DisCoF: Cooperative Pathfinding in Distributed Systems with Limited Sensing and Communication Range

Abstract

Cooperative pathfinding is often addressed in one of two ways in the literature. In fully coupled approaches, robots are considered together and the plans for all robots are constructed simultaneously. In decoupled approaches, the plans are constructed only for a subset of robots at a time. While decoupled approaches can be much faster than fully coupled approaches, they are often suboptimal and incomplete. Although there exist a few decoupled approaches that achieve completeness, global information (which makes global coordination possible) is assumed. Global information may not be accessible in distributed robotic systems. In this paper, we provide a window-based approach to cooperative pathfinding with limited sensing and communication range in distributed systems (called DisCoF). In DisCoF, robots are assumed to be fully decoupled initially, and may gradually increase the level of coupling in an online and distributed fashion. In some cases, e.g., when global information is needed to solve the problem instance, DisCoF would eventually couple all robots together. DisCoF represents an inherently online approach since robots may only be aware of a subset of robots in the environment at any given point of time. Hence, they do not have enough information to determine non-conflicting plans with all the other robots. Completeness analysis of DisCoF is provided.

1 Introduction

Cooperative pathfinding for multi-robot systems has many applications. However, this problem is fundamentally hard in general (i.e., PSPACE-hard [7]). Previous approaches often address this problem in one of two ways. In fully coupled approaches, all robots are considered together and the plans for them are constructed simultaneously. However, given that the complexity grows exponentially with the number of robots, these approaches can easily become impractical. As a result, recent research more often concentrates on decoupled approaches. In decoupled approaches, the plans are constructed (partially or fully) only for a subset of robots at a time; the remaining robots must then take the others’ constructed plans into account when constructing their own plans. While decoupled approaches are often suboptimal and incomplete, they typically run much faster than fully coupled approaches, since the number of robots that need to be coupled can be significantly smaller. While there are decoupled approaches that achieve optimality and completeness, they all assume global information, which implies global coordination. However, global information may not be accessible in distributed robotic systems, since such systems are often subject to limited sensing and communication range. As a result, these approaches cannot be implemented on many distributed systems.

In this paper, we introduce a window-based approach for cooperative pathfinding in distributed systems, called DisCoF, with the window size corresponding to the limited sensing and communication range. DisCoF is inherently online, since a robot may not be aware of all the other robots in the environment at any given point of time, let alone determining a non-conflicting plan with them. In DisCoF, a robot can only communicate directly with robots within its sensing range (i.e., local window) to coordinate. However, two robots can communicate indirectly through other robots using a message relay protocol. All robots are assumed to be fully decoupled initially: they plan and execute independently and simultaneously. Robots can gradually increase the level of coupling in an online and distributed fashion.

To reduce computation, we need to determine when to couple robots and only couple them when necessary. We follow an intuitive approach to achieving this: couple robots only when they have potential conflicts (i.e., predictable conflicts in DisCoF). Furthermore, to efficiently reduce the possibility of future coupling given only local knowledge, instead of making full plans to final goals, robots in each coupling only plan to local goals that minimize conflicts within a pre-specified horizon. This process also ensures that these robots make progress to final goals.

However, given the localized nature of this approach, it is subject to live-locks. We identify a live-lock when robots in a coupling cannot make further progress to final goals within the finite horizon, which is a necessary (but insufficient) condition to detect live-locks. Note that detecting live-locks requires global information in general. DisCoF allows “live-locks” to be detected and resolved in a distributed manner. When a live-lock is detected, robots in the coupling use a technique, called Push and Pull, to keep within each other’s sensing and communication range, while progressing to final goals one at a time.

By combining these methods, DisCoF achieves an efficient solution that also guarantees completeness. Note that for a problem instance that requires global information, DisCoF solves it by eventually coupling all robots together. To the best of our knowledge, this is the first work that guarantees completeness for cooperative pathfinding in distributed systems with limited sensing and communication range. The remainder of this paper is organized as follows. After a brief review of related literature in Sect. 2, we introduce DisCoF in Sect. 3. The live-lock resolution technique is discussed separately in Sect. 4. Conclusions and discussions of future work are presented afterwards.

2 Related Work

The most convenient way to address cooperative pathfinding is to consider robots as fully coupled, since then many existing state-space search algorithms (e.g., A$^*$) can be applied. While this fully coupled search is intractable, approaches have been provided to reduce the branching factors to improve the performance, e.g., [16]. There are also approaches that compile cooperative pathfinding problems into related problem formulations [1, 5, 9, 20] (e.g., maximum flow [20]), and then apply the corresponding algorithms to solve them. However, these approaches are unscalable due to the large state space. Methods for spatial abstraction to reduce the state space have also been discussed [14, 18], but they often suffer optimality and even completeness. By restricting the underlying graphs of problem instances to have certain topologies, optimal solutions can be found fast [12, 13, 19].

More research has been concentrated on decoupled approaches due to its better scalability. One commonly used approach is the hierarchical cooperative A$^*$ (HCA$^*$ [15]), which is a prioritized planning method. HCA$^*$ chooses fixed priorities for robots and makes a plan for a single robot at a time based on its priority, while respecting the computed plans for robots of higher priorities. This process is performed through the use of a reservation table that all robots can access. To reduce the influence of the computed plans for robots of higher priorities (on robots of lower priorities), a windowed HCA$^*$ approach (WHCA$^*$) is also discussed in [15]. In WHCA$^*$, robots only send the portions of their plans within a fixed window size (from their current locations) to the reservation table, which has been shown to enable WHCA$^*$ to solve more problem instances. More recently, an extension of WHCA$^*$ (CO-WHCA$^*$ [2]) is proposed, which improves over WHCA$^*$ by only reserving plans when there are conflicts. Another common decoupled approach is to create traffic laws for the robots to follow, e.g., [8], thus reducing the possibility of conflicts. Although these decoupled approaches can often find solutions fast, they are incomplete.

There are decoupled approaches that achieve completeness and optimality, e.g., [16, 17]. However, these approaches are still intractable for many problem instances due to the inherent complexity. Hence, more recent approaches often relax optimality while maintaining completeness [4, 10]. In [10], a Push and a Swap operation are introduced, which are used to move robots to their goals one at a time; the resulting individual plans are then optimized for all robots. The authors in [4] further introduce a new operation, Rotate, to complement Push and Swap, in order to guarantee completeness in more general problem instances. These approaches, however, assume global information (e.g., the individual plans of all robots at any time). Global information may not be accessible in distributed robotic systems with sensing and communication range, in which each robot must create its individual plan based on its local knowledge (including the sensed and communicated information).

In this paper, we introduce an approach that achieves completeness without assuming global information in distributed systems. While cooperative pathfinding with limited sensing and communication range has been investigated before, e.g., [3, 11, 21], to the best of our knowledge, guarantee of completeness has never been provided. Note that cooperative pathfinding with only local knowledge can be considered as a special case of pathfinding with dynamic obstacles. The difficulty lies partly in the existence of live-locks, as global information is required to detect live-locks in general. To achieve completeness, our approach allows robots to gradually increase the level of coupling when potential live-locks are detected.

3 DisCoF

3.1 Problem Formulation

Given a graph $G = (V, E)$ and a set of robots $\mathcal {R}$, the initial locations of the robots are denoted as $\mathcal {I}\subseteq V$ and the goals are denoted as $\mathcal {G}\subseteq V$. Edges in E are undirected. Any robot can move to any adjacent vertex in one time step or remain where they are. A plan $\mathcal {P}$ is a set of individual plans of robots, and $\mathcal {P}[i]$ denotes the individual plan for robot $i \in \mathcal {R}$. Each individual plan is composed of a sequence of actions. For simplicity of presentation, each action is identified by the next vertex to be visited. We denote by $\mathcal {P}_k[i]$ $(k \ge 1)$ the action to be taken at time step $k - 1$ (or the vertex to be visited at k) for robot i, and by $\mathcal {P}_{k,l}[i]$ $(k\le l)$ the subplan that results by considering only the actions $\mathcal {P}_k[i]$ up to $\mathcal {P}_l[i]$. The goal of cooperative pathfinding is to find a plan $\mathcal {P}$ such that robots start in $\mathcal {I}$ and end in $\mathcal {G}$ after executing it, without any conflicts. The set of locations of robots at time step k is denoted by $\mathcal {S}_k$, and the set of locations of robots after executing a plan $\mathcal {P}$ from $\mathcal {S}$ is denoted by $\mathcal {S}(\mathcal {P})$. Thus, we have $\mathcal {S}_0 = \mathcal {I}$, $\mathcal {S}_0(\mathcal {P})= \mathcal {G}$ and $\mathcal {S}_k = \mathcal {S}_0(\mathcal {P}_{1,k})$. A conflict happens at time step k, if two robots are in the same location, or their locations at $k - 1$ are exchanged. Formally,

$$\begin{aligned} \mathcal {S}_{k}[i] = \mathcal {S}_{k}[j] \vee (\mathcal {S}_{k}[i] = \mathcal {S}_{k - 1}[j] \wedge \mathcal {S}_{k - 1}[i] = \mathcal {S}_{k}[j]) \end{aligned}$$

(1)

in which $i \in \mathcal {R}$, $j \in \mathcal {R}$ and $i \ne j$.

Each robot can independently compute a plan (without considering other robots) to a given goal from a starting location using a shortest-path planner. For simplicity, we assume that when given the same starting location and goal to different robots, the computed shortest-path plans are the same. Hence, we can denote the shortest-path plan that moves a robot from vertex u to v as $P(u, v)$. The length of $P(u, v)$ is denoted as $\mathcal {C}(u, v)$, i.e., $\mathcal {C}(u, v) = |P(u,v)|$. Furthermore, we make the following assumptions:

• 1. Robots are homogeneous and have the same sensing and communication range (this assumption only simplifies the presentation and it can be relaxed).

• 2. Robots are equipped with a communication protocol that allows them to efficiently relay messages.

• 3. Time steps are synchronized (asynchronous time steps are to be investigated in future work).

• 4. Each robot has full knowledge of the environment, i.e., G.

The individual plans are constructed and updated in an online fashion in DisCoF. Initially, for each robot i, the individual plan is constructed as $\mathcal {P}[i] = P(\mathcal {I}[i], \mathcal {G}[i])$. Robots then start executing their individual plans until conflicts can be predicted (discussed later). In such cases, the individual plans of robots that are involved are updated from $\mathcal {P}_{k + 1}$ to avoid these conflicts, given that the current time step is k.

3.2 Local Window

While the window size in WHCA$^*$ [15] is a parameter to determine the number of next plan steps to be sent by each robot to the reservation table, the window size in DisCoF represents the sensing range of the robot. To reduce communication, we only allow a robot to directly communicate with other robots that it can see. However, two robots can communicate indirectly through other robots to coordinate using the message relay protocol. This window is called a local window in DisCoF, which is used in the prediction and resolution of potential conflicts.

Definition 1

(Local Window) At time step k, the local window of robot $i \in \mathcal {R}$, denoted by $\mathcal {W}_k[i]$, is defined as $\mathcal {W}_k[i] = \{v \in V$ (vertices in G)$\; | \; v$ can be reached by i from its current location (i.e., $\mathcal {S}_k[i]$) in $\lambda$ steps$\}$, in which $\lambda$ is the window size, a positive integer that is greater than 1.

When a robot j satisfies $\mathcal {S}_k[j] \in \mathcal {W}_k[i]$, we write $i \vartriangleright _k j$ to indicate that robot i can communicate with robot j. A simplifying assumption made here is that the visibility of the sensor is only influenced by the distance, which can be relaxed. Given our assumptions, $\vartriangleright _k$ is symmetric, i.e., i and j can communicate with each other. We indicate this symmetric relation as $i \vartriangleleft \vartriangleright _k j$. Furthermore, given the communication relay protocol, $\vartriangleleft \vartriangleright _k$ also defines a transitive relation. Namely, if $i \vartriangleleft \vartriangleright _k r$ and $r \vartriangleleft \vartriangleright _k j$, we also have that $i \vartriangleleft \vartriangleright _k j$. The $\vartriangleleft \vartriangleright _k$ relation introduces the coordination graph.

Definition 2

(Coordination Graph) At time step k, the coordination graph $G^*_k = (V^*_k$, $E^*_k)$ of the robots is constructed as follows:

• $V^*_k = \mathcal {R}$.

• $(i, j)\in E^*_k$ if and only if $i \vartriangleleft \vartriangleright _k j$.

Note that the coordination graph is only a structure introduced to facilitate our following discussions. In DisCoF, robots are not required to compute this graph at any time step. Next, we partition the coordination graph into disconnected components that indicate which robots communicate with each other.

Definition 3

(Outer Closure (OC)) At time step k, the coordination graph $G^*_k$ is partitioned into disjoint connected subgraphs. Denote $\varPhi _k$ as the set of vertex sets of these subgraphs. Then, for any $(\phi ^x, \phi ^y) \in \varPhi _k \times \varPhi _k$, the following is satisfied:

$\forall {(i, j) \in \mathcal {R} \times \mathcal {R}}$, if $i \ne j \wedge i \in \phi ^x \wedge j \in \phi ^y$ holds, we have $i \vartriangleleft \vartriangleright _k j$, if and only if $x = y$. Each $\phi \in \varPhi _k$ defines an outer closure.

Since two robots in different outer closures (OCs) do not communicate in DisCoF (whether directly or indirectly), they do not know about each other’s current plan or location (they may not even be aware of each other). Hence, only robots within the same OCs can coordinate with each other.

Definition 4

(Predictable Conflicts) At time step k, given an OC $\phi \in \varPhi _k$, we define that a robot $i \in \phi$ has a predictable conflict with parameter $\delta$, if it would be involved in a conflict at $k + \delta$ ($\delta \le \beta$, in which $\beta$ is a pre-specified finite horizon) with another robot in $\phi$, and that i would not be involved in any conflicts with robots in $\phi$ at any time step earlier than $k + \delta$, assuming that robots in $\phi$ continue with their current individual plans.

The reason for imposing the finite horizon $\beta$ is due in part to the limited sensing range (i.e., visibility) of the robots since resolution for potential conflicts in the far future is likely to only waste computation resource and time. Note that $\lambda$ (i.e., window size) and $\beta$ do not have to be related.

At time step k, if a robot i has a predictable conflict with parameter $\delta$ (see Definition 4), we denote it as $\varDelta _k^i(\delta )$. We also use $\varDelta _k^i$ when the parameter does not need to be identified. Predictable conflicts are associated with the notion of inner closure.

Definition 5

(Inner Closure (IC)) At time step k, the IC $\psi$ of a given OC $\phi \in \varPhi _k$ is the set of robots that satisfy: $\psi = \{i$ | $\varDelta _k^i$ $\wedge$ $i \in \phi \}$.

Similarly, we denote $\varPsi _k$ as the set of ICs for the OCs (there is a one-to-one correspondence) at time step k. Note that the IC of an OC may be empty. We provide an example of OC and IC below.

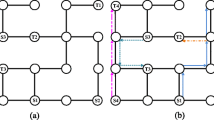
Example 1

Figure 1 visualizes such a scenario for $\lambda = 2$ and $\beta = 2$. Robots are shown at their initial locations at time step 0. The arrows indicate their respective individual plans for the next few steps and the highlighted gray areas their local windows. We have $r_2 \vartriangleleft \vartriangleright _0 r_3$ and $r_3 \vartriangleleft \vartriangleright _0 r_4$ and hence $r_2 \vartriangleleft \vartriangleright _0 r_4$ through $r_3$. Thus, the OC at time 0 are $\phi ^1 = \{r_2,r_3,r_4\}$, and $\phi ^2 = \{r_1\}$. Even though $r_2$, $r_3$, $r_4$ are in the same OC, only $r_3$ and $r_4$ belong to the corresponding IC, since there is a predictable conflict with parameter 1. Hence, $\psi ^1 = \{r_3, r_4\}$ and $\psi ^2 = \emptyset$.

Fig. 1

Scenario that illustrates OC and IC. Two OCs are present, and one of them contains a predictable conflict. Here, $r_i$ indicates the sensing and communication range of each robot i

3.3 Coupling in OC

Given an OC with predictable conflicts, the goal of coupling is to update the individual plans of robots to proactively resolve these conflicts while avoiding introducing new conflicts in the finite horizon (i.e., specified by $\beta$).

At time step k, suppose that conflicts are predicted in an OC $\phi \in \varPhi _k$, robots in $\phi$ need to update their individual plans from $\mathcal {P}_{k + 1}$. Note that robots may join and leave different couplings during the online planning process. To make sure that robots make progress to their final goals as a team, we associate a contribution value $\gamma$ with each robot, which captures the individual contribution of the robot to updating the summation of (shortest) distances between all robots’ current locations and their final goals. Initially, this value is zero (i.e., $\forall {i}, \gamma _0[i]= 0$). For robot i, we denote this value just before the coupling at k by $\gamma _{k-}[i]$ and after $\delta$-steps by $\gamma _{k+\delta }[i]$. When $\delta$ is 0, $\gamma$ represents the updated value immediately after the coupling at k (see below).

First, robots in $\phi$ compute a plan $\mathcal {Q}$ (such that $|\mathcal {Q}| \le \beta$) which satisfies the following two conditions:

$$\begin{aligned}&\sum _{i \in \phi } \mathcal {C}(\mathcal {S}_k[i], \mathcal {G}[i]) + \gamma _{k-}[i] > \sum _{i \in \phi } \mathcal {C}(\mathcal {S}_k[i](\mathcal {Q}[i]), \mathcal {G}[i]) \end{aligned}$$

(2)

$$\begin{aligned}&\qquad \qquad \qquad \qquad \quad \qquad \forall {i \in \phi }, \lnot \varDelta _{k}^i \end{aligned}$$

(3)

in which $\varDelta _{k}^i$ is computed based on the updated individual plans that are constructed as follows: the new individual plan $\mathcal {P}[i]$ for robot $i \in \phi$ is constructed by replacing actions starting from $\mathcal {P}_{k + 1}[i]$ by $\mathcal {Q}[i] + P(\mathcal {S}_k[i](\mathcal {Q}[i]), \mathcal {G}[i])$. Here, $\mathcal {S}_k[i](\mathcal {Q}[i])$ is the local goal for i, which is the location of i (currently at $\mathcal {S}_k[i]$) after executing $\mathcal {Q}[i]$. The $+$ symbol is used here to denote concatenation.

At time step k, and after executing each action in $\mathcal {Q}[i]$, the contribution value for i is updated as follows, until a conflict is predicted or this value becomes 0:

$$\begin{aligned} \gamma _{k+\delta }[i] = \mathcal {C}(\mathcal {S}_k[i](\mathcal {Q}[i]), \mathcal {G}[i]) - \mathcal {C}(\mathcal {S}_{k + \delta }[i], \mathcal {G}[i]) \end{aligned}$$

(4)

in which $0 \le \delta \le |\mathcal {Q}|$, is the steps after the coupling (i.e., number of actions in $\mathcal {Q}$ that are executed). Note that $\mathcal {S}_{k+\delta }[i] = \mathcal {S}_0[i](\mathcal {P}_{1,k + \delta }[i])$ in Eq.  (4) is the location of robot i at time step $k+\delta$ under the updated individual plan $\mathcal {P}[i]$ at time step k.

Lemma 1

Planning (i.e., the computation of $\mathcal {Q}$) in the coupling process converges $\mathcal {R}$ to their final goals as k grows, if Eq. (2) can always be satisfied.

Proof

From Eqs. (2) and (4), we have the following holds:

$$\begin{aligned} \sum _{i \in \phi } \mathcal {C}(\mathcal {S}_k[i], \mathcal {G}[i]) + \gamma _{k-}[i] > \sum _{i \in \phi } \mathcal {C}(\mathcal {S}_{k + \delta }[i], \mathcal {G}[i]) + \gamma _{k+\delta }[i] \end{aligned}$$

(5)

First, Eq. (5) holds for all robots that are still executing the coupled plan (i.e., $\mathcal {Q}$) to move to their local goals; furthermore, Eq. (5) also holds for robots that have already reached their local goals or robots that have not engaged in any coupling yet. As a result, Eq. (5) holds for $\mathcal {R}$. As k grows, we know that $\sum _{i \in \mathcal {R}} \mathcal {C}(\mathcal {S}_{k + \delta }[i], \mathcal {G}[i]) + \gamma _{k+\delta }[i]$ would gradually decrease. This also means that $\sum _{i \in \mathcal {R}} \mathcal {C}(\mathcal {S}_k[i](\mathcal {Q}[i]), \mathcal {G}[i])$ would gradually decrease from Eqs. (2) and (4). Given $|\mathcal {Q}| \le \beta$, the conclusion holds.

Assuming that the condition in Eq. (2) holds, Lemma 1 shows that planning converges to final goals for $\mathcal {R}$. This condition requires robots in a coupling to always make progress jointly within the finite horizon. However, this assumption does not hold in the presence of live-locks. In such cases, robots in a coupling would eventually be unable to find a $\mathcal {Q}$ that satisfies both Eqs. (2) and (3).¹ Furthermore, the limited horizon can also cause the search of $\mathcal {Q}$ to fail. However, we realize that when live-locks are present in distributed systems with only local knowledge, the search is bound to fail eventually even with unlimited horizon. Hence, we do not distinguish the two causes, and consider it as a “live-lock” being detected when when Eq. (2) becomes unsatisfiable (while satisfying Eq. (3)).

3.4 Computing $\mathcal {Q}$

Before discussing how “live-locks” are addressed in DisCoF, we provide details on how $\mathcal {Q}$ is computed. Given that coupled search is expensive, we aim to minimize $|\mathcal {Q}|$ as well as the number of robots that need to be coupled.

To achieve this, we try to construct $\mathcal {Q}$ that satisfies Eqs. (2) and (3) for $\rho$ $(\rho \subseteq \phi )$, which is initially set to be the corresponding IC for $\phi$, while forcing robots in $\rho$ to respect the plans (i.e., avoiding predictable conflicts) of robots in $\phi \setminus \rho$ in the next $\beta$ steps. Note that having $\rho$ instead of $\phi$ satisfy Eq. (2) does not influence the planning convergence.

The search first checks $\mathcal {Q}$ for $\rho$ with $\theta = 1$, in which $\theta = |\mathcal {Q}|$, and gradually increases $\theta$ until $\theta = \beta$. If a valid $\mathcal {Q}$ is found for the current $\theta$, the $\mathcal {Q}$ is returned. Otherwise, if $\phi \setminus \rho \ne \emptyset$, $\rho$ is expanded to include robots in $\phi \setminus \rho$ that are also within the combined region of local windows of robots in $\rho$, and the current $\theta$ is re-checked; else, $\theta$ is incremented or unsatisfiability is returned when $\theta = \beta$.

4 Push and Pull

In DisCoF, when unsatisfiability is returned in computing $\mathcal {Q}$ for an OC $\phi$, we consider it as a “live-lock” (i.e., robots in $\phi$ may have contributed in creating a live-lock situation) being detected. To resolve it, information of all robots in $\phi$ must be accessible. In distributed systems, this requires the robots in $\phi$ to maintain within each other’s sensing and communication range (thus remain coupled). Furthermore, note that a live-lock may not involve all robots in $\mathcal {R}$ and there may be multiple live-locks in the environment. When a live-lock is detected, robots in $\phi$ form a coupling group, $\omega$, which executes a live-lock resolution process described next. This process also allows a coupling group to merge with other groups and robots, thus gradually increasing the level of coupling. In some cases, e.g., when a global live-lock is present, robots in DisCoF can eventually become fully coupled.

4.1 Overview

To achieve completeness, DisCoF uses a technique that is similar to Push and Rotate [4], which we call Push and Pull. To ensure completeness in Push and Rotate, robots must move to goals one at a time according to the priorities of subproblems to which they belong. Robots that have already reached their goals are respected (i.e., considered as obstacles) by the subsequent Push operations. When Push fails, Push and Rotate uses a Swap operation to ensure that these robots move back in their goals as the remaining robots move. Such a priority ordering must also be respected in DisCoF. At time step k, for all coupling groups that have been formed, the basic idea is to: (1) maintain robots in these groups within each other’s sensing and communication range; (2) for each group, move robots to goals one at a time based on a relaxed version of the priority ordering, which is consistent to that in Push and Rotate; (3) add robots that introduce predictable conflicts with a coupling group as robots in the group move to their goals. Each coupling group progresses independently of other robots and coupling groups unless there are predictable conflicts. The main process is described in Algorithm 1.

In Algorithm 1, the coupling of robots in $\omega$ is maintained by the Push and Pull technique. As a result, predictable conflicts can only be introduced by other robots. When a coupling group detects predictable conflicts with another group, two groups are merged. Furthermore, when a robot that has already reached its goal is added to a coupling group in the live-lock resolution process, if the robot’s priority is not the highest among all robots that have not reached their goals after recomputing the priorities, this robot is not considered as having reached its goal in Push and Pull. This means that the Push and Pull operations can move these robots. Also, the priority ordering (i.e., the $\prec$ relations in [4]) is maintained and aggregated by the robots whenever new relations are identified (in Line 5); given that the relaxed priority ordering is consistent with that in Push and Rotate, robots can gradually achieve a consensus of this ordering.

4.2 Assigning Priorities

To ensure completeness, the priorities of subproblems in Push and Rotate [4] must be respected. However, given the limited visibility of the robots, this priority ordering can only be partially computed for each coupling group. This partially computed ordering in DisCoF is kept consistent with the priority ordering in Push and Rotate.

To compute the priorities, first, Push and Rotate identifies the subproblems. Since this computation is only dependent on the graph structure, robots in DisCoF can individually identify the set of subproblems.

Next, Push and Rotate assigns robots to subproblems. DisCoF computes a relaxed version of this assignment to ensure that assignments are only made when they are consistent with those in Push and Rotate. Denote the set of subproblems as $\mathcal {D}$. Algorithm 2 presents the algorithm to compute the assignment in a coupling group $\omega$.

The differences of Algorithm 2 from that in Push and Rotate lie in Line 4, 5, 6 and 9. While the computation for these lines is performed based on the global graph (i.e., G) in Push and Rotate, the computation in DisCoF is based on $G^\omega = (V^\omega , E^\omega )$ (which represents the combined region of the local windows of robots in $\omega$), and G given only robots in $G^{\omega }$. Note that not every robot may be assigned to a subproblem and the unassigned robots are assumed to have the lowest priorities.

Lemma 2

The assignment of robots to subproblems in DisCoF is consistent to that in Push and Rotate [4]: if a robot r is assigned to subproblem $\mathcal {D}_h$ in Algorithm 2, it is also assigned to $\mathcal {D}_h$ in Push and Rotate.

Proof

We only need to prove that: (1) when the condition in Line 6 is satisfied, the corresponding condition in Push and Rotate is also satisfied; (2) $m'$ and $m''$ in Algorithm 2 are smaller than those in [4], and $\lnot m \ge 1$ in Algorithm 2 implies $m' < m$ in [4]. These directly follow from how they are computed.

In the third step, Push and Rotate assigns priorities to the subproblems. Robots within the same subproblems receive the same priorities. Similarly, the reference of global graph is changed to $G^\omega$; otherwise, the process is unchanged.

Lemma 3

The assignment of priorities to subproblems in DisCoF is consistent to that in Push and Rotate [4]: if two subproblems $\mathcal {D}_{h1}$ and $\mathcal {D}_{h2}$ satisfy $\mathcal {D}_{h1} \prec \mathcal {D}_{h2}$, they must also satisfy $\mathcal {D}_{h1} \prec \mathcal {D}_{h2}$ in Push and Rotate.

Proof

This conclusion follows almost directly from Lemma 2 and the process for assigning priorities to subproblems.

Note that this assignment process is executed by each coupling group in DisCoF instead of all robots in Push and Rotate. This means that while the assignments are consistent with that in Push and Rotate, they are computed for different (and disjoint) sets of robots in DisCoF.

4.3 Maintaining and Expanding $\omega$

Robots in a coupling group can use the operations (i.e., Push, Swap and Rotate) in Push and Rotate to move to their goals one at a time (for details, refer to [4]). To maintain robots within $\omega$ in sensing and communication range, we introduce a new operation, called Pull. Denote r as the current robot that is being moved to its final goal in $\omega$. As r moves to its goal, it can use any of the Push, Swap and Rotate operations. Every step that r moves as a result of these operations, it also invokes the Pull operation on the other robots in $\omega$.

The Pull operation computes a shortest-path plan p from r to any robot $s \in \omega \setminus r$. A set $\mathcal {U}$ is created, which contains only r initially. If p does not pass through other robots in $\omega$, and the first step in p leads s closer to r, s is added to $\mathcal {U}$. If the first step in p does not introduce conflicts with other robots in $\omega$, this step is added to the individual plan of s; otherwise, an action to stay is added to the individual plan of s. For robots that have been newly added into $\mathcal {U}$, they recursively apply the Pull operation on robots that are not in $\mathcal {U}$. This process ends until all robots in $\omega$ are in $\mathcal {U}$. The Pull operation is presented in Algorithm 3. Figure 2 illustrates the Pull operation in a simple scenario.

Fig. 2

Scenario that illustrates the Pull operation. Left figure shows that robot $r_2$ is moving to its goal. Right figure shows the same scenario after one time step. Blue arrows show the actions being added to the individual plans of the corresponding robots at each step by the Pull operation

Lemma 4

The Pull operation maintains robots in each coupling group within each other’s sensing and communication range.

Proof

The Pull operation, after execution, ensures that any robot $s \in \omega$ is no further away from one of the robots in $\omega$ before its execution. Hence, the conclusion holds.

Fig. 3

Scenario that illustrates the expanding process, in which two coupling groups, each with two robots, are merged when a conflict is predicted in the next step

Similar to Push, Pull may fail (Line 13 in Algorithm 3) since it must respect the robots (with equal or higher priorities) that have already reached their goals. In such cases, a similar procedure using Swaps as for the Push operation in [4] can be used; these Swaps can cause robots that are being swapped to recursively invoke Pull.

When there are other robots within the combined region of the local windows of robots in $\omega$, robots must plan to consider predicted conflicts. Each coupling group makes a plan for the next $\beta$ steps considering only robots in the group. When no conflicts are predicted, robots continue with this plan. When conflicts are predicted, $\omega$ is expanded as we previously discussed. The expanded coupling group chooses the robot currently with the (equal) highest priority to move to the goal.² Figure 3 illustrates the merge of two coupling groups. In the group on the left ($r_2$ and $r_3$), $r_2$ is moving to its goal, pulling $r_3$, and in the other group, $r_1$ is moving to its goal, puling $r_4$. Since a predictable conflict exists between $r_2$ and $r_1$, the two groups are merged.

4.4 Analysis

To prove the completeness of DisCoF, we use a property that is derived directly from Theorem 2 in Push and Rotate [4].

Corollary 1

If the cooperative pathfinding problem is solvable, the assignment of robots in a coupling group to subproblems remains unchanged unless the group is expanded.

Theorem 1

DisCoF is complete for the class of cooperative pathfinding problems in which there are two or more unoccupied vertices in each connected component.

Proof

We provide the proof sketch here, which is based on the following observations: (1) When every coupling group is independent of other robots and groups, DisCoF is complete; this is almost a direct result from Push and Rotate, since the Pull operation does not influence the other operations. (2) When a coupling group is expanded, robots in the group are maintained within each other’s sensing and communicating range; this is a direct result from Lemma 4. (3) The priority ordering relations (i.e., $\prec$) are maintained and gradually aggregated (to reach a consensus) as they are identified; this is a result from Lemma 2, Lemma 3 and Corollary 1. (4) Robots with the highest priorities are respected (in Push and Pull operations) by the coupling groups in the Push and Pull process (similar to that in Push and Rotate), which moves robots with the highest priorities to goals first.

Since it has been shown in [4] that robots with the highest priorities must be moved to goals first in order to ensure a solution, these robots must eventually be assigned the highest priorities as the coupling groups move. Hence, these robots would be moved to their final goals. This process then continues to robots with the second highest priorities and so on. Hence, DisCoF is complete.

5 Conclusions

In this paper, we introduce a window-based approach for cooperative pathfinding in distributed systems, with the window size corresponding to the limited sensing and communication range in such systems. This approach, called DisCoF, is an inherently online approach. To limit coupling in order to reduce computation, we introduce a formulation that allows robots to avoid future conflicts while still making joint progress to their final goals. This formulation also allows “live-locks” to be detected; in such cases, we use a Push and Pull technique. We show that DisCoF is complete. To the best of our knowledge, this is the first work that guarantees completeness for cooperative pathfinding with limited sensing and communication range in distributed systems. Note that the general definition of conflict potentially allows DisCoF to be applied to cooperative pathfinding with different robotic platforms, e.g., adding the consideration of height for UAVs.

In future work, we plan to provide a detailed evaluation of DisCoF and compare it with other related approaches. We also plan to extend the formulations to consider more complex environment and goal specifications (e.g., using temporal logic specifications [6]). Other directions include extending the approach to support continuous motions, heterogeneous robots, and asynchronous time steps. For recent progresses, refer to https://cpslab.assembla.com/spaces/discof/.