Manifold proximal support vector machine for semi-supervised classification

Abstract

Recently, semi-supervised learning (SSL) has attracted a great deal of attention in the machine learning community. Under SSL, large amounts of unlabeled data are used to assist the learning procedure to construct a more reasonable classifier. In this paper, we propose a novel manifold proximal support vector machine (MPSVM) for semi-supervised classification. By introducing discriminant information in the manifold regularization (MR), MPSVM not only introduces MR terms to capture as much geometric information as possible from inside the data, but also utilizes the maximum distance criterion to characterize the discrepancy between different classes, leading to the solution of a pair of eigenvalue problems. In addition, an efficient particle swarm optimization (PSO)-based model selection approach is suggested for MPSVM. Experimental results on several artificial as well as real-world datasets demonstrate that MPSVM obtains significantly better performance than supervised GEPSVM, and achieves comparable or better performance than LapSVM and LapTSVM, with better learning efficiency.

1 Introduction

Over the last decade, support vector machines (SVMs) have been recognized as a powerful kernel-based tool for machine learning because of their remarkable generalization performance [1–3]. In contrast with the conventional artificial neural networks, which aim to reduce the empirical risk, SVMs are guided by the principle of structural risk minimization (SRM) to guarantee the upper bound of the generalization error [1, 2]. The central idea of SVMs is to construct two optimal parallel hyperplanes that maximize the margin between two classes (data labeled as “+1” or “−1”) by solving a quadratic programming problem (QPP). Within a few years of their introduction, SVMs had already outperformed most machine learning methods in a wide variety of applications [4–8].

Recently, Mangasarian et al. [9] proposed a generalized eigenvalue proximal support vector machine (GEPSVM) for supervised classification problems. GEPSVM aims to generate two nonparallel proximal hyperplanes, with each hyperplane closer to its own class and as far as possible from the other. For this purpose, it solves a pair of relatively smaller optimization problems, instead of the large one considered by traditional SVMs [1]. As a result, the learning procedure of GEPSVM is more efficient than that of SVMs [9]. In addition, GEPSVM is excellent at dealing with “xor” problems. Thus, methods of constructing nonparallel proximal classifiers have been extensively studied, such as improved GEPSVM [10], DGEPSVM [11], TWSVM [12, 13], twin parametric-margin SVM (TPMSVM) [14], structural TWSVM (S-TWSVM) [15] and so on [16–20].

The above nonparallel proximal classifiers are fully supervised, and their generalization performance is very dependent on whether there is sufficient labeled information [21, 22]. That is to say, only labeled data are considered for model training. However, in many real-world learning problems, e.g., natural language parsing [23], spam filtering [24], video surveillance [25] and protein 3D structure prediction [26], the acquisition of labeled data is usually hard or expensive, whereas the collection of unlabeled data is much easier. In such a situation, the performance of these fully supervised classifiers usually deteriorates because of an insufficient volume of labeled information.

To deal with the situation of large amounts of unlabeled data and relatively few labeled data, the paradigm of semi-supervised learning (SSL) has been proposed. Comprehensive reviews of SSL can be found in [21, 22, 27, 28]. Among these, manifold regularization (MR) is one of the most elegant constructions [29, 30]. In the MR framework, two regularization terms are introduced: one concentrates on the complexity of the classifier in the Reproducing Kernel Hilbert Spaces (RKHS), and the other enforces the smoothness of the classifier along the intrinsic manifold. Following the MR framework, Qi et al. [31] first extended the supervised nonparallel proximal classifier to the semi-supervised case and proposed a Laplacian twin support vector machine (LapTSVM). Extensive experimental results [31–33] demonstrated the effectiveness of this approach. However, one of the main challenges in LapTSVM is that the objective functions of its dual QPPs require two matrix inversion operations. These matrices are of size (n+1)×(n+1) for the linear case and (l+u+1)×(l+u+1) for the nonlinear case, where n is the feature dimension and l/u is the number of labeled/unlabeled data. To our knowledge, this matrix inversion is the main bottleneck of LapTSVM, greatly reducing its learning efficiency. Another challenge is that there are at least three predetermined parameters in LapTSVM. Although a grid-based approach can be used to optimize these parameters [31], this makes the model selection of LapTSVM something of a burden. These drawbacks restrict the application of LapTSVM to many real-world problems.

In this paper, we propose a novel nonparallel proximal classifier, termed as a manifold proximal support vector machine (MPSVM), for semi-supervised classification problems. In MPSVM, we not only introduce MR terms to capture as much geometric information as possible from inside the data, but also utilize the maximum distance criterion to characterize the discrepancy between different classes. MPSVM has the following properties:

• MPSVM determines a pair of nonparallel proximal hyperplanes by solving two standard eigenvalue problems, successfully avoiding the matrix inversion operations.

• An efficient particle swarm optimization (PSO)-based model selection (parameter optimization) approach is designed for MPSVM. By applying PSO, our MPSVM achieves better learning efficiency.

• MPSVM has a natural out-of-sample extension property from training data to unseen data. This can handle both the transductive and inductive learning cases.

• Finally, by choosing an appropriate parameter, MPSVM can degenerate to a supervised nonparallel proximal classifier, i.e., GEPSVM [9] and DGEPSVM [11].

The remainder of this paper is organized as follows: In Sect. 2, a brief review of SVM and GEPSVM is given. Our linear and nonlinear MPSVM is formulated in Sect. 3. The relations between MPSVM and some other related methods are also discussed in Sect. 3. In Sect. 4, PSO-based model selection approach for MPSVM is arranged. Experimental results are described in Sect. 5 and concluding remarks are given in Sect. 6.

2 Preliminaries

In this paper, all vectors are column vectors unless transformed to a row vector by a prime superscript ′. A vector of zeros of arbitrary dimension is represented by 0. In addition, we denote e as a vector of ones of arbitrary dimension and I as an identity matrix of arbitrary dimensions.

2.1 Support vector machine

As a state-of-the-art of supervised machine learning method, support vector machine (SVM) [1, 3] has been introduced under the framework of statistical learning theory, which is known as the SRM principle. Consider a binary classification problem in the n-dimensional real space $\mathbb{R}^{n}$. Given a set of labeled data T={(x ₁ ,y ₁),(x ₂ ,y ₂),…,(x _l ,y _l )}, where $\boldsymbol{X}_{\boldsymbol{l}}=\{\boldsymbol {x}_{\boldsymbol{i}}\}_{i=1}^{l} \in\mathbb{R}^{l \times n}$ are inputs and $\boldsymbol{Y}_{l} = \{y_{i}\}_{i=1}^{l} \in\{1, -1\}^{l}$ are corresponding labels. SVM aims to maximize the margin between two different classes by constructing the following separating hyperplane:

$$\begin{aligned} f(\boldsymbol{x}): \boldsymbol{w}'\boldsymbol{x} + b=0, \end{aligned}$$

(1)

where $\boldsymbol{w}\in\mathbb{R}^{n}$ is the normal vector and $b\in \mathbb {R}$ is the bias term. Then, the hyperplane (1) is obtained by solving the following QPP:

$$\begin{aligned} \begin{array}{l@{\quad}l} \displaystyle\min_{\boldsymbol{w}_{1}, b_{1}, \boldsymbol{\xi}} & \displaystyle\frac{1}{2}\|\boldsymbol{w}\|^2 + c\boldsymbol{e}'\boldsymbol{\xi}, \\ \mbox{s.t.} & \boldsymbol{Y}_l(\boldsymbol{X}_{l}\boldsymbol{w} + \boldsymbol{e}b) + \boldsymbol{\xi} \geq\boldsymbol {e},\quad\boldsymbol{\xi} \geq\boldsymbol{0}, \end{array} \end{aligned}$$

(2)

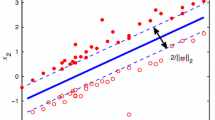
where ∥⋅∥ stands for the L ₂-norm, $\boldsymbol{\xi} \in \mathbb {R}^{l}$ are the slack variables, c>0 is the regularization factor that balances the importance between the maximization of the margin and the minimization of the empirical risks. An intuitive geometric interpretation for the linear SVM is shown in Fig. 1(a).

Fig. 1

Geometric interpretation of SVM, GEPSVM and MPSVM on the toy example (Color figure online)

Note that the minimization of the regularization term $\frac{1}{2} \| \boldsymbol {w}\|^{2}$ is equivalent to the maximization of the margin between two parallel hyperplanes w′x+b=1 and w′x+b=−1. When we obtain the optimal solution of (2), a new point $\boldsymbol{x} \in\mathbb{R}^{n}$ is classified as “+1” or “−1” according to whether the decision function,

$$\begin{aligned} \mathrm{Class}\ i =\operatorname{sign}\bigl(\boldsymbol{w}' \boldsymbol {x} + b\bigr), \end{aligned}$$

(3)

yields “+1” or “−1”.

2.2 Generalized eigenvalue proximal SVM

Generalized eigenvalue proximal SVM (GEPSVM) is one of the most well-known supervised nonparallel proximal classifiers. Let us denote $\boldsymbol{A} \in\mathbb{R}^{m_{1}\times n}$ as the labeled data belonging to “+1” class, and $\boldsymbol{B} \in\mathbb{R}^{m_{2}\times n}$ as the labeled data belonging to “−1” class, where m ₁+m ₂=l. The original idea of GEPSVM [9] is to seek the following two nonparallel proximal hyperplanes¹

$$\begin{aligned} f_1(\boldsymbol{x}): \boldsymbol{w}'_{1} \boldsymbol{x} + b_{1} = 0 \quad\mathrm{and}\quad f_2( \boldsymbol {x}): \boldsymbol{w}'_{2}\boldsymbol{x} + b_{2} = 0, \end{aligned}$$

(4)

where $\boldsymbol{w}_{1}, \boldsymbol{w}_{2} \in\mathbb{R}^{n}$ are the normal vectors and $b_{1}, b_{2} \in\mathbb{R}$ are the bias terms, each hyperplane is closer to its class and is as far as possible from the other. Then, the optimization problems for GEPSVM can be expressed as

(5)

and

(6)

In order to reduce the norm problem of variables (w _i ,b _i ) (i=1,2) in (5) and (6), GEPSVM introduces a Tikhonov regularization term [9, 34] and further regularizes the optimization problems as

(7)

and

(8)

where δ>0 is the regularization parameter. An intuitive geometric interpretation for the linear GEPSVM is shown in Fig. 1(b).

By defining G=[A e ₁]′[A e ₁]+δ I, H=[B e ₂]′[B e ₂], L=[B e ₂]′[B e ₂]+δ I, M=[A e ₁]′[A e ₁], and , we can reformulate (7) and (8) as

$$\begin{aligned} \min_{\boldsymbol{v}_{1} \neq\boldsymbol{0}} \frac{\boldsymbol{v}'_{1}\boldsymbol{G}\boldsymbol {v}_{1}}{\boldsymbol{v}'_{1}\boldsymbol{H}\boldsymbol{v}_{1}} \quad\mathrm{and}\quad \min _{\boldsymbol{v}_{2}\neq\boldsymbol{0}} \frac{\boldsymbol{v}'_{2}\boldsymbol{L}\boldsymbol {v}_{2}}{\boldsymbol{v}'_{2}\boldsymbol{M}\boldsymbol{v}_{2}}. \end{aligned}$$

(9)

According to [9, 35], the above two minimization problems are exactly Rayleigh quotient and the solutions can be readily computed by solving the following two related generalized eigenvalue problems (GEPs)

$$\begin{aligned} \boldsymbol{G}\boldsymbol{v}_{1} = \lambda_1 \boldsymbol {H}\boldsymbol{v}_1 \quad \mathrm{and}\quad\boldsymbol{L}\boldsymbol {v}_{2} = \lambda_2 \boldsymbol{M}\boldsymbol{v}_2. \end{aligned}$$

(10)

Specially, the eigenvectors of (10) corresponding to the smallest eigenvalues are the optimal solutions to (7) and (8). Once the solutions (w ₁,b ₁) and (w ₂,b ₂) are obtained, a new point $\boldsymbol {x}\in\mathbb {R}^{n}$ is assigned to class i (i=“+1” or “−1”), depending on which of the two hyperplanes (4) it lies closer to, i.e.,

$$\begin{aligned} \mathrm{Class}\ i=\arg\min_{k=1,2}~ \frac{|\boldsymbol{w}'_{k}\boldsymbol{x}+b_{k}|}{\|\boldsymbol {w}_{k}\|}, \end{aligned}$$

(11)

where |⋅| is the absolute value.

3 Manifold proximal SVM

3.1 Motivation

Let us denote $\boldsymbol{X}_{u}=\{\boldsymbol{x}_{i}\}_{i=l+1}^{l+u} \in\mathbb{R}^{u \times n}$ as the unlabeled data, and $\boldsymbol{X} = \{\boldsymbol {x}_{i}\} _{i=1}^{l+u} \in\mathbb{R}^{(l+u) \times n}$ as all the training data. As mentioned previously, the optimization problems in both SVM and GEPSVM only consider the labeled data X _l , but omit the distribution information revealed by the unlabeled data X _u . Therefore, their performance will deteriorate when the amount of labeled information is insufficient.

For example, imagine a situation where three labeled data (two positive and one negative) and some unlabeled data are given, as illustrated in Fig. 2(a). If a classifier is constructed using only these three labeled data, an optimal choice appears to be the “mid” hyperplane between them. As a result, SVM and GEPSVM cannot capture the real data distribution/tendency, which is shown in Figs. 2(b) and (c).

Fig. 2

Synthetic smile datasets without noise. The upper part corresponds to positive class, and the lower part corresponds to negative class. The squares denote a large set of unlabeled data points. The red diamond or blue circle denotes the labeled data points of positive or negative class, respectively. The black solid curve is the decision boundary. The blue and red dashed curves are the two kernel-generated hyperplanes. The nonlinear classification accuracy of SVM 87.83 %, GEPSVM 89.41 %, and MPSVM 100.00 % (Color figure online)

Thus, to make full use of both the labeled data X _l and unlabeled data X _u , we primarily propose a novel manifold proximal SVM (MPSVM) for semi-supervised classification problems. Inspired by the maximum distance criterion [9–11] and MR technique [29, 30], our MPSVM incorporates both discriminant information and distribution information by minimizing the following two optimization problems

$$\begin{aligned} f_1^* = \arg \left ( \begin{array}{l@{\quad}l} \displaystyle\min_{f_1 \in\mathcal{H}} & R^{emp}\bigl(f_1(\boldsymbol{X}_l)\bigr) + \gamma _\mathcal{M}\bigl\| f_1(\boldsymbol{X})\bigr\| ^2_{\mathcal{M}}\\ \mbox{s.t.} & \|f_1\|^2_{\mathcal{H}} = 1 \end{array} \right ), \end{aligned}$$

(12)

and

$$\begin{aligned} f_2^* = \arg \left ( \begin{array}{l@{\quad}l} \displaystyle\min_{f_2 \in\mathcal{H}} &R^{emp}\bigl(f_2(\boldsymbol{X}_l)\bigr) + \gamma _\mathcal{M}\bigl\| f_2(\boldsymbol{X})\bigr\| ^2_{\mathcal{M}},\\ \mbox{s.t.} & \|f_2\|^2_{\mathcal{H}} = 1 \end{array} \right ), \end{aligned}$$

(13)

where R ^emp(f) denotes the empirical risks on the labeled data X _l , which are used to extract the discriminant information for MPSVM. In light of the manifold assumption that two points x ₁,x ₂ that are close on the intrinsic manifold $\mathcal {M}$ should share similar labels, the MR term $\|f\|^{2}_{\mathcal{M}}$ enforces the smoothness of f along the underlying distribution (intrinsic manifold $\mathcal{M}$). Moreover, $\|f\|^{2}_{\mathcal{H}}$ is the norm of f in the RKHS, and the constraint controls the complexity of MPSVM to avoid over-fitting. In the following subsections, we will give the derivation of these terms in (12) and (13) for both linear and nonlinear cases.

3.2 Linear MPSVM

For the linear case, our MPSVM finds the following two nonparallel proximal hyperplanes

$$\begin{aligned} f_{1}(\boldsymbol{x}): \boldsymbol{w}'_{1} \boldsymbol{x} + b_{1} = 0 \quad\mbox{and}\quad f_{2}( \boldsymbol {x}): \boldsymbol{w}'_{2}\boldsymbol{x} + b_{2} = 0, \end{aligned}$$

(14)

where $\boldsymbol{w}_{1}, \boldsymbol{w}_{2} \in\mathbb{R}^{n}$ are the normal vectors and $b_{1}, b_{2} \in\mathbb{R}$ are the bias terms.

Motivated by the maximum distance criterion,² we use the “difference” instead of the “ratio” (used in GEPSVM) to characterize the discrepancy between two different classes. Thus, the empirical risk R ^emp(f) in (12) and (13) can be represented as

(15)

and

(16)

where c ₁>0 is the empirical risk penalty parameter that determines the trade-off between the two terms in (15) and (16). That is to say, introducing the parameter c ₁ allows our MPSVM to have a bias factor for different data classes.

Generally, in SSL [29, 30], the MR terms $\|f\| ^{2}_{\mathcal{M}}$ can be approximated by

$$\begin{aligned} \|f_1\|^2_{\mathcal{M}} =& \sum _{i,j=1}^{l+u} w_{ij}\bigl(f_{1}( \boldsymbol {x}_i)-f_{1}(\boldsymbol{x}_j) \bigr)^2 = f'_1(\boldsymbol{X})\boldsymbol {L}f_1(\boldsymbol{X}) \\ =& (\boldsymbol{X}\boldsymbol{w}_1 + \boldsymbol{e}b_1)' \boldsymbol {L}(\boldsymbol{X}\boldsymbol{w}_1 + \boldsymbol{e}b_1), \end{aligned}$$

(17)

and

$$\begin{aligned} \|f_2\|^2_{\mathcal{M}} =& \sum _{i,j=1}^{l+u} w_{ij}\bigl(f_{2}( \boldsymbol {x}_i)-f_{2}(\boldsymbol{x}_j) \bigr)^2 = f'_2(\boldsymbol{X})\boldsymbol {L}f_2(\boldsymbol{X}) \\ =& (\boldsymbol{X}\boldsymbol{w}_2 + \boldsymbol{e}b_2)' \boldsymbol {L}(\boldsymbol{X}\boldsymbol{w}_2 + \boldsymbol{e}b_2), \end{aligned}$$

(18)

where w _ij is the edge-weight defined for a pair of points (x _i ,x _j ) of the adjacency matrix $\boldsymbol{W}= (w_{ij}) \in\mathbb {R}^{(l+u) \times(l+u)}$, f ₁(X)=Xw ₁+e b ₁, f ₂(X)=Xw ₂+e b ₂, and L is the graph Laplacian defined as L=D−W. Furthermore, the diagonal matrix D is given by $D_{ii} = \sum_{j=1}^{l+u}w_{ij}$. More details can be seen in [29].

Similar to [9, 10, 31], we introduce a constraint to control and normalize the norm of the problem variables (w _i ,b _i ) (i=1,2). By defining H=[A e ₁], G=[B e ₂], J=[X e], , and , the primal problems for our MPSVM can be expressed as

$$\begin{aligned} \begin{array}{l@{\quad}l} \displaystyle\min_{\boldsymbol{v}_1} & f_{(1,obj)}(\boldsymbol{v}_1)= \boldsymbol {v}'_1\boldsymbol{H}'\boldsymbol {H}\boldsymbol{v}_1 - c_1\boldsymbol{v}'_1\boldsymbol{G}'\boldsymbol {G}\boldsymbol{v}_1 \\ &\phantom{f_{(1,obj)}(\boldsymbol{v}_1)=}{}+ c_2\boldsymbol{v}'_{1}\boldsymbol {J}'\boldsymbol{L}\boldsymbol{J}\boldsymbol{v}_{1} ,\\ \mbox{s.t.} & \|\boldsymbol{v}_1\|^2 =1, \end{array} \end{aligned}$$

(19)

and

$$\begin{aligned} \begin{array}{l@{\quad}l} \displaystyle\min_{\boldsymbol{v}_2} & f_{(2,obj)}(\boldsymbol{v}_2)= \boldsymbol {v}'_2\boldsymbol{G}'\boldsymbol {G}\boldsymbol{v}_2 - c_1\boldsymbol{v}'_2\boldsymbol{H}'\boldsymbol {H}\boldsymbol{v}_2\\ &\phantom{f_{(2,obj)}(\boldsymbol{v}_2)=}{} + c_2\boldsymbol{v}'_{2}\boldsymbol {J}'\boldsymbol{L}\boldsymbol{J}\boldsymbol{v}_{2},\\ \mbox{s.t.} & \|\boldsymbol{v}_2\|^2 =1, \end{array} \end{aligned}$$

(20)

where c ₂>0 is the MR parameter. An intuitive geometric interpretation for the linear MPSVM is shown in Fig. 1(c). Let us give a detailed explanation of the optimization problem in (19). The first term in the objective function of (19) minimizes the squared sum of values of A (the data labeled “+1”) on f ₁(x), which makes the labeled data A be as close as possible to the “+1” proximal hyperplane f ₁(x). Optimizing the second term leads to B (the data labeled “−1”) being as far as possible from f ₁(x). It is noteworthy that the first and second terms in (19) integrate the supervised information into MPSVM according to the maximum distance criterion. The third term exploits the underlying distribution between the labeled and unlabeled data. Minimizing this term enforces the smoothness of f ₁(x) along the intrinsic manifold. The constraint in (19) controls the model complexity of f ₁(x) to avoid over-fitting.

Because the optimization problem in (20) is similar to that in (19), we mainly focus on the solution of (19). Constructing the Lagrange function of (19) with the multiplier λ ₁, gives

$$\begin{aligned} L(\boldsymbol{v}_1, \lambda_1) =& \boldsymbol{v}'_1\boldsymbol {H}' \boldsymbol{H}\boldsymbol{v}_1 - c_1\boldsymbol {v}'_1\boldsymbol{G}'\boldsymbol{G} \boldsymbol{v}_1 + c_2\boldsymbol {v}'_{1} \boldsymbol{J}'\boldsymbol{L}\boldsymbol{J}\boldsymbol {v}_{1} \\ &{}- \lambda_1\bigl(\|\boldsymbol{v}_{1} \|^{2} - 1\bigr). \end{aligned}$$

(21)

Setting the partial derivatives of v ₁ in (21) equal to zero, we obtain

$$ \nabla_{\boldsymbol{v}_1}L = 2\bigl(\boldsymbol{H}'\boldsymbol{H} - c_1\boldsymbol{G}'\boldsymbol{G} + c_2 \boldsymbol{J}'\boldsymbol {L}\boldsymbol{J}\bigr) \boldsymbol{v}_1 - 2\lambda_1\boldsymbol{v}_{1} = 0, $$

(22)

which is equal to

$$ \bigl(\boldsymbol{H}'\boldsymbol{H} - c_1\boldsymbol{G}'\boldsymbol{G} + c_2 \boldsymbol{J}'\boldsymbol{L}\boldsymbol{J}\bigr) \boldsymbol{v}_1 = \lambda_1\boldsymbol{v}_1. $$

(23)

In fact, λ ₁ is an eigenvalue of the symmetric matrix (H′H−c ₁ G′G+c ₂ J′LJ). In particular, we can rewrite the objective function f _(1,obj)(v) in (19) as

$$\begin{aligned} f_{(1,obj)}(\boldsymbol{v}) =& \boldsymbol{v}'_1 \boldsymbol {H}'\boldsymbol{H}\boldsymbol{v}_1 - c_1\boldsymbol{v}'_1\boldsymbol {G}'\boldsymbol{G}\boldsymbol{v}_1 + c_2 \boldsymbol {v}'_{1}\boldsymbol{J}' \boldsymbol{L}\boldsymbol{J}\boldsymbol {v}_{1} \\ =& \boldsymbol{v}'_1\bigl(\boldsymbol{H}' \boldsymbol{H} - c_1\boldsymbol {G}'\boldsymbol{G} + c_2\boldsymbol{J}'\boldsymbol{L}\boldsymbol {J}\bigr) \boldsymbol{v}_1. \end{aligned}$$

(24)

Then, substituting (23) into (24), we obtain

$$\begin{aligned} f_{(1,obj)}(\boldsymbol{v}_1) =& \boldsymbol{v}'_1\lambda _1 \boldsymbol{v}_1 = \lambda_1\|\boldsymbol {v}_1\|^2 = \lambda_1 \geq \lambda_{(1,s)} \\ =& \boldsymbol{v}'_{(1,s)}\lambda_{(1,s)} \boldsymbol{v}_{(1,s)} = f_{(1,obj)}(\boldsymbol {v}_{(1,s)}) \\ =& f_{(1,obj)}\bigl(\boldsymbol{v}_1^{*}\bigr), \end{aligned}$$

(25)

where λ _(1,s) is the smallest eigenvalue of (23) and v _(1,s) is the corresponding eigenvector. From (25), we can conclude that the eigenvector corresponding to the smallest eigenvalue of (23) is the optimal solution of (19).

In a similar way, we can find the solution of the optimization problem (20) by solving the following standard eigenvalue problem:

$$\begin{aligned} \bigl(\boldsymbol{G}'\boldsymbol{G} - c_1\boldsymbol{H}'\boldsymbol{H} + c_2 \boldsymbol{J}'\boldsymbol{L}\boldsymbol{J}\bigr) \boldsymbol{v}_2 = \lambda_2\boldsymbol{v}_2, \end{aligned}$$

(26)

where the optimal solution is the eigenvector corresponding to the smallest eigenvalue.

Once solutions (w ₁,b ₁) and (w ₂,b ₂) have been obtained by solving the two eigenvalue problems of (23) and (26), a new data $\boldsymbol{x}\in\mathbb{R}^{n}$ is assigned to class i (i=“+1” or “−1”), depending on which of the two proximal hyperplanes (14) it lies closer to, i.e.,

$$\begin{aligned} \mathrm{Class}\ i=\arg\min_{k=1,2}~ \frac{|\boldsymbol{w}'_{k}\boldsymbol{x}+b_{k}|}{\|\boldsymbol {w}_{k}\|}. \end{aligned}$$

(27)

3.3 Nonlinear MPSVM

In order to extend our model to the nonlinear case, we consider the following two kernel-generated proximal hyperplanes

$$\begin{aligned} \begin{aligned} {}&f_{1}(\boldsymbol{x}): \mathcal{K}\bigl( \boldsymbol{x}', \boldsymbol {X}'\bigr) \boldsymbol{w}_1 + b_{1} = 0 \quad\mbox{and}\\ &f_{2}(\boldsymbol{x}): \mathcal{K}\bigl(\boldsymbol{x}', \boldsymbol{X}'\bigr)\boldsymbol{w}_2 + b_{2} = 0, \end{aligned} \end{aligned}$$

(28)

where $\boldsymbol{X} \in\mathbb{R}^{(l+u) \times n}$ denotes all the training data and $\mathcal{K}(\cdot,\cdot)$ is an appropriately chosen kernel, such as the radial basis function (RBF) kernel $\mathcal {K}(\boldsymbol{u}, \boldsymbol {v}) = e^{-\gamma\|\boldsymbol{u}-\boldsymbol{v}\|^{2}}$, γ>0. The optimization problems for the nonlinear MPSVM can be expressed as

$$\begin{aligned} \begin{array}{l@{\quad}l} \displaystyle\min_{\boldsymbol{w}_1, b_1} & \bigl\| \mathcal{K}(\boldsymbol {A},\boldsymbol{X}')\boldsymbol{w}_1 + \boldsymbol{e}_1b_1\bigr\| ^2 \\ &\quad{}- c_1\bigl\| \mathcal{K}(\boldsymbol{B},\boldsymbol{X}')\boldsymbol{w}_1 + \boldsymbol{e}_2b_1\bigr\| ^2 \\ &\quad{} + c_2(\boldsymbol{K}\boldsymbol{w}_1 + \boldsymbol {e}b_1)'\boldsymbol{L}(\boldsymbol{K}\boldsymbol{w}_1 + \boldsymbol {e}b_1),\\ \mbox{s.t.} & \|\boldsymbol{w}_1\|^2 + b_1^2 = 1, \end{array} \end{aligned}$$

(29)

and

$$\begin{aligned} \begin{array}{l@{\quad}l} \displaystyle\min_{\boldsymbol{w}_2, b_2} & \bigl\| \mathcal{K}(\boldsymbol {B},\boldsymbol{X}')\boldsymbol{w}_2 + \boldsymbol{e}_2b_2\bigr\| ^2\\ &\quad{}- c_1\bigl\| \mathcal{K}(\boldsymbol{A},\boldsymbol{X}')\boldsymbol{w}_2 + \boldsymbol{e}_1b_2\bigr\| ^2 \\ &\quad{} + c_2(\boldsymbol{K}\boldsymbol{w}_2 + \boldsymbol {e}b_2)'\boldsymbol{L}(\boldsymbol{K}\boldsymbol{w}_2 + \boldsymbol {e}b_2),\\ \mbox{s.t.} & \|\boldsymbol{w}_2\|^2 + b_2^2 = 1, \end{array} \end{aligned}$$

(30)

where K denotes $\mathcal{K}(\boldsymbol{X}, \boldsymbol{X}')$, c ₁>0 is the empirical risk penalty parameter, c ₂>0 is the manifold regularization parameter, and L is the graph Laplacian.

By defining $\boldsymbol{H}_{\varphi}=[\mathcal{K}(\boldsymbol{A}, \boldsymbol{X}')\ \boldsymbol {e}_{1}]$, $\boldsymbol{G}_{\varphi}=[\mathcal{K}(\boldsymbol{B}, \boldsymbol{X}')\ \boldsymbol{e}_{2}]$, J _φ =[K e], and , the above problems can be rewritten as

$$\begin{aligned} \begin{array}{l@{\quad}l} \displaystyle\min_{\boldsymbol{v}_1 } & \boldsymbol{v}'_1\boldsymbol {H}'_{\varphi}\boldsymbol{H}_{\varphi }\boldsymbol{v}_1 - c_1\boldsymbol{v}'_1\boldsymbol{G}'_{\varphi}\boldsymbol {G}_{\varphi}\boldsymbol{v}_1 + c_2\boldsymbol{v}'_{1}\boldsymbol{J}'_{\varphi}\boldsymbol {L}\boldsymbol{J}_{\varphi}\boldsymbol{v}_{1},\\ \mbox{s.t.} & \|\boldsymbol{v}_1\|^2 = 1, \end{array} \end{aligned}$$

(31)

and

$$\begin{aligned} \begin{array}{l@{\quad}l} \displaystyle\min_{\boldsymbol{v}_2} & \boldsymbol{v}'_2\boldsymbol{G}'_{\varphi }\boldsymbol{G}_{\varphi }\boldsymbol{v}_2 - c_1\boldsymbol{v}'_2\boldsymbol{H}'_{\varphi}\boldsymbol {H}_{\varphi}\boldsymbol{v}_2 + c_2\boldsymbol{v}'_{2}\boldsymbol{J}'_{\varphi}\boldsymbol {L}\boldsymbol{J}_{\varphi}\boldsymbol{v}_{2},\\ \mbox{s.t.} & \|\boldsymbol{v}_2\|^2 = 1. \end{array} \end{aligned}$$

(32)

Similar to the linear case, the solutions of the optimization problem (31) and (32) can be obtained by solving the following two standard eigenvalue problems:

$$\begin{aligned} \bigl(\boldsymbol{H}'_{\varphi} \boldsymbol{H}_{\varphi} - c_1\boldsymbol {G}'_{\varphi} \boldsymbol{G}_{\varphi } + c_2\boldsymbol{J}'_{\varphi} \boldsymbol{L}\boldsymbol {J}_{\varphi} \bigr)\boldsymbol{v}_1 = \lambda_1\boldsymbol{v}_1, \end{aligned}$$

(33)

and

$$\begin{aligned} \bigl(\boldsymbol{G}'_{\varphi} \boldsymbol{G}_{\varphi} - c_1\boldsymbol {H}'_{\varphi} \boldsymbol{H}_{\varphi } + c_2\boldsymbol{J}'_{\varphi} \boldsymbol{L}\boldsymbol {J}_{\varphi}\bigr)\boldsymbol{v}_2 = \lambda_2\boldsymbol{v}_2. \end{aligned}$$

(34)

where the optimal solutions are the eigenvectors corresponding to the smallest eigenvalues.

Once the solutions (w ₁,b ₁) and (w ₂,b ₂) of (31) and (32) are obtained, a new data $\boldsymbol {x} \in\mathbb{R}^{n}$ is assigned to class i (i=“+1” or “−1”), depending on which of the two kernel-generated proximal hyperplanes (28) it lies closer to, i.e.,

$$\begin{aligned} \mathrm{Class}\ i=\arg\min_{k=1,2} \frac{|\mathcal{K}(\boldsymbol{x}',\boldsymbol{X}')\boldsymbol {w}_{k} + b_{k}|}{\sqrt{\boldsymbol {w}'_k\boldsymbol{K}\boldsymbol{w}_k}}. \end{aligned}$$

(35)

3.4 Relationship with some other related methods

3.4.1 Relationship with GEPSVM and DGEPSVM

As mentioned above, in (5) and (6), GEPSVM uses a “ratio” to quantify the discrepancy between two different classes, resulting in the generalized eigenvalue problems. To enhance its performance, DGEPSVM [11] uses the “difference” instead of the “ratio”, leading to simpler optimization problems (standard eigenvalue problems). If we drop the MR terms $\| f(\boldsymbol{X})\| ^{2}_{\mathcal{M}}$ in (12) and (13) by setting c ₂=0, our MPSVM will degenerate to the DGEPSVM. Therefore, we can see that DGEPSVM is a special case of MPSVM. From another perspective, our MPSVM is a useful extension of GEPSVM and DGEPSVM to the semi-supervised case.

3.4.2 Relationship with LapTSVM

Both LapTSVM and MPSVM utilize information about the underlying distribution (via MR) to construct a more reasonable classifier. However, there are several obvious differences between them. First, the empirical risk R ^emp(f) in LapTSVM [31] is implemented by minimizing both the L ₁ and L ₂-norm loss functions for each class, whereas, in (15) and (16), our MPSVM implements R ^emp(f) by maximizing the L ₂-norm distances between two different classes. Second, during the learning procedure, the solutions of LapTSVM are obtained by solving two QPPs with computational-costly matrix inversion operations. In contrast, our MPSVM solves two standard eigenvalue problems without matrix inversion, resulting in more effective learning ability.

4 Model selection for MPSVM

In this section, we consider the model selection (parameter optimization) for MPSVM. The parameters that should be optimized in MPSVM include the empirical risk penalty parameter c ₁, the MR parameter c ₂, and the RBF kernel parameter γ (for the nonlinear case), as detailed in Table 1. Different parameter settings can have a great impact on the performance of MPSVM. However, to our knowledge, the parameter optimization is recognized as a combinatorial optimization problem (NP-hard problem), which is one of the main unsolved problems of computer science [36–38]. Typically, metaheuristics are used to obtain approximate solutions to NP-hard problems [39]. In our implementation, instead of using a genetic algorithm (GA), we apply the excellent population-based PSO metaheuristic [40, 41] to assist the parameter optimization.

Table 1 Summary of parameters in MPSVM

4.1 Concept of particle swarm optimization (PSO)

PSO is an artificial intelligence technique that can be used to seek approximate solutions to extremely difficult numeric optimization problems [40]. Its main idea is that, inspired from the social behavior of organisms, PSO consists of a swarm (population) of particles (potential solutions) that search for the best position (solution) in the multi-dimensional space, and each particle adjusts its moving direction (velocity) according to its personal best position (cognition parts) and the best global position of all particles (social parts) during each iteration. An intuitive illustration for the population-based search behavior of PSO is shown in Fig. 3. The iteration strategy for each particle is described as

$$\begin{aligned} \begin{array}{l} \mbox{Velocity update:}\\ \quad \boldsymbol{v}_i^{t+1} = \boldsymbol {v}_i^{t} + \tau _{1}r_{1}\bigl(\boldsymbol{p}_i^{t} - \boldsymbol{x}_i^{t}\bigr) + \tau _{2}r_{2}\bigl(\boldsymbol{g}^{t} - \boldsymbol {x}_i^{t}\bigr),\\ \mbox{Position update:} \quad\boldsymbol{x}_i^{t+1} = \boldsymbol {x}_i^{t} + \boldsymbol{v}_i^{t+1}, \end{array} \end{aligned}$$

(36)

where superscript t denotes the t-th iteration; v _i =(v _i1,v _i2,…,v _id )′ and x _i =(x _i1,x _i2,…,x _id )′ denote the velocity and position of the particle i in d-dimensional space, respectively; p _i =(p _i1,p _i2,…,p _id )′ represents the personal best position of particle i, and g=(g ₁,g ₂,…,g _d )′ is the best position obtained from p _i for all particles; τ ₁,τ ₂∈(0 2] indicate the cognition and social learning parameter, respectively; r ₁ and r ₂ are the random numbers generated by uniform distribution U[0,1]. More details can be seen in [40, 41].

Fig. 3

The population-based search behavior of PSO. The blue circle denotes a particle and the arrow navigates the particle’s motion (search) direction (Color figure online)

4.2 Parameter optimization for MPSVM

In this subsection, we develop a PSO-based parameter optimization approach for our MPSVM. As indicated above, some parameters must be predetermined. These are the penalty parameters c ₁, c ₂ and an extra RBF kernel parameter γ for the nonlinear case. In our implementation, we first transform the above set of parameters into a particle x, which is composed of (c ₁,c ₂) for the linear case or (c ₁,c ₂,γ) for the nonlinear case. The main process is illustrated in Fig. 4, for which we give the following explanation:

• (1) Initialization: A swarm of N particles is initialized to have position $\boldsymbol{X}^{0} = \{\boldsymbol {x}_{i}^{0}\}_{i=1}^{N}$ and velocity $\boldsymbol{V}^{0} = \{\boldsymbol{v}_{i}^{0}\} _{i=1}^{N}$. Each $\boldsymbol {x}_{i}^{0}$ and $\boldsymbol{v}_{i}^{0}$ are generated by the uniform distribution according to the range shown in Table 1. By default, the cognition learning parameter is set to τ ₁=1.3 and the social learning parameter is set to τ ₂=1.5.

• (2) Fitness evaluation: The fitness of each particle used to train MPSVM is evaluated according to $\mathit{Fit}(\boldsymbol {x}_{i}^{t}) = 1 - \mathit{Acc}(\boldsymbol{x}_{i}^{t})$, where $\mathit{Acc}(\boldsymbol{x}_{i}^{t})$ denotes the classification accuracy of MPSVM under the parameter $\boldsymbol{x}_{i}^{t}$, and the fitness $\mathit{Fit}(\boldsymbol{x}_{i}^{t})$ denotes the corresponding training error.³

• (3) Update operation: If the fitness of $\boldsymbol {x}_{i}^{t}$ is better than its previous best value (i.e., $\mathit{Fit}(\boldsymbol {x}_{i}^{t}) < \mathit{Fit}(\boldsymbol{p}_{i}^{t-1})$), the current position $\boldsymbol {x}_{i}^{t}$ is taken as the new personal best position $\boldsymbol{p}_{i}^{t}$. The best $\{ \boldsymbol{p}_{i}^{t}\} _{i=1}^{N}$ is then chosen as the new best global position g ^t. After finding the two best positions, the particle updates its velocity and position according to (36).

• (4) Stopping criterion: The process is terminated if the minimum error criterion is satisfied or the maximum iteration number is reached.

Fig. 4

The architecture of the proposed PSO-based parameter optimization approach for MPSVM

5 Experimental results

To evaluate the performance of our MPSVM,⁴ we investigated its classification accuracy⁵ and computational efficiency⁶ on both artificial and real-world datasets. In our implementation, we focused on the comparison between MPSVM and several state-of-the-art classifiers, including GEPSVM, LapSVM, and LapTSVM:

• GEPSVM [9]: It is a supervised algorithm for classification. GEPSVM relaxes the universal requirement that the hyperplanes generated by SVMs should be parallel, and attempts to seek a pair of optimal nonparallel proximal hyperplanes by solving generalized eigenvalue problems. The parameter settings in GEPSVM are (δ) for linear and (δ,γ) for nonlinear.

• LapSVM [29]: It is an extension of SVM [1] for semi-supervised classification. LapSVM adopts the manifold assumption, and uses the hinge loss to construct a parallel hyperplane classifier by seeking a maximum margin boundary on both labeled and unlabeled data. The parameter settings in LapSVM are (c ₁,c ₂) for linear and (c ₁,c ₂,γ) for nonlinear.

• LapTSVM [31]: It is an extension of TWSVM [12] for semi-supervised classification. LapTSVM also adopts the manifold assumption and exploits the geometric information embedded in the training data to construct a nonparallel hyperplane classifier. The parameter settings in LapTSVM are (c ₁,c ₂,c ₃) for linear and (c ₁,c ₂,c ₃,γ) for nonlinear.

All the classifiers are implemented in Matlab (R14)⁷ on a personal computer (PC) with an Intel P4 processor (2.9 GHz) and 2 GB random-access memory (RAM). The general eigenvalue problem in GEPSVM and standard eigenvalue problem in MPSVM were solved by the Matlab function “eig( )”. For the QPPs in LapSVM and LapTSVM, we used the Matlab function “quadprog( )”. With regard to parameter selection, we employed the standard 10-fold cross-validation technique [3]. Furthermore, as in [9, 29, 31], we used a grid-based approach to obtain the optimal parameters for GEPSVM, LapSVM, and LapTSVM. For the grid-based approach, the optimal penalty parameters δ, c ₁, c ₂, c ₃ and RBF kernel parameter γ were selected from the set {2ⁱ|i=−5,−4,…,4,5}. Additionally, the PSO-based approach was utilized for our MPSVM. Once selected, the optimal parameters were employed to learn the final decision function.

5.1 Results on artificial datasets

In this subsection, we compare the effectiveness of our MPSVM with GEPSVM, LapSVM and LapTSVM for three semi-supervised artificial datasets, in terms of the classification performance and decision boundary.

First, we consider a two-dimensional “xor” dataset, which is usually used to demonstrate the effectiveness of nonparallel proximal SVM [9, 12, 13]. The “xor” dataset was obtained by perturbing the points that lie on two intersecting planes (lines) with three labeled data points, as shown in Fig. 5(a), where each plane corresponds to one class. Figure 5 shows the one-run results from this dataset of GEPSVM, LapSVM, LapTSVM and MPSVM for the case of a linear kernel. We can see that: (1) supervised GEPSVM obtains poor results because of the insufficient labeled information; (2) although both LapSVM and LapTSVM utilize the unlabeled data to assist training, they are not suited to the “xor” dataset; (3) taking advantage of the maximum distance criterion, our MPSVM is able to deliver a more reasonable decision boundary than the others.

Fig. 5

Synthetic xor dataset with noise. Each cross line corresponds to one class. The squares denote a large set of unlabeled data points. The red diamond or blue circle denotes the labeled data points of positive or negative class, respectively. The black curve is the decision boundary. The blue and red dashed curves are the two linear hyperplanes. The linear classification accuracy of GEPSVM 69.89 %, LapSVM 69.89 %, LapTSVM 68.82 % and MPSVM 100.00 % (Color figure online)

A more challenging case is illustrated in Fig. 6(a), which is a variant of the “smile” dataset corrupted by the Gaussian noise. Figure 6 shows the learning results of each classifiers using an RBF kernel. We can see that: (1) as might be expected, GEPSVM simply constructs the decision boundary across the minpoints of the labeled data points; (2) LapTSVM and MPSVM obtain 100 % classification accuracy. However, our MPSVM obtains a smoother decision boundary, resulting in better generalization ability.

Fig. 6

Synthetic smile datasets with noise. The upper part corresponds to positive class, and the lower part corresponds to negative class. The squares denote a large set of unlabeled data points. The red diamond or blue circle denotes the labeled data points of positive or negative class, respectively. The black curve is the decision boundary. The blue and red dashed curves are the two kernel-generated hyperplanes. The nonlinear classification accuracy of GEPSVM 93.65 %, LapSVM 98.17 %, LapTSVM 100.00 % and MPSVM 100.00 % (Color figure online)

For the third dataset (inverse half-moons, see Fig. 7(a)), we labeled three data points for each moon-shaped class. Figure 7 describes the one-run results from each classifier with this dataset using an RBF kernel. It can be seen that our MPSVM makes full use of the geometric information, and obtains a more reasonable decision boundary, whereas the other classifiers cannot achieve satisfactory performance.

Fig. 7

Synthetic two inverse half-moons datasets with noise. Each half-moon corresponds to one class. The squares denote a large set of unlabeled data points. The red diamond or blue circle denotes the labeled data points of positive or negative class, respectively. The black curve is the decision boundary. The blue and red dashed curves are the two kernel-generated hyperplanes. The nonlinear classification accuracy of GEPSVM 89.41 %, LapSVM 97.81 %, LapTSVM 98.90 % and MPSVM 99.64 % (Color figure online)

We also plot the iterative PSO procedure for our MPSVM, shown in Figs. 5–7(f). We can see that the optimal model/parameters of MPSVM can be obtained after a few PSO iterations. To further illustrate the learning results of these classifiers, Table 2 lists the classification accuracies (Acc), training time (T _train ), optimization parameters, and parameter search time (T _para ) with these three artificial datasets. We have highlighted the best performance. The results indicate that MPSVM obtains the best classification performance among these classifiers. In terms of the training time, LapTSVM and MPSVM are more efficient than GEPSVM and LapSVM. Furthermore, the parameter search time of our PSO-based MPSVM is orders of magnitude faster than the grid-based approach.

Table 2 Results of GEPSVM, LapSVM, LapTSVM and MPSVM on three artificial datasets

5.2 Results on UCI datasets

To further evaluate the performance of MPSVM, we applied each algorithm to several real-world datasets from the UCI machine learning repository,⁸ and investigated the results in terms of classification accuracy, training time, and parameter search time. We used the Hepatitis, Ionosphere, WDBC, Australian and CMC datasets for our comparison. These datasets represent a wide range of fields (include pathology, biological information, finance and so on), sizes (from 155 to 1437) and features (from 6 to 34). Note that all datasets are normalized such that the features scale in [−1 1] before training. Similar to [27, 42], our experiments were set up in the following way. First, each dataset was divided into two subsets: 65 % for training and 35 % for testing. Then, we randomly labeled m of the training set, and used the remainder as unlabeled data, where m is the ratio of labeled data. Finally, we transformed them into semi-supervised tasks. Each experiment is repeated 10 times.

Table 3 lists the learning results of each algorithm using an RBF kernel, and includes the mean and deviation of the testing accuracy for various m from 5 % to 30 %. We have highlighted the best performance. From Table 3, it is easy to see that increasing the ratio of labeled data generally improves the classification performance for all algorithms. For example, in the Australian dataset, the accuracy of MPSVM improved more than 5 % when m increased from 5 % to 10 %. Furthermore, we also find that the traditional proximal algorithm GEPSVM performed relatively poorly with almost all datasets, which was due to insufficient numbers of labeled data. On the contrary, our MPSVM fully utilizes the underlying data information to enable better classification.

Table 3 Mean and standard deviation of testing accuracy with different labeled ratio m on UCI dataset. ▲/▽ indicates whether MPSVM is statistically superior/inferior to the compared algorithm, according to pairwise t-test 95 % significance level. Win/Tie/Loss denotes the number of datasets where MPSVM is significance Superior/Equal/Inferior to the compared algorithm. Ave. mean and std denotes the average mean and standard deviation accuracy of each algorithm over all datasets

To provide more statistical evidence [27, 43], we performed a paired t-test to compare the testing accuracy of GEPSVM, LapSVM, and LapTSVM to that of MPSVM. The significance level (SL) was set to 0.05. That is, when the t-test value is greater than 1.7341, the classification results of the two algorithms significantly different. Consequently, as shown in Table 3, we can see that our MPSVM significantly outperforms GEPSVM and LapSVM with most datasets. A Win/Tie/Loss (W/T/L) summarization based on the t-test is also listed at the bottom of Table 3. This shows that our MPSVM obtains better classification performance than the others. This is because MPSVM combines both the maximum distance criterion and MR to enhance its generalization ability.

The average training time (T _train ) and parameter search time (T _para ) of each algorithm with the above datasets are shown in Figs. 8 and 9, respectively. These reveal that the training time of MPSVM is comparable to that of LapTSVM, and the parameter search time of MPSVM is several orders of magnitude faster than that of the other classifiers.

Fig. 8

The training time T _train of the GEPSVM, LapSVM, LapTSVM and MPSVM on real-world datasets for the case of RBF kernel in the logarithmic scale, where m is the ratio of labeled data (Color figure online)

Fig. 9

The parameter searching time T _para of the GEPSVM, LapSVM, LapTSVM and MPSVM on real-world datasets for the case of RBF kernel in the logarithmic scale, where m is the ratio of labeled data (Color figure online)

5.3 Results for handwritten symbol recognition

In this section, we investigate the impact of the number of unlabeled data on the performance of MPSVM. The USPS handwritten dataset⁹ was used for these experiments. The USPS database consists of grayscale images of handwritten digits from ‘0’ to ‘9’, as shown in Fig. 10. The size of each image is 16×16 pixels with 256 gray levels. Similarly to [31], we choose four pairwise digits (200 images) on raw pixel features for our comparisons, and set up experiments in the following way. First, each dataset was divided into two subsets: 150 images for training and 50 images for testing. Then, we randomly labeled 40 images for the training set with m unlabeled images chosen from the remainder. Finally, we transformed them into semi-supervised tasks. Each experiment was repeated 10 times.

Fig. 10

An illustration of 10 subjects in the USPS database

Figure 11 plots the learning results of each algorithm using a linear kernel, and includes the mean and deviation of testing accuracy for values of m from 20 to 100. As demonstrated in this figure, MPSVM generally has an obvious superiority over the other classifiers.

Fig. 11

The test accuracy and standard deviation of GEPSVM, LapSVM, LapTSVM and MPSVM on USPS dataset for the case of linear kernel (Color figure online)

Overall, our MPSVM obtains significantly better classification accuracy than the other classifiers, but with remarkably lower learning time.

6 Conclusions

In this paper, we have proposed a novel MPSVM for binary semi-supervised classification. MPSVM incorporates both discriminant information and underlying geometric information to construct a more reasonable classifier. The optimal nonparallel proximal hyperplanes of MPSVM are obtained by solving a pair of standard eigenvalue problems. In addition, we designed an efficient PSO-based model selection approach, instead of a conventional grid search. We carried out a series of experiments to analyze our classifier against three state-of-the-art learning classifiers. The results demonstrate that MPSVM obtains significantly better performance than supervised GEPSVM, and achieves comparable or better performance than LapSVM and LapTSVM, with greater computational efficiency (including training time and parameter search time).

One of our future work is to construct the sparse L matrix in $\| f(\boldsymbol{X})\|^{2}_{\mathcal{M}}$ for the underlying manifold (distribution) representation. We also feel that extending our MPSVM to semi-supervised feature selection and multi-category classification would be interesting.