1 Introduction

Data envelopment analysis (DEA) is a nonparametric technique for analyzing the relative efficiency of homogeneous Decision Making Units (DMUs) with multiple inputs and multiple outputs. The relative efficiency is the ratio of the weighted sum of outputs to the weighted sum of inputs. DEA was presented by Charnes et al. (1978). DEA scores unity to efficient DMUs. Therefore, DEA may not discriminate between efficient DMUs. Several ranking approaches have been proposed to break the tie. One of the popular ranking approaches is cross-efficiency assessment. Sexton et al. (1986) discussed the cross-efficiency based on the constant returns-to-scale (CRS) assumption. Lim and Zhu (2015) used the cross-efficiency evaluation in variable returns-to-scale (VRS) production technology. Cross-efficiency evaluation has been employed in many settings (e.g., Cui & Li, 2015; Lim et al., 2014; Wu et al., 2009). On the other hand, one of the most important issues is the existence of alternative optimal solutions in the results of cross-efficiency scores. To address this issue, the concept of secondary goals was presented by Sexton et al. (1986) and Doyle and Green (1994). The secondary goals concern the benevolent and aggressive formulas. The benevolent (aggressive) model determines the optimum weights to retain the efficiency score of DMU under evaluation and increases (decreases) the efficiencies of other DMUs. Some researchers also suggested a neutral perspective based on specific criteria for determining the unique cross-efficiency scores (e.g., Wang & Chin, 2010; Lam, 2010; Wang et al., 2012; Cook & Zhu, 2014; Maddahi et al., 2014; Nasseri and Kiaei, 2019).

Classical cross-efficiency studies are based on black box models and do not care about the internal structure of production processes. For this purpose, network DEA (NDEA) was proposed. The NDEA can determine the efficiency scores of the entire system and its components. Most of the NDEA models assume that the production systems have two stages. In the first stage, some inputs are converted into the intermediate products and some are converted to the outputs. Färe and Grosskopf (2000) developed an NDEA model to assess health systems. Kao and Hwang (2008) proposed a two-stage DEA model to measure the efficiency of insurance companies. There is a considerable amount of research in this field; see Liu and Lu (2012), Kazemi Matin and Azizi (2015), Guo et al. (2017), Ahranjani et al. (2018), Zhu et al. (2018), An et al. (2018), Tavana et al., (2018a, 2018b), Golshani et al. (2019) Kiaei and Kazemi Matin (2020, 2021), Nemati et al. (2020), Kiaei et al. (2020), Lozano and Khezri (2021), Shahbazifar et al. (2021) and Chu and Zhu (2021) among others.

More recently, some researchers have started studying and applying the cross-efficiency method with network structure. Zadmirzaei et al. (2015) used NDEA and cross-efficiency to rank wood and paper companies. Also, Moslemi and Mirzazadeh (2017) suggested an NDEA model for measuring the efficiency of four-stage serial networks in the presence of feedback. To rank the DMUs, they employed the cross-efficiency method. However, they did not determine unique weights. Also, no method was proposed to set inputs and outputs targets to enhance cross-efficiency in NDEA. The target unit can inform the Decision Maker (DM) of the amount (%) by which an inefficient DMU should decrease its inputs and/or increase its outputs to become efficient (Ebrahimnejad & Tavana, 2014). Kao and Liu (2019) used the cross-efficiency method to evaluate the performance of DMUs with a serial and parallel two-stage network. They defined a cross-efficiency score as the geometrical average of the cross-efficiencies in a multi-stage DEA and showed that there is a multiplication relation between the overall cross-efficiency and stages. Örkcü et al. (2019) introduced a neutral cross-efficiency model in NDEA to rank DMUs and sub-DMUs. Meng and Xiong (2021) extended the cross-efficiency to a general two-stage system and applied the leader–follower method for the decomposition of the system's efficiency. Lin and Tu (2021) developed cross-efficiency evaluation in series and parallel structures for use with the directional distance function (DDF). Shao and Wang (2021) proposed the prospect values of DMUs and aggressive, benevolent, and neutral prospect basic two-stage cross-efficiency evaluation models. Wang et al. (2021) suggested a two-stage NDEA with game cross-efficiency to evaluate performance of industrial water resource utilization systems.

The proposed models in the evaluation of cross-efficiency scores in two-stage NDEA consider stages and overall cross-efficiencies’ relations (see Kao & Liu, 2019; Örkcü et al., 2019). In other words, by defining cross-efficiency score as a product of cross-efficiencies, they establish a multiplication relationship between the stages and overall cross-efficiency scores. However, by this definition, they neglect the amount of efficiency they attribute to the units because if the values of cross-efficiency are lower, the product of them will also be very low and almost close to zero. As a result, such a definition of stages and overall cross-efficiencies scores cannot evaluate and rank all units and subunits. Also, so far, no research has reported setting targets for the inputs and outputs to improve cross-efficiency in two-stage NDEA except for Rödder and Reucher (2011) who improved DEA cross-efficiency scores by providing two models based on radial decrease or change in inputs. They have taken weights or virtual prices of a peer DMU into account to improve the efficiencies of all remaining units.

The present paper generalizes Doyle and Green’s (1994) study and provides definitions of the stages and overall cross-efficiency scores in two-stage NDEA. This index is expressed as the arithmetic mean of cross-efficiency in series mode. By this definition, the problem faced in ranking all units and subunits is avoided. To improve the efficiency of units and subunits in two-stage NDEA based on Rödder and Reucher (2011) paper, two approaches are proposed: (a) Radial reduction of the first stage inputs and radial increase of the final outputs (without changing the intermediate productions). (b) Changing the inputs of the first stage and the final outputs without changing the intermediate productions (not necessarily reducing the inputs and increasing the outputs). For the sake of clarity, a real example is presented to show the superiority of the proposed method.

To the best of our knowledge, there is no paper to evaluate the NDEA cross-efficiency and its improvement. The main purpose of this paper is to evaluate cross-efficiency based on the benevolent method using an index to rank all the units and subunits in a two-stage NDEA and to set targets for the inputs and outputs of inefficient units and subunits based on the mentioned two methods to reduce their inefficiency and improve their efficiency. The contributions of this paper are as follows:

  • Using the cross-efficiency and assuming CRS, a new benevolent NDEA model is proposed.

  • The definition of cross-efficiency proposed by Doyle and Green (1994) is generalized.

  • Target setting of inputs and outputs for improving the cross-efficiency scores.

  • A case study is presented.

The rest of the paper is as follows: In Sect. 2, preliminary is given. The proposed model is presented in Sect. 3. In Sect. 4, a case study is given. Section 5 discusses the results of sensitivity analysis. Finally, the Secti. 6 concludes the paper.

2 Preliminary

2.1 Cross-efficiency and the way to improve the cross-efficiency of black-box DMUs

Table 1 depicts the used notations in this paper.

Table 1 The notations
Full size table

Suppose that we have \(n\). DMUs, \( {\text{DMU}}_{j} \left( {j = 1, \ldots ,n} \right)\) and each \({\text{DMU}}_{j} \) employs \(m\). semi-positive inputs \({\varvec{x}}_{{\varvec{j}}} = \left( {x_{1j} , \ldots ,x_{mj} } \right)\) to produce \(s\) semi-positive outputs \(\user2{ y}_{j} = \left( {y_{1j} , \ldots ,y_{sj} } \right)\). The CRS input-oriented model, when \({\text{DMU}}_{{k \in \left\{ {1, \ldots ,n} \right\}}}\) is the DMU under evaluation, is as follows:

$$ \begin{aligned} E_{kk}^{*} = \,\mathop {\max }\limits_{{{\mathbf{u}}_{k} ,\,{{\varvec{\upnu}}}_{k} }} \,\,\,\, & {\mathbf{u}}_{k} {\mathbf{y}}_{k} \\ \,\,\,\,\,\,\,\,\,\,s.t.\,\,\,\,\,\,\,\, & {{\varvec{\upnu}}}_{k} {\mathbf{x}}_{k} = 1, \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & {\mathbf{u}}_{k} {\mathbf{y}}_{j} - {{\varvec{\upnu}}}_{k} {\mathbf{x}}_{j} \le 0,\quad j = 1, \ldots ,n, \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & {\mathbf{u}}_{k} \ge {\mathbf{0}}_{s} , \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & {{\varvec{\upnu}}}_{k} \ge {\mathbf{0}}_{m} . \\ \end{aligned} $$
(1)

Let \(\left( {{\varvec{v}}^{*} ,{\varvec{u}}^{*} } \right)\). are the optimal solution of Model (1). Then, the optimal objective function \(E_{kk}^{*}\). refers to Charnes-Cooper-Rhodes (CCR) efficiency score of \({\text{ DMU}}_{k}\). Such evaluation is known as self-evaluation because the DMU is evaluated in favor of the optimal weights of its inputs and outputs. In contrast, the peer-evaluation \(E_{kj}^{*} = {{\sum\nolimits_{r = 1}^{s} {u_{rk}^{*} y_{rj} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{r = 1}^{s} {u_{rk}^{*} y_{rj} } } {\sum\nolimits_{i = 1}^{m} {v_{ik}^{*} x_{ij} } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{i = 1}^{m} {v_{ik}^{*} x_{ij} } }}\) indicates the cross-efficiency derived from peer evaluation of DMUj by DMUk. The model of each DMU is solved. As a result, n sets of weights of inputs and outputs are obtained for n DMUs. Each DMU (n − 1) iassigned a cross-efficiency score along with a CCR efficiency score. These efficiencies imply that Ekj are the elements located in the kth row and jth column of the matrix. In this case, the matrix is called the cross-efficiency matrix.

Dle and Green (1994) defined the cross-efficiency score of DMUj as the average cross-efficiencies with optimal weights of the other DMUs:

$$ e_{j} = \frac{1}{n}\sum\limits_{k = 1}^{n} {E_{kj}^{*} } \, = \frac{1}{n}\sum\limits_{k = 1}^{n} {\frac{{\sum\nolimits_{r = 1}^{s} {u_{rk}^{*} y_{rj} } }}{{\sum\nolimits_{r = 1}^{s} {v_{ik}^{*} x_{ij} } }}} $$
(2)

If the DMU under evaluation is CCR-efficient, then the optimal solution of Model (1) is not unique. To address the alternative optimal solutions’ issue, the benevolent and aggressive goals were introduced by Sexton et al. (1986). Rödder and Reucher (2011) presented a benevolent model to select a unique optimal solution. Their first model improves the cross-efficiency of DMUj from the viewpoint of DMUk by reducing inputs with respect to the production possibility set (PPS). Their second model may increase the inputs. Although the improved cross-efficiencies of the two methods dominate the cross-efficiencies, the second model improves the cross-efficiencies more than the first model because inputs change are free and feasible. Therefore, the input change can better improve the cross-efficiencies of all DMUs.

2.2 Efficiency evaluation and PPS in two-stage network

Here, we focus on a two-stage structure in which the inputs of the first stage are consumed to produce intermediate products for the second stage to get final outputs. Figure 1 shows the two-stage structure. The first stage consumes all the external inputs \({\mathbf{x}}_{i} ,\,\,i = 1,...,m,\) to produce the intermediate products \({\mathbf{z}}_{g} ,\,g = 1,...,h,\) which are used in the second stage. The second stage produces the final outputs \({\mathbf{y}}_{r} ,\,r = 1,...,s.\)

Fig. 1
figure 1

Two-stage structure

Full size image

Note that the aggregate outputs should be less than or equal to the aggregate inputs in the operations of the stages, which means the consumption of inputs in the second stage should be less than or equal to the production of outputs in the first stage. Assume that the DMU under evaluation is \(\left( {{\mathbf{x}}_{k} ,{\mathbf{z}}_{k} ,{\mathbf{y}}_{k} } \right)\). Also, suppose that at least one component of inputs, one component of intermediate products, and one component of outputs are positive. Assuming CRS, Kao and Hwang (2008) proposed an input-oriented multiplier model, which is as follows:

$$ \begin{aligned} \theta_{kk}^{*} = \mathop {\max }\limits_{{{\mathbf{u}}_{k} ,\,{{\varvec{\upnu}}}_{k} ,\,{\mathbf{w}}_{k} }} \,\,\,\,\, & {\mathbf{u}}_{k} {\mathbf{y}}_{k} \\ s.t.\,\,\,\,\,\,\,\, & {{\varvec{\upnu}}}_{k} {\mathbf{x}}_{k} = 1, \\ & {\mathbf{u}}_{k} {\mathbf{y}}_{j} - {{\varvec{\upnu}}}_{k} {\mathbf{x}}_{j} \le 0,\quad \,j = 1, \ldots ,n, \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & {\mathbf{w}}_{k} {\mathbf{z}}_{j} - {{\varvec{\upnu}}}_{k} {\mathbf{x}}_{j} \le 0,\quad \,j = 1, \ldots ,n, \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & {\mathbf{u}}_{k} {\mathbf{y}}_{j} - {\mathbf{w}}_{k} {\mathbf{z}}_{j} \le 0,\quad \,j = 1, \ldots ,n, \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & {\mathbf{u}}_{k} \ge {\mathbf{0}}_{s} , \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & {{\varvec{\upnu}}}_{k} \ge {\mathbf{0}}_{m} , \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & {\mathbf{w}}_{k} \ge {\mathbf{0}}_{h} . \\ \end{aligned} $$
(3)

where the weight wg corresponds to the intermediate measure \({\mathbf{z}}_{g}\). Note that the second set of constraints is redundant as it is obtained from the third and fourth set of constraints. Thus, it can be removed. The efficiency of the whole system and its stages can be calculated based on the optimal solution of model (3):

$$ \begin{aligned} & \theta_{kk}^{*} = \,\frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{k} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{k} }}\,,\quad j = 1,...,n, \\ & \theta_{kk}^{*(1)} = \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{k} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{k} }}\,,\quad j = 1,...,n, \\ & \theta_{kk}^{*(2)} = \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{k} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{k} }}\,,\quad j = 1,...,n.\, \\ \end{aligned} $$
(4)

Note that the efficiency of whole system is expressed as multiplication of efficiencies of two stages:

$$ \theta_{kk}^{*(1)} \times \theta_{kk}^{*(2)} = \,\,\frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{k} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{k} }} \times \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{k} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{k} }}\, = \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{k} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{k} }}\,\, = \theta_{kk}^{*} $$
(5)

where (\({\mathbf{w}}_{k}^{*T} ,\,{\mathbf{u}}_{k}^{*T} ,\,{{\varvec{\upnu}}}_{k}^{*T}\)) is the optimum solution of model (3), where DMUk is the DMU under evaluation.

A PPS in a two-stage network is introduced. PPS is defined as a set of inputs and outputs in a technology that the non-negative inputs can generate non-negative outputs. PPS in a two-stage network is presented as follows:

$$ {\mathcal{T}}_{TS - NDEA} = \{ ({\mathbf{x}},{\mathbf{y}})|\,\,({\mathbf{x}},{\mathbf{z}}) \in P_{1} ,\,({\mathbf{z}},{\mathbf{y}}) \in P_{2} \,\} $$
(6)

where P1 and P2 are the PPS of the first and the second stage of a two-stage network. In fact, \({\mathbf{x}}\) can produce \({\mathbf{z}}\) in the first stage and \({\mathbf{z}}\), in turn, can produce \({\mathbf{y}}\) in the second stage. To get a better understanding of the role of intermediate inputs and outputs in PPS of a two-stage network, the \({\mathbf{z}}\) is decomposed into intermediate outputs \({\mathbf{z}}^{out}\) in the first stage and intermediate inputs \({\mathbf{z}}^{int}\) in the second stage. \({\mathcal{T}}_{TS - NDEA}\) can be represented as follows:

$$ {\mathcal{T}}_{TS - NDEA} = \{ ({\mathbf{x}},{\mathbf{z}}^{out} ,{\mathbf{z}}^{int} ,{\mathbf{y}})|\,\,({\mathbf{x}},{\mathbf{z}}^{out} ) \in P_{1} ,\,({\mathbf{z}}^{int} ,{\mathbf{y}}) \in P_{2} \,,{\mathbf{z}}^{int} \le {\mathbf{z}}^{out} \} $$
(7)

In a two-stage network, \({\mathbf{z}}^{int}\) has to be less than or equal to \({\mathbf{z}}^{out}\). This is indicated in Expression (7) by the constraint \({\mathbf{z}}^{int} \le {\mathbf{z}}^{out}\).

3 Proposed model

3.1 Decomposition of cross-efficiency in a two-stage network

Note that the cross-efficiency method has two phases in the back-box approach. In the first phase, a unique optimum solution is obtained by the traditional DEA models. In the second phase, the cross-efficiency score is calculated by Expression (2). Similarly, these phases are used to calculate the cross-efficiency scores in a two-stage network. Kao and Liu (2019) defined a geometric mean of cross-efficiencies as a cross-efficiency score in a two-stage network. They presented a multiplicative relationship between the overall and stage cross-efficiency scores by defining the geometric mean. However, their definition faces problem if cross-efficiencies are small. To tackle the problem, we extend Doyle and Green's (1994) definition of cross-efficiency in a two-stage network.

Definition 1

(peer evaluation in two-stage NDEA) To calculate the cross-efficiency of \(DMU_{j}\) from the viewpoint of \(DMU_{k}\), the following expression is used:

$$ \begin{aligned} \theta_{kj}^{*(1)} = & \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{j} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{j} }},\quad j = 1,...,n, \\ \theta_{kj}^{*(2)} = & \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{j} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{j} }},\quad j = 1,...,n, \\ \theta_{kj}^{*} = & \,\frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{j} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{j} }},\quad j = 1,...,n. \\ \end{aligned} $$
(8)

Definition 2

(cross-efficiency scores by the arithmetic mean in two-stage NDEA) Consider the overall and stage cross-efficiency scores of \(DMU_{j}\) in a two-stage network:

$$ \begin{aligned} & \theta_{j}^{*} = \,\frac{1}{n}\,\,\sum\limits_{k = 1}^{n} {\theta_{kj}^{*} } ,\quad j = 1,...,n, \\ & \theta_{j}^{*(1)} = \,\,\frac{1}{n}\,\,\sum\limits_{k = 1}^{n} {\theta_{kj}^{*(1)} } ,\quad j = 1,...,n, \\ & \theta_{j}^{*(2)} = \,\frac{1}{n}\,\,\sum\limits_{k = 1}^{n} {\theta_{kj}^{*(2)} } ,\quad j = 1,...,n.\, \\ \end{aligned} $$
(9)

The overall and stage cross-efficiencies matrix in a two-stage network are represented in Figs. 2, 3, and 4.

Fig. 2
figure 2

Cross-efficiency matrix of stage 1

Full size image
Fig. 3
figure 3

Cross-efficiency matrix of stage 2

Full size image
Fig. 4
figure 4

The overall cross-efficiency matrix

Full size image

Note that the main diagonal elements in the matrix of overall and stage cross-efficiencies are the overall and stage efficiency scores.

Corollary 1

  1. a.

    The cross-efficiency of the DMUj from the viewpoint of the DMUk is the multiplication of the stage cross-efficiencies:

    $$ \theta_{kj}^{*(1)} \times \theta_{kj}^{*(2)} = \theta_{kj}^{*} ,\,\,\,\,\,j = 1,...,n. $$
    (10)
  2. b.

    The multiplicative relationship between the overall and stage cross-efficiency scores by Expression (9) in a two-stage network does not necessarily hold.

  3. c.

    Only the multiplicative relationship between the overall and stage cross-efficiency scores by Expression (9) in a two-stage network holds if one of the stage cross-efficiency scores equals 1.

Proof

  1. a.

    \(\theta_{kj}^{*(1)} \times \theta_{kj}^{*(2)} = \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{j} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{j} }}\, \times \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{j} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{j} }}\, = \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{j} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{j} }} = \theta_{kj}^{*} ,\,\,\,\,\,j = 1,...,n.\)

  2. b.

    \(\begin{aligned} \theta_{j}^{*(1)} \times \theta_{j}^{*(2)} = & \,\,\frac{1}{n}\,\,\sum\limits_{k = 1}^{n} {\theta_{kj}^{*(1)} } \times \frac{1}{n}\,\,\sum\limits_{k = 1}^{n} {\theta_{kj}^{*(2)} } = \frac{1}{{n^{2} }}\sum\limits_{k = 1}^{n} {\sum\limits_{l = 1}^{n} {\theta_{kj}^{*(1)} \times \theta_{lj}^{*(2)} } } \\ \ne & \frac{1}{n}\,\,\sum\limits_{k = 1}^{n} {\theta_{kj}^{*(1)} } \times \theta_{kj}^{*(2)} = \,\frac{1}{n}\,\,\sum\limits_{k = 1}^{n} {\theta_{kj}^{*} } = \theta_{j}^{*} ,\,\,\,\,\,\,\,\,\,\, \\ \Rightarrow & \theta_{j}^{*(1)} \times \theta_{j}^{*(2)} \ne \theta_{j}^{*} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,j = 1,...,n.\, \\ \end{aligned}\)

  3. c.

    Assume that the stage cross-efficiency of the second stage is 1; i.e.,

\(\theta_{j}^{*(2)} = \,\frac{1}{n}\,\,\sum\limits_{k = 1}^{n} {\theta_{kj}^{*(2)} } = 1\). Therefore, for each k, \(\theta_{kj}^{*(2)} = 1\). Thus, we have \(\theta_{j}^{*(1)} \times \theta_{j}^{*(2)} = \,\frac{1}{n}\,\sum\nolimits_{k = 1}^{n} {\theta_{kj}^{*(1)} } \times 1 = \frac{1}{n}\,\sum\nolimits_{k = 1}^{n} {\theta_{kj}^{*(1)} } = \frac{1}{n}\,\sum\nolimits_{k = 1}^{n} {\theta_{kj}^{*(1)} \times \theta_{kj}^{*(2)} } = \,\frac{1}{n}\,\sum\nolimits_{k = 1}^{n} {\theta_{kj}^{*} = \theta_{j}^{*} } .\) Hence, \(\theta_{j}^{*(1)} \times \theta_{j}^{*(2)} = \theta_{j}^{*} ,\,\,j = 1,...,n.\,\)

Likewise, if the cross-efficiency score of the first stage is 1, the same outcome is achieved.

As mentioned in the second part of corollary 1 and given Definition 2, there is no multiplicative relationship between the overall and stage cross-efficiency scores. To address this issue, the definition of Kao and Liu (2019) is used. They show that if the arithmetic mean is replaced by the geometric mean, the overall cross-efficiency score can be decomposed to the multiplication of the stage cross-efficiency scores.

Definition 3

(cross-efficiency scores by geometric mean in a two-stage network). Consider the overall and stage cross-efficiency scores of the \(DMU_{j}\) in a two-stage DEA model as follows:

$$ \begin{aligned} & E_{j}^{*} = \sqrt[n]{{\prod\limits_{k = 1}^{n} {\theta_{kj}^{*} } }}\,,\quad j = 1,...,n, \\ & E_{j}^{*(1)} = \,\sqrt[n]{{\prod\limits_{k = 1}^{n} {\theta_{kj}^{*(1)} } }}\,,\quad j = 1,...,n, \\ & E_{j}^{*(2)} = \,\sqrt[n]{{\prod\limits_{k = 1}^{n} {\theta_{kj}^{*(2)} } }}\,,\quad j = 1,...,n.\, \\ \end{aligned} $$
(11)

Theorem 1

If the overall and stage cross-efficiency scores are derived from Expression (11), then there is a multiplicative relationship between the overall and stage cross-efficiency scores such that:

$$ E_{j}^{*(1)} \times E_{j}^{*(2)} = E_{j}^{*} ,\,\,\,\,\,j = 1,...,n. $$
(12)

Proof

Suppose that the scores of the overall and stage cross-efficiency are obtained from Expression (11). Thus, we have.

$$ E_{j}^{*(1)} \times E_{j}^{*(2)} = \sqrt[n]{{\prod\limits_{k = 1}^{n} {\theta_{kj}^{*(1)} } }} \times \sqrt[n]{{\prod\limits_{k = 1}^{n} {\theta_{kj}^{*(2)} } }}\, = \sqrt[n]{{\prod\limits_{k = 1}^{n} {\theta_{kj}^{*(1)} } \times \prod\limits_{k = 1}^{n} {\theta_{kj}^{*(2)} } }} = \sqrt[n]{{\prod\limits_{k = 1}^{n} {(\theta_{kj}^{*(1)} } \times \theta_{kj}^{*(2)} )}} $$

Hence,

\(\Rightarrow E_{j}^{*(1)} \times E_{j}^{*(2)} = \sqrt[n]{{\prod\limits_{k = 1}^{n} {(\theta_{kj}^{*(1)} } \times \theta_{kj}^{*(2)} )}}\).

On the other hand, according to Expression (10), we have.

\(E_{j}^{*(1)} \times E_{j}^{*(2)} = \sqrt[n]{{\prod\limits_{k = 1}^{n} {(\theta_{kj}^{*(1)} } \times \theta_{kj}^{*(2)} )}} = \sqrt[n]{{\prod\limits_{k = 1}^{n} {\theta_{kj}^{*} } }} = E_{j}^{*}\). As a result, \(E_{j}^{*(1)} \times E_{j}^{*(2)} = E_{j}^{*} ,\,\,\,\,\,j = 1,...,n.\)

Therefore, the proof is completed.\(\hfill\square\)

Theorem 1 shows that the overall cross-efficiency scores can be decomposed as product of the stage cross-efficiency scores. Due to the existence of multiple optimal solutions of model (3) in relations (10) and (12), the decompositions for cross-efficiency scores are not unique. To tackle this problem, we use secondary goals such as benevolent or aggressive approach.

Remark 1

The index which defines the cross-efficiency score should be well defined in ranking all units. Equation (11), defined by Kao and Liu (2019), fails to evaluate all units because if the cross-efficiencies \(\theta_{kj}^{*(1)}\) and \(\theta_{kj}^{*(2)}\) take small values. Then due to the existence of a multiplication relation between them, the values of \(E_{j}^{*(1)}\), \(E_{j}^{*(2)}\) and \(E_{j}^{*}\) will be numerically insignificant such that in computational programs it is assumed to be 0. Therefore, Eq. (11) cannot be a good indicator to determine the amount of cross-efficiency scores. To address this issue, it is obvious that Eq. (9) offers a good definition to measure the stages and the overall efficiency scores as it prevents a zero cross-efficiency score.

Since in model (3), it is possible to have alternative optimal solutions, the cross-efficiency cannot be readily obtained for a two-stage network. To overcome this issue, we introduce a new benevolent approach based on the idea of Rödder and Reucher (2011). To this end, the following model is proposed for the first stage.

$$ \begin{array}{*{20}l} {\mathop {\min }\limits_{{{\mathbf{u}}_{k} ,\,{{\varvec{\upnu}}}_{k} ,\,{\mathbf{w}}_{k} ,{\mathbf{s}}_{j}^{1} ,\,{\mathbf{s}}_{j}^{2} }} } \hfill & {\sum\limits_{j} {{\mathbf{s}}_{j}^{1} } + \sum\limits_{j} {{\mathbf{s}}_{j}^{2} } } \hfill \\ {s.t.} \hfill & {{{\varvec{\upnu}}}_{k} {\mathbf{x}}_{k} = 1,} \hfill \\ {} \hfill & {{\mathbf{u}}_{k} {\mathbf{y}}_{k} = \theta_{kk}^{*} ,{\mathbf{w}}_{k} {\mathbf{z}}_{k} = \theta_{kk}^{*(1)} ,\theta_{kk}^{*(2)} {\mathbf{w}}_{k} {\mathbf{z}}_{k} - {\mathbf{u}}_{k} {\mathbf{y}}_{k} = 0,} \hfill \\ {} \hfill & {{\mathbf{w}}_{k} {\mathbf{z}}_{j} - {{\varvec{\upnu}}}_{k} {\mathbf{x}}_{j} + {\mathbf{s}}_{j}^{1} \ge 0,\,\,\,\,j = 1, \ldots ,n,} \hfill \\ {} \hfill & {{\mathbf{u}}_{k} {\mathbf{y}}_{j} - \,{\mathbf{w}}_{k} {\mathbf{z}}_{j} + {\mathbf{s}}_{j}^{2} \ge 0,\quad \,j = 1, \ldots ,n,} \hfill \\ {} \hfill & {{\mathbf{w}}_{k} {\mathbf{z}}_{j} - {{\varvec{\upnu}}}_{k} {\mathbf{x}}_{j} \le 0,\,\,\,\,j = 1, \ldots ,n,} \hfill \\ {} \hfill & {{\mathbf{u}}_{k} {\mathbf{y}}_{j} - \,{\mathbf{w}}_{k} {\mathbf{z}}_{j} \le 0,\quad \,j = 1, \ldots ,n,} \hfill \\ {} \hfill & {{\mathbf{u}}_{k} \ge {\mathbf{0}}_{s} ,\,{{\varvec{\upnu}}}_{k} \ge {\mathbf{0}}_{m} ,{\mathbf{w}}_{k} \ge {\mathbf{0}}_{h} ,} \hfill \\ {} \hfill & {{\mathbf{s}}_{j}^{1} ,\,{\mathbf{s}}_{j}^{2} \ge {\mathbf{0}},\,j = 1, \ldots ,n.} \hfill \\ \end{array} $$
(13)

In model (13), the first constraint normalizes the input weights. The second constraint ensures that the overall and the stage efficiency of the DMU under evaluation do not change. In the third and fourth constraints, by adding and minimizing the slacks corresponding to the first and the second stages, the cross-efficiency score of the units approximates to one as closely as possible. Unequal constraints are used to guarantee feasible weights in the first and the second stages. In other words, we reduce the slack as much as possible, which implies that the weights are benevolent to the units under evaluation. The fifth and sixth constraints prevent the cross-efficiency of the first and second stages to be more than one. Model (13) selects a solution out of the alternative optimal solutions to maximize the cross-efficiencies of the first and the second stages. Therefore, the overall and the stage cross-efficiency of the jth DMU from the perspective of the kth DMU, based on the benevolent approach, can be calculated by Expression (8), where (\({\mathbf{w}}_{k}^{*T} ,\,{\mathbf{u}}_{k}^{*T} ,{{\varvec{\upnu}}}_{k}^{*T}\)) is the vector of the unique optimum solution of model (13) when DMUk is under evaluation. In the second phase, the overall and the stage cross-efficiency scores of the \(j^{th}\) DMU, based on the benevolent approach, can be computed by Expression (9).

Remark 2

The existing models calculate the cross-efficiency scores using the secondary goal as Model (3) has often multiple optimal solutions. Hence, secondary goals are developed to choose a solution among multiple optimal solutions.

3.2 Setting targets to improve cross-efficiency in a two-stage network

We propose two methods for setting inputs and outputs targets to improve the cross-efficiency score in PPS in a two-stage network. First, to improve the cross-efficiency score in a two-stage network, the outputs of the second stage should be increased and the inputs of the first stage should be reduced. The intermediate measures are unchanged.

Suppose that DMUk is an inefficient DMU, where \({\mathbf{w}}_{k}^{*} ,\,{\mathbf{u}}_{k}^{*} ,{{\varvec{\upnu}}}_{k}^{*}\) are optimal weights of model (13). From the kth DMU aspect, suppose that the cross-efficiency of DMUl concerning the first and second stages is less than 1. Then, we have \(\,{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} - {{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l} < 0\) and \({\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l} - \,{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} < 0\). To improve the cross-efficiency of the lth DMU from the kth DMU perspective, the inputs and outputs are reduced and increased as follows: \(\,{\mathbf{x^{\prime}}}_{l} = {\mathbf{x}}_{l} \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l} }}\) and \({\mathbf{y^{\prime}}}_{l} = {\mathbf{y}}_{l} \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l} }}\,\,\), respectively. Therefore, if the inputs of the first stage are decreased and the outputs of the second stage are increased (intermediate measures remain unchanged), the cross-efficiency of the inefficient stage is given by \(\frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x^{\prime}}}_{l} }} = 1\,\,\) and \(\frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y^{\prime}}}_{l} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }} = 1\). However, such a reduction and increase in the inputs and outputs are not necessarily within the PPS. Thus, the overall and stage cross-efficiency scores do not always become one. To improve the cross-efficiency of the stages in the PPS, the following model is presented:

$$ \begin{array}{*{20}l} {r_{l}^{*} = } \hfill & {\mathop {\min }\limits_{{p_{l} ,\,q_{l} ,\,{\uplambda},\,{{\varvec{\upmu}}}}} \,\,\,\,\,\,\,p_{l} \, - \,q_{l} } \hfill \\ {s.t.} \hfill & {{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} - \,\,{{\varvec{\upnu}}}_{k}^{*} p_{l} {\mathbf{x}}_{l} \,\, \le 0,} \hfill \\ {} \hfill & {p_{l} {\mathbf{x}}_{l} - {\mathbf{X }\uplambda} \ge {\mathbf{0}}_{m} ,} \hfill \\ {} \hfill & {{\mathbf{z}}_{l} - {\mathbf{Z}\uplambda} \le {\mathbf{0}}_{h} ,} \hfill \\ {} \hfill & {{\mathbf{u}}_{k}^{*} q_{l} {\mathbf{y}}_{l} \,\, - \,\,{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} \, \le 0,} \hfill \\ {} \hfill & {q_{l} {\mathbf{y}}_{l} - {\mathbf{Y}}{\varvec{\upmu}} \le {\mathbf{0}}_{s} ,} \hfill \\ {} \hfill & {{\mathbf{z}}_{l} - {\mathbf{Z}}{\varvec{\upmu}} \ge {\mathbf{0}}_{h} ,} \hfill \\ {} \hfill & {p_{l} \le 1,\,q_{l} \ge 1,\,{{\varvec{\uplambda}}},{{\varvec{\upmu}}}\, \ge {\mathbf{0}}_{n} .} \hfill \\ \end{array} $$
(14)

Where \(\left( {{\mathbf{w}}_{k}^{*} ,\,{\mathbf{u}}_{k}^{*} ,{{\varvec{\upnu}}}_{k}^{*} } \right)\) is the optimal weights of model (13) when DMUk is under evaluation. Here, \(p_{l}\). and \(q_{l}\) are the reducing variables from the first stage of the inputs and the increasing variables from the second stage of the outputs of DMUl, respectively. The first constraint seeks to enhance the cross-efficiency score of the DMUl from the viewpoint of DMUk. Given the objective function of model (14), this is done by reducing the inputs of the first stage of DMUl. The second and third constraints guarantee that the inputs of the first stage of the lth DMU are decreased within the PPS of the first stage. The fourth constraint seekso enhance the cross-efficiency of DMUl from the DMUk perspective in the second stage by increasing the output of DMUl. The last two constraints seek to enhance the second stage’s outputs of the lth DMU within the PPS of the second stage.

In Model (14), our goal is to reduce the radial inputs and increase the radial outputs to improve the overall and the stages cross-efficiencies. The radial decrease of the inputs is done by the contraction coefficient \(p_{l}\) and the radial increase of the outputs is carried out by the expansion coefficient \(q_{l}\) such that the weights and activities are feasible. In fact, model (14) is a combination of multiplier and envelopment models.

Remark 3

Assuming \(p_{l} \, = q_{l} = 1\), \({{\varvec{\uplambda}}} = {{\varvec{\upmu}}}\, = (0_{1} ,0_{2} ,...,1_{l} ,...,0_{n} )\), solution \((p_{l} \,,q_{l} ,{{\varvec{\uplambda}}},{{\varvec{\upmu}}})\) is satisfied in the constraints of model (14). Therefore, model (14) is feasible. According to model (14), we have \(p_{l} \le 1\), \(q_{l} \ge 1\) and \(r_{l}^{*} = \,\min \,\,\,p_{l} \, - \,q_{l}\). Hence, \(r_{l}^{*} \le 0\). Also, it is bounded because \(0 \le p_{l} \le 1\). According to the fourth constraint of model (14), we have \(q_{l} \le \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l} }}\). Therefore, \(- \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l} }} \le p_{l} \, - \,q_{l}\). As a result, model (14) is bounded.

Suppose \(p_{j}^{*}\) and \(q_{j}^{*}\) are the optimal solutions of model (14). By augmenting the outputs and reducing the inputs at the same time, the cross-efficiency of the stages and the overall cross-efficiency are improved as follows:

$$ \begin{aligned} & \theta_{kj}^{*(1)} = \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{j} }}{{{{\varvec{\upnu}}}_{k}^{*} p_{j}^{*} {\mathbf{x}}_{j} }}\,,\quad j = 1,...,n, \\ & \theta_{kj}^{*(2)} = \frac{{{\mathbf{u}}_{k}^{*} q_{j}^{*} {\mathbf{y}}_{j} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{j} }}\,,\quad j = 1,...,n, \\ & \theta_{kj}^{*} = \,\frac{{{\mathbf{u}}_{k}^{*} q_{j}^{*} {\mathbf{y}}_{j} }}{{{{\varvec{\upnu}}}_{k}^{*} p_{j}^{*} {\mathbf{x}}_{j} }}\,,\quad j = 1,...,n. \\ \end{aligned} $$
(15)

If, in model (3), DMUk is overall inefficient, then it can improve its performance. In Theorem 2, we show that the efficiency of the remaining DMUs and their stage are not worsened. To this end, see the following model:

$$ \begin{array}{*{20}l} {r_{l}^{c*} } \hfill & { = \mathop {\min }\limits_{{p_{l}^{c} ,\,q_{l}^{c} ,\,{{{\uplambda}}},\,{{\varvec{\upmu}}}}} p_{l}^{c} \, - \,q_{l}^{c} } \hfill \\ {s.t.\,} \hfill & {{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} - \,\,{{\varvec{\upnu}}}_{k}^{*} p_{l}^{c} {\mathbf{x}}{}_{l}^{d} \,\, \le 0,} \hfill \\ {} \hfill & {p_{l}^{c} {\mathbf{x}}{}_{l}^{d} - {\mathbf{ X} \uplambda} \ge {\mathbf{0}}_{m} ,} \hfill \\ {} \hfill & {{\mathbf{z}}_{l} - {\mathbf{Z} \uplambda} \le {\mathbf{0}}_{h} ,} \hfill \\ {} \hfill & {{\mathbf{u}}_{k}^{*} q_{l}^{c} {\mathbf{y}}_{l}^{i} \,\, - \,\,{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} \, \le 0,} \hfill \\ {} \hfill & {q_{l}^{c} {\mathbf{y}}_{l}^{i} - {\mathbf{Y}}{\varvec{\upmu}} \le {\mathbf{0}}_{s} ,} \hfill \\ {} \hfill & {{\mathbf{z}}_{l} - {\mathbf{Z}}{\varvec{\upmu}} \ge {\mathbf{0}}_{h} ,} \hfill \\ {} \hfill & {p_{l}^{c} \le 1,\,q_{l}^{c} \ge 1,\,\,{{\varvec{\uplambda}}},{{\varvec{\upmu}}}\, \ge {\mathbf{0}}_{n} .} \hfill \\ \end{array} $$
(16)

First, solve model (13) for peer k and determine the optimal solution (\({\mathbf{w}}_{k}^{*} ,\,{\mathbf{u}}_{k}^{*} ,{{\varvec{\upnu}}}_{k}^{*}\)). Now, put \({\mathbf{x}}_{k}^{d} = \theta_{kk}^{*(1)} {\mathbf{x}}_{k}\), \({\mathbf{y}}_{k}^{i} = \frac{{{\mathbf{y}}_{k} }}{{\theta_{kk}^{*(2)} }}\), and consider \({\mathbf{x}}_{j}^{d} = {\mathbf{x}}_{j} ,\,{\mathbf{y}}_{j}^{i} = {\mathbf{y}}_{j}\) for \(j \ne k\) and solve model (16). This concludes the following theorem.

Theorem 2

Suppose that \(r_{l}^{c*}\) and \(r_{l}^{*}\) are the optimal objective functions of models (16) and (14), respectively. We have \(r_{l}^{c*} \le r_{l}^{*}\). As a result, the cross-efficiency of DMUj with respect to the DMUk will not become worse.

Proof

Note that a feasible solution of model (14) is also feasible for model (16), when \({\mathbf{x}}_{k}^{d} = \theta_{kk}^{*(1)} {\mathbf{x}}_{k}\), \({\mathbf{y}}_{k}^{i} = \frac{{{\mathbf{y}}_{k} }}{{\theta_{kk}^{*(2)} }}\), \({\mathbf{x}}_{j}^{d} = {\mathbf{x}}_{j} ,\,{\mathbf{y}}_{j}^{i} = {\mathbf{y}}_{j}\), \(j \ne k\). Therefore, the feasible region of model (14) is a subset of feasible region of model (16). As a result, in the objective function, we have \(r_{l}^{c*} \le r_{l}^{*} \le 0\). Thus,

\(p_{l}^{c*} \le p_{l}^{*}\), \(q_{l}^{c*} \ge q_{l}^{*}\), \(\,p_{l}^{c*} {{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l}^{d} \le p_{l}^{*} {{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l}\), \(q_{l}^{c*} {\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l}^{i} \ge q_{l}^{*} {\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l}\). At the end:

$$ \begin{gathered} \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}{{p_{l}^{c*} {{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l}^{d} }} \ge \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}{{p_{l}^{*} {{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l} }}, \hfill \\ \frac{{q_{l}^{c*} {\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l}^{i} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }} \ge \frac{{q_{l}^{*} {\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}, \hfill \\ \frac{{q_{l}^{c*} {\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l}^{i} }}{{p_{l}^{c*} {{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l}^{d} }} \ge \frac{{q_{l}^{*} {\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l} }}{{p_{l}^{*} {{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l} }}. \hfill \\ \end{gathered} $$

The proof is complete.\(\hfill\square\)

Theorem 2 implies that the overall and stage cross-efficiency improvement of DMUl in the weight system of peer k do not suffer from k’s radial input reduction and k’s radial output increase. In the second method, instead of reducing and increasing the inputs and outputs at the same time, the inputs and outputs are simultaneously changed within the PPS. This leads to improved cross-efficiency of stages and overall cross-efficiency. The model is expressed as follows:

$$ \begin{array}{*{20}l} {t_{l}^{*} = } \hfill & {\mathop {\min }\limits_{{{\mathbf{x^{\prime}}}_{l} ,\,{\mathbf{y^{\prime}}}_{l} ,\,{{{\uplambda}}},\,{{\varvec{\upmu}}}}} \,\,\,\,\,\,{{\varvec{\upnu}}}_{k}^{*} \,{\mathbf{x^{\prime}}}_{l} \, - {\mathbf{u}}_{k}^{*} \,{\mathbf{y^{\prime}}}_{l} } \hfill \\ {s.t.} \hfill & {{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} - \,\,{{\varvec{\upnu}}}_{k}^{*} \,{\mathbf{x^{\prime}}}_{l} \,\, \le 0,} \hfill \\ {} \hfill & {{\mathbf{x^{\prime}}}_{l} - {\mathbf{ X} \uplambda} \ge {\mathbf{0}}_{m} ,} \hfill \\ {} \hfill & {{\mathbf{z}}_{l} - {\mathbf{ Z} \uplambda} \le {\mathbf{0}}_{h} ,} \hfill \\ {} \hfill & {{\mathbf{u}}_{k}^{*} \,{\mathbf{y^{\prime}}}_{l} - \,\,{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} \,\, \le 0,} \hfill \\ {} \hfill & {{\mathbf{y^{\prime}}}_{l} - {\mathbf{Y}}{\varvec{\upmu}} \le {\mathbf{0}}_{s} ,} \hfill \\ {} \hfill & {{\mathbf{z}}_{l} - {\mathbf{Z}}{\varvec{\upmu}} \ge {\mathbf{0}}_{h} ,} \hfill \\ {} \hfill & {{{\varvec{\uplambda}}},{{\varvec{\upmu}}}\, \ge {\mathbf{0}}_{n} .} \hfill \\ \end{array} $$
(17)

In model (17), by changing the inputs of the first stage, the first constraint ensures that the cross-efficiency of the first stage of DMUl is improved from the DMUk perspective. The second and the third constraints indicate that the change in the inputs of the first stage should lie within the PPS of the first stage. The fourth constraint, by changing the outputs of the second stage, aims to enhance the cross-efficiency of DMUl in the second stage from DMUk perspective. The fifth and sixth constraints ensure that the outputs of the second stage are changed within the PPS of the second stage.

Model (17) seeks to increase the cross-efficiency using a non-radial approach to change the inputs and outputs. By maintaining the weights and feasible activities, this model does not necessarily reduce or increase all the input and output components, respectively, but its strategy is a trade-off between the input and output components to reduce the weighted inputs and increase the weighted outputs. Thus, the cross-efficiency scores of the first and the second stages, and the overall cross-efficiency are increased. Meanwhile, model (17), like model (14), is a combination of multiplier and envelopment models.

In model (17), \({\mathbf{x^{\prime}}}_{l}^{{}} ,\,{\mathbf{y^{\prime}}}_{l}^{{}}\) are vectors of the inputs and outputs, respectively. They imply the amount of decrease in the inputs of the first stage and the amount of increase in the outputs of the second stage of DMUl from DMUk perspective, respectively. Note that in both models (14) and (17), the unit participation weight, \({{\varvec{\uplambda}}}\) and \({{\varvec{\upmu}}}\), correspond to the first stage and the second stage, respectively.

Assume that \({\mathbf{x^{\prime}}}_{l}^{*} ,\,{\mathbf{y^{\prime}}}_{l}^{*}\) are the optimal solutions of model (17). As a result, by changing the outputs and inputs at the same time, the overall and stage cross-efficiencies are improved as follows:

$$ \begin{aligned} \theta_{kl}^{*(1)} = & \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x^{\prime}}}_{l}^{*} }}\,,\,\,\,\,\,l = 1,...,n, \\ \theta_{kl}^{*(2)} = & \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y^{\prime}}}_{l}^{*} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}\,,\,\,\,\,l = 1,...,n, \\ \theta_{kl}^{*} = & \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y^{\prime}}}_{l}^{*} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x^{\prime}}}_{l}^{*} }}\,,\,\,\,\,\,\,\,\,l = 1,...,n. \\ \end{aligned} $$
(18)

The model simultaneously improves the overall and stage cross-efficiencies by reducing the first stage’s inputs and increasing the second stage’s outputs. Note that, when calculating the improved cross-efficiency, the internal inputs and outputs do not change.

Remark 4

Model (17) similar to model (14) is feasible and bounded because if \({\mathbf{x^{\prime}}}_{l} \, = {\mathbf{x}}_{l} \,\), \({\mathbf{y^{\prime}}}_{l} = {\mathbf{y}}_{l}\), \({{\varvec{\uplambda}}} = {{\varvec{\upmu}}}\, = (0_{1} ,0_{2} ,...,1_{l} ,...,0_{n} )\), then it is feasible. It is also bounded. Due to the first and the fourth constraints of model (17), we have \({\mathbf{u}}_{k}^{*} \,{\mathbf{y^{\prime}}}_{l} \le \,{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} \,\,\), \({\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} \le \,{{\varvec{\upnu}}}_{k}^{*} \,{\mathbf{x^{\prime}}}_{l} \,\,\). As a result, \({\mathbf{u}}_{k}^{*} \,{\mathbf{y^{\prime}}}_{l} \le \,{{\varvec{\upnu}}}_{k}^{*} \,{\mathbf{x^{\prime}}}_{l} \,\,\). Therefore, \(t_{l}^{*} \ge 0\). Since the objective function is minimization, model (17) is bounded.

Here, we re-examine the effect of inefficient DMU on the efficiency improvement of other DMUs when we use model (17). In other words, if we just decrease the input of inefficient \(DMU_{k}\) and increase its output at the same time, the efficiency of other DMUs and stages does not decrease. Consider the following model:

$$ \begin{array}{*{20}l} {t_{l}^{c*} = } \hfill & {\mathop {\min }\limits_{{{\mathbf{x}}_{l}^{\prime d} ,\,{\mathbf{y}}_{l}^{\prime i} ,\,{{{\uplambda}}},\,{{\varvec{\upmu}}}}} \,\,\,\,\,\,{{\varvec{\upnu}}}_{k}^{*} \,{\mathbf{x}}_{l}^{\prime d} \, - {\mathbf{u}}_{k}^{*} \,{\mathbf{y}}_{l}^{\prime i} } \hfill \\ {s.t.} \hfill & {{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} - \,\,{{\varvec{\upnu}}}_{k}^{*} \,{\mathbf{x}}_{l}^{\prime } \,\, \le 0,} \hfill \\ {} \hfill & {{\mathbf{x}}_{l}^{\prime d} -\mathbf{ X} \uplambda \ge {\mathbf{0}}_{m} ,} \hfill \\ {} \hfill & {{\mathbf{z}}_{l} - {\mathbf{ Z} \uplambda} \le {\mathbf{0}}_{h} ,} \hfill \\ {} \hfill & {{\mathbf{u}}_{k}^{*} \,{\mathbf{y}}_{l}^{\prime i} - \,\,{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} \,\, \le 0,} \hfill \\ {} \hfill & {{\mathbf{y}}_{l}^{\prime } - {\mathbf{ Y}}\upmu \le {\mathbf{0}}_{s} ,} \hfill \\ {} \hfill & {{\mathbf{z}}_{l} - {\mathbf{ Z}}\upmu \ge {\mathbf{0}}_{h} ,} \hfill \\ {} \hfill & {{{\varvec{\uplambda}}},{{\varvec{\upmu}}}\, \ge {\mathbf{0}}_{n} .} \hfill \\ \end{array} $$
(19)

where \({\mathbf{x^{\prime}}}_{k}^{d} = \theta_{kk}^{*(1)} .{\mathbf{x^{\prime}}}_{k}\), \({\mathbf{y^{\prime}}}_{k}^{i} = \frac{{{\mathbf{y^{\prime}}}_{k} }}{{\theta_{kk}^{*(2)} }}\), \({\mathbf{x^{\prime}}}_{j}^{d} = {\mathbf{x^{\prime}}}_{j} ,\,{\mathbf{y^{\prime}}}_{j}^{i} = {\mathbf{y^{\prime}}}_{j}\), \(j \ne k\) and \(DMU_{k}\) is inefficient.

Theorem 3

Suppose \(({\mathbf{x^{\prime}}}_{l}^{*d} ,{\mathbf{y^{\prime}}}_{l}^{*i} )\) and \(({\mathbf{x^{\prime}}}_{l}^{*} ,{\mathbf{y^{\prime}}}_{l}^{*} )\) are the optimal solutions of models (19) and (17), respectively. Thus, the cross-efficiency of the rest of DMUs and stages from the perspective of \(DMU_{k}\) does not decrease.

Proof

If \({\mathbf{x^{\prime}}}_{k}^{d} = \theta_{kk}^{*(1)} .{\mathbf{x^{\prime}}}_{k}\), \({\mathbf{y^{\prime}}}_{k}^{i} = \frac{{{\mathbf{y^{\prime}}}_{k} }}{{\theta_{kk}^{*(2)} }}\), \({\mathbf{x^{\prime}}}_{j}^{d} = {\mathbf{x^{\prime}}}_{j} ,\,{\mathbf{y^{\prime}}}_{j}^{i} = {\mathbf{y^{\prime}}}_{j}\), \(j \ne k\), then each feasible solution of model (17) is also feasible for model (19). Therefore, \(0 \le t_{l}^{c*} \le t_{l}^{c}\), \({{\varvec{\upnu}}}_{k}^{*} {\mathbf{x^{\prime}}}_{l}^{*d} \le {{\varvec{\upnu}}}_{k}^{*} {\mathbf{x^{\prime}}}_{l}^{*}\), \({\mathbf{u}}_{k}^{*} {\mathbf{y^{\prime}}}_{l}^{*i} \ge {\mathbf{u}}_{k}^{*} {\mathbf{y^{\prime}}}_{l}^{*}\). Because of the constant \({\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l}\), we have.

$$ \begin{aligned} & \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l}^{\prime *d} }} \ge \frac{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l}^{\prime *} }}, \\ & \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l}^{\prime *i} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }} \ge \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{ll}^{\prime *} }}{{{\mathbf{w}}_{k}^{*} {\mathbf{z}}_{l} }}, \\ & \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l}^{\prime *i} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{l}^{\prime *d} }} \ge \frac{{{\mathbf{u}}_{k}^{*} {\mathbf{y}}_{l}^{\prime *} }}{{{{\varvec{\upnu}}}_{k}^{*} {\mathbf{x}}_{ll}^{\prime *} }}. \\ \end{aligned} $$

The proof is complete.\(\hfill\square\)

4 Case study

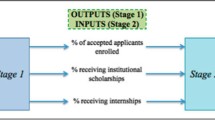
Performance appraisal is an important issue at universities and higher education institutions. DEA has been used extensively for educational purposes, considering departments, colleges, universities, and institutions of higher education as DMUs. NDEA models were also used to evaluate the performance of higher education institutions from different perspectives. For instance, Yadolladi and Matin (2021) evaluated university units by introducing resource allocation models focused on two-stage network systems. Likewise, Hosseini et al. (2019) evaluated the productivity of university units by suggesting a public network model with stochastic data. Ding et al. (2021) also proposed a collective model with a two-stage network structure that evaluated the faculties of some universities in China. Most studies in the performance appraisal literature on the domain of education or research are examined from different perspectives. Twenty branches of the Islamic Azad University for higher education in Iran are examined and their performance is evaluated based on cross-efficiency with a two-stage structure using a new method. The dataset dates back to 2018 and 2019 and was obtained from the Statistics and Information System of Islamic Azad University (www.stat.iau.ir/). Campus branches are made up of different departments. Two offices in campus management are education and research. These parts cooperate in the form of a two-stage network system, which are shown in Fig. 5.

Fig. 5
figure 5

The structure of higher education institutes

Full size image

The inputs, intermediate measures, and outputs are defined in Table 2. Table 3 depicts the dataset.

Table 2 Inputs, intermediate measures, and outputs of higher education institutes
Full size table
Table 3 The dataset
Full size table

Table 4 reports the overall and stage cross-efficiencies derived from models (3) and (13) and Expression (9). As is seen, DMU15 has the best efficiency score of 0.1034 and is ranked first by model (13). However, DMU15 has the overall cross-efficiency score of 0.2193 and the third rank by model (3). As a result, the cross-efficiency in a two-stage network can provide different discrimination between DMUs. Also, in the first stage, DMUs 8, 12, 13, and 14 have the same efficiency score of 1. Therefore, such DMUs cannot be ranked, while these DMUs have the cross-efficiency scores (rank) of 0.5578(8), 0.9353(1), 0.9137(2), and 0.7072(3), respectively. In the second stage, DMUs 5 and 6 have an efficiency score of 1, while these DMUs have the cross-efficiency scores (rank) of 1(1) and 0.5457(2), respectively. Therefore, cross-efficiency has better discrimination power. Note that the overall and stage cross-efficiencies are lower than the overall and stage efficiencies in all DMUs. In addition, more inefficiencies are identified in evaluating DMUs. Also, as is seen in Table 4, the multiplicative relationship between the overall and stage cross-efficiencies does not necessarily hold. For instance, the product of the cross-efficiency of the first and the second stage of DMU3 is 0.6352(0.0836) = 0.0531; whereas the overall cross-efficiency score is 0.0447.

Table 4 The results obtained from Models (3), (13), and Expression (9)
Full size table

Table 5 compares the overall and stage cross-efficiencies derived from model (13) and Expressions (9) and (11). The overall and stage cross-efficiencies obtained from Expression (11) are smaller than the overall and stage cross-efficiencies derived from Expression (9). Also, using Expression (11), there is a multiplicative relationship between the overall and stage cross-efficiencies. For example, the product of the cross-efficiency scores of the first and second stages of DMU3 equals \( 0.592335 \times 0.072089 = 0.042701\); and its overall cross-efficiency score is 0.042701. However, DMUs 7, 17, and 20 cannot be ranked by Expression (11) as the cross-efficiency scores of the first and the second stages are very small.

Table 5 The results obtained from model (13) by expressions (9) and (11)
Full size table

Tables 6 and 7 present the improved overall and stage cross-efficiencies and the measure of changes in inputs and outputs, which are derived from models (14) and (17). As is seen, the improved overall and stage cross-efficiencies obtained from model (17) are higher than models (14) and (13). Also, model (17) increases the overall and stage cross-efficiencies more than model (14). Figures 6, 7, and 8 show the results.

Table 6 Reduction of inputs and enhancement of outputs derived from Model (14)
Full size table
Table 7 Change of inputs and outputs of DMUs from the perspective of DMU1 derived from Model (17)
Full size table
Fig. 6
figure 6

Overall cross-efficiency scores and improvements by Models (13), (14), and (17)

Full size image
Fig. 7
figure 7

Stage 1 cross-efficiency scores and improvements by Models (13), (14), and (17)

Full size image
Fig. 8
figure 8

Stage 2 cross-efficiency scores and improvements by Models (13), (14), and (17)

Full size image

Now, using model (14), assume that we want to improve the overall and stage cross-efficiency of DMU2 from the perspective of DMU1. We only need to reduce the first to the fourth inputs from 178, 1762, 12,277, and 174 to 176.79, 1750.07, 12193.88, and 172.82, respectively. Also, the first and the second outputs are enhanced from 770.7 and 4879 to 1971.25 and 12479.24, respectively. This leads to increased scores for overall and stage cross-efficiency from 0.6266(5), 0.1124(7), and 0.0562(6) to 0.6308(6), 0.2876(13), and 0.1448(9), respectively. Using model (17), assume that we want to improve the overall and stage cross-efficiencies of DMU2 from the perspective of DMU1. It is enough to change the first, the second, the third, and the fourth inputs to 316.79, 1935.7, 23140.15, and 162.71, and change the first and second outputs to 1976.33 and 9910.37, respectively. This leads to increased overall and stage cross-efficiencies 0.7895(11), 0.6192(11), and 0.4264(11). Therefore, model (17) suggests more improvements than model (14). Changes in the inputs and outputs of DMU2 from the perspective of DMU6 are presented in Table 8.

Table 8 Changes in the inputs and outputs of DMUs from the perspective of DMU6 derived from Model (17)
Full size table

Now, the question is how much the cross-efficiency scores of the DMUs change if they are evaluated by black box DEA? As we know, the efficiency scores of the two-stage DEA are lower than the efficiency scores of black box DEA as it considers DMUs with the internal structure. In other words, more inefficient sources are identified in NDEA. Table 9 shows the efficiency scores and cross-efficiency scores obtained from the two-stage DEA and the black box DEA. As is seen, using black-box DEA, \(DMU_{3}\), \(DMU_{5}\), \(DMU_{6}\), \(DMU_{8}\), \(DMU_{9}\), \(DMU_{11}\), \(DMU_{12}\), \(DMU_{13}\), \(DMU_{15}\), \(DMU_{16}\), and \(DMU_{19}\) are efficient and cannot be ranked. Based on the cross-efficiency evaluation, these DMUs received the scores (rank) of 0.9111(5), 0.8935(6), 0.7665(8), 0.6621(9), 0.4747(14), 0.9449(2), 0.9743(1), 0.9344(3), 0.7789(7), and 0.5808(12), respectively. The overall efficiency scores (rank) of these DMUs in the two-stage network are as follows: 0.0558(14), 0.2002(4), 0.2240(2), 0.1481(5), 0.0810(7), 0.0754(10), 0.0556(15), 0.2193(3), 0.2254(1), and 0.0673(12), respectively. The overall cross-efficiency scores (rank) of these DMUs are 0.0447(9), 0.0988(2), 0.0670(4), 0.0425(10), 0.0313(15), 0.0580(5), 0.0467(8), 0.1034(1), 0.0676(3) and 0.0330(14), respectively. Note that, using the cross-efficiency of basic two-stage DEA, the rank of DMU19 is 14, while its rank is first in the black-box CCR method. This is due to the internal structure and the evaluation based on viewpoints of all DMUs. As a result, the cross-efficiency in a two-stage network identifies more inefficient DMUs and provides better discrimination among DMUs. Using the two-stage cross-efficiency model, the cross-efficiency of DMU15 drops to 0.1034. The worst DMU in terms of all methods is DMU17.

Table 9 The efficiency and cross-efficiency scores obtained from two-stage DEA and black box DEA
Full size table

4.1 Managerial implications

Mathematical models provide important information for decision-makers. This paper offers interesting tools for goal setting. The current study helps managers to evaluate DMUs and sub-DMUs irrespective of the influence of the weights. Also, the proposed method recommends improving the performance of DMUs and sub-DMUs by determining the goals for inputs and outputs. In the case study, two approaches are suggested to improve the efficiency of DMUs and sub-DMUs, including (1) decreasing inputs and increasing outputs, simultaneously; (2) Changing the inputs and outputs, simultaneously. If managers wish to further improve the efficiency of DMUs and sub-DMUs, simultaneous change of inputs and outputs produces better results. Our method can evaluate the DMUs that cannot be assessed by Kao and Liu (2019). In addition, in the proposed method, perfect discrimination exists among sub-DMUs.

The cross-efficiency scores of Table 10 are greater or equal to Table 9 (column 2). Also, the changed inputs from the perspective of DMU1 and the improved scores of the cross-efficiency obtained from Rödder and Reucher (2011) are presented in Tables 11. Similarly, all the cross-efficiency scores of Table 11 are higher than Table 9 (column 2). As is seen, the improved cross-efficiency of some DMUs in a two-stage network is bigger than the classic DEA model. For instance, the improved cross-efficiency of DMU5, based on model (17), is 0.9960(1), while it is 0.9777(9) based on Rödder and Reucher (2011). This can be explained by the simultaneous variation of inputs and outputs of a two-stage network. In contrast, in the classical DEA, only the inputs are changed to increase the cross-efficiency scores. In some DMUs, the improved cross-efficiency score of the two-stage network is lower than classical DEA. For instance, using model (17), the improved two-stage cross-efficiency of DMU13, is 0.9814(2) (Table 7), while in the classic DEA it is 0.9987(4). This can be attributed to the presence of intermediate measure, although internal measure remains unchanged.

Table 10 Decrease of inputs, improved cross-efficiency scores, and ranks derived from Rödder and Reucher (2011)
Full size table
Table 11 Change of inputs, improved cross-efficiency scores, and the ranks derived from Rödder and Reucher (2011)
Full size table

5 Discussion and sensitivity analysis

In evaluating the performance of university units, the optimal weights of all units were obtained from different perspectives. In Tables 4, 6, and 7, the overall and stages cross-efficiency scores, their improvements, and their targets for the inputs and final outputs were reported using models (14) and (17). Compared with Tables 3, 6 showed that the radial decrease of inputs and radial increase of final outputs resulted in improvement of the overall and stages cross-efficiency. Furthermore, changing both the inputs and final outputs led to the highest level of improvement in cross-efficiency scores. In a two-stage NDEA, we should not only improve the cross-efficiency, but also the amount of change in the inputs and outputs is important. Target setting of the inputs and outputs should be cost-effective. Although model (17) increases cross-efficiency more than model (14), the change of inputs and outputs is more than model (14). However, dramatic changes of inputs and outputs are so tough for managers. In this paper, targets are set for the inputs and outputs to improve the overall and stages cross-efficiencies of DMUs. According to model (17), by changing the optimal weights from one unit to another, cross-efficiency is improved. The sensitivity analysis of targets for the inputs and outputs can give better insight for managers. To find the least changes of the inputs and outputs and to increase the cross-efficiency from the perspective of optimal weights of DMUs, the following expression is presented:

$$ \begin{gathered} a_{ij}^{k} = \frac{{x_{ij}^{k} }}{{x_{ij} }},\,\,\,k,j = 1,...,n,\,\,i = 1,...,m, \hfill \\ b_{rj}^{k} = \frac{{y_{rj}^{k} }}{{y_{ij} }},\,\,\,k,j = 1,...,n,\,\,r = 1,...,s. \hfill \\ \end{gathered} $$
(20)

In Expression (20), the higher ratio, the more cross-efficiency with fewer changes in inputs and outputs. Therefore, to determine the cost-effectiveness of changes in the inputs and outputs, Expression (20) can be calculated for all DMUs from the perspective of optimal weights of other DMUs. For example, Table 12 shows \(a_{ij}^{k}\) and \(b_{rj}^{k}\) for \(DMU_{1}\) given the optimal weights of all DMUs.

Table 12 Relative changes of inputs and outputs for \(DMU_{1}\) from the perspective of all DMUs derived from Model (17)
Full size table

As is seen in Table 12, the values of \(a_{ij}^{k}\) and \(b_{rj}^{k}\) for \(DMU_{1}\) are the same in terms of the optimal weights of units 1, 8, and 11, and the values are closer to one. Therefore, changing the inputs and final outputs of \(DMU_{1}\) from \((258,4954,18709,233,1480,2420)\) to \((312.6,1910.82,22833.48,160.65,1971.54,9886.37)\) is better than improving the overall and stages cross-efficiency scores by the optimal weights of units, 8, and 11. Also, as is seen in Table 4, the inputs of \(DMU_{1}\). are decreased by factor \(p_{1}^{*} = 0.68\) and the final output is increased by factor \(q_{1}^{*} = 1.33\). In other words, to improve the overall and stages cross-efficiencies, the inputs and outputs of \(DMU_{1}\) are changed from \((258,4954,18709,233,1480,2420)\) to \((174.39,3348.9,12645.75,157.49,1971.54,3223.74)\). Although Model (17), compared to Model (14), takes into account more changes in the inputs and final outputs, the effect of this change can be partially adjusted by a suitable choice of the optimal weights of other DMUs. At this stage, the decision-maker can adopt the necessary strategy to improve the overall and stages cross-efficiency given the goals of the DMUs.

6 Conclusions

The use of cross-efficiency is considered as a form of weight control to avoid unreal weights. This method ranks all DMUs. In many traditional DEA models, the interior structure of DMUs is ignored, and DMUs are treated as black boxes. In this paper, we employed a new benevolent approach in a two-stage cross-efficiency network. It was observed that the overall cross-efficiency scores in a two-stage network are lower than black-box cross-efficiency scores. Also, there was better discrimination among DMUs. In other words, the evaluation of cross-efficiency by considering the internal structure of DMUs has led to further identification of sources of inefficiency of DMUs. At the same time, this helped us to avoid the selection of unrealistic weights in evaluating DMUs with network structures.

By defining the overall and stage cross-efficiency scores based on the geometric mean of overall and stage cross-efficiency of Kao and Liu (2019), we proved that the overall cross-efficiency scores can be decomposed as a multiplicative relationship between the stage cross-efficiency scores. However, Kao and Liu's (2019) definition is not appropriate because some of the overall and stage cross-efficiencies become zero. Therefore, in the two-stage DEA, we proposed a new definition of overall and stage cross-efficiencies.

To improve the overall and stage cross-efficiencies in a two-stage network, two approaches were proposed. Compared with a simultaneous decrease in inputs and increase in outputs, the results showed that the overall and stage cross-efficiencies were improved significantly. Also, it was shown that to improve the cross-efficiency of DMUs, simultaneous output/input change in two-stage network leads to more improvements in cross-efficiency scores of all DMUs. To increase the overall and stage cross-efficiencies, models (14) and (17) do not adopt the same approach. Model (14) follows a radial approach, while model (17) adopts a non-radial and component by component approach to improve cross-efficiency. Each of the models can be used given the real-world situation.

In this paper, the stage and overall cross-efficiency scores were evaluated based on the benevolent method. Including aggressive and neutral approaches can be an interesting research topic. Also, in this study, we assumed that the intermediate measures are fixed. It seems an interesting study to examine the conditions in which the stages efficiency can be improved by changing the intermediate measures. Furthermore, the provided decomposition of overall cross-efficiency score based on the stage scores is straightforward and easy to interpret. The idea of decomposing based on a weighted sum of the stage efficiencies is also another option, which can be considered as an alternative approach. Besides, in this research, assuming CRS, we developed a two-stage cross-efficiency DEA model. Developing a new two-stage cross-efficiency DEA model with VRS assumption will be an interesting topic that can be addressed in future works.