Additive Efficiency Decomposition in Network DEA

Abstract

In conventional data envelopment analysis (DEA), decision making units (DMUs) are generally treated as a black-box in the sense that internal structures are ignored, and the performance of a DMU is assumed to be a function of a set of chosen inputs and outputs. A significant body of work has been directed at problem settings where the DMU is characterized by a multistage process; supply chains and many manufacturing processes take this form. The current chapter presents DEA modeling approaches for network DEA where additive efficiency decompositions are assumed for sub-units/processes/stages. In the additive efficiency decomposition approach, the overall efficiency is expressed as a (weighted) sum of the efficiencies of the individual stages. This approach can be applied under both constant returns to scale (CRS) and variable returns to scale (VRS) assumptions.

Part of this chapter is based upon (i) Chen, Y., Cook, W.D., Li, N. and Zhu, Joe, Additive Efficiency Decomposition in Two-Stage DEA, European Journal of Operational Research, Vol. 196 (2009), 1170–1176 and (ii) Cook, W.D., Zhu, Joe, Yang, F. and Bi, G-B, Network DEA: Additive Efficiency Decomposition, European Journal of Operational Research, Vol. 207, Issue 2 (2010), 1122–1129, with permissions from Elsevier Science.

5.1 Introduction

Data envelopment analysis (DEA) is a tool for measuring the relative efficiency of peer decision making units (DMUs) that have multiple inputs and outputs. In many cases, DMUs may have internal or network structures; see for example, Färe and Grosskopf (1996), Castelli et al. (2004) and Tone and Tsutsui (2009). In the latter case, the authors provide a slacks-based model that captures the overall efficiency of the DMU, and provides, as well, measures for the components (referred to as divisions) or stages that make up the DMU. The overall efficiency is expressed as a weighted average of the component efficiencies, where weights are exogenously imposed to reflect the perceived importance of the components. (see Chap. 11 for detailed discussions.)

Based upon the work of Chen et al. (2009) and Cook et al. (2010), the current chapter focuses on the derivation of a radial measure of efficiency that can be decomposed into a convex combination of radial measures for the individual components that make up the DMU. We note that in these two work, the weights used for individual stage’s efficiency aggregation are variables, and not imposed exogenously.

Chen et al. (2009) present a methodology for representing overall radial efficiency of a DMU as an additive weighted average of the radial efficiencies of the individual stages or components that make up the DMU. While the approach of Chen et al. (2009) can be extended to DMUs that have more than two stages, such an extension requires that the multi-stage processes share the unique feature that all outputs from any stage represent the only inputs to the next stage. In other words, except for the first stage, all other stages do not have their own independent inputs (and/or outputs), that enter (exit) the process at that point. While these closed systems do exist, the more prevalent case is that where each stage is open, that is it has its own inputs (and/or outputs) in addition to the intermediate measures (that exist in-between two stages).

Such open multistage structures are relatively common, particularly in processing industries. Consider, for example, the situation in which a coal mining company wishes to evaluate the efficiency of a set of collieries (mining operations) in a large coal field. Typically, the process of delivering finished products to the customer is multistage in nature. In crude terms, Stage 1 would involve the extraction of the raw or run-of-mine (ROM) coal from underground or open pit coal reserves. At the mine site, the ROM is generally put through a process where screens separate the product into different size categories; e.g. a ‘more than one inch in diameter’ category, and a ‘less than one inch’ category. The resulting ‘size grades’, representing the outputs from this first stage, are then transported to an on-site washing facility, which might be deemed Stage 2. The washing process filters out any material below a certain specific gravity; this portion is unsuitable for sale and is discarded. A portion of the remaining usable coal (outputs from Stage 2) is sold to the open market as a finished product, and at management’s discretion (based on estimates of the demand), the remaining product is sent to Stage 3, the crusher. The crushing process also produces waste or discard, with the remaining material, sometimes referred to as ‘middlings’, being sold or blended with other materials to make such products as briquettes. This latter process might be thought of as Stage 4.

Numerous such examples from processing industries exist. In many cases a portion of the outputs from one stage may be in ‘finished’ form and go to the consumer market, with the remainder being reprocessed at the next stage to get a more pure form of the product. The petrochemical industry, perfume manufacturing and so on, are examples.

It is important to note that the models of Kao and Hwang (2008), Liang et al. (2008) and Chen et al. (2009) concentrate specifically on pure serial processes. Cook et al. (2010) develop linear models for DMUs that have multiple stages, with each stage being open, having its own inputs and outputs. Cook et al. (2010) also obtain an additive efficiency decomposition of the overall efficiency score. The advantage of additive efficiency decomposition is that we can also study performance under assumptions of both constant returns to scale (CRS) and variable returns to scale (VRS).

The current chapter starts with the approach of Chen et al. (2009) where a simple two-stage network process is studies. We then present the work of Cook et al. (2010) where additive efficiency decomposition approach is applied to general network structures. For ease of notation, we begin in Sect. 5.5 by examining open serial systems. We then present a model for measuring the overall radial efficiency of the general serial multi-stage process, and show that this measure can be decomposed into radial measures of efficiency for the components or stages making up the overall process. Section 5.6 then extends this model structure to include more complex multistage processes. Our approach is illustrated in Sect. 5.7 with the supply chain data set in Liang et al. (2006). As well, we re-evaluate the data set provided in Tone and Tsutsui (2009).

5.2 A Two-Stage Network Process: Constant Returns to Scale

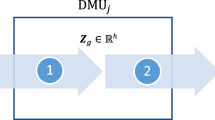
Consider a two-stage process shown in Fig. 5.1. Suppose we have n DMUs, and that each DMU _j (j = 1, 2, …, n) has m inputs to the first stage, x _ij (i = 1, 2, …, m), and D outputs from this stage, z _dj , (d = 1, 2, …, D). These D outputs then become the inputs to the second stage, and are referred to as intermediate measures. The outputs from the second stage are denoted y _rj , (r = 1, 2, …, s). Based upon the CRS model (Charnes et al. 1978), the (CRS) efficiency scores for $DM{U}_{j_o}$ in the first and second stages can be calculated in the following two CRS models (5.1) and (5.2), respectively:

$$ \begin{array}{l}{\theta}_{j_o}^1= \max \frac{{\displaystyle \sum_{d=1}^D{\eta}_d^A{z}_{d{j}_o}}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{i{j}_o}}}\hfill \\ {}\kern0.5em \mathrm{s}.\mathrm{t}.\kern0.5em \frac{{\displaystyle \sum_{d=1}^D{\eta}_d^A{z}_{dj}}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{ij}}}\le 1\kern1em \mathrm{j}=1,\dots, \mathrm{n}\hfill \\ {}\kern2.4em {\eta}_d^A,{v}_i\ge 0\hfill \end{array} $$

(5.1)

$$ \begin{array}{l}{\theta}_j^2= \max \frac{{\displaystyle \sum_{r=1}^s{u}_r{y_{rj}}_o}}{{\displaystyle \sum_{d=1}^D{\eta}_d^B{z_{dj}}_o}}\hfill \\ {}\kern.5em \mathrm{s}.\mathrm{t}.\kern0.5em \frac{{\displaystyle \sum_{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle \sum_{d=1}^D{\eta}_d^B{z}_{dj}}}<1,\kern1em \mathrm{j}=1,\dots, \mathrm{n}\hfill \\ {}\kern2.4em {\eta}_d^B,{u}_r\ge 0\hfill \end{array} $$

(5.2)

The overall CRS efficiency score can be calculated from the following CRS model (5.3)

$$ \begin{array}{l} \max \kern.5em \frac{{\displaystyle \sum_{r=1}^s{u}_r}{y}_{r{j}_o}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{i{j}_o}}}\hfill \\ {}\mathrm{s}.\mathrm{t}.\kern1em \frac{{\displaystyle \sum_{r=1}^s{u}_r}{y}_{rj}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{ij}}}\le 1,\kern1em \mathrm{j}=1,\dots \mathrm{n}\hfill \\ {}\kern2.3em {v}_i,{u}_r\ge 0\hfill \end{array} $$

(5.3)

Fig. 5.1

Two-stage process

In Kao and Hwang’s (2008) and Liang et al. (2008) two-stage network DEA approach, it is required that the input of the second stage to be the expected output of the first stage, i.e., given the inputs to the first stage x _ij , that stage yields the optimal intermediate measure ${\displaystyle \sum_{d=1}^D{\eta}_d^{*}{z}_{dj}}$ which is then used as the (aggregated) input in the second stage. Thus, it is assumed that η ^A _d  = η ^B _d  = η _d , and the overall efficiency of a DMU is given by:

$$ \begin{array}{l}{\theta}_{j_o}= Max\kern.5em \frac{{\displaystyle \sum_{d=1}^D{\eta}_d{z}_{d{j}_o}}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{i{j}_o}}}\bullet \frac{{\displaystyle \sum_{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle \sum_{d=1}^D{\eta}_d{z}_{dj}}}=\frac{{\displaystyle \sum_{r=1}^s{u}_r}{y}_{r{j}_0}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{i{j}_0}}}\hfill \\ {}\kern2.34em s.t.\kern0.9em \frac{{\displaystyle \sum_{d=1}^D{\eta}_d{z}_{dj}}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{ij}}}\le 1,\kern1em \mathrm{j}=1,\dots, \mathrm{n}\hfill \\ {}\kern4.7em \frac{{\displaystyle \sum_{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle \sum_{d=1}^D{\eta}_d{z}_{dj}}}\le 1,\kern1em \mathrm{j}=1,\dots, \mathrm{n}\hfill \\ {}\kern4.8em {v}_i,{u}_r,{\eta}_d\ge 0\hfill \end{array} $$

(5.4)

It can be seen from the objective function of model (5.4) that the overall efficiency is the product of the efficiencies of the two stages, i.e., ${\theta}_{j_0}^1\bullet {\theta}_{j_0}^2=\frac{{\displaystyle \sum_{r=1}^s{u}_o^{*}}{y}_{r{j}_0}}{{\displaystyle \sum_{i=1}^m{v}_o^{*}{x}_{i{j}_0}}}={\theta}_{j_O}$, where ${\theta}_{j_0}^1=\frac{{\displaystyle \sum_{d=1}^D{\eta}_d^{*}{z}_{d{j}_o}}}{{\displaystyle \sum_{i=1}^m{v}_i^{*}{x}_{i{j}_o}}}$ and ${\theta}_{j_0}^2=\frac{{\displaystyle \sum_{r=1}^s{u}_r^{*}{y}_{rj}}}{{\displaystyle \sum_{d=1}^D{\eta}_d^{*}{z}_{dj}}}$ and (*) denotes optimal value from model (5.4).

Note η ^A _d  = η ^B _d is a key and rational assumption in that the value accorded the outputs from the first stage should reasonably be assumed as their value when they assume the additional role as inputs to the second stage. Without this assumption, model (5.4) becomes a non-linear program, as the terms ∑  ^D _d = 1 η ^A _d z _do and ∑  ^D _d = 1 η ^B _d z _do cannot be cancelled in the objective function. Also, without this assumption, solving model (5.4) is equivalent to applying the CRS model to stages 1 and 2 independently, and then taking the geometric mean of the two CCR efficiency scores. Throughout the chapter we therefore maintain the assumption that ∑  ^D _d = 1 η _d z _do is to be the same for the two stages.

In the interest of modeling two-stage processes in a more general way, and specifically to allow for VRS settings, we propose that rather than combine the stages in a multiplicative (geometric) manner as in Kao and Hwang (2008) and Liang et al. (2008), we use a weighted additive (arithmetic mean) approach.

As will be explained below, the multiplicative and additive models are two different, but equally valid ways of aggregating the components of a two-stage process. Thus, we propose to define overall efficiency of the two stage process as

$$ {w}_1\bullet \frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}}+{w}_2\bullet \frac{{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{r{j}_0}}}{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}, $$

(5.5)

Where w ₁ and w ₂ are user-specified weights such that w ₁ + w ₂ = 1. These weights are not optimization variables, but rather are functions of the optimization variables.

We thus propose deriving the overall efficiency of the process by solving the following problem:

$$ \begin{array}{l} Max\left[{w}_1\bullet \frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}}+{w}_2\bullet \frac{{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{r{j}_0}}}{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}\right]\\ {}s.t.\kern0.55em \frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{dj}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{ij}}}\le 1\\ {}\kern1.88em \frac{{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{dj}}}\le 1\\ {}\kern1em {\eta}_d,{u}_r,{v}_i\ge 0,\kern1em j=1,2,\dots, n\end{array} $$

(5.6)

It is observed that model (5.6) cannot be turned into a linear program using the usual Charnes and Cooper (1962) transformation. For example, if we let ${t}_1=\frac{1}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}}$, ${t}_2=\frac{1}{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}$, and set π ¹ _d  = t ₁ • η _d , ω _i  = t ₁ • v _i , μ _r  = t ₂ • u _r , π ² _d  = t ₂ • η _d , then the transformations π ¹ _d  = t ₁ • η _d and π ² _d  = t ₂ • η _d imply a linear relationship between π ¹ _d and π ² _d , namely, ${\pi}_d^1=\frac{{\displaystyle {\sum}_i{\omega}_i{x}_{i{j}_o}}}{{\displaystyle {\sum}_k{\pi}_k^1{z}_{k{j}_o}}}\bullet {\pi}_d^2$. Then, model (5.6) becomes

$$ \begin{array}{l} Max\left[{w}_1\bullet {\displaystyle {\sum}_{d=1}^D{\pi}_d^1{z}_{d{j}_0}}+{w}_2\bullet {\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{r{j}_0}}\right]\\ {}s.t.\kern0.85em {\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{ij}}-{\displaystyle {\sum}_{d=1}^D{\pi}_d^1{z}_{dj}}\ge 0\\ {}\kern2em {\displaystyle {\sum}_{d=1}^D{\pi}_d^2{z}_{dj}}-{\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{rj}}\ge 0\\ {}\kern2em {\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{i{j}_o}=1}\\ {}\kern2em {\displaystyle {\sum}_{d=1}^D{\pi}_d^2{z}_{d{j}_o}}=1\\ {}\kern2em {\pi}_d^1=\frac{{\displaystyle {\sum}_i{\omega}_i\bullet {x}_{i,{j}_0}}}{{\displaystyle {\sum}_k{\pi}_k^1\bullet {z}_{k,{j}_0}}}\bullet {\pi}_d^2\\ {}\kern2em {\pi}_d^1,{\pi}_d^2,{\mu}_r,{\omega}_i\ge 0,\kern1em j=1,2,\dots, n\end{array} $$

(5.7)

which is a non-linear program. We, therefore, seek an alternative way to convert model (5.6) into a linear form, by appropriate choice of the w ₁ and w ₂.

Note that w ₁ and w ₂ are intended to represent the relative importance or contribution of the performances of stages 1 and 2, respectively, to the overall performance of the DMU. One argument is that the ‘size’ of a stage reflects its importance, (as measured by its weight). One reasonable representation of size is the portion of total resources devoted to each stage. Letting ${\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}+{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}$ represent the total size of (amount of resources consumed by) the two-stage process, and ${\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}$ and ${\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}$, the sizes of the stages 1 and 2 respectively, we define

$$ \begin{array}{ll}{w}_1=\frac{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}+{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}\kern1em \mathrm{and}\\{w}_2=\frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}+{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}} \end{array}$$

(5.8)

Then, the objective function of model (5.6) becomes:

$$ \frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}+{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{r{j}_0}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}+{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}} $$

(5.9)

Under the CRS case, model (5.6) becomes

$$ \begin{array}{l} Max\frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}+{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{r{j}_0}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}+{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}\\ {}s.t.\kern0.5em \frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{dj}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{ij}}}\le 1\\ {}\kern1.85em \frac{{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{dj}}}\le 1\\ {}\kern1.85em {\eta}_d,{u}_r,{v}_i\ge 0,\kern1em j=1,2,\dots, n\end{array} $$

(5.10)

Using the Charnes-Cooper transformation, model (5.10) is equivalent to

$$ \begin{array}{l} Max{\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{r{j}_o}}+{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}\\ {}s.t.\kern0.5em {\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{ij}}\le 0\\ {}\kern1.8em {\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}\le 0\\ {}\kern1.8em {\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{i{j}_o}}+{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}=1\\ {}\kern1.8em {\pi}_d,{\mu}_r,{\omega}_i\ge 0,\kern1em j=1,2,\dots, n\end{array} $$

(5.11)

Once we obtain an optimal solution to (5.11), we can calculate efficiency scores for the two individual stages. However, model (5.11) can have alternative optimal solutions. As a result, the decomposition of the overall efficiency defined in (5.5) may not be unique. We here follow Kao and Hwang’s (2008) approach to find a set of multipliers which produces the largest first (or second) stage efficiency score while maintaining the overall efficiency score.

We therefore propose the following procedure. Given the overall efficiency obtained from (5.11) (denoted as θ _o ), we calculate either the first stage’s efficiency (θ ^1 * _j ) or the second stage’s efficiency (θ ^2 * _j ) first, and then derive from that the efficiency of the other stage.

In case the first stage is to be given pre-emptive priority, the following model determines its efficiency (θ ^1 * _o ), while maintaining the overall efficiency score at θ _o calculated from model (5.11).

$$ \begin{array}{l}{\theta}_o^{1*}= Max\frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_o}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_o}}}\\ {}s.t.\kern1.3em \frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{dj}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{ij}}}\le 1\\ {}\kern2.43em \frac{{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{dj}}}\le 1\\ {}\kern2.5em \frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_o}}+{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{r{j}_o}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_o}}+{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_o}}}={\theta}_0\kern2em \\ {}\kern2.5em {\eta}_d,{u}_r,{v}_i\ge 0,\kern1em j=1,2,\dots, n\end{array} $$

(5.12)

or equivalently,

$$ \begin{array}{l}{\theta}_o^{1*}= Max{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}\\ {}s.t.\kern1.2em {\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{ij}}\le 0\\ {}\kern2.5em {\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}\le 0\\ {}\kern2.5em \left(1-{\theta}_o\right){\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}+{\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{r{j}_o}}={\theta}_o\\ {}\kern2.5em {\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{i{j}_o}}=1\\ {}\kern2.5em {\pi}_d,{\mu}_r,{\omega}_i\ge 0,\kern1em j=1,2,\dots, n\end{array} $$

(5.13)

The efficiency for the second stage is then calculated as

$$ {\theta}_o^2=\frac{\theta_o-{w}_1^{*}\cdot {\theta}_o^{1*}}{w_2^{*}} $$

where w ^*₁ and w ^*₂ represent optimal weights obtained from model (5.11) by way of (5.8).

Note that we here use (*) in θ ^1 * _o to indicate that the efficiency of the first stage is given the pre-emptive priority and is optimized first. In this case, the resulting second stage efficiency score is denoted as θ ² _o .

In case the second stage is to be given pre-emptive priority, the following model determines the second stage’s efficiency (θ ^2 * _o ) while maintaining the overall efficiency score at θ _o calculated from model (5.11).

$$ \begin{array}{l}{\theta}_o^{2*}= Max\frac{{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{r{j}_o}}}{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_o}}}\\ {}s.t.\kern1.2em \frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{dj}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{ij}}}\le 1\\ {}\kern2.3em \frac{{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{dj}}}\le 1\\ {}\kern2.3em \frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_o}}+{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{r{j}_o}}}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_o}}+{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_o}}}={\theta}_0\kern2em \\ {}\kern2.4em {\eta}_d,{u}_r,{v}_i\ge 0,\kern1em j=1,2,\dots, n\end{array} $$

(5.14)

Model (5.14) is equivalent to

$$ \begin{array}{l}{\theta}_o^{2*}= Max{\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{r{j}_o}}\\ {}s.t.\kern1.2em {\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{ij}}\le 0\\ {}\kern2.5em {\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}\le 0\\ {}\kern2.5em {\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}+{\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{r{j}_o}}-{\theta}_o{\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{i{j}_o}}={\theta}_o\\ {}\kern2.5em {\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}=1\\ {}\kern2.5em {\pi}_d,{\mu}_r,{\omega}_i\ge 0,\kern1em j=1,2,\dots, n\end{array} $$

(5.15)

and the efficiency for the first stage is calculated as

$$ {\theta}_o^1=\frac{\theta_o-{w}_2^{*}\cdot {\theta}_o^{2*}}{w_1^{*}}. $$

Note that we here use (*) in θ ^2 * _o to indicate that second stage is given pre-emptive priority in terms of its efficiency being optimized first. In this case, the resulting first stage efficiency score is denoted as θ ¹ _o .

Finally, note that if θ ^1 * _o = θ ¹ _o or θ ^2 * _o = θ ² _o , then this indicates that we have a unique efficiency decomposition.

5.3 Two-Stage Network DEA: Variable Returns to Scale

While the discussion in the previous section is based upon the assumption of CRS, the above approach enables us to study the efficiency of two-stage processes under VRS. The VRS efficiency scores for the two stages can be determined by the following VRS models (Banker et al. 1984):

$$ \begin{array}{l} \max {E}_{j_o}^1=\frac{{\displaystyle \sum_{d=1}^D{\eta}_d^A{z}_{d{j}_o}}+{u}^A}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{i{j}_o}}}\hfill \\ {}\kern2.5em \mathrm{s.t.}\kern0.5em \frac{{\displaystyle \sum_{d=1}^D{\eta}_d^A{z}_{dj}}+{u}^A}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{ij}}}\le 1,\kern1em \mathrm{j}=1,\dots, \mathrm{n}\hfill \\ {}\kern4.3em {\eta}_d^A,{v}_i\ge 0\kern1em {u}^A\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign}\hfill \end{array} $$

and

$$ \begin{array}{l} \max {E}_{j_o}^2=\frac{{\displaystyle \sum_{r=1}^s{u}_r{y}_{r{j}_o}}+{u}^B}{{\displaystyle \sum_{d=1}^D{\eta}_d^B{z}_{d{j}_o}}}\hfill \\ {}\kern2.75em \mathrm{s.t.}\ \frac{{\displaystyle \sum_{r=1}^s{u}_r{y}_{rj}}+{u}^B}{{\displaystyle \sum_{d=1}^D{\eta}_d^B{z}_{dj}}}<1,\kern1em \mathrm{j}=1,\dots, \mathrm{n}\hfill \\ {}\kern4.5em {\eta}_d^B,{u}_r\ge 0\kern1em \mathrm{and}\kern1em {u}^B\ \mathrm{free}\ \mathrm{in}\ \mathrm{sign}\hfill \end{array} $$

Note that the approach of Kao and Hwang (2008) and Liang et al. (2008) cannot be extended to the VRS assumption, because ${E}_{j_o}^1\bullet {E}_{j_o}^2$ cannot be converted into a linear form under the condition of η ^A _d  = η ^B _d , due to the free variable u ^A in the numerator of ${E}_{j_o}^1$. On the other hand, using our approach, we have the VRS overall efficiency as using the weights defined under the CRS assumption

$$ \begin{array}{l} Max\frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}+{u}^A+{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{r{j}_0}}+{u}^B}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{i{j}_0}}+{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}\\ {}s.t.\kern0.5em \frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{dj}}+{u}^A}{{\displaystyle {\sum}_{i=1}^m{v}_i{x}_{ij}}}\le 1\\ {}\kern1.8em \frac{{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{rj}}+{u}^B}{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{dj}}}\le 1\\ {}\kern1.8em {\eta}_d,{u}_r,{v}_i\ge 0,\kern1em j=1,2,\dots, n\\ {}\kern1.8em {u}^A,{u}^B,\mathrm{free}\ \mathrm{in}\ \mathrm{sign}\end{array} $$

(5.16)

Note that this is an input-oriented model. If we use output-oriented VRS models, the weights will be defined as ${w}_1=\frac{{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}{{\displaystyle {\sum}_{r=1}^s{u}_r{y}_{r{j}_0}}+{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}$ and ${w}_2=\frac{{\displaystyle {\sum}_{r=1}^s{u}_i{y}_{r{j}_0}}}{{\displaystyle {\sum}_{r=1}^s{u}_i{y}_{r{j}_0}}+{\displaystyle {\sum}_{d=1}^D{\eta}_d{z}_{d{j}_0}}}$.

Model (5.16) is equivalent to the following linear programming program

$$ \begin{array}{l} Max{\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{r{j}_o}}+{u}^1+{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}+{u}^2\\ {}s.t.\kern0.5em {\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{ij}}+{u}^1\le 0\\ {}\kern1.8em {\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}+{u}^2\le 0\\ {}\kern1.8em {\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{i{j}_o}}+{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}=1\\ {}\kern1.8em {\pi}_d,{\mu}_r,{\omega}_i\ge 0,\kern1em j=1,2,\dots, n\\ {}\kern1.8em {u}^1,{u}^2\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign}\end{array} $$

(5.17)

Once we obtain the overall efficiency, models similar to (5.13) and (5.15) can be developed to determine the efficiency of each stage. Specifically, assuming pre-emptive priority for stage 1, the following model determines that stage’s efficiency (E ^1 * _o ), while maintaining the overall efficiency score at E _o calculated from model (5.17).

$$ \begin{array}{l}{E}_o^{1*}= Max{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}+{u}^1}\\ {}\kern0.8em \mathrm{s.t.}\kern0.5em {\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}+{u}^1-{\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{ij}}\le 0\\ {}\kern2.5em {\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{rj}}+{u}^2-{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}\le 0\\ {}\kern2.5em \left(1-{E}_o\right){\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}+{\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{r{j}_o}}+{u}^1+{u}^2={E}_o\\ {}\kern2.4em {\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{i{j}_o}}=1\\ {}\kern2.5em {\pi}_d,{\mu}_r,{\omega}_i\ge 0,\kern1em j=1,2,\dots, n\\ {}\kern2.5em {u}^1,{u}^2\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign}\end{array} $$

(5.18)

Similarly, if stage 2 is to be given pre-emptive priority, the following model determines the efficiency (E ^2 * _j ) for that stage, while maintaining the overall efficiency score at E _o calculated from model (5.17).

$$ \begin{array}{l}{E}_o^{2*}= Max{\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{r{j}_o}}+{u}^2\\ {}\kern0.75em s.t.\kern0.5em {\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}+{u}^1-{\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{ij}}\le 0\\ {}\kern2.5em {\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{rj}}+{u}^2-{\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{dj}}\le 0\\ {}\kern2.5em {\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}+{\displaystyle {\sum}_{r=1}^s{\mu}_r{y}_{r{j}_o}}-{E}_o{\displaystyle {\sum}_{i=1}^m{\omega}_i{x}_{i{j}_o}}+{u}^1+{u}^2={E}_o\\ {}\kern2.5em {\displaystyle {\sum}_{d=1}^D{\pi}_d{z}_{d{j}_o}}=1\\ {}\kern2.5em {\pi}_d,{\mu}_r,{\omega}_i\ge 0,\kern1em j=1,2,\dots, n\\ {}\kern2.5em {u}^1,{u}^2\kern0.5em \mathrm{free}\ \mathrm{in}\ \mathrm{sign}\end{array} $$

(5.19)

Once the efficiency score for one of the stages is calculated using (5.18) or (5.19), the score for the other stage can be derived in the similar manner as in the CRS case.

5.4 Two-Stage Network DEA: Application of Additive Efficiency Decomposition

We here apply the above approach to the 24 Taiwanese non-life insurance companies studied in Kao and Hwang (2008). The two-stage process consists of premium acquisition and profit generation. There are two inputs to the first stage which is characterized by marketing of the insurance and generation of premiums, and two outputs from the second stage which is characterized by investment and generation of profit. The two inputs are operational expenses and insurance expenses, and the outputs are underwriting profit and investment profit. There are also two intermediate measures between the two stages, namely direct written premiums and reinsurance premiums. The data are provided in Table 5.1.

Table 5.1 Data set

The CRS results from models (5.11), (5.13) and (5.15) are reported in Table 5.2. The third column reports the overall CRS efficiency obtained from model (5.11). The optimal weights from model (5.11) for each DMU are reported under columns 4 and 5. The rest of the columns report the efficiency score for each individual stage based upon models (5.13) and (5.15).

Table 5.2 CRS results

It can be seen from Table 5.2 that we have unique efficiency decompositions for all DMUs. This arises from the fact that models (5.13) and (5.15) yield identical efficiency scores for the two stages. (Note that the uniqueness result is only true to this specific data set.)

Since the overall efficiency definition presented herein is different from that assumed by Kao and Hwang (2008), the overall efficiency scores from the two approaches cannot be directly compared. The last three columns of Table 5.3 report the CRS scores based upon Kao and Hwang’s (2008) approach. We, however, note that except for 8 DMUs (7, 8, 11, 13, 14, 17, 21, and 24), our first and second stage’s efficiency scores are identical to those of Kao and Hwang (2008). This indicates that Kao and Hwang’s approach also yields unique efficiency decompositions for the remaining 16 DMUs.

Table 5.3 Ranking of CRS scores

Table 5.3 reports the rankings of the CRS scores based upon our new approach and Kao and Hwang’s (2008). It can be seen they do not yield the same exact ranking. DMUs 9 and 14 show a big ranking difference. In fact, if we apply the average to Kao and Hwang’s (2008) first and second stage scores, a different ranking is obtained. However, the Spearman Rank Correlation coefficient for the rankings in Table 5.3 is 0.971 which is significant at the 0.01 level, indicating an approximately equal ranking based upon the two different approaches. It is also the case that the Pearson Correlation Coefficient for the two sets of raw CRS scores is 98 %.

We next turn to the case of VRS reported in Table 5.4. Two DMUs (5.5 and 5.22) are VRS overall efficient. Also, we have unique VRS efficiency decompositions for all DMUs, as the results obtained from models (5.18) and (5.19) are identical.

Table 5.4 VRS results

Under the standard DEA approach, the scores under the VRS assumption are not less than the ones under CRS assumption. This is true as well for the overall efficiency scores in our models. However, we note that this is not the case for DMUs 1, 12 and 20 for the first stage scores. This may be attributed to the fact that the constraint spaces for (5.13) and (5.18) are not the same, and hence the intermediate scores may not obey the conventional principles.

We finally note that w ₁ and w ₂ as defined in the current chapter, are variables related to the inputs and the intermediate measures. By virtue of the optimization process, it can turn out that either w ₁ = 1 and w ₂ = 0 or w ₁ = 0 and w ₂ = 1 at optimality. To overcome this problem, we can require that w ₁ ≥ α and w ₂ ≥ α in model (5.6), where α is a selected constant and 0 % < α ≤ 50 %. Such additional constraints can also be viewed as user’s preference regarding the relative importance of the two stages. If such additional constraints are need, we can then study the sensitivity of the overall efficiency scores relative to changes in this parameter α.

In the current chapter, however, there is no need to add additional constraints of w ₁ ≥ α and w ₂ ≥ α into models (5.11) and (5.17), because non-zero weights are obtained for both stages. We point out, however, that it is likely that model (5.11) (or model (5.17)) can be infeasible with certain α values. For example, when α = 40 %, model (5.11) is infeasible for DMU22 and when α = 50 %, model (5.11) is infeasible for DMUs 1, 2, 5, 6, 10, 16, 20 and 23. This indicates that the input mixes for these DMUs do not allow such weighting structures.

5.5 General Multi-stage Serial Processes

Consider the P-stage process pictured in Fig. 5.2. We denote the input vector to stage 1 by z _o . The output vectors from stage p (p = 1, …,P) take two forms, namely z ¹ _p and z ² _p . Here, z ¹ _p represents that output that leaves the process at this stage and is not passed on as input to the next stage. The vector z ² _p represents the amount of output that becomes input to the next (p + 1) stage. These types of intermediate measures are called links in Tone and Tsutsui (2009). In addition, there is the provision for new inputs z ³ _p to enter the process at the beginning of stage p + 1. Specifically, when p = 2,3,…, we define

Fig. 5.2

Serial multi-stage DMU

• (i) z ^j1 _pr the rth component (r = 1,.... R _p ) of the R _p -dimensional output vector for DMU j flowing from stage p, that leaves the process at that stage, and is not passed on as an input to stage p + 1.

• (ii) z ^j2 _pk the kth component (k = 1, … S _p ) of the S _p -dimensional output vector for DMU j flowing from stage p, and is passed on as a portion of the inputs to stage p + 1.

• (iii) z ^j3 _pi the ith component (i = 1, … I _p ) of the I _p -dimensional input vector for DMU j at the stage p + 1, that enters the process at the beginning of that stage.

Note that in the last stage P, all the outputs are viewed as z ^j1 _pr , as they leave the process.

We denote the multipliers (weights) for the above factors as

• (i) u _pr is the multiplier for the output component z ^j1 _pr flowing from stage p.

• (ii) η _pk is the multiplier for the output component z ^j2 _pk at stage p, and is as well the multiplier for that same component as it becomes an input to stage p + 1.

• (iii) ν _pi is the multiplier for the input component z ^j3 _pi entering the process at the beginning of stage p + 1.

Thus, when p = 2, 3, …, the efficiency ratio for DMU j (for a given set of multipliers) would be expressed as:

$$ {\theta}_p=\left({\displaystyle \sum_{r=1}^{R_p}{u}_{pr}{z}_{pr}^{j1}+{\displaystyle \sum_{k=1}^{S_p}{\eta}_{pk}{z}_{pk}^{j2}}}\right)/\left({\displaystyle \sum_{k=1}^{S_{p-1}}{\eta}_{p-1k}{z}_{p-1k}^{j2}+{\displaystyle \sum_{i=1}^{I_p}{\nu}_{p-1i}{z}_{p-1i}^{j3}}}\right) $$

(5.20)

Note that there are no outputs flowing into stage 1. The efficiency measure for stage 1 of the process (namely, p = 1), for DMU _j becomes

$$ {\theta}_1=\left({\displaystyle \sum_{r=1}^{R_1}{u}_{1r}{z}_{1r}^{j1}+{\displaystyle \sum_{k=1}^{S_1}{\eta}_{1k}{z}_{1k}^{j2}}}\right)/{\displaystyle \sum_{i=1}^{I_0}{\nu}_{0i}{z}_{0i}^j} $$

(5.21)

where z ^j_0i are the (only) inputs to the first stage represented by the input vector z _o .

We claim that the overall efficiency measure of the multistage process can reasonably be represented as a convex linear combination of the P (stage-level) measures, namely

$\theta ={\displaystyle \sum_{p=1}^P{w}_p{\theta}_p}$ where ${\displaystyle \sum_{p=1}^P{w}_p}=1$.

As in Sect. 5.3, we use ${\displaystyle \sum_{i=1}^{I_0}{\nu}_{0i}{z}_{0i}^j}+{\displaystyle \sum_{p=2}^P\left({\displaystyle \sum_{k=1}^{S_{p-1}}{\eta}_{p-1k}{z}_{p-1k}^{j2}+{\displaystyle \sum_{i=1}^{I_p}{\nu}_{p-1i}{z}_{p-1i}^{j3}}}\right)}$ to represent the total size of or total amount of resources consumed by the entire process, and we define the weight w _p to be the proportion of the total input used at the pth stage. We then have

$$ \begin{array}{c}{w}_1={\displaystyle \sum_{i=1}^{I_0}{\nu}_{0i}{z}_{0i}^j}/\left\{{\displaystyle \sum_{i=1}^{I_0}{\nu}_{0i}{z}_{0i}^j}\right.+\left.{\displaystyle \sum_{p=2}^P\left({\displaystyle \sum_{k=1}^{S_{p-1}}{\eta}_{p-1k}{z}_{p-1k}^{j2}+{\displaystyle \sum_{i=1}^{I_p}{\nu}_{p-1i}{z}_{p-1i}^{j3}}}\right)}\right\},\\ {{w}_{p}}= \left({\displaystyle \sum_{k=1}^{S_{p-1}}{\eta}_{p-1k}{z}_{p-1k}^{j2}+{\displaystyle \sum_{i=1}^{I_p}{\nu}_{p-1i}{z}_{p-1i}^{j3}}}\right)/\left\{{\displaystyle \sum_{i=1}^{I_0}{\nu}_{0i}{z}_{0i}^j}\right.\\ +\left.{\displaystyle \sum_{p=2}^P\left({\displaystyle \sum_{k=1}^{S_{p-1}}{\eta}_{p-1k}{z}_{p-1k}^{j2}+{\displaystyle \sum_{i=1}^{I_p}{\nu}_{p-1i}{z}_{p-1i}^{j3}}}\right)}\right\},p>1\end{array} $$

Thus, we can write the overall efficiency θ in the form

$$ \begin{array}{ll}\theta ={\displaystyle \sum_{p=1}^P\left({\displaystyle \sum_{r=1}^{R_p}{u}_{pr}{z}_{pr}^{j1}+{\displaystyle \sum_{k=1}^{S_p}{\eta}_{pk}{z}_{pk}^{j2}}}\right)}/\left\{{\displaystyle \sum_{i=1}^{I_0}{\nu}_{0i}{z}_{0i}^j}\right.\\+\left.{\displaystyle \sum_{p=2}^P\left({\displaystyle \sum_{k=1}^{S_{p-1}}{\eta}_{p-1k}{z}_{p-1k}^{j2}+{\displaystyle \sum_{i=1}^{I_p}{\nu}_{p-1i}{z}_{p-1i}^{j3}}}\right)}\right\}, \end{array}$$

(5.22)

We then set out to optimize the overall efficiency θ of the multistage process, subject to the restrictions that the individual measures θ _p must not exceed unity, or in the linear programming format, after making the usual Charnes and Cooper transformation,

$$ \begin{array}{l} \max {\displaystyle \sum_{p=1}^P\left({\displaystyle \sum_{r=1}^{R_p}{u}_{pr}{z}_{pr}^{o1}+{\displaystyle \sum_{k=1}^{S_p}{\eta}_{pk}{z}_{pk}^{o2}}}\right)}\hfill \\ {}\mathrm{subject}\kern0.5em \mathrm{to}\hfill \\ {}\kern-.2em \left\{{\displaystyle \sum_{i=1}^{I_0}{\nu}_{0i}{z}_{0i}^o}\right.+\left.{\displaystyle \sum_{p=2}^P\left({\displaystyle \sum_{k=1}^{S_{p-1}}{\eta}_{p-1k}{z}_{p-1k}^{o2}+{\displaystyle \sum_{i=1}^{I_p}{\nu}_{p-1i}{z}_{p-1i}^{o3}}}\right)}\right\}=1\hfill \\ {}\kern-.2em \left({\displaystyle \sum_{r=1}^{R_1}{u}_{1r}{z}_{1r}^{j1}+{\displaystyle \sum_{k=1}^{S_1}{\eta}_{1k}{z}_{1k}^{j2}}}\right)\le {\displaystyle \sum_{i=1}^{I_0}{\nu}_{0i}{z}_{0i}^j}\hfill \\ {}\kern-.3em \left({\displaystyle \sum_{r=1}^{R_p}{u}_{pr}{z}_{pr}^{j1}+{\displaystyle \sum_{k=1}^{S_p}{\eta}_{pk}{z}_{pk}^{j2}}}\right)\le \left({\displaystyle \sum_{k=1}^{S_{p-1}}{\eta}_{p-1k}{z}_{p-1k}^{j2}+{\displaystyle \sum_{i=1}^{I_p}{\nu}_{p-1i}{z}_{p-1i}^{j3}}}\right)\forall j\hfill \\ {}{u}_{pr},{\eta}_{pk},{\nu}_{pi},{\nu}_{0i}\ge 0\hfill \end{array} $$

(5.23)

Note that we should impose the restriction that the overall efficiency scores for each j should not exceed unity, but since these are redundant, this is unnecessary.

Note again that the w _p , as defined above, are variables related to the inputs and the intermediate measures. By virtue of the optimization process, it can turn out that some w _p  = 0 at optimality. To overcome this problem, one can impose bounding restrictions w _p  ≥ β, where β is a selected constant.

5.6 General Multi-stage Processes

In the process discussed in the previous section it is assumed that the components of a DMU are arranged in series as depicted in Fig. 5.2. There, at each stage p, the inputs took one of two forms, namely (1) those that are outputs from the previous stage p-1, and (2) new inputs that enter the process at the start of stage p. On the output side, those (outputs) emanating from stage p take two forms as well, namely (1) those that leave the system as finished ‘products’, and (2) those that are passed on as inputs to the immediate next stage p + 1.

The model presented to handle such strict serial processes is easily adapted to more general network structures. Specifically, the efficiency ratio for an overall process can be expressed as the weighted average of the efficiencies of the individual components. The efficiency of any given component is the ratio of the total output to the total input corresponding to that component. Again, the weight w _p to be applied to any component p is expressed as

$$ {w}_p=\left(\mathrm{component}\ p\;\mathrm{input}\right)/\left(\mathrm{total}\ \mathrm{input}\ \mathrm{across}\ \mathrm{all}\ \mathrm{components}\right). $$

There is no convenient way to represent a network structure that would lend itself to a generic mathematical representation analogous to model (5.23) above. The sequencing of activities and the source of inputs and outputs for any given component will differ from one type of process to another. However, as a simple illustration, consider the following two examples of network structures:

5.6.1 Parallel Processes

Consider the process depicted in Fig. 5.3. Here, an initial input vector z _o enters component 1. Three output vectors exit this component, that is z ¹₁ leaves the process, z ²₁ is passed on as an input to component 2, and z ³₁ as an input to component 3. Additional inputs z ⁴₁ and z ⁵₁ enter components 2 and 3 respectively, from outside the process. Components 2 and 3 have z ¹₂ and z ¹₃ , respectively as output vectors which are passed on as inputs to component 4, where a final output vector z ¹₄ is the result.

Fig. 5.3

Multi-stage DMU with parallel processes

Component Efficiencies

Component 1 efficiency ratio: θ ₁ = (u ₁ z ¹₁  + η ²₁ z ²₁  + η ³₁ z ³₁ )/ν _o z _o

Component 2 efficiency ratio: θ ₂ = η ¹₂ z ¹₂ /(η ²₁ z ²₁  + ν ₁ z ⁴₁ )

Component 3 efficiency ratio: θ ₃ = η ¹₃ z ¹₃ /(η ³₁ z ³₁  + ν ₂ z ⁵₁ )

Component 4 efficiency ratio: θ ₄ = u ₄ z ¹₄ /(η ¹₂ z ¹₂  + η ¹₃ z ¹₃ )

Component Weights

Note that the total (weighted) input across all components is given by the sum of the denominators of θ ₁ through θ ₄, namely

$$ I={\nu}_o{z}_o+{\eta}_1^2{z}_1^2+{\nu}_1{z}_1^4+{\eta}_1^3{z}_1^3+{\nu}_2{z}_1^5+{\eta}_2^1{z}_2^1+{\eta}_3^1{z}_3^1. $$

Now express the w _p as:

$$ \begin{array}{c}{w}_1={\nu}_o{z}_o/I\\ {}{w}_2=\left({\eta}_1^2{z}_1^2+{\nu}_1{z}_1^4\right)/I\\ {}{w}_3=\left({\eta}_1^3{z}_1^3+{\nu}_2{z}_1^5\right)/I\\ {}{w}_4=\left({\eta}_2^1{z}_2^1+{\eta}_3^1{z}_3^1\right)/I\end{array} $$

With this, the overall network efficiency ratio is given by

$$ \theta ={\displaystyle \sum_{p=1}^4{w}_p{\theta}_p}=\left({u}_1{z}_1^1+{\eta}_1^2{z}_1^2+{\eta}_1^3{z}_1^3+{\eta}_2^1{z}_2^1+{\eta}_3^1{z}_3^1+{u}_4{z}_4^1\right)/I, $$

And one then proceeds, as in (5.4) above, to derive the efficiency of each DMU and its components.

5.6.2 Non-immediate Successor Flows

In the previous example all flows of outputs from a stage or component either leave the process entirely or enter as an input to an immediate successor stage. In Fig. 5.2, stage p outputs flow to stage p + 1. In Fig. 5.3, the same is true except that there is more than one immediate successor of stage 1.

Consider Fig. 5.4. Here, the inputs to stage 3 are of three types, namely outputs from stage 2, inputs coming from outside the process, and outputs from a previous, but not immediately previous stage. Again the above rationale for deriving weights w _p can be applied and a model equivalent to (5.23) solved to determine the decomposition of an overall efficiency score into scores for each of the components in the process.

Fig. 5.4

Non-immediate successor flows

5.7 General Multi-stage Processes: An Illustrative Application

We here re-visit the supply chain data set used in Liang et al. (2006). This data set consists of a two-stage process, or a seller-buyer supply chain. The inputs to the first stage (seller) are labor (z ^j₀₁ ), operating cost (z ^j₀₂ ) and shipping cost (z ^j₀₃ ). The outputs from the first stage are number of product A shipped (z ^j2₁₁ ), number of product B shipped (z ^j2₁₂ ) and number of product C shipped (z ^j2₁₃ ). This data set assumes that all outputs from the first stage become inputs to the second stage, i.e., there is no z ¹₁ . There is one input to the second stage (buyer), labor (z ^j3₁₁ ), and two outputs from the second stage, sales (z ^j1₂₁ ) and profits (z ^j1₂₂ ). Table 5.5 provides the data set.

Table 5.5 Data set

In this case, we have, for DMU _o

$$ \begin{array}{c}{w}_1={\displaystyle \sum_{i=1}^3{\nu}_{0i}{z}_{0i}^o}/\left({\displaystyle \sum_{i=1}^3{\nu}_{0i}{z}_{0i}^o}+\left.{\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{o2}+{\nu}_{11}{z}_{11}^{o3}}\right),\right.\\ {}{w}_2=\left({\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{o2}+{\nu}_{11}{z}_{11}^{o3}}\right)/\left({\displaystyle \sum_{i=1}^3{\nu}_{0i}{z}_{0i}^o}\right.+\left.{\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{o2}+{\nu}_{11}{z}_{11}^{o3}}\right)\end{array} $$

$$ \begin{array}{l}\mathrm{Max}{\displaystyle \sum_{k=1}^3{\eta}_{2k}{z}_{1k}^{o2}}+{\displaystyle \sum_{r=1}^2{u}_{2r}}{z}_{2r}^{o1}\hfill \\ {}\mathrm{subject}\kern0.5em \mathrm{to}\hfill \\ {}\kern1em {\displaystyle \sum_{i=1}^3{\nu}_{0i}{z}_{0i}^o}+{\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{o2}+{\nu}_{11}{z}_{11}^{o3}}=1\hfill \\ {}\kern1em {\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{j2}}\le {\displaystyle \sum_{i=1}^3{\nu}_{0i}{z}_{0i}^j},\mathrm{j}=1,\dots, 10\ \left(\mathrm{for}\ \mathrm{stage}\ 1\right)\hfill \\ {}\kern1em {\displaystyle \sum_{r=1}^2{u}_{2r}}{z}_{2r}^{j1}\le {\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{j2}+{\nu}_{11}{z}_{11}^{j3}},\mathrm{j}=1,\dots, 10\ \left(\mathrm{for}\ \mathrm{stage}\ 2\right)\hfill \end{array} $$

(5.24)

where efficiency scores for DMU _o in stages 1 and 2 can be expressed as

$$ \begin{array}{l}{\theta}_1={\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{o2}}/{\displaystyle \sum_{i=1}^3{\nu}_{0i}{z}_{0i}^o}\\ {}{\theta}_2={\displaystyle \sum_{r=1}^2{u}_{2r}}{z}_{2r}^{o1}/\left({\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{o2}+{\nu}_{11}{z}_{11}^{o3}}\right)\end{array} $$

Table 5.6 reports the results from model (5.24) where the last two columns display the efficiency scores derived from the cooperative model of Liang et al. (2006). Note that the differences between the two approaches are not significant. For example, the two approaches yield identical efficiency scores for the two stages for DMUs, 2, 5, 6, and 9. The Liang et al. (2006) approach is based upon a non-linear program and its solution is obtained by using heuristic search. While the current approach uses a linear program and guarantees a global optimal solution.

Table 5.6 Results

Note that the average of the two stages’ efficiency scores is used as the objective function in Liang et al. (2006) non-linear model, namely, the weights for the two individual efficiency scores are equal, w ₁ = w ₂. The current approach yields w ₁ = w ₂ = 0.5 for DMUs 4 and 7. Yet, our results are different from those obtained from Liang et al. (2006). For example, in DMU 7, the efficiency score for the second stage is 0.54762 compared to 0.81888 from Liang et al. (2006). This is due to the fact that our choice of weights actually introduces some sort of value judgment into the DEA model, and restricts the multiplier values in model (5.24). This is why Liang et al. (2006) score is larger than ours when w ₁ = w ₂ = 0.5 in optimality.

Note that weights w _p (p = 1, 2, …, P) defined are actually variables related to the multiplier decision variables. We next, therefore, impose additional restrictions on w ₁ and w ₂ in model (5.24) via

$$ \begin{array}{c}{w}_1=\left\{{\displaystyle \sum_{i=1}^3{\nu}_{0i}{z}_{0i}^o}/\left({\displaystyle \sum_{i=1}^3{\nu}_{0i}{z}_{0i}^o}\right.+\left.{\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{o2}+{\nu}_{11}{z}_{11}^{o3}}\right)\right\}\ge {\beta}_1\\ {}{w}_2=\left\{\left({\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{o2}+{\nu}_{11}{z}_{11}^{o3}}\right)/\left({\displaystyle \sum_{i=1}^3{\nu}_{0i}{z}_{0i}^o}\right.+\left.{\displaystyle \sum_{k=1}^3{\eta}_{1k}{z}_{1k}^{o2}+{\nu}_{11}{z}_{11}^{o3}}\right)\right\}\ge {\beta}_2\end{array} $$

where β ₁ and β ₂ are user-specified parameters. In this way, we can perform sensitivity analysis on w ₁ and w ₂.

We first impose β ₁ = β ₂ and change β ₁ and β ₂ 0.1–0.5 with a 0.1 increment each time. Note that when β ₁ = β ₂ = 0.5, we explicitly require that w ₁ = w ₂ = 0.5 as in Liang et al. (2006). Table 5.7 reports the results when β ₁ = β ₂ = 0.5. Both our approach and Liang et al. (2006) yield identical efficiency scores for DMU9. Except for DMU1, Liang et al. (2006) score is larger than ours when w ₁ = w ₂ = 0.5 in optimality. For DMU1, the definition of our weights and restrictions on our weights turn the efficient stage 1 under Liang et al. (2006) approach into an inefficient stage, and the inefficient stage 2 under Liang et al. (2006) approach into efficient.

Table 5.7 Results with β ₁ = 0.5, β ₂ = 0.5

Table 5.8 reports the results for DMUs 2, 4, 5, 6, 7, 9 and 10 whose efficiency scores along with the optimized weights remain unchanged when β ₁ = β ₂ = 0.1, 0.2, 0.3 and 0.4, respectively.

Table 5.8 Results with β ₁ = β ₂ = 0.1 (0.2, 0.3, 0.4)

Table 5.9 reports the results for DMUs 1, 3 and 8 whose efficiency scores changed when β ₁ and β ₂ are changed (see the last column of Table 5.5). For DMUs 1 and 3, change in the efficiency scores does not occur until β ₁ = β ₂ = 0.4. For DMU 8, a change in the efficiency score for the first stage is observed when β ₁ = β ₂ = 0.3 and 0.4.

Table 5.9 Results for DMUs 1, 3, and 8

It can be seen that up to β ₁ = β ₂ = 0.3, most of the DMUs have the same weights and efficiency scores with respect to different values of β ₁ and β ₂. As expected, when β ₁ = β ₂ = 0.4, some of the resulting weights are different from the previous cases. However, we note that the efficiency scores do not change significantly. We also note that the efficiency scores for the second stage do not change when β ₁ and β ₂ are increased from 0.1 to 0.4.

We also performed calculations when β ₁ is fixed at 0.2 and β ₂ is changed from 0.3 to 0.8 with an increment of 0.1 each time (results are not reported here). In overall, the efficiency scores do not change significantly.

The above sensitivity analysis indicates that efficiency scores obtained based upon our approach are robust with respect to our choice of weights.

We finally apply our approach to the numerical example used in Tone and Tsutsui (2009). Table 5.10 provides the data. We have two intermediate measures or outputs flow from one stage to the other. Table 5.11 reports the results. In this case, if we do not impose a lower bound for the w _p (p = 1, 2, 3), we have some w _p  = 1 at optimality (for DMUs B, D, I and J). Therefore, we impose w _p  > 0.1 (p = 1, 2, 3) in model (5.23). Because our approach is different from Tone and Tsutsui’s (2009) and our choice of weights introduces restrictions on the multipliers, our results are different from theirs.

Table 5.10 Data set in Tone and Tsutsui (2009)

Table 5.11 Results on three-stage process

5.8 Conclusions

The current chapter introduces the DEA approaches of Chen et al. (2009) and Cook et al. (2010) for DMUs that have a general multi-stage or network structure. We first study the simple two-stage network processes where outputs form the first stage become the only inputs to the second stage. We then examine pure serial networks where each stage has its own inputs and two types of outputs. One type of output from any given stage p is passed on as an input to the next stage, and the other type exits the process at stage p. Work closely related to the current chapter is the non-linear approach of Liang et al. (2006) where a two-member supply chain structure is studied. While Liang et al. (2006) developed a heuristic search algorithm after converting the non-linear model into a parametric linear model, their approach cannot be generalized into cases where supply chains have more than two members. The approach of Cook et al. (2010) can, however, handle via a linear model, situations where more than two stages are present.

In general, the intermediate measures are those that exist between two members of the network. In many cases, the intermediate measures are obvious, as indicated in our examples mentioned in the Introduction. Tone and Tsutsui (2009) provides other good examples. Sometimes, the selection of intermediate measures is not so obvious. The important thing is that intermediate measures are neither “inputs” (to be reduced) nor “outputs” (to be increased), rather these measures need to be “coordinated” to determine their efficient levels.

Note that models under Sects. 5.5 and 5.6 are developed under the assumption of CRS. We should point out that these models can directly be applied to VRS by adding the free-in-sign variable in our ratio efficiency definition, just as in the standard VRS DEA model and the two stage network DEA approach discussed in Sect. 5.3.