On a queueing inventory problem with necessary and optional inventories

Abstract

Queueing inventory models are extensively analysed since 1992. Very few among these discuss multi-commodity system. In this paper, we present a multi-commodity queueing inventory problem involving one essential and a set of m optional item(s). Immediately after the service of an essential item, the customer either leaves the system with probability p or with probability 1-p he goes for optional item(s). However, in the absence of an essential item, service will not be provided. More than one optional item can be demanded by the customer. The i th optional item or i th and j th optional items or i th, j th and k th and so on or all the optional items together, could be demanded by a customer, with probabilities $p_{i}$, $p_{ij}$, $p_{ijk}$ $\ldots$ $p_{12\ldots m}$ respectively. If the demanded optional item(s) is(are) not available, the customer leaves the system after purchasing the essential item. With the arrival of customers forming Markovian Arrival Process (MAP), service time of essential item Phase type distributed and that for optional items exponentially distributed( depending on the type(s) of item(s)), all given by the same (single) server, we analyse the system. Then we obtain the system state probability distribution. In-order to get a picture of how the system performs, we derive several characteristics of the system. With control policies for essential and optional items determined respectively, by (s, S) and ($s_{i}$,$S_{i}$),$i=1,2,3,$..., m, we investigate the optimal values of $s,S,s_{i}$ and $S_{i}$s’. To this end, we set up a cost function, involving these control variables.

1 Introduction

Inventory with positive service time or Queueing Inventory (QI) got attention of researchers since 1992 (Melikov and Molchanov 1992; Sigman and Simchi-Levi 1992). Subsequently Berman and Kim (1999), Berman et al. (1993), Berman and Sapna (2002) and later many others contributed to this area of research. A breakthrough occurred when product form solution was introduced in queuing inventory models. The pioneers in this direction are Schwarz M, Daduna H et al. (see their publications Schwarz et al. 2006; Schwarz and Daduna 2006; Schwarz et al. 2007). A few others (such as Saffari et al. 2013; Krishnamoorthy and Viswanath 2013; Baek and Moon 2014 etc.) also contributed to this direction of thoughts. An extensive survey on QI is given in Krishnamoorthy et al. (2019). Unfortunately they missed three papers of the Daduna group. These are given as references Otten et al. (2020), Daduna and Krenzler (2020) and Daduna (2020).

The above mentioned work are all based on a single type commodity. To the best of our knowledge no work is so far reported on multi-commodity QI. Unlike classical inventory on multi commodity, Queueing Inventory with multi-commodity set up looks more complex and hence challenging. In this paper we introduce such a model. Real life examples of the model considered are abundant:

• 1. Consider a dealer of automobiles, for example car. Assume that all stocked items are base models. Thus only the very essential items are in it. Customers, buying the cars, could ask for optional (not essential) items at additional cost. They have the freedom to buy item(s) of their choice. They may prefer not to buy the demanded optional items, in case, one or more of them are out of stock. However, this assumption is not required, though we have introduced that in the modelling.

• 2. An agency sells a single type machines. This is the main item customers ask for. There are m optional items also that customers demand while purchasing the main item. Thus we have an inventory of m+1 items, of which item one is the main which is required by all customers. Some customers do not purchase optional items, others go for one or more of these, depending on the individual taste. We investigate this system in depth.

• 3. Tiller for ploughing fields. Tiller, with minimum required materials for its operation, is on sales. Customers could buy additional items for further safety. A few may opt not to buy any of these, a few others may buy exactly one such item, or two additional items and so on, a few may opt to buy all those additional items.

First we give a glimpse of what has been done in multi-commodity inventory models. We do not claim this list to be complete. Faiz and Hwang (2007) discuss Inventory constrained maritime routing and scheduling for liquid multi-commodity in bulk. They formulate a model for finding a minimum cost routing in a network for a heterogeneous fleet of ships engaged in pickup and delivery of several liquid bulk products. This especially happens while transporting oil and some byproducts from a main port to various other ports. The problem is formulated as a mixed integer non-linear programming problem.

Sadjady and Davoudpour (2012) examine a two-echelon, multi-commodity supply chain network design with mode selection, lead-times and inventory costs. The authors analyse a two-echelon supply chain network design problem in deterministic, single-period, multi-commodity contexts. The problem involves both strategic and tactical levels of supply chain planning including locating and sizing manufacturing plants and distribution warehouses, assigning the retailers’ demands to the warehouses, and the warehouses to the plants and, finally selecting transportation modes. The authors formulate the problem as a mixed integer programming model, which integrates the above mentioned decisions. The authors aim at minimizing total cost of the network including transportation, lead-times, and inventory holding costs for products, as well as opening and operating costs for facilities. Further they develop an efficient Lagrangian based heuristic solution algorithm for solving the real-sized problems in reasonable computational time.

Jin et al. (2009) discuss optimal model and algorithm for multi-commodity logistics network design considering stochastic demand and inventory control. A simultaneous approach that incorporates inventory control decision into facility location model is proposed. This is used to solve the multi-commodity logistics network design problem. Based on the assumption that the stochastic demands of the retailers are normally distributed, a non-linear mixed integer programming model, that simultaneously describe the inventory decision and the facility location decision, is presented. In this, the objective is to minimize the total cost that include location costs, inventory costs, and transportation costs under the certain service level. The Combined Simulated Annealing (CSA) algorithm is developed to solve the problem.

Askin et al. (2014) examine a multi-commodity warehouse location and distribution planning with inventory consideration. The problem of designing a distribution network for a logistics provider that acquires products from multiple facilities and then delivers those products to many retail outlets is discussed. Potential locations for consolidation facilities that combine shipments for cost reduction and service improvements are considered. The problem is formulated with direct shipment and consolidation opportunities. A novel mathematical model is derived to solve a complex facility location problem determining: (i) the location and capacity level of warehouses to open; (ii) the distribution route from each production facility to each retailer outlet; and (iii) the quantity of products stocked at each warehouse and retailer. A genetic algorithm and a specific problem heuristic are designed, tested and compared on several realistic scenarios.

Araya-Sassi et al. (2020) discuss a multi-commodity inventory-location problem with two different review inventory control policies and modular stochastic capacity constraints. They introduced two novel multi-commodity inventory-location models considering continuous and periodic review inventory control policies and modular stochastic capacity constraints. The models address a logistic problem in which a single plant supplies a set of commodities to warehouses where they serve a set of customers or retailers. The problem consists of determining which warehouses should be opened, which commodities are assigned, and which customers should be served by the located warehouses as well as their reorder points and order sizes in order to minimize costs of the system while satisfying service level requirements. This problem is formulated as a mixed-integer nonlinear programming model, which is non-convex in terms of modular stochastic capacity constraints and the objective function. A Lagrangian relaxation and the subgradient method solution approach is proposed. They consider the relaxation of three sets of constraints, including customer assignment, warehouse demand, and variance constraints. Thus a Lagrangian heuristic to determine a feasible integer solution at each iteration of the subgradient method is developed. An experimental study shows that the proposed algorithm provides good quality gaps and near-optimal solutions in a short time. It also evinces significant impacts of the selected inventory control policy into total costs and network design, including risk pooling effects, when it is compared with different review period values and continuous review.

Zadeh et al. (2013) examine a dynamic multi-commodity inventory and facility location problem in steel supply chain network design. This paper focuses on strategic and tactical design of Steel Supply Chain (SSC) networks. Ever-increasing demand for steel products enforces the steel producers to expand their production and storage capacities. The main purpose of the paper includes preparing a countrywide production, inventory distribution, and capacity expansion plan to design an SSC.

Salient features of this paper are:-

• It considers multi-commodity inventory with positive service time.

• First paper to introduce optional items for service.

• Except for one item(essential), all others are optional.

• Customer demand process forms a Markovian arrival process (MAP).

• Service time of customers, being served with the essential inventory, follows phase type distribution and that w.r.t optional item(s) follows exponential distribution. The latter has parameter, depending on the specific item(s) demanded by the customer.

The rest of the paper is arranged as follows. Mathematical formulation is taken up in Sect. 2, which includes stability condition and steady state probability vector. Some important performance measures are derived in Sect. 3. A cost function for optimizing the control variables is given in Sects. 4 and 5 deals with numerical illustrations which includes the numerical analysis of cost function. Section 6 gives the conclusion and it is followed by References.

Some notations and abbreviations used in the sequel:

• (s, S) ordering policy: Maximum inventory level is S and when the inventory level comes down to s, order for replenishment is placed.

• e = Column vector of $1'$s of appropriate order.

• ${\bar{0}}$ = Zero matrix of appropriate order.

• $I_n$ = Identity matrix of order n.

• $[A]_{ij}$ = (i, j)th element of the matrix A.

• CTMC :  Continuous time Markov chain.

• LIQBD :  Level Independent Quasi-Birth and Death process.

• MAP= Markovian arrival process.

• The Kronecker product of two given matrices $A_{m \times n}$ and $B_{p \times q}$ is $A \otimes B$ = $([A]_{ij}B)$ of order $mp \times nq$.

• The Kronecker sum of two square matrices C and D of orders m and n respectively is $C\oplus D = C \otimes I_n +I_m \otimes D$.

• Customer arrival process : $MAP (D_0,D_1)$ of order $m_2$.

• Service time of customers w.r.t essential inventory: $PH(\gamma , T)$ of order $m_1$.

• Service time of customers w.r.t optional inventories: $exp(\mu _{i})$ for $1\le i \le m$.

2 Mathematical formulation

Consider a single server multi-commodity queueing inventory system consisting of one essential and m optional inventories where the essential and optional inventories are under the control policies (s, S) and ($s_{i}$,$S_{i}$) for $i=1,2,3,\ldots ,m$, respectively. Customers arrive according to the Markovian arrival process (MAP)(see Chakravarthy 2001) with representation ($D_{0}$,$D_{1}$) of order $m_{2}$. The arrival in MAP is a special class of semi-Marlov process with underlying CTMC ($\delta (t), t \ge 0$) on the state space { $1,2,3,\ldots ,m_{2}$} with generator $D = D_{0}+ D_{1}$ such that $D_0$ governs transitions corresponding to no arrivals and $D_1$ accounts for transitions corresponding to arrivals. These matrices, $D_0$ and $D_1$, are of the form given by

$$\begin{aligned} {D_0}= & {} \left[ {\begin{array}{*{20}c} {d_{11}^{(0)}} &{} {d_{12}^{(0)}} &{} \cdots &{} {d_{1m_2}^{(0)}} \\ {d_{21}^{(0)}} &{} {d_{22}^{(0)}} &{} \cdots &{} {d_{2m_2}^{(0)}} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {d_{m_21}^{(0)}} &{} {d_{m_22}^{(0)}} &{} \cdots &{} {d_{m_2 m_2}^{(0)}}\\ \end{array}} \right] ,\\ {D_1}= & {} \left[ {\begin{array}{*{20}c} {d_{11}^{(1)}} &{} {d_{12}^{(1)}} &{} \cdots &{} {d_{1m_2}^{(1)}} \\ {d_{21}^{(1)}} &{} {d_{22}^{(1)}} &{} \cdots &{} {d_{2m_2}^{(1)}} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {d_{m_21}^{(1)}} &{} {d_{m_22}^{(1)}} &{} \cdots &{} {d_{m_2 m_2}^{(1)}}\\ \end{array}} \right] \end{aligned}$$

where,

$$\begin{aligned} d_{ii}^{(0)}= - \left( \sum _{j=1,j \ne i}^{m_2}d_{ij}^{(0)}+\sum _{j=1}^{m_2}d_{ij}^{(1)} \right) . \end{aligned}$$

Thus $d_{ij}^{(1)}, 1 \le i,j \le m_2$ represents the rate of transition from i to j through an arrival, while $d_{ij}^{(0)}, 1 \le i,j \le m_2$, represents the rate of transition from i to j without an arrival. Note that transition from i to i is possible only through an arrival and not otherwise. Let $\eta$ be the steady state probability vector of D. Then, $\eta$ satisfy $\eta D$=0 and $\eta e$=1. The fundamental rate $\lambda$ of this MAP is given by $\lambda$= $\eta D_{1} e$ which gives the expected number of arrivals per unit of time.

Service time of customers being served with the essential inventory is phase type distributed with representation $(\gamma , T)$ of order $m_{1}$. This service time can be interpreted as the time untill the underlying Markov chain ($\zeta (t), t \ge 0$) with a finite state space { $1,2,3,\ldots ,m_{1}+1$} gets absorbed into the single absorbing state $m_{1}+1$, conditioned on the fact that the initial state of this process is selected as one of the states { $1,2,3,\ldots ,m_{1}$} according to the initial probability vector $\gamma$=($\gamma _{1},\gamma _{2}, \ldots , \gamma _{m_{1}}$). The transition rates within the set {$1,2,3,\ldots ,m_{1}$} are defined by the generator T and the absorption rates from the individual transient states to the absorption state is given by $T^{0}= -Te$. The mean service time of the customer is calculated by $\mu '$=$-\gamma T^{-1}e$ (see Neuts 1981).

Service time of customers, being served with the optional inventories, are exponentially distributed with parameter $\mu _{i}$, where i $\in$ {$i_{1},i_{1}i_{2},i_{1}i_{2}i_{3},\ldots ,i_{1}i_{2}i_{3}\ldots i_{m}$} in which no element has any order preference, for example $i_{j}i_{k}=i_{k}i_{j}$ with $j \ne k$ where each $i_{k}$ $\in$ {$1,2,3,\ldots ,m$} for $j, k \in \{1,2,3,\ldots ,m\}$.

In this model, after the service of the essential inventory, we assume that, with probability p the customer leaves the system or goes for optional item with complementary probability $1-p$. Each customer demands exactly one unit of the essential inventory whereas, demand for more than one type of optional inventories is permitted with a restriction of maximum one unit from each optional inventories. The i th optional item, i th and j th optional items so on and all the optional items together could be demanded with probability $p_{i}$, $p_{ij}$ and $p_{12\ldots m}$ respectively. If the demanded optional item(s) is(are) not available, the customer leaves the system after purchasing the essential item as well as whatever optional items he/she demanded are available. It is assumed that the server remains idle when there is no customer in the system and/or when there is no essential inventory. The lead time for both essential and optional inventories are exponentially distributed with parameters $\beta$ and $\beta _{i}$ for $1\le i \le m$ respectively.

Fig. 1

Pictorial representation of the model

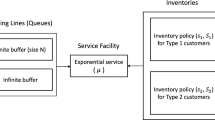
The structure of the system under study is given in Fig. 1.

Let N(t), I(t), $I_{k}(t)$,$J_{1}(t)$ and $J_{2}(t)$ denote respectively, the number of customers in the system, the number of items in the essential inventory, the number of items in the k th optional inventory for $1\le k \le m$, phase of essential service and phase of arrival of the customer arrival process at time t. Also for any time t define the random variable C(t) to denote the status of the server as,

$$\begin{aligned} C(t)=\left\{ \begin{array}{ll} 0^{*}&{} \hbox {Idle server} \\ 0&{} \hbox {Essential service} \\ 1&{} 1^{st} \, \hbox {optional service} \\ \vdots \\ jk&{} j{th} \,\hbox {and} \, k{th} \, \hbox {optional service together} \\ \vdots \\ jkl&{} j{th}, k{th} \, \hbox {and} \, l{th} \, \hbox {optional service together} \\ \vdots \\ 123,...,m&{} \hbox {All optional service together} \\ \end{array} \right. \end{aligned}$$

Let $\Lambda$ be the collection of all the possible combinations of optional items restricted to one from each kind and $C_u$ denotes the server status for u optional items, $1 \le u \le m$ . Thus the process $\Gamma$={$(N(t),I(t), C(t),I_{1}(t),I_{2}(t),\ldots ,I_{m}(t),J_{1}(t),J_{2}(t)) ), t\ge 0$} is a Continuous time Markov chain (CTMC) which is a Level Independent Quasi-Birth and Death process(LIQBD) with state space

{$(0,i,0^*,i_1,i_2,\ldots , i_m,j_2), 0\le i\le S, 0\le i_r\le S_r$ for$1\le r\le m, 1\le j_2 \le m_2$}

$\bigcup$ {$(n,0,0^*,i_1,i_2,\ldots , i_m,j_2),n\ge 1, 0\le i_r\le S_r$ for$1\le r\le m, 1\le j_2 \le m_2$}

$\bigcup$ {$(n,i,0,i_1,i_2,\ldots , i_m,j_1,j_2),n\ge 1, 1\le i \le S, 0\le i_r\le S_r$ for$1\le r\le m, 1\le j_1 \le m_1, 1\le j_2 \le m_2$}

$\bigcup$ {$(n,i,C_1,i_1,i_2,\ldots , i_m,j_2),n\ge 1, 1\le i \le S, C_1 \in \Lambda , 1\le j_2 \le m_2,$

for if $C_1=l$ where $1\le l\le m$ then $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l \}$ and $1 \le i_l \le S_l$}

$\bigcup$ {$(n,i,C_2,i_1,i_2,\ldots , i_m,j_2),n\ge 1, 1\le i \le S, C_2 \in \Lambda , 1\le j_2 \le m_2,$ for if $C_2=lj$ where $l \ne j,1\le l,j\le m$ then $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l,j \}$ and $1 \le i_k \le S_k$ for $k \in \{l,j\}$}

$\bigcup$ {$(n,i,C_3,i_1,i_2,\ldots , i_m,j_2),n\ge 1, 1\le i \le S, C_3 \in \Lambda , 1\le j_2 \le m_2,$ for if $C_3=hjl$ where $h \ne j \ne l,1\le h,j,l\le m$ then $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ h,j, l\}$ and $1 \le i_k \le S_k$ for $k \in \{h,j, l\}$}$\bigcup \ldots$ $\bigcup$ {$(n,i,12\ldots m,i_1,i_2,\ldots , i_m,j_2),n\ge 1, 1\le i \le S, 12\ldots m \in \Lambda , 1\le j_2 \le m_2,$ $1\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}$}.

The transitions rates are:

• 1. Transitions due to arrival of customers.

  • (a) $(0,i,0^*,i_1,i_2,\ldots , i_m,j_2) \rightarrow (1,i,0,i_1,i_2,\ldots , i_m,j_1,j_2^{'} )$ at the rate $\gamma {_{j_1}} [D_1]_{j_2 j_2'}$ for $1 \le j_1 \le m_1$ and $1 \le j_2 ,j_2^{'} \le m_2$ where $1 \le i \le S; 0\le i_r\le S_r$ for$1\le r\le m.$

  • (b) $(n,i,0,i_1,i_2,\ldots , i_m,j_1,j_2) \rightarrow (n+1,i,0,i_1,i_2,\ldots , i_m,j_1^{'},j_2^{'})$ at the rate ${[D_1]_{j_2 j_2'}}$ for ${j_1 = j_1^{'}}$ and rate is 0 when ${j_1 \ne j_1^{'}}$ for $1 \le j_1,j_1^{'} \le m_1$ and $1 \le j_2,j_2^{'} \le m_2$ where $n \ge 1;1 \le i \le S$;

    $0\le i_r\le S_r$ for $1\le r\le m.$

  • (c) $(n,i,C_u,i_1,i_2,\ldots , i_m,j_2) \rightarrow (n+1,i,C_u,i_1,i_2,\ldots , i_m,j_2^{'})$ at the rate ${[D_1]_{j_2 j_2'}}$

    for $1 \le j_2,j_2^{'} \le m_2$ where $1 \le i \le S$ and, when

    $u=1$ and $C_1=l;1\le l \le m,$ then $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l \}$ and$1 \le i_l \le S_l$;

    $u=2$ and $C_2=lj, l\ne j, 1 \le l,j \le m;$ then $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l,j \}$ and$1 \le i_k \le S_k$ for $k \in \{l,j \}$;

    $u=3$ and $C_3=hjl ,h\ne j \ne l, 1 \le h,j,l \le m;$then $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ h,j,l \}$ and$1\le i_k \le S_k$ for $k \in \{ h,j,l \}$; $\ldots$ etc.

    $u=m$ and $C_m=123 \ldots m ;$then $1\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}.$

• 2. Transitions due to the service of essential and optional items.

  • (a) $(1,i,C_u,i_1,i_2,\ldots ,i_l,\ldots , i_m,j_2) \rightarrow (0,i,0^*,i_{1}^*,i_{2}^*,\ldots ,i_{l}^*,\ldots , i_{m}^*,j_2^{'})$ at the rate $\mu _{C_u}$

    for $1 \le j_2,j_2^{'} \le m_2$ where $1 \le i \le S$ and, when

    $u=1$ and $C_1=l;1\le l \le m,$ then$\ i_{k}^*=i_k$ and $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l \}$ and$\ i_{l}^*=i_l -1, 1 \le i_l \le S_l$;

    $u=2$ and $C_2=lj ,l\ne j, 1 \le l,j \le m;$ then$\ i_{k}^*=i_k$, $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l,j \}$ and$\ i_{k}^*= i_k -1$, $1 \le i_k \le S_k$ for $k \in \{l,j \}$;

    $u=3$ and $C_3=hjl, h\ne j \ne l, 1 \le h,j,l \le m; \$then$,\ i_{k}^*=i_k$, $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ h,j,l \}$ and $i_{k}^*=i_k -1$, $1\le i_k \le S_k$ for $k \in \{ h,j,l \}$; $\ldots$ etc.

    $u=m$ and $C_m=123 \ldots m ,\$then$\ i_{k}^*=i_k-1, 1\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}.$

  • (b) $(1,i,0,i_1,i_2,\ldots ,i_l,\ldots , i_m,j_1,j_2) \rightarrow (0,i-1,0^*,i_{1}^*,i_{2}^*,\ldots ,i_{l}^*,\ldots , i_{m}^*,j_2^{'})$ at the rate $T_{j_{1}}$

    for $1 \le j_1 \le m_1$;$1 \le j_2,j_2^{'} \le m_2$ where $1 \le i \le S$ and $i_k = i_k^{*}=0$ for $k \in \{1,2, \ldots ,m\}.$

  • (c) $(1,i,0,i_1,i_2,\ldots ,0,\ldots , i_m,j_1,j_2) \rightarrow (0,i-1,0^*,i_{1}^*,i_{2}^*,\ldots ,0,\ldots , i_{m}^*,j_2^{'})$ at the rate $\eta _{l}T_{j_{1}}$ for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $1 \le i \le S;1 \le i_k=i_k^{*} \le S_k$ for $k \in \{1,2, \ldots ,m\}$ and $\eta _{l}= p+(1-p)\sum p_{{\bar{l}}}$, where $\sum p_{{\bar{l}}}$ is the sum of probabilities of all possible combinations of optional inventories including l th optional inventory.

  • (d) $(1,i,0,i_1,i_2,\ldots ,i_l,\ldots , i_m,j_1,j_2) \rightarrow (0,i-1,0^*,i_{1}^*,i_{2}^*,\ldots ,i_{l}^*,\ldots , i_{m}^*,j_2^{'})$ at the rate $p T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $1 \le i \le S;1 \le i_k=i_k^{*} \le S_k$ for $k \in \{1,2, \ldots , m\}.$

  • (e) $(n,i,C_u,i_1,i_2,\ldots ,i_l,\ldots , i_m,j_2) \rightarrow (n-1,i,C_u,i_{1}^*,i_{2}^*,\ldots ,i_{l}^*,\ldots , i_{m}^*,j_2^{'})$ at the rate $\mu _{C_u}$

    for $1 \le j_2,j_2^{'} \le m_2$ where $n\ge 2; 1 \le i \le S$ and, when

    $u=1$ and $C_1=l;1\le l \le m,$ then$\ i_{k}^*=i_k$ and $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l \}$ and$\ i_{l}^*=i_l -1, 1 \le i_l \le S_l$;

    $u=2$ and $C_2=lj ,l\ne j, 1 \le l,j \le m;$ then$\ i_{k}^*=i_k$, $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l,j \}$ and$\ i_{k}^*= i_k -1$, $1 \le i_k \le S_k$ for $k \in \{l,j \}$;

    $u=3$ and $C_3=hjl, h\ne j \ne l, 1 \le h,j,l \le m; \$then$,\ i_{k}^*=i_k$, $0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ h,j,l \}$ and $i_{k}^*=i_k -1$, $1\le i_k \le S_k$ for $k \in \{ h,j,l \}$; $\ldots$ etc.

    $u=m$ and $C_m=123 \ldots m ,\$then$\ i_{k}^*=i_k-1, 1\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}.$

  • (f) $(n,1,0,i_1,i_2,\ldots ,i_l,\ldots , i_m,j_2) \rightarrow (n-1,0,0^*,i_{1}^*,i_{2}^*,\ldots ,i_{l}^*,\ldots , i_{m}^*,j_2^{'})$

    at the rate $T_{j_{1}}$

    for $1 \le j_1 \le m_1$;$1 \le j_2,j_2^{'} \le m_2$ where $n\ge 2; 1 \le i \le S$ and $i_k = i_k^{*}=0$ for $k \in \{1,2, \ldots ,m\}.$

  • (g) $(n,1,0,i_1,\ldots ,i_l,\ldots , i_m,j_1,j_2) \rightarrow (n-1,0,0^*,i_{1}^*,\ldots ,i_{l}^*,\ldots , i_{m}^*,j_2^{'})$ at the rate $\eta _{l}T_{j_{1}}$ for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n \ge 2;1 \le i \le S;1 \le i_k=i_k^{*} \le S_k$ for $k \in \{1,2, \ldots ,m\}-\{l\}$, $i_l = i_{l}^* =0$ and $\eta _{l}= p+(1-p)\sum p_{{\bar{l}}}$, where $\sum p_{{\bar{l}}}$ is the sum of probabilities of all possible combinations of optional inventories including l th optional inventory. Similarly for $1 \le l \le m.$

  • (h) $(n,1,0,i_1,i_2,\ldots ,i_l,\ldots , i_m,j_1,j_2) \rightarrow (n-1,0,0^*,i_{1}^*,i_{2}^*,\ldots ,i_{l}^*,\ldots , i_{m}^*,j_2^{'})$ at the rate $p T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n \ge 2;1 \le i_k=i_k^{*} \le S_k$ for $k \in \{1,2, \ldots ,m\} .$

  • (i) $(n,i,0,i_1,\ldots ,i_l,\ldots , i_m,j_2) \rightarrow (n-1,i-1,0,i_{1}^*,\ldots ,i_{l}^*,\ldots , i_{m}^*,j_1,j_2)$

    at the rate $T_{j_{1}}$

    for $1 \le j_1 \le m_1$;$1 \le j_2 \le m_2$ where $n\ge 2; 1 \le i \le S$ and $i_k = i_k^{*}=0$ for $k \in \{1,2, \ldots ,m\}.$

  • (j) $(n,i,0,i_1,\ldots ,i_l,\ldots , i_m,j_1,j_2) \rightarrow (n-1,i-1,0,i_{1}^*,\ldots ,i_{1}^*,\ldots , i_{m}^*,j_2^{'})$

    at the rate $\eta _{l}T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n \ge 2;2 \le i \le S;1 \le i_k=i_k^{*} \le S_k$ for $k \in \{1,2, \ldots ,m\}-\{l\}$, $i_l = i_{l}^* =0$ and $\eta _{l}= p+(1-p)\sum p_{{\bar{l}}}$, where $\sum p_{{\bar{l}}}$ is the sum of probabilities of all possible combinations of optional inventories including l th optional inventory. Similarly for $1 \le l \le m.$

  • (k) $(n,i,0,i_1,\ldots ,i_l,\ldots , i_m,j_1,j_2) \rightarrow (n-1,i-1,0,i_{1}^*,\ldots ,i_{l}^*,\ldots , i_{m}^*,j_2^{'})$ at the rate $p T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n \ge 2;2 \le i \le S;1 \le i_k=i_k^{*} \le S_k$ for $k \in \{1,2, \ldots ,m\}.$

• 3. Transitions due to replenishments of the essential and optional items.

  • (a) $(0,i,0^*,i_1,\ldots ,i_l,\ldots , i_m,j_2) \rightarrow (0,i,0^*,i_{1},\ldots ,S_{l},\ldots , i_{m},j_2)$

    at the rate $\beta _{l}$

    for $1 \le j_2 \le m_2$ where $0 \le i \le S; 0 \le i_k \le S_k$for $k \in \{1,2, \ldots ,m\}-\{l\}$; $0 \le i_l \le s_l$. Similarly for $1 \le l \le m.$

  • (b) $(0,i,0^*,i_1,\ldots ,i_l,\ldots , i_m,j_2) \rightarrow (0,S,0^*,i_1,\ldots ,i_l,\ldots , i_m,j_2)$

    at the rate $\beta$

    for $1 \le j_2 \le m_2$ where $0 \le i \le s; 0 \le i_k \le S_k$ for $k \in \{1,2, \ldots ,m\} .$

  • (c) $(n,0,0^*,i_1,\ldots ,i_l,\ldots , i_m,j_2) \rightarrow (n,0,0^*,i_1,\ldots ,S_l,\ldots , i_m,j_2)$

    at the rate $\beta _{l}$

    for$1 \le j_2 \le m_2$ where $n \ge 1; 0\le i_k \le S_k$ for $k \in \{1,2, \ldots ,m\}-\{l\}$; $0 \le i_l \le s_l$. Similarly for $1 \le l \le m.$

  • (d) $(n,0,0^*,i_1,\ldots ,i_l,\ldots , i_m,j_2) \rightarrow (n,S,0,i_1,\ldots ,i_l,\ldots , i_m,j_1,j_2)$

    at the rate $\gamma \otimes \beta I_{m_2}$

    for $1 \le j_1 \le m_1; 1\le j_2 \le m_2$ where $n \ge 1; 0 \le i_k \le S_k$ for $k \in \{1,2, \ldots ,m\}.$

  • (e) $(n,i,0,i_1,\ldots ,i_l,\ldots , i_m,j_1,j_2) \rightarrow (n,i,0,i_1,\ldots ,S_l,\ldots , i_m,j_1,j_2)$ at the rate $\beta _{l}$

    for $1 \le j_1 \le m_1; 1\le j_2 \le m_2$ where $n \ge 1 ; 1 \le i \le S; 0\le i_k \le S_k$ for $k \in \{1,2, \ldots ,m\}-\{l\}$; $0 \le i_l \le s_l$. Similarly for $1 \le l \le m.$

  • (f) $(n,i,C_u,i_1,\ldots ,i_l,\ldots , i_m,j_2) \rightarrow (n,i,C_u,i_1,\ldots ,S_l,\ldots , i_m,j_2)$ at the rate $\beta _{l}$

    for $1\le j_2 \le m_2$ where $n \ge 1;1\le i \le S$;

    $u=1$ and $C_1=l; 0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l \}$ and$0 \le i_l \le s_l.$ Similarly for$1\le l \le m$.

    $u=2$ and $C_2=lj ; 0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l \}$ and $1 \le i_l \le s_l ; 1 \le i_j \le S_j.$ Similarly for $l\ne j, 1 \le l,j \le m$.

    $u=3$ and $C_3=hjl \ 0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{ l \}$ and $1 \le i_l \le s_l ; 1 \le i_k \le S_k$ for $k \in \{h,j\}$. Similarly for $h\ne j \ne l, 1 \le h,j,l \le m.$ $\ldots$ etc.

    $u=m$ and $C_m=123 \ldots m ,\ 1\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}-\{l\}$;

    $1 \le i_l \le s_l .$

  • (g) $(n,i,0,i_1,\ldots ,i_l,\ldots , i_m,j_1,j_2) \rightarrow (n,S,0,i_1,\ldots ,i_l,\ldots , i_m,j_1,j_2)$ at the rate $\beta$

    for $1 \le j_1 \le m_1; 1\le j_2 \le m_2$ where $n\ge 1; 1\le i \le s; 0\le i_k \le S_k$ for $k \in \{1,2,\ldots ,m\}$ for $k \in \{1,2, \ldots ,m\}.$

  • (h) $(n,i,C_u,i_1,\ldots ,i_l,\ldots , i_m,j_2) \rightarrow (n,S,C_u,i_1,\ldots ,i_l,\ldots , i_m,j_2)$ at the rate $\beta$

    for $1 \le j_2 \le m_2$ where $n\ge 1; 1\le i \le s$;

    $u=1$ and $C_1=l; 0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}$ Similarly for$1\le l \le m$.

    $u=2$ and $C_2=lj ; 0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}$ Similarly for $l\ne j, 1 \le l,j \le m$.

    $u=3$ and $C_3=hjl \ 0\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\}$. Similarly for $h\ne j \ne l, 1 \le h,j,l \le m.$ $\ldots$ etc.

    $u=m$ and $C_m=123 \ldots m ,\ 1\le i_k \le S_k$ for $k \in \{ 1,2, \ldots ,m\} .$

The infinitesimal generator ${\mathcal {Q}}$ of the system $\Gamma$ with entries as described above is obtained to be

$$\begin{aligned} {\mathcal {Q}} = \left[ {\begin{array}{*{20}c} {A_{00} } &{} {A_{01} } &{} {} &{} {} \\ {A_{10} } &{} {A_1 } &{} {A_0 } &{} {} \\ &{}{A_2 } &{} {A_1 } &{} {A_0 } &{} {} \\ {} &{} &{}\ddots &{} \ddots &{} \ddots \\ \end{array}} \right] \end{aligned}$$

$A_{00}$ is a square matrix of order a and it contains transitions within level 0. $A_{01}$ represents transitions from level 0 to level 1 and it’s a matrix of order $a \times b$. Matrix $A_{10}$ represents transitions from level 1 to level 0 and is of order $c \times a$. $A_0$ and $A_1$ are square matrices of order c representing transitions from level n to level $n+1$ and within level n respectively for $n\ge 1$ and finally $A_{2}$ is again a square matrix of order c representing transitions from level n to level $n-1$ for $n \ge 2$ where $a=(S+1)\Pi _{k=1}^{m}(S_k +1)m_2$, $b = (S+1)\Pi _{k=1}^{m}(S_k +1)m_1 m_2$ and $c= \Pi _{k=1}^{m}(S_k +1)m_2 + S \sum _{u \in \Lambda } l_u.$

When $u = i,$ then $l_i= \pi _{k=1, k\ne i}^{m}(S_k +1)S_im_2$ for $1 \le i \le m.$

When $u = ij,$ then $l_{ij}= \pi _{k=1, k\ne i,j}^{m}(S_k +1)\Pi _{k \in \{i,j\}}S_k m_2$ for $1 \le i,j \le m$

When $u = hij,$ then $l_{hij}= \pi _{k=1, k\ne h,i,j}^{m}(S_k +1)\Pi _{k \in \{h,i,j\}}S_k m_2$ for $1 \le h, i,j \le m$ and so on. When $u = 12\ldots m,$ then $l_{12 \ldots m}= \pi _{k=1}^{m}S_km_2.$

The structure of $A_{00}$, $A_{01}$, $A_{10}$, $A_0$, $A_1$ and$A_2$ are obtained as

The entries in $A_{01}$ and $A_2$ are as given in transition due to the arrival of customers. The entries in $A_{10}$ and $A_0$ are as given in transition due to the service of essential and optional items. The entries in $A_{00}$ and $A_1$ are as given in transition due to replenishment of the essential and optional items. In addition, the diagonal entries in $A_{00}$ and $A_1$ are non-positive, having value equal to but with negative sign the sum of other elements of the same row found in $A_{01}$, $A_{10}$,$A_0$ and $A_2$.

$\varvec{Illustration: (1)}$ : when m=2, the state space and transition rates are explicitely,

{$(0,i,0^*,i_1,i_2,j_2), 0\le i\le S, 0\le i_1\le S_1, 0\le i_2\le S_2, 1\le j_2 \le m_2$}

$\bigcup$ {$(n,0,0^*,i_1,i_2,j_2),n\ge 1, 0\le i_1\le S_1, 0\le i_2\le S_2, 1\le j_2 \le m_2$}

$\bigcup$ {$(n,i,0,i_1,i_2,j_1,j_2),n\ge 1, 1\le i \le S, 0\le i_1\le S_1, 0\le i_2\le S_2, 1\le j_1 \le m_1, 1\le j_2 \le m_2$}

$\bigcup$ {$(n,i,1,i_1,i_2,j_2),n\ge 1, 1\le i \le S, 1\le i_1\le S_1, 0\le i_2\le S_2, 1\le j_2 \le m_2$}

$\bigcup$ {$(n,i,2,i_1,i_2,j_2),n\ge 1, 1\le i \le S, 0\le i_1\le S_1, 1\le i_2\le S_2, 1\le j_2 \le m_2$}

$\bigcup$ {$(n,i,12,i_1,i_2,j_2),n\ge 1, 1\le i \le S, 1\le i_1\le S_1, 1\le i_2\le S_2, 1\le j_2 \le m_2$}

and the transitions rates are:

• 1. Transitions due to arrival of customers.

  • (a) $(0,i,0^*,i_1,i_2,j_2) \rightarrow (1,i,0,i_1,i_2,j_1,j_2^{'} )$ at the rate $\gamma {_{j_1}} [D_1]_{j_2 j_2'}$ for $1 \le j_1 \le m_1$ and $1 \le j_2, j_2^{'} \le m_2$ where $1 \le i \le S; 0 \le i_1 \le S_1; 0 \le i_2 \le S_2$

  • (b) $(n,i,0,i_1,i_2,j_1,j_2) \rightarrow (n+1,i,0,i_1,i_2,j_1^{'},j_2^{'})$ at the rate ${[D_1]_{j_2 j_2'}}$ for ${j_1 = j_1^{'}}$ and rate is 0 when ${j_1 \ne j_1^{'}}$ for $1 \le j_1,j_1^{'} \le m_1$ and $1 \le j_2,j_2^{'} \le m_2$ where $n \ge 1;1 \le i \le S; 0 \le i_1 \le S_1; 0 \le i_2 \le S_2$

  • (c) $(n,i,C(t),i_1,i_2,j_2) \rightarrow (n+1,i,C(t),i_1,i_2,j_2^{'})$ at the rate ${[D_1]_{j_2 j_2'}}$

    for $1 \le j_2,j_2^{'} \le m_2$ where $1 \le i \le S$ and, when $C(t)=1 \longrightarrow 1\le i_1 \le S_1; 0 \le i_2\le S_2$;

    $C(t)=2 \longrightarrow 0\le i_1 \le S_1; 1 \le i_2\le S_2$; $C(t)=12 \longrightarrow 1\le i_1 \le S_1; 1 \le i_2\le S_2$

• 2. Transitions due to the service of essential and optional items.

  • (a) $(1,i,1,i_1,i_2,j_2) \rightarrow (0,i,0^*,i_1-1,i_2,j_2)$ at the rate $\mu _1$

    for $1 \le j_2 \le m_2,$ where $1 \le i \le S; 1\le i_1 \le S_1; 0 \le i_2 \le S_2$

  • (b) $(1,i,2,i_1,i_2,j_2) \rightarrow (0,i,0^*,i_1,i_2-1,j_2)$ at the rate $\mu _2$

    for $1 \le j_2 \le m_2$ where $1 \le i \le S; 0\le i_1 \le S_1; 1 \le i_2 \le S_2$

  • (c) $(1,i,12,i_1,i_2,j_2) \rightarrow (0,i,0^*,i_1-1,i_2-1,j_2)$ at the rate $\mu _{12}$

    for $1 \le j_2 \le m_2$ where $1 \le i \le S; 1\le i_1 \le S_1; 1 \le i_2 \le S_2$

  • (d) $(1,i,0,0,0,j_1,j_2) \rightarrow (0,i-1,0^*,0,0,j_2)$ at the rate $T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $1 \le i \le S$

  • (e) $(1,i,0,0,i_2,j_1,j_2) \rightarrow (0,i-1,0^*,0,i_2,j_2)$ at the rate $\eta _{1}T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $1 \le i \le S;1 \le i_2 \le S_2$ and $\eta _{1}= p+(1-p)(p_1 +p_{12})$

  • (f) $(1,i,0,i_1,0,j_1,j_2) \rightarrow (0,i-1,0^*,i_1,0,j_2)$ at the rate $\eta _{2}T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $1 \le i \le S;1 \le i_1 \le S_1$ and $\eta _{2}= p+(1-p)(p_2 +p_{12})$

  • (g) $(1,i,0,i_1,i_2,j_1,j_2) \rightarrow (0,i-1,0^*,i_1,i_2,j_2)$ at the rate $p T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $1 \le i \le S;1 \le i_1 \le S_1$ and $1\le i_2 \le S_2$

  • (h) $(n,i,1,i_1,i_2,j_2) \rightarrow (n-1,i,1,i_1-1,i_2,j_2)$ at the rate $\mu _1$

    for $1 \le j_2 \le m_2,$ where $n \ge 2; 1 \le i \le S; 1\le i_1 \le S_1; 0 \le i_2 \le S_2$

  • (i) $(n,i,2,i_1,i_2,j_2) \rightarrow (n-1,i,2,i_1,i_2-1,j_2)$ at the rate $\mu _2$

    for $1 \le j_2 \le m_2$ where $n\ge 2; 1 \le i \le S; 0\le i_1 \le S_1; 1 \le i_2 \le S_2$

  • (j) $(n,i,12,i_1,i_2,j_2) \rightarrow (n-1,i,12,i_1-1,i_2-1,j_2)$ at the rate $\mu _{12}$

    for $1 \le j_2 \le m_2$ where $n \ge 2; 1 \le i \le S; 1\le i_1 \le S_1; 1 \le i_2 \le S_2$

  • (k) $(n,1,0,0,0,j_1,j_2) \rightarrow (n-1,0,0^*,0,0,j_2)$ at the rate $T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n \ge 2$

  • (l) $(n,1,0,0,i_2,j_1,j_2) \rightarrow (n-1,0,0^*,0,i_2,j_2)$ at the rate $\eta _{1}T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n\ge 2;1 \le i_2 \le S_2$ and

    $\eta _{1}= p+(1-p)(p_1 +p_{12})$

  • (m) $(n,1,0,i_1,0,j_1,j_2) \rightarrow (n-1,0,0^*,i_1,0,j_2)$ at the rate $\eta _{2}T_{j_{1}}$

    for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n \ge 2;1 \le i_1 \le S_1$ and

    $\eta _{2}= p+(1-p)(p_2 +p_{12})$

  • (n) $(n,1,0,i_1,i_2,j_1,j_2) \rightarrow (n-1,0,0^*,i_1,i_2,j_2)$ at the rate $p T_{j_{1}}$ for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n \ge 2; 1 \le i_1 \le S_1; 1\le i_2 \le S_2$

  • (o) $(n,i,0,0,0,j_1,j_2) \rightarrow (n-1,i-1,0,0,0,j_1,j_2)$ at the rate $T_{j_{1}}$ for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n\ge 2;2 \le i \le S$

  • (p) $(n,i,0,0,i_2,j_1,j_2) \rightarrow (n-1,i-1,0,0,i_2,j_1,j_2)$ at the rate $\eta _{1}T_{j_{1}}$ for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n \ge 2;2 \le i \le S;1 \le i_2 \le S_2$ and $\eta _{1}= p+(1-p)(p_1 +p_{12})$

  • (q) $(n,i,0,i_1,0,j_1,j_2) \rightarrow (n-1,i-1,0,i_1,0,j_1,j_2)$ at the rate $\eta _{2}T_{j_{1}}$ for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n \ge 2; 2 \le i \le S;1 \le i_1 \le S_1$ and $\eta _{2}= p+(1-p)(p_2 +p_{12})$

  • (r) $(n,i,0,i_1,i_2,j_1,j_2) \rightarrow (n-1,i-1,0,i_1,i_2,j_1,j_2)$ at the rate $p T_{j_{1}}$ for $1 \le j_1 \le m_1;1 \le j_2 \le m_2$ where $n \ge 2;2 \le i \le S; 1 \le i_1 \le S_1;$ and $1\le i_2 \le S_2$

• 3. Transitions due to replenishments of the essential and optional items.

  • (a) $(0,i,0^*,i_1,i_2,j_2) \rightarrow (0,i,0^*,i_1,S_2,j_2)$ at the rate $\beta _{2}$ for $1 \le j_2 \le m_2$ where $0 \le i \le S; 0 \le i_1 \le S_1; 0 \le i_2 \le s_2$

  • (b) $(0,i,0^*,i_1,i_2,j_2) \rightarrow (0,i,0^*,S_1,i_2,j_2)$ at the rate $\beta _{1}$ for $1 \le j_2 \le m_2$ where $0 \le i \le S; 0 \le i_1 \le s_1; 0 \le i_2 \le S_2$

  • (c) $(0,i,0^*,i_1,i_2,j_2) \rightarrow (0,S,0^*,i_1,i_2,j_2)$ at the rate $\beta$ for $1 \le j_2 \le m_2$ where $0 \le i \le s; 0 \le i_1 \le S_1; 0 \le i_2 \le S_2$

  • (d) $(n,0,0^*,i_1,i_2,j_2) \rightarrow (n,0,0^*,i_1,S_2,j_2)$ at the rate $\beta _{2}$ for$1 \le j_2 \le m_2$ where $n \ge 1; 0\le i_1 \le S_1; 0 \le i_2 \le s_2$

  • (e) $(n,0,0^*,i_1,i_2,j_2) \rightarrow (n,0,0^*,S_1,i_2,j_2)$ at the rate $\beta _{1}$ for $1\le j_2 \le m_2$ where $n \ge 1; 0\le i_1\le s_1; 0 \le i_2\le S_2$

  • (f) $(n,0,0^*,i_1,i_2,j_2) \rightarrow (n,S,0,i_1,i_2,j_1,j_2)$ at the rate $\gamma \otimes \beta I_{m_2}$ for $1 \le j_1 \le m_1; 1\le j_2 \le m_2$ where $n \ge 1; 0\le i_1\le S_1; 0 \le i_2\le S_2$

  • (g) $(n,i,0,i_1,i_2,j_1,j_2) \rightarrow (n,i,0,i_1,S_2,j_1,j_2)$ at the rate $\beta _{2}$ for $1 \le j_1 \le m_1; 1\le j_2 \le m_2$ where $n \ge 1 ; 1 \le i \le S; 0 \le i_1 \le S_1$; $0 \le i_2 \le s_2$

  • (h) $(n,i,0,i_1,i_2,j_1,j_2) \rightarrow (n,i,0,S_1,i_2,j_1,j_2)$ at the rate $\beta _{1}$ for $1 \le j_1 \le m_1; 1\le j_2 \le m_2$ where $n \ge 1;1\le i \le S;0 \le i_1 \le s_1$; $0 \le i_2 \le S_2$

  • (i) $(n,i,C(t),i_1,i_2,j_2) \rightarrow (n,i,C(t),i_1,S_2,j_2)$ at the rate $\beta _{2}$ for $1\le j_2 \le m_2$ where $n \ge 1;1\le i \le S$; $C(t)=1 \longrightarrow 1\le i_1 \le S_1; 0 \le i_2\le s_2$; $C(t)=2 \longrightarrow 0\le i_1 \le S_1; 1 \le i_2\le s_2$; $C(t)=12 \longrightarrow 1\le i_1 \le S_1; 1 \le i_2\le s_2$

  • (j) $(n,i,C(t),i_1,i_2,j_2) \rightarrow (n,i,C(t),S_1,i_2,j_2)$ at the rate $\beta _{1}$ for $1\le j_2 \le m_2$ where $n \ge 1;1\le i \le S$; $C(t)=1 \longrightarrow 1\le i_1 \le s_1; 0 \le i_2\le S_2$; $C(t)=2 \longrightarrow 0\le i_1 \le s_1; 1 \le i_2\le S_2$; $C(t)=12 \longrightarrow 1\le i_1 \le s_1; 1 \le i_2\le S_2$

  • (k) $(n,i,0,i_1,i_2,j_1,j_2) \rightarrow (n,S,0,i_1,i_2,j_1,j_2)$ at the rate $\beta$ for $1 \le j_1 \le m_1; 1\le j_2 \le m_2$ where $n\ge 1; 1\le i \le s; 0\le i_1 \le S_1$; $0 \le i_2 \le S_2$

  • (l) $(n,i,C(t),i_1,i_2,j_2) \rightarrow (n,S,C(t),i_1,i_2,j_2)$ at the rate $\beta$ for $1 \le j_2 \le m_2$ where $n\ge 1; 1\le i \le s$; $C(t)=1 \longrightarrow 1\le i_1 \le S_1; 0 \le i_2\le S_2$; $C(t)=2 \longrightarrow 0\le i_1 \le S_1; 1 \le i_2\le S_2$; $C(t)=12 \longrightarrow 1\le i_1 \le S_1; 1 \le i_2\le S_2$

The infinitesimal generator ${\mathcal {Q}}$ of the system $\Gamma$ with entries as described above is obained to be

$$\begin{aligned} {\mathcal {Q}} = \left[ {\begin{array}{*{20}c} {A_{00} } &{} {A_{01} } &{} {} &{} {} \\ {A_{10} } &{} {A_1 } &{} {A_0 } &{} {} \\ &{}{A_2 } &{} {A_1 } &{} {A_0 } &{} {} \\ {} &{} &{}\ddots &{} \ddots &{} \ddots \\ \end{array}} \right] \end{aligned}$$

$A_{00}$ is a square matrix of order a and it contains transitions within level 0. $A_{01}$ represents transitions from level 0 to level 1 and it’s a matrix of order $a \times b$. Matrix $A_{10}$ represents transitions from level 1 to level 0 and is of order $c \times a$. $A_0$ and $A_1$ are square matrices of order c representing transitions from level n to level $n+1$ and within level n respectively for $n\ge 1$ and finally $A_{2}$ is again a square matrix of order c representing transitions from level n to level $n-1$ for $n \ge 2$ where $a=(S+1)(S_1 +1)(S_2 +1)m_2$, $b = (S+1)l_1$ and $c=(S_1 +1)(S_2+1)m_2 + S(l_1+l_2+l_3 +l_4)$ where $l_1=(S_1 +1)(S_2 +1)m_1 m_2, \ l_2=S_1(S_2 +1) m_2,\ l_3 = (S_1 +1)S_2m_2$ and $l4=S_1 S_2 m_2.$

The structure of $A_{00}$, $A_{01}$, $A_{10}$, $A_0$, $A_1$ and$A_2$ are obtained as

$$\begin{aligned}&\hbox {with} \, {Z_0} = \left( {\begin{array}{*{20}c} {I_{s_1+1} \otimes C_1} &{} {e_{s_1+1} \otimes \beta _1 I_{(s_2 +1)m_1m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes C_2} \\ \end{array}} \right) , \, \hbox {where}\\&{C_1} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes B_1} &{} {e_{s_2+1} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes B_2} \\ \end{array}} \right) , \\&{C_2} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes B_3} &{} {e_{s_2+1} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes B_4} \\ \end{array}} \right) ,\\&{B_1} = {\begin{array}{*{20}c} { D - (\beta +\beta _1+\beta _2)I_{ m_2}} \\ \end{array}}, \quad {B_2} = {\begin{array}{*{20}c} { D - (\beta +\beta _1)I_{ m_2}} \\ \end{array}}, \\&{B_3} = {\begin{array}{*{20}c} { D - (\beta +\beta _2)I_{ m_2}} \\ \end{array}}, \quad {B_4} = {\begin{array}{*{20}c} { D - \beta I_{m_2}} \\ \end{array}} .\\&\hat{Z_1} = \left( {\begin{array}{*{20}c} {I_{s_1+1} \otimes \hat{C_1}} &{} {e_{s_1+1} \otimes \beta _1 I_{(s_2 +1)m_1m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes \hat{C_2}} \\ \end{array}} \right) , \, \hbox {where} \\&\hat{C_1} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes \hat{B_1}} &{} {e_{s_2+1} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \hat{B_2}} \\ \end{array}} \right) , \quad \hat{C_2} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes \hat{B_3}} &{} {e_{s_2+1} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \hat{B_4}} \\ \end{array}} \right) ,\\&\hat{B_1} = {\begin{array}{*{20}c} { D_0 - (\beta +\beta _1+\beta _2)I_{ m_2}} \\ \end{array}}, \quad \hat{B_2} = {\begin{array}{*{20}c} { D_0 - (\beta +\beta _1)I_{ m_2}} \\ \end{array}}, \\&\hat{B_3} = {\begin{array}{*{20}c} { D_0 - (\beta +\beta _2)I_{ m_2}} \\ \end{array}}, \quad \hat{B_4} = {\begin{array}{*{20}c} { D_0 - \beta I_{m_2}} \\ \end{array}} .\\&\hat{Z_2} = \left( {\begin{array}{*{20}c} {I_{s_1+1} \otimes \bar{C_1}} &{} {e_{s_1+1} \otimes \beta _1 I_{(s_2 +1)m_1m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes \bar{C_2}} \\ \end{array}} \right) , \, \hbox {where} \\&\bar{C_1} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes \bar{B_1}} &{} {e_{s_2+1} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \bar{B_2}} \\ \end{array}} \right) , \quad \bar{C_2} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes \bar{B_3}} &{} {e_{s_2+1} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \bar{B_4}} \\ \end{array}} \right) ,\\&\bar{B_1} = {\begin{array}{*{20}c} { D_0 - (\beta _1+\beta _2)I_{ m_2}} \\ \end{array}}, \, \bar{B_2} = {\begin{array}{*{20}c} { D_0 - (\beta _1)I_{ m_2}} \\ \end{array}},\\&\bar{B_3} = {\begin{array}{*{20}c} { D_0 - (\beta _2)I_{ m_2}} \\ \end{array}}, \, \bar{B_4} = {\begin{array}{*{20}c} { D_0 } \\ \end{array}}.\\&{\hat{Z}}= \beta I_{(S_1+1)(S_2+1)m_2}, \\&L^* = I_{(S_1 +1)(S_2 +1)} \otimes \gamma \otimes D_1 \end{aligned}$$

$$\begin{aligned}&{m_0}= \left( {\begin{array}{*{20}c} {T^0 \otimes I_{m_2}} &{} {{\bar{0}}} \\ {{\bar{0}}} &{} { I_{S_2} \otimes \eta _{1}T^0 \otimes I_{m_2} } \\ \end{array}} \right) , \, \hbox {where} \, \eta _{1}= p+(1-p)(p_1 +p_{12}). \\&{m_1}= \left( {\begin{array}{*{20}c} {\eta _{2}T^0 \otimes I_{m_2}} &{} {{\bar{0}}} \\ {{\bar{0}}} &{} { I_{S_2} \otimes p T^0 \otimes I_{m_2} } \\ \end{array}} \right) , \, \hbox {where} \, \eta _{2}= p+(1-p)(p_2 +p_{12}). \end{aligned}$$

$$\begin{aligned}&H_1 = I_{S_1 (S_2 +1)} \otimes D_1, \, H_2 = I_{(S_1+1)S_2} \otimes D_1, \, \hbox {and} \, H_{12} = I_{S_1 S_2} \otimes D_1. \end{aligned}$$

$$\begin{aligned}&\hat{m_0}= \left( {\begin{array}{*{20}c} {diag(T^0) \otimes I_{m_2}} &{} {{\bar{0}}} \\ {{\bar{0}}} &{} { I_{S_2} \otimes \eta _{1} diag(T^0) \otimes I_{m_2} } \\ \end{array}} \right) , \\&\hbox {where}, \, \eta _{1}= p+(1-p)(p_1 +p_{12}). \\&\hat{m_1}= \left( {\begin{array}{*{20}c} {\eta _{2} diag(T^0) \otimes I_{m_2}} &{} {{\bar{0}}} \\ {{\bar{0}}} &{} { I_{S_2} \otimes p diag( T^0) \otimes I_{m_2} } \\ \end{array}} \right) , \\&\hbox {where} \, \eta _{2}= p+(1-p)(p_2 +p_{12}). \end{aligned}$$

$$\begin{aligned}&Z^{0}= I_{(S_1+1)(S_2+1)} \otimes (\gamma \otimes I_{m2}),\ Z= \beta I_{l_1 + l_2 + l_3 +l_4} \end{aligned}$$

where,

$$\begin{aligned}&{G_1} = \left( {\begin{array}{*{20}c} {I_{s_1+1} \otimes C_3} &{} {e_{s_1+1} \otimes \beta _1 I_{(S_2 +1)m_1m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes C_4} \\ \end{array}} \right) . \\&{C_3} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes B_5} &{} {e_{s_2+1} \otimes \beta _2 I_{m_1m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes B_6} \\ \end{array}} \right) , \, {C_4} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes B_7} &{} {e_{s_2+1} \otimes \beta _2 I_{m_1m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes B_8} \\ \end{array}} \right) ,\\&{B_5} = {\begin{array}{*{20}c} {T \oplus D_0 - (\beta +\beta _1+\beta _2)I_{m_1 m_2}} \\ \end{array}}, \, {B_6} = {\begin{array}{*{20}c} {T \oplus D_0 - (\beta +\beta _1)I_{m_1 m_2}} \\ \end{array}}, \\&{B_7} = {\begin{array}{*{20}c} {T \oplus D_0 - (\beta +\beta _2)I_{m_1 m_2}} \\ \end{array}}, \, {B_8} = {\begin{array}{*{20}c} {T \oplus D_0 - \beta I_{m_1 m_2}} \\ \end{array}} .\\&{G^{12}}= \left( {\begin{array}{*{20}c} {\bar{0}} \\ {H_1} \\ \end{array}} \right) , \, {H_1} = {\begin{array}{*{20}c} {I_{S_1(S_2 +1)} \otimes (1-p) p_1 (T^0 \otimes I_{m_{2}})} \\ \end{array}}\\&G^{13}= I_{S_1+1} \otimes Z^{*}, \, {Z^{*}}= \left( {\begin{array}{*{20}c} {\bar{0}} \\ { H_2} \\ \end{array}} \right) , \, {H_2} = {\begin{array}{*{20}c} {I_{S_2} \otimes (1-p)p_2 (T^0 \otimes I_{m_2})} \\ \end{array}} .\\&{G^{14}}= \left( {\begin{array}{*{20}c} {\bar{0}} \\ {I_{S_1} \otimes {\bar{Z}}} \\ \end{array}} \right) , \, {{\bar{Z}}}= \left( {\begin{array}{*{20}c} {\bar{0}} \\ { H_3} \\ \end{array}} \right) , \, {H_3} = {\begin{array}{*{20}c} {I_{S_2} \otimes (1-p)p_{12} (T^0 \otimes I_{m_2})} \\ \end{array}},\\&{G_2} = \left( {\begin{array}{*{20}c} {I_{s_1} \otimes C_5} &{} {e_{s_1} \otimes \beta _1 I_{(S_2 +1)m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes C_6} \\ \end{array}} \right) , \, \hbox {where}\\&{C_5} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes B_9} &{} {e_{s_2+1} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes B_{10} } \\ \end{array}} \right) , \, {C_6} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes B_{11}} &{} {e_{s_2+1} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes B_{12} } \\ \end{array}} \right) \\&{B_9} = {\begin{array}{*{20}c} { D_0 - (\beta +\beta _1+\beta _2 +\mu _1)I_{m_2}} \\ \end{array}}, \, {B_{10}} = {\begin{array}{*{20}c} {D_0 - (\beta +\beta _1+\mu _1)I_{m_2}} \\ \end{array}},\\&{B_{11}} = {\begin{array}{*{20}c} { D_0 - (\beta +\beta _2+\mu _1)I_{m_2}} \\ \end{array}}, \, {B_{12}} = {\begin{array}{*{20}c} { D_0 - (\beta +\mu _1)I_{m_2}} \\ \end{array}} . \\&{G_3} = \left( {\begin{array}{*{20}c} {I_{s_1+1} \otimes C_7} &{} {e_{s_1+1} \otimes \beta _1 I_{(S_2 +1)m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes C_8} \\ \end{array}} \right) , \, \hbox {where} \\&{C_7} = \left( {\begin{array}{*{20}c} {I_{s_2} \otimes B_{13}} &{} {e_{s_2} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes B_{14} } \\ \end{array}} \right) , \, {C_8} = \left( {\begin{array}{*{20}c} {I_{s_2} \otimes B_{15}} &{} {e_{s_2} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes B_{16} } \\ \end{array}} \right) \\&{B_{13}} = {\begin{array}{*{20}c} { D_0 - (\beta +\beta _1+\beta _2 +\mu _2)I_{m_2}} \\ \end{array}}, \, {B_{14}} = {\begin{array}{*{20}c} {D_0 - (\beta +\beta _1+\mu _2)I_{m_2}} \\ \end{array}},\\&{B_{15}} = {\begin{array}{*{20}c} { D_0 - (\beta +\beta _2+\mu _2)I_{m_2}} \\ \end{array}}, \, {B_{16}} = {\begin{array}{*{20}c} {D_0 - (\beta +\mu _2)I_{m_2}} \\ \end{array}} .\\&{G_4} = \left( {\begin{array}{*{20}c} {I_{s_1} \otimes C_9} &{} {e_{s_1} \otimes \beta _1 I_{(S_2 +1)m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes C_{10}} \\ \end{array}} \right) , \, \hbox {where} \\&{C_9} = \left( {\begin{array}{*{20}c} {I_{s_2} \otimes B_{17}} &{} {e_{s_2} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes B_{18} } \\ \end{array}} \right) , \, {C_{10}} = \left( {\begin{array}{*{20}c} {I_{s_2} \otimes B_{19}} &{} {e_{s_2} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes B_{20} } \\ \end{array}} \right) \\&{B_{17}} = {\begin{array}{*{20}c} {D_0 - (\beta +\beta _1+\beta _2 +\mu _{12})I_{m_2}} \\ \end{array}}, \, {B_{18}} = {\begin{array}{*{20}c} { D_0 - (\beta +\beta _1+\mu _{12})I_{m_2}} \\ \end{array}},\\&{B_{19}} = {\begin{array}{*{20}c} { D_0 - (\beta +\beta _2+\mu _{12})I_{m_2}} \\ \end{array}}, \, {B_{20}} = {\begin{array}{*{20}c} { D_0 - (\beta +\mu _{12})I_{m_2}} \\ \end{array}} . \end{aligned}$$

where,

$$\begin{aligned}&\hat{G_1} = \left( {\begin{array}{*{20}c} {I_{s_1+1} \otimes \hat{C_3}} &{} {e_{s_1+1} \otimes \beta _1 I_{(S_2 +1)m_1m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes \hat{C_4}} \\ \end{array}} \right) ., \, \hbox {where} \\&\hat{C_3} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes \hat{B_5}} &{} {e_{s_2+1} \otimes \beta _2 I_{m_1m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \hat{B_6}} \\ \end{array}} \right) , \, \hat{C_4} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes \hat{B_7}} &{} {e_{s_2+1} \otimes \beta _2 I_{m_1m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \hat{B_8}} \\ \end{array}} \right) ,\\&\hat{B_5} = {\begin{array}{*{20}c} {T \oplus D_0 - (\beta _1+\beta _2)I_{m_1 m_2}} \\ \end{array}}, \, \hat{B_6} = {\begin{array}{*{20}c} {T \oplus D_0 - (\beta _1)I_{m_1 m_2}} \\ \end{array}}, \\&\hat{B_7} = {\begin{array}{*{20}c} {T \oplus D_0 - (\beta _2)I_{m_1 m_2}} \\ \end{array}}, \, \hat{B_8} = {\begin{array}{*{20}c} {T \oplus D_0 } \\ \end{array}} .\\&\hat{G_2} = \left( {\begin{array}{*{20}c} {I_{s_1} \otimes \hat{C_5}} &{} {e_{s_1} \otimes \beta _1 I_{(S_2 +1)m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes \hat{C_6}} \\ \end{array}} \right) , \, \hbox {where} \\&\hat{C_5} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes \hat{B_9}} &{} {e_{s_2+1} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \hat{B_{10}} } \\ \end{array}} \right) , \, \hat{C_6} = \left( {\begin{array}{*{20}c} {I_{s_2+1} \otimes \hat{B_{11}}} &{} {e_{s_2+1} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \hat{B_{12}} } \\ \end{array}} \right) \\&\hat{B_9} = {\begin{array}{*{20}c} {D_0 - (\beta _1+\beta _2 +\mu _1)I_{m_2}} \\ \end{array}}, \, \hat{B_{10}} = {\begin{array}{*{20}c} { D_0 - (\beta _1+\mu _1)I_{m_2}} \\ \end{array}},\\&\hat{B_{11}} = {\begin{array}{*{20}c} { D_0 - (\beta _2+\mu _1)I_{m_2}} \\ \end{array}}, \, \hat{B_{12}} = {\begin{array}{*{20}c} { D_0 - (\mu _1)I_{ m_2}} \\ \end{array}} . \\&\hat{G_3} = \left( {\begin{array}{*{20}c} {I_{s_1+1} \otimes \hat{C_7}} &{} {e_{s_1+1} \otimes \beta _1 I_{(S_2 +1)m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes \hat{C_8} } \\ \end{array}} \right) ., \, \hbox {where} \\&\hat{C_7} = \left( {\begin{array}{*{20}c} {I_{s_2} \otimes \hat{B_{13}}} &{} {e_{s_2} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \hat{B_{14} }} \\ \end{array}} \right) , \, \hat{C_8} = \left( {\begin{array}{*{20}c} {I_{s_2} \otimes \hat{B_{15}}} &{} {e_{s_2} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \hat{B_{16} }} \\ \end{array}} \right) \\&\hat{B_{13}} = {\begin{array}{*{20}c} { D_0 - (\beta _1+\beta _2 +\mu _2)I_{m_2}} \\ \end{array}}, \, \hat{B_{14}} = {\begin{array}{*{20}c} { D_0 - (\beta _1+\mu _2)I_{m_2}} \\ \end{array}},\\&\hat{B_{15}} = {\begin{array}{*{20}c} { D_0 - (\beta _2+\mu _2)I_{m_2}} \\ \end{array}}, \, \hat{B_{16}} = {\begin{array}{*{20}c} { D_0 - (\mu _2)I_{m_2}} \\ \end{array}} . \\&\hat{G_4} = \left( {\begin{array}{*{20}c} {I_{s_1} \otimes \hat{C_9}} &{} {e_{s_1} \otimes \beta _1 I_{(S_2 +1)m_2}} \\ {\bar{0}} &{} {I_{S_1-s_1} \otimes \hat{C_{10}}} \\ \end{array}} \right) , \, \hbox {where} \\&\hat{C_9} = \left( {\begin{array}{*{20}c} {I_{s_2} \otimes \hat{B_{17}}} &{} {e_{s_2} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \hat{B_{18} }} \\ \end{array}} \right) , \, \hat{C_{10}} = \left( {\begin{array}{*{20}c} {I_{s_2} \otimes \hat{B_{19}}} &{} {e_{s_2} \otimes \beta _2 I_{m_2}} \\ {\bar{0}} &{} {I_{S_2-s_2} \otimes \hat{B_{20} }} \\ \end{array}} \right) \\&\hat{B_{17}} = {\begin{array}{*{20}c} { D_0 - (\beta _1+\beta _2 +\mu _{12})I_{m_2}} \\ \end{array}}, \, \hat{B_{18}} = {\begin{array}{*{20}c} {D_0 - (\beta _1+\mu _{12})I_{ m_2}} \\ \end{array}},\\&\hat{B_{19}} = {\begin{array}{*{20}c} { D_0 - (\beta _2+\mu _{12})I_{m_2}} \\ \end{array}}, \, \hat{B_{20}} = {\begin{array}{*{20}c} {D_0 - (\mu _{12})I_{m_2}} \\ \end{array}} . \end{aligned}$$

2.1 Stability condition

Let $\pi = (\pi _0, \pi _1, \pi _2, \ldots , \pi _S)$ be the steady state probability vector of $A = A_0 + A_1 +A_2.$ Then

$$\begin{aligned} \pi A=0, \pi e =1 \end{aligned}$$

(1)

From (1),

$$\begin{aligned}&\pi _0 N_0 + \pi _1 M_0= 0 \\&\pi _i N_1 + \pi _{i+1}M =0, 1\le i \le s \\&\pi _i N_2 + \pi _{i+1}M =0, s+1\le i \le S-1 \\&\pi _0 Z^0 + \sum _{i=1}^{s } \pi _i Z +\pi _S N_2 =0 \end{aligned}$$

Where,

$$\begin{aligned}&N_0 = Z_0 \\&N_i=L+ Z_i + {\bar{M}}, \, 1\le i \le 2 \\ \end{aligned}$$

Solving the above system of equations, we get

$$\begin{aligned} \pi _i=\left\{ \begin{array}{ll} \pi _S {\mathcal {U}}_{0} &{} i=0\\ \pi _S {\mathcal {U}}_{i} &{} 1 \le i \le s\\ \pi _S {\hat{\mathcal {U}}}_{i} &{} s+1 \le i \le S \\ \end{array} \right. \end{aligned}$$

Where,

$$\begin{aligned}&{\mathcal {U}}_{0}=(-1)^{S}(MN_{2}^{-1})^{S-s-1}(MN_{1}^{-1})^{s}(M_0 N_0^{ -1}) \\&{\mathcal {U}}_{i} = (-1)^{S-i}(MN_{2}^{-1})^{S-s-1}(MN_{1}^{-1})^{s+1-i} \\&{\hat{\mathcal {U}}}_{i} = (-1)^{S-i}(MN_{2}^{-1})^{S-i} \end{aligned}$$

The unknown probability $\pi _S$ can be calculated from the normalising condition

$$\begin{aligned} \pi _S \left( {\mathcal {U}}_{0}+ \sum _{i=1}^{s} {\mathcal {U}}_{i} + \sum _{i=s+1}^{S} {\hat{\mathcal {U}}}_{i} \right) {\varvec{e}}=1, \\ \end{aligned}$$

Theorem 2.1

The queuing inventory system under study is stable if and only if

$$\begin{aligned} \pi _S {\mathcal {H}}_0{\mathcal {V}}_0 < \pi _S \left( {\mathcal {H}}_1 {\mathcal {V}}_1 + {\mathcal {H}}_2 {\mathcal {V}}_2 \right) \end{aligned}$$

Proof

The queueing system with the generator ${\mathcal {Q}}$ under study is stable if and only if

$$\begin{aligned} \pi A_0e < \pi A_2e \end{aligned}$$

(2)

From $A_0$ and $A_2$ mentioned before, we obtain

$$\begin{aligned} \pi A_0e = \pi _S \left( \sum _{i=1}^{s} {\mathcal {U}}_{i} + \sum _{i=s+1}^{S} {\hat{\mathcal {U}}}_{i} \right) L.e \end{aligned}$$

and

$$\begin{aligned} \pi A_2e = \pi _S \left[ {\mathcal {U}}_{1} (M_0 +{\bar{M}}) + \left( \sum _{i=2}^{s} {\mathcal {U}}_{i} + \sum _{i=s+1}^{S} {\hat{\mathcal {U}}}_{i}\right) ({\bar{M}}+M)\right] .e \end{aligned}$$

Let

$$ \begin{aligned}&{\mathcal {H}}_0=\sum _{i=1}^{s} {\mathcal {U}}_{i} + \sum _{i=s+1}^{S} {\hat{\mathcal {U}}}_{i}, \; \; \; {\mathcal {V}}_0 =L.e,\; \; \; {\mathcal {H}}_1 = {\mathcal {U}}_1, \; \; \; {\mathcal {V}}_1 =(M_0+{\bar{M}}).e, \; \; \; \\&{\mathcal {H}}_2=\sum _{i=2}^{s} {\mathcal {U}}_{i} + \sum _{i=s+1}^{S} {\hat{\mathcal {U}}}_{i} \; \; \& \; \;{\mathcal {V}}_2 =({\bar{M}}+M).e \end{aligned}$$

Then by (2) we get the stated result. $\square$

2.2 Steady state probability vector

Assuming that the stability condition is satisfied, the steady state probability vector of the system $\varvec{\Omega }$ is calculated as follows: Let $\mathbf{x }$ denote the steady state probability vector of the generator ${\mathcal {Q}}$. Then we have

$$\begin{aligned} \mathbf{x } {\mathcal {Q}} = 0, \ \ \ \ \ \ \mathbf{x } \mathbf{e } = 1. \end{aligned}$$

(3)

Partitioning $\mathbf{x }$ as $\mathbf{x } = (\mathbf{x }_0, \mathbf{x }_1, \mathbf{x }_2, ...)$, by the above conditions we get

$$\begin{aligned}&\mathbf{x }_ 0 A_{00}+\mathbf{x }_1A_{10} =0 \nonumber \\&\mathbf{x }_0A_{01}+\mathbf{x }_{1}A_1+\mathbf{x }_{2}A_2=0 \nonumber \\&\mathbf{x }_{n-1}A_{0}+\mathbf{x }_{n}A_1+\mathbf{x }_{n+1}A_2=0 ; n \ge 2 \end{aligned}$$

(4)

By assuming the stability condition, we see that $\mathbf{x }$ is obtained as (see Neuts)

$$\begin{aligned} \mathbf{x }_n = \mathbf{x }_1 R^{n-1} ; n \ge 2, \end{aligned}$$

(5)

where R is the minimal non-negative solution of the matrix quadratic equation

$$\begin{aligned} R^2 A_2 + R A_1 + A_0 = 0 \end{aligned}$$

(6)

The boundary conditions are given by

$$\begin{aligned}&\mathbf{x }_ 0 A_{00}+\mathbf{x }_1A_{10} =0 \nonumber \\&\mathbf{x }_0A_{01}+\mathbf{x }_{1}[A_1 +R A_2]=0 \end{aligned}$$

(7)

From Eq. (7) we get,

$$\begin{aligned} \mathbf{x }_1 = \mathbf{x }_0 {\mathcal {K}} \end{aligned}$$

(8)

and hence by the normalising condition in equation number (3), we get

$$\begin{aligned} {[}\mathbf{x }_0 + \mathbf{x }_0 {\mathcal {K}} (I-R)^{-1}]\mathbf{e } =1 \end{aligned}$$

(9)

where

$$\begin{aligned} {\mathcal {K}} = (-A_{01})( A_1+ R A_2)^{-1} \end{aligned}$$

(10)

3 Some system performance measures

• 1. Expected re-ordering rate of essential item

  $$\begin{aligned} E_{RE}= \mu '\sum _{n=1}^{\infty }\sum _{k=1}^{m}\sum _{i_k=1}^{S_k}\sum _{j_1=1}^{m_1}\sum _{j_2=1}^{m_2} \mathbf{x }_n (s+1,0,i_1,\ldots ,i_m,j_1,j_2) \end{aligned}$$

• 2. Expected re-ordering rate of l th optional item, $1\le l \le m$

  $$\begin{aligned} E_{ROI}(l)=\mu _l \sum _{n=1}^{\infty }\sum _{i=1}^{S} \left( \sum _{\begin{array}{c} u \in \Lambda \\ l \in u \end{array}} \sum _{\begin{array}{c} i_k=0,\\ k\not \in u,\\ 1\le k \le m \end{array}}^{S_k} \sum _{\begin{array}{c} i_k=1,\\ k\in u, \\ 1 \le k \le m \end{array}}^{S_k} \right) \sum _{j_2=1}^{m_2} \mathbf{x }_n (i,u,i_1,\ldots ,i_{h-1},s_l +1,i_{h+1},\ldots ,j_2) \end{aligned}$$

• 3. Expected number of customers in the system $E_C = \sum _{i=1}^{\infty }i.\mathbf{x }_i.e$

• 4. Expected number of essential inventories in the system

  $$\begin{aligned} E_{EI}&=\sum _{i=1}^{S} \sum _{k=1}^{m}\sum _{i_k=1}^{S_k} \sum _{j_2=1}^{m_2}i. \mathbf{x }_0 (i,0^*,i_1,\ldots ,i_m,j_2) \\&\quad + \sum _{n=1}^{\infty }\sum _{i=1}^{S}\sum _{k=1}^{m}\sum _{i_k=1}^{S_k} \sum _{j_1=1}^{m_1}\sum _{j_2=1}^{m_2}i. \mathbf{x }_n (i,0,i_1,\ldots ,i_m,j_1,j_2) \\&\quad + \sum _{n=1}^{\infty }\sum _{i=1}^{S} \left( \sum _{u \in \Lambda } \sum _{\begin{array}{c} i_k=0,\\ k\not \in u,\\ 1\le k \le m \end{array}}^{S_k} \sum _{\begin{array}{c} i_k=1,\\ k\in u, \\ 1 \le k \le m \end{array}}^{S_k}\right) \sum _{j_2=1}^{m_2}i. \mathbf{x }_n (i,u,i_1,\ldots ,i_m,j_2) \end{aligned}$$

• 5. Expected number of l th optional inventories in the system for $1 \le l \le m$.

  $$\begin{aligned} E_{{OI}_l}&=\sum _{i=1}^{S} \sum _{k=1}^{m}\sum _{i_k=1}^{S_k} \sum _{j_2=1}^{m_2}i_l. \mathbf{x }_0 (i,0^*,i_1,\ldots ,i_m,j_2) \\&\quad + \sum _{n=1}^{\infty }\sum _{i=1}^{S}\sum _{k=1}^{m}\sum _{i_k=1}^{S_k}\sum _{j_1=1}^{m_1}\sum _{j_2=1}^{m_2}i_l. \mathbf{x }_n (i,0,i_1,\ldots ,i_m,j_1,j_2) \\&\quad + \sum _{n=1}^{\infty }\sum _{i=1}^{S}\left( \sum _{u \in \Lambda } \sum _{\begin{array}{c} i_k=0,\\ k\ne l, k\not \in u,\\ 1\le k \le m \end{array}}^{S_k} \sum _{\begin{array}{c} i_k=1,\\ k=l, k\in u, \\ 1 \le k \le m \end{array}}^{S_k}\right) \sum _{j_2=1}^{m_2}i_l. \mathbf{x }_n (i,u,i_1,\ldots ,i_m,j_2) \end{aligned}$$

• 6. Expected loss rate of customers in the absence of essential item

  $$\begin{aligned} E_L = \lambda \sum _{n=1}^{\infty } \sum _{k=1}^{m}\sum _{i_k=1}^{S_k} \sum _{j_2=1}^{m_2} \mathbf{x }_n (0,0^*,i_1,\ldots ,i_m,j_2) \end{aligned}$$

4 Cost function

In this section, we provide the optimal values of inventory levels $s, S, s_i$ and $S_i$ for $1\le i \le m$. We introduce the cost function,

$$\begin{aligned}&K(s,s_1,\ldots ,s_m,S,S_1, \ldots ,S_m) \\&\quad =C^0 E_{R_E} +\sum _{i=1}^{m}C^i E_{R_{OI}}(i) + C_{EI} E_{EI} +\sum _{i=1}^{m}C_{OI}(i) E_{OI}(i) \\&\qquad + C_1 E_C + C_2 E_L \end{aligned}$$

where

• 1. $C^0$ = Fixed ordering cost due to essential item /unit item

• 2. $C^i$= Fixed ordering cost due to the i th optional item

• 3. $C_{EI}$= Holding cost due to the essential item/ unit

• 4. $C_{OI}(i)$= Holding cost due to the i th optional item/ unit

• 5. $C_1$= Holding cost of customers/ unit time

• 6. $C_2$= Cost due to loss of customers / unit time, in the absence of the essential item

5 Numerical illustration

For numerical illustration, we have considered the model with one eessential and two optional inventories (the case when m=2). The number of phases of the arrival process is taken as 4 where as the number of phases in the service process is taken as 3. Here we take $D_o$, $D_1$, T and $T^0$ as follows.

$$\begin{aligned} D_{0}= & {} \left( {\begin{array}{*{20}c} -6.18 &{} 1.2 &{} 2 &{} 2 \\ 1 &{} -8.213 &{} 3 &{} 3 \\ 2 &{} 3 &{} -10.08 &{} 4 \\ 3 &{} 4 &{} 3 &{} -11.02 \\ \end{array}} \right) ,\\ D_{1}= & {} \left( {\begin{array}{*{20}c} 0.20 &{} 0.23 &{} 0.30 &{} 0.25 \\ 0.31 &{} 0.32 &{} 0.34 &{} 0.243 \\ 0.25 &{} 0.26 &{} 0.27 &{} 0.30\\ 0.27 &{} 0.22 &{} 0.32 &{} 0.21 \\ \end{array}} \right) \\ T= & {} \left( {\begin{array}{*{20}c} -18 &{} 4 &{} 6 \\ 1 &{} -11 &{} 5 \\ 3 &{} 6 &{} -16 \\ \end{array}} \right) , \, T^{0} = \left( {\begin{array}{*{20}c} 8 \\ 5 \\ 7 \\ \end{array}} \right) ,\\ \gamma= & {} \left( {\begin{array}{*{20}c} 0.3 &{} 0.2&{} 0.5 \\ \end{array}} \right) \end{aligned}$$

The variations in the system performance measures with various parameters are numerically shown as follows.

Table 1 Effect of $\beta$: Fix $S=5,S_1= 4, S_2=3,s=3,s_1=2,s_2=1$, $m1=3,m2=4,\mu _1=6, \mu _2=7,\mu _{12}=8, \beta _{1} =5, \beta _{2} =5$

Table 1 shows the effect of the replenishment rate $\beta$ of the essential item on various performance measures. As seen in the table, the values of $E_{RE}, E_{ROI(1)}, E_{ROI(2)}, E_C, E_{OI(1)}$, $E_{OI(2)}$ and $E_L$ seems to be decreasing with increase in the value of $\beta$, where as an increasing tendency is observed with an increased values of $\beta$ in the case of $E_{EI}$.

Table 2 Effect of $\mu _1$ : Fix $S=5,S_1= 4, S_2=3,s=3,s_1=2,s_2=1$, $m1=3,m2=4, \mu _2=4,\mu _{12}=5, \beta =8,\beta _{1} =6, \beta _{2} =5$

Table 3 Effect of $\mu _2$ : Fix $S=5,S_1= 4, S_2=3,s=3,s_1=2,s_2=1, m1=3,m2=4, \mu _1=4,\mu _{12}=5, \beta =8,\beta _{1} =6, \beta _{2} =5$

Table 4 Effect of $\mu _{12}$ : Fix $S=5,S_1= 4, S_2=3,s=3,s_1=2,s_2=1$, $m1=3,m2=4, \mu _1=4,\mu _{2}=5, \beta =8,\beta _{1} =6, \beta _{2} =5$

Tables 2, 3 and 4 shows the effect of $\mu _1, \mu _{2}$ and $\mu _{12}$, the exponential service rates of the first, second and the combined optional services on the performance measures. As seen in the Tables 2, 3 and 4, the values of $E_{RE}, E_{ROI(1)}, E_{ROI(2)},E_{EI}, E_{OI(1)}$, $E_{OI(2)}$ and $E_L$ shows an increasing tendency respectively with increased values of $\mu _1, \mu _{2}$ and $\mu _{12}$ where as $E_C$ shows a decreasing tendency respectively with the incresased values of $\mu _1, \mu _{2}$ and $\mu _{12}$.

5.1 Numerical analysis of cost function

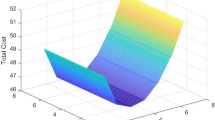
Table 5 shows the effect of the pair (s, S) of the essential inventory on the cost incurred by the system. With the increased values of S the cost showed an increasing tendency as expected as the cost of a single unit of the essential item is high also it’s holding cost adds to this hike. Even though the cost decreased initially with the increased values of s, it later showed an increasing behaviour( at s=4).

Table 6 gives the effect of of the pair $(s_1,S_1)$ with respect to the first optional item in the cost incurred on the system. The cost showed an increasing tendency with increased values of $S_1$ as expected except in the case where $s_1=3$ where the cost decreased initially and then showed an increasing behaviour. As the value of $s_1$ is increased, the cost seems to be decreasing.

Table 5 Effect of (s, S) on the Cost function: Fix $S_1= 4, S_2=3,s_1=2,s_2=1$, $m1=3,m2=4, \mu _1=4,\mu _{2}=5,\mu _{12}=6, \beta =7,\beta _{1} =6, \beta _{2} =5,C^0=120$$, $C^1=35$$, $C^2=40$$, $C_{EI}=110$$, $C_{OI}(1)=500$$, $C_{OI}(2)=450$$, $C_1=70$$, $C_2=50$$

Table 6 Effect of $(s_1,S_1)$ on the Cost function: Fix $S= 4, S_2=3,s=2,s_2=1$, $m1=3,m2=4, \mu _1=4,\mu _{2}=5,\mu _{12}=6, \beta =7,\beta _{1} =6$, $\beta _{2} =5,C^0=120$$, $C^1=35$$, $C^2=40$$, $C_{EI}=110$$, $C_{OI}(1)=500$$, $C_{OI}(2)=450$$, $C_1=70$$, $C_2=50$$

Table 7 Effect of $(s_2,S_2)$ on the Cost function: Fix $S= 4, S_1=3,s=2,s_1=1$, $m1=3,m2=4, \mu _1=4,\mu _{2}=5,\mu _{12}=6, \beta =7,\beta _{1} =6$, $\beta _{2} =5,C^0=120$$, $C^1=35$$, $C^2=40$$, $C_{EI}=110$$, $C_{OI}(1)=500$$, $C_{OI}(2)=450$$, $C_1=70$$, $C_2=50$$

Table 7 gives the effect of the pair $(s_2,S_2)$ with respect to the second optional item in the cost incurred on the system. The cost showed an increasing tendency with increased values of $S_2$ as expected. As the value of $s_2$ is increased, the cost seems to be decreasing. The optimum values of the control variables are when the values of S and $S_i$ for $1\le i \le m$ are kept minimum together with the values of s and $s_i$ fixed close to those of S and $S_i$ respectively for $1 \le i \le m$.

6 Conclusion

We analyzed a multi-commodity queueing inventory system with one essential and m optional items. Immediately after the service of an essential item, the customer either leaves the system with probability p or with probability 1-p he/she goes for optional item(s). However, in the absence of an essential item, service will not be provided. With the arrival of customers forming Markovian arrival process (MAP), service time of essential item Phase type distributed and that for optional items exponentially distributed( depending on the type(s) of item(s)), all given by a single server, the system was analysed. Then we obtained the system state probability distribution. Under stability condition, we computed the long run system state distribution. A cost function involving these control variables was established. An optimization of the control variables w.r.t the cost function is also done numerically and it is the same as what we see around us. For example, in car showroom, huge machinery showroom etc., only a few items (main item) will be displayed and orders will be taken as per the requirement of the customers.

Extending the model discussed by introducing random/ Markovian environments is proposed as a future work. This will be quite challenging.