Two-machine flowshop scheduling problem with coupled-operations

Abstract

This paper addresses a generalization of the coupled-operations scheduling problem in the context of a flow shop environment. We consider the two-machine scheduling problem with the objective of minimizing the makespan. Each job consists of a coupled-operation to be processed first on the first machine and a single operation to be then processed on the second machine. A coupled-operation contains two operations separated by an exact time delay. The single operation can start on the second machine only when the coupled-operation on the first machine is completed. We prove the NP-completeness of two restricted versions of the general problem, whereas we also exhibit several other well solvable cases.

1 Introduction

The coupled-operations scheduling problem was first introduced by Shapiro (1980). It consists of a set of n jobs to be scheduled on a single machine. Each job j consists of a coupled-operation. A coupled-operation is made of two operations that have to be processed with an intermediate exact delay $L_{j}$, i.e., if $C_j^1$ and $S_j^2$ denote the completion time and the start time of the first and the second operation of job j, respectively, then, in a valid schedule, we have $S_j^2-C_j^1=L_j$. Each job j is thus described by a triplet $(a_{j},L_{j},b_{j})$, where $a_{j}$ and $b_{j}$ denote the processing times of the first and the second operation of job j, respectively, separated by the exact time delay $L_{j}$, as illustrated in Fig. 1. The objective we seek to minimize is the overall completion time (known as the makespan) or some other regular objective functions. Orman and Potts (1997) denoted this problem as $(a_{j},L_{j},b_{j})$.

Fig. 1

Examples of job interleaving

The motivation for the coupled-operation scheduling problem comes from the radar activities, where two subsequent pulses are used to compute the speed and the trajectory of a moving object. The emission pulse and the receptive pulse to detect an object are separated by a fixed time delay (Shapiro 1980). Other applications in robotic cells are cited in Brauner et al. (2009).

Orman and Potts (1997) studied the $(a_{j},L_{j},b_{j})$ problem where they enumerated several problems and arranged them hierarchically according to their complexity status. Ageev and Kononov (2007) provided several approximation algorithms depending on the values of $a_{j}$ and $b_{j}$. Ageev and Baburin (2007) proposed a 7/4-approximation algorithm for that problem. A few works considered additional constraints to the coupled-operation problem. We may cite Blazewicz et al. (2010) where it is shown that the $(a_{j}=b_{j}=1,L_{j}=l)$ problem is NP-hard if precedence constraints between the coupled operations are considered. However, for a tree, the corresponding problem is solvable in linear time. Simonin et al. (2010) showed that the $(a_j=b_j=1,L_j)$ problem with precedence and compatibility constraints among the coupled operations is NP-hard. Let us also mention the paper of Ahr et al. (2004) for the (a, L, b) problem for which an algorithm with a time complexity $O(nr^{2L})$ is presented, where $r \le \root a-1 \of {a}$. A general survey on this problem is presented in Blazewicz et al. (2012).

In the context of the standard flowshop, research has mainly focused on cases with minimum time delays in which a minimum time delay must elapse between two successive operations of a job. The mostly studied problem is the two-machine case with respect to the makespan, denoted $F2|L_j|C_{\max }$. The corresponding problem with unit-time operations is NP-hard (Yu et al. 2004). In the approximation front, Dell’Amico (1996) provided a 2-approximation algorithm for $F2|L_j|C_{\max }$, Karuno and Nagamochi (2003) improved on this and gave an $\frac{11}{6}$-approximation algorithm. Ageev (2008) showed that the worst case ratio could be improved to $\frac{3}{2}$ if $a_j=b_j$ for each job, $j=1, \ldots , n$. However, if we restrict the problem to the permutation case, Mitten (1958) provides a polynomial time algorithm.

Another model has also been proposed in the literature in which, in addition to the minimal time delay constraints, a maximal time delay is imposed on the processing of jobs (i.e., the following operation of a job must be processed within a time interval during their processing). For more details, see e.g. (Fondrevelle et al. 2006, 2008). Let us note that the flowshop scheduling problem with exact time delays is a special case of the problem minimum time delays. This problem received little attention in the literature.

In this paper we consider the two-machine flowshop scheduling problem with coupled-operations with exact delays. More precisely, in this model, each job consists of a coupled-operation processed on the first machine and a single operation that has to be processed on the second machine. The coupled-operation on the first machine comprises of two parts separated by an exact time delay. Moreover, the operation on the second machine can start only when the coupled-operation on the first machine is completed. The motivation of flowshop scheduling problems with coupled-operations is encountered in chemical workshop production systems where each machine must carry out several operations of the same job and an exact delay is imposed between the execution of each two consecutive operations on the same machine due to some chemical reactions (Chu and Proth 1994).

This paper is organized as follows. In Sect. 2, a description and classification of problems under study are presented. In Sect. 3, we provide NP-hardness results for several restricted versions of the general problem, whereas, in Sect. 4, we discuss several well solvable cases. Section 5 is our conclusion.

2 Problem description and classification

We consider the flowshop scheduling problem with two machines $M_1$ and $M_2$. A set $J =\{1, \ldots , n\}$ of jobs needs to be scheduled first on $M_1$, and then on $M_2$. Each job j consists of a coupled-operation $O_{1,j}$ and a single operation $O_{2,j}$. Each coupled-operation $O_{1,j}$ of job j is described by a triplet $(a_j , L_j , b_j)$ where $a_j$ and $b_j$ are the processing times of the first and the second part, respectively, and $L_j$ denotes the exact time delay that separates the processing of the two parts. Operation $O_{2,j}$ is described by its processing time $c_j$. For each job j, operation $O_{2,j}$ can start only when the two parts of $O_{1,j}$ are completed on machine $M_1$. The objective is to minimize the makespan. This problem is denoted hereafter by $F2(a_j,L_j,b_j,c_j)$.

Orman and Potts (1997) studied the coupled-operations on a single machine, and derived several results depending on the values of $a_j$, $L_j$ and $b_j$. They also provided a classification of these problems depending on their complexity status. Clearly, all NP-hard problems on a single machine remain NP-Hard in the case of a flowshop. Thus, in this paper, we focus our attention on problems that are already polynomially solvable in the case of a single machine. Figure 2 provides a graph of all polynomially solvable problems discussed in Orman and Potts (1997) and the relations between these problems. In this graph arc directed from a special case to a more general problem and edges connect identical problems. For instance, problem $(a_j=a, b_j=L_j=p)$ is a special case of problem $(a_j, b_j=L_j=p)$, where $a_j$ ($j=1, \ldots , n$) is unrestricted.

We thus extend the complexity graph to the two-machine flowshop environment as in Fig. 3. Table 1 summarizes the results of two-machine flow shop environment with coupled-operations.

Before developing our contributions, we recall here two main results of the literature that will be used along this paper. The first result concerns the scheduling of n jobs in two machines flowshop problem. Given a set S of n jobs, each job $J_j$ is characterized by its processing times $p_{1,j}$ and $p_{2,j}$ on first and second machines respectively, the objective is minimizing makespan. Johnson (1954) proposed a polynomial time algorithm in O(nlogn) that proceed as in Algorithm 0.

Fig. 2

Polynomially solvable problems (Orman and Potts 1997)

Fig. 3

Two-machine flowshop complexity classification problems

The second result concerns the scheduling of n jobs with time-lags on two machines flowshop problem. Time lag is an additional time delay must elapse between completing a job at first machine and starting it at the second machine. More precisely, each job is characterized by $p_{1,j}$, $p_{2,j}$ and $l_j$ where $p_{1,j}$ and $p_{2,j}$ are the processing times and $l_j$ is the time lag. When there are no lags, a permutation schedule is always optimal in a two-machine flowshop for any regular criteria. However with time-lag this is no longer true. When the job order cannot change from machine one to machine two, i.e., we seek for permutation solution, Mitten (1958) observed that the O(nlogn) algorithm of Johnson could be extended to handle time lag. Mitten’s algorithm apply Jonhson’s algorithm to modified job processing times, in which processing times $p_{1,j}$ and $p_{2,j}$ are replaced by $p_{1,j}+l_j$ and $p_{2,j}+l_j$, respectively.

Table 1 Complexity status of two-machine flowshop scheduling with coupled-operations

Table 2 Jobs processing times

3 NP-hardness results

This section is entirely devoted to NP-completeness proofs of several variants of the problem we are considering in this paper.

3.1 Problem $F2(a_{j},p,p,c_{j})$

In this section, we consider the problem $F2(a_{j},p,p,c_{j})$. We show its NP-hardness from the partition problem with equal size, known to be NP-Hard (Garey and Johnson 1979).

The partition with equal size decision problem (PES) is stated as follows: Given is a set $E=\{e_{1},e_{2},\ldots ,e_{2n}\}$ of 2n positives integers, where $\sum _{j=1}^{2n} e_{j}=2B$ for some integer B. Does there exist a partition of E into two disjoint subsets $E_{1}$ and $E_{2}$ such as $\sum _{j\in E_{1}} e_{j}=\sum _{j\in E_{2}} e_{j}=B$ and $|E_{1}|=|E_{2}|=n$? In our proof we assume that $e_j>1$, $j=1, \ldots , 2n$.

Given an arbitrary instance of PES, we construct an instance $\mathcal I$ of problem $F2(a_{j},p,p,c_{j})$ with a set of $4n+2$ jobs as follows:

• Jobs of type U, denoted $U_{j}$, $j=1, \ldots , 2n$;

• n identical jobs denoted V;

• $n+1$ identical jobs denoted W;

• One job denoted T;

For all jobs, we set $L_{j}=b_{j}=p$, $j=1, \ldots , 4n+2$, where $p>B$. The processing times of jobs on $M_1$ and $M_2$ are given in Table 2.

We show that the PES problem has a solution if, and only if, the scheduling problem admits a solution S with $C_{max}(S) \le y$, where $y=4(2n+1)p+1$.

In the following, the notation (XY)-job where $X,Y \in \{T,U,V,W\}$ refers to the composite job (XY) in which jobs X and Y are interleaved and the first operation of X is on the first position. For instance, the composite job (VW) can be seen as a compact job with processing times $4p+1$ and 4p on machines $M_1$ and $M_2$, respectively, and a time-lag $l=-p$ (see Fig. 4).

Fig. 4

Example of composite job (VW)

Lemma 1

If PES problem has a solution then instance ${{\mathcal {I}}}$ of $F2(a_{j},p,p,c_{j})$ has a feasible solution S such that $C_{max}(S) \le y$.

Proof

Let $E_1$ and $E_2$ be the partition of set E such that $\sum _{j \in E_1} e_j = \sum _{j \in E_2} e_j = B$ where each set $E_1$ and $E_2$ contains exactly n elements. We can schedule the jobs of instance ${\mathcal {I}}$ as follows:

Let $I_1$ and $I_2$ be the subset of U-jobs corresponding to $E_1$ and $E_2$, respectively. Let S be a feasible schedule of instance ${\mathcal {I}}$ in which U-jobs of $J_1$ ($J_2$) are interleaved with V-jobs (W-jobs), and the job T is interleaved with job W. Let (VU)-jobs = $\{(VU)_1, \ldots , (VU)_n\}$, (UW)-jobs = $\{(UW)_1, \ldots , (UW)_n\}$ and (WT)-job be the composite jobs obtained by the interleaving operation. The Schedule S is constructed as follows (see Fig. 5): start by scheduling (VU)-jobs, followed by (TW)-job, then complete the schedule with (UW)-jobs. The composite jobs of set (VU)-jobs ((UW)-jobs) in schedule S can be chosen in an arbitrary order. Clearly in S there is no idle-time between composite jobs on $M_1$ and $M_2$. It then follows

$$\begin{aligned} C_{max}(S)= & {} p+1+2p+4np+\sum _{j \in J_1} e_j + (4n+1)p - 2B + \sum _{j \in J_2} e_j \\= & {} 4p+ 8np + 1 = 4(2n+1)p+1. \end{aligned}$$

$\square$

Fig. 5

Schedule S

Let $A_j$ and $B_j$ be the processing times of the composite jobs on $M_1$ and $M_2$, respectively, and $\ell _j$ the time lag of the composite jobs, as shown in Fig. 7. Table 3 summarizes the values of $A_j$, $B_j$ and $\ell _j$ of all possible composite jobs related to instance ${\mathcal {I}}$.

Table 3 Processing times of composite jobs

Fig. 6

Some notations

Depending on the processing times of the composite jobs, we have

• In a composite job (TU), job T can only be in the first position.

• The processing time of composite job $(U_jW)$ is smaller than the processing time of $(WU_j)$ on $M_1$, then in schedule S, all composite jobs $(WU_j)$ can be transformed into $(U_jW)$ by changing the interleaving order of jobs W and $U_j$ without increasing the value of the makespan.

Let S be a feasible schedule of instance ${\mathcal {I}}$ and let $X_1$, $X_2$, $Y_1$ and $Y_2$ be the processing times of interleaved jobs related to the position of job T in schedule S as shown in Fig. 6. Clearly, $LB=X_1+\max \{X_2,Y_2\}$ is a lower bound on the makespan.

Lemma 2

If instance ${\mathcal {I}}$ admits a feasible solution S with $C_{max}(S) \le y$, then PES problem has a solution.

Proof

In order to proof this lemma, we need the following claims. $\square$

Claim 2.1

In a feasible schedule S, all jobs are interleaved.

Proof of Claim 2.1

Assume that in a schedule S at least two jobs are not interleaved. Let us consider that the U-jobs are indexed in non increasing order of $e_j$ values of their processing time $a_j$. Since the total processing time of composite jobs on first machine is a lower bound on the makespan, then the best interleaving operation of jobs that minimize the total processing time on the first machine is a lower bound on S.

Let us consider the following interleaving operation of jobs: n composite jobs (VW), one composite job (TW), and $n-1$ composite jobs $(U_iU_k)$ where $i=n, \ldots , 2n-2$; $k=1, \ldots , n-1$, and jobs $U_{2n-1}$ and $U_{2n}$ are scheduled alone, respectively. It is easy to see that this interleaving operation of jobs provides the minimal total processing time of jobs on the first machine when exactly two jobs not interleaved. Thus, comparing the makespan of S with the total processing times of jobs in S on the first machine, we have

$$\begin{aligned} C_{max}(S)\ge & {} (B+p+1-n+3p)+n(4p+1)+4np+2p-\sum \limits _{j=n-1}^{2n-2} e_{j} -e_{2n-1} - e_{2n}\\\ge & {} 4(2n+1)p+1+2p+B-\sum \limits _{j=n-1}^{2n} e_{j}\\\ge & {} y+2p+B-\sum \limits _{j=n-1}^{2n} e_{j} \end{aligned}$$

Since $p>B$ and $\sum \nolimits _{j=n-1}^{2n} e_{j}<2B$, we have $2p+B-\sum \nolimits _{j=n-1}^{2n} e_{j}>0$ hence $C_{max}(S)> y$. It then follows that in a feasible solution all jobs are interleaved. $\square$

Claim 2.2

In a feasible schedule S, there is no composite (UU)-jobs.

Proof of Claim 2.2

Assume that there exists one composite job (UU) in schedule S. Assume that this (UU)-job is composed of a pair $(U_{i},U_{j})$ of jobs in which $U_{i}$ is interleaved with $U_{j}$ and the others U-jobs are interleaved with V-jobs, W-jobs and T-job. We distinguish the following cases:

• (a) T is interleaved with W. Then nW-jobs, nV-jobs and $(2n-2)$U-jobs remain. Depending on these remaining jobs, two ways of their interleaving are possible, namely,

  • 1. (TW), (WW), $(VU_{k})_{k\in I_1}$, $(U_{k}W)_{k\in I_2}$, where $|I_1|=n$, $|I_2|=n-2$ and $I_1\cup I_2\cup \{i,j\}=\{1,\ldots ,2n\}$.

  • 2. (TW), (VW), $(VU_{k})_{k\in I_1}$, $(U_{k}W)_{k\in I_2}$, where $|I_1|=n-1$, $|I_2|=n-1$ and $I_1\cup I_2\cup \{i,j\}=\{1,\ldots ,2n\}$.

• (b) T is interleaved with an U-job. Then nV-jobs, $(n+1)$W-jobs and $(2n-3)$U-jobs remain. Again, depending on these remaining jobs, three ways of their interleaving are possible, namely,

  • 1. $(TU_{r})$, (WW), (WW), $(VU_{k})_{k\in I_1}$, $(U_{k}W)_{k\in I_2}$, where $|I_1|=n$, $|I_2|=n-3$ and $I_1\cup I_2\cup \{i,j,r\}=\{1,\ldots ,2n\}$.

  • 2. $(TU_{r})$, (WW), (VW), $(VU_{k})_{k\in I_1}$, $(U_{k}W)_{k\in I_2}$, where $|I_1|=n-1$, $|I_2|=n-2$ and $I_1\cup I_2\cup \{i,j,r\}=\{1,\ldots ,2n\}$.

  • 3. $(T,U_{r})$, (VW), (VW), $(VU_{k})_{k\in I_1}$, $(U_{k}W)_{k\in I_2}$, where $|I_1|=n-2$, $|I_2|=n-1$ and $I_1\cup I_2\cup \{i,j,r\}=\{1,\ldots ,2n\}$.

In the following we examine the value of the makespan of each sequence of interleaving jobs.

Case a.1: According to Mitten’s algorithm (Fondrevelle et al. 2006), the optimal schedule of the composite jobs is given by the sequence $S=\langle (VU_{k})_{k\in I_1}, (TW), (U_{i}U_{j}), (U_{k}W)_{k\in I_2}, (WW)\rangle$. Depending on the processing times of these composite jobs given in Table 3, the parameters $X_1$, $X_2$, $Y_1$ and $Y_2$ (see Fig. 6) of sequence S are as follows:

$$\begin{aligned} \begin{array}{ll} X_1=4np+3p+B+1, &{}\quad X_2=4pn+p-\left( \sum \limits _{k\in I_2}e_k+e_i\right) .\\ Y_1=4np+\left( \sum \limits _{k\in I_1}e_k\right) , &{}\quad Y_2=4np+p-2B+\left( \sum \limits _{k\in I_2}e_k+e_i+e_j\right) . \end{array} \end{aligned}$$

Then, the lower bound of $C_{max}(S)$ is

$$\begin{aligned} LB= & {} X_1+\max \{X_2,Y_2\}\\= & {} 8np+4p+1+\max \left\{ B-\left( \sum \limits _{k\in I_2}e_k+e_i\right) ,\left( \sum \limits _{k\in I_2}e_k+e_i+e_j\right) -B\right\} \\= & {} y+\max \left\{ B-\left( \sum \limits _{k\in I_2}e_k+e_i\right) ,\left( \sum \limits _{k\in I_2}e_k+e_i+e_j\right) -B\right\} \end{aligned}$$

Since $\max \{B-(\sum \nolimits _{k\in I_2}e_k+e_i),(\sum \nolimits _{k\in I_2}e_k+e_i+e_j)-B\}>0$ then $LB> y$. Thus S is not a feasible solution with $C_{max}(S)\le y$.

Case a.2: The optimal sequence in this case is $S=\langle (VU_{k})_{k\in I_1}, (TW), (VW), (U_{i}U_{j}), (U_{k}W)_{k\in I_2}\rangle$. The parameters $X_1$, $X_2$, $Y_1$ and $Y_2$ are as follows.

$$\begin{aligned} \begin{array}{ll} X_1=4np-p+B, &{}\quad X_2=4np+5p+1-\left( \sum \limits _{k\in I_2}e_k+e_i\right) \\ Y_1=4np-4p+\left( \sum \limits _{k\in I_1}e_k\right) , &{}\quad Y_2=4np+5p-2B+\left( \sum \limits _{k\in I_2}e_k+e_i+e_j\right) . \end{array} \end{aligned}$$

The lower bound LB is such that

$$\begin{aligned} LB= & {} X_1+\max \{X_2,Y_2\}\\= & {} 8np+4p+1+\max \left\{ B-\left( \sum \limits _{k\in I_2}e_k+e_i\right) ,\left( \sum \limits _{k\in I_2}e_k+e_i+e_j\right) -B-1\right\} .\\= & {} y+\max \left\{ B-\left( \sum \limits _{k\in I_2}e_k+e_i\right) ,\left( \sum \limits _{k\in I_2}e_k+e_i+e_j\right) -B-1\right\} \end{aligned}$$

Since $\forall k, e_k>1$, we have $\max \{B-(\sum \nolimits _{k\in I_2}e_k+e_i),(\sum \nolimits _{k\in I_2}e_k+e_i+e_j)-B-1\}> 0$, then $LB>y$. Thus S is not a feasible solution with $C_{max}(S)\le y$.

Case b.1: The optimal sequence of the composite jobs in this case is defined by

$S= \langle (VU_{k})_{k\in I_1}, (TU_{r}), (U_{i}U_{j}), (U_{k}W)_{k\in I_2}, (WW), (WW)\rangle$. The parameters $X_1$, $X_2$, $Y_1$ and $Y_2$ are:

$$\begin{aligned} \begin{array}{ll} X_1=4np+B+3p+1, &{}\quad X_2=4np+p-\left( \sum \limits _{k\in I_2}e_k+e_i\right) \\ Y_1=4np+\sum \limits _{l\in k_1}e_k, &{}\quad Y_2=4np+p-2B+\left( \sum \limits _{k\in I_2}e_k+e_i+e_j+e_r\right) . \end{array} \end{aligned}$$

Then the lowed bound of $C_{max}(S)$ is $LB = X_1+\max \{X_2,Y_2\} = y+\max \{B-(\sum \nolimits _{l\in I_2}e_l+e_i),(\sum \nolimits _{l\in I_2}e_l+e_i+e_j+e_k)-B\}$. Since $\max \{B-(\sum \nolimits _{l\in I_2}e_l+e_i),(\sum \nolimits _{l\in I_2}e_l+e_i+e_j+e_k)-B\}>0$ then $LB>y$. Thus S is not a feasible solution with $C_{max}(S)\le y$.

Case b.2: The optimal sequence of the composite jobs in this case is defined by

$$\begin{aligned} S=\langle (VU_{k})_{k\in I_1}, (TU_{r}), (VW), (U_{i}U_{j}), (U_{k}W)_{k\in I_2}, (WW)\rangle . \end{aligned}$$

The parameters $X_1$, $X_2$, $Y_1$ and $Y_2$ are:

$$\begin{aligned} \begin{array}{ll} X_1=4np-p+B, &{}\quad X_2=4np+5p-\left( \sum \limits _{k\in I_2}e_k+e_i\right) \\ Y_1=4np-4p+\left( \sum \limits _{k\in I_1}e_k\right) , &{}\quad Y_2=4np+5p-2B+(\sum \nolimits _{k\in I_2}e_k+e_i+e_r). \end{array} \end{aligned}$$

Then the lowed bound of $C_{max}(S)$ is $LB=X_1+\max \{X_2,Y_2\}=y+\max \{B-(\sum \nolimits _{k\in I_2}e_k+e_i+1), (\sum \nolimits _{k\in I_2}e_k+e_i+e_j+e_r)-B-1\}$. Since $\forall k, e_k> 1$, then $\max \{B-(\sum \nolimits _{k\in I_2}e_k+e_i+1),(\sum \nolimits _{k\in I_2}e_k+e_i+e_j+e_r)-B-1\}>0$, then $LB>y$. Thus S is not a feasible solution with $C_{max}(S)\le y$.

Case b.3: The optimal sequence of the composite jobs of this case is defined by

$S= \langle (VU_{k})_{k\in I_1}, (TU_{r}), (VW), (VW), (U_{i}U_{j}), (U_{k}W)_{k\in I_2}$. The parameters $X_1$, $X_2$, $Y_1$ and $Y_2$ are:

$$\begin{aligned} \begin{array}{ll} X_1=4np-5p-1+B, &{}\quad X_2=4np+9p+2-\left( \sum \limits _{k\in I_2}e_k+e_i\right) \\ Y_1=4np-8p+\left( \sum \limits _{k\in I_1}e_k\right) , &{}\quad Y_2=4np+9p-2B+\left( \sum \limits _{k\in I_2}e_k+e_i+e_j+e_r\right) . \end{array} \end{aligned}$$

Then the lowed bound of $C_{max}(S)$ is $LB=X_1+\max \{X_2,Y_2\}=y+\max \{B-(\sum \nolimits _{k\in I_2}e_k+e_i),(\sum \nolimits _{k\in I_2}e_k+e_i+e_j+e_r)-B-1\}$. Since $\forall k, e_k>1$, we have $\max \{B-(\sum \nolimits _{k\in I_2}e_k+e_i),(\sum \nolimits _{k\in I_2}e_k+e_i+e_j+e_r)-B-1\}>0$, then $LB>y$. Thus S is not a feasible solution with $C_{max}(S)\le y$.

Note that if we have more than one interleaving (UU)-jobs then $X_2$ increases and $LB>y$.

$\square$

Claim 2.3

In a feasible schedule S, the T-job is interleaved with W-job.

Proof of Claim 2.3

Assume that in a schedule S, T is interleaved with U-job, and let $U_r$ be that job. From Claims 2.1 and 2.2, the only possible composite jobs are

• 1. $(VU_{k})_{k\in I_1}$, $(U_{k}W)_{k\in I_2}$, (VW) where $|I_1|=n-1$, $|I_2|=n$ and $I_1\cup I_2\cup \{r\}=\{1,\ldots ,2n\}$.

• 2. $(VU_{k})_{k\in I_1}$, $(U_{k}W)_{k\in I_2}$, (WW) where $|I_1|=n$, $|I_2|=n-1$ and $I_1\cup I_2\cup \{r\}=\{1,\ldots ,2n\}$.

For above cases the optimal sequences are

• Case 1. $S= \langle (VU_{k})_{k\in I_1}, (TU_r), (VW), (U_{k}W)_{k\in I_2}\rangle$

• Case 2. $S= \langle (VU_{k})_{k\in I_1}, (TU_r), (U_{k}W)_{k\in I_2}, (WW)\rangle$

Similarly to the proof of Claim 2.2, it is easy to show that for each case, we have $C_{max}(S)> y$, then in schedule S job T is interleaved with job W. $\square$

Let S be a feasible solution of instance ${\mathcal {I}}$ such that $C_{max}(S) \le y$. From Claims 2.1, 2.2 and 2.3, the unique interleaved operations of jobs in schedule S is $(VU_k)_{k\in I_1}$, (TW) and $(U_kW)_{k\in I_2}$ where $|I_1|=n$, $|I_2|=n$ and $I_1\cup I_2=\{1,\ldots ,2n\}$. The optimal sequence of these composite jobs is $S=\langle (VU_k)_{k\in I_1}$, (TW), $(U_kW)_{k\in I_2} \rangle$. The parameters $X_1$, $Y_1$, $X_2$ and $Y_2$ of this sequence are,

$$\begin{aligned} \begin{array}{ll} X_1=4np+p+1+B, &{}\quad X_2=4np+p-\sum \limits _{k\in I_2}e_k\\ Y_1=4np+\sum \limits _{k\in I_1}e_k, &{}\quad Y_2=4np+p-2B+\sum \limits _{k\in I_2}e_k. \end{array} \end{aligned}$$

The lower bound LB of $C_{max}(S)$ is $LB=X_1+\max \{X_2,Y_2\}=y+\max \{B-\sum \nolimits _{k\in I_2}e_k, \sum \nolimits _{k\in I_2}e_k - B\}$. Since $C_{max}(S) \le y$, then $\max \{B-\sum \nolimits _{k\in I_2}e_k, \sum \nolimits _{k\in I_2}e_k - B\} = 0$. Thus $\sum \nolimits _{k\in I_2}e_k= B$ and $\sum \nolimits _{k\in I_1}e_k = B$. Then we obtain a solution for the PES problem. $\square$

From Lemmas 1 and 2, we have the following result.

Theorem 1

The problem $F2(a_{j},p,p,c_{j})$ is binary NP-hard.

3.2 Problem $F2(p,p,b_{j},c_{j})$

In this section, we show that $F2(p,p,b_{j},c_{j})$ is NP-hard using a reduction from the Partition problem with Equal Size. Given an arbitrary instance of the PES problem, we build an instance ${\mathcal {I}}$ of problem $F2(p,p,b_{j},c_{j})$ with a set of $4n+4$ jobs as follows:

• Jobs of type U, denoted $U_{j}$, $j=1, \ldots , 2n$;

• n identical jobs denoted V;

• $n+2$ identical jobs denoted W;

• One job denoted T;

• One job denoted R;

For all the jobs, we set $a_{j}=L_{j}=p$, $j=1, \ldots , 4n+4$, where $p>B$. Processing times of jobs on $M_1$ and $M_2$ are given in Table 4.

Table 4 Jobs processing times

We show that PES problem has a solution if, and only if, instance $({\mathcal {I}})$ admits a feasible solution with $C_{\max }(S) \le y$, where $y=9(n+1)p+n+2$.

Lemma 3

If PES problem has a solution, then there exists a schedule S with $C_{\max }(S) \le y$.

Proof

Assume that PES problem has a solution, and let $E_1$ and $E_2$ be the required subset of E such that $\sum _{j \in E_1} e_j = \sum _{j \in E_2} e_j = B$ and $\vert E_1\vert =\vert E_2 \vert = n$. Let $I_1$ and $I_2$ be the subsets of U-jobs corresponding to the sets $E_1$ and $E_2$, respectively. Then the desired schedule S exists where the completion time $C_{\max }(S)$ of schedule S is equal to $9(n+1)p+n+2$. The composite jobs and their schedule is given by sequence $S=\langle (U_kV)_{k\in J_1},(WT),(WU_k)_{k\in J_2},(WR)\rangle$. $\square$

Assume now that there exists a schedule S with makespan $\le y$, then we show that PES problem has a solution.

As presented in Sect. 3.1, Table 5 summarizes the values of $A_j$, $B_j$ and $l_j$ of all possible composite jobs related to the instance ${\mathcal {I}}$.

Table 5 Processing times of the composite jobs

Lemma 4

If instance ${\mathcal {I}}$ admits a feasible solution with $C_{max}(S) \le y$, then PES problem has a solution.

Proof

In order to proof this result we need the following claims. Proof of Claims 4.1, 4.2 and 4.3 are similar to that of Claims 2.1, 2.2 and 2.3, respectively. $\square$

Claim 4.1

In a feasible schedule S, all jobs are interleaved.

Claim 4.2

In a feasible schedule S, there is no composite (UU)-jobs.

Claim 4.3

In a feasible schedule S, T is interleaved with W.

Claim 4.4

In a feasible schedule S, R is interleaved with W.

Proof of Claim 4.1

Assume that in schedule S, job R is not interleaved with job W but with a job of type U. Let $U_r$ be the U-job interleaved with R. From Claims 4.1, 4.2 and 4.3, the only possible composite jobs are

• 1. (WT), $(U_rR)$, $(U_{k}V)_{k\in I_1}$, $(WU_{k})_{k\in I_2}$, and (WW) where $|I_1|=n$, $|I_2|=n-1$ and $I_1\cup I_2\cup \{r\}=\{1, \ldots , 2n\}$.

• 2. (WT), $(U_rR)$, (WV), $(VU_{k})_{k\in I_1}$, and $(U_{k}W)_{k\in I_2}$, where $|I_1|=n-1$, $|I_2|=n$ and $I_1\cup I_2\cup \{r\}=\{1,\ldots ,2n\}$.

For cases 1 and 2, the optimal sequences are

• Case 1. $S= \langle (VU_{k})_{k\in I_1}, (WT), (U_{k}W)_{k\in I_2}, (U_rR), (WW)\rangle$.

• Case 2. $S= \langle (VU_{k})_{k\in I_1}, (WV), (WT), (U_{k}W)_{k\in I_2}, (U_rR)\rangle$.

Similarly to the proof of Claim 2.2, it is easy to show that for each above case $C_{max}(S)> y$, then in schedule S job R is interleaved with job W. $\square$

From Claims 4.1, 4.2, 4.3 and 4.4, the unique interleaved jobs operations in schedule S is (WT), (WR), $(U_{k}V)_{k\in I_1}$, $(WU_{k})_{k\in I_2}$ where $|I_1|=n$, $|I_2|=n$ and $I_1\cup I_2=\{1, \ldots , 2n\}$. The optimal sequence of these composite jobs is $S=\langle (U_kV)_{k\in I_1}$, (WT), $(WU_k)_{k\in I_2} (WR )\rangle$. The parameters $X_1$, $X_2$ and $Y_2$ of this sequence are,

$$\begin{aligned} \begin{array}{ll} X_1=5np+5p+B+n+1, &{}\quad X_2=4np+4p+1-\sum \limits _{k\in I_2}e_k\\ Y_2=4np+4p+1-2B+\sum \limits _{k\in I_2}e_k. &{}\quad \end{array} \end{aligned}$$

The lower bound LB of $C_{max}(S)$ is $LB=X_1+\max \{X_2,Y_2\}=y+\max \{B-\sum \nolimits _{k\in I_2}e_k, \sum \nolimits _{k\in I_2}e_k - B\}$. since $C_{max}(S) \le y$, then $\max \{B-\sum \nolimits _{k\in I_2}e_k, \sum \nolimits _{k\in I_2}e_k - B\} = 0$. Thus $\sum \nolimits _{k\in I_2}e_k= B$ and $\sum \nolimits _{k\in I_1}e_k = B$. Then we obtain a solution for the PES problem. $\square$

From Lemmas 3 and 4, we have the following result.

Theorem 2

$F2(p,p,b_{j},c_{j})$ is binary NP-hard.

4 Well solvable cases

In this section, we discuss special cases that can be solved polynomially.

4.1 Problem $F2(a, p,p,c_{j})$

In this section we consider the problem $F2(a, p,p,c_{j})$. Clearly, interleaving operation is possible only if $a\le p$, otherwise each job is scheduled separately. In the following we assume that $a\le p$. The following lemmas are useful to provide a polynomial algorithm for $F2(a, p,p,c_{j})$.

Lemma 5

There exists an optimal schedule in which all jobs are interleaved except one if the number of jobs is odd.

Proof

Let S be an optimal schedule. Assume that there exist in S two jobs $J_i$ and $J_j$ that are scheduled separately, and assume that job $J_i$ is scheduled before $J_j$. Let us consider a new schedule $S'$ obtained from S in which $J_j$ is interleaved with $J_i$ to form a new composite job $(J_iJ_j)$, and the new composite job is scheduled at the position of $J_i$ in S. The total processing time of $S'$ on $M_1$ is reduced by $p+a$ with respect to S, and the makespan of $S'$ is not increased. Therefore, $S'$ is an optimal schedule. Repeating this argument generates a schedule with interleaved jobs except the last if the number of jobs is odd. $\square$

Lemma 6

There exists un optimal schedule in which jobs are scheduled in non increasing order of $c_j$ on the second machine.

Proof

Let S be an optimal schedule in which Lemma 6 does not hold. Let $J_i$ and $J_j$ be the first two jobs of S for which $c_i \le c_j$ and $J_i$ is scheduled before $J_j$. Consider a new schedule $S'$ in which $J_i$ and $J_j$ exchange their positions. Since all composite jobs have the same processing time on $M_1$, then the completion time of $S'$ on $M_1$ remains unchanged. Furthermore, the completion time of the composite job that contains $J_i$ in $S'$ is not greater than jobs in S. Thus, the new schedule $S'$ is also optimal. Repeating this operation yields a schedule with the desired properties. $\square$

A polynomial algorithm for the problem $F2(a,p,p,c_{j})$ is detailed below.

Theorem 3

Algorithm 1 provides an optimal solution for $F2(a,p,p,c_{j})$ in $O(n\log n)$-time.

Proof

If $a>p$ jobs cannot be interleaved, then an optimal schedule is obtained by applying Johnson’s algorithm. If $a \le p$, then from Lemmas 5 and 6, all jobs are interleaved expect the last job if n is odd, and jobs are scheduled in nonincreasing order of their processing times on the second machine. Algorithm 1 generates an optimal schedule with respect to Lemmas 5 and 6. Furthermore, this solution is generated in $O(n\log n)$-time. $\square$

We end this section by a remark on problem $F2(p,p,b,c_{j})$. Since composite jobs of problems $F2(p,p,a,c_{j})$ and $F2(a,p,p,c_{j})$ have same processing times on the first machine, then $F2(p,p,b,c_{j})$ and $F2(a,p,p,c_{j})$ are similar and results of Lemmas 5 and 6 remain valid for $F2(p,p,b,c_{j})$. Thus, Algorithm 1 provides an optimal solution for $F2(p,p,b,c_{j})$ in $O(n\log n)$-time.

4.2 Problem $F2(p,L,p,c_{j})$

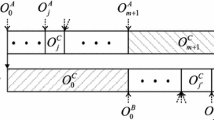
In this section, we consider the problem $F2(p,L,p,c_{j})$. When $L<p$, the interleaving operation is not possible, and jobs are scheduled using Johnson Algorithm where processing times of jobs on machines $M_1$ and $M_2$ are $p_{1j} =2p+L$ and $p_{2j} =c_j$, $j=1, \ldots , n$, respectively. Otherwise we assume, without loss of generality, that $L=vp+r$ where $r<p$ and v is non-negative integer value. In the following a composite job is called full if it consists of $(v+1)$ interleaved jobs (see Fig. 1). Such composite job has processing time $(v+2)p+L$ on the first machine. Clearly there is an optimal schedule for the problem $F2(p,L,p,c_{j})$ in which jobs are processed on the first machine as early as possible. Such schedule contains full composite jobs except one if the number of jobs is not multiple of $(v+1)$ (Fig. 7).

Fig. 7

Example of composite job

Lemma 7

In an optimal schedule, all composite jobs are full except one if the number of jobs is not a multiple of $(v+1)$.

Proof

Let S be an optimal schedule containing the composite jobs $B_1, \ldots , B_u$. Let $B_j$ be the first not full composite job of S. Let $B_k$ be another not full composite job of S scheduled after $B_j$ in S. A new schedule $S'$ is built from S by completing $B_j$ with jobs from $B_k$ and shifting all composite jobs that follow $B_k$ in the schedule to the right. Clearly the completion time of $S'$ is not greater than the makespan of S. Therefore $S'$ is an optimal schedule. Repeating such modification yields a schedule whose composite jobs are full excepting the last if the number of jobs is not a multiple of $(v+1)$$\square$

Lemma 8

There is at least one optimal schedule in that jobs are scheduled in non increasing order of $c_j$ on the second machine.

Proof

Let S be an optimal schedule in which Lemma 8 does not hold. Let $J_i$ and $J_j$ be the two first jobs of S for which $c_i \le c_j$ and $J_i$ is scheduled before $J_j$. Consider a new schedule $S'$ in which $J_i$ and $J_j$ exchange their positions. Since all composite jobs have the same processing time on the first machine, then the completion time of $S'$ on $M_1$ is not changed. Furthermore, the completion time of the composite job that contains $J_i$ in $S'$ is not greater than the completion time of the composite job that contains job $J_j$ in S. Thus, the new schedule $S'$ is also optimal. Repeating this operation yields a schedule with the desired properties. $\square$

A polynomial algorithm for $F2(p,L,p,c_{j})$ is detailed below.

Theorem 4

Algorithm 2 provides an optimal solution for the problem $F2(p,L,p,c_{j})$ in O(nlogn)-time.

Proof

If $L<p$ jobs cannot be interleaved, then an optimal schedule is obtained by applying Johnson’s algorithm on the jobs. If $L \ge p$, then according to Lemmas 7 and 8, all composite jobs are full expect the last job if n is not a multiple of $(v+1)$ where $L=vp+r$, and jobs are assigned to composite jobs in non increasing order of their processing times on the second machine. Algorithm 2 generates a schedule with respect to Lemmas 5 and 8. Furthermore, this solution is provided in O(nlogn)-time. $\square$

4.3 Problem $F2(a_{j}, p,p, c)$

In this section, we consider the problem $F2(a_{j}, p,p, c)$. Let $K_1=\{J_j \;\vert \; a_j> p\}$ and $K_2=\{J_j \;\vert \; a_j \le p\}$, $n_1$ and $n_2$ the size of sets $K_1$ and $K_2$, respectively. We assume that jobs in $K_1$ and $K_2$ are indexed in nondecreasing order of their $a_i$. Clearly, jobs of $K_1$ can only be interleaved with jobs of $K_2$, where a job of $K_1$ is in the first position of the composite job. However, a job of $K_2$ can be interleaved with a job of either $K_1$ or $K_2$.

Let $S_\ell$ be the set of all jobs in which exactly $\ell$ jobs of $K_1$ are interleaved with $\ell$ jobs of $K_2$, $0\le \ell \le \min \{n_1,n_2\}$, and the other jobs of $K_1$ remain single. The rest of jobs of $K_2$ may either be interleaved between them or not. The following results are useful to build a polynomial algorithm.

Lemma 9

There exists an optimal schedule of set $S_\ell$ in which the $\ell$ last jobs of $K_2$ are interleaved with the $\ell$ first jobs of $K_1$.

Proof

We first prove that if in an optimal schedule of set $S_{\ell }$ the $\ell$ last jobs of $K_2$ are interleaved, then we show that jobs of $K_2$ are interleaved with the $\ell$ first jobs of $K_1$.

(i) Let $S^0$ be an optimal schedule of $S_\ell$ that does not satisfy the first statement of Lemma 9. Then there exists a job $J^{K_2}_i$, $i\le n_2-\ell$, which is interleaved with a job of $K_1$. Since exactly $\ell$ jobs of $K_1$ are interleaved with jobs of $K_2$, then there exists a job $J^{K_2}_j$, $j\ge n_2-\ell$, such that $J^{K_2}_j$ is not interleaved in schedule $S^0$. Let us consider a new schedule $S^*$ of set $S_\ell$ obtained from schedule $S^0$ by exchanging $J^{K_2}_i$ with $J^{K_2}_j$. Since $a_j \ge a_i$ and $J^{K_2}_i$ and $J^{K_2}_j$ have the same processing time on $M_2$, then we have $C_{\max }(S^*) \le C_{\max }(S^0)$. Repeating this arguments establishes the first statement of Lemma 9.

(ii) Let $S^0$ be an optimal schedule of $S_\ell$ that satisfies the first statement of Lemma 9 but not the second statement. Then there exists two jobs $J^{K_1}_i$ and $J^{K_1}_j$, $i<j$, $j> \ell$, such that $J^{K_1}_j$ is interleaved with job $J^{K_2}_k$ and $J^{K_1}_i$ is scheduled on its own. In $S^0$ we have either $J^{K_1}_j$ scheduled before $J^{K_1}_i$ or scheduled after $J^{K_1}_i$ depending on their processing times. Let us distinguish two cases.

• 1. $J^{K_1}_i$is scheduled before $J^{K_1}_j$. In this case we distinguish three situations depending on the contribution of $J^{K_1}_i$ and $J^{K_1}_j$ to the value of $C_{\max }(S^0)$: (i) $J^{K_1}_i$ and $J^{K_1}_j$ are on the critical path on $M_1$, i.e., $J^{K_1}_i$ and $J^{K_1}_j$ contribute to the value of makespan with their processing times on $M_1$, (ii) $J^{K_1}_i$ and $J^{K_1}_j$ are not on the critical path on $M_1$, and (iii) job $J^{K_1}_i$ is on the critical path on $M_1$ but not $J^{K_1}_j$. Let us consider a new schedule $S^*$ of set $S_\ell$ obtained from schedule $S^0$ in which $J^{K_2}_k$ form a new composite job with $J^{K_1}_i$, and let $C_{\max }(S^*)$ be the makespan of $S^*$. If $C_{\max }(S^0)$ is given by Case (i) or (ii) then it is easy to see that $C_{\max }(S^*)= C_{\max }(S^0)$. If $C_{\max }(S^0)$ is given by Case (iii) (see Fig. 8) then we have $c>p$. From Fig. 8, we have

  $$\begin{aligned} C_{\max }(S^*)\le & {} t+p+ \max \{0, c-\delta -p\}+L -c\\\le & {} t+L+ \max \{p-c, -\delta \}\\\le & {} t+L = C_{\max }(S^0) \end{aligned}$$

• 2. $J^{K_1}_i$is scheduled after $J^{K_1}_j$. Again we distinguish the same three points as in Case 1, depending on the contribution of $J^{K_1}_i$ and $J^{K_1}_j$ to the value of $C_{\max }(S^0)$. The proof of point (i) and (ii) is similar to that of Case 1. We consider only the case in which job $J^{K_1}_j$ is on the critical path on $M_1$ and job $J^{K_1}_i$ is not on the critical path.

  Let us consider a new schedule $S^*$ of set $S_\ell$ obtained from schedule $S^0$ in which we exchange $J^{K_2}_i$ with $J^{K_2}_j$ and $J^{K_2}_k$ is interleaved with $J^{K_2}_i$. Let $C_{\max }(S^*)$ be the makespan of $S^*$. From Fig. 9, we have $C_{\max }(S^*)=t+L-\min \{\delta , a_j-a_i\} \le C_{\max }(S^0)$.

Fig. 8

The third point of Case 1 (after the transfer of job $J^{K_2}_k$)

Fig. 9

The third situation of Case 2 (after exchanging $J^{K_2}_i$ with $J^{K_2}_j$)

Repeating the arguments of Case 1 and 2 establishes the second statement of Lemma 9. $\square$

In the following, we assume that set $S_\ell$ satisfies the statement of Lemma 9.

Lemma 10

There exists an optimal schedule of set $S_\ell$ in which

• 1. All remaining jobs of $K_2$ are interleaved between them, except one if their number is odd.

• 2. Jobs $J^{K_2}_1, \ldots , J^{K_2}_{\lceil \frac{n_2-\ell }{2}\rceil }$ are in the first positions in the new composite jobs.

Proof

(1) Let $S^0$ be an optimal schedule of $S_\ell$ that does not satisfy Lemma 10. Let $J_i$ and $J_j$ be two jobs of $K_2$ where $i<j$ and $J_i$ and $J_j$ are processed on their own. According to Mitten Algorithm, job $J_i$ is scheduled before $J_j$. Depending on the contribution of $J_i$ and $J_j$ to the value of $C_{\max }(S^0)$, we distinguish three cases, (i) $J_i$ and $J_j$ are on the critical path on the first machine, (ii) $J_i$ and $J_j$ are not on the critical path on $M_1$, and (iii) job $J_i$ is on the critical path on $M_1$ but not $J_j$.

Let $S^*$ be a new schedule of set $S_\ell$ obtained from schedule $S^0$ in which a new composite job ($J_iJ_j$) is created and scheduled at the position of $J_i$, and $C_{\max }(S^*)$ its makespan. Clearly if $C_{\max }(S^0)$ is given either by case (i) or (ii), we have $C_{\max }(S^*) \le C_{\max }(S^0)$. It follows $S^*$ is optimal. If $C_{\max }(S^0)$ is given by Case (iii), we have $c<3p$. In this case $C_{\max }(S^*)$ decreases by $\delta$ (see Fig. 10), i.e., $C_{\max }(S^*)=t+(c-\delta )+(L-c)=C_{\max }(S^0)-\delta$. Repeating this argument establishes the statement of Lemma 10.

Fig. 10

The third point (after the transfer of the jobs $J_j$)

(2) The second statement of Lemma 10 can be easily established with an exchange argument. $\square$

From Lemmas 9 and 10, the following result is straightforward.

Lemma 11

Mitten algorithm generates an optimal schedule for set $S_\ell$ in O(n)-time.

Let us consider the following algorithm.

Theorem 5

Algorithm 3 solves $F2(a_{i},p,p,c)$ in $O(n^2)$-time.

Proof

In Algorithm 3, for each value of $\ell$, the constructed set of composite jobs satisfies Lemmas 9 and 10. Furthermore, Algorithm 3 selects the best solution among all values of $\ell$ leading to an optimal solution for $F2(a_{j},p,p,c)$. Clearly, Algorithm 3 runs in $O(n^2)$-time.

$\square$

We end this section by a remark on problem $F2(p,p,b_j,c)$. Since composite jobs of problems $F2(a_j,p,p,c)$ and $F2(p,p,a_j,c)$ have same processing times on the first machine, then $F2(p,p,b_j,c)$ and $F2(a_j,p,p,c)$ are similar and results of Lemmas 9 and 10 remain valid for $F2(p,p,b_j,c)$. Thus, Algorithm 3 in which jobs of $K_1$ and $K_2$ are now sorted in nondecreasing order of their $b_i$ provides an optimal solution for $F2(p,p,b_j,c)$ in $O(n^2)$-time.

5 Conclusion

In this paper, we have considered the two-machine flowshop scheduling problem with coupled operations on the first machine. We showed that the two problems $F2(a_{j},p,p,c_{j})$ and $F2(p,p,b_{j},c_{j})$ are weakly NP-hard. Besides, we designed polynomial algorithms for several special cases. Let us mention a symmetric model, with respect to the makespan, may be derived from the model we considered in this paper, namely the model in which the coupled operations are now on the second machine. For further research, it would be interesting to generalize our study to the case where the coupled-operations occur on both machines.