Two-machine flowshop scheduling with three-operation jobs subject to a fixed job sequence

Abstract

This paper studies the problem of scheduling three-operation jobs in a two-machine flowshop subject to a predetermined job processing sequence. Each job has two preassigned operations, which are to be performed on their respective dedicated machines, and a flexible operation, which may be processed on either of the two machines subject to the processing order as specified. Five standard objective functions, including the makespan, the maximum lateness, the total weighted completion time, the total weighted tardiness, and the weighted number of tardy jobs are considered. We show that the studied problem for either of the five considered objective functions is ordinary NP-hard, even if the processing times of the preassigned operations are zero for all jobs. A pseudo-polynomial time dynamic programming framework, coupled with brief numerical experiments, is then developed for all the addressed performance metrics with different run times.

1 Introduction

This paper investigates a two-stage flowshop problem for scheduling a given sequence of jobs, each of which consists of three operations. The setting without the presumption of a fixed job sequence is formulated and studied by Gupta et al. (2004) for the performance metric of makespan. The three-operation flowshop scheduling problem is described as follows. A set of n jobs $\mathcal{J}=\{J_1,\ldots ,J_n\}$ is to be processed in a two-machine flowshop, consisting of machine A at stage 1 and machine B at stage 2. Each job $J_j\in \mathcal{J}$ has three operations, $O^A_j$, $O^B_j$, and $O^C_j$ with non-negative processing times $a_j$, $b_j$, and $c_j$, respectively, and is associated with due date $d_j$ and weight $w_j$. The three operations of each job must follow the processing order $(O^A_j, O^C_j, O^B_j)$. Operations $O^A_j$ and $O^B_j$ are preassigned to be performed on their respective dedicated machines A and B. Operation $O^C_j$ is flexible and may be processed on either of the two machines subject to the processing order as specified. The problem with makespan minimization is at least binary NP-hard for it corresponds to the parallel machine scheduling problem $P2||C_{\max }$ when $a_j=b_j=0$ for all jobs $J_j\in \mathcal{J}$. This problem becomes the traditional two-machine flowshop scheduling problem, which can be solved by Johnson’s rule (Johnson 1954), provided that an optimal assignment of the flexible operations to the two machines is given (Gupta et al. 2004). Gupta et al. (2004) presented a $\frac{3}{2}$-approximation algorithm and developed a polynomial time approximation scheme.

The above problem with identical jobs was discussed by Crama and Gultekin (2010), Gultekin (2012), and Uruk et al. (2013). Crama and Gultekin (2010) proposed some optimality properties and polynomial-time algorithms for various cases where the number of jobs is either finite or infinite, and where the buffer capacity in between machines is either zero, limited, or unlimited. Gultekin (2012) later considered the scenario of non-identical machines, viz., the processing times of the flexible operation are different on the two machines, and developed a constant-time solution procedure for the cases with no buffer and unlimited buffer capacity in between machines. Uruk et al. (2013) investigated the scenario where the processing times of the preassigned and flexible operations are controllable and can be any value within the given interval, and the manufacturing cost of an operation is a nonlinear function of its processing time. Mixed integer nonlinear programs were derived for the bi-criteria objective of makespan and total manufacturing cost, and a heuristic algorithm was designed for large-scale instances. The practical applications of the three-operation flowshop scheduling problem could be found in flexible manufacturing systems with machine linkage, inventory control transit centers with bar-coding operations, and scheduling in farming (Gupta et al. 2004). Crama and Gultekin (2010) also described the industrial settings in the assembly of printed circuit boards and in automated computer numerical control machines.

Since the three-operation flowshop scheduling problem is intractable and involves the decisions of partitioning and sequencing, it could be worth investigating the restricted problem where one of the decisions is predetermined, especially from the perspective on solution approach development which will be addressed later. In this paper, we discuss the problem subject to the assumption of a fixed job sequence, i.e., the processing sequence of all jobs is known and given a priori. Five standard objective functions, namely the makespan ($C_{\max }$), the maximum lateness ($L_{\max }$), the total weighted completion time ($\sum w_jC_j$), the total weighted tardiness ($\sum w_jT_j$), and weighted number of tardy jobs ($\sum w_jU_j$), are considered. Without loss of generality, the predetermined job sequence is $(J_1,J_2,\ldots ,J_n)$. The condition of a fixed job sequence requires that on machine A as well as machine B, job $J_i$ should precede job $J_j$ if $i<j$.

In the design of branch-and-bound algorithms, local search-based methods and meta-heuristics for handling intractable problems, the sequence- or permutation-based representations for candidate solutions are commonly adopted. It is demanded to have efficient algorithms for determining the objective values of given job/operation sequences. In the classification of complexity status, special properties, e.g. agreeable conditions, could also suggest the optimality of specific job orderings. One envisaged industrial application of the fixed-job-sequence setting in the three-operation flowshop scheduling problem could be the scheduling of bar-coding operations in inventory or stock control systems, where the First-Come-First-Served principle is applied. For each item $J_j\in \mathcal{J}$, operations $O^A_j$, $O^C_j$, and $O^B_j$ are unpacking, bar-coding process, and repacking, respectively. It is commonly regarded fair by customers and easy to be implemented by processors that the unpacking and repacking sequences of items are identical and predetermined by the item/order receiving times. Other theoretical and practical justifications of the fixed-job-sequence assumption from the technological or managerial considerations can be found in, e.g. Shafransky and Strusevich (1998), Lin and Hwang (2011), Hwang et al. (2012, (2014) and Lin et al. (2016).

The remainder of this paper is organized as follows. In Sect. 2, we discuss the NP-hardness of the studied problem for the considered performance metrics. Section 3 contains the development of pseudo-polynomial time dynamic programming algorithms. We conclude the paper and suggest some research issues in Sect. 4.

2 NP-hardness

The requirement of operation processing order and the condition of fixed job sequence jointly imply the standard format of a feasible schedule, where for each job $J_j$ the flexible operation $O^C_j$ is immediately preceded by the corresponding preassigned operation $O^A_j$ or immediately followed by the corresponding preassigned operation $O^B_j$. The studied fixed-job-sequence problem can thus be regarded as the problem of finding an optimal partition of the flexible operations. The determination of its complexity status, however, is not straightforward as will be shown later. Before proving the NP-hardness of the problem under study, an optimality property is described as follows.

Lemma 1

For any regular objective function, there exists an optimal schedule in which the flexible operation of the first job, i.e. $O^C_1$, goes to machine B and that of the last job, i.e. $O^C_n$, goes to machine A.

Proof

Let $\sigma$ be an optimal schedule that does not satisfy the specified property. We move operation $O_1^C$ from machine A to machine B to derive another schedule $\sigma '$. Depletion of the processing on machine A lets all the operations behind $O_1^A$ on machine A start earlier by $c_1$ units of time. Merging $O^C_1$ into $O^B_1$ will not defer the completion of any operation on machine B. Therefore, the completion times $C_j(\sigma ')\le C_j(\sigma )$ for all jobs $J_j\in \mathcal{J}$. Next, we consider operation $O^C_n$. Depleting $O_n^C$ from machine B will decrease machine B’s completion time by $c_n$. Appending it to machine A will delay the start time of operation $O_n^B$ by at most $c_n$. Therefore, the derived schedule has a regular objective function value not greater than that of $\sigma '$ and thus $\sigma$. $\square$

Theorem 1

The studied fixed-job-sequence problem for makespan minimization is NP-hard in the ordinary sense, even if $a_j=b_j=0$ for all jobs $J_j\in \mathcal{J}$.

Proof

Let integer bound E and integer sizes $e_1,e_2,\ldots , e_m$ with $\sum _{j=1}^m e_j=2E$ be an instance of Partition. We create a scheduling instance with $m+2$ jobs as follows:

$$\begin{aligned}&\hbox {Job }J_0: c_0=E;\\&\hbox {Job }J_j: c_j=e_j, j\in \{1,\ldots ,m\};\\&\hbox {Job }J_{m+1}: c_{m+1}=E. \end{aligned}$$

Note that $a_j=b_j=0$ for all $j\in \{0,1,\ldots ,m+1\}$ and the jobs abide by the processing sequence $(J_0, J_1,\ldots , J_{m+1})$. We claim that the answer to Partition is affirmative if and only if there is a feasible schedule with a makespan of 2E. Recall that it is necessary and sufficient to consider the schedules where each flexible operation $O^C_j$ is immediately preceded by the corresponding operation $O^A_j$ or immediately followed by the corresponding operation $O^B_j$.

Let $X_1$ and $X_2$ be a partition of the m indices in Partition. A feasible schedule is constructed as follows. Machines A and B are initialized with two processing sequences of operations $(O_0^A, O_1^A,\ldots , O_{m+1}^A)$ and $(O_0^B, O_1^B,\ldots , O_{m+1}^B)$, respectively. Then operations $O_0^C$ and operation $O_{m+1}^C$ are assigned to machine B and machine A, respectively. Let each operation $O_{j}^C$, $j\in X_1$ processed on machine A immediately preceded by $O_j^A$, and each operation $O_{j'}^C$, $j'\in X_2$ processed on machine B immediately followed by $O_{j'}^B$. The makespan is exactly 2E as depicted in Fig. 1.

Assume now that there is a feasible schedule the makespan of which is exactly 2E. Since the sum of the processing loads of all jobs is 4E, no idle time is allowed on either machine. By Lemma 1, we assume that $O_0^C$ and $O_{m+1}^C$ are processed on machine B and machine A, respectively. Let the set $\mathcal{J}_A$ contain the jobs whose flexible operations are assigned to machine A. If $\sum _{J_j\in \mathcal{J}_A} c_j>E$, then the completion time of $O_{m+1}^C$ on machine A is larger than 2E, which contradicts the assumption. On the other hand, if $\sum _{J_j\in \mathcal{J}_A} c_j<E$, then $\sum _{J_j\in \{J_1,\ldots ,J_m\}\setminus \mathcal{J}_A} c_j>E$ and the completion time of machine B is greater than 2E. Therefore, we must have $\sum _{J_j\in \mathcal{J}_A} c_j=E$, and a partition is obtained. $\square$

Fig. 1

Configuration of a feasible schedule with a makespan of 2E

The relationships between the standard objective functions lead to the following corollary.

Corollary 1

The studied fixed-job-sequence problem for $L_{\max }, \sum w_jC_j, \sum T_j$ or $\sum U_j$ is NP-hard in the ordinary sense, even if $a_j=b_j=0$ for all jobs $J_j\in \mathcal{J}$.

Proof

The minimization of maximum lateness is a natural generalization of makespan minimization since $C_{\max }$ is a special case of $L_{\max }$ by setting $d_j=0$ for all jobs $J_j\in \mathcal{J}$. In the studied fixed-job-sequence problem, makespan minimization also corresponds to a special case of minimizing $\sum w_jC_j$ with $w_j=0, j\in \{1,2,\ldots ,n-1\}$ and $w_n=1$. As for the objective function $\sum T_j$ or $\sum U_j$, the proof technique utilized in Theorem 1 can be applied to show the NP-hardness by deploying arguments with $d_j=2E$ for all jobs $J_j\in \mathcal{J}$ and a feasible schedule retaining $\sum T_j=0$ or $\sum U_j=0$. $\square$

3 Pseudo-polynomial time dynamic programs

In this section, pseudo-polynomial time dynamic programs are proposed for the five addressed objective functions $C_{\max }$, $L_{\max }$, $\sum w_jC_j$, $\sum w_jT_j$, and $\sum w_jU_j$. The notion of the developed dynamic programming stems from the observation that a feasible schedule can be decomposed into several subschedules separated by the machine-B idle times. Then a subschedule in some state can be defined by the schedule shape characteristics. In the designed two-phase dynamic programming framework, optimal subschedules of all states are constructed in the first phase. Then an optimal schedule can be assembled by concatenating appropriate optimal subschedules in the second phase.

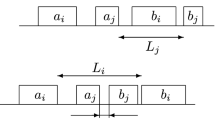
3.1 Makespan

For a particular subschedule, the difference between the completion times of the two machines is called the lag of this subschedule. Define a subschedule named schedule block in state $(k,i,j,\ell )$ as a subschedule for jobs $\{J_i,J_{i+1},\ldots ,J_j\}$ satisfying the following conditions: (1) no idle time exists between any two consecutive operations on the machines, i.e. block property; (2) the first flexible operation $O^C_i$ goes to machine $k\in \{A,B\}$; (3) the lag is exactly $\ell$. The shape characteristics of the schedule blocks in some state can be delineated in terms of the above three conditions. A schedule block in state $(k,i,j,\ell )$, where $i<j$, can be built up by suffixing $J_j$ to an appropriate schedule block in state $(k,i,j-1,\ell ')$. Two possible construction scenarios are depicted in Fig. 2, where $k=A$. Let function $f(k,i,j,\ell )$ denote the minimum machine-A processing span among the blocks in state $(k,i,j,\ell )$. The schedule block retaining $f(k,i,j,\ell )$ is called the optimal block in state $(k,i,j,\ell )$. To facilitate further presentation, define the Kronecker delta

$$\begin{aligned} \delta _{kB}=\left\{ \begin{array}{ll} 0,&{} \quad \text{ if } \; k=A;\\ 1,&{} \quad \text{ if } \; k=B, \end{array}\right. \end{aligned}$$

and the aggregate quantities $a_{[i:j]}=\sum _{h=i}^j a_h$, $c_{[i:j]}=\sum _{h=i}^j c_h$, $b_{[i:j]}=\sum _{h=i}^j b_h$, and $w_{[i:j]}=\sum _{h=i}^j w_h$, $1\le i\le j\le n$. The block property of a schedule block in state $(k,i,j,\ell )$, where $i<j$, implies

$$\begin{aligned}&c_i\delta _{kB}+b_{[i:j]}-a_{[i+1:j]}-c_{[i+1:j]}\le \ell \le c_i\delta _{kB}\\&\quad +\, b_{[i:j]}+c_{[i+1:j]}-a_{[i+1:j]}, \end{aligned}$$

and the block exists only if $\ell \ge b_j$. Denote

$$\begin{aligned} \underline{\ell }=\max \{b_j,c_i\delta _{kB}+b_{[i:j]}-a_{[i+1:j]}-c_{[i+1:j]}\}, \end{aligned}$$

and

$$\begin{aligned} \overline{\ell }=c_i\delta _{kB}+b_{[i:j]}+c_{[i+1:j]}-a_{[i+1:j]}. \end{aligned}$$

It thus suffices to consider $\ell$ over the interval $\left[ \underline{\ell },\overline{\ell }\right]$, which is valid if the condition $\overline{\ell }\ge b_j$ can be ensured. Actually, given a 3-tuple k, i, j, the value $\overline{\ell }$, which denotes the upper limit to $\ell$, is calculated by assuming that the flexible operation(s) including $O_{j}^C$ go to machine B, and thus a schedule block can be constructed only if $\overline{\ell }\ge c_j+b_j$. The dynamic programs for block construction can be described in the following.

Fig. 2

Construction of a block in state $(A,i,j,\ell )$ from a block in state $(A,i,j-1,\ell ')$

Block construction ($C_{\max }$)

Initial conditions:

$f(k,i,j,\ell )=\left\{ \begin{array}{ll} a_i+c_i,&{} \text{ if } k=A, i=j, \text{ and } \ell =b_i;\\ a_i,&{} \text{ if } k=B, i=j, \text{ and } \ell =c_i+b_i;\\ \infty , &{}\text{ otherwise. } \end{array}\right.$

Recursions:

for each 4-tuple $k,i,j,\ell$ satisfying $k\in \{A,B\}$, $1\le i< j\le n$, and $\underline{\ell }\le \ell \le \overline{\ell }$,

$/*$ The recursion runs only if $\overline{\ell }\ge c_j+b_j$.$*/$

Case 1 (Operation $O_j^C$ being assigned to machine A):

$y_1= f(k,i,j-1,\ell +a_j+c_j-b_j)+(a_j+c_j),$                        (1)

Case 2 (Operation $O_j^C$ being assigned to machine B):

$y_2=\left\{ \begin{array}{ll} f(k,i,j-1,\ell +a_j-c_j-b_j)+a_j,&{} \text{ if } \ell \ge c_j+b_j; \\ \infty ,&{} \text{ otherwise },\\ \end{array}\right.$

$\displaystyle f(k,i,j,\ell )=\min \{y_1, y_2\}$.

The formulation is justified as follows. Given a feasible combination of $k,i,j,\ell$, the derivation of $f(k,i,j,\ell )$ can be done by considering two scenarios regarding the assignment of the last flexible operation $O_j^C$. Case 1 is for assigning operation $O_j^C$ to machine A, as shown in Fig. 2a. By suffixing the two operations $O_j^A$ and $O_j^C$ on machine A, and operation $O_j^B$ on machine B to the optimal block in state $(k,i,j-1,\ell ')$, we have $(a_j+c_j)+\ell =\ell '+b_j$, subject to the condition of block property $\ell '\ge a_j+c_j$. Thus, it can be shown that $\ell '=\ell +a_j+c_j-b_j$, as given in Eq. (1), subject to the condition $\ell +a_j+c_j-b_j\ge a_j+c_j$, i.e. $\ell \ge b_j$, which is satisfied anyway in the recursions owing to the definition of $\underline{\ell }$, the lower limit on $\ell$. In Case 2 where operation $O_j^C$ is processed on machine B as shown in Fig. 2b, we have $a_j+\ell =\ell '+(c_j+b_j)$, subject to the condition $\ell '=\ell +a_j-c_j-b_j\ge a_j$, i.e. $\ell \ge c_j+b_j$. Note that the two cases are not disjoint about the associated conditions $\ell \ge b_j$ and $\ell \ge b_j+c_j$ and the first condition subsumes the second one. If $\ell \ge c_j+b_j$ is satisfied, then operation $O_j^C$ is allowed to be dispatched to either of the machines.

After the block construction, a complete schedule can be generated with a concatenation of appropriate optimal blocks in backward recursion. Notice that in a schedule any two adjacent optimal blocks are separated by an inserted idle time on machine B to ensure that each optimal block is maximal for inclusion. Define by a partial schedule in state (k, i) a schedule of jobs $\{J_i,J_{i+1},\ldots ,J_n\}$, the prefix of which is an optimal block having the leading job $J_i$ and operation $O_i^C$ processed on machine k. Denote by g(k, i) the minimum makespan among all the partial schedules in state (k, i). The dynamic program for schedule concatenation, where we need a dummy job $J_{n+1}$ with $a_{n+1}=c_{n+1}=\infty$, is depicted in Schedule Concatenation $(C_\mathrm{max})$.

The algorithm procedure is validated as follows. There are two cases for assembling a partial schedule in (k, i) by prefixing an optimal block in $(k,i,j,\ell )$. In Case 1, the optimal block in $(k,i,j,\ell )$ is attached to the front end of the optimal partial schedule in $(A,j+1)$, as illustrated in Fig 3a, where $k=B$. To satisfy the schedule concatenation property about idle times, the inequality $\ell < a_{j+1}+c_{j+1}$ is required. As for Case 2, we have the optimal block in $(k,i,j,\ell )$ prefixed to the optimal partial schedule in $(B,j+1)$ as shown in Fig. 3b (where $k=B$), and thus $\ell < a_{j+1}$. Notice again that the first associated condition $\ell < a_{j+1}+c_{j+1}$ subsumes the second one $\ell < a_{j+1}$. The term $\ell \lfloor {\frac{j}{n}\rfloor }$ is added for the scenario where $j=n$.

Schedule concatenation $(C_{\max })$

Initial conditions:

for each $k\in \{A,B\}$,

$g(k,i)=\left\{ \begin{array}{ll} 0,&{} \text{ if } i=n+1,;\\ \infty , &{}\text{ otherwise. } \end{array}\right.$

Recursions:

for each 2-tuple k, i satisfying $k\in \{A,B\}$, and $1\le i\le n$,

$g(k,i)=\min _{\begin{array}{c} i\le j\le n;\\ \underline{\ell }\le \ell \le \overline{\ell } \end{array}}\{z_1, z_2\}$,                                                      (2)

where $z_1$ and $z_2$ are calculated as in the following:

Case 1 (The optimal block in $(k,i,j,\ell )$ being attached to the optimal partial schedule in $(A,j+1)$):

$z_1=\left\{ \begin{array}{ll} f(k,i,j,\ell )+\ell \lfloor {\frac{j}{n}\rfloor }+g(A,j+1),&{} \text{ if } \ell < a_{j+1}+c_{j+1}; \\ \infty , &{}\text{ otherwise },\\ \end{array}\right.$

Case 2 (The optimal block in $(k,i,j,\ell )$ being attached to the optimal partial schedule in $(B,j+1)$):

$z_2=\left\{ \begin{array}{ll} f(k,i,j,\ell )+\ell \lfloor {\frac{j}{n}\rfloor }+g(B,j+1),&{} \text{ if } \ell < a_{j+1}; \\ \infty ,&{} \text{ otherwise }.\\ \end{array}\right.$

Goal: $\displaystyle \min _{k\in \{A,B\}}\{g(k,1)\}.$

Fig. 3

Schedule concatenation ($C_{\max }$) for assembling a partial schedule in state (B, i) by prefixing an optimal block in $(B,i,j,\ell )$

The run time of the developed dynamic program can be analysed as follows. In the block construction, there are at most $O(n^2 \sum _{h=1}^n c_h)$ states, each of which needs O(1) time for calculation, since the size of the interval $\left[ \underline{\ell },\overline{\ell }\right]$ is in the order of $O(\sum _{h=1}^n c_h)$. Thus, the run time for block construction is $O(n^2 \sum _{h=1}^n c_h)$. In the schedule concatenation, there are O(n) states, each of which takes at most $O(n \sum _{h=1}^n c_h)$ time due to the loops over all possible subscripts of the $\min$ operator in Eq. (2). So the run time for schedule concatenation is $O(n^2 \sum _{h=1}^n c_h)$. The total run time of the presented dynamic program is therefore $O(n^2 \sum _{h=1}^n c_h)$.

Theorem 2

The studied fixed-job-sequence problem for makespan minimization is pseudo-polynomially solvable in $O(n^2 \sum _{h=1}^n c_h)$ time.

In the following subsections, we extend the design of the above dynamic programming algorithm to the performance metrics of $L_{\max }$, $\sum w_jC_j$, $\sum w_jT_j$, and $\sum _j w_jU_j$. The development starts with the maximum lateness and the total weighted completion time. The solution procedure will then be adapted for the total weighted tardiness and weighted number of tardy jobs.

3.2 Maximum lateness and total weighted completion time

In the previous subsection, the block construction is carried out by minimizing the processing span of machine A subject to a specified lag. For the objective function of $L_{\max }$, we however cannot obtain a shortest machine-A processing span of a block while minimizing the maximum lateness within this block. The same difficulty also arises in the pursuit of the minimum total weighted completion time. Therefore, we introduce another parameter to freeze machine-A processing spans of the constructed blocks.

Define a schedule block in state $(k,i,j,S,\ell )$ as a subschedule for jobs $\{J_i,J_{i+1},\ldots ,J_j\}$ satisfying the following four conditions: (1) no idle time is inserted between any two consecutive operations on the machines; (2) the first flexible operation $O^C_i$ is assigned to machine $k\in \{A,B\}$; (3) the machine-A processing span is exactly S; (4) the lag is exactly $\ell$. Let function $f(k,i,j,S,\ell )$ denote the optimal maximum lateness of the jobs $\{J_i,J_{i+1},\ldots ,J_j\}$ among the blocks in state $(k,i,j,S,\ell )$. Then, the dynamic program for block construction is formulated as follows.

Block construction ($L_{\max }$)

Initial conditions:

$f(k,i,j,S,\ell )=\left\{ \begin{array}{ll} a_i+c_i+b_i-d_i,&{} \text{ if } k=A, i=j, S=a_i+c_i, \text{ and } \ell =b_i;\\ a_i+c_i+b_i-d_i,&{} \text{ if } k=B, i=j, S=a_i, \text{ and } \ell =c_i+b_i;\\ \infty , &{}\text{ otherwise. } \end{array}\right.$

Recursions:

for each 5-tuple $k,i,j,S,\ell$ satisfying $k\in \{A,B\}$, $1\le i< j\le n$, $a_{[i:j]}\le S\le a_{[i:j]}+c_{[i:j]}$, and $\underline{\ell }\le \ell \le \overline{\ell }$,                                     $/*$ The recursion runs only if $\overline{\ell }\ge c_j+b_j$.$*/$

Case 1 (Operation $O_j^C$ being assigned to machine A, as shown in Fig. 4):

$y_1=\max \{f(k,i,j-1,S-a_j-c_j,\ell +a_j+c_j-b_j),S+\ell -d_j\}),$

Case 2 (Operation $O_j^C$ being assigned to machine B):

$y_2=\left\{ \begin{array}{ll} \max \{f(k,i,j-1,S-a_j,\ell \!+\!a_j-c_j-b_j), S+\ell -d_j\},&{} \text{ if } \ell \ge c_j+b_j; \\ \infty ,&{} \text{ otherwise },\\ \,\end{array}\right.$

$\displaystyle f(k,i,j,S,\ell )=\min \{y_1, y_2\}$.

Fig. 4

Construction of a block in $(A,i,j,S,\ell )$ from a block in $(A,i,j-1,S',\ell ')$

After the block construction procedure, we can then generate complete schedules for a sequence of jobs with idle times inserted between blocks. Let a partial schedule in state (k, i) be a schedule of jobs $\{J_i,J_{i+1},\ldots ,J_n\}$, the prefix of which is an optimal block having the leading job $J_i$ and operation $O_i^C$ processed on machine k. Denote by g(k, i) the optimal maximum lateness among all the partial schedules in state (k, i). The dynamic program for schedule concatenation, where we introduce a dummy job $J_{n+1}$ with $a_{n+1}=c_{n+1}=\infty$, is shown below.

Schedule concatenation $(L_{\max })$

Initial conditions:

for $k\in \{A,B\}$,

$g(k,i)=\left\{ \begin{array}{ll} -\infty ,&{} \text{ if } i=n+1,;\\ \infty , &{}\text{ otherwise. } \end{array}\right.$

Recursions:

for each 2-tuple k, i satisfying $k\in \{A,B\}$, and $1\le i\le n$,

$g(k,i)=\min _{\begin{array}{c} i\le j\le n;\\ a_{[i:j]}\le S\le a_{[i:j]}+c_{[i:j]};\\ \underline{\ell }\le \ell \le \overline{\ell } \end{array}}\{z_1, z_2\}$,

where $z_1$ and $z_2$ are calculated as in the following:

Case 1 (The optimal block in $(k,i,j,S,\ell )$ being attached to the optimal partial schedule in $(A,j+1)$, as illustrated in Fig. 5):

$z_1=\left\{ \begin{array}{ll} \max \{f(k,i,j,S,\ell ),S+g(A,j+1)\},&{} \text{ if } \ell < a_{j+1}+c_{j+1}; \\ \infty , &{}\text{ otherwise },\\ \end{array}\right.$

Case 2 (The optimal block in $(k,i,j,S,\ell )$ being attached to the optimal partial schedule in $(B,j+1)$):

$z_2=\left\{ \begin{array}{ll} \max \{f(k,i,j,S,\ell ),S+g(B,j+1)\},&{} \text{ if } \ell < a_{j+1}; \\ \infty ,&{} \text{ otherwise }.\\ \end{array}\right.$

Goal: $\displaystyle \min _{k\in \{A,B\}}\{g(k,1)\}.$

Regarding the run time, there are at most $O(n^2 (\sum _{h=1}^n c_h)^2)$ states, each of which needs O(1) time for calculation of $f(k,i,j,S,\ell )$. Thus, the run time for block construction is thus $O(n^2 (\sum _{h=1}^n c_h)^2)$. In the schedule concatenation, there are O(n) states, each of which takes at most $O(n (\sum _{h=1}^n c_h)^2)$ time due to the loops over all possible subscripts of the $\min$ operator. So the run time for schedule concatenation is $O(n^2 (\sum _{h=1}^n c_h)^2)$. The total run time of the presented dynamic program is therefore $O(n^2 (\sum _{h=1}^n c_h)^2)$.

Theorem 3

The studied fixed-job-sequence problem for minimizing the maximum lateness is pseudo-polynomially solvable in $O(n^2 (\sum _{h=1}^n c_h)^2)$ time.

Fig. 5

Case-1 schedule concatenation ($L_{\max }$) for assembling a partial schedule in state (B, i)

Next, we consider the objective function of total weighted completion time. The algorithm framework for maximum lateness minimization can be readily adapted for the minimization of total weighted completion time with slight modifications. Let $f(k,i,j,S,\ell )$ be the minimum total weighted completion time of the state $(k,i,j,S,\ell )$. Definitions of initial conditions, $z_1$, and $z_2$ used in Block construction ($L_{\max }$) are modified as

$$\begin{aligned}&f(k,i,j,S,\ell )\\&\quad =\left\{ \begin{array}{ll} w_i(a_i+c_i+b_i),&{} \quad \text{ if } \; k=A, i=j, S=a_i+c_i, \text{ and } \ell =b_i;\\ w_i(a_i+c_i+b_i),&{} \quad \text{ if } \; k=B, i=j, S=a_i, \text{ and } \ell =c_i+b_i;\\ \infty , &{}\text{ otherwise, } \end{array}\right. \\&y_1=f(k,i,j-1,S-a_j-c_j,\ell +a_j +c_j-b_j)+w_j(S+\ell ),\\&y_2\\&\quad =\left\{ \begin{array}{ll} f(k,i,j-1,S-a_j,\ell \!+\!a_j-c_j-b_j)\!+\!w_j(S\!+\!\ell ),&{} \text{ if } \ell \!\ge \! c_j+b_j; \\ \infty ,&{} \text{ otherwise }.\\ \end{array}\right. \end{aligned}$$

Definitions of initial conditions, $z_1$, and $z_2$ used in Schedule concatenation ($L_{\max }$) are also modified as

$$\begin{aligned}&g(k,i)=\left\{ \begin{array}{ll} 0,&{} \quad \text{ if } \; i=n+1,;\\ \infty , &{} \quad \text{ otherwise. } \end{array}\right. \\&z_1\\&\quad =\left\{ \begin{array}{ll} f(k,i,j,S,\ell )+g(A,j+1)+w_{[j+1:n]}S,&{} \quad \text{ if } \ell< a_{j+1}+c_{j+1}; \\ \infty , \quad &{}\text{ otherwise },\\ \end{array}\right. \\&z_2\\&\quad =\left\{ \begin{array}{ll} f(k,i,j,S,\ell )+g(B,j+1)+w_{[j+1:n]}S,&{} \quad \text{ if } \ell < a_{j+1}; \\ \infty ,&{} \quad \text{ otherwise }.\\ \end{array}\right. \end{aligned}$$

Theorem 4

The studied fixed-job-sequence problem for minimizing the total weighted completion time is pseudo-polynomially solvable in $O(n^2 (\sum _{h=1}^n c_h)^2)$ time.

3.3 Total weighted tardiness and weighted number of tardy jobs

To design pseudo-polynomial time algorithms for the two objective functions, $\sum w_jT_j$ and $\sum w_jU_j$, some further modifications are needed. The tardiness status of the jobs within the blocks and partial schedules created via the procedures for $L_{\max }$ and $\sum w_jC_j$ cannot be fathomed. We therefore instead determine the optimal objective value for $\sum w_jT_j$ or $\sum w_jU_j$ within the blocks and partial schedules subject to the condition that the first job starts at a specified time point. In both Block construction and Schedule concatenation procedures, we introduce an extra parameter $\lambda$, which is the lead time to specify the exact total length before the start of the block or partial schedule. Define state $(k,i,j,S,\ell ,\lambda )$ to include the subschedules for jobs $\{J_i,J_{i+1},\ldots ,J_j\}$ which satisfy the following conditions: (1) no idle time is inserted between any two consecutive operations on the machines; (2) the first flexible operation $O^C_i$ is assigned to machine $k\in \{A,B\}$; (3) the machine-A processing span is exactly S; (4) the lag is exactly $\ell$; (5) job i starts at time $\lambda$, which is the lead time strictly imposed in front of the block. Let function $f(k,i,j,S,\ell ,\lambda )$ denote the optimal total weighted tardiness of the jobs $\{J_i,J_{i+1},\ldots ,J_j\}$ among the blocks in state $(k,i,j,S,\ell ,\lambda )$. To facilitate notation, we denote the tardiness and the tardiness status of job $J_j$ completing at time t in some block, respectively, by $T_j(t)=\max \{0,t-d_j\}$ and

$$\begin{aligned} U_j(t)=\left\{ \begin{array}{ll} 1, &{} \quad \text{ if } t>d_j;\\ 0, &{} \quad \text{ otherwise }.\\ \end{array}\right. \end{aligned}$$

A dummy job $J_0$ with $a_0=c_0=0$ is needed for the following procedures as shown below.

Block construction ($\sum w_jT_j$)

Initial conditions:

for each $\lambda$ satisfying $a_{[0:i-1]}\le \lambda \le a_{[0:i-1]}+c_{[0:i-1]}$,

$f(k,i,j,S,\ell ,\lambda )=\left\{ \begin{array}{ll} w_iT_i(\lambda +a_i+c_i+b_i),&{} \text{ if } k=A, i=j, S=a_i+c_i, \text{ and } \ell =b_i;\\ w_iT_i(\lambda +a_i+c_i+b_i),&{} \text{ if } k=B, i=j, S=a_i, \text{ and } \ell =c_i+b_i;\\ \infty , &{}\text{ otherwise. }\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \,\,\,(3) \end{array}\right.$

Recursions:

for each 6-tuple $k,i,j,S,\ell ,\lambda$ satisfying $k\!\in \!\{A,B\}$, $1\le i< j\le n$, $a_{[i:j]}\le S\le a_{[i:j]}+c_{[i:j]}$, $\underline{\ell }\le \ell \le \overline{\ell }$, and $a_{[0:i-1]}\le \lambda \le a_{[0:i-1]}+c_{[0:i-1]}$,

$/*$ The recursion runs only if $\overline{\ell }\ge c_j+b_j$.$*/$

Case 1 (Operation $O_j^C$ going to machine A, as shown in Fig. 6):

$y_1=f(k,i,j-1,S-a_j-c_j,\ell +a_j+c_j-b_j,\lambda )+w_jT_j(\lambda +S+\ell )$,                                                                                                       (4)

Case 2 (Operation $O_j^C$ going to machine B):

$y_2=\left\{ \begin{array}{ll} f(k,i,j-1,S-a_j,\ell +a_j-c_j-b_j,\lambda )+w_jT_j(\lambda +S+\ell ),&{} \text{ if } \ell \ge c_j+b_j; \\ \infty ,&{} \text{ otherwise },\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \, (5) \\ \end{array}\right.$

$\displaystyle f(k,i,j,S,\ell ,\lambda )=\min \{y_1, y_2\}$.

With the derived blocks, we can then find an optimal complete schedule through the concatenation of optimal blocks. Let state $(k,i,\lambda )$ include the partial schedules consisting of jobs $\{J_i,J_{i+1},\ldots ,J_n\}$ that are prefixed with an optimal block having operation $O_i^C$ processed on machine k and job $J_i$ starting exactly at time $\lambda$. Denote by $g(k,i,\lambda )$ the optimal total weighted tardiness among all the partial schedules in state $(k,i,\lambda )$. The dynamic program for schedule concatenation with another dummy job $J_{n+1}$ retaining $a_{n+1}=c_{n+1}=\infty$ is shown below.

Schedule concatenation $(\sum w_jT_j)$

Initial conditions:

for each 2-tuple $k,\lambda$ satisfying $k\in \{A,B\}$, and $a_{[1:n]}\le \lambda \le a_{[1:n]}+c_{[1:n]}$,

$g(k,i,\lambda )=\left\{ \begin{array}{ll} 0,&{} \text{ if } i=n+1,;\\ \infty , &{}\text{ otherwise. } \end{array}\right.$

Recursions:

for each 3-tuple $k,i,\lambda$ satisfying $k\in \{A,B\}, 1\le i\le n$, and $a_{[0:i-1]}\le \lambda \le a_{[0:i-1]}+c_{[0:i-1]}$,

$g(k,i,\lambda )=\min _{\begin{array}{c} i\le j\le n;\\ a_{[i:j]}\le S\le a_{[i:j]}+c_{[i:j]};\\ \underline{\ell }\le \ell \le \overline{\ell } \end{array}}\{z_1, z_2\}$,

where $z_1$ and $z_2$ are calculated as in the following:

Case 1 (The optimal block in $(k,i,j,S,\ell ,\lambda )$ being attached to the optimal partial schedule in $(A,j+1,S+\lambda )$, as shown in Fig. 7):

$z_1=\left\{ \begin{array}{ll} f(k,i,j,S,\ell ,\lambda )+g(A,j+1,S+\lambda ),&{} \text{ if } \ell < a_{j+1}+c_{j+1}; \\ \infty , &{}\text{ otherwise },\\ \end{array}\right.$

Case 2 (The optimal block in $(k,i,j,S,\ell ,\lambda )$ being attached to the optimal partial schedule in $(B,j+1,S+\lambda )$):

$z_2=\left\{ \begin{array}{ll} f(k,i,j,S,\ell ,\lambda )+g(B,j+1,S+\lambda ),&{} \text{ if } \ell < a_{j+1}; \\ \infty ,&{} \text{ otherwise }.\\ \end{array}\right.$

Goal: $\displaystyle \min _{k\in \{A,B\}}\{g(k,1,0)\}.$

The procedures Block construction $(\sum w_jT_j)$ and Schedule concatenation $(\sum w_jT_j)$ both requires $O(n^2 (\sum _{h=1}^n c_h)^3)$, in which the lead time parameter $\lambda$ induces an extra term $\sum _{h=1}^n c_h$. The following theorem follows.

Table 1 Average run times (in seconds) of 25 instances for $10\le n\le 100$ and $100\le \sum _{h=1}^n c_h\le 300$

Theorem 5

The studied fixed-job-sequence problem for minimizing the total weighted tardiness is pseudo-polynomially solvable in $O(n^2 (\sum _{h=1}^n c_h)^3)$ time.

The above two procedures for $\sum w_jT_j$ can be easily adapted for the minimization of weighted number of tardy jobs with the same time complexity by replacing function $T_j(\cdot )$ with $U_j(\cdot )$ in Eq. (3), (4), and (5).

Theorem 6

The studied fixed-job-sequence problem for minimizing the weighted number of tardy jobs is pseudo-polynomially solvable in $O(n^2 (\sum _{h=1}^n c_h)^3)$ time.

Fig. 6

Construction of a block in $(A,i,j,S,\ell ,\lambda )$ from a block in $(A,i,j-1,S',\ell ',\lambda )$

Fig. 7

Case-1 schedule concatenation ($\sum w_jT_j$) for assembling a partial schedule in state $(B,i,\lambda )$

3.4 Computational experiments

To demonstrate the practical performance of the developed dynamic programming framework, we conducted brief computational experiments for the objective function $C_{\max }$. The numerical experiments were implemented in Mathematica 10.1 on a laptop computer equipped with an Intel Core i5-4310M CPU, 8GB RAM and Windows 7 64-bit operating system. Regarding the experimental setting, the processing time $a_j$ or $b_j$ for each job $J_j\in \mathcal{J}$ was generated as an uniformly distributed random number within the interval [0, 20]. The processing times of the flexible operations were produced by a random partition of a given amount $\sum _{h=1}^n c_h$ into n values such that $c_j\ge 0$, $j\in \{1,\ldots ,n\}$. The first experiment was performed for $10\le n\le 100$ (with an interval of 5) and $100\le \sum _{h=1}^n c_h\le 300$ (with an interval of 10). For each combination of n and $\sum _{h=1}^n c_h$, we generate 25 random test instances. The average run times of 25 instances for all combinations are given in Table 1, and the regression result is illustrated in Fig. 8, where the dots denote the experimental data of test instances and the associated best-fit regression polynomial reflects the computational complexity $O(n^2 \sum _{h=1}^n c_h)$.

Fig. 8

Regression surface of the average run time and $(n,\sum _{h=1}^n c_h)$

Table 2 Average and maximum run times (in seconds) of 25 instances for $50\le n\le 200$ and $500\le \sum _{h=1}^n c_h\le 1000$

The second experiment was concerned with large-scale instances, where $50\le n\le 200$ (with an interval of 50) and $500\le \sum _{h=1}^n c_h\le 1000$ (with an interval of 500). Table 2 summarizes the average and maximum run times of 25 random test instances. Given $n=50$, even the maximum run time is no more than 26 s for the case with $\sum _{h=1}^n c_h=1000$. If $n=200$ is considered, then the average run time is less than 118 s for $\sum _{h=1}^n c_h=500$ and 296 s for $\sum _{h=1}^n c_h=1000$.

4 Conclusions

This paper investigated the problem of scheduling three-operation jobs in a two-machine flowshop subject to a given job processing sequence for five standard performance metrics, viz. $C_{\max },L_{\max },\sum w_jC_j,\sum w_jT_j, \mathrm{and} \sum w_jU_j$. We showed that the studied problem is ordinary NP-hard even if the processing times of the preassigned operations are all zero. Although the extremely restricted case remains NP-hard, the general setting is pseudo-polynomially solvable with the development of dynamic programs. The detailed complexity results of the studied fixed-job-sequence problem is provided in Table 3. It shall be highlighted that this study is mainly aimed at contributing to the three-operation flowshop scheduling problem from the perspective on solution technique development.

Table 3 Complexity results of the studied fixed-job-sequence problems

For future research, we could first clarify the complexity status of the total completion time minimization problem, the polynomial solvability of which is not ruled out. The following two observations suggest that a polynomial-time dynamic programming algorithm design similar to Hwang et al. (2012, (2014) may not be applicable to the $\sum C_j$ problem:

• (1) In the development of a dynamic program with backward (or forward) recursion for the open problem, the shape of the block (or partial schedule) cannot be fixed with a constant number of state variables the ranges of which are polynomial in the number of jobs, i.e., the machine-A or machine-B processing span of a block (or partial schedule) cannot be realized without specifying exactly which flexible operations are on machine A or B. Thus, it is inevitable to include a temporal state variable S to enumerate the machine-A processing span in the recursive function.

• (2) If the aforementioned difficulty can be overcome by some technique, then we will be able to avoid the temporal state variable $\ell$ with the same approach. It thus will make the studied problem for the makespan minimization polynomially solvable, which contradicts the NP-hardness result in Theorem 1.

Therefore, the development of an algorithm other than block-based dynamic program is suggested for investigating the polynomial solvability. It would be essential to delve into the structural properties of schedules with respect to the objective function $\sum C_j$. As for the conjecture about NP-hardness, an unconventional proving scheme could be necessary for the flexibility in job manipulation could be limited by the fixed-job-sequence assumption. Another direction is to devise fully polynomial time approximation schemes for the five considered performance metrics. A further extension is to investigate the generalized fixed-sequence scenario where the requirement for the flexible operation being immediately preceded or followed by the corresponding preassigned operations is relaxed. This relaxation may render much more interleaving combinations of operations on either machine, and make the problem more challenging. The consideration of preemption, particularly for the flexible operations could also be an interesting extension.