Abstract
In this paper, our aim is to revisit the nonparametric estimation of a square integrable density f on \({\mathbb {R}}\), by using projection estimators on a Hermite basis. These estimators are studied from the point of view of their mean integrated squared error on \({\mathbb {R}}\). A model selection method is described and proved to perform an automatic bias variance compromise. Then, we present another collection of estimators, of deconvolution type, for which we define another model selection strategy. Although the minimax asymptotic rates of these two types of estimators are mainly equivalent, the complexity of the Hermite estimators is usually much lower than the complexity of their deconvolution (or kernel) counterparts. These results are illustrated through a small simulation study.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Consider an i.i.d. n-sample \(X_1, \ldots ,X_n\) from an unknown density f. The nonparametric estimation of f has been the subject of such a huge number of contributions in the past decades that it is difficult to make an exhaustive list of references. Roughly speaking, there are two main approaches to estimate \(f\), kernel or projection method. In the projection method which is our concern here, for f belonging to \({\mathbb {L}}^2({\mathbb {R}})\), considering an orthonormal basis in \({\mathbb {L}}^2({\mathbb {R}})\), estimators are built by estimating a finite number of coefficients of the development of \(f\in {\mathbb {L}}^2({\mathbb {R}})\) on the basis. Fourier and wavelet bases, for instance, are commonly used. Bases of orthogonal polynomials are also used for compactly supported densities (see e.g., Donoho et al. 1996; Birgé and Massart 2007; Efromovich 1999; Massart 2007; Tsybakov 2009 for reference books). For densities with a non-compact support included in \({\mathbb {R}}^+\), recent contributions use bases composed of Laguerre functions (see e.g., Comte and Genon-Catalot 2015; Belomestny et al. 2016; Mabon 2017).
To our knowledge, for densities on \({\mathbb {R}}\), the use of a Hermite basis is only considered in Schwartz (1967) and Walter (1977). In this paper, we are going to revisit the nonparametric estimation of \(f\in {\mathbb {L}}^2({\mathbb {R}})\) by using projection estimators on a Hermite basis. To find the minimax asymptotic rates of convergence, authors generally assume that the unknown density belongs to a function space specifying some regularity properties of f. Here, we consider the Sobolev-Hermite spaces which are naturally associated with the Hermite basis and are defined in Bongioanni and Torrea (2006). It turns out that the Sobolev-Hermite space of regularity index s is included in the classical Sobolev space with same index. Therefore, we are led to compare the performances of the projection estimators on the Hermite basis with those of the deconvolution estimators which are projection estimators on the sine cardinal basis. Deconvolution estimators have been widely studied mainly for observations with additive noise and also for direct observations (see e.g., Comte et al. 2008). The optimal \({\mathbb {L}}^2\)-risk for density estimation on a Sobolev ball with regularity index s is of order \(O(n^{-2s/(2s+1)})\), see Schipper (1996), Efromovich (2008) and Efromovich (2009). For densities having a fifth-order moment belonging to a Sobolev Hermite ball with the same regularity index s, we obtain the same rate. Therefore, from the asymptotic point of view, no difference can be made between these two classes of estimators at least for non-heavy tailed densities. Apart from Sobolev spaces, we consider a class of Gaussian mixtures where Hermite-based estimators also achieve the minimax convergence rates. Finally, we study Hermite projection estimators in a different context, the estimation of the Lévy density of a Lévy process in the pure-jump case.
While most papers focus on deriving minimax convergence rates, the computational efficiency of the proposed estimator is not often considered. This issue is especially important for densities with a non-compact support. We prove that the Hermite estimators have usually a much lower complexity than the deconvolution estimators, resulting in a noteworthy computational gain.
The plan of the paper is as follows. In Sect. 2, we present the Hermite basis, and the \({\mathbb {L}}^2\)-risk of the associated projection estimators is studied together with the possible orders for the variance term. A data-driven choice of the dimension is proposed and the associated estimator is proved to be realize adequately the bias–variance trade-off. In Sect. 3, results on deconvolution estimators are presented. Section 4 is devoted to the study of asymptotic rates of convergence. From this point of view, the two approaches of the previous sections are proved to be equivalent, except in some special cases. Then, we compare the complexity of the procedures and conclude that the Hermite method has a substantial advantage from this point of view. Section 4.6 is devoted to numerical simulation results and aims at illustrating the previous findings. In Sect. 5, the estimation of the Lévy density is considered in the same framework as Belomestny et al. 2015, Chapter “Adaptive estimation for Lévy processes.” A short conclusion is delivered in Sect. 6, and proofs are gathered in Sect. 7.
2 Projection estimators on the Hermite basis
2.1 Hermite basis
Below, we denote by \(\Vert .\Vert \) the \({\mathbb {L}}^2\)-norm on \({\mathbb {R}}\) and by \(\langle \cdot , \cdot \rangle \) the \({\mathbb {L}}^2\)-scalar product.
The Hermite polynomial of order j is given, for \(j\ge 0\), by:
Hermite polynomials are orthogonal with respect to the weight function \(\hbox {e}^{-x^2}\) and satisfy: \( \int _{{\mathbb {R}}} H_j(x) H_\ell (x) \hbox {e}^{-x^2}\hbox {d}x= 2^j j! \sqrt{\pi } \delta _{j,\ell } \) (see e.g., Abramowitz and Stegun 1964). The Hermite function of order j is given by:
The sequence \((h_j,j\ge 0)\) is an orthonormal basis of \({\mathbb {L}}^2({\mathbb {R}})\). The density f to be estimated can be developed in the Hermite basis \(f=\sum _{j\ge 0}a_j(f)h_j\) where \(a_j(f)=\int _{{\mathbb {R}}} f(x)h_j(x)\hbox {d}x=\langle f, h_j\rangle \).
We define \(S_m = \mathrm{span}(h_0, h_1, \dots , h_{m-1})\) the linear space generated by the m functions \(h_0, \dots , h_{m-1}\) and \(f_m=\sum _{j=0}^{m-1} a_j(f) h_j\) the orthogonal projection of f on \(S_m\).
2.2 Hermite estimator and risk bound
Consider a sample \(X_1, \dots , X_n\) of i.i.d. random variables with density f, belonging to \({\mathbb {L}}^2({\mathbb {R}})\). We define for each \(m\ge 0\), \({\hat{f}}_m=\sum _{j=0}^{m-1}\hat{a}_jh_j\) a projection estimator of f, with \(\hat{a}_j=n^{-1}\sum _{i=1}^n h_j(X_i)\), that is, an unbiased estimator of \(f_m=\sum _{j=0}^{m-1}a_j(f) h_j\).
These estimators are considered in Schwartz (1967) and then in Walter (1977). As usual, the \({\mathbb {L}}^2\)-risk is split into a variance and a square bias term. We give a more accurate rate for the variance term than in the latter papers. Indeed, we have the classical decomposition
where
The infinite norm of \(h_j\) satisfies (see Abramowitz and Stegun 1964; Szegö 1975, p. 242):
Therefore, we have \(V_m\le \varPhi _0^2 m\), as usual for projection density estimator, see Massart (2007), Chapter 7. However, more precise properties of the Hermite functions provide refined bounds:
Proposition 1
-
(i)
There exists constant c such that, for any density f and for any integer m,
$$\begin{aligned} V_{m} \le c m^{5/6}. \end{aligned}$$ -
(ii)
If \({\mathbb E}|X|^5 <+\infty \), then there exists constant \(c'\) such that for any integer m,
$$\begin{aligned} V_{m} \le c' m^{1/2}. \end{aligned}$$ -
(iii)
Assume that there exists \(K>0\) with
$$\begin{aligned} |f(x)|\le g(x):= \alpha \frac{1}{(1+|x|)^{a}}, \text{ for } |x|\ge K \text{ and } \alpha>0,a>1. \end{aligned}$$Then, there exists \(c''\) such that, for m large enough, \(V_{m}\le c'' m^{\frac{a+2}{2(a+1)}}\).
Proposition 1(i) shows that \(V_m\) is at most of order \(m^{5/6}\), a property obtained in Walter (1977). However, (ii)–(iii) show that this order can be improved depending on additional assumptions on f. At this point, it is worth stressing that, under the moment assumption of (ii), the rate of variance term \(V_m/n\) is not m / n as usual but \(m^{1/2}/n\). This means that, in this approach, the role of the dimension is played by \(m^{1/2}\). This fact, together with the regularity spaces introduced below to evaluate the rate of the bias term, allows to prove that the Hermite projection estimators is asymptotically equivalent to the sine cardinal estimators.
In the next paragraph, we make no assumption on the regularity properties of f. Moreover, because the variance order depends on assumptions on f, we do not want to consider it as given unlike in most model selection strategies. Our proposal of data-driven m leads to an estimator whose \({\mathbb {L}}^2\)-risk automatically realizes the bias–variance trade-off in a non-asymptotic way without knowing the regularity of the function f nor knowing the rate of the variance term.
2.3 Model selection
For model selection, we must estimate the bias and the variance term. Define \({\mathcal M}_n=\{1, \dots , m_n\}\), where \(m_n\) is the largest integer such that \(m_n^{5/6}\le n/\log (n)\) and set
where \(\kappa \) is a numerical constant. The quantity \(-\Vert \hat{f}_m\Vert ^2\) estimates \(-\Vert f_m\Vert ^2=\Vert f-f_m\Vert ^2 -\Vert f\Vert ^2\), and we can ignore the (unknown) constant term \(\Vert f\Vert ^2\). Usually, the penalty is chosen equal to \( \kappa \varPhi _0^2 m/n\), which is the known upper bound of the variance term, where \(\varPhi _0\) is defined by (4). Here, we know that this rate is not the adequate one and the fact that the order of \(V_m\) varies according to the assumptions on f justifies that we rather use \( {\widehat{V}}_m\), an unbiased estimator of \(V_m\). We can prove the following result.
Theorem 1
Assume that f is bounded and that \(\inf _{a\le x\le b} f(x)>0\) for some interval [a, b]. Then there exists \(\kappa _0\) such that, for \(\kappa \ge \kappa _0\), the estimator \({\hat{f}}_{{\hat{m}}}\) where \({\hat{m}}\) is defined by (5) satisfies
where C is a numerical constant (\(C=4\) suits) and \(C'\) is a constant depending on \(\Vert f\Vert _\infty \).
The estimator \({\hat{f}}_{{\hat{m}}}\) is adaptive in the sense that its risk bound achieves automatically the bias–variance compromise, up to a negligible term of order O(1 / n). It follows from the proof that \(\kappa _0=8\) is possible. This value of \(\kappa _0\) is certainly not optimal; finding the optimal theoretical value of \(\kappa \) in the penalty is not an easy task, even in simple models (see for instance Birgé and Massart (2007) in a Gaussian regression model). This is why it is standard to calibrate the value \(\kappa \) in the penalty by preliminary simulations, as we do in Sect. 4.6. Actually, the assumption \(\inf _{a\le x\le b} f(x)>0\) is due to the fact that the proof requires the condition
Condition (6) holds, as we can prove:
Proposition 2
If \(\inf _{a\le x\le b} f(x)>0\) for some interval [a, b], then, for m large enough, \(V_{m} \ge c'' m^{1/2}\) where \(c''\) is a constant.
3 Deconvolution estimators
As we want to compare the performances of projection estimators on the Hermite basis to those of projection estimators on the sine cardinal basis, we recall the definition of the latter estimators, i.e., the deconvolution estimators. Let \(\varphi (x)=\sin (\pi x)/(\pi x)\) which satisfies \(\varphi ^*(t)=1_{[-\pi , \pi ]}(t)\), where \(\varphi ^*\) denotes the Fourier transform of \(\varphi \). The functions \((\varphi _{\ell ,j}(x)= \sqrt{\ell }\varphi (\ell x-j),j\in {\mathbb Z})\) constitute an orthonormal system in \({\mathbb {L}}^2({\mathbb {R}})\). The space \(\varSigma _{\ell }\) generated by this system is exactly the subspace of \({\mathbb {L}}^2({\mathbb {R}})\) of functions having Fourier transforms with compact support \([-\pi \ell , \pi \ell ]\). The orthogonal projection \({\bar{f}}_{\ell }\) of f on \(\varSigma _{\ell }\) satisfies \({\bar{f}}_{\ell }^*= f^*1_{[-\pi \ell , \pi \ell ]}\). Therefore,
The projection estimator \({{\widetilde{f}}}_\ell \) of f is defined by:
This expression corresponds to the fact that:
Contrary to \({{\hat{f}}}_m\), the estimator \({{\widetilde{f}}}_\ell \) cannot be expressed as the corresponding sum with the estimated coefficients \({{\tilde{a}}}_{\ell ,j}=\frac{1}{n} \sum _{k=1}^n \varphi _{\ell ,j}(X_k)\) as this sum would be infinite and not defined. To compute it in concrete, one can use (8) or a truncated version
which creates an additional bias but is comparable to the previous Hermite estimator. We give the results for \({{\widetilde{f}}}_\ell \) and \({{\widetilde{f}}}_\ell ^{(n)}\).
Proposition 3
The estimator \({{\widetilde{f}}}_\ell \) satisfies
If moreover \(M_2=\int x^2f^2(x)\mathrm{d}x<+\infty \), then the estimator \({\widetilde{f}}_\ell ^{(n)}\) satisfies
If \(\ell \le n\) and \(K_n\ge n^2\), the last term is of order \(O(\ell /n)\) and can be associated to the variance term \(\ell /n\). Note that condition \(K_n\ge n^2\) implies that the computation of a large number of coefficients is required for \({\widetilde{f}}_{\ell }^{(n)}\), for large n. In practice, we take \(K_n\) even smaller than n in order to keep reasonable computation times.
As in the previous case, we can define a data-driven choice of the cutoff parameter \(\ell \) and build adaptive estimators:
where \({\tilde{\kappa }}\) is a numerical constant. Note that
We give the result for \({\widetilde{f}}^{(n)}_\ell \) only, as \(\Vert {\widetilde{f}}_\ell ^{(n)}\Vert ^2\) is faster to compute if \(K_n\) is chosen in a restricted range, \(K_n\le n\), see Sects. 4.5 and 4.6. The following result holds.
Theorem 2
If \(K_n\ge n^2\) and \(M_2=\int x^2f^2(x)\hbox {d}x<+\infty \), then there exists a numerical constant \({{\tilde{\kappa }}}_0\) such that, for \({{\tilde{\kappa }}}\ge {{\tilde{\kappa }}}_0\), the estimator \({\widetilde{f}}_{{\tilde{\ell }}_n}^{(n)}\) where \({\tilde{\ell }}_n\) is defined by (9) satisfies
where \(C_1\) is a numerical constant and \(C_2\) is a constant depending on \(\Vert f\Vert _\infty \).
For \({\widetilde{f}}_{{\tilde{\ell }}}\), an analogous risk bound may be obtained, without condition \(M_2<+\infty \) and without the term \(\ell (M_2+1)/n\) in the bound. For Theorem 2, we refer to Comte et al. (2008), Proposition 5.1, p. 97.
4 Comparison of rates of convergence and discussion
In this section, we compute the rates of convergence that can be deduced from the optimization of the upper bounds of \({\mathbb {L}}^2\)-risks. This requires to assess the rate of decay of the bias terms \(\Vert f-f_m\Vert ^2\) in the Hermite case, \(\Vert f-{\bar{f}}_\ell \Vert ^2\) in the deconvolution framework. The latter is usually obtained by assuming that the unknown density f belongs to a Sobolev space. For the former, we consider the Sobolev-Hermite spaces which are naturally linked with the Hermite basis.
4.1 Sobolev and Sobolev-Hermite regularity
For \(s>0\), the Sobolev-Hermite space with regularity s may be defined by:
where \(a_n(f)=\langle f,h_n\rangle \) is the n-th component of f in the Hermite basis. We refer to Bongioanni and Torrea (2006) for a definition using operator theory. Let \({\mathcal F}= \left\{ \sum _{j\in J} a_j h_j, J\subset {\mathbb N}, \text{ finite } \right\} \) be the set of finite linear combinations of Hermite functions and \(C_c^{\infty }\) the set of infinitely derivable functions with compact support. The sets \(C_c^{\infty }\) and \({\mathcal F}\) are dense in \(W^s\). As the Fourier transform of \(h_n\) satisfies
\(f\in W^s\) if and only if \( f^* \in W^s\). We now describe \(W^s\) when s is integer. Let
The following result is proved in Bongioanni and Torrea (2006). For sake of clarity, we give a simplified proof.
Proposition 4
For s integer, the Sobolev-Hermite space \(W^{s}\) is equal to:
Moreover, the following statements are equivalent: for s integer,
-
(1)
\(f \in W^{s}\),
-
(2)
f admits derivatives up to order s which satisfy \(f, f', \ldots ,f^{(s)}, x^{s-\ell }f^{(\ell )}, \ell =0, \ldots ,s-1 \) belong to \({\mathbb {L}}^2({\mathbb {R}})\).
The two norms \(\Vert f\Vert _{s, \mathrm{sobherm}}\) and \(\Vert |f\Vert |_{s,\mathrm{sobherm}}\) are equivalent.
Now, we recall the definition of usual Sobolev spaces. The Sobolev space with regularity index s is defined by
If s is integer, then
The two norms \(\Vert |\cdot \Vert |_{s,\mathrm{sob}}\) and \(\Vert \cdot \Vert _{s,\mathrm{sob}}\) are equivalent. Therefore, for s integer, \(W^s \subset {\mathcal W}^s\). Moreover, the following properties are proved in Bongioanni and Torrea (2006): for all \(s>0\),
-
\(W^s \varsubsetneq {\mathcal W}^s\). If \(f\in {\mathcal W}^s\) has compact support, then \(f \in W^s\).
-
$$\begin{aligned} f \in W^s \Rightarrow x^s f\in {\mathbb {L}}^2({\mathbb {R}}). \end{aligned}$$(13)
4.2 Rates of convergence
Now, we look at asymptotic rates of convergence. We first consider rates for Hermite projection estimators. We already studied the variance rate \(V_m/n\) (see the bounds for \(V_m\) in Proposition 1). If f belongs to
then \( \Vert f-f_m\Vert ^2\le L m^{-s}\). Plugging this and the bounds of Proposition 1 in Inequality (2) gives the following rates of the \({\mathbb {L}}^2({\mathbb {R}})\)-risk.
Proposition 5
Assume that \(f\in W^s(L)\) and consider the three cases (i), (ii), (iii) of Proposition 1.
Case (i) (general case). For \(m_{\mathrm{opt}}=[n^{1/(s+(5/6))}]\), \(\displaystyle \;\;{\mathbb E}(\Vert {\hat{f}}_{m_{\mathrm{opt}}} -f\Vert ^2)\lesssim n^{-\frac{s}{s+(5/6)}} \).
Case (ii). For \(m_{\mathrm{opt}} =[n^{1/(s+(1/2))}]\), \(\displaystyle \;\; {\mathbb E}(\Vert {\hat{f}}_{m_{\mathrm{opt}}}-f\Vert ^2)\lesssim n^{-\frac{s}{s+1/2}}\).
Case (iii). For \(m_{\mathrm{opt}} =[n^{1/(s+ (a+2)/(2(a+1))}]\), \(\displaystyle \;\;{\mathbb E}(\Vert {\hat{f}}_{m_{\mathrm{opt}}} -f\Vert ^2)\lesssim n^{-\frac{s}{s+ (a+2)/[2(a+1)]}}\).
Case (ii) gives the best rate. In view of the constraint on \(m_n\) in Theorem 1, the adaptive procedure reaches this best rate if \(m_{\mathrm{opt}}^{5/6}\le n/\log (n)\), that is \(s>1/3\). Note that the rate in case (iii) is strictly better than in case (i) as \((a+2)/(a+1) <5/3\) as soon as \(a>1/2\). Cases (ii)–(iii) improve the results of Schwartz (1967) and Walter (1977).
Now, we can compare the rates to those of projection estimators in the sine cardinal basis. The following result is deduced from Proposition 3 and (7).
Proposition 6
If
and \( \ell _{\mathrm{opt}}=n^{1/(2s+1)}\), we have \({\mathbb E}(\Vert {\widetilde{f}}_{ \ell _\mathrm{opt}}-f\Vert ^2)\lesssim n^{-2s/(2s+1)}\). If moreover \(K_n\ge n^2\), \({\mathbb E}(\Vert {\widetilde{f}}_{ \ell _\mathrm{opt}}^{(n)}-f\Vert ^2)\lesssim n^{-2s/(2s+1)}\).
In Schipper (1996), it is proved that this rate is minimax optimal (with exact Pinsker constant) on Sobolev balls (at least for an integer \(s\)), see also Efromovich (2009) for \(s<1/2\). Rigollet (2006) uses the blockwise Stein method to build an adaptive deconvolution estimator, which reaches the optimal rate with exact constant for any \(s>1/2\).
Let us compare results of Proposition 6 and of Proposition 5. As \(W^s \subset {\mathcal W}^s\), see Sect. 4.1, the comparison is relevant. In case (i), we see that the estimator \({{\widetilde{f}}}_{ \ell _\mathrm{opt}}\) has a better rate than \({\hat{f}}_{m_\mathrm{opt}}\). In case (ii), the estimators have the same rate. In case (iii), the estimator \({{\widetilde{f}}}_{ \ell _\mathrm{opt}}\) is slightly better than \({\hat{f}}_{m_\mathrm{opt}}\). In view of case (ii), the Hermite method is competitive. Indeed, the moment condition for (ii) is not very strong. In this case, sine cardinal estimators with cutoff parameter \(\ell \) and Hermite projection estimators on the space \(S_m\) are asymptotically equivalent when \(\ell = m^{1/2}\).
4.3 Rates of convergence in some special cases
When the density f belongs to \(W^s\) for all s, we must obtain directly the exact rate of decay of the bias term. This is possible for Gaussian and some related densities as one can make an exact computation of the coefficients \(a_j(f)\). Let
and
for X a standard Gaussian variable. The distribution \(f_{p,\sigma }(x)\hbox {d}x\) is equal to \(\varepsilon G^{1/2}\) for \(\varepsilon \) a symmetric Bernoulli variable, G a \(\mathrm{Gamma}(p+(1/2), 1/(2\sigma ^2))\) variable, independent of \(\varepsilon \).
Proposition 7
Assume that \(f=f_\mu \). Then for \(m_{\mathrm{opt}} =[(\log (n)/\log (2)) +e\mu ^2]\), we have
Assume that \(f=f_{\sigma }\). Then for \(m_{\mathrm{opt}} = [(\log {n})/\lambda ]\) where \(\lambda = \log {\left( \frac{\sigma ^2+1}{\sigma ^2-1}\right) ^2}\), we have
The same result holds for \(f=f_{p,\sigma }\) or any finite mixture of such distributions.
For \(f=f_{\sigma }\), the estimator \({{\widetilde{f}}}_\ell \) satisfies,
For \(\ell _{\mathrm{opt}}= \sigma \sqrt{2\log {n}}\), the rate of \({{\widetilde{f}}}_{\ell _{\mathrm{opt}}}\) is \(\sqrt{\log {n}}/n\). The rate is identical to the one obtained in Proposition 7. The result is analogous for \(f=f_{p,\sigma }\).
Finally, the Cauchy density will provide a counter-example. Let
From Proposition 1, case (iii), we take \(a=2\) and obtain for the variance term \(V_m\lesssim m^{2/3}\). Using Proposition 4, we check that \(f\in W^1\), \(f\notin W^2\). Moreover, by (13), \(x^s f \notin W^s\) for \(s\ge 3/2\). Therefore, \(f\notin W^{3/2}\), so the best rate we can obtain is \(n^{-s/s+(2/3)}\) with \(s<3/2\), for \(m_{\mathrm{opt}}=[n^{1/(s+(2/3))}]\).
For the sine cardinal method, \(f^*(t)= \exp {(-|t|)}\), so that \(\Vert f-f_\ell \Vert \lesssim \exp {(-2\pi \ell })\). Therefore, for \(\ell _\mathrm{opt}= \log {n}/2\pi \), the estimator \({{\widetilde{f}}}_{\ell _\mathrm{opt}}\) has a risk with rate \(\log {n}/n\). This is much better than for the Hermite estimator.
This discussion on rates of convergence points out the interest of the adaptive method. Indeed, it automatically realizes the bias–variance compromise and thus the previous rates are reached without any specific knowledge on f.
4.4 Rates of convergence for Gaussian mixtures
Kim (2014) provides optimal rates of convergence for estimating densities that are mean mixtures of normal distributions, that is for densities f in the class
where \(\phi \) denotes the standard normal density and \({\mathcal P}({\mathbb {R}})\) the set of all probability measures on the real line. The minimax optimal rate for the mean square risk is \(\sqrt{\log (n)}/n\). Moreover, the sine cardinal estimator \({\widetilde{f}}_\ell \) reaches the upper bound for the \({\mathbb {L}}^2\)-risk on the class \({\mathcal F}\), for \(\ell \propto \sqrt{\log (n)}\).
We study Hermite projection estimators for mean mixtures of Gaussian but also for variance mixtures. We consider, as suggested in Kim (2014), the subclass \({\mathcal F_\mathrm{sub}}({\mathbb {R}})=\cup _{C>0}{\mathcal F_\mathrm{sub}}(C),\)
where
Proposition 8
For \(f\in {\mathcal F}_\mathrm{sub}(C)\) and \(m_{\mathrm{opt}} = [\log (n)(eC+1/\log (2))]\), we have
Now we define the class of variance mixtures that we consider: let \(v >1\),
In other words, \(f\in {\mathcal G}(v)\) is the density of \(\sigma X\) with \(X \sim {\mathcal N}(0,1)\), \(\sigma \sim \varPi \), \(\sigma \in [1/v, v]\) with \(\sigma \) and X independent.
Proposition 9
For \(f\in {\mathcal G}(v)\), let
For \(m_{\mathrm{opt}} = [\log (n)/|\log (\rho _0)|]\), we have
In the class of variance mixtures of Gaussians, the lower bound rate is not known. However, in Ibragimov and Has’minskii (1980), Ibragimov (2001), the estimation of a density on a compact set [a, b] which is analytical in the vicinity of [a, b] is considered. The authors prove that the rate \(\log (n)/n,\) is optimal in this class. The restricted class given by \({\mathcal G}(v)\) considered in Proposition 9 gives a slightly improved rate, which is coherent with the result of Proposition 7.
4.5 Complexity
In this paragraph, we compare the Hermite and deconvolution estimators from another point of view: the computational efficiency.
Consider an estimator \({\hat{f}}_n\) of a function f whose \({\mathbb {L}}^2\)-risk can be evaluated on a ball B(L) of some functional space. Define its complexity \({\mathcal C}_{{\hat{f}}_n}(\varepsilon )\) as the minimal cost of computing \({\hat{f}}_n\) at the observation points \(X_1, \dots , X_n\), given that
Let us compute the complexity of the estimate \({\widetilde{f}}_{\ell _{\mathrm{opt}}}\) on the Sobolev ball \({\mathcal W}^s(L)\). As we need to evaluate the function \(\frac{\sin (\pi \ell \cdot )}{\pi \cdot }\) at all points \((X_k-X_j)\), \(1\le k, j \le n\), the cost of computing \({\widetilde{f}}_{\ell _{\mathrm{opt}}}\) is of order \(n^2\). Thus \(\varepsilon ^2 \asymp n^{-2s/(2s+1)}\) yields \(n\asymp \varepsilon ^{-2-1/s}\) so that \(C_{{\widetilde{f}}_{\ell _{\mathrm{opt}}}}(\varepsilon ) \asymp \varepsilon ^{-4-2/s}\) as \(\varepsilon \rightarrow 0\). So even in the case of infinitely smooth densities, the complexity of the deconvolution estimate can not be (asymptotically) lower than \(\varepsilon ^{-4}.\) A natural question is whether one can find an estimate with lower order of complexity. Note that the complexity would be the same for a kernel estimator on a ball of a Nikol’ski class with regularity s, see Tsybakov (2009), at least for kernels with a non-compact support used in Ibragimov and Has’minskii (1980).
For the truncated estimator \({\widetilde{f}}^{(n)}_{\ell _{\mathrm{opt}}}\), the cost is of order \(nK_n\): indeed, one must compute the \(\varphi _{\ell , j}(X_i)\) for \(i=1, \dots , n\) and \(|j|\le K_n\). Consequently, compared to the previous one, this estimate is competitive in term of computational cost as soon as \(K_n < n\) (however, this choice would contradict Theorem 3.1 where \(K_n\ge n^2\)).
Now, let us look at the projection estimator \({\hat{f}}_{m_{\mathrm{opt}}}\) for \(f\in W^s(L)\). The cost of computing a projection estimator \({\hat{f}}_m\) at observation points \(X_1, \dots , X_n\) corresponds to the cost of computing \(h_j(X_i)\) for \(i=1, \dots , n\) and \(j=0, \dots , m-1\), i.e., is of order nm. Thus, we derive the following proposition.
Proposition 10
Assume that \(f\in W^s(L)\) and consider the three cases (i), (ii), (iii) of Proposition 1. The complexity of the estimate \({\hat{f}}_{m_{\mathrm{opt}}}\) is given by \(\mathcal {C}_{{\hat{f}}}(\varepsilon )\sim \varepsilon ^{-2-\frac{2(\alpha +1)}{s}}\) with \(\alpha = 5/6,1/2,(a+2)/[2(a+1)],\), respectively.
Proof of Proposition 10
Taking \(\varepsilon ^2 \asymp n^{-2s/(2s+1)}\), hence \(n \asymp \varepsilon ^{-2-1/s}\), and the three values of \(m_{\mathrm{opt}}\) given Proposition 5 yield the result. \(\square \)
As can be seen, the complexity order of the Hermite-based estimate \({\hat{f}}_{m_{\mathrm{opt}}}\) is lower than the complexity order of the deconvolution estimate \({\widetilde{f}}_{\ell _{\mathrm{opt}}}\) provided \(s>\alpha .\) So in the case of densities with finite fifth moment already for \(s>1/2,\) our approach leads to estimates with much lower complexity. The difference between the estimates \({\hat{f}}_{m_{\mathrm{opt}}}\) and \({\widetilde{f}}_{\ell _{\mathrm{opt}}}\) becomes especially pronounced in the limiting case \(s\rightarrow \infty ,\) where \(\mathcal {C}_{{\hat{f}}_{m_{\mathrm{opt}}}}( \varepsilon )\asymp \varepsilon ^{-2}\) while \(\mathcal {C}_{{\widetilde{f}}_{\ell _{\mathrm{opt}}}}(\varepsilon )\asymp \varepsilon ^{-4}\) as \(\varepsilon \rightarrow 0\), resulting in a huge computational gain.
For any projection estimator, the cost of computation if of order \(nm_{\mathrm{opt}}\) where \(m_{\mathrm{opt}}\) is the optimal dimension. In the case of a density with compact support A, if we evaluate the \({\mathbb {L}}^2\)-risk of a projection estimator on a Besov ball of \(B_{2, s, \infty }(A)\) , we have \(\varepsilon ^2\asymp n^{-2s/(2s+1)}\) with \(m_{\mathrm{opt}}\asymp n^{1/(2s+1)}\), thus a cost of order \(\varepsilon ^{-2 -2/s}\), see Barron et al. (1999) for rates and definition of Besov spaces. All these results are summarized in Table 1.
4.6 Simulation illustrations
In this section, we propose a few illustrations of the previous theoretical findings. To that aim, we consider several densities, fitting different assumptions of our setting.
-
(i)
A Gaussian \({\mathcal N}(0,1)\),
-
(ii)
A Gaussian \({\mathcal N}(0,\sigma ^2)\), \(\sigma =0.5\),
-
(iii)
A mixed Gaussian density \(0.4{\mathcal N}(-3,\sigma ^2)+0.6 {\mathcal N}(3,\sigma ^2)\), \(\sigma =0.5\),
-
(iv)
A Gamma \(\gamma (3,0.5)\) density,
-
(v)
A mixed Gamma \(0.4\gamma (2, 1/2) + 0.6 \gamma (16, 1/4)\)
-
(vi)
A beta density \(\beta (3,3)\),
-
(vii)
A beta density \(\beta (3,6)\),
-
(viii)
Laplace density \(f(x)=\hbox {e}^{-|x|}/2\),
-
(ix)
A Cauchy density, \(f(x)=5/[\pi (1+(5x)^2)]\).
Density (i) is proportional to the first basis function \(h_0\) and should be perfectly estimated in the Hermite procedure, densities (vi) and (vii) are compactly supported and density (ix) does not admit any moment (in particular no fifth moment, so it does not fit case (ii) of Proposition 1). Hermite functions are recursively computed via (34) and with normalization (1).
We plot in Fig. 1, the representation of \(m\mapsto {\widehat{V}}_m/\sqrt{m}\) for 1 and 10 samples drawn from densities (i), (iv), (vi), (ix) (see (5)). It seems that the ratio is stable along the repetitions and converges to a fixed value, which is the same in the first three cases. On the contrary, \(m\mapsto {\widehat{V}}_m/m^{5/6}\) given for (i) and (ix) seems to decrease and to tend to zero in any case. It is tempting to conclude from these plots that the order of \(V_m\) is \(O(m^{1/2})\) in a rather general case.
Left: \(m\mapsto {\widehat{V}}_m/\sqrt{m}\) for 1 sample of densities (i) (blue line), (iv) (cyan stars), (vi) (red dashed), (ix) (green x marks) and \(m\mapsto {\widehat{V}}_m/m^{5/6}\) for 1 sample of densities (i) (blue dashed) and (ix) (green dash-dot). Right: the same as previously for 10 samples color figure online
We have implemented the Hermite projection estimator \({\hat{f}}_{{\hat{m}}}\) with \({\hat{m}}\) given in (5), \({\widetilde{f}}^{(n)}_{{\tilde{\ell }}_n}\) with \({\tilde{\ell }}_n\) given by (9) and the kernel estimator given by the function ksdensity of Matlab. For the model selection steps of the first two estimators, the two constants \(\kappa \) and \({\tilde{\kappa }}\) of the procedures have been both calibrated by preliminary simulations including other densities than the ones mentioned above (to avoid overfitting): the selected values were \(\kappa ={\tilde{\kappa }} =4\). We considered two sample sizes \(n=250\) and \(n=1000\), but as the sine cardinal procedure is rather slow, we only took \(K_{250}=K_{1000}=100\). The theoretical value \(K_n=n^2\) is unreachable in practice (the computing time becomes much too large), and our choice of \(K_n\) is consistent with the complexity considerations of Sect. 4.5.
For \(m_n\), we should take \((n/\log (n))^{6/5}\), which is of order 100 for \(n=250\) and 400 for \(n=1000\). We took \(m_{250}=m_{1000}=200\) as a compromise. The cutoff \(\ell \pi \) is selected among 100 equispaced values between 0 and 10. For each distribution, we present in Table 2 the MISE computed over 200 repetitions, together with the standard deviation. In the three cases, we provide also the mean (and standard deviations in parenthesis) of the selected dimension (Hermite), cutoff (Sine cardinal) or bandwidth (kernel).
We can see from the results of Table 2 that the Hermite and sine cardinal methods give very similar results, except for the \({\mathcal N}(0,1)\) where the Hermite projection is much better as expected, as the procedure most of the time chooses \(m=1\). The kernel method seems globally less satisfactory. The noteworthy difference between the first two methods is the computation time: as the models are nested in the Hermite projection strategy, all coefficients can be computed once for all, and then, the dimension is selected. In the sine cardinal strategy, each time \(\ell \) is changed, all the coefficients have to be recalculated. For instance, when the maximal dimension proposed \(m_n\) is 50, and \(K_n\) is 100, the elapsed times for 100 simulations is: for \(n=250\), around 0.5s for Hermite, 41s for sine cardinal; for \(n=1000\), around 1.2s for Hermite, 137s for sine cardinal, all times measured on the same personal computer to give an order of the difference. This is coherent with the lower complexity property of the Hermite method.
Table 2 also provides the selected dimensions, cutoffs and bandwidths. As could be expected, \({\hat{m}}\) , \({\tilde{\ell }}\) vary in opposite way, compared to \({\hat{h}}\). Without surprise also, the selected dimensions and cutoffs increase when the sample size increases. What is remarkable is the values of the selected dimensions for \(\beta \)-distributions, which are very large. Globally, we can see that these values are very different from one distribution to the other. Contrary to the theoretical result, the Cauchy density is estimated with similar MISEs in the Hermite and sine cardinal methods.
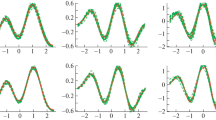
True density f in bold blue for Model (iii) (first two lines), Model (vii) (third line) and Model (ix) (fourth line), together with 25 estimates (green/gray) with \(n=250\) (lines 1 and 3) or \(n=1000\) (lines 2 and 4). First column: Hermite; second column: Sine cardinal; third column: kernel. Above each plot: MISE \(\times \) 1000 and std \(\times \) 1000 in parenthesis, followed par the mean of selected dimensions, cutoffs and bandwidths (all means over the 25 samples) color figure online
In Fig. 2, density and 25 estimators are plotted for models (iii), (vii) and (ix). Risks and standard deviation for the 25 curves are given above each plot, together with the mean of the selected dimension, cutoff or bandwidth. The methods are comparable, even for the Cauchy distribution, except for the mixtures, where the kernel method fails. The first two lines illustrate the improvement obtained when increasing n. We note again that the selected dimensions in the Hermite method are possibly rather high (see the beta and the Cauchy densities). However, computation time remains very short.
5 Pure jump Lévy processes
We now look at projection Hermite estimators in a different context, namely the estimation of the Lévy density of a Lévy process.
Let \((L_t, t \ge 0)\) be a real-valued Lévy process, i.e., a process with stationary independent increments with characteristic function of the form:
where we assume that the Lévy density \(n(\cdot )\) satisfies
-
(H1)
\(\displaystyle \int _{\mathbb {R}} |x| n(x) \hbox {d}x < \infty .\)
Uner (H1) and (17), the process \((L_t)\) is of pure jump type, has no drift component, finite variation on compacts and satisfies \({\mathbb E}(|L_t|)<+\infty \) (see e.g., Bertoin 1996, Chap. 1). The distribution of \((L_t)\) is entirely specified by \(n(\cdot )\), which describes the jumps behavior. We assume that the process is discretely observed with sampling interval \(\varDelta \) and set \((Z_k= Z_k^{\varDelta }= L_{k\varDelta }- L_{(k-1)\varDelta } , k= 1, \ldots , n)\) which are independent, identically distributed random variables with common characteristic function \(\phi _{\varDelta }(u)\). In Belomestny et al. (2015), second chapter, “Adaptive estimation for Lévy processes,” methods of estimation of the function
in this context are presented and studied under the asymptotic framework of high-frequency data, i.e., the sampling interval \(\varDelta =\varDelta _n\) tends to 0 while n and the total length time of observations \(n\varDelta _n\) tend to infinity.
In here, we consider the same framework and propose estimators of g using the Hermite functions basis. For simplicity, we omit the index n in notations and denote \(\varDelta =\varDelta _n\), \(Z_k= Z_k^{\varDelta _n},k= 1, \ldots , n\). The following additional assumptions are required.
-
(H2)
The function g belongs to \({\mathbb {L}}^{2}(\mathbb {R})\).
-
(H3)
\(\int _{\mathbb {R}} |x|^{7} n(x) \hbox {d}x <\infty \).
Assumption (H2) is obviously needed for the projection method. Assumption (H3) implies that \({\mathbb E}|Z_1|^7<+\infty \). Let \(P_\varDelta \) denote the distribution of \(Z_1\). In the above reference, the following property is proved (Proposition 3.3, p. 84): the measure
where \(g_\varDelta (x)= {\mathbb E}g(x-Z_1)= \int g(x-z)P_\varDelta (\hbox {d}z)\) and \(\mu _\varDelta (\hbox {d}x)\) weakly converges to \(g(x)\hbox {d}x\) as \(\varDelta \rightarrow 0\). In view of this property, the measure
will play the role of empirical measure for the estimation of g. By (H2), the function g can be developed in the Hermite basis:
We define, for \(m\ge 0\), the projection estimator \({\hat{g}}_m\) of g on the space \(S_m\) by:
Now, \({\hat{a}}_j\) is no more an unbiased estimator of \(a_j(g)\). For t a function, we set when it is well defined,
Thus, we have \({\mathbb E}{\hat{a}}_j= a_j(g)+R(h_j)\). The following holds:
Proposition 11
Assume that (H1)–(H3) hold. Consider for \(m \ge 0\), the estimator \({\hat{g}}_m\) of g and denote by \(g_m\) the orthogonal projection of g on \(S_m\). Then
where
and
(\(\Vert g\Vert _1\) denotes the \({\mathbb {L}}^1\)-norm of g).
First, let us recall some small sample properties of moments and absolute moments of \(Z_1\), see e.g., Belomestny et al. (2015). Under (17), (H1) and (H3), it holds that
where o(1) means that the term tends to 0 as \(\varDelta \) tends to 0 (see Proposition 3.1 and 3.2, pp. 82–83). Now, let us compare the projection Hermite estimators \(({\hat{g}}_m, m\ge 0)\) to the estimators studied in the latter reference. In Section 4.1, p. 87, a deconvolution estimator is studied, given by:
Looking at Proposition 4.3, p. 90 and Proposition 4.4, p. 91, we see that the sine cardinal estimators and the projection Hermite estimators are equivalent for \(\ell = m^{1/2}\) with the same optimal rates of convergence. Then, in Section 4.2, p. 105, the estimation of \(g1_A\) where A is a compact subset of \({\mathbb {R}}\) is considered by a projection method on finite dimensional subspaces of \({\mathbb {L}}^2(A)\). Here, on the contrary, the Hermite method gives better results as can be seen from Proposition 4.6, p. 110. The difference lies in the additional bias term \(\rho _{_{m, \varDelta }} \) which is smaller.
6 Concluding remarks
This paper is concerned with the nonparametric estimation of the density of an i.i.d. sample. Although there is an ocean of papers on this topic, it seems that the method developed here has not received yet much attention. Under the assumption that the unknown density belongs to \({\mathbb {L}}^2({\mathbb {R}})\), we build and study projection estimators using an orthonormal basis composed of Hermite functions. Usually, for projection estimators, the variance term of the \({\mathbb {L}}^2\)-risk is proportional to the dimension of the projection space. The special feature of the Hermite function basis is that the variance term is governed by the square root of the dimension. Moreover, we introduce specific regularity function spaces to evaluate the order of the bias term, namely the Sobolev Hermite spaces. This allows to prove that Hermite estimators are asymptotically equivalent to sine cardinal estimators. From the practical point of view, Hermite estimators are much faster to compute.
Adaptive estimators are studied, using an appropriate data-driven choice of the dimension.
This paper is only concerned with \({\mathbb {L}}^2\)-risks, but \({\mathbb {L}}^p\)-risks have also been studied by many authors (see the classical reference Donoho et al. 1996). Moreover, the \({\mathbb {L}}^1\)-approach is especially developed in Devroye and Györfi (1985). In this setting, adaptive estimators have been constructed by Devroye and Lugosi (2001). The study of \({\mathbb {L}}^p\)-risks with the Hermite approach would be an interesting field of further investigation.
7 Proofs
7.1 Proof of Propositions 1 and 2
We start by proving Proposition 1.
(i). The following bound comes from Szegö (1975, p. 242) where an expression of \(C_{\infty }\) is given:
Therefore, \( V_{m} \le C_{\infty }^2 \sum _{j=0}^{m-1}(j+1)^{-(1/6)}\le \frac{6}{5}C_{\infty }^2 m^{5/6}. \)
(ii). Now, as in Walter (1977), we use the following expression for the Hermite function \(h_n\) (see Szegö (1975, p. 248)):
where \(\lambda _j=|h_j(0)|\) if j is even, \(\lambda _j=|h^{'}_j(0)|/(2j+1)^{1/2}\) if j is odd and
By the Cauchy–Schwarz inequality, \( \xi _j^2(x)\le \int _0^{|x|}t^4 \hbox {d}t \int _0^{|x|}h_j^2(t)\hbox {d}t \le \frac{|x|^5}{5} \times \frac{1}{2}. \) Moreover,
By the Stirling formula and its proof, \(\lambda _{2j }\sim \pi ^{-1/2} j^{-1/4}\), \(\lambda _{2j+1}\sim \pi ^{-1/2} j^{-1/4}\) and for all j, there exists constants \(c_1,c_2\) such that, for all \(j\ge 1\),
Therefore, \( h_j^2(x)\le 2 \frac{c_2^2}{\pi j^{1/2}}+ \frac{1}{2j+1}\frac{|x|^5}{5}. \) This yields:
which implies \(V_m\lesssim m^{1/2}\).
Now, we study case (iii). The following bound for \(h_j\) is given in Markett (1984, p. 190): There exist positive constants \(C, \gamma \), independent of x and j, such that, for \(J=2j+1\),
Consider a sequence \((a_j)\) such that \(a_j\rightarrow +\infty \), \(a_j/ \sqrt{j}\rightarrow 0\) with \(J=2j+1 \) large enough to ensure \(\frac{a_J}{\sqrt{J}}\le 1/\sqrt{2}, a_J\ge K\). As \(\int h_j^2(x)\hbox {d}x=1\), \(a_J< \sqrt{J}\), \(a_J\ge K\) and g is decreasing,
Set \(x= (J^{1/3}+J)^{1/2}y\) in the integral. This yields:
as for \(0\le x\le 1/\sqrt{2}\), \(\text{ Arcsin }x\le 2x\). Now, we choose the sequence \((a_j)\) and consider \(a_j=j^{1/(2(a+1))}\). We deduce \( \int h_j^2(x)f(x)\hbox {d}x \lesssim j^{-a/(2(a+1))}, \) which leads to
\(\square \)
Now we turn to the proof of Proposition 2 and we look at the lower bound. We have, setting \(c=\inf _{a\le x \le b} f(x)\), and using (26),
We have \(j^{-3/4}c_1/\sqrt{\pi }\le \frac{2\lambda _j}{(2j+1)^{1/2}}\le j^{-3/4} \sqrt{2/\pi }c_2 \) and
Thus, the second term is lower bounded by \(-C j^{-3/4}c_1/\sqrt{\pi }\). For the first term, \(\lambda _j^2 \ge j^{-1/2} c_1^2/\pi \) and
Therefore, \( \int h_j^2(x)f(x)\hbox {d}x \ge c j^{-1/2} c_1^2/\pi \left[ \frac{b-a}{2} + O(\frac{1}{j^{1/2}})\right] -C j^{-3/4}c_1/\sqrt{\pi }. \) Consequently, for j large enough, \(\int h_j^2(x)f(x)\hbox {d}x \ge c'j^{-1/2}\). This implies, \(V_m\ge c'' m^{1/2}\). \(\square \)
7.2 Proof of Theorem 1
Let \(S_m\) be the space spanned by \(\{h_0, \ldots , h_{m-1}\}\) and \(B_m=\{t\in S_m, \Vert t\Vert =1\}\). We have \({\hat{f}}_m=\arg \min _{t\in S_m}\gamma _n(t)\) where \(\gamma _n(t)=\Vert t\Vert ^2 -2n^{-1}\sum _{i=1}^n t(X_i)\) and \(\gamma _n({\hat{f}}_m)=-\Vert {\hat{f}}_m\Vert ^2\). Now, we write, for two functions \(t,s \in {\mathbb {L}}^2({\mathbb {R}})\) ,
where
Then, for any \(m\in {\mathcal M}_n=\{1 \le m\le m_n\}\), \(m_n\le n/\log {n}\), and any \(f_m\in S_m\),
This yields \( \Vert {\hat{f}}_{{\hat{m}}} -f\Vert ^2 \le \Vert f-f_m\Vert ^2 + \widehat{\mathrm{pen}}(m)-\widehat{\mathrm{pen}}({\hat{m}}) +2\nu _n({\hat{f}}_{{\hat{m}}}-f_m). \) We use that
and some classical algebra to obtain:
We can choose p(m) such that
Indeed, for this, we apply the Talagrand Inequality (see Klein and Rio 2005):
where \({\mathbb E} \left( \sup _{t\in B_{m}} \nu _n^2(t)\right) \le \frac{V_m}{n}:=H^2\), \(\sup _{t\in B_{m}}\mathrm{Var}(t(X_1))\le \sup _{t\in B_{m}}{\mathbb E}(t^2(X_1))\le \Vert f\Vert _\infty :=v^2\) and \(\sup _{t\in B_{m}}\sup _x |t(x)| \le \sqrt{\sup _x\sum _{j=0}^{m-1} h_j^2(x)} \le C'_\infty m^{5/12}\le C'_\infty \sqrt{n}:=M_1\) (see (25)). Therefore, we obtain
Therefore, with the choice \(p(m)=4V_m/n\), (31) holds under condition (6) which is ensured by Proposition 2. Taking expectation in (30) yields
Let us define
and the set inspired by Bernstein Inequality \(\varOmega :=\)
with \(C''_\infty :=(C'_\infty )^2\) and \(C'_\infty \) is the constant appearing in \(M_1\) above. We split the term to study in (32) as follows:
On \(\varOmega \),
using that \(2xy\le x^2+y^2\) applied to \( \sqrt{2 V A}=2\sqrt{V/2} \sqrt{A}\le V/2 + A\) with \(V=V_{{\hat{m}}}\) and \(A=C''_\infty {\hat{m}}^{5/6}\log (n)/n\). Thus, by definition of \({\mathcal M}_n\),
On the other hand, \({\mathbb E}\left[ (\mathrm{pen}({\hat{m}}) - \widehat{\mathrm{pen}}({\hat{m}}))_+{\mathbf 1}_{\varOmega ^c}\right] \le 2\kappa {\mathbb P}(\varOmega ^c).\) Now, by applying Bernstein inequality, we get
Indeed, we have \({\mathbb P}(|S_n/n|\ge \sqrt{2v^2x/n}+ bx/(3n))\le 2\hbox {e}^{-x}\) for \(S_n=\sum _{i=1}^n (U_i-{\mathbb E}(U_i))\), Var\((U_1) \le v^2\), \(|U_i|\le b\). In our case \(U_i=Y_i^{(m)}\) and \(v^2=V_mC''_\infty m^{5/6}\), \(b= C''_\infty m^{5/6}\) and we took \(x=2\log (n)\).
So Eq. (32) becomes
Now we note that, for \(\kappa \ge 8:=\kappa _0\), \(4p(m\vee {\hat{m}})- \frac{1}{2} \mathrm{pen}({\hat{m}})\le \mathrm{pen}(m).\) Finally, we get, for all \(m \in {\mathcal M}_n\),
which ends the proof. \(\square \)
7.3 Proof of Proposition 3
The first inequality is standard. Let us study \({{\widetilde{f}}}_\ell ^{(n)}(x)\). We write that
The term \(\Vert {\bar{f}}_\ell -f\Vert ^2\) is the usual bias term. Moreover,
because \(\sum _{j\in {\mathbb Z} } |\varphi _{\ell ,j}(x)|^2\le \ell \). This is the standard variance term order.
The new term is
We write that \(ja_{\ell ,j}= j\sqrt{\ell } \int \varphi (\ell x-j) f(x)\hbox {d}x = \sqrt{\ell }(I_1+I_2)\) where
and we bound \(I_1\) and \(I_2\).
On the other hand, \(|I_2| \le \sup _{u\in {\mathbb {R}}}|u\varphi (u)| \int f(x)\hbox {d}x\le 1.\) We obtain:
Plugging this in (33), we find the bound: \(\Vert {\mathbb E}({{\widetilde{f}}}_\ell ^{(n)})-{\bar{f}}_\ell \Vert ^2\le 4\ell ^2(M_2+1)/K_n.\) This term is \(O(\ell /n)\) if \(\ell \le n\) and \(K_n\ge n^2\). \(\square \)
7.4 Proof of Proposition 4
Using the relations (see e.g., Abramowitz and Stegun 1964):
we get:
We deduce:
Assume first that \(f \in {\mathbb {L}}^2({\mathbb {R}})\), f admits derivatives up to order s, and for \(j_1,\ldots , j_m \in \{-,+\}\) and \( 1\le m\le s\), \(A_{j_1}\ldots A_{j_m}f \in {\mathbb {L}}^2({\mathbb {R}})\). We prove that \(\sum _{n\ge 0}n^s a_n^2(f)<+\infty . \) We do the proof only for f compactly supported and refer to Bongioanni and Torrea (2006) otherwise.
For the proof, set \(A_{-1}=A_{-}\), \(A_{+1}=A_{+}\) so that, for \(n-j\ge 0\), \(A_jh_n= \sqrt{2(n+d_j)} h_{n-j}\), \(d_j=0\) if \(j=1\), \(d_j=1\) if \(j=-1\) . Thus, for \(n-j_1-j_2-\cdots -j_m\ge 0\),
Now, for f compactly supported,
Iterating yields, for \(n+j_1+j_2+\cdots +j_m\ge 0\),
Therefore, \( \sum _{n\ge 0}(\langle A_{j_1}\ldots A_{j_m}f, h_n\rangle )^2<+\infty \) is equivalent to
Now assume that \(\sum _{n\ge 0}n a_n^2(f)<+\infty .\) We have \(f=\sum _{n\ge 0} a_n(f) h_n\). We can write for \(n_1\) large enough:
Thus, the series for f converges uniformly, f is continuous and satisfies for all x, \(f(x)=\sum _{n\ge 0} a_n(f) h_n(x)\). Therefore, we have:
Set \(S_N(t)= \sum _{n= 1}^N a_n(f)(\sqrt{n}\;h_{n-1}(t)-\sqrt{n+1}h_{n+1}(t)) \) and \(S(t)=\sum _{n\ge 1} a_n(f) (\sqrt{n}\;h_{n-1}(t)-\sqrt{n+1}h_{n+1}(t))\). The function S(t) is well defined by assumption and \(S_N\) converges to S in \({\mathbb {L}}^2({\mathbb {R}})\). Therefore, as N tends to infinity, \( \int _x^y |S_N(t)-S(t)|\hbox {d}t\le \sqrt{y-x} \Vert S_N-S\Vert \rightarrow 0. \) We have proved that
Thus, f is absolutely continuous and \(f'=S\) belongs to \({\mathbb {L}}^2({\mathbb {R}})\). Analogously, we prove that xf belongs to \({\mathbb {L}}^2({\mathbb {R}})\). Thus, \(A_+f, A_-f\) belong to \({\mathbb {L}}^2({\mathbb {R}})\).
Next, by the same reasoning as above, using that \(\sum _n n^2 a_n(f)<+\infty \) the series for \(f'(t)=S(t)\) is uniformly convergent and \(f'(t)\) is continuous. We proceed analogously to prove that \(f'\) is absolutely continuous and that \(xf'\) and \(f''\) belong to \({\mathbb {L}}^2({\mathbb {R}})\). Iterating the reasoning, we obtain that f admits continuous derivatives up to \(s-1\) and that \(f^{(s-1)}\) is absolutely continuous and that \(f, f', \ldots , f^{(s)}, x^{k-m}f^{(k-m)}, m=0, \ldots , s-1\) all belong to \({\mathbb {L}}^2({\mathbb {R}})\). This shows that, for \(j_1,\ldots , j_m \in \{-,+\}, 1\le m\le s\), \(A_{j_1}\ldots A_{j_m}f\) belongs to \({\mathbb {L}}^2({\mathbb {R}})\). \(\square \)
7.5 Proof of Proposition 7
Let \(f_{\mu }\) be the density \({\mathcal N}(\mu ,1)\), then
Now, we use the following formula, obtained by the Taylor formula and the recurrence relation \(H'_n=2nH_{n-1}\):
This yields
and \( \int _{{\mathbb {R}}} H_k(v) \hbox {e}^{-v^2} \hbox {d}v=(1/(c_kc_0))\langle h_k, h_0\rangle = 0\) if \(k\ne 0\). Therefore, we get
Then
Using Stirling’s formula, we get
Therefore \(m_{\mathrm{opt}} = [(\log (n)/\log (2))+ e\mu ^2]\) yields \(\Vert f_\mu -(f_\mu )_{m_{\mathrm{opt}}}\Vert ^2\lesssim 1/(n\sqrt{\log (n)})\). Combining with Proposition 1, we obtain the first result.
To prove the second result, we use the following proposition.
Proposition 12
Recall that \(a_j(f)= \int f(x)h_j(x)\mathrm{d}x\). For \(j\ge 0\), we have:
For \(n\ge p\), \(j\ge 0\),
We can now deduce the risk of \({{\hat{f}}}_m\) when \(f=f_{\sigma }\). We have:
Therefore, setting \(\lambda = \log \left[ \left( \frac{\sigma ^2+1}{\sigma ^2-1}\right) ^2\right] \) yields \(\Vert f-f_m\Vert ^2 \lesssim \frac{1}{\sqrt{m}} \exp {(-\lambda m)}.\) Combining with Proposition 1, we obtain \({\mathbb E}(\Vert {\hat{f}}_m-f\Vert ^2)\lesssim \frac{1}{\sqrt{m}} \exp {(-\lambda m)}+n^{-1}\sqrt{m }\), and thus Proposition 7. \(\square \)
Proof of Proposition 12
We first compute the coefficients of the centered Gaussian density. As Hermite polynomials of odd index are odd, the coefficients with odd index are null. We compute the coefficients with even index. Let
Note that if \(2{\bar{\sigma }}^2 =1\), i.e., \(\sigma ^2=1\), the coefficients are null except for \(n=0\).
We have
Using that (see e.g., Lebedev 1972, formula (4.9.2), p. 60)
we obtain:
Note that \(|(\sigma ^2-1)/(1+\sigma ^2)|<1\). Analogously,
Now, we use the following result which is proved in Chaleyat-Maurel and Genon-Catalot (2006, Lemma 3.1, p. 1459):
After some computations, we get:
Therefore,
which allows to bound \(|a_{2j}(f_{p, \sigma })|\) and ends the proof. \(\square \)
7.6 Proof of Proposition 8
Let \(f\in {\mathcal F}_\mathrm{sub}(C)\). We have from (36),
Therefore
Let us look at the first term of the sum above.
where we used that \(1/(j+m)!\le 1/(j!\; m!)\). Now, gathering the two terms again, we get
By Stirling’s formula
We choose \(\lambda =1/(2e)\); thus, the decrease of the square bias term is exponentially fast. The choice \(m_{\mathrm{opt}}=[\mathtt{a} \log (n)]\) with \(\mathtt{a}= eC+ 1/\log (2)\). Combining this with Proposition 1 gives the rate \(\sqrt{\log (n)}/n\) for the \({\mathbb {L}}^2\)-risk of the estimator. \(\square \)
7.7 Proof of Proposition 9
From Proposition 12 and formula (37), we have
Now for \(f\in {\mathcal G}(v)\), we get
where \(\rho _0\) is given by (16). Therefore, choosing \(m_{\mathrm{opt}}=[\log (n)/|\log (\rho _0)|]\) gives a squared bias of order \(1/(n\sqrt{\log (n)})\) and a variance of order \(\sqrt{\log (n)}/n\), thus a rate of order \(\sqrt{\log (n)}/n\).
7.8 Proofs of Proposition 11
Using notation (21), we have:
First, \(\sum _{j=0}^{m-1} R^2(h_j) =\sup _{t\in S_m, \Vert t\Vert =1} R^2(t)\) and the bound for this term follows from the following Lemma:
Lemma 1
Let \(t\in S_m\) and assume that (H1) and (H2) hold.
(1) If \(C:=\int u^2|g^*(u)|^2du<+\infty \), then
(2) Otherwise:
On the other hand, we have:
We need to bound \(z^2h_j^2(z)\). To that aim, we use relation (26) for \(h_j\). We bound \(\xi _j(x)\) given by (27) as in the proof of Proposition 1 by: \(|\xi _j(x)|^2\le |x|^5/10\), and using (28) we obtain for \(j\ge 1\),
As a consequence
The bound on \({\mathcal V}_m\) given in (23) follows. \(\square \)
Proof of Lemma 1
For case (1), we refer to Comte and Genon-Catalot (2009), Proposition 4.1, p. 4099.
For case (2), we have (see (21) and (18)) for \(t\in S_m\),
Thus,
Under (17), (H1), we have
(see Proposition 3.2, p. 83 in Belomestny et al. 2015). Now, by Lemma 2 below, \(\Vert t'\Vert \le \sqrt{2 m} \Vert t\Vert \) so the proof of Lemma 1 is complete. \(\square \)
Lemma 2
\(\forall m\ge 0, \quad \forall t\in S_m, \quad \Vert t'\Vert ^2\le 2m\Vert t\Vert ^2\).
Proof of Lemma 2
A function \(t \in S_m\) can be written \(t=\sum _{j=0}^{m-1} a_j h_j\). Thus, \(t'=\sum _{j=0}^{m-1} a_j h'_j\). We use \(h'_0(x)=-h_1(x)/\sqrt{2}\) and Formula (35) to obtain:
This implies, for \(m\ge 2\)
For \(m=0,1\), the same inequality holds obviously. \(\square \)
References
Abramowitz, M., Stegun, I. A. (1964). Handbook of mathematical functions with formulas, graphs, and mathematical tables. National Bureau of Standards Applied Mathematics Series, 55 for sale by the Superintendent of Documents. Washington, DC: U.S. Government Printing Office.
Barron, A., Birgé, L., Massart, P. (1999). Risk bounds for model selection via penalization. Probability Theory and Related Fields, 113, 301–413.
Belomestny, D., Comte, F., Genon-Catalot, V., Masuda, H., Reiss, M. (2015). Lévy matters. IV. Estimation for discretely observed Lévy processes. Lecture Notes in Mathematics, 2128. Lévy Matters. Cham: Springer.
Belomestny, D., Comte, F., Genon-Catalot, V. (2016). Nonparametric Laguerre estimation in the multiplicative censoring model. Electronic Journal of Statistics, 10, 3114–3152.
Bertoin, J. (1996). Lévy processes. Cambridge tracts in mathematics, 121. Cambridge, NY: Cambridge University Press.
Birgé, L., Massart, P. (2007). Minimal penalties for Gaussian model selection. Probability Theory and Related Fields, 138, 33–73.
Bongioanni, B., Torrea, J. L. (2006). Sobolev spaces associated to the harmonic oscillator. Proceedings of the Indian Academy of Sciences: Mathematical Sciences, 116(3), 337–360.
Chaleyat-Maurel, M., Genon-Catalot, V. (2006). Computable infinite-dimensional filters with applications to discretized diffusion processes. Stochastic Processes and Their Applications, 116, 1447–1467.
Comte, F., Genon-Catalot, V. (2009). Nonparametric estimation for pure jump Lévy processes based on high frequency data. Stochastic Processes and Their Applications, 119, 4088–4123.
Comte, F., Genon-Catalot, V. (2015). Adaptive Laguerre density estimation for mixed Poisson models. Electronic Journal of Statistics, 9, 1113–1149.
Comte, F., Dedecker, J., Taupin, M. L. (2008). Adaptive density deconvolution with dependent inputs. Mathematical Methods of Statistics, 17, 87–112.
Devroye, L., Györfi, L. (1985). Nonparametric density estimation. The L1 view. Wiley series in probability and mathematical statistics: Tracts on probability and statistics. New York: Wiley.
Devroye, L., Lugosi, G. (2001). Combinatorial methods in density estimation. Springer series in statistics. New York: Springer.
Donoho, D. L., Johnstone, I. M., Kerkyacharian, G., Picard, D. (1996). Density estimation by wavelet thresholding. The Annals of Statistics, 24, 508–539.
Efromovich, S. (1999). Nonparametric curve estimation. Methods, theory, and applications. Springer series in statistics. New York: Springer.
Efromovich, S. (2008). Adaptive estimation of and oracle inequalities for probability densities and characteristic functions. The Annals of Statististics, 36, 1127–1155.
Efromovich, S. (2009). Lower bound for estimation of Sobolev densities of order less 1/2. Journal of Statistical Planning and Inference, 139, 2261–2268.
Ibragimov, I. (2001). Estimation of analytic functions. In M. de Gunst, C. Klaasen, A. van der Vaart (Eds.) State of the art in probability and statistics (Leiden, 1999). Institute of mathematical statistics lecture notes—Monograph series 36 (pp. 359–383). Beachwood, OH: Institute of Mathematical Statistics.
Ibragimov, I. A., Has’minskii, R. Z. (1980). An estimate of the density of a distribution. Studies in mathematical statistics, IV. Zapiski Nauchnykh Seminarov Leningradskogo Otdeleniya Matematicheskogo Instituta imeni V. A. Steklova Akademii Nauk SSSR (LOMI) 98, 61–85, 161–162 (in Russian).
Kim, A. K. H. (2014). Minimax bounds for estimation of normal mixtures. Bernoulli, 20, 1802–1818.
Klein, T., Rio, E. (2005). Concentration around the mean for maxima of empirical processes. The Annals of Probability, 33, 1060–1077.
Lebedev, N. N. (1972). Special functions and their applications (Revised edition, translated from the Russian and edited by Richard A. Silverman. Unabridged and corrected republication). New York: Dover Publications, Inc.
Mabon, G. (2017). Adaptive deconvolution on the nonnegative real line. Scandinavian Journal of Statistics: Theory and Applications, 44, 707–740.
Markett, C. (1984). Norm estimates for \((C,\delta )\) means of Hermite expansions and bounds for \(\delta _{{\rm eff}}\). Acta Mathematica Hungarica, 43, 187–198.
Massart, P. (2007). Concentration inequalities and model selection. Lectures from the 33rd summer school on probability theory held in Saint-Flour, July 6–23, 2003. With a foreword by Jean Picard. Lecture notes in mathematics, 1896. Berlin: Springer.
Rigollet, P. (2006). Adaptive density estimation using the blockwise Stein method. Bernoulli, 12, 351–370.
Schipper, M. (1996). Optimal rates and constants in L2-minimax estimation of probability density functions. Mathematical Methods of Statistics, 5, 253–274.
Schwartz, S. C. (1967). Estimation of a probability density by an orthogonal series. The Annals of Mathematical Statistics, 38, 1261–1265.
Szegö, G. (1975). Orthogonal polynomials (4th ed.). American Mathematical Society, Colloquium Publications, Vol: XXIII. Providence, RI: American mathematical Society.
Tsybakov, A. B. (2009). Introduction to nonparametric estimation. Springer series in statistics. New York: Springer.
Walter, G. G. (1977). Properties of Hermite series estimation of probability density. The Annals of Statistics, 5, 1258–1264.
Author information
Authors and Affiliations
Corresponding author
Additional information
D.B. acknowledges the financial support from the Russian Academic Excellence Project “5-100” and from the Deutsche Forschungsgemeinschaft (DFG) through the SFB 823 “Statistical modeling of nonlinear dynamic processes”.
About this article
Cite this article
Belomestny, D., Comte, F. & Genon-Catalot, V. Sobolev-Hermite versus Sobolev nonparametric density estimation on \({\mathbb {R}}\). Ann Inst Stat Math 71, 29–62 (2019). https://doi.org/10.1007/s10463-017-0624-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10463-017-0624-y