Optimal Adaptive Estimation on ${\mathbb{R}}$ or ${\mathbb{R}}^{{+}}$of the Derivatives of a Density

Abstract

In this paper, we consider the problem of estimating the $d$-th order derivative $f^{(d)}$ of a density $f$, relying on a sample of $n$ i.i.d. observations $X_{1},\dots,X_{n}$ with density $f$ supported on ${\mathbb{R}}$ or ${\mathbb{R}}^{+}$. We propose projection estimators defined in the orthonormal Hermite or Laguerre bases and study their integrated ${\mathbb{L}}^{2}$-risk. For the density $f$ belonging to regularity spaces and for a projection space chosen with adequate dimension, we obtain rates of convergence for our estimators, which are optimal in the minimax sense. The optimal choice of the projection space depends on unknown parameters, so a general data-driven procedure is proposed to reach the bias-variance compromise automatically. We discuss the assumptions and the estimator is compared to the one obtained by simply differentiating the density estimator. Simulations are finally performed. They illustrate the good performances of the procedure and provide numerical comparison of projection and kernel estimators

1 INTRODUCTION

1.1 Motivations and Content

Let $X_{1},\dots,X_{n}$ be $n$ i.i.d. random variables with common density $f$ with respect to the Lebesgue measure. The problem of estimating $f$ in this simple model has been widely studied. In some contexts, it is also of interest to estimate the $d$th order derivative $f^{(d)}$ of $f$, for different values of the integer $d$. Density derivatives provide information about the slope of the curves, local extrema or saddle points, for instance. Several examples of use of derivatives are developed in [33, 39]. The most common cases are those with $d\in\{1,2\}$. The first order density derivative permits to reach information, such as mode seeking in mixture models and in data analysis, see e.g., [10, 12]. The second order derivative of the density can be used to estimate one parameter scale of exponential families (see [17]), to develop tests for mode (see [12]), to select the optimal bandwidth parameter for density estimation (see [37]). Let us detail two specific contexts.

(1) The question arises when considering regression models. The estimation of the so-called ‘‘average derivative’’ defined by $\delta={\mathbb{E}}[Y\psi(X)]$, with $\psi(x)=f^{(1)}(x)/f(x),$ and $f$ is the marginal distribution of $X$ (see [19, 21]) relies on the estimation of the derivative of the density of $X$. This quantity enables to quantify the relative impact of $X$ on the variable of interest $Y$. In an econometric context, the average derivative is also used to verify empirically the law of demand: it allows to compare two economies with different price systems (see [19, 20], Section 3). In [7], the study of sea shore water quality leads the authors to estimate the derivative of the regression function, and the derivative of a Nadaraya–Watson estimator involves the derivative of a density estimator. Regression curves (see [30]) also involve derivatives of densities, consider $r(x)={\mathbb{E}}(Y|X=x)$, [39] (see Eq. (2.1)) establishes that for specific families of conditional distributions of $Y$ given $X$, on can express $r(x)=\psi(x)$ as $\psi(x)=f^{(1)}(x)/f(x)$, where $f$ is a density (see (2.1) in [39]).

(2) Derivatives also appear in the study of diffusion processes. Let $(X_{t})_{t\geqslant 0}$ be the solution of

$$dX_{t}=b(X_{t})dt+\sigma(X_{t})dW_{t},\quad X_{0}=\eta,$$

where $W_{t}$ is a standard Brownian independent of $\eta$. There exists a solution under standard assumptions on $b$ and $\sigma$. The model is widely used, for example in finance and biology. One related statistical problem is to estimate the drift function $b$, from discrete time observations of the process $X$. Under additional conditions (see [34]), the model is stationary, admits a stationary distribution $f$ and it holds that

$$\frac{f^{(1)}(x)}{f(x)}\varpropto\frac{2b(x)}{\sigma^{2}(x)}-2\frac{\sigma^{\prime}(x)}{\sigma(x)}.$$

If the variance $\sigma$ is either a constant or known, estimating $f$ and $f^{(1)}$ lead to an estimator of $b$.

These examples illustrate the interest of the mathematical question of nonparametric estimation of derivatives as a general inverse problem.

Most proposals for estimating the derivative of a density are built as derivatives of kernel density estimators, see [8, 10, 11, 28, 32, 35, 37] or [18], either in independent or in $\alpha$-mixing settings, in univariate or in multivariate contexts. A slightly different proposal still based on kernels can be found in [38]. The question of bandwidth selection is only considered in the more recent papers. For instance, [10] proposes a general cross-validation method in the multivariate case for a matrix bandwidth, see also the references therein. Most recently, [27] proposed a general original approach to bandwidth selection, and applies it to derivative estimation in a multivariate $\mathbb{L}^{p}$ setting and for anisotropic Nikol’ski regularity classes. This paper is, to the best of our knowledge, the first to study the risk of an adaptive kernel estimator.

Projection estimators have also been considered for density and derivatives estimation. More precisely, using trigonometric basis, [15] proposes a complete study of optimality and sharpness of such estimators, on Sobolev periodic spaces. Lately, [18] proposes a projection estimator and provide an upper bound for its $\mathbb{L}^{p}$-risk, $p\in[1,\infty]$. In a dependent context, [34] studies projection estimators in a compactly supported basis constrained on the borders or a non compact multi-resolution basis: she considers dependent $\beta$-mixing variables and a model selection method is proposed and proved to reach optimal rates on Besov spaces. In most results, the rate obtained for estimating $f^{(d)}$ the $d$th order derivative assumed to belong to a regularity space associated to a regularity $\alpha$, is of order $n^{-2\alpha/(2\alpha+2d+1)}$. Recently, a bayesian approach has been investigated in [36] relying on a $B$ spline basis expansion, the procedure requires the knowledge of the regularity of the estimated function.

In the present work, we consider projection estimators on projection spaces generated by Hermite or Laguerre basis, which have non compact supports, ${\mathbb{R}}$ or ${\mathbb{R}}^{+}$. When using compactly supported bases, one has to choose the basis support: it is generally considered as a fixed interval say $[a,b]$, but the bounds $a$ and $b$ are in fact determined from the data. Hermite and Laguerre bases do not require this preliminary choice. Moreover, in a recent work, [6] proves that estimators represented in Hermite basis have a low complexity and that few coefficients are required for a good representation of the functions: therefore, the computation is numerically fast and the estimate is parsimonious. If the $X_{i}$’s are nonnegative, then one should use the Laguerre basis: thus, this basis is of natural use in survival analysis where most functions under study are ${\mathbb{R}}^{+}$-supported. Lastly, we mention that derivatives of Laguerre or Hermite functions have interesting mathematical properties: their derivatives are simple and explicit linear combination of other functions of the bases. This property is fully exploited to construct our estimators.

The integrated ${\mathbb{L}}^{2}$-risk of such estimators is classically decomposed into a squared bias and a variance term. The specificity of our context is threefold.

(1) The bias term is studied on specific regularity spaces, namely Sobolev Hermite and Sobolev Laguerre spaces, as defined in [9], enabling to consider non compact estimation support ${\mathbb{R}}$ or ${\mathbb{R}}^{+}$.

(2) The order of the variance term depends on moment assumptions. This explains why, to perform a data driven selection of the projection space, we propose a random empirical estimator of the variance term, which has automatically the adequate order.

(3) In standard settings, the dimension of the projection space is the relevant parameter that needs to be selected to achieve the bias-variance compromise. In our context, this role is played by the square root of the dimension.

We also mention that our procedure provides parsimonious estimators, as few coefficients are required to reconstruct functions accurately. Moreover, our regularity assumptions are naturally set on $f$ and not on its derivatives, contrary to what is done in several papers. Our random penalty proposal is new, and most relevant in a context where the representative parameter of the projection space is not necessarily its dimension, but possibly the square root of the dimension. We compare our estimators with those defined as derivatives of projection density estimators, which is the strategy usually applied with kernel methods. Finally, we also propose a numerical comparison between our projection procedure and a sophisticated kernel method inspired by the recent proposal in density estimation of [25].

The paper is organized as follows. In the remaining of this section, we define the Hermite and Laguerre bases and associated projection spaces. In Section 2, we define the estimators and establish general risk bounds, from which rates of convergence are obtained, and lower bounds in the minimax sense are proved. A model selection procedure is proposed, relying on a general variance estimate; it leads to a data-driven bias-variance compromise. Further questions are studied in Section 3: the comparison with the derivatives of the density estimator leads in our setting to different developments depending on the considered basis: interestingly Hermite and Laguerre cases happen to behave differently from this point of view. Lastly, a simulation study is conducted in Section 4, in which kernel and projection strategies are compared.

1.2 Notations and Definition of the Basis

The following notations are used in the remaining of this paper. For $a$, $b$ two real numbers, denote $a\vee b=\max(a,b)$ and $a_{+}=\max(0,a)$. For $u$ and $v$ two functions in $\mathbb{L}^{2}(\mathbb{R})$, denote $\langle u,v\rangle=\int_{-\infty}^{+\infty}u(x)v(x)dx$ the scalar product on $\mathbb{L}^{2}(\mathbb{R})$ and $||u||=\big{(}\int_{-\infty}^{+\infty}u(x)^{2}dx\big{)}^{1/2}$ the norm on $\mathbb{L}^{2}(\mathbb{R})$. Note that these definitions remain consistent if $u$ and $v$ are in $\mathbb{L}^{2}(\mathbb{R}^{+})$.

1.2.1. The Laguerre basis. Define the Laguerre basis by:

$$\ell_{j}(x)=\sqrt{2}L_{j}(2x)e^{-x},\quad L_{j}(x)=\sum_{k=0}^{j}\dbinom{j}{k}(-1)^{k}\frac{x^{k}}{k!},\quad x\geqslant 0,\quad j\geqslant 0,$$

(1)

where $L_{j}$ is the Laguerre polynomial of degree $j$. It satisfies: $\int_{0}^{+\infty}L_{k}(x)L_{j}(x)e^{-x}dx=\delta_{k,j}$ (see [1], 22.2.13), where $\delta_{k,j}$ is the Kronecher symbol. The family $(\ell_{j})_{j\geqslant 0}$ is an orthonormal basis on $\mathbb{L}^{2}(\mathbb{R}^{+})$ such that $||\ell_{j}||_{\infty}=\sup_{x\in\mathbb{R}^{+}}|\ell_{j}(x)|=\sqrt{2}$. The derivative of $\ell_{j}$ satisfies a recursive formula (see Lemma 8.1 in [13]) that plays an important role in the sequel:

$$\ell_{0}^{\prime}=-\ell_{0},\quad\ell_{j}^{\prime}=-\ell_{j}-2\sum_{k=0}^{j-1}\ell_{k},\quad\forall j\geqslant 1.$$

(2)

1.2.2. The Hermite basis. Define the Hermite basis $(h_{j})_{j\geqslant 0}$ from Hermite polynomials $(H_{j})_{j\geqslant 0}$ :

$$h_{j}(x)=c_{j}H_{j}(x)e^{-x^{2}/2},\quad H_{j}(x)=(-1)^{j}e^{x^{2}}\frac{d^{j}}{dx^{j}}(e^{-x^{2}}),\quad c_{j}=(2^{j}j!\sqrt{\pi})^{-1/2},\quad x\in\mathbb{R},\ j\geqslant 0.$$

(3)

The family $(H_{j})_{j\geqslant 0}$ is orthogonal with respect to the weight function $e^{-x^{2}}$: $\int_{\mathbb{R}}H_{j}(x)H_{k}(x)e^{-x^{2}}dx=2^{j}j!\sqrt{\pi}\delta_{j,k}$ (see [1], 22.2.14). It follows that $(h_{j})_{j\geqslant 0}$ is an orthonormal basis on $\mathbb{R}$. Moreover, $h_{j}$ is bounded by

$$||h_{j}||_{\infty}=\underset{x\in\mathbb{R}}{\text{sup}}|h_{j}(x)|\leqslant\phi_{0}\text{ with }\phi_{0}=\pi^{-1/4}$$

(4)

(see [1], Chap. 22.14.17 and [22]). The derivatives of $h_{j}$ also satisfy a recursive formula (see [13], Eq. (52) in Section 8.2),

$$h_{0}^{\prime}=-h_{1}/\sqrt{2},\quad h_{j}^{\prime}=(\sqrt{j}\ h_{j-1}-\sqrt{j+1}h_{j+1})/\sqrt{2},\quad\forall j\geqslant 1.$$

(5)

In the sequel, we denote by $\varphi_{j}$ either for $h_{j}$ in the Hermite case or for $\ell_{j}$ in the Laguerre case. Let $g\in\mathbb{L}^{2}(\mathbb{R})$ or $g\in\mathbb{L}^{2}(\mathbb{R}^{+})$, $g$ develops either in the Hermite basis or the Laguerre basis:

$$g=\sum_{j\geqslant 0}a_{j}(g)\varphi_{j},\quad a_{j}(g)=\langle g,\varphi_{j}\rangle.$$

Define, for an integer $m\geqslant 1$, the space

$$S_{m}=\text{Span}\{\varphi_{0},\dots,\varphi_{m-1}\}.$$

The orthogonal projection of $g$ on $S_{m}$ is given by: $g_{m}=\sum_{j=0}^{m-1}a_{j}(g)\varphi_{j}$.

2 ESTIMATION OF THE DERIVATIVES

2.1 Assumptions and Projection Estimator of $f^{(d)}$

Let $X_{1},\dots,X_{n}$ be $n$ i.i.d. random variables with common density $f$ with respect to the Lebesgue measure and consider the following assumptions. Let $d$ be an integer, $d\geqslant 1$.

(A1) The density $f$ is $d$-times differentiable and $f^{(d)}$ belongs to $\mathbb{L}^{2}(\mathbb{R}^{+})$ in the Laguerre case or $\mathbb{L}^{2}(\mathbb{R})$ in the Hermite case.

(A2) For all integer $r$, $0\leqslant r\leqslant d-1$, we have $||f^{(r)}||_{\infty}<+\infty$.

(A3) For all integer $r$, $0\leqslant r\leqslant d-1$, it holds $\lim_{x\to 0}f^{(r)}(x)=0$.

Assumption (A3) is specific to the Laguerre case and avoids boundary issue. In particular, it permits to establish Lemma 2.1 below that is central to define our estimator. This assumption can be removed at the expense of additional technicalities, see Section 3. Under (A1), we develop $f^{(d)}$ in the Laguerre or Hermite basis, its orthogonal projection on $S_{m}$, $m\geqslant 1$, is

$$f^{(d)}_{m}=\sum_{j=0}^{m-1}a_{j}(f^{(d)})\varphi_{j},\quad\text{where},\quad a_{j}(f^{(d)})=\langle f^{(d)},\varphi_{j}\rangle.$$

(6)

The estimator is built by using the following result, proved in Appendix A.

Lemma 2.1. Suppose that (A1) and (A2) hold in the Hermite case and that (A1), (A2), and (A3) hold in the Laguerre case. Then $a_{j}(f^{(d)})=(-1)^{d}\mathbb{E}[\varphi_{j}^{(d)}(X_{1})],$ $\forall j\geqslant 0.$

Remark 1. If the support of the density $f$ is a strict compact subset $[a,b]$ of the estimation support (here ${\mathbb{R}}$ and $a<b$ or ${\mathbb{R}}^{+}$ and $0<a<b$), then the regularity condition (A1) implies that $f$ must be null in $a,b$, as well as its derivatives up to order $d-1$( i.e. $f(x_{0})=f^{(1)}(x_{0})=\dots=f^{(d-1)}(x_{0})=0$ for $x_{0}\in\{a,b\}$). On the contrary, Assumption (A3) in the Laguerre case can be dropped out (see Section 3) and this shows that a specific problem occurs when the density support coincides with the estimation interval. This point presents a real difficulty and is either not discussed in the literature, or hidden by periodicity conditions.

We derive the following estimator of $f^{(d)}$ (see also [18] p. 402): let $m\geqslant 1$,

$$\widehat{f}_{m,(d)}=\sum_{j=0}^{m-1}\widehat{a}^{(d)}_{j}\varphi_{j}\quad\text{with}\quad\widehat{a}^{(d)}_{j}=\frac{(-1)^{d}}{n}\sum_{i=1}^{n}\varphi_{j}^{(d)}(X_{i}).$$

(7)

For $d=0$, we recover an estimator of the density $f$.

2.2 Risk Bound and Rate of Convergence

We consider the $\mathbb{L}^{2}$-risk of $\widehat{f}_{m,(d)}$, defined in (7),

$$\mathbb{E}\big{[}||\widehat{f}_{m,(d)}-f^{(d)}||^{2}\big{]}=||{f^{(d)}_{m}}-f^{(d)}||^{2}+\mathbb{E}\big{[}||\widehat{f}_{m,(d)}-{f^{(d)}_{m}}||^{2}\big{]},$$

(8)

where $f_{m}^{(d)}:=\sum_{k=0}^{m-1}a_{j}(f^{(d)})\varphi_{j}.$ The study of the second right-hand-side term of the equality (variance term) leads to the following result.

Theorem 2.1. Suppose that (A1) and (A2) hold in the Hermite case and that (A1), (A2), and (A3) hold in the Laguerre case. Assume that

$$\mathbb{E}[X_{1}^{-d-1/2}]<+\infty\textit{ in the Laguerre case and }\mathbb{E}[|X_{1}|^{2/3}]<+\infty\textit{ in the Hermite case}.$$

(9)

Then, for sufficiently large $m\geqslant d$, it holds that

$$\mathbb{E}\big{[}||\widehat{f}_{m,(d)}-f^{(d)}||^{2}\big{]}\leq||{f^{(d)}_{m}}-f^{(d)}||^{2}+C\frac{m^{d+\frac{1}{2}}}{n}-\frac{||f_{m}^{(d)}||^{2}}{n}$$

(10)

for a positive constant $C$ depending on the moments in condition (9) (but not on $m$ nor $n$).

Remark 2. In the Laguerre case, condition (9) is a consequence of (A3) and $f^{(d)}(0)<+\infty$. Indeed, (A3) imposes that $f(x)\underset{x\to 0}{\sim}x^{d}f^{(d)}(x)$ which, under $f^{(d)}(0)<+\infty$, ensures integrability of $x^{-d-1/2}f(x)$ around $0^{+}$ (i.e., $\int_{0}x^{-d-1/2}f(x)dx<\infty$); integrability near $\infty$ is a consequence of $f\in\mathbb{L}^{1}([0,\infty))$.

The bound obtained for $\widehat{f}_{m,(d)}$ in Theorem 2.1 is sharp. Indeed, we can establish the following lower bound.

Proposition 2.1. Under the assumptions of Theorem 2.1, it holds, for some constant $c>0$, that

$$\mathbb{E}\Big{[}||\widehat{f}_{m,(d)}-f^{(d)}||^{2}\Big{]}\geqslant||{f^{(d)}_{m}}-f^{(d)}||^{2}+c\frac{m^{d+\frac{1}{2}}}{n}-\frac{||f^{(d)}_{m}||^{2}}{n}.$$

2.3 Definition of Regularity Classes and Rate of Convergence

The first two terms in the right hand side of (10) have an antagonistic behavior with respect to $m$: the first term, $||{f^{(d)}_{m}}-f^{(d)}||^{2}$ is a squared bias term which decreases when $m$ increases, while the second $m^{d+1/2}/n$ is a variance term which increases with $m$. Thus, the optimal choice of $m$ requires a bias-variance compromise which allows to derive the rate of convergence of $\widehat{f}_{m,(d)}$. To evaluate the order of the bias term, we introduce Sobolev–Hermite and Sobolev–Laguerre regularity classes for $f$ (see [9, 13]).

2.3.1. Sobolev–Hermite classes. Let $s>0$ and $D>0$, define the Sobolev–Hermite ball of regularity $s$

$$W_{H}^{s}(D)=\{\theta\in\mathbb{L}^{2}(\mathbb{R}),\sum_{k\geqslant 0}k^{s}a_{k}^{2}(\theta)\leqslant D\},$$

(11)

where $a_{k}^{2}(\theta)=\langle\theta,h_{k}\rangle$ and $k^{s}$ is to be understood as $(\sqrt{k})^{2s}$, see Remark 3 below. The following Lemma 2.2 relates the regularity of $f^{(d)}$ and the one of $f$.

Lemma 2.2. Let $s\geqslant d$ and $D>0$, assume that $f$ belongs to $W_{H}^{s}(D)$ and (A1), then there exist a constant $D_{d}>D$ such that $f^{(d)}$ is in $W_{H}^{s-d}(D_{d}).$

2.3.2. Sobolev–Laguerre classes. Similarly, consider the Sobolev–Laguerre ball of regularity $s$

$$W_{L}^{s}(D)=\{\theta\in\mathbb{L}^{2}(\mathbb{R}^{+}),|\theta|_{s}^{2}=\sum_{k\geqslant 0}k^{s}a_{k}^{2}(\theta)\leqslant D\},\quad D>0,$$

(12)

where $a_{k}(\theta)=\langle\theta,\ell_{k}\rangle$. If $s\geqslant 1$ an integer, there is an equivalent norm of $|\theta|_{s}^{2}$ (see Section 7.2 of [4]) defined by

$$|||\theta|||_{s}^{2}=\sum_{j=0}^{s}||\theta||_{j}^{2},\quad||\theta||_{j}^{2}=||x^{j/2}\sum_{k=0}^{j}\binom{j}{k}\theta^{(k)}||^{2}.$$

(13)

This inspires the definition, for $s\in\mathbb{N}$ and $D>0$, of the subset $\widetilde{W}_{L}^{s}(D)$ as

$$\widetilde{W}_{L}^{s}(D)=\{\theta\in\mathbb{L}^{2}(\mathbb{R}^{+}),\ \theta^{(j)}\in C([0,\infty)),\ x\mapsto x^{k/2}\theta^{(j)}(x)\in\mathbb{L}^{2}(\mathbb{R}^{+}),\ 0\leqslant j\leqslant k\leqslant s,|\theta|^{2}_{s}\leqslant D\}.$$

(14)

It is straightforward to see that $\widetilde{W}_{L}^{s}(D)\subset W_{L}^{s}(D)$. Moreover, we can relate the regularity of $f^{(d)}$ and the one of $f$.

Lemma 2.3. Let $s\in\mathbb{N},$ $s\geqslant d\geqslant 1$, $D>0$ and $\theta\in\widetilde{W}_{L}^{s}(D)$, then, $\theta^{(d)}\in\widetilde{W}_{L}^{s-d}(D_{d})$ where $D\leqslant D_{d}<\infty$.

2.3.3. Rate of convergence of $\widehat{\boldsymbol{f}}_{\boldsymbol{m,(d)}}$. Assume that $f\in W_{H}^{s}(D)$ or $f\in\widetilde{W}_{L}^{s}(D)$, then Lemmas 2.2 and 2.3 enable a control of the bias term in (10)

$$||{f^{(d)}_{m}}-f^{(d)}||^{2}=\sum_{j\geqslant m}(a_{j}(f^{(d)}))^{2}=\sum_{j\geqslant m}j^{s-d}(a_{j}(f^{(d)}))^{2}j^{-(s-d)}\leqslant D_{d}m^{-(s-d)}.$$

Injecting this in (10) yields

$$\mathbb{E}\big{[}||\widehat{f}_{m,(d)}-f^{(d)}||^{2}\big{]}\leqslant D^{\prime}m^{-(s-d)}+c\frac{m^{d+\frac{1}{2}}}{n}.$$

Remark 3. We stress that the squared bias and variance terms have orders specific to the use of Laguerre or Hermite bases. For instance if $d=0$, the latter bound becomes $m^{-s}+c\sqrt{m}/n$ showing that the associated spaces are represented by the square root of their dimension and not their dimension. Analogously in the context of derivatives, the role of the dimension in [34] is played in our case by $\sqrt{m}$.

Consequently, selecting $m_{\textrm{opt}}=[n^{2/(2s+1)}]$ gives the rate of convergence

$$\mathbb{E}\big{[}||\widehat{f}_{m_{\textrm{opt}},(d)}-f^{(d)}||^{2}\big{]}\leqslant C(s,d,D)n^{-\frac{2(s-d)}{2s+1}},$$

(15)

where $C(s,d,D)$ depends only on $s$, $d$, and $D$, not on $m$. This rate coincides with the one obtained by [34] in the dependent case and by [18]. Contrary to [32] and [27], we set the regularity conditions on the function $f$ and not on its derivatives: for a regularity $s$ of $f^{(d)}$, they obtain a quadratic risk $n^{-2(s-d)/(2s+1)}$ (case $p=2$ in [27] and dimension 1). Interestingly, $m_{\textrm{opt}}$ does not depend on $d$. This is in accordance with [27]’s strategy, which consists in plugging in the derivative kernel estimator the bandwidth selected for the direct density estimation problem. Note that, for $d=0$ in (15), we recover the optimal rate for estimation of the density $f$.

Remark 4. If $f$ is a mixture of Gaussian densities in the Hermite case or a mixture of Gamma densities in the Laguerre case, it is known from Section 3.2 in [13] that the bias decreases with exponential rate. The computations therein can be extended to the present setting and imply in both Hermite and Laguerre cases that $m_{\textrm{opt}}$ is then proportional to $\log(n)$. Therefore the risk has order $[\log(n)]^{d+\frac{1}{2}}/n$: for these collections of densities, the estimator converges much faster than in the general setting.

2.4 Lower Bound

Contrary to the lower bound given in Proposition 2.1, which ensures that the upper bound derived in Theorem 2.1 for the specific estimator $\widehat{f}_{m,(d)}$ is sharp, we provide a general lower bound that guarantees that the rate of the estimator $\widehat{f}_{m,(d)}$ is minimax optimal. The following assertion states that the rate obtained in (15) is the optimal rate.

Let $s\geqslant d$ be an integer and $\widetilde{f}_{n,d}$ be any estimator of $f^{(d)}$. Then for $n$ large enough, we have

$$\inf_{\widetilde{f}_{n,d}}\sup_{f\in W^{s}(D)}\mathbb{E}[||\widetilde{f}_{n,d}-f^{(d)}||^{2}]\geqslant cn^{-\frac{2(s-d)}{2s+1}},$$

(16)

where the infimum is taken over all estimator of $f^{(d)}$, $c$ a positive constant depending on $s$ and $d$, and $W^{s}(D)$ stands either for $W_{L}^{s}(D)$ or for $W_{H}^{s}(D)$.

We provide in Section 5.3 the key elements to establish (16). We emphasize that the proof relies on compactly supported test functions, implying that the lower bound on usual Sobolev spaces and the present one coincide, as these functions belong to both. This had to be checked since Hermite Sobolev spaces are strict subspaces of usual Sobolev spaces. Similar lower bounds were known for this model for different regularity spaces. We mention e.g., (7.3.3) in[16], which considers perdiodic Lispchitz spaces, or [27], which examines general Nikol’ski spaces.

2.5 Adaptive Estimator of $f^{(d)}$

The choice of $m_{\textrm{opt}}=[n^{2/(2s+1)}]$ leading to the optimal rate of convergence is not feasible in practice. In this section we provide an automatic choice of the dimension $m$, from the observations $(X_{1},\ldots,X_{n})$, that realizes the bias-variance compromise in (10). Assume that $m$ belongs to a finite model collection $\mathcal{M}_{n,d}$, we look for $m$ that minimizes the bias-variance decomposition (8) rewritten as

$$\mathbb{E}\big{[}||\widehat{f}_{m,(d)}-f^{(d)}||^{2}\big{]}=||{f^{(d)}_{m}}-f^{(d)}||^{2}+\frac{1}{n}\sum_{j=0}^{m-1}{\textrm{Var}}\left[\varphi_{j}^{(d)}(X_{1})\right].$$

Note that the bias is such that $||{f^{(d)}_{m}}-f^{(d)}||^{2}=||f^{(d)}||^{2}-||f^{(d)}_{m}||^{2}$ where $||f^{(d)}||^{2}$ is independent of $m$ and can be dropped out. The remaining quantity $-||f^{(d)}_{m}||^{2}$ is estimated by $-||\widehat{f}_{m,(d)}||^{2}$. The variance term is replaced by an estimator of a sharp upper bound, given by

$$\widehat{V}_{m,d}=\frac{1}{n}\sum_{i=1}^{n}\sum_{j=0}^{m-1}(\varphi_{j}^{(d)}(X_{i}))^{2}.$$

(17)

Finally, we set

$$\widehat{m}_{n}:=\underset{m\in\mathcal{M}_{n,d}}{\text{argmin}}\{-||\widehat{f}_{m,(d)}||^{2}+\widehat{{\textrm{pen}}}_{d}(m)\},\quad\textrm{where}\quad\widehat{{\textrm{pen}}}_{d}(m)=\kappa\frac{\widehat{V}_{m,d}}{n},$$

(18)

where $\kappa$ is a positive numerical constant. If we set $V_{m,d}:=\sum_{j=0}^{m-1}\operatorname{\mathbb{E}}[(\varphi_{j}^{(d)}(X_{1})^{2})]$, it holds $\mathbb{E}[\widehat{{\textrm{pen}}}_{d}(m)]=\kappa{V_{m,d}}/{n}$. In the sequel, we write ${\textrm{pen}}_{d}(m):=\kappa{V_{m,d}}/{n}$. To implement the procedure a value for $\kappa$ has to be set. Theorem 2.2 below provides a theoretical lower bound for $\kappa$, which is however generally too large. In practice this constant is calibrated by intensive preliminary experiments, see Section 4. General calibration methods can be found in [3] for theoretical explanations and heuristics, and in the associated package, for practical implementation.

Remark 5. Note that in the definition of the penalty, instead of (18), we can plug the deterministic upper bound on the variance and take $c\,m^{d+\frac{1}{2}}/n$ as a penalty (see Theorem 2.1) as Proposition 2.1 ensures its sharpness. However, this upper bound relies on additional assumptions given in (9) and depends on non explicit constants (see [2]). This is why we choose to estimate directly the variance by $\widehat{V}_{m,n}$ and use $\widehat{V}_{m,n}/n$ as the penalty term.

Theorem 2.2. Let $\mathcal{M}_{n,d}:=\{d,\dots,m_{n}(d)\}$, where $m_{n}(d)\geqslant d$. Assume that (A1) and (A2) hold, and that (A3) holds in the Laguerre case, and that $||f||_{\infty}<+\infty$.

AL. Set $m_{n}(d)=\lfloor(n/\log^{3}(n))^{\frac{2}{2d+1}}\rfloor$, assume that $\sup_{x\in\mathbb{R}^{+}}\frac{f(x)}{x^{d}}<+\infty$ in the Laguerre case.

AH. Set $m_{n}(d)=\lfloor n^{\frac{2}{2d+1}}\rfloor$ in the Hermite case.

Then, for any $\kappa\geqslant\kappa_{0}:=32$ it holds that

$$\mathbb{E}\Big{[}||\widehat{f}_{\widehat{m}_{n},(d)}-f^{(d)}||^{2}\Big{]}\leqslant C\inf_{m\in\mathcal{M}_{n,d}}\left(||{f^{(d)}_{m}}-f^{(d)}||^{2}+{\textrm{pen}}_{d}(m)\right)+\frac{C^{\prime}}{n},$$

(19)

where C is a universal constant ($C=3$ suits) and $C^{\prime}$ is a constant depending on $\sup_{x\in\mathbb{R}^{+}}\frac{f(x)}{x^{d}}<+\infty$ and $\mathbb{E}[X_{1}^{-d-1/2}]<+\infty$ (Laguerre case) or $||f||_{\infty}$ (Hermite case).

The constraint on the the largest element $m_{n}(d)$ of the collection $\mathcal{M}_{n,d}$ ensures that the variance term, which is upper bounded by $m^{d+\frac{1}{2}}/n$ vanishes asymptotically. The additional $\log$ term does not influence the rate of the optimal estimator: the optimal (and unknown) dimension $m_{\textrm{opt}}\asymp n^{\frac{2}{2s+1}}$, with $s$ the regularity index of $f$, is such that $m_{\textrm{opt}}\ll n^{\frac{2}{2d+1}}$ as soon as $s>d$. For $s=d$, a log-loss in the rate would occur in the Laguerre case, but not in the Hermite case.

Note that, in the Laguerre case, condition $\sup_{x\in\mathbb{R}^{+}}\frac{f(x)}{x^{d}}<+\infty$ implies ${\mathbb{E}}(X_{1}^{-d-1/2})<+\infty$ (see condition (9)) and is clearly related to (A3). Inequality (19) is a key result and expresses that $\widehat{f}_{\widehat{m}_{n},(d)}$ realizes automatically a bias-variance compromise and is performing as well as the best model in the collection, up to the multiplicative constant $C$, since clearly, the last term $C^{\prime}/n$ is negligible. Thus, for $f$ in $\widetilde{W}_{L}^{s}(D)$ or $W_{H}^{s}(D)$ and under the assumptions of Theorem 2.2, we have $\mathbb{E}\big{[}||\widehat{f}_{\widehat{m},(d)}-f^{(d)}||^{2}\big{]}=\mathcal{O}(n^{-2(s-d)/(2s+1)})$, which implies that the estimator is adaptive.

3 FURTHER QUESTIONS

We investigate here additional questions, and set for simplicity $d=1$. Mainly, we compare our estimator to the derivative of a density estimator, and discuss condition (A3) in the Laguerre case.

3.1 Derivatives of the Density Estimator

When using kernel strategies, it is classical to build an estimator of the derivative of $f$ by differentiating the kernel density estimator, as already mentioned in the Introduction. For projection estimators, we find more relevant to proceed differently. Indeed, our aim is to obtain an estimator expressed in an orthonormal basis; unfortunately, the derivative of an orthonormal basis is a collection of functions but not an orthonormal basis. So, our proposal (7) is easier to handle. Moreover, our estimator can be seen as a contrast minimizer, which makes model selection possible to settle up.

However, Laguerre and Hermite cases are somehow different and can be more precisely compared. Let us recall that the projetion estimator of $f$ on $S_{m}$ is defined by (see [13] or (7) for $d=0$):

$$\widehat{f}_{m}:=\sum_{k=0}^{m-1}\widehat{a}_{k}^{(0)}\varphi_{k},\quad\text{where }\quad\widehat{a}_{k}^{(0)}:=\frac{1}{n}\sum_{j=0}^{n}\varphi_{k}(X_{j}).$$

As the functions $(\varphi_{j})_{j}$ are infinitely differentiable, both in Hermite and Laguerre settings, this leads to the natural estimator of $f^{(d)}$, $d\geqslant 1$,

$$(\widehat{f}_{m})^{(d)}=\sum_{k=0}^{m-1}\widehat{a}_{k}^{(0)}\varphi_{k}^{(d)}.$$

(20)

For $d=1$, we write $(\widehat{f}_{m})^{(1)}=(\widehat{f}_{m})^{\prime}$. We want to compare $(\widehat{f}_{m})^{\prime}$ to $\widehat{f}_{m,(1)}$. In both Hermite and Laguerre cases, this estimator is consistent, under adequate regularity assumptions and for adequate choice of $m$ as a function of $n$.

3.2 Comparison of $\widehat{f}_{m,(1)}$ with $(\widehat{f}_{m})^{\prime}$ in the Hermite Case

Using the recursive formula (5), in (20) and (7), respectively, straightforward computations give

$$(\widehat{f}_{m})^{\prime}=\frac{1}{\sqrt{2}}\widehat{a}_{1}^{(0)}h_{0}+\sum_{j=1}^{m-1}\left(\sqrt{\frac{j+1}{2}}\widehat{a}_{j+1}^{(0)}-\sqrt{\frac{j}{2}}\widehat{a}_{j-1}^{(0)}\right)h_{j}-\sqrt{\frac{m}{2}}\left(\widehat{a}_{m}^{(0)}h_{m-1}+\widehat{a}_{m-1}^{(0)}h_{m}\right),$$

whereas

$$\widehat{f}_{m,(1)}=\frac{1}{\sqrt{2}}\widehat{a}_{1}^{(0)}h_{0}+\sum_{j=1}^{m-1}\left(\sqrt{\frac{j+1}{2}}\widehat{a}_{j+1}^{(0)}-\sqrt{\frac{j}{2}}\widehat{a}_{j-1}^{(0)}\right)h_{j}.$$

Therefore, it holds that $\mathbb{E}[||(\widehat{f}_{m})^{\prime}-\widehat{f}_{m,(1)}||^{2}]={m}/{2}\big{\{}\operatorname{\mathbb{E}}\big{[}(\widehat{a}^{(0)}_{m})^{2}\big{]}+\operatorname{\mathbb{E}}\big{[}(\widehat{a}^{(0)}_{m-1})^{2}\big{]}\big{\}}$ and

$$\mathbb{E}[||(\widehat{f}_{m})^{\prime}-\widehat{f}_{m,(1)}||^{2}]\leqslant\frac{m}{2}(a^{2}_{m-1}(f)+a^{2}_{m}(f))+\frac{m}{2n}\left(\int h^{2}_{m}(x)f(x)dx+\int h^{2}_{m-1}(x)f(x)dx\right).$$

Using Lemma 8.5 in [13] under ${\mathbb{E}}[|X_{1}|^{2/3}]<+\infty$ and for $f$ in $W^{s}_{H}(D)$, $s>1$, it follows for some positive constant $C$ that,

$$\mathbb{E}[||(\widehat{f}_{m})^{\prime}-\widehat{f}_{m,(1)}||^{2}]\leqslant\frac{D}{2}m^{-s+1}+C\frac{\sqrt{m}}{n}.$$

Under the same assumptions, (10) for $d=1$ implies

$$\mathbb{E}[||(\widehat{f}_{m})^{\prime}-f^{\prime}||^{2}]\leqslant D^{\prime}m^{-s+1}+c\frac{m^{3/2}}{n}.$$

Therefore, by triangle inequality, this implies that $(\widehat{f}_{m})^{\prime}$ reaches the same (optimal) rate as $\widehat{f}_{m,(1)}$, under the same assumptions.

3.3 Comparison of $\widehat{f}_{m,(1)}$ with $(\widehat{f}_{m})^{\prime}$ in the Laguerre Case

In the Laguerre case, assumption (A3) is required for the estimator $\widehat{f}_{m,(1)}$ to be consistent, while it is not for the estimator $(\widehat{f}_{m})^{\prime}$.

Proceeding as previously and taking advantage of the recursive formula (2) in (20) and (7), respectively, straightforward computations give, for $m\geqslant 1$,

$$(\widehat{f}_{m})^{\prime}=\sum_{j=0}^{m-1}\left(\widehat{a}_{j}^{(0)}-2\sum_{k=j}^{m-1}\widehat{a}_{k}^{(0)}\right)\ell_{j},\quad\textrm{whereas}\quad\widehat{f}_{m,(1)}=\sum_{j=0}^{m-1}\left(\widehat{a}_{j}^{(0)}+2\sum_{k=0}^{j-1}\widehat{a}_{k}^{(0)}\right)\ell_{j}.$$

(21)

Therefore, in the Laguerre case, the coefficients of $\widehat{f}_{m,(1)}$ in the basis $(\ell_{j})_{j}$ do not depend on $m$ while those of $(\widehat{f}_{m})^{\prime}$ do. Moreover, computing the difference between the estimators leads to $\widehat{f}_{m,(1)}-(\widehat{f}_{m})^{\prime}=2\sum_{j=0}^{m-1}(\sum_{k=0}^{m-1}\widehat{a}_{k}^{(0)})\ell_{j}$ and

$$||\widehat{f}_{m,(1)}-(\widehat{f}_{m})^{\prime}||^{2}=4m\left(\sum_{k=0}^{m-1}\widehat{a}_{k}^{(0)}\right)^{2}.$$

Heuristically, if $f(0)=0$, as $f(0)=\sqrt{2}\sum_{j\geqslant 0}a_{j}(f)=0$, it follows that $\sum_{j=0}^{m-1}a_{j}(f)$ should be small for $m$ large enough. Consequently, its consistent estimator $\sum_{k=0}^{m-1}\widehat{a}_{k}^{(0)}$ should also be small. This would imply that, when $f(0)=0$, the distance $||\widehat{f}_{m,(1)}-(\widehat{f}_{m})^{\prime}||^{2}$ can be small; on the contrary, the distance should tend to infinity with $m$ if $f(0)\neq 0$. This is due to the fact that $\widehat{f}_{m,(1)}$ is not consistent, while $(\widehat{f}_{m})^{\prime}$ is. Indeed, in the general case ($f(0)\neq 0$), the risk bound we obtain for $(\widehat{f}_{m})^{\prime}$ is the following.

Proposition 3.1. Assume that (A1) and (A2) hold for $d=1$ and that $f$ belongs to $W_{L}^{s}(D)$. Then, it holds

$$\mathbb{E}||(\widehat{f}_{m})^{\prime}-f^{\prime}||^{2}\leqslant Cm^{-s+2}+\frac{3}{n}||f||_{\infty}m^{2}.$$

(22)

Obviously, for suitably chosen $m$ the estimator is consistent and by selecting $m_{{\textrm{opt}}}\asymp n^{1/s}$, it reaches the rate: $\mathbb{E}[||(\widehat{f}_{m_{{\textrm{opt}}}})^{\prime}-f^{\prime}||^{2}]\leqslant C(s,D)n^{-(s-2)/s}.$ This rate is worse than the one obtained for $\widehat{f}_{m,(1)}$ but it is valid without (A3), and thus $\widehat{f}_{m,(1)}$ is consistent to estimate an exponential density, or any mixture involving exponential densities. Note that both the order of the bias and the variance in (22) are deteriorated compared to (10), and we believe these orders are sharp.

In the following section, we investigate if the rate can be improved, if (A3) is not satisfied, by correcting our estimator (6).

3.4 Estimation of $f^{\prime}$ on $\mathbb{R}^{+}$ with $f(0)>0$

Assumption (A3) excludes some classical distribution such as the exponential distribution or Beta distributions $\beta(a,b)$ with $a=1$. If $f(0)>0$, Lemma 2.1 no longer holds, and one has $a_{j}(f^{\prime})=-f(0)\ell_{j}(0)-\mathbb{E}[\ell_{j}^{\prime}(X_{1})]$ instead. Therefore, $f(0)$ has to be estimated and we consider

$$\widehat{a}_{j,K}^{(1)}=-\ell_{j}(0)\widehat{f}_{K}(0)-\frac{1}{n}\sum_{i=1}^{n}\ell_{j}^{\prime}(X_{i}),\text{ with }\widehat{f}_{K}=\sum_{j=0}^{K-1}\widehat{a}_{j}^{(0)}\ell_{j},\text{ }\widehat{a}_{j}^{(0)}=\frac{1}{n}\sum_{i=1}^{n}\ell_{j}(X_{i}).$$

(23)

We estimate $f^{\prime}$ as follows

$$\widetilde{f}_{m,K}^{\prime}=\sum_{j=0}^{m-1}\widehat{a}_{j,K}^{(1)}\ell_{j},\text{ with }\widehat{a}_{j,K}^{(1)}=-\frac{1}{n}\sum_{i=1}^{n}\ell_{j}^{\prime}(X_{i})-\widehat{f}_{K}(0)\ell_{j}(0).$$

(24)

Obviously, $\widehat{a}_{j,K}^{(1)}$ is a biased estimator of $a_{j}(f^{\prime})$, implying that $\widetilde{f}_{m,K}^{\prime}$ is a biased estimator of $f_{m}^{\prime}$. Now there are two dimensions $m$ and $K$ to be optimized. We can establish the following upper bound.

Proposition 3.2. Suppose (A1) is satisfied for $d=1$, then it holds that

$$\mathbb{E}\big{[}||\widetilde{f}_{m,K}^{\prime}-f^{\prime}||^{2}\big{]}\leq||f^{\prime}-f_{m}^{\prime}||^{2}+\frac{2}{n}\sum_{j=0}^{m-1}\operatorname{\mathbb{E}}\big{[}\big{(}\ell_{j}^{\prime}(X_{1})\big{)}^{2}\big{]}+4m(\textrm{Var}(\widehat{f}_{K}(0))+(f(0)-f_{K}(0))^{2}),$$

(25)

where $f_{K}$ is the orthogonal projection of $f$ on $S_{K}$ defined by: $f_{K}=\sum_{j=0}^{K-1}a_{j}(f)\ell_{j}$.

The first two terms of the upper bound seem similar to the ones obtained under (A3), but as we no longer assume $f(0)=0,$ Assumption (9) for $d=1$ cannot hold and the tools used to bound the variance term $V_{m,1}$ by $m^{3/2}$ no longer apply: we only get an order $m^{2}$ for this term, under $||f||_{\infty}<+\infty$.

The last two terms of (25) correspond to $m$ times the pointwise risk of $\widehat{f}_{K}(0)$. Then, using $||\ell_{j}||_{\infty}\leqslant\sqrt{2}$, we obtain $\textrm{Var}(\widehat{f}_{K}(x))\leqslant 4K^{2}/n$. If $||f||_{\infty}<\infty$, this can be improved in $\textrm{Var}(\widehat{f}_{K}(x))\leqslant||f||_{\infty}\,K/n,$ using the orthonormality of $(\ell_{j})_{j}$.

To sum up, if $f\in\widetilde{W}_{L}^{s}(D)$, and $||f||_{\infty}<\infty$, then

$$\mathbb{E}\big{[}||\widetilde{f}_{m,K}^{\prime}-f^{\prime}||^{2}\big{]}\leqslant C(s,D,||f||_{\infty})\left\{m^{-s+2}+\frac{m^{2}}{n}+m\left(K^{-s+1}+\frac{K}{n}\right)\right\}.$$

Choosing $K_{{\textrm{opt}}}=cn^{1/s}$ and $m_{{\textrm{opt}}}=cn^{1/s}$ gives the rate $\mathbb{E}\big{[}||\widetilde{f}_{m_{{\textrm{opt}}},K_{{\textrm{opt}}}}^{\prime}-f^{\prime}||^{2}\big{]}\leqslant Cn^{-(s-2)/s}$, that is the same rate as the one obtained for $(\widehat{f}_{m_{{\textrm{opt}}}})^{\prime}$. Then, renouncing to Assumption (A3) has a cost, it renders the procedure burdensome and leads to slower rates.

We propose a model selection procedure adapted to this new estimator. Let

$$\widehat{f^{\prime}}_{m,K}=\arg\min_{t\in S_{m}}\gamma_{n}(t),$$

(26)

where $\gamma_{n}(t)=||t||^{2}+\frac{2}{n}\sum_{i=1}^{n}t^{\prime}(X_{i})+2t(0)\widehat{f}_{K}(0).$ Here, we consider that $K=K_{n}$ is chosen so that $\widehat{f}_{K_{n}}$ satisfies

$$\left[{\mathbb{E}}(\widehat{f}_{K_{n}}(0))-f(0)\right]^{2}\leqslant\frac{K_{n}\log(n)}{n}.$$

(27)

This assumption is likely to be fulfilled for a $K$ selected in order to provide a squared bias/variance compromise, see the pointwise adaptive procedure for density estimation in [31]; however therein, the choice of $K$ is random while we set $K_{n}$ as fixed, here. Then, we select $m$ as follows:

$$\widehat{m}_{K}=\arg\min_{m\in{\mathcal{M}}_{n}}\left\{\gamma_{n}(\widehat{f^{\prime}}_{m,K})+{\textrm{pen}}_{K}(m)\right\},\;{\mathcal{M}}_{n}=\{1,\dots,[\sqrt{n}]\}$$

(28)

with

$${\textrm{pen}}_{K}(m)=c_{1}||f||_{\infty}\frac{m^{2}\,\log(n)}{n}+c_{2}(||f||_{\infty}\vee 1)\frac{m\,K\,\log(n)}{n}:={\textrm{pen}}_{1}(m)+{\textrm{pen}}_{2,K}(m).$$

(29)

It is easy to ckeck that $\gamma_{n}(\widehat{f^{\prime}}_{m,K})=-||\widehat{f^{\prime}}_{m,K}||^{2}$. We prove the following result.

Theorem 3.1. Let $\widehat{f^{\prime}}_{m,K_{n}}$ be defined by (26) with $m=\widehat{m}_{K_{n}}$ selected by (28), (29) and $K_{n}$ such that (27) holds. Then for $c_{1}$ and $c_{2}$ larger than fixed constants $c_{0,1},c_{0,2}$, we have

$${\mathbb{E}}\left(||f^{\prime}-\widehat{f^{\prime}}_{\widehat{m},K_{n}}||^{2}\right)\leqslant C\left(||f^{\prime}-f_{m}^{\prime}||^{2}+m^{2}\frac{\log(n)}{n}+m\frac{K_{n}\log(n)}{n}\right)+\frac{C^{\prime}}{n},$$

where $C$ is a numerical constant and $C^{\prime}$ depends on $f$ .

Theorem 3.1 implies that the adaptive estimator $\widehat{f^{\prime}}_{m,K_{n}}$ provides the adequate compromise, up to log terms.

4 NUMERICAL EXAMPLES

In this section, we provide a nonexhaustive illustration of our theoretical results.

4.1 Simulation Setting and Implementation

We illustrate the performances of the adaptive estimator $\widehat{f}_{\widehat{m}_{n},(d)}$ defined in (7), with $\widehat{m}$ selected by (17), (18), for different distributions and values of $d$ ($d=1,2$). In the Hermite case we consider the following distributions which are estimated on the interval $I$, which we fix to ensure reproducibility of our experiments:

(i) Gaussian standard $\mathcal{N}(0,1)$, $I=[-4,4],$

(ii) Mixed Gaussian $0.4\mathcal{N}(-1,1/4)+0.6\mathcal{N}(1,1/4)$, $I=[-2.5,2.5],$

(iii) Cauchy standard, density: $f(x)=(\pi(1+x^{2}))^{-1}$, $I=[-6,6],$

(iv) Gamma $\Gamma(5,5)/10$, $I=[0,7],$

(v) Beta $5\beta(4,5)$, $I=[0,5]$.

In the Laguerre case we consider densities (iv), (v) and the two following additional distributions

(vi) Weibull $W(4,1)$, $\textrm{I}=[0,1.5],$

(vii) Maxwell with density $\sqrt{2}x^{2}e^{-x^{2}/(2\sigma^{2})}/(\sigma^{3}\sqrt{\pi})$, with $\sigma=2$ and $\textrm{I}=[0,8].$

All these distributions satisfy Assumptions (A1), (A2) and densities (iv)-(vii) satisfy (A3). The moment conditions given in (9) are fulfilled for $d=1,2$, even by the Cauchy distribution (iii) which has finite moments of order $2/3<1$. For the adaptive procedure, the model collection considered is $\mathcal{M}_{n,d}=\{d,\dots,m_{n}(d)\}$, where the maximal dimension is $m_{n}(d)=50$ in the Laguerre case and $m_{n}(d)=40$ in the Hermite case, for all values of $n$ and $d$ (smaller values may be sufficient and spare computation time). In practice, the adaptive procedure follows the steps.

$\bullet$ For $m$ in $\mathcal{M}_{n,d}$, compute $-\sum_{j=0}^{m-1}(\widehat{a}_{j}^{(d)})^{2}+\widehat{{\textrm{pen}}}_{d}(m)$, with $\widehat{a}_{j}^{(d)}$ given in (7) and $\widehat{{\textrm{pen}}}_{d}(m)$ in (18).

$\bullet$ Choose $\widehat{m}_{n}$ via $\widehat{m}_{n}=\underset{m\in\mathcal{M}_{n,d}}{\text{argmin }}\{-\sum_{j=0}^{m-1}(\widehat{a}_{j}^{(d)})^{2}+\widehat{{\textrm{pen}}}_{d}(m)\}$.

$\bullet$ Compute $\widehat{f}_{\widehat{m}_{n},(d)}=\sum_{j=0}^{\widehat{m}-1}\widehat{a}_{j}^{(d)}\varphi_{j}$.Then, we compute the empirical mean integrated squared errors (MISE) of $\widehat{f}_{\widehat{m}_{n},(d)}$. For that, we first compute the ISE by Riemann discretization in 100 points: for the $j$th path, and the $j$th estimate $\widehat{g}_{\widehat{m}}^{(j)}$ of $g$, where $g$ stands either for the density $f$ or for its derivative $f^{\prime}$, we set

$$||g-\widehat{g}_{\widehat{m}}^{(j)}||^{2}\approx\frac{\text{length}(I)}{K}\sum_{k=1}^{K}(\widehat{g}^{(j)}_{\widehat{m}}(x_{k}))-g(x_{k}))^{2},\quad x_{k}=\min(I)+k\frac{\text{length}(I)}{K},\quad k=1,\dots,K,$$

for $j=1,\dots R$. To get the MISE, we average over $j$ of these $R$ values of ISEs. The constant $\kappa$ in the penalty is calibrated by preliminary experiments. A comparison of the MISEs for different values of $\kappa$ and different distributions (distinct from the previous ones to avoid overfitting) allows to choose a relevant value. We take $\kappa=3.5$ for the density and its first derivative and $\kappa=5$ for the second order derivative in the Laguerre case or $\kappa=4$ for the density and its first derivative and $\kappa=6.5$ for the second order derivative in the Hermite case.

Comparison with kernel estimators. We compare the performances of our method with those of kernel estimators, and start by density estimation ($d=0$). The density kernel estimator is defined as follows

$$\widehat{f}_{h}(x)=\frac{1}{nh}\sum_{i=1}^{n}K\left(\frac{X_{i}-x}{h}\right),\quad x\in\mathbb{R},$$

where $h>0$ is the bandwidth and $K$ a kernel such that $\int K(x)dx=1$. These two quantities ($h$ and $K$) are user-chosen. For density estimation, we use the function implemented in the statistical software R called density, where the kernel is chosen Gaussian and the bandwidth selected by plug-in (R-function bw.SJ), see Tables 2 and 4.

For the estimation of the derivative, the kernel estimator we compare with (see Tables 3 and 5) is defined by:

$$\widehat{f}_{h}^{\prime}(x)=-\frac{1}{nh^{2}}\sum_{i=1}^{n}K^{\prime}\left(\frac{X_{i}-x}{h}\right).$$

In that latter case there is no ready-to-use procedure implemented in R; therefore, we generalize the adaptive procedure of [25] from density to derivative estimation. To that aim, we consider a kernel of order 7 (i.e. $\int x^{j}K(x)dx=0$, for $j=1,\dots,7$) built as a Gaussian mixture defined by:

$$K(x)=4n_{1}(x)-6n_{2}(x)+4n_{3}(x)-n_{4}(x),$$

(30)

where $n_{j}(x)$ is the density of a centered Gaussian with a variance equal to $j$: the higher the order, the better the results, in theory (see [42]) and in practice (see [14]). By analogy with the proposal of [25] for density estimation, we select $h$ by:

$$\widehat{h}=\underset{h\in\mathcal{H}}{\text{argmin}}\{||\widehat{f}_{h}^{\prime}-\widehat{f}_{h_{\textrm{min}}}^{\prime}||^{2}+{\textrm{pen}}(h)\}\text{ with }{\textrm{pen}}(h)=\frac{4}{n}\langle K_{h}^{\prime},K_{{h}_{\textrm{min}}^{\prime}}\rangle,$$

where $h_{\textrm{min}}=\min\mathcal{H}$, for $\mathcal{H}$ the collection of bandwidths chosen in $[c/n,1]$ and $K_{h}(x)=\frac{1}{h}K(\frac{x}{h})$. Note that

$${\textrm{pen}}(h)=\frac{4}{n}\langle K_{h}^{\prime},K_{{h}_{\textrm{min}}^{\prime}}\rangle=\frac{4}{nh^{2}h_{\textrm{min}}^{2}}\int K^{\prime}\left(\frac{u}{h}\right)K^{\prime}\left(\frac{u}{h_{\textrm{min}}}\right)du$$

and this term can be explicitely computed with the definition of $K$ in (30).

4.2 Results and Discussion

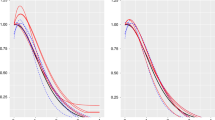
Figures 1 and 2 show 20 estimated $f$, $f^{\prime}$, $f^{\prime\prime}$ in case (ii), for two values of $n$, 500 and 2000. These plots can be read as variability bands illustrating the performance and the stability of the estimator. We observe that increasing $n$ improves the estimation and, on the contrary, that increasing the order of the derivative makes the problem more difficult. The means of the dimensions selected by the adaptive procedure are given in Table 1. Unsurprisingly, this dimension increases with the sample size $n$. In average, these dimensions are comparable for $d\in\{0,1,2\}$, this is in accordance with the theory: the optimal value $m_{\textrm{opt}}$ does not depend on $d$.

Fig. 1

20 estimates $\widehat{f}_{\widehat{m}_{n},(d)}$ in the Hermite basis of a Mixed Gaussian distribution (ii), with $n=500$ (first line) and $n=2000$ (second line). The true quantity is in bold red and the estimate in dotted lines (left $d=0$, middle $d=1$, and right $d=2$).

Fig. 2

20 estimates $\widehat{f}_{\widehat{m}_{n},(d)}$ in the Laguerre basis of a Gamma distribution (iv), with $n=500$ (first line) and $n=2000$ (second line). The true quantity is in bold red and the estimate in dotted lines (left $d=0$, middle $d=1$, and right $d=2$).

Table 1 Mean of selected dimensions $\widehat{m}_{n}$ presented in Figs. 1 and 2

Tables 2 and 4 for $d=0$ and Tables 3 and 5 for $d=1$ allow to compare the MISEs obtained with our method and the kernel method for different sample sizes and densities.The error decreases when the sample size increases for both methods. For density estimation ($d=0$), the results obtained with our Hermite projection method in Table 2 are better in most cases than the kernel competitor, except for smallest sample size $n=100$ and Gamma (iv) and Beta (v) distributions. Table 3 gives the risks obtained for derivative estimation in the Hermite basis: our method is better for densities (i)–(iii) (except for $n=100$ for Gaussian distribution (i)), but the kernel method is often better for densities (iv) and (v); they correspond to Gamma and beta densities which are in fact with support included in ${\mathbb{R}}^{+}$.

Table 2 Empirical MISE $100\times\mathbb{E}||\widehat{f}_{\widehat{m},(0)}-f||^{2}$ (left) and $100\times\mathbb{E}||\widehat{f}_{\widehat{h}}-f||^{2}$ (right, Kernel Estimator) for $R=100$ in the Hermite case

Table 3 Empirical MISE $100\times\mathbb{E}||\widehat{f}_{\widehat{m},(1)}-f^{\prime}||^{2}$ (left) and $100\times\mathbb{E}||\widehat{f}_{\widehat{h}}^{\prime}-f^{\prime}||^{2}$ (right) for $R=100$ in the Hermite case

Table 4 Empirical MISE ($100\times\mathbb{E}||\widehat{f}_{\widehat{m},(0)}-f||^{2}$ (left) and $100\times\mathbb{E}||\widehat{f}_{\widehat{h}}-f||^{2}$ (right) for $R=100$ in the Laguerre case

Table 5 Empirical MISE $100\times\mathbb{E}||\widehat{f}_{\widehat{m},(1)}-f^{\prime\prime}||^{2}$ (left) and $100\times\mathbb{E}||\widehat{f}_{\widehat{h}}^{\prime}-f^{\prime\prime}||^{2}$ (right) for $R=100$ in the Laguerre case

In Table 4, we compare the errors obtained for densities (iv)–(vii) with support in ${\mathbb{R}}^{+}$. Our method is always better than the R-kernel estimate. For the derivatives, in Table 5, our method and the kernel estimator seem equivalent. Lastly, Table 6 allows to compare Laguerre and Hermite bases for the estimation of the second order derivatives of functions (iv) and (v), for larger sample sizes. As expected, the risks are larger, because the degree of ill posedness increases and thus the rate deteriorates. For these ${\mathbb{R}}^{+}$-supported functions, the Laguerre basis is clearly better. It is possible that scale of the functions themselves also increase (multiplicative factors appearing by derivation). Note that the same phenomenon is observed for the ${\mathbb{L}}^{1}$-risk computed in [36], see their Table 1.

Table 6 Empirical MISE $100\times\mathbb{E}||\widehat{f}_{\widehat{m},(2)}^{(2)}-f^{(2)}||^{2}$ for $R=100$

5 PROOFS

In the sequel $C$ denotes a generic constant whose value may change from line to line and whose dependency is sometimes given in indexes.

5.1 Proof of Theorem 2.1

Following (8) we study the variance term, notice that $\mathbb{E}\big{[}||\widehat{f}_{m,(d)}-{f^{(d)}_{m}}||^{2}\big{]}=\sum_{j=0}^{m-1}\textrm{Var}(\widehat{a}_{j}^{(d)})$. By definition of $\widehat{a}_{j}^{(d)}$ given in (7), we have

$$\textrm{Var}(\widehat{a}_{j}^{(d)})=\textrm{Var}\left(\frac{(-1)^{d}}{n}\sum_{i=1}^{n}\varphi_{j}^{(d)}(X_{i})\right)=\frac{1}{n}\textrm{Var}(\varphi_{j}^{(d)}(X_{1}))=\frac{1}{n}\mathbb{E}[(\varphi_{j}^{(d)}(X_{1}))^{2}]-\frac{a_{j}^{2}(f^{(d)})}{n}.$$

(31)

Clearly, $\sum_{j=0}^{m-1}a_{j}^{2}(f^{(d)})=||f_{m}^{(d)}||^{2}$. In the sequel we denote by $V_{m,d}$ the quantity

$$V_{m,d}=\sum_{j=0}^{m-1}\mathbb{E}[(\varphi_{j}^{(d)}(X_{1}))^{2}].$$

(32)

The remaining of the proof consists in showing that under (9) we have $V_{m,d}\leqslant cm^{d+1/2}.$ For that, write

$$V_{m,d}=\sum_{j=0}^{m-1}\int(\varphi_{j}^{(d)}(x))^{2}f(x)dx=\left(\sum_{j=0}^{d-1}\int(\varphi_{j}^{(d)}(x))^{2}f(x)dx+\sum_{j=d}^{m-1}\int(\varphi_{j}^{(d)}(x))^{2}f(x)dx\right),$$

(33)

where

$$\sum_{j=0}^{d-1}\int(\varphi_{j}^{(d)}(x))^{2}f(x)dx\leqslant\sum_{j=0}^{d-1}||\varphi_{j}^{(d)}||_{\infty}^{2}:=c(d).$$

(34)

To bound the second term in (33), we consider separately Hermite and Laguerre cases.

5.1.1. The Laguerre case. We derive from (1) that

$$\ell^{(d)}_{j}(x)=\sqrt{2}\sum_{k=0}^{d}(-1)^{d-k}\binom{d}{k}L_{j}^{(k)}(2x)e^{-x}.$$

Using [24], Eq. (2.10), we derive

$$L_{j}^{(k)}(x)=\frac{d^{k}}{dx^{k}}L_{j}(x)=(-1)^{k}L_{j-k,(k)}(x),\quad\textrm{where}\quad L_{p,(\delta)}(x)=\frac{1}{p!}e^{x}x^{-\delta}\frac{d^{p}}{dx^{p}}\left(x^{\delta+p}e^{-x}\right)\mathbf{1}_{\delta\leqslant p}.$$

Moreover, introduce the orthonormal basis on $\mathbb{L}^{2}(\mathbb{R}^{+})$ $(\ell_{k,(\delta)})_{0\leqslant k<\infty}$ by

$$\ell_{k,(\delta)}(x)=2^{\frac{\delta+1}{2}}\left(\frac{k!}{\Gamma(k+\delta+1)}\right)^{1/2}L_{k,(\delta)}(2x)x^{\frac{\delta}{2}}e^{-x}.$$

(35)

Therefore, $(L_{j}(2x))^{(k)}=2^{k}L_{j-k,(k)}(2x)\mathbf{1}_{j\geqslant k}$, so that

$$\ell^{(d)}_{j}(x)=(-1)^{d}\sum_{k=0}^{d}\binom{d}{k}2^{\frac{k}{2}}x^{-k/2}\left(\frac{j!}{(j-k)!}\right)^{\frac{1}{2}}\ell_{j-k,(k)}(x),$$

(36)

where $\ell_{j,(\delta)}$ is defined in (35). Using the Cauchy Schwarz inequality in (36), we derive that

$$\sum_{j=d}^{m-1}\int\limits_{0}^{\infty}[\ell_{j}^{(d)}(x)]^{2}f(x)dx\leqslant 3^{d}\sum_{j=d}^{m-1}\sum_{k=0}^{d}\dbinom{d}{k}\frac{j!}{(j-k)!}\int\limits_{0}^{+\infty}x^{-k}[\ell_{j-k,(k)}(x)]^{2}f(x)dx$$

$${}\leqslant C_{d}\sum_{j=d}^{m-1}\sum_{k=0}^{d}j^{d}\int\limits_{0}^{+\infty}x^{-k}(\ell_{j-k,(k)}(x/2))^{2}f(x/2)dx.$$

Now we rely on the following Lemma, proved in Appendix A.

Lemma 5.1. Let $j\geqslant k\geqslant 0$ and suppose that $\mathbb{E}[X^{-k-1/2}]<+\infty$, it holds, for a positive constant $C$ depending only on $k$, that

$$\int\limits_{0}^{+\infty}x^{-k}\left[\ell_{j-k,(k)}(x/2)\right]^{2}f(x/2)dx\leqslant\frac{C}{\sqrt{j}}.$$

From Lemma 5.1, we obtain

$$\sum_{j=d}^{m-1}\int(\ell_{j}^{(d)}(x))^{2}f(x)dx\leqslant C\sum_{j=d}^{m-1}\sum_{k=0}^{d}j^{d-1/2}\leqslant Cm^{d+1/2}.$$

Plugging this and (34) in (33), gives the result (10) and Theorem 2.1 in the Laguerre case.

5.1.2. The Hermite case. We first introduce a useful technical result, its proof is given in Appendix A.

Lemma 5.2. Let $h_{j}$ given in (3), the dth derivative of $h_{j}$ is such that

$$h_{j}^{(d)}=\sum_{k=-d}^{d}b^{(d)}_{k,j}h_{j+k},\quad\text{where}\quad b^{(d)}_{k,j}=\mathcal{O}(j^{d/2}),\quad j\geqslant d\geqslant|k|.$$

(37)

Using successively Lemma 5.2, the Cauchy Schwarz inequality and Lemma 8.5 in [13] (using that $\operatorname{\mathbb{E}}[|X_{1}|^{2/3}]<\infty$), we obtain, for $k+j$ large enough,

$$\sum_{j=d}^{m-1}\int(h_{j}^{(d)}(x))^{2}f(x)dx\leqslant(2d+1)\sum_{j=d}^{m-1}\sum_{k=-d}^{d}(b_{k,j}^{(d)})^{2}\int h_{j+k}(x)^{2}f(x)dx\leqslant d(2d+1)^{2}\sum_{k=-d}^{d}\sum_{j=d}^{m-1}cj^{d-\frac{1}{2}}$$

$${}\leqslant c^{\prime}(d)m^{d+\frac{1}{2}}.$$

(38)

Plugging (38) and (34) in (33) leads to inequality (10) and Theorem 2.1 in the Hermite case.

5.2 Proof of Proposition 2.1

We build a lower bound for (8). Recalling (31) and notation $V_{m,d}=\sum_{j=0}^{m-1}\mathbb{E}[(\varphi_{j}^{(d)}(X_{1}))^{2}]$, to establish Proposition 2.1, we have to build a minorant for $V_{m,d}.$ We consider separately the Laguerre and Hermite cases.

5.2.1. The Laguerre case. Using (36), we have

$$\ell_{j}^{(d)}(x)=(-1)^{d}2^{d/2}x^{-d/2}\Big{(}\frac{j!}{(j-d)!}\Big{)}^{1/2}\ell_{j-d,(d)}(x)+(-1)^{d}\sum_{k=0}^{d-1}\binom{d}{k}2^{\frac{k}{2}}x^{-k/2}\left(\frac{j!}{(j-k)!}\right)^{\frac{1}{2}}\ell_{j-k,(k)}(x)$$

$${}:=T_{1}(x)+T_{2}(x).$$

It follows that

$$\int\limits_{0}^{+\infty}(\ell_{j}^{(d)})^{2}(x)f(x)dx\geqslant\int\limits_{0}^{+\infty}T_{1}(x)^{2}f(x)dx+2\int\limits_{0}^{+\infty}T_{1}(x)T_{2}(x)f(x)dx:=E_{1}+E_{2}.$$

For the first term, as (A1) ensures that $f$ is a continuous density, there exist $0\leqslant a<b$ and $c>0$, such that $\inf_{a\leqslant x\leqslant b}f(x)\geqslant c>0.$ We derive

$$E_{1}\geqslant 2^{d}\frac{j!}{(j-d)!}\int\limits_{0}^{+\infty}x^{-d}\ell_{j-d,(d)}^{2}(x)f(x)dx\geqslant c2^{d}(j-d)^{d}b^{-d}\int\limits_{a}^{b}\ell_{j-d,(d)}^{2}(x)dx.$$

By Theorem 8.22.5 in [40], for $\delta>-1$ an integer, and for $\underline{b}/j\leqslant x\leqslant\bar{b}$, where $\underline{b}$, $\bar{b}$ are arbitrary positive constants, it holds

$$\ell_{j,(\delta)}(x)={\mathfrak{d}}(jx)^{-\frac{1}{4}}\left(\cos\left(2\sqrt{2}\sqrt{jx}-\frac{\delta\pi}{2}-\frac{\pi}{4}\right)+(jx)^{-\frac{1}{2}}\mathcal{O}(1)\right),$$

(39)

where $\mathcal{O}(1)$ is uniform on $[\underline{b}/j,\bar{b}]$ and $\mathfrak{d}=2^{1/4}/\sqrt{\pi}$. It follows that,

$$\ell_{j,(\delta)}^{2}(x)=\frac{\mathfrak{d}^{2}}{2}(jx)^{-\frac{1}{2}}\left[1+\cos\left(4\sqrt{2}\sqrt{jx}-\delta\pi-\frac{\pi}{2}\right)\right]+(jx)^{-1}\mathcal{O}(1).$$

We derive that $\int_{a}^{b}\ell_{j-d,(d)}^{2}(x)dx\geqslant C(j-d)^{-1/2},$ after a change of variable $y=\sqrt{x},$ for some positive constant $C$ depending on $a,b$, and $d$. Consequently, it holds

$$E_{1}\geqslant C(j-d)^{d-\frac{1}{2}}\geqslant C^{\prime}j^{d-\frac{1}{2}},\quad\forall j\geqslant 2d,$$

(40)

where $C^{\prime}$ depends on $a$, $b$, $c$, and $d$. For the second term, we have

$$|E_{2}|\leqslant 2\int\limits_{0}^{+\infty}|T_{1}(x)T_{2}(x)|f(x)dx$$

$${}\leqslant 2j^{\frac{d}{2}}j^{\frac{d-1}{2}}\sum_{k=0}^{d-1}\dbinom{d}{k}2^{\frac{k+d}{2}}\left[\int\limits_{0}^{+\infty}x^{-d}\ell_{j-d,(d)}^{2}(x)f(x)dx+\int\limits_{0}^{+\infty}x^{-k}\ell_{j-k,(k)}^{2}(x)f(x)dx\right].$$

By Lemma 5.1, it follows that

$$|E_{2}|\leqslant Cj^{\frac{d}{2}}j^{\frac{d-1}{2}}j^{-\frac{1}{2}}\sum_{k=0}^{d-1}\dbinom{d}{k}2^{\frac{k+d}{2}}\leqslant Cj^{d-1}.$$

This together with (40), lead to $\int_{0}^{+\infty}(\ell_{j}^{(d)})^{2}(x)f(x)dx\geqslant C^{\prime}j^{d-\frac{1}{2}},\quad j\geqslant 2d$ where $C$ depends on $a,b,c$, and $d$. We derive

$$V_{m,d}\geqslant Cm^{d+\frac{1}{2}},$$

(41)

which ends the proof in the Laguerre case.

5.2.2. The Hermite case. The proof is similar to the Laguerre case. Consider the following expression of $h_{j}$ (see [40], p. 248):

$$h_{j}(x)=\lambda_{j}\cos\left((2j+1)^{\frac{1}{2}}x-\frac{j\pi}{2}\right)+\frac{1}{(2j+1)^{\frac{1}{2}}}\xi_{j}(x),\quad\forall x\in\mathbb{R},$$

(42)

where $\lambda_{j}=|h_{j}(0)|$ for $j$ even or $\lambda_{j}=|h_{j}^{\prime}(0)|/(2j+1)^{1/2}$ for $j$ odd and

$$\xi_{j}(x)=\int\limits_{0}^{x}\sin\left((2j+1)^{\frac{1}{2}}(x-t)\right)t^{2}h_{j}(t)dt.$$

By Stirling formula, it holds

$$\lambda_{2j}=\frac{(2j)!^{\frac{1}{2}}}{2^{j}j!\pi^{1/4}}\sim\pi^{-1/2}j^{-1/4}\quad\text{and}\quad\lambda_{2j+1}=\lambda_{2j}\frac{\sqrt{2j+1}}{\sqrt{2j+3/2}}\sim\pi^{-1/2}j^{-1/4}.$$

(43)

Differentiating (42), we get

$$h_{j}^{(d)}(x)=\lambda_{j}(2j+1)^{\frac{d}{2}}\cos\left((2j+1)^{\frac{1}{2}}x-\frac{j\pi}{2}+\frac{d\pi}{2}\right)+\frac{1}{\sqrt{2j+1}}\xi_{j}^{(d)}(x).$$

Note that if $d=2$ it holds

$$\xi_{j}^{(2)}(x)=\sqrt{2j+1}x^{2}h_{j}(x)-(2j+1)\xi_{j}(x).$$

(44)

From (A1), there exists $a<b$ and $c>0$ such that $\inf_{a\leqslant x\leqslant b}f(x)\geqslant c>0.$ It follows

$$\int\limits_{\mathbb{R}}h_{j}^{(d)}(x)^{2}f(x)dx\geqslant c(2j+1)^{d}\lambda_{j}^{2}\int\limits_{a}^{b}\cos^{2}\left((2j+1)^{\frac{1}{2}}x-(j+d)\frac{\pi}{2}\right)dx$$

$${}+2{c\lambda_{j}}{(2j+1)^{\frac{d-1}{2}}}\int\limits_{a}^{b}\cos\left((2j+1)^{\frac{1}{2}}x-(j+d)\frac{\pi}{2}\right)\xi_{j}^{(d)}(x)dx:=E_{1}+E_{2}.$$

For the first term, using $\cos^{2}(x)=(1+\cos(2x))/2$ and (43), we get

$$E_{1}=c(2j+1)^{d}\lambda_{j}^{2}\left(\frac{b-a}{2}+\mathcal{O}(\frac{1}{\sqrt{j}})\right)\geqslant c^{\prime}j^{d-\frac{1}{2}}\left(\frac{b-a}{2}+\mathcal{O}(\frac{1}{\sqrt{j}})\right).$$

For the second term we first show that

$$\forall x\in[a,b],\quad\forall j\geqslant 0,\quad\forall d\geqslant 0,\quad\xi_{j}^{(d)}(x)=\mathcal{O}(j^{d/2}).$$

(45)

To establish (45) we first note, using (44), that for $d\geqslant 2$, $\forall x\in\mathbb{R}$,

$$\xi_{j}^{(d)}(x)+(2j+1)\xi_{j}^{(d-2)}(x)=(\xi_{j}^{(2)}(x)+(2j+1)\xi_{j}(x))^{(d-2)}=\sqrt{2j+1}(x^{2}h_{j}(x))^{(d-2)}=:\Psi_{j,d}(x).$$

Together with Lemma 5.2, one easily obtains by induction that $\forall x\in[a,b]$, $\forall j\geqslant 0$, $\Psi_{j,d}(x)=\mathcal{O}(j^{\frac{d-1}{2}}).$ The latter result gives $\xi_{j}^{(d)}=-j\xi_{j}^{(d-2)}+\Psi_{j,d}$ and an immediate induction on $d$ leads to (45). Injecting this in $E_{2}$ gives, together with (43), $|E_{2}|\leqslant Cj^{d-\frac{3}{4}},$ for a positive constant $C$ depending on $a,\ b,\ c$, and $d$. Gathering the bound on $E_{1}$ and $E_{2}$ lead to

$$\int\limits_{\mathbb{R}}h_{j}^{(d)}(x)^{2}f(x)dx\geqslant c^{\prime}j^{d-\frac{1}{2}}\left(\frac{b-a}{2}+\mathcal{O}(\frac{1}{\sqrt{j}})\right)-\mathcal{O}(j^{d-\frac{3}{4}})\geqslant C_{d}^{\prime}j^{d-\frac{1}{2}}$$

and

$$V_{m,d}\geqslant c_{d}m^{d+\frac{1}{2}},$$

(46)

which ends the proof of the Hermite case.

5.3 Proof of (16)

We apply Theorem 2.7 in [42]. We start by the construction of a family of hypotheses $(f_{\theta})_{\theta}$. The construction is inspired by [5]. Define $f_{0}$ by

$$f_{0}(x)=P(x)\mathbf{1}_{]0,1[}(x)+\frac{1}{2}x\mathbf{1}_{[1,2]}(x)+Q(x)\mathbf{1}_{]2,3]}(x),$$

(47)

where $P$ and $Q$ are positive polynomials, for $0\leqslant k\leqslant s,$ $P^{(k)}(0)=Q^{(k)}(3)=0$, $P^{(k)}(1)=\lim_{x\downarrow 1}(x/2)^{(k)}$, $Q^{(k)}(2)=\lim_{x\uparrow 2}(x/2)^{(k)}$ and finally $\int_{0}^{1}P(x)dx=\int_{2}^{3}Q(x)dx=\frac{1}{8}$. Consider $f_{\theta}$ defined as a perturbation of $f_{0}$

$$f_{\theta}(x)=f_{0}(x)+\delta K^{-(\gamma+d)}\sum_{k=0}^{K-1}\theta_{k+1}\psi\big{(}(x-1)(K+1)-k\big{)}\quad\text{with $K\in\mathbb{N}$}$$

(48)

for some $\delta>0$, ${\theta}=(\theta_{1},\dots,\theta_{K})\in\{0,1\}^{K}$, $\gamma>0$ and $\psi$ which is supported on $[1,2]$, admits bounded derivatives up to order $s$ and is such that $\int_{1}^{2}\psi(x)dx=0$. The lower bound (16) is a consequence of the following Lemma 5.3.

Lemma 5.3. $(i)$. Let $s\geqslant d$, $\forall\text{ }\theta\in\{0,1\}^{K}$, there exist $\delta$ small enough and $\gamma>0$ such that $f_{\theta}$ is density. There exists $D>0$ such that $f_{\theta}$ belongs to $W_{H}^{s}(D)$. If in addition $\gamma\geqslant s-d$, $f_{\theta}$ belongs to $W_{L}^{s}(D)$.

$(ii)$. Let $M$ an integer, for all $j<l\leqslant M$, $\forall\theta^{(j)}$, $\theta^{(l)}$ in $\{0,1\}^{K}$, it holds $||f^{(d)}_{\theta^{(j)}}-f^{(d)}_{\theta^{(l)}}||^{2}\geqslant C\delta^{2}K^{-2\gamma}$.

$(iii)$. For $\delta$ small enough, $K=n^{1/(2\gamma+2d+1)}$ and for all $(\theta^{(j)})_{1\leqslant j\leqslant M}\in(\{0,1\}^{K})^{M}$, it holds

$$\frac{1}{M}\sum_{j=1}^{M}\chi^{2}\left({f_{\theta^{(j)}}}^{\otimes n},{f_{0}}^{\otimes n}\right)\leqslant\alpha M,$$

where $0<\alpha<1/8$ and $\chi^{2}(g,h)$ denotes the $\chi^{2}$ divergence between the distributions $g$ and $h$ .

Choosing $\gamma=s-d$, $K=n^{1/(2\gamma+2d+1)}$ and $\delta$ small enough, we derive from Lemma 5.3 that,

$$||f^{(d)}_{\theta^{(j)}}-f^{(d)}_{\theta^{(l)}}||^{2}\geqslant C\delta^{2}n^{-2\frac{(s-d)}{2s+1}},\quad\forall\theta^{(j)},\ \theta^{(l)}\in\{0,1\}^{K}.$$

The announced result is then a consequence of Theorem 2.7 in [42]. Proof of Lemma 5.3 is omitted, but can be found in the hal-preprint version of the paper.

5.4 Proof of Theorem 2.2

Consider the contrast function defined as follows:

$$\gamma_{n,d}(t)=||t||^{2}-\frac{2}{n}\sum_{i=1}^{n}(-1)^{d}t^{(d)}(X_{i}),\quad t\in\mathbb{L}^{2}(\mathbb{R}),$$

for which $\widehat{f}_{m,(d)}=\underset{t\in S_{m}}{\text{argmin}}\gamma_{n,d}(t)$ (see (7)) and $\gamma_{n}(\widehat{f}_{m,(d)})=-||\widehat{f}_{m,(d)}||^{2}$. For two functions $t,s\in\mathbb{L}^{2}(\mathbb{R})$, consider the decomposition:

$$\gamma_{n,d}(t)-\gamma_{n,d}(s)=||t-f^{(d)}||^{2}-||s-f^{(d)}||^{2}-2\nu_{n,d}(t-s),$$

(49)

where

$$\nu_{n,d}(t)=\frac{1}{n}\sum_{i=1}^{n}\left((-1)^{d}t^{(d)}(X_{i})-\langle t,f^{(d)}\rangle\right).$$

By (18), it holds for all $m\in\mathcal{M}_{n,d}$, that $\gamma_{n,d}(\widehat{f}_{\widehat{m}_{n},(d)})+\widehat{{\textrm{pen}}}_{d}(\widehat{m}_{n})\leqslant\gamma_{n,d}({f^{(d)}_{m}})+\widehat{{\textrm{pen}}}_{d}(m).$ Plugging this in (49) yields, for all $m\in\mathcal{M}_{n,d}$,

$$||\widehat{f}_{\widehat{m}_{n},(d)}-f^{(d)}||^{2}\leq||{f^{(d)}_{m}}-f^{(d)}||^{2}+\widehat{{\textrm{pen}}}_{d}(m)+2\nu_{n,d}\left(\widehat{f}_{\widehat{m}_{n},(d)}-{f^{(d)}_{m}}\right)-\widehat{{\textrm{pen}}}_{d}(\widehat{m}_{n}).$$

(50)

Note that for $t\in\mathbb{L}^{2}(\mathbb{R})$, $\nu_{n,d}(t)=||t||\nu_{n,d}\big{(}{t}/{||t||}\big{)}\leq||t||\sup_{s\in S_{m}+S_{\widehat{m}},||s||=1}|\nu_{n,d}(s)|.$ Consequently, using $2xy\leqslant x^{2}/4+4y^{2}$, we obtain

$$2\nu_{n,d}\left(\widehat{f}_{\widehat{m}_{n},(d)}-{f^{(d)}_{m}}\right)\leqslant\frac{1}{2}||\widehat{f}_{\widehat{m}_{n},(d)}-f^{(d)}||^{2}+\frac{1}{2}||{f^{(d)}_{m}}-f^{(d)}||^{2}+4\sup_{t\in S_{m}+S_{\widehat{m}},||t||=1}|\nu_{n,d}(t)|^{2}.$$

(51)

It follows from (50) and (51) that:

$$\frac{1}{2}||\widehat{f}_{\widehat{m}_{n},(d)}-f^{(d)}||^{2}\leqslant\frac{3}{2}||{f^{(d)}_{m}}-f^{(d)}||^{2}+\widehat{{\textrm{pen}}}_{d}({m})+4\sup_{t\in S_{m}+S_{\widehat{m}},||t||=1}|\nu_{n,d}(t)|^{2}-\widehat{{\textrm{pen}}}_{d}(\widehat{m}_{n}).$$

Introduce the function $p(m,m^{\prime})=4\frac{V_{m\vee m^{\prime},d}}{n}$, we get, after taking the expectation,

$$\frac{1}{2}\mathbb{E}\left[||\widehat{f}_{\widehat{m}_{n},(d)}-f^{(d)}||^{2}\right]\leqslant\frac{3}{2}||{f^{(d)}_{m}}-f^{(d)}||^{2}+{\textrm{pen}}_{d}(m)$$

$${}+4\mathbb{E}\left[\left(\sup_{t\in S_{m}+S_{\widehat{m}},||t||=1}|\nu_{n,d}(t)|^{2}-p(m,\widehat{m}_{n})\right)_{+}\right]$$

$${}+\mathbb{E}[4p(m,\widehat{m}_{n})-{\textrm{pen}}_{d}(\widehat{m}_{n})]+\mathbb{E}\left[\left({\textrm{pen}}_{d}(\widehat{m}_{n})-\widehat{{\textrm{pen}}}_{d}(\widehat{m}_{n})\right)_{+}\right].$$

The remaining of the proof is a consequence of the following Lemma 5.4.

Lemma 5.4. Under the assumptions of Theorem 2.2, the following hold.

(i) There exists a constant $\Sigma_{1}$ such that:

$$\mathbb{E}\left[\left(\sup_{t\in S_{m}+S_{\widehat{m}},||t||=1}|\nu_{n,d}(t)|^{2}-\text{p}(m,\widehat{m}_{n})\right)_{+}\right]\leqslant\frac{\Sigma_{1}}{n}.$$

(ii) There exists a constant $\Sigma_{2}$ such that:

$$\mathbb{E}\left[\left({\textrm{pen}}_{d}(\widehat{m}_{n})-\widehat{{\textrm{pen}}}_{d}(\widehat{m}_{n})\right)_{+}\right]\leqslant\frac{1}{2}\mathbb{E}[{\textrm{pen}}_{d}(\widehat{m}_{n})]+\frac{\Sigma_{2}}{n}.$$

Lemma 5.4 yields

$$\frac{1}{2}\mathbb{E}\left[||\widehat{f}_{\widehat{m}_{n},(d)}-f^{(d)}||^{2}\right]\leqslant\frac{3}{2}||{f^{(d)}_{m}}-f^{(d)}||^{2}+{\textrm{pen}}_{d}(m)+4\frac{\Sigma_{1}}{n}+\mathbb{E}[4p(m,\widehat{m}_{n})-\frac{1}{2}{\textrm{pen}}_{d}(\widehat{m}_{n})]+\frac{\Sigma_{2}}{n}.$$

Next, for $\kappa\geqslant 32=:\kappa_{0}$, we have, $4p(m,\widehat{m}_{n})\leq{\textrm{pen}}_{d}(\widehat{m}_{n})/2+{\textrm{pen}}_{d}(m)/2$. Therefore, we derive

$$\mathbb{E}\left[||\widehat{f}_{\widehat{m}_{n},(d)}-f^{(d)}||^{2}\right]\leqslant 3||{f^{(d)}_{m}}-f^{(d)}||^{2}+3{\textrm{pen}}_{d}(m)+2\frac{4\Sigma_{1}+\Sigma_{2}}{n},\quad\forall m\in\mathcal{M}_{n,d}.$$

Taking the infimum on $\mathcal{M}_{n,d}$, $C=3$ and $C^{\prime}=2(4\Sigma_{1}+\Sigma_{2})/n$ completes the proof.

5.5 Proof of Proposition 3.1

First, it holds that

$$\mathbb{E}\Big{[}||(\widehat{f}_{m})^{\prime}-f^{\prime}||^{2}\Big{]}\leqslant 2\Big{[}||(f_{m})^{\prime}-f^{\prime}||^{2}+\mathbb{E}[||(\widehat{f}_{m})^{\prime}-(f_{m})^{\prime}||^{2}]\Big{]}$$

$${}=2\int\limits_{0}^{+\infty}\left(\sum_{j\geqslant m}a_{j}(f)\ell_{j}^{\prime}(x)\right)^{2}dx+2\mathbb{E}\left[\left|\left|\sum_{j=0}^{m-1}(\widehat{a}_{j}^{(0)}-a_{j}(f))\ell_{j}^{\prime}\right|\right|^{2}\right].$$

For the first bias term, we derive from (2) that $\langle\ell_{j}^{\prime},\ell_{k}^{\prime}\rangle=2+4j\wedge k$ for $j\neq k$ and $\langle\ell_{j}^{\prime},\ell_{j}^{\prime}\rangle=1+4j$, and we derive that

$$\int\limits_{0}^{+\infty}\left(\sum_{j\geqslant m}a_{j}(f)\ell_{j}^{\prime}(x)\right)^{2}dx=\sum_{j\geqslant m}a_{j}(f)^{2}(1+4j)+2\sum_{m\leqslant j<k}a_{j}(f)a_{k}(f)(2+4j).$$

First, for $f$ in $W_{L}^{s}(D)$, we have

$$\sum_{j\geqslant m}a_{j}(f)^{2}(1+4j)\leqslant m^{-s}\sum_{j\geqslant m}j^{s}a_{j}(f)^{2}+4m^{-s+1}\sum_{j\geqslant m}j^{s}a_{j}(f)^{2}\leq 5Dm^{-s+1},$$

and by the Cauchy–Schwarz inequality, it holds for a positive constant $C$,

$$\sum_{m\leqslant j<k}a_{j}(f)a_{k}(f)\leqslant\left(\sum_{m\leqslant j<k}j^{s}a_{j}(f)^{2}k^{s}a_{k}(f)^{2}\right)^{\frac{1}{2}}\left(\sum_{m\leqslant j<k}j^{-s}k^{-s}\right)^{\frac{1}{2}}$$

$${}\leqslant\sum_{j\geqslant m}j^{s}a_{j}(f)^{2}\sum_{j\geqslant m}j^{-s}\leqslant DCm^{-s+1}$$

$$\sum_{m\leqslant j<k}j|a_{j}(f)a_{k}(f)|\leqslant\sum_{j\geqslant m}j|a_{j}(f)|\left(\sum_{k\geqslant j}k^{s}a_{k}(f)^{2}\sum_{k\geqslant j}k^{-s}\right)^{\frac{1}{2}}$$

$${}\leqslant\sqrt{DC}\sum_{j\geqslant m}j^{\frac{s}{2}-s+\frac{3}{2}}|a_{j}(f)|\leqslant DCm^{-s+2}.$$

Thus, it comes

$$2||(f_{m})^{\prime}-f^{\prime}||^{2}\leqslant Cm^{-(s-2)},$$

(52)

where $C>0$ depends on $D$. Second, for the variance term, straightforward computations lead to

$$\mathbb{E}\left[\left|\left|\sum_{j=0}^{m-1}(\widehat{a}_{j}^{(0)}-a_{j}(f))\ell_{j}^{\prime}\right|\right|^{2}\right]$$

$${}=\frac{1}{n}\int\limits_{0}^{+\infty}\textrm{Var}\left(\sum_{j=0}^{m-1}\ell_{j}(X_{1})\ell_{j}^{\prime}(x)\right)dx\leqslant\frac{1}{n}\int\limits_{0}^{+\infty}\mathbb{E}\left[\left(\sum_{j=0}^{m-1}\ell_{j}(X_{1})\ell_{j}^{\prime}(x)\right)^{2}\right]dx.$$

By the orthonormality of $(\ell_{j})_{j}$ and (A2), we obtain

$$\int\limits_{0}^{+\infty}\limits\mathbb{E}\left[(\sum_{j=0}^{m-1}\ell_{j}(X_{1})\ell_{j}^{\prime}(x))^{2}\right]dx\leqslant||f||_{\infty}\sum_{j,k=0}^{m-1}\int\limits_{0}^{+\infty}\limits\int\limits_{0}^{+\infty}\limits\ell_{j}(u)\ell_{j}^{\prime}(x)\ell_{k}(u)\ell_{k}^{\prime}(x)dudx$$

$${}=||f||_{\infty}\sum_{j=0}^{m-1}(1+4j)\leqslant 3||f||_{\infty}m^{2}.$$

From this and (52), the result follows.

5.6 Proof of Proposition 3.2

By the Pythagoras Theorem, we have the bias-variance decomposition $\mathbb{E}\big{[}||\widetilde{f}_{m,K}^{\prime}-f^{\prime}||^{2}\big{]}=||f^{\prime}-f_{m}^{\prime}||^{2}+\mathbb{E}\big{[}||\widetilde{f}_{m,K}^{\prime}-f_{m}^{\prime}||^{2}\big{]}.$ As $\ell_{j}(0)=\sqrt{2}$, it follows that

$$\widetilde{f}_{m,K}^{\prime}-f_{m}^{\prime}=\sum_{j=0}^{m-1}\left[-\sqrt{2}(\widehat{f}_{K}(0)-f(0))-\frac{1}{n}\sum_{i=1}^{n}(\ell_{j}^{\prime}(X_{i})-\mathbb{E}[\ell_{j}^{\prime}(X_{i})])\right]\ell_{j}.$$

From the orthonormality of $(\ell_{j})_{j}$, it follows

$$\mathbb{E}\big{[}||\widetilde{f}_{m,K}^{\prime}-f_{m}^{\prime}||^{2}\big{]}=\sum_{j=0}^{m-1}\mathbb{E}\left[-\sqrt{2}(\widehat{f}_{K}(0)-f(0))-\frac{1}{n}\sum_{i=1}^{n}(\ell_{j}^{\prime}(X_{i})-\mathbb{E}[\ell_{j}^{\prime}(X_{i})])\right]^{2}$$

$${}\leqslant 4m\mathbb{E}\left[(\widehat{f}_{K}(0)-f(0))^{2}\right]+2\sum_{j=0}^{m-1}\operatorname{\mathbb{E}}\left[\left(\frac{1}{n}\sum_{i=1}^{n}(\ell_{j}^{\prime}(X_{i})-\mathbb{E}[\ell_{j}^{\prime}(X_{i})])\right)^{2}\right].$$

Finally, using that the $(X_{i})_{i}$ are i.i.d. lead to the result in the second variance term.

5.7 Proof of Theorem 3.1

We have the decomposition:

$$\gamma_{n}(t)-\gamma_{n}(s)=||t-f^{\prime}||^{2}-||s-f^{\prime}||^{2}-2\langle s-t,f^{\prime}\rangle-\frac{2}{n}\sum_{i=1}^{n}(s^{\prime}-t^{\prime})(X_{i})-2(s(0)-t(0))\widehat{f}_{K}(0)$$

and as $\langle t,f^{\prime}\rangle=-t(0)f(0)-\int t^{\prime}f,$ we get

$$\gamma_{n}(t)-\gamma_{n}(s)=||t-f^{\prime}||^{2}-||s-f^{\prime}||^{2}-2\nu_{n}(s-t)-2(s(0)-t(0))(\widehat{f}_{K}(0)-f(0))$$

$$\textrm{with}\quad\nu_{n}(t)=\frac{1}{n}\sum_{i=1}^{n}t^{\prime}(X_{i})-\langle t^{\prime},f\rangle.$$

(53)

First note that for

$$f_{m,K}^{\prime}=\sum_{j=0}^{m-1}a_{j,K}^{(1)}\ell_{j},\quad a_{j,K}^{(1)}={\mathbb{E}}[\widehat{a}_{j,K}^{(1)}]=\langle f^{\prime},\ell_{j}\rangle+\ell_{j}(0)(f(0)-{\mathbb{E}}[\widehat{f}_{K}(0)]$$

it holds that

$$||f^{\prime}-f_{m,K}^{\prime}||^{2}=\left|\left|\sum_{j=0}^{\infty}\langle f^{\prime},\ell_{j}\rangle\ell_{j}-\sum_{j=0}^{m-1}\langle f^{\prime},\ell_{j}\rangle\ell_{j}-\sum_{j=0}^{m-1}\ell_{j}(0)\big{(}f(0)-{\mathbb{E}}[\widehat{f}_{K}(0)]\big{)}\ell_{j}\right|\right|^{2}$$

$${}=\sum_{j\geqslant m}\langle f^{\prime},\ell_{j}\rangle^{2}+2\sum_{j=0}^{m-1}\big{(}f(0)-{\mathbb{E}}[\widehat{f}_{K}(0)]\big{)}^{2}=||f^{\prime}-f_{m}^{\prime}||^{2}+2m\,\big{(}f(0)-{\mathbb{E}}[\widehat{f}_{K}(0)]\big{)}^{2}.$$

Let us start by writing that, by definition of $\widehat{m}_{K}$, it holds, $\forall m\in{\mathcal{M}}_{n}$,

$$\gamma_{n}(\widehat{f^{\prime}}_{\widehat{m}_{K},K})+{\textrm{pen}}_{K}(\widehat{m}_{K})\leqslant\gamma_{n}(f_{m,K}^{\prime})+{\textrm{pen}}_{K}(m),$$

which yields, with (53) and notations introduced in (29),

$$||\widehat{f^{\prime}}_{\widehat{m}_{K},K}-f^{\prime}||^{2}\leqslant||f_{m,K}^{\prime}-f^{\prime}||^{2}+{\textrm{pen}}_{K}(m)+2\nu_{n}(f_{m,K}^{\prime}-\widehat{f^{\prime}}_{\widehat{m}_{K},K})-{\textrm{pen}}_{1}(\widehat{m}_{K})$$

$${}+2(f_{m,K}^{\prime}(0)-\widehat{f^{\prime}}_{\widehat{m}_{K},K}(0))(\widehat{f}_{K}(0)-f(0))-{\textrm{pen}}_{2,K}(\widehat{m}_{K})$$

$${}\leqslant||f_{m,K}^{\prime}-f^{\prime}||^{2}+{\textrm{pen}}_{K}(m)+\frac{1}{4}||f_{m,K}^{\prime}-\widehat{f^{\prime}}_{\widehat{m}_{K},K}||^{2}+8\sup_{t\in S_{m\vee\widehat{m}_{K}}}\nu_{n}^{2}(t)-{\textrm{pen}}_{1}(\widehat{m}_{K})$$

$${}+16(m\vee\widehat{m}_{K})[\widehat{f}_{K}(0)-f(0)]^{2}-{\textrm{pen}}_{2,K}(\widehat{m}_{K}).$$

To get the last line, we write that, for any $t\in S_{m}$,

$$|t(0)|=\sqrt{2}\left|\sum_{j=0}^{m-1}a_{j}(t)\right|\leqslant\sqrt{2m\sum_{j=0}^{m}a_{j}^{2}(t)}\leqslant\sqrt{2m}||t||,$$

and we use that $2xy\leqslant x^{2}/8+8y^{2}$ for all real $x,y$. We obtain

$$\frac{1}{2}||\widehat{f^{\prime}}_{\widehat{m}_{K},K}-f^{\prime}||^{2}\leqslant\frac{3}{2}||f_{m,K}^{\prime}-f^{\prime}||^{2}+{\textrm{pen}}_{K}(m)+16m(\widehat{f}_{K}(0)-f(0))^{2}$$

$${}+8\left(\sup_{t\in S_{m\vee\widehat{m}_{K}},||t||=1}\nu_{n}^{2}(t)-p_{1}(m\vee\widehat{m}_{K})\right)_{+}+8p_{1}(m\vee\widehat{m}_{K})-{\textrm{pen}}_{1}(\widehat{m}_{K})$$

$${}+16\widehat{m}_{K}\left[(\widehat{f}_{K}(0)-f(0))^{2}-c_{2}(||f||_{\infty}\vee 1)K\frac{\log(n)}{n}\right],$$

(54)

where

$$p_{1}(m)={\texttt{b}}(1+2\log(n))||f||_{\infty}\frac{m^{2}}{n},\quad{\texttt{b}}>0.$$

The following Lemma 5.5 can be proved using the Talagrand inequality (see Appendix B.2).

Lemma 5.5. Under the assumptions of Theorem 3.1, and ${\texttt{b}}\geqslant 6$,

$$\sum_{m\in{\mathcal{M}}_{n}}{\mathbb{E}}\left[\sup_{t\in S_{m},||t||=1}\nu_{n}^{2}(t)-p_{1}(m)\right]_{+}\leqslant\frac{c}{n}.$$

It follows that

$${\mathbb{E}}\left(\sup_{t\in S_{m\vee\widehat{m}_{K}},||t||=1}\nu_{n}^{2}(t)-p_{1}(m\vee\widehat{m}_{K})\right)_{+}$$

$${}\leqslant\sum_{m^{\prime}\in{\mathcal{M}}_{n}}{\mathbb{E}}\left(\sup_{t\in S_{m^{\prime}\vee m},||t||=1}\nu_{n}^{2}(t)-p_{1}(m\vee m^{\prime})\right)_{+}\leqslant\frac{c}{n}.$$

(55)

This implies that $8p_{1}(m\vee\widehat{m}_{K})\leqslant{\textrm{pen}}_{1}(m)+{\textrm{pen}}_{1}(\widehat{m}_{K})$ for $c_{1}$–defined in (29)–large enough.Moreover, let ${\texttt{a}}>0$ and

$$\Omega_{K}:=\left\{\left|\frac{1}{n}\sum_{i=1}^{n}(Z_{i}^{K}-{\mathbb{E}}(Z_{i}^{K}))\right|\leqslant\sqrt{{\texttt{a}}(||f||_{\infty}\vee 1)\frac{K\log(n)}{n}}\right\},$$

where $Z_{i}^{K}:=\sum_{j=0}^{K-1}\ell_{j}(X_{i})$. To apply the Bernstein Inequality (see Appendix B.3), we compute $s^{2}=||f||_{\infty}K$ and $b=\sqrt{2}K$ and note that $K\log(n)/n\leqslant 1$. Thus, we get that there exist constants $c_{0}$, $c$ such that

$$\textrm{for\ {{a}}}>c_{0},\quad{\mathbb{P}}(\Omega_{K}^{c})\leqslant\frac{c}{n^{4}}.$$

(56)

On $\Omega_{K}$, it holds that

$$(\widehat{f}_{K}(0)-f_{K}(0))^{2}=\left(\frac{1}{n}\sum_{i=1}^{n}(Z_{i}^{K}-{\mathbb{E}}(Z_{i}^{K}))\right)^{2}\leqslant 2{\texttt{a}}(||f||_{\infty}\vee 1)K\frac{\log(n)}{n}.$$

(57)

For any $K_{n}\leqslant[n/\log(n)]$ satisfying condition (27), we have

$${\mathbb{E}}\left\{\widehat{m}_{K_{n}}\left[(\widehat{f}_{K_{n}}(0)-f(0))^{2}-c_{2}(||f||_{\infty}\vee 1)K_{n}\frac{\log(n)}{n}\right]\right\}$$

$${}\leqslant{\mathbb{E}}\left\{\widehat{m}_{K_{n}}\left[(\widehat{f}_{K_{n}}(0)-f_{K_{n}}(0))^{2}-(c_{2}-2)(||f||_{\infty}\vee 1)K_{n}\frac{\log(n)}{n}\right]\right\}.$$

Now we note that $|\widehat{f}_{K}(x)|\leqslant 2K$ for all $x\in{\mathbb{R}}^{+}$ and any integer $K$ and by using the definition of (57), provided that $c_{2}>2{\texttt{a}}+2$, we obtain

$${\mathbb{E}}\left\{\widehat{m}_{K_{n}}\left[(\widehat{f}_{K_{n}}(0)-f_{K_{n}}(0))^{2}-(c_{2}-2)(||f||_{\infty}\vee 1)K_{n}\frac{\log(n)}{n}\right]\right\}$$

$${}\leqslant{\mathbb{E}}\left\{\widehat{m}_{K_{n}}\left[(\widehat{f}_{K_{n}}(0)-f_{K_{n}}(0))^{2}-(c_{2}-2)(||f||_{\infty}\vee 1)K_{n}\frac{\log(n)}{n}\right]{\mathbf{1}}_{\Omega_{K_{n}}}\right\}$$

$${}+{\mathbb{E}}\left\{\widehat{m}_{K_{n}}\left[(\widehat{f}_{K_{n}}(0)-f_{K_{n}}(0))^{2}-(c_{2}-2)(||f||_{\infty}\vee 1)K_{n}\frac{\log(n)}{n}\right]{\mathbf{1}}_{\Omega_{K_{n}}^{c}}\right\}$$

$${}\lesssim Cn^{5/2}{\mathbb{P}}(\Omega_{K_{n}}^{c})\lesssim\frac{1}{n},$$

the term on $\Omega_{K_{n}}$ being less than or equal to 0. Plugging this and (55) into (54), we get

$${\mathbb{E}}\left(||\widehat{f^{\prime}}_{\widehat{m}_{K},K}-f^{\prime}||^{2}\right)\leqslant 3||f_{m,K}^{\prime}-f^{\prime}||^{2}+4{\textrm{pen}}_{K}(m)+32m(\widehat{f}_{K}(0)-f(0))^{2}+\frac{c}{n},$$

which gives the result of Theorem 3.1. $\Box$

APPENDIX A

PROOFS OF AUXILIARY RESULTS

A.1. Proof of Lemma 2.1

In the Hermite case $\varphi_{j}=h_{j}$ and $f:\mathbb{R}\mapsto[0,\infty),$ allowing $d$ successive integration by parts, it holds that

$$a_{j}(f^{(d)})=\int\limits_{\mathbb{R}}f^{(d)}(x)h_{j}(x)dx=\left[\sum_{k=0}^{d-1}(-1)^{k}f^{(d-1-k)}(x)h_{j}^{(k)}(x)\right]^{+\infty}_{-\infty}+(-1)^{d}\int\limits_{\mathbb{R}}h_{j}^{(d)}(x)f(x)dx.$$

(A.1)

By definition for all $j\geqslant 0$, $h_{j}(x)=c_{j}H_{j}(x)e^{-\frac{x^{2}}{2}}$ where $H_{j}$ is a polynomial. Then, its $k$th derivative, $0\leqslant k\leqslant d-1$, is a polynomial multiplied by $e^{-{x^{2}}/{2}}$ and $\lim_{|x|\to+\infty}h_{j}^{(k)}(x)=0$. This together with (A2), gives that the bracket in (A.1) is null and the result follows.

Similarly in the Laguerre case, (A.1) holds integrating on $[0,\infty)$ instead of $\mathbb{R}$ and replacing $h_{j}$ by $\ell_{j}$. The term in the bracket is null at 0 from (A3). It is also null at infinity using (A2) together with the fact that $\ell_{j}$ are polynomials multiplied by $e^{-x}$ leading similarly to $\lim_{x\to\infty}f^{(d-1-k)}(x)\ell^{(k)}_{j}(x)=0$, $0\leqslant k\leqslant d-1$, $j\geqslant 0$. The result follows.

A.2. Proof of Lemma 2.2

We control the quantity

$$\sum_{j\geqslant 0}j^{s-d}\langle f^{(d)},h_{j}\rangle^{2}=\sum_{j=0}^{d-1}j^{s-d}\langle f^{(d)},h_{j}\rangle^{2}+\sum_{j\geqslant d}j^{s-d}\langle f^{(d)},h_{j}\rangle^{2}.$$

(A.2)

The first term is a constant which depending on $d$. For the second term using Lemma 5.2, we obtain

$$\sum_{j\geqslant d}j^{s-d}\langle f^{(d)},h_{j}\rangle^{2}=\sum_{j\geqslant d}j^{s-d}\left(\sum_{k=-d}^{d}b_{k,j}^{(d)}\int h_{j+k}(x)f(x)dx\right)^{2}$$

$${}\leqslant C_{d}\sum_{j\geqslant d}j^{s}\sum_{k=-d}^{d}\left(\int h_{j+k}(x)f(x)dx\right)^{2}=C_{d}\sum_{k=-d}^{d}\sum_{j\geqslant d}j^{s}\langle h_{j+k},f\rangle^{2}$$

$${}=C_{d}\sum_{k=-d}^{d}\left(\sum_{j\geqslant d+k}|j-k|^{s}\langle h_{j},f\rangle^{2}\right)\leqslant C_{d}\sum_{k=-d}^{d}\left(\sum_{j\geqslant 0}2^{s}j^{s}\langle h_{j},f\rangle^{2}\right)=(2d+1)2^{s}DC_{d}.$$

Inserting this in (59), we obtain the announced result.

A.3. Proof of Lemma 2.3

We establish the result for $d=1$, the general case is an immediate consequence. It follows from the definition of $\widetilde{W}_{L}^{s}(D)$ that $(\theta^{\prime})^{(j)}$, $0\leqslant j\leqslant s-1$ are in $C([0,\infty))$. Moreover, it holds that $x\mapsto x^{k/2}(\theta^{\prime})^{(j)}(x)\in\mathbb{L}^{2}(\mathbb{R}^{+})$ for all $0\leqslant j<k\leqslant s-1$. The case $k=j$ is obtained using that $\theta^{(j)}$ is continuous on $C([0,\infty))$ and that $x\mapsto x^{(j+1)/2}(\theta^{\prime})^{(j)}(x)\in\mathbb{L}^{2}(\mathbb{R}^{+}).$ It follows that

$$|||\theta^{\prime}|||_{s}^{2}=\sum_{j=0}^{s-1}\Big{|}\Big{|}x^{j/2}\sum_{k=0}^{j}\binom{j}{k}(\theta^{\prime})^{(k)}\Big{|}\Big{|}^{2}\leqslant 2\sum_{j=0}^{s-1}\Big{|}\Big{|}x^{j/2}\sum_{k=0}^{j-1}\binom{j}{k}(\theta^{\prime})^{(k)}\Big{|}\Big{|}^{2}+2\sum_{j=0}^{s-1}\Big{|}\Big{|}x^{j/2}(\theta^{\prime})^{(j)}\Big{|}\Big{|}^{2}$$

$${}\leqslant C+2\sum_{j=0}^{s-1}||x^{(j+1)/2}(\theta^{\prime})^{(j)}(x)||^{2}<\infty,$$

where $C$ depends on $D$. Finally, using the equivalence of the norms $|.|_{s}$ and $|||.|||_{s}$, the value of $D^{\prime}$ follows from the latter inequality.

A.4. Proof of Lemma 5.1

Consider the decomposition

$$\int\limits_{0}^{+\infty}x^{-k}(\ell_{j-k,(k)}(x/2))^{2}f(x/2)dx=\sum_{i=1}^{6}I_{i},$$

where for $\nu=4j-2k+2$, $j\geqslant k$, we used the decomposition $(0,\infty)=(0,\frac{1}{\nu}]\cup(\frac{1}{\nu},\frac{\nu}{2}]\cup(\frac{\nu}{2},\nu-\nu^{1/3}]\cup(\nu-\nu^{1/3},\nu+\nu^{/13}]\cup(\nu+\nu^{1/3},3\nu/2]\cup(3\nu/2,\infty).$ Using [2] (see Appendix B.1) and straightforward inequalities give

$$I_{1}\lesssim\int\limits_{0}^{\frac{1}{\nu}}x^{-k}(x\nu)^{k}f(x/2)dx\leqslant\int\limits_{0}^{\frac{1}{\nu}}x^{-k}(x\nu)^{-1/2}f(x/2)dx\lesssim\nu^{-1/2}\mathbb{E}[X^{-k-1/2}],$$

$$I_{2}\lesssim\int\limits_{1/\nu}^{\frac{\nu}{2}}x^{-k}((x\nu)^{-1/4})^{2}f(x/2)dx=\nu^{-1/2}\int\limits_{1/\nu}^{\frac{\nu}{2}}x^{-k-1/2}f(x/2)dx\leqslant\nu^{-1/2}\mathbb{E}[X^{-k-1/2}],$$

$$I_{3}\lesssim\int\limits_{\frac{\nu}{2}}^{\nu-\nu^{1/3}}x^{-k}(\nu^{-1/4}(\nu-x)^{-1/4})^{2}f(x/2)dx=\nu^{-1/2}\int\limits_{\frac{\nu}{2}}^{\nu-\nu^{1/3}}x^{-k}(\nu-x)^{-1/2}f(x/2)dx\lesssim\nu^{-1/2},$$

$$I_{4}\lesssim\int\limits_{\nu-\nu^{1/3}}^{\nu+\nu^{1/3}}x^{-k}(\nu^{-1/3})^{2}f(x/2)dx\leqslant\nu^{-2/3}\int\limits_{\frac{\nu}{2}}^{\nu+\nu^{1/3}}x^{-k}f(x/2)dx\lesssim\nu^{-1/2}\nu^{-k}\leqslant\nu^{-1/2},$$

$$I_{5}\lesssim\int\limits_{\nu+\nu^{1/3}}^{3\nu/2}x^{-k}\nu^{-1/2}(x-\nu)^{-1/2}e^{-2\gamma_{1}\nu^{-1/2}(x-\nu)^{3/2}}f(x/2)dx\lesssim\nu^{-1/2}\nu^{-1/6}\nu^{-k}\int f(x/2)dx\lesssim\nu^{-1/2},$$

$$I_{6}\lesssim\int\limits_{3\nu/2}^{+\infty}x^{-k}e^{-2\gamma_{2}x}f(x/2)dx\lesssim e^{-3\gamma_{2}\nu/2}=\mathcal{O}(\nu^{-1/2}).$$

Gathering these inequalities give the announced result.

A.5. Proof of Lemma 5.2

The result is obtained by induction on $d$. If $d=1$, $h_{j}^{\prime}$ is given by (5), with $b^{(1)}_{-1,j-1}=j^{1/2}/\sqrt{2}$, $b_{0,j}=0$ and $b^{(1)}_{1,j}=(j+1)^{1/2}/\sqrt{2}$, $\forall j\geqslant 1$. Thus, it holds $b_{k,j}^{(1)}=\mathcal{O}(j^{1/2})$ and (37) is satisfied for $d=1$. Let $\text{P}(d)$ the proposition given by Eq. (37) and assume $\text{P}(d)$ holds and we establish $\text{P}(d+1)$. It holds using successively $\text{P}(d)$ and (5) that

$$h_{j}^{(d+1)}(x)=\sum_{k=-d}^{d}b_{k,j}^{(d)}\left[\frac{\sqrt{j+k}}{\sqrt{2}}h_{j+k-1}-\frac{\sqrt{j+k+1}}{\sqrt{2}}h_{j+k+1}\right]$$

$${}=\sum_{k^{\prime}=-d-1}^{d-1}b_{k^{\prime}+1,j}^{(d)}\frac{\sqrt{j+k^{\prime}+1}}{\sqrt{2}}h_{j+k^{\prime}}-\sum_{k^{\prime}=-d+1}^{d+1}b_{k^{\prime}-1,j}^{(d)}\frac{\sqrt{j+k^{\prime}}}{\sqrt{2}}h_{j+k^{\prime}}:=\sum_{k=-d-1}^{d+1}b_{k,j}^{(d+1)}h_{j+k^{\prime}},$$

where $b^{(d)}_{k,j}=\mathcal{O}(j^{d/2})$, $\forall j\geqslant d\geqslant|k|$ and $b_{k,j}^{(d+1)}=b_{k+1,j}^{(d)}\frac{\sqrt{j+k+1}}{\sqrt{2}}\mathbf{1}_{|k|\leqslant d-1}-b_{k-1,j}^{(d)}\frac{\sqrt{j+k}}{\sqrt{2}}\mathbf{1}_{|k|\leqslant d+1}$. It follows that $|b_{k,j}^{(d+1)}|\leqslant 2\sqrt{({j+d+1})/{2}}j^{\frac{d}{2}}\leqslant C_{d}j^{\frac{d+1}{2}},$ $|k|\leqslant d\leqslant j$, which completes the proof.

Proof of Lemma 5.4

A.6.1. Proof of part (i). First, it holds that

$$\mathbb{E}\left[\left(\sup_{t\in S_{m}+S_{\widehat{m}},||t||=1}|\nu_{n,d}(t)|^{2}-p(m,\widehat{m}_{n})\right)_{+}\right]$$

$${}\leqslant\sum_{m^{\prime}\in\mathcal{M}_{n,d}}\mathbb{E}\left[\left(\sup_{t\in S_{m}+S_{{m^{\prime}}},||t||=1}|\nu_{n,d}(t)|^{2}-p(m,{m^{\prime}})\right)_{+}\right],$$

(A.3)

which we bound applying a Talagrand Inequality (see Appendix B.2). Following notations of Appendix B.2, we have three terms $H^{2},v$, and $M_{1}$ to compute. Let us denote by $m^{*}=m\vee m^{\prime}$, for $t\in S_{m}+S_{{m^{\prime}}}$, $||t||=1$, it holds

$$||t||^{2}=\left|\left|\sum_{j=0}^{m^{*}-1}a_{j}\varphi_{j}\right|\right|^{2}=\sum_{j=0}^{m^{*}-1}a_{j}^{2}=1.$$

Computing $\boldsymbol{H}^{\mathbf{2}}$. By the linearity of $\nu_{n,d}$ and the Cauchy–Schwarz inequality, we have

$$\nu_{n,d}(t)^{2}=\left(\sum_{j=0}^{m^{*}-1}a_{j}\nu_{n,d}(\varphi_{j})\right)^{2}\leqslant\sum_{j=0}^{m^{*}-1}a_{j}^{2}\sum_{j=0}^{m^{*}-1}\nu_{n,d}^{2}(\varphi_{j})=\sum_{j=0}^{m^{*}-1}\nu_{n,d}^{2}(\varphi_{j}).$$

One can check that the latter is an equality for $a_{j}=\nu_{n,d}(\varphi_{j}).$ Therefore, taking expectation, it follows

$$\mathbb{E}\left[\sup_{t\in S_{m}^{*},||t||=1}\nu^{2}_{n,d}(t)\right]=\sum_{j=0}^{m^{*}-1}\textrm{Var}(\nu_{n,d}(\varphi_{j}))=\frac{1}{n}\sum_{j=0}^{m^{*}-1}\textrm{Var}(\varphi_{j}^{(d)}(X_{1}))$$

$${}\leqslant\frac{1}{n}\sum_{j=0}^{m^{*}-1}\mathbb{E}\left[\varphi_{j}^{(d)}(X_{1})^{2}\right]=\frac{V_{m^{*},d}}{n}=:H^{2}.$$

Computing $\boldsymbol{v}$. It holds for $t\in S_{m}+S_{{m^{\prime}}}$, $||t||=1$,

$$\textrm{Var}\left((-1)^{d}t^{(d)}(X_{1})\right)\leqslant\int t^{(d)}(x)^{2}f(x)dx=\int\left(\sum_{j=0}^{m^{*}-1}a_{j}\varphi_{j}^{(d)}(x)\right)^{2}f(x)dx$$

$${}\leqslant 2\int\left(\sum_{j=0}^{d-1}a_{j}\varphi_{j}^{(d)}(x)\right)^{2}f(x)dx+2\int\left(\sum_{j=d}^{m^{*}-1}a_{j}\varphi_{j}^{(d)}(x)\right)^{2}f(x)dx.$$

(A.4)

The first term of the previous inequality is a constant depending only on $d$. For the second term, we consider separately the Laguerre and Hermite cases.

The Laguerre case ($\varphi_{j}=\ell_{j}$). Using (36) and the Cauchy–Schwarz inequality, it holds that

$$\int\left(\sum_{j=d}^{m^{*}-1}a_{j}\ell_{j}^{(d)}(x)\right)^{2}f(x)dx\leqslant 3^{d}\sum_{k=0}^{d}\binom{d}{k}\int\left(\sum_{j=d}^{m^{*}-1}a_{j}\left(\frac{j!}{(j-k)!}\right)^{\frac{1}{2}}x^{-\frac{k}{2}}\ell_{j-k,(k)}(x)\right)^{2}f(x)dx$$

$${}\leqslant 3^{d}\sum_{k=0}^{d}\binom{d}{k}\sup_{x\in\mathbb{R}^{+}}\frac{f(x)}{x^{k}}\sum_{j=d}^{m^{*}-1}a_{j}^{2}\frac{j!}{(j-k)!}\leqslant C(d)(m^{*})^{d},$$

(A.5)

where we used the orthonormality of $(\ell_{j,(k)})_{j\geqslant 0}$ and where $C(d)$ is a constant depending only on $d$ and $\sup_{x\in\mathbb{R}^{+}}\frac{f(x)}{x^{k}}$.

The Hermite case ($\varphi_{j}=h_{j}$). Similarly, using Lemma 5.2 and the orthonormality of $h_{j}$, it follows

$$\int\left(\sum_{j=d}^{m^{*}-1}a_{j}h_{j}^{(d)}(x)\right)^{2}f(x)dx\leqslant(2d+1)\sum_{k=-d}^{d}\int\left(\sum_{j=d}^{m^{*}-1}a_{j}b_{k,j}h_{j+k}(x)\right)^{2}f(x)dx$$

$${}\leqslant C(d)||f||_{\infty}(m^{*})^{d}.$$

(A.6)

Plugging (A.5) or (A.6) in (A.4), we set in the two cases $v:=c_{1}(m^{*})^{d}$ where $c_{1}$ depends on $d$ and either on $\sup_{x\in\mathbb{R}^{+}}\frac{f(x)}{x^{k}}$ (Laguerre case) or $||f||_{\infty}$ (Hermite case).

Computing $\boldsymbol{M}_{\mathbf{1}}$. The Cauchy Schwarz Inequality and $||t||=1$ give

$$||(-1)^{d}t^{(d)}||_{\infty}=\left|\left|\sum_{j=0}^{m^{*}-1}(-1)^{d}a_{j}\varphi_{j}^{(d)}\right|\right|_{\infty}\leqslant\sup_{x\in\mathbb{R}}\sqrt{\sum_{j=0}^{m^{*}-1}\varphi_{j}^{(d)}(x)^{2}}.$$

(A.7)

The Laguerre case. We use the following Lemma whose proof is a consequence of (2) and an induction on $d$.

Lemma A.1. For $\ell_{j}$ given in (1), the $d$th derivative of $\ell_{j}$ is such that $||\ell_{j}^{(d)}||_{\infty}\leqslant C_{d}(j+1)^{d}$, $\forall j\geqslant 0$ and where $C_{d}$ is a positive constant depending on $d$ .

Using Lemma A.1, we obtain

$$\sum_{j=0}^{m^{*}-1}\ell_{j}^{(d)}(x)^{2}\leqslant C_{d}^{2}(m^{*})^{2d+1}.$$

(A.8)

The Hermite case. The $d$ first terms in the sum in (A.7) can be bounded by a constant depending only on $d$. For the remaining terms, Lemma 5.2 and $||h_{j}||_{\infty}\leqslant\phi_{0}$ (see (4)) give

$$\sum_{j=d}^{m^{*}-1}[h_{j}^{(d)}(x)]^{2}\leqslant C_{d}^{2}\phi_{0}^{2}\sum_{k=-d}^{d}\sum_{j=d}^{m^{*}-1}j^{d}\leqslant C(m^{*})^{d+1},$$

(A.9)

where $C$ is a positive constant depending on $d$ and $\phi_{0}$.

Injecting either (A.8) or (A.9) in (A.7), we set $M_{1}=\mathcal{O}(m^{d+\frac{1}{2}})$ in the Laguerre case or $M_{1}=\mathcal{O}(m^{\frac{d}{2}+\frac{1}{2}})$ in the Hermite case.

Now, we apply the Talagrand inequality see Appendix B.2 with $\varepsilon=1/2$, it follows

$$\mathbb{E}\left[\left(\sup_{t\in S_{m}+S_{{m^{\prime}}},||t||=1}|\nu_{n,d}(t)|^{2}-4H^{2}\right)_{+}\right]\leqslant\frac{C_{1}}{n}\left(v\exp\left(-C_{2}\frac{nH^{2}}{v}\right)+C_{3}\frac{M_{1}^{2}}{n}\exp\left(-C_{4}\frac{nH}{M_{1}}\right)\right)$$

$${}:=\frac{C_{1}}{n}\left(U_{d}(m^{*})+V_{d}(m^{*})\right).$$

The Laguerre case. We have

$$U_{d}(m^{*})=c_{1}(m^{*})^{d}\exp\left(-C_{2}\frac{V_{m^{*},d}}{c_{1}(m^{*})^{d}}\right)$$

$$\text{and}\quad V_{d}(m^{*})=C_{3}c_{2}\frac{(m^{*})^{2d+1}}{n}\exp\left(-C_{4}\sqrt{n}\frac{\sqrt{V_{m^{*},d}}}{c_{2}(m^{*})^{d+\frac{1}{2}}}\right).$$

From (41) and the value of $m_{n}(d)$, we obtain

$$U_{d}(m^{*})\leqslant c_{1}{(m^{*})^{d}}\exp(-C_{2}^{\prime}m^{*}{{}^{\frac{1}{2}}})\quad\textrm{and}\quad V_{d}(m^{*})\leqslant C_{3}c_{2}(m^{*})^{{d+\frac{1}{2}}}\exp(-C_{4}^{\prime}{\sqrt{n}}{(m^{*})^{-\frac{d}{2}-\frac{1}{4}}}).$$

Using the value $m_{n}(d)$, it holds $(m^{*})^{d+1/2}\leqslant{n}/{\log^{3}(n)}$, which implies (recall $m^{*}=m\vee m^{\prime}$)

$$\sum_{m^{\prime}\in\mathcal{M}_{n,d}}V_{d}(m^{*})\leqslant C\sum_{m^{\prime}\in\mathcal{M}_{n,d}}(m^{*})^{{d+\frac{1}{2}}}\exp\left(-{C_{4}}\log^{2}(n)\right)\leqslant\Sigma_{d,2},$$

where $\Sigma_{d,2}$ is a constant depending only on $d$. Next, it follows

$$\sum_{m^{\prime}=1}^{n}U_{d}(m^{*})=\sum_{m^{\prime}=1}^{m}U_{d}(m^{*})+\sum_{m^{\prime}=m}^{n}U_{d}(m^{*})=c_{1}m^{d+1}\exp(-C_{2}^{\prime}m^{\frac{1}{2}})+\sum_{m^{\prime}=m}^{n}c_{1}(m^{\prime})^{d}\exp(-C_{2}^{\prime}m^{\prime\frac{1}{2}}).$$

The function $m\mapsto m^{d+1}\exp(-C_{2}^{\prime}m^{\frac{1}{2}})$ is bounded and the sum is finite on $m^{\prime}$, it holds

$$C_{1}\sum_{m^{\prime}=1}^{n}U_{d}(m^{*})\leqslant\Sigma_{d,1},\text{ where }\Sigma_{d,1}\text{ depends only on }d.$$

The Hermite case. Only the second term $V_{d}(m^{*})$ changes. Here, it is given by

$$V_{d}(m^{*})=C_{3}c_{2}\frac{(m^{*})^{d+1}}{n}\exp\left(-C_{3}\sqrt{n}\frac{\sqrt{V_{m^{*},d}}}{c_{2}(m^{*})^{\frac{d}{2}+\frac{1}{2}}}\right)\leqslant C_{3}c_{2}(m^{*})^{1/2}\exp(-C_{4}^{\prime}{\sqrt{n}(m^{*})^{-\frac{1}{4}}})$$

$${}\leqslant C_{3}c_{2}(m^{*})^{1/2}\exp(-C_{4}^{\prime}{(m^{*})^{\frac{d}{2}}}),$$

where we used (46) and the value of $m_{n}(d)$. We derive that $\sum_{m^{\prime}\in\mathcal{M}_{n,d}}V_{d}(m^{*})\leqslant\Sigma_{d,2}$.

Gathering all terms, it follows

$$\mathbb{E}\left[\left(\sup_{t\in S_{m}+S_{{m^{\prime}}},||t||=1}|\nu_{n,d}(t)|^{2}-4H^{2}\right)_{+}\right]\leqslant\frac{\Sigma}{n},\text{ where }\Sigma=\Sigma_{d,1}+\Sigma_{d,2}.$$

Plugging this in (A.3) gives the announced result.

A.6.2. Proof of part (ii). We use the Bernstein Inequality (see Appendix B.3) to prove the result. Define

$$Z_{i}^{(m)}=\sum_{j=0}^{m-1}(\varphi_{j}^{(d)}(X_{i}))^{2},\quad\textrm{then, }\quad\widehat{V}_{m,d}=\frac{1}{n}\sum_{i=1}^{n}Z_{i}^{(m)}$$

We select $s^{2}$ and $b$ such that $\textrm{Var}(Z_{i}^{(m)})\leqslant s^{2}$ and $|Z_{i}^{(m)}|\leqslant b$. By the computation of $M_{1}$ (see proof of part (i)), we set $b:=C^{*}m^{\alpha}$, with $\alpha=2d+1$ (Laguerre case) or $\alpha=d+1$ (Hermite case), where $C^{*}$ depends on $d$. For $s^{2}$, using that $\textrm{Var}(Z_{i}^{(m)})\leqslant\mathbb{E}[(Z_{i}^{(m)})^{2}]\leqslant b\sum_{j=0}^{m-1}\mathbb{E}\left[(\varphi_{j}^{(d)}(X_{i}))^{2}\right]=C^{*}m^{\alpha}V_{m,d}=:s^{2}$. Applying the Bernstein inequality, we have for $S_{n}=n(\widehat{V}_{m,d}-V_{m,d})$

$$\mathbb{P}\left(\left|\frac{S_{n}}{n}\right|\geqslant\sqrt{\frac{2xC^{*}m^{\alpha}V_{m,d}}{n}}+\frac{C^{*}m^{\alpha}x}{3n}\right)\leqslant 2e^{-x},\quad\forall x>0.$$

(A.10)

Choose $x=2\log(n)$ and define the set

$$\Omega:=\left\{m\in\mathcal{M}_{n,d},\ \frac{1}{n}|S_{n}|\leq 2\sqrt{\frac{C^{*}m^{\alpha}\log(n)V_{m,d}}{n}}+\frac{2C^{*}m^{\alpha}\log(n)}{3n}\right\}.$$

Consider the decomposition,

$$\mathbb{E}\left[\left({\textrm{pen}}_{d}(\widehat{m}_{n})-\widehat{{\textrm{pen}}}_{d}(\widehat{m}_{n})\right)_{+}\right]\leqslant\mathbb{E}\left[\left({\textrm{pen}}_{d}(\widehat{m}_{n})-\widehat{{\textrm{pen}}}_{d}(\widehat{m}_{n})\right)_{+}\mathbf{1}_{\Omega}\right]$$

$${}+\mathbb{E}\left[\left({\textrm{pen}}_{d}(\widehat{m}_{n})-\widehat{{\textrm{pen}}}_{d}(\widehat{m}_{n})\right)_{+}\mathbf{1}_{\Omega^{c}}\right].$$

Using $2xy\leqslant x^{2}+y^{2}$, we have on $\Omega$

$$|\widehat{V}_{\widehat{m},d}-V_{\widehat{m},d}|\leqslant\frac{V_{\widehat{m},d}}{2}+\frac{2C^{*}\widehat{m}^{\alpha}\log(n)}{n}+\frac{2C^{*}\widehat{m}^{\alpha}\log(n)}{3n}=\frac{V_{\widehat{m},d}}{2}+\frac{8}{3}\frac{C^{*}\widehat{m}^{\alpha}\log(n)}{n}.$$

The constraint on $m_{n}$ gives $\widehat{m}^{d+1/2}\leqslant C{n}/{(\log(n))^{2}}$ together with (41) giving $V_{\widehat{m},d}\geqslant c^{*}\widehat{m}^{d+1/2}$ give for $\alpha=2d+1$ (Laguerre case) that $\frac{8C^{*}}{3}\frac{\widehat{m}^{\alpha}\log(n)}{n}\leqslant\frac{8CC^{*}}{3c^{*}}\frac{V_{\widehat{m},d}}{\log(n)}\leqslant\frac{V_{\widehat{m},d}}{4},$ for $n$ large enough and

$$\mathbb{E}\left[\left({\textrm{pen}}_{d}(\widehat{m}_{n})-\widehat{{\textrm{pen}}}_{d}(\widehat{m}_{n})\right)_{+}\mathbf{1}_{\Omega}\right]\leqslant\frac{3}{4}\mathbb{E}[{\textrm{pen}}_{d}(\widehat{m}_{n})].$$

(A.11)

In the Hermite case ($\alpha=d+1$) computations are similar as $\widehat{m}^{d+1}\leqslant\widehat{m}^{2d+1}$. For the control on $\Omega^{c}$, we write, using (A.10),

$$\mathbb{E}\left[\left({\textrm{pen}}_{d}(\widehat{m}_{n})-\widehat{{\textrm{pen}}}_{d}(\widehat{m}_{n})\right)_{+}\mathbf{1}_{\Omega^{c}}\right]\leqslant 2\kappa\mathbb{P}(\Omega^{c})\leqslant 2\kappa\sum_{m\in\mathcal{M}_{n,d}}2e^{-2\log(n)}:=\frac{\Sigma_{2}}{n}.$$

(A.12)

Gathering (A.11) and (A.12), we get the desired result.

Appendices

APPENDIX B

SOME INEQUALITIES

2.1 B.2. Asymptotic Askey and Wainger Formula

From [2], we have for $\nu=4k+2\delta+2$, and $k$ large enough

$$|\ell_{k,(\delta)}(x/2)|\leqslant C\begin{cases}\textrm{a)}(x\nu)^{\delta/2}\quad\textrm{ if }\quad 0\leqslant x\leqslant 1/\nu\\ \textrm{b)}(x\nu)^{-1/4}\quad\textrm{ if }\quad 1/\nu\leqslant x\leqslant\nu/2\\ \textrm{c)}\nu^{-1/4}(\nu-x)^{-1/4}\quad\textrm{ if }\quad\nu/2\leqslant x\leqslant\nu-\nu^{1/3}\\ \textrm{d)}\nu^{-1/3}\quad\textrm{ if }\quad\nu-\nu^{1/3}\leqslant x\leqslant\nu+\nu^{1/3}\\ \textrm{e)}\nu^{-1/4}(x-\nu)^{-1/4}e^{-\gamma_{1}\nu^{-1/2}(x-\nu)^{3/2}}\quad\textrm{ if }\quad\nu+\nu^{1/3}\leqslant x\leqslant 3\nu/2\\ \textrm{f)}e^{-\gamma_{2}x}\quad\textrm{ if }\quad x\geqslant 3\nu/2,\end{cases}$$

where $\gamma_{1}$ and $\gamma_{2}$ are positive and fixed constants.

2.2 B.2. A Talagrand Inequality

The Talagrand inequalities have been proven in [41] and reworked by [26]. This version is given in [23]. Let $(X_{i})_{1\leqslant i\leqslant n}$ be independent real random variables and

$$\nu_{n}(t)=\frac{1}{n}\sum_{i=1}^{n}(t(X_{i})-\mathbb{E}[t(X_{i})])$$

for $t$ in $\mathcal{F}$ a class of measurable functions. If there exist $M_{1}$, $H$, and $v$ such that:

$$\sup_{t\in\mathcal{F}}||t||_{\infty}\leqslant M_{1},\quad\mathbb{E}[\sup_{t\in\mathcal{F}}\mid{\nu_{n}(t)}\mid]\leqslant H,\quad\sup_{t\in\mathcal{F}}\dfrac{1}{n}\sum_{i=1}^{n}\textrm{Var}(t(X_{i}))\leqslant v,$$

then, for $\varepsilon>0$,

$$\mathbb{E}\left[\left(\sup_{t\in\mathcal{F}}|{\nu^{2}_{n}(t)}|-2(1+2\varepsilon)H^{2}\right)_{+}\right]\leqslant\frac{4}{K_{1}}\left(\frac{v}{n}\exp\left(-K_{1}\varepsilon\frac{nH^{2}}{v}\right){}\right.$$

$${}\left.+\frac{49M_{1}^{2}}{K_{1}C^{2}(\varepsilon)n^{2}}\exp\left(-K_{1}^{\prime}C(\varepsilon)\sqrt{\varepsilon}\dfrac{nH}{M_{1}}\right)\right),$$

where $C(\varepsilon)=(\sqrt{1+\varepsilon}-1)\wedge 1$, $K_{1}=1/6$ and $K_{1}^{\prime}$ a universal constant.

2.3 B.3. Bernstein Inequality ([29])

Let $X_{1},\dots X_{n}$, $n$ independent real random variables. Assume there exist two constants $s^{2}$ and $b$, such that $\textrm{Var}(X_{i})\leqslant s^{2}$ and $|X_{i}|\leqslant b$. Then, for all $x$ positive, we have

$$\mathbb{P}\left(|{S_{n}}|\geqslant\sqrt{2ns^{2}x}+\frac{bx}{3}\right)\leqslant 2e^{-x}\quad\text{with}\quad S_{n}=\sum_{i=1}^{n}(X_{i}-\mathbb{E}[X_{i}]).$$