1 Introduction

Mean-variance portfolio selection problem is concerned with the trade-off between profit (expected return) maximization and risk (variance) minimization. The pioneering work of Markowitz (1952) laid the foundation for portfolio selection under the mean-variance criterion in a single-period setting. By applying an embedding technique and taking advantage of the stochastic linear-quadratic control theory, Li and Ng (2000) and Zhou and Li (2000) extended Markowitz’s work to a multi-period and continuous-time setting, respectively. A notable feature of Zhou and Li (2000) is that the exogenous parameter processes are assumed to be only constants or deterministic functions. To generalize Zhou and Li (2000)’s results to more realistic environments, Lim and Zhou (2002) considered a complete market where the model coefficients are assumed to be uniformly bounded stochastic processes. By exploiting the backward stochastic differential equation (BSDE) theory (El Karoui et al. 1997), they solved the mean-variance problem by relating the optimal strategy to the solution to the associated BSDEs. Lim (2004) went a step forward by extending the results and methods of Lim and Zhou (2002) to an incomplete market setting under similar model assumptions. The uniform boundedness hypothesis, however, precludes the applications of local volatility and stochastic volatility models to the mean-variance portfolio selection problem, such as the constant elasticity of variance (CEV) model, Heston model (Heston 1993), 3/2 model (Lewis 2000), and the state-of-the-art 4/2 model (Grasselli (2017)). For this reason, many researchers drew on a more general market by relaxing the uniform boundedness hypothesis in recent years. For example, Shen et al. (2014) investigated a mean-variance portfolio selection problem under the CEV model, and explicit solutions were obtained by using a BSDE approach and assuming that the market price of volatility risk satisfies exponential integrability of infinitely large order. Shen and Zeng (2015) further considered the optimal investment-reinsurance problem for a mean-variance insurer in an incomplete market, where the market price of risk is proportional to a Markovian, affine-form, and square-root factor process. By using similar techniques, Tian et al. (2021) studied a mean-variance investment-reinsurance problem when the return rate of the stock follows an Ornstein-Uhlenbeck (OU) process. As the literature on the mean-variance portfolio selection problems is abundant, the above review is not exhaustive. Other relevant works include Chiu and Wong (2011); Yu (2013); Lv et al. (2016), Sun and Guo (2018); Sun et al. (2020), to name but only a few.

Although the mean-variance portfolio selection problems have been extensively investigated in the last decade, two aspects deserve further exploration. First, most of the preceding literature assumes that the interest rates are constants or deterministic functions, which violates the well-documented evidence that the short rates are stochastic, mainly referred to Vasicek (1977), Cox et al. (1985), and Duffie and Kan (1996). It is noteworthy that, in the last few years, some research results on the portfolio optimization problems with stochastic interest rates have been achieved. For example, Ferland and Watier (2010) considered a portfolio selection problem under the mean-variance criterion in a complete market with an extended CIR interest rate, and obtained the optimal strategy by using a BSDE approach. Assuming that the stochastic interest rate follows the Vasicek model, Shen and Siu (2012) studied an asset allocation problem with regime switching in an exponential utility maximization framework by using the dynamic programming approach. Chang (2015) concerned a mean-variance problem with random liabilities and Vasicek’s stochastic interest rate, and solved the problem explicitly for two special cases by using the dynamic programming approach. Guan and Liang (2014) investigated a defined contribution pension management problem under power utility in the presence of stochastic interest rates and stochastic volatility. By using similar methods to Guan and Liang (2014), Guan and Liang (2015) considered a similar problem under the mean-variance criterion with an affine-form stochastic interest rate and a stochastic return rate driven by an OU process. Recent works on the portfolio selection problems with stochastic interest rates include Yao et al. (2016); Pan and Xiao (2017), Escobar et al. (2017, 2018), Chang et al. (2020), and references therein.

Second, the optimal investment strategies derived in most of the aforementioned literature on the mean-variance portfolio selection problems are time-inconsistent (Strotz 1956), in the sense that the optimal strategies determined at the initial time might not be optimal at a future time point since the nonlinear operator within the objective function under the mean-variance criterion precludes the use of Bellman’s principle of optimality. In recent years, there has been a growing interest in developing time-consistent mean-variance approaches. To deal with the time inconsistency under the mean-variance criterion, Basak and Chabakauri (2010) applied a backward recursion approach starting from the terminal date to determine a time-consistent optimal strategy. Alternatively, Björk et al. (2017) proposed the Nash equilibrium approach by imposing a time-consistent constraint on the optimal strategy and derived the equilibrium optimal strategy and equilibrium value function by essentially solving an HJB equation under the Markovian market settings. Along this approach, readers may refer to Li et al. (2012), Wei and Wang (2017), and Zhang et al. (2020). Different from the equilibrium approach, the dynamic optimal approach championed by Pedersen and Peskir (2017) tackled the time inconsistency of the static optimal (time-inconsistent) strategy by performing an infinite number of the static optimality over the investment period, and they, therefore, derived a dynamic optimal (time-consistent) strategy. For other previous works along this line, one can refer to Pedersen and Peskir (2018), Zhang (2021a, 2021b), and references therein.

Motivated by the above aspects, in this paper, we study a mean-variance portfolio selection problem that takes into consideration interest rate and volatility risks within the framework developed by Pedersen and Peskir (2017). Three primitive assets, one risk-free asset, one risky asset, and one zero-coupon bond, can be freely traded in the market. We assume that the stochastic interest rate is described by the Vasicek model. Inspired by Escobar et al. (2018), the risky asset price exhibits not only stochastic volatility but also stochastic covariance with the interest rate. As opposed to most of the above-mentioned literature on the mean-variance portfolio selection problems, the risky asset’s return rate and volatility are not specifically given. We only assume that the market price of volatility risk relies on a Cox-Ingersoll-Ross (CIR) process, which embraces the family of the state-of-the-art 4/2 stochastic volatility models (Cheng and Escobar 2021) as a particular case. By applying a BSDE approach and solving the associated BSDE explicitly, closed-form expressions for the static optimal (time-inconsistent) strategy and optimal value function (efficient frontier) are derived. Following the methodology of Pedersen and Peskir (2017), we further consider a dynamic formulation of the mean-variance problem, and the explicit expression for the dynamic optimal (time-consistent) strategy is obtained by solving an infinite number of the static optimality over the investment period. Moreover, analytical solutions to some special cases of our model are provided. Finally, the economic impact of some model parameters on the efficient frontier as well as on the static and dynamic optimal asset allocations is illustrated with numerical examples. To sum up, the main contributions of this paper are as follows: (1) we consider a mean-variance portfolio selection problem in an incomplete market with interest rate and volatility risks, where the stochastic interest rate follows the Vasicek model while the market price of volatility risk is driven by a CIR process recovering the Heston model, 3/2 model, and 4/2 model as special cases. (2) Explicit expressions for the static optimal (time-inconsistent) and dynamic optimal (time-consistent) strategies are obtained by applying a BSDE approach. (3) The impact of some model parameters on the efficient frontier and the static and dynamic optimal asset allocations is shown.

The remainder of this paper is structured as follows. Section 2 introduces the financial market and formulates the mean-variance portfolio selection problems. In Sect. 3, we explore the solvability of a BSRE and a linear BSDE and obtain the explicit solutions. Section 4 presents both the static and dynamic optimality of the mean-variance problem, and closed-form solutions to some special cases are recovered. In Sect. 5, some numerical experiments are implemented to illustrate our theoretical results. Section 6 concludes the paper.

2 Formulation of the problem

Let [0, T] be a fixed and finite horizon of decision making and \((\Omega ,{\mathcal {F}},\mathbb {F},\mathrm{P})\) be a filtered complete probability space satisfying the usual conditions on which are defined three one-dimensional, mutually independent Brownian motions \(\left\{ W^{0}_{t}\right\} _{t\in [0,T]},\left\{ W^{1}_{t}\right\} _{t\in [0,T]},\) and \(\left\{ W^{2}_{t}\right\} _{t\in [0,T]}\). where filtration \(\mathbb {F}:=\left\{ {\mathcal {F}}_{t}\right\} _{t\in [0,T]}\) is generated by the above three Brownian motions, and \(\mathrm{P}\) is a real-world probability measure.

2.1 Financial market

We consider a financial market with interest rate and volatility risks, where a risk-free asset (cash), a zero-coupon bond, and a risky asset (stock) can be continuously traded. Assume that the price of the risk-free asset, denoted by \(S^{0}_{t}\), satisfies the following dynamics:

$$\begin{aligned} dS^{0}_{t} = r_{t}S^{0}_{t}\,dt \end{aligned}$$

with initial value \(S^{0}_{t_{0}}= s_{0}\) at time \(t_{0}\in [0,T)\) fixed and given, and that the instantaneous interest rate \(r_{t}\) is governed by the Vasicek model:

$$\begin{aligned} dr_{t} = (a-br_{t})\,dt -\sigma _{r}\,dW^{0}_{t}, \end{aligned}$$
(1)

with initial value \(r_{t_{0}}=r_{0}\), where \(b\in \mathbb {R}^{+}\) is the mean-reversion speed, \(a/b\in \mathbb {R}^{+}\) is the long-run level, and \(\sigma _{r}\) is the volatility of the interest rate. Suppose that the market price of interest rate risk is \(\lambda _{r}\in \mathbb {R}^{+}\). From Vasicek (1977), the price process \(B_{t}(u)\) of the zero-coupon bond with bond maturity u satisfies the following stochastic differential equation (SDE):

$$\begin{aligned} dB_{t}(u) = r_{t}B_{t}(u)\,dt + h_{0}(u-t)B_{t}(u)\sigma _{r}\left( \lambda _{r}\,dt + dW^{0}_{t}\right) ,\ t\le u \end{aligned}$$
(2)

with boundary condition \(B_{u}(u) =1\), where the deterministic function \(h_{0}(t)\) is given by

$$\begin{aligned} h_{0}(t) = \frac{1}{b}\left( 1-e^{-bt}\right) . \end{aligned}$$

We notice that the maturity of the zero-coupon bond \(B_{t}(u)\), \(u-t\), varies continuously as time t evolves. However, as it is stated in Boulier et al. (2001), there may not exist zero-coupon bonds with any maturity in the market. We, therefore, introduce a rollover bond with a fixed time-to-maturity \(K\in \mathbb {R}^{+}\) into the market. Denote by \(B_{t}(K)\) the price of the rollover bond at time t. Then, the rollover bond \(B_{t}(K)\) is of the form:

$$\begin{aligned} dB_{t}(K) = r_{t}B_{t}(K)\,dt + h_{0}(K)\sigma _{r}B_{t}(K)\left( \lambda _{r}\,dt + dW^{0}_{t}\right) . \end{aligned}$$
(3)

The risky asset price process \(S^{1}_{t}\) is related to the risk of interest rate and governed by the following general stochastic volatility model:

$$\begin{aligned} dS^{1}_{t} =S^{1}_{t}\left[ \mu \left( t,r_{t},\alpha _{t}\right) \,dt + \eta _{r}\sigma _{r}\,dW^{0}_{t}+\sigma \left( t,\alpha _{t}\right) \,dW^{1}_{t}\right] ,\ S^{1}_{t_{0}}=s^{1}_{0}\in \mathbb {R}^{+}, \end{aligned}$$
(4)

where \(\mu \) and \(\sigma \ne 0\) are two possibly unbounded and continuous functions and related to each other via:

$$\begin{aligned} \mu (t,r_{t},\alpha _{t})-r_{t} = \lambda \sqrt{\alpha _{t}}\sigma (t,\alpha _{t})+\lambda _{r}\eta _{r}\sigma _{r} \end{aligned}$$

with \(\lambda ,\eta _{r}\in \mathbb {R}\), and \(\alpha _{t}\) is an observable stochastic factor process following the CIR model:

$$\begin{aligned} d\alpha _{t} =\kappa (\theta -\alpha _{t})\,dt +\sigma _{\alpha }\sqrt{\alpha _{t}}\left( \rho \,dW^{1}_{t}+\sqrt{1-\rho ^{2}}\,dW^{2}_{t}\right) ,\ \alpha _{t_{0}}=\alpha _{0}\in \mathbb {R}^{+}, \end{aligned}$$
(5)

where \(\kappa \in \mathbb {R}^{+}\) is the speed of mean reversion, \(\theta \in \mathbb {R}^{+}\) is the long-run mean, \(\sigma _{\alpha }\) is the volatility of the factor process \(\alpha _{t}\), and \(\rho \in [-1,1]\) is the correlation coefficient between the risky asset price and factor process. In particular, we posit that the Feller condition is satisfied, i.e. \(2\kappa \theta \ge \sigma _{\alpha }^{2}\), so that the factor process \(\alpha _{t}\) driving the volatility of the risky asset price is strictly positive \(\mathbb {P}\) almost surely, for \(t\in [t_{0},T]\).

Remark 1

Notice that the risky asset price process (4) exhibits not only stochastic volatility via the function \(\sigma \) and factor process \(\alpha _{t}\) (5), but also stochastic instantaneous correlation \(\frac{\eta _{r}\sigma _{r}}{\sqrt{\eta _{r}^{2}\sigma _{r}^{2}+\sigma ^{2}(t,\alpha _{t})}}\in [-1,1]\) with the interest rate process \(r_{t}\) (1), in which the parameter \(\eta _{r}\) measures the impact of the interest rate dynamics on the risky asset price, and the specification \(\eta _{r}=0\) corresponds to the case when the interest rate and risky asset price are uncorrelated. It is also noteworthy that functions \(\mu \) and \(\sigma \) allow for more flexibility in modeling the risky asset price. In what follows, we shall see that the modeling framework includes the family of the state-of-the-art 4/2 stochastic volatility models, as an exceptional case.

Example 1

(The 4/2 model) If \(\sigma \left( t,\alpha _{t}\right) =c_{1}\sqrt{\alpha _{t}}+\frac{c_{2}}{\sqrt{\alpha _{t}}}\), \(\mu \left( t,\alpha _{t},r_{t}\right) =r_{t}+\lambda (c_{1}\alpha _{t}+c_{2})+\lambda _{r}\eta _{r}\sigma _{r}\) with constants \(c_{1}\ge 0\) and \(c_{2}\ge 0\), and \(\alpha _{t}=V_{t}\), then the risky asset price process is given by the 4/2 model (Grasselli 2017):

$$\begin{aligned} \left\{ \begin{aligned} dS^{1}_{t}=&\, S^{1}_{t}\left[ \left( r_{t}+\lambda (c_{1}V_{t}+c_{2})+\lambda _{r}\eta _{r}\sigma _{r}\right) \,dt+\left( c_{1}\sqrt{V_{t}}+\frac{c_{2}}{\sqrt{V_{t}}}\right) \,dW^{1}_{t}+\eta _{r}\sigma _{r}\,dW^{0}_{t}\right] ,\\ dV_{t} =&\,\kappa (\theta -V_{t})\,dt+\sigma _{\alpha }\sqrt{V_{t}}\left( \rho \,dW^{1}_{t}+\sqrt{1-\rho ^{2}}\,dW^{2}_{t}\right) , \end{aligned} \right. \nonumber \\ \end{aligned}$$
(6)

where \(V_{t}\) is the instantaneous variance driver process, and parameters \(c_{1}\) and \(c_{2}\) characterize the superposition of the two embedded parsimonious models, the Heston model (Heston 1993) and 3/2 model (Lewis 2000). More specifically, the case \((c_{1},c_{2})=(1,0)\) stands for the Heston model, while \((c_{1},c_{2})=(0,1)\) corresponds to the 3/2 model.

Suppose that the investor has an initial wealth \(x_{0}\in \mathbb {R}^{+}\) at time \(t_{0}\). Denote by two Markovian controls \(\pi _{B}(t,\alpha _{t},r_{t},X^{\pi }_{t})\) and \(\pi _{S^{1}}(t,\alpha _{t},r_{t},X^{\pi }_{t})\) the market value of wealth invested in the rollover bond \(B_{t}(K)\) and risky asset \(S^{1}_{t}\), respectively, where \(\pi :=\left( \left\{ \pi _{B}(\cdot )\right\} _{t\in [t_{0},T]},\left\{ \pi _{S^{1}}(\cdot )\right\} _{t\in [t_{0},T]}\right) \) represents the investment strategy and \(X^{\pi }_{t}\) is the associated wealth process. Under a self-financing condition, the wealth of the investor evolves according to

$$\begin{aligned} \begin{aligned} dX^{\pi }_{t} =&\, \left[ r_{t}X^{\pi }_{t}+\pi _{B}(t,\alpha _{t},r_{t},X^{\pi }_{t})h_{0}(K)\sigma _{r}\lambda _{r}+\pi _{S^{1}}(t,\alpha _{t},r_{t},X^{\pi }_{t})\bigg (\sigma \left( t,\alpha _{t}\right) \lambda \sqrt{\alpha _{t}}\right. \\&\left. +\lambda _{r}\eta _{r}\sigma _{r}\bigg )\right] \,dt+\left( \pi _{B}(t,\alpha _{t},r_{t},X^{\pi }_{t})h_{0}(K)\sigma _{r}+\pi _{S^{1}}(t,\alpha _{t},r_{t},X^{\pi }_{t})\eta _{r}\sigma _{r}\right) \,dW^{0}_{t}\\&+\pi _{S^{1}}(t,\alpha _{t},r_{t},X^{\pi }_{t})\sigma (t,\alpha _{t})\,dW^{1}_{t}. \end{aligned} \nonumber \\ \end{aligned}$$
(7)

Throughout the rest of the paper, we denote by \(\mathrm{P}_{t_{0}}\) the probability measure with initial data \((\alpha _{t_{0}},r_{t_{0}},X^{\pi }_{t_{0}})=(\alpha _{0},r_{0},x_{0})\) at time \(t_{0}\in [0,T]\), and \(\mathrm{E}_{t_{0}}[\cdot ]\) and \(\mathrm{Var}_{t_{0}}(\cdot )\) denote the associated expectation and variance, respectively.

Definition 1

(Admissible strategy) Given any fixed initial time \(t_{0}\in [0,T)\), a Markovian investment strategy \(\pi \) is said to be admissible if the following conditions are met:

  1. 1.

    SDE (7) associated with \(\pi \) has a pathwise unique solution;

  2. 2.

    \(\mathrm{E}_{t_{0}}\left[ \int _{0}^{T}\pi ^{2}_{B}(t,\alpha _{t},r_{t},X^{\pi }_{t})+\pi ^{2}_{S_{1}}(t,\alpha _{t},r_{t},X^{\pi }_{t})\,dt\right] <+\infty \);

  3. 3.

    \(\mathrm{E}_{t_{0}}\left[ \int _{0}^{T}\pi ^{2}_{S_{1}}(t,\alpha _{t},r_{t},X^{\pi }_{t})\sigma ^{2}(t,\alpha _{t})\,dt\right] <+\infty \);

  4. 4.

    \(\mathrm{E}_{t_{0}}\left[ \sup _{t\in [t_{0},T]}\vert X^{\pi }_{t}\vert ^{4}\right] <+\infty \).

The set of admissible strategies is denoted by \({\mathcal {A}}\).

Remark 2

Due to the unboundedness of interest rate process \(r_{t}\) and factor process \(\alpha _{t}\) in the meantime, the square integrability condition for the associated wealth process adopted by some preceding literature, such as Tian et al. (2021), Sun et al. (2020), and Zhang (2021a, 2021b), is not sufficient to apply the dominated convergence theorem on the left-hand side of (A10) to exchange the order of limit and expectation. We, therefore, opt for the fourth-order integrability condition for the wealth process \(X^{\pi }_{t}\), i.e. condition 4 in Definition 1.

2.2 Optimization problems

We consider the investor who wants to trade over the time interval \([t_{0},T]\) to minimize the variance of the terminal wealth, while the expected value is exogenously determined, i.e., under the mean-variance criterion. Formally, the mean-variance portfolio selection problem is defined as follows.

Definition 2

The mean-variance portfolio problem is a constrained stochastic optimization problem:

$$\begin{aligned} \left\{ \begin{aligned}&\min _{\pi \in {\mathcal {A}}}\ \mathrm{Var}_{t_{0}}(X^{\pi }_{T})\\&\mathrm{subject \ to}\ \mathrm{E}_{t_{0}}[X^{\pi }_T]= \xi , \end{aligned} \right. \end{aligned}$$
(8)

where \(\xi \) is a fixed and given constant. We denoted by \(V_{MV}(t_{0},\alpha _{0},r_{0},x_{0})\) and \(\pi ^{*}\) the optimal value function and optimal investment strategy, respectively.

Considering the time inconsistency of the mean-variance criterion as discussed in the introduction, it is expected to see that the resulting optimal strategy relies on the initial value of state variables \((t_{0},\alpha _{0},r_{0},x_{0})\) and might not be guaranteed to be optimal at a future time point. To address this problem, we opt for the dynamic optimal approach introduced by Pedersen and Peskir (2017). For the readers’ convenience, we now present the definition of dynamic optimality, which is slightly modified from Definition 2 in Pedersen and Peskir (2017), to adapt to the current context.

Definition 3

(Dynamic optimality) Given any fixed initial time \(t_{0}\in [0,T)\), a Markovian investment strategy \(\pi ^{d*}=:\left( \left\{ \pi ^{d*}_{B}(\cdot )\right\} _{t\in [t_{0},T]},\left\{ \pi ^{d*}_{S^{1}}(\cdot )\right\} _{t\in [t_{0},T]}\right) \) is referred to as the dynamic optimality for the mean-variance problem (8) if for every \((t,\alpha ,r,x)\in [t_{0},T)\otimes \mathbb {R}^{+}\otimes \mathbb {R}\otimes \mathbb {R}\) and every admissible strategy \(u\in {\mathcal {A}}\) with \(u(t,\alpha ,r,x)\ne \pi ^{d*}(t,\alpha ,r,x)\) and \(\mathrm{E}_{t,\alpha ,r,x}[X^{u}_{T}]=\xi \), there is a Markovian strategy w satisfying \(w(t,\alpha ,r,x)=\pi ^{d*}(t,\alpha ,r,x)\) and \(\mathrm{E}_{t,\alpha ,r,x,}[X^{w}_{T}]=\xi \) such that

$$\begin{aligned} \mathrm{Var}_{t,\alpha ,r,x}(X^{w}_{T})<\mathrm{Var}_{t,\alpha ,r,x}(X^{u}_{T}), \end{aligned}$$

where \(\mathrm{E}_{t,\alpha ,r,x}[X^{\pi }_{T}] =\mathrm{E}[X^{\pi }_{T}\vert \ \alpha _{t}=\alpha ,r_{t}=r,X^{\pi }_{t}=x]\) and \(\mathrm{Var}_{t,\alpha ,r,x}(X^{\pi }_{T})= \mathrm{E}_{t,\alpha ,r,x}[(X^{\pi }_{T})^{2}]-(\mathrm{E}_{t,\alpha ,r,x}[X^{\pi }_{T}])^{2}\).

Remark 3

According to Pedersen and Peskir (2017), the dynamic optimality \(\pi ^{d*}\) is essentially derived by solving the static optimal strategy, i.e., \(\pi ^{*}\) at each time and implementing it in an infinitesimally small period of time. In other words, the static optimality shall be considered in the first place.

Since the mean-variance problem (8) involves a convex objective functional, the associated linear constraint \(\mathrm{E}_{t_{0}}[X^{\pi }_T]= \xi \) can be eliminated by introducing the following auxiliary Lagrange dual function:

$$\begin{aligned} \begin{aligned} {\mathcal {L}}(\alpha _{0},r_{0},x_{0};\pi ,\theta )&:= \mathrm{E}_{t_{0}}[(X^{\pi }_{T}-\xi )^{2}] +2\theta \mathrm{E}_{t_{0}}[X^{\pi }_{T}-\xi ]\\&= \mathrm{E}_{t_{0}}\left[ (X^{\pi }_{T}-(\xi -\theta ))^{2}\right] -\theta ^{2}, \end{aligned} \end{aligned}$$
(9)

where \(\theta \in \mathbb {R}\) is the Lagrange multiplier. According to the Lagrangian duality theorem (see, for example, Luenberger 1968), problem (8) is equivalent to the following min-max problem:

$$\begin{aligned} \max _{\theta \in \mathbb {R}}\min _{\pi \in {\mathcal {A}}}{\mathcal {L}}(\alpha _{0},r_{0},x_{0};\pi ,\theta ), \end{aligned}$$
(10)

which implies that it remains to first consider the following benchmark problem:

$$\begin{aligned} \min _{\pi \in {\mathcal {A}}}J(\alpha _{0},r_{0},x_{0};\pi ,\gamma ) := \min _{\pi \in {\mathcal {A}}}\mathrm{E}_{t_{0}}\left[ (X^{\pi }_{T}-\gamma )^{2}\right] , \end{aligned}$$
(11)

where \(\gamma = \xi -\theta \in \mathbb {R}\).

3 Solution to the benchmark problem

In this section, we mainly focus on the benchmark problem (11) using a BSDE approach. Before introducing the BSDEs associated with the benchmark problem (11), we present the following auxiliary results on the Vasicek model (1) and CIR model (5), which are modified from Lemma 4.3 in Benth and Karlsen (2005), Lemma 4.1 in Wei and Wang (2017), and Theorem 5.1 in Zeng and Taksar (2013), respectively.

Lemma 3.1

For the Vasicek model (1), when c is a constant such that \(c<\frac{b}{2\sigma _{r}^{2}(T-t_{0})}\), the Laplace transform of \(r_{t}^{2}\) is well-defined, i.e.,

$$\begin{aligned} \mathrm{E}_{t_{0}}\left[ \exp \left\{ c\int _{t_{0}}^{T}r_{t}^{2}\,dt\right\} \right] <+\infty . \end{aligned}$$

Lemma 3.2

For the Vasicek model (1), \(\vert r_{t}\vert \) has exponential moment of all order, i.e.,

$$\begin{aligned} \mathrm{E}_{t_{0}}\left[ \sup _{t\in [t_{0},T]}e^{p\vert r_{t}\vert }\right] <+\infty ,\ \forall p\ge 0. \end{aligned}$$

Lemma 3.3

For the CIR model (5), when c is a constant such that \(c\le \kappa ^{2}/2\sigma _{\alpha }^{2}\), the Laplace transform of \(\alpha _{t}\) is well-defined, i.e.,

$$\begin{aligned} {\mathrm{E}}_{t_{0}}\left[ \exp \left\{ c\int _{t_{0}}^{T}\alpha _{t}\,dt\right\} \right] <+\infty . \end{aligned}$$

Having reviewed the above preliminary results, we now impose the following assumption to facilitate further discussions:

Assumption 3.4

\(48\sigma _{r}^{2}T<b\) and \(\max \bigg \{24\lambda (\lambda +\sigma _{\alpha }\vert \rho b(t_{0})\vert ),(276+48\sqrt{33})(\lambda ^{2}+\sigma _{\alpha }^{2}b^{2}(t_{0}))\bigg \}\le \kappa ^{2}/2\sigma _{\alpha }^{2}\), where function b(t) is given by (20) below.

Remark 4

The monotonicity of function b(t) shown in Proposition 3.8 implies that \(\vert b(t)\vert \) decreases to 0 as T approaches 0, which indicates the mathematical feasibility of the assumption above when the investment horizon is small enough. From an economic point of view, Assumption 3.4 presents an upper bound for the slope \(\lambda \) of the market price of volatility risk. As stated in Korn and Kraft (2003), when \(\lambda \) is too large, undertaking volatility risk is rewarded too much by the market, and the optimal investment strategy might not be uniquely determined. Mathematically speaking, if the above technical condition is violated, the uniqueness result to the following BSRE (12) and linear BSDE (13) might not be ensured.

Considering the following BSRE and linear BSDE:

$$\begin{aligned} \left\{ \begin{aligned} dP_{t} =&\, \left\{ \left[ -2r_{t}+\lambda _{r}^{2}+\lambda ^{2}\alpha _{t}\right] P_{t} +2\lambda _{r}\Gamma _{0,t}+2\lambda \sqrt{\alpha _{t}}\Gamma _{1,t}+\frac{\Gamma _{0,t}^{2}}{P_{t}}+\frac{\Gamma _{1,t}^{2}}{P_{t}}\right\} \,dt\\&+ \Gamma _{0,t}\,dW^{0}_{t}+\Gamma _{1,t}\,dW^{1}_{t}+\Gamma _{2,t}\,dW^{2}_{t},\\ P_{T} =&\, 1,\\ P_{t} >&0,\ \text {for all}\ t\in [t_{0},T], \end{aligned} \right. \end{aligned}$$
(12)

and

$$\begin{aligned} \left\{ \begin{aligned} dY_{t}&= (r_{t}Y_{t} + Z_{t}\lambda _{r})\,dt + Z_{t}\,dW^{0}_{t},\\ Y_{T}&=-\gamma . \end{aligned} \right. \end{aligned}$$
(13)

Here, a solution to (12) is a triplet of \(\mathbb {F}\)-adapted stochastic processes \((P_{t},\Gamma _{0,t},\Gamma _{1,t},\Gamma _{2,t})\); a solution to (13) is a pair of \(\mathbb {F}\)-adapted stochastic processes \((Y_{t},Z_{t})\). It is noteworthy that these two kinds of BSDEs are with unbounded coefficients due to the unboundedness of the interest rate process \(r_{t}\) and factor process \(\alpha _{t}\), and thus, the results in Lim (2004) and El Karoui et al. (1997) cannot be used in our case. Nevertheless, by observing that the driver of linear BSDE (13) follows a stochastic Lipschitz continuity (Bender and Kohlmann 2000), we derive the unique solution to BSDE (13) in the next lemma.

Lemma 3.5

Suppose that Assumption 3.4 holds true. The unique solution \((Y_{t},Z_{t})\) to linear BSDE (13) is given by

$$\begin{aligned} \left\{ \begin{aligned} Y_{t}&= -\gamma \exp \left\{ g(t)+h(t)r_{t}\right\} ,\\ Z_{t}&= -\sigma _{r}h(t)Y_{t}, \end{aligned} \right. \end{aligned}$$
(14)

where functions g(t) and h(t) are given by

$$\begin{aligned} \left\{ \begin{aligned} g(t) =&\,\left( \frac{\sigma _{r}^{2}}{2b^{2}}-\frac{a+\sigma _{r}\lambda _{r}}{b}\right) (T-t)+ \left( \frac{a+\lambda _{r}\sigma _{r}}{b^{2}}-\frac{\sigma _{r}^{2}}{b^{3}}\right) \left( 1-e^{-b(T-t)}\right) \\&+\frac{\sigma _{r}^{2}}{4b^{3}}\left( 1-e^{-2b(T-t)}\right) ,\\ h(t) =&\, \frac{1}{b}\left( e^{-b(T-t)}-1\right) . \end{aligned} \right. \end{aligned}$$
(15)

Proof

See Appendix A.1. \(\square \)

By using the Markovian structures of the interest rate process \(r_{t}\) and factor process \(\alpha _{t}\), we next manage to derive one explicit solution to BSRE (12) and show its uniqueness.

Lemma 3.6

One solution \((P_{t},\Gamma _{0,t},\Gamma _{1,t},\Gamma _{2,t})\) to BSRE (12) is given by

$$\begin{aligned} P_{t} = \exp \left\{ a(t)r_{t}+b(t)\alpha _{t}\right\} \phi (t), \end{aligned}$$
(16)

and

$$\begin{aligned} (\Gamma _{0,t},\Gamma _{1,t},\Gamma _{2,t}) = (-\sigma _{r}a(t)P_{t},\sigma _{\alpha }\rho b(t)\sqrt{\alpha _{t}}P_{t},\sigma _{\alpha }\sqrt{1-\rho } b(t)\sqrt{\alpha _{t}}P_{t}), \end{aligned}$$
(17)

where functions a(t), b(t),  and \(\phi (t)\) are solutions to the following ordinary differential equations (ODEs):

$$\begin{aligned} \left\{ \begin{aligned} \frac{da(t)}{dt}-ba(t)+2&=0,\ a(T)=0,\\ \frac{db(t)}{dt}-(\kappa +2\rho \sigma _{\alpha }\lambda )b(t)+\left( \frac{1}{2}-\rho ^{2}\right) \sigma _{\alpha }^{2}b^{2}(t)-\lambda ^{2}&=0,\ b(T)=0,\\ \frac{d\phi (t)}{dt} +\left[ (a+2\sigma _{r}\lambda _{r})a(t) +\kappa \theta b(t)-\frac{1}{2}a^{2}(t)\sigma _{r}^{2}-\lambda _{r}^{2}\right] \phi (t)&=0,\ \phi (T)=1. \end{aligned} \right. \end{aligned}$$
(18)

Proof

See Appendix A.2. \(\square \)

In the next proposition, we derive explicit solutions to ODEs (18), which provides the closed-form solution to BSRE (12).

Proposition 3.7

The explicit solutions of a(t), b(t),  and \(\phi (t)\) to ODEs (18) are given as follows:

$$\begin{aligned} a(t) =\frac{2}{b}\left( 1-e^{-b(T-t)}\right) , \end{aligned}$$
(19)

and

$$\begin{aligned} b(t) =\left\{ \begin{aligned}&\frac{\lambda ^{2}}{k+2\lambda \rho \sigma _{\alpha }}\left( e^{(k+2\lambda \rho \sigma _{\alpha })(t-T)}-1\right) ,&\rho ^{2}=\frac{1}{2},\ k+2\lambda \rho \sigma _{\alpha }\ne 0;\\&\lambda ^{2}(t-T),&\rho ^{2}=\frac{1}{2},\ k+2\lambda \rho \sigma _{\alpha }=0;\\&\frac{n_{1}n_{2}(1-e^{\sqrt{\Delta }(T-t)})}{n_{1}-n_{2}e^{\sqrt{\Delta }(T-t)}},&\rho ^{2}\ne \frac{1}{2},\ \Delta >0;\\&\frac{\sigma _{\alpha }^{2}(\rho ^{2}-\frac{1}{2})(T-t)n_{0}^{2}}{\sigma _{\alpha }^{2}(\rho ^{2}-\frac{1}{2})(T-t)n_{0}-1},&\rho ^{2}\ne \frac{1}{2},\ \Delta =0;\\&\frac{\sqrt{-\Delta }}{\sigma _{\alpha }^{2}(2\rho ^{2}-1)}\tan \left( \arctan \left( \frac{k+2\lambda \rho \sigma _{\alpha }}{\sqrt{-\Delta }}\right) -\frac{\sqrt{-\Delta }}{2}(T-t)\right) +n_{0},&\rho ^{2}\ne \frac{1}{2},\ \Delta <0, \end{aligned} \right. \end{aligned}$$
(20)

and

$$\begin{aligned} \phi (t) =\exp \left\{ \int _{t}^{T}(a+2\sigma _{r}\lambda _{r})a(s) +\kappa \theta b(s)-\frac{1}{2}a^{2}(s)\sigma _{r}^{2}-\lambda _{r}^{2}\,ds\right\} , \end{aligned}$$
(21)

where \(\Delta ,n_{0},n_{1},\) and \(n_{2}\) are given by

$$\begin{aligned} \left\{ \begin{aligned} \Delta&=(k+2\lambda \rho \sigma _{\alpha })^{2}-(4\rho ^{2}-2)\sigma _{\alpha }^{2}\lambda ^{2},\ n_{0}=\frac{-(k+2\lambda \rho \sigma _{\alpha })}{\sigma _{\alpha }^{2}(2\rho ^{2}-1)},\\ n_{1}&=\frac{-(k+2\lambda \rho \sigma _{\alpha })+\sqrt{\Delta }}{\sigma _{\alpha }^{2}(2\rho ^{2}-1)},\ n_{2}=\frac{-(k+2\lambda \rho \sigma _{\alpha })-\sqrt{\Delta }}{\sigma _{\alpha }^{2}(2\rho ^{2}-1)}. \end{aligned} \right. \end{aligned}$$
(22)

Proof

See Appendix A.3. \(\square \)

The next proposition shows that b(t) is a strictly increasing function over \([t_{0},T]\). In other words, the maximum value of \(\vert b(t)\vert \) is attained at the initial time \(t_{0}\).

Proposition 3.8

Function b(t) is monotonically increasing over \([t_{0},T]\).

Proof

See Appendix A.4. \(\square \)

Lemma 3.9

Suppose that Assumption 3.4 holds true, then the solution \((P_{t},\Gamma _{0,t},\Gamma _{1,t},\Gamma _{2,t})\) given in (16) and (17) is the unique solution to BSRE (12).

Proof

See Appendix A.5. \(\square \)

Having derived the uniqueness results of BSRE (12) and linear BSDE (13), we now define the following two stochastic exponential processes \(\Pi _{0,t}\) and \(\Pi _{1,t}\), for \(t\in [t_{0},T]\),

$$\begin{aligned} \left\{ \begin{aligned} \Pi _{0,t}&= \exp \left\{ -\int _{t_{0}}^{t}(\lambda _{r}-\sigma _{r}a(s))\,dW^{0}_{s}-\int _{t_{0}}^{t}\frac{1}{2}\left( \lambda _{r}-\sigma _{r}a(s)\right) ^{2}\,ds\right\} ,\\ \Pi _{1,t}&= \exp \left\{ -\int _{t_{0}}^{t}(\lambda +\sigma _{\alpha }\rho b(s))\sqrt{\alpha _{s}}\,dW^{1}_{s}-\int _{t_{0}}^{t}\frac{1}{2}(\lambda +\sigma _{\alpha }\rho b(s))^{2}\alpha _{s}\,ds\right\} . \end{aligned} \right. \nonumber \\ \end{aligned}$$
(23)

In the next lemma, we investigate the integrability of \(\Pi _{0,t}\) and \(\Pi _{1,t}\), which shall be used in the Proof of Proposition 3.11 below.

Lemma 3.10

Suppose that Assumption 3.4 holds true. The stochastic exponential processes \(\Pi _{0,t}\) and \(\Pi _{1,t}\) defined in (23) satisfy

$$\begin{aligned} \mathrm{E}_{t_{0}}\left[ \sup _{t\in [t_{0},T]}\vert \Pi _{0,t}\vert ^{12}+\vert \Pi _{1,t}\vert ^{12}\right] <+\infty . \end{aligned}$$

Proof

See Appendix A.6. \(\square \)

Based on the preceding results, we are ready to present the first main result of this paper, which relates the optimal strategy and optimal value function of the benchmark problem (11) to the solutions to BSRE (12) and linear BSDE (13).

Proposition 3.11

Suppose that Assumption 3.4 holds true. For any initial data \((t_{0},\alpha _{0},r_{0},x_{0})\in [0,T)\otimes \mathbb {R}^{+}\otimes \mathbb {R}\otimes \mathbb {R}\) fixed and given, the optimal investment strategy, denoted by \(\pi ^{*}\), of the benchmark problem (11) is given by

$$\begin{aligned} \left\{ \begin{aligned} \pi ^{*}_{S^{1}}(t,\alpha _{t},r_{t},X^{*}_{t}) =&\, -\frac{(X^{*}_{t}+Y_{t})\left( \frac{\Gamma _{1,t}}{P_{t}}+\lambda \sqrt{\alpha _{t}}\right) }{\sigma (t,\alpha _{t})},\\ \pi ^{*}_{B}(t,\alpha _{t},r_{t},X^{*}_{t}) =&\,-\frac{(X^{*}_{t}+Y_{t})\left( \frac{\Gamma _{0,t}}{P_{t}}+\lambda _{r}\right) +Z_{t}+\pi ^{*}_{S^{1}}(t,\alpha _{t},r_{t},X^{*}_{t})\eta _{r}\sigma _{r}}{h_{0}(K)\sigma _{r}}, \end{aligned} \right. \nonumber \\ \end{aligned}$$
(24)

where \(Y_{t},Z_{t},P_{t},\Gamma _{0,t}\), and \(\Gamma _{1,t}\) are given by (14), (16), and (17), respectively. The optimal value function is given by

$$\begin{aligned} J(\alpha _{0},r_{0},x_{0};\pi ^{*},\gamma ) = P_{t_{0}}\left( x_{0}+Y_{t_{0}}\right) ^{2}, \end{aligned}$$
(25)

and the wealth process \(X^{*}_{t}\) associated with the optimal strategy (24) evolves as

$$\begin{aligned} \begin{aligned} X^{*}_{t} =&\, \left( x_{0}-\gamma e^{g(t_{0})+h(t_{0})r_{0}}\right) \exp \left\{ \int _{t_{0}}^{t}r_{s}-(\lambda _{r}^{2}-\lambda _{r}\sigma _{r}a(s))-(\lambda ^{2}+\lambda \sigma _{\alpha }\rho b(s))\alpha _{s}\,ds\right\} \\&\times \Pi _{0,t}\Pi _{1,t}+\gamma e^{g(t)+h(t)r_{t}}, \end{aligned} \end{aligned}$$
(26)

where \(g(t),h(t),a(t),b(t),\Pi _{0,t}\), and \(\Pi _{1,t}\) are given in (15), (19), (20), and (23), respectively. Moreover, the optimal strategy given in (24) is admissible.

Proof

See Appendix A.7. \(\square \)

4 Static and dynamic optimality of the problem

In this section, we derive the static and dynamic optimality of the mean-variance problem (8). The static optimal investment strategy and optimal value function (efficient frontier) of problem (8) are obtained by solving (9) and (11) in a backward sequence.

Specifically, based on the relationship between the mean-variance problem (8) and benchmark problem (11) as shown in (10), we have

$$\begin{aligned} \begin{aligned}&V_{MV}(t_{0},\alpha _{0},r_{0},x_{0})\\&\quad =\max _{\theta \in \mathbb {R}}J(\alpha _{0},r_{0},x_{0};\pi ^{*},\xi -\theta )-\theta ^{2}\\&\quad = \max _{\theta \in \mathbb {R}}\bigg \{\left[ \exp \left\{ b(t_{0})\alpha _{0}+2g(t_{0})\right\} \phi (t_{0})-1\right] \theta ^{2}\\&\qquad + 2\exp \left\{ (a(t_{0})+h(t_{0}))r_{0}+b(t_{0})\alpha _{0}+g(t_{0})\right\} \phi (t_{0})\left( x_{0}-\xi e^{g(t_{0})+h(t_{0})r_{0}}\right) \theta \\&\qquad + \exp \left\{ a(t_{0})r_{0}+b(t_{0})\alpha _{0}\right\} \phi (t_{0})\left( x_{0}-\xi e^{g(t_{0})+h(t_{0})r_{0}}\right) ^{2}\bigg \}. \end{aligned}\nonumber \\ \end{aligned}$$
(27)

It can be easily checked that the leading coefficient of the above quadratic function of \(\theta \) is negative, i.e,

$$\begin{aligned} \begin{aligned} \exp \left\{ b(t_{0})\alpha _{0}+2g(t_{0})\right\} \phi (t_{0})<\exp \left\{ -\int _{t_{0}}^{T}\left( \frac{a(t)\sigma _{r}}{2}-\lambda _{r}\right) ^{2}\,dt\right\} \le 1, \end{aligned} \end{aligned}$$

where the strict inequality follows from the negativeness of function b(t) implied by Proposition 3.8. As such, the maximum of the right-hand side of (27) is attained at

$$\begin{aligned} \theta ^{*} = \frac{\exp \left\{ (a(t_{0})+h(t_{0}))r_{0}+b(t_{0})\alpha _{0}+g(t_{0})\right\} \phi (t_{0})\left( \xi e^{g(t_{0})+h(t_{0})r_{0}}-x_{0}\right) }{\exp \left\{ b(t_{0})\alpha _{0}+2g(t_{0})\right\} \phi (t_{0})-1}.\nonumber \\ \end{aligned}$$
(28)

Now we are ready to state our second main result.

Theorem 4.1

Suppose that Assumption 3.4 holds true. For any initial data \((t_{0},\alpha _{0},r_{0},x_{0})\in [0,T)\otimes \mathbb {R}^{+}\otimes \mathbb {R}\otimes \mathbb {R}\) fixed and given, the static optimal investment strategy of the mean-variance problem (8) is given by

$$\begin{aligned} \left\{ \begin{aligned} \pi ^{*}_{S^{1}}(t,\alpha _{t},r_{t},X^{*}_{t}) =&\, -\frac{\left( X^{*}_{t}-(\xi -\theta ^{*})e^{g(t)+h(t)r_{t}}\right) (\lambda +\sigma _{\alpha }\rho b(t))\sqrt{\alpha _{t}}}{\sigma (t,\alpha _{t})},\\ \pi ^{*}_{B}(t,\alpha _{t},r_{t},X^{*}_{t}) =&\,-\frac{(X^{*}_{t}-(\xi -\theta ^{*})e^{g(t)+h(t)r_{t}})(\lambda _{r}-\sigma _{r}a(t))+(\xi -\theta ^{*})\sigma _{r}h(t)e^{g(t)+h(t)r_{t}}}{h_{0}(K)\sigma _{r}}\\&-\frac{\pi ^{*}_{S^{1}}(t,\alpha _{t},r_{t},X^{*}_{t})\eta _{r}}{h_{0}(K)}, \end{aligned} \right. \end{aligned}$$
(29)

where \(\theta ^{*}\) is given by (28), and g(t), h(t), a(t),  and b(t) are given by (15), (19), and (20), respectively. The optimal value function (efficient frontier) is given by

$$\begin{aligned} V_{MV}(t_{0},\alpha _{0},r_{0},x_{0})= \frac{\exp \left\{ a(t_{0})r_{0}+b(t_{0})\alpha _{0}\right\} \phi (t_{0})\left( x_{0}-\xi e^{g(t_{0})+h(t_{0})r_{0}}\right) ^{2}}{1-\exp \left\{ b(t_{0})\alpha _{0}+2g(t_{0})\right\} \phi (t_{0})}, \end{aligned}$$
(30)

and the wealth process \(X^{*}_{t}\) associated with (29) evolves according to

$$\begin{aligned} \begin{aligned} X^{*}_{t} =&\, \left( x_{0}-(\xi -\theta ^{*})e^{g(t_{0})+h(t_{0})r_{0}}\right) \\&\exp \left\{ \int _{t_{0}}^{t}r_{s}-(\lambda _{r}^{2}-\lambda _{r}\sigma _{r}a(s))-(\lambda ^{2}+\lambda \sigma _{\alpha }\rho b(s))\alpha _{s}\,ds\right\} \\&\times \Pi _{0,t}\Pi _{1,t}+(\xi -\theta ^{*}) e^{g(t)+h(t)r_{t}}, \end{aligned} \end{aligned}$$
(31)

where \(\Pi _{0,t}\) and \(\Pi _{1,t}\) are given by (23). Moreover, the static optimality (29) is admissible.

Proof

Replacing the constant \(\gamma \) in (24) and (26) by \(\xi -\theta ^{*}\) leads to the static optimal strategy (29) and the associated wealth process (31), respectively. Plugging \(\theta ^{*}\) given in (28) back into the right-hand side of (27) yields the optimal value function (30). Moreover, following the Proof of Proposition 3.11, it is evident that the static optimal strategy (29) is admissible, i.e., \(\pi ^{*}\in {\mathcal {A}}\). \(\square \)

The next corollary provides the explicit results for one special case of our model, the 4/2 stochastic volatility model.

Corollary 4.2

(The 4/2 model) Suppose that Assumption 3.4 holds true. If the risky asset price \(S^{1}_{t}\) follows the 4/2 model (6), then the static optimal investment strategy and optimal value function of the mean-variance problem (8) are, respectively, given by

$$\begin{aligned} \left\{ \begin{aligned} \pi ^{*}_{B}(t,V_{t},r_{t},X^{*}_{t}) =&\,-\frac{(X^{*}_{t}-(\xi -\theta ^{*})e^{g(t)+h(t)r_{t}})(\lambda _{r}-\sigma _{r}a(t))+(\xi -\theta ^{*})\sigma _{r}h(t)e^{g(t)+h(t)r_{t}}}{h_{0}(K)\sigma _{r}}\\&-\frac{\pi ^{*}_{S^{1}}(t,V_{t},r_{t},X^{*}_{t})\eta _{r}}{h_{0}(K)},\\ \pi ^{*}_{S^{1}}(t,V_{t},r_{t},X^{*}_{t}) =&\, -\frac{\left( X^{*}_{t}-(\xi -\theta ^{*})e^{g(t)+h(t)r_{t}}\right) (\lambda +\sigma _{\alpha }\rho b(t))\sqrt{V_{t}}}{c_{1}\sqrt{V_{t}}+\frac{c_{2}}{\sqrt{V_{t}}}}, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} V_{MV}(t_{0},v_{0},r_{0},x_{0}) = \frac{\exp \left\{ a(t_{0})r_{0}+b(t_{0})v_{0}\right\} \phi (t_{0})\left( x_{0}-\xi e^{g(t_{0})+h(t_{0})r_{0}}\right) ^{2}}{1-\exp \left\{ b(t_{0})v_{0}+2g(t_{0})\right\} \phi (t_{0})}. \end{aligned}$$

Proof

Plugging the specified parameters of the 4/2 model (6) given in Example 1 into (29)–(30) leads to the above results. \(\square \)

Remark 5

If we further specify \((c_{1},c_{2})=(1,0)\) and \((c_{1},c_{2})=(0,1)\) in Corollary 4.2, explicit solutions to the embedded Heston model and 3/2 stochastic volatility model are derived, respectively. To the best of our knowledge, there is no existing literature on the portfolio selection problems reporting the above results for the hybrid Vasicek-4/2 model under the mean-variance criterion.

As discussed in Sect. 2, the static optimal investment strategy given in Theorem 4.1 is time-inconsistent because it depends on the initial value of the state variables via \(\theta ^{*}\), and thus, the mean-variance investor might deviate from it whenever any new position at a future time is arrived at. Now, we proceed to derive the dynamic optimality of the mean-variance problem (8) within the framework championed by Pedersen and Peskir (2017), which is the third main result of this paper.

Theorem 4.3

Suppose that Assumption 3.4 holds true. For any initial data \((t_{0},\alpha _{0},r_{0},x_{0})\in [0,T)\otimes \mathbb {R}^{+}\otimes \mathbb {R}\otimes \mathbb {R}\) fixed and given, the dynamic optimal investment strategy \(\pi ^{d*}\) of the mean-variance problem (8) is given by

$$\begin{aligned} \left\{ \begin{aligned} \pi _{S^{1}}^{d*}(t,\alpha _{t},r_{t},X^{d*}_{t}) =&\,\frac{\left( X^{d*}_{t}-\xi e^{g(t)+h(t)r_{t}}\right) (\lambda +\sigma _{\alpha }\rho b(t))\sqrt{\alpha _{t}}}{(\exp \left\{ b(t)\alpha _{t}+2g(t)\right\} \phi (t)-1)\sigma (t,\alpha _{t})},\\ \pi _{B}^{d*}(t,\alpha _{t},r_{t},X^{d*}_{t}) =&\,\frac{X^{d*}_{t}\left( \lambda _{r}-\sigma _{r}a(t)-\exp \left\{ b(t)\alpha _{t}+2g(t)\right\} \phi (t)h(t)\sigma _{r}\right) }{(\exp \left\{ b(t)\alpha _{t}+2g(t)\right\} \phi (t)-1)h_{0}(K)\sigma _{r}}\\&-\frac{\xi e^{g(t)+h(t)r_{t}}\left( \lambda _{r}+h(t)\sigma _{r}\right) }{(\exp \left\{ b(t)\alpha _{t}+2g(t)\right\} \phi (t)-1)h_{0}(K)\sigma _{r}}\\&-\frac{\pi ^{d*}_{S^{1}}(t,\alpha _{t},r_{t},X^{d*}_{t})\eta _{r}}{h_{0}(K)}, \end{aligned} \right. \end{aligned}$$
(32)

where \(X^{d*}_{t}\) is the wealth process associated with \(\pi ^{d*}\) and evolves according to

$$\begin{aligned} \begin{aligned} X^{d*}_{t}=&\,\xi e^{g(t)+h(t)r_{t}}+\exp \left\{ \int _{t_{0}}^{t}\Bigg [\frac{\lambda _{r}\left( \lambda _{r}-\exp \left\{ b(u)\alpha _{u}+2g(u)\right\} \phi (u)h(u)\sigma _{r}-\sigma _{r}a(u)\right) }{\exp \left\{ b(u)\alpha _{u}+2g(u)\right\} \phi (u)-1}\right. \\&\left. +\frac{(\lambda +\sigma _{\alpha }\rho b(u))\lambda \alpha _{u}}{\exp \left\{ b(u)\alpha _{u}+2g(u)\right\} \phi (u)-1}+r_{u}\Bigg ]\,du\right\} \Pi _{2,t}\Pi _{3,t}\left( x_{0}-\xi e^{g(t_{0})+h(t_{0})r_{0}}\right) , \end{aligned}\nonumber \\ \end{aligned}$$
(33)

with \(\Pi _{2,t}\) and \(\Pi _{3,t}\) given by

$$\begin{aligned} \left\{ \begin{aligned} \Pi _{2,t}=&\,\exp \left\{ \int _{t_{0}}^{t}\frac{(\lambda +\sigma _{\alpha }\rho b(u))\sqrt{\alpha _{u}}}{\exp \left\{ b(u)\alpha _{u}+2g(u)\right\} \phi (u)-1}\,dW^{1}_{u}\right. \\&\left. -\frac{1}{2}\int _{t_{0}}^{t}\frac{(\lambda +\sigma _{\alpha }\rho b(u))^{2}\alpha _{u}}{\left( \exp \left\{ b(u)\alpha _{u}+2g(u)\right\} \phi (u)-1\right) ^{2}}\,du\right\} ,\\ \Pi _{3,t}=&\,\exp \left\{ \int _{t_{0}}^{t}\frac{\lambda _{r}-\sigma _{r}a(u)-\exp \left\{ b(u)\alpha _{u}+2g(u)\right\} \phi (u)h(u)\sigma _{r}}{\exp \left\{ b(u)\alpha _{u}+2g(u)\right\} \phi (u)-1}\,dW^{0}_{u}\right. \\&\left. -\frac{1}{2}\int _{t_{0}}^{t}\frac{(\lambda _{r}-\sigma _{r}a(u)-\exp \left\{ b(u)\alpha _{u}+2g(u)\right\} \phi (u)h(u)\sigma _{r})^{2}}{(\exp \left\{ b(u)\alpha _{u}+2g(u)\right\} \phi (u)-1)^{2}}\,du\right\} . \end{aligned} \right. \end{aligned}$$

Furthermore, if the initial data satisfies \(x_{0}\le \xi e^{g(t_{0})+h(t_{0})r_{0}}\), then it holds that \(X^{d*}_{t}\le \xi e^{g(t)+h(t)r_{t}}\), \(\mathrm{P}_{t_{0}}\) almost surely.

Proof

See Appendix A.8. \(\square \)

Corollary 4.4

(The 4/2 model) Suppose that Assumption 3.4 holds true. If the risky asset price \(S^{1}_{t}\) follows the 4/2 model (6), then the dynamic optimal investment strategy \(\pi ^{d*}\) of the mean-variance problem (8) is given by

$$\begin{aligned} \left\{ \begin{aligned} \pi _{S^{1}}^{d*}(t,V_{t},r_{t},X^{d*}_{t}) =&\,\frac{\left( X^{d*}_{t}-\xi e^{g(t)+h(t)r_{t}}\right) (\lambda +\sigma _{\alpha }\rho b(t))V_{t}}{(\exp \left\{ b(t)V_{t}+2g(t)\right\} \phi (t)-1)(c_{1}V_{t}+c_{2})},\\ \pi _{B}^{d*}(t,V_{t},r_{t},X^{d*}_{t}) =&\,\frac{X^{d*}_{t}\left( \lambda _{r}-\sigma _{r}a(t)-\exp \left\{ b(t)V_{t}+2g(t)\right\} \phi (t)h(t)\sigma _{r}\right) }{(\exp \left\{ b(t)V_{t}+2g(t)\right\} \phi (t)-1)h_{0}(K)\sigma _{r}}\\&-\frac{\xi e^{g(t)+h(t)r_{t}}\left( \lambda _{r}+h(t)\sigma _{r}\right) }{(\exp \left\{ b(t)V_{t}+2g(t)\right\} \phi (t)-1)h_{0}(K)\sigma _{r}}\\&-\frac{\pi ^{d*}_{S^{1}}(t,V_{t},r_{t},X^{d*}_{t})\eta _{r}}{h_{0}(K)}, \end{aligned} \right. \end{aligned}$$

where the wealth process \(X^{d*}_{t}\) satisfies that \(X^{d*}_{t}\le \xi e^{g(t)+h(t)r_{t}}\), for \(t\in [t_{0},T]\), \(\mathrm{P}_{t_{0}}\) almost surely.

Proof

Substituting the specified parameters of the 4/2 model (6) given in Example 1 into (32) yields the results immediately. \(\square \)

Remark 6

Setting either \((c_{1},c_{2})=(1,0)\) or \((c_{1},c_{2})=(0,1)\) in Corollary 4.4, we provide the closed-form expressions for the dynamic optimal strategies under the Heston model and 3/2 model, respectively.

5 Numerical analysis

This section investigates the impact of the model parameters on the efficient frontier and the static and dynamic optimal investment strategies. The formula of efficient frontier is given by (30) and the closed-form expressions for the static and dynamic optimality are presented in (29) and (32), respectively. We show the case when the market model is characterized by the hybrid Vasicek-Heston model. Throughout this section, unless otherwise stated, the values of the parameters modified from Escobar et al. (2017) are listed below: \(a=0.0125,b=0.266,\sigma _{r}=0.013,\lambda _{r}=0.689,\eta _{r}=0.4,\lambda =2.234,\kappa =2.115,\theta =0.051,\sigma _{\alpha }=0.505,\rho =-0.514,x_{0}=1,r_{0}=0.05,v_{0}=0.03,T=1,\xi =3,K=20\).

5.1 Efficient frontier

In this subsection, we present how the model parameters affect the efficient frontier. In the following numerical experiments, we vary the value of one parameter with others fixed and given.

Figure 1 contributes to the impact of parameters \(\lambda _{r},a,\) and \(\eta _{r}\) on the efficient frontier. We observe from Fig. 1a that given the fixed expected value of terminal wealth, the efficient frontier moves downwards as \(\lambda _{r}\) increases from 0.689 to 0.889. Since \(\lambda _{r}\) characterizes the market price of interest rate risk, a greater value of \(\lambda _{r}\) implies that the investor can obtain higher returns by investing in the roll-over bond. As such, the investor can take fewer risks from the market if he wants to gain the same expected wealth at the terminal date. Figure 1b shows the relationship between the efficient frontier and parameter a. We find that along with the growth of a, the variance of terminal wealth decreases. As revealed by (1), parameter a partially depicts the long-run mean of the short interest rate. As a increases, the return rate of the risk-free asset becomes higher, while the risk premiums of investing in both the roll-over bond and the risky asset are not influenced. In such a case, the investor can bear fewer risks if the same expected terminal wealth is acquired. From Fig. 1c, we find that the scale parameter \(\eta _{r}\) has no impact on the efficient frontier. This is consistent with our intuition that although \(\eta _{r}\) changes the optimal allocations on the roll-over bond and risky asset, the optimal risk exposures to the interest rate and volatility risks remain unchanged. Therefore, the investor undertakes the same investment risks, and he has the same variance of terminal wealth if he acquires the same expected terminal wealth.

Fig. 1
figure 1

Impact of parameters \(\lambda _{r},a,\) and \(\eta _{r}\) on the efficient frontier

Full size image

Figure 2 reveals the relationship between the efficient frontier and parameters \(\lambda ,\sigma _{\alpha },\) and \(\rho \). From Fig. 2a, we find that the efficient frontier moves down as \(\lambda \) increases from 2.234 to 3.234. \(\lambda \) characterizes the slope of the market price of volatility risk. So, along with the growth of \(\lambda \), the investor can obtain a higher volatility risk premium. In such a case, the investor can invest less in the risky asset to obtain the same expected terminal wealth. In Fig. 2b, we vary \(\sigma _{\alpha }\) from 0.505 to 0.705, and find that the efficient frontier moves down. In other words, as \(\sigma _{\alpha }\) increases, to derive a fixed expected terminal wealth, the investor will undertake fewer risks. One explanation is that as the volatility of volatility \(\sigma _{\alpha }\) increases, the fluctuation of the stochastic volatility becomes larger, and thus, the return rate of the risky asset is more likely to increase, which helps the investor derive the same expected return by investing less in the risky asset and hence bearing fewer risks. In Fig. 2c, we vary \(\rho \) from \(-0.314\) to \(-0.714\), and find that the efficient frontier moves down. This can be explained by the fact that as the correlation parameter \(\rho \) approaches \(-1\), the risky asset price and its instantaneous variance become more negatively correlated. Therefore, the offset between the risk caused by fluctuations of the risky asset price and its volatility becomes more. Consequently, investing the same amount in the risky asset reduces the investor’s exposure to volatility risk.

Fig. 2
figure 2

Impact of parameters \(\lambda ,\sigma _{\alpha },\) and \(\rho \) on the efficient frontier

Full size image

5.2 Static and dynamic optimal strategies

In this subsection, we investigate the impact of some model parameters and the fixed expected terminal wealth \(\xi \) on the behavior of the static and dynamic optimal investment strategies. For simplicity, we pay attention to the results at time \(t_{0}=0\) in the following numerical experiments. From the definition of dynamic optimality above (see Definition 3), we know that \(\pi ^{*}=\pi ^{d*}\) at the initial time \(t_{0}\).

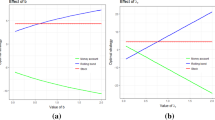
Figure 3 illustrates the relationship between the parameters \(\lambda _{r},a,\) and \(\eta _{r}\) on the dynamic and static optimal investment strategies. In Fig. 3a, we vary \(\lambda _{r}\) from 0.689 to 0.889 and find that the market value of wealth invested in the roll-over bond is positively correlated with \(\lambda _{r}\), while the investment in the risky asset is negatively correlated with \(\lambda _{r}\). As the previous section explains, as the market price of interest rate risk \(\lambda _{r}\) increases, the investor can obtain a higher risk premium from investing in the roll-over bond. It is thus better to allocate more in the roll-over bond to reduce the overall risks when the same expected terminal wealth is acquired. Figure 3b shows that the amount of wealth invested in both the roll-over bond and the risky asset decreases as a increases from 0.125 to 0.25. Indeed, as a becomes larger, the long-run level of the short rate a/b increases, such that the return rate of the risk-free asset is amplified. Hence, the investor can undertake fewer risks by investing more in the risk-free asset. It is shown from Fig. 3c that as \(\eta _{r}\) increases from 0 to 1, the amount of wealth invested in the roll-bond is reduced, while the investment in the risky asset remains unchanged. As a matter of fact, the overall interest rate and volatility risks are not changed when \(\eta _{r}\) varies since it only measures the impact of the interest rate dynamics on the risky asset price. Namely, when \(\eta _{r}\) becomes larger, the investor faces the same amount of volatility and interest rate risks, but the interest rate risk can be more easily hedged against by investing in the risky asset.

Fig. 3
figure 3

Impact of parameters \(\lambda _{r},a,\) and \(\eta _{r}\) on the dynamic and static optimality

Full size image
Fig. 4
figure 4

Impact of parameters \(\lambda ,\sigma _{\alpha },\) and \(\xi \) on the dynamic and static optimality

Full size image

Figure 4 shows how the dynamic and static optimal investment strategies change with respect to the parameters \(\lambda ,\sigma _{\alpha },\) and \(\xi \). From Fig. 4a, we find that as \(\lambda \) increases, the investor is willing to invest more in the risky asset and less in the roll-over bond. This can be explained by the fact that \(\lambda \) characterizes the slope of the market price of volatility risk, and the investor can derive a higher risk premium from the risky asset as \(\lambda \) becomes larger. In Fig. 4b, we vary \(\sigma _{\alpha }\) from 0.505 to 0.905 and find that the amount of wealth invested in the risky asset becomes larger as \(\sigma _{\alpha }\) increases. One of the possible explanations is that as the volatility of volatility \(\sigma _{\alpha }\) increases, it is more likely for the investor to derive a higher volatility risk premium from the risky asset, i.e., \(\lambda \sqrt{V_{t}}\). In such a case, the investor tends to adopt a more aggressive investment strategy. In the meantime, since the optimal risk exposure to the interest rate risk is not affected by the change of \(\sigma _{\alpha }\), the investor can invest less in the roll-over bond to hedge against the interest rate risk due to the stochastic correlation between interest rate and risky asset price. Finally, we see from Fig. 4c that the amount of wealth invested in the roll-over bond and the risky asset has a positive relationship with the expected terminal value \(\xi \). This is consistent with our intuition that to obtain a greater value of the expected terminal wealth, the investor has to invest more in both the roll-over bond and the risky asset such that the overall interest rate and volatility risks can be hedged against.

To end this subsection, we highlight the difference between static and dynamic optimality, i.e., \(\pi ^{*}\) and \(\pi ^{d*}\). By setting 500 equidistant time points over the investment horizon [0, 1] and using some Monte Carlo techniques, we simulate two paths of \(X^{*}_{t}\) and \(X^{d*}_{t}\), as well as one path of the stochastic process \(\xi e^{g(t)+h(t)r_{t}}\), which is referred to as the bound in Fig. 5. As shown in Fig. 5, the trajectories of two optimal wealth processes \(X^{*}_{t}\) and \(X^{d*}_{t}\) are significantly different even though the same random numbers are used. In particular, we observe that the dynamic optimal wealth process \(X^{d*}_{t}\) is strictly below the process \(\xi e^{g(t)+h(t)r_{t}}\), which is consistent with the theoretical results derived in Theorem 4.3 above.

Fig. 5
figure 5

Two trajectories of static and dynamic optimality

Full size image

6 Conclusion

In this paper, we consider dynamic mean-variance portfolio selection problems in a stochastic environment. The risks in the market come from the interest rate and the risky asset. The interest rate follows the Vasicek model while the risky asset’s return rate not only relies on a CIR process but also exhibits stochastic covariance with the interest rate. The modeling framework embraces the family of the state-of-the-art 4/2 stochastic volatility models, as an exceptional case. Given the time inconsistency of the mean-variance criterion, the problems are investigated in line with the dynamic optimal approach. For this, we first address the static optimal (time-inconsistent) strategy by using a BSDE approach. Under the assumption of some model parameters, the associated BSDEs are solved explicitly. Analytical expressions for the static optimality and optimal value function (efficient frontier) are derived via the explicit solutions to the BSDEs. By recomputing the static optimality in an infinitesimally small period of time, we derive, in closed form, the dynamic optimal (time-consistent) strategy. Moreover, results on the Vasicek-Heston, Vasicek-3/2, and Vasicek-4/2 models are provided, as particular cases. Finally, the economic impact of some model parameters on the efficient frontier as well as on the static and dynamic optimal asset allocations is illustrated with numerical examples. As far as we know, there is no existing literature on the mean-variance portfolio selection problems considering the time-inconsistent and time-consistent solutions in the presence of stochastic volatility and interest rate. So, this study is meaningful from both theoretical and practical perspectives.

Built on the present paper, several potential topics in the future may be followed; for instance, one may extend the current framework with a single risky asset to that with multiple risky assets. In addition, since it is difficult to estimate the return rate of the risky asset and interest rate with precision in practice, the investor might be ambiguous about the financial market. It is thus of interest to explore the mean-variance portfolio selection problems with stochastic interest rate and volatility under model ambiguity.