1 Introduction

Over the past two decades, a remarkable progress has been made in the field of biotechnology, biomedical and bio-chemical processes, attributed primarily to the rapid advancement of microfluidic technology (Stone et al. 2004; Li and Zhou 2013). Pertaining to the applications mentioned above, the conjugation of microfluidic technology has offered a few distinctive beneficial features, which include a reduction in reagent/sample volume, decreasing the analysis time, increasing sensitivity, augmented specificity, etc. It may be mentioned here that various flow actuation mechanisms have already established their pertinence to transport liquid in microfluidic set-up namely, electric field modulated transport (Devasenathipathy et al. 2002; Mondal et al. 2015; Gaikwad et al. 2016; Abhimanyu et al. 2016; Gaikwad and Mondal 2017), pressure-driven flow (Chen et al. 2004), thermocapillary actuated transport (DasGupta et al. 2014; Mondal and Chaudhry 2018), magnetic field-induced flow (Gorthi et al. 2017), surface tension driven transport (Gaikwad et al. 2020a, b; Gorthi et al. 2019). Among these, flow actuation parameter consistent with the combined influences of applied pressure gradient and electric field has gained huge prominence at the microfluidic scale (Shuai et al. 2022; Jiali et al. 2022) owing to its capability of ensuring better dispersion, finer control over the underlying flow.

Most of the biological fluids exhibit non-Newtonian behavior and as witnessed in the reported literature (Cho and Kensey 1991), several constitutive laws have been used to characterize their non-Newtonian rheology as well (Goswami et al. 2015; Siva et al. 2020; Mehta et al. 2021; Gaikwad et al. 2019a; Anantha et al. 2018a; Anantha et al. 2019; Ventaka et al. 2021).The Carreau fluid model (Carreau et al. 1979), established as the most commonly used non-Newtonian model in describing several biofluids (Zhao and Yang 2011), offers flexibility in describing the fluid rheological behavior at relatively high shear rates. In particular, this rheological model describes the accurate physical behavior of inelastic non-Newtonian fluids as compared to the power-law model in regions where the shear rate tends to be zero. The solution of transport equations governing the flow dynamics of non-Newtonian fluids even in the paradigm of microscale transport, typically known as low Reynolds number flows, is analytically intractable, attributed primarily to involved non-linearity stemming from the constitutive laws (Chaffin and Rees 2018; Jing et al. 2019; Sun et al. 2021). The underlying solution process becomes even more convoluted pertaining to the transportation of rheological fluid under the combined influences of electric field and applied pressure gradient (Gaikwad et al. 2016b). Accounting for this inevitable complexity in solving applied field-driven flows (precisely, the transport equations) using the analytical framework, researchers have mostly focused on several numerical methods for describing the flow field of non-Newtonian fluids (Gaikwad et al. 2016, 2018, 2019b; Ferrás et al. 2016). Albeit the solution of the transport equations governing the flow dynamics of non-Newtonian fluids using analytical/semi-analytical tools is deemed to be of demanding importance in the arena of micro/nanofluidics, this endeavor is indeed scarce in the open literature.

In the present work, we demonstrate a semi-analytical formalism, consistent with the perturbation method, to describe the flow dynamics of non-Newtonian fluid driven by the combined effects of applied electric field and pressure gradient in a microchannel. We here consider the Carreau fluid model to describe the rheology of the non-Newtonian fluid. The deviatoric stress tensor of the Carreau fluid model reads as (Johnston et al. 2004)

$${\varvec{\tau}}=\mu \left(\dot{\gamma }\right)\left[\nabla {\varvec{U}}+{\left(\nabla {\varvec{U}}\right)}^{T}\right],$$
(1)

with \(\mu \left(\dot{\gamma }\right)={\mu }_{\infty }+\left({\mu }_{0}-{\mu }_{\infty }\right){\left(1+{\left(\lambda \dot{\gamma }\right)}^{2}\right)}^{\frac{n-1}{2}},\) where \(\mu (\dot{\gamma })\) is the apparent viscosity; \(\dot{\gamma }=\left(\sqrt{(1/2){\varvec{S}}:{\varvec{S}}}\right)\) is the invariant rate of deformation tensor with strain rate tensor \({\varvec{S}}=[\nabla \varvec{U}+{\left(\nabla \varvec{U}\right)}^{{T}}]\); \({\mu }_{\infty }\) is the infinite-shear rate viscosity and \({\mu }_{0}\) is the zero-shear rate viscosity. The parameter \(n\) represents the degree of shear-thinning, while the parameter \(\lambda\) is a time constant which indicates the onset of the shear-thinning behavior. It is worth mentioning here that the method proposed here is capable of providing flow-field distribution of Carreau fluid for any values, including non-integers, of parameter \(n\) without requiring time-consuming and complex computational simulations. This part, although remained unexplored in the literature until present endeavor, is unique pertaining to the field-driven transport of non-Newtonian Carreau fluid at microfluidic scale.

2 Problem formulation

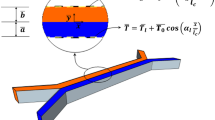
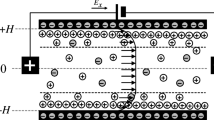
We consider hydrodynamically fully developed, laminar, incompressible flow of an inelastic non-Newtonian fluid (electrolyte) through a microchannel of height 2H. As mentioned in Eq. (1), we consider the Carreau model to represent the rheology of inelastic non-Newtonian fluid in this analysis. The flow is driven by the combined effects of both applied pressure gradient and electroosmosis. The geometry and coordinate system of microchannel is shown in Fig. 1. The length and width of the channel are sufficiently larger than the height of the channel. The channel walls are considered to bear a net charge as manifested in terms of surface potential \({\psi }^{^{\prime}}\), which leads to the formation of the electrical double layer (EDL) in contact with ionic liquid (Masliyah and Bhattacharjee 2006). The externally applied electric field \({E}_{x}\) along the axial direction sets in the underlying flow of the chosen fluid by virtue of electroosmosis. Below, in sub-section A, we write the momentum transport equations in their generic form. However, in sub-sections B–C, the transport equations are written in their reduced form pertinent to the assumptions made above together with the case of non-overlapping EDLs and uniform surface potential.

Fig. 1
figure 1

Schematic diagram showing the flow configuration. Flow takes place along the x direction under the combined influences of applied pressure gradient and electroosmosis. The coordinate system is attached at the left center of the channel

Full size image

2.1 Transport equations

We begin with the full set of momentum transport equations as written below.

Continuity equation:

$$\nabla \cdot {\varvec{U}} = 0.$$
(2)

Momentum equation:

$$\rho \left(\frac{\partial {\varvec{U}}}{\partial t}+{\varvec{U}}\cdot \nabla \varvec{U}\right)=-\nabla {p}+\nabla \cdot {\varvec{\tau}}+{\varvec{F}},$$
(3)

where \({\varvec{U}}\) is the velocity vector, \({p}\) is the fluid pressure, \(\rho\) is the fluid density, \({\varvec{F}}\) is the electroosmotic body force per unit volume. Note that \({\varvec{\tau}}\) in Eq. (3) is the stress tensor, and its expression following the constitutive behavior of the Carreau model is already described in Eq. (1).

2.2 Electric double-layer phenomenon: development of induced potential

For the description of induced potential due to interfacial electrochemical interaction, we invoke the Poisson–Boltzmann equation in this analysis. Consistent with the one-dimensional form of the Poisson–Boltzmann equation, the EDL potential distribution \({\psi }^{^{\prime}}\left(y\right)\) pertaining to the problems considered here and for symmetric electrolyte using the Debye–Hückel approximation can be written as (Masliyah and Bhattacharjee 2006):

$$\frac{{d}^{2}{\psi }^{^{\prime}}}{d{y}^{2}}=-\frac{{\rho }_{e}}{\varepsilon }=\frac{2{n}_{0}ez}{\varepsilon }\left(\frac{ez{\psi }^{^{\prime}}}{{T}_{0}{k}_{B}}\right),$$
(4)

where \(e, z, {n}_{0} ,\varepsilon , {T}_{0}\) and \({k}_{B}\) signify the single electron charge, valence number of ions, bulk ionic concentration, electric permittivity, reference temperature and Boltzmann constant, respectively.

Introducing non-dimensional number \(Y=\frac{y}{H}\) and \(\psi =\frac{ze{\psi }^{^{\prime}}}{{k}_{B}{T}_{0}}\); we can write Eq. (4) in the following form as

$$\frac{{d}^{2}\psi }{d{Y}^{2}}={\overline{\kappa }}^{2}\psi .$$
(5)

Here, \(\kappa \left(=\sqrt{\frac{2{n}_{0}{e}^{2}{z}^{2}}{\varepsilon {k}_{B}{T}_{0}}}\right)\) and inverse of this quantity, i.e., \({\kappa }^{-1}={\lambda }_{D}\) is the characteristic EDL thickness (also, known as the Debye length). Note that \(\overline{\kappa }=\kappa H\) is the dimensionless EDL thickness (Soong et al. 2010). In order to solve Eq. (5), we employ the following boundary conditions.

$$Y=0,\frac{d\psi }{dY}=0, \,\mathrm{and}\, \psi =0.$$
(6)

Note that the boundary condition in Eq. (6) is justified due to symmetry and non-overlapping EDL situation. Hence, Eq. (5) can be simplified as:

$$\psi \left(Y\right)=\zeta \frac{\mathrm{cosh}\left(\overline{\kappa }Y\right)}{\mathrm{cosh}\overline{\kappa }},$$
(7)

where \(\zeta\) is the zeta potential.

2.3 Description of flow field

In a steady-state and hydrodynamically fully developed flow, the momentum equation [Eq. 3] pertinent to present problem can be written as

$$\frac{d\left({\tau }_{xy}\right)}{dy} = - \frac{dp}{ dx}+{F}_{x}.$$
(8)

Note that \({F}_{x}\) in Eq. (8) includes the forcing due to the electroosmotic effect. Pertaining to the present flow scenario, the electroosmotic body force can be written in the following form (Sarma et al. 2018; Sadeghi and Saidi 2010):

$${F}_{x}={\rho }_{e}{E}_{x},$$
(9)

where \({E}_{x}\) is an applied external electric field along the \(x\) direction and \({\rho }_{e}\) is the net electric charge density (Gaikwad et al. 2016). For this case, the momentum transport equation (Eq. 8) can be written as

$$\frac{d\left({\tau }_{xy}\right)}{dy} = - \frac{dp}{ dx}+{\rho }_{e}{E}_{x}.$$
(10)

From Eq. (4), using \({\rho }_{e}=-\varepsilon \frac{{d}^{2}{\psi }^{^{\prime}}}{d{y}^{2}}\) in Eq. (10), we get

$$\frac{d\left({\tau }_{xy}\right)}{dy} = - \frac{dp}{ dx}-\varepsilon {E}_{x}\frac{{d}^{2}{\psi }^{^{\prime}}}{d{y}^{2}}.$$
(11)

From Eq. (1), the stress tensor \({\tau }_{xy}\) of Carreaufluidpertinent to the flow configuration considered in this analysis can be expressed as (Cho and Kensey 1991; Johnston et al. 2004):

$${\tau }_{xy}=\left[{\mu }_{\infty }+\left({\mu }_{0}-{\mu }_{\infty }\right){\left(1+{\left(\lambda \frac{du}{dy}\right)}^{2}\right)}^{\frac{n-1}{2}}\right]\left(-\frac{du}{dy}\right).$$
(12)

For the solution of Eq. (11), the following boundary conditions are used.\({\tau }_{xy}=0\) at \(y\) = 0 and \(u=0\) at \(y=H.\)

We invoke to the symmetric EDL potential condition and assuming the zero-shear stress at the center of the microchannel (Sarma et al. 2018), i.e., at \(y=0, {\tau }_{xy}=\frac{d{\psi }^{^{\prime}}}{dy}=0\) to obtain the solution of Eq. (10). Now, on integrating Eq. (11), we get,

$${\tau }_{xy}= - \frac{dp}{ dx}y-\varepsilon {E}_{x}\frac{d{\psi }^{^{\prime}}}{dy}.$$
(13)

On substituting Eq. (13) into Eq.  (12),we get the following:

$$-\frac{dp}{ dx}y-\varepsilon {E}_{x}\frac{d{\psi }^{^{\prime}}}{dy}=\left[{\mu }_{\infty }+\left({\mu }_{0}-{\mu }_{\infty }\right){\left(1+{\left(\lambda \frac{du}{dy}\right)}^{2}\right)}^{\frac{n-1}{2}}\right]\left(-\frac{du}{dy}\right).$$
(14)

Now by making use of the dimensionless numbers mentioned in Section II.B, the following non-dimensional numbers are defined as:

$$U = \frac{u}{{u_{HS} }},{\Gamma } = \lambda^{2} \frac{{u_{HS}^{2} }}{{H^{2} }}.$$
(15)

with \({u}_{HS}(=-\frac{\varepsilon {E}_{x}{k}_{B}{T}_{0}}{ze{\mu }_{0}} )\) as a Helmholtz–Smoluchowski velocity, the Eq. (14) can be simplified to the following:

$$- \frac{dp}{ dx}YH-\frac{\varepsilon {E}_{x}{k}_{B}{T}_{0}}{Hze}\frac{d\psi }{dY}=\frac{{\mu }_{\infty }{u}_{HS}}{H}\left(-\frac{dU}{dY}\right)+\frac{{u}_{HS}\left({\mu }_{0}-{\mu }_{\infty }\right)}{H}\left[{\left(1+{\Gamma \left(\frac{dU}{dY}\right)}^{2}\right)}^{\frac{n-1}{2}}\right]\left(-\frac{dU}{dY}\right).$$
(16)

3 Solution methodology

3.1 Semi-analytical solution

The non-dimensional form of the momentum transport equation governing the flow dynamics of the Carreau fluid as in Eq. (16), obtained under the framework of a few assumptions, is highly non-linear in nature. Hence, we look for the solutions for the velocity profile (and the corresponding flow rate) by using a semi-analytical framework consistent with the perturbation method. Following this method, the analytical solution for Carreau fluid flow in microchannel can be obtained by considering \(\Gamma ={\lambda }^{2}\frac{{u}_{HS}^{2}}{{H}^{2}}\) is small \(\left(\Gamma \ll 1\right)\) and \(\frac{{\mu }_{\infty }}{{\mu }_{0}}\ll 1\). We here take an effort to establish the typical values of these two quantities through their order of magnitude analysis as follows: For a channel height H~100 μm, which is typical to microfluidic configuration and \({u}_{HS}={10}^{-4}\,\mathrm{m}/s\) (Mukerjee et al. 2017; Hsieh and Yang 2006; Hsieh et al. 2016), we obtain the order of \(\Gamma \sim {10}^{-2}\) for a relaxation parameter \(\lambda =0.1\,\mathrm{s}\), the zero-shear rate viscosity \(\mu_{0} = 38.73\,{\text{Pa}} \cdot {\text{s}}\) and infinite-shear rate viscosity \(\mu_{\infty } = 0.05 \,{\text{Pa}} \cdot {\text{s}}\). Hence, the ratio of \(\frac{{\mu }_{\infty }}{{\mu }_{0}}\) for Carreau fluid becomes \({10}^{-3}\)(Sun et al. 2021). This order of magnitude analysis is justifiable for applying the perturbation method as employed here to solve the transport equation.

Consistent with the methodology employed here, the solution for flow velocity can be written in the form as written below.

$$U={U}_{0}+\Gamma {U}_{1}+O\left({\Gamma }^{2}\right).$$
(17)

Note that the leading order solution refers to the solution for the Newtonian fluid.

3.1.1 Zeroth-order solution

For \(\Gamma =0\), the corresponding \(U={U}_{0}\) is the solution of the following zeroth-order equation:

$$-\frac{dp}{ dx}YH-\frac{\varepsilon {E}_{x}{k}_{B}{T}_{0}}{Hze}\frac{d\psi }{dY}=-\frac{{\mu }_{0}{u}_{HS}}{H}\frac{d{U}_{0}}{dY}.$$
(18)

Equation(18) can be further simplified using the Eqs. (5) and (7) as:

$$-\frac{dp}{ dx}YH-\frac{\varepsilon {E}_{x}{k}_{B}{T}_{0}}{zeH}\overline{\kappa }\frac{\mathrm{sinh}\left(\overline{\kappa }\mathrm{Y}\right)}{\mathrm{cosh}\overline{\kappa }}=-\frac{{\mu }_{0}{u}_{HS}}{H}\frac{d{U}_{0}}{dY}.$$
(19)

Now, by defining \(A=-\frac{{ H}^{2}}{{\mu }_{0}{u}_{HS}}\frac{dp}{ dx}\), and for \({u}_{HS}=-\frac{\varepsilon {E}_{x}{k}_{B}{T}_{0}}{ze{\mu }_{0}}\); we can write Eq. (19) in the following form as given below.

$$-\frac{d{U}_{0}}{dY}=AY+\overline{\kappa }\frac{\mathrm{sinh}\left(\overline{\kappa }{Y}\right)}{\mathrm{cosh}\overline{\kappa }}.$$
(20)

Now, integrating Eq. (20), we get zeroth-order solution as follows:

$${U}_{0}=-A\frac{{Y}^{2}}{2}-\frac{\mathrm{cosh}\left(\overline{\kappa }{Y}\right)}{\mathrm{cosh}\overline{\kappa }}+{C}_{1}.$$
(21)

The constant of integration \({C}_{1}\) can be determined by the boundary conditions \(Y=1, {U}_{0}=0\).

Hence, the dimensionless zeroth-order velocity \({U}_{0}\) is obtained as:

$${U}_{0}=\frac{A}{2}\left({1-Y}^{2}\right)-\frac{\mathrm{cosh}\left(Y\overline{\kappa }\right)}{\mathrm{cosh}\left(\overline{\kappa }\right)}+1.$$
(22)

Henceforth, we remove overbar symbol from the dimensionless EDL thickness for the sake of convenience in writing only.

3.1.2 First-order solution

We next take an effort to obtain the solution of the first-order problem for small value of \(\Gamma\). In doing so, the first-order solution \(\left(U={U}_{0}+\Gamma {U}_{1}\right)\) is substituted into Eq. (19). We consider the non-linear part of Eq. (19), which reads as

$$N\left(\Gamma \right)=\left[{\left(1+{\Gamma \left(\frac{d\left({U}_{0}+\Gamma {U}_{1}\right)}{dY}\right)}^{2}\right)}^{\frac{n-1}{2}}\right]\left(-\frac{d\left({U}_{0}+\Gamma {U}_{1}\right)}{dY}\right).$$
(23)

Denoting:

$${N}_{1}\left(\Gamma \right)={\left(1+{\Gamma \left(\frac{d{U}_{0}}{dY}\right)}^{2}+2{\Gamma }^{2}\frac{d{U}_{0}}{dY}\frac{d{U}_{1}}{dY}+{\Gamma }^{3}{\left(\frac{d{U}_{1}}{dY}\right)}^{2}\right)}^{\frac{n-1}{2}}.$$
(24a)

Linearization of Eq. (24a) yields:

$${N}_{1}\left(\Gamma \right)\approx {N}_{1}\left(\Gamma =0\right)+{\left.\frac{d{N}_{1}\left(\Gamma \right)}{d\Gamma }\right|}_{\Gamma =0}\Gamma +\dots$$
$$=1+\frac{\left(n-1\right)}{2}{{\left[1+{\Gamma \left(\frac{d{U}_{0}}{dY}\right)}^{2}+2{\Gamma }^{2}\frac{d{U}_{0}}{dY}\frac{d{U}_{1}}{dY}+{\Gamma }^{3}{\left(\frac{d{U}_{1}}{dY}\right)}^{2}\right]}_{\Gamma =0}}^{\frac{n-3}{2}}{\left[{\left(\frac{d{U}_{0}}{dY}\right)}^{2}+4\Gamma \frac{d{U}_{0}}{dY}\frac{d{U}_{1}}{dY}+ {3\Gamma }^{2}{\left(\frac{d{U}_{1}}{dY}\right)}^{2}\right]}_{\Gamma =0}\Gamma +\dots$$
(24b)

Accordingly, the linear expression for \(N\left(\Gamma \right)\) reads as

$$N\left( {\Gamma } \right) \approx \left[ {1 + {\Gamma }\frac{{\left( {n - 1} \right)}}{2}\left( {\frac{{dU_{0} }}{dY}} \right)^{2} } \right]\left( { - \frac{{dU_{0} }}{dY} - {\Gamma }\frac{{dU_{1} }}{dY}} \right) \approx - \frac{{dU_{0} }}{dY} - {\Gamma }\frac{{dU_{1} }}{dY} - {\Gamma }\frac{{\left( {n - 1} \right)}}{2}\left( {\frac{{dU_{0} }}{dY}} \right)^{3} .$$
(25)

Now, on substituting Eqs. (20), (25) into Eq. (16) and equating the terms proportional to (of like powers of) \(\Gamma\), we get the following and written as:

$$-\frac{d{U}_{1}}{dY}={\frac{\left(1-n\right)}{2}\left(-\frac{d{U}_{0}}{dY}\right)}^{3}.$$
(26)

The Eq. (26) further implies.

$$- \frac{{dU_{1} }}{dY} = \frac{{\left( {1 - n} \right)}}{2}\left( {AY + k\frac{{\sinh \left( {kY} \right)}}{\cosh k}} \right)^{3} .$$
(27)

On integrating Eq. (27), we get

$${U}_{1}=\frac{\left(n-1\right)}{2}\left(\frac{1}{4}{A}^{3}{Y}^{4}+\frac{3{{A}}^{2}\mathrm{cos}h\left({kY}\right){{Y}}^{2}}{\mathrm{cos}h\left(k\right)}+\frac{3}{2}\frac{A\mathrm{ sin}h\left(kY\right)\mathrm{cos}h\left(kY\right)kY}{\mathrm{cos}h{\left(k\right)}^{2}}-\frac{3}{4}\frac{A{k}^{2}{Y}^{2}}{\mathrm{cos}h{\left(k\right)}^{2}}-\frac{Y6{A}^{2}\mathrm{sin}h\left(kY\right)}{\mathrm{cos}h\left(k\right)k} +\frac{1}{3}\frac{\mathrm{cos}h{\left(kY\right)}^{3}{k}^{2}}{\mathrm{cos}h{\left(k\right)}^{3}}-\frac{3}{4}\frac{\mathrm{A cos}h{\left(kY\right)}^{2}}{\mathrm{cos}h{\left(k\right)}^{2}}+\frac{6{{A}}^{2}\mathrm{cos}h\left(kY\right)}{\mathrm{cos}h\left(k\right){k}^{2}}-\frac{{{k}}^{2}\mathrm{cos}h\left(kY\right)}{\mathrm{cos}h{\left(k\right)}^{3}}\right)+{C}_{2}.$$
(28)

Now, by utilizing the boundary conditions (\(U=0\) at \(Y=1\)), the constant \({C}_{2}\) is obtained as follows.

$${C}_{2}=-\frac{\left(n-1\right)}{2}\left(\begin{array}{c}\frac{1}{4}{A}^{3}+3{A}^{2}+\frac{3kA\mathrm{tanh}\left(\kappa \right)}{2}-\frac{3}{4}\frac{A{k}^{2}}{\mathrm{cosh}{\left({k}\right)}^{2}}-\frac{6{A}^{2}\mathrm{tanh}\left(\kappa \right)}{k}+\frac{1}{3}{k}^{2}\\ -\frac{3}{4}A+\frac{6{A}^{2}}{{k}^{2}}-\frac{{k}^{2}}{\mathrm{cosh}{\left(k\right)}^{2}}\end{array}\right).$$
(29)

Hence, the solution for the first-order problem \({(U}_{1})\) is given by

$${U}_{1}=\frac{\left({n}-1\right)}{2}\left[\left(\frac{1}{4}{A}^{3}{Y}^{4}+\frac{3{{A}}^{2}\mathrm{cosh}\left(kY\right){{Y}}^{2}}{\mathrm{cosh}\left(k\right)}+\frac{3}{2}\frac{\mathrm{A sinh}\left(kY\right)\mathrm{cosh}\left(kY\right)\mathrm{kY}}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{2}}-\frac{3}{4}\frac{A{k}^{2}{Y}^{2}}{\mathrm{cos}h{\left(k\right)}^{2}}-\frac{Y6{A}^{2}\mathit{sinh}\left(kY\right)}{\mathrm{cosh}\left(k\right)k}+ +\frac{1}{3}\frac{\mathrm{cosh}{\left(kY\right)}^{3}{\mathrm{k}}^{2}}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{3}}-\frac{3}{4}\frac{\mathrm{Acosh}{\left(kY\right)}^{2}}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{2}}+\frac{6{\mathrm{A}}^{2}\mathrm{cosh}\left(kY\right)}{\mathrm{cosh}\left(\mathrm{k}\right){\mathrm{k}}^{2}}-\frac{{\mathrm{k}}^{2}\mathrm{cosh}\left(kY\right)}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{3}}\right)-\left(\frac{1}{4}{A}^{3}+3{A}^{2}+ \frac{3kA\mathrm{tan}h\left(\kappa \right)}{2}- \frac{3}{4}\frac{A{k}^{2}}{\mathrm{cosh}{\left(k\right)}^{2}}-\frac{6{\mathrm{A}}^{2}\mathrm{tan}h\left(\kappa \right)}{k}+\frac{1}{3}{k}^{2}-\frac{3}{4}A+\frac{6{A}^{2}}{{k}^{2}}-\frac{{k}^{2}}{\mathrm{cosh}{\left(k\right)}^{2}}\right)\right].$$
(30)

Finally, we obtain an approximate solution for \(U\) up to the first order of the perturbation parameter \(\Gamma\) following the perturbation method as used in this analysis. Thus, the final solution of \(U\), which is obtained by substituting the expressions of zeroth-order solution \({U}_{0}\) and first-order solution \({U}_{1}\) from Eqs. (22) and (30), into Eq. (17), reads as:

$$U=\frac{A}{2}\left({1-Y}^{2}\right)-\frac{\mathrm{cosh}\left(Y\kappa \right)}{\mathrm{cosh}\left(\kappa \right)}+1$$
$$+\Gamma \left(\frac{\left(n-1\right)}{2}\left[\left(\frac{1}{4}{A}^{3}{Y}^{4}+\frac{3{\mathrm{A}}^{2}\mathrm{cosh}\left(\mathrm{kY}\right){\mathrm{Y}}^{2}}{\mathrm{cosh}\left(\mathrm{k}\right)}+\frac{3}{2}\frac{\mathrm{A sinh}\left(\mathrm{kY}\right)\mathrm{cosh}\left(\mathrm{kY}\right)\mathrm{kY}}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{2}}-\frac{3}{4}\frac{{\mathrm{Ak}}^{2}{\mathrm{Y}}^{2}}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{2}}-\frac{\mathrm{Y}6{\mathrm{A}}^{2}\mathrm{sinh}\left(\mathrm{kY}\right)}{\mathrm{cosh}\left(\mathrm{k}\right)\mathrm{k}}+ +\frac{1}{3}\frac{\mathrm{cosh}{\left(\mathrm{kY}\right)}^{3}{\mathrm{k}}^{2}}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{3}}-\frac{3}{4}\frac{\mathrm{Acosh}{\left(\mathrm{kY}\right)}^{2}}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{2}}+\frac{6{\mathrm{A}}^{2}\mathrm{cosh}\left(\mathrm{kY}\right)}{\mathrm{cosh}\left(\mathrm{k}\right){\mathrm{k}}^{2}}-\frac{{\mathrm{k}}^{2}\mathrm{cosh}\left(\mathrm{kY}\right)}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{3}}\right)-\left(\frac{1}{4}{\mathrm{A}}^{3}+3{\mathrm{A}}^{2}+ \frac{3kA\mathrm{tanh}\left(\kappa \right)}{2}-\frac{3}{4}\frac{{\mathrm{Ak}}^{2}}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{2}}-\frac{6{\mathrm{A}}^{2}\mathrm{tanh}\left(\kappa \right)}{k}+\frac{1}{3}{\mathrm{k}}^{2}-\frac{3}{4}\mathrm{A}+\frac{6{\mathrm{A}}^{2}}{{\mathrm{k}}^{2}}-\frac{{\mathrm{k}}^{2}}{\mathrm{cosh}{\left(\mathrm{k}\right)}^{2}}\right)\right]\right).$$
(31)

3.2 Numerical solution

To establish the efficacy of the perturbation method as employed in this study, we also take an effort to compare the approximate analytical results with the corresponding numerical solutions as well. To this end, we look for the numerical solutions of the flow configuration considered in this analysis from two perspectives as discussed next.

3.2.1 Shooting technique

First, we appeal to shooting method, which is simple and an efficient technique, to solve the non-linear boundary value problems (Eqs. 10, 11) (Hoffman 1992; Keskin 2019). In this method, we first transform the differential equations into the system of first order equations (initial value problems (IVPs)), which are then solved using Runge–Kutta fourth-order scheme (Anantha et al. 2018b, 2022a, b). The given boundary conditions on one side of the interval considered as initial conditions. Other required initial conditions are assumed, and first order equations (IVPs) are solved. The initial conditions assumed on one boundary are iterated until the boundary conditions on the other boundary are satisfied.

From Eqs. (11) and (12), we have the following

$$- \frac{dp}{ dx}-\varepsilon {E}_{x}\frac{{d}^{2}\psi }{d{y}^{2}}=\left[{\mu }_{\infty }+\left({\mu }_{0}-{\mu }_{\infty }\right){\left(1+{\left(\lambda \frac{du}{dy}\right)}^{2}\right)}^{\frac{n-1}{2}}\right]\left(-\frac{{d}^{2}u}{d{y}^{2}}\right)$$
$$+\left(-\frac{du}{dy}\right)\left[(n-1)\left({\mu }_{0}-{\mu }_{\infty }\right){\left(1+{\left(\lambda \frac{du}{dy}\right)}^{2}\right)}^{\frac{n-1}{2}}\lambda \frac{du}{dy}\frac{{d}^{2}u}{d{y}^{2}}\right].$$
(32)

On using non-dimensional quantities, as defined in Eq. (15), the above equation [Eq. 32] can be written as

$$- A-{k}^{2}\frac{\mathrm{cosh}\left(kY\right)}{\mathrm{cosh}\left(k\right)}=\left[\frac{{\mu }_{\infty }}{{\mu }_{0}}+\left(1-\frac{{\mu }_{\infty }}{{\mu }_{0}}\right){\left(1+{\Gamma \left(\frac{dU}{dY}\right)}^{2}\right)}^{\frac{n-1}{2}}\right]\left(\frac{{d}^{2}U}{d{Y}^{2}}\right)$$
$$+\left[\left(n-1\right)\left(1-\frac{{\mu }_{\infty }}{{\mu }_{0}}\right){\left(1+{\Gamma \left(\frac{dU}{dY}\right)}^{2}\right)}^{\frac{n-3}{2}}\Gamma {\left(\frac{dU}{dY}\right)}^{2}\frac{{d}^{2}U}{d{Y}^{2}}\right].$$
(33)

We solve Eq. (33) numerically using shooting method consistent with the Runge–Kutta scheme.

3.2.2 Full-scale simulations

To obtain full-scale simulated results for the flow field of the chosen set-up, we use finite element framework of COMSOL® Multiphysics to solve the transport equations described above in Eqs. (2–4), accounting for the expression of electrical forcing given in Eq. (8). The transport equations are solved by adapting Multiphysics modules (laminar flow model for the momentum transport equations describing the Carreau fluid transport and the classical PDE module for the Poisson’s equation for potential distribution. Since we take this endeavor essentially for the comparison of our approximate analytical solutions with the full-scale simulated results, we consider only electroosmotic effect as the flow forcing parameter (corresponds to trivially small forcing comparison parameter \(\mathrm{A}(=\ll 1)\), as defined in sub-section A.1) and consider channel length is much higher than the channel width. For the numerical computations, we fix the relative residual criteria as \({10}^{-6}\) satisfying the convergence of all the field variables. For the solution of momentum transport equation, we consider no slip condition at the channel walls, while gauge pressure is considered to be zero at both ends of the channel. For the description of potential distribution, we consider specified wall potential, while no flux condition is imposed at other boundaries.

4 Volumetric flow rate and wall shear stress

The dimensionless flow rate is obtained by integrating the normalized velocity profile across the channel height

$$Q=2{\int }_{0}^{1}Udy.$$
(34)

The expression of wall shear stress in non-dimensional form is given by

$${\tau }_{w}=\frac{{\left({\tau }_{xy}\right)}_{y=H}}{{\mu }_{0}{u}_{HS}/H}={\frac{{\mu }_{\infty }}{{\mu }_{0}}\left(-\frac{dU}{dY}\right)}_{Y=1}+\left(1-\frac{{\mu }_{\infty }}{{\mu }_{0}}\right)\left[{\left(1+{\Gamma {\left(\frac{dU}{dY}\right)}_{Y=1}}^{2}\right)}^{\frac{n-1}{2}}\right]{\left(-\frac{dU}{dY}\right)}_{Y=1}.$$
(35)

5 Model benchmarking

To ascertain the efficacy of the proposed method, we also benchmark our theoretical model from different perspectives. In Fig. 2, we have shown the comparison analysis of present approximate analytical results with full scale numerical solutions for two distinct values of shear-thinning parameter \(n=0.356 \ \mathrm{and} \ 0.818\). The lines are used to denote the approximate analytical solutions while the markers are used to indicate the simulated results. The other parameters considered for this plotting being \(\mathrm{A}=0.01\), \(\kappa =20\) and \(\Gamma =0.01\). As seen in Fig. 2, approximate solutions match with the full-scale simulated results in a fairly accurate manner. For both the cases (\(n=0.356\ \mathrm{and} \ 0.818\)), the approximate analytical solutions match well with the reported experimental results. These observations justify the credibility of the proposed theoretical modeling framework in predicting the flow physics of our interest.

Fig. 2
figure 2

Plot depicting the variation of flow velocity along the transverse direction of the channel, obtained for \(n=0.356, 0.818\). The lines are used to denote the approximate analytical solutions while markers are used to indicate the simulated results. The other parameters considered for this plotting are \(\mathrm{A}=0.01\), \(\kappa =20\) and \(\Gamma =0.01\). As seen, approximate solutions match with the full-scale simulated results in a fairly accurate manner

Full size image

6 Results and discussion

In this section, we discuss the variation of flow variables like flow velocity, flow rate, and shear stress for a window of parameters typically considered in microscale set-up such as \(A=0.01, 0.1, 2\), rheological parameter \(\Gamma =0.01, 0.05, 0.08\), and the Debye–Hückel parameter \(\kappa =15, 20, 25\). The chosen range of the parameters is in accordance with their permissible values typically considered in the microfluidic set-up (Siva et al. 2020; Sun et al. 2021; Horiuchi et al. 2006; Gaikwad et al. 2020a, b). It is worth mentioning here that conforming with the prime focus of this analysis, i.e., to obtain analytical solution for any arbitrary value of shear-thinning parameter \(n\), we primarily consider several values of \(n=0.356, 0.528, 0.818\) (Cho and Kensey 1991). These values are used to describe the non-Newtonian rheology of many fluids, including biofluids, typically used in the realm of practical applications (Cho and Kensey 1991). Note that seeking for a purely analytical solution of the transport equation [Eq. (10)] for these selected values of \(n\), which is otherwise not impossible using numerical method, is indeed a convoluted task. Nevertheless, we have also shown the variation of flow velocity obtained for \(n=0.3, 0.5, 0.6, 0.8\), as given in inset of Fig. 3a. Albeit the results demonstrated in this analysis are typical to microscale transport under the combined influences of applied pressure gradient and electrokinetic effect, nevertheless, we take an effort in this endeavor to represent results for several non-integers of \(n\) (for the chosen values of \(n\) analytical solution is deemed impossible) with the prime objective of establishing the efficacy of the proposed approximate analytical method. For the sake of completeness, we must mention here that, for each case, we plot the variation obtained from both approximate analytical method and numerical solutions obtained from shooting technique (Section B.1). The effect of the aforementioned parameters on the flow velocity, net throughput and wall shear stress is aptly discussed in the forthcoming paragraphs.

Fig. 3
figure 3

Plot depicting the variation of velocity distribution a for different value of shear-thinning parameter \(n\), while other parameters are fixed at \(\mathrm{A}=0.01\), \(\kappa =20\) and \(\Gamma =0.01\); and b for different values of pressure gradient parameter \(A\), keeping at \(n=0.356\), \(\kappa =20\) and \(\Gamma =0.01\)

Full size image

6.1 Description of flow velocity

  1. (i)

    Effect of force comparison parameter

The variation of flow velocity \((U)\) distribution obtained from the approximate analytical technique is presented graphically in Figs. 3, 4, 5 for different values of pertinent parameters, i.e., \(n, A\) and \(\kappa\) with fixed value of \(\Gamma\). Also, we take an effort here to confirm the accuracy of approximate solutions obtained from perturbation technique with the results obtained from numerical analysis, consistent with the shooting technique. To do this, in Figs. 3, 4, we plot and compare the approximate analytical solutions of flow velocity \((U)\) vis-à-vis the numerical results, obtained for different values of \(n\), \(A\) and \(\kappa\). In all the cases, the approximate analytical solutions show excellent match with numerical results, which largely emphasizes the efficacy of the methodology employed in the present work. The effect of \(n\) on the flow velocity \(U\) of the Carreau fluid (for definite values of \(A, \kappa ,\mathrm{and \ \Gamma }\)) is shown in Fig. 3a. As seen in Fig. 3a, with increasing the value of \(n\), the flow velocity \(U\) decreases. The smaller the values \(n\), the stronger is the shear-thinning behavior of the fluid. It is because of the increasing shear-thinning nature of the fluids with lower \(n\), the underlying flow velocity of these fluids becomes relatively higher as witnessed in Fig. 3a. This primary reason behind this observation is attributed to the lesser apparent viscosity of the fluids having smaller \(n\) and so is the lesser viscous resistance being offered to the underlying transport. However, as seen in Fig. 3a, with increasing the value of \(n\), the flow velocity decrease and tends to exhibit Newtonian fluid velocity (the maximum velocity approaches to 1).

Fig. 4
figure 4

Plot of the velocity variation for different value of Debye parameter \(\kappa\). The other parameters considered are \(n=0.356\), \(\mathrm{A}=0.01\) and \(\Gamma =0.01\)

Full size image
Fig. 5
figure 5

Plot showing the variation of velocity distribution obtained for different value of Carreau fluid parameter \(\Gamma\) with respect to a pressure-gradient parameter \(A\), keeping fixed \(n=0.356\), \(\kappa =20\); and b Debye parameter \(\kappa\), while other parameters being \(n=0.356\), \(\mathrm{A}=0.01\)

Full size image

The dimensionless \(U\)-velocity profile for distinct values of pressure-gradient parameter \(A\) with fixed \(\kappa =20, n=0.356\) and \(\Gamma =0.01\) is demonstrated in Fig. 3b. The value of \(A\) considered for plotting Fig. 3b ranges from 0.01 to 1.0. In Fig. 3b, the shape of \(U\)-velocity profile changes from plug-like to parabolic profile as the pressure-gradient parameter \(A\) increases from 0.01 to 1.0. The flow field corresponding to smaller value of \(A \left(=0.01\right)\) conforms to electro-osmotic flow scenario to the closer extent. On the other hand, for a higher value of \(A(=1.0)\), the velocity resembling with the combined pressure-driven and electroosmotic flows. As witnessed in Fig. 3b, for \(A=0.01\), velocity profile becomes plug-type (uniform flow) in the core region. Also, as can be verified from Fig. 3b, the effect of pressure gradient combined with electroosmotic effect is seen to be higher i.e., \(A>0.01\), while with increasing the magnitude of \(A\), the \(U\)-velocity increases significantly and attains its maximum value at the central region. The approximate analytical results, as plotted in Fig. 3b, are also compared with the corresponding numerical results. A good match between approximate solutions and numerical results indeed vouches for the efficacy of the proposed method employed in this analysis.

  1. (ii)

    Effect of electrokinetic parameter

We next look into the impact of Debye parameter \(\kappa\) on velocity distribution \(\left(U\right)\) as graphically shown in Fig. 4. The value of \(\kappa\) considered for the variations plotted in Fig. 4 are \(\kappa =15, 20 \ \mathrm{and} \ 25\). Important to mention here that \({\kappa }^{-1}\) signifies the characteristics EDL thickness. For the value of \(A=0.01\), a case signifying the prominence of electrokinetic effect on the underlying transport, considered in plotting Fig. 4, the velocity profile showing similarity with a purely electroosmotic flow looks like plug-type (Gaikwad et al. 2016b). It is seen that, the dimensionless flow velocity (\(U\)-velocity) profile increases for increasing the value of \(\kappa\). From the definition, for higher value of \(\kappa\), the EDL becomes thinner and a greater number of ions get squeezed in a smaller region (EDL is thinner). This effect, in turn, boosts-up the electrical body force being applied on the fluid mass inside the EDL, and results in an enhance of flow velocity with \(\kappa\) as witnessed in Fig. 4. For a thinner EDL (higher \(\kappa\)), a stronger electroosmotic body force enhances the flow velocity even by reducing the electro-viscous effect in the EDL and a relatively higher velocity gradient near the wall region (precisely, within EDL) for higher \(\kappa\) is the results as confirmed by the inset of Fig. 4.

  1. (iii)

    Effect of fluid rheological parameter

In Fig. 5a, the effect \(\Gamma\) on the variation of flow velocity is shown for two distinct values of \(A\) with fixed \(\kappa =20\) and \(n=0.356\). For plotting Fig. 5a, the value of \(\Gamma\) varies in the range \(0.01<\Gamma <0.08\). When pressure-gradient parameter \(A (=0.01)\) is considered to be lesser, the flow velocity profile exhibits plug-like shape for different value of \(\Gamma\) considered. This is mainly because of the dominating effect of electroosmotic actuation on the underlying transport pertaining to smaller value of \(A\). On the other hand, for the higher value of \(A (=1.0)\), the velocity profile takes a parabolic shape for the chosen values of \(\Gamma\), and this observation underlines the negligible electroosmotic effect on the flow dynamics for this case. Having a look at the variations plotted in Fig. 5a, it is seen that the for both the values of \(A\) considered, the magnitude of flow velocity increases significantly with increasing the value of \(\Gamma\). The Carreau fluid parameter \(\Gamma\) is directly related to time constant \(\lambda\), which affect the fluid’s shear-thinning behavior. Precisely, the higher value of \(\Gamma\) decrsaes the shear rate and the Carreau fluid behaves like a Newtonian fluid. As such, this lower shear rate leads to an enhancement of the flow velocity as witnessed in Fig. 5a.

Figure 5b plots the approximate analytical solutions of flow velocity \((U)\) vis-à-vis the numerical results, obtained for different values of Carreau fluid parameter, depicted for varying values of \(\kappa\) ranging from 15 to 30. It is seen from Fig. 5b that for higher \(\kappa\)(i.e., for thinner EDL), the influence of \(\Gamma\) on the underlying flow velocity becomes much more prominent. A higher \(\kappa\), being the representative measure of thinner EDL, results in a stronger flow velocity gradient inside EDL (cf. inset of Fig. 4). Note that the variations depicted in Fig. 5b correspond to \(A=0.01\), and hence pertaining this case, the electroosmotic effect becomes the main driving force for the underlying flow. Thus, a higher shear rate developed inside the EDL for higher \(\kappa\) (since, the velocity gradient is higher) brings about a notable change in the flow velocity with a change in \(\Gamma\) for this case as seen from the depicted variations in Fig. 5b. It is worth adding here that for the chosen values of \(\Gamma =0.01, 0.05\ \mathrm{and} \ 0.08\), the approximate analytical solutions match well with the corresponding numerical results. This observation once more underlines the efficacy of the semi-analytical method as proposed in this endeavor.

6.2 Description of net throughput/flow rate

We here briefly discuss the variation of net throughput/flow rate with a change in parameters pertinent to this analysis. In particular, we depict the variation of \({Q}_{Carreau}/{Q}_{N}\), which henceforth is termed as the ‘flow rate ratio’ only to establish the relative enhancement of the net throughput/flow rate of the Carreau fluid in the chosen flow configuration. Figure 6a, b plot the flow rate ratio versus force comparison parameter, obtained for different values of shear-thinning parameter \(n\) and Carreau fluid parameter \(\Gamma ,\) respectively. It is interesting to observe two distinct regimes from Fig. 6a, b, the existence of those is explained later. The decreasing trend of flow rate ratio \(({Q}_{Carreau}/{Q}_{N})\) with increasing the value of \(n\) is observed for the range of \(A\) considered. With increasing the value of \(n\), the flow velocity of Carreau fluid reduces (cf. Fig. 3a), which in turn leads to a decrease in the flow rate ratio to unity. Flow rate ratio for smaller \(A(<1)\) is almost independent of shear-thinning parameter (regime-I), while for \(A(>1)\), i.e., in regime-II, the flow rate ratio is seen to be greater than unity, signifying a relatively higher flow rate of Carreau fluid. The higher flow rate ratio \(({Q}_{Carreau}/{Q}_{N}>1)\) for higher \(A(>1)\) is suggestive of a relatively higher flow rate of Carreau fluid pertaining to this range of analysis, which is witnessed by the variation shown in inset of Fig. 6a as well. For the smaller \(A\), the underlying transport is mainly governed by the electroosmotic effect for which the shear rate being developed in the flow field becomes lesser. Since at low shear rate, the Carreau fluid behaves like a Newtonian fluid, we observe the flow rate ratio to remain constant and that too is independent of shear-thinning parameter \(n\). Also, a change in flow rate ratio becomes insignificant with a change in \(n\) in this range of \(A\). However, for the higher values of \(A(>10)\), the larger magnitude of shear rate being developed in flow field gives rise to a substantial velocity of the underlying flow of Carreau fluid and results in a higher flow rate (see inset of Fig. 6a) as well as flow rate ratio. Notably, it is because of the higher shear rate, we see a noticeable change in flow rate ratio with a change in shear-thinning (shear-thinning effect is largely dependent on shear rate of the Carreau fluid) parameter \(n\).

Fig. 6
figure 6

Simulated volumetric flow rate ratio of Carreau fluid to the Newtonian with \(A\) a for different values of shear-thinning parameter \(n\), while other parameters being \(\kappa =20\) and \(\Gamma =0.01\). b For different values of rheological parameter \(\Gamma\), but keeping fixed value of \(n=0.356\) and \(\kappa =20\)

Full size image

Figure 6b represents the variation of \({Q}_{Carreau}/{Q}_{N}\) for increasing value of \(\Gamma\). As witnessed in the inset of Fig. 6b, \({Q}_{Carreau}\) increases weakly with increasing \(\Gamma\) for smaller \(A(<1)\), while exhibit substantial increasing trend with increasing the value of \(\Gamma\) for higher \(A(>10)\). As discussed in the context of Fig. 6a, for higher \(\Gamma\), the shear rate of the Carreau fluid decreases and it behaves like a Newtonian fluid. This characteristic feature of the Carreau fluid leads to a mild increase of underlying flow velocity with increasing \(\Gamma\) for smaller \(A(<1)\) (see inset of Fig. 6b). For higher \(A(>10)\), however, the higher shear rate imposed by the driving forcing overshadows the reduction of shear rate due to increasing \(\Gamma\) and results drastic increase in flow rate of the Carreau fluid (cf. Fig. 6b). It is worth adding here that the imposed shear rate in the flow field at higher \(A(>10)\) makes a substantial increase in flow velocity even for higher \(\Gamma\) and its eventual impact is the significant rise of the flow rate ratio as seen in regime-II of Fig. 6b.

The variation of flow rate ratio \({Q}_{\mathrm{Carreau}}/{Q}_{N}\) with Debye parameter \(\kappa\) is illustrated in Fig. 7, considering different values of \(n\) (Fig. 7a) and \(\Gamma\) (Fig. 7b). In Fig. 7a, b, for \(\kappa\) (> 15), typically used for microscale transport, a marked difference in the flow rate ratio with a change in \(n\) and \(\Gamma\) is witnessed. It may be reiterated here that the higher value of \(\kappa\) implies the thinner EDL, which in principle, augments the net body force being applied to take place the fluid movement by increasing scale of characteristics shear gradient. The higher electroosmotic body force for higher \(\kappa\) increases the flow rate of the Carreau fluid \({(Q}_{\mathrm{Carreau}})\) substantially (see inset of Fig. 7a, b), which consequently results in higher flow rate ratio \({(Q}_{\mathrm{Carreau}}/{Q}_{N})\) as seen from regime-II of Fig. 7a, b.

Fig. 7
figure 7

Simulated volumetric flow rate ratio of Carreau fluid to the Newtonian with \(\kappa\) a for different values of shear-thinning parameter \(n\) with fixed \(\mathrm{A}=0.01\), \(\Gamma =0.01\); and b for different values of rheological parameter \(\Gamma\) with fixed \(n=0.356\), \(\mathrm{A}=0.01\)

Full size image

6.3 Description of wall shear stress

Finally, the variation of non-dimensional wall shear stress \({\tau }_{w}\), computed using Eq. (35), is shown for different values of \(n\) in Fig. 8a, b, plotted as a function of \(A\) and \(\kappa ,\) respectively. Two distinct regimes of the variation of wall shear stress \({\tau }_{w}\) with \(A\) is seen in Fig. 8a. For smaller \(A(<1)\), the variation of \({\tau }_{w}\) with a change in shear-thinning parameter \(n\) is miniscule, which is apparent from regime-I of Fig. 8a. This observation is attributed to the lower shear rate being developed in the flow field for \(A<1\). It is because of the low shear rate, the change in flow velocity and so is the shear rate with \(n\) is insignificant. However, for \(A(>10)\), a higher shear rate being developed in the flow field gives rise to a substantial increase in the flow velocity and so is the shear stress, which becomes even noticeable with a change in \(n\) (see regime-II of Fig. 8a).

Fig. 8
figure 8

Plot showing the variation of wall shear stress \({\tau }_{w}\) with \(A\) obtained a for different values of shear-thinning parameter \(n\) but for fixed \(\kappa =20\), \(\Gamma =0.01\); and b for different values of electrokinetic parameter \(\kappa\), while other parameters being \(\mathrm{A}=0.01\) and \(\Gamma =0.01\)

Full size image

Figure 8b plots the variation of wall shear stress \({\tau }_{w}\) versus \(\kappa\), obtained for different values of \(n(=0.356, 0.528, 0.818)\). Note that other parameters considered are \(A=0.01\) and \(\Gamma =0.01\). The value of \(A\) chosen for plotting the variations in Fig. 8b is suggestive of electroosmotic effect dominated underlying transport and hence, shear rate developed in the flow field becomes lesser. As such, for smaller value of \(\kappa (<10)\), a relatively lesser electroosmotic body force eventually reduces shear stress as witnessed in regime-I of Fig. 8b. On the other hand, for \(\kappa >10\), a higher electroosmotic body force leads to a higher shear stress following higher velocity gradient in the near wall region, i.e., within EDL (cf. inset of Fig. 4) that too is verified from regime-II of Fig. 8b. Another important observation to be discussed here is the variation of \({\tau }_{w}\) with a change in \(n\), as seen from Fig. 8b. A relatively lesser flow velocity for smaller \(n\) results in a lesser wall shear stress \({\tau }_{w}\). However, the variation of \({\tau }_{w}\) with \(n\) is indeed significant for \(\kappa >10\), attributed primarily to a relatively higher flow velocity in this range of electrokinetic parameter \(\kappa\).

7 Conclusions

In this study, we have discussed the flow characteristics of non-Newtonian Carreau fluid in a microchannel under the combined influences of applied pressure gradient and electrokinetic effect. We have developed a semi-analytical methodology in the framework of perturbation technique to solve the non-linear transport equations. By validating present theoretical results for any arbitrary values of shear-thinning parameter \(n\) with the numerical solutions considering identical flow configuration, we have established the efficacy of the proposed approximate analytical scheme. Certainly, the variation of flow velocity, obtained for shear-thinning parameters those describing the non-Newtonian viscosity of many fluids, including biofluids, of practical use, are demonstrated as well and the depicted variations are found to be physically consistent with the chosen set-up and applied forcing strength. Also, we have benchmarked the proposed theoretical model by comparing our results with the experimental results available in the literature for the limiting case of a purely electroosmotic flow. We have shown that the proposed method, accounting for the effect that stems from the double-layer phenomenon, is capable of describing the flow-field accurately for any values of shear-thinning parameter \(n\), including non-integers up to three decimal points. The semi-analytical scheme developed in this study can be of beneficial use for describing the flow-field of other complex non-Newtonian fluids, typically used in several bio-microfluidic applications, under varied flow actuation scenarios.