Analysis of pressure-driven electrokinetic flows in hydrophobic microchannels with slip-dependent zeta potential

Abstract

The present study is an analysis of pressure-driven electrokinetic flows in hydrophobic microchannels with emphasis on the slip effects under coupling of interfacial electric and fluid slippage phenomena. Commonly used linear model with slip-independent zeta potential and the nonlinear model at limiting (high-K) condition with slip-dependent zeta potential are solved analytically. Then, numerical solutions of the electrokinetic flow model with zeta potential varying with slip length are analyzed. Different from the general notion of “the more hydrophobic the channel wall, the higher the flowrate,” the results with slip-independent and slip-dependent zeta potentials both disclose that flowrate becomes insensitive to the wall hydrophobicity or fluid slippage at sufficiently large slip lengths. Boundary slip not only assists fluid motion but also enhances counter-ions transport in EDL and, thus, results in strong streaming potential as well as electrokinetic retardation. With slip-dependent zeta potential considered, flowrate varies non-monotonically with increasing slip length due to competition of the favorable and adverse effects with more complicated interactions. The influence of the slip on the electrokinetic flow is eventually nullified at large slip lengths for balance of the counter effects, and the flowrate becomes insensitive to further hydrophobicity of the microchannel. The occurrence of maximum, minimum, and insensitivity on the flowrate-slip curves can be premature at a higher zeta potential and/or larger electrokinetic separation distance.

1 Introduction

In microchannels at the interface of aqueous electrolyte solution and charged walls there is a thin electric double layer (EDL), where the unbalance of positive and negative ions results in electric force and affects the fluid flow. On the other hand, the pressure-driven fluid motion causes migration of mobile ions in EDL and generates a streaming potential. The electrokinetic flow mechanism can be manifested by the interactions of the electric and flow fields (Soong and Wang 2003). The boundary slip is another interfacial phenomenon influential to the hydrodynamics at micro- and nanoscales (Zhu and Granick 2001; Tretheway and Meinhart 2002) and can be characterized by the slip length, L _S, in Navier’s formula, U _S = L _S(∂U/∂n) _w , where U _S denotes the slip velocity and (∂U/∂n) _w the normal velocity gradient at walls. Hydrophobicity of a solid surface can be reflected by the fluid slippage at the solid–liquid interface, while the slippage depends on a few factors such as properties of and interactions between solid and liquid, surface conditions, etc. Therefore, slip length can be used as an index for wall hydrophobicity. A recent review (Veronov et al. 2008) provided extensive data of fluid slippage, from which it is found that, although molecular dynamics simulation usually predicts slip lengths as low as several nanometers, the measured slip lengths may extend from nanometers up to the orders of microns, tens microns, or higher, e.g., O(1 μm) (Zhu and Granick 2001), O(10 μm) (Majumder et al. 2005; Choi and Kim 2006), and even high up to O(10² μm) in the cases of carbon nanotube (Truesdell et al. 2006).

Recently, liquid slip has attracted a number of investigations and, based on the results obtained, it was concluded that, in microchannel flows either driven by pressure-gradient or electric field, fluid slip can reduce the flow resistance as well as save the driving power required (Eijkel 2007). For example, in a series of works invoking constant property and Debye–Hückel approximations, Yang and Kwok (2003a, b, 2004) studied pressure-driven and electroosmotic flows in two-dimensional flat channel, circular tube, and rectangular duct as well. Their results demonstrated that slip affects the electrokinetic flow characteristics and increases the flow efficiency. Most recently, to investigate the effects of heat flux and boundary slip on electrokinetic flows, Ngoma and Erchiqui (2007) developed analytic solution of the linearized model and drawn the same conclusions. In the above-mentioned analyses of electrokinetic flow with boundary slip, to facilitate analytic solutions, linearized model with constant properties and Debye–Hückel approximation based on assumption of small zeta potential were employed.

It seems that we can hydrophobize wall surfaces to enhance fluid transport in microchannels. Is it always true? The answer is probably negative. Since the previous studies have the following restrictions: (1) the adverse effects of boundary slip in pressure-driven electrokinetic flows were not explored; (2) only small dimensionless slip lengths (≤0.1) were considered; and (3) zeta potential was assumed independent of fluid slippage. Physically, in the pressure-driven microchannel flow with the presence of EDL, the slip effect assists fluid motion and increases the flowrate, but it also enhances the counter-ions transport in EDL and thus the streaming potential, which, in turn, leads to a stronger electrokinetic retardation to the flow. It implies that simply enhancing hydrophobicity of the channel wall results in two counter effects on fluid transport, and what the resultant effect would be in a quite hydrophobic channel has not been investigated. In addition, fluid slippage has noticeable influence on zeta potential, which was not considered in the previous analysis mentioned above. In a recent review (Tandon and Kirby 2008), a few expressions of zeta potential with slip length developed previously were dealt with. With the complicated interactive mechanisms in the presence of fluid slip, how the resultant effect influences the fluid transport in a hydrophobic microchannel is worthy to investigate. The phenomenon of streaming potential and the related retardation effect are quite different from the electroosmotic flow, in which increase in zeta potential enhances the electroosmotic velocity rather than retards the fluid motion. In this study, slip effect on pressure-driven electrokinetic flows is analyzed with a typical model of parallel-plate hydrophobic microchannel. At first, solution to the commonly used model with slip-independent zeta potential is solved analytically and will be employed as a basis for comparison. Then, numerical solutions of the electrokinetic flow model with zeta potential varying with slip length are analyzed. The electric potential is obtained from solution to the nonlinear Poisson–Boltzmann equation without invoking Debye–Hückel linearization. In order to verify the numerical predictions, an analytic solution at limiting condition of large electrokinetic separation distance is also provided. The slip effects on the electric potential, fluid velocity, streaming potential, and flowrate at various conditions of electrokinetics and slip length are investigated.

2 Theoretical model

2.1 Governing equations

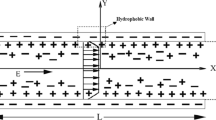
In order to explore the coupling effects, we consider the electrokinetic flow in parallel-plate microchannels of height 2a and length L as the physical model, as shown in Fig. 1. The liquid flow is assumed of constant properties, i.e., dynamic viscosity, μ, permittivity, ε, and bulk liquid electric conductivity, λ. In addition, U is used to denote the axial velocity, P the pressure, T the temperature, and Ψ the electric potential. The electric charge density is evaluated by $\rho_{e} = \sum\nolimits_{i} {{e}n_{i} z_{i} }$ with e standing for the elementary charge, n _i for the concentration, and z _i for the valance of the ith ion species. At equilibrium state, the ion concentrations can be described by Boltzmann distribution, i.e., $n_{ \pm } = n_{0} \exp ( \mp ez\Uppsi /k_{\text{B}} T)$ with n ₀ denoting salt concentration and k _B the Boltzmann constant. The charge density for symmetric electrolyte of valence z₊ = −z₋ = z can be expressed as ρ _e  = ez(n ₊−n ₋) = −2n ₀ ez sinh(ezΨ/k _B T). The coordinate system OXY lies at the channel center with X and Y, respectively, denoting the longitudinal and transverse directions. In order to non-dimensionlize the governing equations, we use the transformations u = U/U ₀, v = V/U ₀, x = X/a, y = Y/a, p = P/ρU ²₀ , ψ = ezΨ/k _B T, $E_{\text{s}}^{*} = ezE_{\text{s}} /k_{\text{B}} T$, $\rho_{e}^{*} = \rho_{e} /\left( {ezn_{0} } \right)$, $n_{ \pm }^{*} = n_{ \pm } /n_{0}$, G ₁ = a ² P _X /μU ₀, P _X  = −dp/dX, G ₂ = n ₀ a ² k _B T/LμU ₀, and K = κa, where U ₀ is the mean velocity used as a reference, κ = (2n ₀ e ² z ²/εk _B T ₀)^1/2 is the Debye–Hückel parameter, κ ⁻¹ is the characteristic thickness of EDL, K = a/κ ⁻¹ is thus the dimensionless electrokinetic separation distance. Without external field applied, streaming potential is the electric potential along the channel, E _x = E _s/L. The parameter $E_{\text{x}}^{*} \; \equiv \;E_{\text{s}}^{*} /\left( {L/a} \right)$ is the dimensionless streaming potential gradient generated in the pressure-driven flow. The dimensionless form of the momentum equation and Poisson–Boltzmann equation for fully developed flow can be depicted as

$$ {\text{d}}^{2} u/{\text{d}}y^{2} + G_{1} - 2G_{2} E_{S}^{*} \sinh \psi = 0, $$

(1)

$$ {\text{d}}^{2} \psi /{\text{d}}y^{2} = K^{2} \sinh \psi . $$

(2)

Fig. 1

Physical model of the pressure-driven electrokinetic flow in hydrophobic microchannels with slip effects

The system of Eqs. 1 and 2 is the nonlinear Poisson–Boltzmann (NPB) model for electrokinetic flows.

2.2 Boundary conditions

The two channel walls are assumed at the same conditions; therefore, the velocity and electrical potential both are symmetrical at the channel center (y = 0). The boundary conditions are:

$$ y = 0:\partial u/\partial y = \partial \psi /\partial y = 0; $$

(3)

$$ y = 1:u = - L_{S}^{*} ({\text{d}}u/{\text{d}}y)_{w}\;{\text{and }}\psi = \zeta_{\text{a}}^{*} $$

(4)

where $L_{S}^{*} \; \equiv \; L_{S} /a$ is the dimensionless slip length, $\zeta_{\text{a}}^{*} \; \equiv \; ez\zeta_{\text{a}} /k_{\text{B}} T$ is the dimensionless apparent zeta potential with the presence of slip effect.

For a solid of specific material with a given liquid over it, the true zeta potential can be measured and some of them can be found in literature; while as the wall surface is treated either by a physical or chemical means to modify its surface condition, the wall hydrophobicity or the slip characteristic is changed. This modification of the interfacial condition may result in a change in zeta potential. It is difficult to model the details of the surface condition such as roughness or gas bubble attached, but the resultant fluid slippage is usually described by using the Navier formula with slip length as an index just like the slippage data listed by Veronov et al. (2008). Although the Navier slip expression is not always very accurate for quantifying the slip phenomenon, it is a useful approximation before we have a more appropriate model. Thereby the apparent zeta potential of the wall is expressed as the true zeta potential with a function of slip length at the solid–liquid interface. In a previous work (Churaev et al. 2002), a simple linear relationship between zeta potential and slip length, in terms of the present notations, $\zeta_{\text{a}}^{*} = \zeta^{*} ( 1+ KL_{S}^{*} )$, was employed, where ζ ^* ≡ ezζ/k _B T is the dimensionless true zeta potential. In a study of simultaneously determining slip and zeta potential, Yang and Kwok (2002) developed a modified expression of the form $\zeta_{\text{a}}^{*} = \zeta^{*} ( 1+ KL_{S}^{*} )/f_{\text{m}} ,$ where f _m is the modification factor. The above formulas are appropriate for low zeta potentials in the Debye–Hückel limit. In the work of Joly et al. (2004), using molecular dynamics simulations they disclosed that the immobile layer disappears in the cases of non-wetting (i.e., hydrophobic) surface, and the zeta potential deduced from electrokinetic effects is thus considerably amplified by the existence of a slippage at the solid surface.

Most recently, a nonlinear expression for a dilute z–z symmetric electrolyte was proposed in the review article by Tandon and Kirby (2008). With the present nomenclature, this slip-dependent zeta potential can be expressed as

$$ \zeta_{\text{a}}^{ * } = \zeta^{ * } + L_{S}^{ * } \cdot K \cdot \sinh \zeta^{ * } . $$

(5)

It can be re-written in an alternative form, $\zeta_{\text{a}}^{*} = \zeta^{*} [ 1+ KL_{S}^{*} ({ \sinh }\zeta^{*} /\zeta^{*} )]$. For very small zeta potential, sinh ζ ^*/ζ ^* ≈ 1, Eq. 5 reduces to the simple linear correlation, $\zeta_{\text{a}}^{*} = \zeta^{*} ( 1+ KL_{S}^{*} ).$ In the present nonlinear analysis, Eq. 5 is employed to account for the influence of wall hydrophobicity or fluid slippage on zeta potential.

3 Results and discussion

3.1 General analytic considerations

Analytically, velocity distributions can be obtained from the resultant equation of combining Eqs. 1 and 2 with the sinh-term eliminated,

$$ u = {\frac{{G_{1} }}{2}}\left( {1 - y^{2} } \right) + G_{1} L_{S}^{*} - {\frac{{2G_{2} E_{S}^{*} }}{{K^{2} }}}\left[ {2KL_{S}^{*} \sinh {\frac{{\zeta_{\text{a}}^{*} }}{2}} + \zeta_{\text{a}}^{*} - \psi (y)} \right] $$

(6)

in which the electric potential ψ(y) can be obtained from solution of Eq. 2. The solution ψ(y) of the nonlinear Poisson–Boltzmann equation, Eq. 2, can be obtained analytically with ψ(y) at y = 0 known a priori. This addition data can be found somehow, e.g., by using an approximation or a numerical method. In the discussion of the present section on the qualitative natures, we do not intend to solve it. The streaming potential can be determined with balance of streaming current, I _S, and the conductive current, I _C, at steady state. The streaming potential is defined as $I_{S} \equiv \int_{{A_{\text{C}} }} {U\rho_{e} } W{\text{d}}Y$ and its dimensionless form is $I_{S}^{*} \equiv {{I_{\text{s}} } \mathord{\left/ {\vphantom {{I_{\text{s}} } {2n_{0} evU_{0} Wa = - \int_{ - 1}^{1} {u\sinh \psi {\text{d}}y,} }}} \right. \kern-\nulldelimiterspace} {2n_{0} evU_{0} Wa = - \int_{ - 1}^{1} {u\sinh \psi {\text{d}}y,} }}$ where W denotes the channel width and for this two-dimensional model, unit width W = 1 is taken. The conductive current consists of two parts, bulk flow and surface, i.e., I _C = I _C,b + I _C,S = A _C λ _b E _S/L + 2 Wλ _S E _S/L = 2 W(aλ _b + λ _S)E _S/L. At steady state, I _S + I _C = 0 or $\int_{{A_{C} }} {U\rho_{e} } WdY + 2W\left( {a\lambda_{0} + \lambda_{S} } \right)E_{S} /L = 0.$ With definition of the dimensionless parameter G ₃ = a(aλ _b + λ _S)/ɛLU ₀, finally, we have $E_{S}^{*} = \left( {{{K^{2} } \mathord{\left/ {\vphantom {{K^{2} } {G_{3} }}} \right. \kern-\nulldelimiterspace} {G_{3} }}} \right)\int_{ - 1}^{1} {u\sinh \psi dy}$ or

$$ E_{S}^{*} = - {\frac{{K^{ 2} \left( {G_{1} F_{1} - G_{1} F_{2} + 2G_{1} L_{S}^{*} F_{1} } \right)}}{{ 2\left[ { 2G_{ 2} F_{ 3} - 4G_{ 2} KL_{S}^{*} \sinh \left( {{{\zeta_{\text{a}}^{ *} } \mathord{\left/ {\vphantom {{\zeta_{\text{a}}^{ *} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)F_{1} - 2G_{ 2} \zeta_{\text{a}}^{ *} F_{1} - G_{ 3} } \right]}}} $$

(7)

where $F_{ 1} = \int_{ - 1}^{1} {\sinh \psi {\text{d}}y} ,F_{ 2} = \int_{ - 1}^{1} {y^{ 2} \sinh \psi {\text{d}}y}$ and $F_{ 3} = \int_{ - 1}^{1} {\psi \sinh \psi {\text{d}}y}$.

Dimensionless flowrate in the microchannel can be evaluated with $Q^{*} = \int_{ - 1}^{1} {udy}$ and

$$ Q^{*} = 2G_{1} / 3+ 2G_{1} L_{S}^{*} - 4G_{2} E_{S}^{*} {{\left[ {2KL_{S}^{*} \sinh \left( {{{\zeta_{\text{a}}^{*} } \mathord{\left/ {\vphantom {{\zeta_{\text{a}}^{*} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) + \zeta_{\text{a}}^{*} - F_{ 4} } \right]} \mathord{\left/ {\vphantom {{\left[ {2KL_{S}^{*} \sinh \left( {{{\zeta_{\text{a}}^{*} } \mathord{\left/ {\vphantom {{\zeta_{\text{a}}^{*} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) + \zeta_{\text{a}}^{*} - F_{ 4} } \right]} {K^{2} }}} \right. \kern-\nulldelimiterspace} {K^{2} }} $$

(8)

where $F_{ 4} \equiv \int_{ - 1}^{1} {\psi {\text{d}}y} .$ Using the conventional Poiseuille flowrate $Q_{p}^{*} = 2G_{1} /3$ (with $L_{S}^{*} = 0$ and $\zeta^{*} = E_{S}^{*} = 0$) as the reference, we define the volumetric flowrate ratio as $r_{Q} \equiv Q^{*} /Q_{p}^{*} .$ Therefore, the following formula for r _Q can be developed.

$$ r_{Q} = 1 + 3L_{S}^{*} - {{6G_{2} E_{S}^{*} \left[ {2KL_{S}^{*} \sinh \left( {{{\zeta_{\text{a}}^{*} } \mathord{\left/ {\vphantom {{\zeta_{\text{a}}^{*} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) + \zeta_{\text{a}}^{*} - F_{ 4} } \right]} \mathord{\left/ {\vphantom {{6G_{2} E_{S}^{*} \left[ {2KL_{S}^{*} \sinh \left( {{{\zeta_{\text{a}}^{*} } \mathord{\left/ {\vphantom {{\zeta_{\text{a}}^{*} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) + \zeta_{\text{a}}^{*} - F_{ 4} } \right]} {G_{1} K^{2} }}} \right. \kern-\nulldelimiterspace} {G_{1} K^{2} }}. $$

(9)

Since the flowrate is normalized by the Poiseuille flowrate, the parameter r _Q can be employed to indicate the change in flowrate under the interactions of slip and electrokinetics. On the right-hand side of Eq. 9, the first term (unity) simply stands for the Poiseuille flowrate, the second term ($3L_{S}^{*}$) for purely hydrodynamic slip effect, and the last part with three terms in the square parenthesis includes the change in flowrate related to the EDL effects and the electro-hydrodynamic interaction. In this part, at non-slip condition ($L_{S}^{*} = 0$), the terms $\zeta_{\text{a}}^{*}$ and F ₄ reduce to their counterparts of pure electrokinetic; while the most complicated coupling term of $2KL_{S}^{*} \sinh \left( {{{\zeta_{\text{a}}^{*} } \mathord{\left/ {\vphantom {{\zeta_{\text{a}}^{*} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)$ becomes zero as $L_{S}^{*} = 0$.

In the present flow problem, the major unknowns to be solved are fluid velocity u(y) and electrical potential ψ(y), thereby the flowrate and streaming potential can be derived. The dimensionless parameters involved in this flow configuration are G ₁, G ₂, G ₃, K, ζ ^*, and $L_{S}^{*}$, where a number of dimensional quantities and constants are involved and have to be assigned for evaluation of the above six dimensionless groups. As an example, for the electrokinetic flow of a dilute (n ₀ = 10⁻⁶ M) aqueous 1–1 electrolyte solution (z = 1) at T ₀ = 298 K with the physical constants $\varepsilon = 6. 9 4 2 5 \times 10^{ - 10} {\text{C}}/{\text{m}} \;{\text{V}},$ k _B = 1.3805 × 10⁻²³ J/K, and e = 1.6021 × 10⁻¹⁹ C, then EDL characteristic length is κ ⁻¹ = (2n ₀ e ² z ²/ɛk _B T ₀)^−1/2 = 0.304 μm. Assume the height of the microchannel is 2a = 6.08 μm, the parameter K = a/κ ⁻¹ = 10 is determined. In this pressure-driven electrokinetic flow without external electric field applied, for a given pressure-gradient −dP/dX = 4.265 × 10⁴ N/m³, the corresponding Poiseuille flow velocity U ₀ = 1.472 × 10⁻⁴ m/s rather than the Helmholtz–Smoluchowski velocity is used as the reference velocity. The parameters G ₁ = a ²(−dP/dX)/μ ₀ U ₀ = 3 and G ₂ = n ₀ a ² k _B T ₀/(Lμ ₀ U ₀) = 0.573 can be evaluated with fluid viscosity μ ₀ = 8.9226 × 10⁻⁴ Ns/m², density ρ ₀ = 997 kg/m³, and reference channel length L = 100a. The conduction current parameter is G ₃ = a(aλ _b + λ _S)/ɛLU ₀ = 4.455, in which the bulk electrical conductivity λ _b = 1.4979 × 10⁻⁵ Ω⁻¹ m⁻¹ is taken but the effect of surface conductivity λ _S ignored. Surface electrical conductivity may become important for low bulk concentration and high zeta potential. Although, it can be neglected for large K (Gong et al. 2008) or very small ratio λ _S/λ _b, e.g., the value is of order 10⁻⁷ for aqueous solution through the glass surface (Chun et al. 2003). Besides, the significance of the surface conductivity seems uncertain as we learned from the previous work of Li (2001). Therefore, the effect of λ _S is not included in the present parametric evaluation.

The above is considered as a baseline case in the present study. In order to explore the interaction of the fluid slippage and electrokinetics, the parameters K, ζ ^*, and $L_{S}^{*}$ characterizing electrokinetic separation distance, zeta potential, and fluid slippage (or wall hydrophobicity), respectively, are allowed to vary in parametric analysis. For fixed values of G ₁ = 3, G ₂ = 0.573, and G ₃ = 4.455, the cases of K = 10 (corresponding to a = 3.04 μm and U ₀ = 1.472 × 10⁻⁴ m/s), K = 7.5 (a = 2.28 μm and U ₀ = 1.104 × 10⁻⁴ m/s), and K = 5 (a = 1.52 μm and U ₀ = 7.361 × 10⁻⁵ m/s) are studied. The range of $L_{S}^{*}$ spans from O(10⁻³) up to O(1) for superhydrophobic surface. With the baseline case of a = 3.04 μm, the corresponding values of the dimensional slip length L _S thus ranges from O(1 nm) to O(10 μm). The magnitudes of zeta potential |ζ| ≤ 200 mV, i.e., ζ ^* ≤ 8, are considered. The slip length data for some materials can be found elsewhere, e.g., the review article by Veronov et al. (2008), and some measured data of zeta potentials for various conditions of solid–liquid interface are listed in Table 1 for reference.

Table 1 Some zeta potential data for electrokinetic flows in microchannels

3.2 Solutions with conventional boundary condition of slip-independent zeta potential

In this section, we solve the problem with boundary condition of zeta potential independent of slip or ψ = ζ ^* at walls, which is a commonly used boundary condition in the previous investigations. Although this solution of weak coupling may become inappropriate in the cases of significant slip, it can be used as a basis for comparison to show the differences between the results with slip-dependent and slip-independent zeta potential. Equations 1 and 2 will be solved numerically with zeta potential high up to ζ ^* = 8. In the meantime, to facilitate analytic solutions, the Debye–Hückel approximation for low zeta potential (ζ ^* < 2) with $\sinh \psi \approx \psi$ is invoked. The dimensionless form of the simplified model for fully developed electrokinetic flow in parallel-plate microchannels can be depicted as

$$ {\text{d}}^{2} u/{\text{d}}y^{2} + G_{1} - 2G_{2} E_{S}^{*} \psi = 0 $$

(1a)

$$ {\text{d}}^{2} \psi /{\text{d}}y^{2} = K^{2} \psi . $$

(2a)

This is the so-called linearized Poisson–Boltzmann (LPB) model versus the full PB model of Eqs. 1 and 2. The boundary conditions for the solutions of u(y) and ψ(y) are ∂u/∂y = ∂ψ/∂y = 0 at y = 0; $u = - L_{S}^{*} \left( {{\text{d}}u/{\text{d}}y} \right)_{w}$ and ψ = ζ ^* at y = 1. The linearized solutions of velocity and electric potential, and the derivative quantities such as the streaming potential, flowrate, and flowrate ratio defined in the previous section, respectively, are

$$ \psi (y) = {{(e^{K} - e^{ - K} )(e^{Ky} + e^{ - Ky} )\zeta^{*} } \mathord{\left/ {\vphantom {{(e^{K} - e^{ - K} )(e^{Ky} + e^{ - Ky} )\zeta^{*} } {2\sinh 2K}}} \right. \kern-\nulldelimiterspace} {2\sinh 2K}}, $$

(10)

$$ u(y) = {{G_{1} \left( {1 + 2L_{S}^{*} - y^{2} } \right)} \mathord{\left/ {\vphantom {{G_{1} \left( {1 + 2L_{S}^{*} - y^{2} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2} - {{2\zeta^{*} G_{2} E_{S}^{*} \left[ {1 + KL_{S}^{*} \tanh (K) - \cosh (Ky)\text{sech} (K)} \right]} \mathord{\left/ {\vphantom {{2\zeta^{*} G_{2} E_{S}^{*} \left[ {1 + KL_{S}^{*} \tanh (K) - \cosh (Ky)\text{sech} (K)} \right]} {K^{2} }}} \right. \kern-\nulldelimiterspace} {K^{2} }}, $$

(11)

$$ E_{S}^{*} = {\frac{{2G_{1} \zeta^{*} \left[ {K - \left( {1 - K^{2} L_{S}^{*} } \right)\tanh K} \right]}}{{KG_{3} + 2G_{2} \zeta^{*2} \left( {\tanh K + 2KL_{S}^{*} \tanh^{2} K - K\text{sech}^{2} K} \right)}}}, $$

(12)

$$ Q^{*} {{ = {{2G_{1} (1 + 3L_{S}^{*} )} \mathord{\left/ {\vphantom {{2G_{1} (1 + 3L_{S}^{*} )} 3}} \right. \kern-\nulldelimiterspace} 3} - 4G_{2} E_{S}^{*} \zeta^{ *} [K - (1 - K^{2} L_{S}^{*} )\tanh (K)]} \mathord{\left/ {\vphantom {{ = {{2G_{1} (1 + 3L_{S}^{*} )} \mathord{\left/ {\vphantom {{2G_{1} (1 + 3L_{S}^{*} )} 3}} \right. \kern-\nulldelimiterspace} 3} - 4G_{2} E_{S}^{*} \zeta^{ *} [K - (1 - K^{2} L_{S}^{*} )\tanh (K)]} {K^{3} }}} \right. \kern-\nulldelimiterspace} {K^{3} }}, $$

(13)

$$ r_{Q} = 1 + 3L_{S}^{*} - {{6G_{2} \zeta^{*} E_{S}^{*} \left[ {K - \left( {1 - K^{2} L_{S}^{*} } \right)\tanh K} \right]} \mathord{\left/ {\vphantom {{6G_{2} \zeta^{*} E_{S}^{*} \left[ {K - \left( {1 - K^{2} L_{S}^{*} } \right)\tanh K} \right]} {K^{3} G_{1} }}} \right. \kern-\nulldelimiterspace} {K^{3} G_{1} }}. $$

(14)

The sensitivity of flowrate to the variation of slip length, ${{\partial r_{Q} } \mathord{\left/ {\vphantom {{\partial r_{Q} } {\partial L_{S}^{*} }}} \right. \kern-\nulldelimiterspace} {\partial L_{S}^{*} }},$ can be developed and expressed as

$$ {\frac{{\partial r_{Q} }}{{\partial L_{S}^{*} }}} = {\frac{{3{\text{sech}}^{4} K\left[ {K^{2} G_{3} \cosh^{2} K - G_{2} \zeta^{*2} \left( {2 + 2K^{2} - 2\cosh 2K + K\sinh 2K} \right)} \right]^{2} }}{{K^{2} \left[ {KG_{3} + 2G_{2} \zeta^{*2} \left( { - K{\text{sech}}^{2} K + \tanh K + 2KL_{S}^{*} \tanh^{2} K} \right)} \right]^{2} }}}. $$

(15)

It is found that the sensitivity ${{\partial r_{Q} } \mathord{\left/ {\vphantom {{\partial r_{Q} } {\partial L_{S}^{*} }}} \right. \kern-\nulldelimiterspace} {\partial L_{S}^{*} }}$ reduces with either increasing zeta potential ζ ^* or slip length $L_{S}^{*}$. Equation 15 reveals two characteristic behaviors: (1) for the case of conventional Poiseuille flow (ζ ^* = K = 0) with slip boundary condition, ${{\partial r_{Q} } \mathord{\left/ {\vphantom {{\partial r_{Q} } {\partial L_{S}^{*} }}} \right. \kern-\nulldelimiterspace} {\partial L_{S}^{*} }} = 3$ for all $L_{S}^{*}$; (2) with the presence of electrokinetic effect (ζ ^* ≠ 0 and K ≠ 0) ${{\partial r_{Q} } \mathord{\left/ {\vphantom {{\partial r_{Q} } {\partial L_{S}^{*} }}} \right. \kern-\nulldelimiterspace} {\partial L_{S}^{*} }} \to 0$ as $L_{S}^{*} \; \to \;\infty$ or at sufficiently large slip.

For the cases of K = 10 and $L_{S}^{*} \; = \; 1$ shown in Fig. 2, both the analytic (LPB) solutions of velocity distributions for ζ ^* ≤ 2 and the numerical solutions of the full PB model for wider range of zeta potential ζ ^* ≤ 8 are presented. The agreement of LPB model with the full PB model is quite good for ζ ^* ≤ 1 and acceptable even at ζ ^* = 2. The results demonstrate that the flow velocity is reduced with increasing zeta potential. The velocity slip at the wall boundary is also observed. The close-up view shows the occurrence of negative slip velocities at higher zeta potentials, ζ ^* ≥ 6, with emergence of flow reversal.

Fig. 2

Velocity distributions at conditions of K = 10, $L_{S}^{*} = 1$ and various ζ ^* with zeta potential independent of slip

Since the streaming potential generated in a microchannel depends on the channel length, streaming potential gradient is more appropriate for dealing with fluid transport performance. In the following discussion, the streaming potential gradient $E_{\text{x}}^{*} \equiv E_{\text{s}}^{*} /(L/a)$ generated in the microchannel is dealt with. The variations of the streaming potential parameter $E_{\text{x}}^{*}$ with slip length at various zeta potentials are presented in Fig. 3. Streaming potential is null at ζ ^* = 0. In the low-ζ ^* range, ζ ^* ≤ 0.75, $E_{\text{x}}^{*}$ increases with the increasing zeta potential, whereas the trend reverses as zeta potential rises further, i.e., ζ ^* ≥ 1. The slip effect on $E_{\text{x}}^{*}$ is also quite noticeable in the low-ζ ^* range; while for higher zeta potentials, the fluid slip effects become moderate with increasing slip length and saturated eventually. The underlying physical mechanisms with the electro-hydrodynamic interactions can be addressed as follows.

Fig. 3

Slip effects on the steaming potential parameter at conditions of K = 10 and various ζ ^* with zeta potential independent of slip

In this model configuration of microchannel flow, electrokinetics reduces fluid velocity while the boundary slip generally tends to alleviate flow resistance and enhance the inertia of fluid motion. However, besides the above individual effects, the enhanced fluid motion with slip may also result in an additional increment in the streaming potential and, in turn, the electrokinetic retardation. Owing to the coupling of electric and flow fields, the advantage of the fluid slip is counteracted by the extra retarding effect. The resultant effects on the flowrate parameter r _Q are shown in Fig. 4. As the qualitative trend predicted by the linearized theory (LPB model), the slope ${{\partial r_{Q} } \mathord{\left/ {\vphantom {{\partial r_{Q} } {\partial L_{S}^{*} }}} \right. \kern-\nulldelimiterspace} {\partial L_{S}^{*} }}$ reduces and approaches zero asymptotically with sufficiently high ζ ^*. Due to strong electrokinetic retardation, the asymptotic flowrate drops a little below the conventional Poiseuille flowrate (r _Q  < 1) for the high zeta potentials (ζ ^* ≤ 4). We define a numerical criterion for reasonably ignoring slip effect, i.e., ${{\partial r_{Q} } \mathord{\left/ {\vphantom {{\partial r_{Q} } {\partial L_{S}^{*} }}} \right. \kern-\nulldelimiterspace} {\partial L_{S}^{*} }} \; < \; 0.01$. In Fig. 5, the critical values of slip length ($L_{\text{S,C}}^{*}$) for ${{\partial r_{Q} } \mathord{\left/ {\vphantom {{\partial r_{Q} } {\partial L_{S}^{*} }}} \right. \kern-\nulldelimiterspace} {\partial L_{S}^{*} }}\; = \;0.01$ are plotted versus ζ ^*. The results show a rapid reduction of $L_{\text{S,C}}^{*}$ with zeta potential and a little different trend for ζ ^* > 5 due to the occurrence of the flow reversal.

Fig. 4

Slip effects on the flowrate ratio at conditions of K = 10 and various ζ ^* with zeta potential independent of slip

Fig. 5

Critical conditions for asymptotic criterion ${{\partial r_{Q} } \mathord{\left/ {\vphantom {{\partial r_{Q} } {\partial L_{S}^{*} }}} \right. \kern-\nulldelimiterspace} {\partial L_{S}^{*} }} < 0.01$ in variations of slip effects on r _Q based on the solution with slip-independent zeta potential

3.3 Limiting solution of nonlinear model at high K with slip-dependent zeta potential

At limiting condition of high K, the electric potential at the channel center can be approximately assumed zero. The analytic expressions of electric potential and fluid velocity can be developed, viz.,

$$ \psi (y) = 4\tanh^{ - 1} \left[ {\text{e}^{K(y - 1)} \tanh \left( {{\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right)} \right] $$

(16)

$$ \begin{aligned} u(y) = & {\frac{{G_{1} }}{2}}\left( {1 - y^{2} } \right) + G_{1} L_{S}^{*} \\ - {\frac{{2G_{2} E_{S}^{*} }}{{K^{2} }}}\left[ {2KL_{S}^{*} \sinh \left( {{\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{2}}} \right) + \zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } - \psi (y)} \right]. \\ \end{aligned} $$

(17)

The streaming potential can be derived from the above solutions and have the following form:

$$ E_{\text{s}}^{*} = {\frac{{\left( {2G_{1} \left( \begin{gathered} 2K\tanh^{ - 1} \left( {e^{2K} \coth {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right) - {\text{Li}}_{2} \left( { - e^{K} \coth {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right) + \hfill \\ {\text{Li}}_{2} \left( {e^{K} \coth {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right) + {\text{Li}}_{2} \left( { - e^{2K} \coth {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right) - \hfill \\ {\text{Li}}_{2} \left( {e^{2K} \coth {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right) + {\text{Li}}_{2} \left( { - \tanh {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right) - \hfill \\ {\text{Li}}_{2} \left( {\tanh {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right) - {\text{Li}}_{2} \left( { - e^{ - K} \tanh {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right) + \hfill \\ {\text{Li}}_{2} \left( {e^{ - K} \tanh {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right) + {\frac{{K\left( {\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } } \right)}}{2}} + \hfill \\ K^{2} L_{S}^{*} \sinh {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{2}}\left( {1 - {\frac{1}{{\sinh 2K\cosh {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{2}} + \cosh 2K}}}} \right) \hfill \\ \end{gathered} \right)} \right)}}{{\left( \begin{gathered} KG_{3} + \hfill \\ {\frac{{8e^{2K} G_{2} \sinh {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{2}}}}{{\left( \begin{gathered} 1 + e^{4K} + \hfill \\ \left( { - 1 + e^{4K} } \right)\cosh {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{2}} \hfill \\ \end{gathered} \right)}}}\left( \begin{gathered} 4\tanh^{ - 1} \left( {e^{ - 2K} \tanh {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{4}}} \right) + \hfill \\ KL_{S}^{*} \sinh 2K \cdot \sinh \left( {\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } } \right) - \hfill \\ \left( {\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } } \right) + \hfill \\ 4\sinh K\sinh {\frac{{\zeta^{ * } + KL_{S}^{ * } \sinh \zeta^{ * } }}{2}} \times \hfill \\ \left( {\left. {\cosh K + KL_{S}^{ * } \sinh K} \right)} \right. \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right)}}}, $$

(18)

where Li₂(x) is the so-called Euler dilogarithm function defined as $\text{Li}_{2} \left( x \right) = \sum\nolimits_{n = 1}^{\infty } {x^{n} /n^{2} } = - \int_{0}^{x} {\left[ {\log \left( {1 - t} \right)/t} \right]} {\text{d}}t$ in the interval of 0 ≤ x ≤ 1. The ratio of volumetric flowrate is then expressed as

$$ \begin{gathered} r_{Q} = 1 + 3L_{S}^{*} - \hfill \\ \, {\frac{{6G_{2} E_{S}^{*} }}{{G_{1} K^{3} }}}\left( \begin{gathered} - 4\text{Li}_{2} \left( {\tanh {\frac{{\zeta^{ * } + L_{S}^{ * } K\sinh \zeta^{ * } }}{4}}} \right) + 4\text{Li}_{2} \left( {e^{ - K} \tanh {\frac{{\zeta^{ * } + L_{S}^{ * } K\sinh \zeta^{ * } }}{4}}} \right) + \hfill \\ \text{Li}_{2} \left( {\tanh^{2} {\frac{{\zeta^{ * } + L_{S}^{ * } K\sinh \zeta^{ * } }}{4}}} \right) - \text{Li}_{2} \left( {e^{ - 2K} \tanh^{2} \left({\frac{{\zeta^{ * } + L_{S}^{ * } K\sinh \zeta^{ * } }}{4}}\right)} \right) + \hfill \\ 2K^{2} L_{S}^{*} \sinh {\frac{{\zeta^{ * } + L_{S}^{ * } K\sinh \zeta^{ * } }}{2}} + K\left( {\zeta^{ * } + L_{S}^{ * } K\sinh \zeta^{ * } } \right) \hfill \\ \end{gathered} \right). \hfill \\ \end{gathered} $$

(19)

3.4 Numerical method and model verification

In the following text, numerical solutions of the complete model, Eqs. 1–4, are to be dealt with. The governing equations are discretized by finite volume method with central difference for diffusion terms, and the resultant system of algebraic equations is solved by tri-diagonal matrix algorithm (TDMA) (Ferziger and Perić, 1999). With the presence of high potential slope at high-K condition, non-uniform grid system with grid lines clustered toward walls is arranged. The smallest grid size of Δy = 10⁻⁵ next to walls is employed. For grid independence, simulations of the parameters of typical case of K = 10 were carried out on grid systems of 27, 52, 77, 102, 127, 152, and 177 points. Predictions of streaming potential gradient $E_{\text{x}}^{*}$, which is a key parameter of pressure-driven electrokinetic flow, show that the maximum deviation between the solutions on 152 and 177 grids is <0.02%. This concludes the validation of the grid-independence test, and the grid of 152 points is used in this study. In Fig. 6, at K = 10 and various values of $L_{S}^{*}$ and ζ ^*, the numerical predictions agree excellently with the analytic solutions of high-K limiting case.

Fig. 6

Comparison of numerical predictions and the analytic solutions of $E_{\text{x}}^{*}$ at K = 10 and various conditions of $L_{S}^{*}$ and ζ ^*

In this study, some cases of high zeta potentials are studied and, even at lower ζ ^* such as ζ ^* < 2, slip effect may enhance the apparent zeta potential. In order to avoid the possible errors induced by linearization, we employ nonlinear PB model in the analysis but abandon the simplicity provided by the Debye–Hückel approximation. The results at K = 10 in Fig. 7 demonstrate noticeable deviations between linear and nonlinear solutions at higher ζ ^* and/or $L_{S}^{*}$, which corroborates the necessity of using nonlinear PB model for this class of analysis.

Fig. 7

Comparison of linear and nonlinear solutions of $E_{\text{x}}^{*}$ at K = 10 and various conditions of $L_{S}^{*}$ and ζ ^*

3.5 Analysis of solutions with slip-dependent zeta potential

Considering the boundary conditions of zeta potential dependent of slip length, solutions of electrokinetic flows in hydrophobic microchannels governed by Eqs. 1 and 2 are obtained numerically. In Fig. 8a, at K = 10 and ζ ^* = 1, electric potential distributions with various slip lengths are presented. Dependence of ψ(y) on the slip length $L_{S}^{*}$ reflects strong influences of fluid slippage. As the electrokinetic separation distance reduces to K = 7.5 and 5, Fig. 8b and c, although the multiplier K in $\zeta_{a}^{*} (K,L_{S}^{*} )$ expression decreases, while the EDL becomes thicker, thus the slip effects remain obvious. The augmentation of zeta potential with slip length penetrates into the interior of the microchannel and increases the local potential.

Fig. 8

Slip effects on electric potential distributions at ζ ^* = 1 with slip-dependent zeta potential. a K = 10; b K = 7.5; c K = 5

The velocity profiles at three values of parameter K and ζ ^* = 1 shown in Fig. 9 show a very similar quantitative nature. In the first stage of low $L_{S}^{*}$, the slip effect is dominant and the fluid velocity increases with the increasing $L_{S}^{*}$. In Fig. 9a, for example, fluid velocity increases with $L_{S}^{*}$ in the range of $L_{S}^{*} = 0{\text{ to }}0. 1 1$. Then, the increasing electrokinetic retardation becomes strong enough to draw the fluid velocity down and even to the level less than the Poiseuille flow, the cases of $L_{S}^{*} = 0. 2 5 {\text{ and }}0. 4$. However, the low fluid velocity in EDL region also weakens the ions transport and, in turn, the electrokinetic retardation. In this situation, further increasing $L_{S}^{*}$ tends to recover the fluid velocity. The favorable and the adverse effects balance each other, and eventually the fluid motion approaches the Poiseuille flow profile asymptotically as the profiles for $L_{S}^{*} = 1. 3$. In order to analyze the electro-hydrodynamic interactions involved in this complicated flow, the predictions of streaming potential gradient $E_{\text{x}}^{*}$ are presented in Fig. 10. It is revealed that, different from the results shown in Fig. 3, the $E_{\text{x}}^{*} \; \sim \;L_{S}^{*}$ curves obtained with the slip-dependent zeta potential are of a non-monotonic behavior with a vanishing tendency at large $L_{S}^{*}$. The underlying mechanisms are more complicated due to the strongly nonlinear coupling nature from the apparent zeta potential $\zeta_{a}^{*} (K,L_{S}^{*} )$. Take the cases at K = 10 and ζ ^* = 1 as illustrative examples, it is observed that an increase in $L_{S}^{*}$ enhances fluid flow and streaming potential in the region of slip dominance, i.e., $L_{S}^{*} < 0. 2$. Besides the retarding effect from the enhanced streaming potential, the augmentation in the apparent zeta potential with increasing slip length further enhances the retarding effect. The retarded flow then leads to a reduction in $E_{\text{x}}^{*}$ as $L_{S}^{*} > 0. 2$, where the electrokinetic retardation dominates. As a consequence of stronger retardation with apparent zeta potential $\zeta_{\text{a}}^{*}$ enhanced by $L_{S}^{*}$, reversed flow occurs as the slip length lies up to $L_{S}^{*} = 0. 4$. Beyond this value, $E_{\text{x}}^{*}$ diminishes continuously and the fluid velocity recovers gradually. The velocity distribution approaches the Poiseuille flow as $L_{S}^{*} \ge 1. 3$ in Fig. 9a due to cancellation of the favorable slippage effect and the electrokinetic retardation at large $L_{S}^{*}$.

Fig. 9

Slip effects on velocity distributions at ζ ^* = 1 with slip-dependent zeta potential. a K = 10; b K = 7.5; c K = 5

Fig. 10

Slip effects on streaming potential at various ζ ^* with slip-dependent zeta potential. a K = 10; b K = 7.5; c K = 5

In the situation of zero or small slip length, $E_{\text{x}}^{*}$ is lower at a lower zeta potential for weak EDL effect, and the enhancement of fluid slippage is relatively more pronounced until $E_{\text{x}}^{*}$ reaches a maximum. While at a high zeta potential, the streaming potential $E_{\text{x}}^{*}$ can be high even at a small slip length, but too strong EDL effect renders a premature development of slip effect. The turning points of the $E_{\text{x}}^{*} \sim L_{S}^{*}$ curve and the nullified $E_{\text{x}}^{*}$ occur earlier. At K = 7.5 and 5, as shown in Figs. 9b, c and 10b, c, similar behaviors present. The lower values of K in general result in a lower $E_{\text{x}}^{*}$ as that demonstrated previously, e.g., Soong and Wang (2003). However, comparing with that at K = 10, the weak augmentation of apparent zeta potential with lower K, Eq. 5, reduces the levels of $E_{\text{x}}^{*}$ generated at K = 7.5 and 5. Meanwhile, in the case of ζ ^* = 4 with very strong EDL effect, the favorable slip effect is little and, as $L_{S}^{*} > 4 \; \times \; 10^{ - 3}$, the slip-enhanced retardation reduces $E_{\text{x}}^{*}$ almost monotonically with increasing $L_{S}^{*}$.

The resultant electro-hydrodynamic effect on the fluid transport in microchannels is reflected on the flowrate parameter r _Q in Fig. 11. At K = 10 in Fig. 11a, it is revealed that too small slip length has little influence, and the noticeable effect emerges as $L_{S}^{*}$ up to the order of 10⁻², which correspond to the dimensional slip length L _S over 10 nm. Except the cases of high zeta potential ζ ^* = 4, in general, with the favorable slip effect dominant in low-$L_{S}^{*}$ regimes the flowrate is enhanced and reaches a local maximum at a certain slip length $L_{S,C1}^{*}$, e.g., $L_{S,C1}^{*} \approx 0.11$ in the case of ζ ^* = 1. As that mentioned earlier, increase in $L_{S}^{*}$ also augments zeta potential and in turn the electrokinetic retardation. The slip effect reverses after r _Q reaches the maximum. The flow reversal emerges at large $L_{S}^{*}$ and flowrate has a local minimum at $L_{S,C2}^{*}$, e.g., $L_{S,C2}^{*} \approx 0.4$ for ζ ^* = 1. Since the reversed flow in the near-wall region tends to move the counter-ions upstream and then diminishes $E_{\text{x}}^{*}$ and electrokinetic retardation as well. Under this condition, further increasing slip length over $L_{S,C2}^{*}$ brings the flowrate to recover and approach to the conventional Poiseuille flowrate (r _Q  = 1) as the resultant slip effect vanishes. In the low-K cases presented in Fig. 11b and c, the EDL effects are stronger and then the flowrates at the limiting condition of zero/low slip are lower due to stronger retardation than that for K = 10. However, with slip effect acting, Eq. 5 shows that a lower K results in weaker augmentation in apparent zeta potential and therefore the weaker electrokinetic retardation. Since $E_{\text{x}}^{*}$ is lower at lower K, the peaks of slip-enhanced flowrate are relatively higher in the cases of K = 7.5 and 5. On the other hand, at lower values of K the minima of r _Q are relatively lower due to the presence of the stronger flow reversal as that shown in Fig. 7. Using the criterion ${{\partial r_{Q} } \mathord{\left/ {\vphantom {{\partial r_{Q} } {\partial L_{S}^{*} }}} \right. \kern-\nulldelimiterspace} {\partial L_{S}^{*} }} < 0.01$ defined in the Section 3.2, the critical condition for asymptotically vanishing slip effect is denoted as $L_{S,C3}^{*}$. As an example, $L_{S,C3}^{*} \approx 1.3$ for ζ ^* = 1. In Fig. 12, the three critical conditions are plotted against zeta potential ζ ^*. It is revealed that the critical parameters all reduce with increases in zeta potential ζ ^* as well as in electrokinetic parameter K.

Fig. 11

Slip effects on flowrate ratio at various ζ ^* with slip-dependent zeta potential. a K = 10; b K = 7.5; c K = 5

Fig. 12

Critical conditions for occurrence of local maximum, local minimum, and asymptotic criterion ${{\partial r_{Q} } \mathord{\left/ {\vphantom {{\partial r_{Q} } {\partial L_{S}^{*} }}} \right. \kern-\nulldelimiterspace} {\partial L_{S}^{*} }} < 0.01$ in variations of slip effects on r _Q . Solution with zeta potential independent of slip

4 Concluding remarks

In the present study, slip effects on fluid transport of pressure-driven electrokinetic flows in hydrophobic microchannels have been analyzed by using a model with zeta potentials independent and dependent of slip length. Based on the present theory and numerical predictions, the following conclusions can be drawn.

• (1) The present analysis with a more realistic boundary condition of slip-dependent zeta potential reveals strong electro-hydrodynamic coupling natures in pressure-driven electrokinetic flows. The electric potential, fluid velocity, streaming potential, and flowrate vary remarkably with the change in slip length. Relatively, the conventional model with zeta potentials independent of slip length is oversimplified.

• (2) The slip effect on fluid transport varies non-monotonically with increasing slip length due to competition of slip-assisting effect and slip-enhanced electrokinetic retardation. Beyond a sufficiently large slip length, the flowrate becomes insensitive to the fluid slippage due to cancellation of the two counter effects. The critical conditions for occurrence of maximum, minimum, and insensitivity in flowrate-slip length correlation can be premature at a higher zeta potential and/or larger electrokinetic separation distance.

• (3) In the cases analyzed, the non-monotonic and asymptotic behaviors in the flowrate variations with slip length can be observed with a dimensional slip length of 10² nm or even lower order of 10 nm at conditions of high K or high zeta potential.

• (4) Most strikingly, the non-monotonic and vanishing tendencies of slip effect disclosed presently are quite different from the general notion of the more hydrophobic the channel wall, the higher the flowrate. It implies that further hydrophobizing the channel wall to enhance flowrate or save the pumping power does not necessarily work. Slip-assisting effect works only in the range of small slip lengths.

• (5) The present results offer some information for further understanding of microscale electrokinetic flow with complicated electro-hydrodynamic interactions, which might be useful in design of micro/nanofluidic devices. Currently, there is no experimental evidence available to support the present novel viewpoints. Although experimental work will encounter challenges, development of techniques for modifying/controlling surface characteristics, measurement of slip length and zeta potential at various conditions, correlation of slip-zeta potential, etc. are all extremely worthwhile investigations in future.