Effects of surface roughness on the stability and dynamics of microtubes conveying internal fluid

Abstract

In this article, the instability and dynamic characteristics of fluid-conveying microtubes with surface roughness are studied. A theoretical model is presented to describe the dynamic behaviors of rough microtubes by introducing correction factors, which account for the effects of the surface roughness both on the structure and the internal fluid. The results demonstrate that the surface roughness has little effect on the correction factors for structure, but dramatically decreases the correction factors for fluid, which indicates that the Coriolis force and centripetal force caused by the internal fluid are reduced. For clamped–clamped microtubes, the surface roughness makes the nondimensional critical velocity for divergence and the natural frequency increase. And as the roughness height or the wave number increases, both the critical velocity and the frequency increase. For cantilevered microtubes, the critical velocity for fluttering depends on the surface roughness and the mass ratio. Curves describing the relationship between the nondimensional critical velocity $\hat{U}_{\text{cr}}$ and the mass ratio $\beta$ for smooth and rough microtubes are presented. Each curve contains a S-shaped segment, which is associated with the instability–restabilization–instability sequence. The surface roughness induces the curve shifting to the upper right of the $\hat{U}_{\text{cr}}$ − $\beta$ plane. In the region far away from the S-shaped segment, the critical velocity increases with the increasing of roughness height. And in the vicinity of S-shaped segment, the critical velocity for the rough microtube may be less than the value for the smooth microtube because of the sharply varying of critical velocity with mass ratio. The effects of surface roughness on the frequency of cantilevered microtubes are also analyzed and discussed.

1 Introduction

As one classical fluid–structure interaction problem, dynamic analysis of fluid-conveying pipes/tubes has been a hot topic for scholars from decades ago (Paidoussis, 1998) to recent years (Dai et al., 2020; Giacobbi et al., 2020; Li et al., 2020; Lyu et al., 2020; Peng et al., 2018, 2019), due to the rich and interesting properties in their dynamic behaviors. Microtubes conveying fluid have a wide range of applications in micro/nano electromechanical systems, such as mass sensing (Kim et al., 2016), drug injection (Schwengber et al., 2015), fluid transporting (Mainak et al., 2005) and so on. Because of the complex interactions between the structure and fluid, fluid-conveying microtubes exhibit rich dynamic behaviors, including buckling, flutter, chaos, etc. As a result, a number of researchers paid much attention to the dynamics and stability of microtubes conveying fluid (Dehrouyeh-Semnani et al., 2017; Ghayesh et al., 2019; Ghazavi et al., 2018; Hu et al., 2016).

Owing to the small size of microtubes, the behaviors of both micro-structures and micro-flows are quite different from macro tubes. To accurately predict dynamic characteristics, both the micro-structure and micro-fluid should be appropriately addressed. Numerous researchers focused on modeling micro-structures and developed several methods, including modified couple stress theory (Hu et al., 2016; Wang, 2010), strain gradient theory (Ghazavi et al., 2018; Hosseini and Bahaadini, 2016), nonlocal elasticity theory (Li et al., 2016; Rahmati and Khodaei, 2018), second strain gradient theory (Ghazavi et al., 2018) and so on. Wang (Wang, 2010) firstly developed a theoretical model to describe dynamic behaviors of microtubes conveying fluid based on the modified couple stress theory. The Hamilton’s principle was used to derive the equations of motion and the differential quadrature method was adopted to solve the equations. The results showed that the critical flow velocities obtained using the modified couple stress theory were higher than the ones obtained based on the classical continuum theory. Ghazavi et al. (2018) adopted the second strain gradient theory for modeling the micro/nano tubes conveying fluid. According to the second strain gradient theory, the critical velocities were higher than those predicted by the classical theory and strain gradient theory. Li et al. applied nonlocal strain gradient theory along with the Timoshenko and Euler–Bernoulli models to describe the dynamics and stability of fluid-conveying microtubes. The results demonstrated that the critical flow velocity increased as the material length scale parameter increased or the nonlocal parameter decreased.

The microscale fluid also has a significant effect on the stability and dynamic behaviors of fluid-conveying microtubes. For the macro tube, the flow is usually turbulent (Paidoussis, 1998). Consequently, the flow velocity is assumed to be constant across the cross section and is treated as a solid moving at a constant velocity (Li et al., 2016). However, the Reynolds numbers for fluid flowing in microtubes are quite small and hence the fluid flows are usually laminar. For laminar flows, the velocities are not constant across the cross section and the velocity profiles should be taken into consideration. Guo et al. (2010) modified the centripetal force term of governing equations for microtubes conveying fluid by considering the non-uniformity of flow velocities. The results demonstrated that because of the velocity profile, the critical velocities for divergence and flutter were lower than those with plug flow. Wang et al. (2013) studied the in-plane and out-of-plane vibration of fluid-conveying microtubes with different cross-sectional shapes. The size effects of micro-structure and micro-flow were both taken intoconsideration. Bobovnik and Kutin (2018) studied the fluid–structure forces induced by laminar fluid in vibrating pipes using CFD numerical models. It was found that the centripetal correction factor was affected by vibration frequencies, lengths of the pipe and vibration amplitudes.

Surface roughness is an inherent byproduct of almost all fabrication techniques (Parfenyev et al., 2019). For microstructures, it is very likely to generate rough surfaces due to the limitation of fabrication processes. The dynamic behaviors of microstructures were dependent on the surface roughness. Shaat and Faroughi (2018) firstly researched the effect of surface integrity on the vibration characteristics of microbeams. The surface roughness, altered layer and surface excess energy were taken into account. The results showed that surface integrity may decrease/increase the beam natural frequency. Shaat et al. (2020) investigated the buckling behaviors of beam-typed micro/nano structures under the influence of surface roughness. It was revealed that surface roughness distorted the buckling configurations and post-buckling mode shapes. Furthermore, a post-buckling mode inversion due to surface roughness was found. Surface roughness also has significant effect on the flow characteristics in rough microtubes. In general, the characteristic height of generated surface roughness ranges from tens of nanometers to several micrometers (Jaeger et al., 2012; Zhou et al., 2017), which is comparable to the characteristic length of microtubes. A number of researches have researched the effect of surface roughness on the fluid flows in microtubes through experimental, theoretical and numerical methods (Akyildiz and Siginer, 2017; Dey et al., 2021; Duan et al., 2008; Mala and Li, 1999; Song et al., 2018; Tang et al., 2007). As early as 1999, Mala and Li (Mala and Li, 1999) experimentally studied liquid flow through microtubes with diameters ranging from 50 to 254 μm and found that the friction factor was obviously higher than that predicted by the Poiseuille flow theory. Tang et al. (2007) summarized the experimental results of flow characteristics in microtubes and indicated that surface roughness led to the increasing of friction factors. Duan et al. (2008) studied the influences of corrugated surface roughness on laminar flow in microtubes based on the Stokes equation. An analytical model was presented through a perturbation method to predict velocity distributions and friction factors for rough microtubes. Song et al. (2018) investigated flow characteristics in circular microtubes with periodically structured surface roughness. The flow field and pressure drop were analyzed and discussed based on a theoretical model and numerical simulations. Marusic-Paloka and Pazanin (2020) studied the influences of both surface roughness and inertia on the flow in a corrugated pipe and proposed a high order correction of the Hagen–Poiseuille velocity. Based on these results, a new formula for the Darcy friction coefficient was developed.

According to the results published in the literature, surface roughness not only affects the dynamic behaviors of microstructures, but also has important effect on the fluid flow through rough microtubes. It is well known that the fluid-conveying microtube is a typical fluid–structure coupling system. Consequently, the stability and dynamic properties of the microtube is dependent on the surface roughness. To the authors’ best knowledge, there is no single study related to the roughness-dependent stability and dynamic behaviors of rough microtubes. Therefore, this article aims to analytically explore this topic.

The article is outlined as follows. In Sect. 2, a theoretical model is developed by considering the surface roughness of microtube to characterize the stability and dynamic behaviors of rough microtubes. The effects of surface roughness on the dynamics of microtubes with different boundary conditions are analyzed and discussed in Sect. 3. Some conclusions are drawn in Sect. 4.

2 Model development

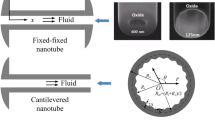
Figure 1a shows microtubes with surface roughness (Kim et al., 2016). These microtubes were fabricated through the silicon-on-nothing process and were utilized for mass sensing. It can be found that in the axial direction the inner wall of the microtube is almost smooth. And in the circumferential direction, there exists obvious surface roughness. Furthermore, the distribution of roughness height is approximately periodic. Hence, a microtube with sinusoidally wavy wall is considered, as illustrated in Fig. 1b. The mean radius of the microtube is denoted as $R_{\text{m}}$. A cylindrical coordinate system (r, θ, x) is adopted, where x axis is the direction of fluid flow. The surface roughness of the inner wall is described by

$$R_{\text{i}} = R_{\text{m}} \left[ {1 + \varepsilon \sin \left( {\lambda \theta } \right)} \right],$$

(1)

Fig. 1

a Microtubes with periodic surface roughness. b Schematic for a rough microtube conveying fluid

where $R_{\text{i}}$ is the real radius of the inner wall, $\varepsilon$ is the relative roughness which is defined as $\varepsilon = {\Delta \mathord{\left/ {\vphantom {\Delta {R_{\text{m}} }}} \right. \kern-\nulldelimiterspace} {R_{\text{m}} }}$, $\lambda$ is the wave number that can be expressed as $\lambda = {{2\pi R_{\text{m}} } \mathord{\left/ {\vphantom {{2\pi R_{\text{m}} } b}} \right. \kern-\nulldelimiterspace} b}$ and $\theta$ is the circumferential coordinate. The parameters $\Delta$ and b are the amplitude and wavelength of the surface roughness, as shown in Fig. 1b.

Generally, the length of the microtube is much larger than the diameter. Hence, its dynamic characteristics can be described by the Euler–Bernoulli beam theory. Generally, beam element and fluid element are subjected to many forces, including fluid pressure, gravity, friction, tension, shear force, bending moment, etc. In this paper, the influences of surface roughness on the dynamic characteristics of fluid-conveying microtubes are focused on. In order to obtain a concise and clear dynamic control equation, the gravity, tensioning and pressurization effects are neglected. If readers are interested in these effects, please refer to Paidoussis’s work (Paidoussis, 1998). Figure 2a shows the forces and moments acting on a beam element. According to the theory of fluid mechanics, the fluid in the beam element can be regarded as composed of a large number of fluid particles, whose density is $\rho_{\text{f}}$, volume is $\Delta V_{\text{p}}$ and acceleration is $a_{\text{py}}$. Applying the Newton’s second law to the beam element, yields:

$$\frac{\partial Q}{{\partial x}}\Delta L = \rho_{\text{t}} V_{\text{t}} a_{\text{ty}} + \sum\limits_{{V_{\text{f}} }} {\rho_{\text{f}} \Delta V_{\text{p}} a_{\text{py}} } ,$$

(2)

$$Q = \frac{\partial M}{{\partial x}} = - EI^{(r)} \frac{{\partial^{3} w}}{{\partial x^{3} }},$$

(3)

Fig. 2

a Forces and moments acting on the beam element. b Motion of the fluid particle in the relative coordinate system

where Q is the transverse shear force, $\Delta L$ is the length of the microtube element, M is the moment, $\rho_{\text{t}}$ and $\rho_{\text{f}}$ are the densities of the microtube and fluid, $V_{\text{t}}$ and $V_{\text{f}}$ are the volumes of the microtube element and fluid element, $a_{\text{ty}}$ is the acceleration of the beam element, $\Delta V_{\text{p}}$ is the volume of a fluid particle, E is the Young’s modulus and $I^{(r)}$ is the second moment of cross-sectional area. The acceleration of microtube can be easily given by $a_{\text{ty}} = {{\partial^{2} w} \mathord{\left/ {\vphantom {{\partial^{2} w} {\partial t^{2} }}} \right. \kern-\nulldelimiterspace} {\partial t^{2} }}$. In order to obtain $a_{\text{py}}$, the motion of a fluid particle is analyzed.

As shown in Fig. 2b, the fluid particle moves at a velocity of u in the relative coordinate system $x^{\prime} - o^{\prime} - y^{\prime}$. Because of the effect of viscosity and surface roughness, the velocity of fluid particle is nonuniform and depends on the position. The microtube is considered to be slender and its lateral motions, w(x, t), to be small and of long wavelength as compared to the diameter. As a result, the curvilinear coordinate s along the centerline of the microtube and the coordinate x can be used interchangeably. According to the theorem of acceleration composition, the acceleration of fluid particle in the absolute coordinate system is composed of the convected acceleration, the relative acceleration and the Coriolis acceleration. The acceleration of coordinate system $x^{\prime} - o^{\prime} - y^{\prime}$ relative to the absolute coordinate system is ${{\partial^{2} w} \mathord{\left/ {\vphantom {{\partial^{2} w} {\partial t^{2} }}} \right. \kern-\nulldelimiterspace} {\partial t^{2} }} + {{\partial^{3} w} \mathord{\left/ {\vphantom {{\partial^{3} w} {\partial x\partial^{2} t}}} \right. \kern-\nulldelimiterspace} {\partial x\partial^{2} t}}$. The former term indicates the translational acceleration while the latter indicates the rotational acceleration. Considering the small-deflection approximation, yields ${{\partial^{2} w} \mathord{\left/ {\vphantom {{\partial^{2} w} {\partial t^{2} }}} \right. \kern-\nulldelimiterspace} {\partial t^{2} }} \gg {{\partial^{3} w} \mathord{\left/ {\vphantom {{\partial^{3} w} {\partial x\partial^{2} t}}} \right. \kern-\nulldelimiterspace} {\partial x\partial^{2} t}}$. Hence, the convected acceleration is expressed as ${{\partial^{2} w} \mathord{\left/ {\vphantom {{\partial^{2} w} {\partial t^{2} }}} \right. \kern-\nulldelimiterspace} {\partial t^{2} }}$. Based on the Euler–Bernoulli beam theory, the curvature of microtube element is expressed as ${{\partial^{2} w} \mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x^{2} }}} \right. \kern-\nulldelimiterspace} {\partial x^{2} }}$. Hence, the acceleration of fluid particle in the relative coordinate system $x^{\prime} - o^{\prime} - y^{\prime}$ can be given as $u^{2} \cdot {{\partial^{2} w} \mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x^{2} }}} \right. \kern-\nulldelimiterspace} {\partial x^{2} }}$. Relative to the absolute coordinate system, the coordinate system $x^{\prime} - o^{\prime} - y^{\prime}$ has a rotational velocity ${{\partial^{2} w} \mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x\partial t}}} \right. \kern-\nulldelimiterspace} {\partial x\partial t}}$. The Coriolis acceleration of fluid particle is expressed as $2u \cdot {{\partial^{2} w} \mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x\partial t}}} \right. \kern-\nulldelimiterspace} {\partial x\partial t}}$. Consequently, the acceleration of fluid particle in the absolute coordinate system can be given by

$$a_{\text{py}} = \frac{{\partial^{2} w}}{{\partial t^{2} }} + u^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2u\frac{{\partial^{2} w}}{\partial x\partial t}.$$

(4)

Because the cross-section area keeps constant along the axial direction, the velocity of fluid particle is assumed as constant in the direction. Moreover, considering that the vibration amplitude of the microtube is very small, the velocity of fluid particle in the vibrating microtube is assumed to be equal to the one in the static microtube. Hence, the governing equation for the vibration of rough microtube can be expressed as:

$$EI^{(r)} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \left( {\rho_{\text{t}} A_{\text{t}} + \rho_{\text{f}} A_{\text{f}} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\rho_{\text{f}} \left( {\int_{{S_{\text{f}} }} {u_{x} {\text{d}}S} } \right)\frac{{\partial^{2} w}}{\partial x\partial t} + \rho_{\text{f}} \left( {\int_{{S_{\text{f}} }} {u_{x}^{2} dS} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0,$$

(5)

where $u_{x}$ is the fluid velocity in the axial direction of the rough microtube. For clamped–clamped microtubes, the boundary conditions are subjected to:

$$\begin{aligned} & w\left( {0,t} \right) = 0,\quad \frac{{\partial w\left( {0,t} \right)}}{\partial x} = 0, \\ & w\left( {L,t} \right) = 0,\quad \frac{{\partial w\left( {L,t} \right)}}{\partial x} = 0. \\ \end{aligned}$$

(6)

For cantilevered microtubes, the boundary conditions are subjected to:

$$\begin{aligned} & w\left( {0,t} \right) = 0,\quad \frac{{\partial w\left( {0,t} \right)}}{\partial x} = 0, \\ & \frac{{\partial^{2} w\left( {L,t} \right)}}{{\partial x^{2} }} = 0,\quad \frac{{\partial^{3} w\left( {L,t} \right)}}{{\partial x^{3} }} = 0. \\ \end{aligned}$$

(7)

In order to obtain the flow velocity $u_{x}$, the flow characteristics in the rough microtube should be analyzed. Duan et al. (2008) has developed an analytic formula for fluid velocities in corrugated microtubes using a perturbation method. For the completeness of the article, the analysis process of flow characteristics is briefly introduced. And interested readers can refer to the reference (Duan et al. 2008). The Navier–Stokes equations for steady flow in the cylindrical coordinate system can be written as:

$$\begin{aligned} & \rho_{\text{f}} \left( {u_{\text{r}} \frac{{\partial u_{\text{r}} }}{\partial r} + \frac{{u_{\theta } }}{r}\frac{{\partial u_{\text{r}} }}{\partial \theta } + u_{x} \frac{{\partial u_{\text{r}} }}{\partial x} - \frac{{u_{\theta }^{2} }}{r}} \right) = - \frac{\partial p}{{\partial r}} + \mu \left( {\frac{{\partial^{2} u_{\text{r}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{\text{r}} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u_{\text{r}} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} u_{\text{r}} }}{{\partial x^{2} }} - \frac{2}{{r^{2} }}\frac{{\partial u_{\theta } }}{\partial \theta } - \frac{{u_{\text{r}} }}{{r^{2} }}} \right) \\ & \rho_{\text{f}} \left( {u_{\text{r}} \frac{{\partial u_{\theta } }}{\partial r} + \frac{{u_{\theta } }}{r}\frac{{\partial u_{\theta } }}{\partial \theta } + u_{x} \frac{{\partial u_{\theta } }}{\partial x} + \frac{{u_{\text{r}} u_{\theta } }}{r}} \right) = - \frac{1}{r}\frac{\partial p}{{\partial \theta }} + \mu \left( {\frac{{\partial^{2} u_{\theta } }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{\theta } }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u_{\theta } }}{{\partial \theta^{2} }} + \frac{{\partial^{2} u_{\theta } }}{{\partial x^{2} }} + \frac{2}{{r^{2} }}\frac{{\partial u_{\text{r}} }}{\partial \theta } - \frac{{u_{\theta } }}{{r^{2} }}} \right) \\ & \rho_{\text{f}} \left( {u_{\text{r}} \frac{{\partial u_{x} }}{\partial r} + \frac{{u_{\theta } }}{r}\frac{{\partial u_{x} }}{\partial \theta } + u_{x} \frac{{\partial u_{x} }}{\partial x}} \right) = - \frac{\partial p}{{\partial x}} + \mu \left( {\frac{{\partial^{2} u_{x} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{x} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u_{x} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} u_{x} }}{{\partial x^{2} }}} \right). \\ \end{aligned}$$

(8)

where $u_{\text{r}}$, $u_{\theta }$ and $u_{x}$ are components of flow velocities in the radial, circumferential and axial directions, respectively, and $\mu$ is the fluid viscosity. The considered rough microtube is axisymmetric and the cross-section keeps constant in the axial direction. As a result, the velocity components $u_{\text{r}}$ and $u_{\theta }$ are zero, and the velocity component $u_{x}$ does not vary along the flow direction. Consequently, Eq. (8) is reduced to

$$- \frac{{{\text{d}}p}}{{{\text{d}}x}} + \mu \left( {\frac{{\partial^{2} u_{x} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{x} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u_{x} }}{{\partial \theta^{2} }}} \right) = 0.$$

(9)

The boundary condition for the flow can be given as

$$u_{x} \left( {r,\theta } \right) = 0\;\;{\text{at}}\;\;r = R_{\text{m}} \left[ {1 + \varepsilon \sin \left( {\lambda \theta } \right)} \right].$$

(10)

Using the perturbation method, the velocity u_x is expanded in terms of $\varepsilon$

$$u_{x} \left( {r,\theta } \right) = u_{x}^{\left( 0 \right)} \left( {r,\theta } \right) + \varepsilon u_{x}^{\left( 1 \right)} \left( {r,\theta } \right) + \varepsilon^{2} u_{x}^{\left( 2 \right)} \left( {r,\theta } \right) + \cdots$$

(11)

By substituting Eq. (11) into Eqs. (9) and (10), the expressions of $u_{x}^{\left( 0 \right)}$, $u_{x}^{\left( 1 \right)}$ and $u_{x}^{\left( 2 \right)}$ can be given after some mathematical calculations,

$$u_{x}^{\left( 0 \right)} = - \frac{{{\text{d}}p}}{{{\text{d}}x}} \cdot \frac{1}{\mu } \cdot \frac{{R_{\text{m}}^{2} - r^{2} }}{4},$$

(12)

$$u_{x}^{\left( 1 \right)} = - \frac{{{\text{d}}p}}{{{\text{d}}x}} \cdot \frac{1}{\mu } \cdot \left[ {\frac{1}{2}R_{\text{m}}^{2} \left( {\frac{r}{{R_{\text{m}} }}} \right)^{\lambda } \sin \left( {\lambda \theta } \right)} \right],$$

(13)

$$u_{x}^{\left( 2 \right)} = - \frac{{{\text{d}}p}}{{{\text{d}}x}} \cdot \frac{1}{\mu } \cdot \left[ {\frac{1 - 2\lambda }{8}R_{\text{m}}^{2} - \frac{1 - 2\lambda }{8}R_{\text{m}}^{2} \left( {\frac{r}{{R_{\text{m}} }}} \right)^{2\lambda } \cos \left( {2\lambda \theta } \right)} \right].$$

(14)

As a result, the parameters in Eq. (5) associated with the fluid velocity $u_{x}$ are given by

$$\begin{gathered} \int_{{S_{\text{f}} }} {u_{x} } {\text{d}}S = \frac{{ - {{{\text{d}}p} \mathord{\left/ {\vphantom {{{\text{d}}p} {{\text{d}}x}}} \right. \kern-\nulldelimiterspace} {{\text{d}}x}}}}{\mu }\frac{1}{8}\pi R_{\text{m}}^{4} \left[ {1 - \left( {2\lambda - 3} \right)\varepsilon^{2} } \right] \hfill \\ \int_{{S_{\text{f}} }} {u_{x}^{2} {\text{d}}S} = \left( {\frac{{ - {{{\text{d}}p} \mathord{\left/ {\vphantom {{{\text{d}}p} {{\text{d}}x}}} \right. \kern-\nulldelimiterspace} {{\text{d}}x}}}}{\mu }} \right)^{2} \pi R_{\text{m}}^{6} \left[ {\frac{1}{48} + \frac{1}{{8\left( {\lambda + 1} \right)}}\varepsilon^{2} + \frac{1}{32}\left( {1 - 2\lambda } \right)\varepsilon^{2} } \right]. \hfill \\ \end{gathered}$$

(15)

The governing equation for the vibration of the rough microtube conveying fluid can be expressed as

$$EI^{(r)} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \left( {\rho_{\text{t}} A_{\text{t}}^{(r)} + \rho_{\text{f}} A_{\text{f}}^{(r)} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\rho_{\text{f}} A_{\text{f}}^{(s)} \left( {{\text{CFF}}_{1} } \right)U_{\text{s}} \frac{{\partial^{2} w}}{\partial x\partial t} + \frac{4}{3}\left( {{\text{CFF}}_{2} } \right)\rho_{\text{f}} A_{\text{f}}^{(s)} U_{\text{s}}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} = 0,$$

(16)

where $A_{\text{t}}^{(r)}$ and $A_{\text{f}}^{(r)}$ are the structure cross-sectional area and the fluid cross-sectional area of the rough microtube, respectively, $A_{\text{f}}^{(s)} = \pi R_{\text{m}}^{2}$ is the fluid cross-sectional area of the smooth microtube, CFF₁ and CFF₂ are correction factors for fluid due to the surface roughness, and $U_{\text{s}}$ is the averaged fluid velocity of smooth microtube. The above parameters are written as

$$I^{\left( r \right)} = \frac{1}{4}\pi R_{o}^{4} - \frac{1}{4}\pi R_{\text{m}}^{4} - \frac{3}{4}\pi \varepsilon^{2} R_{\text{m}}^{4} - \frac{3}{32}\pi \varepsilon^{4} R_{\text{m}}^{4} ,$$

(17)

$$A_{\text{t}}^{\left( r \right)} = \pi R_{o}^{2} - \pi R_{\text{m}}^{2} - \frac{1}{2}\pi \varepsilon^{2} R_{\text{m}}^{2} ,$$

(18)

$$A_{\text{f}}^{\left( r \right)} = \pi R_{\text{m}}^{2} + \frac{1}{2}\pi \varepsilon^{2} R_{\text{m}}^{2} ,$$

(19)

$${\text{CFF}}_{1} = 1 - \left( {2\lambda - 3} \right)\varepsilon^{2} ,$$

(20)

$${\text{CFF}}_{2} = 1{ + }\frac{6}{{\left( {\lambda { + }1} \right)}}\varepsilon^{2} { + }\frac{{3\left( {1{ - }2\lambda } \right)}}{2}\varepsilon^{2} ,$$

(21)

$$U_{\text{s}} = \frac{{ - {{{\text{d}}p} \mathord{\left/ {\vphantom {{{\text{d}}p} {{\text{d}}x}}} \right. \kern-\nulldelimiterspace} {{\text{d}}x}}}}{\mu }\frac{1}{8}R_{\text{m}}^{2} ,$$

(22)

where $R_{o}$ is the outer radius of the microtube. When the surface roughness is not considered, Eq. (16) reduces to the governing equation for smooth microtube conveying fluid,

$$EI^{(s)} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \left( {\rho_{\text{t}} A_{\text{t}}^{(s)} + \rho_{\text{f}} A_{\text{f}}^{(s)} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\rho_{\text{f}} A_{\text{f}}^{(s)} U_{\text{s}} \frac{{\partial^{2} w}}{\partial x\partial t} + \frac{4}{3}\rho_{\text{f}} A_{\text{f}}^{(s)} U_{\text{s}}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} = 0.$$

(23)

In order to compare the stability and dynamic characteristics of rough microtubes and smooth microtubes, the governing Eqs. (16) and (23) are separately nondimensionalized,

$$\eta^{\prime\prime\prime\prime} + \ddot{\eta } + 2\sqrt \beta \hat{U}\dot{\eta^{\prime}} + \frac{4}{3}\hat{U}^{2} \eta^{\prime\prime} = 0,$$

(24)

$$\left( {{\text{CFS}}_{{1}} } \right)\eta^{\prime\prime\prime\prime} + \left( {{\text{CFS}}_{2} } \right)\ddot{\eta } + \left( {{\text{CFF}}_{{1}} } \right)2\sqrt \beta \hat{U}\dot{\eta^{\prime}} + \left( {{\text{CFF}}_{2} } \right)\frac{4}{3}\hat{U}^{2} \eta^{\prime\prime} = 0,$$

(25)

where

$$\begin{gathered} \eta = \frac{w}{L},\quad \xi = \frac{x}{L},\quad {\text{CFS}}_{1} = \frac{{I^{(r)} }}{{I^{(s)} }},\quad {\text{CFS}}_{2} = \frac{{\rho_{\text{t}} A_{\text{t}}^{\left( r \right)} + \rho_{\text{f}} A_{\text{f}}^{\left( r \right)} }}{{\rho_{\text{t}} A_{\text{t}}^{\left( s \right)} + \rho_{\text{f}} A_{\text{f}}^{\left( s \right)} }} \hfill \\ \tau = \sqrt {\frac{{EI^{(s)} }}{{\rho_{\text{t}} A_{\text{t}}^{\left( s \right)} + \rho_{\text{f}} A_{\text{f}}^{\left( s \right)} }}} \frac{t}{{L^{2} }},\quad \hat{U} = \sqrt {\frac{{\rho_{\text{f}} A_{\text{f}}^{(s)} }}{{EI^{(s)} }}} U_{\text{s}} L,\quad \beta = \frac{{\rho_{\text{f}} A_{\text{f}}^{(s)} }}{{\rho_{\text{t}} A_{\text{t}}^{\left( s \right)} + \rho_{\text{f}} A_{\text{f}}^{\left( s \right)} }}, \hfill \\ \end{gathered}$$

(26)

and the spatial and temporal derivatives are given by $\eta^{\prime} = \left( {{{\partial \eta } \mathord{\left/ {\vphantom {{\partial \eta } {\partial \varepsilon }}} \right. \kern-\nulldelimiterspace} {\partial \varepsilon }}} \right)$ and $\dot{\eta } = \left( {{{\partial \eta } \mathord{\left/ {\vphantom {{\partial \eta } {\partial \tau }}} \right. \kern-\nulldelimiterspace} {\partial \tau }}} \right)$. The parameters CFS₁ and CFS₂ are correction factors for structure induced by the surface roughness. The boundary conditions in nondimensional form are expressed as:

$$\eta \left( {0,t} \right) = 0,\quad \eta^{\prime}\left( {0,t} \right) = 0,\quad \eta \left( {1,t} \right) = 0,\quad \eta^{\prime}\left( {1,t} \right) = 0,$$

(27)

for clamped–clamped microtubes and

$$\eta \left( {0,t} \right) = 0,\quad \eta^{\prime}\left( {0,t} \right) = 0,\quad \eta^{\prime\prime}\left( {1,t} \right) = 0,\quad \eta^{\prime\prime\prime}\left( {1,t} \right) = 0,$$

(28)

for cantilevered microtubes. In the next, by solving Eqs. (24) and (25) through the Galerkin method, the effect of surface roughness on the stability and dynamic behaviors of microtubes conveying fluid are analyzed and discussed.

3 Results and discussions

3.1 Correction factors

Equation (24) is the classical governing equation for smooth fluid-conveying microtubes. The four terms on the left side sequentially represent the elastic force of the structure, the inertial force of the fluid and structure, the Coriolis force and the centripetal force caused by the fluid flow. By comparing Eqs. (25) to (24), it is found that surface roughness affects all these four terms, which can be characterized by four correction factors, CFS₁, CFS₂, CFF₁ and CFF₂.

Parameters CFS₁ and CFS₂ are correction factors for structure. The surface roughness changes the geometry of the microtube, and hence affects the elastic force and the inertial force. From Eqs. (17)–(19) and Eq. (26), it is known that CFS₁ and CFS₂ depend on the roughness height $\varepsilon$ and have nothing to do with the wave number $\lambda$. The parameter CFS₁ indicates the effect of surface roughness on the elastic force. Surface roughness changes the cross-section of microtube and consequently affects the bending stiffness. Figure 3 demonstrates the variation of CFS₁ for different geometrical parameters. The parameter $\gamma$ is defined as $\gamma = {{\left( {R_{o} - R_{\text{m}} } \right)} \mathord{\left/ {\vphantom {{\left( {R_{o} - R_{\text{m}} } \right)} {R_{\text{m}} }}} \right. \kern-\nulldelimiterspace} {R_{\text{m}} }}$, which means the ratio of the thickness to the nominal inner radius of microtube. As shown in Fig. 3, for $\gamma = 1$, as surface roughness increases, the parameter CFS₁, almost keeps constant. This indicates that the elastic force of microtube is almost independent on surface roughness when the microtube is thick enough. However, when the microtube is thin, surface roughness can reduce the bending stiffness up to about 5%. The parameter CFS₂ characterizes the relationship between the surface roughness and the inertial force. By affecting the cross-section shape of the microtube, the surface roughness also influences the mass of structure and fluid per unit length, thus having an effect on the inertial force, which is described by the parameter CFS₂. As demonstrated in Fig. 4, CFS₂ not only depends on the surface roughness $\varepsilon$ and the geometrical parameter $\gamma$, but also affected by the ratio of structure density to fluid density ${{\rho_{\text{t}} } \mathord{\left/ {\vphantom {{\rho_{\text{t}} } {\rho_{\text{f}} }}} \right. \kern-\nulldelimiterspace} {\rho_{\text{f}} }}$. When ${{\rho_{\text{t}} } \mathord{\left/ {\vphantom {{\rho_{\text{t}} } {\rho_{\text{f}} }}} \right. \kern-\nulldelimiterspace} {\rho_{\text{f}} }}$ is less than one, CFS₂ increases as the surface roughness increases. However, when ${{\rho_{\text{t}} } \mathord{\left/ {\vphantom {{\rho_{\text{t}} } {\rho_{\text{f}} }}} \right. \kern-\nulldelimiterspace} {\rho_{\text{f}} }}$ is larger than one, CFS₂ decreases as the surface roughness increases. In general, the density of structure is larger than the one of fluid. Hence, the case that the parameter ${{\rho_{\text{t}} } \mathord{\left/ {\vphantom {{\rho_{\text{t}} } {\rho_{\text{f}} }}} \right. \kern-\nulldelimiterspace} {\rho_{\text{f}} }}$ is larger than 1 is focused on. From Fig. 4c, d, it can be found that the relationship between the CFS₂ and surface roughness is similar to that of CFS₁. When the microtube is thick, the surface roughness has no obvious effect on CFS₂. And when the microtube is thin, the surface roughness makes CFS₂ decrease. In addition, when the density of structure is much larger than the one of fluid, the effect of surface roughness is more significant. On the other hand, if the structure density equals to the fluid density, CFS₂ keeps constant as unity.

Fig. 3

Variation of CFS₁ with surface roughness for different geometrical parameters

Fig. 4

Variation of CFS₂ with surface roughness for different geometrical parameters a ${{\rho_{\text{t}} } \mathord{\left/ {\vphantom {{\rho_{\text{t}} } {\rho_{\text{f}} }}} \right. \kern-\nulldelimiterspace} {\rho_{\text{f}} }} = 0.1$ b ${{\rho_{\text{t}} } \mathord{\left/ {\vphantom {{\rho_{\text{t}} } {\rho_{\text{f}} }}} \right. \kern-\nulldelimiterspace} {\rho_{\text{f}} }} = 0.5$ c ${{\rho_{\text{t}} } \mathord{\left/ {\vphantom {{\rho_{\text{t}} } {\rho_{\text{f}} }}} \right. \kern-\nulldelimiterspace} {\rho_{\text{f}} }} = 2$ and d ${{\rho_{\text{t}} } \mathord{\left/ {\vphantom {{\rho_{\text{t}} } {\rho_{\text{f}} }}} \right. \kern-\nulldelimiterspace} {\rho_{\text{f}} }} = 10$

Parameters CFF₁ and CFF₂ are correction factors for fluid. Surface roughness affects the flow characteristics in the microtube, and hence influences the Coriolis force and centripetal force. In order to clarify the effect of surface roughness on the flow velocity and verify the correctness of the theoretical results obtained by the perturbation method, numerical simulations are performed using the finite volume method. The nominal radius of microtubes is 30 μm, and the pressure gradient is 10⁷ Pa/m. Figure 5 shows the contours of fluid velocity in smooth and rough microtubes. The values of velocity are normalized by the maximum velocity in the smooth microtube. Figure 6 demonstrates the distribution of flow velocities in the radial direction with a comparison between the theoretical and numerical results. It can be found that the surface roughness has two main effects on the fluid flow in the microtube. Firstly, the surface roughness decreases the flow velocity. As shown in Figs. 5c and 6, the surface roughness with parameters $\varepsilon = 0.05$ and $\lambda = 20$ reduces the maximum velocity by about 10%. Secondly, The surface roughness disturbs the fluid flow near the wall, which makes the velocity contours no longer circular. And this disturbance decreases with the increasing of the distance between the fluid and the wall until it disappears. In addition, as shown in Fig. 6, the theoretical results for flow velocities agree well with the numerical results, which indicates that the analytical results can accurately characterize the flow behaviors in rough microtubes.

Fig. 5

Contours of fluid velocities in smooth and rough microtubes

Fig. 6

Distribution of fluid velocities in the radial direction for smooth and rough microtubes with a comparison between the theoretical and numerical results

Because the surface roughness reduces the flow velocities in the microtube, both the Coriolis force and centripetal force induced by fluid flow decrease with the increasing of surface roughness height, as shown in Fig. 7. Moreover, the increase in the wave number $\lambda$ aggravates the influence of roughness height on the correction factors for fluid. By comparing Fig. 7 to Fig. 3 and Fig. 4, it can be found that the surface roughness has much more significant effect on correction factors for fluid than that on correction factors on structure. As demonstrated in Fig. 7, for a very rough microtube with parameters $\varepsilon = 0.1$ and $\lambda = 30$, the correction factor CFF₁ can be reduced by more than 50% and the factor CFF₂ is decreased by more than 80%. For the same roughness parameter, the variation of correction factors for structure is about within 4%. Therefore, it can be inferred that the surface roughness mainly affects the dynamics of the microchannel by influencing the fluid flow. In the next, the stability and dynamic behaviors of rough microtubes for different boundary conditions are analyzed and discussed.

Fig. 7

The variation of CFF₁ and CFF₂ with the increasing of the surface roughness height for different wave numbers

3.2 Clamped–clamped microtubes

Solving the governing equations for smooth and rough microtubes subjected to the clamped–clamped boundary condition using the Galerkin method, the complex eigenfrequencies $\hat{\omega }$ are obtained. The real part of $\hat{\omega }$ is the dimensionless oscillation frequency, and the ratio of the imaginary to the real parts is the damping ratio of the system. As shown in Fig. 8, whether the microtube is smooth or rough, the frequency decreases and the damping ratio keeps constant as zero with the increasing of the flow velocity. And once the flow velocity exceeds the critical value, the instability of divergence occurs. Hence, the surface roughness does not change the instability mode of clamped–clamped microtubes. However, it has obvious effect on the critical flow velocity for divergence. Figure 8a shows the Argand diagram for a smooth microtube. All the four correction factors equal to 1. Figure 8b is for a rough microtube with a thick wall. As discussed in Sect. 3.1, when the microtube is thick enough, the surface roughness has little effect on the correction factors for structure. Hence, Fig. 8b mainly represents the influence of fluid flow on the instability of a rough microtube. By comparing Fig. 8b to a, it is found that the critical flow velocity increases by about 13.6% as the surface roughness increases. This is because the surface roughness can reduce the flow velocity in microtubes, as illustrated in Figs. 5 and 6. Figure 8c is for a rough microtube with a thin wall. For this condition, the surface roughness slightly decreases the bending stiffness of the microtube. It is known that the instability of the clamped–clamped microtube is caused by the elastic restoring force of the structure less than the centripetal force induced by the fluid flow. Consequently, the critical flow velocity for a thin microtube decreases due to the decreasing of bending stiffness. This means that the thin microtube is more prone to instability. In addition, it is noted that the effect of surface roughness on the bending stiffness is so little that the critical flow velocity only decreases about 0.8%.

Fig. 8

The variation of dimensionless complex frequencies with the increasing of the dimensionless flow velocity for smooth and rough microtubes a Smooth, $\gamma = 1$ b rough, $\varepsilon = 0.05,\;\lambda = 30,\;\gamma = 1$ c rough,$\varepsilon = 0.05,\;\lambda = 30,\;\gamma = 0.15$

The natural frequency is one key dynamic behavior for microtubes. Figure 9 demonstrates the variation of nondimensional frequency with nondimensional flow velocity for smooth and rough microtubes. It is found that as the flow velocity increases, the nondimensional natural frequency decreases. When the velocity reaches the critical value, the natural frequency decreases to 0 and the microtube loses stability. Furthermore, as the roughness height or wave number increases, which indicates that the surface becomes more rough, the natural frequency increases. This is because for clamped–clamped microtubes, the centripetal force can be equivalent to the axial pressure which makes the structure “softer”. The increase of surface roughness can reduce the fluid velocity, thus reducing the stiffness softening effect caused by the centripetal force. In addition, as the roughness height or wave number increases, the critical flow velocity also increases, which means that the microtube is less prone to instability. Figure 10 illustrates the variation of frequency for smooth and rough microtubes with different wall thickness. When the internal fluid flows in a certain velocity, the nondimensional frequencies for smooth microtubes with various wall thickness are different. This is because the wall thickness affects the parameter $\beta$, which characterizes the inertial force induced by the structure and fluid. In addition, it can be found that the wall thickness has no effect on the critical flow velocity for divergence. This is because for smooth microtubes the wall thickness only affects the mass ratio $\beta$, while the variation of $\beta$ does not influence the nondimensional critical velocity, as shown in Table 1. The parameter $\beta$ is always associated with velocity-dependent terms in the equation of motion, while divergence of the clamped–clamped microtube represents a static loss of stability (Paidoussis, 1998). For rough microtubes, the wall thickness influences the correction factors for structure, thus affecting the critical velocity. However, because this influence is very small, the critical velocity only decreases about 0.5% as $\gamma$ decreases from 1.0 to 0.15, which can be neglected.

Fig. 9

Variation of nondimensional frequency with nondimensional flow velocity for smooth and rough microtubes with different roughness parameters

Fig. 10

Variation of nondimensional frequency with nondimensional flow velocity for smooth and rough microtubes with different wall thickness

Table 1 The effects of mass ratio $\beta$ on the nondimensional critical velocity for clamped–clamped microtubes

As discussed in the above, it can be concluded that the surface roughness mainly affects the dynamic characteristics by influencing the flow velocity in the microtube. Figure 11 shows the variation of nondimensional critical velocity with the surface roughness. It is obvious that as the roughness height or the wave number increases, the critical flow velocity dramatically increases. Moreover, the larger the surface roughness height is, the faster the critical velocity increases with the roughness height. The nondimensional critical velocity for the smooth microtube is about 5.44, while the value for the rough microtube with $\varepsilon = 0.05$ and $\lambda = 30$ is about 6.16. The surface roughness makes the critical velocity increase about 13.2%.

Fig. 11

Variation of nondimensional critical velocity with the surface roughness

3.3 Cantilevered microtubes

The dynamic behaviors of cantilevered microtubes are very different from the clamped–clamped ones. According to the analysis in the above, the effect of surface roughness on correction factors for structure is so small that it can be neglected. Hence, CFF₁ and CFF₂ are assumed to be 1. Figure 12 illustrates the typical Argand diagram of smooth and rough cantilevered microtubes for different mass ratios. The parameters for the surface roughness is $\varepsilon = 0.05$ and $\lambda = 30$. It can be found that for different mass ratios, the dynamic behaviors of microtubes are very different. And the effect of surface roughness is also distinct. For $\beta = 0.2$, as the flow velocity increases, the imaginary part of $\hat{\omega }$ which indicates the damping of the system, first increases and then decreases. Once the flow velocity exceeds the critical value, the damping becomes negative and the microtube conveying fluid loses stability by fluttering. For the smooth microtube, the nondimensional critical velocity is about 4.44, while the value is about 4.96 for the rough microtube with $\varepsilon = 0.05$ and $\lambda = 30$. The surface roughness increases the critical velocity. For $\beta = 0.4$, the dynamic behavior is so different. As the flow velocity increases, the imaginary part of $\hat{\omega }$ goes through the process of increasing, decreasing, increasing and finally decreasing. For the first decreasing, the imaginary part of $\hat{\omega }$ reduces to about 0.1 and then increases, which means that the system is still stable. And for the second decreasing, the imaginary part of $\hat{\omega }$ drops below 0 and the microtube loses stability by fluttering. The surface roughness changes the trend of the imaginary part of $\hat{\omega }$ with the increasing flow velocity, as illustrated in Fig. 12d. The imaginary part of $\hat{\omega }$ also goes through the increasing–decreasing–increasing–decreasing process, but it reduces to below 0 for the first decreasing. As a result, the critical velocity for the rough microtube is less than the value for the smooth microtube. The surface roughness decreases the critical velocity, which is opposite to the case of $\beta = 0.2$. For $\beta = 0.6$, the damping of the second order mode is always positive and the one of the third order mode decreases to below 0 as the flow velocity exceeds the critical value. In other words, the microtubes conveying fluid loses stability by the fluttering of the third mode. Moreover, the surface roughness makes the critical velocity increase from about 7.86 to about 8.76, which is similar to the case of $\beta = 0.2$.

Fig. 12

The variation of dimensionless complex frequencies with the increasing of the dimensionless flow velocity for smooth and rough microtubes

To clarify the phenomenon shown in Fig. 12c, d, the variation of nondimensional critical velocity with the mass ratio for smooth and rough microtubes are demonstrated by Fig. 13. It is found that every curve contains a S-shaped segment, which indicates each $\beta$ corresponds to three nondimensional critical velocities. This phenomenon is associated with the instability–restabilization–instability sequence (Paidoussis, 1998). Furthermore, in the vicinity of S-shaped segment, the nondimensional critical velocity changes sharply with $\beta$, which induces that the nondimensional flow velocity for the rough microtube is less than the value for the smooth microtube, as shown in Fig. 12c, d. In the region far away from the S-section, the nondimensional flow velocity increases slowly with $\beta$ and the surface roughness makes the critical velocity increase, as illustrated in Fig. 12a, b, e, f. Figure 14 shows the instability–restabilization–instability sequence. For $\beta = 0.395$, as the flow velocity increases, the imaginary part of the second order $\hat{\omega }$ for the smooth microtube reduces to below zero at the nondimensional velocity 6.36. After decreasing to the local maximum, it increases to larger than zero at the nondimensional velocity 6.70, which means the microtube conveying fluid gains stability. Finally, the system again loses stability by fluttering at the nondimensional velocity 7.14. It can be found that there exist three critical velocities when the microtube undergoes the instability–restabilization–instability sequence, which corresponds to the S-shaped segment illustrated in Fig. 13. For $\beta = 0.415$, the rough microtube with $\varepsilon = 0.05$ and $\lambda = 30$ goes through the instability–restabilization–instability process, as shown in Fig. 14b. The three critical velocities are about 7.04, 7.80, 8.00.

Fig. 13

Variation of the nondimensional critical velocity with mass ratio $\beta$ for smooth and rough microtubes

Fig. 14

The variation of imaginary part of $\hat{\omega }$ with the nondimensional flow velocity for smooth and rough microtubes a $\beta = 0.395$ b $\beta = 0.415$

Figure 15 demonstrates the variation of the first and second order frequencies as the flow velocity increases. The first order frequency increases and the second order frequency decreases with the increasing of the flow velocity. Moreover, as the roughness height increases, the first order frequency decreases while the second order frequency increases. The difference can be attributed to the different mode shapes of the two modes (Yan et al., 2017). For the first mode, the centripetal force acts towards to the position of equilibrium and it can be regarded as the restoring force. Consequently, the effective stiffness of the fluid-conveying microtube increases with the increasing of flow velocity, which causes the first order frequency increasing. Moreover, because the surface roughness can reduce the flow velocity, the effective stiffness and the frequency decrease as the roughness height increases. For the second mode, the centripetal force acts away from the position of equilibrium and it works like a “negative” spring. As a result, the effect of flow velocity and surface roughness on the second order frequency is opposite to the one on the first order frequency.

Fig. 15

The variation of the first and second order frequencies with the nondimensional flow velocity for smooth and rough microtubes

3.4 Dimensional flow velocity

The instability of fluid-conveying microtubes with surface roughness is analyzed and discussed in Sects. 3.2 and 3.3 and the principal results can be summarized in terms of the nondimensional critical flow velocities. For the microtube, the corresponding dimensional values of the critical flow velocities can be directly derived according to Eq. (26), which is written as (Rinaldi et al., 2010),

$$U_{\text{cr}} = \hat{U}_{\text{cr}} \sqrt {\frac{{EI^{(s)} }}{{\rho_{\text{f}} A_{\text{f}}^{(s)} }}} \frac{1}{L} = \hat{U}_{\text{cr}} \sqrt {\frac{E}{{\rho_{\text{f}} }}} \frac{{\sqrt {1 - \lambda_{1}^{4} } }}{{4\lambda_{1} \lambda_{2} }},$$

(29)

where $U_{\text{cr}}$ is the dimensional critical velocity, $\lambda_{1} = {{R_{\text{m}} } \mathord{\left/ {\vphantom {{R_{\text{m}} } {R_{o} }}} \right. \kern-\nulldelimiterspace} {R_{o} }}$ is the cross-sectional aspect ratio and $\lambda_{2} = {L \mathord{\left/ {\vphantom {L {2R_{o} }}} \right. \kern-\nulldelimiterspace} {2R_{o} }}$ is the slenderness ratio.

Assume a clamped–clamped rough microtube with $R_{\text{m}} = 2\;{\mu m}$, $R_{o} = 4\;{\mu m}$, $\varepsilon = 0.05$ and $\lambda = 30$. The fluid flowing this microtube is water, whose density is 998 kg/m³. It's easy to get a nondimensional critical velocity of 6.18 for this microtube by solving Eq. (25). According to Eq. (29), the dimensional critical velocity is not only related to the nondimensional value, but also to the Young's modulus and the length of microtube. Figure 16 illustrated the critical flow velocity as a function of the microtube length for several common engineering materials: rubber (~ 0.1 GPa), plastic (~ 1 GPa), silicon dioxide (~ 70 GPa) and steel (~ 210 GPa). It is demonstrated that when the microtube is short ($\lambda_{2} < 10$), the critical flow velocities exceed 100 m/s for all materials. However, for slender microtubes ($\lambda_{2} > 100$), the dimensional critical velocities can be reduced to about 10 m/s, which implies that the instability should be taken into account. This analysis can readily be extended to analyze the effects of different materials and cross-sectional shapes on dimensional critical velocities.

Fig. 16

The effects of material properties and microtube length on the dimensional critical velocities for instability

4 Conclusions

A theoretical model is presented to describe effect of surface roughness on the instability and dynamic behaviors of fluid-conveying microtubes. Four correction factors are introduced to account for the influences of the surface roughness on the structure and the internal fluid. As the results demonstrated, the surface roughness has little effect on structure, but dramatically decreases the Coriolis force and centripetal force caused by the internal fluid. In other words, the surface roughness mainly affects the dynamic characteristics by influencing the flow velocity in the microtube. For clamped–clamped microtubes, as the roughness height or the wave number increases, which means the surface becomes more rougher, and both the critical velocity and the frequency increase. For cantilevered microtubes, the dynamic behaviors are more complex. The critical velocity for fluttering depends on the mass ratio, which can be described by the $\hat{U}_{\text{cr}}$ − $\beta$ curves. Each curve contains a S-shaped segment, which is associated with the instability–restabilization–instability sequence. It is found that the surface roughness induces the curve shifting to the upper right of the $\hat{U}_{\text{cr}}$-$\beta$ plane. In the vicinity of S-shaped segment, the critical velocity sharply varies as $\beta$ increases, inducing the critical velocity for the rough microtube less than the value for the smooth microtube. In the region far away from the S-shaped segment of the curve, the critical velocity increases with the increasing of roughness height. The effects of surface roughness on the frequency of cantilevered microtubes are also analyzed and discussed. The results also demonstrate that the first order frequency of the cantilevered microtube increases and the second order frequency decreases with the increasing of the flow velocity. Moreover, as the roughness height increases, the first order frequency decreases while the second order frequency increases. The phenomenon is related to the different mode shapes of the two modes.