1 Introduction

Multiphase flows through ducts and pipes are widespread in engineering applications such as power plants and crude oil transport. Depending on the volume fraction of the gaseous phase, one distinguishes bubbly, slug, churn, and annular flows (Weisman 1983; Brennen 2005). In recent years, there has been a strong interest in using structured or porous surfaces soaked with a liquid to create surfaces being robustly repellent to another fluid (Wong et al. 2011; Grinthal and Aizenberg 2013). In that context, a simple process has been demonstrated to impregnate planar walls with a stable, nondewetting water-repelling film (Eifert et al. 2014). When functionalizing microchannel walls based on these methods, flow patterns similar to annular flows prevail, where a fluid is pumped through channels whose walls are coated with a thin liquid film. Such flows may give rise to instabilities, which are, in fact, quite common in nature. One of the most well-known related phenomena is the Kelvin–Helmholtz instability, appearing on the initially flat interface between two inviscid fluid layers flowing parallel to each other. If the velocity of the two fluids differs, the system may be unstable to small disturbances in the flow field (Drazin and Reid 2004). The disturbances are escalated by the corresponding variations in the dynamic (Bernoulli) pressure and grow into a vortex sheet (Chandrasekhar 2013). If the viscous stresses are not negligibly small, they may also trigger the formation of patterns at interfaces. An example is the formation of ripples on sand beds sheared by a liquid flow (Charru and Hinch 2006). Therefore, for general co-current fluid flows, it is reasonable to consider the variations in both the pressure and the viscous stresses to obtain the time evolution of the system. Since the early discussion of Yih (1967), the instability of the parallel flow of fluids with different viscosities has been the subject of numerous papers. For instance, as a far from exhaustive selection, the reader is referred to Gondret and Rabaud (1997), Joseph et al. (1984), and Hooper and Boyd (1983), as well as to Yiantsios and Higgins (1988). The shear number of other studies referencing this selection of papers illustrates the importance and considerable challenge the analysis of co-current viscous flow often poses.

This paper investigates the coupled hydrodynamic instabilities of two thin liquid films coating flat walls opposite to each other when exposed to gas flow. Apart from the already mentioned example of liquid-infused surfaces, the corresponding flow patterns are important for a number of applications such as microchannel cooling (Kandlikar 2012; Houshmand and Peles 2013; Kabov et al. 2011). In addition, the understanding of interfacial instabilities in gas–liquid flows is vital for the mapping of the different flow regimes in confined multiphase systems. These maps have been explored analytically (Taitel and Dukler 1976), experimentally (Saisorn and Wongwises 2008; Triplett et al. 1999), and numerically (Talimi et al. 2012). Although core-annular flows have, in general, different properties than planar flows, their features are similar as long as the tube curvature and the corresponding capillary effects are negligibly small (Renardy 1987). Core-annular gas flow can be utilized as a model system for the discussion of the closure of airways (Heil et al. 2008; Johnson et al. 1991; Halpern et al. 2008). A review of various instabilities of core-annular flows was given by Joseph et al. (1997).

For thin liquid films, interfacial instabilities are strongly influenced by surface tension. The stabilizing effect of capillarity dampens sharp deformations of the interface, so that, for sufficiently thin films, the evolution of the instabilities can be described by the long-wavelength approximation. The analyses of these systems have shown that the co-current flow of two superposed liquid films with large interfacial tension is governed by the Kuramoto–Sivashinsky equation (Hooper and Grimshaw 1985; Shlang et al. 1985). The analysis of this nonlinear partial differential equation is remarkably challenging. Interfacial instabilities occurring in the planar flow of three superposed liquid films have been first discussed by Li (1969). Although the systems may be studied by linear stability analysis (Kliakhandler and Sivashinsky 1995), the large influence of the nonlinear terms severely limits the range of validity of the linearized problem. It has been argued that the weakly nonlinear equations of stratified films should take the form of coupled Kuramoto–Sivashinsky equations (Papaefthymiou et al. 2013; Papaefthymiou and Papageorgiou 2017). The analysis of the equations revealed that in contrast to double-layer configurations, these systems can become unstable even if inertial effects are negligibly small. These novel instabilities were found to be either the result of a resonance-like coupling between the interfaces or were assumed to be a fourth-order generalization of the Majda–Pego instability (Majda and Pego 1985; Papaefthymiou et al. 2013).

The mathematical complexity of multilayer systems hinders their analytical description. This restricts the investigations to either numerical simulations or to the discussion of simplified configurations (Renardy 1987; Kliakhandler and Sivashinsky 1995; Papaefthymiou et al. 2013; Papaefthymiou and Papageorgiou 2017). For the long-wavelength instability driven by a planar gas flow between thin liquid films, the disparity between the viscosities of the liquid and the gas phase allows for a simplification of the governing equations. This is the focus of this paper. Section 2 discusses the derivation of the evolution equations for the film thicknesses. Section 3 addresses symmetric systems, where the compact form of the equations and the small number of independent parameters permits a deeper analytical treatment. Finally, in Sect. 4, a brief summary is given of the results obtained by numerically simulating asymmetric systems. Based on linear stability analysis, a qualitative explanation for the observed behavior is given.

2 Evolution equations of the interfaces

2.1 Governing equations

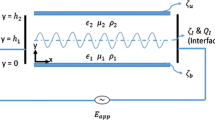
In this section, the evolution equations for the gas and liquid-film flows are derived. The analysis in two spatial dimensions is restricted to immiscible, incompressible, Newtonian fluids. The latter two assumptions imply sufficiently small flow velocities and shear rates, respectively. Furthermore, the flow is assumed to be driven solely by an externally imposed pressure gradient. According to the notations introduced in Fig. 1, the momentum equations in the bulk fluids and the stress balance at the interfaces are given by the following:

(1)
(2)

where the liquid films are assumed to be sufficiently thin to neglect the gravitational force. The subscript i defines the fluid film or the interface the physical quantity is referring to. In this sense and as illustrated in Fig. 1, in Eq. (1), the three phases are referred to as “1”, “g”, and “2” from bottom to top. In a similar manner, in Eq. (2), the lower interface is denoted by “1” and the upper one by “2”. The gradient along interface i is denoted by \(\varvec{\nabla _i}\), and its normal vector by \({\hat{{\mathbf {n}}}}_{{\varvec{i}}}\). The directions of \({\hat{{\mathbf {n}}}_{{\varvec{i}}}}\) are defined in Fig. 1. The symbols \(\rho _i\) and \(\gamma _i\) refer to the mass densities of the fluids and the constant surface tensions, respectively. The velocity field is denoted by \({\varvec{v}}=(v_1,v_2)\), and its material (or substantial) time derivative by \({{\mathrm{d}}}{\varvec{v}}/{\mathrm{d}}t\) \(\equiv \partial {\varvec{v}}/\partial t + {\varvec{v}} \cdot {\varvec{\nabla }} {\varvec{v}}\). The stress tensors, Ti, are composed of the scalar hydrodynamic pressures \(p_i\) and the viscous stress tensors: Ei.

(3)

where the identity matrix is referred to by \({{{\mathbf {\mathsf{{I}}}}}}\), while \(\mu _i\) denote the dynamic viscosities. This study is limited to instabilities with characteristic time scales much smaller than the gravitational time scale, i.e., for films with a small Bond number. Most prominently and as assumed in this work, this condition is met for sufficiently thin films, so that the effects of interfacial stresses markedly exceed those of the volumetric forces.

Fig. 1
figure 1

Illustration of gas flow between two liquid films

Full size image

For the nondimensionalization of the equations, one introduces \(\lambda _{\mathrm{char}}\) as a characteristic length scale of the variation of the flow field along the horizontal direction. An educated guess for this quantity is the still unknown linear approximation of the characteristic wavelength of the instability. It is emphasized that a different choice for this scaling length does not affect the underlying physics of the problem. One simply has to ensure posteriori that no horizontal characteristic length scale found in the course of the analysis is significantly smaller than the chosen one. Consequently, the \(x_1\) coordinate is nondimensionalized by \(X=x_1/\lambda _{\mathrm{char}}\). With d denoting the separation distance between the walls, the quantities \(Y=x_2/d\) and \(H_i=h_i/d\) are introduced as the dimensionless vertical coordinate and film thickness, respectively. The volume flux of the gas flow at the entrance of the channel, Q, is utilized for defining the dimensionless velocities \({\varvec{V}}=(V_X,V_Y)=(v_1,v_2/\epsilon )d/Q\). In this definition, the \(\epsilon =d/\lambda _{\mathrm{char}}\) parameter appearing in the vertical velocity originates from the different spatial scalings applied in the horizontal and the vertical directions. The rescaled time variable reads \(\tau =tQ/(\lambda _{\mathrm{char}}d)\). The dimensionless pressures are given by \(P_i=p_i\epsilon d^2/(\mu _g Q)\), with \(\mu _g\) being the dynamic viscosity of the gaseous medium. Finally, the viscosity ratios \({\textit{M}}_i=\mu _i/\mu _g\) and density ratios \({\textit{R}}_i=\rho _i/\rho _g\) are introduced. With these new variables, the momentum equations take the form

$$\begin{aligned} \begin{aligned} \epsilon {\textit{Re}}\, {\textit{R}}_i\frac{{\mathrm{d}}V_X}{{\mathrm{d}}\tau }=&{\textit{M}}_i\left( \epsilon ^2\frac{\partial ^2 V_X}{\partial X^2}+\frac{\partial ^2 V_X}{\partial Y^2}\right) -\frac{\partial P_i}{\partial X},\\ \epsilon ^3 {\textit{Re}}\,{\textit{R}}_i\frac{{\mathrm{d}}V_Y}{{\mathrm{d}}\tau }=&{\textit{M}}_i\left( \epsilon ^4\frac{\partial ^2 V_Y}{\partial X^2}+\epsilon ^2\frac{\partial ^2 V_Y}{\partial Y^2}\right) -\frac{\partial P_i}{\partial Y}. \end{aligned} \end{aligned}$$
(4)

The Reynolds number is denoted by \({\textit{Re}}=\rho _gQ/\mu _g\). The interfacial stress balance in the tangential and the normal directions is given by the following:

$$\begin{aligned}&\left( \epsilon ^2\frac{\partial V_Y}{\partial X}{\Bigg |}_{g}+\frac{\partial V_X}{\partial Y}{\Bigg |}_{g}\right) -{\textit{M}}_i{\Bigg (}\epsilon ^2\frac{\partial V_Y}{\partial X}{\Bigg |}_i+\frac{\partial V_X}{\partial Y}{\Bigg |}_i{\Bigg )} \\&\quad =-\frac{4 \epsilon ^2\partial H_i/\partial X}{1-\epsilon ^2 (\partial H_i/\partial X)^2}\left( \frac{\partial V_Y}{\partial Y}{\Bigg |}_{g}-{\textit{M}}_i\frac{\partial V_Y}{\partial Y}{\Bigg |}_i\right) , \\&P_{i}-P_{g}+2\epsilon ^2\frac{1+\epsilon ^2(\partial H_i/\partial X)^2}{1-\epsilon ^2(\partial H_i/\partial X)^2}{\Bigg (}\frac{\partial V_Y}{\partial Y}{\Bigg |}_{g}-{\textit{M}}_i\frac{\partial V_Y}{\partial Y}{\Bigg |}_i{\Bigg )} \\&\quad =(-1)^i\frac{\epsilon }{{\textit{Ca}}_i}\frac{\partial ^2H_i/\partial X^2}{[\epsilon ^2(\partial H_i/\partial X)^2+1]^{3/2}} \quad i\in [1,2]. \end{aligned}$$

The capillary numbers are denoted by \({\textit{Ca}}_i=\mu _gQ/(\epsilon ^2d\gamma _i)\). This definition ensures that the capillary number is of O(1).

Finally, the dimensionless continuity equation in the layers read

$$\begin{aligned} \frac{\partial V_X}{\partial X}+\frac{\partial V_Y}{\partial Y}=0, \end{aligned}$$
(5)

while the kinematic condition along the interfaces leads to

$$\begin{aligned} \begin{aligned} \frac{\partial H_1}{\partial \tau }+V_X{\Big |}_{H_1}\frac{\partial H_1}{\partial X}-V_Y{\Big |}_{H_1}&=0,\\ \frac{\partial H_2}{\partial \tau }+V_X{\Big |}_{1-H_2}\frac{\partial H_2}{\partial X}+V_Y{\Big |}_{1-H_2}&=0.\\ \end{aligned} \end{aligned}$$
(6)

2.2 Framework of the analysis

The current paper focuses on systems where the material properties of the liquids are identical. Formally, this implies that \({\textit{M}}_1={\textit{M}}_2\equiv {\textit{M}}\), \({\textit{Ca}}_1={\textit{Ca}}_2\equiv {\textit{Ca}}\) and \({\textit{R}}_1={\textit{R}}_2\equiv R\). To ease the mathematical analysis, the following simplifications are introduced.

Assumption 1 :

  The dominant influence of capillarity and viscosity on the behavior of thin liquid films dampens short-wavelength deformations and instabilities along their interfaces. Therefore, the long-wavelength approximation (Oron et al. 1997) is utilized.

Assumption 2 :

  In contrast to related work (Papaefthymiou and Papageorgiou 2017), inertial effects in the gas flow are included. However, to limit the scope of the present analysis, the Reynolds number for the gas will be restricted to configurations where \(O(\epsilon {\textit{Re}}) < 1\). Consequently, terms of \(O(\epsilon {\textit{Re}})^2\) and higher are negligible. Nevertheless, given the high viscosity ratio between the liquid and the gaseous medium, the Reynolds number and the corresponding nonlinear terms in the momentum equation of the liquid layers are negligible.

Assumption 3 :

  To reduce the set of equations to only two evolution equations, it is sufficient to apply the previous two assumptions. However, these equations are highly complex, and related studies usually focus on either the numerical analysis of these systems for a restricted parameter space (Papaefthymiou et al. 2013) or utilize strong simplifications, such as negligible surface tension and inertia (Papaefthymiou and Papageorgiou 2017). To facilitate analytical studies and to retain some of the physical insight of the problem, the current work is based in the assumption that the viscosity of the gas is much smaller than that of the liquid so that \({\textit{M}}^2\gg 1\). In the following, this assumption is referred to as the assumption of semi-rigidness of the liquid films. Consequently, all terms containing second or higher orders of \(1/{\textit{M}}\) are neglected from the equations of the current study. As detailed in Appendix 1, this assumption yields a good approximation for the time evolution of the system as long as \(O({1}/{{\textit{M}}})\le O(\epsilon )\).

The mathematical implementation of these assumptions is straightforward and is summarized in Appendix 1. It is found that, to leading order of \(\epsilon\) and \(1/{\textit{M}}\), the system is characterized by the equations:

$$\begin{aligned}&\begin{aligned} \frac{\partial H_1}{\partial \overline{\tau }}&=-\frac{\partial }{\partial \overline{X}}{\Bigg \{}\frac{H_1^2(3+H_1-3H_2)}{\epsilon (1-H_1-H_2)^3}+\frac{H_1^3}{3}\frac{\partial ^3 H_1}{\partial \overline{X}^3}\\&\quad +{\textit{Re}}\,\root 3 \of {{\textit{Ca}}}\frac{3H_1^2(1+5H_1-H_2)}{35(1-H_1-H_2)^3}\left( \frac{\partial H_1}{\partial \overline{X}}+\frac{\partial H_2}{\partial \overline{X}}\right) {\Bigg \}}, \end{aligned} \end{aligned}$$
(7)
$$\begin{aligned}&\begin{aligned} \frac{\partial H_2}{\partial \overline{\tau }}&=-\frac{\partial }{\partial \overline{X}}{\Bigg \{}\frac{H_2^2(3+H_2-3H_1)}{\epsilon (1-H_1-H_2)^3}+\frac{H_2^3}{3}\frac{\partial ^3 H_2}{\partial \overline{X}^3}\\&\quad +{\textit{Re}}\,\root 3 \of {{\textit{Ca}}}\frac{3H_2^2(1+5H_2-H_1)}{35(1-H_1-H_2)^3}\left( \frac{\partial H_1}{\partial \overline{X}}+\frac{\partial H_2}{\partial \overline{X}}\right) {\Bigg \}}. \end{aligned} \end{aligned}$$
(8)

To obtain these equations, the temporal and spatial coordinates have been rescaled as \(\overline{\tau }=\tau \epsilon \root 3 \of {{\textit{Ca}}}/{\textit{M}}\) and \(\overline{X}=\root 3 \of {{\textit{Ca}}}X\). In the following, to avoid complicated notations, the overbars will be omitted.

It is noted that, in the previous studies, it has already been implied that the evolution equations for the liquid-film thicknesses take a form similar to Eqs. (7) and (8), even for arbitrary viscosity ratios (Papaefthymiou et al. 2013). In the general case, these equations are remarkably complex, and, to the best of our knowledge, the full evolution equations have not been presented in the literature so far, neither for arbitrary \(1/{\textit{M}}\) nor for \(1/{\textit{M}}<1\).

In contrast to other applications of the lubrication approximation to study the dynamics of thin films, Eqs. (7) and (8) explicitly depend on the scaling parameter \(\epsilon\). First, given the underlying expansion of the governing equations in \(\epsilon\), the final evolution equations will, in general, always contain terms of mixed order in \(\epsilon\). Most prominently, the capillary term is of cubic order in \(\epsilon\), but this is commonly hidden in the use of the scaled capillary number. While, in the absence of a gas flow, the stress terms in the film evolution equation are typically of linear and cubic order in \(\epsilon\), for systems with a gas flow this is supplemented by a stress term of zeroth order. This represents the stress from the base gas flow onto the liquids and as such has no characteristic length scale in the spread direction of the films. In essence, the evolution of the interfaces depends on the stresses of both the base flow and the additional perturbative effects caused by the inertia of the gaseous medium and the capillary pressure. The significance of the latter two effects relative to that of the base flow is expressed by \(\epsilon\). This parameter simply scales the nondimensional stress terms in a fashion, such that naturally evolving spatial periodicity is properly scaled to the chosen lateral length scale of the (nondimensional) domain. In a dimensionful notation, \(\epsilon\) would not be present.

Nevertheless, although Eqs. (7) and (8) seem to imply that there is a singularity in the equations for \(\epsilon \rightarrow 0\), it can be verified that it only appears due to the introduction of \(\overline{X}\) and \(\overline{\tau }\) to Eqs. (7) and (8). Even in the limit \(\epsilon \rightarrow 0\), a nonsingular evolution of the system is obtained for the original temporal and spatial variables.

2.3 Physical interpretation of the problem

In Fig. 2, to provide an intuitive understanding of the physical background for Eqs. (7) and (8), an example of the flow field of the gaseous medium for \({\textit{Re}}=2\) and \(\epsilon =0.1\) in a symmetrically deformed channel is shown. Within the framework of the current study, liquid interfaces deformed in the same way as the channel walls of Fig. 2 would generate identical flow profiles in the gas. The Mathematica® software package is used to evaluate the obtained analytic formulas with the given nondimensional numbers. In the first row of Fig. 2, the pressure drop and the streamlines of the zeroth-order (Stokes) flow are shown, while the inertial first-order perturbation is depicted in the second row. The full (non-Stokesian) flow field can be obtained by superimposing the two results. The figure indicates that the base flow simply corresponds to a channel flow with periodically undulated walls. The first-order flow supports two instability mechanisms. First, the pressure in the narrower section is lower which will promote reducing the cross section even further. The corresponding pressure gradient is given by the following:

$$\begin{aligned} \frac{\partial P_g}{\partial X}{\Bigg |}_{H_1} = \frac{\partial P_g}{\partial X}{\Bigg |}_{1-H_2} =-\frac{6 \left[ 70+9 \epsilon {\textit{Re}}\left( \frac{\partial H_1}{\partial X}+\frac{\partial H_2}{\partial X}\right) \right] }{35 \left( 1-H_1-H_2\right) {}^3}. \end{aligned}$$
(9)

Second, the periodic lateral pressure fluctuations cause counter-rotating vortices, which deform the film interfaces by viscous stresses. These are given by

$$\begin{aligned} {E{|}_{H_1}}={-E{|}_{1-H_2}} = \frac{6 \left[ 35+\epsilon {\textit{Re}}\left( \frac{\partial H_1}{\partial X}+\frac{\partial H_2}{\partial X}\right) \right] }{35 \left( 1-H_1-H_2\right) {}^2}. \end{aligned}$$
(10)

In a later section and based on this illustration, the significance of the normal stresses to induce the instability will be compared to that of the shear stresses.

Furthermore, one may ask how the film deformation affects the pressure gradient to maintain a constant volumetric flow rate. Based on Eq. (9), one can calculate the pressure drop along the channel of length L. Assuming that the deformations at its ends are negligibly small yields

$$\begin{aligned} P_g(L)-P_g(0)=-\int \limits _0^{L}{\frac{12}{(1-H_1-H_2)^3}\,{\mathrm{d}}X}. \end{aligned}$$
(11)

The effect of the gas dragging the liquid films is not considered in the expression, since the corresponding term contributes to the evolution equations only at higher orders of the viscosity ratios. This is beyond the scope of the current analysis. Assuming the system to be mirror-symmetric, the notation \(H_1=H_2=H_0+\varDelta H\) is introduced. Here, \(H_0\) represents the initial uniform film thickness and the local deviation from that state is given by \(\varDelta H\). The integral takes the form

$$\begin{aligned} P_g(L)-P_g(0)&=-\int \limits _0^{L} \left[ \frac{12}{(1-2H_0)^3}+\frac{72 \varDelta H}{(1-2H_0)^4}\right. \\&\quad \left. +\frac{288 \varDelta H^2}{(1-2H_0)^5}+\frac{960 \varDelta H^3}{(1-2H_0)^6}+\cdots \right] {\mathrm{d}}X. \end{aligned}$$
(12)

The linear term in \(\varDelta H\) drops out, since the total volume of the liquid films does not change during their evolution. Thus, since, in relevant scenarios, \(|\varDelta H/(1-2H_0)|\ll 1\), the term scaling with \(\varDelta H^2\) defines the dominant effect of the deformations of the liquid surfaces. In comparison to the case of undeformed films, this term implies the pressure drop to be \(1+O(\varDelta H)^2\times 24/(1-2H_0)^2\) times larger due to the instability of the interfaces.

Fig. 2
figure 2

Pressure drop and streamlines of an exemplary gas flow in a channel with symmetrically deformed walls. The Stokes flow (primary flow) is depicted in the first row, while the first-order correction arising from the nonzero inertial terms is shown in the second one. The full flow field corresponds to the superposition of the two results (\({\textit{Re}}=2\), \(\epsilon =0.1\))

Full size image

3 Symmetric systems

This section discusses systems where the undisturbed liquid-film thicknesses are equal, i.e., the undisturbed system is completely symmetric with respect to the channel center plane. The question arises whether or not the mirror symmetry breaks down during the evolution of the system. As a similar problem, the breakdown of axial symmetry in core-annular flows has been observed in experiments (Hewitt and Hall-Taylor 1970) and in analytical studies (Renardy 1987), supporting the significance of this question for planar flows.

With the initial film thickness \(H_0\), we denote the film deformations as \(\varDelta H_1=H_1-H_0\) and \(\varDelta H_2=H_2-H_0\). In the case of small deformations \(\varDelta H_1\equiv \epsilon \eta _1\), \(\varDelta H_2\equiv \epsilon \eta _2\) are introduced, where \(\textit{O}(\eta _1)=\textit{O}(\eta _2)=\textit{O}(1)\), while \(0<\epsilon <1\). Then, one finds that, after neglecting second or higher orders of \(\epsilon\), Eqs. (7) and (8) transform to

$$\begin{aligned} \frac{\partial \eta _1}{\partial \tau }&=-\frac{\partial }{\partial X}\left\{ \frac{6H_0[(1-H_0)\eta _1+H_0\eta _2]}{\epsilon (1-2H_0)^4}\right. \\&\quad +{\textit{Re}}\root 3 \of {{\textit{Ca}}}\frac{3H_0^2(1+4H_0)}{35(1-2H_0)^3}\left( \frac{\partial \eta _1}{\partial X}+\frac{\partial \eta _2}{\partial X}\right) \\&\quad +\frac{3[(1-H_0)\eta _1+H_0\eta _2]}{(1-2H_0)^5}[(1+H_0(3-2H_0))\eta _1 \\&\quad \left. +\,H_0(3+2H_0)\eta _2]+\frac{H_0^3}{3}\frac{\partial ^3 \eta _1}{\partial X^3}\right\} , \end{aligned}$$
(13)
$$\begin{aligned} \frac{\partial \eta _2}{\partial \tau }&=-\frac{\partial }{\partial X}\left\{ \frac{6H_0[(1-H_0)\eta _2+H_0\eta _1]}{\epsilon (1-2H_0)^4}\right. \\&\quad +{\textit{Re}}\root 3 \of {{\textit{Ca}}}\frac{3H_0^2(1+4H_0)}{35(1-2H_0)^3}\left( \frac{\partial \eta _1}{\partial X}+\frac{\partial \eta _2}{\partial X}\right) \\&\quad +\frac{3\left[ (1-H_0)\eta _2+H_0\eta _1\right] }{(1-2H_0)^5} [(1+H_0(3-2H_0))\eta _2 \\&\quad \left. +\,H_0(3+2H_0)\eta _1]+\frac{H_0^3}{3}\frac{\partial ^3 \eta _2}{\partial X^3}\right\} . \end{aligned}$$
(14)

The first and the second terms in the curly brackets represent the stresses acting from the primary flow of the gas on the film. The governing equations remain nonlinear in \(\eta _1\) and \(\eta _2\). In general, such a nonlinearity can not be scaled out by a Galilean transformation (Papaefthymiou et al. 2013). This restricts the validity of the linear stability analysis of the equations to a very narrow region around the equilibrium state.

3.1 Linear stability analysis

The remaining nonlinear terms of Eqs. (13) and (14) imply that their linearization in \(\eta _1\) and \(\eta _2\) is only expected to reliably approximate the evolution of the interfaces for extremely small deformations. However, the analysis is helpful for a subsequent discussion of the weakly nonlinear equations. Furthermore, the linear analysis also gives approximate values for the scaling parameters of the system.

Assuming that, instead of \(\textit{O}(\eta _1)=\textit{O}(\eta _2)=\textit{O}(1)\) proposed for Eqs. (13) and (14), \(\eta _1,\eta _2\ll \epsilon <1\), one can neglect the second-order terms in the deformations from Eqs. (13) and (14). The resulting system of linear partial differential equations can be analyzed utilizing Fourier transformation (Cross and Greenside 2009). One finds the solution of the equations to be given by

$$\begin{aligned} \left( \begin{array}{l} \eta _{1}\\ \eta _{2} \end{array}\right)= & {} \int \limits _{-\infty }^{\infty }{\left( A_ +{\varvec{v}}_{+}{\mathrm{e}}^{\sigma _+\tau } +A_-{\varvec{v}}_{-}{\mathrm{e}}^{\sigma _-\tau }\right) {\mathrm{e}}^{{{\text{i}}}kX}dk},\quad \text{where} \\&\quad {\varvec{v}}_{+}=\left( \begin{array}{l} 1 \\ 1\end{array} \right) ,\quad \sigma _{+}=-{{\text{i}}}k \frac{6H_0}{\epsilon (1-2H_{0})^{4}}-k^{4}\frac{H_{0}^{3}}{3} \\&\qquad +k^{2}{\textit{Re}}\root 3 \of {{\textit{Ca}}}\frac{6}{35}\frac{H_{0}^{2}(1+4H_{0})}{(1-2H_{0})^3}, \\&\quad {\varvec{v}}_{-}=\left( \begin{array}{l} 1\\ -1 \end{array} \right) ,\quad \sigma _{-}=-{{\text{i}}}k \frac{6H_{0}}{\epsilon (1-2H_{0})^3}-k^{4}\frac{H_{0}^{3}}{3}, \end{aligned}$$
(15)

with k being the dimensionless wave number and \(A_{\pm }(k)\) being the Fourier amplitudes. From this, it is apparent that the deformations of the interfaces are the superposition of a symmetric instability, \(\varvec{v_+}\), and a linearly independent antisymmetric one, \(\varvec{v_-}\). As \({{\text{Im}}}(\sigma _\pm )\propto k\), the propagation speeds of the linear interfacial waves are independent of the wavenumber and, therefore, do not disperse. Furthermore, \({{\text{Re}}}(\sigma _-)<0\) for all wavenumbers, while \({{\text{Re}}}(\sigma _+)>0\) for sufficiently small wavenumbers. Consequently, the interfaces are always linearly unstable for the symmetric deformations, while the antisymmetric ones are linearly stable.

On one hand, the characteristic (i.e., dominant) wavenumber of the deformations can be assumed to correspond to the wavenumber maximizing \(\sigma _+\) (i.e., the fastest growing wavenumber), which is given by

$$\begin{aligned} k_{\mathrm{char}}=\left[ {\frac{9}{35}{\textit{Re}}\root 3 \of {{\textit{Ca}}}\frac{1+4H_0}{H_0(1-2H_0)^3}}\right] ^{1/2}. \end{aligned}$$
(16)

Hence, owing to the negligible effect of gravity, the films are always inherently unstable to disturbances of a sufficiently small wavenumber for nonvanishing \({\textit{Re}}\).

On the other hand, according to Sect. 2.2, the dimensionless X coordinate is given by \(X=x_1\root 3 \of {{\textit{Ca}}}/\lambda _{\mathrm{char}}\), where \(\lambda _{\mathrm{char}}\) is the linear approximation of the characteristic dimensional wavelength of the deformations. Thus, consistent scaling requires that \(k_{\mathrm{char}}=2\pi /\root 3 \of {Ca}\). The equivalence of this wavenumber to the one from Eq. (16) provides an expression for \({\textit{Ca}}\) given by

$$\begin{aligned} {\textit{Ca}}=\frac{140\pi ^2H_0(1-2H_0)^3}{9{\textit{Re}}(1+4H_0)}. \end{aligned}$$
(17)

With the definition of the capillary number, one may also compute \(\epsilon\) to be given by

$$\begin{aligned} \epsilon =\sqrt{\frac{9\mu _g Q{\textit{Re}}(1+4H_0)}{140\pi ^2d\gamma H_0(1-2H_0)^3}}=\sqrt{\frac{9\rho _g Q^2(1+4H_0)}{140\pi ^2d\gamma H_0(1-2H_0)^3}}. \end{aligned}$$
(18)

As shown in Eq. (18), if \(\epsilon\) is defined consistently, it is merely a parameter predetermined by the properties of the system. The neutrally stable wavenumber is obtained from the condition \(\text{Re}(\sigma _+)=0\). According to Eq. (15), this condition is satisfied at \(k_{\mathrm{max}}=\sqrt{2}k_{\mathrm{char}}\).

To illustrate the application range of the current study, typical values of the dimensionless numbers used in the examples presented in the following sections are summarized in Table 1.

Table 1 Dimensionless quantities, their definitions, and typical values of the dimensionless numbers employed in the numerical simulations of the study
Full size table

3.1.1 Physical interpretation of the results

First, one may utilize the results of the linear stability analysis to judge the relative influence of the pressure gradient and the viscous stresses, respectively, on the instability. For this purpose, one assumes that both effects may be considered separately from one another. Without the presence of viscous stresses along the interface, the system would still be unstable, but with the characteristic wavenumber \(k_{\mathrm{char}}^\text{P}\). This instability emerges due to a mechanism analogous to the Venturi effect. Namely, it is caused by the fluctuation in the dynamic pressure of the gas flow triggered by the widening or narrowing of the gas layer with changing liquid-layer thicknesses. An equivalent mechanism is responsible for the Kelvin–Helmholtz instability. This is depicted in the bottom-left graph of Fig. 2. Similarly, if the pressure gradient is omitted from the evolution equations, one obtains \(k_{\mathrm{char}}^\text{T}\) for the characteristic wavenumber. The instability driven by the viscous stresses is triggered by the “sweeping” mechanism of the counter-rotating vortices of the secondary air flow before and after an elevation of the liquid–gas interface. This is shown in the bottom-right graph of Fig. 2. A straightforward calculation leads to

$$\begin{aligned} k_{\mathrm{char}}^\text{P}&=\left[ \frac{54}{35}{\textit{Re}}\root 3 \of {{\textit{Ca}}}\frac{1}{(1-2H_0)^3}\right] ^{1/2}, \end{aligned}$$
(19)
$$\begin{aligned} k_{\mathrm{char}}^\text{T}&=\left[ \frac{9}{35}{\textit{Re}}\root 3 \of {{\textit{Ca}}}\frac{1}{(1-2H_0)^2H_0}\right] ^{1/2}. \end{aligned}$$
(20)

The obtained wavenumbers can be related to the original one given by Eq. (16) with the expression \(k_{\mathrm{char}}^2=(k_{\mathrm{char}}^\text{P})^2\) \(+(k_{\mathrm{char}}^\text{T})^2\). Moreover, as long as \(H_0<0.125\) (\(H_0>0.125\)), \(k_{\mathrm{char}}^\text{T}>k_{\mathrm{char}}^\text{P}\) (\(k_{\mathrm{char}}^\text{T}<k_{\mathrm{char}}^\text{P}\)). This suggests that, at small film thicknesses, the interfaces are mainly deformed by viscous stresses, while, for larger film thicknesses, the instabilities are driven by pressure gradients.

Second, one may be interested in the effect which the coupling between the two interfaces has on the emergence of the patterns. That is, one can analyze how the properties of the instability of the two coupled interfaces differ from those of the instability that would appear if the deformation of one layer would not affect the other interface (Vécsei et al. 2014). The mathematical implementation of the latter scenario corresponds to setting \(\eta _2=0\) in Eq. (13) and \(\eta _1=0\) in Eq. (14). Performing a linear stability analysis indicates that the characteristic wavenumber of such a configuration is given by

$$\begin{aligned} k_{\mathrm{char}}'=\left[ {\frac{9}{70}{\textit{Re}}\root 3 \of {{\textit{Ca}}}\frac{1+4H_0}{H_0(1-2H_0)^3}}\right] ^{1/2}. \end{aligned}$$
(21)

Hence, the characteristic wavenumber is \(\sqrt{2}\) times smaller than for the coupled system. Furthermore, its corresponding growth rate is one-fourth of the growth rate of the coupled system at \(k=k_{\mathrm{char}}\). Hence, the coupling between the interfaces further destabilizes the system.

3.1.2 Validity range of the assumptions

With respect to assumption 1 Regarding the requirement that \(\epsilon ^2\ll 1\), the permittable volumetric fluxes as a function of \(H_0\) and the material properties are readily given by Eq. (18).

With respect to assumption 2 With respect to \(\epsilon {\textit{Re}}\), the corresponding first-order perturbation approach is readily justified for small \(\epsilon {\textit{Re}}\). Nevertheless, one expects the calculation to be sufficiently accurate as long as the advection-related corrections to the pressure gradient and the shear stresses in the gas layer, expressed by those terms in Eqs. (9) and (10) multiplied by \(\epsilon Re\), remain small. The results of the linear stability analysis can be used to demonstrate that Eqs. (7) and (8) remain valid also at larger values of \(\epsilon {\textit{Re}}\). To show this, one assumes that \(\text{O}(\partial H_1/\partial X)\approx \text{O}(\partial H_2/\partial X)\approx \varDelta Hk_{\mathrm{char}}\). According to Eqs. (9) and (10), if these corrections are small, then the perturbation approach for the inertial flow is justified even for larger values of \(\epsilon Re\). For an antisymmetric deformation, the correction vanishes completely, while, for a symmetric deformation, the relative contribution of inertia to the pressure gradient is given by

$$\begin{aligned} \varDelta P'\approx \frac{9}{35}\epsilon {\textit{Re}}k_{\mathrm{char}}\varDelta H. \end{aligned}$$
(22)

An equivalent estimate for the relative contribution of inertia to the shear stresses along the interfaces is given by \(\varDelta { E}'=\varDelta P'/4.5\). Thus, as long as \((\varDelta P')^2\ll 1\), the perturbation approach remains valid also at larger values of \(\epsilon Re\).

With respect to assumption 3 Estimating the error introduced by neglecting terms of higher order than \(1/{\textit{M}}\) from the evolution equations requires a more careful approach, as \({\textit{M}}\) is absent from Eqs. (7) and (8). Although the linear behavior of multilayer systems of arbitrary viscosities has been discussed in previous studies (Anturkar et al. 1990; Renardy 1987), these were not limited to interfaces undergoing long-wavelength instabilities. Therefore, the equations arising from these calculations are more complicated and could only be solved by numerical simulations. Thus, to perform a detailed analytical description for arbitrary viscosities but within the framework of the long-wavelength approximation, it is necessary to re-derive the linearized equations, starting from Eqs. (4)–(6). For asymmetric systems, the calculations are overly complicated, but, for symmetric systems, the solution of the linearized problem can be separated into a symmetric and an independent antisymmetric instability mode. This is possible even if the intermediate layer has an arbitrary viscosity. Formally, the linear solution takes the same form as Eq. (15), where the eigenvectors remain unchanged and the difference only arises in the expression for the eigenvalues. Given the linear independency of the eigenvectors, one may calculate the growth rates for the symmetric and the antisymmetric modes separately. To this end, one first assumes that the small interfacial deformation of the interfaces is symmetric, which corresponds to eigenvector \(\varvec{v_+}\). This leads to a single evolution equation for the deformations \(\eta _1=\eta _2\). Examining its Fourier transform will give the value of \(\text{Re}(\sigma _+)\). Similarly, one obtains \(\text{Re}(\sigma _-)\) by solving the linearized problem while assuming an antisymmetric deformation of the interfaces. The calculations are straightforward and were performed with the Mathematica® software. A comparison of the formulas obtained with this method and the numerical results of Renardy (1987) is presented in Fig. 3. The graphs show a good agreement between the two approaches. The complete expressions for the growth rates at arbitrary viscosity ratios and a more detailed discussion of the governing parameters of Fig. 3 are given in Appendix 2.

Fig. 3
figure 3

Comparison of the growth rates of the symmetric \(\sigma _+\) and the antisymmetric \(\sigma _-\) mode, according to expressions (39) and (40), with the numerical results of Renardy (1987). The dots represent the numerical results, which are taken from Figures 2, 4 and 3, respectively, of the referred paper. The lines correspond to the analytical formulas: [\(\mu _1=\mu _3=1.56605\times 10^{-6}\,\text{Pa}\,\text{s}\), \(d=200\,\upmu\text{m}\), \(\rho _1=\rho _2=\rho _3=1\,\text{kg}\,\text{m}^{-3}\), \(\partial p/\partial x=19.62\,\text{Pa}\,\text{m}^{-1}\), \(\gamma \rightarrow 0\) (see Appendix 2 for explanation), \(k=0.01/H_0\)]

Full size image

With these results, it is useful to calculate the relative error between the exact (linear) growth rates for arbitrary viscosities and those obtained for the simplified problem, where the middle layer has a much smaller viscosity than the liquid films. Denoting the real part of the exact growth rates by \(\text{Re}(\sigma _{+}^{e})\) and \(\text{Re}(\sigma _{-}^{e})\), the relative error of the simplification is defined by

$$\begin{aligned} \varDelta \sigma _\pm ^2=\frac{\int \limits _0^{k_{\mathrm{max}}}{\left[ \text{Re}(\sigma _{\pm }^{ e})-\text{Re}(\sigma _{\pm })\right] ^2{\mathrm{d}}k}}{\int \limits _0^{k_{\mathrm{max}}}{\left[ \text{Re}(\sigma _{\pm }^{ e})\right] ^2{\mathrm{d}}k}}. \end{aligned}$$
(23)

The linearly neutrally stable wavenumber (\(k_{\mathrm{max}}=\) \(\sqrt{2}k_{\mathrm{char}}\) with \(k_{\mathrm{char}}\) defined by (16)) is taken as the limit of the integrals, as one is mainly interested in the regime of unstable wavenumbers (\(k<k_{\mathrm{max}}\)), for which \(\text{Re}(\sigma _+)\ge 0\). After substituting the expressions for the growth rates into (23), one finds that \(\varDelta \sigma _\pm ^2\) are independent of the Reynolds and the capillary number. This is an important property, as it shows that even though the growth rates are functions of \({\textit{Re}}\root 3 \of {{\textit{Ca}}}\), the error introduced by the assumption of semi-rigidness is only a function of the viscosity, density ratios, and \(H_0\). For instance, this implies that after its validity has been verified for a given setup, semi-rigidness remains a valid assumption even if some of the system parameters, such as the flux of the gas flow, are changed. An example of the results for a water–air system is depicted in Fig. 4. Values for the material properties at \(25~^\circ \text{C}\) and \(1~\text{bar}\) used to generate this figure are summarized in Table 2.

Table 2 Material properties of air, water (Lide and Haynes 2010), and \(10\,\text{cSt}\) silicone oil (VanHook et al. 1997) for different temperatures at \(1\text{ bar}\) pressure
Full size table
Fig. 4
figure 4

Real part of the eigenvalues, \(\sigma _+\) and \(\sigma _-\), for the linearized water–air system as a function of the wavenumber. The continuous lines indicate the results obtained under the assumption of semi-rigidness of the films (\(M\gg 1\)), while the exact eigenvalues for the actual value of \({\textit{M}}\) are plotted with dashed lines. The initial thickness \(H_0 = h_0/d\) of the symmetric liquid films is varied for each plot, as indicated (\(d=200\,\upmu \text{m}\), mean air velocity \(1\,\text{m}\,\text{s}^{-1}\), \({\textit{Re}}\approx 10\), \({\textit{Ca}}\approx 0.56\))

Full size image

Figure 4 confirms intuition in the sense that the assumption of semi-rigidness becomes less accurate with increasing the blockage of the total channel width by the liquid films. For the examples shown, this is particularly noticeable for \(H_0 \ge 0.11\). While approximations estimating the accuracy of the assumption of semi-rigidness are only valid for the equations linearized in \(\eta _1\) and \(\eta _2\), one does not expect the order of the relative error to change considerably for the nonlinear equations. This can be explained by the linearity of the viscous stress term in the Navier–Stokes equation.

3.2 Weakly nonlinear analysis

As the eigenvectors of the linear equations \(\varvec{v_+}\) and \(\varvec{v_-}\) form a complete set for the function space of possible solutions, one can assume without loss of generality that the solutions of the weakly nonlinear equations take the form

$$\begin{aligned} \begin{pmatrix}\eta _1\\ \eta _2\end{pmatrix}=\int \limits _{-\infty }^{\infty }{\left[ A_+(k,\tau )\varvec{v_+}{\mathrm{e}}^{\sigma _+\tau }+A_-(k,\tau )\varvec{v_-}{\mathrm{e}}^{\sigma _-\tau }\right] {\mathrm{e}}^{{{\text{i}}}kX}{\mathrm{d}}k}. \end{aligned}$$
(24)

This expression is formally identical to the one presented in Eq. (15), except that here the Fourier coefficients are not only functions of the wavenumber k but are also time-dependent. This occurs due to the mixing of the linear modes through the nonlinear terms of the evolution equations. The growth rates \(\sigma _\pm\) are still defined by the same expressions as in Eq. (15). After substituting this integral into Eqs. (13) and (14), one obtains the relationships between the Fourier coefficients to be given by

$$\begin{aligned}&\frac{\partial A_{+}}{\partial \tau }{\mathrm{e}}^{\sigma _+ \tau }+{{\text{i}}}k\left[ \frac{3(1+6H_0)}{(1-2H_0)^5}(A_+{\mathrm{e}}^{\sigma _+\tau } )\underset{k}{*}(A_+{\mathrm{e}}^{\sigma _+\tau })\right. \\&\quad \left. +\frac{3(1+2H_0)}{(1-2H_0)^3}(A_-{\mathrm{e}}^{\sigma _-\tau }) \underset{k}{*}(A_-{\mathrm{e}}^{\sigma _-\tau })\right] =0, \\&\frac{\partial A_{-}}{\partial \tau }{\mathrm{e}}^{\sigma _- \tau }+{{\text{i}}}k\frac{6(1+4H_0)}{(1-2H_0)^4}(A_+{\mathrm{e}}^{\sigma _+\tau }) \underset{k}{*}(A_-{\mathrm{e}}^{\sigma _-\tau })=0, \end{aligned}$$
(25)

where \(f\underset{k}{*}g:=\int \nolimits _{-\infty }^\infty {f(k-k')g(k'){\mathrm{d}}k'}\) is the convolution of the functions with respect to the wavenumber. The derivation of these equations is discussed in detail in Appendix 3. For the calculations and the discussion of the actual film deformations, it is useful to introduce the variables

$$\begin{aligned} \begin{aligned} \zeta _+(\xi ,\tau )&=\int \limits _{-\infty }^{\infty }{A_+{{\text{exp}}}[{{{\text{Re}}}(\sigma _+)\tau +{{\text{i}}}k \xi }]\,{\mathrm{d}}k} \\ \zeta _-(\xi ,\tau )&=\int \limits _{-\infty }^{\infty }{A_-{{\text{exp}}}[{{\text{Re}}}(\sigma _-)\tau +{{\text{i}}}k \xi ]\,{\mathrm{d}}k}. \end{aligned} \end{aligned}$$
(26)

Since, in the definition of \(\zeta _-\) and \(\zeta _+\), the imaginary parts of the growth rates were omitted, one needs to consider them as a shift along the spatial coordinate. Formally, the film deformations are given by

$$\begin{aligned} \eta _1(X,\tau )&=\zeta _+(X-6H_0/\left[ \epsilon (1-2H_0)^4\right] \tau ,\tau ) \\&\quad +\,\zeta _-(X-6H_0/\left[ \epsilon (1-2H_0)^3\right] \tau ,\tau ), \end{aligned}$$
(27)
$$\begin{aligned} \eta _2(X,\tau )&=\zeta _+(X-6H_0/\left[ \epsilon (1-2H_0)^4\right] \tau ,\tau ) \\&\quad -\,\zeta _-(X-6H_0/\left[ \epsilon (1-2H_0)^3\right] \tau ,\tau ), \end{aligned}$$
(28)

i.e., \(\zeta _+\) and \(\zeta _-\) define the magnitude of the symmetric and the asymmetric deformations at a point along the horizontal coordinate. An inverse Fourier transformation of Eq. (25) results in the partial differential equations

$$\begin{aligned}&\begin{aligned} 0&=\frac{\partial \zeta _+}{\partial \tau }+\frac{H_0^3}{3}\frac{\partial ^4 \zeta _+}{\partial \xi ^4}+ {\textit{Re}}\root 3 \of {{\textit{Ca}}}\frac{6}{35}\frac{H_0^2(1+4H_0)}{(1-2H_0)^3}\frac{\partial ^2 \zeta _+}{\partial \xi ^2}\\&\quad +\frac{3(1+6H_0)}{(1-2H_0)^5}\frac{\partial \zeta _+^2}{\partial \xi }+\frac{3(1+2H_0)}{(1-2H_0)^3}\frac{\partial \zeta _-^2}{\partial \xi }{\Bigg |}_{\xi +\frac{12H_0^2}{\epsilon (1-2H_0)^4}\tau }, \end{aligned} \end{aligned}$$
(29)
$$\begin{aligned}&\begin{aligned} 0&=\frac{\partial \zeta _-}{\partial \tau }+\frac{H_0^3}{3}\frac{\partial ^4 \zeta _-}{\partial \xi ^4} \\&\quad +\frac{6(1+4H_0)}{(1-2H_0)^4}\frac{\partial \left[ \zeta _-\left( \zeta _+{\Big |}_{\xi -\frac{12H_0^2}{\epsilon (1-2H_0)^4}\tau }\right) \right] }{\partial \xi }. \end{aligned} \end{aligned}$$
(30)

The subscript \(X\pm 12H_0^2/[\epsilon (1-2H_0)^4]\tau\) represents the differences in the phase velocities of the symmetric and the antisymmetric mode. It indicates that one evaluates the corresponding function at a shifted value of X. For verification, the expressions of Eqs. (27) and (28) may be substituted directly into Eqs. (13) and (14). This has been found to also lead to Eqs. (29) and (30). Note that all terms of the derived equations are \(O(\epsilon ^0)\). This has been obtained by a fundamentally different approach than the one used in the previous studies. Those were limited to systems for which the application of a Galilean transformation was sufficient to avoid terms scaling with different orders of \(\epsilon\) in the governing equations (Papaefthymiou et al. 2013). Herein, such a transformation would have been impractical as the velocities of the two modes are not identical. This is apparent from Eqs. (27) and (28). It is noted that due to the vastly different viscosity ratios of the systems discussed in other related works (Papaefthymiou et al. 2013; Kliakhandler and Sivashinsky 1995), no direct comparison between the results is possible. Furthermore, as the work of Papaefthymiou and Papageorgiou (2017) focuses on inertialess multilayer systems with negligible surface tension, their results are also not applicable for the present study.

The equations show that, while the (weakly nonlinear) symmetric deformation is affected by the inertial flow, the antisymmetric mode is not influenced by it directly. Furthermore, by introducing the variables \(\zeta _+\) and \(\zeta _-\), the advective terms of Eqs. (13) and (14) transform into a nonlocal coupling effect between the instability modes. To describe this coupling, it is useful to transform the equations. Similar to the approach used to analyze the Kuramoto–Sivashinsky equations (Chang and Demekhin 2002), one multiplies Eqs. (29) and (30) with \(\zeta _+\) and \(\zeta _-\), respectively, and integrates the resulting equations along \(-\infty<\xi <\infty\). Assuming that, for every \(\tau\), the deformations and their derivatives vanish as \(\xi \rightarrow \pm \infty\) (i.e., at a fixed point in time, the interfaces are pinned at \(X\rightarrow \pm \infty\) with a contact angle of \(90^\circ\)), one finds that

$$\begin{aligned}&\begin{aligned} 0&=\frac{\partial }{\partial \tau }\left<\zeta _+^2\right>+\frac{2H_0^3}{3}\left<\left( \frac{\partial ^2 \zeta _+}{\partial \xi ^2}\right) ^2\right>\\&\quad -\,{\textit{Re}}\root 3 \of {{\textit{Ca}}} \frac{12}{35}\frac{H_{0}^2(1+4H_{0})}{(1-2H_{0})^3}\left<\left( \frac{\partial \zeta _+}{\partial \xi }\right) ^2\right>\\&\quad -\,\frac{6(1+2H_0)}{(1-2H_0)^3}{\text{corr}}\left( \frac{\partial \zeta _+}{\partial \xi },\zeta _-^2\right) {\Bigg |}_{\textstyle \frac{12H_0^2}{\epsilon (1-2H_0)^4}\tau }, \end{aligned} \end{aligned}$$
(31)
$$\begin{aligned}&\begin{aligned} 0&=\frac{\partial }{\partial \tau }\left<\zeta _-^2\right>+ \frac{2H_0^3}{3}\left<\left( \frac{\partial ^2 \zeta _-}{\partial \xi ^2}\right) ^2\right>\\&\quad +\frac{6(1+4H_0)}{(1-2H_0)^4}{\text{corr}}\left( \frac{\partial \zeta _+}{\partial \xi },\zeta _-^2\right) {\Bigg |}_{\textstyle \frac{12H_0^2}{\epsilon (1-2H_0)^4}\tau }, \end{aligned} \end{aligned}$$
(32)

where corr \(\left( \frac{\partial \zeta _+}{\partial \xi },\zeta _-^2\right) {\Bigg |}_{\varDelta \xi }=\int \nolimits _{-\infty }^{\infty } {\frac{\partial \zeta _+}{\partial \xi }{\Bigg |}_{\xi }\zeta _-^2{\Bigg |}_{\xi +\varDelta \xi }{\mathrm{d}}\xi }\) denotes the correlation function. The equations remain the same if—instead of the condition of pinned interfaces—periodic boundary conditions are applied at the domain boundaries. The operator \(\langle f(\xi )\rangle\) represents the integration of \(f(\xi )\) on \([-\infty ,\infty ]\). The quantities \(\langle \zeta _+^2\rangle\) and \(\langle \zeta _-^2\rangle\) characterize the magnitude of the symmetric and the antisymmetric instability mode, respectively, over the whole length of the interface. As \(\langle ({\partial \zeta _+}/{\partial \xi })^2\rangle\) is nonnegative, the perturbation due to the inertial term always leads to an increase of the symmetric deformations. Similarly, \(\langle ({\partial ^2 \zeta _+}/{\partial \xi ^2})^2\rangle\) is always nonnegative as well, so that capillarity always decreases the deformation amplitudes. Therefore, the interfaces are not susceptible to capillary-induced instabilities. The absence of such instabilities in the system is discussed in more detail in Appendix 4.

As summarized in Appendix 5, from numerical simulations, it was found that the antisymmetric mode is always dampened out. Intuitively, this can be understood as follows: Eqs. (31) and (32) suggest that the antisymmetric instability mode can only be destabilized if the correlation function between the antisymmetric and the symmetric modes is negative. In this case, Eq. (31) indicates that \(\langle \zeta _+^2\rangle\) grows slower than for configurations for which the correlation is positive. In turn, for a positive correlation function, the symmetric deformation further dampens the antisymmetric instability. Thus, one expects the symmetric instability mode to have a generally stabilizing effect on the antisymmetric one. Moreover, as \(\tau \rightarrow \infty\), the spatial distance over which the correlation is evaluated also tends to infinity. Although dissipative systems are known to exhibit long-range coherent behavior (Nicolis and Prigogine 1977), the correlation function still needs to vanish in physically realistic setups as the shift between \(\zeta _+\) and \(\zeta _-\) tends to infinity. Therefore, after sufficiently long time, the coupling between the instability modes will have a negligible effect on the film evolution. Both arguments, supported by numerical tests, suggest that the antisymmetric instability mode decays during the long-time evolution of the interfaces, which can be formally expressed by \(\langle \zeta _-^2\rangle \rightarrow 0\), and thus, \(\zeta _-\rightarrow 0\) at every point. Hence, as long as the symmetric mode is unstable, one may assume that as time proceeds \(\zeta _-\ll \zeta _+\). From this and Eq. (29), one can deduce that the physically relevant symmetric instability mode will evolve according to the Kuramoto–Sivashinsky equation given by

$$\begin{aligned} 0&=\frac{\partial \zeta _+}{\partial \tau }+\frac{H_0^3}{3}\frac{\partial ^4 \zeta _+}{\partial \xi ^4}+ {\textit{Re}}\root 3 \of {{\textit{Ca}}}\frac{6}{35}\frac{H_0^2(1+4H_0)}{(1-2H_0)^3}\frac{\partial ^2 \zeta _+}{\partial \xi ^2} \\&\quad +\,\frac{3(1+6H_0)}{(1-2H_0)^5}\frac{\partial \zeta _+^2}{\partial \xi }, \end{aligned}$$
(33)

which is noted to be independent of the parameter \(\epsilon\). This implies that although the initial behavior of the system is affected by this parameter, it only influences the dimensionless velocity of the emerging waves at large times according to Eqs. (27) and (28). Substituting the definition of Eqs. (27) and (28) permits to transform this equation into evolution equations of \(\eta _1\) and \(\eta _2\). Nonlinear partial differential equations of this type have been first derived for reaction–diffusion systems (Kuramoto and Tsuzuki 1976) and for liquid-film instabilities (Sivashinsky and Michelson 1980). They have been the subject of extensive analytical (Chang and Demekhin 2002; Kudryashov 1990) and numerical studies (Cvitanovic et al. 2010; Kevrekidis et al. 1990). Therefore, the further analysis of these equations will not be discussed here in detail; the reader is referred to the existing literature on the topic.

After calculating \(\zeta _+\) with Eq. (33) (under the assumption that the coupling to the antisymmetric mode is negligibly small), one can solve Eq. (30) independently to obtain \(\zeta _-\). It is noted that even when \(\zeta _-\) is not negligibly small compared to \(\zeta _+\), Eqs. (29) and (30) are still reducible to a single evolution equation. The derivation of this quite complicated equation is discussed in Appendix 6.

In the long-time limit, equations of the form

$$\begin{aligned} \frac{\partial u}{\partial t}+\nu \frac{\partial ^4 u}{\partial x^4}+\frac{\partial ^2 u}{\partial x^2}+\frac{1}{2}\frac{\partial u^2}{\partial x}=0 \end{aligned}$$
(34)

should have a bounded solution (Hyman and Nicolaenko 1986), where an upper bound scales like \(\nu ^{-1/4}\). After rescaling of Eq. (33) to take the same form as Eq. (34), this condition transforms to

$$\begin{aligned} \lim \limits _{\tau \rightarrow \infty }\text{sup}(\zeta _+)\le \beta \left[ \frac{(1+6H_0)^2}{H_0^3(1-2H_0)(1+4H_0)^3CaRe^3}\right] ^{-1/4}. \end{aligned}$$
(35)

Therefore, the amplitudes of the interfacial deformation cannot increase indefinitely, but should be stabilized by the nonlinear terms in the evolution equation. While this property is consistent with physical intuition, giving an exact upper limit for the deformation amplitudes is not possible due to the unknown constant \(\beta\) on the right-hand side of the expression.

As mentioned above, to examine the long-term damping of the antisymmetric instability mode, a number of simulations of the full evolution equations [Eqs. (7) and (8)] were conducted. The finite-element method with quadratic (Lagrangian) shape functions was applied for solving the equations. The calculations were performed with Comsol (2014) using the Matlab Livelink environment. The dimensionless parameters were varied according to \(H_0\in [0.01,0.3]\), \(\epsilon \in [0.01,0.5]\), \({\textit{Re}}\in [1,50]\), and \({\textit{Ca}}\in [0.125,5]\). The simulation results are summarized in Appendix 4. They all indicate that the antisymmetric mode is quickly damped out. Thus, for symmetric systems, the films fully synchronize in phase and amplitude.

An example of the evolution of \(\langle \zeta _-^2\rangle\) and \(\langle \zeta _+^2\rangle\) is depicted in Fig. 5. As for all of the simulations conducted, the length of the simulated domain was \(L=40\pi /k_{\mathrm{char}}\) with periodic boundary conditions. This corresponds to a sampling rate of \(k_{\mathrm{char}}/20\) in Fourier space. The length was divided into 200 cells. Hence, according to the Nyquist theorem, the maximal numerically resolvable wavenumber would be \(5k_{\mathrm{char}}\) if the domain was discretized with a finite-different scheme. The finite-element discretization with quadratic Lagrangian shape functions utilized for the simulations exceeds this resolution. In any case, although the strong nonlinearity of the evolution equations suggests that higher wavenumbers than \(k_{\mathrm{max}}=\sqrt{2}k_{\mathrm{char}}\) should also appear during the evolution, the highest unstable wavenumber in the full nonlinear simulations was still found to be considerably smaller than \(5k_{\mathrm{char}}\). As an initial condition, the interfaces were assumed to be flat except for a small white-noise perturbation with an amplitude of \(0.01H_0\) added to the surface of the lower film. Since the upper film was initially undeformed (\(\eta _2=0\)), it was ensured that at the beginning \(\langle \zeta _-^2\rangle =\langle \zeta _+^2\rangle\).

Fig. 5
figure 5

Example for the numerical results obtained by solving (7) and (8) for \(H_0 = 0.2\), \({\textit{Re}}= 23.46\), \({\textit{Ca}}= 0.15\), and \(\epsilon =0.12\). Plot a shows the interfaces along the channel at \(\tau =1\), b depicts the absolute values of the Fourier coefficients of \(\zeta _+\) at \(\tau =1\). The values of \(k_{\mathrm{max}}\) and \(k_{\mathrm{char}}\) correspond to the two dashed vertical lines. Plot c shows the time evolution of the symmetric and the antisymmetric instability mode. The approximate solution according to the Kuramoto–Sivashinsky (KS) equation is shown for comparison

Full size image

For the simulations referred to in Fig. 5, silicone oil (\(10\text{ }\text{cSt}\)) and air at a temperature of \(50\text{ }^\circ \text{C}\) and at \(1\text{ bar}\) pressure were assumed as the working fluids. Their material properties are summarized in Table 2. The undisturbed film thicknesses were \(H_0=0.2\), which corresponds to an error of \(\varDelta \sigma _+\approx 0.005\) and \(\varDelta \sigma _-\approx 0.006\) in the (linear) growth rates caused by the truncation of the viscosity-ratio expansion [see Eq. (23)]. Therefore, for this configuration, the assumption of semi-rigid liquid films is valid. The channel width was set to \(d=200~\upmu \text{m}\), and the mean air-flow velocity was assumed to be \(3.5~\text{m}\,\text{s}^{-1}\). The corresponding Reynolds and capillary numbers are \({\textit{Re}}\approx 23.46\) and \({\textit{Ca}}\approx 0.15\), while \(\epsilon \approx 0.12\). The maximal deformation of the interfaces was found to be \(\varDelta H\approx 0.028\); thus, the relative contribution to the pressure field due to inertia was approximately 0.23 according to Eq. (22). Hence, all assumptions necessary for the validity of Eqs. (7) and (8) were fulfilled during the simulation.

Plot (a) of Fig. 5 shows the interface shapes at \(\tau = 1\), while plot (b) depicts the spectrum of the absolute values of the Fourier coefficients of the symmetric deformation, \(\zeta _+\), at the same time instance. From this plot, one can deduce that there is no well-defined characteristic (i.e., dominating) wavelength of the instability, which is a consequence of the pronounced nonlinearity of the evolution equations. Similarly, while high wavenumbers are damped, the nonlinearity of Eqs. (7) and (8) implies that wavenumbers larger than \(k_{\mathrm{max}}\) (obtained from the linear analysis) are unstable, as well. This does not cause any problems in the simulations, as the largest appearing wavenumber is still much smaller than the resolution of the mesh, \(5k_{\mathrm{char}}\).

Figure 5c shows the time evolution of \(\langle \zeta _+^2\rangle\) and \(\langle \zeta _-^2\rangle\). As one expects, the antisymmetric instability mode is damped quickly, and \(\langle \zeta _+^2\rangle\) becomes much larger than \(\langle \zeta _-^2\rangle\) after a short initial transition period. For comparison, a simulation of the Kuramoto–Sivashinsky equation [Eq. (33)] was also performed. As the initial condition, the initial distribution of \(\zeta _+\) from the previous simulation was utilized (i.e., the initial white-noise distribution is identical). One finds that the graph of \(\langle \zeta _+^2\rangle\) obtained from the simulation of the full evolution equations [Eqs. (7) and (8)] is essentially identical to the one calculated from the simplified problem \(\langle \zeta _+^2\rangle _{\text{KS}}\). This comparison was also performed for three other systems. For the first one, all parameters were the same as in Fig. 5, but the mean air velocity was changed to \(u=5~\text{m}\,\text{s}^{-1}\). Similarly, for the second and third simulation, the governing parameters were unchanged, except that the nondimensional film thickness was \(H_0=0.1\) and the channel width was \(d=100~\upmu \text{m}\), respectively. For all the cases, the simplified equation was found to provide a good approximation of the behavior of the full system, even at early times. The accuracy of the approximation is comparable to what is shown in Fig. 5c. Thus, these results verify numerically that Eq. (33) accurately approximates the time evolution of the original nonlinear equations, Eqs. (7) and (8).

Returning to the question posed at the beginning of Sect. 3, one may conclude that the mirror symmetry of the system does not break down dynamically. Even if the fluctuations along the interfaces are not symmetric, they do not give rise to a self-sustaining asymmetric deformation of the interfaces. This can intuitively be understood by the mechanism explained in the context of Fig. 2: An initial thickness disturbance on one film will lead to pressure fluctuations and shear stress variations along the surface of the other film. They act in a direction that always fosters a deformation of that film not only at the same location and in the same direction as the initial disturbance but—given the identical initial thickness of both films—also of the same amplitude. Since this mechanism applies to all thickness disturbances, the evolutions of both films are completely synchronized. However, it should be noted that such an intuition is only correct if the liquid films are much more viscous than the fluid in between. Indeed, if the viscosity ratio M is not sufficiently large, then both the symmetric and the antisymmetric mode can become unstable, so that this conclusion does no longer hold. This is apparent from the formulas for the corresponding (linear) growth rates given in Appendix 2. Hence, the initial symmetry alone does not ensure a fully synchronized evolution of both films.

Less intuitive is the finding that the coupled system becomes more unstable than the isolated films under identical base flow conditions, as indicated by the enlarged wavenumber of the fastest growing mode in the linear theory. In the weakly nonlinear regime, the saturation deformation amplitude is seen to be affected by the coupling, as well. However, in light of the complex and partially unknown properties of the Kuramoto–Sivashinsky equation, no upper bound can be given for this quantity, neither for the single nor for the double film system. Therefore, the magnitude of the coupling effect on that parameter cannot be quantified, in general.

4 Asymmetric systems

In realistic systems, complete mirror symmetry of the undisturbed system is not a valid assumption. For broken symmetry, it is possible to perform a second perturbation analysis for the deviation from the symmetric configuration. Nevertheless, to get a qualitative overview of systems with high asymmetry, it is favorable to use numerical calculations. For this purpose, the initial thicknesses of the liquid films are allowed to differ by a nondimensional quantity \(\delta\), which defines the difference between the initial thicknesses of the undisturbed films according to

$$\begin{aligned} \begin{aligned}&H_1(t=0) = H_0(1+\delta /2), \\&H_2(t=0) = H_0(1-\delta /2), \quad \delta \in [0,2). \end{aligned} \end{aligned}$$
(36)

The goal of the present analysis is to find how the coupling between the two films changes with \(\delta\). For this purpose, the evolution of the liquid films was simulated with the same numerical method as introduced in the previous section. Furthermore, the quantities used for nondimensionalization were defined in the same way as for symmetric systems. Given that the evolution of the film thicknesses is still described by Eqs. (7) and (8), the dynamics of the interfaces should be only governed by the four dimensionless numbers, \(\epsilon\), \({\textit{Re}}\root 3 \of {Ca}\), \(H_0\), and \(\delta\).

To quantify the coupling strength between the layers, the normalized correlation of the interface deformation amplitudes \(\varDelta H_1\) and \(\varDelta H_2\) is defined by

$$\begin{aligned} C(\tau )=\frac{\int \limits _{-\infty }^{\infty }{\varDelta H_1(\tau ,X)\varDelta H_2(\tau ,X)}\,{\mathrm{d}}X}{\sqrt{\int \limits _{-\infty }^{\infty }{\varDelta H_1^2(\tau ,X)\,{\mathrm{d}}X}\int \limits _{-\infty }^{\infty }{\varDelta H_2^2(\tau ,X)\,{\mathrm{d}}X}}}. \end{aligned}$$
(37)

A convenient property of C is that it is invariant under the transformation \(\varDelta H_1\rightarrow \alpha _1\varDelta H_1\), \(\varDelta H_2\rightarrow \alpha _2\varDelta H_2\) as long as \(\alpha _1\times \alpha _2\) is positive and independent of X. Thus, even if the magnitudes of the deformations are different, the normalized correlation function may remain the same. This is useful, since one expects the thinner film to have a smaller deformation than the thicker one. For phase-synchronized deformations, \(C=1\), while \(C=0\), if the film deformations are uncorrelated. At the \(C=-1\) limit, the interfaces are in antiphase, i.e., \(\varDelta H_1=-\alpha \varDelta H_2\), where \(\alpha>0\) is independent of X.

All simulations indicate that, at \(\delta =0\), the correlation function tends to unity as \(\tau \rightarrow \infty\). For symmetric systems, this is to be expected, since—as discussed above—in those cases, the antisymmetric mode disappears in the long-time limit. Hence, for symmetric systems, \(\varDelta H_1\approx \varDelta H_2\) after a sufficiently long-time period. Relative to the symmetric case, the correlation is seen to decrease with increasing values of \(\delta\). A number of simulations were performed for the dimensionless parameters \(H_0\in [0.04,0.2]\), \(Re\root 3 \of {Ca}\in [1,10]\), \(\delta \in [0,1.999]\), and \(\epsilon \in [0.01,0.125]\). The value of C was found to be nonnegative in all the cases studied. Consequently, even for the asymmetric configuration, the deformations of the two films have predominantly the same sign.

In Fig. 6, examples of the evolution of the correlation function with \(\delta\) are shown. Once again, the silicone oil of Table 2 was considered as the liquid medium, while air was chosen for the intermediate gas layer. For the first set of simulations, the channel thickness was \(d=50~\upmu \text{m}\). The dimensionless initial liquid-layer thicknesses at \(\delta =0\) were \(H_0=0.04\), and the mean air velocity was \(u=5~\text{m}\,\text{s}^{-1}\). For the second and third sets of simulations, these parameters were \(d=50~\upmu \text{m}\), \(H_0=0.08\), \(u=5~\text{m}\,\text{s}^{-1}\) and \(d=100~\upmu \text{m}\), \(H_0=0.15\), \(u=3~\text{m}\,\text{s}^{-1}\), respectively. For the last set of simulations, the values were \(d=100~\upmu \text{m}\), \(H_0=0.2\), \(u=3~\text{m}\,\text{s}^{-1}\). In dimensionless coordinates, the channel length was set to 20, while it was divided into at least 500 cells to ensure grid independence. The time evolution of \(\langle \varDelta H_1^2\rangle\) and \(\langle \varDelta H_2^2\rangle\) strongly resembles the graph of \(\langle \zeta _+^2\rangle\) in Fig. 5c). Therefore, for the current analysis, the simulated time interval after which C was evaluated was chosen to be long enough to ensure that the values of \(\langle \varDelta H_1^2\rangle\) and \(\langle \varDelta H_2^2\rangle\) only oscillated around their asymptotic value in the last \(10\%\) of the time interval. The corresponding dimensionless time was 1600 in the first, 1000 in the second, 160 in the third and 120 in the fourth set of simulations. These correspond to approximately \(849~\text{s}\), \(822~\text{s}\), \(977~\text{s}\), and \(909~\text{s}\) in real time. It is noted that the highest value of \(\delta\) for the last set of simulations was 1.7 due to the increase in the computational requirements of the calculations with \(\delta\) and \(H_0\). The correlation function was calculated as the average of the correlation between the film thicknesses in the final \(10\%\) of the simulated time interval.

Fig. 6
figure 6

Dependence of the correlation function C on the thickness difference \(\delta\) for systems with different nominal film thicknesses \(H_0\). (The velocities and channel thicknesses for \(H_0=0.2\) were \(u=3\,\text{m}\,\text{s}^{-1}\) and \(d=100\,\upmu \text{m}\). For \(H_0=0.15\), they were \(u=3\,\text{m}\,\text{s}^{-1}\), \(d=100\,\upmu \text{m}\); for \(H_0=0.08\): \(u=5\,\text{m}\,\text{s}^{-1}\), \(d=50\,\upmu \text{m}\); and for \(H_0=0.04\): \(u=5\,\text{m}\,\text{s}^{-1}\), \(d=50\,\upmu \text{m}\))

Full size image

All simulations show similar characteristics. Initially, the correlation function decreases with increasing values of \(\delta\). This was found to be a consequence of a very slowly emerging instability of the thinner liquid layer, detuning the two interfaces. As \(\delta\) further increases, this process either disappears or its growth rate becomes small enough to no longer affect the patterns within the simulated time interval, leading to an increase of the correlation between the films. At \(\delta \approx 2\), when the ratio of the undisturbed film thicknesses is about 100, C drops sharply. This is not a surprising result, since, at this point, the order of magnitude of the terms in the evolution equations [Eqs. (7) and (8)] is very different for each film, and one does no longer expect the layers to have a qualitatively similar behavior. The unevenness of the curves is a consequence of the small, \(\delta\)-dependent rate of the detuning. Given that obtaining a single data point took in some cases several days to compute, performing longer simulations was generally not possible due to limitations in computational resources. Therefore, it is presumed that the simulated time interval was not sufficiently large to capture the full development of the detuning for all simulations. In these cases, the correlation function may not have reached its stationary value. However, the behavior of the system is not a numerical artifact: the spectrum of unstable wavenumbers of the interfacial deformations stayed within the range of the numerical resolution of the simulations, and no rapid temporal variations emerged during the calculations.

Notably, the correlations of most systems were close to unity for \(\delta \in [0,2)\) for several minutes. This result indicates that, even in a highly asymmetric system, one may often utilize the assumption that at the initial stages of their development the patterns on the two interfaces are identical apart from a constant factor between their amplitudes. For highly asymmetric systems, the deformation of the thinner film is expected to have a smaller effect on the pattern of the thicker film than vice versa. Therefore, at high values of \(\delta\), where \(C\approx 1\), this indicates that the deformation of the thinner film is enslaved by the instability of the thicker one.

To a certain degree, the synchronization of the interfaces can be explained qualitatively by examining the linear properties of the system. For this purpose, one considers the uncoupled liquid layers, i.e., similarly as for Eq. (21), it is assumed that only the thicker (thinner) liquid layer may deform, while the deformation of the thicker (thinner) liquid interface is suppressed. By performing a linear stability analysis for these systems, one may obtain the characteristic length scales of the patterns that would emerge on the interfaces if the deformations of the two interfaces did not affect each other. The calculation is straightforward, and Fig. 7 depicts the normalized characteristic wavenumber for the thinner and the thicker liquid layer for a set of parameters. These plots show that even up to \(\delta =1.5\), for which the lower film is seven times thicker than the upper one, the characteristic wavenumbers of the two interfaces are very similar. The difference between the characteristic length scales increases with decreasing \(H_0\) and increasing \(\delta\). This implies that, for a large range of parameters, the deformational wavelengths would be comparable, even if the interfaces were uncoupled. For the coupled system, Eqs. (9) and (10) show that both the pressure drop and the viscous stresses destabilizing the layers are more prominent if the two interfaces deform in phase with each other. Therefore, if the characteristic length scales of the emerging patterns of the uncoupled interfaces are comparable, even a weak coupling is sufficient to promote their synchronization. If these quantities are principally different, a stronger coupling would be necessary to synchronize the two interfaces. Therefore, one expects the correlation function to decrease for \(\delta \rightarrow 2\) as well as for \(H_0\rightarrow 0\), which agrees with the results of Fig. 6. The increase of the correlation function near \(\delta =1\) and beyond is presumably a consequence of the very slow self-patterning of the thinner liquid layer, combined with its coupling to the rapid pattern formation process of the thicker layer. At \(\delta =1\), the linear analysis shows that the growth rate of the most unstable wavenumber is about an order of magnitude larger for the uncoupled thicker layer in comparison with the thinner one. At \(\delta =1.9\), it is generally more than two orders of magnitude larger.

Fig. 7
figure 7

Normalized characteristic wavenumber of the uncoupled layers for different values of \(\delta\) and \(H_0\)

Full size image

5 Conclusion

In this paper, the hydrodynamic coupling between the long-wavelength instabilities emerging at the interfaces of thin liquid films, which cover the walls of a plane-parallel microchannel and are exposed to a gaseous flow along the channel center plane, has been investigated. To the best of our knowledge, this setup has not been analyzed in detail in the previous studies, despite its practical relevance. The governing equations were simplified by employing the long-wavelength approximation and by assuming moderate values for the Reynolds number. The small viscosity ratios of the gaseous to the liquid media were utilized to simplify the system further, so that it can be described and analyzed by two relatively compact evolution equations. The fully and weakly nonlinear forms of the governing equations correspond to the expectations based on the previous analyses. While Papaefthymiou et al. (2013) treated similar systems numerically, the discussion of the current study is focused on the analytical characterization of the unstable modes of the system. In contrast to the analytical results of Papaefthymiou and Papageorgiou (2017), employing substantially different physical assumptions, inertia and surface tension effects were accounted for.

Based on the simplified model, it was shown that, for initially symmetric films on both walls (i.e., identical material properties and initial thicknesses), the interface deformations can be described by the superposition of a symmetric and a linearly independent antisymmetric mode. It was found that the interfaces are not destabilized by capillary forces, agreeing with the implications of previous studies. By means of a linear and weakly nonlinear stability analysis, it was found that the symmetric mode is linearly unstable but grows only up to a maximum deflection amplitude. The linear analysis implies that, for liquid films thinner than 1 / 8 of the total channel width, this mode is mainly driven by variations of the viscous stresses along the interfaces. For thicker films, variations in the pressure gradient are the main source of this mode of instability. The weakly nonlinear analysis indicates that the large contribution of the nonlinear terms significantly widens the spectrum of unstable wavenumbers in comparison to the linear regime. A characteristic wavelength clearly dominating the pattern cannot be identified. In contrast to the symmetric mode, the antisymmetric mode is not inherently unstable, but can only exhibit an instability due to its coupling to the symmetric mode. At long times, the antisymmetric mode disappears, so that in the weakly nonlinear regime the system is governed by a single Kuramoto–Sivashinsky equation. This surprising finding stands in contrast to systems addressed in the related studies. It is noted that this result does not necessarily hold if the intermediate layer has an arbitrary viscosity. To verify this, the study provides analytical expressions for the (linear) growth rates for such systems, which were found to be in complete agreement with numerical simulations conducted for selected cases by other researchers. With respect to the hydrodynamic coupling between the two films it was shown that the interaction enhances the degree of instability. Namely, the wavenumber of the fastest growing mode in the linear theory is \(\sqrt{2}\) times larger than if both films were to evolve under the same conditions but isolated from each other. In the weakly nonlinear regime, the maximal deformation amplitude was seen to be affected by the coupling as well.

For asymmetric systems, a numerical and linear analysis has been performed as well. For long elapsed time periods, it was found that the correlation between the interfacial deformations remains close to unity for an extended period of time even for highly asymmetric configurations. This implies that, even for such systems, the patterns of the two interfaces often remain approximately phase-synchronized for a long time. Nevertheless, after much longer than this initial period, the films are expected to detune from each other due to their inherently different patterning processes.

Finally, it is emphasized that the method used for the analysis of this system can be easily generalized to more complex systems. For instance, introducing Marangoni stresses or gravitational forces to the equations will only add a new term to the evolution equations [Eqs. (7) and (8)], but the approach to tackle these problems is essentially the same as the one discussed in this paper. Our findings are relevant for systems where the walls of narrow ducts are coated by thin liquid films, which do not severely obstruct the gas flow in the center. Examples are air flow in respiratory ducts coated with mucus, boiling in microchannels, or the flow of a supersaturated gas in a narrow duct, such that liquid condenses at the channel walls.