Wavy Dynamics of Confined and Inclined Falling Liquid Films

Abstract

We present direct numerical simulations of thin viscous films falling in inclined channel of constant relative confinement, η = 2. The two films with the same Kapitza number, Ka = 509.5, flow in a passive and quiescent atmosphere of air, in presence of gravity, with a suitable monochromatic perturbation, applied at the liquid-velocity inlets. The study is made for different values of liquid flow Reynolds number, Re as a control parameter defined in terms of Nusselt flat film solution. Any orientation of films other than vertical leads to symmetry breaking causing the waves to grow differently on both interfaces. Variations of film flow characteristics such as wave amplitude (h), streamwise velocity (u), and minimum occlusion distance (d_min) are examined with Re for both films. The oscillatory behavior of films ranging from progressive periodic to solitary waves with flow reversals is observed for different values of Re. These flow variations are subjected to suppression when the films undergo strong confinement. Suitable scaling law is reported for d_min as a function of Re for two different values of channel inclination.

1 Introduction

Liquid film flow in narrow channels has numerous industrial applications. For example, transport operations in microelectronic equipment [1] and distilled columns in structural packing [2] employ liquid films to perform desired functions. In these applications, the wavy interaction between phases becomes important as it governs the efficiency of the concerned technological operation. Films over solid and inclined surfaces undergo an interfacial instability often referred to as hydrodynamic or Kapitza instability [3]. The waves on the liquid–air interface evolve either naturally, or “forced” via the imposition of inlet frequency forcing, which ensures that waves are of constant amplitude on the films within a finite length of the domain [4]. When excited at low frequencies, films exhibit solitary waves, which are large amplitude humps with long tails and steep fronts, along with front running capillary ripples at the interface [5]. The fluctuation of velocity underneath the wave trough and capillary wave region was observed to have much higher values as compared to the other flow regions, due to the large interfacial curvature there [6]. Backflow phenomena or flow reversals in the capillary region due to its short wavelength and curvature are reported for laminar falling liquid films [7, 8]. These reversals are prone to occur due to adverse pressure gradients acting in opposite direction to streamwise gravity. The variations in solitary wave characteristics on inertia-dominated falling films were studied for Reynolds number, plate inclination angle, and other control parameters, and suitable scaling laws were proposed [9]. Films flowing underneath the solid surfaces are also subjected to Rayleigh–Taylor instability apart from the hydrodynamic one [10]. Similar to films flowing over surfaces, these films also show the dependence of wave characteristics on Reynolds number and inclination angle.

Wavy films may experience flooding in the form of wave coalescence or occlusion when three fluid systems flow in a confined environment such as a channel or tube. The trigger of wave occlusion was observed to have a strong dependence on higher values of both Reynolds number and inclination angle [11, 12]. The occlusion scenarios were numerically examined by Dietze et al. [13] in terms of minimum occlusion distance variation with gravity, inertia, and surface tension coefficients. The occlusion was found to get delayed with gravity but precipitated with an increase in inertia and surface tension.

The occlusion scenarios in wavy films flowing in a three-layer system lead to plug formation (or slug flow) that causes enormous stress on the solid walls as well as drastically affects the performance of the desired industrial application [14]. To the best of our knowledge, less attention has been focused on film flows in such geometries. Moreover, a similar study with inclined films motivates us to investigate and compare the wave evolution on films on each channel wall for different orientations and identify the critical parameter(s) that ultimately leads to occlusion scenarios. As far as wave evolution and propagation are concerned, the channel orientation leads to the growth of waves differently on both interfaces. Consequently, it will also affect the flow structures and momentum transport between different fluid phases. In the present work, we study the variation of wave characteristics on two films with time at different Reynolds numbers, such that the channel is oriented at a specific angle. Consequently, we also compare the occlusion distance variation with ${\text{Re}}$ to that of vertically oriented films and deduce a suitable scaling law.

2 Methodology

The solver, interFoam based on FVM framework from OpenFOAM 7.0 toolbox [15, 16] is used to study the present work. It utilizes the volume of fluid (VOF) method [17] particularly to solve multiphase problems of isothermal, incompressible, and immiscible fluids.

2.1 Physical System and Governing Equations

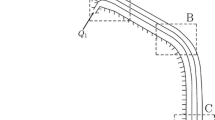
We consider a laminar flow system of two viscous liquid films in a quiescent atmosphere of air and confined between two planar walls of an inclined channel (see Fig. 1). The two films flow under gravity as shown in the figure. The fluid system is initially assumed to have well defined flat liquid–gas interfaces such that by Nusselt’s theory, film thickness and fully developed stream-wise velocity is given by $h_{{\text{N}}} = \left( {3\nu_{{\text{l}}}^{2} {\text{Re}} /g\sin \theta } \right)^{1/3}$ and $u_{{\text{N}}} = g\sin \theta h_{{\text{N}}}^{2} /3\nu_{{\text{l}}}$ respectively, where $\nu_{{\text{l}}} = \mu_{{\text{l}}} /\rho_{{\text{l}}}$ is the kinematic viscosity of the liquid films. The two walls of the channel are separated from each other by a constant confinement ratio, $\eta = H/2h_{{\text{N}}} = 2$ so that $H = 4h_{{\text{N}}}$. The length, $L$ of the walls is also considered as a function of film thickness, equal to $500h_{{\text{N}}}$. Such a choice of variable length was found to be sufficient to accommodate the fully developed waves [6]. The Reynolds number for the liquid film is defined as ${\text{Re}} = u_{{\text{N}}} h_{{\text{N}}} /\nu_{{\text{l}}}$, which compares flow inertia to the viscous effects. The two films are considered to be of the same Kapitza number, ${\text{Ka}} = 509.5$. The $x$ and $y$ coordinate axes are aligned as shown in the figure such that the channel is symmetrical about the $x$-axis. The left, right, and top walls of the channel are subjected to no slip and no flux conditions. The two liquid films enter the domain each through an inlet section which is taken the same as the corresponding value of $h_{{\text{N}}}$. The inlet velocity of the liquid film is considered as $u_{{{\text{in}}}} = 6u_{{\text{N}}} \left[ {\left( {\frac{Y}{{h_{{\text{N}}} }}} \right) - \left( {\frac{Y}{{h_{{\text{N}}} }}} \right)^{2} } \right]. \left[ {1 + \varepsilon \sin \left( {2\pi ft} \right)} \right]$. where $Y=\pm \left( {H/2 - y} \right)$ such that the variation in y is valid only in the liquid regions; the positive sign stands for the right film while the negative sign for the left film. The above form of scaled parabolic inlet velocity is coupled with a monochromatic perturbation with amplitude and frequency as $\varepsilon = 0.05$ and $f = 15$ Hz respectively [18].

Fig. 1

Schematic diagram of wavy falling films in an inclined channel

The fluid flow in the present system is described by Navier–Stokes equations through the VOF method which is based on solving a single set of conservation equations of continuity and momentum for a hypothetical fluid of density $\rho$ and dynamic viscosity $\mu$. These properties of the fluid are calculated as the weighted average of the corresponding properties of individual fluids: $\rho = \alpha \rho_{{\text{l}}} + \left( {1 - \alpha } \right)\rho_{{\text{g}}}$ and $\mu = \alpha \mu_{{\text{l}}} + \left( {1 - \alpha } \right)\mu_{{\text{g}}}$. The quantity $\alpha$ corresponds to the volume fraction of the reference fluid. Subscripts ${\text{l}}$ and ${\text{g}}$ stand for the liquid and gas phases respectively. The relevant continuity and momentum equations are:

$$\nabla .\vec{u} = 0$$

(1)

$$\rho \frac{{D(\vec{u})}}{Dt} = - \nabla p + \mu \nabla .(\nabla \vec{u} + (\nabla \vec{u})^{T} ) + \rho \vec{g} + \vec{F}_{s}$$

(2)

where $\vec{u}$ is the velocity, $p$ is the pressure and $\overrightarrow {{F_{{\text{s}}} }}$ represents additional forces due to interfacial surface tension which is distributed over a thin interfacial layer. The continuum surface force (CSF) has been employed to model surface tension [19]. With the introduction of weighted average α, the interface between the phases is tracked by solving an additional advection equation 3 of scalar α.

$$\frac{\partial \alpha }{{\partial t}} + \nabla .(\vec{u}\alpha ) = 0$$

(3)

α = 0.5 is used for the representation of the liquid–gas interface. In all our simulations, an adaptive time step was used such that the maximum Courant number did not exceed the value of 0.3.

2.2 Validation

To assure the validity of the methodology, validation is carried out for the non-linear wave evolution on falling liquid films over plane surfaces (see Fig. 2) with the same flow conditions and transport properties as reported by Dietze et al. [18]. The plots in the figure show good agreement for film height.

Fig. 2

Validation: Comparison of time variation of dimensional liquid film (in mm) at location x = 120 mm from inlet for simulated vertical falling film with Ka = 509.5, Re = 15, f = 16 Hz

3 Results and Discussion

Falling films over flat surfaces are subjected to hydrodynamic instabilities in which the streamwise component of gravity, $g\sin \theta$ assists the waves to grow at the liquid–air interface. The cross-stream component, $g\cos \theta$ acts normal and towards the surface resisting wave growth [3]. On the other hand, films flowing underneath the flat surfaces (hanging films) are subjected to Rayleigh–Taylor instabilities along with the hydrodynamic one [10]. In these cases, $g\cos \theta$ also acts normally but away from the planar surface, thus assisting the wave growth along with that of $g\sin \theta$.

Figure 3 depicts the time variation of liquid film’s heights on both walls at $x/L = 0.75$ and $\theta = 60^\circ$. The heights are normalized with their respective Nusselt thicknesses, $h_{{\text{N}}}$. For ${\text{Re}} = 5$ (see Fig. 3a), the waves on the surfaces of the two films vary almost out of phase with each other such that the waves on the right film show higher amplitude as compared to that of the left film. This is because the right film is the hanging one subjected to both hydrodynamic and Rayleigh–Taylor instability. At this Reynolds number, the inertia plays only a perturbative role and the amplitudes of the waves result due to the competition between gravity and viscous forces. These waves are progressive periodic waves resembling the appearance of Stokes waves. At ${\text{Re}} = 10$, the inertia becomes dominant over both gravity and viscous forces. Consequently, the disturbances over film interfaces also increase showing the formation of large wave humps with small front running capillary ripples. These wave humps are nothing but solitary waves that are of constant amplitudes and occupy the maximum span of the film interfaces. The difference in phases of both films is reduced and the amplitudes with respect to Nusselt thickness are increased. The heights of the films increase further at ${\text{Re}} = 15$ with two additional differences observed as compared to that of ${\text{Re}} = 10$. The first difference is that the number of smaller ripples ahead of the wave hump increase. The second is, the left film responds to the disturbance lately as compared to the right film such that the waves on the left film lag the right one which was the opposite in the case of ${\text{Re}} = 10$. With increase in ${\text{Re}}$, the difference in wave amplitudes of both films reduce such that at ${\text{Re}} = 17$ (not shown here), the amplitude becomes equal. For ${\text{Re}} \le 17$, a higher amplitude is found for the right film as compared to the left film. However, at ${\text{Re}} = 20$ (see Fig. 3d) a suppression of instability is observed for the hanging film such that the maximum height of this film decreases as compared to the left one. Instead, the maximum height of the left film was observed to rise with an increase in ${\text{Re}}$ even after ${\text{Re}} \ge 17$ (till the maximum value of ${\text{Re}}$ examined), dominating the spatial region in the cross-stream direction. The growth of disturbance makes both the films come in proximity such that they start interacting in a manner that the one that lags in response to disturbance, dominates the other. At ${\text{Re}} = 20$ the left film lags and hence dominates the hanging film.

Fig. 3

Variation of normalized film height with time of both the films at $x/L = 0.75, \theta = 60^\circ$ for different Reynolds number

Figure 4 shows the time variation of the stream-wise velocity field at location $x/L = 0.75$ measured from the inlet for four different Reynolds numbers. The velocity field is normalized with Nusselt flat film average velocity, $u_{{\text{N}}}$. The reason for normalization is that it eases the understanding of the response of the velocity field to the disturbance with respect to the average velocity. Two different location points in the liquid bulk: $\frac{Y}{{h_{{\text{N}}} }} = \pm 0.1$ where $Y = \pm \left( {\frac{H}{2} - y } \right)$ are considered for computing the velocities in the liquid domain close to the walls. At ${\text{Re}} = 5,$ velocity fields are enslaved to film height evolution with space and time and show similar oscillatory behaviour even though the location of sample points is far from the respective liquid–air interfaces. The velocities vary differently in phases but with the same maximum amplitude. At ${\text{Re}} = 10$ (see Fig. 4b), the fluctuation of velocity fields is almost the same in phase for both films. However, a momentarily negative velocity (in the form of sharp valleys) can be observed that depicts the reverse flow within the liquid film that takes place at a particular instant. The reverse flow is due to the adverse pressure gradient acting in front of the main hump [7]. It is found to be higher in the hanging film as compared to the other one. In the case of ${\text{Re}} = 15$, the velocity fields vary neck to neck for both the films with a slight increment in both peaks and valleys of the right film compared to that of the left film. At ${\text{Re}} = 20$ (see Fig. 4d), a decrement in both maximum and minimum velocities is observed compared to that at ${\text{Re}} = 10$ and $15$ for both films. It is important to note that the dimensional velocities would have higher values at this ${\text{Re}}$ as compared to that of lower ${\text{Re}}$ values. At this Reynolds number, the films interact with each other as they come under close confinement leading to the suppression of instability. This too causes a decrement in the growth of disturbance on the velocity field, which possibly would not have been observed if the films were largely confined.

Fig. 4

Variation of normalized streamwise velocity with time in bulk of both the films close to the wall for different Reynolds number. Locations 1, 2: $(x/L,\mp(H/2-y)/h_N ) = (0.75,0.1), \theta = 60^\circ$

Figure 5 depicts the variation of minimum occlusion $d_{\min }$ with ${\text{Re}}$ for the two different channel inclination values. $d_{\min }$ is calculated by taking the average of all valleys after the waves attained the fully developed state till the final simulation time. For both the angles, $d_{\min }$ decreases with an increase in ${\text{Re}}$ with an approximate fit:

$$\delta = d_{\min } /H = a{\text{Re}}^{2} - b{\text{Re}} + c$$

(4)

where $a$, $b$, $c$ are constants that depend on the value of $\theta$. The values of fitting parameters are given in Table1. It is important to note that at every ${\text{Re}}$ value, the magnitude of $d_{\min }$ for $\theta = 60^\circ$ is higher as compared to that of $\theta = 90^\circ$. When the channel is vertically oriented, the two films are symmetrical to each other and only the stream-wise component of gravity acts on both films without any presence of a cross-stream component. Therefore, the waves on both films grow and propagate symmetrically with maximum amplitude and phase and minimum occlusion distance is least for vertically oriented falling films. When the channel is oriented at any angle other than $\theta = 90^\circ$ ($\theta = 60^\circ$ in the present case), the symmetry breaks due to different actions of the cross-stream component of gravity on both films. The left film now is subjected to only hydrodynamic instability while the right film is subjected to both hydrodynamic and Rayleigh–Taylor instabilities. This leads to a difference in both the growth of wave amplitudes and phases. The peaks now do not lay one over the other as in the case of vertically oriented films, rather their locations are somewhat relatively misaligned. Consequently, the minimum occlusion distance is higher as compared to that of vertical films.

Table 1 The values of the fitting parameters corresponding to the fitting equation in Fig. 5

Fig. 5

Variation of minimum occlusion distance with Reynolds number

4 Conclusions

In this chapter, two-dimensional numerical simulations of wavy liquid films in inclined channels are performed using the VOF method. The two films with the same Kapitza number were considered to flow in a quiescent atmosphere between them along with monochromatic forcing applied at their respective inlets. The effects on flow parameters were studied for Reynolds number (${\text{Re}}$) as the control parameter. On increasing ${\text{Re}}$, it was found that the interfacial disturbance grows with space and time on the interface of both the liquid films. Symmetry breaking is observed for films oriented at an angle $\theta = 60^\circ$ due to different actions of the cross-stream component of gravity on both films (which is not applicable for the case of θ = $90^\circ$). The hanging film on the right wall showed a higher amplitude than that of the other film at lower ${\text{Re}}$ values. However, at comparatively higher ${\text{Re}}$ values, the waves on films grow and come under proximity to influence each other such that the film that lags in response to disturbance (left film) dominates the other (hanging film). In this case, the stabilizing (left) film occupies the space of destabilizing film suppressing its maximum height. Similar behaviour is reflected in the time variation of the velocity field such that the growth of disturbance on the velocity field suppresses at a higher Reynolds number. Reverse flow is observed at values of ${\text{Re}} \ge 10$. However, the strength of reverse flow decreases when the films come under strong confinement. The minimum occlusion distance is found to vary quadratically with ${\text{Re}}$ for both channel inclinations. The behaviour of the films so observed should be true for all other inclinations and is open for further investigation.