1 Introduction

In recent years, the microfluidic platform has been emerged as an advanced technology for biological and chemical analysis in the field of microfluidics lab-on-a-chip systems (Madou et al. 2006; Geschke et al. 2004; Ducrée et al. 2007; Gorkin et al. 2010). One particular area of microfluidics research is the development of microfluidics compact disc (CD) platforms that operate on the basis of centrifugal pumping. Compared to the other driving methods such as the electroosmotic flow (Moles 2002) and pressure-driven flow (Oh et al. 2012), the most attractive advantage of centrifugal technique is its simple driving mechanism which reduces the need for an external pumping system. Furthermore, this microfluidic CD platform also has the advantages of low-cost, easy operation, parallel detection, fast response suitable for point of care and minimum sample usage.

By this way, several microfluidic functions such as cascade micromixing, capillary valving and Coriolis force based on switching can be integrated into the CD by balancing the centrifugal force and the capillary force more easily. Hence, the related researches of microvalve and Coriolis force had been done, such as the capillary-burst microvalve by Man et al. (1998), Leu and Chang (2004), Cho et al. (2007), and Chen et al. (2008), passive flow switching valves by Kim et al. (2008), and patterning of flow and mixing by Ducrée et al. (2006). In addition, microscale flow in rotating channels had been investigated by Marliani et al. (1997), Maruyama and Maeuchi (2008), and Kim et al. (2008), which mainly concentrated on centrifugal-force-driven steady flow, and lack of understanding of the transient flow behavior.

Nevertheless, the spatial and temporal behavior of fluid flow inside the microchannel is a key issue for designing a precise centrifugal microfluidic channel system. A physical modeling and numerical analysis for the centrifugal-force-driven transient filling flow into a rectangular and circular microchannel had been researched by Kim and Kwon (2006a, b). The results showed that the filling flow driven by centrifugal force was affected by three dimensionless parameters which combine fluid properties, rectangular channel geometry and processing condition of rotational speed. However, their physical modeling was simply derived on the basis of ignoring the surface tension effect. In the case of considering the dynamic contact angle and the hydrophobic inner surface of the microchannel, a theoretical model for determining time-dependent flow behaviors in a 3D rotating rectangular microchannel was proposed by Liu et al. (2008). However, the model has no velocity distribution and displacement expression, but only has a coupling form of velocity, acceleration and displacement. Moreover, in order to obtain the filling speed of a channel up to distance L(t) by capillary action, a theoretical model used the Washburn equation for high-aspect ratio channels been proposed by Garcia-Cordero et al. (2010). The Washburn equation neglects inertial effects, gravity and deviations from a fully developed flow profile and a dynamic contact angle, which leads to discrepancies between calculated and measured values. In this study, a simple analytical expression and experimental methods of centrifugal-force-driven transient filling flow into rectangular microchannel on a rotating disk are presented.

Figure 1 shows a schematic diagram of a rectangular cross-sectional microchannel on a CD-type centrifugal microfluidic system. Without rotation, the liquid stored in the reservoir will flow to fill the hydrophilic channel but stop at the inlet to the suddenly expanded valve due to the capillary force (stage 1). By spinning the disk, the centrifugal force overcomes the capillary force and the fluid is pumped from the center toward the edge of the disk (stage 2). This point of capillary pressure depends on the geometry of the channel and the properties of the liquid. For capillary valves in the rectangular microchannel and a sudden opening of β = 90°, the maximum barrier pressure at the liquid front termed the burst pressure P cap is given by Zeng et al. (2000).

$$P_{{{\text{cap}}1}} = 2\cos \theta_{c} \gamma_{la} \left( {\frac{1}{H} + \frac{1}{W}} \right)$$
(1)

where θ c , γ la , H and W are the contact angle of the liquid with the solid channel wall, liquid–air surface energies per unit area, the height and width of a rectangular microchannel, respectively. The 1D theory of Eq. (1) may suffer significant error when the microchannel geometry deviates largely from the assumed circular shape. Then, in order to predict the critical burst pressure accurately, Chen et al. (2008) presented the 3D modeling and analysis of the capillary-burst microfluidic valves for rectangular transport channels with various aspect ratios. The analytical expression of burst pressure derived from the 3D model was compared with the results of 1D and 2D theories by means of the visualization experiments. The measurements of burst rotational speeds for the capillary valves are in good agreement with the predictions in their 3D model. The burst pressure in their 3D model can be expressed as:

$$P_{{{\text{cap}}2}} = \frac{{2\gamma_{la} }}{W}\left[ { - \frac{W}{H}\cos \theta_{c} - \cos \left( {\theta_{c} + \beta } \right)} \right]$$
(2)

where β is the opening angle of capillary valve. The rotational frequency at which the centrifugal force overcomes the capillary force to open a valve called the burst frequency ω c , which can be expressed as:

$$\omega_{c} = \sqrt {\frac{{P_{\text{cap}} }}{{\rho\Delta r\bar{r}}}}$$
(3)

where ρ and Δr are the mass density and the difference between the top and bottom of the liquid levels at rest with respect to the center of the CD, and \(\bar{r}\) is the average distance of the liquid from the center of the CD.

Fig. 1
figure 1

Schematic diagram of the transient filling flow into a rectangular microchannel on the centrifugal microfluidic system. Dark black area represents a region occupied by the sample fluid, lt indicating the flow front

Full size image

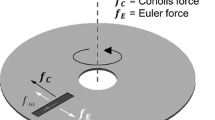
As viewed from the non-inertial rotating frame rotating at \(\vec{\omega }\), the liquid traveling at a speed \(\vec{u}\) down the channel is affected by the centrifugal force \(\vec{f}_{c}\) (perpendicular to the direction of \(\vec{u}\)) and the Coriolis force \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {f}_{\omega }\) (parallel to the direction of \(\vec{u}\)). A fluid of mass density ρ rotating at a distance r from a central axis at an angular velocity ω experiences the centrifugal force, which is formulated as:

$$\vec{f}_{\omega } = - \rho \cdot \vec{\omega } \times \left( {\vec{\omega } \times \vec{r}} \right)$$
(4)

The Coriolis force is written as:

$$\vec{f}_{c} = - 2\rho \cdot \vec{\omega } \times \vec{u}$$
(5)

The Coriolis force induces the transversal flow inside the microchannel relative to the axial down channel flow, so the flow becomes fully three-dimensional.

A reasonable model and analytical method contributes to a more precise microchannel system and a better understanding of the physical behavior of flow inside the microchannel. In the following sections, the transient flow modeling and analysis of the time-dependent centrifugal microflows for hydrophilic rectangular channels will be presented. Then the experimental apparatus developed for visualization and measurements of the liquid flow in the rotating microfluidics will be described. Thus, we can get the sequential images of the flow front displacement up on time by the visualization experiments. According to the experimental results, we will analyze the rationality of our model for predicting the time-dependent behaviors of the moving front, estimate the relative implications of various forces acting on the fluid and discuss parameters that are known to affect the moving front, such as the length l, the height H and the width W of the channel, and the rotational frequency.

2 Analysis of transient flow

2.1 Governing equations

In order to obtain analytic solutions for the transient flow into a rectangular microchannel, the Coriolis force effect is assumed to be negligible in a mild rotational speed in comparison with the centrifugal force effect. Brenner et al. (2005) suggested that the secondary flow was too weak to modify the primary flow along the axial direction of the channel unless the flow over the rotational speed of 350 rad/s for a microchannel of which the width and depth are 360 and 125 μm, respectively. Kim et al. (2008) showed that the Coriolis force started to affect the flow switching at an angular frequency of 80 rad/s. This is a significantly reduced frequency compared to the threshold frequency (i.e., 350 rad/s), which is made possible due to their unique junction geometry. In addition, only the centrifugal force was considered as an external force in a mild rotational speed (Duffy et al. 1999; Zoval and Madou 2004; Haeberle et al. 2005; Kim and Kwon 2006a, b; Liu et al. 2008; Kim et al. 2008). Therefore, at the relatively low rotational speed, the Coriolis force could be neglected relative to the centrifugal force.

Thus, the continuous equation for an incompressible fluid can be drawn as:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0$$
(6)

In the case of neglecting Coriolis force, the continuous equation can be simplified as:

$$\frac{\partial w}{\partial z} = 0$$
(7)

The momentum conservation equation in the Z direction can be drawn as:

$$\begin{aligned} & \rho \frac{\partial w}{\partial t} + \rho \left( {u\frac{\partial w}{\partial x} + v\frac{\partial w}{\partial y} + w\frac{\partial w}{\partial z}} \right) \\ & \quad = \mu \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) - \frac{\partial p}{\partial z} + f_{z} \\ \end{aligned}$$
(8)

where f z is the centrifugal force per unit. Thus, one can obtain the following relationship

$$\rho \frac{\partial w}{\partial t} - \mu \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) = - \frac{\partial p}{\partial z} + f_{z}$$
(9)

One might recognize the partial differential equation for velocity field. The velocity and pressure can be written as the form of w = w(x, y, t) and p = p(z). Thus, no-slip boundary conditions imposed on w (x, y, t) are mathematically described as:

$$w\left( {x = \pm \frac{W}{2},y,t} \right) = 0$$
(10)
$$w\left( {x,y = \pm \frac{H}{2},t} \right) = 0$$
(11)
$$w\left( {x,y,t = 0} \right) = 0$$
(12)

The inner surface of the microchannel is hydrophilic, so when the rotational speed of the disk exceeds a threshold value in the front of microchannel, the centrifugal force will become larger than the capillary force causing the liquid to burst into the rectangular channel. The surface pressure is negative at this point. However, when the liquid fills into the microchannel, the surface pressure will become positive. Herein, the stage of the liquid filling into the rectangular channel is researched on the basis of ignoring the entrance effect. According to Eqs. (1) and (2), p(z = 0) can be drawn as:

$$\begin{aligned} p\left( {z = 0} \right) & = P_{0} - P_{{{\text{cap}}2}} + P_{{{\text{cap}}1}} \\ & = \rho \omega^{2}\Delta rr_{c} - \frac{{2\gamma_{la} }}{W}\left[ { - \frac{W}{H}\cos \theta_{c} - \cos \left( {\theta_{c} + \beta } \right)} \right] \\ & \quad + 2\gamma_{la} \cos \theta_{c} \left( {\frac{1}{W} + \frac{1}{H}} \right) \\ \end{aligned}$$
(13)

where Δr = r 2 − r 1 is the length of the liquid plug with its fronts located r 1 in the reservoir and r 2 in the capillary-burst valve from the rotational center, and r c  = (r 1 + r 2)/2. P 0 is the apparent hydrostatic pressure. Moreover, at the outlet of the microchannel z = l, the pressure p (z = l) could be assumed to be zero for connecting with the atmospheric pressure. Thus, the boundary conditions of p(z) as follows:

$$p\left( {z = 0} \right) = \rho \omega^{2}\Delta rr_{c} - \frac{{2\gamma_{la} }}{W}\left[ { - \frac{W}{H}\cos \theta_{c} - \cos \left( {\theta_{c} + \beta } \right)} \right] + 2\gamma_{la} \cos \theta_{c} \left( {\frac{1}{W} + \frac{1}{H}} \right)$$
(14)
$$p\left( {z = l} \right) = 0$$
(15)

2.2 Analytic solutions

A fluid of mass density ρ on a planar substrate (Fig. 1) rotating at a distance l 0 from a central axis at an angular velocity ω experiences the centrifugal force

$$f_{z} = \rho \omega^{2} \left( {z + l_{0} } \right),\quad 0 \le z \le l$$
(16)

It is well known that the term, −∂p/∂z + f z , only depends on z. From the partial differential Eq. (9), it should be noted that once the equation established, both sides should be constant. Hence, an assumption is given as:

$$- \frac{\partial p}{\partial z} + \rho \omega^{2} \left( {z + l_{0} } \right) = P^{*}$$
(17)

where P* is the modified pressure gradient (Maruyama and Maeuchi 2008). We can integrate the above equation with respect to z from 0 to z, as below:

$$\begin{aligned} \int\limits_{0}^{l} {\frac{\partial p}{\partial z}{\text{d}}z} & = p\left( {z = l} \right) - p\left( {z = 0} \right) \\ & = \int\limits_{0}^{l} {\left( {\rho \omega^{2} \left( {z + l_{0} } \right) - P^{*} } \right){\text{d}}z} \\ \end{aligned}$$
(18)

Substituting boundary conditions of pressure at z = 0 and z = l into Eq. (18), one can get an equation for constant P* as below:

$$\begin{aligned} P^{*} & = \frac{1}{2}\rho \omega^{2} l + \rho \omega^{2} l_{0} \\ & \quad + \frac{{\rho \omega^{2}\Delta rr_{c} + \frac{{2\gamma_{la} }}{W}\left[ {\frac{W}{H}\cos \theta_{c} + \cos \left( {\theta_{c} + \beta } \right)} \right] + 2\gamma_{la} \cos \theta_{c} \left( {\frac{1}{W} + \frac{1}{H}} \right)}}{l} \\ \end{aligned}$$
(19)

By substituting Eq. (19) into Eq. (17), and integrating Eq. (17) with respect to z from 0 to z, one can get the pressure distribution inside the rectangular microchannel as:

$$\begin{aligned} p\left( z \right) & = \frac{1}{2}\rho \omega^{2} z^{2} - \left[ {\frac{1}{2}\rho \omega^{2} l} \right. \\ & \quad \left. { + \frac{{\rho \omega^{2}\Delta rr_{c} + \frac{{2\gamma_{la} }}{W}\left[ {\frac{W}{H}\cos \theta_{c} + \cos \left( {\theta_{c} + \beta } \right)} \right] + 2\gamma_{la} \cos \theta_{c} \left( {\frac{1}{W} + \frac{1}{H}} \right)}}{l}} \right]z \\ \end{aligned}$$
(20)

Based on Eq. (20), one can get the variation of pressure up on the moving front displacement (Fig. 2). It can be found in Fig. 2 that a larger rotational speed results in a larger pressure gradient. Moreover, the pressure distribution is parabolic rather than linear in the axial direction. Figure 2 also shows that the pressure distribution in microchannel could be divided into two distinctive regions: (1) the region from the inlet reservoir to the critical point (the minimum value of pressure) with a negative pressure gradient and (2) the other region from the critical point to the outlet reservoir with a positive pressure gradient. Similar results of numerical analysis had been obtained by Kim and Kwon (2006a) and Liu et al. (2008) in their centrifugal microfluidic systems.

Fig. 2
figure 2

Variation of pressure up on the moving front displacement for a rectangular channel (W = 400 μm, H = 300 μm, L = 0.025 μm) with rotational speed ranging from 80 to 120 rad/s. Interfacial properties γ = 0.064 mN/m and θ c  = 62°, liquid properties (85 % glycerol) ρ = 1.229 g/cm3, and other dimensions r 1 = 0.024 m, Δr = 0.0066 m were used for the calculations

Full size image

Now, by substituting the constant P* to Eq. (9), along with boundary conditions, one can obtain a final form of velocity distribution inside the rectangular microchannel using Green’s functions as:

$$\begin{aligned} w\left( {x,y,t} \right) & = \frac{16}{{\pi^{2} \mu }}\left[ {\frac{1}{2}\rho \omega^{2} l + \rho \omega^{2} l_{0} } \right. \\ & \quad \left. { + \frac{{\rho \omega^{2}\Delta rr_{c} + \frac{{2\gamma_{la} }}{W}\left[ {\frac{W}{H}\cos \theta_{c} + \cos \left( {\theta_{c} + \beta } \right)} \right] + 2\gamma_{la} \cos \theta_{c} \left( {\frac{1}{W} + \frac{1}{H}} \right)}}{l}} \right] \\ & \quad \times \sum\limits_{m = 1,3,5 \ldots }^{\infty } {\sum\limits_{1,3,5}^{\infty } {\frac{{\left( { - 1} \right)^{m + n} }}{{\left( {2m - 1} \right)\left( {2n - 1} \right)\lambda }}} } \left( {1 - {\text{e}}^{{ - \lambda \frac{\mu }{\rho }t}} } \right) \\ & \quad \times \,{ \cos }\frac{{2\varepsilon_{m} }}{W}x\,{ \cos }\frac{{2\varepsilon_{n} }}{H}y \\ \end{aligned}$$
(21)

where

$$\lambda = \frac{{4\varepsilon_{m}^{2} }}{{W^{2} }} + \frac{{4\varepsilon_{n}^{2} }}{{H^{2} }},\quad \varepsilon_{m} = \pi \left( {m - \frac{1}{2}} \right),\quad \varepsilon_{n} = \pi \left( {n - \frac{1}{2}} \right)$$
(22)

Here, in order to simplify equations, the following relation is assumed

$$D = \frac{{\left( { - 1} \right)^{m + n} }}{{\left( {2m - 1} \right)\left( {2n - 1} \right)\lambda }}$$
(23)

One can obtain the expression of the total flow rate over time, Q t , as follows:

$$Q_{t} = WH\frac{{{\text{d}}l_{t} }}{{{\text{d}}t}} = \int\limits_{{ - \frac{W}{2}}}^{{\frac{W}{2}}} {\int\limits_{{ - \frac{H}{2}}}^{{\frac{H}{2}}} {w\left( {x,y,t} \right){\text{d}}x{\text{d}}y} }$$
(24)

Thus, by substituting Eq. (21) to Eq. (24), and integrating Eq. (24) with respect to t from 0 to t, one can obtain the equation for the flow front advancement, namely lt, as follows:

$$\begin{aligned} lt & = \frac{16}{{\pi^{2} \mu }}\left[ {\frac{1}{2}\rho \omega^{2} l + \rho \omega^{2} l_{0} } \right. \\ & \quad \left. { + \frac{{\rho \omega^{2}\Delta rr_{c} + \frac{{2\gamma_{la} }}{W}\left[ {\frac{W}{H}\cos \theta_{c} + \cos \left( {\theta_{c} + \beta } \right)} \right] + 2\gamma_{la} \cos \theta_{c} \left( {\frac{1}{W} + \frac{1}{H}} \right)}}{l}} \right] \\ & \quad \times \sum\limits_{m = 1,3,5 \ldots }^{\infty } {\sum\limits_{n = 1,3,5}^{\infty } {D\left( {t + \frac{\rho }{\lambda \mu }\left( {{\text{e}}^{{ - \lambda \frac{\mu }{\rho }t}} - 1} \right)} \right)\frac{1}{{\varepsilon_{m} \varepsilon_{n} }}} } \\ \end{aligned}$$
(25)

It is found from Eq. (25) that the parameters of microchannel and rotating speed dominantly affected the flow front advancement when the liquid is determined. In summary, once the fluid properties, geometry of microchannel and processing conditions are given, one can calculate the velocity distribution w = w (x, y, t) via Eq. (21) and then determine the exact filling flow front advancement as a function of time according to Eq. (25).

3 Experimental details

3.1 Experimental setup

Experimental work is carried out on a custom-made CD spin test system. The system comprises a signal control board, image-capturing unit, sensor unit, motor unit and a computer for displaying the images. A schematic of the experimental setup is shown in Fig. 3. The centrifugal pumping is achieved by employing a brush less DC motor (WS55-180, 0–12,500 rad/min) to drive the disk. The angular position of the microchannel on the disk is acquired and controlled through a Holzer sensor (HAL-506S, 1 HZ–45 kHZ). The signals from the sensor are used to synchronize the image-capturing unit. High-speed video camera (Phantom, v641, America) is mounted on a microscope (Nikon SMZ1000) to visually capture the process of transient flow. When the same position of the CD passes under the camera, the shoot button will be triggered. The high-speed camera having a frame rate of 1450 fr/s (resolution, 2560 × 1600) can be triggered to allow one shot of the targeted object on the rotating disk per revolution.

Fig. 3
figure 3

Experimental arrangement for flow visualization on centrifugal microfluidic system

Full size image

3.2 Rotating test

In our test system, the motor is controlled by the pulse width modulation (PWM), so the angular velocity that corresponds to the width of the PWM signal was tested before the experiment. For example, we need the angular velocity of 80 rad/s, and then the given PWM value should be 30. In the program, two methods are designed to control the motor speed: one is gradual increase and the other is step increase. The process of increasing speed in step increase mode is shown in Fig. 4. As shown in Fig. 4, when the starting speed and the target speed were set up, the speed increase will be divided into three stages: (1) the speed increases from zero to the starting speed gradually, (2) it keeps this speed for 3 s, and (3) then it reaches the target speed quickly. Furthermore, in order to guarantee the liquid front stops at the capillary valve, the starting speed should be slower than the critical speed of the capillary valve which can be achieved by using Eq. (2).

Fig. 4
figure 4

Process of increasing speed in step increase mode. Red line represents the target speed, and green line represents the starting speed (color figure online)

Full size image

3.3 Fabrication of devices and material

The microfluidic chip is tested using a mixture of glycerol (85 %) with red dye (at ratio of 1 part dye to 10 part water) in the experiment. The basic properties of liquid are given in Table 1. The microfluidic chip is fabricated from layers of polymethyl methacrylate (PMMA) plastic and a pressure-sensitive adhesive (PSA). Each chip consists of three layers: two layers of PMMA bound with a layer of PSA. The contact angle between the fluid and the PMMA surface is measured using a dynamic contact angle system (DSA30, KRUSS, Germany) at 62 ± 1°. As given in Table 2, we use microchannels of different cross-sectional dimensions (200, 300 and 400 μm in width and 150, 240 and 300 μm in depth) and length (18 and 25 mm). For each microchannel, three different rotating speeds are adopted. The position of the inlet reservoir r 1 = 24 mm and the radius of reservoir are all designed as 3 mm.

Table 1 Physical properties of DI water and glycerol for the temperature 298 K
Full size table
Table 2 Geometrical parameters of the microchannels used for testing
Full size table

4 Results and discussion

The synchronized image-capturing system developed in the present study enables us to visualize the change of the moving front displacement; also, the process of the bursts out at the capillary valve to fill the expanded volume can be acquired. Figure 5a shows flow visualization images of the liquid blocked by the capillary valve with β = 90° and channel cross section of W = 400 μm, H = 300 μm on a stationary disk (80 rad/s). It is observed that the liquid stops at the capillary valve with its meniscus curving outward to balance the centrifugal force. Figure 5b, c displays images of the liquid flow that bursts into the valve as the angular speed is increased to 48 rad/s which is higher than the predicted burst value of 44.7 rad/s. The burst pressure of experiment is in good agreement with the predictions by Eq. (2). Moreover, it can be seen from the Fig. 5b, c that the process of liquid front passing though the capillary valve is continuous. Hereby, it is suggested that the displacement of moving front when the liquid bursts out the capillary valve to fill into the rectangular microchannel is zero.

Fig. 5
figure 5

Liquid front passes though the sudden opening of the capillary valve (W = 400 μm, H = 300 μm, ω = 80 rad/s and β = 90°) on a resting disk

Full size image

Based on Eq. (2) and the above-investigated parameters, the angular velocities used in the following parametric studies are larger than the burst frequency. By carrying out image processing on the sequential picture, we can get the flow front curve of displacement in rectangular microchannel. For each of the data points presented, the flow displacement was repeatedly examined at least three times. The uncertainty of the flow displacement presented in the following figures is approximately within ±3 %. In the following sections, the parameters and the driving force that are known to affect the displacement of the moving front will be discussed.

4.1 Microchannel dimensions

Figure 6 shows the characterization of liquid filling the different microchannels at different angular velocities. As shown in Fig. 6, the displacement of the moving front versus time is plotted, while the travel length of the advancing flow is set as 10 mm. As expected, the time-dependent motion of the centrifugal driven flow is strongly affected by the angular velocity. It is observed that the development of a centrifugal microflow to its steady state takes a short period of time, normally on the order of milliseconds, and then displacement of the moving front increases linearly with time. This indicates that the capillary flow has fully developed before the fluid reaches the position of 10 mm of the microchannel. It is also observed that, for all microchannels investigated in this study, the time to reach the specified position decreases as the angular velocity increases.

Fig. 6
figure 6

Characterization of liquid filling the different microchannels at different angular velocities by experiment (points are averages of three measurements), and the travel length of the advancing flow is set as 10 mm. The angular velocities we used are 80, 100 and 120 rad/s, and the length of the microchannel, L, is all 25 mm. Lower right schematic shows the centrifugal force, f z , acting on the plug of liquid displaced by a distance L: a type C1, the section size: W/H = 0.4/0.3 (mm); b type C2, the section size: W/H = 0.4/0.24 (mm); and c type C3, the section size: W/H = 0.3/0.24 (mm)

Full size image

As shown in Fig. 6a, b, under the condition of the same angular velocity (80, 100 and 120 rad/s), a comparison of the flow time between types C1 and C2 microchannels shows that increasing the channel height while keeping the same width will lead to a larger increase in the flow velocity. For example, when the rotation at an angular velocity of 80 rad/s, the flow front in types C1 and C2 can reach the position of 10 mm in 0.529 and 0.685 s. As shown in Fig. 6b, c, a comparison of the flow time between types C2 and C3 microchannels shows that while keeping the same channel height and increasing the width will lead to a larger increase in the flow velocity. For example, when the rotation at an angular velocity of 120 rad/s, the flow front in types C2 and C3 can reach the position of 10 mm in 0.355 and 0.305 s. Overall, the flow velocity of liquid increases with the increase in the channel width and height. Since the angular velocity is much larger than the burst frequency, the effect of the centrifugal force will dominate the loading process, and the room for the centrifugal force to be exerted is limited for a channel with relatively low section size.

Furthermore, by comparing Fig. 6a–c, it can be seen that the height of the microchannel has a greater influence on the flow velocity than the width. Under the condition of the same angular velocity of 100 rad/s, for the cases of Fig. 6a–c, the time to reach the position of 10 mm is 0.34, 0.43 and 0.49 s, respectively. It is observed that the time decreases 90 ms with the height increases 60 μm, but the time only decreases 60 ms when the microchannel width increases 100 μm.

In addition, the advancing velocity of the moving front also depends on the location of the inlet reservoir, which provides an apparent hydrostatic pressure to the liquid plug. The farther the microchannel locates from the center of rotation, the larger the centrifugal force the liquid plug receives.

It should be noted that the advancing velocity is also affected by the length of microchannel. As shown in Fig. 7, the advancing speed of the capillary front will increase as the dimension of the channel length increased since the increased channel length leads to larger value of −∂p/∂z + f z (Eq. 9). It is also observed that the differences between the two lines of types C3 and C4 are not obvious when the angular velocity is large (green line), but with the decrease in the angular velocity, the differences become obvious (red line), such as when the rotation at an angular velocity of 80 rad/s, the flow front in types C3 and C4 can reach the position of 10 mm in 0.73 and 0.802 s, respectively.

Fig. 7
figure 7

Comparison of the moving front versus flow time for types C3 and C4 microchannels. The section size of types C3 and C4 are W/H = 0.3/0.24 mm

Full size image

4.2 Force analysis

In an effort to understand the underlying flow characteristics, one may perform an order of magnitude analysis to estimate the relative implications of various forces acting on the fluid. Several important non-dimensional parameters indicative of the competing effects expressed as ratio of different forces are given as:

  • Reynolds number: \(\text{Re} = \frac{\rho wH}{\mu }\) (the inertial force to the viscous force)

  • Weber number: \({\text{We}} = \frac{{\rho w^{2} H}}{\sigma }\) (inertial force to the surface tension force)

  • Rossby number: \(R_{0} = \frac{w}{{\omega_{c} \bar{r}}}\) (Coriolis force to the centrifugal)

  • Capillary number: \({\text{Ca}} = \frac{\mu w}{\sigma }\) (the viscous force to the surface tension force).

For most microfluidic applications, the fluid flow usually has a small Re due to the small characteristic length of a microchannel. In our research, Reynolds number ranges from 10−1 to 10−2. It means that the inertial force is small compared with the viscous force.

As mentioned earlier, the Coriolis force induces the transversal flow inside the microchannel relative to the axial down channel flow so that the flow becomes fully three-dimensional. In order to compare the effects of Coriolis force and centrifugal force, Rossby number versus angular frequency is calculated using five types of microchannels, shown in Fig. 8.

Fig. 8
figure 8

Calculated Rossby number as a function of angular frequency where w and \(\bar{r}\) are the average velocity of radial and average displacement of liquid

Full size image

From Fig. 8, one can observe that Rossby number R 0 increases with the increasing angular frequency and channel dimensions. It means that the effect of Coriolis force will increase as angular frequency and channel dimensions increase. However, the R 0 is still very small, and the maximum value is only 0.012. Furthermore, this result can also verify the rationality of our model of neglecting the influence of Coriolis force.

Figure 9 shows the effect of angular frequency on capillary number. Figure 9 shows that the capillary number increases as the angular frequency increased. In addition, under the condition of same angular velocity, the capillary number increases as channel dimensions increased. It means that the effect of the capillary force on the flow will become weaker as the microchannel dimension increases. In a nutshell, the capillary number is smaller in our study, and the viscous force is 2 orders of magnitude smaller than the surface tension. Hence, the surface tension should be considered in the model.

Fig. 9
figure 9

Calculated capillary number as a function of angular frequency where w is the average velocity of radial

Full size image

4.3 Model analysis

Ignoring the surface tension effect and initial pressure the simplified model problem, Kim and Kwon (2006a, b) had developed the physical modeling and carried out the analysis for the centrifugal-force-driven transient filling flow into a rectangular microchannel. The moving front advancement in their model, l(t), was expressed as:

$$l\left( t \right) = l_{0} \left[ {2{\text{e}}^{Dt} - 1} \right]$$
(26)

where

$$D = \frac{{32\rho \omega^{2} }}{\mu }\sum\limits_{m = 1,3,5 \ldots }^{\infty } {\sum\limits_{n = 1,3,5 \ldots }^{\infty } {\frac{1}{{\lambda_{mn} m^{2} n^{2} \pi^{4} }}} }$$
(27)
$$\lambda_{mn} = \frac{D\rho }{\mu } + \left[ {\left( {\frac{m\pi }{W}} \right)^{2} + \left( {\frac{n\pi }{H}} \right)^{2} } \right]$$
(28)

In this section, a comparison of the displacement of the moving front obtained from Eqs. (25) and (26) with experimental data results are shown in Fig. 10a–d. On the whole, it is observed that the results of the moving front advancement obtained from the experimental data show a trend similar to those obtained from the theoretical calculations (Eqs. 25 and 26). However, over a range of channel sizes and angular velocity, the theoretical results from Eq. (25) are more reasonable than Kim’s model (Eq. 26) to provide a good prediction of the experimental data for the five types (given in Table 2) of microchannels used in this study. The reasons for this are due to the fact that Kim’s model did not consider the initial pressure. Actually, the effect of the initial pressure [P(z = 0)] is large enough to dominate the loading process at the beginning. Additionally, the capillary force could not be neglected especially for the small size of the microchannel, since the total centrifugal force is only slightly larger than the summation of the capillary force and the wall shear force (Liu et al. 2008).

Fig. 10
figure 10

Comparison of the moving front advancement versus flow time for types C1, C2, C3 and C5 microchannels [symbols experimental value, solid lines theoretical value (Eq. 25), dotted lines theoretical value (Kim’s model, Eq. 26)] where a type C1, b type C2, c type C3 and d type C5: a type C1, the section size: W/H = 0.4/0.3 (mm); b type C2, the section size: W/H = 0.4/0.24 (mm); c type C3, the section size: W/H = 0.3/0.24 (mm); and d type C5, the section size: W/H = 0.2/0.14 (mm)

Full size image

In addition, according to the experimental curves and theoretical curves presented by Eq. (25), for types C1–C3 and C5 microchannels with an angular velocity varying from 80 to 120 rad/s, all the experimentally determined data are higher than the predicted curves, as shown in Fig. 10. This means that the pressure gradient (−∂p/∂z) in our theoretical model is less than the experimental value results in terms of −∂p/∂z + f ω . This may be partly due to the parabolic pressure distribution in the model, and the pressure gradient inside a CD-based microchannel flow may be linear (Madou et al. 2001).

Moreover, under the condition of the same microchannel length, Fig. 10a–c shows, with the decrease in the section size, the larger discrepancy between the experimentally obtained data and theoretical value. For example, the discrepancy of flow time (to arrive at 10 mm) for the case of 80 rad/s for types C1–C3 is 6.8, 8.6 and 19 %, respectively.

With the overall angular velocity ranging from 80 to 120 rad/s (based on the experimental data obtained for five sets of microchannels being studied), compared with the theoretical model proposed in this study, the average errors between the predicted values and the most experimental results are 14 %. It should be noted that the average discrepancy of types C1–C4 is 8.4, 8.7, 15 and 13.4 %, but type C5 is 25 %. This means that the cross-section size of the microchannel is larger, and the error between theoretical and the experimental is smaller. This may be partly due to difference on the pressure gradient and the fact that our theoretical model does not consider the variety of dynamic contact angle. Overall, the theoretical model and experimental results are deemed to be in good agreement.

5 Conclusions

An analytical study has been carried out to investigate the transient filling flow into rectangular hydrophilic microchannel in centrifugal microfluidics. By neglecting the Coriolis force, an analytical expression of simple form, including the velocity profile, flow rate, the moving front, and the pressure distribution along the microchannel, was presented. This simple expression relates the moving front to the channel dimensions (W, H and l), the rotating speed ω and the liquid property (ρ and μ) as well as the surface property (θ c and γ la ). This model is developed to predict the time-dependent behaviors of the moving front in lab-on-a-CD systems or centrifugal pumping.

For different types of the microchannels used in this study, the results from our model provide a good prediction (with an average discrepancy of 14 %) of experimental data over a wide range of channel sizes and angular velocity. Also, the larger the cross-section size of the microchannel is, the less the error between theoretical and the experimental will be. Moreover, by comparing our model and Kim’s model as well as experiment data, the initial pressure and surface tension have a great influence on the flow velocity especially for small section size of the microchannel. Both the theory and the experiment consistently show that the displacement of the moving front depends on the angular velocity, locations of reservoirs and section size. It should be noted that the advancing velocity is also affected by the length of microchannel due to the change of pressure distribution in the microchannel. In conclusion, by means of accurate prediction model, one can easily determine the microchannel dimensions and the rotational speed to meet the design requirements for centrifugal microfluidic system.