1 Introduction

Microfluidic systems take advantage of the peculiar scaling of surface-to-volume ratios towards the microworld, which brings about severe changes in the design paradigms towards microdimensions (Gravesen et al. 1993; Ho 2001; Nguyen and Steve 2002; Tay FEH 2002; Ducrée et al. 2005). On the one hand, the high surface-to-volume ratios allow the implementation of surface- or field-mediated liquid transport mechanisms, for instance, capillary action and electroosmosis. On the other hand, the large shear stresses connected to the high surface-to-volume ratios and the low channel cross sections severely limit the volume flux and impose strictly laminar flow conditions.

For applications in which the diffusion limited the speed of mixing in such laminar flows is a major problem; mixing must be accelerated by “engineering of chaos" via hydrodynamic stretching-and-folding or multilamination schemes. The particular choice of the mixing scheme depends on various criteria, among them are volume throughput, power efficiency, compatibility with properties of processed fluid, compatibility with fabrication and operation of other up- and downstream components and the overall fabrication costs.

The main focus of this paper is on applications in chemical microprocess engineering, where the paramount issues are the speed and homogeneity of mixing, volume throughput and often power efficiency (Branebjerg et al. 1996; Henzler 2000; Hessel et al. 2003; Hardt and Schönfeld 2003; Nguyen and Wu 2005; Hardt et al. 2005; Hessel et al. 2005). Under these premises, one of the best trade-offs is achieved by multilamination schemes of continuous, pressure-driven flows through high-aspect-ratio microstructures often displaying a three-dimensional architecture. However, these complex structures are costly to fabricate.

We will present in this contribution a novel method for the mixing of flows based on centrifugal microfluidics, jointly addressing the problems of fabrication, throughput and parallelization. Centrifugal microfluidic technologies have formerly been introduced to elegantly implement hydrodynamic pumping and parallelization in miniaturized analytical assays (Madou and Kellogg 1998; Man et al. 1998; Duffy et al. 1999; Ekstrand et al. 2000; Eckersten et al. 2001; Tooke et al. 2001; Palm et al. 2001; Brenner et al. 2004; Grumann et al. 2004). Flow control is often achieved by “capillary burst valves" based on hydrophobic constrictions (McNeely et al. 1999). The rotation creates an artificial gravity to pulselessly pump the liquid in the radial direction. We demonstrate how, apart from the pumping, the centrifugal acceleration significantly enhances mixing between concurrent, centrifugally pumped flows by means of the apparent Coriolis force.

Previously, the secondary hydrodynamic motion, which is connected to the Coriolis force Eq. 7, has already been considered for heat exchangers or centrifugation (Barua 1954; Benton 1956; Alfredsson and Persson 1989; Brouwers 1995, 2002). In this work, we examine for the first time its influence on flows through microchannels spinning at comparatively high speeds of rotation.

This paper is structured in the following way. The next Sect. 2 outlines how the Navier–Stokes equation is transferred in the rotating reference frame to yield the (apparent) centrifugal and Coriolis force. In Sect. 3, we then show numerical simulations which illustrate how the streamlines are distorted as fluid moves at a finite speed in a channel in the radial direction to induce distinct flow patterns. These basic hydrodynamic effects are in agreement with experimental observations presented in Sect. 4. Finally, in Sect. 5, we summarize the basic outcomes and provide an outlook on future work.

2 Hydrodynamics in a rotating reference frame

2.1 Hydrodynamic equations of motion

The continuum mechanics of incompressible fluids in a centrifugally driven flow at the angular frequency, ω=2 π ν, is governed by the Navier–Stokes equation

$$ \varrho \underbrace{\left[ {{\partial}\over {\partial t}}\vec{v} + (\vec{v} \cdot \nabla) \vec{v} \right]}_{\hbox{D} \vec{v} / {\hbox{D} t}} = -\nabla p + \eta \nabla^2 \vec{v} $$
(1)

and the continuity equation

$$ \nabla \cdot \vec{v} = 0 $$
(2)

for the velocity field \(\vec{v}.\) The differential operator \({\hbox{D}\vec{v}} / {\hbox{D} t}\) on the left-hand side of Eq. 1 is named the material derivative. The constant parameters \(\varrho\) and η denote the density and viscosity of the liquid, respectively.

The flow is driven by the centrifugal field

$$ \vec{f}_\omega = \varrho r \omega^2 \hat{e}_{\rm r} $$
(3)

at a radial position r along the radial \(\hat{e}_{\rm r}{\text{-direction}}.\) Equation 3 is implicitly incorporated into Eq. 1 by the boundary condition for the wall of the radial channel which steadily moves at an angular speed \( \vec {\omega}.\) Externally imposed pressure differences Δp, e.g., between the inlet and the outlet of the open channel, as well as gravity will be discarded in this work.

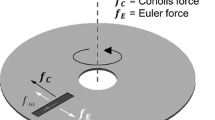
The centrifugally driven flow of a liquid plug through a channel of width Δx and a height h rotating at an angular velocity vector ω=2 π ν is displayed in Fig. 1. The plug possesses a length \( l = r_{>} - r_{<} \) and a mean radial position \( \bar{r} = 0.5(r_{<} + r_{>} ) \) between its inner and outer boundaries \( r_{<} \) and \(r_{>},\) respectively.

Fig. 1
figure 1

Geometry and forces on a disk spinning at the angular velocity vector \(\vec{\omega}\) pointing for positive, i.e., counter-clockwise rotation, out of the paper plane towards the reader. The local radial unit vector is given by \(\hat{e}_{\rm r},\) the local azimuthal direction is represented by \(\hat{e}_{\rm x}.\) The rectangular radial channel exhibits a width Δx and a height h. A liquid plug of length \( l = r_{>} - r_{<} \) and mean radial position \( \bar{r} = 0.5(r_{<} + r_{>} ) \) is characterized by its inner and outer boundaries \( r_{<} \) and \(r_{>},\) respectively. The liquid traveling at a speed \(\vec{v}\) down the channel is exposed to the mean centrifugal force density \(\vec{f}_\omega \propto \bar{r} \omega^2 \hat{e}_{\rm r}\) (Eq. 3) and to the Coriolis force density \(\vec{f}_{\rm C} \propto \vec{v} \times \vec{\omega}\) (Eq. 7) when viewed from the non-inertial rotating frame rotating at \(\vec{\omega}\)

Full size image

2.2 Transformation into disk frame

We want to express the centrifugal liquid motion in its ‘‘generic’’ frame of reference rotating with the disk at an angular velocity vector \(\vec{\omega}.\) In this non-inertial frame, the material derivative \(\hbox{D} \vec{v} / {\hbox{D}} t \) on the left-hand side of the Navier–Stokes equation 1 transforms

$$ {{\hbox{D} \vec{v}}\over {{\hbox{D}} t}} \mapsto {{{\hbox{D}} \vec{v}}\over {{\hbox{D}} t}} + \vec{\omega} \times \left( \vec{\omega} \times \vec{r} \right) + 2 \vec{\omega} \times \vec{v} $$
(4)

with the velocity \(\vec{v}\) and its (spatial) derivatives now referring to measurement in the rotating frame.

Implementing Eq. 4, we thus obtain

$$ \varrho \left[ {{\partial}\over {\partial t}}\vec{v} + (\vec{v} \cdot \nabla) \vec{v} \right] = -\nabla p + \eta \nabla^2 \vec{v} \underbrace{- \varrho \vec{\omega} \times \left( \vec{\omega} \times \vec{r} \right)}_{\vec{f}_\omega} \underbrace{- 2 \varrho \vec{\omega} \times \vec{v}}_{\vec{f}_{\rm C}} $$
(5)

as the equation of motion with static boundary conditions, i.e., where the channel walls remain at rest. Formally, Eq. 5 differ with Eq. 1 by two pseudo forces, the centrifugal term

$$ \vec{f}_\omega = -\varrho \vec{\omega} \times \left( \vec{\omega} \times \vec{r} \right) $$
(6)

which corresponds to the centrifugal force \(\vec{f}_\omega.\) Equation 3 for the geometry considered here \(\angle(\vec{\omega}, \vec{v}) = 90^{\circ}.\) and the velocity-dependent constituent

$$ \vec{f}_{\rm C} = - 2 \varrho \vec{\omega} \times \vec{v} $$
(7)

which is called the Coriolis force.

2.3 Flow profile

We now evaluate the axial velocity profile v r(x)=v(x) of a centrifugally driven flow along the transversal \(\hat{e}_{\rm x}\hbox{-direction}\) within a radial channel rotating at an angular frequency ω (Fig. 1). For the moment, we disregard the Coriolis-induced transversal components of the velocity field \(\vec{v}\) which neither contribute to the radial flow nor do they add up to an overall net flow in the transversal direction due to the confining walls.

In order to allow a simple analytical treatment of Eq. 1, we assume a flow through a narrow gap at a constant spacing, 2 x 0=Δx and \(h \mapsto \infty,\) instead of the rectangular channel (with a finite h) in Fig. 1. We further restrict the discussion to steady-state conditions, i.e., \(\partial \vec{v} / \partial t = 0.\) Due to the neglect of the Coriolis force, the laminar centrifugal flow field \(\vec{v}(\vec{r})\) in the radial channel is approximately represented by its radial component \(v_{\rm r} \hat{e}_{\rm r}\) and continuity Eq. 2 requires \(v_{\rm r}(\vec{r}) = v_{\rm r}(x).\) This way, \(\partial \vec{v} / \partial r = 0\) and also the inertial term \(\left(\vec{v} \cdot \nabla\right) \vec{v}\) vanishes.

We thus obtain \(\hbox{D} \vec{v} / {\rm D t} = 0\) for the material derivative on the left-hand side of Eq. 5 to arrive at

$$ \eta {{\partial^2 v}\over {\partial x^2}} = -{{\hbox{D} p}\over {{\rm d} r}} - \varrho \omega^2 r $$
(8)

which is the Navier–Stokes equation for the two-dimensional velocity profile v=v r(r, x). The condition ∂v/∂r=0 also allows to average Eq. 8 over the radial component,

$$ \eta {{\partial^2 v}\over {\partial x^2}} = -\Delta p - \varrho \omega^2 \bar{r} $$
(9)

i.e., to integrate along the r-axis and divide by the radial length of the channel l.

Discarding external pressure differences Δp=0 between the inlet and the outlet boundaries, we can now derive the parabolic flow profile

$$ v(x) = v_{\rm max} - {{\varrho \omega^2 \bar{r}}\over {2 \eta}} x^2 $$
(10)

which fulfills Eq. 9 under no-slip boundary conditions v(±x 0)=v r (±x 0)=0. This parabolic profile exhibits a maximum velocity

$$ v_{\rm max} = {{\varrho \omega^2 \bar{r}}\over {2 \eta}} x_0^2 $$
(11)

in the center of the tube at x=0. Note that the velocity profile v(x) in Eq. 10 depends on the mean radial position \(\bar{r}\) while the parabolic profile of a pressure-driven Hagen–Poiseuille flow scales with the inverse of the overall length of the channel.

Using the material properties of water (\(\varrho \approx 1,000\,\hbox{kg}\,\hbox{m}^{-3},\) η ≈ 1 mPa s), a typical channel radius x 0=100 μm and a mean position of the liquid plug \(\bar{r} = 3\) cm, a scaling

$$ v_{\rm max} = 1.5 \times 10^{-4}\rm m s^{-1} \cdot \omega^2[{\rm rad\,s^{-1}}] $$
(12)

is derived from Eq. 11. At a typical frequency ν=1,000 rpm, the flow velocity Eq. 12 thus amounts to roughly 1.65 m s−1, implying a residence time of 12 ms, only, in a 2-cm long channel which can be easily accommodated on a standard Compact Disc (CD).

2.4 Scaling of forces

The scaling of forces in centrifugal flows can be investigated by dimensionless numbers. For the following rule-of-thumb approximations, we consider the Coriolis force \(\vec{f}_{\rm C}\) Eq. 7 interacting with an initially radial centrifugal flow. We also assume a characteristic radial velocity \(0.5 v_{\rm max} \hat{e}_{\rm r}\) and \(\nabla \vec{v} \approx v_{\rm max} / x_0\) where v max is set equal to Eq. 11. We thus obtain a characteristic scaling

$$ f_{\rm C} = {{\varrho^2 \bar{r} x_0^2 \omega^3}\over {2 \eta}} $$
(13)

of the Coriolis force Eq. 7 with x 20 ω 3.

To understand the evolution of transversal components in the velocity field \(\vec{v}\) of a centrifugal flow, it is most interesting to study the ratio

$$ {{f_\omega}\over {f_{\rm C}}} = {{2 \eta}\over {\varrho x_0^2 \omega}} $$
(14)

between the centrifugal force \(\vec{f}_\omega\) Eq. 3 pointing in the radial direction and the transversal Coriolis force \(\vec{f}_{\rm C}\) (Eq. 7). The ratio Eq. 14 amounts to roughly 200 ω−1 for the liquid characteristics of water and a channel measuring x 0=100 μm. This shows that for angular speeds ω beyond about 200 rad s−1 ≈ 1900 rpm, the Coriolis force prevails over the centrifugal force!

To consider all possible interactions in experiments, we also need to look at the impact of the capillary force. The corresponding force per unit mass

$$ f_\Theta = {{p_\Theta}\over {l}} \approx {{2 \sigma}\over {x_0 l}} \cos\Theta $$
(15)

is associated with the capillary pressure p Θ as a function of the contact angle Θ and the surface tension σ which is, of course, independent of ω. The ratio between f Θ and the Coriolis force

$$ {{f_\Theta}\over {f_{\rm C}}} = {{4 \eta \sigma \cos\Theta}\over {\varrho^2 l \bar{r} \omega^3 x_0^3}} $$
(16)

turns out to be highly dependent on ω and x 0. Inserting the surface tension σ=72.9 mN m−1 for water, perfect wetting (Θ=0) and again x 0=100 μm, \(\bar{r} = 3\) cm and l =2 cm, the equilibrium between f Θ and f C is reached at about 78.6 rad s−1 ≈ 750 rpm. For growing contact angles Θ, i.e., an increasingly hydrophobic character of the surface, the equilibrium frequency continuously drops until the capillary force is eliminated at Θ=90°.

In the presented experiments, the capillary force only plays a role during the short priming period of the microfluidic network which is on the order of 10 ms Eq. 12. Thereafter, capillary forces only occur within incompletely filled channels. However, the situation may change when gas-liquid-solid interfaces emerge, e.g., at expansions or bifurcations of the channel structure. For the following simulations carried out under steady-state conditions and complete filling of the channels, capillary forces are entirely discarded.

2.5 Schematic patterning of flow

Figure 2 sketches how the Coriolis force impacts a flow through a duct spinning at an angular frequency \(\vec{\omega}.\) Similar to a pressure-driven flow, the centrifugal force \(\vec{f}_\omega\) Eq. 3 induces a parabolic flow profile. Therefore, the velocity-dependent Coriolis force \(\vec{f}_{\rm C}\) (Eq. 7) displays its largest values, where \(\vec{v}\) peaks in the center of the channel from where the fluid is driven towards the side wall.

Fig. 2
figure 2

Schematic of the patterning of flow in a fluidic duct spinning at an angular frequency ω. The centrifugal force \(\vec{f}_\omega\) Eq. 3 generates a parabolic profile \(\vec{v}\) pointing (mainly) in radial direction. The Coriolis force \(\vec{f}_{\rm C}\) (Eq. 7) seeks to deflect the flow in transversal direction. As the transversal motion in the filled channel is restricted by the side walls, the non-uniform flow field \(\vec{v}\) in a cross section of the channel leads to an inhomogeneous field distribution of the Coriolis force \(\vec{f}_{\rm C}(\vec{v}) \perp \vec{v}.\) The field peaks in the center of the channel where the liquid is pushed towards the side wall. From these, the liquid escapes along the upper and lower side wall. This way, transversal swirling patterns \(\vec{v}(\vec{f}_{\rm C})\) are generated

Full size image

As the force field \(\vec{f}_{\rm C}\) uniformly points towards the same wall addressed by the sense of rotation, the liquid next to the wall must escape along the upper and lower side walls where the counteracting field \(\vec{f}_{\rm C}\) is minimum due to the no-slip boundary condition. Overall, the Coriolis force drives a transversal stirring, while the centrifugal force \(\vec{f}_\omega\) drives the flow in the radial direction.

3 Simulation of basic hydrodynamic effects

To investigate the impact of the Coriolis force on the flow patterns in a more quantitative fashion, we have carried out extensive numerical simulations with the commercial code ACE+ (CFD-GUI Revision 2002.2.16, CFD-ACEU solver Revision 2002.0.40) from ESI-Group (2000). The simulations are performed in the reference frame where the channel walls remain at rest, i.e.,the reference frame rotates at the same speed as the disk. The three-dimensional simulations obtained for steady-state conditions \((\partial \vec{v} / \partial t = 0)\) are carried out under fixed-pressure boundary conditions.

In this non-inertial reference system, a centrifugal force \(\vec{f}_\omega\) Eq. 3 and a Coriolis force \(\vec{f}_{\rm C}\) (Eq. 7) are experienced by the liquid. In the (inertial) lab frame, the liquid is not exposed to any external forces. The experimentally observed hydrodynamics is rather induced by the moving wall of the rotating disk (which are at rest in the rotating frame) and inertia. In the following simulations, we use a plug length of l=2 cm which starts at a distance of \(r_{<} = 2\) cm from the center of the disk (Fig. 1). For the liquids, we set the above-mentioned parameters of (distilled) water at room temperature.

3.1 Flipping

Figure 3 displays the reshaping of the initial vertical interface line between the water-like liquid streams indicated by the black and light gray shading, respectively. Further downstream, the Coriolis force pointing in the direction of \(\vec{v} \times \vec{\omega}\) pulls the two liquids on the right-hand wall. The gray liquid escapes by the top and bottom of the channel. After a distance of 2 cm, the positions of the adjacent streams have almost completely switched without any passive structures to guide the flow! Note that diffusion is disabled in the simulation, and the mixing observed at the interface region is an artifact resulting from the numerical algorithm (‘‘numerical diffusion’’).

Fig. 3
figure 3

Flipping of two parallel flows. The black flow is introduced on the left, the light gray flow on the right-hand side of the channel measuring Δx=h =100 μm, \( r_{<} = 2\;{\text{cm}} \) and l=2 cm at ω= 50 rad  s−1

Full size image

3.2 Stirring and mixing

In order to still obey the continuity equation (2), the reshaping of the flow in Fig. 3 must be accompanied by some helical motion, i.e., transversal components add to the initially merely radial velocity field. This “stirring” action convectively accelerates mixing on the disk. The behavior resembles the well-known Taylor dispersion (Taylor 1953) in pressure-driven flows, where the parabolic flow profile enhances mixing in axial direction.

To understand the mixing process, we recall Fick’s law

$$ \vec{j} = -D \nabla c $$
(17)

for the mass diffusion flux \(\vec{j}\) resulting from a gradient in the concentration ∇ c. D denotes the constant of diffusion. The overall flux is given by the surface integral of \(\vec{j}\) (Eq. 17) over the interfacial area. When observing the patterning of the flow in Fig. 3, it can be clearly recognized that the interfacial surface is significantly increased and the characteristic thickness d of the adjacent layers is greatly reduced in downstream direction. As a rule of thumb, the mixing time

$$ t_D \propto {{d^2}\over {D}} $$
(18)

scales with the square of d.

In Fig. 4, we have adjusted the speed of rotation to ω=150 rad s−1 while keeping all other parameters constant to better illustrate the stirring process. Note again the D has been virtually eliminated (D=2×10−20 m2 s−1 due to technical reasons) for the simulation, but still the above-mentioned numerical diffusion softens the interfacial region. It can, however, be seen that diffusion distances d are reduced compared to the upstream entrance to sizably speed up the diffusive mixing.

Fig. 4
figure 4

Stirring of two parallel flows. The black flow is introduced on the left, the gray flow on the right-hand side in the same channel geometry (l=2 cm, Δx=h =100 μm, \( r_{<} = 2\;{\text{cm}} \) cm) as Fig. 3. Now the angular velocity is increased to ω = 150 rad s−1. The first graphs following the entrance indicate the transversal flow patterns induced by the Coriolis force

Full size image

The (simulated) maximum velocity of the liquid plug obtained in the CFD-simulation is 0.58 m s−1 in the center of the channel, implying a lower limit of the residence time of t res ≈ 34 ms. Compared to the diffusion time t D ≈ d 2/D=950 ms Eq. 18 for the undistorted profile in the entrance region with d=Δx/2=50 μm and D=2.62×10−9 m2 s−1 (self-diffusion of H2O), this residence time t res≪t D is negligible. (In other words, the Peclet number for mass transport Pe m=v l/D amounts to about 4.4×106, i.e., the contribution of pure diffusive mixing can be discarded on the way through the channel). Considering that the distance d shrinks by about a factor of three in the downstream flow pattern at the end of the channel, this time reduces only by a factor of 9, i.e., t D ≈ 100 ms! This means the Coriolis-induced mixing proceeds on the same time-scale as the residence time t res (which can easily be prolonged by extending the length of the channel).

3.3 Impact of aspect ratio

For nearly all microfabrication techniques, e.g., silicon micromachining, injection molding and hot embossing, the fabrication of high-aspect-ratio structures is expensive compared to low-aspect-ratio structures. On the other hand, such structures are required to reach short diffusion times t D (Eq. 18) for large liquid volumes to be mixed. For these cases, rather complex and expensive techniques such as LIGA have been employed. Here we show that very efficient mixing can also be reached for wide, low-aspect-ratio channels due to the nature of the Coriolis force.

In Fig. 5, the same simulation parameters have been applied as in the previous Fig. 3, but the channel widths Δx have been extended from 100 to 250 μm (top) and 500 μm (bottom). It can be seen that characteristic diffusion length d roughly amounts to half of the channel width at the channel entrance. At the channel exit, the favorable patterning of flow by the Coriolis force now makes the smaller height of the channel to represent the characteristic dimension, thus significantly shrinking the characteristic diffusion time t D Eq. 18. For the 500-micron channel, this means a factor of 10 in the characteristic length, i.e., a reduction by a factor 102=100 (from half of the channel width d=250 μm to one quarter of the height, i.e., h = 25 μm) in diffusion time!

Fig. 5
figure 5

Impact of the aspect ratio on the flow pattern at an angular speed ω=50 rad s−1 with Δx=250 μm (top), Δx=500 μm (bottom) and all other geometric parameters unchanged from Figs. 3 and 4 (l=2 cm, h=100 μm, \( r_{<} = 2\;{\text{cm}} \))

Full size image

4 Comparison to experiments

We have developed a measurement set-up to experimentally investigate the patterning of flow on a centrifugal disk by a stroboscopic principle (Grumann et al. 2005). The PC-controlled set-up contains a rotating drive unit spinning the disk at a defined frequency of rotation up to 150 Hz. The image-capturing unit is composed of a stroboscopic flash (Drelloscope 255-01, Drello GmbH) and a 1280×1024-pixel CCD camera (Sensicam fast shutter, PCO Computer Optics GmbH) which is mounted on a microscope (Leica MZ12.5, Leica Microsystems GmbH) to obtain a tenfold magnification of the captured image. The high-speed CCD camera allows very short exposure times down to 100 ns, thus delivering a solution below 5 μm, even at an extraordinary high frequency of 150 Hz.

With this optical set-up, images of water and ink flows are captured by a black-and-white camera located at a fixed position above the rotating disk. The disk was manufactured by precision engineering and sealed with adhesive tape. The green ink solution was prepared from commercial Pelikan 4001 flasks diluted with 50% of water. This mixture proved to provide the optimum contrast while not measurably changing the viscosity of the water. The degree of mixing has been assigned to the gray-scale intensities have been by a calibration series using premixed ink-water solutions at known mixing ratios.

In the experiment, the water and the ink solutions were stored in two separate on-disk reservoirs which were large enough to allow the evolution of steady-state flow conditions within the common radial mixing channel. In our investigations of the Coriolis-induced mixing, we can, thus, directly compare the accumulated gray-scale intensity of each pixel to the numerically integrated value of the corresponding simulations under steady-state conditions.

We first look at the simulation and corresponding experiment in Fig. 6 displaying a top view of the channel. While experiencing the Coriolis force at ω=300 rad s−1, the dark fluid successively spreads into the lane of the clear liquid as the flow proceeds in down the channel (l=2.1 cm, h=65 μm, Δx=320 μm, \( r_{<} = 3\;{\text{cm}} \)). The figure illustrates a clear experimental evidence for the strong impact of the Coriolis pseudo force on the lateral convection in centrifugal flows.

Fig. 6
figure 6

Lateral spreading of two concurrent centrifugal flows A (clear) and B (dark) due to Coriolis force \(\vec{f}_{\rm C}\) for an angular frequency ω = 300 rad s−1 in a rectangular radial channel of length l=2.1 cm, height h = 65 μm and width Δx = 320 μm starting at \( r_{<} = 3\;{\text{cm}} \). The right hand side shows a top-view photography of the lateral spreading in the corresponding experiment. (Note the different length scales apply to the x- and y-axis.)

Full size image

Figure 7 resolves the transversal flow patterns in a rectangular channel at different radial positions. Under the impact of \(\vec{f}_{\rm C}\), the initially undisturbed flow pattern is increasingly deformed in downstream direction. At 3/4 of the channel length, the dark liquid has protruded far into the other liquid. In this vertical stack (‘‘sandwich’’)of thin liquid layers, the characteristic diffusion length d has been reduced by about a factor of three to cut down diffusion times t D ∝ d 2 by a factor of nine in an ordinary, straight microchannel! It is obvious that this effect is even more pronounced towards decreasing (!) aspect-ratios which can easily be manufactured by standard microfabrication equipment. Figure 8 examines the flow patterns recorded at a fixed location near the outlet as a function of ω.

Fig. 7
figure 7

Experiments and simulation of Coriolis-induced patterning of concurrent flows through a radial channel of length l=2 cm, h=65 μm and Δx=320 μm, starting at a radius of \( r_{<} = 2\;{\text{cm}} \) from the center and rotating at ω=300 rad s−1, at different downstream positions. The intensities represent the integral concentration accumulated along the dashed line, d indicates the characteristic diffusion length

Full size image
Fig. 8
figure 8

Experiments and simulation of flow profiles at the fixed position of the outlet of the l=2 cm long radial channel with h=65 μm, Δx=320 μm and \( r_{<} = 2\;{\text{cm}} \). At ω = 50 rad  s−1, the flow is still widely undisturbed by F C. Proceeding to ω=200 rad s−1, a vertical stacking ("sandwich") takes place. Reaching ω=300 rad s−1, the order of the two flows is flipped and a large contact surface forms. (Note that the right-hand simulation corresponds to the profile at the outlet for the series portrayed in Fig. 7)

Full size image

The comparison of the simulations and the experiments reveals a qualitative agreement which both comply with the suggested inversion of the layering. On the one hand, the quantitative deviations root in the simplified simulation model discards the full geometry and gas–liquid interfacial effects within the inlet and outlet sections. On the other hand, photographic artifacts like shadows thrown by the channel walls, reflections and impurities cannot be taken into account.

5 Summary and outlook

In this paper, we have studied the role of the apparent Coriolis force in centrifugally driven flow through straight microchannels pointing in radial direction on a rotating disk. It could be shown by numerical simulations and accompanying experiments that transversal flow components could be induced to stir and flip concurrent liquid flows through a radial channel.

The key impact parameters governing the Coriolis-induced reshaping of the contact surface are the channel length, its aspect ratio and the rate of rotation. Satisfactory agreement has been reached between simulations and accompanying experiments.

Overall, centrifugal microfluidic platforms excel with their modular set-up, featuring a fixed and reusable drive and detection unit on the one side, and a possibly disposable disk cartridge on the other. Due to the simple (rectangular) channel structure in a planar architecture as well as the absence of active components and moving parts, the disk is readily amenable to standard polymer microfabrication. The problems of fouling and clogging of particle suspensions are potentially reduced by the straight, constriction-free geometry of the mixing channel as well as the centrifugal volume force.

Furthermore, the contact-free transmission of the centrifugal field obviates the need for external pumps and pressure-tight interfaces to facilitate the handling of the system. The centrifugal actuation also allows throughputs of milliliters per second and channel which can be greatly enhanced by a generic parallelization scheme displaying a set of channels aligned in a spoke-like ‘‘wagon-wheel’’ geometry.

At the moment, work is under way to utilize the Coriolis-induced flow patterning for engineering several new functional elements such as a hydrodynamically actuated flow switch (Brenner et al. 2005) and a centrifugal microreactor (Haeberle et al. 2005).