1 Introduction

Over the past decade, a wide range of applications of integrated microfluidic systems has been observed in the fields of miniaturized analytical systems for chemistry and biology such as genomic and proteomic analyses, clinical diagnostics and micro total analysis systems (Auroux et al. 2002; Reyes et al. 2002). In recent years, these miniaturized analytical microfluidic systems enable a point-of-care or ubiquitous diagnosis and treatment of patients with minimizing sample and reagents volumes. The integrated microfluidic systems generally contain several microfluidic functions (Auroux et al. 2002; Reyes et al. 2002) such as pump, valve, mixing, reaction, separation and so on. In order to achieve desirable functions with the microfluidic systems in a precise manner, the control of the fluid flow is inherently required.

Recently, a centrifugal pumping method for a CD type microfluidic device equipped with a rotational motor was reported as a new controlling method for the flow in microchannels (Duffy et al. 1999; Madou et al. 2001; Gyros™ Microlaboratory, http://www.gyros.com). The centrifugal force generates fluid flow with little sensitivity to the physicochemical properties of the working fluid such as ionic strength, pH and so on (Duffy et al. 1999). It can also provide parallel pumping flows to several microchannels simultaneously on the same CD type microfluidic chip. It is important to understand the spatial and temporal behavior of fluid flow inside the microchannel for a precise design of a centrifugal microfluidic channel system. So far, most of previous studies in the literature simply adopted capillary stop valves making use of a surface tension effect for the purpose of controlling fluid flow, with lack of detailed understanding of the centrifugal flow behavior.

Numerical simulation could help us to design the desirable microchannel system more precisely and to understand the physical behavior of such microchannel flows. However, relying on a numerical analysis tool is very time consuming and costly at the first design step, especially for the cases of a complex microchannel network system or transient filling flow into microchannels. In contrast, an analytical solution approach, if available, provides a physical insight into flow behavior inside the microchannel. And moreover, it can offer a simple design guide at the first design step so that the design time and cost could be remarkably reduced. In this regard, we have already carried out the physical modeling and analysis for the centrifugal force driven transient filling flow into a circular microchannel and suggested the simple design equations for the circular microchannel (Kim and Kwon 2006). However, the cross-sectional geometry of microchannels which were fabricated by the conventional photolithography is usually rectangular rather than circular in most practical cases. It might be possible to apply the analytical results for the circular microchannel to the design of arbitrary cross-sectional microchannels such as a trapezoidal cross-sectional microchannel, based on the definition of the hydraulic radius. But, the analytical solutions for the rectangular microchannel are definitely useful and precise to understand and design the flow inside the rectangular microchannel.

In this paper, we define a specific physical problem for the radial flow into a rectangular microchannel on a rotating disk, as a simplified model of the centrifugal flow. For such a model problem, physical modeling is carried out based on the fundamental balance equations of mass and force. A dimensional analysis is then performed to understand the effects of related forces on the defined system according to the physical modeling. Two types of analytical solutions are achieved: (1) a pseudo-static approximate solution when the inertia force is negligible, and (2) an exact solution with the inertia force taken into account. The solution provides important information such as filling flow front advancement, velocity profile and pressure distribution as functions of both time and geometry. The obtained analytical results show that the filling flow driven by centrifugal force is affected by three dimensionless parameters which combine fluid properties, rectangular channel geometry and rotating conditions. Finally, we propose a design tool for a rectangular microchannel in which the flow is driven by centrifugal force with application examples.

2 Problem statement

This paper aims not only at analyzing the transient filling flow into a rectangular microchannel which is driven by centrifugal pumping but also at providing a simple design tool to determine a rectangular microchannel geometry and disk rotational speed to meet a specific flow requirement for the given fluid material properties.

In this regard, we define a model problem to represent the transient flow into a microchannel driven by a rotation of a disk in this section. At this stage, we focus on the rectangular cross-sectional microchannel. The model problem can be described as follows.

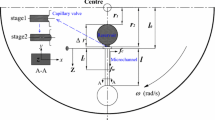
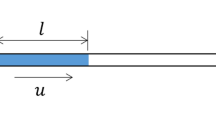
Figure 1 shows a schematic diagram of a rectangular cross-sectional microchannel on a CD type centrifugal microfluidic system. The width and height of the microchannel are denoted by W and H, respectively. A sample fluid, such as reagents or drugs having physical fluid properties of density, ρ, and viscosity, μ, is injected into a reservoir which is placed at a certain radial location of the CD plate, so that the microchannel starts from the radial location of L 0 away from the center of the CD as indicated in Fig. 1. Now the fluid flow can be considered when a rotational motor starts the CD plate in a constant rotational speed of ω. The material will flow out of the reservoir into the microchannel due to the centrifugal force and the flow front gradually advances along the radial direction of the CD. It is in our interest to be able to determine the flow front advancement as a function of time t, denoted by l(t). Of course, this flow front advancement will depend on the rotational speed, ω, as well as the location of reservoir, rectangular microchannel geometry and material properties of the fluid.

Fig. 1
figure 1

Schematic diagram of the transient filling flow into a rectangular microchannel on the CD type centrifugal microfluidic system. Dark area represents a region occupied by the sample fluid, l(t) indicating the flow front

Full size image

As for the design aspects of a microfluidic system with several microchannels on a CD plate, it is supposed that a design objective is to deliver sample fluids to specifically desired locations in the disk at the desired times through the multiple rectangular microchannels via centrifugal force induced by the rotational motion of the CD. A designer has to decide where to put the reservoirs (L 0), the widths and heights of the microchannels (W and H) for each channel along with the rotational speed (ω) of the disk. With this kind of design objective in mind, a simple analytic solution is indeed of great use in designing such a centrifugal microfluidic system. For instance, if the analytical expression of l(t) is available in terms of the design parameters, one can easily design the centrifugal microchannels.

In this regard, we would like to obtain an analytical solution for l(t) as a function of time for given sample fluid (ρ and μ), microchannel geometry (W, H and L 0) and processing condition (ω) which are regarded as the important design parameters in the centrifugal microchannel system. Of course, in obtaining an analytical solution for l(t), we also find expressions of the detailed velocity profile as well as the pressure distribution for the transient filling flow inside the rectangular microchannel. Finally, we suggest a simple analytical design tool of a rectangular microchannel on the CD plate for the given conditions.

3 Physical modeling and governing equations

Figure 2 shows various forces applied to an infinitesimal control volume of fluid inside the centrifugal microchannel of a rectangular cross-section. The centrifugal force is developed in the downchannel direction, i.e., the radial direction of the CD plate. Shear force and pressure are also developed according to the developed fluid flow. To investigate the centrifugal force driven transient flow analytically, we simplified the complicated problem by introducing several assumptions described below and then derived governing equations associated with the transient flow.

Fig. 2
figure 2

An infinitesimal control volume of fluid with the applied forces inside a rectangular microchannel in which flow is driven by centrifugal force

Full size image

3.1 Assumptions

Assumption 1

In this study, as a simple constitutive equation, material is assumed to be a Newtonian fluid. (non-Newtonian case needs a numerical simulation method since there is no analytic solution available.)

Assumption 2

As the first attempt to obtain analytic solutions for the transient flow into a rectangular microchannel, the Coriolis force effect is assumed to be negligible in a mild rotational speed in comparison with the centrifugal force effect. (Brenner et al. (2003) showed that the Coriolis force dominantly affects the flow over the rotational speed of 350 rad s−1, or equivalently about 3,350 rpm, for a microchannel of which width and depth are 360 and 125 μm, respectively. The Coriolis force induces the transversal flow inside the microchannel relative to the axial downchannel flow so that the flow becomes fully three-dimensional. At the relatively low rotational speed, however, the Coriolis force could be neglected relative to the centrifugal force.) Under this assumption, the flow can be assumed to be an axial flow, i.e., u = v = 0 and w ≠ 0 where u, v and w are velocity components in the direction of x, y and z, respectively.

Assumption 3

Surface tension effect is neglected in this study, again as the first attempt to obtain analytic solutions for the transient flow into a rectangular microchannel. (It might be noted here that surface tension becomes important in the microscale transient flow (Duffy et al. 1999; Kim et al. 2002; Madou et al. 2001; Gyros™ Microlaboratory, http://www.gyros.com) depending upon the surface properties. However, it may be reasonable to neglect surface tension effect when a polymer substrate of which the contact angle of a sample fluid is almost 90°. For example, the contact angles between water and native surfaces of polydimethylsiloxane (PDMS) and cyclic olefin copolymer (COC) substrates are about 90° (Duffy et al. 1999) and 92° (Puntambekar et al. 2002), respectively, with no surface modification. With this kind of case in mind, we ignored the surface tension effect for the present simplified model problem.)

3.2 Governing equations

The local continuity equation for an axial downchannel flow assumption (u = v = 0) is simply,

$$\frac{{\partial w}}{{\partial z}} = 0,$$
(1)

which implies that w is independent of z, i.e., w = w(x, y, t).

As for the momentum conservation equation, from the free body diagram depicted in Fig. 2, one can obtain the following relationship:

$$\rho \frac{{\partial w}}{{\partial t}} - \frac{{\partial \tau_{{xz}} }}{{\partial x}} - \frac{{\partial \tau_{{yz}} }}{{\partial y}} = - \frac{{\partial p}}{{\partial z}} + \rho \omega^{2} z,$$
(2)

where τ xz , τ yz and p are shear stresses in xz- and yz-planes and pressure, respectively. It should be noted that the material derivative, Dw/Dt becomes just the time derivative, ∂w/∂t in this case since w is a function of x, y and t only.

For a Newtonian fluid case, τ xz and τ yz , with a sign convention defined in Fig. 2, can be expressed as

$$\tau_{xz}(x,y,t)=\mu\frac{\partial w}{\partial x},$$
(3a)
$$\tau_{yz}(x,y,t)=\mu\frac{\partial w}{\partial y}.$$
(3b)

Then Eq. 2 becomes

$$\rho \frac{{\partial w}}{{\partial t}} - \mu {\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)} = - \frac{{\partial p}}{{\partial z}} + \rho \omega^{2} z,\quad \hbox{for} \; L_{0} \leq z \leq l(t)\; \hbox{and}\; t > 0.$$
(4)

Equation 4 is a partial differential equation for velocity field, w(x, y, t), and pressure field, p(z, t). The domains of interest for z and t are also expressed in Eq. 4. It should be noted that the region occupied by fluid is increasing as flow proceeds since l(t) increases with the time, which is a peculiar nature of this transient flow (Kim and Kwon 2006). One might recognize that the domain of z at t = 0 is null so that the velocity field is not defined at t = 0. In this regard, the conventional initial velocity of w is not to be considered in this study. Therefore, one has to solve Eq. 4 to obtain w(x, y, t) and p(z, t) just with appropriate boundary conditions as follows:

$$w(x = 0,y,t) = 0,\quad w(x = W,y,t) = 0,$$
(5a)
$$w(x,y = 0,t) = 0,\quad w(x,y = H,t) = 0,$$
(5b)

and

$$p(L_{0},t) = 0,$$
(6a)
$$p(l(t),t) = 0.$$
(6b)

Equation 5a, b means no-slip condition of the velocity on the wall. Equation 6a indicates that the pressure head of the inlet reservoir is zero. The pressure head at the inlet is induced by the gravity force in the reservoir and it is generally much less than the viscous and centrifugal forces inside the microchannel. In this regard, we neglected the inlet pressure to simplify the problem in this study. The pressure at the flow front, i.e., at z = l(t), is set to be zero in Eq. 6b by the assumption of neglecting the surface tension effect (Assumption 3).

In addition to the continuity and momentum equations, as a peculiar feature of this particular problem, one has to take into account the global mass conservation with regard to the flow front advancement. From the expression of the total flow rate, Q(t), one can obtain the equation for the flow front advancement, namely l(t), as below

$$Q(t) = WH\frac{{\hbox{d}l(t)}}{{\hbox{d}t}} = {\int\limits_0^H {{\int\limits_0^W {w(x,y,t)\hbox{d}x\,\hbox{d}y} }} },$$
(7)

the second equation in Eq. 7 being the governing equation for l(t) with the associated initial condition

$$l(t) = L_{0} \quad \hbox{at}\; t = 0.$$
(8)

Once the velocity field is obtained, the flow advancement can be determined via Eq. 7.

In summary, one has to obtain analytic solutions for w(x, y, t), p(z, t) and l(t) from Eqs. 4 and 7 with boundary conditions, Eqs. 5a, b and 6a, b and initial condition, Eq. 8.

4 Analytic solutions

In this section, we first manipulate the basic governing equations further to obtain more convenient forms of equations to deal with. Then we will introduce dimensionless forms of the governing equations for the sake of understanding the nature of the flow more efficiently. From the dimensionless equations, we will derive two types of analytic solutions: (1) for a pseudo-static flow as an approximation of low Reynolds number (Re) limiting case, and (2) for the general transient flow case as an exact solution.

Equation 4 can be recast to the following form:

$$\frac{{\partial p}}{{\partial z}} = \rho \omega^{2} z - {\left[ {\rho \frac{{\partial w}}{{\partial t}} - \mu {\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)}} \right]}.$$

One can easily integrate the above equation with respect to z from L 0 to z at instant time t, recognizing that three terms in the bracket are independent of z, to result in

$$p(z,t) - p(L_{0}, t) = \frac{{\rho \omega^{2} }}{2}{\left( {z^{2} - L_{0}^{2} } \right)} - {\left[ {\rho \frac{{\partial w}}{{\partial t}} - \mu {\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)}} \right]}{({z - L_{0} })}.$$
(9)

Substituting l(t) for z in Eq. 9, along with boundary conditions of Eqs. 6a, b at z = L 0 and z = l(t), respectively, gives rise to an interesting equation as below:

$$\rho \frac{{\partial w}}{{\partial t}} - \mu {\left( {\frac{{\partial ^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)} = \frac{{\rho \omega^{2} }}{2}{({l(t) + L_{0} })}.$$
(10)

Making use of Eq. 10 and boundary condition of Eq. 6a, one can rewrite Eq. 9 as

$$p(z,t) = \frac{{\rho \omega^{2} }}{2}{({z - L_{0} })}\,{({z - l(t)})}.$$
(11)

Now, in summary, the governing equations for w(x, y, t) and l(t) are Eqs. 10 and 7, respectively, along with boundary conditions, Eq. 5a, b, and an initial condition, Eq. 8. Note that they are coupled with each other. Once w(x, y, t) and l(t) are known by solving them, one can calculate the pressure distribution from Eq. 11. It may be noted that Eq. 11 shows that pressure distribution is parabolic in the axial direction at any instant time t (it will be discussed later).

4.1 Dimensionless governing equations

Dimensionless form of equations would be more convenient to identify a group of dimensionless parameters which affect the flow rather than the dimensional form of equations, thus enabling one to gain the physical insight into the problem more clearly. In this regard, Eqs. 7 and 10 are nondimensionalized. For this purpose, we introduced characteristic quantities as listed below:

  • Characteristic lengths: (1) W (width of the rectangular microchannel), (2) H (height of the rectangular microchannel), and (3) L (characteristic downchannel length, e.g., distance from the center of a CD plate to inlet reservoir.)

  • Characteristic velocities: (1) U (mean downchannel velocity of fluid flow), and (2) V (rotational velocity defined by V = L ωc, where ωc is the characteristic angular velocity).

  • Characteristic times: (1) T c (characteristic time for downchannel flow defined by T c = L/U), and (2) 1/ωc (characteristic time for rotational motion defined by 1/ωc = L/V).

  • Characteristic pressure: P c = (1/2)ρ U 2.

The dimensionless variables using such characteristic quantities are listed below:

$$\begin{aligned} &x^{*} = x/W, y^{*} = y/H, z^{*} = z/L, t^{*} = t/T_{{\rm c}} = tU/L, \omega ^{*} = \omega /\omega_{{\rm c}} = \omega L/V,\\ &w^{*} (x^{*}, y^{*}, t^{*}) = w(x,y,t)/U, p^{*} (z^{*}, t^{*}) = p(z,t)/P_{{\rm c}} = 2p/{({\rho U^{2} })}, l^{*} (t^{*}) = l(t)/L,\\ \end{aligned} $$
(12)

where superscript asterisk stands for corresponding dimensionless parameters.

Then, dimensionless form of Eq. 10 could be stated as

$$Re\,G_{{\rm A}} \frac{{\partial w^{*} }}{{\partial t^{*} }} - C_{{\rm A}}^{2} \frac{{\partial^{2} w^{*} }}{{\partial x^{*2} }} - \frac{{\partial^{2} w^{*} }}{{\partial y^{*2} }} = \frac{1}{2}Re\,G_{{\rm A}} \overline{V}^{2} \omega^{*2} {\left( {l^{*} (t^{*}) + L_{0}^{*} } \right)},$$
(13)

with the corresponding boundary conditions

$$w^{*} (0,y^{*}, t^{*}) = 0, \quad w^{*} (1,y^{*}, t^{*}) = 0,$$
(14a)
$$w^{*} (x^{*}, 0,t^{*}) = 0, \quad w^{*} (x^{*}, 1,t^{*}) = 0,$$
(14b)

where Re, G A, C A and \(\overline{V}\) denote the Reynolds number, Re = ρ UH/μ, geometrical (global) aspect ratio of height of the rectangular microchannel to downchannel length, G A = H/L, microchannel aspect ratio of height to width of the rectangular microchannel, C A = H/W, and ratio of rotational velocity to downchannel flow velocity, \(\bar{V} = {V}/{U},\) respectively. It should be noted that the first term on the left-hand side of Eq. 13 represents the inertia force effect; the second two terms on the left-hand side express the effect of viscous force; and the term on the right-hand side comes from the centrifugal (rotational) force effect. It is found from Eq. 13 that three different dimensionless groups dominantly affect the fluid flow behavior: \(Re\,G_{{\rm A}}, \overline{V}\omega^{*} \) and C A. Re G A represents the ratio of inertia force to viscous force, which enables us to estimate the inertia force effect on the flow system. \(\overline{V} \omega^{*}\) is equal to ω L/U, which is in fact the ratio of the rotational velocity of a disk to the downchannel flow velocity, associated with the centrifugal force as shown in Eq. 13. And, C A shows the effect of the cross-sectional shape of the rectangular microchannel on flow behaviors.

Dimensionless form of Eq. 7 can be written as

$$Q^{*} = \frac{Q}{{WHU}} = \frac{{\hbox{d}l^{*} }}{{\hbox{d}t^{*} }} = {\int\limits_0^1 {{\int\limits_0^1 {w^{*} \,\hbox{d}x^{*} \hbox{d}y^{*} } }} },$$
(15)

with an initial condition

$$l^{*} (0) = L_{0}^{*}.$$
(16)

Finally, a dimensionless equation for pressure distribution was also derived from Eq. 11 as:

$$p^{*} (z^{*}, t^{*}) = \bar{V}^{2} \omega^{*2} {\left( {z^{*} - L_{0}^{*} } \right)}{\left( {z^{*} - l^{*} (t^{*})} \right)}.$$
(17)

In summary, one has to solve w* (x*, y*, t*) and l* (t*) from the coupled Eqs. 13 and 15. Once they are solved, one can determine the pressure distribution from Eq. 17.

For most of microfluidic applications, the fluid flow usually has a small Re due to the small characteristic length of a microchannel. In this regard, we present two types of analytic solutions below for: (1) a pseudo-static approximate solution, which is corresponding to the relatively simple case when \(Re\,G_{{\rm A}} \ll 1,\) and (2) an exact solution. It might be mentioned that the pseudo-static solution enables us to check the validity of the exact solution since the pseudo-static solution is corresponding to the asymptotic behavior of exact solution as Re G A → 0.

4.2 Pseudo-static approximate solution

The microchannel flow usually has a small Re (i.e., \(Re \ll 1.\)) The very small G A also justifies \(Re\,G_{{\rm A}} \ll 1,\) even when Re is relatively large. For the case of \(Re\,G_{{\rm A}} \ll 1\) while maintaining \(Re\,G_{{\rm A}} \bar{V}^{2} \omega^{*2} \sim O(1),\) the effect of inertia force in Eq. 13 becomes negligible compared with the effects of viscous and centrifugal forces so that Eq. 13 can be reduced to

$$ - C_{{\rm A}}^{2} \frac{{\partial^{2} w^{*} }}{{\partial x^{*2} }} - \frac{{\partial^{2} w^{*} }}{{\partial y^{*2} }} = \frac{1}{2}Re\,G_{{\rm A}} \overline{V}^{2} \omega^{*2} {\left( {l^{*} (t^{*}) + L_{0}^{*} } \right)},$$
(18)

with the boundary conditions of Eq. 14a, b, at instant time t*. The solution of Eq. 18 is called the pseudo-static approximate solution since the inertia term does not play a role as if the viscous force were just balanced with the centrifugal force. It should be noted that the dimensionless velocity, w* is still a function of geometry (x* and y*) and time (t*) although we neglect the inertia force term.

From Eq. 18 with boundary conditions, Eq. 14a, b, one can obtain a dimensionless velocity profile inside the rectangular microchannel based on the eigenfunction expansion method

$$w^{*} (x^{*}, y^{*}, t^{*}) = 8Re\,G_{{\rm A}} \overline{V} ^{2} \omega^{*2} {\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda _{{mn,{\rm static}}} mn\pi^{2} }}\sin m\pi x^{*} \sin n\pi y^{*} } }} }{\left( {l^{*} (t^{*}) + L_{0}^{*} } \right)},$$
(19)

where the eigenvalues of the pseudo-static approximate flow, λ mn,static are

$$\lambda_{{mn,{\rm static}}} = C_{{\rm A}}^{2} m^{2} \pi^{2} + n^{2} \pi^{2} \quad \hbox{for} \; m = 1, 3, 5, \ldots \; \hbox{and} \; n = 1, 3, 5,\ldots.$$
(20)

Applying Eq. 19 to Eq. 15 yields the following equation for l*(t*),

$$\frac{{\hbox{d}l^{*} }}{{\hbox{d}t^{*} }} = 32Re\,G_{{\rm A}} \overline{V}^{2} \omega^{*2} {\sum\limits_{m = 1,3,5, \ldots }^\infty{{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda_{{mn,{\rm static}}} m^{2} n^{2} \pi^{4} }} }, }} }{\left( {l^{*} (t^{*}) + L_{0}^{*}} \right)}.$$
(21)

One can integrate Eq. 21 and apply the initial condition, Eq. 16 to obtain the final solution of a dimensionless pseudo-static flow front advancement, l*(t*):

$$l^{*} (t^{*}) = L_{0}^{*} {\left( {2\exp {\left[ {32Re\, G_{{\rm A}} \overline{V}^{2} \omega^{*2} {\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda _{{mn,{\rm static}}} m^{2} n^{2} \pi^{4} }}} }} }t^{*} } \right]} - 1} \right)}.$$
(22)

Equation 22 shows that the filled region of microchannel exponentially increases with the time, t*, and Re G A times \(\bar{V}^{2} \omega^{*2} \) and also with the inverse summation of C 2A (in λ mn,static) appearing in an exponent. The flow front is thus strongly affected by Re G A, \(\bar{V}^{2} \omega^{*2}\) and C 2A . The flow front is also found to be just proportional to L 0*, the entrance location of the microchannel.

Substitution of Eq. 22 to Eq. 19 gives the final solution of the dimensionless pseudo-static velocity profile inside the rectangular microchannel:

$$\begin{aligned} w^{*} (x^{*}, y^{*}, t^{*}) &= 16 Re\,G_{{\rm A}} \overline{V}^{2} \omega^{*2} L_{0}^{*} {\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda_{{mn,{\rm static}}} mn\pi^{2} }}\sin m\pi x^{*} \sin n\pi y^{*} } }} } \\ & \quad \times \exp {\left[ {32Re\,G_{{\rm A}} \overline{V}^{2} \omega^{*2} {\sum\limits_{m^{\prime} = 1,3,5, \ldots }^\infty {{\sum\limits_{n^{\prime} = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda _{{m^{\prime}n^{\prime},{\rm static}}} m^{\prime 2} n^{\prime 2} \pi^{4} }}} }} }t^{*} } \right]}. \\ \end{aligned}$$
(23)

It is interesting to mention that the maximum velocity of the pseudo-static flow increases exponentially with the time.

Finally, by substituting Eq. 22 to Eq. 17, one can obtain a final form of the dimensionless pseudo-static pressure distribution inside the rectangular microchannel:

$$\begin{aligned} p^{*} (z^{*}, t^{*}) &= \overline{V}^{2} \omega ^{*2} {\left( {z^{*} - L_{0}^{*} } \right)}\\ & \quad {\left( {z^{*} + L_{0}^{*} - 2L_{0}^{*} \times\exp {\left[ {32Re\,G_{{\rm A}} \overline{V}^{2} \omega^{*2} {\sum\limits_{m = 1,3,5, \ldots}^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda _{{mn,{\rm static}}} m^{2} n^{2} \pi^{4} }}} }} }t^{*} } \right]}} \right)}.\\ \end{aligned}$$
(24)

In summary, for given fluid properties, geometry of rectangular microchannel and processing conditions (i.e., rotational speed), one can determine the pseudo-static filling flow characteristics: filling flow front advancement, velocity profile and pressure distribution as the filling flow proceeds from Eqs. 22, 23 and 24, respectively.

4.3 Exact solution

In this section, we just present the exact solution to the coupled differential Eqs. 13 and 15. One may refer to Appendix 1 for the detailed derivation of l*(t*) and w*(x*, y*, t*).

The exact solution of the dimensionless filling flow front advancement into the rectangular microchannel is found to be

$$l^{*} (t^{*}) = L_{0}^{*} {\left[ {2\hbox{e}^{{Dt^{*} }} - 1} \right]},$$
(25)

indicating that the filled region of microchannel exponentially increases with the time as in the case of the pseudo-static approximation. The exponential growth rate is denoted by the exponent D which can be determined from the following nonlinear equation

$$D = 32Re\,G_{{\rm A}} \overline{V}^{2} \omega^{*2} {\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots}^\infty {\frac{1}{{\lambda_{{mn}} m^{2} n^{2} \pi^{4} }}} }} },$$
(26)

where the eigenvalues of the exact flow, λ mn are

$$\lambda_{{mn}} = Re\,G_{{\rm A}} D + C_{{\rm A}}^{2} m^{2} \pi ^{2} + n^{2} \pi^{2},\quad \hbox{for}\; m = 1, 3, 5, \ldots \; \hbox{and} \; n = 1, 3, 5,\ldots.$$
(27)

It should be noted that the exponent D, in this study, is the most important parameter to govern the centrifugal force driven transient filling flow into the rectangular microchannel as discussed like in Kim and Kwon (2006). D represents an inverse of a characteristic time indicating how fast the filling flow front into the rectangular microchannel advances: the higher D is, the faster flow front advances. Comparison between Eqs. 22 and 25 leads to the definition of D static, exponential growth rate for the pseudo-static case as

$$D_{{{\rm static}}} = 32Re\,G_{{\rm A}} \overline{V}^{2} \omega ^{*2} {\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda_{{mn,{\rm static}}} m^{2} n^{2} \pi^{4} }}} }} },$$
(28)

where λ mn,static are expressed in Eq. 20.

The exact dimensionless velocity profile inside the rectangular microchannel was also obtained as

$$w^{*} (x^{*}, y^{*}, t^{*}) = 16Re\,G_{{\rm A}} \overline{V} ^{2} \omega^{*2} L_{0}^{*} {\left[ {{\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda _{{mn}} mn\pi^{2} }}\sin m\pi x^{*} \sin n\pi y^{*} } }} }} \right]}\hbox{e}^{{Dt^{*} }}.$$
(29)

It is noted that the velocity profile of the exact case deviates from the pseudo-static approximation case due to the difference of eigenvalues, λ mn . But the maximum velocity of the exact solution also increases exponentially with the time like the pseudo-static one. Furthermore, the dimensionless average velocity, W avg*(t*) can be obtained from Eqs. 15 and 25:

$$W_{{\rm avg}}^{*} (t^{*}) = \frac{{\hbox{d}l^{*} (t^{*})}}{{\hbox{d}t^{*} }} = 2DL_{0} ^{*} \hbox{e}^{{Dt^{*}}}.$$
(30)

Finally, the exact dimensionless pressure distribution inside the rectangular microchannel can be expressed as

$$p^{*} (z^{*}, t^{*}) = \bar{V}^{2} \omega^{*2} {\left( {z^{*} - L_{0}^{*} } \right)} {\left[ {z^{*} + L_{0}^{*} - 2L_{0}^{*} \hbox{e}^{{Dt^{*} }} } \right]}.$$
(31)

In summary, for the given fluid properties, geometry of microchannel and processing conditions, one can calculate the exponent D via Eqs. 26 and 27 and then determine the exact filling flow front advancement, velocity profile and pressure distribution as a function of time from Eqs. 25, 29 and 31, respectively.

Meanwhile, one can be easily aware that asymptotic λ mn of Eq. 27 as Re G A → 0 is reduced to λ mn,static of Eq. 20 and therefore, asymptotic behaviors of the exact solutions (Eqs. 26, 25, 29, 31) as Re G A → 0 are reduced to those of the pseudo-static case (Eqs. 28, 22, 23, 24, respectively) while maintaining \(Re\,G_{{\rm A}} \bar{V}^{2} \omega^{*2} \sim O(1),\) as they should.

Finally, for the sake of readers’ convenience, we also summarized important results of analytic solutions in a dimensional form in Appendix 2 since it is sometimes easier to understand the flow behavior if equations are expressed in a dimensional form rather than in a dimensionless form.

5 Analysis results and discussion

5.1 Parametric study for exponent D

As discussed above, the exponential growth rate, exponent D is the most important governing parameter in this transient flow, representing how fast the front of filling flow advances into the rectangular microchannel. In this regard, we will discuss the parametric study of D in this section.

As shown in Eqs. 20 and 26, 27, 28, D is determined by three sets of dimensionless parameters, Re G A, \(\overline{V} \omega^{*} \) and C A, which are associated with fluid properties, geometric data and processing conditions. Therefore, once \(Re\,G_{{\rm A}}, \overline{V} \omega ^{*} \) and C A are determined from the information on a sample fluid, rectangular microchannel geometry and processing conditions, it is rather straightforward to determine D by solving the nonlinear Eqs. 20 and 26, 27, 28. For the parametric study, we extensively carried out computations of D for various combinations of \(Re\,G_{{\rm A}}, \overline{V}\omega^{*}\) and C A.

Figure 3 shows the calculated D for both pseudo-static (curves) and exact (symbols) cases as a function of Re G A (Fig. 3a, b), \(\overline{V} \omega^{*} \) (Fig. 3c, d) and C A (Fig. 3e, f). Since D static for the pseudo-static case is proportional to Re G A and square of \(\overline{V} \omega^{*} \) as expressed in Eq. 28, D static varies linearly for Re G A and \(\overline{V} \omega^{*} \) in logarithmic scale, which are represented as linear lines in all Fig. 3a–d. It might be mentioned that the gap between adjacent linear curves of Fig. 3a (one order change of \(\overline{V} \omega^{*}\)) is wider than that of Fig. 3c (one order change of Re G A) due to the square proportionality of D to \(\overline{V} \omega^{*}.\) Since D for the exact case asymptotically behaves like the pseudo-static D static under the condition of \(Re\,G_{{\rm A}} \ll 1,\) the calculated D lies on the lines of D static as shown in Fig.  3a–c, e while \(Re\,G_{{\rm A}} \ll 1\) even at high \(\overline{V} \omega^{*},\) as expected. But, as Re G A increases, D becomes smaller than D static, which implies that the flow advancement in the exact solution is not as fast as the pseudo-static approximation case. This deviation is due to the inertia force effect (the first term in Eq. 13) which tends to restrain fluid mass from accelerating rapidly. As Re G A increases further, D deviates more and more from the curves of D static.

Fig. 3
figure 3

The calculated exponent D as a function of a Re G A when C A = 0.2, b Re G A when \(\overline{V} \omega^{*} =1,\) c \(\overline{V} \omega^{*} \) when C A = 0.2, d \(\overline{V} \omega ^{*} \) when Re G A = 1, e C A when \(\overline{V} \omega^{*} =1,\) and f C A when Re G A = 1 (symbols from exact D, and curves from pseudo-static D static)

Full size image

From Fig. 3e, f, one can observe the effect of C A on the D: (1) D decreases as C A increases, and (2) the exact D deviates more from the curves of the pseudo-static D static as C A decreases when Re G A is large enough. These trends can be explained as follows. (1) Mathematically, D is proportional to inverse summation of λ mn and λ mn is proportional to C 2A as explicitly expressed in Eqs. 20 and 26, 27, 28. In physical sense, a large C A means a large characteristic length (the height of the channel in this case). For a given Re G A, the large characteristic length results in the small characteristic velocity so as to maintain the same Re G A. Therefore, D decreases as C A increases. And it might be mentioned that for the region of the small C A, the flow inside the microchannel acts as a two-dimensional plane flow so that the variation of D in response to the change of C A becomes small. But, for the region of C A > 0.1, one can expect the three-dimensional flow inside the microchannel and therefore, D drastically decreases in the response to the small change of C A compared with the behavior at the region of small C A. (2) When C A decreases, the characteristic velocity increases and also the inertia force effect increases. As discussed above, the larger inertia force is, the larger deviation of D from D static becomes. Therefore, D deviates more from D static as C A decreases.

5.2 Parametric study for flow behavior

In order to provide a physical insight into the centrifugal microfluidic system in this study, we extensively performed parametric studies on the flow behavior in terms of the flow front advancement, the velocity profile and the pressure distribution as functions of the time and various combinations of Re G A, \(\overline{V} \omega^{*} \) and C A.

5.2.1 Filling flow front advancement

Figure 4 shows the effects of Re G A (Fig. 4a), \(\overline{V} \omega^{*} \) (Fig. 4b) and C A (Fig. 4c) on the behavior of the dimensionless filling flow front advancement, l*(t*), with respect to the dimensionless time, t*, for both the pseudo-static (dotted curves) and exact (solid curves) cases. For the case of Fig.  4a, various values of Re G A are chosen: 0.01, 0.1, 0.4, 0.8, 1, 2, 4 and 10 when \(L_{0}^{*}=1, \overline{V} \omega^{*} =1\) and C A = 0.2. D static corresponding to those values of Re G A are found to be 0.000364146, 0.00364146, 0.0145658, 0.0291317, 0.0364146, 0.0728292, 0.145658 and 0.364146, respectively, from Eqs. 28 and 20, and D corresponding to them are 0.000364146, 0.00364134, 0.014558, 0.0290691, 0.0362926, 0.0718729, 0.138558 and 0.28792, respectively (Eqs. 26, 27). For the case of Fig. 4b, we vary the values of \(\overline{V} \omega^{*}\) as 0.1, 0.4, 0.8, 1, 2, 4 and 10 while maintaining L 0* = 1, Re G A = 1 and C A = 0.2. The values of D static corresponding to these \(\overline{V} \omega^{*}\prime{\rm s} \) become 0.000364146, 0.00582634, 0.0233053, 0.0364146, 0.145658, 0.582634 and 3.64146, respectively, and D are 0.000364134, 0.0058232, 0.0232553, 0.0362926, 0.143746, 0.554232 and 2.8792, respectively. In Fig. 4c, C A varies as 0.01, 0.1, 0.6, 1, 2, 6 and 10 when L 0* = 1, Re G A = 1 and \(\overline{V} \omega^{*} =1.\) The corresponding calculated D static are 0.0414041, 0.0390406, 0.0260765, 0.0175721, 0.0071463, 0.00103583 and 0.000390406, respectively, and D are 0.0412345, 0.0388946, 0.0260284, 0.0175572, 0.00714532, 0.00103583 and 0.000390406, respectively.

Fig. 4
figure 4

Filling flow front advancements into the rectangular microchannel for both cases of the pseudo-static (dotted curves) and exact (solid curves) solutions with respect to the variation of the time: a effect of Re G A when \(\overline{V} \omega^{*}=1, C_{{\rm A}}=0.2\) and L 0* = 1, b effect of \(\overline{V} \omega^{*} \) when Re G A = 1, C A = 0.2 and L 0* = 1, and c effect of C A when \(Re\,G_{{\rm A}}=1, \overline{V} \omega^{*} =1\) and L 0* = 1

Full size image

It is noted that l*(t*) shows, in the logarithmic scale of the ordinate, a nonlinear behavior near t* = 0 due to the term −1 inside the bracket of Eqs. 22 and 25, as plotted in all Fig. 4a–c. However, as t* is sufficiently large, the term, −1 becomes negligible in comparison with the exponential term of\(2\hbox{e}^{{Dt^{*} }}, \) and therefore l*(t*) shows a linear behavior in the logarithmic scale of the ordinate. It might also be noted that the curves of pseudo-static and exact l*(t*) almost coincide with each other at small Re G A and \(\overline{V} \omega^{*} \) (Fig. 4a, b) and at large C A (Fig. 4c) since the values of D static and D are almost the same at those values.

As clearly shown in Fig. 4a, b, the behavior of l*(t*) is more sensitively affected by the change of \(\overline{V} \omega^{*}\) than Re G A due to the fact that the exponent D is proportional to the square of \(\overline{V} \omega^{*} \) while it is linearly proportional to Re G A. Meanwhile, as Re G A increases, the deviation between the pseudo-static and exact cases gets larger as indicated in Fig. 4a, due to the inertia force effect as discussed earlier. On the other hand, Fig. 4b shows a very small deviation between the pseudo-static and exact cases due to a relatively small Re G A (in this case, Re G A = 1). For Fig. 4c, one can find that the rate of l*(t*) decreases as C A increases due to the inverse proportionality of D to C A and, as well, the relative decrease of the characteristic velocity for increasing C A when the other conditions are kept the same, as discussed above.

5.2.2 Velocity profile

Plotted in Fig. 5 are typical behaviors of dimensionless velocity profile, w*(x*, y*, t*), with respect to t* (a–c), Re G A (d, e), \(\overline{V} \omega^{*} \) (f, g) and C A (h, i) for both cases of pseudo-static (dotted curves) and exact (solid curves) solutions. Figure 5a shows a typical three-dimensional transient velocity profile in one quarter of the rectangular microchannel when \(Re\,G_{{\rm A}}=10, \bar{V}\omega^{*} =0.2\) and C A = 0.2 with L 0* = 1 at t* = 80 (the corresponding D = 0.0143746). Figure 5b, c shows the typical cross-sectional velocity profile development according to the increase of the time (in this case t* = 20, 40, 60, 80 and 100) for a specific case of \(Re\,G_{{\rm A}}=10, \overline{V} \omega^{*} = 0.2\) and C A = 0.2 with L 0* = 1. The corresponding D static and D are 0.0145658 and 0.0143746, respectively. The maximum value of the velocity exponentially increases with the time as expressed in Eqs. 23 and 29. Since the flow front position gets exponentially away from the center with the time as illustrated in Fig. 4, the induced centrifugal force which is a flow driving force in the system exponentially increases with the time, resulting in the exponential increase of the maximum velocity. It is noted that due to a smaller value of D than D static, the exact velocity profile is getting smaller than the pseudo-static one as time proceeds. In other words, since the inertia force restrains the rapid velocity increase, the real velocity profile development becomes more deviated from the pseudo-static case with the time even at Re G A = 10.

Fig. 5
figure 5figure 5

Velocity profiles, w*(x*, y*, t*): typical three-dimensional transient velocity profile in one quarter of the rectangular microchannel when \(Re\,G_{{\rm A}}=10, \bar {V}\omega^{*} =0.2\) and C A = 0.2 at t* = 80 (a), the change of cross-sectional velocity profile inside the rectangular microchannel with respect to the variation of t* when \(Re\,G_{{\rm A}}=10, \bar {V}\omega^{*} =0.2\) and C A = 0.2 at y* = 0.5 (b) and at x* = 0.5 (c), effect of Re G A when \( \bar {V}\omega^{*} =1, C_{{\rm A}}=0.2\) and t* = 5 on velocity at y* = 0.5 (d) and at x* = 0.5 (e), effect of \( \bar {V}\omega^{*} \) when Re G A = 1, C A = 0.2 and t* = 5 on velocity at y* = 0.5 (f) and at x* = 0.5 (g), and effect of C A when \(Re\,G_{{\rm A}}=1, \bar {V}\omega^{*} =1\) and t* = 5 on velocity at y* = 0.5 (h) and at x* = 0.5 (i) (solid curves exact velocity, dotted curves pseudo-static velocity). L 0* = 1 for all the cases

Full size image

The variations of cross-sectional velocity profile in response to Re G A,\(\overline{V} \omega^{*} \) and C A are shown in Fig.  5d–i, respectively, at the same instant time, t* = 5 when L 0* = 1 . In Fig. 5d, e, Re G A varies as 1, 2, 4, 6 and 8 when \(\overline{V} \omega^{*} =1\) and C A = 0.2. The corresponding calculated D static are 0.0364146, 0.0728292, 0.145658, 0.218488 and 0.291317, respectively, and D are 0.0362926, 0.0718729, 0.138558, 0.196993 and 0.246519, respectively. For the case of Fig. 5f, g, \(\overline{V} \omega^{*} \) varies as 0.6, 0.8, 1, 2 and 4 when Re G A = 1 and C A = 0.2. The corresponding D static are calculated as 0.0131093, 0.0233053, 0.0364146, 0.145658 and 0.582634, respectively, and D are 0.0130934, 0.0232553, 0.0362926, 0.143746 and 0.554232, respectively. In Fig. 5h, i, C A varies 0.1, 0.4, 0.8, 1, 2, 4 and 6 when Re G A = 1 and \(\overline{V} \omega^{*}=1.\) The corresponding D static are 0.0390406, 0.0311706, 0.0214666, 0.0175721, 0.0071463, 0.00219385 and 0.00103583, respectively, and D are 0.0388946, 0.0310906, 0.0214394, 0.0175572, 0.00714532, 0.00219382 and 0.00103583, respectively. Due to the dependency of the exponent D on the square of \(\overline{V} \omega^{*},\) the velocity profile is more sensitively affected by the change of \(\overline{V} \omega^{*} \) (Fig. 5f, g) than Re G A (Fig. 5d, e). However, it is noted that the higher Re G A is, the more deviation between the pseudo-static and exact cases is, which is the same trend as l*(t*), due to the inertia force effect restraining a rapid velocity increase. And also, the maximum velocity decreases as C A increases due to the inverse proportionality of D to C A as shown in Fig. 5h, i like the behavior of l*(t*). It might be mentioned that Fig.  5d, e, and f, g plot the velocity profiles only in the vicinity of the wall for the case of Re G A = 8 and \(\overline{V} \omega^{*} =4,\) respectively, since the velocity magnitude in the other region exceeds the given ranges of the ordinate.

5.2.3 Pressure distribution

Plotted in Fig. 6 are typical pressure distributions with respect to (a) t*, (b) Re G A, (c) \(\overline{V} \omega^{*} \) and (d) C A for both cases of pseudo-static (dotted curves) and exact (solid curves) solutions. Figure 6a shows the typical development of the pressure distribution as time increases (in this case t* = 20, 40, 60, 80 and 100) for a specific case of \(Re\,G_{{\rm A}}=10, \overline{V} \omega ^{*} =0.2\) and C A = 0.2 with L 0* = 1. The corresponding D static and D are calculated as 0.0145658 and 0.0143746, respectively. As expected from Eq. 17, both the pseudo-static and exact pressure distributions show parabolic shapes and negative value of pressure over the microchannel. The first zero pressure of one fixed end point of the parabola represents the starting position, i.e., the reservoir, L 0*, (in this case, L 0* = 1), and the second zero pressure of the other moving end point corresponds to the advancing position of flow front, l*(t*), at the indicated time, t*. Due to the difference of D static and D, the positions of the second zero pressure point at the same instant time deviate more and more from each other as time proceeds. The filled portion of a microchannel could be divided to two distinctive regions: (1) the left half region from the starting point (the reservoir) to the center (the center of filled region inside the microchannel at the indicated time) having a negative pressure gradient; and (2) the right half region from the center to the other second end point (the position of the filling flow front) showing a positive pressure gradient. At the center of the filled channel, i.e., between the two regions, the pressure gradient is zero. These trends can be explained by the force balance among the centrifugal force, pressure gradient and shear stress based on the assumptions in this study. It might be reminded that the velocity component, w, is a function of x and y only (not z) at any instant time, thus the shear stress becomes a function of x and y only at an instant time, thus remaining the same over the entire filled region of the microchannel. The centrifugal force linearly increases with the radial location of the CD plate. In response to the increasing centrifugal force with the radial direction, the pressure is developed to maintain the same shear force throughout the filled region inside the microchannel as follows. A small centrifugal force in the left half region needs a negative pressure gradient (a favorable pressure gradient to the flow), while a positive pressure gradient (an adverse pressure gradient to the flow) should compensate for a large centrifugal force in the right half region, in order to match exactly the average centrifugal force (with zero pressure gradient) at the center. This is how a parabolic and negative pressure distribution is built up along the downchannel direction of the microchannel.

Fig. 6
figure 6

The change of pressure distribution for both cases of pseudo-static (dotted curves) and exact (solid curves) solutions with respect to the variation of a t* when \(Re\,G_{{\rm A}}=10, \bar {V}\omega ^{*} =0.2\) and C A = 0.2, b Re G A when \( \bar {V}\omega^{*} =1\) and C A = 0.2 at t* = 5, c \(\overline{V} \omega^{*} \) when Re G A = 1 and C A = 0.2 at t* = 5, and d C A when Re G A = 1 and \( \bar {V}\omega^{*} =1\) at t* = 5. L 0* = 1 for all the cases

Full size image

Figure 6b–d shows the pressure distributions with regard to the change of\(Re\,G_{{\rm A}}, \overline{V} \omega^{*} \) and C A, respectively, at the same instant time, t* = 5 when L 0* = 1. For the case of Fig. 6b, Re G A varies as 1, 2, 4, 6 and 8 when \(\overline{V} \omega^{*} =1\) and C A = 0.2. The corresponding D static are 0.0364146, 0.0728292, 0.145658, 0.218488 and 0.291317, respectively, and D are 0.0362926, 0.0718729, 0.138558, 0.196993 and 0.246519, respectively. In Fig. 6c, \(\overline{V} \omega^{*} \) varies as 0.6, 0.8, 1 and 2 when Re G A = 1 and C A = 0.2. The corresponding D static are calculated as 0.0131093, 0.0233053, 0.0364146 and 0.145658, respectively, and D are 0.0130934, 0.0232553, 0.0362926 and 0.143746, respectively. In Fig. 6d, C A varies 0.1, 0.4, 0.8, 1 and 2 when Re G A = 1 and \(\overline{V} \omega^{*} =1.\) The corresponding D static are 0.0390406, 0.0311706, 0.0214666, 0.0175721 and 0.0071463, respectively, and D are 0.0388946, 0.0310906, 0.0214394, 0.0175572 and 0.00714532, respectively. Like the change of velocity profile, the pressure distribution is more sensitively influenced by the change of \(\overline{V} \omega^{*}\) (Fig. 6c) than Re G A (Fig. 6b). And the higher Re G A is, the more deviation one can observe between the pseudo-static and exact pressure distributions as explained above. And also, the second zero pressure point (the position of the flow front) decreases as C A increases which is the same trend of l*(t*) as shown in Fig.  6d. It might be mentioned that the pressure distributions for the cases of Re G A = 8 and \(\overline{V} \omega^{*} =2\) are plotted only near the two ends of the filled channel within the given ranges of the ordinate in Fig. 6b, c, respectively.

Finally, we want to comment on the limitations and potentials of the modeling and analysis developed in this study with respect to applications. First, we neglected the Coriolis force in obtaining the analytic solutions of this transient filling flow problem. This assumption is valid under the relatively low rotational speed, e.g., below the order of 1,000 rpm with a typical microchannel size of the order of 100 μm (Kim and Kwon 2006). The analytic solutions presented in this study may not be accurate at a very high rotational speed. However, the analytic solutions still enable us to get a physical insight into the centrifugal force driven fluid flow and help us design such a microchannel system for a wide range of a rotational speed. One may refer to Kim and Kwon (2006) for the detailed magnitude analysis for the centrifugal force and the Coriolis force. Second, we neglected surface tension effect at the boundary of the flow front. As discussed before, if one applies a plastic substrate of which the contact angle of a sample liquid is nearly 90°, the assumption is valid. When the surface tension plays an essential role in the hydrophilic/phobic fluidic control, incorporating the surface tension effect into the analytical approach might become important. In this regard, we are currently investigating the effect of surface tension in the context of the present model problem, which will be the subject of a separate paper in the future.

6 Design application examples

As already described above, one of the principal objectives of this work is to provide a simple analytical design tool at the first design step. In this regard, we present two different application examples as typical design problems in which the width (or height) of a microchannel or the processing condition of rotational speed is determined so as to meet the design requirements by means of the results of modeling and analysis performed in this study.

Suppose a microfluidic designer wants to deliver a sample fluid from the reservoir location, L 0, to the desired radial downchannel location, L d, at a desired time, t d. There are two possible design cases: (1) case I, where one has to design the width (or height) of a microchannel for a new microfluidic system to be fabricated with a specific rotational speed of a disc driving system already fixed, and (2) case II, where one has to determine a rotational speed of a disc with a given microchannel geometry (width and height) in an existing microfluidic system fabricated already.

To meet the design requirement, one can use the following design equations in sequence. The first design equation can be obtained by rearranging Eq. 57 in Appendix 2 as follows

$$ \hbox{Design equation I}: \quad D = \frac{1}{{t_{{\rm d}} }}\ln {\left[ {\frac{1}{2}{\left( {\frac{{L_{{\rm d}} }}{{L_{0} }} + 1} \right)}} \right]},$$
(32)

which is to determine a dimensional value of D for the given values of L 0, L d and t d. And the second design equation can be obtained by combining Eqs. 60 and 61 in Appendix 2 as below:

$$\hbox{Design equation II}: \quad D = \frac{{32\rho \omega^{2} }}{\mu }{\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{(D\rho / \mu) + {\left[ {{\left( {{{m\pi }}/{W}} \right)}^{2} + {\left( {{{n\pi }}/{H}} \right)}^{2} } \right]}m^{2} n^{2} \pi^{4} }}} }} },$$
(33)

from which the width, W (or height H), or the rotational speed, ω, is subsequently determined for given conditions with the calculated D.

As a specific design example, let the sample fluid properties and design requirements be as follows:

  • Fluid properties: ρ = 103 kg m−3 and μ = 10−3 Pa s, which are the same order as those of water.

  • Position of reservoir (i.e., entrance location of microchannel): L 0 = 5 mm.

  • Design requirements: L d = 40 mm and t d = 2 s.

Therefore, for the given values of L 0, L d and t d, D is determined as D = 0.752 s−1 from Design equation I, Eq. 32. Then, depending on the design case, one can determine the other parameter as below.

6.1 Case I: determination of W or H for a given rotational speed, ω

Suppose that a designer wants to deliver the sample to the desired radial position on a CD plate which is rotated with a specific rotational speed, ω. This problem is typically encountered at the design step.

Let the CD be rotated with ω = 60 rad s−1 ≈ 573 rpm. (1) If the height, H, is given to be 80 μm, the corresponding width can be determined via Design equation II, Eq. 33 as W = 233 μm. (2) In contrast, if the width, W, is given to be 400 μm, the corresponding height can be calculated as H = 75.4 μm from Design equation II. The corresponding hydraulic radii of the designed microchannels of (1) and (2) (R h = WH/(W + H) for the case of the rectangular channel) are 59.6 and 63.4 μm, respectively. It should be noted that the required hydraulic radius of circular microchannel becomes the similar value of 57.8 μm to achieve the design requirements with the same condition in this case, which is calculated based on the design equations for the circular microchannel derived in Kim and Kwon (2006). This result shows that one can determine the geometry of rectangular microchannel roughly with the design equations in Kim and Kwon (2006) based on the definition of hydraulic radius, but the present analysis enables us to determine the geometry of rectangular microchannel more precisely.

6.2 Case II: determination of ω for given width, W, and height, H, of a microchannel

The cross-sectional area of microchannel may be given already in an existing microfluidic system or may be first assigned in the design step of a new system especially when the sample volume to be delivered is specifically given. The sample fluid can be delivered to the desired radial position at a desired time by adjusting the rotational speed. This problem is typically encountered at the experimental step.

If the width and height of a microchannel on the CD plate are assigned to (or given by) W = 250 μm and H = 100 μm (C A=0.4), the corresponding rotational speed can be determined as ω ≈ 49.1 rad s−1 ≈ 469 rpm from Design equation II.

As illustrated through cases I and II, a microfluidic designer can determine the width (or height) of a microchannel or the rotational speed for given experimental conditions and design requirements by means of Design equations I and II (Eqs. 32, 33).

7 Conclusion

In this paper, we have developed the physical modeling and carried out the analysis for the transient filling flow into a rectangular microchannel driven by centrifugal force. By means of the modeling and analysis, we have successfully provided not only a physical insight into such a rectangular microchannel flow but also a simple design tool.

The governing equations for the filling flow were developed from the fundamental force balance (among viscous force, inertia force and centrifugal force) for an infinitesimal control volume in the rectangular microchannel together with the continuity equation. With the developed physical modeling in a dimensionless form, first, a pseudo-static approximate solution was derived for the case when the inertia force is negligible, and secondly, an exact analytic solution was derived with the inertia force effect taken into account.

The analytical results showed that the filled region into the rectangular microchannel exponentially increases with the time for the centrifugal force driven filling flow. The transient flow behavior is very sensitively affected by three dimensionless parameters of Re G A (related with the inertia force effect), \(\overline{V} \omega^{*} \) (associated with the centrifugal force effect) and C A (effect of the cross-sectional geometry of the rectangular channel) which are combinations of fluid properties, microchannel geometries and processing condition of the rotational speed.

The exponential growth rate, exponent D which represents an inverse of a characteristic time for flow front advancement, i.e., indicating how fast the microchannel is filled, is found to be the most important parameter in this study. The parametric study on D showed that the filling flow behavior is more sensitively influenced by the change of \(\overline{V} \omega^{*} \) than Re G A since D is proportional to the square of \(\overline{V} \omega^{*} \) and linearly proportional to Re G A. And, as Re G A increases, the inertia force effect becomes more important in the system, resulting in the increase of the deviation between the pseudo-static approximation solution and exact one since the inertia force effect tends to restrain flow velocity from a rapid acceleration. The parametric study also showed that if C A decreases, the relative characteristic velocity increases for a given Re G A, resulting in an increase of D and, as well, the more deviation between D and D static when Re G A is large enough.

The parametric studies on filling flow front advancement, l*(t*), velocity profile, w*(x*, y*, t*), and pressure distribution, p*(z*, t*), were also carried out to understand the flow behavior. All l*(t*), w*(x*, y*, t*) and p*(z*, t*) are more sensitively affected by the change of \(\overline{V} \omega^{*} \) than Re G A as expected from the behavior of D. It is also expected that the higher Re G A induces the larger deviation between the pseudo-static and exact solutions for all three flow characteristic variables. It is noted that the maximum velocity increases with the time. And, the pressure is negative and has a parabolic distribution along the downchannel direction for both pseudo-static and exact cases so as to maintain the force balance in the filled region of a microchannel.

With regard to the design tool for the system, two design equations have been proposed and two types of design application examples are demonstrated successfully. By means of two design equations, a microfluidic designer can easily determine the width (or height) of a microchannel or the rotational speed to meet the design requirements for given conditions.

As a final remark, this study might become a platform for the analytic approaches not only for an arbitrary channel path but also for a complex microchannel network system in which the fluid flow is driven by centrifugal force.