1 Introduction

Air damping cannot be ignored in micro-electro-mechanical systems (MEMS) devices due to its lager surface area to volume ratio of the moving parts (Bao 2005), and it is a significant factor of the dynamic characteristics because it affects the amplitude, phase and response time. For a torsion mirror, the dynamic performance is especially important since it determines the devices performance directly. It must be taken into consideration when designing and optimizing the MEMS torsion mirror. According to the movement direction of plate, air damping can be classified into slide-film damping and squeeze-film damping, and the torsion mirror is governed by squeeze-film damping.

As the MEMS torsion mirror has been widely used in barcode reader, micro-projector, medical examination, spectrometers and so on (Yalcinkaya et al. 2007; Sprague et al. 2005; Sakai et al. 2011; Chen et al. 2013), the research of squeeze-film air damping in MEMS torsion mirror is very meaningful. Pan et al. (1998) found the expression of damping torque for a rectangular torsion mirror in the Fourier series solution and in the double sine series solution under the assumption of small displacements. Hao et al. (2002) solved the Reynolds equation which was linearized for the analytical formula describing the air-damping effect with Green’s function method. Chang et al. (2002) proposed an analytical solution that is obtained from the linearized modified molecular gas film lubrication (MMGL) equation. Minikes et al. (2005) presented a squeeze-film model with artificial viscosity and the molecular dynamics model are adapted for the case of a torsion mirror under a wide range of vacuum levels. Bao et al. (2006) simplified the nonlinear Reynolds equation and deduced the expression of damping torque by solving the equation. Veijola (2007) presented simple but accurate compact models for the squeeze-film damping of rectangular mirror. Pandey et al. simulated the effect of squeeze-film damping by progressively refining the model for the boundary conditions to show how the numerically computed results get close to the experimental value (2007) and presented a squeeze-film damping model in a double-gimballed torsional mirror with two conditions—a large air gap to plate length ratio and complicated boundary conditions (2008). Li (2008) analyzed effects of gas rarefaction and surface roughness of squeeze-film damping by using the linearized average Reynolds type equation. Li and Fang used molecular dynamics method (2010a) and wavelet interpolation Galerkin method (2010b) for the numerical simulation of torsion mirror under the effect of squeeze-film damping, respectively. Leung et al. (2011) validated the modified Reynolds equation method for the prediction of low-pressure squeeze-film damping compared with Monte Carlo simulation method. Moeenfard et al. used the extended Kantorovich method to analytically solve the problem of squeezed-film damping of micro-mirrors (2011), and in (2012), they extended Bao’s model to analytically solve the problem of squeeze-film damping in micro-mirrors considering the bending of torsion beams. Pantano et al. (2012) proposed a numerical study of both parallel and torsion plates at decreasing pressure by numerically solving a full 3D Navier–Stokes equation and compared different formulations that are solved by both analytical and numerical means to determine which is the most performing (2014). Gugat (2013) presented a transformation that allowed a fast and reliable numerical evaluation of the coefficient of damping torque for torsion mirrors. Famileh et al. (2015) solved the governing equations of squeeze-film damping numerically by the entropy generation analysis. But all of them focused on rectangular torsion mirrors, and expressions of squeeze-film damping torque of circular or elliptical torsion mirrors have not been reported.

In order to calculate the damping of circular and elliptical torsion mirrors, the nonlinear Reynolds equation is solved in polar coordinate and elliptical coordinate. First, it is solved in polar coordinate, and the expression of damping torque of circular torsion mirror is given in Sect. 2. Then, in Sect. 3, it is solved in elliptical coordinate when rotation axis is minor axis and major axis, followed by the expression of damping torque of elliptical torsion mirror. Section 4 presents the numerical simulation of squeeze air damping in comparison with the result of the formula deduced by this paper, and Sect. 5 discusses the applicable condition of the equation. In Sect. 6, conclusions are drawn.

2 Circular torsion mirror

The simplified nonlinear Reynolds equation was deduced by Bao et al. (2006), and the equation is:

$$\frac{{{\partial ^2}p}}{{\partial {x^2}}} + \frac{{{\partial ^2}p}}{{\partial {y^2}}} = - \frac{{12\mu }}{{{(h-\varphi x)^3}}}\frac{{\partial \varphi }}{{\partial t}}x$$
(1)

where p is a deviatory pressure caused by the squeeze-film air damping, \(\mu\) the viscosity, h the height between mirror and bottom, \(\varphi\) the torsion angle. And this equation is established under the condition:

$$\phi \ll \frac{4 \mu a_{{\rm m}}^2}{h^2 p_{{{{\rm max}}}}}\frac{{\partial \phi }}{{\partial t}}$$
(2)

where \(\phi =\varphi a_{{\rm m}} h^{-1}, a_{{\rm m}}\) is half length of the mirror and \(\phi\) normalized angle. The right part of Eq. (1) can be expanded into a Taylor series, and this is the basic equation of this paper:

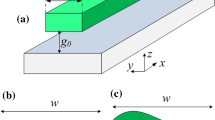
$$\frac{{{\partial ^2}p}}{{\partial {x^2}}} + \frac{{{\partial ^2}p}}{{\partial {y^2}}} = - \sum _{n=1}^{\infty }\frac{{6\mu n(n+1) }}{{{h^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}\varphi ^{n-1}x^n$$
(3)

The schematic diagram of circular torsion mirror is shown in Fig. 1a. The boundary condition of basic equation in this situation is \(p(x,y)|_{x^2+y^2=r_0^2}=0\), where \(r_0\) is radius of the mirror. It is much easier to solve it in polar coordinate than in Cartesian coordinate. The boundary condition in polar coordinate is \(p(r=r_0)=0\) ,and the basic equation is:

$$\begin{aligned}& \frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{{{\partial }p}}{{\partial {r}}} \right)+ \frac{1}{r^2}\frac{{{\partial ^2}p}}{{\partial {\theta ^2}}} \nonumber \\ &\quad= -\, \sum _{n=1}^{\infty }\frac{{6\mu n(n+1) }}{{{h^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}\varphi ^{n-1}(r \cos \theta )^n \end{aligned}$$
(4)
Fig. 1
figure 1

The schematic diagram of circular and elliptical torsion mirror. a Circular torsion mirror, b elliptical torsion mirror with torsion axis in minor axis, c elliptical torsion mirror with torsion axis in major axis and d cross section of torsion mirror

Full size image

Equation (4) can be solved by the method of eigenfunction expansions (Asmar 2005). The eigenfunction of this equation is (Liang et al. 2010):

$$p=r^m(C_{{\rm m}} \cos m \theta + D_{{\rm m}} \sin m\theta)$$
(5)

With the method of eigenfunction expansions, p can be assumed as:

$$p=\sum _{l=0}^{\infty }\sum _{k=0}^{\infty }r^l(C_{lk} \cos k\theta +D_{lk} \sin k\theta )$$
(6)

According to the characteristic of trigonometric functions, \(\cos ^n \theta\) can be expanded to:

$$\cos ^n \theta =\left\{ \begin{array}{ll} \frac{1}{2^{n-1}}\sum \nolimits_{{{{\rm odd}}}\, k}^{n} {{{\rm C}}}_{n}^{\frac{n-k}{2}}\cos k \theta &{}\quad n \in {{{\rm odd}}}\\ \frac{1}{2^{n-1}}\sum\nolimits_{{{{\rm even}}}\, k}^{n} {{{\rm C}}}_{n}^{\frac{n-k}{2}}\cos k \theta +\frac{1}{2^{n}}{{{\rm C}}}_{n}^{\frac{n}{2}} &{}\quad n \in {{{\rm even}}}\\ \end{array} \right.$$
(7)

With Eqs. (6) and (7), Eq. (4) can be expanded:

$$\begin{aligned}&\sum _{l=0}^{\infty } \sum _{k=0}^{\infty }(l^2-k^2)r^{l-2}(C_{lk} \cos k\theta + D_{lk} \sin k \theta ) \\&\quad =-\,\sum _{{{{\rm odd}}}\, n}^{\infty }\frac{{6\mu n(n+1) }}{{{2^{n-1}h^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}\varphi ^{n-1}r^n\sum _{{{{\rm odd}}}\, k}^{n}{{{\rm C}}}_{n}^{\frac{n-k}{2}}\cos k\theta \\&\quad \quad -\,\sum _{{{{\rm even}}}\, n}^{\infty }\frac{{6\mu n(n+1) }}{{2^{n-1}h^{n+2}}}\frac{{\partial \varphi }}{{\partial t}}\varphi ^{n-1}r^n \sum _{{{{\rm even}}}\, k}^{n}{{{\rm C}}}_{n}^{\frac{n-k}{2}}\cos k\theta \\&\quad \quad -\,\sum _{{{{\rm even}}}\, n}^{\infty }\frac{{6\mu n(n+1) }}{{{2^nh^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}\varphi ^{n-1}r^n{{{\rm C}}}_{n}^{\frac{n}{2}} \end{aligned}$$
(8)

The coefficients of the variables r and \(\theta\) in both side should equal in Eq. (8), so we have \(l=n+2\), and with boundary condition \(p(r=r_0)=0\), the coefficients are:

$$C_{l0} =-\frac{{{{\rm C}}}_{n}^{\frac{n}{2}}\varphi ^{n-1}}{2^{n}(n+2)^2}\frac{{6\mu n(n+1) }}{{{h^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}$$
(9a)
$$C_{lk} =-\frac{{{{\rm C}}}_{n}^{\frac{n-k}{2}}\varphi ^{n-1}}{2^{n-1}[(n+2)^2-k^2]}\frac{{6\mu n(n+1) }}{{{h^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}$$
(9b)
$$C_{00} =\sum _{{{{\rm even}}}\, n}^{\infty }\frac{{{{\rm C}}}_{n}^{\frac{n}{2}}\varphi ^{n-1}}{2^{n}(n+2)^2}\frac{{6\mu n(n+1) }}{{{h^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}r_0^{n+2}$$
(9c)
$$C_{kk} =\sum _{n=k,k+2\ldots }^{\infty }\frac{{{{\rm C}}}_{n}^{\frac{n-k}{2}}\varphi ^{n-1}}{2^{n-1}[(n+2)^2-k^2]}\frac{{6\mu n(n+1) }}{{{h^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}r_0^{n+2-k}$$
(9d)

where l is even and greater than zero in Eq. (9a). l and k are both odd or both even, and l is greater than k greater than zero in Eq. (9b). In Eq. (9d), k is greater than zero. And in other cases, \(C_{lk}=D_{lk}=0\). So p is:

$$p=\sum _{l=0}^{\infty }\sum _{k=0}^{\infty }C_{lk}r^l \cos k\theta$$
(10)

when torsion angle is small, the Taylor series of Eq. (4) approximates to its first order, and thus, the max value of n is 1. The expression of deviatory pressure p in this situation is shown in Eq. (11), and 3D diagram is shown in Fig. 2.

$$p= \frac{3\mu }{{2h_0^{3}}}\frac{{\partial \varphi }}{{\partial t}}\left( r_0^2 r-r^3 \right) \cos \theta$$
(11)

The damping torque is \(T_{{\rm cir}}=\int p x {\rm d}x {\rm d}y =\int p r \cos \theta r {\rm d}r {\rm d}\theta.\) Because of the orthogonality of trigonometric functions, the result of integration is not zero only when k equals 1. So, we arrive at:

$$\begin{aligned} T_{{\rm cir}}&=\sum _{{{{\rm odd}}}\, n}^{\infty }\int _0^{r_0}\int _0^{2\pi }\frac{{{{\rm C}}}_{n}^{\frac{n-k}{2}}\varphi ^{n-1}}{2^{n-1}[(n+2)^2-k^2]}\\ &\quad\times\,\frac{{6\mu n(n+1) }}{{{h^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}(r_0^{n+1}r-r^{n+2})r^2\cos ^2\theta {\rm d} r {\rm d}\theta \\&=\sum _{{{{\rm odd}}} \, n}^{\infty }\frac{1}{2^{n}}\frac{{3\mu n(n+1) }}{(n+3)(n+5)}{{{\rm C}}}_{n}^{\frac{n-1}{2}}\frac{\pi r_0^{n+5}}{h^{n+2}}\frac{{\partial \varphi }}{{\partial t}}\varphi ^{n-1} \\&= \frac{ \mu \pi r_0^{6}}{8h^{3}}\frac{{\partial \varphi }}{{\partial t}} \sum _{ {{{\rm odd}}} \, n}^{\infty }\frac{24}{2^{n}}\frac{{ n(n+1) }}{(n+3)(n+5)}{{{\rm C}}}_{n}^{\frac{n-1}{2}} \phi ^{n-1} \\&=\frac{ \mu \pi r_0^{6}}{8h^{3}}\frac{{\partial \varphi }}{{\partial t}} \gamma (\phi ) \end{aligned}$$
(12)

where \(\phi =\varphi r_0 h^{-1}, \gamma (\phi )\) can be calculated:

$$\gamma (\phi )=\frac{160-152\phi ^2+16\phi ^4-160\sqrt{1-\phi ^2} +72\phi ^2\sqrt{1-\phi ^2}}{\phi ^6\sqrt{1-\phi ^2}}$$
(13)

Let the damping torque \(T_{{\rm cir}}=T_{{\rm cir}}(0) \gamma (\phi )\), where \(T_{{\rm cir}}(0)\) is the damping torque when \(\phi\) equals zero. And the curve of function \(\gamma (\phi )\) is shown in Fig. 3. With \(T_{{\rm cir}}=c_{{\rm cir}}\tfrac{{\partial \varphi }}{{\partial t}}\), the coefficient of damping torque is:

$$c_{{\rm cir}}=c_{{\rm cir}}(0)\gamma (\phi )= \frac{ \mu \pi r_0^{6}}{8h^{3}}\gamma (\phi )$$
(14)

where \(c_{{\rm cir}}(0)\) means the coefficient of damping torque when \(\phi\) equals zero.

Fig. 2
figure 2

The deviatory pressure of circular mirror when torsion angle is small

Full size image
Fig. 3
figure 3

The function \(\gamma (\phi )\) versus \(\phi\)

Full size image

3 Elliptical torsion mirror

The basic equation, which refers to the Taylor series form of simplified nonlinear Reynolds equation, Eq. (3), should be changed into elliptical coordinate form to facilitate solving. The elliptical coordinate is shown in Fig. 4 (Elliptic 2013). The relationship between Cartesian coordinate and elliptical coordinate is (Korn and Korn 2000):

$$x =c\cosh \xi \cos \eta$$
(15a)
$$y =c\sinh \xi \sin \eta$$
(15b)

where c is focal length of the ellipse, \(\xi\) a nonnegative real number and \(\eta \in [0,2\pi )\).

Fig. 4
figure 4

The schematic of elliptical coordinate

Full size image

The major axis length of elliptical mirror is a, and the minor axis is b. Substitute \(\xi =\cosh ^{-1}(a/c)\) into Eq. (15) and we have:

$$\frac{x^2}{a^2 }+\frac{y^2}{b^2 } =1$$
(16)

Assuming \(\xi _0=\cosh ^{-1}(a/c)\), it can be seen from above that \(\xi =\xi _0\) describes the outline of the elliptical mirror. So, boundary condition in elliptical coordinate is \(p(\xi =\xi _0)=0.\) There are two cases in this situation that torsion axis is in minor axis or major axis.

3.1 Torsion axis in minor axis

When torsion axis is in minor axis, as shown in Fig. 1b, the basic equation in this situation is:

$$\begin{aligned}&\frac{1}{c^2(\sinh ^2\xi +\sin ^2 \eta )} \left( \frac{{{\partial ^2}p}}{{\partial {\xi ^2}}} + \frac{{{\partial ^2}p}}{{\partial {\eta ^2}}} \right) \nonumber \\&\quad =-\,\sum _{n=1}^{\infty}\frac{{6\mu n(n+1) }}{{{h^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}\varphi ^{n-1}c^n\cosh ^n \xi \cos ^n \eta \end{aligned}$$
(17)

As in previous section, the method of eigenfunction expansions is still used. The eigenfunction of Eq. (17) is solved by separation of variables method. Let \(p(\xi,\eta )=\varXi (\xi )H(\eta ),\) and thus, we have \(\varXi (\xi )=A_{{\rm m}} \cosh m \xi + B_{{\rm m}} \sinh m \xi\) and \(H(\eta )=C_{{\rm m}} \cos m \eta +D_{{\rm m}} \sin m \eta\), where m is a natural number. So, we have:

$$\begin{aligned} p(\xi,\eta )&=(A_{{\rm m}} \cosh m \xi + B_{{\rm m}} \sinh m \xi ) (C_{{\rm m}} \cos m \eta +D_{{\rm m}} \sin m \eta )\nonumber \\&= A_{{\rm m}} C_{{\rm m}} \cosh m \xi \cos m \eta +B_{{\rm m}} D_{{\rm m}} \sinh m \xi \sin m \eta \nonumber \\&\quad +\,A_{{\rm m}} D_{{\rm m}} \cosh m \xi \sin m \eta +B_{{\rm m}} C_{{\rm m}} \cosh m \xi \sin m \eta \end{aligned}$$
(18)

For \(\cosh m \xi \sin m \eta\), it is not continuous since its left-sided limit \(\sin m \eta\) and right-sided limit \(-\sin m \eta\) are not equal in y direction of Cartesian coordinate, which is shown in Fig. 5. For \(\sinh m \xi \cos m \eta\), it is not smooth since its left derivative \(m\cot m \eta\) and right derivative \(-m\cot m \eta\) with respect to y are not equal, which is shown in Fig. 6. For function p, which describes a natural variable, it is not reasonable to include a discontinuous or non-smooth expression. Then, the eigenfunction can be simplified to:

$$p(\xi,\eta )= A_{{\rm m}} \cosh m \xi \cos m \eta + B_{{\rm m}} \sinh m \xi \sin m \eta$$
(19)

With the method of eigenfunction expansions, expression p can be assumed as:

$$p(\xi,\eta )=\sum _{l=0}^{\infty }\sum _{k=0}^{\infty } A_{lk} \cosh l \xi \cos k \eta + B_{lk} \sinh l \xi \sin k \eta$$
(20)

and according to the characteristic of hyperbolic functions, \(\cosh ^n \xi\) can be expanded to:

$$\cosh ^n \xi =\left\{ \begin{array}{ll} \frac{1}{2^{n-1}}\sum\nolimits_{{{{\rm odd}}}\, l}^{n} {{{\rm C}}}_{n}^{\frac{n-l}{2}}\cosh l \xi &{}\quad n \in {{{\rm odd}}}\\ \frac{1}{2^{n-1}}\sum\nolimits_{{{{\rm even}}}\, l}^{n} {{{\rm C}}}_{n}^{\frac{n-l}{2}}\cosh l \xi +\frac{1}{2^{n}}{{{\rm C}}}_{n}^{\frac{n}{2}} &{}\quad n \in {{{\rm even}}}\\ \end{array} \right.$$
(21)

With Eqs. (20), (21) and (7), Eq. (17) becomes:

$$\begin{aligned}&\sum _{l=0}^{\infty }\sum _{k=0}^{\infty } (l^2-k^2)(A_{lk} \cosh l \xi \cos k \eta + B_{lk} \sinh l \xi \sin k \eta ) \\&\quad = - \sum _{n=1}^{\infty }\frac{{6\mu n(n+1) }}{{{2^{2n}h^{n+2}}}}c^{n+2}\frac{{\partial \varphi }}{{\partial t}}\varphi ^{n-1} \\&\quad \quad \times \,\left[ \sum _{{{{\rm odd}}}\, l}^{n+2} \sum _{{{{\rm odd}}}\, k}^{n+2}f(n,l,k)\cosh l \xi \cos k \eta \right. \\&\quad \quad +\,\sum _{{{{\rm even}}}\, l}^{n+2} \sum _{{{{\rm even}}}\, k}^{n+2} f(n,l,k)\cosh l \xi \cos k \eta \\&\quad \quad +\,\frac{1}{2} \sum _{{{{\rm even}}}\, l}^{n+2} f(n,l,0)\cosh l \xi \\&\quad \quad +\,\left. \frac{1}{2}\sum _{{{{\rm even}}}\, k}^{n+2} f(n,0,k)\cos k \eta \right] \end{aligned}$$
(22)

where \(f(n,l,k)={{{\rm C}}}_{n+2}^{\frac{n+2-l}{2}} {{{\rm C}}}_{n}^{\frac{n-k}{2}}-{{{\rm C}}}_{n}^{\frac{n-l}{2}}{{{\rm C}}}_{n+2}^{\frac{n+2-k}{2}}\). For both side of Eq. (22), the coefficients of variables \(\xi\) and \(\eta\) should be equal. When k and l are exchanged in Eq. (22), it can be easily found that \(A_{lk}=A_{kl}\) since \((l^2-k^2)=-(k^2-l^2)\) and \(f(n,l,k)=-f(n,k,l)\). And the coefficients are:

$$A_{l0}= -\frac{1}{l^2} \sum _{{{{\rm even}}}\, n}^{\infty }\frac{{6\mu n(n+1) }}{{{2^{2n+1}h^{n+2}}}}c^{n+2}\frac{{\partial \phi }}{{\partial t}}\phi ^{n-1} f(n,l,0)$$
(23a)
$$A_{lk}=-\frac{1}{l^2-k^2} \sum _{n=1}^{\infty }\frac{{6\mu n(n+1) }}{{{2^{2n}h^{n+2}}}}c^{n+2}\frac{{\partial \phi }}{{\partial t}}\phi ^{n-1}f(n,l,k)$$
(23b)
$$A_{kk}=-\sum _{l=0}^{\infty }A_{lk}\frac{\cosh l \xi _0}{\cosh k \xi _0}$$
(23c)

where l is even and l is greater than zero in Eq. (23a). In Eq. (23b), l, k and n are all odd or all even and l is greater than k greater than zero. In Eq. (23c), l is not equal to k. And in other cases, \(A_{lk}=B_{lk}=0\). So, p here is:

$$p=\sum _{l=0}^{\infty }\sum _{k=0}^{\infty }A_{lk}\cosh l \xi \cos k \eta$$
(24)

When torsion angle is small, as before, the expression of deviatory pressure p in this situation can be simplified and 3D diagram is shown in Fig. 7.

Fig. 5
figure 5

The function of \(\cosh m \xi \sin m \eta\)

Full size image
Fig. 6
figure 6

The function of \(\sinh m \xi \cos m \eta\)

Full size image
Fig. 7
figure 7

The deviatory pressure of elliptical mirror with axis in minor axis when torsion angle is small

Full size image

The equation of damping torque is \(T_{{\rm minor}}=\int p c \cosh \xi \cos \eta c^2(\cosh ^2 \xi -\cos ^2\eta ){\rm d}\xi {\rm d}\eta.\) Because of the orthogonality of trigonometric function, the result of integration is not zero only when k equals 1 or 3. Thus, we have:

$$\begin{aligned} T_{{\rm minor}}&=\sum _{{{{\rm odd}}}\, n}^{\infty}\frac{{12\pi \mu n(n+1) {{{\rm C}}}_{n}^{\frac{n-1}{2}}}}{2^{n}(n+3)(n+5)}\frac{ (c \cosh \xi _0)^{n+5}}{h_0^{n+2}}\frac{\sinh ^3 \xi _0}{\cosh 3\xi _0}\frac{{\partial \phi }}{{\partial t}}\phi ^{n-1} \nonumber \\ &= \frac{ \pi \mu (c \cosh \xi _0)^6}{2h^3}\frac{\sinh ^3 \xi _0}{\cosh 3\xi _0}\frac{{\partial \varphi }}{{\partial t}}\gamma (\phi ) \end{aligned}$$
(25)

When \(\xi _0\) approaching infinity, the elliptical mirror approaches a circular mirror. In this situation, the major axis length can be considered as the radius of mirror. And Eq. (25) becomes:

$$\begin{aligned} \lim _{\xi _0 \rightarrow \infty }T_{{\rm minor}}&=\lim _{\xi _0 \rightarrow \infty } \frac{ \pi \mu (c \cosh \xi _0)^6}{2h^3}\frac{\sinh ^3 \xi _0}{\cosh 3\xi _0}\frac{{\partial \varphi }}{{\partial t}}\gamma (\phi )\nonumber \\&=\frac{ \pi \mu (r_0)^6}{2h^3}\frac{{\partial \varphi }}{{\partial t}}\gamma (\phi )\lim _{\xi _0 \rightarrow \infty } \frac{\sinh ^3 \xi _0}{4\cosh ^3 \xi _0 -3\cosh \xi _0} \\&=\frac{ \pi \mu r_0^6}{8h^3}\frac{{\partial \varphi }}{{\partial t}}\gamma (\phi ) \end{aligned}$$
(26)

This result is entirely consistent with the torque damping of circular mirror. With \(T_{{\rm minor}}=c_{{\rm minor}}\tfrac{{\partial \varphi }}{{\partial t}}\) and Eq. (25), the coefficient of damping torque is:

$$c_{{\rm minor}}= \frac{ \pi \mu (c \cosh \xi _0)^6}{2h^3}\frac{\sinh ^3 \xi _0}{\cosh 3\xi _0}\gamma (\phi )$$
(27)

3.2 Torsion axis in major axis

When torsion axis is in major axis, as shown in Fig. 1c, the torsion axis is x axis. The basic equation becomes:

$$\begin{aligned}&\frac{1}{c^2(\sinh ^2\xi +\sin ^2 \eta )} \left( \frac{{{\partial ^2}p}}{{\partial {\xi ^2}}} + \frac{{{\partial ^2}p}}{{\partial {\eta ^2}}} \right) \nonumber \\&\quad =-\,\sum _{n=1}^{\infty}\frac{{6\mu n(n+1) }}{{{h^{n+2}}}}\frac{{\partial \phi }}{{\partial t}}\phi ^{n-1}c^n\sinh ^n \xi \sin ^n \eta \end{aligned}$$
(28)

With the method of eigenfunction expansions, the expression of p can be assumed as Eq. (20). And according to the characteristic of trigonometric functions and hyperbolic function, \(\sinh ^n \xi\) and \(\sin ^n \eta\) can be expanded to:

$$\begin{aligned} \sin ^n \eta&= {} \left\{ \begin{array}{ll} \frac{1}{2^{n-1}}\sum\nolimits_{{{{\rm odd}}}\, k}^{n} (-1)^{\frac{k-1}{2}} {{{\rm C}}}_{n}^{\frac{n-k}{2}}\sin k \eta &{}\quad n \in {{{\rm odd}}}\\ \frac{1}{2^{n-1}}\sum\nolimits_{{{{\rm even}}}\, k}^{n} (-1)^{\frac{k}{2}} {{{\rm C}}}_{n}^{\frac{n-k}{2}}\cos k \eta +\frac{1}{2^{n}}{{{\rm C}}}_{n}^{\frac{n}{2}} &{}\quad n \in {{{\rm even}}}\\ \end{array} \right. \end{aligned}$$
(29)
$$\begin{aligned} \sinh ^n \xi&= {} \left\{ \begin{array}{ll} \frac{1}{2^{n-1}}\sum\nolimits_{{{{\rm odd}}}\, l}^{n} (-1)^{\frac{n-l}{2}} {{{\rm C}}}_{n}^{\frac{n-l}{2}}\sinh l \xi &{}\quad n \in {{{\rm odd}}}\\ \frac{1}{2^{n-1}}\sum\nolimits_{{{{\rm even}}}\, l}^{n} (-1)^{\frac{n-l}{2}} {{{\rm C}}}_{n}^{\frac{n-l}{2}}\cosh l \xi +\frac{1}{2^{n}}(-1)^{\frac{n-l}{2}}{{{\rm C}}}_{n}^{\frac{n}{2}} &{}\quad n \in {{{\rm even}}}\\ \end{array} \right. \end{aligned}$$
(30)

With Eqs. (20), (29) and (30), Eq. (28) becomes:

$$\begin{aligned} \sum _{l=0}^{\infty }\sum _{k=0}^{\infty }&(l^2-k^2)(A_{lk} \cosh l \xi \cos k \eta + B_{lk} \sinh l \xi \sin k \eta ) \\&\quad = - \sum _{n=1}^{\infty }\frac{{6\mu n(n+1) }}{{{2^{2n}h^{n+2}}}}c^{n+2}\frac{{\partial \varphi }}{{\partial t}}\varphi ^{n-1}\nonumber \\&\quad \quad \times \,\left[ \sum _{{{{\rm odd}}}\, l}^{n+2} \sum _{{{{\rm odd}}}\, k}^{n+2}(-1)^{\frac{n-l+k+1}{2}}f(n,l,k)\sinh l \xi \sin k \eta \right. \\&\quad \quad +\,\sum _{{{{\rm even}}}\, l}^{n+2} \sum _{{{{\rm even}}}\, k}^{n+2} (-1)^{\frac{n-l+k+2}{2}}f(n,l,k)\cosh l \xi \cos k \eta \\&\quad \quad +\,\frac{1}{2} \sum _{{{{\rm even}}}\, l}^{n+2}(-1)^{\frac{n-l+2}{2}} f(n,l,0)\cosh l \xi \\&\quad \quad \,+\left. \frac{1}{2}\sum _{{{{\rm even}}}\, k}^{n+2}(-1)^{\frac{n+k+2}{2}} f(n,0,k)\cos k \eta \right] \end{aligned}$$
(31)

The coefficients of variables \(\xi\) and \(\eta\) in both sides should equal in Eq. (31). In the same way, it is also found that \(A_{lk}=A_{kl}\) and \(B_{lk}=B_{kl}\), and the coefficients are:

$$A_{l0}=-\sum _{n=1}^{\infty } \frac{(-1)^{\frac{n-l+2}{2}} }{l^2} \frac{{6\mu n(n+1) }}{{{2^{2n+1}h^{n+2}}}}\frac{{\partial \varphi }}{{\partial t}}c^{n+2}\varphi ^{n-1}f(n,l,0)$$
(32a)
$$A_{lk} =-\sum _{{{{\rm even}}}\, n}^{\infty }\frac{(-1)^{\frac{n-l+k+2}{2}}}{l^2-k^2} \frac{{6\mu n(n+1) }}{{{2^{2n}h^{n+2}}}}\frac{{\partial \phi }}{{\partial t}}c^{n+2}\phi ^{n-1}f(n,l,k)$$
(32b)
$$B_{lk} =-\sum _{{{{\rm odd}}}\, n}^{\infty }\frac{(-1)^{\frac{n-l+k+1}{2}}}{l^2-k^2} \frac{{6\mu n(n+1) }}{{{2^{2n}h^{n+2}}}}c^{n+2}\frac{{\partial \phi }}{{\partial t}}\phi ^{n-1}f(n,l,k)$$
(32c)
$$A_{kk} =-\sum _{{{{\rm even}}}\, l}^{\infty }A_{lk}\frac{\cosh l \xi _0}{\cosh k \xi _0}$$
(32d)
$$B_{kk} =-\sum _{{{{\rm odd}}}\, l}^{\infty }B_{lk}\frac{\sinh l \xi _0}{\sinh k \xi _0}$$
(32e)

where l is even and l is greater than zero in Eq. (32a). And l and k are both odd in Eq. (32b), while they are both even in Eq. (32c) and l is greater than k greater than zero. In Eqs. (32d) and (32e), l is not equal to k. In other cases, \(A_{lk}=B_{lk}=0\). Thus, p is:

$$p=\sum _{l=0}^{\infty }\sum _{k=0}^{\infty }(A_{lk}\cosh l \xi \cos k \eta +B_{lk}\sinh l \xi \sin k \eta )$$
(33)

when torsion angle is small, as before, the expression of deviatory pressure p in this situation can be simplified and 3D diagram is shown in Fig. 8.

Fig. 8
figure 8

The deviatory pressure of elliptical mirror with axis in major axis when torsion angle is small

Full size image

The damping torque in this case is \(T_{{\rm major}}=\int p c \sinh \xi \sin \eta c^2(\sinh ^2 \xi +\sin ^2\eta ){\rm d} \xi {\rm d} \eta.\) Because of the orthogonality of trigonometric function, the result of integration is not zero only when k equals 1 or 3. Thus, we have:

$$\begin{aligned} T_{{\rm major}}&=\sum _{{{{\rm odd}}}\, n}^{\infty}\frac{{12\pi \mu n(n+1) {{{\rm C}}}_{n}^{\frac{n-1}{2}}}}{2^{n}(n+3)(n+5)}\frac{ (c \sinh \xi _0)^{n+5}}{h_0^{n+2}}\frac{\cosh ^3 \xi _0}{\sinh 3\xi _0}\frac{{\partial \phi }}{{\partial t}}\phi ^{n-1} \nonumber \\&= \frac{ \pi \mu (c \sinh \xi _0)^6}{2h^3}\frac{\cosh ^3 \xi _0}{\sinh 3\xi _0}\frac{{\partial \varphi }}{{\partial t}}\gamma (\phi ) \end{aligned}$$
(34)

Since \(\sinh 3\xi _0=4 \sinh ^3 \xi +3 \sinh \xi\), the limit of Eq. (34) is also exactly the same with the damping torque of circular mirror when \(\xi _0\) approaching infinity. With \(T_{{\rm major}}=c_{{\rm major}}\tfrac{{\partial \varphi }}{{\partial t}}\) and Eq. (34), the coefficient of damping torque is:

$$c_{{\rm major}}= \frac{ \pi \mu (c \sinh \xi _0)^6}{2h^3}\frac{\cosh ^3 \xi _0}{\sinh 3\xi _0}\gamma (\phi )$$
(35)

4 Numerical simulation

CoventorWare® is a reliable software to simulate MEMS devices, which uses finite element modelling (FEM) or boundary element method (BEM) solvers to do simulation. Consequently, its simulation results can be used to verify the accuracy of numerical solution of the formula before.

3D model of mirror is established and meshed in extruded bricks type, as shown in Fig. 9. The 3D meshed model of circular mirror whose radius is 500 \(\upmu\)m is shown in Fig. 3. In the field solvers, DampingMM module is chosen to acquire the coefficient of damping torque. In the setting dialogue, squeezed or slide-film flow is selected and the 3D model is simulated with the damping coefficient ranging from 10 to \(10^6\,\hbox {Hz}\) with a 101 kPa pressure and 300 K temperature. The boundary condition is “edge”, which means that the relative (to ambient) pressure at the specified edge will be set to zero. The specified edge is the intersection of the boundary of mirror and the surface of mirror which faces the air.

From the results of simulation, it is clear that the squeeze damping coefficient of rotation mirror hardly changes with the frequency and shows a good consistence with the results of formula. The comparisons of damping coefficient between formula and simulation are shown in Figs. 10, 11 and 12.

Fig. 9
figure 9

The mesh model of micro-torsion mirror

Full size image
Fig. 10
figure 10

Comparison between the coefficient of damping torque calculated by CoventorWare® (scatter) and formula (line) of circular mirror

Full size image
Fig. 11
figure 11

Comparison between the coefficient of damping torque calculated by CoventorWare® (scatter) and formula (line) of elliptical mirror with torsion axis in minor axis

Full size image
Fig. 12
figure 12

Comparison between the coefficient of damping torque calculated by CoventorWare® (scatter) and formula (line) of elliptical mirror with torsion axis in major axis

Full size image

Figure 10 compares the damping coefficient results of different radius of circular mirror when the gap between substrate and mirror is 100, 200 and 300 \(\upmu\)m. The lines are the results of formula and the triangles; squares and dots are the results of simulation. The maximum relative error is 3.8 %, based on the results simulated.

Figures 11 and 12 compare the damping coefficient of elliptical mirror with different eccentricity when its major axis is 500, 1000 and 1500 \(\upmu\)m. The rotation axis is the major axis and minor axis, respectively, when the gap between substrate and mirror is 200 \(\upmu\)m. Similarly, the lines are the results of formula and the triangles; squares and dots are the results of simulation. It is also clear that the results of simulation and formula are well consistent with the maximum relative error of 3.2 % for major axis as the rotation axis, while the minor axis is 3.1 %. When the eccentricity is zero, the eclipse becomes circular. The result of the formula of eclipse mirror when the eccentricity is zero is perfectly consistent with the result of simulation of circular mirror, which further proves the accuracy of the formula.

In addition, the squeeze damping coefficient getting from formula is continuous. Consequently, we can figure out the variation tendency of the damping coefficient when one of the mirror parameters changes, which means the formula will be a useful tool to optimize the structure of mirror with lower damping torque.

5 Discussion

We discuss the range of application of the basic equation in this section. From the expression of damping torque, the maximum damping pressure is \(p_{{{{\rm max}}}}=p_{{{{\rm max}}}}(0)\gamma (\phi )\). \(p_{{{{\rm max}}}}(0)\) of elliptical mirror is smaller than circular mirror when its major axis length is identical with the radius of the circular mirror, so we could use the derivation of Eq. (11), the expression of circular mirror, to get the max value of p:

$$p_{{{{\rm max}}}}=\left( \frac{r_0^2 \mu }{\sqrt{3} h^2}\frac{\partial \phi }{\partial t} \right) \gamma (\phi )$$
(36)

Apply Eq. (36) to Eq. (2):

$$\phi \gamma (\phi ) \ll 6.96$$
(37)

With Eq. (13) and Fig. 3, we have \(\phi \gamma (\phi )=1.44\) when \(\phi\) equal 0.6 and \(\phi \gamma (\phi )=2.45\) when \(\phi\) equal 0.7. Therefore, \(\phi\) should be \(<\)0.7, and it is same as Bao’s conclusion (Bao et al. 2006).

6 Conclusions

Nonlinear Reynolds equation is solved in polar coordinate and elliptical coordinate, and the squeeze-film air-damping torque of circular and elliptical torsion mirrors is deduced in this paper. The method of eigenfunction expansions is used to solve the nonlinear Reynolds equation, and then, we have the series solution of deviatory pressure. With integral, the damping torque is calculated and the expression can be generalized to \(T_{{\rm sq}}=T_{{\rm sq}}(0)\gamma (\phi )\). \(T_{{\rm sq}}(0)\) is the damping torque when torsion angle is zero, which is a function of mirror’s parameters, viscosity of air and angular velocity. \(\gamma (\phi )\) is strongly nonlinear function of \(\phi\). We find that when \(\xi _0\) approaching infinity, i.e., the shape of elliptical mirror approaching circularity, its damping torque expression approaches circular mirrors. Compared with numerical simulations, the formula calculated results meet well with the simulated results of CoventorWare®. And the expression is valid under the condition \(\phi <0.7\).