1 Introduction

As the size of devices becomes smaller, the surface to volume ratio increases, and the gas–surface interaction becomes important in microscale gas flows. Thus, surface forces become more dominant than body forces in micro systems. The dynamic behavior of movable parts in MEMS is largely affected by the ambiance due the presence of gas engulfing the microstructure, e.g., low vacuum conditions for micro-accelerometers (Starr 1990), ultra-thin gas film in magnetic head/disk interfaces (Hwang et al. 1996), and tilting micro-mirrors in DLP type projectors (Chang et al. 2002; Hornbeck). The main effect occurs in these examples is the squeeze film. The energy losses in the systems are lowered by many methods (lowering the ambient pressure Starr 1990, perforations kim et al. 1999) to increase the quality factor. Squeeze film dampers are also widely used in many mechanical applications (Kim and Lee 2005; San Andreś and De Santiago 2004; Suciu et al. 2000).

In the modeling of gas flow in squeeze film, the amplitude of an oscillating plate is restricted to be small and thus resulting in small variation in pressure from ambient pressure. Traditionally, the compressible Reynolds equation (widely used as the governing equation for continuum problems) is linearized by introducing the pressure and film thickness perturbation parameters (Griffin et al. 1966; Ausman 1967; Langlois 1962; Blech 1983). The dynamic coefficients (stiffness and damping coefficients) and cutoff frequencies (the frequency at which the spring and damping coefficients are equal, K′ = B′) in compressible squeeze film have been analyzed for parallel or tilting motions of infinite strips, thin annuli and circular plates. A detailed review was given by Andrews et al. (1993). To solve the linearized compressible Reynolds equation, Darling et al. (1998) utilized the Green’s function method to find the solution analytically for arbitrary acoustic venting conditions along the edges of a movable structure. The resulting forces from compressible squeeze film damping can be calculated by integrating the complex perturbed pressure over the squeeze surface. Arbitrary deflection profiles can also be treated, enabling the calculation of damping effects for cantilevers, diaphragms, tilting plates and drum-head modes. Pan et al. (1998) investigated the dynamic behavior of a tilting mirror in atmosphere pressure only and verify the results experimentally. Both the Fourier series solution and the double sine series solution are derived analytically from the linearized Reynolds equation, which is obtained under the assumption of small tilting amplitude. However, the above results (Griffin et al. 1966; Ausman 1967; Langlois 1962; Blech 1983; Andrews et al. 1993; Darling et al. 1998; Pan et al. 1998) are only applicable to continuum cases with smooth surfaces.

In micro devices, the effects of gas rarefaction (including Knudsen number and surface accommodations effects) and surface roughness become important (Li 2004) under the conditions of low spacing or low ambient pressure. Three important parameters in micro devices are: the Knudsen number (Kn = λ/h 0), the ACs \((\alpha_{1},\alpha_{2})\) and the film thickness ratio (H S0 = h 0 /σ).

  1. (1)

    The Knudsen number (Kn = λ/h0) is defined as the ratio of the mean free path of gas to the characteristic length of the squeeze film (film thickness), which is an indicators of gas rarefaction. The effect of gas rarefaction increases as the inverse Knudsen number \(\left(D = \frac{\sqrt \pi}{2Kn} = \frac{\sqrt \pi}{2}\frac{h}{\lambda}\right)\) decreases. The continuum hypothesis (valid for Kn < 0.001) is questionable under ultra low spacing (small h) or low ambient pressure (large λ) conditions. The flow regimes can be divided into various regimes as Kn increases from 0 to infinity: continuum, slip, transition and free-molecular flow regimes. Many slip-flow models, first-order (Burgdorfer 1959), second-order (Hsia and Domoto 1983), 1.5-order (Mitsuya 1993), high-order (Hwang et al. 1996) and databases (Fukui and Kaneko 1990; Kang 1997; Li 2002, 2003) are proposed to modify the compressible Reynolds equation to be applicable in a wider range of Knudsen numbers. The first-order slip-flow model is simple and applicable to the present micro-mirror analysis (0.001 < Kn < 0.1). The first-order velocity slip on the solid boundary without thermal creep is \(v_{s} = \frac{2 - \alpha}{\alpha}\lambda \frac{\partial v}{\partial n}\left| {_{{\rm wall}}} \right..\)

  2. (2)

    The accommodation coefficient (AC, α) (also called the tangential momentum accommodation coefficient, TMAC) is an indicator of the average tangential momentum exchange of the collision between gas molecules and the solid boundary (Karniadakis and Beskok 2002). Many experiments (shown in Table 1 of Finger et al. 2007) show that the TMACs is not in perfectly diffuse reflection, and always in the range of 0 < α ≤ 1. AC(α) represents the fraction of the gas molecules that interact with solid boundaries in a diffusive manner (as molecules incident on the solid bearing surfaces: α = 1, the diffuse reflections, the molecules are reflected on a microscopically rough surface with zero average tangential velocity; α = 0, the specular reflections, zero skin friction (Jang and Wereley 2006). Incident particles keep the (1 − α) part of the information about their state before collisions and lose the α part of the information. Due to the small size of the incident molecular, the microscale roughness affects the molecular–solid interactions more significantly than the macroroughness does. However, the macroscale roughness affects the gas flow between squeezing surfaces more significantly than the microscale roughness does.

  3. (3)

    The film thickness ratio (HS0 = h0 /σ) is defined as the ratio of the nominal film thickness h0 to the standard deviation of composite roughness \({\sigma}\left({\sigma}={\sqrt {\sigma_{1}^{2}+\sigma_{2}^{2} }}\right),\) which is an indicator of surface roughness. The effect of roughness increases as HS0 decreases (as σ is comparable to minimum film thickness), i.e., the macroscale roughness affects the average flow significantly. The average flow model (the flow factor method) is widely used in modeling the flow between rough surfaces. Due to the small size of the molecular incident on the microscopic roughness in (2), the scale of roughness in (3) is much greater than the microscopic roughness in (2). Thus, the microscale roughness affects the AC significantly, whereas the macro-scale roughness affects the squeeze flow significantly.

Table 1 The product \({\bar{Q}}_{P}\left(\phi^{p}_{x}\right)_{0}\) at D 0 = 10, γ = 9, H S0 = 3.0, and β′  = 2
Full size table

To account for the effects of gas rarefaction, Veijola et al. (1995) and Li and Hughes (2000) proposed the “effective coefficient of viscosity” to modify the compressible Reynolds equation to be used in a wide range of Knudsen numbers. In the low vacuum region, another models based on the free molecular dynamic are also developed (Christian 1966; Bao et al. 2002; Hutcherson and Ye 2004). The damping of a microresonator torsion mirror (operating with rarefied gas ambience) was also discussed for a wide range of vacuum levels (Minikes et al. 2005). They found the theoretical model agree favorably with the experimental data. To account for the effects of gas rarefaction and surface roughness on squeeze film, Bhushan and Tonder (1989a, b) use the effective viscosity and pressure flow factors separately in the ARTE. Latter, the coupling effects of gas rarefaction and surface roughness on lubricating film were proposed in the ARTE by Li and Weng (1997), and were applied in squeeze film for arbitrary Knudsen number conditions (Li 1999). In addition, the effects of accommodation coefficients (ACs) and gas rarefaction are considered in the modeling of squeeze film damping (Veijola et al. 1997), flow in microchannel (Jang and Wereley 2006), and gas bearing of magnetic head sliders flying on a rotating disk (Huang and Bogy 2000). However, the effects of surface roughness are not considered in Veijola et al. (1995, 1997), and Huang and Bogy (2000).

Recently, the author presents a model which is valid in the slip-flow region (Li 2004). The effects of gas rarefaction, symmetric ACs (α1 = α2), and surface roughness on the modeling of lubrication film are included in the model. The model is applicable and reasonable for the modeling of the present MEMS micromirrors in micrometer scale. In the derivation of flow factors for the ARTE, the symmetric conditions (same ACs on the two lubricating surfaces, α1 = α2) are made for applications to hard disk drives, where both the Couette and Poiseuille flow exist. However, the existence of Couette flow corrector, \({\bar{Q}}_{C} (\alpha_{1}, \alpha _{2}, D),\) makes the derivation of flow factors unreachable. The flow factors cannot be obtained under the conditions of non-symmetric ACs due to the Couette and Poiseuille flow exist simultaneously (Li 2004). The flow factors can only be expressed as functions of symmetric ACs (α1 = α2), inverse Knudsen number \(\left(D = \frac{{{\sqrt \pi}}}{2}\frac{1}{{Kn}}\right),\) and roughness parameters (H S0 and γ). For the present squeeze film problem, only Poiseuille flow exists. Thus, the non-symmetric conditions for ACs (α1 ≠ α2) on flow factors could be discussed. The flow factors can be derived and expressed as functions of non-symmetric ACs (α1 ≠ α2), inverse Knudsen number \(\left(D = \frac{{{\sqrt \pi }}}{2}\frac{1}{{Kn}}\right),\) and roughness parameters (H S0 and γ). The effects of non-symmetric ACs, inverse Knudsen number and surface roughness parameters on the flow factors and the dynamic coefficients of torsion micromirrors are discussed.

2 Derivation

The first-order slip flow model is accurate enough to model the gas film in MEMS scale. The coupling effects of gas rarefactions and surface roughness in squeeze film are included in the ARTE. The flow factors that consider the effects of non-symmetric ACs are first proposed and discussed.

2.1 Governing equation

Following the usual assumption of hydrodynamic lubrication, and the non-symmetric first-order slip boundary conditions \((u - u_{1} = \frac{{2 - \alpha_{1} }}{{\alpha_{1}}}\frac{{\partial u}}{{\partial y}}\,\hbox{at}\, y=0 \quad \hbox{and} \quad u - u_{2} = - \frac{{2 - \alpha_{2}}}{{\alpha_{2}}}\frac{{\partial u}}{{\partial y}}\,\hbox{at}\, y=h)\) to correct the traditional no-slip boundary conditions, we can derive the modified Reynolds equation, i.e.,

$$ \frac{\partial}{{\partial x}} \left[\frac{{\rho h^{3}}}{{12\mu}}\frac{{\partial p}}{{\partial x}}{\bar{Q}}_{P} \right] + \frac{\partial}{{\partial y}}\left[\frac{{\rho h^{3}}}{{12\mu}}\frac{{\partial p}}{{\partial y}}{\bar{Q}}_{P} \right] = \frac{{\partial (\rho h)}}{{\partial t}} + \frac{\partial}{{\partial x}}\left[\frac{{u_{1} + u_{2}}}{2} \cdot h \cdot {\bar{Q}}_{C} \right] + \frac{\partial}{{\partial y}}\left[\frac{{v_{1} + v_{2}}}{2} \cdot h \cdot {\bar{Q}}_{C} \right] $$
(1)

where p, ρ, h, D, and μ0 are the pressure, the density, the film thickness, the inverse Knudsen number, and the viscosity of gas, respectively. The inverse Knudsen number is defined as, \(D = \frac{{{\sqrt \pi}h}}{{2\lambda }} = \frac{{{\sqrt \pi}h_{0}}}{{2\lambda_{a} }}\frac{p}{{p_{a}}}\frac{h}{{h_{0}}} = D_{0} \frac{p}{{p_{a}}}\frac{h}{{h_{0}}}\) where the reference inverse Knudsen number, \(D_{0} = \frac{{p_{a} h_{0}}}{{\mu _{0} {\sqrt {2RT}}}} = \frac{{{\sqrt \pi}h_{0}}}{{2\lambda _{a}}}.\) The non-symmetric molecular/solid interactions (α1 ≠ α2) between lubricating surfaces is included in the equation. The gas rarefaction corrector for Poiseuille flow in the slip flow region with non-symmetric ACs is defined as \({\bar{Q}}_{P} = 1 + \frac{{3{\sqrt \pi}}}{D}\left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right) - \frac{{3\left(\frac{1}{{\alpha _{1}}} - \frac{1}{{\alpha_{2}}}\right)^{2} \frac{\pi}{{D^{2} }}}}{{1 + \frac{{{\sqrt \pi}}}{D}\left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right)}}.\) The equation of state of gas is p/ρη = constant, where η = 1 corresponds to the isothermal process, and η = c p /c v = k corresponds to adiabatic process with c p and c v are the specific heat for constant pressure and for constant volume, respectively. Although the gas rarefaction corrector for Couette flow also exists (not equal 1.0, \({\bar{Q}}_{C} = 1 + \frac{{u_{2} - u_{1} }}{{u_{2} + u_{1}}}\frac{{\left(\frac{1}{{\alpha_{1}}} - \frac{1}{{\alpha_{2}}}\right)\frac{{{\sqrt \pi}}}{D}}}{{1 + \frac{{{\sqrt \pi}}}{D}\left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right)}}\)) for non-symmetric boundary conditions, it still has no effects on the present squeeze film problems (u i  = v i  = 0). The modified Reynolds equation for squeeze film is

$$ \frac{\partial}{{\partial x}}\left[\frac{{\rho h^{3}}}{{12\mu}} \frac{{\partial p}}{{\partial x}}{\bar{Q}}_{P} \right] + \frac{\partial}{{\partial y}}\left[\frac{{\rho h^{3}}}{{12\mu}}\frac{{\partial p}}{{\partial y}}{\bar{Q}}_{P} \right] = \frac{{\partial (\rho h)}}{{\partial t}} $$
(2)

The average flow model (Li 2004, Li and Weng 1997) is utilized to derive the ARTE. One important assumption is that the length scale of roughness is large enough that does not affect the ACs. Following the procedure proposed in Li (2004), the ARTE, which includes the coupling effects of gas rarefaction (first-order slip-flow model with symmetric ACs, α1 = α2), and surface roughness, is modified to model the pressure distributions in the squeeze film between the tilting micro-mirrors and substrates with non-symmetric ACs, α1 ≠ α2. Under the conditions of zero roughness orientation angles (θ1 = θ2 = 0°), zero sliding velocity (only squeeze effects), and non-symmetric ACs (α1 ≠ α2), the ARTE can be modified into

$$ \frac{\partial}{{\partial x'}}{\left[ {\phi^{p}_{x} \overline{Q}_{P} (D,\;\alpha_{1}, \;\alpha_{2})\frac{{\rho h^{3}}}{{12\mu_{0}}}\frac{{\partial p}}{{\partial x'}}} \right]} + \frac{\partial}{{\partial y'}}{\left[ {\phi^{p}_{y} \overline{Q}_{P} (D,\;\alpha_{1}, \;\alpha_{2})\frac{{\rho h^{3}}}{{12\mu_{0}}}\frac{{\partial p}}{{\partial y'}}} \right]} = \frac{\partial}{{\partial t}}(\rho h) $$
(3)

where θ i , ϕ p x , ϕ p y , and \({\bar{Q}}_{P}\) are the orientation angles of representative asperity in ith surface, pressure flow factor in x-direction, pressure flow factor in y-direction, and the gas rarefaction corrector, respectively.

The pressure flow factors that include the coupling effects of gas rarefaction (first-order slip-flow model with non-symmetric ACs, α1 ≠ α2) and surface roughness can be expressed as

$$ \phi^{p}_{x} = 1 + g \times \left(\frac{\sigma}{h}\right)^{2} {\left({1 - \frac{{f^{2}}}{g}\frac{1}{{\gamma + 1}}} \right)} $$
(4)
$$ \phi^{p}_{y} = 1 + g \times (\frac{\sigma}{h})^{2} {\left({1 - \frac{{f^{2}}}{g}\frac{\gamma}{{\gamma + 1}}} \right)} $$
(5)

where

$$ \frac{1}{{\gamma + 1}} = \left(\frac{{\sigma_{2}}}{\sigma}\right)^{2} \frac{1}{{\gamma_{2} + 1}} + \left(\frac{{\sigma_{1}}}{\sigma}\right)^{2} \frac{1}{{\gamma_{1} + 1}} $$
(6)
$$ f = 3 + \frac{{D \times d{\bar{Q}}_{p} /dD}}{{\bar{Q}}_{p}} $$
(7)
$$ g = 3 + \frac{{3D \times d{\bar{Q}}_{p} /dD}}{{\bar{Q}}_{p}} + \frac{{D^{2}}}{2}\frac{{d^{2} {\bar{Q}}_{p} /dD^{2}}}{{\bar{Q}}_{p}} $$
(8)

and σ i is the standard deviation of ith surface, \({\sigma}= \sqrt{\sigma_{1}^{2}+\sigma_{2} ^{2}}\) is the composite standard deviation of the two surfaces, γ i is the Peklenik number of ith surface.

The first and second derivative of gas rarefaction corrector with respective to D are

$$ \frac{{d{\bar{Q}}_{P}}}{{dD}} = \frac{{- 3{\sqrt \pi}}}{{D^{2}}} \left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right) + \frac{{6\left(\frac{1}{{\alpha_{1}}} - \frac{1}{{\alpha_{2}}}\right)^{2} \frac{\pi}{{D^{3}}}}}{{1 + \frac{{{\sqrt \pi}}}{D}\left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right)}} - \frac{{3\left(\frac{1}{{\alpha_{1}}} - \frac{1}{{\alpha_{2}}}\right)^{2} \left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right)\frac{{\pi^{{3/2}}}}{{D^{4}}}}}{{{\left[ {1 + \frac{{{\sqrt \pi}}}{D}\left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right)} \right]}^{2}}} $$
(9)

and

$$ \frac{{d^{2} {\bar{Q}}_{P}}}{{dD^{2}}} = \frac{{6{\sqrt \pi}}}{{D^{3}}} \left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right) - \frac{{18\left(\frac{1}{{\alpha_{1}}} - \frac{1}{{\alpha_{2}}}\right)^{2} \frac{\pi}{{D^{4}}}}}{{1 + \frac{{{\sqrt \pi}}}{D}\left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right)}} + \frac{{18\left(\frac{1}{{\alpha_{1}}} - \frac{1}{{\alpha_{2}}}\right)^{2} \left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right)\frac{{\pi^{{3/2}}}}{{D^{5}}}}}{{{\left[ {1 + \frac{{{\sqrt \pi}}}{D}\left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right)} \right]}^{2}}} - \frac{{6\left(\frac{1}{{\alpha_{1}}} - \frac{1}{{\alpha_{2}}}\right)^{2} \left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right)^{2} \frac{{\pi^{2}}}{{D^{6}}}}}{{{\left[ {1 + \frac{{{\sqrt \pi}}}{D}\left(\frac{1}{{\alpha_{1}}} + \frac{1}{{\alpha_{2}}} - 1\right)} \right]}^{3}}} $$
(10)

2.2 Linearized average Reynolds type equation (Linearized ARTE)

The variation (δp) from ambient pressure (p a) in the squeeze film is also small for small variations (δh) in gap spacing (h 0). Introducing the perturbation parameters, p = p a  + δp and h = h 0 + δh (p a and h 0 are constants), the pressure flow factors and gas rarefaction corrector may thus be expressed as the following series expansion,

$$ \phi^{p}_{x} = (\phi^{p}_{x})_{0} + {\left({\frac{{\partial \phi^{p}_{x}}} {{\partial p}}} \right)}_{0} \times \delta p + {\left({\frac{{\partial \phi^{p}_{x}}}{{\partial h}}} \right)}_{0} \times \delta h $$
(11)
$$ \phi^{p}_{y} = (\phi^{p}_{y})_{0} + {\left({\frac{{\partial \phi^{p}_{y}}} {{\partial p}}} \right)}_{0} \times \delta p + {\left({\frac{{\partial \phi^{p}_{y}}}{{\partial h}}} \right)}_{0} \times \delta h $$
(12)
$$ \overline{Q}_{P} = (\overline{Q}_{P})_{0} + {\left({\frac{{\partial \overline{Q}_{P}}}{{\partial p}}} \right)}_{0} \times \delta p + {\left({\frac{{\partial \overline{Q}_{P}}}{{\partial h}}} \right)}_{0} \times \delta h $$
(13)

From the equation of state of gas, we can obtain

$$ \rho \; \propto \;p^{{\frac{1}{\eta}}} = (p_{a} + \delta p)^{{\frac{1}{\eta}}} \cong p_{a}^{{\frac{1}{\eta}}} + \frac{1}{\eta}p_{a}^{{\frac{1}{\eta} - 1}} \delta p $$
(14)

Substituting Eqs. (11–14) into Eq. (3), the solution of the steady equation is p = p a for all h = h 0. The first order equations is

$$ \frac{\partial}{{\partial x'}}\left[{\left({\phi^{p}_{x}} \right)}_{0} \frac{{p_{a}^{{\frac{1}{\eta}}} \cdot h_{0}^{3}}}{{12\mu}}\frac{{\partial \delta p}}{{\partial x'}}\right] + \frac{\partial}{{\partial y'}}\left[{\left({\phi^{p}_{y}} \right)}_{0} \frac{{p_{a}^{{\frac{1}{\eta}}} \cdot h_{0}^{3}}}{{12\mu}}\frac{{\partial \delta p}}{{\partial y'}}\right] = \frac{\partial}{{\partial t}}(p_{a}^{{\frac{1}{\eta}}} \cdot \delta h \cdot + h_{0} \cdot \frac{1}{\eta}p_{a}^{{\frac{1}{\eta} - 1}} \delta p) $$
(15)

where \(\mu = \frac{{\mu_{0}}}{{({\bar{Q}}_{P})_{0}}}\) is the effective viscosity of gas with gas rarefaction effects corrected. Two dimensionless parameters are defined here, i.e., \(P = \frac{{\delta p}}{{p_{a}}}\) is the local pressure variation, and \(H(x,y,t) = \frac{{\delta h(x,y,t)}}{{h_{0} }}\) is the local film thickness variation. Equation (15) can be rearranged to

$$ {\left({\phi^{p}_{x}} \right)}_{0} \frac{\partial}{{\partial x'}}{\left[ {\frac{{\partial P}}{{\partial x'}}} \right]} + {\left({\phi^{p}_{y}} \right)}_{0} \frac{\partial}{{\partial y'}}{\left[ {\frac{{\partial P}}{{\partial y'}}} \right]} = \xi^{2} {\left[ {\eta \frac{{\partial H}}{{\partial t}} + \frac{{\partial P}}{{\partial t}}} \right]} $$
(16)

where \(\xi^{2} = \frac{{12\mu}}{{\eta h_{0}^{2} p_{a}}} = \frac{\mu}{{\mu_{0}}}\xi_{0}^{2} = \frac{1}{{{\bar{Q}}_{P} (D_{0})}}\xi_{0}^{2}\) is a constant.

By the following coordinate transformation,

$$ x = \frac{{x'}}{{{\sqrt {(\phi^{p}_{x})_{0}}}}}, \quad y = \frac{{y'}} {{{\sqrt {(\phi^{p}_{y})_{0}}}}} $$
(17)

also the dimension of the micromirror is changed from l × w in x − y coordinate into \(l = \frac{{l'}}{{{\sqrt {(\phi^{p}_{x})_{0}}}}}\) and \(w = \frac{{w'}}{{{\sqrt {(\phi^{p}_{y})_{0}}}}}\) in x′ − y′ coordinate, Eq. (16) becomes

$$ \frac{\partial}{{\partial x}}{\left[ {\frac{{\partial P}}{{\partial x}}} \right]} + \frac{\partial}{{\partial y}}{\left[ {\frac{{\partial P}}{{\partial y}}} \right]} - \xi^{2} \frac{{\partial P}}{{\partial t}} = \xi^{2} \eta \frac{{\partial H}}{{\partial t}} $$
(18)

For the tilting micromirror, the dimensionless film thickness has the following relations, i.e., \(H(x,y,t) = \frac{{\delta h(x,y,t)}}{{h_{0}}} = \frac{{x\varepsilon (t)}}{{h_{0}}} = 2X\frac{l}{{2h_{0}}}\varepsilon (t) = 2X{\kern 1pt} H'e^{{j\omega t}},\) where \(\varepsilon (t) = \frac{{2h_{0}}}{l}H'e^{{j\omega t}}, \quad X = x/l,\) and \(j = {\sqrt {- 1}}.\)

Now, Eq. (18) has the form of a linear diffusion equation with a source term ξ2η∂H/∂t, which is the same as that derived previously by Darling et al. (1998) and Pan et al. (1998). Thus, we can use the analytical solution by Darling et al. (1998 Eq. 17) in the transformed domain (x − y), and then the inverse coordinate transformation of Eq. (17) is utilized to find the solutions in the real world (x′ − y′).

The dimensionless form of Eq. (18) is rearranged as

$$ \frac{\partial}{{\partial X}}{\left[ {\frac{{\partial P}}{{\partial X}}} \right]} + \frac{\partial}{{\partial Y}}{\left[ {\frac{{\partial P}}{{\partial Y}}} \right]} - \Gamma^{2} \frac{{\partial P}}{{\partial \tau}} = \Gamma^{2} \eta \frac{{\partial H}}{{\partial \tau}} $$
(19)

where the modified squeeze number Γ = α2ωl 2, and we have the following relations

$$ \Gamma = \frac{{12\mu \omega l^{2}}}{{\eta p_{a} h_{0}^{2}}} = \left(\frac{l}{{l'}}\right)^{2} \left(\frac{\mu}{{\mu_{0}}}\right)\frac{{12\mu_{0} \omega l^{'2}}}{{\eta p_{a} h_{0}^{2}}} = \left(\frac{l}{{l'}}\right)^{2} \left(\frac{\mu}{{\mu_{0}}}\right)\Gamma_{0} = \frac{{\Gamma_{0}}}{{\bar{Q}}_{P} (D_{0}, \alpha_{1}, \alpha_{2})(\phi^{p}_{{xx}})_{0}} $$
(20)

with conventional squeeze number Γ0 = ξ 20 ωl ′2.

2.3 Solution procedure

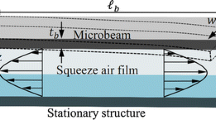
As shown in Fig. 1, a rectangular mirror with dimension l′ × w′ is tilting about the y-axis. The analysis domain of the squeeze film (mirror size) is \( - \frac{{l'}}{2} < x' < \frac{{l'}}{2}\) and \( - \frac{{w'}}{2} < y' < \frac{{w'}}{2}.\) The maximum displacement in z-direction occurs at \(x = \pm \frac{{l'}}{2}.\) Modifying the procedure in the previous publication (Li 1999), the dynamic coefficients of the squeeze gas film between a tilting micromirror and the substrate can be easily obtained. The solution procedure for the present problem is as follows:

  1. (1)

    Given: operating conditions \((h_{0}, \;p_{a}, \;\mu_{0}, {\;\omega,}\;H'),\) roughness parameters \((\sigma_{1},\;\sigma_{2}, \;\gamma_{1}, \;\gamma_{2}),\) mirror size (l′ × w′), and surface ACs \((\alpha_{1}, \;\alpha_{2}).\)

  2. (2)

    Calculate the inverse Knudsen number, \(D_{0} = \frac{{p_{a} h_{0}}}{{\mu_{0} {\sqrt {2RT_{0}}}}};\) the gas rarefaction corrector, \({\bar{Q}}_{p} (D_{0}, \alpha_{1}, \alpha_{2});\) the plate aspect ratio, \(\beta' = \frac{{l'}}{{w'}};\) the film thickness ratio, H S0 = h 0/σ; the pressure flow factors, (ϕ p x )0 and (ϕ p y )0; and the conventional squeeze number, \(\Gamma_{0} =\frac{{12\mu _{0} {\omega}l^{'2}}}{{{\eta}p_{a} h_{0}^{2}}}.\)

  3. (3)

    By the coordinate transformation, \(l = \frac{{l'}}{{{\sqrt {(\phi^{p}_{x})_{0}}}}}\) and \(w = \frac{{w'}}{{{\sqrt {(\phi^{p}_{y})_{0}}}}},\) the modified aspect ratio, \(\beta = \frac{l}{w} = \beta '{\sqrt {\frac{{(\phi^{p}_{y})_{0}}}{{(\phi^{p}_{x})_{0}}}}},\) and the modified squeeze number, \(\Gamma = \frac{12\mu \omega l^{2}}{\eta p_{a} h_{0}^{2}} = \frac{\Gamma _{0}}{{\bar{Q}}_{P} (D_{0}, \alpha_{1}, \alpha_{2})(\phi ^{p}_{x})_{0}},\) are then obtained.

  4. (4)

    The dimensionless dynamic pressure distributions can be obtained directly from that proposed by Darling et al. (1998) (which is the same as that obtained by Pan et al. (1998), i.e.,

    $$ P = {\sum\limits_{\begin{subarray}{l} m = even \\ n = odd \end{subarray}}^\infty \frac{{16(- 1)^{{\frac{m}{2} - 1}} (- 1)^{{\frac{{n - 1}}{2}}}}}{{\pi^{2} mn}}\frac{{- j\Gamma \eta H'e^{{j\omega t}}}}{{j\Gamma + m^{2} \pi^{2} + \beta^{2} n^{2} \pi^{2}}} \times \sin \frac{{m\pi x}}{l}\cos \frac{{n\pi y}}{w}} $$
    (21)

    From Eq. (21), we can obtain the dimensionless torque acting on the mirror, i.e.,

    $$T_{d} = \frac{\tau_{d}}{wl^{2} \frac{p_{a}}{2}} = {\sum\limits_{\begin{subarray}{l} {m = even }\\ {n = odd} \end{subarray}}^\infty {\frac{{64}}{{\pi^{4} m^{2} n^{2}}}\frac{{- j\Gamma \eta H'e^{{j\omega t}}}}{{j\Gamma + m^{2} \pi^{2} + \beta^{2} n^{2} \pi^{2}}}}}$$
    (22)

    We can rearrange Eq. (22) into

    $$\left(\frac{{2h_{0}}}{l}\right)T_{d} = \frac{{64\eta}}{{\pi^{4}}}\left\{{\varepsilon {\sum\limits_{\begin{subarray}{l} m = {\rm even} \\ n = {\rm odd} \end{subarray}}^\infty {\frac{1}{{m^{2} n^{2}}}\frac{{\Gamma^{2}}}{{\Gamma^{2} + (m^{2} \pi^{2} + \beta^{2} n^{2} \pi^{2})^{2}}}}}} \right. \left. {-\frac{{\dot{\varepsilon}}}{\omega}{\sum\limits_{\begin{subarray}{l} m = {\rm even} \\ n = {\rm odd}\\ \end{subarray}}^\infty {\frac{1}{{m^{2} n^{2}}}\frac{{\Gamma (m^{2} \pi^{2} + \beta^{2} n^{2} \pi^{2})}}{{\Gamma^{2} + (m^{2} \pi^{2} + \beta^{2} n^{2} \pi^{2})^{2}}}}}} \right\}$$
    (23)

    where \(\varepsilon (t) = \frac{{2h_{0}}}{l}H'e^{{j\omega t}}\) and \(\dot{\varepsilon}(t) = \frac{{{{\rm d}}\varepsilon (t)}}{{{{\rm d}}t}}\) are the tilting angle and angular velocity of the rectangular tilt micromirror (Fig. 1). The dimensionless stiffness and damping coefficients in transformed domain are, respectively,

    $$ K = \operatorname{Re} \left[\left(\frac{{2h_{0}}}{l}\right)T_{d} /\varepsilon \right] = \frac{{64\eta}}{{\pi^{4}}}{\sum\limits_{\begin{subarray}{l} {m = {\rm even}}\\ {n = {\rm odd}} \end{subarray}}^\infty {\frac{1}{{m^{2} n^{2}}}\frac{{\Gamma^{2}}}{{\Gamma^{2} + (m^{2} \pi^{2} + \beta^{2} n^{2} \pi^{2})^{2}}}}} $$
    (24a)

    and

    $$ B = \operatorname{Im} [{(\frac{{2h_{0}}}{l})T_{d}} \mathord{\left/ {\vphantom {{(\frac{{2h_{0}}}{l})T_{d}} {(\frac{{\dot{\varepsilon}}}{\omega})}}} \right. \kern-\nulldelimiterspace} {(\frac{{\dot{\varepsilon }}}{\omega})}] = \frac{{- 64\eta}}{{\pi^{4} }}{\sum\limits_{\begin{subarray}{l} {m = {\rm even}}\\ {n = {\rm odd}} \end{subarray}}^\infty {\frac{1}{{m^{2} n^{2} }}\frac{{\Gamma (m^{2} \pi^{2} + \beta^{2} n^{2} \pi ^{2})}}{{\Gamma^{2} + (m^{2} \pi^{2} + \beta^{2} n^{2} \pi ^{2})^{2}}}}}. $$
    (24b)

    Under the conditions of small squeeze number, Γ (small tilting frequency), the damping force is dominate as compared to the spring force. The damping force in the transformed domain is the same as that proposed by Pan et al. (1998). In addition, as the squeeze number is small, Γ2 ≪ π2, Pan’s results can be reduced to the damping coefficient proposed by Minkies et al. (2005).

  5. (5)

    Therefore, the solution in the real world (x′ − y′) can be obtained by the inverse coordinate transform, i.e.,

    $$ \left(\frac{{2h_{0}}}{{l'}}T_{d} '\right) = \frac{{2h_{0}}}{{l'}}\frac{{\tau_{d}}}{{l^{'2} w'p_{a} /2}} = \frac{{l^{3}}}{{l^{'3}}}\frac{w}{{w'}}\frac{{2h_{0}}}{l}\frac{{\tau_{d}} }{{l^{2} wp_{a} /2}} = \frac{1}{{(\phi^{p}_{x})_{0}^{{3/2}}}}\frac{1}{{(\phi^{p}_{y})_{0}^{{1/2 }}}} \left(\frac{{2h_{0}}}{l}T_{d}\right) $$
    (25)

    The dimensionless torque acting on the mirror in the x′ − y′ coordinate, \(\frac{{2h_{0}}}{{l'}}T_{d} ',\) is equal to the dimensionless torque that acting on the mirror with smooth surfaces, \(\frac{{2h_{0}}}{l}T_{d},\) multiplied by \(\frac{1}{{(\phi^{p}_{x})_{0}^{{3/2}}}}\frac{1}{{(\phi ^{p}_{y})_{0}^{{1/2}}}}.\)

  6. (6)

    The real part of \(\frac{{2h_{0}}}{{l'}}T_{d} '\) is now defined as the dimensionless stiffness coefficient, and the imaginary part of \(\frac{{2h_{0}}}{{l'}}T_{d} '\) is defined as the dimensionless damping coefficient. Thus, the dimensionless stiffness and damping coefficients in real domain are \(K' = \frac{1}{{(\phi^{p}_{x})_{0}^{{3/2}}}}\frac{1}{{(\phi^{p}_{y})_{0}^{{1/2}}}}K,\) and \(B' = \frac{1}{{(\phi^{p}_{x})_{0}^{{3/2}}}}\frac{1}{{(\phi^{p}_{y})_{0}^{{1/2}}}}B.\)

  7. (7)

    The cut-off frequency is defined as the frequency at which the stiffness is equal to the damping, i.e., K′ = B′.

Fig. 1
figure 1

Schematic diagram of a rectangular torsion mirror

Full size image

3 Results and discussion

Following the solution procedure, the dynamic coefficients of the tilting micromirror are obtained as the operating conditions, and roughness parameters are given. The isothermal case (η = 1) is discussed here. The inverse Knudsen number (D 0) is 10.0 for the present MEMS scale. The value of AC is as low as 0.25 for deposited metal on mica surfaces under stringent scattered vacuum condition (Lord 1976). Therefore, ACs in the range of 0.3 ≤ α i  ≤ 1.0 are discussed. In this squeeze film problem, only Poiseuille flow exists. The symmetric relation of gas rarefaction corrector follows, \({\bar{Q}}_{P} (D,\alpha_{1}, \alpha_{2}) = {\bar{Q}}_{P} (D,\alpha_{2}, \alpha_{1}).\) As the effects of gas rarefaction and surface roughness are neglected, we have \({\bar{Q}}_{P} \to 1, \quad \phi^{p}_{x} \to 1,\) and ϕ p y  → 1. The squeeze ARTE (Eq. 3) is reduced to the traditional Reynolds equation for squeeze film and Eq. (24b) is exactly the same as the results proposed by Pan et al. (1998). In addition, the present results reduce to the results of Li (1999) in the slip flow region under fully diffuse reflection (α1 = α2 = 1) with roughness effects considered. As shown in Fig. 2, the gas rarefaction correctors, \({\bar{Q}}_{p} (D,\alpha_{1}, \alpha_{2}),\) are plotted as functions of AC (α2, on one squeezed surface) for various ACs (α1, on the other squeezed surface). \({\bar{Q}}_{p} (D,\alpha_{1}, \alpha_{2})\) is a nonlinear function of AC. The gas rarefaction corrector decreases as the AC (α) increases or D 0 increases. At higher D 0 (Li 2003) or higher AC (α), the flow in the lubricating film is more restricted (Li 2004). Therefore, we have smaller gas rarefaction effects and thus smaller \({\bar{Q}}_{p} (D,\alpha_{1}, \alpha _{2}).\)

Fig. 2
figure 2

Gas rarefaction correctors as functions of α2 for various of α1

Full size image

The pressure flow factors, ϕ p x and ϕ p y , are plotted for various combination of ACs as shown in Fig. 3a and b, respectively. The coupling effects of the three parameters are also appeared in Eqs. (11–13) or in Fig. 3a and b. The roughness parameters and operating conditions are: film thickness ratio (H S0 = 3), Peklenik number (γ = 9), and inverse Knudsen number (D 0 = 10). The plate aspect ratio is β′ = 2.0. In our previous results (Li and Weng 1997), the roughness effect decreases as the gas rarefaction effect increases. As the molecular solid interactions become smaller (smaller ACs), the more fraction of specular reflection the molecules act, and the more rarefied they are. The pressure flow factor is a correction of Poiseuille flow rate within rough surfaces. The flow is more enhanced (restricted) as the pressure flow factor increases (decreases) further from 1.0. The roughness effect is more diluted due to smaller ACs and/or smaller D 0, i.e., ϕ p x  → 1.0 as D 0 and /or α decreases. As shown in Fig. 3a, the pressure flow factors in the transverse direction (ϕ p xx ) increases monotonously as AC increases. In addition, the pressure flow in the perpendicular direction (ϕ p yy ) decreases monotonously as AC increases (Fig. 3b). The combined effects of ACs on the two squeezing surfaces affect the pressure flow factors significantly. \({\sqrt {\phi^{p}_{{xx}} \times \phi^{p}_{{yy}}}}\) [Li and Weng 1997] and \({\sqrt {(\phi^{p}_{{xx}})^{3} \times \phi^{p}_{{yy}}}}\) are always smaller than 1.0. Therefore, the values of dynamic coefficients in real domain are always greater than those in transformed domain, i.e., from solution procedure (6), K′ > K and B′ > B.

Fig. 3
figure 3

a Pressure flow factor (ϕ p x ) plotted as functions of α2 for various of α1. b Pressure flow factor (ϕ p y ) plotted as functions of α2 for various of α1

Full size image

The squeeze number (\(\Gamma_{0} = \frac{{12\mu_{0} \omega l^{'2}}}{{p_{a} h_{0}^{2}}}\) for isothermal cases) increases as the tilting frequency increases and/or h 0 decreases. The gas molecules in squeeze film can escape (or be squeeze out) rapidly at low squeeze number regime. On the contrary, the gas molecules do not have enough time to escape (or be trapped in the squeeze film) at high squeeze number regime. As shown in Fig. 4a and b, the stiffness and damping coefficients are plotted for various combinations of ACs at a constant modified squeeze number \(\left(\Gamma = 10.0, \Gamma = \frac{{12\mu \omega l^{2} }}{{\eta p_{a} h_{0}^{2}}} = \frac{{\Gamma_{0} }}{{\bar{Q}}_{P} (D_{0}, \alpha_{1}, \alpha_{2})(\phi ^{p}_{x})_{0}}\right).\) At higher modified squeeze number (Γ = 100), the stiffness and damping coefficients are plotted as shown in Fig. 5a and b for various combinations of ACs. In Figs. 4a and 5a, the spring force increases as AC increases. In Fig. 4b, the damping force has the same tendency as that the spring force acts at low Γ region. In Fig. 5b, the damping force has the reverse tendency as the spring force acts at high Γ region. In Fig.4a the effect of ACs on the stiffness variations is as large as 14% for 0.3 ≤ α ≤ 1.0. However, the effect of ACs on the dynamic coefficients is not significant at high modified squeeze number. From Eq. (24a) and (24b), we have \(K \to \frac{{64\eta}}{{\pi^{4} }}{\sum\limits_{\begin{subarray}{l} m = {\rm even} \\ n = {\rm odd} \end{subarray}}^\infty {\frac{1}{{m^{2} n^{2}}}} } = \frac{1}{3}\) and B → 0 as the modified squeeze number increases to infinity (Γ → ∞). The effects of roughness and gas rarefaction should be treated as important matters except in the high squeeze number.

Fig. 4
figure 4

a Dimensionless stiffness coefficients plotted as functions of α2 for various of α1. b Dimensionless damping coefficients plotted as functions of α2 for various of α1

Full size image
Fig. 5
figure 5

a Dimensionless stiffness coefficients plotted as functions of α2 for various of α1. b Dimensionless damping coefficients plotted as functions of α2 for various of α1

Full size image

The effects of squeeze number on the dynamic coefficients are shown in Fig. 6a and b. As the squeeze number increases, the gas film is stiffened, and the dissipation of energy in the squeeze film is suppressed. The spring force increases with the tilting frequency, and the damping force increases till the cut-off frequency is reached and decreases thereafter. As presented in (Li 1999), the spring force increases as Γ0 increases, γ increases, or H S0 decreases. Four combinations of ACs are discussed for the gas rarefaction. The four discussion cases are: A(α1 = 0.5, α2 = 1), B(α1 = 0.8, α2 = 0.8), C(α1 = 0.8, α2 = 1.0), and D(α1 = 1.0, α2 = 1.0). The effects of AC on the spring force and damping force are plotted in Fig.6a. The spring force has the following relations: A < B < C < D. The damping force has the following relation: A < B < C < D at low tilting frequency, and A < B < C < D at high tilting frequency. The squeeze number and the modified squeeze number has the following relation, \(\Gamma_{0} = {\bar{Q}}_{P} \times (\phi ^{p}_{x})_{0} \times \Gamma.\) For the present longitudinal type roughness (γ = 9), the pressure flow factor is greater than 1.0, i.e., (ϕ p x )0 > 1. So, the product \({\bar{Q}}_{P} \times (\phi^{p}_{x})_{0}\) is always greater than 1.0. As the gas rarefaction effect increases, the increase in Poiseuille flow corrector \({\bar{Q}}_{P}\) is more significant than the decreases in the pressure flow factor. In Table 1, the product \({\bar{Q}}_{P} \cdot (\phi ^{p}_{x})_{0}\) for these four cases are shown at the operating conditions of D 0 = 10, γ = 9, H S0 = 3.0, and β′ = 2. The product \({\bar{Q}}_{P} \times (\phi^{p}_{x})_{0}\) increases as the effect of gas rarefaction increases. As the product \({\bar{Q}}_{P} \times (\phi^{p}_{x})_{0}\) increases further, the horizontal axis (Γ) in the original curve of dynamic coefficients in the transformed domain (Eqs. 24a and 24b) is more stretched to the present Fig. 6a. So, as the gas rarefaction increase, the dynamic coefficients decrease except for the damping coefficients in the high squeeze number region. In Fig. 6b, the room-in view of Fig. 6a are plotted. From Fig. 7, the cut-off frequency (Γ0C ) increases as the effect if gas rarefaction increases (AC decreases or D 0 decreases). The variation of cut-off frequency in the region of α1(0.3–1.0) is smaller at larger D 0.

Fig. 6
figure 6

a Dimensionless stiffness and damping coefficients plotted as functions of squeeze number for various combinations of (α1, α2). b Dimensionless stiffness and damping coefficients plotted as functions of squeeze number for various combinations of (α1, α2)—room in view

Full size image
Fig. 7
figure 7

Cut-off squeeze number plotted as functions of α2 for various of α1 and D 0

Full size image

4 Conclusion

The present analysis proposed a close form expression of stiffness and damping coefficients for tilting micromirrors. The coupling effects of surface roughness and gas rarefaction (first-order slip-flow model with non-symmetric ACs) are considered simultaneously. The results show that ACs affect the dynamic coefficient significantly. The decreases in inverse Knudsen number and/or decreases in AC will increase the gas rarefaction. Thus, the dynamic coefficients decreases except for the damping coefficients at high squeeze number region. Also, the cut-off frequency increases as the gas rarefaction effects increase.