1 Introduction

The exponential growth of technology, together with a rapid dissemination of knowledge, made us question the validity of some “empirical laws” that were considered an absolute truth in the past, as happens for the no-slip boundary condition at walls. Based on the experiments with Newtonian fluids, the no-slip boundary condition became popular and, above all, it was considered as a law, as stated in many books on the subject of fluid mechanics. However, the no-slip boundary condition is nothing more than an empirical model, which is an excellent approximation in most cases.

For some non-Newtonian fluids, such as polymer melts, it is nowadays consensually accepted the existence of slip velocity between the fluid and the solid wall (Brochard and de Gennes 1992; de Gennes 1979; Denn 2001; Inn and Wang 1996; Kraynik and Schowalter 1981; Léger et al. 1999; Migler et al. 1993; Schowalter 1988; Wan 1999). The same applies to electro-osmotic flow (Marry et al. 2003; Herr et al. 2000), flow in microfluidic devices (Gad-el-Hak 1999; Stone et al. 2004), biological processes (Zhang et al. 2003; Beebe et al. 2002), and gas flow (incidentally, the assumption that gases may exhibit wall slip was first introduced by Maxwell 1879).

Even for Newtonian fluids, where the no-slip boundary condition fits well the macroscopic experimental data, some recent experiments in microfluidic flows showed the inaccuracy of such boundary condition (Pit et al. 2000; Craig et al. 2001; Zhu and Granick 2001; Horn et al. 2000; Baudry et al. 2001; Bonaccurso et al. 2002).

In the last decade, we have witnessed a fast evolution in micro- and nanofluidics, and electro-osmotic flows have also attracted the scientific community, especially due to its applicability to chemical analysis, medical research, and possibly in the mixing of fluids with microscale flows.

Several works have been published on electro-osmotic flow, such as the ones of Soong et al. (2008) and Jamaati et al. (2010), regarding the Newtonian pressure-driven electrokinetic flows in hydrophobic and planar microchannels. For non-Newtonian fluids, Afonso et al. (2009, 2011) presented analytical solutions of mixed electro-osmotic/pressure-driven viscoelastic fluids in microchannels for electro-osmotic flow under symmetric and asymmetric zeta potentials using the Phan-Thien and Tanner (1977, 1978) model to describe the viscoelasticity; Dhinakaran et al. (2010) analyzed the full PTT model with nonzero second normal stress difference; and Afonso et al. (2012) derived the analytical solution for fully developed electro-osmosis-driven flow of polymer solutions, described by the sPTT and FENE-P models with a Newtonian solvent contribution.

The existence of slip between the fluid and the wall is an interfacial phenomenon that influences the hydrodynamics of micro- and nanoflows, as discussed in Tretheway and Meinhart (2002, 2002), Tandon and Kirby (2008), and Tandon et al. (2008), and therefore, appropriate boundary conditions should be used to properly model the flow process. The Navier slip boundary condition (Navier 1827) is the most widely used model to describe such effect.

In microfluidics, it is common to use channels with walls made from different materials. For instance, in soft lithography, the channels are often made in polydimethylsiloxane (PDMS) except for the top wall that is often made of glass for optical access, which emphasizes the practical relevance of asymmetric flows.

In this work, we present an analytical solution for mixed pressure-driven electrokinetic slip flows of viscoelastic fluids in hydrophobic microchannels, with asymmetric zeta potential and under the influence of the Navier slip boundary condition at the channel walls.

Section 2 starts with the set of governing equations including the nonlinear Poisson–Boltzmann equation governing the electric double-layer (EDL) field and the added body force to the momentum equation, caused by the applied electrical potential field. In Sect. 3, we present the analytical solution for the sPTT and FENE-P models, including the particular case of streaming potential. A discussion of the Navier slip coefficient effects upon the flow characteristics and the main conclusions obtained closes this work.

2 Governing equations

The governing equations for this type of flow are the continuity equation,

$$ \nabla\cdot{\bf u}=0 $$
(2.1)

and the momentum equation,

$$ \rho\frac{\hbox{D}{\bf u}}{\hbox{D}t}=\nabla\cdot \varvec{\tau}-\nabla p+\rho_{e}{\bf E} $$
(2.2)

where u is the velocity vector, p the pressure, t the time, ρ the constant fluid density (incompressible flow), and \({\varvec{\tau}}\) the polymeric extra-stress contribution, which is here described by the sPTT constitutive model (Phan-Thien and Tanner 1977; Phan-Thien 1978),

$$ f(\tau_{kk})\varvec{\tau}+\lambda \left(\frac{\hbox{D}\varvec{\tau}}{\hbox{D}t}- \nabla{\bf u}^{{\rm T}}\cdot\varvec{\tau}- \varvec{\tau}\cdot\nabla{\bf u}\right)=2\eta{\bf D}, $$
(2.3)

where D is the rate of deformation tensor (\({\bf D}=\frac{1}{2}\left(\nabla{\bf u}+ \nabla{\bf u}^{{\rm T}}\right)\)), λ is the relaxation time of the fluid, η is the viscosity coefficient, \(\tau_{kk}=\tau_{xx}+\tau_{yy}+ \tau_{zz}\) is the trace of the extra-stress tensor and \(f(\tau_{kk})=1+\frac{\varepsilon\lambda}{\eta} \tau_{kk}\) (the linear version of the function). Note that although the transient term is present in the full Eqs. (2.2) and (2.3), this study is carried out assuming a steady-state flow; thus, the unsteady terms are discarded in the remaining analysis.

In Eq. (2.2), ρ e E represents a body force term, where E is the applied external electric field and ρ e is the net electric charge density associated with the spontaneously formed electric double layers (EDL, see Bruus 2008 for more details), which are assumed here not to be affected by the imposed electric field. The electric field is related to a potential (\(\Upphi\)), \({\bf E}=-\nabla{\Upphi}\), with \(\Upphi=\psi+\phi\), where ϕ is the applied streamwise potential and ψ is the equilibrium-induced potential at the channel walls, associated with the interaction between the ions of the fluid and the wall dielectric properties.

The different concentrations of counterions and co-ions lead to the creation of a varying potential field, within the electric double layer, that can be expressed by means of a Poisson equation:

$$ \nabla^{2}\psi=-\frac{\rho_{e}}{\epsilon} $$
(2.4)

where ψ denotes the EDL potential and \(\epsilon\) is the dielectric constant of the solution.

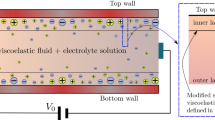
In this work, we assume that the microchannel walls can be made of different materials (e.g., glass and PDMS), leading to different hydrophobic characteristics, different zeta wall potentials (see Fig. 1), and different slip boundary conditions. In some previous works dealing with Newtonian fluids (Soong et al. 2010), a slip-dependent zeta potential is employed. Information on this issue is still rather limited and is essentially focused on Newtonian fluids. The addition of macromolecules to water to produce viscoelastic solutions has a strong impact upon the interaction between the fluid and the wall (for instance, adsorption or the formation of a skimming layer are two examples), so that the relationship between the zeta potential and slip coefficients of rheologically complex fluids is still unknown. Therefore, we have decided to carry out this work assuming those two quantities can be independent of each other in order to arrive at a more general analytical solution, which can be easily modified in the future to account for the slip-dependent zeta potential relationship. As boundary condition, we assume the linear Navier slip law with different slip coefficients (Navier 1827), \(\mathcal{L}_{1}\) and \(\mathcal{L}_{2}\), for the bottom and top walls, respectively,

$$ \left\{ \begin{array}{cc} u_{\Vert {\rm wall1}} =+{\mathcal{L}}_{1}\tau_{xy\Vert {\rm wall1}}\\ \\ u_{\Vert {\rm wall2}} =-{\mathcal{L}}_{2}\tau_{xy\Vert {\rm wall2}}\end{array}\right. $$
(2.5)

where u is the streamwise velocity component and τ xy is the shear stress at the wall, which is parallel to the x−axis (cf. coordinate system in Fig. 1).

Fig. 1
figure 1

Schematic view of the flow in a parallel plate microchannel

Full size image

For the symmetric case, we will also consider the nonlinear Navier slip boundary condition,

$$ \left|u_{\Vert wall}\right|={\mathcal{L}}_{s}\left|\tau_{xy\Vert wall}\right|^{m} $$
(2.6)

where m is the slip exponent.

We remark that for pure pressure-driven flows of viscoelastic fluids, one can find in the literature that values of m range from 1 (Newtonian) to 4 (Chatzimina et al. 2009). For electro-osmotic flows of viscoelastic fluids under the influence of slip, the literature is scarce and we could not find any experimental data. Therefore, as was done in the past for pressure-driven flows, we extend the Navier slip law (used for Newtonian fluids) to a more general model that is able to deal with wall slip boundary conditions for viscoelastic fluids. In this way, we obtain a more general solution that can cope with various degrees of slip and different classes of fluids.

3 Analytical solution

3.1 Asymmetric boundary conditions

Considering the flow between parallel plates (Fig. 1) and by assuming the Debye–Hückel approximation, (\(\frac {{\text d^{2}}\psi}{{\text{d}}{y^{2}}}\,=\,{\kappa^{2}}{\psi},\) where \(\kappa^{2}\,=\,{2{n_0}e^{2}z^{2}}/{\epsilon{k_B}{T}}\) is the Debye–Hückel parameter—more details in Afonso et al. 2011), together with different zeta potential at the walls, \(\psi_{\Vert y=-H}=\zeta_{1}\) and \(\psi_{\Vert y=H}=\zeta_{2}\), Eq. (2.4) leads to:

$$ \psi(y)=\zeta_{1}\left(\Uppsi_{1}\hbox{e}^{\kappa y}-\Uppsi_{2}\hbox{e}^{-\kappa y}\right) $$
(3.1)

The net electric charge density is given by (Afonso et al. 2011)

$$ \rho_{e}=-\epsilon\kappa^{2}\zeta_{1}\left(\Uppsi_{1}\hbox{e}^{\kappa y}-\Uppsi_{2}\hbox{e}^{-\kappa y}\right)=-\epsilon\kappa^{2}\zeta_{1}\Upomega_{1}^{-}(y), $$
(3.2)

where \(\Uppsi_{1}=\frac{\left(R_{\zeta}\hbox{e}^{\kappa H}-\hbox{e}^{-\kappa H}\right)}{2\sinh(2\kappa H)}\), \(\Uppsi_{2}=\frac{\left(R_{\zeta}\hbox{e}^{-\kappa H}-\hbox{e}^{\kappa H}\right)}{2\sinh(2\kappa H)}, R_{\zeta}=\zeta_{2}/\zeta_{1}\) denotes the ratio of the zeta potentials of the two walls within the range −H ≤ y ≤ H, and \(\Upomega_{p}^{\pm}(y)=\Uppsi_{1}^{p}\left(\hbox{e}^{\kappa y}\right)^{p}\pm\Uppsi_{2}^{p}\left(\hbox{e}^{-\kappa y}\right)^{p}\).

Assuming the fully developed flow of a fluid modeled by the sPTT model, the constitutive equation (Eq. 2.3) can be further simplified (for more details, see Afonso et al. 2011), leading to

$$ f(\tau_{kk})\tau_{xx}=2\lambda\dot{\gamma}\tau_{xy} $$
(3.3)
$$ f(\tau_{kk})\tau_{xy}=\eta\dot{\gamma}, $$
(3.4)

where \({\tau}_{kk}={\tau}_{xx}\) is the trace of the extra-stress tensor (note that τ yy  = τ zz  = 0) and \(\overset{\cdot}{\gamma}=\hbox{d}u/\hbox{d}y\) is the velocity gradient. The ratio between Eqs. (3.3) and (3.4) leads to

$$ \tau_{xx}=2\frac{\lambda}{\eta}\tau_{xy}^{2} $$
(3.5)

For the particular flow conditions considered, the momentum equation (Eq. 2.2) can also be simplified to

$$ \frac{\hbox{d}\tau_{xy}}{\hbox{d}y}=-\rho_{{\rm e}} E_{x}+p_{,x}, $$
(3.6)

where \(p_{,x}\equiv\hbox{d}p/\hbox{d}x, E_{x}\equiv-\hbox{d}\phi/\hbox{d}x\) and ϕ is the electric potential of the applied external field, which is characterized by a constant streamwise gradient. The external electrical field is positive if in accordance with Fig. 1 and negative otherwise.

Integration of Eq. (3.6) yields the following expression for the shear stress distribution,

$$ \tau_{xy}=\epsilon\kappa\zeta_{1}E_{x}\Upomega_{1}^{+}(y)+p_{,x}y+ \tau_{1}, $$
(3.7)

and making use of Eq. (3.5), the normal stress component is given by

$$ \tau_{xx}=2\frac{\lambda}{\eta}\left(\epsilon\kappa\zeta_{1}E_{x} \Upomega_{1}^{+}(y)+p_{,x}y+\tau_{1}\right)^{2}. $$
(3.8)

where τ1 is a shear stress integration constant to be quantified later from the slip boundary conditions.

If we combine Eqs. (3.4), (3.7), and (3.8), the velocity gradient distribution is obtained, given as

$$ \overset{\cdot}{\gamma} \equiv\frac{\hbox{d}u}{\hbox{d}y}=\left[1+2\varepsilon\lambda^{2} \left(\frac{\epsilon E_{x}\zeta_{1}}{\eta}\kappa\Upomega_{1}^{+}(y)+ \frac{p_{,x}}{\eta}y+\overset{\cdot}{\gamma_{1}}\right)^{2}\right] \left(\frac{\epsilon E_{x}\zeta_{1}}{\eta}\kappa\Upomega_{1}^{+}(y)+ \frac{p_{,x}}{\eta}y+\overset{\cdot}{\gamma_{1}}\right) $$
(3.9)

where the shear rate asymmetry coefficient is defined as \(\overset{\cdot}{\gamma_{1}}=\tau_{1}/\eta\). Eq. (3.9) can be integrated subject to the slip boundary condition at the lower wall (y =  − H)

$$ u_{\Vert y=-H}={\mathcal{L}}_{1}\tau_{xy\Vert y=-H}. $$
(3.10)

resulting in a velocity profile that depends on \(\overset{\cdot}{\gamma_{1}}\). The restriction imposed by the upper wall \(\left(y=H\right)\) slip boundary condition (Eq. 3.11) provides the equation for \(\overset{\cdot}{\gamma_{1}}\)

$$ u_{\Vert y=H}=-{\mathcal{L}}_{2}{\tau}_{xy\Vert y=H} $$
(3.11)

Note that the slip velocity can assume different directions as illustrated in Fig. 2. This is a consequence from the fact that \({{\tau}}_{xy\Vert y=H}\) can be either positive or negative, depending on the flow direction. We note, however, from Eqs. (3.3) and (3.5) that τ xy and the velocity gradient have necessarily the same sign.

Fig. 2
figure 2

Schematic view of the flow in a parallel plate microchannel with different flow conditions at the upper wall: a positive slip velocity; b negative slip velocity

Full size image

After integration and introducing the normalizations \(\bar{y}=y/H\) and \(\bar{\kappa}=\kappa H\), the dimensionless velocity profile is then given by

$$ \begin{aligned} \frac{u}{u_{sh}} &=-\overline{{\mathcal{L}}_{1}}\left(\overline{\kappa} \overline{\Upomega}_{1}^{+}(-1)+\Upgamma-\overline{\overset{\cdot}{ \gamma}}_{1}\right)\\ &\quad +\overline{\overset{\cdot}{\gamma}}_{1}\left(\overline{y}+1\right) \left(1+2\overline{\overset{\cdot}{\gamma}}_{1}^{2}\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\right)-\left(1+6 \overline{\overset{\cdot}{\gamma}}_{1}^{2}\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\right)\overline{\Upomega}_{1,1}^{-} (\overline{y}) \\ &\quad +2\overline{\overset{\cdot}{\gamma}}_{1}\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}}\left(6\Uppsi_{1}\Uppsi_{2}\overline{\kappa}\left(\overline{{y}}+1\right)+\frac{3}{2}\overline{\Upomega}_{2,1}^{-}(\overline{y})\right) \\ &\quad -2\varepsilon Wi_{\kappa}^{2}\left(\frac{1}{3}\overline{\Upomega}_{3,1}^{-}(\overline{y})+3\Uppsi_{1}\Uppsi_{2}\overline{\Upomega}_{1,1}^{-}(\overline{y})\right) \\ &\quad +\frac{1}{2}\Upgamma\left(\overline{y}^{2}-1\right)\left(1+6\overline{\overset{\cdot}{\gamma}}_{1}^{2}\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}+\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\Upgamma^{2}\left(\overline{y}^{2}+1\right)\right) \\ &\quad +2\overline{\overset{\cdot}{\gamma}}_{1}\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\Upgamma^{2}\left(\overline{y}^{3}+1\right) \\ &\quad -12\overline{\overset{\cdot}{\gamma}}_{1}\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{3}}\Upgamma\left(\overline{\Upomega}_{1,2}^{-}(\overline{y})-\overline{\Upomega}_{1,1}^{+}(\overline{y})\right) \\ &\quad +6\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\Upgamma\left(\Uppsi_{1}\Uppsi_{2}\overline{\kappa}^{2}\left(\overline{{y}}^{2}-1\right)+\frac{1}{2}\overline{\Upomega}_{2,2}^{-}(\overline{y})-\frac{1}{4}\overline{\Upomega}_{2,1}^{+}(\overline{y})\right) \\ &\quad -6\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{4}}\Upgamma^{2}\left(\overline{\Upomega}_{1,3}^{-}(\overline{y})+2\overline{\Upomega}_{1,1}^{-}(\overline{y})-2\overline{\Upomega}_{1,2}^{+}(\overline{y})\right) \end{aligned} $$
(3.12)

where \(\overline{\Upomega}_{p,q}^{\pm}(y)\) is the normalized operator defined as

$$ \overline{\Upomega}_{p,q}^{\pm}(\overline{y}) =\left(\overline{\kappa}\; \overline{y}\right)^{(q-1)}\overline{\Upomega}_{p}^{\pm}(\overline{y}) -(-1)^{(q+1)}\overline{\kappa}^{(q-1)}\overline{\Upomega}_{p}^{\pm}(-1) $$
(3.13)

with \(\overline{\Upomega}_{p}^{\pm}(\overline{y})= \Uppsi_{1}^{p}\left(\hbox{e}^{\overline{\kappa} \;\overline{y}}\right)^{p} \pm\Uppsi_{2}^{p}\left(\hbox{e}^{-\overline{\kappa}\;\overline{y}}\right)^{p}\). The parameter \(\Upgamma=-\frac{H^{2}}{\epsilon\zeta_{1}}\frac{\mathit{p_{,x}}}{E_{x}}\) represents the ratio of pressure to electro-osmotic driving forces, \(\overline{\overset{\cdot}{\gamma}}_{1}= \frac{\overset{\cdot}{\gamma}_{1}H}{u_{sh}}\), \({\overline{\mathcal{L}_{1}}=\mathcal{L}_{1}\frac{\eta}{H}}\), and \(Wi_{\kappa}=\frac{\lambda u_{sh}}{\xi}=\lambda\kappa u_{sh}\) is the Weissenberg number based on the EDL thickness and on the Helmholtz–Smoluchowski electro-osmotic velocity, \(u_{sh}=-\frac{\epsilon\zeta_{1}E_{x}}{\eta}\) (Park and Lee 2008). For simplicity, the above terms were based on the zeta potential at the bottom wall (\(\psi_{\Vert y=-H}=\zeta_{1}\)).

The dimensionless shear rate asymmetry coefficient is calculated from the following cubic equation

$$ \overline{\overset{\cdot}{\gamma}}_{1}^{3}+\overline{a}_{1} \overline{\overset{\cdot}{\gamma}}_{1}^{2}+\overline{a}_{2} \overline{\overset{\cdot}{\gamma}}_{1}+\overline{a}_{3}=0, $$
(3.14)

with coefficients

$$ \begin{aligned} \overline{a}_{1} & =-\frac{3}{2}\overline{\Upomega}_{1,1}^{-}(1) \\ \overline{a}_{2} & =\frac{\overline{\kappa}^{2}}{2\varepsilon Wi_{\kappa}^{2}}+\Upgamma^{2}+6\overline{\kappa}^{2}\Uppsi_{1} \Uppsi_{2}+\frac{3}{4}\overline{\kappa}\overline{\Upomega}_{2,1}^{-}(1) -3\frac{\Upgamma}{\overline{\kappa}}\left(\overline{\Upomega}_{1,2}^{-}(1) -\overline{\Upomega}_{1,1}^{+}(1)\right)\\ &\quad +\frac{\overline{\kappa}^{2}\left(\overline{{\mathcal{L}}_{1}}+ \overline{{\mathcal{L}}_{2}}\right)}{4\varepsilon Wi_{\kappa}^{2}} \\ \overline{a}_{3} & =-\frac{1}{4}\frac{\overline{\kappa}^{2} \overline{\Upomega}_{1,1}^{-}(1)}{\varepsilon Wi_{\kappa}^{2}} -\frac{1}{2}\overline{\kappa}^{2}\left(\frac{1}{3} \overline{\Upomega}_{3,1}^{-}(1)+3\Uppsi_{1}\Uppsi_{2} \overline{\Upomega}_{1,1}^{-}(1)\right) \\ &\quad +\frac{3}{2}\Upgamma\left(\frac{1}{2}\overline{\Upomega}_{2,2}^{-}(1)- \frac{1}{4}\overline{\Upomega}_{2,1}^{+}(1)\right)-\frac{3}{2} \frac{\Upgamma^{2}}{\overline{\kappa}^{2}}\left(\overline{\Upomega}_{1,3}^{-} (1)+2\overline{\Upomega}_{1,1}^{-}(1)-2\overline{\Upomega}_{1,2}^{+}(1)\right)\\ &\quad +\frac{\overline{\kappa}^{3}}{4\varepsilon Wi_{\kappa}^{2}}\left(- \overline{{\mathcal{L}}_{1}}\;\overline{\Upomega}_{1}^{+}(-1)-\overline{{\mathcal{L}}_{2}}\;\overline{\Upomega}_{1}^{+}(1)\right)+\frac{\overline{\kappa}^{2}\Upgamma\left(- \overline{{\mathcal{L}}_{1}}+\overline{{\mathcal{L}}_{2}}\right)}{4 \varepsilon Wi_{\kappa}^{2}}. \end{aligned} $$
(3.15)

The relevant solution of this cubic equation is given in Eq. 3.21. Performing the integration of the velocity profile (Eq. 3.12) over the channel width, the following expression relating \(\overline{Q}\) and \(\Upgamma\) is obtained,

$$ \begin{aligned} \overline{Q} & = \frac{Q}{2Hu_{sh}}=\frac{\overline{u}}{u_{sh}}= \frac{1}{2}\int\limits_{-1}^{1}\frac{u}{u_{sh}}\rm{d}\overline{y}= -{\overline{{\mathcal{L}}}_{1}}\left(\overline{\kappa} \overline{\Upomega}_{1}^{+}(-1)+\Upgamma-\overline{\overset{\cdot}{ \gamma}}_{1}\right)\\ &\quad +{\overline{\overset{\cdot}{\gamma}}_{1}\left(1+2\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\overline{\overset{\cdot}{ \gamma}}_{1}^{2}\right)}-\frac{1}{2}\Upgamma\left(\frac{4}{5} \frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\Upgamma^{2}+ \frac{2}{3}\left(1+6\overline{\overset{\cdot}{\gamma}}_{1}^{2} \frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\right)\right) \\ &\quad +2\overline{\overset{\cdot}{\gamma}}_{1}\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\Upgamma^{2}-\frac{1}{2}\left(1+6 \frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}} \overline{\overset{\cdot}{\gamma}}_{1}^{2}\right)\left( \frac{\overline{\Upomega}_{1,1}^{+}(1)}{\overline{\kappa}}- 2\overline{\Upomega}_{1}^{-}(-1)\right) \\ &\quad +{\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}} \overline{\overset{\cdot}{\gamma}}_{1}\left(12\Uppsi_{1}\Uppsi_{2} \overline{\kappa}+\frac{3}{2}\left(\frac{\overline{\Upomega}_{2,1}^{+}( 1)}{2\overline{\kappa}}-2\overline{\Upomega}_{2}^{-}(-1)\right)\right)}\\ &\quad- {\varepsilon Wi_{\kappa}^{2}\left(\frac{\overline{\Upomega}_{3,1}^{+} (1)}{9\overline{\kappa}}-\frac{2}{3}\overline{\Upomega}_{3}^{-}(-1)+3 \Uppsi_{1}\Uppsi_{2}\left(\frac{\overline{\Upomega}_{1,1}^{+}(1)}{\overline{ \kappa}}-2\overline{\Upomega}_{1}^{-}(-1)\right)\right)} \\ &\quad -6\overline{\overset{\cdot}{\gamma}}_{1}\frac{\varepsilon Wi_{ \kappa}^{2}}{\overline{\kappa}^{4}}\Upgamma\left[\overline{\Upomega}_{1,2}^{+} (1)-2\overline{\Upomega}_{1,1}^{-}(1)+2\overline{\kappa}\left( \overline{\kappa}\overline{\Upomega}_{1}^{-}(-1)+\overline{\Upomega}_{1}^{+}(-1)\right)\right] \\ &\quad +3\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}} \Upgamma\left(\frac{1}{4\overline{\kappa}}\left(\overline{\Upomega}_{2,2}^{+} (1)-\overline{\Upomega}_{2,1}^{-}(1)\right)-\frac{4}{3}\Uppsi_{1}\Uppsi_{2} \overline{\kappa}^{2}+\overline{\kappa}\overline{\Upomega}_{2}^{-}(-1)+ \frac{1}{2}\overline{\Upomega}_{2}^{+}(-1)\right) \\ &\quad -3\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{5}} \Upgamma^{2}\left(\overline{\Upomega}_{1,3}^{+}(1)-4\overline{\Upomega}_{1,2}^{-} (1)+6\overline{\Upomega}_{1,1}^{+}(1)\right) \\ &\quad +6\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{4}} \Upgamma^{2}\left(\left(\overline{\kappa}^{2}+2\right) \overline{\Upomega}_{1}^{-}(-1)+2\overline{\kappa}\overline{\Upomega}_{1}^{+} (-1)\right). \end{aligned} $$
(3.16)

The expressions for the dimensionless shear and normal stress components are easily obtained from Eqs. (3.5) and (3.7), once \(\tau_{1}=\eta\overset{\cdot}{\gamma}_{1}\) is evaluated (from Eq. 3.14 in the form of the normalized \(\overline{\overset{\cdot}{\gamma}}_{1}\)).

The analytical solution for the FENE-P model can be easily derived from the sPTT solution, provided suitable substitutions are made (see Cruz et al. 2005).

3.2 Symmetric boundary conditions

Assuming equal zeta potentials at the walls, \(\psi_{\Vert y=-H}=\psi_{\Vert y=H}=\zeta\, (R_{\zeta}=1)\), analytical solutions can be derived using the linear \(\left(u_{\Vert wall}=\pm\mathcal{L}_{s}\tau_{xy\Vert wall}\right)\) and also the nonlinear Navier slip boundary condition \(\left(\left|u_{\Vert wall}\right|=\mathcal{L}_{s}\left|\tau_{xy\Vert wall}\right|^{m}\right)\).

Considering again the fully developed flow conditions, the dimensionless velocity profile is given by

$$ \begin{aligned} \frac{u}{u_{sh}} & =\overline{{\mathcal{L}}_{s}}\left|\overline{\kappa}\overline{D}-\Upgamma\right|^{m-1}\left(\overline{\kappa}\overline{D}-\Upgamma\right)+(1-2\overline{C}\varepsilon Wi_{\kappa}^{2})(1-\overline{A})+\frac{2}{3}\varepsilon Wi_{\kappa}^{2}(1-\overline{A}^{3}) \\ &\quad -\frac{1}{2}\Upgamma\left(1-\bar{y}^{2}\right)\left[1+\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{2}}\Upgamma^{2}\left(1+\bar{y}^{2}\right)\right] \\ &\quad +\frac{3}{2}\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{2}}\Upgamma\left[1-\overline{A}^{2}+\bar{\kappa}^{2}(1-\overline{y}^{2})\overline{C}+2\overline{\kappa}\overline{D}\left(\overline{y}\overline{A}\;\overline{B}-1\right)\right] \\ &\quad -\frac{12\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{4}}\Upgamma^{2}\left[\bar{\kappa}\overline{D}\left(1-\overline{y}\overline{B}\right)+(1+\frac{1}{2}\left(\bar{\kappa}\bar{y}\right)^{2})\overline{A}-(1+\frac{1}{2}\bar{\kappa}^{2})\right] \end{aligned} $$
(3.17)

where \(\overline{A}=\frac{\cosh\left(\bar{\kappa}\bar{y}\right)}{\cosh \left(\bar{\kappa}\right)}\), \(\overline{B}=\frac{\sinh\left( \bar{\kappa}\bar{y}\right)}{\sinh\left(\bar{\kappa}\right)}\), \(\overline{C}=\frac{1}{\cosh^{2}\left(\bar{\kappa}\right)}\), \(\overline{D}=\tanh\left(\bar{\kappa}\right)\), \({\overline{\mathcal{L}}=\mathcal{L}\left(\frac{\eta}{H}\right)^{m} \left|u_{sh}\right|^{m-1}}\), and the expression for the normalized flow rate is

$$ \begin{aligned} \overline{Q} & =\frac{Q}{{2}{Hu_{sh}}}=\frac{\overline{u}}{u_{sh}}=\int\limits_{0}^{1}\frac{u}{u_{sh}}\rm{d}\overline{\it {y}}=\overline{{\mathcal{L}}_{s}}\left|\bar{\overline{\kappa}}\overline{\it{D}}-\Upgamma\right|^{{\it{m}}-1}\left(\bar{\overline{\kappa}}\overline{\it {D}}-\Upgamma\right) \\ &\quad +\left(1-2\overline{C}\varepsilon Wi_{\kappa}^{2}\right)\left(1-\frac{\overline{D}}{\bar{\kappa}}\right)+\frac{2}{3}\varepsilon Wi_{\kappa}^{2}\left(1-\frac{1}{3}\frac{\overline{D}}{\bar{\kappa}}\left(1+2\overline{C}\right)\right)-\Upgamma\left(\frac{2}{5}\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{2}}\Upgamma^{2}+\frac{1}{3}\right) \\ &\quad +\frac {3}{2}\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{2}}\Upgamma\left(2-\frac{\overline{D}}{\bar{\kappa}}-\overline{C}+\frac{2}{3}\overline{C}\bar{\kappa}^{2}-2\bar{\kappa}\overline{D}\right)-\frac{12\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{4}}\Upgamma^{2}\left(-3+3\frac{\overline{D}}{\bar{\kappa}}+\frac{3}{2}\bar{\kappa}\overline{D}-\frac{1}{2}\bar{\kappa}^{2}\right) \end{aligned} $$
(3.18)

Equation (3.17) and (3.18) agree with Eqs. (3.12) and (3.16) when symmetric boundary conditions are used (\(R_{\zeta}=1\) and \(\overline{\overset{\cdot}{\gamma}}_{1}=0\)) and m = 1, but the former are preferred because of their simplicity (and the possibility of using the nonlinear Navier slip law).

For Navier slip coefficient with m = 1, 2, and 3, this is a cubic equation on \(\Upgamma\) and the solution of the inverse problem (calculation of \(\Upgamma\) for a given \(\overline{Q}\)) involves the determination of \(\Upgamma\), which can be done using the Cardano–Tartaglia solution for cubic algebraic equations. In many practical applications, the finite electric double layer is very small, about 1 to 3 orders of magnitude smaller than the thickness of the microfluidic channel (\( 10\; \lesssim \;\bar{\kappa }\; \lesssim \;10^{3} \)). In these circumstances, \(\cosh\left(\bar{\kappa}\right)\gg1\) and \(\overline{D}=\tanh\left(\bar{\kappa}\right)\approx1\), so the above equations for the velocity profile can be further simplified. In particular, the normalized flow rate becomes

$$ \begin{aligned} \overline{Q} & \simeq\overline{{\mathcal{L}}_{s}}\left|\overline{\kappa}-\Upgamma\right|^{m-1}\left(\overline{\kappa}-\Upgamma \right)+\left(\frac{\bar{\kappa}-1}{\bar{\kappa}}\right)+\frac{2}{3}\varepsilon Wi_{\kappa}^{2}\left(\frac{3\bar{\kappa}-1}{3\bar{\kappa}}\right)-\Upgamma\left(\frac{2}{5}\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{2}}\Upgamma^{2}+\frac{1}{3}\right) \\ & +\frac {3}{2}\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{2}}\Upgamma\left(\frac{2\bar{\kappa}-1-2\bar{\kappa}^{2}}{\bar{\kappa}}\right)-\frac{12\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{4}}\Upgamma^{2}\left(\frac{\bar{\kappa}}{2}\left(3-\bar{\kappa}\right)+\frac{3-3\bar{\kappa}}{\bar{\kappa}}\right) \end{aligned} $$
(3.19)

which is simpler than Eq. (3.18), but still cubic in \(\Upgamma\) for m = 1, 2, and 3. This expression can be written in a more compact form as

$$ \Upgamma^{3}+a_{1}\Upgamma^{2}+a_{2}\Upgamma+a_{3}=0 $$
(3.20)

for m = 1, 2 or 3. Eq. (3.20) comprises the explicit solution of the inverse problem, giving the ratio of pressure to electro-osmotic driving forces as a function of the dimensionless flow rate, viscoelastic model parameters, and relative microchannel ratio. The solution is obtained using the Cardano–Tartaglia formula (for simplicity, here we consider the usual case \(\overline{\kappa}-\Upgamma\;>\;0\)),

$$ \begin{aligned} \Upgamma & =\sqrt[3]{-\frac{b_{1}}{2}+\sqrt{\frac{b_{1}^{2}}{4}+ \frac{a^{3}}{27}}}+\sqrt[3]{-\frac{b_{1}}{2}-\sqrt{\frac{b_{1}^{2}}{4}+ \frac{a^{3}}{27}}}-\frac{a_{1}}{3} \\ a & =a_{2}-\frac{a_{1}^{2}}{3} \\ b_{1} & =a_{3}-\frac{a_{1}a_{2}}{3}+\frac{2a_{1}^{3}}{27} \end{aligned} $$
(3.21)

with

$$ \begin{aligned} a_{1} & =\frac{12\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{4}}\left(\frac{\bar{\kappa}}{2}\left(3-\bar{\kappa}\right)+\frac{3-3\bar{\kappa}}{\bar{\kappa}}\right)-\left(m-1\right)\overline{{\mathcal{L}}_{s}}\left(\frac{3}{2}\overline{\kappa}\right)^{m-2}}{\left(\frac{2}{5}\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{2}}+\delta_{m3}\overline{{\mathcal{L}}_{s}}\right)} \\ a_{2} & =\frac{\frac{1}{3}-\frac{3}{2}\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{2}}\left(\frac{2\bar{\kappa}-1-2\bar{\kappa}^{2}}{\bar{\kappa}}\right)+m\overline{{\mathcal{L}}_{s}}\overline{\kappa}^{m-1}}{\left(\frac{2}{5}\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{2}}+\delta_{m3}\overline{{\mathcal{L}}_{s}}\right)}\\ a_{3} & =\frac{\overline{Q}-\left(\frac{\bar{\kappa}-1}{\bar{\kappa}}\right)-\frac{2}{3}\varepsilon Wi_{\kappa}^{2}\left(\frac{3\bar{\kappa}-1}{3\bar{\kappa}}\right)-\overline{{\mathcal{L}}_{s}}\overline{\kappa}^{m}}{\left(\frac{2}{5}\frac{\varepsilon Wi_{\kappa}^{2}}{\bar{\kappa}^{2}}+\delta_{m3}\overline{{\mathcal{L}}_{s}}\right)} \end{aligned} $$
(3.22)

where δ m3 is a Kronecker delta that assumes the value of 1 for m = 3 and 0 for m = 1 or 2.

4 Results and discussion

In order to understand the influence of the slip velocity on the fluid flow, we present the results for the velocity profiles of an sPTT fluid under the mixed influence of electro-osmotic/pressure-driven forces and symmetric/asymmetric hydrophobic wall zeta potentials, and assuming different slip coefficients at both walls. The influence of the slip velocity on the coefficient of asymmetry is also studied.

4.1 Symmetric boundary conditions

4.1.1 Newtonian fluid with mixed drive forcings and wall slip

For a Newtonian fluid, the Weissenberg number vanishes (Wi κ = 0); thus, Eq. (3.17) becomes

$$ \frac{u}{u_{sh}}=\overline{{\mathcal{L}}_{s}}\left|\overline{\kappa} \overline{D}-\Upgamma\right|^{m-1}\left(\overline{\kappa}\overline{D}-\Upgamma\right)\,+\,(1-\overline{A})-\frac{1}{2}\Upgamma \left(1-\bar{y}^{2}\right) $$
(4.1)

under the mixed influence of electro-osmotic and pressure-driven forcings. For \(\Upgamma\rightarrow0\), the last term on the right-hand side of Eq. (4.1) vanishes, the flow becomes governed solely by the electro-osmosis, and the velocity profile is only a function of the wall distance and the relative microchannel ratio, \(\bar{\kappa}\). When \(\frac{1}{\Upgamma}\rightarrow0\), pressure forcing dominates the momentum transport and the classical laminar parabolic velocity profile is recovered. Figure 3 shows velocity profiles for various ratios of pressure gradient to electro-osmotic driving forcings at \(\bar{\kappa}=20\) and \(\bar{\kappa}=100\) for two different values of the slip coefficient, \({\overline{\mathcal{L}_{s}}=0}\) and 0.002 (m = 1). When \(\Upgamma=0\) the velocity profiles correspond to a pluglike flow. The cases \(\Upgamma<0\) and \(\Upgamma>0\) correspond to mixed Poiseuille/electro-osmotic flows with favorable and adverse pressure gradients, respectively. Equation (4.1) predicts negative velocities at \(\bar{y}=0\) when \({\Upgamma>\frac{2}{2\overline{\mathcal{L}_{s}}+1} \left(\frac{\cosh\left(\bar{\kappa}\right)-1}{\cosh \left(\bar{\kappa}\right)}\right)+\frac{2 \overline{\mathcal{L}_{s}}}{2\overline{\mathcal{L}_{s}}+1} \overline{\kappa}\tanh\left(\bar{\kappa}\right)}\), for the linear Navier slip law \(\left(m=1\right)\). For small Debye lengths, \( \bar{\kappa }\; \gtrsim \;10 \), the velocity becomes negative in the central region of the channel for \({\Upgamma\gtrsim\frac{2+2 \overline{\mathcal{L}_{s}}\overline{\kappa}}{2 \overline{\mathcal{L}_{s}}+1}}\), which, as expected, reduces to the solution without slip, \(\Upgamma\gtrsim2\), as found in Afonso et al. (2009) when \({\overline{\mathcal{L}_{s}}\rightarrow0}\). When comparing with the no-slip solutions, we can conclude that the presence of slip velocity affects the velocity profile and requires larger adverse pressure gradients to obtain negative velocities.

Fig. 3
figure 3

Velocity profiles for various ratios of pressure to electro-osmotic driving forcings, \(\Upgamma\), and various slip coefficients, \({\bar{\mathcal{L}_{s}}=0}\) (solid line) and 0.002 (dashed line), for Newtonian fluids with m = 1 and relative microchannel ratio of (a) \(\bar{\kappa}=20\) and (b) \(\bar{\kappa}=100\)

Full size image

4.1.2 Viscoelastic fluid flow driven by electro-osmosis with wall slip

For pure electro-osmotic flow (\(\Upgamma=0\)) of a viscoelastic fluid, Eq. (3.17) reduces to

$$ \frac{u}{u_{sh}} =\overline{{\mathcal{L}}_{s}}\left(\overline{\kappa} \overline{D}\right)^{m}+(1-2\overline{C}\varepsilon Wi_{\kappa}^{2})(1-\overline{A})+\frac{2}{3}\varepsilon Wi_{\kappa}^{2}(1-\overline{A}^{3}) $$
(4.2)

Figure 4a, b show the dimensionless velocity profiles as a function of \(\sqrt{\varepsilon}Wi_{\kappa}\) for two relative microchannel ratios \(\bar{\kappa}=20\) and \(\bar{\kappa}=100, \) with and without slip at the wall. By comparing with the Newtonian case, we see that a pluglike velocity profile is again obtained, but now \(\sqrt{\varepsilon}Wi_{\kappa}\) and \({\overline{\mathcal{L}_{s}}}\) both contribute to an increase in the velocity plateau, especially for \(\bar{\kappa}=100\) where the effect of the slip velocity is more significant. The influence of \(\bar{\kappa}\) on the velocity profile is restricted to the effective EDL thickness, with the velocity profiles for higher values of \(\bar{\kappa}\) exhibiting thinner EDL layers and consequently larger velocity gradients (or shear rates). In Fig. 5, we analyze the effect of the slip law exponent m on the velocity profile. The profiles show that an increase in m leads to an increase in the velocity plateau, with the influence of m on the increase in the flow rate being more important than that of \({\overline{\mathcal{L}_{s}}}\).

Fig. 4
figure 4

Dimensionless velocity profiles of a PTT fluid for various values of \(\sqrt{\varepsilon}Wi_{\kappa}\) under pure electro-osmotic flow (\(\Upgamma=0\)) (\({\bar{\mathcal{L}_{s}}=0}\) solid lines, \({\bar{\mathcal{L}_{s}}=0.002}\) dashed lines). a \(\bar{\kappa}=20\) and b \(\bar{\kappa}=100\)

Full size image
Fig. 5
figure 5

Dimensionless velocity profiles of a PTT fluid for various values of \(\sqrt{\varepsilon}Wi_{\kappa}\), m and \({\bar{\mathcal{L}_{s}}}\) and constant \(\bar{\kappa}=20\) under pure electro-osmotic flow (\(\Upgamma=0\))

Full size image

4.1.3 Viscoelastic fluid with mixed drive forcings and wall slip

The viscoelastic flow characteristics under the combined action of electro-osmosis and pressure gradient forcings are discussed in this section, based on Eq. (3.17). Figure 6a, b present dimensionless velocity profiles for flows with favorable \(\left(\Upgamma<0\right)\) and adverse \(\left(\Upgamma>0\right)\) pressure gradients, respectively. In both cases, the velocity profiles increase with \(\sqrt{\varepsilon}Wi_{\kappa}\) and \({\overline{\mathcal{L}_{s}}}\), and, as also shown in Fig. 4, the increase due to the slip coefficient \({\overline{\mathcal{L}_{s}}}\) contribution is more intense for higher values of \(\sqrt{\varepsilon}Wi_{\kappa}\).

Fig. 6
figure 6

Dimensionless velocity profiles for a PTT fluid under the mixed influence of electro-osmotic/pressure-driven forces as a function of \(\sqrt{\varepsilon}Wi_{\kappa}\) and \({\bar{\mathcal{L}_{s}}}\) with a relative microchannel ratio of \(\bar{\kappa}=20\) (\({\overline{\mathcal{L}_{s}}} = 0\) (solid line); \({\overline{\mathcal{L}_{s}}} = 0.002\) , m = 1 (dashed line)): a favorable pressure gradient (\(\Upgamma=-1\)) and b adverse pressure gradient (\(\Upgamma=2.5\))

Full size image

The effect of the slip velocity on the velocity profile can be evaluated by imposing a constant dimensionless flow rate \(\overline{Q}\). Fig. 7a, b present velocity profiles as a function of \({\overline{\mathcal{L}_{s}}}\) at the flow rate \(\overline{Q}=\frac {1}{2}\), for the cases \(\sqrt{\varepsilon}Wi_{\kappa}=0\) and \(\sqrt{\varepsilon}Wi_{\kappa}=2\). The influence of viscoelasticity leads to a decrease in the centerline velocity (see Fig. 7b) when compared to the Newtonian case (see Fig. 7a), and the slip velocity enhances this effect. Simultaneously, an increase in the velocity gradients in the EDL layers is observed for higher \(\sqrt{\varepsilon}Wi_{\kappa}\) and \({\overline{\mathcal{L}_{s}}}\). This is mainly a consequence of shear thinning, inherent to the viscoelastic model employed, which promotes higher velocity gradients near the wall, and consequently lower velocities near the symmetry plane for the same flow rate. Figure 7c, d show similar results, but now for a higher dimensionless flow rate, \(\overline{Q}=\frac {3}{2}\).

Fig. 7
figure 7

Dimensionless velocity profiles for Newtonian (\(\sqrt{\varepsilon}Wi_{\kappa}=0\)) and PTT fluids (\(\sqrt{\varepsilon}Wi_{\kappa}=2\)) under the mixed influence of electro-osmotic/pressure-driven forces for different values of the slip coefficient \({\bar{\mathcal{L}_{s}}}\) and \(\overline{\kappa}=20\): a \(\overline{Q}=\frac {1}{2}\) and \(\sqrt{\varepsilon}Wi_{\kappa}=0\); b \(\overline{Q}=\frac{1}{2}\) and \(\sqrt{\varepsilon}Wi_{\kappa}=2\); c \(\overline{Q}=\frac{3}{2}\) and \(\sqrt{\varepsilon}Wi_{\kappa}=0\); d \(\overline{Q}=\frac{3}{2}\) and \(\sqrt{\varepsilon}Wi_{\kappa}=2\)

Full size image

In order to assess the influence of \(\Upgamma\) on the dimensionless flow rate \(\overline{Q}\), in Fig. 8, we show the variation of \(\frac{\overline{Q}}{\overline{Q}_{N}}\) (\(\overline{Q}_{N}\) is the flow rate that would be observed for a Newtonian fluid with no-slip velocity for each \(\Upgamma\)) with \(\Upgamma\) for \(\overline{\kappa}=20\) and different values of \({\bar{\mathcal{L}_{s}}}\) and \(\sqrt{\varepsilon}Wi_{\kappa}\). For \(\sqrt{\varepsilon}Wi_{\kappa}=0\) (Newtonian fluid) we can see that the dimensionless flow rate always increases with \(\Upgamma\) (except at the critical value \(\Upgamma = 2.85\), for which \(\overline{Q}_N = 0\)) while for the other values of \(\sqrt{\varepsilon}Wi_{\kappa}\) and \({\bar{\mathcal{L}_{s}}}\) the dimensionless flow rate is non-monotonic. This can also be seen in Fig. 9, which illustrates the variation of \(\frac{\overline{Q}}{\overline{Q}_{N}}\) as a function of \(\sqrt{\varepsilon}Wi_{\kappa}\) and \({\bar{\mathcal{L}_{s}}}\), for two different values of \(\Upgamma\). The parameter \(\sqrt{\varepsilon}Wi_{\kappa}\) leads to a significant increase in \(\frac{\overline{Q}}{\overline{Q}_{N}}\) , due to the shear shinning effect mentioned above, and an increase in the slip velocity also enhances \(\frac{\overline{Q}}{\overline{Q}_{N}}\), as expected.

Fig. 8
figure 8

Dimensionless flow rate \(\frac{\overline{Q}}{\overline{Q}_{N}}\) as a function of \(\Upgamma\) for pressure-driven/electro-osmotic flow of a PTT fluid for \(\overline{\kappa}=20\) and different values of the slip coefficient, \({\bar{\mathcal{L}_{s}}}\), and \(\sqrt{\varepsilon}Wi_{\kappa}\)

Full size image
Fig. 9
figure 9

Variation of the dimensionless flow rate \(\frac{\overline{Q}}{\overline{Q}_{N}}\) with \(\sqrt{\varepsilon}Wi_{\kappa}\) and the slip coefficient \({\bar{\mathcal{L}_{s}}}\) (m = 1)for the pressure-driven/electro-osmotic flow of a PTT fluid for relative microchannel ratio \(\overline{\kappa}=20\): a favorable pressure gradient (\(\Upgamma=-1\)) and b adverse pressure gradient (\(\Upgamma=2.5\))

Full size image

4.2 Asymmetric boundary conditions

4.2.1 Pure electro-osmosis

For the sPTT fluid under pure electro-osmotic driving force, the simplified velocity solution is derived by setting \(\Upgamma=0\) in Eq. (3.12), which reduces to

$$ \begin{aligned} \frac{u}{u_{sh}} & =-\overline{{\mathcal{L}}_{1}}\left(\overline{\kappa}\overline{\Upomega}_{1}^{+}(-1)-\overline{\overset{\cdot}{\gamma}}_{1}\right)\\ &\quad +\overline{\overset{\cdot}{\gamma}}_{1}\left(\overline{y}+1\right)\left(1+2\overline{\overset{\cdot}{\gamma}}_{1}^{2}\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\right)-\left(1+6\overline{\overset{\cdot}{\gamma}}_{1}^{2}\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}^{2}}\right)\overline{\Upomega}_{1,1}^{-}(\overline{y}) \\ &\quad +2\overline{\overset{\cdot}{\gamma}}_{1}\frac{\varepsilon Wi_{\kappa}^{2}}{\overline{\kappa}}\left(6\Uppsi_{1}\Uppsi_{2}\overline{\kappa}\left(\overline{{y}}+1\right)+\frac{3}{2}\overline{\Upomega}_{2,1}^{-}(\overline{y})\right)-2\varepsilon Wi_{\kappa}^{2}\left(\frac{1}{3}\overline{\Upomega}_{3,1}^{-}(\overline{y})+3\Uppsi_{1}\Uppsi_{2}\overline{\Upomega}_{1,1}^{-}(\overline{y})\right). \end{aligned} $$
(4.3)

For symmetric boundary conditions with no-slip (\({R_{\zeta}=1, \,\overline{\mathcal{L}_{1}}= \overline{\mathcal{L}_{2}}=0}\); leading to \(\overline{\overset{\cdot}{\gamma}}_{1}=0\)) the above equation reduces to that presented by Afonso et al. (2011), but for \(R_{\zeta}\neq1\) and \({\overline{\mathcal{L}_{1,2}}\neq0}\) the dimensionless shear rate asymmetry coefficient, \(\overline{\overset{\cdot}{\gamma}}_{1}\), depends on the fluid rheological properties. For a Newtonian fluid, the dimensionless shear rate asymmetry coefficient is a linear function of \(R_{\zeta}\), as expressed by \({\frac{\overline{\Upomega}_{1,1}^{-}(1)+\overline{\mathcal{L}_{1}} \overline{\kappa}\left(\overline{\Upomega}_{1}^{+}(-1)+R_{\mathcal{L}} \overline{\Upomega}_{1}^{+}(1)\right)}{2+\overline{\mathcal{L}_{1}} \left(1+R_{\mathcal{L}}\right)}}\), that simplifies to \({\overline{\overset{\cdot}{\gamma}}_{1}=\frac{1}{2}{ \overline{\Upomega}_{1,1}^{-}(1)}=\frac{1}{2}}\left(R_{\zeta}-1\right)\), when \({\overline{\mathcal{L}_{1}}=0}\) as shown in Afonso et al. (2011).

Assuming the no-slip boundary condition at both walls, for a viscoelastic fluid and \(R_{\zeta}<1\), \(\overline{\overset{\cdot}{\gamma}}_{1}\) is always negative, decreasing with the increase in\(\sqrt{\varepsilon}Wi_{\kappa}\), an indication that the shear stress is also decreasing as \(\sqrt{\varepsilon}Wi_{\kappa}\) increases. For \(R_{\zeta}>1\), \(\overline{\overset{\cdot}{\gamma}}_{1}\) is always positive and increases with \(\sqrt{\varepsilon}Wi_{\kappa}\), due to the increasing shear-thinning behavior of the fluid, leading to higher normalized shear stresses. Afonso et al. (2011) showed that all curves asymptote to the same limiting curve when \(\sqrt{\varepsilon}Wi_{\kappa}\rightarrow\infty\), with the absolute value of \(\overline{\overset{\cdot}{\gamma}}_{1}\) increasing when \(\bar{\kappa}\) increases.

The dependence of the dimensionless shear rate asymmetry coefficient on the slip coefficients \({\left(\overline{\mathcal{L}_{1}}, \overline{\mathcal{L}_{2}}\right)}\) is shown in Fig. 10, for the particular case of \(\sqrt{\varepsilon}Wi_{\kappa}=1\). To capture the influence of both slip coefficients on \(\overline{\overset{\cdot}{\gamma}}_{1}\), and based on the data obtained from Afonso et al. (2011), we selected three different values of \(R_{\zeta}\), \(R_{\zeta}=-1, 1, 2\) and plotted the variation of \(\overline{\overset{\cdot}{\gamma}}_{1}\) for two particular cases, \({\overline{\mathcal{L}_{1}}=0}\) and \({\overline{\mathcal{L}_{1}}=\overline{\mathcal{L}_{2}}}\).

Fig. 10
figure 10

Variation of \(\overline{\overset{\cdot}{\gamma}}_{1}\) with the slip coefficients, \({\overline{\mathcal{L}_{1}}, \overline{\mathcal{L}_{2}}}\), for m = 1 and constant values of \(R_{\zeta}\) and \(\sqrt{\varepsilon}Wi_{\kappa}=1\) with a relative microchannel ratio of \(\overline{\kappa}=20\)

Full size image

For the first value, \(R_{\zeta}=-1\), \(\overline{\overset{\cdot}{\gamma}}_{1}\) is negative and decreases in both situations, being smaller for \({\overline{\mathcal{L}_{1}}=\overline{\mathcal{L}_{2}}}\). The same happens with \(R_{\zeta}=2\), with the difference that \(\overline{\overset{\cdot}{\gamma}}_{1}\) is now positive and increases for both cases (\({\overline{\mathcal{L}_{1}}=0}\) and \({\overline{\mathcal{L}_{1}}=\overline{\mathcal{L}_{2}}}\)). The decrease in \(\overline{\overset{\cdot}{\gamma}}_{1}\) was expected, because the shear stress is reduced when wall slip is present. We can see that the variation of \(\overline{\overset{\cdot}{\gamma}}_{1}\) with the slip velocity is similar to the variation of \(\overline{\overset{\cdot}{\gamma}}_{1}\) with \(\sqrt{\varepsilon}Wi_{\kappa}\). Additionally, we observe that the slip coefficient enhances the viscoelastic effects.

For \(R_{\zeta}=1\), only the variation of \(R_{\zeta}\) with \({\overline{\mathcal{L}_{2}}}\) (\({\overline{\mathcal{L}_{1}}=0}\)) was analyzed, because when \({\overline{\mathcal{L}_{1}}=\overline{\mathcal{L}_{2}}}\) the flow is symmetric and \(\overline{\overset{\cdot}{\gamma}}_{1}=0\). For this case, we found that \(\overline{\overset{\cdot}{\gamma}}_{1}\) increases with \({\overline{\mathcal{L}_{2}}}\).

Figure 11 shows the velocity profiles for asymmetric slip boundary conditions (with \({\overline{\mathcal{L}_{1}}=0}\)). Note that for \(R_{\zeta}=1\) the velocity profile is skewed due to the asymmetry imposed by the slip velocity. We can also see, as expected, an increase in the normalized velocity magnitude with the slip coefficient \({\overline{\mathcal{L}_{2}}}\).

Fig. 11
figure 11

Dimensionless velocity profiles as a function of \({\overline{\mathcal{L}_{2}}}\) (m = 1) for constant \({\overline{\mathcal{L}_{1}}=0}\), for the electro-osmotic flow of a PTT fluid with \(R_{\zeta}=-1, 1\) and \(\sqrt{\varepsilon}Wi_{\kappa}=1\)

Full size image

4.2.2 Mixed driving forces

In this section, we investigate the sPTT fluid flow under the combined action of electro-osmosis, pressure gradient, and slip boundary conditions (Fig. 12).

Fig. 12
figure 12

Variation of \(\overline{\overset{\cdot}{\gamma}}_{1}\) with the slip coefficients, \({\overline{\mathcal{L}_{1}}, \overline{\mathcal{L}_{2}}}\), for constant values of \(R_{\zeta}\) and \(\sqrt{\varepsilon}Wi_{\kappa}=1\) with a relative microchannel ratio of \(\overline{\kappa}=20\) and a favorable pressure gradient \(\Upgamma=-1\)

Full size image

Afonso et al. (2011) showed (for the asymptotic limit of \(\sqrt{\varepsilon}Wi_{\kappa}\rightarrow\infty\)) that increasing the favorable pressure gradient (decreasing \(\Upgamma\) for negative values), \(\overline{\overset{\cdot}{\gamma}}_{1}\) increases, especially for \(R_{\zeta}<1\), and increasing \(\Upgamma\) for adverse pressure gradient conditions also leads to an increase in \(\overline{\overset{\cdot}{\gamma}}_{1}\), especially for \(-1<R_{\zeta}<1\). Notice that for the asymptotic limit of large \(\sqrt{\varepsilon}Wi_{\kappa}\) the cubic equation that needs to be solved is independent of the slip boundary conditions; therefore, we followed the same procedure adopted for the pure electro-osmotic case. For this case, we studied the variation of \(\overline{\overset{\cdot}{\gamma}}_{1}\) with the slip coefficients \({\overline{\mathcal{L}_{1}}}\) and \({\overline{\mathcal{L}_{2}}}\) for \(R_{\zeta}=-1, 1, 2\) and \(\Upgamma=-2, -1, 0, 1, 2\). The results obtained are similar to those obtained with \(\Upgamma=0\), with the difference that the absolute values of \(\overline{\overset{\cdot}{\gamma}}_{1}\) increase with \(\Upgamma\).

Figure 13a, b present the dimensionless velocity profiles for slip flows with symmetric (\(R_{\zeta}=1\)) and antisymmetric zeta potentials (\(R_{\zeta}=-1\)), respectively, for \(\sqrt{\varepsilon}Wi_{\kappa}=1\). For both, favorable (\(\Upgamma<0\)) and adverse pressure gradients (\(\Upgamma>0\)), Fig. 13a shows that the velocity profile increases with \({\overline{\mathcal{L}_{2}}, }\) due to the consequent reduction in the shear stress near the wall. For the case of \(R_{\zeta}=-1, \) Fig. 13b shows that the slip velocity increases in the direction of the flow. For this case, the flow near the upper wall is in the adverse direction and, therefore, the slip velocity increases (in magnitude) in that direction.

Fig. 13
figure 13

Dimensionless velocity profiles as a function of \({\overline{\mathcal{L}_{2}}}\) (m = 1) for \({\overline{\mathcal{L}_{1}}=0}\), for the electro-osmotic flow of a PTT fluid with \(\sqrt{\varepsilon}Wi_{\kappa}=1\) (a) \(R_{\zeta}=1\) (b) \(R_{\zeta}=-1\)

Full size image

5 Conclusions

In this work, we derived analytical solutions for the fully developed channel flow of symmetric z-z electrolyte viscoelastic fluid (sPTT) under the mixed influence of electro-osmosis and pressure gradient forcings, for the cases of symmetric and asymmetric wall zeta potentials and assuming different slip coefficients at the bottom and top walls, representing different hydrophobic characteristics of the microchannels walls. The combined effects of the slip boundary conditions, fluid rheology, electro-osmotic, and pressure gradient forcings on the fluid velocity distribution are also discussed in terms of the relevant dimensionless numbers. The results demonstrate that both the presence of the slip velocity and viscoelasticity induce an increase in the dimensionless velocity profiles and the flow rate. We also found that an increase in the slip coefficient influences the asymmetry coefficient, with \(\overline{\dot{\gamma }}_{1}\) decreasing for \(R_{\zeta}<0\) and increasing for \(R_{\zeta}>0\).