1 Introduction

Squeeze film damping is a common phenomenon which occurs in many devices that involves a surface moving in a normal direction in close proximity to another solid surface. The relative motion alternately squeezes out and draws in fluid between the two surfaces. This causes a pressure field to arise within the fluid, which may affect the movement of the surfaces. If the fluid film thickness is small enough compared to the wall width, such a phenomenon plays a significant role in energy loss and often dominates the dynamic motion of the system (Williams 2005).

Derived from integrated circuit fabrication technology, microelectromechanical systems (MEMS) have driven a great amount of research and number of applications, due to their potential of performing sensing and actuation at unprecedented levels of miniaturization (Hsu 2008). The study of a fluid film squeezed between two solid surfaces is important in many MEMS applications that involve the out-of-plane vibration of beams or plates in the proximity of a surface, such as accelerometers (Houlihan and Kraft 2005), resonators (Zhang et al. 2004), optical switches (Horsley et al. 2005), microtorsion mirrors (Pan et al. 1998), and others. As size shrinks, the volume forces such as gravity become less important, while surface forces like those due to hydrodynamics often comprise the largest source of parasitic losses (Bao and Yang 2007).

Depending on the design criteria and operating conditions, squeeze film damping influences the behavior of MEMS in different ways. For instance, in a resonant sensor, to achieve a high Q-factor, the damping should be reduced as much as possible for the best resolution (Homentcovschi and Miles 2010). On the other hand, system damping may provide stability to certain devices with inherent tendencies to instability, such as microaccelerometers (Houlihan and Kraft 2005). All these devices are greatly affected by squeeze film forces on their resonance frequency, Q-factor, velocity, and amplitude. Hence, it is essential to understand the flow mechanisms and evaluate fluid forces accurately to optimize the design of microdevices.

The fluid force on a surface associated with squeeze film flow can be interpreted as the sum of two forces: an inertia force which is proportional to the acceleration of the confining surface (the proportionality constant is called the added mass coefficient) and likewise a corresponding viscous force which is proportional to the velocity (the proportionality constant being the viscous damping coefficient (Huang et al. 2011)). In this paper, the terms damper or damping are used to characterize these devices in general, although by a stricter terminology, damping refers only to energy dissipation due to viscosity.

Extensive efforts have been devoted to the developing of mathematical models for squeeze film forces acting on MEMS devices. The publications in this area are based almost exclusively on the well-known Reynolds equation and the behavior of linear systems (Zhang et al. 2004; Starr 1990; Veijola et al. 1995; Darling et al. 1998; Kwok et al. 2005; Pandey and Rudra 2007; Pandey and Pratap 2008). The linearized models are applicable for only small amplitude oscillation devices, and when convective inertia effects are negligible. However, large amplitude oscillations are common in many microdevices such as the RF switch, deformable mirrors, and pull-in pressure sensors (Chigullapalli et al. 2012; Pandey and Pratap 2003). These devices require a more sophisticated model that accounts for the nonlinear behavior of the squeeze film forces.

A few researchers have addressed squeeze film damping of microdevices oscillating at large amplitude. Pandey and Pratap (2003) studied the nonlinear effect of viscous, unsteady, compressible, and laminar air flow between two parallel plates with a narrow gap. The results showed that nonlinear effects in the squeeze film model become significant once the amplitude of vibration exceeds 10 % of the initial gap. De and Aluru (2006) investigated the complex nonlinear oscillations for an electrostatically actuated microstructure. Moghimi Zand and Ahmadian (2007) presented a model to analyze pull-in phenomenon and nonlinear vibrational behavior and dynamics of multi-layer microplates subjected to an electric field. In the above works, finite element or finite difference methods were applied to study nonlinear dynamic systems without the prerequisite of small amplitude oscillation.

However, in all these studies, fluid inertia effects were neglected. Nevertheless, inertia may become significant when the velocity or oscillation frequency of the system is high or when the system is operated in a dense (i.e., liquid) medium. For instance, from lubrication theory, the force resisting the motion of a plate moving perpendicular to a close parallel substrate is proportional to \(\dot{h}/h^{3},\) where h is the fluid film thickness, or the distance between the two surfaces (Williams 2005). However, recent experimental data from such systems of micrometer size operating in a liquid environment seem to not exhibit this dependency (Naik et al. 2003; Harrison et al. 2007). Specifically, in Naik et al., the viscous damping coefficient was found to be proportional to the inverse of the fluid thickness to the first power (1/h), the same as the inertia added mass coefficient. In Harrison et al. where a similar problem was studied, powers of −1 and −1/2 were measured for viscous and added mass coefficients. However, this study was later followed up by a report from the same group, showing that the fluid force indeed scales as 1/h 3 even when the plate is far away from the wall, i.e., when the thin film assumption is not applicable (Fornari et al. 2010). These authors expressed frustration due to “the lack of a well-described theory” in the literature.

A complete solution for specified properties and kinematic conditions that considers the effects of viscosity and inertia at large oscillation could be obtained by directly solving the Navier-Stokes equations via commercial simulation software (Turowski et al. 1999; Pandey et al. 2007). Although commercial software for such computation fluid dynamics simulations is efficient and readily available, the cost and effort of solving a complete fluid model coupled to finite element structural elastic behavior (fluid–structure interaction or FSI) is still substantial. The objective of this study is to achieve the similar goal via a fast, accurate, and low cost method. This paper presents an investigation of both inertia and viscous fluid effects on the dynamic response of a system employing a microplate parallel to a substrate and undergoing large normal vibrations. A compact expression for the incompressible hydrodynamic forces with separate viscous and inertia terms is developed. The dynamic response of the system is solved numerically for realistic cases. In the Results and Discussion section, parameters that have effects on the behavior of the linear and nonlinear model are discussed in detail. The critical oscillation amplitude (i.e., the largest amplitudes at which linear model is applicable) is also found for a wide range of actuation frequencies.

2 Analysis

2.1 Governing equations

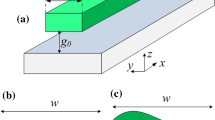
The system of interest consists of a rigid, rectangular plate, as shown in Fig. 1, whose dimensions are L and W along the x- and z-directions in a laboratory reference system. Under the plate lies an infinite substrate, and a thin film of fluid is confined in between. The positions of the plate and the substrate are y p and y s , respectively. The plate has an effective mass m and is connected to the substrate by an elastic structure with effective spring constant k. The plate has single degree of freedom in the y-direction of squeezing. The flow between the plate and substrate can be idealized strictly as two-dimensional when W ≫ L. According to lubrication texts (e.g., Szeri 1998), in the cases where W∼ L, it is still an accepted approximation to regard the flow as two-dimensional.

Fig. 1
figure 1

a Rigid rectangular plate supported elastically and vibrating in the y-direction, normal to a parallel substrate. A viscous fluid is confined between the plate and substrate, while normal sinusoidal displacement is imposed on the latter. b Lumped element representation, assuming that the system has a single degree of freedom

Full size image

Assuming that under an external sinusoidal excitation this system undergoes arbitrary vertical (normal) vibrations, the position of the substrate y s can be expressed as:

$$y_{s}=Y_{\rm s0}+\delta H_{n} \sin \left(\omega t \right),\quad \omega = 2\pi f,$$
(1)

where Y s0 is the initial position of the substrate, δ is a dimensionless parameter representing the dimensionless oscillation amplitude (δ > 0), H n is the nominal gap (the gap in the absence of both the driving force and the plate effective mass), t is time, ω is the angular frequency and f is the excitation frequency in Hz.

In the analysis, the displacement of the plate y p(t) is sought. However, in the case of finite or large oscillation, one cannot assume a sinusoidal motion of the plate. From Newton’s second law, the equation describing the motion of the plate is

$$m\frac{{\rm d}^{2}y_{\rm p}}{{\rm d}t^{2}}=F_{\rm g}+F_{\rm el}+F_{\rm fl},$$
(2)

where F g is the gravity force which is equal to −mg with g as the gravitational constant, F el is the elastic force of the beams, and F fl is the hydrodynamic force acting upon the plate by the fluid.

The dynamic gap (or the thickness of the fluid film) between the plate and substrate is

$$h=y_{\rm p}-y_{\rm s}.$$
(3)

An expression for the dynamic elastic force is straightforward

$$F_{\rm el}=-k\left[ \left(y_{\rm p}-y_{\rm s}\right)-H_{n}\right].$$
(4)

2.2 Derivation of hydrodynamic forces

The squeeze film fluid force F fl can be considered as the sum of a viscous force F v and an inertia force F i. Determination of these quantities for incompressible fluids follows the methodology of Tichy and Modest (1978) and Tichy and Winer (1977). In the more general (nonlinear) case, we write:

$$\begin{aligned} F_{\rm fl}&=F_{\rm v}+F_{\rm i},\\ F_{\rm v}&=-\frac{L^{3}W}{h^{3}}\eta c_{\rm v}\left(\frac{{\rm d}y_{\rm p}}{{\rm d}t}-\frac{{\rm d}y_{s}}{{\rm d}t}\right), \end{aligned}$$

and

$$F_{\rm i}=F_{\rm iC}+F_{\rm iU}=-\frac{L^{3}W}{h^{2}}\rho c_{\rm iC}\left(\frac{{\rm d}y_{p}}{{\rm d}t} -\frac{\rm {d}y_{\rm s}}{{\rm d}t}\right)^{2}-\frac{L^{3}W}{h}\rho c_{iU} \left(\frac{{\rm d}^{2}y_{p}}{{\rm d}t^{2}}-\frac{{\rm d}^{2}y_{s}}{{\rm d}t^{2}}\right),$$
(5)

where η is fluid viscosity and ρ is the density. The inertia force includes both convective F iC and unsteady F iU terms. The symbols c v, c iC, and c iU denote dimensionless viscous, convective inertia, and unsteady inertia coefficients. The incompressible condition (liquids or gasses undergoing small pressure excursions relative to atmospheric) eliminates the so-called fluid spring force. In the case of parallel rectangular plates, the numerical values are c v = 1, c iC = 17/70, and c iU = 1/10, respectively. The method of analysis is to express the inertia terms of the Navier-Stokes equations (left-hand-side) as a first-order correction to the viscous Stokes flow solution. The linear Stokes flow equations (the right-hand-side of the Navier-Stokes equations), when integrated across the film, give rise to Reynolds equation. The convective term of Eq. (5) is generated by the nonlinear convective terms of the Navier-Stokes equations such as vdv/dx, while the unsteady term of Eq. (5) is generated by the local unsteady term such as dv/dt. The analytical method, known to be highly accurate to modified Reynolds number about 10, is described in detail in Szeri’s text (1998). The numerical values of the coefficients are also reported by Szeri.

For other plate geometries, e.g., a circular disk, the coefficients c v, c iC, and c iU would have different numerical values but the structure of the equations is the same (Hamrock 1994).

2.3 Numerical solution for the dynamic system

To solve the Eqs. (2)–(5) for plate displacement y p, a set of state equations is attributed to the system:

$$\begin{aligned} \dot{y}_{\rm p}&\,=\,v_{\rm p},\quad \dot{v}_{\rm p}\,=\,\frac{1}{m+m_{i}}\left(-k (y_{\rm p}-y_{\rm s}-H_{0})+F_{\rm flT}\right),\quad m_{i}\,=\,\frac{L^{3}W}{h}\rho c_{\rm iU},\\ v_{s}&\,=\,\dot{y}_{\rm s}\,=\,\delta H_{n} \omega \cos (\omega t),\quad \dot{v}_{\rm s}\,=\,-\delta H_{n} \omega^{2} \sin (\omega t),\\ F_{\rm flT}&\,=\,-\frac{L^{3}W}{h^{3}}\eta c_{\rm v} \left(v_{\rm p}-v_{\rm s}\right)-\frac{L^{3}W}{h^{2}}\rho c_{\rm iC} \left(v_{\rm p}-v_{\rm s}\right)^{2}+\frac{L^{3}W}{h}\rho c_{\rm iU} \dot{v}_{\rm s}, \end{aligned}$$
(6)

where the dot superscript means d/dt, v p is the velocity of the plate, v s is the velocity of the substrate, m i is the added mass associated with unsteady inertia force, and F flT is a term of the inertia fluid force. Nonlinearities in the plate response y p arise due to the convective velocity squared terms \((\sim (\dot{y}_{\rm p}-\dot{y}_{\rm s})^{2})\), and the reciprocal of the film thickness term (∼ 1/(y p − y s)) raised to powers one, two, and three. Although the viscous and unsteady terms of the Navier-Stokes equations are linear in the fluid mechanical sense, they cause nonlinear forces on the oscillating plate.

The governing equations can be nondimensionalized using:

$$y^{*}_{\rm p}=\frac{y_{\rm p}}{H_{0}},\quad F^{*}=\frac{F H_{0}^{3}}{\eta L^{3} W},\quad \omega_{0}=\sqrt{\frac{k}{m}},\quad t^{*}=\omega_{0} t,\quad y^{*}_{s}=\delta \sin (\omega^{*} t^{*}),\quad h^{*}=y^{*}_{\rm p}-y^{*}_{s},$$

to obtain:

$$\begin{aligned}v^{*}_{\rm p}& =\dot{y}^{*}_{\rm p},\quad \dot{v}^{*}_{\rm p}=\frac{1}{1+c_{\rm iU} N_{\rm v} N_{Re0}/h^{*}}\left(-(y^{*}_{\rm p}-y^{*}_{\rm s}-1)+F^{*}_{\rm flT}\right),\\ F^{*}_{\rm flT}& =-c_{\rm v} N_{\rm v} \frac{v^{*}_{p}-v^{*}_{\rm s}}{h^{*3}}-c_{\rm iC} N_{\rm v} N_{Re0}\frac{(v^{*}_{\rm p}-v^{*}_{\rm s})^{2}}{h^{*2}}+c_{\rm iU} N_{\rm v} N_{Re0} \frac{\dot{v}^{*}_{\rm s}}{h^{*}}. \end{aligned}$$
(7)

The following governing dimensionless parameters of the problem emerge:

$$\begin{aligned} \omega^{*}&=\frac{\omega}{\omega_{0}},\quad \delta=\frac{\Updelta y_{\rm s}}{H_n},\quad A=\frac{H_{0}}{L},\\ N_{\rm v}& =\frac{L^{3} W \eta}{m \omega_{0} H_{0}^{3}}=\frac{W \eta}{m \omega_{0}A^{3}},\quad N_{Re}=\frac{\rho \omega H_{0}^{2}}{\eta},\quad \hbox{ and }\quad N_{Re0}=\frac{\rho \omega_{0} H_{0}^{2}}{\eta}, \end{aligned}$$
(8)

where ω 0 is the vacuum resonance frequency of the system in radians per second, ω * is frequency ratio, Δy s is the oscillation amplitude of the substrate and A is an aspect ratio of the gap size. The parameter N v is a dimensionless “viscous number” which represents the ratio of viscous fluid force to the inertia force of the structure (as opposed to inertia force of the fluid). The symbol N Re is the usual unsteady Reynolds number, which is the ratio of inertia force of the fluid to the viscous force, and N Re0 is the Reynolds number at resonant frequency.

When the state variables of the system undergo large vibrations, the nonlinear Eq. (6) can be integrated numerically, using, for example, an ode command in MATLAB (Senturia 2001). A series of solvers provided by MATLAB can be used to solve initial value problems for ordinary differential equations (ODE). Selection of the particular solver depends on the characteristics of the ODE (e.g., the matrix stiffness), the requirements of accuracy, and cost. Solver ode45 (explicit Runge-Kutta 4th and 5th order formulation) is chosen in this study. On the other hand, when the system undergoes small displacement around its balance position (δ ≪ 1), the hydrodynamic force can then be linearized and solved analytically in a closed form (Huang et al. 2011):

$$\begin{aligned} F_{\rm fl}&=F_{\rm v}+F_{i},\\ F_{\rm v}&=-\frac{L^{3}W}{H_{0}^{3}}\eta c_{\rm v}\left(\frac{\rm {d}y_{\rm p}}{\rm {d}t} -\frac{\rm {d}y_{\rm s}}{\rm {d}t}\right), \end{aligned}$$

and

$$F_{i}=F_{\rm iU}=-\frac{L^{3}W}{H_{0}}\rho c_{\rm iU}\left(\frac{\rm {d}^{2}y_{\rm p}}{\rm {d}t^{2}} -\frac{\rm {d}^{2}y_{\rm s}}{\rm {d}t^{2}}\right),$$
(9)

where H 0 is the mean gap value (i.e., the gap between the plate and the substrate including the static effect of gravity and elastic force), which can be expressed as:

$$H_{0}=H_{n}-\frac{m g}{k}.$$
(10)

3 Results and discussion

To thoroughly examine all aspects of the behavior of the system, two output dimensionless parameters F * and y *p would need to be shown as functions of input parameters A, δ, ω *, N v, and N Re0. Such a detailed investigation would not be appropriate to the goals of this study and have diminishing returns. Instead, to understand under which circumstances the small amplitude oscillation assumption can be applied, a case study is presented herein. In the system under consideration, to demonstrate the applicability of the method, the starting point is a base case typical of many microsystem applications: the plate length and width are taken as 500 μm (see Fig. 1). The length and width of the suspension beams are 2 mm and 100 μm, respectively. Using the physical parameters of the most common material in microfabrication (silicon), the effective elastic constant k is calculated as 810 N/m for these dimensions. Unless specified otherwise, the confined fluid is taken as water \((\rho = 1000 \,\hbox{kg}/\hbox{m}^{3}, \eta = 0.001 \hbox{Pa}\cdot\hbox{s})\), the nominal gap H n is set to 50 μm, and the natural frequency of the plate in vacuum is chosen as 3,000 Hz, the same range as used by Naik et al. (2003) and Harrison et al. (2007) by taking the effective mass m as 2.28 mg.

3.1 Effect of frequency ratio and oscillation amplitude on displacement and force

First, the comparison between the full and linear solution predictions is carried out for a system oscillating well below its resonant frequency (ω * = 0.5). Two cases are investigated, namely when the oscillation amplitude of the substrate is small δ = 0.1 and large δ = 1.0. The figures on the left-hand side, Fig. 2a, c, show the film thickness and displacement of the substrate and plate as a function of time. The figures on the right-hand side, Fig. 2b, d present the inertia and viscous forces for the same time interval and the same conditions.

Fig. 2
figure 2

Steady periodic displacement and fluid forces. Comparison between the linear and nonlinear solution for dynamic motion of substrate at half the resonant frequency ω * = 0.5, aspect ratio A = 0.1 (with N v  = 0.01, N Re0 = 47.07). For a and b δ = 0.1; For c and d δ = 1.0. In legend, “film” denotes the thickness of fluid film h, Eq. (3)

Full size image

As seen from these figures, for relative amplitude δ = 0.1, the linear and nonlinear solutions of plate displacement and fluid forces are imperceptibly different (Fig. 2a, b). However, surprisingly, when oscillation amplitude becomes much larger (δ = 1.0), the linear and nonlinear solutions of plate displacement are still nearly identical (Fig. 2c) although the forces differ drastically. It is worth noticing that at this condition, the substrate and plate go through large oscillations (amplitudes of 50 and 70 μm, respectively), but the film oscillations are relatively small (20 μm). In addition, due to high Reynolds number, inertia force dominates over viscous force. Conditions of high Reynolds number often appear to be the norm rather than the exception in squeeze film microsystems applications. A phase shift between the inertia and viscous force can be observed since the former is proportional to the acceleration and the latter is proportional to the velocity of the system. As expected, the magnitudes of both forces increase with increasing oscillation amplitude.

Next, the same exercise is performed at resonant frequency (ω * = 1.0). Figure 3 shows a similar comparison between the linear and nonlinear models. In contrast to findings for the previous case discussed above, this time the linear and nonlinear model predictions coincide only for ultra-small δ = 0.001, Fig. 3a, b. At relative amplitude δ = 0.1, where the linear and nonlinear solutions nearly coincide when the system oscillates below resonance in Fig. 2a, b, the linear solution here shows that the plate penetrates the substrate (i.e., in effect, a negative film), which is obviously physically incorrect (Fig. 3c). This result is also in disagreement with nonlinear result in Fig. 3c. The forces now differ widely between linear and nonlinear, and at larger δ, they are no longer sinusoidal (Fig. 3d). The solution of the nonlinear model is a complicated sum of nonlinear terms, such as \(\dot{h}/h^{3}, \dot{h}^{2}/h^{2}\) and \(\ddot{h}/h,\) so a wide range of nonsinusoidal behavior is not surprising. Note that in the linear case, Eq. (9), the denominators of these terms are the constant H 0. Also, comparing to the circumstances portrayed at ω * = 0.5, the amplitude of current forces is some 20 times larger.

Fig. 3
figure 3

Steady periodic displacement and fluid forces. Comparison between linear and nonlinear solution for dynamic motion of substrate at the resonant frequency ω * = 1.0, aspect ratio A = 0.1 (with N v = 0.01, N Re0 = 47.07). For a and b \(\delta = 0.001;\) for c and d δ = 0.1

Full size image

3.2 Effect of aspect ratio on displacement and force

In addition to frequency ratio and oscillation amplitude, the aspect ratio between the gap thickness and plate length significantly impacts the dynamic response of the system. To illustrate this, the system under consideration is excited at a similar situation as in Fig. 3c, d (ω * = 1.0, δ = 0.1) but a smaller aspect ratio A = 0.02 versus A = 0.1. It is shown that linear and nonlinear solutions for the plate motions and fluid forces are exceedingly close when aspect ratio is smaller (Fig. 4a, b), and the difference increases as aspect ratio increases (Fig. 3c, d). The fluid film thickness becomes negative for linear solution when aspect ratio increases to 0.1 (Fig. 3c). The result once again shows that when the system is excited at resonance frequency and aspect ratio is large, for the linearized model to be hold, the relative amplitude δ has to be extremely small.

Fig. 4
figure 4

Steady periodic displacement and fluid forces. Comparison between linear and nonlinear solution for dynamic motion of substrate at small aspect ratio A = 0.02  (ω * = 1.0, δ = 0.1, N v = 7.29, N Re0 = 47.07)

Full size image

3.3 Effect of Reynolds number on displacement and force

Reynolds number is another factor that may influence the dynamic response of the squeeze film system. To investigate, the properties of 50 cSt silicone oil are applied \((\rho = 960\hbox{ kg}/\hbox{m}^{3}, \eta = 0.048\hbox{ Pa}\cdot\hbox{s})\) instead of water. Silicone oils are widely used and commercially available liquids. The system is excited again at the natural frequency (ω * = 1.0) and amplitude δ equals 0.1. Reynolds number N Re0 now drops to 0.93 compared to 47.1 with water. The dynamic performance of the system is shown in Fig. 5. Compared to the results shown in Fig. 3c, the linear and nonlinear solutions for plate motions are close to each other when Reynolds number is small (Fig. 5a). While dominant inertia force brings nonlinearity into the picture (Fig. 3d), low Reynolds number or stronger viscous force has the opposite tendency, causing linearity of the system (Fig. 5b).

Fig. 5
figure 5

Steady periodic displacement and fluid forces. Comparison between linear and nonlinear solution for dynamic motion of substrate when Reynolds number N Re0 = 0.93  (ω * = 1.0, δ = 0.1, A = 0.1, N v = 0.56)

Full size image

It is worth pointing out that as shown in Eq. (5), the total fluid force is the sum of the viscous force, convective inertia force, and unsteady inertia force. Convective inertia force is often neglected when Reynolds equation applies (Bao and Yang 2007; Marrero et al. 2010). The dimensionless numbers discussed above, i.e., ω *, δ, A, and N Re0 determine the relative importance of convective inertia force. When excitation frequency is close to the natural frequency, oscillation amplitude and aspect ratio are large, or Reynolds number is high, convective force will be important and must be taken into account. Figure 6 gives an example showing the comparison of the complete fluid force and the one neglecting convective inertia for two different cases. The system is excited at the same conditions as in Figs. 3d and 5b respectively. As can be seen in Fig. 6a, when Reynolds number is high, the fluid force including convective inertia is ∼ 25 % greater than the one omitting it. Moreover, due to the term \(\dot{y}_{\rm p}^{2},\) the behavior of the complete force solution is more irregular than the one only considering viscous and unsteady force. On the other hand, these results indicate that convective force can be neglected if Reynolds number is small or the viscous effect dominates (Fig. 6b).

Fig. 6
figure 6

Importance of convective inertia force (ω * = 1.0, δ = 0.1, A = 0.1). For a N v = 0.01, N Re0 = 47.07; For b N v = 0.56, N Re0 = 0.93

Full size image

3.4 Selecting the range for ‘small’ amplitude oscillation

As discussed above, the linear solution is valid only when oscillation amplitude is sufficiently small, and otherwise, the nonlinear model is required. However, the boundary between “small” and “large” amplitude oscillation is vague. Normally, δ ∼ 0.1 is considered to be small vibration (Pandey and Pratap 2003; Huang et al. 2011). Nevertheless, as shown above, for low Reynolds number, low aspect ratio or for actuation frequency away the resonant frequency, the linear solution can be very close to the nonlinear solution even when the relative amplitude δ is large (order one). On the other hand, in some situations, especially when the system is actuated very near to resonant frequency, δ ∼ 0.1 is not small enough, as illustrated in previous sections.

Therefore, the criterion for “small oscillation” is not the same for different situations, and instead, it depends on the system properties and actuation frequency. The maximum δ which is valid for a linear approximation is desirable for specific condition in design and experiment. Hence, an approximate method for seeking the maximum δ for linearity is proposed here. A critical value δ 0 can be associated with the case when the linear solution shows the plate starts to penetrate the substrate. This condition of a negative film h < 0 is an unambiguous indicator that the linear analysis is no longer valid, although significant errors may occur sooner.

As an example, again the nominal gap H n is set to 50 μm, the natural frequency is 3,000 Hz, and the effective mass is 2.28 mg. Figure 7 shows the critical oscillation amplitude δ 0 at a wide range of actuation frequencies. Step intervals of frequency f and dimensionless amplitude δ are chosen to be 250 Hz and 0.02, respectively. Water and silicone oil 50 cSt are taken as fluid media in Fig. 7a, b, respectively, and Reynolds numbers N Re0 are 47.07 and 0.93 accordingly. For comparison, three lines associated with viscous numbers at different orders of magnitude are presented. It can be seen in the figure that, for all the N Re0 and N v , the critical δ 0 can be one or higher when frequency is sufficiently low: less than 2,000 Hz in the current case. As frequency increases, the critical δ 0 decreases and has its smallest value near the resonant frequency. Further increasing frequency, the critical amplitude rises again as the frequency is farther away from the resonance point. However, the critical value never reaches as high as when the frequency is less than resonance. In addition, as N v increases, the critical δ 0 increases as well. It is worth noticing that when both N Re0 and N v are large (Fig. 7a, N v = 0.11), the frequency at which δ 0 has the lowest value shifts to the left instead being at resonant frequency in other cases.

Fig. 7
figure 7

Critical amplitude δ 0 which indicates the limit of the linear model as function of excitation frequency (f 0 = 3000 Hz, H n  = 50 μm, m = 2.28 mg). For a N Re0 = 47.07; For b N Re0 = 0.93

Full size image

4 Conclusions

SFD effects on MEMS systems have long been investigated, almost exclusively based on a linearized equation of the dynamic mechanical system, using Reynolds equation to account for the fluid film forces. Both of these equations neglect fluid inertia effects, while the former also assumes small oscillation amplitude. However, fluid inertia can be important, or can even dominate the system, at the large vibrations common in many microdevices. Neglecting these effects may lead to errors in interpreting experimental measurements and to inadequate design of microsystems.

In this paper, a nonlinear solution has been presented for the single degree of freedom dynamic system consisting of a plate supported elastically above a substrate, confining a viscous fluid, and undergoing large normal oscillations. The nonlinear viscous and inertia forces have been characterized separately in a simple and compact manner. Due to the large number of dimensionless parameters which define the design space of this problem, a case study approach is taken and the behavior is examined in selected regions of interest in microsystems applications.

Comparisons between the linear and nonlinear solution of the dynamic system are given in different situations (i.e., varying the excitation frequency, aspect ratio, and Reynolds number). The results show that when the system is excited at sufficiently small amplitude, the linear and nonlinear solutions are almost identical. The difference between the two solutions increases as the amplitude of excitation increases, and at some point, the linear model is clearly no longer valid, and a nonlinear model is essential. The criterion used as the limit of linear model is when it predicts a negative film thickness, i.e., the surfaces penetrate one another. The maximum critical amplitude for a small vibration assumption is not fixed but depends on the system geometry and kinematics. For example, the linear solution can still be valid when the excitation amplitude is “large” (δ = 1) if the system is actuated at a frequency considerably less than resonance. By contrast, the linear solution may not be valid when the excitation amplitude is “small” (δ = 0.1) if the system excitation is near resonance.