A comparative study of analytical squeeze film damping models in rigid rectangular perforated MEMS structures with experimental results

Abstract

Several analytical models exist for evaluating squeeze film damping in rigid rectangular perforated MEMS structures. These models vary in their treatment of losses through perforations and squeezed film, in their assumptions of compressibility, rarefaction and inertia, and their treatment of various second order corrections. We present a model that improves upon our previously reported work by incorporating more accurate losses through holes proposed by Veijola and treating boundary cells and interior cell differently as proposed by Mohite et al. We benchmark all these models against experimental results obtained for a typical perforated MEMS structure with geometric parameters (e.g., perforation geometry, air gap, plate thickness) that fall well within the acceptable range of parameters for these models (with the sole exception of Blech’s model that does not include perforations but is included for historical reasons). We compare the results and discuss the sources of errors. We show that the proposed model gives the best result by predicting the damping constant within 10% of the experimental value. We study the validity of the proposed model over the entire range of perforation ratios (PR) by comparing its results with numerically computed results from 3D Navier-Stokes equation. These results are also compared with other analytical models. The proposed model shows considerably better results than other models, especially for large values of PR.

1 Introduction

Squeeze film damping, which dominates over other losses (Hosaka et al. 1995), plays a significant role in the performance of many MEMS devices such as accelerometers, gyroscopes, torsional mirrors, etc. It has been extensively studied for various cases such as vibration of parallel rigid plates (Blech 1983; Bao 2000; Hwang et al. 1996) and flexible plates (Nayfeh and Younis 2004) with thin to ultra-thin gaps and from smooth to rough surfaces (Hwang et al. 1996; Pandey and Pratap 2004). Perforations in MEMS structures, often used as etch holes (Madou 1997), play a significant role in controlling the squeeze-film damping in most MEMS devices.

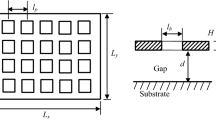
To model perforation effects on squeeze-film damping, there are two common approaches used in the literature. The basic idea used in both approaches is to consider the vibrating plate as a set of uniformly distributed cells. Each cell contains a single hole. The shape and size of a particular cell depends on the nature of the flow around the hole and the pitch of the hole distribution over the plate. Based on the nature of the flow, one can divide the holes into two categories: boundary holes, located along the boundary; and internal holes, located in the interior of the plate as shown in Fig. 1a. These cells are also called the domain of influence of the corresponding holes. The flow pattern is asymmetric around the boundary hole which gives its conjoint cell an asymmetric shape because of asymmetric boundary conditions. When the perforation ratio (defined as the ratio of hole size to hole pitch) is small, such as the case shown in Fig. 1c, the flow around the internal holes near the boundary also show asymmetric flow pattern mainly because of the pressure gradient that exists along the length of the oscillating plate due to squeeze-film flow. In general, however, the flow pattern around the internal holes are considered to be symmetric because of the symmetric boundary conditions around each cell. This assumption is more realistic when the perforation ratio is large, in which case, the pressure gradient drops, especially in the interior of the domain, due to the reduction of maximum pressure as shown in Fig. 1d.

Fig. 1

a Maximum pressure distribution due to squeeze film flow in a system with perforated plate of length 100 μm, width 50 μm, thickness 5 μm, air-gap 4 μm, and perforation ratio, PR (hole size to hole pitch) 0.3 at a particular instant of time during an oscillatory motion of frequency 10 kHz. Pressure variation along section A–A′ in b a non-perforated plate, i.e., PR = 0; maximum pressure = 3.01 × 10⁻² Pa; c a perforated plate with PR = 0.1; maximum pressure = 2.84 × 10⁻² Pa; d a heavily perforated plate with PR = 0.7; maximum pressure = 3.49 × 10⁻³ Pa. A trivial pressure boundary condition is applied on the plate boundaries and outer rim of the holes. Air is used as a fluid medium (μ = 1.67 × 10⁻⁵ N s/m²)

In the first approach, the squeeze-film damping within a single cell is calculated by solving the Reynolds equation over the cell using suitable boundary conditions. The total damping is then calculated by multiplying the damping due to the single cell with the total number of cells. This approach is more suitable for systems with large perforation ratios where the pressure distribution under different cells is largely invariant. This condition can be observed in Fig. 1d where the perforation ratio is 0.7. The pressure distribution is almost flat across the plate except on the boundaries. Assuming incompressible flow and using the first approach, Škvor (1967–1968) has modelled squeeze film damping within a cell by taking ambient pressure boundary condition on the hole rim (i.e., neglecting flow through the hole) and zero flow rate across the cell boundary. Mohite et al. (2005) has extended Škvor’s model to include compressibility and rarefaction effects under the same boundary conditions. By comparing the numerical and experimental results for different perforation model, Kim et al. (1999) have shown that the zero pressure boundary condition on the hole rim, which is used in the Škvors’ model, underestimates the damping. For incompressible flow in a system with circular holes, Homentcovschi and Miles (2004, 2005) have calculated fluid damping as the sum of squeeze film damping and the loss through the holes. Kwok et al. (2005) have also derived a damping model to include perforations and compared it with experimental results but their formula is valid for large perforations only. In this approach, there are two major sources of error. First, the nature and magnitude of flow is taken to be identical for each cell, which leads to a significant error in the net damping calculations in case small and medium sized holes. This is because the holes on the boundaries and the holes in the interior have considerably different pressure distribution. The difference in pressure distribution results in large errors especially when the perforation ratio is small and the number of holes on the boundary are comparable to the number of holes in the interior. The other source of error is the assumption of zero velocity condition on the outer boundary of a cell. In general, the pressure distribution across the length of the plate is not constant as shown in Fig. 1b, c. Therefore, a net flow will result across the boundaries of each cell. The magnitude of error in the second case becomes high as the ratio of the hole radius to cell radius decreases (i.e., for small hole radius) necessitating a large loss through the squeeze effect which, in turn, enhances the spatial variation of pressure as shown in Fig. 1c. To reduce the error contributed by the asymmetric flow pattern in the boundary cells, recently Mohite et al. (2006) have included the effect of asymmetric flow pattern on the net squeeze-film damping calculations, thus improving their own model derived in (Mohite et al. 2005). They have shown through numerical experiments that the damping in a square cell with one open side is about 0.6 times the damping in any of the interior cells with all sides closed, Similarly, the damping in a cell with two sides open (i.e., cells at the corner of a plate) is roughly one third the damping of an interior cell. As these weights are not constant for all perforation ratios, it needs to be calculate for the perforation ratio under considerations. To reduce the second error due to the consideration of no-flow boundary condition on the outer boundary of a cell, the flow through the holes and that through the gap between the parallel plates has to be coupled, which is taken up in the second approach of modelling perforations.

In the second approach, the loss through the holes and the squeeze-film damping are combined in a single governing equation. Veijola and Mattila (2001) have modelled the perforation effect, along with the compressibility effect, in the modified Reynolds equation. Bao et al. (2003) have derived a modified Reynolds equation under the assumption of incompressible flow for system operating at low frequencies by subtracting the pressure relief due to perforations. In another study, Veijola (2006) has recently obtained expressions for several secondary losses such as those due to the open ends of the holes, due to the bending of flow from horizontal to vertical, etc. Thus, the modelling of different loss mechanisms in a single cell is improved even further which is then incorporated into the formula derived by Veijola. All the above models which are based on this approach give good results for dense perforations with small hole size. We have extended Bao’s model to include large range of perforation sizes along with rarefaction and compressibility effects in one of our work (Pandey et al. 2006). This study also includes the effect of plate elasticity in computing the overall damping.

Apart from the above approaches to derive analytical models for simple perforated structure, Schrag and Wachutka (2002, 2004) have proposed mixed level approach to model perforations of arbitrary shape and size in complex structures. In this paper the simple analytical models which are derived based on the two approaches discussed above are summarized in the text. Since the success of both these approaches depends on how well the different dissipation mechanisms are modelled and how correctly the flow patterns in a single cell and across its boundaries are captured, we use the best analytical model which includes most of the effects under a single cell. We follow the same approach discussed in (Pandey et al. 2006) to cover a large range of perforation ratios in the analytical solution obtained by Veijola (2006). To further improve the result, we also consider the effect of boundary holes in the governing equation by adding a correction term. We compare several damping models, including the modified solution presented in this paper, with experimental results obtained from measurements of dynamic response of a perforated MEMS structure using a scanning laser vibrometer. In all models considered here, inertial effect is neglected.

2 Governing equations

The squeeze-film flow is governed by Reynolds equation irrespective of which approach one uses to calculate the squeeze-film damping. To briefly describe the procedure, we consider a rectangular plate of length L along the x-axis, width W along the y-axis, and thickness T _p along the z-axis, as shown in Fig. 2a. The plate has M × N uniformly distributed square holes of size L _h with a pitch q along both x and y-directions. Here, N is the number of holes in any row (along the length) and M is that in any column (along the width). So, the total number of holes is N _h  = M × N. The equivalent hole radius b is calculated by comparing the resistance through a circular pipe and a square channel of the same length, while the cell radius a is calculated by equating the areas of the circular and square shape. Thus, we get b = 1.096 L _h /2 and ${a=q/\sqrt{\pi}}$ (Veijola 2006) (see Fig. 2b). The hole length is equal to the plate thickness, T _p . When the moving plate oscillates with a velocity V _z with respect to the fixed plate, the air under the plate tries to move from its position. We consider the dynamics of air flow through a typical cell shown in Fig. 2b. The figure shows that when the plate oscillates at a certain frequency, the air volume, trapped under the annular cell, gets compressed under the cell and a part of it flows through the hole and causes dissipation. Here, the flow through the hole is assumed to be incompressible, inertialess and fully developed.

Fig. 2

Schematic diagram of the system under consideration with perforation for squeeze film damping: a isometric view of oscillating perforated plate and the fixed plate; b a dynamical view of air flow under a typical hole-cell combination

The form of the governing equation which is used to calculate squeeze-film damping in two approaches (as discussed in the preceding section) can be briefly described below:

• 1. In the first approach, the squeeze-film damping under a single cell, as shown in Fig. 2, can be calculated by solving the conventional Reynolds equation in cylindrical co-ordinate system using suitable boundary conditions on the inner and the outer boundary of the cell (Škvor 1967; Mohite et al. 2005; Kwok et al. 2005). The conventional Reynolds equation in cylindrical co-ordinates is given by

  $$ \frac{1}{r}\frac{\partial}{\partial r} \left(r \frac{\rho h^{3}Q_{\rm ch}}{12\mu} \frac{\partial P}{\partial r}\right) = \frac{\partial (\rho h)}{\partial t} $$

  (1)

  The total damping is then calculated by multiplying the net damping obtained for a single cell with the total number of cells. While this approach can be improved by considering the proper edge correction for the holes lying on the boundaries, it neglect the losses due to the flow across the cell boundaries, hence a more general approach is required which is valid for large range of perforations. The second approach, which is discussed below, considers this particular effect.

• 2. In the second approach, which is used in this paper, the Reynolds equation is modified to couple the flow through the gap between the plates and that through the holes. By equating the total mass flow rate based on the principle of conservation of mass, the conservation of linear momentum and the universal gas law, the non-linear modified Reynolds equation, which includes perforation, compressibility and rarefaction effects, is obtained (Veijola and Mattila 2001; Bao et al. 2003; Pandey et al. 2006). Thus, we get

  $$ \frac{\partial}{\partial {x}} \left(\frac{\rho h^{3}Q_{\rm ch}}{12\mu} \frac{\partial {p}}{\partial {x}}\right)+ \frac{\partial}{\partial {y}} \left(\frac{\rho h^{3}Q_{\rm ch}} {12\mu} \frac{\partial {p}}{\partial {y}}\right)-\frac{\rho p L W} {N_{R} R_{P}}=\frac{\partial {(\rho h)}}{\partial {t}}. $$

  (2)

  where μ is the viscosity of air at ambient conditions. The contribution of internal and boundaries holes can be clubbed into N _R  = (A ₀ N _0s  + A ₁ N _1s  + A ₂ N _2s  + A ₂ N _2s  + A ₃ N _3s ) based on the result and discussion in (Mohite et al. 2006) where A ₀, A ₁, A ₂, and A ₃ are weights calculated by comparing the losses under a hole-cell combination with different boundary conditions and an internal cell with all sides closed (see Sect. 4.1 for details); N _0s is the total number of internal cells whereas N _1s , N _2s and N _3s are the total number of boundary cells with one side open, two sides open, and three sides open along the boundaries of the plate, respectively; and N _h  = N _0s  + N _1s  + N _2s  + N _3s is the total number of cells (or holes). R _P is the net resistance offered to the fluid flow in a hole-cell combination with all sides closed (Veijola 2006), which is given by Eq. (26) in "Appendix A”; Q _ch and Q _th are the flow rate factors which account for rarefaction effect in the flow through the parallel plates and through the holes, respectively. The expression for Q _ch over the entire flow regimes (i.e., the molecular, the transition, the slip and the continuum flow regimes) in the air-gap between the parallel plates (Hwang et al. 1996) and Q _th for the slip flow regime (Veijola 2006) in holes are given by

  $$ \begin{aligned} Q_{\rm ch} &= 1+3 {\frac{0.01807\sqrt{\pi}}{D_{0}}}+6{\frac{1.35355}{D_{0}^{1.17468}}}\\ Q_{\rm th} &= 1+4Kn_{\rm th} \end{aligned} $$

  (3)

  where ${D_{0}={\frac{\sqrt{\pi}}{2 Kn_{\rm ch}}}, {Kn}_{\rm ch}={\frac{\lambda}{h_{0}}}, {Kn}_{\rm th}={\frac{\lambda}{b}}}$ and ${\lambda={\frac{0.0068}{p_{a}}}}$ at ambient temperature and pressure p _a (Sharipov 1999).

Equation (2) can be linearized under the assumption of small amplitude vibration (h = h ₀ + Δh) and small pressure variation (p = p _a  + Δp) through the film thickness, where p _a and h ₀ are constants representing the ambient pressure and the nominal gap thickness, respectively. Now, introducing ${P={\frac{\Delta p} {p_{a}}}}$ and ${H={\frac{\Delta h}{h_{0}}},}$ the linearized modified Reynolds equation for an isothermal process (i.e., ρ ∝ p), becomes

$$ {\frac{\partial^{2} {P}}{\partial {x}^{2}}}+{\frac{\partial^{2} {P}}{\partial {y}^{2}}}-{\frac{P}{l^{2}}}= \alpha^{2}{\frac{\partial {P}}{\partial {t}}}+\alpha^{2} {\frac{\partial {H}}{\partial {t}}} $$

(4)

where ${l=\sqrt{{\frac{Q_{\rm ch} h_{0}^{3} R_{P} N_{R}}{12\mu L W}}}, \alpha^{2}={\frac{12 \mu}{h_{0}^{2}p_{a}Q_{\rm ch}}}}$ is a constant.

3 Different analytical models

Equation (4) is first transformed and solved (Polianin 2002) over a 2D domain as shown in Fig. 2a, with ambient pressure boundary condition (i.e., P = 0) and ambient initial condition, P(t = 0) = 0. The squeeze film damping force is found by following the procedure given in Pandey et al. (2006).

For harmonic displacement H(t) = δe ^iωt about the equilibrium position, i.e., H(0) = 0, we get the non-dimensional pressure distribution P(x,y,t) as

$$ P(x,y,t)=\sum_{m,n={\rm odd}}\frac{16(-1)^{{\frac{m+n-2}{2}}}}{\pi^{2} m n} \frac{-i \omega \delta e^{i \omega t}}{\kappa^{2}+k_{mn}^{2}/\alpha^{2}+i\omega}\cos\frac{m\pi x}{L}\cos\frac{n\pi y}{W} $$

(5)

where ${k_{mn}={\frac{m^{2} \pi^{2}}{L^{2}}}+{\frac{n^{2} \pi^{2}}{W^{2}}}, \kappa={\frac{1}{l \alpha}}.}$ The total reaction force F(t) on the moving perforated plate is calculated by integrating the pressure distribution p _a P(x,y,t) over the domain S = {(x,y)|−L/2 ≤ x ≤ L/2, −W/2 ≤ y ≤ W/2} and then subtracting from it the force contribution due to the total area of the individual holes. The net force after normalizing it with LWp _a is given by

$$ {\frac{F(t)}{LWp_{a}}}=f_{{\rm tot}}=\sum_{m,n={\rm odd}}\frac{16}{\pi^{4} m^{2} n^{2}} \frac{-i \omega \delta e^{i\omega t}}{(\kappa^{2}+k_{mn}^{2}/\alpha^{2})+i\omega} \left[ 4-f_{\rm{perf}}\right] $$

(6)

Here, a negative sign shows the opposite relationship between the back force and the direction of motion. The expression for f _perf is given by:

• If N and M are odd

  $$ \begin{aligned} f_{\rm{perf}} &= (-1)^{{\frac{m+n-2}{2}}} \sum^{{\frac{N-1} {2}}}_{i=-{\frac{N-1}{2}}} \sum^{{\frac{M-1}{2}}}_{j=-{\frac{M-1} {2}}}\int_{i q-L_{h}/2}^{i q+L_{h}} \int_{j q-L_{h}/2}^{j q+L_{h}/2} \cos{{\frac{m \pi x}{L}}} \cos{{\frac{n \pi y}{W}}} \hbox{d} x \hbox{d} y\\ f_{\rm{perf}} & =(-1)^{{\frac{m+n-2}{2}}}\sum^{{\frac{N-1} {2}}}_{i=-{\frac{N-1}{2}}} \left[\sin{{\frac{m \pi (i q+L_{h}/2)} {L}}}-\sin{{\frac{m \pi (i q-L_{h}/2)}{L}}}\right] \\ &\quad \times \sum^{{\frac{M-1}{2}}}_{j=-{\frac{M-1}{2}}}\left[\sin{{\frac{n \pi (j q+L_{h}/2)}{W}}}-\sin{{\frac{n \pi (j q-L_{h}/2)}{W}}}\right] \\ & = 4(-1)^{{\frac{m+n-2}{2}}}\sin{{\frac{m\pi L_{h}}{2L}}}\sin{{\frac{n\pi L_{h}}{2W}}}\sum^{{\frac{N-1}{2}}}_{i=-{\frac{N-1}{2}}} \cos{{\frac{m\pi i q}{L}}} \sum^{{\frac{M-1}{2}}}_{j=-{\frac{M-1}{2}}} \cos{{\frac{n\pi j q}{W}}} \end{aligned} $$

  where ${i\in \left\{\left[-{\frac{N-1}{2}},{\frac{N-1}{2}}\right]: i\rightarrow i+1\right\}}$ and ${j\in \left\{\left[-{\frac{M-1}{2}},{\frac{M-1}{2}}\right]: j\rightarrow j+1\right\}}$

• If N and M are even

  $$ \begin{aligned} f_{\rm{perf}} & = (-1)^{{\frac{m+n-2}{2}}}\sum^{(N-1)}_{i=-(N-1)} \left[\sin{{\frac{m \pi (i q+L_{h})}{2L}}}-\sin{{\frac{m \pi (i q-L_{h})}{2L}}}\right] \\&\quad \times \sum^{(M-1)}_{j=-(M-1)}\left[\sin{{\frac{n \pi (j q+L_{h})}{2W}}}-\sin{{\frac{n \pi (j q-L_{h})}{2W}}}\right]\\& =4(-1)^{{\frac{m+n-2}{2}}}\sin{{\frac{m\pi L_{h}}{2L}}}\sin{{\frac{n\pi L_{h}}{2W}}}\sum^{(N-1)}_{i=-(N-1)} \cos{{\frac{m\pi i q}{2L}}} \sum^{(M-1)}_{j=-(M-1)} \cos{{\frac{n\pi j q}{2W}}} \end{aligned} $$

  where i∈{[−(N−1),(N−1)]: i → i + 2} and j∈{[−(M−1),(M−1)]: j→ j + 2}. Note that i and j are odd numbers.

• If N is odd and M is even

  $$ \begin{aligned} f_{\rm{perf}} & = (-1)^{{\frac{m+n-2}{2}}}\sum^{{\frac{N-1} {2}}}_{i=-{\frac{N-1}{2}}} \left[\sin{{\frac{m \pi (i q+L_{h}/2)} {L}}}-\sin{{\frac{m \pi (i q-L_{h}/2)}{L}}}\right] \\& \quad \times \sum^{(M-1)}_{j=-(M-1)}\left[\sin{{\frac{n \pi (j q+L_{h})} {2W}}}-\sin{{\frac{n \pi (j q-L_{h})}{2W}}}\right] \\& = 4(-1)^{{\frac{m+n-2}{2}}}\sin{{\frac{m\pi L_{h}}{2L}}}\sin{{\frac{n\pi L_{h}}{2W}}}\sum^{{\frac{N-1}{2}}}_{i=-{\frac{N-1}{2}}} \cos{{\frac{m\pi i q}{L}}} \sum^{(M-1)}_{j=-(M-1)} \cos{{\frac{n\pi j q}{2W}}} \end{aligned} $$

  where ${i\in \left\{\left[-{\frac{N-1}{2}},{\frac{N-1}{2}}\right]: i\rightarrow i+1\right\}}$ and j∈{[−(M−1),(M−1)]: j → j + 2}.

Now, the non-dimensional damping force f _dp is calculated by taking the imaginary part of f _tot. Taking the absolute value of the non-dimensional damping force, we get

$$ f_{\rm d p}={\frac{16 \delta \sigma}{\pi^{6}}}\sum_{m,n={\rm odd}}{\frac{\left(\Gamma^{2}/\pi^{2}+m^{2} \chi^{2}+n^{2}\right)\left[ 4-f_{\rm{perf}}\right]}{(mn)^{2}\{[\Gamma^{2}/\pi^{2}+m^{2} \chi^{2}+n^{2}]^{2}+\sigma^{2}/\pi^{4}\}}} $$

(7)

where ${\Gamma=\kappa \alpha W={\frac{W}{l}}= W\sqrt{{\frac{12\mu L W }{Q_{\rm ch} h_{0}^{3} R_{P} N_{R}}}}}$ is a constant that captures the perforation effect; ${\sigma = \alpha^{2}W^{2}\omega={\frac{12\mu W^{2}\omega}{h^{2}_{0}p_{a}Q_{\rm ch}}}}$ is the well known squeeze number (Blech 1983) that captures the compressibility effect; and ${\chi={\frac{W}{L}}}$ is the plate aspect ratio. Generally, W is the smallest dimension chosen out of length L and width W of the plate (in this case, we have taken width W as the smallest dimension). The corresponding damping constant due to squeeze-film assuming viscous damping is given by

$$ C_{\rm squeeze}=\frac{16 \sigma}{\pi^{6}}\frac{p_{a} \chi L^{2}}{\omega h_{0}}\sum_{m,n={\rm odd}}{\frac{\left({\frac{\Gamma^{2}}{\pi^{2}}}+m^{2} \chi^{2}+n^{2}\right)\left[ 4-f_{\rm{perf}}\right]}{(mn)^{2}\{[{\frac{\Gamma^{2}}{\pi^{2}}}+m^{2} \chi^{2}+n^{2}]^{2}+{\frac{\sigma^{2}}{\pi^{4}}}\}}}. $$

(8)

The damping constant due to the loss through holes and their end effects is given by [see Eq. (20) in "Appendix A" (Veijola 2006)]:

$$ C_{\rm hole}=8 \pi \mu \left({\frac{T_{p}} {Q_{\rm th}}}+\Delta_{E} b \right) \times N_{\rm h} $$

(9)

where T _p is the thickness of the perforated plate, Q _th is the relative flow rate to account for the rarefaction effect in the hole [see Eq. (3)], Δ _E is the relative elongation of the hole length due to open end effects [see Eq. (20)]. Finally the net damping constant of the system is given by

$$ C_{\rm total}=C_{\rm squeeze}+C_{\rm hole}. $$

(10)

For higher perforations ratios, the squeeze area reduces and eventually the loss through the holes becomes the dominant term in fluid damping.

The same damping constant obtained from other models that include perforation modelling, are summarized below.

• 1. By substituting f _perf = 0 in Eq. (8) and N _R  = N _h in Γ and neglecting σ term from the denominator we retrieve Veijola’s formula (Veijola 2006)

  $$ C_{\rm Veijola}={\frac{768 \mu L W}{h0^{3} \pi^{6} Q_{{\rm ch}}}}\sum_{m,n={\rm odd}}{\frac{1}{(mn)^2\left[{\frac{m^{2}} {L^{2}}}+{\frac{n^{2}}{W^{2}}}+{\frac{768 \mu LW}{64 \pi^{2}h_{0}^{3}Q_{{\rm ch}}N_{h} R_{p}}} \right]}} $$

  (11)

• 2. Bao’s formula (Bao et al. 2003), which is derived assuming incompressible flow, gives the following expression for the damping constant:

  $$ \begin{aligned} C_{\rm Bao} &= 3 \gamma^2-6\gamma^3\frac{\sinh^{2}{({\frac{1}{\gamma}})}} {\sinh({\frac{2}{\gamma}})}-24 \gamma^3 \frac{\chi}{\pi^2} \frac{\mu} {Q_{\rm ch}}\frac{W^{3} L}{h_{0}^3}\\&\quad \times \sum_{n={\rm odd}} {\frac{\tanh\left({\frac{\sqrt{1+(n \pi \gamma/2)^2}}{\gamma \chi}}\right)}{n^2(1+(n \pi \gamma/2)^2)^{3/2}}} \end{aligned} $$

  (12)

  where ${\gamma = {\frac{2}{W}}\sqrt{{\frac{2h_{0}^{3}T_{\rm eff}\eta(\beta)Q_{\rm ch}}{3 \beta^{2} b^{2}Q_{\rm th}}}}, \beta=b/a}$ is the ratio of the hole to cell radius, ${T_{\rm eff}(=T_{p}+{\frac{3 \pi b}{8}})}$ is the effective hole length, ${\eta(\beta)=\left(1+{\frac{3b^{4}K(\beta)Q_{\rm th}}{16 T_{\rm eff} h^{3}Q_{\rm ch}}}\right),}$ and K(β) = 4β²−β⁴−4lnβ−3. Q _ch and Q _th are given by Eq. (3). In the original equation given by Bao, rarefaction effect in the pipe flow and the flow through the gap between the parallel plates has not been modelled. In Eq. (7), we have included rarefaction effect which is inevitable in small air-gap thickness and the holes of small radius.

• 3. The expression of damping constant given by Kwok et al. (2005) is based on the solution of Reynolds equation under a single hole-cell combination with non-trivial pressure boundary condition on the inner boundary and trivial pressure boundary condition on the outer boundary of the cell. The net damping is then obtained by summing up the contribution of all hole-cell combinations. The expression of damping constant is given by

  $$ C_{\rm Kowk}=\frac{3}{8} \frac{\mu}{Q_{\rm ch}} \frac{q^4 N_{h}}{ h_{0}^3} K(\beta)+8 \pi T_{p} N_{h} \frac{\mu}{Q_{\rm th}} \frac{(q^2-L_{h}^2)^2}{L_{h}^4}. $$

  (13)

  The first term captures the loss due to squeeze-film flow under the cells and the second term captures the additional loss due to non-trivial pressure boundary conditions arising from the flow through the holes. In this formula, although the effect of flow through the holes is considered on the squeeze-film damping, the drag force on the side walls of the holes is not included. Therefore, the formula is valid for thin plates only.

• 4. Ŝkvor’s (1967) formula for fluid damping is derived by solving the Reynolds equation with the trivial pressure boundary condition on both the inner boundary and zero flux on the outer boundary of a single cell. The total damping is calculated by summing the contributions of all cell and hole combinations. The damping constant in this case is given by

  $$ C_{\rm \hat{S}kvor} = 3 \pi \frac{\mu}{Q_{\rm ch}} \frac{a^4 N_{h}}{2 h_{0}^{3}} K(\beta) $$

  (14)

  If it is compared with Kowk’s model, it is clearly seen that the negligence of flow through the holes omits the second term in Eq. (13). Thus, this formula is suitable in those cases where the loss through the holes is negligible, e.g., perforations with large holes and small plate thickness.

• 5. Mohite et al. (2005) modified the Ŝkvor’s formula to include rarefaction and compressibility effect. Later, they found that the damping contribution of boundary cells are not same as the internal cells, and therefore, they modified the formula to include additional boundary effects.

  $$ \begin{aligned} C_{\rm Mohite} &= {\frac{p_{a} a^{2} \pi}{h_{0} \omega}}\\ &\quad \times \hbox{Img} {\left[ {\frac{{2R_i {\left[{I_{1} ({\sqrt {\sigma _aj}R_o})K_{1} ({\sqrt{\sigma _a j}R_i }) -I_{1} ({\sqrt{\sigma _{\rm a} j}R_i })K_{1} ({\sqrt{\sigma _a j}R_o})} \right]}}} {{{\sqrt {\sigma _a j} }{\left[ {I_{0} ({\sqrt {\sigma _a j}R_i })K_{1} ({\sqrt {\sigma _a j}R_o }) +I_{1} ({\sqrt {\sigma _aj}R_i} })K_{0} ({\sqrt {\sigma _a j}R_i})\right]}}} - {\left({R^{2}_{o} - R^{2}_{i} } \right)}} \right]}\\ &\quad \times (A_{0}N_{0s}+A_{1}N_{1s}+A_{2}N_{2s}+A_{3}N_{3s}) \end{aligned} $$

  (15)

  where ${\sigma_{a} = {\frac{12\mu a^{2}\omega}{h^{2}_{0}p_{a}Q_{\rm ch}}}}$ is the squeeze number corresponding to a single hole/cell combination; I ₀ and I ₁ are the modified Bessel functions of the first kind of order zero and one, respectively; K ₀ and K ₁ are the modified Bessel functions of the second kind of order zero and one, respectively; A ₀ = 1, A ₁ = 0.6154, A ₂ = 0.3407, A ₃ = 0.1758, R _o  = 1, R _i  = b/a, N _os is the total number of internal hole-cell combinations whereas N _1s , N _2s and N _3s are the total number of boundary hole-cell combinations with one side, two sides, and three sides along the boundaries of the plate, respectively. In this formula, the flow through the holes is neglected.

We point out that if perforations are not considered in the modelling, the formula presented in this paper [i.e., Eq. (7)] reduces to Blech’s formula (Blech 1983) for f _perf = 0, Γ = 0 and C _Hole = 0. The Blech’s formula, after taking effective viscosity in σ, is given by

$$ C_{\rm Blech}=\frac{64 \sigma}{\pi^{6}}\frac{p_{a} \chi L^{2}}{\omega h_{0}}\sum_{m,n={\rm odd}}{\frac{\left(m^{2} \chi^{2}+n^{2}\right)}{(mn)^{2}\{[m^{2} \chi^{2}+n^{2}]^{2}+\sigma^{2}/\pi^{4}\}}}. $$

(16)

For viscous damping, the damping force is given by ${F_{d}=c_{a} \dot{x},}$ where x is the displacement during oscillations. Now, for x = A sinω t, where A is the amplitude of oscillation and t is the time, the velocity of oscillation is given by ${\dot{x}=A \omega \cos{\omega t}}.$ If m is the effective mass of the vibrating system, then, using the definition of quality factor (Clough and Penzien 1993), we calculate quality factor as:

$$ Q_{\rm anal}=2\pi \frac{E_{\rm input}}{\Delta E_{\rm loss}\ {\rm per\,cycle}}=2\pi{\frac{{\frac{1}{2}}m A^{2} \omega^{2}}{\int_{0}^{2\pi /\omega}F_{d} \dot{x} dt}}={\frac{m \omega}{c_{a}}} $$

(17)

where ω is the frequency of oscillation. For comparing with the experimental results, we use Eq. (17) to calculate the quality factor analytically for all the models described above.

4 Experimental validation

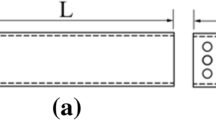
We take a polysilicon MEMS structure shown in Fig. 3a for an experimental validation of the analytical models. The dimensions of the structure and the properties of polysilicon used in calculations are given in Table 1.

Fig. 3

a A picture of the MEMS structure with probes on the electrical pads (shown partially). The central perforated plate is suspended by four anchor beams (see Table 1 for dimensions). There is an electrode below the perforated plate. The structure can oscillate in-plane (actuated by combdrives) or out-of-plane (actuated by parallel plate electrodes). In this study, the structure is made to oscillate out-of-plane by applying actuating voltage between the perforated plate and the bottom electrode. b Side view of the MEMS structure along A–A′. c Frequency response of the first out-of-plane mode of the MEMS structure shown in a

Table 1 Dimensions of MEMS structure shown in Fig. 3a

Assuming that the plate oscillates as a single rigid body, rigidly, the approximate effective mass m _eff = m _plate + m _combs + m _beam, where m _plate = (L ² _p −N _h L ² _h )T _pρ_poly = 1.77 × 10⁻⁹ kg is the mass of the plate involved in out of plane motion, m _combs = N _c L _c W _c T _p ρ_poly = 9.79 × 10⁻¹¹ kg is the mass of the total combs, m _beam = 4 × 0.37L _b W _b T _p ρ_poly = 1.45 × 10⁻¹¹ kg is the effective mass (Rao 1995) of the anchor beams. Here, the beam is considered as a guided beam. Thus, for the given MEMS structure, the net effective mass, m _eff is 1.88 × 10⁻⁹ kg. For computing the first resonant frequency theoretically, we need to find the residual stress in the structure. Such large structure suspended with straight anchored beams (as compared to folded beams) tend to have large residual stresses. We carried out experiments on a few structures on the same wafer (fabricated with the same process) and used independent results to determine the values of the Young’s modulus (E) and the residual stress (τ) (Wylde and Hubbard 1999). The experimentally determined values of E and τ turn out to be 171 GPa and 77.6 MPa, respectively.

For the experiments, we use MSA 400 microsystem analyzer—a Polytec product to characterize the out-of-plane vibrations by Scanning Laser-Doppler Vibrometry (http://www.polytec.com). To find the quality factor and the damped natural frequency of the structure, we apply 4 V DC and 1 V AC pseudorandom signal with frequencies ranging from 1 to 40 kHz. From the captured modes and frequencies, the first natural frequency is found to be 17.30 kHz. The process is repeated 10 times and the results are found to be the same. To verify the spectral response to the pseudorandom signal, we apply a 1 V AC signal (over a 4 V DC bias) of a single frequency at a time and record the steady state response amplitude of the structure. We repeat this process over hundred chosen frequencies between 10 and 27 kHz. Here, we apply electrical signal using an internal function generator across the bottom electrode and the upper perforated plate. The frequency response curve for the displacement on the plate is shown in Fig. 3c. The out-of-plane mode corresponding to this frequency is shown in Fig. 4.

Fig. 4

Transverse motion of the proof mass a top view; b oblique view

To calculate the damping ratio and the quality factor, we use the frequency response curve shown in Fig. 3c. The largest amplitude of oscillation is found to be about 165 nm and the first natural frequency, f _d , to be 17.30 kHz. To calculate the quality factor directly from the response curve, we apply the half-width method (Clough and Penzien 1993). The expression of the experimental quality factor Q _exp is given by

$$ Q_{\rm exp}\approx{\frac{1}{2 \xi}}={\frac{f_{d}} {f_{2}-f_{1}}}. $$

(18)

where f ₁ and f ₂ are frequencies at which the amplitude of the displacement is equal to ${1/\sqrt{2}}$ times the maximum amplitude, and f _d is the resonance frequency. To calculate the quality factor based on the response shown in Fig. 3c, we get f _d  = 17.30 kHz, f ₁ = 14.86 kHz and f ₂ = 19.99 kHz, and finally, Q _exp = 3.37 from Eq. (18). Thus, we get Q _exp≈ 3.37. The damping ratio corresponding to the Q _exp is 0.14 and the the damping constant is obtained by using the relationship C _exp = m _effω _d /Q _exp = 6.09 × 10⁻⁵ N s/m, where ${\omega_{n} =\omega_{d}/\sqrt{1-\xi^2}=1.01 \times \omega_{d} \approx \omega_{d} = 108.7 \times 10^{3} }$ rad/s is the natural angular frequency and m _eff is the effective mass of the structure. The stiffness of all the beams with the given stress residual effects is 22.7 N/m.

4.1 Comparison of different analytical models with experiment

We first calculate the damping constant using different damping models given in Eqs. (7)–(16). Then, we estimate the corresponding quality factor by substituting the damping constants in Eq. (17). We also compute the percentage error in each model with respect to the experimental value of the damping constant and discuss the results.

First, we calculate the weights A’s for border holes in the given structure shown in Fig. 3a. Figure 5 shows the pressure distribution and the corresponding fluid velocities in a typical cell with no-flow boundary condition on the boundaries of the fluid domain. The boundary conditions in an internal cell are shown in Fig. 5a. The numerical procedure is validated by comparing the value of damping constant obtained with the theoretical value from Eq. (26) for a cell with no-flow boundary condition on all the four sides. It is found that the numerical value 3.786 × 10⁻⁷ N-s/m² of damping constant for an interior cell is extremely close to the analytical value 3.785 × 10⁻⁷ N-s/m². To calculate damping in the border cells, appropriate boundary conditions must be used which are listed in Table 2. In Table 2, we calculate the damping constant in a square cell of size 31.25 μm, a square hole of size 11.25 μm, and the air-gap thickness of 6 μm under different boundary conditions. The pressure distribution on the square cell and on the corresponding area of the back plate are shown in the second and third columns. The numerical values of the damping constant, which are obtained by solving the 3D Navier-Stokes equation in ANSYS, are listed in column four. The ratio of the damping constant in different cases with respect to the fully closed condition, which assumes the boundary condition around a typical internal hole-cell combination, are listed in column five. In the structure shown in Fig. 3a, there are two types of border cells: 4 corner cells with two adjacent sides open, i.e., case CL₂OP₂; and 28 cells on the boundaries with one side open, i.e., case CL₃OP₁. In short, out of N _h  = 256 total hole-cell combinations, there are N _0s  = 226 internal cells with weights A ₀ = 1, N _1s  = 28 border cells of type CL₃OP₁ with weights A ₁ = 0.39, and N _2s  = 4 corner cells of type CL₂OP₂ with weights A ₂ = 0.22. All other type of cell numbers N′s and the corresponding weights A′s are zero. These values are subsequently used in calculating the damping constant in the test structure using the present formula.

Fig. 5

Sectional view of 3D flow behavior in a cell with no-flow condition on the boundaries of the air-gap: a pressure distribution; b net fluid velocity; c net velocity vector when the plate moves downwards

Table 2 Damping constant and weights with respect to fully closed boundary condition for different boundary conditions. Here, CL₄OP₀ denote all the sides closed, CL₃OP₁ three sides closed and one side open, CL₂OP₂ two adjacent sides closed and two adjacent sides open

Blech’s formula (Blech 1983), which is valid only for non-perforated structures, is used to calculate damping constant by taking the effective plate area (based on effective length) of the perforated plate. The effective length is obtained by reducing the original length of the plate by the net perforation length (L _eff = L _p−N L _h = 320 μm). It gives an error of 476% in the damping constant. This is obviously not a relevant formula for the perforated plate considered here as it does not take different effects into account such as the pressure relief due to perforations, etc. Ŝkvor’s (1967) formula, which neglects the loss through the holes, gives an error of 74.5%. This formula is derived based on the repetitive pressure pattern over the structure around each hole. Mohite et al. (2005), included the compressibility and rarefaction effect and recently (Mohite et al. 2006) modified the formula by modelling the effect of boundary holes and internal holes, separately. When compared with experimental result, it gives an error of 76.9%. The formula derived by Kwok et al. (2005) improves the Ŝkvor’s model by including the loss through the holes and gives an error of 51.2%. Both Ŝkvor and Kwok formulas are based on the first approach discussed in section I and they do not consider the loss due to drag on the sides walls of the holes. That is the reason their models fail if for thick perforated plate. But these models can be extended by adding the damping due to drag on the side walls of the holes to their models. In (Bao et al. 2003), modified the conventional Reynolds equation to include perforation effect by equating the net flow through all the holes and thus they include spatial variation of pressure also in the governing equation. Their formula gives an error of 32.4%. Recently, Veijola (2006) has modelled the loss under a single cell-hole combination by considering other factors such as the loss due to turning of flow from horizontal to vertical, the loss due to change in flow profile from the region under the cell to that under the hole, etc. (see “Appendix A”), in addition to the losses included in Bao’s model. When compared with the experimental result, Veijola’s model gives an error of 34.6%. However, our formula, given by Eq. (7), which is an improvement over Veijola’s formula, does the best and gives the least amount of error—only 2.0%. This improvement is due to the consideration of reduction in the damping force by f _perf as well as the distinction made between the boundary cells and the interior cells in the total force calculation. We find that both these factors contribute significantly in this case, reducing the error approximately by 23 and 15%, respectively, from the values obtained with Veijola’s model (Table 3; Fig. 6).

Table 3 Comparison of damping constant C _anal in N-s/m² obtained from different analytical models including the present model with respect to the experimental result, C _exp = 6.09 × 10⁻⁵ N-s/m² of MEMS structure shown in Fig. 3b. (Percentage error is calculated with respect to the experimental result, i.e., ${\left|{\frac{C_{\rm exp}-C_{\rm anal}}{C_{\rm exp}}}\right|\times 100)}$

Fig. 6

Damping constant and its percentage error with respect to experimental result using different analytical models for the MEMS structure shown in Fig. 3a

4.2 Numerical validation of f _perf

In order to compare different analytical models at different values of perforation ratios and discuss the effect of pressure relief, we carry out numerical simulations to calculate damping constant in a perforated structure shown in Fig. 7 with the following dimensions: square plate of length 200 μm, perforation distribution 8 × 8, plate thickness 3.5 μm, and air-gap thickness 8 μm. Perforation ratios of 0.0, 0.3-0.9 are considered with a constant value of pitch q = 25.0 μm. We solve the 3D Navier-Stokes equation on the domain shown in Fig. 7 with the following boundary conditions: zero pressure boundary condition on the dotted boundaries (i.e., on the side boundaries and the outer end of the holes), zero velocities on the fixed plate, and non-zero but small velocity with a frequency of 500 Hz on the solid portion of the perforated plate as shown in Fig. 7c. After calculating the pressure distribution on the back plate and the perforated plate, and shear stresses on the side walls of the holes, we calculate the net back force based on three different areas: (1) the top surface of the back plate; (2) the bottom surface of the perforated plate; and (3) the bottom surface of the perforated plate along with the side walls of the holes. We then calculate the phase difference between the velocity and the net back force in all the cases and subsequently find their damping and spring components. The damping constant is then obtained under the assumption of viscous damping in which damping force is proportional to the velocity.

Fig. 7

a Pressure distribution on the perforated plate of PR = 0.6; b pressure distribution on the back plate; c average velocity vector

For analytical models, we vary perforation ratios from 0.01 to 0.99 for the same values of pitch and other dimensions as mentioned above. The extreme values of PR considered here are not practical. However, good theoretical models are expected to predict the correct behavior close to these extreme values on theoretical grounds. Since, the zero pressure boundary condition is taken on the outer ends of the holes in the numerical simulation, we also neglect the outer ends effect of the holes in the analytical model. Moreover, to stress the importance of f _perf in the present model we neglect any modification due to boundary holes (i.e., all the holes are assumed to affect the pressure distribution uniformly).

In order to point out some of the factors under different perforation ratios, we define regions of smaller holes, medium sized holes, and larger holes as shown in Fig. 8.

Fig. 8

Comparison of different analytical models over different values of hole size for a given value of the hole pitch (25.0 μm) and plate thickness (3.5 μm)

For smaller perforation ratios, the average pressure relief due to perforations is small as shown in Fig. 8. Thus, the squeeze-film damping dominates over the loss through the holes. In this case, the formulas, which are derived using the first approach are not valid, the reason being the squeeze-film flow across the cell boundaries due to the existence of non-trivial pressure gradient. The present model, Bao’s model and Veijola’s model fit well under this range. As the perforation area is very small compared to that of the non-perforated plate, the term f _perf in the present model will be very small. So, the present model gives values very close to the Veijola’s and the Bao’s model. These three models match well with the numerical values. It is also observed that the numerical value of damping constant based on the three different areas—the top surface of the back plate, the bottom surface of the perforated plate, and the bottom surface and side walls of the perforated plate—are the same under this range.

For medium sized holes, the effect of perforations start increasing and reaches to a level where one can consider a no flow boundary condition on the cell boundaries to find the total fluid damping. In this case, as the area of the perforation increases, the fluid flow through the holes increases. So, the fluid will less likely to cross the cell boundaries and set the condition for first approach to be valid. Since the net area, over which the back force due to the squeeze-film is applied, decreases, this effect is accounted for subtracting the back force on the perforated areas. In the present formula, this condition is captured by calculating f _perf. In addition there is a loss due to drag force on the side walls of the holes. In this regime, Veijola’s model which is based on the back plate area gives higher values than the numerical values which are based on the area consisting of the bottom surface and the side walls of the perforated plate, while the Bao’s model gives lower values because it does not consider all types of losses which exist under a particular cell-hole combination. On the other hand, the present model matches well with numerical values also over this range. These three formulas can be used to calculate damping in this range with different minor errors. If the numerical results based on the three different areas are compared, it is found that results based on the back plate area give larger values of damping than the other two cases. And the difference in other two cases at the end of this range shows that the drag force on the side walls becomes significant compared to the squeeze-film damping.

For large sized holes where perforation ratio becomes very high, the contribution of holes due to the drag on the side walls in total fluid damping become significant which is given by C _hole from Eq. (9). It is also clear from the numerical results based on these three different areas. It can also be observed from Fig. 8 that out of Veijola’s, Bao’s and the present models, the present model matches well with the numerical results with an error of 10% at PR = 0.9 (Fig. 9). In the case of large sized holes, generally the first approach is used to calculate damping. But in these models, the flow from the boundaries of the plate, and the loss due to the drag on side walls of the holes are not considered. The models which are given by Kwok et al. (2005) and Škvor (1967) can be corrected by adding the effect of side walls of the holes from Eq. (9). Finally it is observed that only the present model matches well with the numerical result over different perforation ratios, hence it is best suited for modelling the effect of perforations in squeeze-film damping.

To validate the formula for thin as well as thick structures, we compare the analytical damping constants obtained from the Veijola’s formula and present formula with numerical results for the plate thicknesses of 1 and 10 μm as shown in Fig. 10. In both the cases, we find that the present formula captures the perforation effect effectively.

Since the present formula is a modification of Veijola’s model, we compare the percentage error obtained from Veijola’s model and the present (modified) model with respect to the numerical results for a plate of thickness 3.5 μm in Fig. 9. We find that the Veijola’s model gives an error of about 150% compared to 10% error in the present model at the perforation ratio of 0.9. Finally, we point out that Eq. (7) is valid for larger range of perforation ratios. It is because the factor f _perf due to perforations and the corrections for boundary and interior holes are included in Eq. (7) (Fig. 10).

Fig. 9

Percentage error in calculating damping constant from the Veijola’s model and the present model with respect to numerical results for a plate of thickness 3.5 μm

Fig. 10

Comparison of Veijola’s model and present model with respect to numerical results for a plate thickness of a 1 μm, and b 10 μm

4.3 Frequency limits

There are two main assumptions used in the derivation of the present model: (1) the amplitude of displacement is small, i.e., δ(t) ≪ h ₀; and (2) the inertial effect is negligible, i.e., Re ≪ 1. While the first assumption helps in the linearization of the governing equation, the second assumption limits the operating frequency range.

For the valid frequency range, the Reynolds number must be less than 1. By an order of magnitude analysis of the equation of squeeze-film flow through the gap between the plates and the equation of flow through the holes, we get the following conditions:

• For inertialess flow in the gap between the plates, the frequency should satisfy the condition ${f_{1} < < {\frac{\mu}{2 \pi \rho h_{0}^{2}Q_{\rm ch.}}}}$

• For inertialess flow in the holes, the frequency should satisfy the condition ${f_{2} < < {\frac{\mu}{2 \pi\rho b^{2}Q_{\rm th.}}}}$

Therefore, the maximum allowable frequency is given by min(f ₁, f ₂).

5 Conclusions

We present a model for squeeze film damping in perforated MEMS structures that takes into account various losses associated with perforations as well as the spatial variation of pressure in 2D domains. This model is an improvement over the model proposed by Veijola as it uses the elaborate calculations for losses through holes proposed by him, and, in addition, incorporates corrections in squeeze-film damping calculation due to perforations and differential contributions of boundary cells and interior cells. We compare the current model with various other analytical models available in the literature for computing squeeze film damping and compare their predicted values with the experimental value obtained for a typical perforated MEMS structure. We show that the model presented in this paper gives the closest results to the experimentally obtained value. To test the validity of the present model over a large range of perforation ratios, a comparative study is carried out with numerical simulations using 3D Navier Stokes equation and the results are compared with other analytical models as well. The results from the present model are compared in details with results from Veijola’s model to show the effect of modifications included in the present model. The result show that the proposed modifications improve the analytical prediction considerably for perforation ratios over 0.5.

Resistance in a single cell

Total resistance R _P in a single perforation cell as shown in Fig. 2b can be divided into three regions (Veijola 2006):

• 1. Squeeze-film region: The flow resistance in this case is given by R _S

  $$ R_{S}={\frac{3 \pi \mu a^{4}}{2 Q_{{\rm ch}} h_{0}^{3}}} K(\beta) $$

  (19)

  where K(β) = 4β²−β⁴−4lnβ−3, β = b/a, b is the hole radius, a is the cell radius, μ is the dynamic viscosity of fluid, Q _ch is the relative flow rate coefficient which accounts for rarefaction effect in the gap h ₀ between the moving part and the fixed part.

• 2. Perforation and end effect:

  $$ R_{C}+R_{E}=8 \pi \mu \left({\frac{T_{p}} {Q_{{\rm th}}}}+\Delta_{E} b \right) $$

  (20)

  where

  $$ \begin{aligned} \Delta_{E} &= {\frac{0.944 \times 3 \pi (1+0.216 Kn_{{\rm th}})}{16}} \left( 1+0.2 \beta^{2} - 0.754 \beta^{4} \right) f_{E} \left( {\frac{b}{h_{0}}}\right), \quad f_ {E}(x)&=1+{\frac{x^{3.5}}{178(1+17.5 Kn_{{\rm ch}})}} \end{aligned} $$

  where T _p is the thickness of the cell, Q _th is the relative flow rate to account for rarefaction effect in the hole, Δ _E is the relative elongation of the hole length due to end effects (Sharipov 1999) (open end only).

• 3. Intermediate region: It consists of R _IS , R _IC , and R _IB . R _IS is the loss due to the change in the flow profile when flow just enters the region under the hole (see Fig. 2b). R _IC is the loss due to turning of flow from horizontal to vertical. R _IB is the loss due to the change in velocity profile at large perforation ratio. The expression for these losses are given by:

  $$ R_{IS}={\frac{6 \pi \mu (a^2-b^2)^2}{b h_{0}^{2}}} \Delta_{S}, \quad R_{IC}=8 \pi \mu b \Delta_{C}, \quad R_{IB}=8 \pi \mu b \Delta_{B} $$

  (21)

  where

  $$ \Delta_{S}= {\frac{0.56-0.32 \beta+0.86 \beta^2}{1+2.5 Kn_{ch}}} $$

  (22)
  $$ \Delta_{C}= (1+0.6 Kn_{th})(0.66 - 0.41 \beta -0.25 \beta^2) $$

  (23)
  $$ \Delta_{B}= 1.33 (1-0.812 \beta^{2}){\frac{1+0.732 Kn_{th}} {1+Kn_{ch}}} f_{B}\left({\frac{b}{h_{0}}},{\frac{T_{p}}{h_{0}}} \right) $$

  (24)
  $$ f_{B}(x,y)=1+{\frac{x^4 y^3}{7.11 (43 y^3+1).}} $$

  (25)

Finally, the net resistance is given by

$$ R_{P}=R_{S}+R_{IS}+R_{IB}+{\frac{1} {\beta^4}}\left(R_{IC}+R_{C}+R_{E} \right). $$

(26)