1 Introduction

When a portion (band) of a solute is entrained by a hydrodynamic flow through a channel, one observes broadening of the band. At sufficiently high flow velocities, the rate of the band broadening can substantially exceed that due to molecular diffusion of the solute. This effect is referred to as hydrodynamic dispersion (HD).

The theory of HD in a flow through a straight channel was developed in the classical papers (Taylor 1953; Aris 1956). According to these studies, the HD of a non-adsorbing solute occurs due to the non-uniformity of the flow velocity within the channel cross-section. In the presence of longitudinal concentration gradient of solute, such non-uniformity gives rise to a transverse redistribution of solute within the channel cross-section. The additional convective flux, which is associated with the deviation of solute concentration from the cross-sectional mean value, turns out to be proportional to both the squared cross-sectional mean velocity and the solute longitudinal concentration gradient. Importantly, this flux is always directed against the concentration gradient. Consequently, such an additional convective flux has properties of an apparent diffusion flux. While dealing with a solute portion (band) transported by a hydrodynamic flow, this apparent diffusion flux is added to the molecular diffusion flux and intensifies the broadening of the entrained band. At sufficiently high velocity, such an apparent diffusion flux exceeds the molecular diffusion flux by orders of magnitude and, thus, becomes completely responsible for the band broadening.

The HD strongly affects both the resolution and the throughput of devises of analytical and bio-analytical chemistry. Due to the HD, a solute (analyte) band entrained by a hydrodynamic flow is broadened thereby decreasing the resolution of analytical separations. The rate of such a broadening increases with increasing the flow velocity. Note that increasing the flow velocity is a major method of increasing the throughput of analytical separations. Consequently, increase in the device throughput results in a deterioration of analytical device resolution. Clearly, a minimization of the HD is one of the most important issues to be addressed while developing new versions of analytical techniques.

The above-discussed apparent diffusional flux is proportional to a square of length scale parameter characterizing the flow non-uniformity within the channel cross-section. For the pressure-driven (Poiseuille) flow, such a length scale parameter coincides with that characterizing the cross-section geometry (Taylor 1953, Aris 1956). For electroosmosis, the flow uniformity is characterized by the inverse Debye parameter (the Debye length), \( \kappa^{ - 1} \), where \( \kappa \) is given as,

$$ \kappa^{2} = \frac{{F^{2} \sum\nolimits_{k} {z_{k}^{2} C_{k} } }}{\varepsilon RT} $$
(1)

In Eq. (1), \( \varepsilon \) is the dielectric permittivity of the electrolyte solution, T is the absolute temperature, F and R are the Faraday and gas constants, \( C_{k} \) and \( z_{k} \) are the kth ion concentration and valence, respectively.

For 10−3 M 1:1 aqueous electrolyte solution, \( \kappa^{ - 1} \approx 10{\text{ nm}} \) and decreases with increasing the electrolyte concentration. Hence, for channels whose cross-sectional dimension exceeds \( 100\;{\text{nm}} \), while using the electroosmotic instead of the Poiseuille flow, one can expect a decrease in the above-discussed apparent diffusion flux by more than two orders of magnitude. The latter results in a weaker HD than that produced by the Poiseuille flow and, thus, higher device resolutions can be observed at the same throughput. Such a weaker HD is one of explanations of the existing trend in developing analytical technique: the use of electrically rather than pressure-driven flows in separation columns and transportation channels of analytical devices (Knox and Grant 1987; Legido-Quigley et al. 2003; Li 2004; Karniadakis et al. 2005; Haeberle and Zengerle 2007). This trend motivates the interest of researchers in the theoretical analysis of the HD produced by electroosmotic flow (Martin and Guiochon 1984; Datta and Kotamarthi 1990; Datta 1990; Griffiths and Nilson 1999, 2000; Gas and Kenndler 2002; Zholkovskij et al. 2003, 2006; Ghosal 2006; De Leebeek, and Sinton 2006; Dutta 2007, 2008; Paul and Ng 2012a, b). The afore-referenced studies confirm the above qualitative conclusion for relatively weak HD in purely electroosmotic flow though straight channels with uniform zeta potential.

As shown by many authors, a substantially stronger HD is produced in the case of electroosmotic flow through a straight channel with longitudinal non-uniformity of zeta potential of channel walls (Anderson and Idol 1985; Herr et al. 2000; Ghosal 2002a, b, 2006; Zholkovskij et al. 2010). This non-uniformity can occur due to random factors as well as regular factors originating from specific technology of channel fabrication In the presence of the longitudinal non-uniformity of zeta potential, Poiseuille flow component is generated by applying electric field in spite of overall zero pressure difference. The Poiseuille flow component occurs to maintain the continuity of total hydrodynamic flow since a purely electroosmotic flow cannot be continuous for a straight channel with the longitudinal variation of zeta potential. Consequently, such un-intentional Poiseuille flow substantially increases the HD.

The above-cited studies have dealt with the walls longitudinal variation of zeta potential. At the same time, a transverse variation of zeta potential can occur due to exactly the same causes as the longitudinal variations. It would be expected that transverse variations (walls of different zeta potentials but uniform in the longitudinal direction) would also make contribution to the flow non-uniformity and thus to HD.

Andreev et al. (1997), in their pioneering study, demonstrated that an increased HD takes place in the case of a slit channel whose walls have different zeta potentials. In this publication, the authors determined the hydrodynamic field within a straight channel having rectangular cross-section with given different values of zeta potentials attributed to each of the walls. For analyzing HD, the authors considered the limiting case of rectangle aspect ratio approaching zero by assuming that this limiting case corresponds to a slit channel. For such a velocity field, the authors numerically applied the Taylor–Aris scheme of addressing the HD and obtained curves that clearly showed a drastic increase in the band broadening when the zeta potentials of the slit channel walls are different.

Having confined themselves to presenting two numerical examples corresponding to a certain set of parameters (the channel width, 10 µm, buffer concentration, \( 10^{ - 5} {\text{M}} \), etc.), Andreev et al. (1997) did not derive analytical expressions that would describe the HD for arbitrary combination of parameters. At the same time, the modern developments of analytical techniques require information about the parameters of analytical separations at much higher concentrations and smaller channel dimensions. In general, for optimizing separation and transport processes, it is useful to have analytical expressions capable of addressing the HD within wide ranges of parameters (channel width, wall zeta potentials, electrolyte concentration, etc.). Obtaining and analyzing such analytical expressions are the major objectives of the present paper. Finally, it will be demonstrated how the derived expressions can be used for practical considerations.

2 Parameters of band broadening

It is convenient to characterize a given band width by the band variance, \( \sigma \), which is the root-mean-square deviation of the molecule coordinate from the coordinate of the band mass center (Fig. 1). Due to band broadening, the variance increases with time. The dispersion coefficient, D, describes the rate of the change of squared variance with time. It is defined as

Fig. 1
figure 1

Solute band moving along axis x with speed \( u_{c} \)

Full size image
$$ D = \frac{1}{2}\frac{{{\rm{d}}\sigma^{2} (t)}}{{{\rm{d}}t}} $$
(2)

Another parameter, which describes changes in the variance during the band displacement at the unit distance, is referred to as the plate height, H

$$ H = \frac{{{\rm{d}}\sigma^{2} (x_{c} )}}{{{\rm{d}}x_{c} }} $$
(3)

where \( x_{c} \) is the coordinate of the band center of mass (Fig. 1). Thus, Eqs. (2) and (3) define the major parameters employed in the literature for describing the band broadening.

For a band of a non-adsorbing solute flowing through a straight channel, the center-of-mass velocity coincides with the cross-sectional mean velocity \( \left\langle u \right\rangle \)

$$ \left\langle u \right\rangle = \frac{{{\rm{d}}x_{c} }}{{{\rm{d}}t}}. $$
(4)

By combining Eqs. (2)–(4), we obtain

$$ D = \frac{1}{2}\left\langle u \right\rangle H. $$
(5)

The above equation yields important relationship between the plate height and the dispersion coefficient.

The plate height, H, is a function of the cross-sectional mean velocity, \( \left\langle u \right\rangle \). A rather general form of this function is given by classical Van Deemter et al. (1956) equation whose version for a non-adsorbing solute in a laminar flow through a straight channel can be written in this form

$$ H = \frac{{2D_{\rm{m}}}}{\left\langle u \right\rangle } + \frac{\left\langle u \right\rangle }{{8D_{\rm {m}}}}H_{\hbox{Min} }^{2} $$
(6)

where \( D_{\rm{m}} \) is the molecular diffusion coefficient and \( H_{\hbox{Min} } \) is a length scale parameter that is determined by using the velocity distribution within a channel cross-section. The first term on the right-hand side of Eq. (6) describes the changes in the squared variance due to the molecular diffusion. This term decreases with increasing the speed of the band center of mass, \( \left\langle u \right\rangle \). The second term, which increases with increasing \( \left\langle u \right\rangle \), reflects the contribution of HD. The length scale parameter \( H_{\hbox{Min} } \) is the only parameter in Eq. (6) that is defined by the flow structure. Simultaneously, \( H_{\hbox{Min} } \) turns out to be the minimum achievable plate height for a given structure of the velocity distribution within a cross-section. The curve of Fig. 2 was plotted using Eq. (6) to illustrate the non-monotonous behavior of the plate height as a function of the mean velocity \( \left\langle u \right\rangle \).

Fig. 2
figure 2

Dependency of the normalized plate height on the normalized mean velocity

Full size image

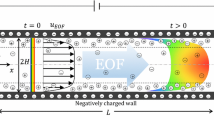
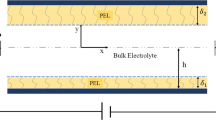
Following the Taylor (1953) and Aris (1956) approach to the description of dispersion coefficient, D, taking into account Eqs. (5) and (6), and realizing that, in a sufficiently long slit channel (Fig. 3), the local velocity depends on a single transverse Cartesian coordinate, y, the minimum plate height is represented in this form

$$ H_{\hbox{Min} }^{2} = \frac{8}{h}\int\limits_{ - h}^{h} {\delta u\left( y \right)\omega \left( y \right){\rm{d}}y} $$
(7)

where the function \( \omega \left( y \right) \) is a quantity proportional to the a normalized transverse fluctuation of the solute concentration, which is the solution of equation

$$ \frac{{{\rm{d}}^{2} \omega }}{{{\rm{d}}y^{2} }} = - \delta u\left( y \right) $$
(8)

subject to the boundary conditions

$$ \frac{{{\rm{d}}\omega }}{{{\rm{d}}y}}\left( { - h} \right) = 0 $$
(9)
$$ \int\limits_{ - h}^{h} {\omega \left( y \right)} {\rm{d}}y = 0 $$
(10)
Fig. 3
figure 3

Slit channel with different zeta potentials of the walls

Full size image

Condition (9) imposes zero normal flux at the wall whose surface has coordinate \( y = - h \) (Fig. 3). As for the similar condition at opposite wall (at \( y = h \)), it is automatically satisfied when (9) is satisfied. Such a situation occurs because the function \( \delta u\left( y \right) \) in Eqs. (8) and (9) is the normalized fluctuation of the velocity

$$ \delta u\left( y \right) = 2h\frac{u(y)}{{\int\nolimits_{ - h}^{h} {u(y){\rm{d}}y} }} - 1. $$
(11)

Accordingly, \( \int\nolimits_{ - h}^{h} {\delta u\left( y \right){\rm{d}}y} \equiv 0 \). Boundary condition (10) reflects the same property of the transverse concentration fluctuation.

The boundary value problem given by Eqs. (8–10) can be reduced to quadratures for velocity distribution of the general type, \( u(y) \). Substituting the expression obtained in such a manner into Eq. (7) and conducting straightforward transformations based on integration by parts one obtains

$$ H_{\hbox{Min} }^{2} = \frac{8}{h}\int\limits_{ - h}^{h} {\left[ {\int\limits_{ - h}^{y} {\delta u(y^{\prime})} {\rm{d}}y^{\prime}} \right]^{2} {\rm{d}}y} . $$
(12)

Thus, by combining Eqs. (11) and (12), one can predict the minimum plate height, \( H_{\hbox{Min} } \), for any given velocity distribution within a slit channel, \( u(y) \). An equation equivalent to (12) was employed by Andreev et al. (1997) in the numerical scheme they used for obtaining the plate height. Next, for electroosmotic flow through a slit channel with different wall zeta potentials, we will determine the function \( u(y) \) which is necessary to obtain \( H_{\hbox{Min} } \) using Eqs. (11) and (12)

3 Velocity distribution

For addressing the electroosmotic flow in a slit channel (Fig. 3), we will use the 1-D version of the Stokes equation containing electrical force originating from the electric field \( \vec{E} \) acting on the space charge of equilibrium electric double layer. At zero applied pressure difference, one should omit the pressure gradient term. Accordingly, the Stokes equation takes its widely used form (see, for example, Masliyah and Bhattacharjee 2006)

$$ \eta \frac{{{\rm{d}}^{2} u}}{{{\rm{d}}y^{2} }} - E\varepsilon \frac{{{\rm{d}}^{2} \Uppsi }}{{{\rm{d}}y^{2} }} = 0. $$
(13)

The first term of Eq. (13) describes the local shear stresses. Accordingly, \( \eta \) is the liquid viscosity. The second term yields the electric force where the equilibrium electric double-layer space charge whose density is \( \left( { - \varepsilon d^{2} \Uppsi /{\rm{d}}y^{2} } \right) \) [\( \Uppsi (y) \) is the electric potential distribution between the parallel planes in absence of the applied electric field].

Using Fig. 3, one can set boundary conditions of zero velocity at the channel walls, as

$$ u(h) = 0; \,\,\,\,\,\,\, u( - h) = 0 $$
(14)

Integrating Eq. (13) twice and taking into account boundary conditions (14), one obtains the velocity distribution in the following form

$$ u\left( y \right) = \frac{\varepsilon E}{\eta }\left[ {\Uppsi \left( y \right) - \frac{{\zeta_{1} + \zeta_{2} }}{2} + \frac{y}{2h}\left( {\zeta_{2} - \zeta_{1} } \right)} \right] $$
(15)

where \( \zeta_{1} \) and \( \zeta_{2} \) are the equilibrium electric potentials of to the wall surfaces.:

$$ \Uppsi \left( h \right) = \zeta_{1}; \,\,\,\,\, \Uppsi \left( { - h} \right) = \zeta_{2} . $$
(16)

The electric potential, \( \Uppsi \left( y \right) \), and the wall potentials, \( \zeta_{1} \) and \( \zeta_{2} \), are defined with reference to an electroneutral electrolyte solution being in thermodynamic equilibrium with the electric double layer formed near the cannel walls. Simultaneously, the ion concentrations, \( C_{k} \), represented in Eq. (1) are attributed to this equilibrium electroneutral solution. In the case of non-overlapping double layers, \( \kappa h > 1 \), this electroneutral solution is presented within the channel.

At \( \kappa h < 1 \), when the whole space within the channel is occupied by the equilibrium electric space charge of the double layer, such an equilibrium solution is considered to be in large reservoirs presented in the macro–nano-fluidic system containing the channel under consideration. For example, while dealing with a porous membrane placed between two identical solutions, the potentials \( \Uppsi (y) \), \( \zeta_{1} \) and \( \zeta_{2} \), are defined with reference to any of these solutions, and \( C_{k} \) is the common kth ion concentration in these solutions.

In some situations, the above-mentioned equilibrium electroneutral solution is not present in the system at all. In such cases, one can always found a hypothetical electroneutral solution which would be in thermodynamic equilibrium with the solution inside the channel. Such a hypothetical solution is characterized by a unique set of the ion concentrations, \( C_{k} \). Accordingly, the potentials \( \Uppsi (y) \), \( \zeta_{1} \) and \( \zeta_{2} \), have physical meanings of electric potential difference which would establish between the wall and the hypothetical equilibrium solution while bringing them in contact, i.e., the reference point for electric potential is placed in the hypothetical solution. Some authors use another reference point for potential by placing the reference point in the center of channel (see, for example, Qu and Li 2000)

Thus, using Eq. (15), one can obtain velocity distribution when the equilibrium potential distribution, \( \Uppsi (y) \), is known. This distribution is obtained from the Poisson–Boltzmann equation subject to boundary condition (16). In the present study, similarly to Andreev et al. (1997), we will consider a linearized version of the above-mentioned equation that is valid for relatively low zeta potentials:

$$ \frac{{{\rm{d}}^{2} \Uppsi }}{{{\rm{d}}y^{2} }} = \kappa^{2} \Uppsi . $$
(17)

In Eq. (17), the Debye parameter, \( \kappa \), is given by Eq. (1) where the ion concentrations relate to the above-discussed equilibrium electroneutral solution.

Solution of the boundary value problem given by Eqs. (16) and (17) is

$$ \Uppsi (y) = \frac{{\zeta_{1} + \zeta_{2} }}{2\cosh (\kappa h)}\cosh (\kappa y) + \frac{{\zeta_{1} - \zeta_{2} }}{2\sinh (\kappa h)}\sinh (\kappa y) $$
(18)

Consequently, combining Eqs. (17) and (18), one obtains

$$ u(y) = \frac{\varepsilon E}{2\eta }\left( {\zeta_{1} + \zeta_{2} } \right)\left[ {\frac{\cosh (\kappa y)}{\cosh (\kappa h)} - 1} \right] + \frac{\varepsilon E}{2\eta }\left( {\zeta_{1} - \zeta_{2} } \right)\left[ {\frac{y}{h} - \frac{\sinh h(\kappa y)}{\sinh (\kappa h)}} \right] $$
(19)

Thus, Eq. (19) describes distribution of the electroosmotic velocity within the plane parallel channel with different potentials of the walls.The first term on the right hand side of Eq. (19) coincides with the expression obtained by Burgreen and Nakache (1964) for the electroosmotic velocity distribution inside a slit channel whose walls would bear a common equilibrium potential \( \zeta = \left( {\zeta_{1} + \zeta_{2} } \right)/2 \). The second term is proportional to the difference of the wall potentials, \( \left( {\zeta_{1} - \zeta_{2} } \right) \), and is an odd function of the transverse coordinate y (Fig. 3). Accordingly, the second term does not contribute into the cross-sectional mean velocity, \( \left\langle u \right\rangle \) which defines the speed of the band mass center. Consequently, using Eq. (20) leads to the following expression for \( \left\langle u \right\rangle \)

$$ \left\langle u \right\rangle = \frac{1}{2h}\int\limits_{ - h}^{h} {u(y){\rm{d}}y = } - \frac{{\varepsilon E(\zeta_{1} + \zeta_{2} )}}{2\eta }\left[ {1 - \frac{\tanh (kh)}{\kappa h}} \right] $$
(20)

Thus, as it could be expected, the cross-sectional mean velocity \( \left\langle u \right\rangle \) given by Eq. (20) is defined by the contribution of the first term on the right-hand side of (19) and, hence, coincides with that following at low zeta potential from the Burgreen and Nakache (1964) solution obtained for a common wall potential \( \zeta \) provided that \( \zeta = \left( {\zeta_{1} + \zeta_{2} } \right)/2 \).

Let us now consider the limiting transition \( \kappa h \to \infty \) (Smoluchowski regime) for the velocity distribution given by Eq. (19). Such a transition yields the following asymptotic expression

$$ u = - \frac{\varepsilon E}{2\eta }\left( {\zeta_{1} + \zeta_{2} } \right) + \frac{\varepsilon E}{2\eta }\left( {\zeta_{1} - \zeta_{2} } \right)\frac{y}{h} $$
(21)

Thus, in the Smoluchowski regime, the velocity distribution is represented as a superposition of the plug-like and Couette flows.

It should be noted that, in contrast with the velocity distribution given by Eq. (19), the asymptotic expression of Eq. (21) is valid for arbitrary, not necessarily low, values of \( \zeta_{1} \) and \( \zeta_{2} \) \provided that \( \kappa h \to \infty \). The latter becomes clear from Eq. (15) which was deduced without preliminary assumptions about low values of wall zeta potentials. In Eq. (15), at \( \kappa h \to \infty \), \( \Uppsi \left( y \right) = 0 \) everywhere except for the vanishingly thin electric double-layer regions adjacent to the channel walls. Accordingly, outside these vanishingly thin region, Eq. (15) reduces to Eq. (21) for arbitrary values of \( \zeta_{1} \) and \( \zeta_{2} \).

Now, we consider the asymptotic form of the velocity distribution given by Eq. (19) at \( \kappa h \to 0 \). Applying the condition \( \kappa h \to 0 \), one obtains

$$ u = - \frac{{\varepsilon E\left( {\zeta_{1} + \zeta_{2} } \right)\left( {kh} \right)^{2} }}{4\eta }\left[ {1 - \left( \frac{y}{h} \right)^{2} } \right]\left\{ {1 - \frac{1}{3}\frac{{\zeta_{1} - \zeta_{2} }}{{\zeta_{1} + \zeta_{2} }}\frac{y}{h} + O\left[ {\left( {kh} \right)^{2} } \right]} \right\} $$
(22)

Remarkably, in contrast to the results obtained by Burgreen and Nakache (1964) for equal zeta potentials, the leading term in the series expansion of the velocity by powers of \( \kappa h \) given by Eq. (22) does not have the spatial structure similar to that of pressure driven flow.

The curves plotted in Figs. 4a, b and c show the velocity profiles within the slit channel cross-section. In the figures, we observe non-monotonous distribution which is asymmetric when \( \zeta_{1} \ne \zeta_{2} \). When \( \zeta_{1} = - \zeta_{2} \), the velocity distribution becomes anti-symmetric and contains minimum and maximum. At \( \kappa h = 0.1 \), the asymptotic formula (22) gives nearly perfect match between the exact and asymptotic solutions. For \( \kappa h = 1 \), Eq. (22) gives a good approximation for the anti-symmetric case, \( \zeta_{1} = - \zeta_{2} \), only, and noticeably overpredicts the result for two other displayed cases. At \( \kappa h = 10 \), there are three distinct zones. Two of them (zones of the equilibrium space charge having thickness of order of \( \kappa^{ - 1} \)) are adjacent to the walls. In the third, middle, zone, one observes a nearly linear velocity profile which is perfectly approximated by the asymptotic formula of Eq. (21). In the next section, we will show that, at \( \zeta_{1} \ne \zeta_{2} \), the non-uniformity of the local velocity within the third zone results in the substantial HD even for the case of \( \kappa h \gg 1 \).

Fig. 4
figure 4

Velocity distribution within cross-section for \( \zeta_{1} = - 2RT/F \) a \( \kappa h = 0.1 \); b \( \kappa h = 1 \); c \( \kappa h = 10 \)

Full size image

4 Plate height

Now using (12), we obtain an expression for the minimum plate height, \( H_{\hbox{Min} } \). To this end, we will preliminary determine the normalized fluctuation \( \delta u\left( y \right) \) which is represented under the integral in Eq. (12) and given by Eq. (11). Consequently, by combining Eqs.(11), (19) and (20), one obtains

$$ \delta u\left( y \right) = - \frac{{\kappa h\cosh \left( {ky} \right) - \sinh \left( {kh} \right)}}{{\kappa h\cosh \left( {kh} \right) - \sinh \left( {kh} \right)}} + \frac{{\zeta_{1} - \zeta_{2} }}{{\zeta_{1} + \zeta_{2} }}\frac{{\frac{{\sinh\left( {\kappa y} \right)}}{{\sinh \left( {\kappa h} \right)}} - \frac{y}{h}}}{{1 - \frac{{\tanh \left( {kh} \right)}}{\kappa h}}} $$
(23)

Substituting the obtained function \( \delta u\left( y \right) \) into Eq. (12), after some transformations, we arrive at the following expression for

$$ \left( {\frac{{H_{\hbox{Min} } }}{h}} \right)^{2} = f\left( {\kappa h} \right) + \left( {\frac{{1 - \zeta_{2} /\zeta_{1} }}{{1 + \zeta_{2} /\zeta_{1} }}} \right)^{2} g\left( {\kappa h} \right) $$
(24)

where the dimensionless functions \( f\left( {\kappa h} \right) \) and \( g\left( {\kappa h} \right) \) are represented, as

$$ f\left( {\kappa h} \right) \,=\, \frac{8}{3}\frac{{2\left[ {6 + \left( {kh} \right)^{2} } \right]\tanh^{2} \left( {kh} \right) - 9\kappa h\tanh \left( {\kappa h} \right) - 3\left[ {\frac{kh}{{\cosh \left( {kh} \right)}}} \right]^{2} }}{{\left( {kh} \right)^{2} \left[ {\kappa h - \tanh \left( {kh} \right)} \right]^{2} }} $$
(25)
$$ g\left( {\kappa h} \right) = \frac{8}{15}\frac{{2\left[ {2\left( {\kappa h} \right)^{4} + 15\left( {\kappa h} \right)^{2} - 30} \right] - 5\kappa h\left[ {4\left( {\kappa h} \right)^{2} - 3} \right]\coth \left( {\kappa h} \right) + 45\left[ {\frac{kh}{{\sinh \left( {kh} \right)}}} \right]^{2} }}{{\left( {\kappa h} \right)^{2} \left[ {\kappa h - \tanh \left( {\kappa h} \right)} \right]^{2} }}. $$
(26)

The squared normalized minimum plate height, \( \left( {H_{\hbox{Min} } /h} \right)^{2} \), is represented by Eq. (24) as a sum of two terms. The first term gives the result obtained earlier by Griffiths and Nilson (1999) who addressed the band broadening in electroosmotic flow through a slit channel with equal wall zeta potentials. According to the results of this reference, the function \( f\left( {\kappa h} \right) \) approaches the limits defined by the following relationships

$$ \begin{aligned} \mathop {\lim }\limits_{\kappa h \to 0} f\left( {\kappa h} \right) &= \frac{32}{105} \hfill \\ \mathop {\lim }\limits_{\kappa h \to \infty } \left[ {\left( {\kappa h} \right)^{2} f\left( {\kappa h} \right)} \right] &= \frac{16}{3} \hfill \\ \end{aligned} $$
(27)

The second term on the right hand side of Eq. (24) yields the contribution into the minimum plate height due to the difference of zeta potentials. Analysis of the liming cases \( \kappa h \to 0 \) and \( \kappa h \to \infty \) yields

$$ \begin{aligned} \mathop {\lim }\limits_{\kappa h \to 0} g\left( {\kappa h} \right) &= \frac{32}{315} \hfill \\ \mathop {\lim }\limits_{\kappa h \to \infty } g\left( {\kappa h} \right) &= \frac{32}{15} \hfill \\ \end{aligned} $$
(28)

Consequently, the asymptotic expressions for the minimum plane height become

$$ \begin{gathered} \left( {\frac{{H_{\hbox{Min} } }}{h}} \right)^{2} = \frac{32}{105}\left[ {1 + \frac{1}{3}\left( {\frac{{1 - \zeta_{2} /\zeta_{1} }}{{1 + \zeta_{2} /\zeta_{1} }}} \right)^{2} } \right]{\rm{ for }}\,\kappa h \ll 1 \hfill \\ \left( {\frac{{H_{\hbox{Min} } }}{h}} \right)^{2} = \frac{16}{3}\left[ {\frac{1}{{\left( {\kappa h} \right)^{2} }} + \frac{2}{5}\left( {\frac{{1 - \zeta_{2} /\zeta_{1} }}{{1 + \zeta_{2} /\zeta_{1} }}} \right)^{2} } \right]{\rm{ for }}\, \kappa h \gg 1 \hfill \\ \end{gathered} $$
(29)

The families of curves given in Figs. 5 a and b display the behavior of the normalized plate height, \( H_{\hbox{Min} } /h \), as a function of the parameter \( \kappa h \) and the ratio of the wall zeta potentials (\( \zeta_{2} /\zeta_{1} \)). At \( \kappa h \ll 1 \), all the curves of Fig. 5a approach the horizontal asymptote defined by Eq. (28). The curve plotted in Fig. 5a for \( \zeta_{2} /\zeta_{1} = 1 \) corresponds to the Griffiths and Nilson 1999 term [the first one on the right hand-side of Eq. (24)] which describes \( H_{\hbox{Min} } \) for channels having equal zeta potentials of the walls. When \( \kappa h < 1 \) and \( \zeta_{2} /\zeta_{1} > 0 \), the contribution of the Griffiths and Nilson (1999) term always exceeds that arising due to the difference in the zeta potentials [the second term on the right-hand side of Eq. (24)]. When the deviation of the ratio \( \zeta_{2} /\zeta_{1} \) from unity is sufficiently large, both the contributions have the same order of value and make the minimum plate height to be of the order of h which, under condition \( \kappa h < 1 \), does not exceed the Debye length, \( \kappa^{ - 1} \). Remarkably, when \( \zeta_{2} /\zeta_{1} \) is near −1, the term associated with the difference between the wall zeta potentials can increase without bound.

Fig. 5
figure 5

Normalized minimum plate height, \( H_{\hbox{Min} } /h \), as function of a \( \kappa h \) for different ratios of the wall zeta potentials, \( \zeta_{2} /\zeta_{1} \); b \( \zeta_{2} /\zeta_{1} \), for different \( \kappa h \)

Full size image

For the case of equal zeta potentials, \( \zeta_{2} /\zeta_{1} = 1 \), the normalized minimum plate height, \( H_{\hbox{Min} } /h \), demonstrates the behavior corresponding to the Griffiths and Nilson (1999) prediction: it decreases with increasing \( \kappa h \), and, at \( \kappa h \gg 1 \), approaches the value being the square root of the aforementioned asymptotic expression, \( \left( {\sqrt {16/3} \, / \, \kappa h} \right) \), Fig. 5a. The latter asymptotic result means that \( H_{\hbox{Min} } \to \sqrt {16/3} \, \kappa^{ - 1} \approx 2.3\kappa^{ - 1} \), i.e., at \( \zeta_{2} /\zeta_{1} = 1 \) and \( \kappa h \gg 1 \), the minimum plate height is of the order of Debye length which is much smaller than the channel thickness, 2 h. Another behavior with increasing \( \kappa h \) is observed for \( \zeta_{2} /\zeta_{1} \ne 1 \) when the minimum plate height remains of the order of h, or even substantially exceeds h that is observed when \( \zeta_{2} /\zeta_{1} < 0 \).

The most substantial difference between the predictions based on the models of equal and different wall zeta potentials is observed at \( \kappa h \gg 1 \). It is seen in Fig. 5b that, at \( \kappa h = 1000 \), even 10 % deviation of the ratio \( \zeta_{2} /\zeta_{1} \) from unity results in an increase in \( H_{\hbox{Min} } \) by more than one order of magnitude. Larger deviations of \( \zeta_{2} /\zeta_{1} \) from unity lead to values of \( H_{\hbox{Min} } \) that exceed the minimum plate height attributed to the case of equal zeta potentials by several orders of magnitude. A special situation occurs when \( \zeta_{2} /\zeta_{1} \to - 1 \). In this case, \( H_{\hbox{Min} } \to \infty \). Accordingly, the minimum plate height acquires especially large values when the ratio of zeta potentials is close to −1. In particular, when \( \zeta_{2} /\zeta_{1} \to - 1.1 \) and \( \kappa h \) = 1,000, the minimum plate height exceed the channel width, 2 h, by more than one order of magnitude (Fig. 5b).

The above-discussed behavior at \( \zeta_{2} /\zeta_{1} \to - 1 \) can easily be explained by taking into account that, under such a condition, the cross-sectional mean velocity approaches zero. Hence, the speed of the band center of mass approaches zero as well. Consequently, a finite increase in the band variance is observed at zero band displacement. Using the plate height definition given by Eq. (3) we arrive at the conclusion that both H and \( H_{\hbox{Min} } \) should infinitely increase when a finite band broadening takes place at zero band speed. The-above discussed system with anti-symmetric wall potentials can be employed for micro-mixing of substances. Potentialities of such an application will be discussed in the next section.

When \( \kappa h \gg 1 \) and the ratio \( \zeta_{2} /\zeta_{1} \) deviates from unity sufficiently strong, the first term in brackets on the right-hand side of the second equation in (29) can be omitted for being small. Importantly, the approximate expression obtained in such a manner is valid for arbitrary, not necessarily small, values of the wall zeta potentials. The latter follows from the fact that such an expression can be derived in an alternative manner by combining Eq. (21), which is valid for arbitrary zeta potentials at \( \kappa h \gg 1 \), with Eqs. (11) and (12).

While inspecting Fig. 5a, one can conclude that, at \( \kappa h \le 0.5 \), the first asymptotic expression of Eq. (29) yields error less than 10 %. As well, the error less than 10 % is yielded while using the second expression of Eq. (29) at \( \kappa h \ge 20 \)

5 Discussion on the result applications

In the present section, we give a brief survey of possible applications using the results obtained in the previous sections.

5.1 Minimization of the band broadening

While optimizing separation processes, it is often important to choose a working regime which provides a minimum broadening of a band transported by a liquid flow. Such a minimum broadening is achieved at the flow regime corresponding to the minimum plate height (Fig. 2). For a non-adsorbing solute considered in the present study, such an optimal regime can be chosen using Eq. (6) and/or the plot in Fig. 2 Accordingly, the cross-sectional mean flow velocity, \( \left\langle u \right\rangle_{\hbox{Min} } \), which provides the minimum value of the plate height, is

$$ \left\langle u \right\rangle_{\hbox{Min} } = \frac{{4D_{\rm{m}}}}{{H_{\hbox{Min} } }}. $$
(30)

By combining Eqs. (20), (24) and (30), we obtain expression for the electric field strength, \( E_{\hbox{Min} } \), which provides the minimum plate height for a solute band entrained by electroosmotic flow through a slit channel with different wall zeta potentials.

$$ E_{\hbox{Min} } = \frac{{E_{ * } }}{{\left( {\tilde{\zeta }_{1} + \tilde{\zeta }_{2} } \right)\left[ {\kappa h - \tanh \left( {kh} \right)} \right]\sqrt {f\left( {\kappa h} \right) + \left( {\frac{{1 - \zeta_{2} /\zeta_{1} }}{{1 + \zeta_{2} /\zeta_{1} }}} \right)^{2} g\left( {\kappa h} \right)} }} $$
(31)

where

$$ \begin{aligned} E_{ * } = \frac{{8D_{\rm {m}} \eta \kappa F}}{RT\varepsilon }\quad ({\rm{a}}) \hfill \\ \tilde{\zeta }_{1,2} = \frac{{\zeta_{1,2} F}}{RT}\quad ({\rm{b}}) \hfill \\ \end{aligned} $$
(32)

The parameter \( E_{ * } \) given by Eq. (32a) has the dimension of electric field strength. Assuming that \( D_{\rm {m}} = 10^{ - 10} {\rm{m}}^{ 2} / {\rm{s}} \); η = 10−3 kg/m × s; \( \kappa^{ - 1} = 10\;{\text{nm}} \); \( \varepsilon = 7 \times 10^{ - 10} {\rm{F/m}} \), \( RT/F = 30{\rm{ mV}} \) we arrive at the following estimation \( E_{ * } \approx 38{\text{ kV/cm}} \). Hereafter, we refer to \( E_{\hbox{Min} } \) as optimum field strength.

The curves plotted in Fig. 6 describe the behavior of the normalized optimum field strength, \( E_{\hbox{Min} } /E_{ * } \), as a function of \( \kappa h \) for different sets of the wall zeta potentials, \( \zeta_{1} \) and \( \zeta_{2} \). When \( \kappa h \to 0 \), \( E_{\hbox{Min} } /E_{ * } \) diverges being proportional to \( \left( {\kappa h} \right)^{ - 3} \) that defines its high value, of order of 103, at \( \kappa h = 0.1 \). When \( \kappa h \to \infty \), Eq. (31) is transformed into the following asymptotic expression

$$ E_{\hbox{Min} } = \frac{{\sqrt 3 E_{ * } }}{{4\left( {\tilde{\zeta }_{1} + \tilde{\zeta }_{2} } \right)\sqrt {1 + \frac{2}{5}\left( {\kappa h} \right)^{2} \left( {\frac{{1 - \zeta_{2} /\zeta_{1} }}{{1 + \zeta_{2} /\zeta_{1} }}} \right)^{2} } }}. $$
(33)
Fig. 6
figure 6

Normalized electric field strength providing minimum band broadening as a function of \( \kappa h \) for different sets of the wall zeta potentials

Full size image

Remarkably at \( \zeta_{1} = \zeta_{2} = \zeta \), the normalized optimum field strength, \( E_{\hbox{Min} } /E_{ * } \), approaches a constant value \( \sqrt 3 E_{ * } /8\tilde{\zeta } \). The dotted curve in Fig. 6 indicates this asymptote. However, when \( \zeta_{1} \ne \zeta_{2} \) the limiting expression (33) can be rewritten in the form

$$ E_{\hbox{Min} } = \frac{1}{4}\sqrt \frac{15}{2} \frac{{E_{ * } }}{{\kappa h\left| {\tilde{\zeta }_{1} - \tilde{\zeta }_{2} } \right|}}\left\{ {1 + O\left[ {\frac{1}{{\left( {\kappa h} \right)^{2} }}} \right]} \right\}. $$
(34)

Thus, at \( \kappa h \gg 1 \) and \( \zeta_{1} \ne \zeta_{2} \), the electric field strength providing the minimum plate height depends on the difference between the wall zeta potentials. The latter explains why the solid and dash–dot curves in Fig. 6 merge with each other at \( \kappa h \gg 1 \).

5.2 Determining zeta potentials of the walls

Now, we discuss an interesting possibility of determining zeta potentials of both the walls forming a slit channel. Earlier, Bianchi et al. (2001) and Yan et al. (2006) suggested methods of determining wall zeta potentials of rectangular channels based on studying the hydrodynamic field within the crosssection. Below, we will show that, in the case of slit channel, the couple of zeta potentials can be obtained while studying the cross-sectional mean electroosmotic velocity and the dynamics of band broadening.

Clearly, the couple of zeta potentials can be obtained as a solution of the equation set formed by Eqs. (20) and (24) that express the mean velocity and the minimum plate height, respectively, through the zeta potentials and other system parameters. Consequently, the obtained zeta potentials will be functions of mean cross-sectional velocity and plate height. The latter quantity can be obtained by applying Eqs. (3) and (6) to experimentally measured changes in the variance of tracer band.

Let us discuss in more details the simplest version of the above-proposed idea. We consider the case of \( \kappa h > 200 \) that corresponds to h > 2 µm for ionic strengths \( 10^{ - 3} {\rm{M}} \). For such a micro-fluidic format of the channel, according to the estimations given below Eq. (32) and the data given in Fig. 6, the magnitude of electric field, \( E_{\hbox{Min} } \), which provides the minimum plate height value, \( H_{\hbox{Min} } \), is lower than \( 1{\text{ kV/cm}} \). While conducting electroosmosis through the channel and observing band broadening for a given tracer transported at a given distance, one can determine both the electric field strength providing the minimum broadening, \( E_{\hbox{Min} } \), and the cross-sectional mean electroosmotic velocity corresponding to this field, \( \left\langle u \right\rangle_{\hbox{Min} } \).

Now, we determine the wall zeta potentials by solving Eq. set (20) and (34) specified for the limiting case \( \kappa h \to \infty \). Using relationships (30) and (32), the obtained results is represented in the form

$$ \begin{gathered} \zeta_{h} = - \frac{\eta }{{E_{\hbox{Min} } \varepsilon }}\left( {\left\langle u \right\rangle_{\hbox{Min} } + \sqrt \frac{15}{2} \frac{{D_{\rm {m}} }}{h}} \right) \hfill \\ \zeta_{l} = - \frac{\eta }{{E_{\hbox{Min} } \varepsilon }}\left( {\left\langle u \right\rangle_{\hbox{Min} } - \sqrt \frac{15}{2} \frac{{D_{\rm {m}} }}{h}} \right) \hfill \\ \end{gathered} $$
(35)

where we slightly changed the notation by denoting as \( \zeta_{h} \) and \( \zeta_{l} \), instead of \( \zeta_{1} \) a \( \zeta_{2} \), the higher and the lower zeta potentials, respectively. Thus, measuring both the cross-sectional mean velocity, \( \left\langle u \right\rangle_{\hbox{Min} } \), and the driving electric field strength, \( E_{\hbox{Min} } \), that result in the minimum broadening of a tracer band entrained by electroosmotic flow, one can determine the wall potentials \( \zeta_{h} \) and \( \zeta_{l} \) with the help of Eqs. (35). The estimated error for using asymptotic relationships (35) at \( \kappa h > 100 \) is less than 1 %.

Clearly, to use Eq. (35), in addition to the conventional data employed for the interpretation of zeta potential measurements (solution viscosity, \( \eta \), and dielectric permittivity, \( \varepsilon \)) one should know the tracer molecular diffusion coefficient, \( D_{\rm {m}} \). However, when \( D_{\rm {m}} \) is not known, one can use the idea of Taylor (1954) who suggested a method of measuring molecular diffusion coefficient by studying the band broadening. Accordingly, one can obtain \( D_{\rm {m}} \) by considering the band broadening in pressure driven flow through the same channel. For example, one can determine the mean cross-sectional velocity for pressure-driven flow which provides minimum band broadening, \( \left\langle u \right\rangle_{\hbox{Min} }^{p} \). The minimum plate height for the pressure-driven flow is given as \( H_{\hbox{Min} }^{p} /h = 4\sqrt {2/105} \) (Aris 1956). Combining the latter expression with relationship (30) one obtains

$$ \frac{{D_{\rm {m}} }}{h} = \sqrt \frac{2}{105} \left\langle u \right\rangle_{\hbox{Min} }^{p} $$
(36)

Finally, combining Eqs. (35) and (36) we arrive at the following expressions

$$ \begin{gathered} \zeta_{h} = - \frac{\eta }{{E_{\hbox{Min} } \varepsilon }}\left( {\left\langle u \right\rangle_{\hbox{Min} } + \frac{{\left\langle u \right\rangle_{\hbox{Min} }^{p} }}{\sqrt 7 }} \right) \hfill \\ \zeta_{l} = - \frac{\eta }{{E_{\hbox{Min} } \varepsilon }}\left( {\left\langle u \right\rangle_{\hbox{Min} } - \frac{{\left\langle u \right\rangle_{\hbox{Min} }^{p} }}{\sqrt 7 }} \right) \hfill \\ \end{gathered} $$
(37)

Hence, the experiment of obtaining the zeta potential of the walls amounts to the following scheme. One should measure both the electroosmotic velocity \( \left\langle u \right\rangle_{\hbox{Min} } \) and the respective driving electric field \( E_{\hbox{Min} } \) that correspond to the minimum band broadening during transport of a tracer band over a given distance. In addition, one should determine the velocity of pressure driven flow, \( \left\langle u \right\rangle_{\hbox{Min} }^{p} \), which results in the minimum broadening of the same solute band while traveling over a given distance. The measured quantities, \( \left\langle u \right\rangle_{\hbox{Min} } \), \( E_{\hbox{Min} } \) and \( \left\langle u \right\rangle_{\hbox{Min} }^{p} \), should be substituted into Eq. (37) that yield the values of wall zeta potentials.

Clearly, the above described method does not allow one to conclude which potential, \( \zeta_{h} \) or \( \zeta_{l} \), is attributed to a given wall. In many cases, such a conclusion can be made using some other data. If such preliminary known data are absent, one can replace one of the two walls by the third wall and conduct the above-discussed measurements with the new channel. Consequently, one of the zeta potentials obtained for such a new channel will coincide with the potentials determined in the previous experiment.

It should be stressed that the use of Eqs. (35) and (37) is correct provided that the wall potentials do differ. Using Eq. (33), it can be demonstrated that the small term on the right-hand side of Eq. (34) has the following structure: \( O\left[ {1/\left( {\kappa h} \right)^{2} } \right] = 5\left( {\zeta_{1} + \zeta_{2} } \right)^{2} /4\left( {\zeta_{1} - \zeta_{2} } \right)^{2} \left( {\kappa h} \right)^{2} \). Considering small differences \( \left( {\zeta_{h} - \zeta_{l} } \right)/\zeta_{h} \ll 1 \) and setting condition \( O\left[ {1/\left( {\kappa h} \right)^{2} } \right] \)≪1, we arrive at the following strong inequality:

$$ \frac{{\zeta_{h} - \zeta_{l} }}{{\zeta_{h} }} \gg \frac{\sqrt 5 }{\kappa h} $$
(38)

Inequality (38) yields a criterion of applicability of Eqs. (35) and (37). While dealing with systems for which \( \kappa h > 100 \), the restriction given by criterion (38) is not dramatic and enables one to measure the potentials which differ by less than 10 %.

5.3 Longitudinal electroosmotic homogenization of solute in micro-channel

The HD is a parasite effect in the case of substance separation. At the same time, in some cases it is necessary to spread out a given portion of solute within the whole volume of channel, uniformly. A purely molecular diffusion mechanism takes a long time. For example, consider a channel having the length \( L = 10{\text{ cm}} \). The time, \( \tau_{\rm {m}} \), which is necessary to level the concentration of a solute previously injected as a small portion can be estimated as

$$ \tau_{m} \simeq L^{2} /D_{\rm {m}} . $$
(39)

Assuming that \( D_{\rm {m}} \simeq 10^{ - 10} {\text m^{2} /{\text s}} \), the estimation yields \( \tau_{m} \simeq 10^{8} {\text {s}} \) that is about 3 years.

Let us now consider homogenization of a solute by electroosmotic flow through a slit channel where the band center of mass does not move and is intensively broadened. As it follows from Eq. (20), this situation occurs for opposite zeta potentials of the walls, \( \zeta_{1} = \zeta \) and \( \zeta_{2} = - \zeta \). To evaluate the homogenization time, \( \tau \), we will replace in Eq. (39) the molecular diffusion coefficient, \( D_{\rm {m}} \), by the dispersion coefficient, D. Accordingly, the evaluations amounts to scaling the right-hand side of Eq. (20) by the ratio \( D_{\rm {m}} /D \) which is obtained by combining Eqs. (5) and (6)

$$ \frac{{D_{\rm {m}} }}{D} = \frac{1}{{1 + \left( {\frac{{\left\langle u \right\rangle H_{\hbox{Min} } }}{{4D_{\rm {m}} }}} \right)^{2} }} $$
(40)

where the combination of parameters in the denominator is obtained by combining Eqs. (20) and (24). Assuming that \( \zeta_{1} = \zeta \) and \( \zeta_{2} = - \zeta \) and considering limiting case of \( \kappa h \gg 1 \), one obtains

$$ \left( {\frac{{H_{\hbox{Min} } \left\langle u \right\rangle }}{{4D_{\rm {m}} }}} \right)^{2} = \frac{2}{15}\left( {h\zeta \frac{\varepsilon }{{\eta D_{\rm {m}} }}E} \right)^{2} . $$
(41)

Let us now assume that \( \zeta = 50{\text{ mV}} \); \( \varepsilon = 7 \times 10^{ - 10} {\text{F/m}} \), h = 10 µm, η = 10−3 kg/m × s, \( E = 10{\text{ kV/cm}} \). By using these values of the parameters we arrive at \( D_{\rm {m}} /D \simeq 6 \times 10^{ - 7} \). Thus, the estimated time of homogenization becomes, \( \tau = \tau_{m} D_{\rm {m}} /D \simeq 60 \, \rm s \). Thus, instead of the 3 years, which are required for the homogenization of solute due to its molecular diffusion, we obtained the time around 1 min for the case of electroosmotic mixing.

Remarkably, in the study of Paul and Ng (2012a), the authors analyzed the possibility of electroosmotic mixing in AC electric field where the space charge, which is acted by this AC field, is created by applying oscillatory electric potentials to the walls of a slit channel. Having analyzed the expression for the dispersion coefficient derived for such a configuration, Paul and Ng (2012a) arrived at a conclusion that the dispersion coefficient reaches a maximum value when the phase shift between the oscillatory potentials applied to the slit channel walls is equal to \( \pi \). The latter situation is somewhat similar to the above-considered case of opposite zeta potential of the walls although the present analysis deals with zeta potentials constant in time and with DC externally applied field.

6 Physical plausibility of results

The possibility of practical use of the results obtained in the present paper depends on whether the channel formed by two unbounded parallel planes is a good model for addressing the channel having rectangular crosssection with high aspect ratio. It should be stressed that many authors (Doshi et al.1978; Chatwin and Sullivan 1982; Desmet and Baron 2002; Zholkovskij et al. 2003; Dutta 2007, 2008; Paul and Ng 2012b), who studied HD in pressure and/or electrically driven flows through rectangular channels, report about a result which looks somewhat paradoxical: when the rectangle aspect ratio infinitely increases, the parameters describing HD for rectangular channel are not transformed into those describing HD in the channel formed by unbounded parallel planes.

To understand the origin of such asymptotic behavior, recall that the Taylor (1953) and Aris (1956) result was obtained within the frameworks of approximation considering quasi-stationary concentration distribution of solute within the channel crosssection. Consequently, this analysis is valid for addressing the band broadening during the elution times, \( t_{\rm {e}} \), that are much longer than the relaxation times responsible for establishing the quasi-stationary concentration field within the crosssection. In the case of rectangular crosssection with high aspect ratio, there are two substantially different diffusion relaxation times, \( \tau_{\rm {h}} = h^{2} /D_{\rm {m}} \) and \( \tau_{l} = l^{2} /D_{\rm {m}} \), where l is the longer aspect of rectangle. When \( l/h \gg 1 \) and, thus, \( \tau_{\rm {h}} /\tau_{\rm {l}} \ll 1 \), one can find a range of elution times, \( t_{\rm {e}} \), which satisfy the inequality \( \tau_{\rm {h}} \ll t_{\rm {e}} \ll \tau_{\rm {l}} \). For the elution times satisfying the latter inequality, the expressions obtained for slit channel are valid. However, when \( \tau_{\rm {l}} \ll t_{\rm {e}} \), its impossible to address dispersion by representing rectangle as two unbounded parallel planes. In this case, it is necessary to deal with addressing rectangular geometry of crosssection. The above qualitative conclusions are confirmed by the quantitative consideration recently reported by Paul and Ng (2012b).

The inequality \( \tau_{\rm {h}} \ll t_{e} \ll \tau_{\rm {l}} \) defines another inequality which should be satisfied by the band speed, \( u_{c} = \left\langle u \right\rangle = L/t_{\rm {e}} \)

$$ LD_{\rm {m}} /l^{2} \ll \left\langle u \right\rangle \ll LD_{\rm {m}} /h^{2} $$
(42)

Assuming that \( D = 10^{ - 10} {\rm{m}}^{ 2} / {\rm{s}} \), \( L = 5{\text{ cm}} \), \( l = 1{\text{ mm}} \), we obtain that 〈u〉 ≫ 5 µm/s. Thus, for the present channel geometry, the first of inequalities (42) is satisfied at reasonable electroosmotic velocities. To demonstrate that, we apply Eq. (20) to the following example: \( \kappa h \gg 1 \); \( \left( {\zeta_{1} + \zeta_{1} } \right)/2 = 50{\text{ mV}} \); η = 10−3; \( \varepsilon = 7 \times 10^{ - 10} {\text{F/m}} \). Consequently, the use of the band speeds satisfying inequality 〈u〉 ≫ 5 µm/s requires the electric field whose strengths satisfies the inequality \( E >> 1.4{\text{ V/cm}} \). Note that the fields stronger by orders than \( 1.4{\text{ V/cm}} \) are widely employed microfluidics. While considering 〈u〉 = 500 µm/s, h = 10 µm, and the above given values of all other of parameter, one can see that the second inequality in (42) is satisfied, as well.

Now, we will demonstrate that the above example is characterized by a substantial contribution of HD, which originates from the difference between the wall zeta potentials, into the band broadening. While inspecting Fig. 2, one can conclude that HD manifests itself when \( \left\langle u \right\rangle H_{\hbox{Min} } /4D_{\rm {m}} \ge 1 \). Otherwise, the band broadening is defined by longitudinal molecular diffusion. Let us consider the case of \( \zeta_{2} /\zeta_{1} = 2 \) and \( \kappa h \gg 1 \) for which \( H_{\hbox{Min} } /h = 0.5 \) (Figs. 5a, b). For this case, using values of parameters given in the previous paragraphs yields \( \left\langle u \right\rangle H_{\hbox{Min} } /4D_{\rm {m}} \approx 5 > 1 \).

In summary, the estimations given in the present section demonstrate that, within broad ranges of parameters, HD in rectangular channels with high aspect ratio can successfully be addressed by using model of unbounded parallel walls.

7 Conclusions

The analysis conducted in the present paper enabled us to derive analytical expressions for the minimum achievable plate height, \( H_{\hbox{Min} } \), which characterizes the broadening of an electrically neutral non-adsorbing solute band entrained by electroosmotic flow through a slit channel with different zeta potentials of the walls. The obtained analytical result is given by Eqs. (24)–(26) that represent the minimum plate height normalized by the half of channel width, \( H_{\hbox{Min} } /h \), as a function of two dimensionless parameters, namely, the half of channel width normalized by the Debye length, \( \kappa h \), and the ratio of the wall zeta potentials, \( \zeta_{1} /\zeta_{2} \). Using the general result of Eqs. (24)–(26), we obtained simple asymptotic expressions (28) and (29) describing the minimum plate height for the limiting cases \( \kappa h \ll 1 \) and \( \kappa h \gg 1 \), respectively.

When \( \zeta_{1} /\zeta_{2} \to 1 \), the obtained result given by Eqs. (24)–(26) reduces to the expression derived earlier by Griffiths and Nilson 1999. When \( \zeta_{1} /\zeta_{2} \ne 1 \), the obtained result substantially deviates from the predictions given by the model of equal zeta potentials. This deviation becomes especially important for \( \kappa h \gg 1 \) when the minimum plate height can be of the order of channel width, h, whereas the analysis conducted for the case of \( \zeta_{1} /\zeta_{2} \to 1 \) yields value of the order of the Debye length, \( \kappa^{ - 1} \ll h \).

The predicted minimum plate height, \( H_{\hbox{Min} } \), is a length-scale parameter represented in the Eq. (6) being a particular version of the Van Deemter equation. By substituting in Eq. (6) the known values of \( H_{\hbox{Min} } \) and the cross-sectional mean velocity \( \left\langle u \right\rangle \) given by Eq. (20), one can predict the normalized plate height, \( H/h \), for given values of applied field, E, wall zeta potentials \( \zeta_{1} \) and \( \zeta_{2} \), parameter \( \kappa h \), and molecular diffusion coefficient, \( D_{\rm {m}} \). The plate height, H, determined in such a manner turns out to be dependent on the applied field strength with a minimum. Expression for the field strength, \( E_{\hbox{Min} } \), corresponding to such a minimum band broadening, is given by Eqs. (31) and (32). We also obtained simple asymptotic expressions describing \( E_{\hbox{Min} } \) for the limiting case of \( \kappa h \gg 1 \), Eqs. (33) and (34).

The conducted analysis enabled us to propose an experimental method of simultaneous determination of different zeta potentials of slit channel walls. The method amounts to measuring both the electric field strength, \( E_{\hbox{Min} } \), and the cross-sectional mean velocity, \( \left\langle u \right\rangle_{\hbox{Min} } \), that correspond to minimum broadening of the tracer band. When the molecular diffusion coefficient of the tracer, \( D_{\rm {m}} \), is known, one obtains the zeta potentials from relationships (35). Otherwise, one should additionally measure the cross-sectional mean velocity which results in the minimum band broadening in the pressure-driven flow, \( \left\langle u \right\rangle_{\hbox{Min} }^{p} \). In the latter case, the zeta potentials are obtained from relationships (38).

It was shown that channels with opposite zeta potentials of the walls can serve as effective tools for electro-osmotic micro-mixing of solute.