1 Introduction

In the recent years, there have been great interest to study the electroosmotic flow (EOF) through nanofluidic channels because of its versatile application ranging from the industries of pharmaceutical and biomedicine, chemical engineering, environmental sciences, to name a few [1,2,3,4,5,6,7]. The nanofludic channel in which the rigid walls are covered with soft polymeric materials is often termed as soft nanochannel. For such a channel, the soft layers, typically represented by polyelectrolyte layers (PELs) are sandwiched between rigid walls and the bulk electrolyte solution. The PEL carries immobile charges due to the presence of ionizable functional group within it and results in an increment in the Donnan potential across the PEL. On the other hand, since the PEL is made of polymeric material which offers additional drag force on the fluid flow. Combination of these two electrohydrodynamic effects may lead to several remarkable features of the EOF and transport of ionic species through the soft nanochannel.

Several researchers have attempted to model the electrokinetic transport of ionized solution through soft nanochannel due to its wide varieties of applications, e.g., in energy conversion systems [8], cell membranes [9], bio-sensor [10], drug delivery [11], etc. One of the earliest work in this direction was made by Donath and Voigt [12] to study the electrokinetic theory of surfaces covered with PEL. They have introduced a new model based on the non-linear Poisson–Boltzmann equation in order to calculate the distribution of fixed charges across the structured surfaces. Later Ohshima and Kondo [13] extends their work to study the EOF through a parallel plate soft nanochannel. Starov and Solomentsev [14] studied the EOF though cylindrical capillary grafted with a porous gel layer, by taking into account the specific ion interaction with the porous layer. Keh and Liu [15] studied analytically the EOF in a circular capillary where the PEL is grafted on its walls. Later Keh and Dong [16] considered the effect of pH-regulated PEL-charge on the electrokinetic flow through a soft capillary nanotube or nanoslit. Wu and Keh [17] studied the combined diffusioosmotic and electroosmotic flow through a capillary slit in which the channel walls are covered by adsorbed PEL.

Das et al. [18,19,20] studied extensively the pressure driven flow through a soft nanochannel. They have shown that for such a nanofluidic device, the electrochemomechanical energy conversion is highly efficient and the efficiency is significantly higher than that of the rigid nanochannel. Later Poddar et al. [21] studied the generation of streaming potential through a soft nanochannel under pressure driven flow by taking the ion partitioning effect into account. A theoretical study on the combined electroosmotic and pressure driven flow through soft nanochannel has been reported by Matin and Ohshima [22]. Later they [23] have further extended their study to consider the thermal transport characteristics of an electrolyte solution through a soft nanochannel. Recently Xing and Jian [24] studied extensively the steric effect on the EOF through soft nanochannel.

In all these aforementioned studies, the transition from the PEL to an electrolyte solution is sharp and a step-like function is considered to represent the PEL-electrolyte interface. The charge density as well as the polymer segments are considered to be uniformly distributed within the PEL. Duval and his coresearchers [25,26,27] made a significant contribution on the eletrokinetics of diffuse soft interface. In their studies they have assumed the Boltzmann distribution for the spatial variation of mobile ions. Considering the Nernst-Planck equation for the spatial distribution of ionic species, recently Bag et al. [28] studied numerically the modulation of EOF through slit soft nanochannel in which the PELs are of diffuse in nature.

The ion transport phenomena have drawn great interest because of its important practical applications such as ionic current signals in nanopore-based biosensing [29], separation of biomolecules [30], drug delivery [31], etc. For a nanofludic channel, several interesting features on ion transport phenomena including ion selectivity have been reported by Yeh et al. [32]. The selectivity of mobile ions results from the consequence of the charges distributed along the channel walls that favours the movement of counterions and obturate the coions. As a result the ionic current due to counterions is higher than that of the coions. Ali et al. [33] experimentally designed an ion selective nanopore in which the walls are functionalized with layer-by-layer assemblies of polyelectrolytes. They have shown that such devices are capable to manipulate and control the movement of chemical and biochemical species flowing through it. Several theoretical studies [28, 34] have shown that the surface PEL has the potential to modulate the ionic current through a soft nanochannel.

In all the earlier studies on the EOF and transport of ionic species through a soft nanochannel, the background electrolyte is taken as a symmetric 1:1 electrolyte solution and physicochemical properties of the surface PELs grafted on the lower and upper rigid walls are taken to be same. However Zheng et al. [35] demonstrate that the multivalent ions have significant effect on the modulation of EOF through a rigid micro/nanochannel filled with general electrolytes. In a recent article Hsu et al. [36] studied the effect of salt valence on the ionic current rectification behaviour of charged conical nanochannel. The scenario may be even more complicated for a soft nanochannel. In addition depending on the physicochemical and hydrodynamic properties of the upper and lower PELs, several interesting electrokinetic effects may arise. Therefore, extending the earlier studies on EOF through a soft nanochannel to take effect of multiple ionic species as well similar/dissimilar PELs properties into account is very desirable. This is conducted in the present study by considering the nonlinear model based on the coupled Poisson–Boltzmann equation for electric double layer (EDL) potential and the Darcy–Brinkman extended Stokes equation for fluid flow.

2 Problem formulation

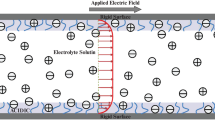
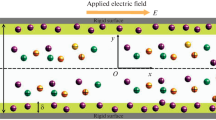
The study on EOF through an infinitely long slit soft nanochannel of height 2h under an externally applied electric field of strength \(E_0\) (Fig. 1) is presented. The channel is filled with general electrolyte, which is either a pure electrolyte or a mixture of pure electrolytes. The channel walls are grafted with an ion and fluid penetrable PEL. The thicknesses of lower and upper PELs are given by \(\delta _1\) and \(\delta _2\), respectively. The net additional charges entrapped within the lower and upper PELs are \(\rho _{f1}=Z_1F N_1\) and \(\rho _{f2}=Z_2FN_2\), respectively, where F is the Faraday constant. The valence and the molar concentration of the immobile charges present within the lower and upper PELs are \(Z_1\), \(N_1\) and \(Z_2\), \(N_2\), respectively. In our present study two different situations is considered, e.g., the lower and upper PELs entrap either similar (\(Z_1Z_2>0\)) or dissimilar (\(Z_1Z_2<0\)) immobile charges. The permittivity of the PELs and the electrolyte medium are considered to be the same, \(\epsilon _f\) and this assumption is reasonable for a PEL with sufficiently high water content [25,26,27]. Below the governing equations along with the numerical method is presented.

Fig. 1
figure 1

Schematic of the present situation

Full size image

2.1 Mathematical model and numerical method

The EDL induced electric potential is governed by the Poisson equation given as

$$\begin{aligned} -\epsilon _f \frac{d^2 \varphi }{dy^2}=\left\{ \begin{array}{ll} \rho _{e}(y)+\rho _{f1} &{} \hbox {: }-h< y \le -h+\delta _1\\ \rho _{e}(y) &{} \hbox {: }-h+\delta _1< y \le h-\delta _2 \\ \rho _{e}(y)+\rho _{f2} &{} \hbox {: }h-\delta _2 < y \le h \end{array} \right. \end{aligned}$$
(1)

Here \(\rho _e(y)=\sum _jFz_jn_j\) is the net charge density due to the mobile ions, where \(z_j\) and \(n_j\) are respectively the valence and the molar concentration of the \(j{\text {th}}\) ionic species. Here the summation is carried over all the species present in the system. The spatial distribution of concentration of mobile electrolyte ions are considered to follow the Boltzmann distribution, i.e.,

$$\begin{aligned} n_j(y)= n_j^\infty \exp \left( \frac{-e z_j \varphi (y)}{K_BT}\right) \end{aligned}$$
(2)

Here e, \(K_B\) and T are the elementary charge, gas constant and absolute temperature, respectively. The bulk molar concentration of the \(j{\text {th}}\) ion is denoted by \(n_j^\infty\). The rigid walls are assumed to be electrically neutral and non-slip in nature. The appropriate boundary conditions associated with equation (1) are

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d \varphi }{dy}|_{-h}=0, \\ \frac{d \varphi }{dy}|_{(-h+\delta _1)^-}=\frac{d \varphi }{dy}|_{(-h+\delta _1)^+}, \\ \varphi |_{(-h+\delta _1)^-}=\varphi |_{(-h+\delta _1)^+}, \\ \frac{d \varphi }{dy}|_{(h-\delta _2)^-}= \frac{d \varphi }{dy}|_{(h-\delta _2)^+}, \\ \varphi |_{(h-\delta _2)^-}=\varphi |_{(h-\delta _2)^+}, \\ \frac{d \varphi }{dy}|_h=0, \\ \end{array} \right. \end{aligned}$$
(3)

The fluid within the soft nanochannel flows under the influence of external electric field. The flow field within creeping flow regime is governed by Darcy–Brinkman extended Stokes equation within the PELs and Stokes equation governs the flow field outside of it. Under fully developed flow condition, the governing equation for the axial velocity u(y) is given by

$$\begin{aligned} \left\{ \begin{array}{ll} \mu \frac{d^2 u}{d y^2}+\rho _e E_0-\mu _{c,1} u=0 &{} : -h< y \le -h+\delta _1 \\ \mu \frac{d^2 u}{d y^2}+\rho _e E_0=0 &{} : -h+\delta _1< y \le h-\delta _2\\ \mu \frac{d^2 u}{d y^2}+\rho _e E_0-\mu _{c,2} u=0 &{} : h-\delta _2 < y \le h\\ \end{array} \right. \end{aligned}$$
(4)

where \(\mu\) is the viscosity of the fluid. The terms \(-\mu _{c,1} u\) and \(-\mu _{c,2} u\) appearing in Eq. (4) represent the frictional force due to presence of polymer segments within the lower and upper PELs, respectively. Here \(\mu _{c,i} (i=1,2)\) is the drag coefficient of the respective PELs.

The axial velocity may be obtained by solving the Eq. (4) subject to the following boundary conditions

$$\begin{aligned} \left\{ \begin{array}{l} u|_{-h}=0, \\ u|_{(-h+\delta _1)^-}=u|_{(-h+\delta _1)^+},\\ \frac{du}{dy}|_{(-h+\delta _1)^-}= \frac{du}{dy}|_{(-h+\delta _1)^+}, \\ u|_{(h-\delta _2)^-}=u|_{(h-\delta _2)^+}, \\ \frac{du}{dy}|_{(h-\delta _2)^-}=\frac{du}{dy}|_{(h-\delta _2)^+}, \\ u|_{h}=0, \end{array} \right. \end{aligned}$$
(5)

Introducing the non-dimensional variables \(\bar{y}=y/h\), \(\bar{\varphi }=\varphi /\varphi _0\) and \(\bar{u}=u/U_{HS}\) where \(\varphi _0=RT/F\) and \(U_{HS}(=\varepsilon _e E_{0} \varphi _0/\mu )\) is the Helmholtz-Smoluchowski velocity, the nondimensional form of the Eqs. (1) and (4) can be written as

$$\begin{aligned} -\frac{d^2\bar{\varphi }}{d\bar{y}^2}=\left\{ \begin{array}{ll} (\kappa h)^2\left[ \bar{\rho }_e+Z_1\bar{N}_1\right] &{} \hbox {: }-1< \bar{y} \le -1+\bar{\delta }_1 \\ (\kappa h)^2\bar{\rho }_e &{} \hbox {: }-1+\bar{\delta }_1< \bar{y} \le 1-\bar{\delta }_2 \\ (\kappa h)^2\left[ \bar{\rho }_e+Z_2\bar{N}_2\right] &{} \hbox {: }1-\bar{\delta }_2 < \bar{y} \le 0 \end{array} \right. \end{aligned}$$
(6)

and

$$\begin{aligned} \frac{d^2\bar{u}}{d \bar{y}^2}+(\kappa h)^2\bar{\rho }_e=\left\{ \begin{array}{ll} \beta _1^2 \bar{u} &{} \hbox {: }-1< \bar{y} \le -1+\bar{\delta }_1 \\ 0 &{} \hbox {: }-1+\bar{\delta }_1< \bar{y} \le 1-\bar{\delta }_2 \\ \beta _2^2 \bar{u} &{} \hbox {: }1-\bar{\delta }_2 < \bar{y} \le 0 \end{array} \right. \end{aligned}$$
(7)

where variables with ‘bar’ represent the corresponding non-dimensional values. Here \(\bar{\rho }_e=\frac{\sum _jz_jn_j^\infty \exp {(-z_j\bar{\varphi })}}{\sum _jz_j^2n_j^\infty }\) is the non-dimensional form of the net charge density due to mobile electrolyte ions. The Debye layer thickness is denoted as \(\kappa ^{-1}\) with \(\kappa ^{-1}=\sqrt{\varepsilon _f \varphi _0/F\sum _jz_j^2n_j^\infty }\). Here \(\bar{N_i}=\frac{N_i}{\sum _jz_j^2n_j^\infty }\) and \(\beta _i(=\mu _{c,i}h^2/ \mu ) (i=1,2)\) are, respectively, the scaled molar concentration of the immobile PEL-charges and softness parameters of the respective PELs. The dimensionless forms of the boundary conditions (3) and (5) are as follows

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d \bar{\varphi }}{d\bar{y}}|_{-1}=0, \\ \frac{d \bar{\varphi }}{d\bar{y}}|_{(-1+\bar{\delta }_1)^-}=\frac{d \bar{\varphi }}{(d\bar{y}}|_{(-1+\bar{\delta }_1)^+}, \\ \bar{\varphi }|_{(-1+\bar{\delta }_1)^-}=\bar{\varphi }|_{(-1+\bar{\delta }_1)^+}, \\ \frac{d \bar{\varphi }}{d\bar{y}}|_{(1-\bar{\delta }_2)^-}=\frac{d \bar{\varphi }}{d\bar{y}}|_{(1-\bar{\delta }_2)^+}, \\ \bar{\varphi }|_{(1-\bar{\delta }_2)^-}=\bar{\varphi }|_{(1-\bar{\delta }_2)^+}, \\ \frac{d \bar{\varphi }}{d\bar{y}}|_1=0 \end{array} \right. \end{aligned}$$
(8)

and

$$\begin{aligned} \left\{ \begin{array}{l} \bar{u}|_{-1}=0, \\ \frac{d\bar{u}}{d\bar{y}}|_{(-1+\bar{\delta }_1)^-}=\frac{d \bar{u}}{d\bar{y}}|_{(-1+\bar{\delta }_1)^+}, \\ \bar{u}|_{(-1+\bar{\delta }_1)^-}=\bar{u}|_{(-1+\bar{\delta }_1)^+}, \\ \frac{d\bar{u}}{d\bar{y}}|_{(-1+\bar{\delta }_1+\bar{\delta }_2)^-}=\frac{d \bar{u}}{d\bar{y}}|_{(1-\bar{\delta }_2)^+}, \\ \bar{u}|_{(1-\bar{\delta }_2)^-}=\bar{u}|_{(1-\bar{\delta }_2)^+}, \\ \bar{u}|_{1}=0 \end{array} \right. \end{aligned}$$
(9)

The governing equations for induced potential (6) and velocity field (7) are nonlinear and coupled in nature. The discretized form of the Eqs. (6) and (7) are obtained by using finite difference method through a second order central difference scheme. The tridiagonal matrix algorithm (TDMA) is used to solve the discretized algebraic equations. A iterative method is employed to solve the algebraic equations for both the potential and flow field equations in a coupled manner. We first solve the Eq. (6) subject to the boundary condition (8) iteratively. Initially iteration procedure starts with a guess value of the potential which is considered to be its bulk value (zero potential), and the iterations are continued until the absolute difference between two successive iterations becomes smaller than the tolerance limit \(10^{-6}\). With the known potential a similar iterative method is used to solve the fluid flow Eq. (7) subject to the boundary condition (9).

2.2 Current density and selectivity of mobile ions

In this subsection the mathematical expressions for the ionic current density and the ion selectivity parameter is provided. The ionic current density of jth ionic species is given by

$$\begin{aligned} \left. \begin{array}{ll} \mathbf I _j=z_jF\mathbf M _j \end{array} \right. \end{aligned}$$
(10)

where the molar flux of the jth species is given by

$$\begin{aligned} \left. \begin{array}{ll} \mathbf M _j=-D_j\bigtriangledown n_j+(\mu _j\mathbf E +\mathbf q )n_j \end{array} \right. \end{aligned}$$
(11)

where \(\mathbf q\) is the velocity vector, \(D_j\) and \(\mu _j(=z_j D_j F/RT)\) are the diffusion coefficient and electrophoretic mobility of the jth species, respectively. We have assumed that the mobility of the mobile ions can take the same value within PEL and electrolyte medium. According to Stigter [37], the drag coefficient of an ion of radius a in a Brinkman medium of Brinkman parameter \(\lambda ~(=\sqrt{\mu _{c,i}/\mu })\) is \(6 \pi \mu a \left( 1+\lambda a+ (\lambda a)^2/9 \right)\). In the present article we have approximated the correction factor \(\left( 1+\lambda a+ (\lambda a)^2/9 \right)\) by unity, since \(\lambda a\) is usually less than 1 so that ions can be treated as essentially point charges. Hence the ion mobility within the PEL may be considered to be same as that in electrolyte medium.

The axial component of the ionic current \(\mathbf M _j\) is given as

$$\begin{aligned} \left. \begin{array}{ll} M_{x,j}=-D_j\frac{\partial {n_j}}{\partial {x}}+\left[ \mu _jE_0+u(y)\right] n_j \end{array} \right. \end{aligned}$$
(12)

The non dimensional form of the axial component of ionic current (i.e., \(I_{x,j}\)), scaled by \(I_0 (=F n_j^\infty U_{HS})\), is given by

$$\begin{aligned} \left. \begin{array}{ll} \bar{I}_{x,j}=-\frac{z_j}{Pe_{j}}\frac{\partial {\bar{n}_j}}{\partial {\bar{x}}}+\Lambda \frac{z_j^2\bar{n}_j}{Pe_{j}}+z_j\bar{n}_j\bar{u} \end{array} \right. \end{aligned}$$
(13)

where the scaled quantity \(Pe_j (=u_{HS}h/D_j)\) is the Peclet number. The respective terms in the right hand side of the above equation represents the contribution due to concentration gradient, convection and electromigration along the axial direction of the slit soft nanochannel. It may be noted that for the EOF through infinitely extended slit soft nanochannel, the contribution due to concentration gradient along the axial direction vanishes and hence one can write

$$\begin{aligned} \left. \begin{array}{ll} \bar{I}_{x,j}=\Lambda \frac{z_j^2\bar{n}_j}{P_{e_j}}+z_j\bar{n}_j\bar{u} \end{array} \right. \end{aligned}$$
(14)

The average axial current density is given by

$$\begin{aligned} \left. \begin{array}{ll} \bar{I}_j=\frac{1}{2}\int _{-1}^1 \bar{I}_{x,j} dy \end{array} \right. \end{aligned}$$
(15)

and the total current in the system can be obtained as

$$\begin{aligned} \left. \begin{array}{ll} \bar{I}=\sum \limits _j \bar{I}_j \end{array} \right. \end{aligned}$$
(16)

where the summation is considered for all the electrolyte ions present in the system. In order to quantify the preference for the ions transported through a soft nanochannel we have defined the nondimensional quantity termed as ionic selectivity (S) and is given by

$$\begin{aligned} \left. \begin{array}{ll} S=\frac{\bar{I}_c-\bar{I}_a}{\bar{I}} \end{array} \right. \end{aligned}$$
(17)

\(\bar{I}_a\), \(\bar{I}_c\) are the anionic and catatonic currents, respectively.

3 Results and discussions

In this section some of the representative results of this rigorous study are presented. The computed solution for the EDL potential and the axial velocity are validated with the corresponding analytical results derived under the Debye–Huckel approximation. A detailed discussion of the derivation of the corresponding analytical solution and the validation of our computed results are provided in Appendix. The present numerical results are presented subsequently by considering much larger ranges of the parameter space. Below the dimensional values of the pertinent parameters considered in this study are enlisted.

The strength of the externally applied electric field is taken to be \(E_0=10^3\) V/m. The channel height (2h) is 20nm and the thicknesses of the lower and upper PELs are varied from 0 to 0.2h. The hydrodynamic penetration length of the PEL is varied from 1nm to 10 nm so that the scaled softness parameter may range from 1 to 10. The PEL-charges are considered to be either positive or negative with valence \(Z=\pm\)1 and the molar concentration of the PEL-charges ranges from low to high (100 mM). Such typical values of physicochemical parameters may appear in biointerface problems [18,19,20,21,22,23,24,25,26,27,28]. The results are presented here when a soft nanochannel is filled with binary symmetric, asymmetric electrolytes as well mixed electrolytes and its bulk concentration is varied from low to high to cover a wide span of EDL thickness. For illustration the binary symmetric as well as asymmetric electrolytes are taken to be KCl (1:1 electrolyte) \(\hbox {MgCl}_2\) (2:1 electrolyte) and \(\hbox {LaCl}_3\) (3:1 electrolyte). In addition the results are presented for general electrolytes, i.e., a mixture of these binary electrolytes with different proportionate. Such types of electrolytes are often considered as background aqueous media for transport of fluid across the micro/nanofluidic based devices [36, 38]. The values of the diffusivity of the mobile electrolyte ions are given by \(D_{{\mathrm{K}}^+}=1.943\times 10^{-9}\,{\mathrm{m}}^2/{\mathrm{s}}\), \(D_{{\mathrm{Mg}}^{+2}}= 0.70\times 10^{-9}\,{\mathrm{m}}^2/{\mathrm{s}}\), \(D_{La^{+3}}= 0.874\times 10^{-9}\,{\mathrm{m}}^2/{\mathrm{s}}\) and \(D_{{\mathrm{Cl}}^{-1}}=2.047\times 10^{-9}\,{\mathrm{m}}^2/{\mathrm{s}}\). The bulk concentrations of 1:1, 2:1 and 3:1 electrolytes are denoted by \(n_1^0\), \(n_2^0\) and \(n_3^0\), respectively with the bulk concentration of corresponding electrolyte ions are \(n_j^\infty\). The running index j can take the values 1, 2 for electrolyte ions present in 1:1 electrolyte; 3, 4 for 2:1 electrolyte; and 5,6 for 3:1 electrolyte, respectively. It may be noted that the bulk concentration of the electrolytes ions may be obtained from the corresponding concentration of the bulk electrolytes and the relation are given explicitly as [39] \(n_1^\infty =n_2^\infty =n_1^0\) (for 1:1 electrolyte); \(n_3^\infty =n_2^0\), \(n_4^\infty =2n_2^0\) (for 2:1 electrolyte); and \(n_5^\infty =n_3^0\), \(n_6^\infty =3n_3^0\) (for 3:1 electrolyte).

The rest of the article is organized as follows. In Sect. 3.1 the results are presented for similar physicochemical properties of the upper and lower PELs. The background solution is taken to be either binary symmetric/asymmetric electrolytes (e.g., 1:1 or 2:1 or 3:1) or a mixed solution of these electrolytes with different proportionate. The thickness and the softness parameter of both the lower and upper PELs are considered to be the same. Section 3.2 contains the results for the modulation of EOF through a soft nanochannel filled with a binary symmetric electrolyte (1:1 electrolyte). Here the physicochemical properties of the PELs are considered to be different in nature, e.g., the thickness of the lower and upper PELs are different and entrap oppositely charged immobile ions. In each of these sections the effect of pertinent parameters on the overall flow modulation as well as the transport of the mobile ions are discussed in great detail. Finally in Sect. 4 we have provided a brief summary of our findings.

Fig. 2
figure 2

The EDL induced potential distribution is shown for different choice of background electrolytes with fixed bulk concentration \(n_0=10\) mM. The results are shown here when both the lower and upper PELs entrapped either a negative immobile charges (\(Z_1=Z_2=-1\)) or b positive immobile charges (\(Z_1=Z_2=1\)) with fixed \(N_1=N_2=100\) mM, \(\beta (=\beta _1=\beta _2)=1\) and PEL thickness \(\delta (=\delta _1=\delta _2)=0.1h\)

Full size image

3.1 Both the upper and lower PELs bear similar charges

In Figs. 2 and 3 the EDL induced potential and axial velocity are shown when the soft nanochannel is filled with either pure symmetric/asymmetric electrolyte or mixed electrolyte. The component electrolytes are present in the mixed electrolyte with same proportion. The thicknesses of both the PELs are considered to be the same \(\delta (=\delta _1=\delta _2)=0.1h\) with a hydrodynamic softness parameter \(\beta (=\beta _1=\beta _2)=1\). The lower and upper PELs entrap either negative (\(Z_1=Z_2=-1\)) or positive (\(Z_1=Z_2=1\)) immobile charges. The bulk concentration of the background electrolyte solution (\(n_0\)) is taken to be 10 mM.

Fig. 3
figure 3

The axial velocity components are shown in a, b. The parameters are considered to be the same as in Fig. 2

Full size image

It is clear from the results presented in Figs. 2 and 3 that the induced potential distribution and hence the axial velocity profile depends on the choice of the background electrolyte. The magnitude of the induced potential and its decay within the PEL depends strongly on the characteristic EDL thickness (\(\kappa ^{-1}\)). With the fixed bulk concentration \(n_0=10\) mM, the EDL thickness \(\kappa ^{-1}=1.77\) nm when the background electrolyte is 2:1 electrolyte, and is smaller than that of the 1:1 electrolyte (\(\kappa ^{-1}=3.08\) nm). Hence for the 1:1 electrolyte the surface polymer layer is engulfed by the thick EDL and the PEL-charge have strong impact on the EDL induced potential and hence the axial velocity. On the other hand for 2:1 electrolyte, the screening of the PEL-charge increases because of the thin EDL where the PEL extends beyond the EDL. As a result when the background solution is 2:1 electrolyte, the magnitude of EDL induced potential and hence the axial velocity profile are lower and are much sharper within the PEL in comparison with that for the 1:1 electrolyte. A similar justification can be made for the other background electrolytes.

Fig. 4
figure 4

The variation of average velocity (\(\bar{u}_{avg}\)) with bulk concentration (\(n_0\)) for different choice of background electrolytes. The results are shown here when both the PELs entraps a negative charges (\(Z_1=Z_2=-1\)); and b positive charges (\(Z_1=Z_2=1\)) with fixed concentration of PEL-charge (\(N_1=N_2=100\) mM), softness parameter \(\beta (=\beta _1=\beta _2)=1\) and PEL thickness (\(\delta _1=\delta _2=0.1h\)). The inset figure corresponds to the value of the EDL potential along the central line of the channel (i.e., \(\bar{\phi }_c\))

Full size image

Another interesting feature of the EDL induced potential and flow pattern are evident from Figs. 2 and 3. There is an interplay between the choice of the background electrolytes and the nature of the immobile charges entrapped within the surface PEL. It is evident from Figs. 2 and 3 when the aqueous medium is binary symmetric electrolyte (1:1 electrolyte) the magnitude of the EDL potential and axial velocity are same for negative and positively charged PELs. On the other hand when the background solution is either binary asymmetric or mixed electrolytes, the EDL potential as well as axial velocity follows different pattern for negative and positively charged PELs. For binary asymmetric electrolytes, (e.g., 2:1, 3:1 electrolytes) the valence of the counterion with respect to the negatively charged PEL is higher than that of the positively charged PEL. So the charge neutralisation due to the penetration of counterions across the PEL is higher for the negatively charged surface PEL which in turn results in a reduction in magnitude of the net effective charges entrapped within the surface PEL. Hence the magnitude of EDL potential and the axial velocity across the soft nanochannel with negatively charged surface PEL is lower than that of the positively charged surface PEL. On the other hand for symmetric electrolytes the magnitude of EDL induced potential and so the axial velocity are not affected by the choice of PEL-charge since the valence of both cations and anions are the same. A similar justification can be made on the mixture of electrolytes.

Fig. 5
figure 5

The dependence of a, b total current density (\(\bar{I}\)) and c, d anionic and cationic current densities (\(\bar{I_a}\), \(\bar{I_c}\)) with bulk electrolyte concentration (\(n_0\)) on different choice of background electrolytes. The results are shown here when both the PELs entraps a, c negative charges (\(Z_1=Z_2=-1\)); and b, d positive charges (\(Z_1=Z_2=1\)) with fixed concentration of PEL-charge \(N_1=N_2=100\) mM, softness parameter \(\beta (=\beta _1=\beta _2)=1\) and PEL thickness \(\delta _1=\delta _2=0.1h\)

Full size image

Next the effect of bulk electrolyte concentration (\(n_0\)) on the overall flow modulation is shown. To provide a quantitative measurement we have presented the variation of average axial velocity (\(\bar{u}_{avg}\)) in Fig. 4 with the bulk electrolyte concentration, where \(\bar{u}_{avg}=0.5\int _{-1}^1 \bar{u}(\bar{y}) dy\). The results are presented here for binary electrolytes as well as general electrolytes in which the component electrolytes are mixed with same proportions. Fig. 4a illustrate the results when both the PELs bear negative charges with \(Z_1=Z_2=-1\) and the results for positively charged PELs with \(Z_1=Z_2=1\) are presented in Fig. 4b. It is observed that the magnitude of \(\bar{u}_{avg}\) reduces with the increase in bulk concentration of the background electrolyte (\(n_0)\). It may be noted that for higher values of electrolyte concentration, the shielding effect is strong enough to reduce the net effective charge entrapped within the PEL and leads to a reduction in magnitude of the average flow rate. On the otherhand for low concentration of bulk electrolyte the average flow rate may attain a local maximum (minimum) when both the PELs are negatively (positively) charged. It may be noted that the occurrence of local maxima or minima in profile for average flow rate is evident for all types of undertaken electrolytes with low concentration. A similar observation has been reported by Haywood et al. [40] for EOF through rigid nanochannel (\(\delta _1=\delta _2=0)\) filled with a binary symmetric electrolyte. It may be noted that at a low electrolyte concentration, the overlapping of adjacent thick EDLs results in a nonzero net charge along the bulk fluid region and it produces a non zero value of EDL potential along the central line of the channel (see inset figures in Fig. 4). If we further decrease the electrolyte concentration from its critical values at which \(u_{avg}\) attains its maximum value, the electrostatic interaction between the overlapped EDL increases and results in a further reduction of average flow rate.

The effect of bulk electrolyte concentration (\(n_0\)) on the average current (cationic, anionic and total current) densities is shown in Fig. 5. The results in Fig. 5a, c are illustrated when the upper and lower PELs entraps negative immobile charges (\(Z_1=Z_2=-1\)) and the results for positively charged PELs (\(Z_1=Z_2=1\)) are shown in Fig. 5b, d. Results are presented here for fixed value of \(N_1=N_2=100\) mM, \(\beta (=\beta _1=\beta _2)=1\) and PEL thickness \(\delta _1=\delta _2=0.1h\). The background electrolyte is taken to be either pure symmetric/asymmetric electrolyte and mixed electrolyte in which the component electrolytes are present with same proportions. It is evident from Fig. 5 that the average current density approaches to a constant value for strong electrolyte concentrations. For a thick EDL at low electrolyte concentrations, the fluid convection has significant role on the transport of the mobile ions and the flow rate decreases significantly with the rise in electrolyte concentration (Fig. 4). Hence for higher values of electrolyte concentration, the electromigration dominates the transport behaviour of the mobile ions and results in a constant value. As expected for binary symmetric (1:1) electrolyte, the average current density when the PEL entraps the positive charges (Fig. 5a, c) is the same as that of negatively charged PEL (Fig. 5b, d). It is reasonable since the valence of cation and anion are the same. In addition for a symmetric electrolyte the cationic (anionic) current density dominates over anionic (cationic) current for negatively (positively) charged PEL, since the majority of transported ions are cations (anions) and hence leads to a higher cationic (anionic) current. On the otherhand when the background electrolyte comprises of either binary asymmetric electrolytes (2:1 or 3:1) or mixture electrolytes, the current density profiles for negatively and positively charged PEL are completely different. Here a strong interplay between cationic and anionic current may occur depending on the charge properties of the surface PEL and choice of background electrolyte solution.

Fig. 6
figure 6

The dependence of ion selectivity on the bulk electrolyte concentration \(n_0\) is shown. Results are presented in a when both the lower and upper PELs entrapped negative immobile charges (\(Z_1=Z_2=-1\)) and in b for positively charged PELs (\(Z_1=Z_2=1\)). The other parameters are considered to be the same as in Fig. 5

Full size image
Fig. 7
figure 7

The variation of selectivity (S) with with the parameter zN is shown for bulk electrolyte concentration a\(n_0=1\) mM , b\(n_0=10\) mM, c\(n_0=10^3\) mM. Here \(z(=Z_1=Z_2)\) and \(N(=N_1=N_2)\) are valence and molar concentration of the surface PEL, respectively. For a mixed electrolyte the component electrolytes are present with same proportions. Results are presented for fixed softness parameter \(\beta (=\beta _1=\beta _2)=1\) and PEL thickness \(\delta _1=\delta _2=0.1h\)

Full size image

To provide a quantitative measurement of the interplay between the cationic and anionic currents we have shown the results for ion selectivity parameter (S), and is defined earlier in Eq. (17). The positive, negative and zero values of S stand for cation selective, anion selective and nonselective nanochannel, respectively. The results for negatively and positively charged PELs are presented Fig. 6a, b, respectively.

Fig. 8
figure 8

The variation of selectivity (S) with the parameter zN is shown for a mixture of 1:1 and 2:1 b mixture of 1:1 and 3:1 electrolytes. Here \(z(=Z_1=Z_2)\) and \(N(=N_1=N_2)\) are valence and molar concentration of the surface PEL, respectively. Results are presented for different electrolyte concentration ratio \(f_2(=n_2^0/n_1^0)\) and \(f_3(=n_3^0/n_1^0)\) with fixed \(n_1^0=10\) mM for fixed softness parameter \(\beta (=\beta _1=\beta _2)=1\) and PEL thickness \(\delta _1=\delta _2=0.1h\). The results for binary electrolytes (either 1:1, or 2:1, or 3:1 electrolyte) with bulk electrolyte concentration 10 mM are also included

Full size image

It is interesting to note that the cationic, anionic as well as net current depends strongly on the choice of salt type and hence leads to various pattern of ion selectivity parameter. For the choice of binary symmetric electrolyte as background medium, the value of the ion selectivity parameter S is positive (negative) when the PEL is negatively (positively) charged (Fig. 6). Here the cationic (anionic) current dominates anionic (cationic) current (Fig. 5c, d) and leads to positive value of S. On the otherhand when the background electrolyte is either binary asymmetric or general electrolytes we observed several interesting features of the ion transport across the soft nanochannel. Fig. 6a depict that the value of S always lies within [0,1] when the PEL is negatively charged. It is reasonable for negatively charged PEL where the cationic current dominate the anionic current (Fig. 5c). On the otherhand if the PEL is positively charged and the background electrolyte is either binary asymmetric or general electrolytes, we found a critical value of electrolyte concentration beyond which the ion selectivity parameter S may switch its value from negative to positive. For low electrolyte concentrations, the neutralisation of PEL-charge due to shielding effect is insignificant. For such a situation the effective PEL-charge is sufficient enough to create a strong anionic current which dominates over the cationic current and leads to a negative value of S. On the other hand for high electrolyte concentrations where the thin EDL is engulfed by the PEL, the screening of PEL-charge is significant and hence the effective PEL-charge is not enough to create strong anionic current to dominate the conduction current due to electromigration of cations (PEL-coions) with higher valence. As a result the cationic current dominates and leads to a positive value of ion selectivity (S).

In order to show explicitly the effect of PEL-charge on the regulation of ion selectivity, the results in Fig. 7 are shown by varying PEL-charge from negative to positive for low, moderate and high bulk electrolyte concentrations (\(n_0\)). Fig. 7a depicts that the PEL-charge has significant effect on the ion selectivity for low electrolyte concentrations. We observed that the value of S is zero for uncharged PEL (\(N=0\)) when background electrolyte is symmetric in nature. On the other hand if the background electrolyte is binary asymmetric or mixed in nature, the channel may behave like a nonselective channel (i.e., \(S\ne 0\)) even for uncharged PEL. For such a case even though there is no net fluid flow across the channel but the conduction currents due to cations and anions are unequal, leading to a nonzero value of ion selectivity parameter S. The channel behaves like a perfect ion selective channel (\(S=\pm 1\)) at higher values of PEL-charge at low electrolyte concentrations (Fig. 7a). As expected at low electrolyte concentration, the value of S gradually reduces from 1 to 0 with the decrease in PEL-charge of negative polarity. In addition the value of ion selectivity parameter S approaches to -1 for further increase in positive PEL-charge. On the otherhand at high electrolyte concentrations (Fig. 7b, c), the profile for S with PEL-charge ceases to its symmetric pattern for binary asymmetric or mixed electrolytes. Here a strong interplay between reduced PEL-charge due to strong charge neutralisation and charge properties of the background electrolyte ions leads to such a typical pattern in ion selectivity parameter S.

In Fig. 8 we have shown the results for ion selectivity parameter S for a mixed electrolyte in which component electrolytes are present in different proportionate. The results are presented here for mixture of 1:1 and 2:1 electrolytes in Fig. 8a and in Fig. 8b for a mixture of 1:1 and 3:1 electrolytes, by varying the PEL-charge. The results for binary electrolytes (either 1:1, or 2:1, or 3:1 electrolyte) with bulk electrolyte concentration 10 mM are also presented. The results are presented for different values of concentration ratio \(f_1\) and \(f_2\) where \(f_1=n_2^0/n_1^0\) and \(f_2=n_3^0/n_1^0\), respectively with fixed \(n_1^0=10\) mM. Figure 8 suggests that for a mixed electrolytes, a small change in concentration ratio \(f_1\) or \(f_2\) may lead to a considerable change in the ion selectivity parameter and hence the transport phenomena. For positively charged PEL the ion selectivity parameter S follows some specific pattern. For such a case the common counterion is \(\text {Cl}^{-}\) ion. For smaller values of \(f_2\) (or \(f_3\)) the value of S is close to that of 1:1 electrolyte. As expected with the increase in concentration ration \(f_2\) (or \(f_3\)), the selectivity for mixed electrolyte approaches towards that of the 2:1 (or 3:1) electrolyte. However such a pattern is not possible when the PEL is negatively charged. This difference is due to the fact that there are two different counter ions (i.e., \(\text {K}^{+}\) and \(\text {Mg}^{2+}\)) with different valences.

Fig. 9
figure 9

The a induced potential (\(\bar{\varphi }\)) and baxial velocity(\(\bar{u}\)) are shown for different values of PEL thickness with fixed value of softness parameter \(\beta (=\beta _1=\beta _2)=1\) and bulk electrolyte concentration \(n_0=10\) mM. The lower and upper PELs entraps positive and negative immobile charges, respectively (i.e., \(Z_1=+1, Z_2=-1\)) with fixed \(N_1=N_2=100\) mM

Full size image

3.2 Upper and lower PELs bear opposite charges

Fig. 10
figure 10

The variation of a average velocity \(\bar{u}_{avg}\) and b ion selectivity parameter S, with the electrolyte concentration is shown. The results are presented for different values of PEL thickness and fixed softness parameter \(\beta (=\beta _1=\beta _2)=1\) and the lower and upper PELs entrap positive and negative immobile charges, respectively (i.e., \(Z_1=+1, Z_2=-1\)) with fixed \(N_1=N_2=100\) mM

Full size image

In Figs. 9 and 10 the effect of asymmetric physicochemical and hydrodynamic properties of the upper and lower PELs on the flow modulation and transport of ionic species are shown. The background electrolyte is considered to be a binary symmetric (1:1) electrolyte with bulk concentration \(n_0\). The thickness of both the PELs are considered to be either same or different. In Figs. 9 and 10 we have shown the results for different values of PEL thickness with fixed values \(\beta _1=\beta _2=1\). The PEL grafted on the lower and upper walls of the soft nanochannel bear opposite charges with \(N_1=N_2=100\) mM. In addition we have included the case where one of the wall is grafted with PEL and another one is left uncoated.

An asymmetric pattern of the induced potential and hence the axial velocity is evident from Fig. 9. When the thicknesses of the lower and upper PELs are same (i.e., \(\delta _1=\delta _2\)), the profile for induced potential and axial velocity on the upper half of the channel is just opposite to that of the lower portion and which may lead to a zero flow rate. On the otherhand for a soft nanochannel where \(\delta _1 \ne \delta _2\), even the upper and lower PELs entrap opposite charges a nonzero flow rate may be achieved (Fig. 10a). The average flow rate reduces with the rise in electrolyte concentration (\(n_0\)) and at a critical value of electrolyte concentration the average flow rate may attains a local maxima. For thick EDL at low electrolyte concentrations, the overlapped EDL result in an occurrence of the local maxima on the flow profile (Fig. 10a). In Fig. 10b, we have shown the variation of ion selectivity parameter S with electrolyte concentration \(n_0\). The value of S is close to zero when the thicknesses of both the PELs are equal. For such a case, the net flow rate is zero and ions are transported across the channel only because of electromigration. On the otherhand for \(\delta _1\ne \delta _2\), the fluid convection plays an important role at least for the thick EDL where the screening of PEL-charge is insignificant. In addition for \(\delta _1\ne \delta _2\), the magnitude of the net charges entrapped within lower and upper PELs are different. Hence the cationic current differs from that of the anions and it leads to a nonzero value of ion selectivity parameter S. The effect of convective transport diminishes with the rise in electrolyte concentration and leads to a constant value of S.

4 Conclusion

In this article we have analyzed extensively the modulation of EOF and transport of mobile ions through a slit soft nanochannel. The background electrolyte is considered to be either binary symmetric, asymmetric electrolyte or mixed electrolyte solution. The soft PELs are grafted on the lower and upper walls may have similar/dissimilar physicochemical properties. Some important observations on the flow modulation are as follows.

  • The screening of PEL-charge and hence the magnitude of induced potential as well as axial velocity across the nanochannel depends strongly on the choice of background electrolyte and its bulk concentration.

  • At a low electrolyte concentration when the EDL becomes comparable to the channel half height, the overlapping of adjacent EDLs impacts significantly on the overall flow modulation. The average flow rate decreases with the rise in bulk concentration.

  • For a symmetric electrolyte, the magnitude of EDL induced potential and hence the axial velocity are not influenced by the polarity of the PEL-charge, while for binary asymmetric or mixed electrolyte as background solution the polarity of PEL-charge has strong impact.

  • An asymmetric flow pattern may be achieved for a dissimilar physicochemical and hydrodynamic properties of the surface PELs.

In addition, depending on the choice of the charge properties of the PEL and electrolyte medium we observed several interesting features of the transport of mobile ions. If the symmetric electrolyte is the background solution, a cation (anion) selective characteristics is achieved when both the PEL entrap negative (positive) charges. The scenario is even more complicated when the background electrolyte is either binary asymmetric or mixed in nature. A cation-selective characteristics of the undertaken soft nanochannel is evident from the results when both PELs entrap negative charges. On the other hand for positively charged PEL, depending on the concentration of bulk electrolyte the channel may show a cation-selective, anionic-selective or non-selective characteristics. It is interesting to note that soft nanochannel may behave like a perfect ion selective channel at higher values of PEL-charge and at low electrolyte concentrations. Such a typical situation may occur irrespective of the choice of background solution. In addition when the physicochemical and hydrodynamic properties of the lower and upper PELs are different in nature, a cation or anion selective characteristics may be achieved by suitably tuning the PELs electrohydrodynamical properties.