Abstract
Accurate modeling of gas microflow is crucial for the microfluidic devices in MEMS. Gas microflows through these devices are often in the slip and transition flow regimes, characterized by the Knudsen number of the order of 10−2~100. An increasing number of researchers now dedicate great attention to the developments in the modeling of non-equilibrium boundary conditions in the gas microflows, concentrating on the slip model. In this review, we present various slip models obtained from different theoretical, computational and experimental studies for gas microflows. Correct descriptions of the Knudsen layer effect are of critical importance in modeling and designing of gas microflow systems and in predicting their performances. Theoretical descriptions of the gas-surface interaction and gas-surface molecular interaction models are introduced to describe the boundary conditions. Various methods and techniques for determination of the slip coefficients are reviewed. The review presents the considerable success in the implementation of various slip boundary conditions to extend the Navier–Stokes (N–S) equations into the slip and transition flow regimes. Comparisons of different values and formulations of the first- and second-order slip coefficients and models reveal the discrepancies arising from different definitions in the first-order slip coefficient and various approaches to determine the second-order slip coefficient. In addition, no consensus has been reached on the correct and generalized form of higher-order slip expression. The influences of specific effects, such as effective mean free path of the gas molecules and viscosity, surface roughness, gas composition and tangential momentum accommodation coefficient, on the hybrid slip models for gas microflows are analyzed and discussed. It shows that although the various hybrid slip models are proposed from different viewpoints, they can contribute to N–S equations for capturing the high Knudsen number effects in the slip and transition flow regimes. Future studies are also discussed for improving the understanding of gas microflows and enabling us to exactly predict and actively control gas slip.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With the rapid development of microelectromechanical systems (MEMS), microscale rarefied gas flows have attracted considerable attention and become a new and important research field (Ho and Tai 1998; Gad-el-Hak 1999; Karniadakis and Beskok 2002). Gas microflows in microfluidic devices have the potential and broad range of applications, such as extracting biological samples, cooling integrated circuits and actively controlling aerodynamic flows (Barber and Emerson 2006; Tang et al. 2008). However, the flows at the microscale are quite different from those at the macroscale (Cao et al. 2006). For understanding fundamental flow physics, it is essential to predict the performances and provide optimal designs and fabrications for microfluidic devices in MEMS, including microchannel, microduct, microtube, microbearing, and micropipe.
Gas microflows are usually in the slip flow and transition regimes and experience a range of non-equilibrium phenomena (Pan et al. 1999). In these flows, the mean free path (MFP) of the gas molecules becomes significant relative to the characteristic dimension of the device, and the continuum hypothesis for the Navier–Stokes (N–S) equations breaks down (Lilley and Sader 2008; Dongari et al. 2009). An important feature in these flows is that velocity slip appears at the solid boundary. The original Maxwell’s slip model and its derived forms have been widely presented and used during the past 130 years. In practice, most gas flows in microfluidic devices experience a wide range of Knudsen numbers and this makes it even more difficult to develop a generalized slip model (Tang et al. 2008; Dongari et al. 2011a). One important inference from the slip models is that the applicability of the N–S slip boundary conditions should be extended into the transition regime (Dongari et al. 2010; Badur et al. 2011). Sharipov and Seleznev (1998) presented an excellent critical review and recommended data on rarefied gas flows. Some researchers subsequently presented unified slip models to extend the conventional N–S equations and Maxwell’s slip model to investigate the gas flows through microfluidic devices in MEMS (Beskok and Karniadakis 1999; Dongari et al. 2007; Lockerby and Reese 2008). The slip models become more complex when the influences of rarefication and compressibility effect, KL effect, surface condition and gaseous mixture are considered for gas microflows. A brief introduction and review of the available slip models can be found in the literature (Karniadakis and Beskok 2002; Karniadakis et al. 2005; Barber and Emerson 2006; Dongari et al. 2007; Colin 2005; Cao et al. 2009).
The objective of this paper is to present a review of investigations on slip models for gas microflows. In this review, Sect. 2 describes a brief introduction of the general properties of the gas microflows. The KL effect on the gas microflows and the capturing approaches are presented in Sect. 3. Section 4 focuses on the theoretical descriptions of the gas-surface interaction and gas-surface molecular interaction models. Section 5 summarizes and reviews the main theoretical, numerical, and experimental slip coefficients and relative various slip models, including first-order, second-order, higher-order and hybrid types, which are widely used to extend the N–S equations in the slip flow and transition regimes. The effects of effective MFP and viscosity, gaseous mixture, surface roughness and TMAC on the slip coefficients and slip models are analyzed and discussed in detail. Finally, Sect. 6 provides final remarks and conclusions. Throughout the review, we emphasized the discrepancies among the various slip models in order to focus on future research efforts into providing an understanding of the velocity slip boundary conditions for gas microflows through the microfluidic devices in MEMS.
2 General physics of gas microflows
The analysis and modeling of gas microflow depend on some important characteristic length scales and parameters (Barber and Emerson 2006; Colin 2005). Gad-el-Hak (2001, 2006) reported the general flow physics in MEMS and broadly reviewed available methodologies to model the transport phenomena in microdevices. Colin (2005) and Barber and Emerson (2006) discussed and reviewed the rarefaction and compressibility effects on gas microflows and provided several characteristic length scales.
At the level of molecules, the relationship between the mean molecular spacing δ and mean molecular diameter d is an important parameter. For the dilute gases, gases satisfy δ/d > 7 (Bird 1994; Gad-el-Hak 2003; Barber and Emerson 2006) or d/δ ≪ 1(Colin 2005). In these cases, most of the intermolecular interactions are binary collisions. Conversely, the gas can be regarded as a dense one. The dilute gas approximations lead to the classical kinetic theory of gases and the Boltzmann transport equation.
For a gas of hard sphere (HS) molecules in thermodynamic equilibrium, Bird (1994) gave the definition of the MFP as:
where n g is the number density of the gas and n g = δ −3.
2.1 Rarefaction effect
The rarefaction effect in microsystems is attributed to the MFP of the gas microflow. In practice, the validity of the thermodynamic equilibrium assumption in the N–S equations can be related to the Knudsen number (Barber and Emerson 2006). Gad-el-Hak (2003) also discussed that the N–S equations remain to be valid when the three fundamental assumptions (Newtonian framework, continuum approximation, and thermodynamic equilibrium) are satisfied. Typically, rarefaction effect can be characterized by the Knudsen number, which is the key parameter to indicate the degree of rarefaction or state of non-equilibrium of gas flows and defined as:
where L 0 is the characteristic length of the microflow system and \( \Upphi_{0} \) is a quantity of interest, such as the gas density, pressure or temperature (Tang et al. 2008). Practically, a local Knudsen number can be used as a global measure to avoid the ambiguity of selecting L 0 in large or complex systems (Oran et al. 1998). The ratio of L 0/δ satisfies to be larger than 100 in order to obtain a statistically stable estimation of the macroscopic properties (Bird 1994).
2.2 Compressibility effect
In general for gas microflows in MEMS, the effects of rarefaction and compressibility are coupled and tend to conflict with each other (Morini et al. 2004, 2005). The compressibility is significant when the Mach number approaches unity. From the classical kinetic theory, the Knudsen number is related to the Reynolds number \( Re \) and Mach number Ma by:
where \( \gamma \) is the ratio of specific heats of the gas. Li et al. (2000) demonstrated experimentally that the effect of compressibility can be neglected only for an average Mach number lower than 0.3, while Colin (2005) recommended that the compressibility effect should be taken into account when Ma > 0.2.
For the rarefaction degree of the gas, it can calculate the Reynolds number for which the Mach number is less than 0.2. For the Knudsen numbers in the slip flow and early transition regimes, Fig. 1 illustrates the range of Reynolds numbers for which the flow can be divided into two zones, i.e., incompressible and compressible flows. The dividing line is different for monatomic and diatomic gases. It is evident that the compressibility effects can be neglected for high Knudsen numbers only when the Reynolds number is very low. However, the gas flow at lower Knudsen numbers can be considered incompressible within a larger range of Reynolds numbers. Therefore, the coupled effects of rarefaction and compressibility on the gas flow in microfluidic devices should be considered simultaneously and systematically for predicting the microflow characteristics.
Validity of the assumption of incompressibility in terms of the Reynolds numbers as a function of the Knudsen number for monatomic and diatomic gases (Colin 2005)
2.3 Classification of the flow regime
The classification of rarefied gas flow was originally proposed by Schaaf and Chambre (1961), and the gas flow is generally divided into four regimes according to the Knudsen number as follows:
-
1.
For Kn < 10−2 (the continuum regime), the continuum and thermodynamic equilibrium assumptions are appropriate, and the flow can be described by the N–S equations with conventional no-slip boundary conditions, although Gad-el-Hak (1999) suggested that the regime should be changed as Kn < 10−3 because of the breakdown in the thermodynamic equilibrium assumption that was discernible in this range.
-
2.
For 10−2 < Kn < 10−1 (the slip flow regime), the non-equilibrium effects dominate near the walls. The no-slip boundary condition fails to provide agreement between theoretical predictions and experimental results, although continuum conservation equations can still be used to describe the bulk flow (Karniadakis et al. 2005; Dongari et al. 2009). However, the gas microflow can still be analyzed by solving the N–S equations with slip velocity and temperature jump boundary conditions.
-
3.
For 10−1 < Kn < 10 (the transition regime), the rarefaction effects dominate and the continuum and thermodynamic equilibrium assumptions of the N–S equations begin to break down. The difficulty in analyzing the transition regime from a continuum assumption arises from the fact that the stress-strain relationship for the gas flow becomes nonlinear near the KL (Barber and Emerson 2006). The slip models become more complex, and the alternative methods, such as direct simulation Monte Carlo (DSMC) method (Bird 1994) or a solving approach derived from BE (Lilley and Sader 2008), should be taken into account.
-
4.
For Kn > 10 (the free molecular regime), the intermolecular collisions are negligible as compared with the collisions between the gas molecules and wall surfaces (Beskok and Karniadakis 1999; Karniadakis and Beskok 2002).
This division of the flow regimes is very important in order to choose the methods used for the modeling and prediction of the gas microflows. Figure 2 describes different regimes and governing equations of the gas microflow depending on the Knudsen number. As the Knudsen number increases, the rarefaction effects become more obvious and eventually the continuum assumption breaks down. The exploration of the Knudsen paradox and its full understanding requires consideration of the entire transport regimes from a small to a large Knudsen number (Dongari et al. 2010).
The local Knudsen numbers in the above classification are somewhat empirical and the boundary conditions among the various gas flow regimes often depend on the particular microfluidic devices (Barber and Emerson 2006). Figure 3 shows a graphical representation of the flow regimes experienced by a range of gas microfluidic devices reported by Beskok (2001), Karniadakis and Beskok (2002), and Karniadakis et al. (2005). It can be found that most microfluidic devices currently operate in the slip flow or early transition regimes. The simple flow can be predicted analytically or semi-analytically. However, the rapid developments of microfabricated techniques can enable the microfluidic devices to be constructed at sub-micro scale and thus make the flow enter the transition regime (Barber and Emerson 2006).
3 Knudsen layer
The Knudsen layer (KL) is an important rarefaction phenomenon and the region of local non-equilibrium extends a thickness of a few MFPs from the wall in gas microflows (Zhang et al. 2006a, b). Although the classical kinetic theory has been extensively used to characterize the KL, either by solving the linearized Boltzmann equation (LBE) (Ohwada et al. 1989; Loyalka et al. 1975) or by DSMC (Bird 1994), the N–S constitutive equations cannot capture the nonlinear stress/strain-rate behavior within the KL (Lockerby et al. 2005a; Hare et al. 2007). Approximately 70 % of the mass flow rate increase results from the velocity slip at the wall, and 30 % of this increase is attributed to the non-Newtonian structure of the KL (Lockerby et al. 2005b). Therefore, it is essential to capture the KL characteristics for modeling rarefied flows at microscale and nanoscale systems (Lilley and Sader 2008).
Figure 4 shows a typical velocity slip profile within the KL near a solid wall (Lockerby et al. 2005a; Watari 2010). In the quasi-equilibrium state (B–C), the flow can be governed by N–S equations and the KL is employed with macro slip boundary conditions (Watari 2010). If the actual velocity slip u s (B–D) is taken into account at the boundary in the KL, the prediction of the velocity profile both inside and outside the KL is poor (Lockerby et al. 2005a; Hare et al. 2007). The molecules collide in the surface more frequently than they impact with each other within the KL (Gallis et al. 2006). The main drawback of the macro slip approach is that some part of the gas microflow is defined fictitiously.
Correct descriptions of the KL are of critical importance in modeling and designing of gas microflows and in predicting their performances (Lockerby et al. 2005a, b). Although lacking a universal description of the KL, it shows from Fig. 4 that the velocity profile decreases rapidly away from the solid wall and is virtually zero outside the KL. Hare et al. (2007) described two possible approaches, phenomenological model and physical approach, to simulate the KL effect.
3.1 Description approaches
3.1.1 Wall-function method
The wall-function approach is a phenomenological one, which can capture the characteristics of the gas microflows with the KL (Hare et al. 2007). For diffuse scattering of the gas molecules, Cercignani (2000) provided the velocity profile in the KL for Kramer’s problem as:
where k u is the velocity gradient in the bulk flow, y is the distance normal to the wall, and I is a function which represents the velocity defect in the KL.
Lockerby et al. (2005a) presented a wall-function model to study the velocity profile within the KL with a curve-fitting approximation from the kinetic theory data. With the wall function \( I(y/\lambda ) \approx 7/20(1 + y/\lambda )^{ - 2} \), the velocity profile can be written as:
The wall function shows the velocity gradient equals to 1.7 at the wall. However, this model does not consider the accommodation coefficient and is limited at a relatively low Knudsen number up to 0.1 for planar surfaces (Hare et al. 2007). Zheng et al. (2006) addressed a formulation of the wall function incorporating the accommodation coefficient to explain this problem.
3.1.2 Higher-order continuum model
Higher-order continuum model can be regarded as an appealing strategy to capture the KL effect (Guo et al. 2007a, b). Some models beyond the N–S equations, such as the Burnett, BGK–Burnett, and super-Burnett models, had been proposed (Zhong et al. 1993; Jin and Slemrod 2001; Struchtrup and Torrilhon 2003; Balakrishnan 2004). These models are usually derived from LBE using the Chapman–Enskog expansion and truncating at certain orders (Cercignani 1988). Lockerby et al. (2005b) explained as to why there are so many different higher-order models with three basic reasons: (1) constitutive relations of higher-order than the N–S equations have indicated potential in modeling rarefied flows; (2) all these models depend on the numerical and physical instability; and (3) no single equation has the ability to predict the important non-equilibrium effects in the rarefied gas microflows.
The velocity profile predicted by the super-Burnett equations can be given by (Lockerby et al. 2005b):
where k s1~k s4 are constants.
Lockerby et al. (2005b) considered the velocity gradient from the wall and developed an expression to approximate the KL as:
where C L depends on the hydrodynamic model, and \( C_{\text{L}} = \sqrt {\pi /2} \) for the BGK–Burnett equation; \( C_{\text{L}} = \sqrt {5\pi /54} \) for the regularized Burnett equation; \( C_{\text{L}} = \sqrt {3\pi } \) for Zhong’s augmented Burnett equation; and \( C_{\text{L}} = \sqrt {5\pi /18} \) for the R13 equation (Lockerby et al. 2005b). C L = 1 represents that the velocity profile is very close to the results obtained from both the LBE and DSMC simulations for Kramer’s problem (Zheng et al. 2006). However, these extended continuum models are exposed to some criticisms and the validity of the Chapman–Enskog expansion in the KL is questionable (Cercignani 1988). Moreover, these higher-order models cannot even capture the KL for the simple Kramer’s problem (Lockerby et al. 2005b). Lilley and Sader (2008) discussed that the wall function, various hydrodynamic models, and Fichman and Hetsroni models (Fichman and Hetsroni 2005) do not capture the asymptotic form of the velocity profile in the KL near the wall.
3.1.3 Power-law model
The lattice Boltzmann method (LBM) can be used to resolve the KL; in this method the wall-function approach can alter the dynamics near the wall by adjusting the relaxation time or applying the mean-field theory (Zheng et al. 2006; Guo et al. 2006), and the higher-order continuum models can be included in the LBM, such as the Burnett, super-Burnett, Grad 13-moment, or beyond (Aidun and Clausen 2010). However, the higher-order continuum model cannot provide a proper treatment of the boundary conditions at the wall (Gu and Emerson 2007; Struchtrup and Torrilhon 2008), and is formally valid outside the KL (Hadjiconstantinou 2006). The power-law description is obtained from the LBE and DSMC solutions of the BE (Lilley and Sader 2008), and it indicates that the velocity gradient singularity comes naturally from the BE.
Lilley and Sader (2007) used the solutions from LBE and DSMC calculations to examine the KL, and discovered that the bulk gas velocity can be accurately described by the remarkably simple power-law behavior as:
where α p ≈ 0.8 applies for HS molecules near a diffusely reflecting wall. The expression establishes the existence of a velocity gradient singularity at the wall, which cannot be captured by the higher-order continuum model (Lockerby et al. 2005b) and wall-function model (Lockerby et al. 2005a).
Lilley and Sader (2008) also presented the entire velocity profile including the KL as:
where σ v is the tangential momentum accommodation coefficient (TMAC), \( \tilde{u} = u/\alpha_{\text{p}} \lambda \) and \( \tilde{y} = y/\lambda \). The functional dependencies of \( \tilde{u}(0,\sigma_{v} ) \), \( C_{\text{L}} (\sigma_{v} ) \), \( \alpha_{p} (\sigma_{v} ) \), and \( \tilde{\xi }(\sigma_{v} ) \) on \( \sigma_{v} \) were determined empirically as: \( \tilde{u}(0,\sigma_{v} ) = 2.01/\sigma_{v} - 1.39 + 0.19\sigma_{v} \), \( C_{\text{L}} (\sigma_{v} ) = 1.58 - 0.33\sigma_{v} \), \( \alpha_{\text{p}} (\sigma_{v} ) = 0.69 + 0.13\sigma_{v} \), and \( \tilde{\xi }(\sigma_{v} ) = 2.01/\sigma_{v} - 0.73 - 0.16\sigma_{v} \), respectively. Lilley and Sader (2008) suggested that the power-law description is a general physical phenomenon.
3.2 Knudsen layer thickness
The KL thickness can be approximated by l c and given by (Gusarov and Smurov 2002):
where k B is the Boltzmann constant, T is the absolute temperature, and p is the gas pressure.
The thickness of KL is of the order of a few MFPs and can be predicted with the kinetic theory and DSMC simulation quantitatively. A comparison of the KL thickness obtained with various approaches is listed in Table 1. It can be seen that the solution obtained from the kinetic theory distinguishes from the DSMC data and MD simulation. The thickness calculated by kinetic theory is about 1.4 λ and those obtained by various higher-order continuum models are in the range from 0.9 λ to 4.9 λ (Lockerby et al. 2005b), and that simulated by molecular dynamics (MD) method is 2.5 λ (Galvin et al. 2007).
4 Theory description
In this section, we review and discuss theoretical descriptions focusing on the physics of problems of engineering interest in the velocity slip at the wall.
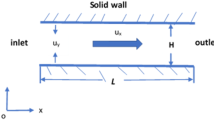
The concept of the slip boundary condition was first presented by Navier and shown schematically in Fig. 5. In Navier’s model, the magnitude of the slip velocity u s is proportional to the magnitude of the flow shear rate at the wall:
where L s is the slip length. Maxwell first quantified the slip length of gas flowing over a solid wall. Badur et al. (2011) for the time analyzed and compared the formulations and mechanics of the slip boundary conditions based on the concepts of Navier, Stokes, Reynolds, and Maxwell. The history and formulation of the slip boundary condition is listed in Table 2, in which the symbols refer to Badur et al. (2011).
4.1 Gas-surface interaction: kinetic theory
In the kinetic theory, the gas-surface interaction forms a boundary condition between the gas molecules and the solid wall. It is important to investigate the gas-surface interaction for understanding the gas microflows. The microflow near a wall is strongly influenced by the gas-surface interaction, which can be governed by the typical models, such as the Maxwell (elastic-diffuse) model or the Cercignani–Lampis (CL) model (McCormick 2005). Although various gas-surface interaction models have been proposed since Maxwell in 1879, the validity of these models remains under question for rarefied flow conditions. The slip effect should be considered to make a correction based on the degree of non-equilibrium near the wall.
4.1.1 Maxwell model
Maxwell (1879) proposed the first and most fundamental description of the gas-surface interaction with two processes, i.e., incidence and reflection. When combining these two processes, the classical description of the velocity slip in rarefied gases in vector form is given by (Lockerby et al. 2004):
where \( \vec{u}_{\text{s}} \) is the tangential slip velocity of the gas, \( \vec{\tau } \) is the tangential shear stress, \( \mu \) is the gas viscosity, \( P_{\text{r}} \) is the Prandtl number, and \( \vec{q} \) is the heat flux. The molecular MFP λ is defined as:
where \( \rho \) is the gas density.
However, the Maxwell’s gas-surface interaction model describes the momentum and energy transport together and considered just one parameter σ v , which is widely used to calculate tangential momentum transport and varies from zero (specular reflection) to unity (diffuse scattering) (Wu and Bogy 2001; Lockerby et al. 2004; Lockerby and Reese 2008). However, the Maxwell model is only applicable for the gas flows where the rarefaction and roughness effects are not evident (Cao et al. 2009). For rarefied flows involving a significant amount of intermolecular collisions, it is necessary to obtain the re-emitted molecular property distributions. Maxwell presented a one-dimensional expression for the shear stress as:
where n is the coordinate normal to the wall, u s is the slip velocity, u w is the wall velocity, and \( \sigma_{p} = \alpha_{\text{s}} (2 - \sigma_{v} )/\sigma_{v} \) is the slip coefficient, in which α s is a controversial coefficient and will be discussed in Sect. 5. Maxwell (1879) first estimated the coefficient and assumed that the incident molecules have the same distributions as those in the midst of the gas, and obtained \( \alpha_{\text{s}} = \sqrt \pi /2 \). This slip boundary condition can provide useful prediction for certain gas microflows (Hare et al. 2007).
When the thermal creep effects due to the axial temperature gradient are neglected, the first-order slip boundary condition can be written as:
In the case of wall with curvature, the slip boundary condition at the wall in two dimensions becomes (Lockerby et al. 2004):
where u n is the gas velocity normal to the wall and x t is the coordinate tangential to the wall. The additional derivative ∂ u n/∂ x t should also be considered for microfluidic devices with significant roughness inducing two components of the velocity close to the wall (Colin 2012). However, the first term at the right hand side is the order of \( {\rm O}(Kn) \), while the second term is the order of \( {\rm O}(Kn^{2} ) \), which were often modified as \( \partial u/\partial x_{\text{t}} \) or neglected, or improved by adding a correction term in theoretical analyses (Khadem et al. 2009; Hossainpour and Khadem 2010; Colin 2012).
To et al. (2010) derived a slip model for gas microflows induced by external body forces based on Maxwell’s collision theory between gas molecules and the wall. The slip boundary condition yields:
where \( \gamma_{\text{T}} \) is the molecular acceleration, \( \bar{c} \) is the thermal speed of the gas, β T denotes a constant, which denotes the difference between the idealized condition used to derive the slip model and the realistic one and is expected to be close to unity.
Second-order boundary conditions have been proposed in the literature (Karniadakis et al. 2005; Barber and Emerson 2006; Dongari et al. 2007; Weng and Chen 2008) and the general form can be expressed as:
where C 1 and C 2 are the first- and second-order slip coefficients, respectively.
From the tangential momentum flux analyses, Beskok and Karniadakis (1996) and Beskok and Karniadakis (1999) derived a high-order slip boundary condition for an isothermal surface in the following form:
where u λ is the tangential component of gas velocity one MFP away from the surface. The boundary condition predicts accurate wall slip velocity when Kn < 0.5, although resulting in poor mass flow rate prediction (Karniadakis et al. 2005). Using a Taylor series expansion of u λ about u s (Beskok and Karniadakis 1999), yields:
Attempts to implement the above slip boundary condition using numerical simulation methods are rather difficult. Second-order and higher derivatives of velocity cannot be computed and simulated accurately near the wall (Gad-el-Hak 1999).
Zhang et al. (2010a, b) considered the effect of relative position of the slip surface in the KL on the slip boundary condition and developed a new slip model in the form:
Compared with the classical second-order slip boundary condition proposed by Beskok and Karniadakis (1999), the coefficient \( C_{\text{Z}} = \xi_{\text{s}} /\lambda \) (\( C_{\text{Z}} \in [0,1] \)), in which \( \xi_{\text{s}} \) is the distance between the wall and the slip surface, is proposed in the corrected second-order boundary condition. The corrected second-order slip boundary condition was used to solve the N–S equations for confined fluids at the microscale and nanoscale (Zhang et al. 2012a, b).
4.1.2 Cercignani–Lampis (CL) model
To provide a more physical description of the gas-surface interaction, the CL model was presented to satisfy the fundamental scattering kernel principles and distinguish the momentum and energy accommodation coefficients (Albertoni et al.1963; Cercignani and Lampis 1971; Loyalka et al. 1975; Ohwada et al. 1989; Garcia and Siewert 2010).
Klinc and Kuscer (1972) presented the variation result for the slip coefficient \( \sigma_{p} \) for the CL gas-surface model as:
where σ 22 = σ 25 = σ v and σ 55 is the coefficient depending on the energy accommodation coefficient \( \sigma_{n} \), μ f is defined to be the first-order approximation to the viscosity μ as computed by Chapman and Cowling (1970), and μ f/μ = 1 for Maxwellian molecules and μ f/μ = 0.984219 for rigid-sphere gas interactions (McCormick 2005). This expression agrees identically with the analytic equation for the velocity slip coefficient derived from a different variational approach by Cercignani and Lampis (1989).
McCormick (2005) deduced the relationship between σ 55 and σ n , and gave the CL gas-surface interaction model and rigid-sphere gas interaction including σ v and σ n as:
where \( 0.915 \le K_{M} \le 1 \). The combination of σ v = 0 and σ n = 0 corresponds to the specular reflection and the combination of σ v = 1 and σ n = 1 refers to the diffuse scattering.
In addition, Lord (1991, 1995) presented a transformation of the CL model with the DSMC method and extended it widely to rarefied gas microflows. The Maxwell model and the Cercignani, Lampis and Lord (CLL) model are the most common gas-surface interaction models used with the DSMC method.
4.2 Gas-surface molecular interaction: surface adsorption theory
A physical approach can be developed to describe the slip effect by considering the interfacial interaction between the gas molecules and surface (Langmuir 1933; Myong et al. 2005). In this approach, the gas molecules are assumed to interact with the surface of the solid via a long range force, and consequently the gas molecules can be adsorbed onto the surface (Langmuir 1933). The Langmuir slip model based on the surface chemistry theory can be explained by surface adsorption isotherm.
Using the Langmuir adsorption isotherm, the Langmuir slip model had been developed by Eu et al. (1987) and Myong (2001, 2004a, 2005), for the gas-surface molecular interaction and the velocity slip can be expressed as:
where the subscript loc denotes the local value adjacent to the wall. α M is the fraction of the surface covered by adsorbed atoms at thermal equilibrium and \( \alpha_{M} = \beta_{M} p/(1 + \beta_{M} p) \) and \( \alpha_{M} = \sqrt {\beta_{M} p} /(1 + \sqrt {\beta_{M} p} ) \) for monatomic and diatomic gas molecules, respectively (Myong 2004b). The parameter β M is a function of the interfacial interaction parameters K M and the wall temperature T and can be expressed as β M = K M /k B T. β M plays a crucial role on the reaction constant for gas-surface molecule interaction (Choi and Lee 2008) and it has the simplest expression as:
where \( \omega_{M} \) is a function of the interaction parameters and shows very similar to the slip coefficient σ p in Maxwell model (Myong 2004a). Myong et al. (2005) pointed out that the slip coefficient ω M in the Langmuir model is a physical parameter of heat adsorption while the accommodation coefficient σ v in the Maxwell model is a free parameter from the concept of diffusive reflection. Comparisons of the slip flows between the Maxwell model and Langmuir model using the LBM were reported by Kim et al. (2007) and Chen and Tian (2010). Zhang (2011) reviewed that the slip models were specified in the boundary treatments as the input to match empirical or analytical descriptions. The boundary slip observed from LBM simulations is more phenomenal than physical as those from other methods, such as numerical results from the BE and DSMC method (Guo and Zheng 2008; Zhang 2011).
5 Slip coefficient and model
The no-slip boundary condition is assumed to apply at the solid–fluid interface under normal conditions. However, it is well known that at higher Knudsen number this condition is violated and the gas slips at the wall (Dongari et al. 2007). Maxwell (1879) first proposed a first-order slip model to calculate the slip velocity at the wall for atomically smooth walls. Later many other heuristic extended slip models have been proposed even for atomically rough walls and are comprehensively summarized by Karniadakis et al. (2005). Slip models have been proposed to improve the predictions of continuum methods for the non-equilibrium regions near solid boundaries. The idea is to relax the traditional no-slip boundary condition to allow the rarefied gas to slip at the wall (Mcnenly et al. 2005). Brenner (2011) offered a simple macroscopic approach to the question of the slip boundary condition to be imposed upon the tangential component of the slip velocity at a solid boundary.
The slip coefficient provides simple conditions for gas dynamic problems (McCormick 2005). However, experimental studies revealed that large discrepancies between the experimental results of the slip coefficients and the theoretical values proposed in the literature (Maurer et al. 2003; Barber and Emerson 2006; Ewart et al. 2007a; Agrawal and Prabhu 2008a, b). Lacking of well-founded and rigorously derived value of the slip coefficient makes it difficult to investigate the real capabilities of the N–S equations and to extend slip flow predictions into the transition regime (Cercignani and Lorenzani 2010).
Robust slip-flow models are always preferred as alternatives since the difficulty in solving the N–S equation is negligible compared with the cost of these alternative methods (Hadjiconstantinou 2006). The detailed methods and techniques to obtain the slip coefficients can be found in the literature. The various values of the slip coefficients and the determination methods are reviewed and discussed in this section.
5.1 Determination methods and techniques
5.1.1 Kinetic-model based method
Various kinetic models have been reported to calculate the slip coefficient at the gas–solid interaction. Loyalka et al. (1975) considered the KL effect and calculated the slip coefficient using the Bhatnagar–Gross–Krook (BGK) kinetic model and a Maxwell diffuse-specular scattering kernel. A simple modified expression of the slip coefficient S with the accommodation coefficients σ v was proposed by:
where S(1) is the slip coefficient for σ v = 1 and equals to 1.016, i.e., the value obtained theoretically by Albertoni et al. (1963). Porodnov et al. (1974) provided the experimental data of the slip coefficient and the corresponding values of σ v for some gases and showed that the slip coefficient is higher than unity for light gases, such as helium and neon.
Gabis et al. (1996) presented a spinning rotor gauge model to describe the torque that an unbounded gas of rigid sphere molecules inducing on a macroscopic sphere and introduced an estimation of the slip coefficient by:
where ω G is a constant and ω G = 0.94146.
Siewert and Sharipov (2002) and Sharipov (2003) used the Sharipov’s kinetic model to determine the slip coefficient with the CL boundary condition, and obtained that the slip coefficient weakly depends on the energy accommodation coefficient σ n (σ n = 1) and can be expressed as:
The experimental data from Porodnov et al. (1974) can also be used to verify the perfect accommodation coefficients. Equation (28) provides more reliable relation of the slip coefficient with the momentum accommodation coefficient, which can be measured by the mass flow rate easily in the free molecular range (Siewert and Sharipov 2002).
To compare the dependence of slip coefficient on the different gas-surface interactions, McCormick (2005) deduced the approximate analytical expressions of the slip coefficient with three boundary conditions. For the Maxwell gas-surface model and CL gas-surface interaction model, the slip coefficients can be written as:
and
where K M = 1 refers to the rigid-sphere gas interaction. When σ v = 1, the slip coefficient S M = S RS = 0.97576 and S CL = 0.97577 for the Maxwell model, rigid-sphere model and CL model, respectively, while S S = 0.98733 obtained by Siewert (2003).
Sharipov (2011) compared the results corresponding to the CL scattering law with the data obtained by applying the BE and presented the following expression:
For a single gas under the assumption of diffuse scattering, Sharipov and Seleznev (1998) and Sharipov (2011) summarized that the values of the slip coefficient based on all kinds of models vary in the range of \( 0.968 \le \sigma_{p} \le 1.03 \). Sharipov and Seleznev (1998), Siewert and Sharipov (2002), and Sharipov (2011) also presented and reviewed the data on the slip coefficient based on diffuse-specular scattering kernel for the Maxwell boundary condition. Table 3 presents the numerical results based on various models, including the BGK model (Loyalka et al. 1975; Sharipov 2011), the LBE (Wakabayashi et al. 1996; Siewert 2003), the S-model (Siewert and Sharipov 2002) and the MC-model (McCormick 2005). It can be seen that the values of the slip coefficient obtained from the LBE (Wakabayashi et al. 1996; Siewert 2003) are slightly smaller than unity. The BGK models (Loyalka et al. 1975; Sharipov 2011) provide the value slightly larger than unity. Therefore, the analytical solutions (26) and (29a, 29b) provide values close to those numerical results and can be successfully used in practical predictions and calculations.
5.1.2 Polynomial expansion approach
In slip flow and near transition regimes, the experimental mass flow rate data can be fitted with first- and second-power polynomial forms of the Knudsen number using a nonlinear least-squares method (Maurer et al. 2003), that yields:
where \( A_{j}^{\exp } \) and \( B_{j}^{\exp } \) are the coefficients obtained by the nonlinear least-squares Marquard–Levenberg algorithm, in which \( j \) denotes the order of the polynomial (Ewart et al. 2007b).
Aubert and Colin (2001) considered a pressure-driven flow in the rectangular microducts and calculated the second-order model for slip flow between parallel plates using the boundary conditions from Deissler (1964), the polynomial expression is given by:
where α AC1 and α AC2 are the coefficients depending on the ratio of the cross-section of the microchannel and momentum accommodation coefficient.
Roohi and Darbandi (2009) presented an IP (information preservation)-based slip coefficient model as:
where a R1 and a R2 are defined as \( a_{{{\text{R}}1}} = 11.72 + \frac{42.253}{{1 + (0.21 + 0.47/Kn_{\text{O}} )(0.21 + 0.47\Uppi /Kn_{\text{O}} )}} \) and \( a_{{{\text{R}}2}} = \frac{{1 + 0.89Kn_{\text{O}} + 4.7Kn_{\text{O}}^{2} }}{{\Uppi^{2} + 0.89Kn_{\text{O}} \Uppi + 4.7Kn_{\text{O}}^{2} }} \). For the general form of the second-order boundary condition, the coefficient is deduced using the IP scheme as:
where Kn O is the Knudsen number outlet, \( \Uppi \) is the ratio of the inlet and outlet pressures, and C 1 = (2 − σ v )/σ v and C 2 = 9/8 (Aubert and Colin 2001). Arkilic et al. (1997) proposed an experimental investigation on the gaseous slip flow in long microchannels for accurately measuring the mass flow and obtained the first-order slip coefficient \( S = 1 + 12C_{1} \frac{{Kn_{\text{O}} }}{\Uppi + 1} \).
5.1.3 DSMC method
From the definition of slip flow, the slip coefficient should be affected not only by the macro-parameters (temperature and speed of solid wall), but also the micro-parameters (the mass, diameter and number density of gas molecules) (Pan et al. 1999). During the past decades, a series of test cases were performed using the DSMC method to study the slip coefficient.
Pan et al. (1999) synthesized Bird’s conclusion (Bird 1994) and discussion from Beskok and Karniadakis (1994) and expressed a general slip coefficient in the form:
where L c is the local characteristic length, and k B T is the average kinetic energy parameter. The slip coefficient is easy to determine from the numerical calculations using the DSMC method (Bird 1994) by:
where S l and \( U_{\text{g}}^{l} \) are the slip coefficient and the gas flow velocity at the lower plate, respectively; and S u and \( U_{\text{g}}^{u} \) are the slip coefficient and the gas flow velocity at the upper plate, respectively.
Pan et al. (1999) finally obtained the functional relationship between the slip coefficient and the MFP
where the coefficient C P is determined to C P = 1.1254 using the least squares approach, and concluded that the slip coefficient is only a function of the MFP excluding any experiential parameter.
Mcnenly et al. (2005) selected the N–S solution from the family that best fits the DSMC data by performing a linear least-squares fit of the DSMC velocity profile with:
where S uy and S yy are the relative position and velocity parameters in the DSMC cell. The slip coefficient can be determined to best capture the non-equilibrium flow as:
where \( \Updelta U \) is the velocity drop between the lower and upper wall velocities. Ng and Liu (2002) devoted to develop an improved slip model, called the stress-density ratio model, applicable especially to transition regime by the DSMC method for the ultra-thin film gas lubrication. The shear stress on the wall is produced by the definition in DSMC as:
where \( u_{{{\text{N}}1}} \) and \( u_{{{\text{N}}2}} \) are the components of molecular velocity. The slip coefficient can be obtained from DSMC results as:
5.1.4 Linearized Boltzmann method
There are considerable successes in extending the N–S equations with high-order slip boundary condition into the transition regime. In order to provide analytical expressions for the first- and second-order velocity slip coefficients, Cercignani and Lorenzani (2010) and Lorenzani (2011) considered the LBE for HS molecules and used the CL scattering kernel to describe the gas-wall interaction. The BE can be linearized about a Maxwellian \( f_{{{\text{M}}0}} \) by:
where f B is the distribution function for the molecular velocity and h B is the small perturbation on the basic equilibrium state. The LBE had been solved by considering the BGK model of the collisional Boltzmann operator (Cercignani and Lorenzani 2010; Lorenzani 2011).
The slip factor in terms of deviations from asymptotic near-continuum solutions of the BE can be given by:
where \( \sigma_{{{\text{L}}0}} = \left( {4\sqrt \pi } \right)^{ - 1} \left[ {\frac{96}{\pi }J_{{{\text{L}}1}} + 48\sqrt \pi } \right] \), \( \sigma_{{{\text{L}}1}} = \left( {4\sqrt \pi \alpha_{\text{t}} A_{\text{L}} } \right)^{ - 1} \left[ {D_{\text{L}} - \frac{16}{9}\pi \alpha_{\text{t}} C_{\text{L}} } \right] \), \( \sigma_{{{\text{L}}2}} = \left( {4\sqrt \pi \alpha_{\text{t}} A_{\text{L}} } \right)^{ - 1} \left[ {\varepsilon_{\text{L}} + \frac{16}{9}\pi \alpha_{\text{t}} C_{\text{L}}^{2} - \frac{16}{9}\pi \alpha_{\text{t}} B_{\text{L}}^{2} - C_{\text{L}} D_{\text{L}} } \right] \), in which the relative parameter was reported by Lorenzani (2011). The first-order and second-order coefficients can be written as \( C_{1} = \sigma_{{{\text{L}}0}} \sigma_{{{\text{L}}1}} /(3\sqrt \pi ) \) and \( C_{2} = \sigma_{{{\text{L}}0}} \sigma_{{{\text{L}}2}} /(3\pi ) \) according to the solution of the N–S equations obtained by \( S = 1 + 6C_{1} Kn + 12C_{2} Kn^{2} \). To check the reliability of the analysis approach, Lorenzani (2011) compared the first-order slip coefficient with the highly accurate numerical results from Siewert (2003), and found that the BGK first-order slip coefficients are similar to those determined by the solution of the BE for HS molecules. The second-order slip coefficients were found to be significantly dependent on the interaction models, such as the Maxwell kernel and the CL model. In the case of a fully diffusive boundary σ v = 1, Cercignani and Lorenzani (2010) predicted the model performs well even further into the transition regime, while Hadjiconstantinou’s second-order slip model (Hadjiconstantinou 2003) and Lockerby’s Maxwell–Burnett slip model (Lockerby et al. 2004) only capture the flow accurately up to Kn < 0.4 and Kn ≤ 1.60, respectively.
5.1.5 Lattice Boltzmann method (LBM)
Modeling of microscale and nanoscale flows has been an active application area for the research of LBM (Zheng et al. 2006; Li and Kwok 2003). Cornubert et al. (1991) presented the first analysis of the slip velocity using the LBM, in which the slip velocity was demonstrated analytically and numerically for the bounce-back and specular reflection boundary conditions. This method has proved to be effective when dealing with microflow of moderate Knudsen number and has some success at predicting the KL (Aidun and Clausen 2010). When the gas microflows beyond the slip flow regime, a higher-order LBM needs to provide a quantitative prediction as well as to reproduce the presence of the KL (Shan et al. 2006; Ansumali et al. 2007). Recently, Zhang (2011) reviewed and discussed the models and applications of the LBM for microfluidics.
Kim et al. (2008) presented an analytic solution of the D2Q9 LBE for Poiseuille flow. To obtain a correct value of the slip coefficient, the effective diffuse scattering condition was introduced by combining the diffuse scattering boundary condition and the bounce-back scheme. The slip coefficient in the general form of the second-order boundary condition can be given by:
where r K is the fraction of gas particles reflected with the bounce-back rule and it influences only the first-order slip coefficient when \( f(r_{\text{q}} ) = 1 \). Sbragaglia and Succi (2005) suggested that the construction of the body force in the LBM should be modified to adjust the second-order slip coefficient. When the energy flux term is taken into account, \( f(r_{\text{q}} ) \) satisfies \( f(r_{\text{q}} ) = 1/r_{\text{q}} \), in which \( r_{q} \) is set to 0.9 for matching the mass flow rate of the LBE to the second-order of Knudsen number. A general lack of agreement exists in the definition of Kn and λ in the LBMs, which should be considered to allow comparison with existing experimental and analytical results (Guo et al. 2006; Aidun and Clausen 2010).
For the modified LBE with the effective diffuse scattering boundary condition (Kim et al. 2008), the normalized slip velocity with discrete lattice effects can be written as:
where N K is the index of the fluid lattices. The problem of discrete effects in the kinetic boundary condition was also addressed by Guo et al. (2007a, b). Watari (2009) conducted the velocity slip simulations in the slip flow regime using a multispeed finite-difference lattice Boltzmann method (FDLBM).
5.1.6 Experimental measurement
Kuhlthau (1949) presented the experimental setup consisting of a rotating inner cylinder with radius R 1 and stationary outer cylinder with radius R 2 with a low pressure gas in the gap. Agrawal and Prabhu (2008a) examined the experimental data of Kuhlthau (1949) and deduced the slip coefficient in the form:
where T r is the torque, ω r is the angle velocity, L r is the length of the inner cylinder, and C F is the correction factor and C F = 1.91. Agrawal and Prabhu (2008a) suggested from the analysis on Kuhlthau’s data that S = 0.13 for Kn < 0.1 and S = 1.70 for 0.1 < Kn < 8.3.
Maurer et al. (2003) performed gas flow experiments in a shallow microchannel and presented new sets of accurate measurements for a well-resolved range of Knudsen number. The slip factor was defined as:
where Q v is the volumetric flow rate, P O is the outlet pressure, ΔP is the pressure drop, P m is the average pressure, w, b, and L are the width, thickness and length of the channel, respectively.
A development of slip factor was proposed in the form
Agrawal and Prabhu (2008b) summarized the experimental measurements of the values of slip coefficients as reported by Sreekanth (1969), Ewart et al. (2007a, b), Maurer et al. (2003), and Yamaguchi et al. (2011), as listed in Table 4. The principle of measurement applied by Ewart et al. (2007b) is similar to that of Maurer et al. (2003). Since the experimental measurements had been proposed to certain geometric microdevice or material, the differences among them are unavoidable. For instance, Ewart et al. (2007a) performed experimental measurements in silica microtube with diameter of 25.2 μm, which is different from Yamaguchi et al. (2011) with diameter of 320 μm.
5.2 First-order slip model
Velocity field in the slip flow regime can be determined from the N–S equations subject to the velocity slip boundary condition. Neglecting the thermal creep effects, the first-order slip velocity boundary condition is given by (Maxwell 1879):
where the value of slip coefficient, originally derived by Maxwell, is C 1 = 1.
Bird (1994) used the DSMC method to simulate the Couette flow using the VHS molecular model and concluded that the slip velocity is very close to \( \lambda \partial U/\partial n \). The conclusion has a very strong attraction for researchers who prefer to use the N–S equations with velocity slip boundary conditions to investigate the slip flow characteristics (Pan et al. 1999). More accurate values for the slip coefficient have been determined using BE, DSMC, MD simulations, and experimental measurements (Maurer et al. 2003; Bahukudumbi et al. 2003; Bahukudumbi and Beskok 2003; Agrawal and Prabhu 2008a). Table 5 provides the values and modified formulations for the slip coefficient in the literature. The above research represents only a fraction of the proposed models, yet almost all of them can be considered an extension of Maxwell’s original model.
Lockerby et al. (2005a) pointed out that the kinetic theory and molecular simulations indicate Maxwell’s first-order slip coefficient C 1 = 1 is sometimes not quite accurate and overestimates the amount of microscopic actual slip velocity (Li et al. 2011). By using an approximate method in the kinetic theory, Loyalka (1971), Loyalka et al. (1975), Bahukudumbi et al. (2003) and Lilley and Sader (2008) had presented the modifications of Maxwell’s argument. Then, the second-order or higher-order slip coefficient is believed to play an important role in simulating rarefied gas microflows at larger Knudsen numbers. Solutions of the BE for the slip coefficients were originally obtained for the significantly simpler BGK model. Early work by Cercignani (1988) and recent results for the HS gas show that the first-order coefficients are fairly insensitive to the gas models (e.g., HS, BGK) (Hadjiconstantinou 2006).
Figure 6 shows the comparison of experimental data of Maurer et al. (2003) with those derived from other slip models in the literature. It can be seen that Ewart’s model (Ewart et al. 2007b) and Maurer’s model (Maurer et al. 2003) agree well with the scattered experimental data (Maurer et al. 2003) in the entire range of investigated Knudsen numbers. Porodnov’s model (Porodnov et al. 1974), Colin’s model (Colin et al. 2004) and Pan’s model (Pan et al. 1999) underestimate the slip coefficients due to their lacking of the second-order term compared to the experimental data (Maurer et al. 2003). Colin’s model (Colin et al. 2004) with the smallest first-order coefficient (C 1 = 1.02) performs the worst prediction. Aubert and Colin’s model (Aubert and Colin 2001) underestimates the slip coefficient at smaller Knudsen number and performs well when Kn > 0.8. The theoretical analyses proposed by Fichman and Hetsroni (2005) agree very well with the experiments in the range of low Knudsen numbers (Kn < 0.2). The reason might be, for higher Knudsen numbers, the interaction of molecules with the opposite wall should be taken into account as well. Figure 6 also illustrates that the experimental and analytical slip coefficients increase much faster than the prediction obtained by the first-order slip theory (Porodnov et al. 1974; Pan et al. 1999; Colin et al. 2004) in the transition regime, which indicates that the contribution of second-order slip should be taken into account.
Comparison of experimental data for the slip coefficient \( S \) for helium (Maurer et al. 2003) with theoretical expressions in the literature
5.3 Second-order slip model
Various slip models have been proposed to calculate the slip velocity at higher Knudsen number in the literature. A simple extension of Maxwell’s model with the second-order term can be written as:
For isothermal flows, the slip velocity of all the second-order slip models can be expressed in a general form when σ v = 1, yields
Inclusive reviews of the slip boundary condition choices were also provided by Colin (2005), Barber and Emerson (2006), Dongari et al. (2007), Tang et al. (2007a, b), Weng and Chen (2008), Cao et al. (2009), Chen and Bogy (2010). They often validated their second-order slip models by demonstrating the capability of predicting an accurate flow rate (Li et al. 2011).
So far, there is no general agreement on the values of the slip coefficients. Slip coefficient in the slip models usually is investigated in two different means taking σ v into account. One way is to fix the value of σ v . For the case of σ v = 1, Table 6 presents a comparison of the values of the second-order slip coefficients that have been proposed in the literature. In Hadjiconstantinou’s model (Hadjiconstantinou 2003), C 2 = 0.61 is used for local velocity distribution and C 2 = 0.31 for mean velocity and friction factor. For the case of the lubrication microbearings, the slip model and coefficient are chosen differently according to their configurations, gas film characteristic length and surface effect (Ng and Liu 2002; Zhang et al. 2009, 2010a, b, 2011; Chen and Bogy 2010).
In Table 6, Lockerby et al. (2004) proposed that the value of the second-order slip coefficient should be in the range of 0.145–0.19, which depends on the Prandtl number of the gas flow but irrespective of the values of the accommodation coefficient. The estimation approach proposed by Lorenzani (2011) and Cercignani and Lorenzani (2010) to obtain the second-order slip coefficients seems inconsistent with most of the available theoretical models, but the estimated values are very close to those obtained by experimental measurements (Maurer et al. 2003; Ewart et al. 2007b). The results gave a better match to direct solutions of the BEs than the reduced equations without considering KL effect (Struchtrup and Torrilhon 2008). Moreover, Li et al. (2011) found that the flow rate obtained with C 2 = 0.8 best fit the solution of the LBE. Kim et al. (2008) concluded their analysis of the slip coefficients based on the second-order equilibrium and forcing terms for the D2Q9 LBE are higher than those for the LBE, which results from the discretization in the velocity space.
Figure 7 compares the non-dimensional flow rate \( Q_{\text{N}} = \sqrt \pi \left( {1 + 6C_{1} Kn + 126C_{2} Kn^{2} } \right)/\left( {12Kn} \right) \) (Hadjiconstantinou and Simek 2002) as a function of the Knudsen number Kn for various slip models. The predictions from all the slip models have small discrepancies when Kn < 0.1. The higher the first-order coefficient is, the larger the flow rate prediction occurs. Kim’s model (Kim et al. 2008) performs the largest prediction with \( C_{1} = \sqrt {6/\pi } \), while Wu and Bogy’s model (Wu and Bogy 2003) presents the smallest one with C 1 = 2/3. However, the predictions have significant discrepancies and the second-order coefficient dominates the flow rate when Kn > 0.1. The slip models with positive second-order coefficients (C 2 > 0) overestimates the flow rate while the slip models with C 2 < 0 underestimates the rate flow compared to the Maxwell’s model. The prediction of Shen’s model (Shen et al. 2007), which has the largest second-order coefficient C 2 = 2, performs the largest deviation to higher side while Karniadakis and Beskok’s model (Beskok and Karniadakis 1999) gives the largest deviation to the lower side with C 2 = −0.5. It indicated that the first-order slip coefficient dominates the slip flow rate for lower Knudsen numbers while the second-order slip coefficient plays a more important role for higher Knudsen numbers.
The other way is to treat the expression as a function of σ v . Table 7 summarizes the comparison of the expressions of the second-order slip coefficients reported in the available literature. It is difficult to obtain the expression of slip coefficients, and most of them are derived from the simulation results of using N–S, quasi-gas dynamic (QGD) and BEs. The first-order slip coefficients relate to σ v , while the second-order slip coefficients are quite different.
Figure 8 illustrates the variation of inverse slip coefficient with Knudsen number at the outlet of microchannel considering \( \Uppi = 1.8 \) and σ v = 0.93. It is observed that Li’s model (Li et al. 2011) shows the closest agreement with the experimental data (Colin et al. 2004). Aubert and Colin’s model (Aubert and Colin 2001) departs from the given data when Kn > 0.25. Karniadakis and Beskok’s model (Karniadakis and Beskok 2002) and Beskok and Karniadakis’ model (Beskok and Karniadakis 1999) do not match the experimental data due to their second-order coefficients C 2 < 0 in the expressions. It can be clearly seen that the first-order slip model (Arkilic et al. 1997) cannot give an accurate prediction when Kn < 0.2. IP-based model (Roohi and Darbandi 2009) and Wu’s model (Wu 2008) yield well agreement in the range of the Knudsen number Kn > 0.2, but depart from the experimental data for the rest of the Knudsen number range. These more complicated boundary conditions produce more accurate velocity profiles than the usual first-order slip models for slightly larger Knudsen numbers.
Variation of the inverse slip coefficient expressions with Knudsen number for different analytical slip models and the experimental data (Colin et al. 2004) with \( \Uppi = 1.8 \) and \( \sigma_{v} = 0.93 \)
5.4 High-order slip model
Most of the first-order and second-order slip models can be simplified from the high-order slip ones. Bahukudumbi et al. (2003) derived an empirical shear model using a modified slip boundary condition for steady and quasi-steady oscillatory Couette flows
Hwang et al. (1995) determined the slip coefficients from the LBE with considering the molecules reflecting at the boundaries diffusively, and presented the high-order slip boundary conditions for uniform microchannels as:
Try to investigate the gaseous flow in microtubes at arbitrary Knudsen numbers, Weng et al. (1999) presented a new model to describe the gas flow behavior in microtubes avoiding time-consuming calculations and compared with the results obtained by Loyalka (1969). The high-order slip flow boundary condition can be written as:
Ng and Liu (2005) investigated and analyzed the performance of conventional slip models among various regimes of Knudsen number, and developed a new multi-coefficient velocity slip model, by using Taguchi quality control techniques, given by:
Beskok and Karniadakis (1996) and Beskok and Karniadakis (1999) also provided the non-dimensional boundary condition from Eq. (20) in the form
where \( (\partial /\partial n) \)represents the gradients normal to the wall surface.
Based on the asymptotic analysis, Beskok and Karniadakis (1999) and Karniadakis and Beskok (2002) developed a physics-based empirical flow model and proposed the following general velocity slip boundary condition for the compressible flow:
where \( b_{\text{BK}} \) is a generalized slip coefficient, which is an empirical parameter to be determined either experimentally or from LBE or DSMC data. Moreover, its physical meaning is the velocity flux into the surface divided by the velocity of flow field on the surface. Beskok and Karniadakis (1999) determined the value \( b_{\text{BK}} \) and provided some results for transition and free-molecular regimes.
Xue and Fan (2000) put a step forward and presented a high-order slip expression with replacing Kn by \( \tanh (Kn) \) as:
This statement involves only the first derivation of the velocity, which leads to results close to those calculated by DSMC method even in relatively high Knudsen number.
5.5 Hybrid slip model
5.5.1 Effective mean free path (MFP)
(1) Various definitions The MFP λ of gas molecules is an average distance traveled by a molecule before colliding with another one in the equilibrium state and also can be defined as:
where \( \upsilon \) is the collision frequency.
Peng et al. (2004) incorporated Bird’s definition (Bird 1994) and the approximation result from Chapmann and Enskog (Chapman and Cowling 1970) by taking the specific gas constant \( R_{\text{P}} = k_{\text{B}} /m \) and obtained the following formulation:
Using the Chapman and Enskog method, the MFP λ can be rewritten regarding of the viscosity as:
where \( v_{\text{g}} \) is the kinematic viscosity.
When collisions due to the intermolecular interaction are not well defined, Cercignani (1988) proposed to use the viscosity-based MFP
The viscosity-based MFP is very close to the exact result for HS molecules (Kim et al. 2008). The MFP for the BGK molecules can be defined as:
where \( \tau_{\text{g}} \) is the relaxation time in the Boltzmann–BGK equation.
In the description of experimental results, the viscosity-based MFP is widely used to define the Knudsen number. However, considering the nature of MFP, the definition of MFP can be different for various studies, except for HS molecules (Shan et al. 2006).
(2) Molecular model Although the HS model is widely used for its simplicity, the rate of effective cross-section decreases directly related to the change of the coefficient of viscosity with temperature. Bird (1994) proposed the modified MFP for the variable hard sphere (VHS) model as:
where μ ref and T ref are the reference conditions, ω m is a constant which determined by the type of the gas and can be obtained from experimental data.
To describe the actual transport properties, Koura and Matsumoto (1992) introduced the variable soft sphere (VSS) model as:
where \( \vartheta_{\text{m}} \) is also a value which can be determined by the same method for \( \omega_{\text{m}} \). For air, in the VSS model \( \vartheta_{\text{m}} = 1.5775 \) and \( \omega_{\text{m}} = 0.7 \), while in the VHS model \( \vartheta_{\text{m}} = 1.0 \) and \( \omega_{\text{m}} = 0.7 \). When \( \vartheta_{\text{m}} = 1.0 \) and \( \omega_{\text{m}} = 0.5 \), the expression of the VSS model reduces to the HS model (Sun et al. 2002).
Bird (1994) and Koura and Matsumoto (1992) compared the VHS model and VSS model with the HS model and derived the expressions for the effective MFP as:
and
Sun et al. (2002) presented new analytical slip models incorporating the VHS and VSS molecular effects and obtained the slip coefficients for the VHS model with C 1 = 0.62228 and C 2 = 0.3872 and VSS model with C 1 = 0.63875 and C 2 = 0.408, respectively.
(3) Wall-function approach For an isothermal, incompressible flow, Zheng et al. (2006) incorporated the wall-function approach into a D2Q9 LBE model and presented the effective MFP expression as:
This approach can be applied to more complex geometries by assuming that the influence of overlapping KLs is additive. Outside the KL, the effective MPF approaches the MFP in the bulk flow, while, at the wall (y = 0), the effective mean free path is 1.7 times smaller than in the bulk flow (Zheng et al. 2006).
(4) Matthiessen rule The Matthiessen rule had been widely used to consider the boundary scattering effects on electron and phonon transport (Ascroft and Mermin 1976). To explain the boundary scattering, the MFP can be evaluated using this rule as:
where λ s is the MFP from molecular scattering and can be simply calculated as \( \lambda_{\text{s}} = \lambda /\sqrt 3 \), and \( \lambda_{\text{b}} \) is the MFP due to boundary scattering.
Shen et al. (2007) took the film thickness H/2 for λ b to account for the fact that there are two overlapping KLs and calculated the effective MFP using the Matthiessen rule (Ascroft and Mermin 1976) as:
The effective MFP should be modified with different geometries. Chen and Bogy (2010) remarked that Shen’s slip model (Shen et al. 2007) is also a second-order type without considering the effective MFP and the rule is seldom used for rarefied gas dynamics. The application of the Matthiessen rule to rarefied gases is not supported by the BE (Chen and Bogy 2010).
(5) Probability distribution function approach The influence of a solid wall on the MFP of the gas molecules can be analyzed by considering the probability of the free path of a gas molecule. The idea of using transport parameters that are influenced by an effective MFP was presented by Stops (1970). Many researchers (Stops 1970; Peng et al. 2004; Guo et al. 2007a, b, 2008; Arlemark et al. 2010; Dongari et al. 2011b) had paid more attention on deducing the effective MFP for various gas flows in MEMS/NEMS.
Figure 9 shows the distribution of the molecule free path in terms of the molecule traveling a distance r. Stops (1970) presented the free path of a molecule following a probability distribution function
Using this probability distribution function, Guo et al. (2007a, b) and Guo et al. (2008) derived a geometry-dependent effective MFP for the two parallel plates, i.e.,
where \( \alpha = y/\lambda \), \( \beta = (H - y)/\lambda \), \( E_{\text{i}} (x) \) denotes the exponential integral function defined by \( E_{\text{i}} (x) = \int_{1}^{\infty } {t^{ - 1} e^{ - xt} dt} \), in which H is the distance between the two parallel plates, and \( \Upphi \) is a monotonous function of Kn and satisfying \( \mathop {\lim }\limits_{{K_{\text{n}} \to 0}} \Upphi (Kn) = 1 \). Guo et al. (2006) mentioned that the function \( \Upphi (Kn) \) derived by Stops is very complicated and is difficult for practical applications. The reason may be that it contains an exponential integral function \( E_{\text{i}} (x) \), which needs a numerical integration and leads to considerable computations (Li et al. 2011). Moreover, heuristic expressions of effective viscosity should be proposed to enable the computation efficient and the implementation ease.
Guo et al. (2006) presented the expression of the effective MFP with an approximation to replace Stops’ expression as follows:
Integrating the density function \( \psi (r) \), Arlemark et al. (2010) applied a probability function \( \Upphi (r) = \int {\psi (r)dr} \) and developed a three-dimensional probability function-based effective MFP \( \lambda_{{{\text{eff}}({\text{A}})}} \) as:
Comparison of both effective MFP models (Stops 1970; Arlemark et al. 2010) with MD simulation data (Dongari et al. 2011a) shows that both models are useful only up to Knudsen numbers of about 0.2 (Dongari et al. 2011b). Moreover, the Stops’ probability distribution is only valid under equilibrium conditions (Dongari et al. 2011a, b).
To extend the N–S–Fourier (N–S–F) equations used for the gas flows at microscales and nanoscales in the transition regime, Dongari et al. (2011b) proposed a power-law-based effective MFP model. For non-equilibrium gas, a power-law form of the distribution function with diverging higher-order moments was hypothesized and expressed as:
where a D and C D are constants with positive values, which are determined through the zero and first moments, and exponent nn can be obtained by making one of the higher-order moments divergent.
The effective MFP based on the power-law distribution function can be given by (Dongari et al. 2011b):
The power-law-based effective MFP (Dongari et al. 2011b) was validated against MD simulation data (Dongari et al. 2011a) up to K n = 1, and also compared with the theoretical models from Stops (1970) and Arlemark et al. (2010).
To study the unidirectional flow of the rarefied gas near the boundary region, Peng et al. (2004) presented a nanoscale effect function \( \lambda_{{{\text{eff}}({\text{P}})}} /\lambda \) to describe the gas behavior between two parallel plates based on the kinetic theory. The probability density of the direction distribution of molecule velocity is:
where θ P, β P are random variables uniformly distributed in the whole space, and the integration of \( \Uptheta (\theta_{\text{P}} ,\beta_{\text{P}} ) \) in the whole integration space is clearly equal to 1. The effective MFP considering the nanoscale boundary effects can be expressed as (Peng et al. 2004):
Chen and Bogy (2010) argued that the modified MFP is not necessary for Fukui and Kaneko’s (FK) model (Fukui and Kaneko 1988) in which the MFP is characterized by the BGK gas molecules in the equilibrium state.
5.5.2 Effective viscosity
Gas viscosity is an important property to account for the momentum exchange between gas molecules. The effective viscosity is a mathematical construct with no connection to real gas properties, and its value will change with flow geometry (Lilley and Sader 2008).
MFP and viscosity are two interactive parameters and many research works pay more attention on their combinations for gas microflows with different boundary conditions. Their relationship can be expressed as (Dongari et al. 2010)
To distinguish the differences between some heuristic effective MFP and viscosity models for gas microflows from different viewpoints, the effective viscosity models are reviewed in this section.
(1) Various definitions For HS molecules, the coefficient of viscosity μ can be obtained by using the Chapman and Enskog method (Chapman and Cowling 1970) as:
The bulk viscosity of dilute gases for the HS model can also be derived from the Chapman–Enskog theory and given by:
Where \( \bar{c} = \sqrt {8k_{\text{B}} T/\pi m_{\text{g}} } \) and \( \rho = p/(R_{p} T) \).
A simple kinetic theory based result proposed by Maxwell for the bulk viscosity is (Pollard and Present 1948):
Alexander et al. (1998) used the Green–Kubo theory to evaluate the transport coefficients in DSMC and derived from the dilute gas Enskog values for the viscosity as:
where \( d_{\text{c}} \) is the collision diameter, \( L_{\text{x}} \) is the width of the cell.
Hadjiconstantinou (2000) considered the convergence with respect to a finite time step when the cell size is negligible and examined the effects of the discretization error in DSMC calculations of the viscosity using the Green–Kubo theory. The resulting expression of the viscosity becomes:
where \( c_{\text{m}} \) is the most probable speed of the gas molecules.
(2) KL-based model Considering the effect of KL, Lilley and Sader (2008) investigated gas flow for small Knudsen numbers and suggested a power-law dependence of viscosity on the dimensionless distance from the solid surface as:
where \( C_{{\tilde{y}}} \) and \( \delta_{{\tilde{y}}} \) can be obtained from the LBE and the empirical determinations of the functional dependencies of \( C_{{\tilde{y}}} \) and \( \delta_{{\tilde{y}}} \) on the thermal accommodation coefficient \( \sigma_{T} \) are \( C_{{\tilde{y}}} (\sigma_{\text{T}} ) = 1.58 - 0.33\sigma_{\text{T}} \) and \( \delta_{{\tilde{y}}} (\sigma_{\text{T}} ) = 0.69 + 0.13\sigma_{\text{T}} \) (Lilley and Sader 2008). The DSMC calculations showed that the KL for VSS molecules is very similar to that for the HS ones and the power-law description is weakly dependent on the molecular model (Lilley and Sader 2007).
To evaluate the isothermal microflows, Lockerby et al. (2005a) proposed a wall-function type of viscosity in the KL derived from a curve fit to the KL velocity profile originally derived by Cercignani (1990) as:
When a part of the molecules is reflected diffusively and another one is reflected specularly, Fichman and Hetsroni (2005) presented the effective viscosity as:
Reese et al. (2007) reviewed the Fichman and Hetsroni model (Fichman and Hetsroni 2005) that it cannot capture the asymptotic form of the velocity profile in the KL near the surface and provided the expression for the effective viscosity required to reproduce the KL structure within an N–S–F model as:
where \( A_{\text{R}} \), \( D_{\text{R}} \) and \( E_{\text{R}} \) are the curve-fitting coefficients. If \( \tilde{y} \) becomes large outside the KL, the effective viscosity tends to be of the actual viscosity and the scaling effect does not work on it. Reese et al. (2007) obtained the coefficients for two different gas molecular models, A R = - 2.719 (HS) and A R = - 2.025 (BGK), with α R = 1 from the data in the literature (Loyalka and Hickey 1989a, b; Wakabayashi et al. 1996). They also found that the coefficient \( A_{\text{R}} \) is almost independent of the surface accommodation α R, and D R = −0.293 and E R = 0.531 for HS model, and D R = −0.328 and E R = 0.612 for the BGK model, respectively (Reese et al. 2007). Moreover, the effective viscosity does not generate artificial stresses in the KL.
(3) Karniadakis-style model Some heuristic effective viscosity models had been proposed in previous studies for gas microflows from different viewpoints (Beskok and Karniadakis 1999; Sun and Chan 2004; Roohi and Darbandi 2009; Michalis et al. 2010), which can also be expressed in the form:
where \( \Uppsi (Kn) \) has different form. The researchers (Zheng et al. 2006; Guo et al. 2006) found that the viscosity corrections can improve the numerical accuracy to some extent, but still cannot give satisfactory results for the gas flows at a higher Knudsen number (Li et al. 2011).
Karniadakis et al. (2005) considered the rarefaction effects and proposed a hybrid formula for the viscosity coefficient as follows:
where \( \alpha_{\text{K}} \) is a coefficient and should be adjusted with a complicated inverse hyperbolic-tangent function. Beskok and Karniadakis (1999) first suggested an expression for the viscosity in the transition regime and conducted numerical computations of flow in cylinders and channels using the N–S formulation complemented with a slip boundary condition at \( \alpha_{\text{K}} = 2.2 \). Sun and Chan (2004) reported that they found good agreement of their model with DSMC and with the LBE results at \( \alpha_{\text{K}} = 2 \).
Michalis et al. (2010) investigated the rarefaction effect on gas viscosity via DSMC modeling of rarefied channel flows and also found such an expression with a Bosanquet-type approximation:
They confirmed this expression through a direct calculation of the gas viscosity from its shear-stress-based definition and the rarefaction factor was found to be \( \alpha_{\text{K}} \approx 2 \) in the transition flow regime. The result is same as that presented by Sun and Chan (2004).
It can be seen from Stops’ expression that the local effective MFP is a function of the distance from the wall. However, the Bosanquet-type effective viscosity is independent of the distance due to its value averaging over the cross section. The overall rarefaction effect on the gas viscosity should be taken into account with the Bosanquet-type effective viscosity (Guo et al. 2006; Li et al. 2011). Michalis et al. (2010) also confirmed that a Bosanquet-type expression of effective viscosity describes satisfactorily the dependence of gas viscosity on the Knudsen number in the transition regime.
(4) Shear stress model Bahukudumbi et al. (2003) derived an empirical shear model, which is uniformly valid in the entire Knudsen regime for steady and quasi-steady oscillatory Couette flows with an effective viscosity, which is given by:
where \( f(Kn) \) can be regarded as a generalized formulation as a function of the Knudsen number from shear-stress models (Cercignani 1969; Sone et al. 1990; Veijola and Turowski 2001; Bahukudumbi et al. 2003). Table 8 gives several expresses of the generalized formulation of \( f(Kn) \).
Considering the IP wall shear stress, Roohi and Darbandi (2009) derived an expression for the viscosity coefficient as a function of Knudsen number in the form:
where V t is the particle information velocity, τ w,IP is the wall shear stress and \( \tau_{{{\text{w}},{\text{IP}}}} = \tau_{\text{w}}^{{({\text{NS}})}} + \tau_{\text{w}}^{{({\text{B}})}} + \tau_{\text{w}}^{{({\text{AB}})}} + \cdots \), in which the superscripts NS, B, and AB denote the N–S, the Burnett, and the augmented Burnett equations, respectively.
The NS-based and IP-based viscosity coefficient expressions are expressed as (Roohi and Darbandi 2009):
where the subscript NS and IP refer to the fact that there have been derived from the NS-based mass flow rate relation and the IP simulation data, respectively.Moreover, Bahukudumbi et al. (2003) pointed that it is not possible to construct a shear stress model from N–S-level constitutive equations that are uniformly valid in the entire Knudsen number regime (Park et al. 2004). Therefore, in a rarefied gas flow system confined by solid walls, the path of gas molecule colliding with the walls will be shorter than the MFP defined in unbounded systems (Tang et al. 2008; Guo et al. 2006, 2008; Li et al. 2011). As mentioned in the above two sections, some modifications or corrections on the MFP and the viscosity have been developed to reflect the effect of gas molecule/wall interactions.
Figure 10 shows comparison of the normalized viscosity coefficients predicted by various methods, such as the HS DSMC results (Bahukudumbi et al. 2003), linearized Boltzmann solution of Sone et al. (1990), and IP simulations by Roohi and Darbandi (2009). It can be found that the normalized viscosity coefficient decreases as the Knudsen number increases. Differences among the variational solution (Cercignani 1969), empirical model (Veijola and Turowski 2001), the DSMC results (Bahukudumbi et al. 2003) and linearized Boltzmann solution (Sone et al. 1990) are almost invisible and the maximum deviation is less than 1 %. The NS-based viscosity coefficient is close to the IP-based model at a lower Knudsen number. NS-based and IP-based models are similar to the DSMC predictions for \( Kn < 0.1 \), and gradually underestimate the viscosity at higher Knudsen number ranges. The Karniadakis model (Karniadakis et al. 2005) with \( \alpha_{\text{K}} = 2.2 \) agrees with the Sun and Chan model and is close to the IP-based model when \( Kn > 0.2 \). The viscosity coefficient is not the sole parameter in determining the mass flow and should be combined with the slip boundary condition (Roohi and Darbandi 2009). Although the various heuristic effective viscosity models are proposed from different viewpoints, they can contribute to N–S equations for capturing the high Knudsen number effects in the transition regime (Guo et al. 2006).
5.5.3 Gaseous mixture
Though in practice one meets mixtures more often than a single gas, there are very few investigations on the slip coefficient for gaseous mixtures (Sharipov and Kalempa 2003). The slip boundary condition for a gaseous mixture is more complicated due to the slip coefficient for a gaseous mixture differing from that for a single gas. The concentration gradient near a solid surface causes a slip of the mixture along the surface. Some slip coefficients were provided for a mixture obtained by the moment method applied to BE (Ivchenko et al. 1997; Sharipov and Kalempa 2003; Garcia and Siewert 2007). Naris et al. (2004) provided an efficient methodology to solve internal flows of binary gaseous mixtures through microchannels over the whole range of the Knudsen number. Pitakarnnop et al. (2010) also verified that the implementation of the linearized BGK and McCormack models for solving rarefied flows through microchannels is valid for the gaseous mixture.
The definition of the slip coefficient for a mixture is very similar to that for a single gas. Equation (15) can be rewritten as (Sharipov and Kalempa 2003)
where \( v_{0} \) is the characteristic molecular velocity of the mixture and \( v_{0} = (2k_{\text{B}} T/m)^{1/2} \), in which the mean molecular mass of the mixture is defined as:
where \( m_{1} \) and \( m_{2} \) are the molecular mass of species and the molar concentration \( C_{0} = n_{01} /(n_{01} + n_{02} ) \), in which n 01 and n 02 are the equilibrium number densities of the species.
Comparisons of the slip coefficients \( \sigma_{\text{p}} \) of the mixtures (He–Xe and He–Ar) as a function of molar concentration \( C_{0} \) for various models are listed in Table 9. Figure 11 also shows the comparisons of the slip coefficients \( \sigma_{\text{p}} \) of the binary mixtures as a function of the molar concentration \( C_{0} \) for various models. It can be seen that the four different methods, including McCormack model (Siewert and Valougeorgis 2004; Garcia and Siewert 2007), Lennard–Jones model (Sharipov and Kalempa 2003), rigid spheres model (Ivchenko et al. 1997) and the moment method applied to the LBE (Garcia and Siewert 2007), are in a good agreement with each other. The slip coefficient is very weakly sensitive to the intermolecular interaction potential. At the limits corresponding to a single gas (C 0 = 0 and C 0 = 1), the slip coefficient σ p = 1.018 for McCormack model (Garcia and Siewert 2007) is exactly the same as that obtained from the Lennard–Jones potential model (Sharipov and Kalempa 2003), and the moment model (Siewert and Valougeorgis 2004) under the assumption of diffuse reflection. The largest deviation of the slip coefficient for a mixture from that for a single gas occurs at C 0 = 0.75 approximately. The results indicate that the value of the slip coefficient for a mixture is larger than that for a single gas, which can be applied to optimize the design of the slip boundary conditions in microflows.
Slip coefficient σ p of the mixtures (He–Xe and He–Ar) as a function of molar concentration C 0 for four different methods, including McCormack model (Siewert and Valougeorgis 2004; Garcia and Siewert 2007), Lennard–Jones model (Sharipov and Kalempa 2003), rigid spheres model (Ivchenko et al. 1997), and the moment method applied to the LBE (Garcia and Siewert 2007)
For the adsorption of a gas mixture within the formulation (24), the fraction of the surface at thermal equilibrium may be expressed as (Myong 2004a):
where \( V_{{{\text{g}}1}} \) and \( V_{{{\text{g}}2}} \) denote the fraction of components in volume and \( V_{{{\text{g}}1}} + V_{{{\text{g}}2}} = 1 \).
For the rarefied flow of binary gas mixture in the vicinity of an isothermal surface, Zahmatkesh et al. (2011) presented a second-order slip model for the whole mixtures using the generalized form derived by Karniadakis et al. (2005) as:
where \( \chi_{\text{M}} = n_{02} m_{2} /(n_{01} m_{1} ) \), λ 1 and λ 2 are the MFPs of the binary gas mixtures, respectively.
5.5.4 Effect of surface roughness
Due to limitations in current micromachining technologies, the microfabricated microfluidic devices typically exhibit some degree of roughness (Duan and Muzychka 2008). The average roughness of the silicon surface created by the DRIE process is 6.43 nm, and the root mean square roughness of the sidewall is reported to be about 30 nm (Chabloz et al. 2000). Maurer et al. (2003) measured a shallow microchannel and estimated the roughness to be 20 nm with the channel deep 1.14 μm. Tang et al. (2007a, b) found that the increase of the pressure drop for the stainless steel tube with relative roughness 3.2 % with respect to smooth one is about 28 %. Surface roughness plays an increasingly important role in gas flow in microfluidic devices, but it is difficult to quantify its effects theoretically and numerically. In practice, the surface roughness can be characterized by atomic force microscope (AFM), scanning tunneling microscope (STM), and scanning electron microscope (SEM) (Fukui and Kaneko 1993). Therefore, understanding the effect of surface roughness on gas flow is highly desirable for microfluidic devices.
From the definition of the Knudsen number \( Kn = \lambda /L_{0} \), it can be found that the characteristic length \( L_{0} \) should be modified to take the surface roughness effect into account and can be expressed as a general form:
where \( L_{{0,{\text{sm}}}} \) denotes the characteristic length of smooth surface, \( f(R_{\text{a}} ,\sigma ) \) is the roughness height, in which \( R_{a} \) and \( \sigma \) are the average roughness and standard deviation, respectively, and both of them are the major concerning parameters. The ratio of the roughness to the MFP is a good criterion to determine the slip boundary condition in the N–S equations (Cao et al. 2009). Two main approaches had been proposed to treat the roughness effect, including averaging method and homogenization method (Buscaglia and Jai 2004; Almqvist et al. 2007).
Surface topographies are critical in momentum transport of the gas microflows in microfluidic devices. The effect of the surface roughness is apparent not only at the slip length and velocities but also at the overall flow characteristics (Einzel et al. 1990; Asproulis and Drikakis 2010). The idea is to replace the constitutive boundary condition at the rough surface by a homogenized or effective one at the smooth surface (Dalibrard and Varet 2011). In this way, the rough micromachined surfaces can be described as periodic and random types, as listed in Table 10.
Various models have been proposed to account for the effects of roughness on gas microflows. Many reported computational and experimental investigations (Li et al. 2002; Chen and Cheng 2003; Kleinstreuer and Koo 2004; Lilly et al. 2007; Zhang and Meng 2009) have drawn a conclusion that surface roughness has a significant influence on the gas flow in microfluidic devices, such as microchannel, microtube, micropipe, microbearing, and microduct. To simply model the roughness effect on gas microflows, some researchers represented the surface roughness as periodic distributions, including sinusoidal, rectangular, triangular, elliptical and trapezoidal surface roughness, for two-dimensional simulation (Sun and Faghri 2003; Wang et al. 2005; Ji et al. 2006; Cao et al. 2006; Duan and Muzychka 2008; Zhang and Meng 2009; Xiong and Chung 2010). Sun and Faghri (2003) modeled the roughness by an array of rectangular modules using DSMC method. Zhang and Meng (2009) analyzed the flow characteristics of the microbearing considering the coupled rarefaction and roughness effects with a new second-order slip model (Wu 2008). The roughness was described by the simple sinusoidal waves. For three-dimensional simulations, rectangular prism elements or conical elements were used to express the roughness effect on the gas microflow depending on the roughness element geometry (Hu et al. 2003; Rawool et al. 2006; Baviere et al. 2006; Lilly et al. 2007; Kunert and Harting 2007). Hu et al. (2003) developed a three-dimensional finite volume based numerical model to simulate the flow in microchannels with rectangular prism rough elements on the surface. Kunert and Harting (2007) used a three-dimensional LB model to simulate the flow in rough microchannels with periodic surfaces, including cosines, squares, and triangles.
However, the rough surface topography is a nonstationary random process (Chen et al. 2009; Xiong and Chung 2010). Some researchers carried out more efforts to model the random roughness even if there are many difficulties. Croce and Agaro (2004) explicitly modeled the surface roughness through a set of random generated peaks along an ideal smooth surface in the microchannels. Li et al. (2002) investigated the effects of surface roughness on the slip flow in long microtubes. The rough surface was represented as a porous film based on the Brinkman-extended Darcy model. However, Blanchard and Ligrani (2007) mentioned that slip is independent of the surface roughness magnitude and mostly due to rarefaction. Bahrami et al. (2006) developed a model to predict the flow in rough microtubes with a Gaussian isotropic distribution. Xiong and Chung (2010) combined a bi-cubic Coons patch with Gaussian distributed roughness heights and presented a three-dimensional random surface roughness model to investigate the laminar flow in microtubes. Cao et al. (2006) investigated the effect of surface roughness on slip flow in microchannels using non-equilibrium MD simulation method. The surface roughness can be modeled by triangular, rectangular, sinusoidal, and randomly triangular waves. The roughness effect is indicated to be significant for gas microflows at the small Knudsen number. The power-law behavior obtained from AFM images for MEMS surfaces was similar to fractal Weierstrass–Mandelbrot (W–M) surface results (Bora et al. 2005). Chen et al. (2009) used W–M function to characterize the multiscale self-affine roughness in a rectangular microchannel. Several probabilistic models, such as the mixed model (Fukui and Kaneko 1993), the model with flow factor (Chen et al. 2004) and the striated rough surface (White 2010) had also been proposed to describe the roughness effects.
In addition, some studies have attempted to extend the slip models to flows over the curved or rough surfaces (Myong et al. 2005). Table 11 presented a simple overview of the roughness model and slip model for several typical microfluidic devices reported in the literature. Although some researchers have paid more attention to the roughness effect on gas flows in different microfluidic devices, the slip boundary condition has been described with a simple form (Cao et al. 2006; Duan and Muzychka 2008; Khadem et al. 2009) or even without consideration (Lilly et al. 2007; Xiong and Chung 2010; Ozalp 2011). Very few experimental investigations have concentrated on the effect of surface roughness on boundary slip. Neto et al. (2005) summarized some challenges, including difficult to produce suitable surfaces of controlled roughness, additional undesired changes at the interface, uncertainly associated with roughness and lack of appropriate theoretical description of the realistic surface roughness, in predicting the roughness effect. Therefore, it is necessary to get a better understanding of the coupled effects of surface roughness and velocity slip on gas microflows. The suitable and efficient models must be developed and applied to estimate the roughness and velocity slip effects in the practical engineering design of microfluidic devices in MEMS.
5.6 Tangential momentum accommodation coefficient (TMAC)
As one of the most important parameters for determining the degree of the slip in all of the slip models, the TMAC can be used to characterize the tangential momentum transport between the gas and wall (Cao et al. 2009) and should be predicted in slip and transition flow regimes for microflows and nanoflows (Agrawal and Prabhu 2008b; Veltzke and Thoming 2012). Most of the analytical, numerical, and experimental investigations concerning rarefaction effects on gas microflows relate to the TMAC.
The TMAC \( \sigma_{v} \) is defined as the fraction of gas molecules reflected diffusively from a solid surface in rarefied gas microflows (Pitakarnnop et al. 2010), and can be expressed as:
where \( \tau_{\text{i}} \) and \( \tau_{\text{r}} \) are the average incident and reflected gas molecules, respectively. Since the incident and reflected molecules cannot be confirmed generally, the TMAC is usually estimated from experimental measurements and simulations, nor predicted from theoretical solutions (Agrawal and Prabhu 2008b; Cao et al. 2009). Although many investigations have demonstrated that the TMAC is sensitive to gas–solid interface conditions, the significant effects of the gas species, surface materials, surface temperature, and other surface conditions on the TMAC are not well understood.
The slip velocity coefficient \( \sigma_{\text{p}} \) is a function of the TMAC and can be expressed for the Maxwell scattering model as:
Empirically, the TMAC is often taken to be unity for most of the practical engineering conditions. However, some studies have demonstrated that the TMAC is sensitive to gas and surface conditions (Ho and Tai 1998). The TMAC plays an important role in determining the slip velocity at the solid boundary. As in Maxwell scattering model, the value of the coefficient \( \alpha_{\text{s}} \) is unity. However, Barber and Emerson (2002) reviewed some rigorous kinetic analyses of the BE for the planar flows (Albertoni et al. 1963; Loyalka et al. 1975; Wakabayashi et al. 1996), and explained that:
The value 1.016191 was obtained numerically by Loyalka et al. (1975) from the kinetic equation BGK model under the assumption of a full accommodation of the molecules at the wall, whereas Wakabayashi et al. (1996) obtained a value of 0.98737 by solving the LBE. Young (2011) obtained the values for the linearized Grad 13-moment (LG13) and linearized Regularized 13-moment (LR13) BGK models are 0.886 and 0.919, respectively. Ewart et al. (2007b) obtained the value of \( \alpha_{\text{s}} = 0.933 \pm 0.003 \) for helium using the first-order fitting, while Graur et al. (2009) obtained the most pertinent values of \( \alpha_{\text{s}}^{{1{\text{st}}}} = 0.889 \pm 0004 \) and \( \alpha_{\text{s}}^{{2{\text{nd}}}} = 0.956 \pm 0005 \) for the first-order and second-order treatments, respectively, for nitrogen using the same criteria as those performed by Ewart et al. (2007b). Table 7 also provides various values and formulations of slip coefficients concerning α s obtained from different approaches. Barber and Emerson (2002) concluded that the different solutions between the BE and Maxwell estimation of \( \alpha_{\text{s}} \) lead to considerable confusion and prevent the clear understanding of gas microflows.
As listed in Table 12, it can be observed that the obvious differences among the various experimental and data-fitting approaches. For the first- and second-order polynomial fitting approaches, the TMAC of second order is closer to unity than that of first order. The different values of σ p and σ v obtained for various gases indicate that nature of the gas plays a significant role on the slip characteristics in the gas microflows.
5.6.1 Experimental measurement
The experimental measurement of the TMAC is very important and valuable. Agrawal and Prabhu (2008b) reviewed different measurement approaches to determine the TMAC with various gas–surface combinations and conditions and clearly described the mechanisms of accurate experimental measurements. Finger et al. (2007) summarized that the TMACs obtained from most of the experimental measurements are in the range of 0.85–1.06, while some researchers had experimentally observed TMACs to be between 0.2 and 1.0 (Gad-el-Hak 1999; Karniadakis and Beskok 2002).
Generally, the determination of the TMAC depends on the mass flow measurement. Table 13 provides several typical experimental measurement methods to obtain the TMACs for helium from the literature. Even for the same gas of helium, the TMAC values have differences for different measurement methods and at various Knudsen ranges. Although many experiments are performed to determine the TMAC, there has no methodology, which can predict the TMAC for a given set of conditions. The difference and uncertainty in the measurements unavoidably lead to widely varying TMACs. Therefore, the results of these previous works on the measurements of the TMACs cannot be directly used in a quantitative way for micro- and nanoflows.
To verify the differences from several methods, Yamaguchi et al. (2011) employed the constant-volume method presented by Arkilic et al. (2001) and Ewart et al. (2007b) to measure the mass flow rate through a single microtube and deduced the TMAC from the slip coefficients using the Maxwell model, Loyalka model (Loyalka et al. 1975) and Sharipov model (Sharipov 2004). As listed in Table 14, the TMACs are smaller than unity, and \( \sigma_{\text{v}}^{\text{L}} \) and \( \sigma_{\text{v}}^{\text{S}} \) are more accurate than \( \sigma_{\text{v}}^{\text{M}} \) from the viewpoint of the kinetic theory. The results show that the differences in gas species are small and a little difference in two geometry conditions (Yamaguchi et al. 2011).
Barber and Emerson (2002) verified that the TMAC is substantially a function of molecular weight of the gas, energy of the incoming molecules, wall material, and surface roughness. The surface roughness plays a significant effect on the TMAC. The TMAC values can vary about 15 % with the surface roughness effect even for the same surface material (Thomas and Lord 1974; Jang and Wereley 2006). However, there are two kinds of controvertible results. On the one hand, Blanchard and Ligrani (2007) designed and performed experiments to measure the TMAC on the walls with different rough surfaces, and found that a smaller value of TMAC is obtained for the rougher surface. A strong dependence of the TMAC on the surface roughness can be seen from Table 15 for both air and helium. Turner et al. (2004) also obtained that the effects of surface roughness on friction factors, accommodation coefficients, and slip velocity are generally insignificant. On the other hand, Chew (2009) summarized the comparison of TMAC measurements from the literature, as listed in Table 16. In the comment, it can be observed obviously that most of the TMACs are significantly below unity, but the TMAC increases above unity for rough surfaces. Sun and Li (2008) verified that the surface roughness often causes the gas molecules colliding with the wall more frequently so that the TMAC increases with the increase of the roughness. Neither the diffusive proportion nor the mass flow rate is influenced by the surface topology (Veltzke and Thoming 2012). Therefore, it is necessary to find a universal measurement method to determine the TMAC with surface roughness effects.
5.6.2 Analytical model
Since it is currently impossible to make a direct measurement of the TMAC, the TMAC value should be inferred by other methods. Barber and Emerson (2002) suggested that the TMAC varies with the Knudsen number based on an analytical model from the experimental observations (Arkilic et al. 2001; Maurer et al. 2003). The analytical model to calculate TMAC should consider the consistent relationship between the slip coefficients and slip models (Agrawal and Prabhu 2008b; Cao et al. 2009).
From the determination of the first-order slip coefficient \( C_{1} \) reviewed in Sect. 4, one can deduce the TMAC using the following formulation:
Maurer et al. (2003) presented a formulation of the TMAC based on the regression analysis method (Arkilic et al. 2001) and gave the determination expression as:
where the slip coefficient \( S \) can be referred to the mass flow rate. Maurer et al. (2003) suggested that it allows reducing the uncertainty on the determination of the TMAC by taking the second-order term into account. Moreover, Eq. (30) is also an appropriate expression for calculating the TMAC from the slip coefficient definition (Sharipov 2011). However, the validity of the existing models should be verified with further works.
Agrawal and Prabhu (2008b) presented the correlation between the TMAC and Knudsen number based on the available data by the following expression:
The equation was chosen to be \( \sigma_{\text{v}} \to 1 \) as \( K_{\text{n}} \to 0 \) and the explanation of the decrease of the TMAC with the increase of Knudsen number was not reported (Agrawal and Prabhu 2008b).
McCormick (2005) estimated the accommodation coefficient as an inverse problem from the experimental data (Siewert 2003) with an iterative method. The accommodation coefficients for the Maxwell one-parameter model and CL two-parameter model are estimated as:
and
To explain the effect of Knudsen number on the TMAC, Fig. 12 shows variation of the TMAC as a function of Knudsen number from different experiment data and analytical results. It can be found that the TMAC varies irregularly and fluctuates near the unity with the change of Knudsen number in the slip and transition flow regimes. Most of the TMAC values are less than unity in the transition flow regime, especially for the analytical results. The TMAC value decreases monotonically with the increasing of Knudsen number from the analytical models presented by Maurer et al. (2003) and Agrawal and Prabhu (2008a, b). However, the TMAC has larger difference between these two methods in the slip flow regime. From the experimental measurements, Gabis et al. (1996) and Maurer et al. (2003) predicted that the TMAC decreases generally with the increase of Knudsen number for helium. Yamamoto et al. (2006) also found the same result for nitrogen. However, the TMAC does not decrease monotonically with increasing Knudsen number for argon (Gabis et al. 1996). Even for the same gas such as air, the TMAC displays different varying trends in the slip and transition flow regimes. Whatever the Knudsen number range and whatever the analytical approach, it can be found that the values of TMAC decrease with the increase of molecular weights of the gas (Graur et al. 2009). The effect of Knudsen number on the TMAC is still not clarified from the literature and should be predicted from the experimental measurements.
5.6.3 Simulation and numerical model
Experimental measurements are specific to some given conditions and not easily applied or extended to new situations in micro- and nanoflows. Some researchers suggested that it has become common practice in numerical modeling and simulation of gas microflows to predict the TMAC (Finger et al. 2007). Various numerical and simulation approaches, such as the MD method (Cao et al. 2005; Kovalev et al. 2011; Barisik and Beskok 2011), DSMC method(Bird 1994; Gallis and Torczynski 2011), LB method (Sbragaglia and Succi 2005; Homayoon et al. 2011), are widely used to model the gas-surface interactions at the wall.
For a given set of gas atoms colliding in a surface, Finger et al. (2007) used the MD simulation model to estimate the TMAC of rarefied gas, and defined the TMAC as:
where N a is the total number of gas atoms, in and fin denote the initial and final values before and after the gas atom collides with a solid surface.
Using the MD simulation model, Cao et al. (2005) and Kovalev et al. (2011) investigated the effect of temperature on the TMAC and found that the TMAC decreases with the increase of temperature following an exponential decay law, and is more sensitive to lower temperatures than to higher ones. Moreover, the adsorbed materials may be in multiple layers and their surface effects should be taken into account (Gad-el-Hak 1999; Finger et al. 2007). Sun and Li (2008) studied the effect of gas adsorption on the TMAC in gas microflows using MD simulations. The gas adsorption can lead to a longer gas-wall interaction time, which will cause the TMAC increasing and reaching the maximum value when an explicit gas layer is formed. MD and DSMC methods can be used to predict the TMAC and model micro- and nanoflows for a wide range of the Knudsen number (Cao et al. 2009). However, the computational cost of these molecular based methods is prohibitively high such that they cannot be widely used for practical fluid flow simulations at the micro- and nanoscales. Although the LB method can be used to simulate gas flows in all regimes upon appropriate adjustments (Sbragaglia and Succi 2005; Homayoon et al. 2011), it needs to be improved and extended to accurately predict the value of TMAC.
It is evident from the above review and discussion that the TMACs are regularly assumed or approximated using different definitions. The reason is that there has no universal methodology which can estimate or predict the TMAC based on the mechanisms involved in the momentum transport for the gas-surface interactions at the wall (Agrawal and Prabhu 2008b; Cao et al. 2009). All of these will prevent the development of reliable modeling of the gas microflows.
6 Conclusions
The slip models have experienced tremendous developments from the original Maxwell’s model and have been widely used to simulate various gas microflow behaviors in the slip flow regime, and even extending the N–S equations into the transition regime.
In this review, we have summarized currently available slip models for modeling isothermal gas microflows through the microfluidic devices in MEMS. Although lacking a universal description of the KL effect on the slip boundary condition, it is essential to capture the KL characteristics using the phenomenological model and physical approach. The slip effect should be considered to make a correction based on the degree of non-equilibrium near the surface. The use of higher-order slip conditions with the N–S constitutive equations can be justified because rarefied flows are dominated by gas-surface interactions at the wall (Barber et al. 2004). Not only gas-surface interaction model but also gas-surface molecular interaction one can be used to describe the boundary condition. It shows that there are significant differences on the values of first-order slip coefficients obtained from whatever theoretical analyses or experimental measurements. In addition, various methods and techniques have been presented to determine the value of the second-order slip coefficient. However, there is no agreement among them and it is very difficult to compare them and to indicate the reliable ones. The large variation in the second-order slip coefficient and the lack of exact expression for the second-order component seem to hinder the extending of the N–S equations for gas microflows. Therefore, new techniques and methods should be developed to accurately measure the mass flow rate, and then to extract the slip coefficient and model for gas microflow studies.
The influences of the effective MFP and viscosity of the gas molecules, surface roughness, gaseous mixture and TMAC on the hybrid slip models for gas microflows are analyzed and discussed in detail. Although different effective MFP and viscosity models are proposed from different viewpoints, they all can be contributed to extend N–S equations for gaseous microflows with higher Knudsen numbers. Furthermore, it indicates that the value of the slip coefficient for a mixture is larger than that for a single gas, which can be applied to optimize the design of the slip boundary condition in gas microflows. The TMAC also governs the degree of slip at the surface, and its value can usually be obtained by comparing the experimental or simulation data of boundary velocities to the solutions of the N–S equations with specified velocity-slip boundary conditions. The review also reports the conflicting results existed in the literature that some predicting the roughness increases TMAC, some predicting the roughness decreases TMAC, and some mentioning the relationship between the roughness and TMAC is more complex. Surface roughness proves to have a dominating influence on the slip and should be appropriately described to investigate its effect on the gas microflows. Furthermore, experimental data within the KL will be very useful for validating the higher-order slip boundary conditions and understanding the gas microflows.
In brief, it is a great challenge to provide accurate data on the velocity slip and allow a precise verification on the validity of the best boundary conditions, as well as on the limits of applicability of the extended N–S equations. Further researches are required to investigate the extensions of current slip coefficients and models for the non-isothermal rarefied gas microflows. Theoretical, numerical and experimental data, both for steady or unsteady rarefied gas microflows, will be provided to reach a good agreement in the future work.
Abbreviations
- AB:
-
Augmented Burnett
- MD:
-
Molecular dynamics
- BE:
-
Boltzmann equation
- MEMS:
-
Microelectromechanical systems
- CL:
-
Cercignani–Lampis
- MFP:
-
Mean free path
- HS:
-
Hard sphere
- N–S:
-
Navier–Stokes
- LBE:
-
Linearized Boltzmann equation
- N–S–F:
-
Navier–Stokes–Fourier
- LBM:
-
Lattice Boltzmann method
- QGD:
-
Quasi-gas dynamic
- BGK:
-
Bhatnagar Gross Krook
- TMAC:
-
Tangential momentum accommodation coefficient
- DSMC:
-
Direct Simulation Monte Carlo
- VHS:
-
Variable hard sphere
- IP:
-
Information preservation
- VSS:
-
Variable soft sphere
- KL:
-
Knudsen layer
- W–M:
-
Weierstrass–Mandelbrot
- a D, \( C_{\text{D}} \) :
-
Constant with positive values
- \( nn \) :
-
Exponent constant
- \( a_{{{\text{R}}1}} \), \( a_{{{\text{R}}2}} \) :
-
Various coefficients
- \( N_{\text{a}} \) :
-
Total number of gas atoms
- \( A_{\text{R}} \), \( D_{\text{R}} \), \( E_{\text{R}} \) :
-
Curve-fitting coefficients
- \( N_{\text{K}} \) :
-
Index of the fluid lattices
- \( b \) :
-
Channel thickness
- p :
-
Pressure
- \( b_{\text{BK}} \) :
-
Generalized slip coefficient
- \( P_{\text{m}} \) :
-
Average pressure
- \( c_{\text{m}} \) :
-
Most probable speed
- \( P_{\text{O}} \) :
-
Outlet pressure
- \( \bar{c} \) :
-
Thermal speed of the gas
- \( P_{\text{r}} \) :
-
Prandtl number
- \( C_{0} \) :
-
Molar concentration
- \( \vec{q} \) :
-
Heat flux
- \( C_{1} \), C 2 :
-
First and second order slip coefficients
- Q N :
-
Non-dimensional flow rate
- C F :
-
Correction factor
- Q v :
-
Volumetric flow rate
- C L :
-
Variable parameter
- r :
-
Traveling distance
- C p, r q :
-
Constants
- \( r_{\text{K}} \) :
-
Fraction of gas particles
- \( C_{{\tilde{y}}} \) :
-
Variable parameter
- \( R_{1} \), \( R_{2} \) :
-
Inner and outer radius
- \( C_{\text{Z}} \) :
-
Variable \( \xi_{\text{s}} /\lambda \)(\( C_{\text{Z}} \in [0,1] \))
- \( R_{\text{a}} \) :
-
Average roughness
- \( d \) :
-
Mean molecular diameter
- \( Re \) :
-
Reynolds number
- \( d_{\text{c}} \) :
-
Collision molecular diameter
- \( R_{\text{P}} \) :
-
Specific gas constant
- \( f \) :
-
Roughness height function
- \( S \) :
-
Slip coefficient function
- \( f_{\text{B}} \) :
-
Distribution function
- \( S_{\text{uy}} \), \( S_{\text{yy}} \) :
-
Relative position and velocity parameters
- \( h_{\text{B}} \) :
-
Small perturbation;
- \( T \) :
-
Absolute temperature
- \( H \) :
-
Film thickness
- T r :
-
Torque
- I :
-
Velocity defect function
- u :
-
Velocity
- k B :
-
Boltzmann constant
- \( \tilde{u} \) :
-
Velocity ratio \( \tilde{u} = u/\alpha_{\text{p}} \lambda \)
- \( K_{\text{M}} \) :
-
Variable parameter
- \( u_{\text{n}} \) :
-
Velocity normal to the wall
- \( Kn \) :
-
Knudsen number
- \( u_{{{\text{N}}1}} \), \( u_{{{\text{N}}2}} \) :
-
Velocity components
- \( Kn_{\text{O}} \) :
-
Knudsen number outlet
- \( u_{\text{s}} \) :
-
Slip velocity
- k s1–k s4 :
-
Constants
- \( \vec{u}_{\text{s}} \) :
-
Tangential slip velocity
- \( k_{\text{u}} \) :
-
Velocity gradient
- \( u_{\text{w}} \) :
-
Wall velocity
- \( l_{\text{c}} \) :
-
Knudsen layer thickness
- \( u_{\lambda } \) :
-
Tangential velocity component
- \( L \) :
-
Channel length
- \( U_{\text{g}} \) :
-
Gas flow velocity
- \( L_{0} \) :
-
Characteristic length
- \( U_{\text{s}} \) :
-
Non-dimensional slip velocity
- \( L_{\text{c}} \) :
-
Local characteristic length
- \( U_{\text{w}} \) :
-
Non-dimensional wall velocity
- \( L_{\text{r}} \) :
-
Inner cylinder length
- \( v_{0} \) :
-
Mixture velocity
- \( L_{\text{s}} \) :
-
Slip length
- \( v_{\text{g}} \) :
-
Kinematic viscosity
- \( L_{\text{x}} \) :
-
Width of the cell
- \( V_{{{\text{g}}1}} \), \( V_{{{\text{g}}2}} \) :
-
Fraction of components
- \( m \) :
-
Molecular mass
- \( V_{\text{t}} \) :
-
Particle information velocity
- \( m_{1} \), \( m_{2} \) :
-
Molecular mass of species
- \( w \) :
-
Channel width
- \( Ma \) :
-
Mach number
- \( x_{t} \) :
-
Coordinate tangential to the wall
- \( n \) :
-
Coordinate normal to the wall
- \( y \) :
-
Distance normal to the wall
- \( n_{01} \), \( n_{02} \) :
-
Equilibrium number densities
- \( \tilde{y} \) :
-
Relative variable \( \tilde{y} = y/\lambda \)
- \( n_{\text{g}} \) :
-
Number density of the gas
- α AC1, α AC2 :
-
Ratio coefficients
- σ v :
-
Tangential momentum accommodation coefficient
- α K :
-
Adjustable coefficient
- ωm, ωG :
-
Constants
- α M :
-
Fraction parameter
- ω M :
-
Interaction parameter
- α p :
-
Applied parameter
- ω r :
-
Angle velocity
- α s :
-
Controversial coefficient
- \( \vartheta_{\text{m}} \) :
-
Variable coefficient
- β M :
-
Interaction parameter
- μ :
-
Gas viscosity (12)
- β T :
-
Difference constant
- μ f :
-
First-order approximation
- θ P, \( \beta_{\text{P}} \) :
-
Random variables
- \( \chi_{\text{M}} \) :
-
Parameter \( \chi_{\text{M}} = n_{02} m_{2} /(n_{01} m_{1} ) \)
- δ :
-
Mean molecular spacing
- ξs :
-
Distance
- \( \delta_{{\tilde{y}}} \) :
-
Variable parameter
- \( \upsilon \) :
-
Collision frequency
- ρ :
-
Gas density
- τ g :
-
Relaxation time
- λ :
-
Mean free path
- τ N :
-
Shear stress
- λ 1, λ 2 :
-
MFP of the binary gas mixtures
- τ w :
-
Wall shear stress
- λ s, λ b :
-
MFP from molecular and boundary scatterings
- \( \vec{\tau } \) :
-
Tangential shear stress
- γ:
-
Ratio of specific heats
- \( \Upphi_{0} \) :
-
Quantity (gas density, pressure or temperature)
- γT :
-
Molecular acceleration
- \( \Upphi \) :
-
Function of Knudsen number
- σ :
-
Standard deviation
- \( \Uptheta \) :
-
Probability density
- σ 22, σ 25, σ 55 :
-
TMAC Coefficients
- ψ:
-
Probability distribution function
- σ L0, σ L1, σ L2 :
-
Variable parameters
- \( \Uppi \) :
-
Pressure ratio
- σ n :
-
Energy accommodation coefficient
- ΔP :
-
Pressure drop
- σ p :
-
Slip coefficient
- ΔU :
-
Velocity drop
- σ T :
-
Thermal accommodation coefficient
- 1st:
-
First-order
- M:
-
Maxwell model
- 2nd:
-
Second-order
- S:
-
Sharipov model
- L:
-
Loyalka model
- c:
-
DSMC cell
- NS:
-
Navier–Stokes
- eff:
-
Effective relations
- r:
-
Reflected gas molecule
- i:
-
Incident gas molecules
- ref:
-
Reference conditions
- in, fin:
-
Initial and final values
- s:
-
Slip boundary condition
- IP:
-
Information preservation
- sm:
-
Smooth surface
- j :
-
The order of the polynomial
- S:
-
Solid wall
- l:
-
Lower plate
- u:
-
Upper plate
- Loc:
-
Local value
References
Agrawal A, Prabhu SV (2008a) Deduction of slip coefficient in slip and transition regimes from existing cylindrical Couette flow data. Exp Therm Fluid Sci 32:991–996
Agrawal A, Prabhu SV (2008b) Survey on measurement of tangential momentum accommodation coefficient. J Vac Sci Technol A 26:634–645
Aidun CK, Clausen JR (2010) Lattice-Boltzmann method for complex flows. Annu Rev Fluid Mech 42:439–472
Albertoni S, Cercignani C, Gotusso L (1963) Numerical evaluation of the slip coefficient. Phys Fluid 6:993–996
Alexander FJ, Garcia AL, Alder BJ (1998) Cell size dependence of transport coefficients in stochastic particle algorithms. Phys Fluid 10:1540–1542
Almqvist A, Lukkassen D, Meidell A, Wall P (2007) New concepts of homogenization applied in rough surface hydrodynamic lubrication. Int J Eng Sci 45:139–154
Ansumali S, Karlin IV, Arcidiacono S, Abbas A, Prasianakis N (2007) Hydrodynamics beyond Navier–Stokes: exact solution to the Lattice Boltzmann hierarchy. Phys Rev Lett 98:124502
Arkilic EB, Schmidt MA, Breuer KS (1997) Gaseous slip flow in microchannels. J Microelectromech Syst 6:167–174
Arkilic EB, Breuer KS, Schmidt MA (2001) Mass flow and tangential momentum accommodation in silicon micromachined channels. J Fluid Mech 437:29–43
Arlemark EJ, Dadzie SK, Reese JM (2010) An extension to the Navier-Stokes equations to incorporate gas molecular collisions with boundaries. ASME J Heat Transf 132:041006
Ascroft NW, Mermin ND (1976) Solid state physics. Saunders College press, Philadelphia
Asproulis N, Drikakis D (2010) Surface roughness effects in micro and nanofluidic devices. J Comput Theoret Nanosci 7:1825–1830
Aubert C, Colin S (2001) High-order boundary conditions for gaseous flows in rectangular microducts. Microscale Thermophys Eng 5:41–54
Badur J, Karcz M, Lemanski M (2011) On the mass and momentum transport in the Navier–Stokes slip layer. Microfluid Nanofluid 11:439–449
Bahrami M, Yovanovich MM, Culham JR (2006) Pressure drop of fully developed laminar flow in rough microtubes. ASME J Fluid Eng 128:632–637
Bahukudumbi P, Beskok A (2003) A phenomenological lubrication model for the entire Knudsen regime. J Micromech Microeng 13:873–884
Bahukudumbi P, Park JH, Beskok A (2003) A unified engineering model for steady and quasi-steady shear-driven gas microflows. Microscale Thermophys Eng 7:291–315
Balakrishnan R (2004) An approach to entropy consistency in second-order hydrodynamic equations. J Fluid Mech 503:201–245
Barber RW, Emerson DR (2002) Numerical simulation of low Reynolds number slip flow past a confined sphere. In: 23rd international symposium on rarefied gas dynamics, Whistler, Canada, Daresbury Laboratory, Daresbury, Warrington, England
Barber RW, Emerson DR (2006) Challenges in modeling gas-phase flow in microchannels: from slip to transition. Heat Transf Eng 27:3–12
Barber RW, Sun Y, Gu XJ, Emerson DR (2004) Isothermal slip flow over curved surfaces. Vaccum 76:73–81
Barisik M, Beskok A (2011) Molecular dynamics simulations of shear-driven gas flows in nano-channels. Microfluid Nanofluid 11:611–622
Baviere R, Gamrat G, Favre-Marinet M, Le Person S (2006) Modelling of laminar flows in rough-wall microchannels. ASME J Fluids Eng 128:734–741
Beskok A (2001) Validation of a new velocity-slip model for separated gas microflows. Num Heat Transfer Part B 40:451–471
Beskok A, Karniadakis GE (1994) Simulation of heat and momentum transfer in complex microgeometries. J Thermophys Heat Transf 8:647–655
Beskok A, Karniadakis GE (1996) Rarefaction and compressibility effects in gas microflows. J Fluid Eng 118:448–456
Beskok A, Karniadakis GE (1999) A model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophys Eng 3:43–77
Bird GA (1994) Molecular gas dynamics and the direct simulation of gas flows. Clarendon Press, Oxford
Blanchard D, Ligrani P (2007) Slip and accommodation coefficients from rarefaction and roughness in rotating microscale disk flows. Phys Fluid 19:063602
Bora CK, Flater EE, Street MD, Redmond JM, Starr MJ, Carpick RW, Plesha ME (2005) Multiscale roughness and modeling of MEMS interfaces. Tribol Lett 19:37–48
Brenner H (2011) Beyond the no-slip boundary condition. Phys Rev E 84:046309
Buscaglia GC, Jai M (2004) Homogenization of the generalized Reynolds equation for ultra-thin gas film and its resolution by FEM. ASME J Tribol 126:547–552
Cao BY, Chen M, Guo ZY (2005) Temperature dependence of the tangential momentum accommodation coefficient for gases. Appl Phys Lett 86:091905
Cao BY, Chen M, Guo ZY (2006) Effect of surface roughness on gas flow in microchannels by molecular dynamics simulation. Inter J Eng Sci 44:927–937
Cao BY, Sun J, Chen M, Guo ZY (2009) Molecular momentum transport at fluid-solid interfaces in MEMS/NEMS: a review. Int J Mol Sci 10:4638–4706
Cercignani C (1969) A variational principle for boundary value problems in kinetic theory. J Stat Phys 1:297–311
Cercignani C (1975) Theory and application of the Boltzmann equation. Scottish Academic Press, Edinburgh
Cercignani C (1988) The Boltzmann equation and its applications. Springer-Verlag, New York
Cercignani C (1990) Mathematical methods in kinetic theory. Plenum, New York
Cercignani C (2000) Rarefied gas dynamics. Cambridge University Press, Cambridge
Cercignani C, Lampis M (1971) Kinetic model for gas-surface interaction. Transp Theory Stat Phys 1:101–114
Cercignani C, Lampis M (1989) Variational calculation of the slip coefficient and the temperature jump for arbitrary gas-surface interactions. In: Rarefied gas dynamics: space related studies, American Institute of Aeronautics and Astronautics, Washington, pp 553–561
Cercignani C, Lorenzani S (2010) Variational derivation of second-order slip coefficients on the basis of the Boltzmann equation for hard-sphere molecules. Phys Fluids 22:062004
Chabloz M, Sasaki Y, Matsuura T, Tsutsumi K (2000) Improvement of sidewall roughness in deep silicon etching. Microsyst Technol 6:86–89
Chapman S, Cowling TG (1970) The mathematical theory of nonuniform gases, 3rd edn. Cambridge University Press, New York
Chen D, Bogy DB (2010) Comparisons of slip-corrected Reynolds lubrication equations for the air bearing film in the head-disk interface of hard disk drives. Tribol Lett 37:191–201
Chen Y, Cheng P (2003) Fractal characterization of wall roughness on pressure drop in microchannels. Int Commun Heat Mass Transf 30:1–11
Chen S, Tian Z (2010) Simulation of thermal micro-flow using lattice Boltzmann method with Langmuir slip model. Inter J Heat Fluid Flow 31:227–235
Chen MD, Lin JW, Lee SC, Chang KM, Li WL (2004) Application of modified molecular gas lubrication equation to the analysis of micromotor bushings. Tribol Int 37:507–513
Chen Y, Zhang C, Shi M, Peterson GP (2009) Role of surface roughness characterized by fractal geometry on laminar flow in microchannels. Phys Rev E 80:026301
Chew AD (2009) Comment on “Survey on measurement of tangential momentum accommodation coefficient” [J Vac Sci Technol A 26, 634 (2008)]. J Vac Sci Technol A 27:591–592
Choi H, Lee D (2008) Computations of gas microflows using pressure correction method with Langmuir slip model. Comput Fluid 37:1309–1319
Colin S (2005) Rarefaction and compressibility effects on steady and transient gas flows in microchannels. Microfluid Nanofluid 1:268–279
Colin S (2012) Gas microflows in the slip flow regime: a critical review on convective heat transfer. ASME J Heat Transf 134:020908
Colin S, Lalonde P, Caen R (2004) Validation of a second-order slip flow model in rectangular microchannels. Heat Transf Eng 25:23–30
Cornubert R, d’Humieres D, Levermore D (1991) A Knudsen layer theory for lattice gases. Physica D 47:241–259
Croce G, Agaro P (2004) Numerical analysis of roughness effect on microtube heat transfer. Superlattices Microstr 35:601–616
Dalibrard AL, Varet DG (2011) Effective boundary condition at a rough surface starting from a slip condition. J Differ Equ 251:3450–3487
Deissler RG (1964) An analysis of second-order slip flow and temperature jump boundary conditions for rarefied gases. Int J Heat Mass Transf 7:681–694
Dongari N, Agrawal A, Agrawal A (2007) Analytical solution of gaseous slip flow in long microchannels. Int J Heat Mass Transf 50:3411–3421
Dongari N, Sambasivam R, Durst F (2009) Extended Navier–Stokes equations and treatments of micro-channel gas flows. J Fluid Sci Tech 4:454–467
Dongari N, Durst F, Chakraborty S (2010) Predicting microscale gas flows and rarefaction effects through extended Navier–Stokes–Fourier equations from phoretic transport considerations. Microfluid Nanofluid 9:831–846
Dongari N, Zhang YH, Reese JM (2011a) Molecular free path distribution in rarefied gases. J Phys D Appl Phys 44:125502
Dongari N, Zhang YH, Reese JM (2011b) Modeling of Knudsen layer effects in micro/nanoscale gas flows. J Fluid Eng 133:071101
Duan Z, Muzychka YS (2008) Effects of corrugated roughness on developed laminar flow in microtubes. ASME J Fluid Eng 130:031102
Duan Z, Muzychka YS (2010) Effects of axial corrugated roughness on low Reynolds number slip flow and continuum flow in microtubes. ASME J Heat Transf 132:041001
Einzel D, Panzer P, Liu M (1990) Boundary condition for fluid flow: curved or rough surfaces. Phys Rev Lett 64:2269
Eu BC, Khayat RE, Billing GD, Nyeland C (1987) Nonlinear transport coefficients and plane Couette flow of a viscous, heat conducting gas between two plates at different temperatures. Can J Phys 65:1090–1103
Ewart T, Perrier P, Graur IA, Meolans JG (2007a) Tangential momentum accommodation in microtube. Microfluid Nanofluid 3:689–695
Ewart T, Perrier P, Graur IA, Meolans JG (2007b) Mass flow rate measurements in a microchannel, from hydrodynamic to near free molecular regimes. J Fluid Mech 584:337–356
Fichman M, Hetsroni G (2005) Viscosity and slip velocity in gas flow in microchannels. Phys Fluid 17:123102
Finger GW, Kapat JS, Bhattacharya A (2007) Molecular dynamics simulation of adsorbent layer effect on tangential momentum accommodation coefficient. ASME J Fluids Eng 129:31–39
Fukui S, Kaneko R (1988) Analysis of ultra-thin gas film lubrication based on linearized Boltzmann equation: first report-derivation of a generalized lubrication equation including thermal creep flow. ASME J Tribol 110:253–262
Fukui S, Kaneko R (1993) Estimation of gas film lubrication effects beneath sliding bushings of micromotors using a Molecular gas film lubrication equation. Wear 168:175–179
Gabis DH, Loyalka SK, Storvick TS (1996) Measurements of the tangential momentum accommodation coefficient in the transition flow regime with a spinning rotor gauge. J Vac Sci Technol A 14:2592–2598
Gad-el-Hak M (1999) The fluid mechanics of microdevices—the Freeman scholar lecture. ASME J Fluid Eng 121:5–33
Gad-el-Hak M (2001) Flow physics in MEMS. Mec Ind 2:313–341
Gad-el-Hak M (2003) Comments on “Critical view on new results in micro-fluid mechanics”. Int J Heat Mass Transf 46:3941–3945
Gad-el-Hak M (2006) Gas and liquid transport at the microscale. Heat Transf Eng 27:13–29
Gallis MA, Torczynski JR (2011) Direct simulation Monte Carlo-based expressions for the gas mass flow rate and pressure profile in a microscale tube. Phys Fluid 24:012005
Gallis MA, Torczynski JR, Rader DJ, Tij M, Santos A (2006) Normal solutions of the Boltzmann equation for highly nonequilibrium Fourier flow and Couette flow. Phys Fluids 18:017104
Galvin JE, Hrenya CM, Wildman RD (2007) On the role of the Knudsen layer in rapid granular flows. J Fluid Mech 585:73–92
Garcia RDM, Siewert CE (2007) The viscous-slip, diffusion-slip, and thermal-creep problems for a binary mixture of rigid spheres described by the linearized Boltzmann equation. Eur J Mech B/Fluid 26:749–778
Garcia RDM, Siewert CE (2010) Viscous-slip, thermal-slip, and temperature-jump coefficients based on the linearized Boltzmann equation (and five kinetic models) with the Cercignani_Lampis boundary condition. Eur J Mech B/Fluid 29:181–191
Gibelli L (2012) Velocity slip coefficients based on the hard-sphere Boltzmann equation. Phys Fluid 24:022001
Graur IA, Meolans JG, Zeitoun DE (2006) Analytical and numerical description for isothermal gas flows in microchannels. Microfluid Nanofluid 2:64–77
Graur IA, Perrier P, Ghozlani W, Meolans JG (2009) Measurements of tangential momentum accommodation coefficient for various gases in plane microchannel. Phys Fluid 21:102004
Gu XJ, Emerson DR (2007) A computational strategy for the regularized 13 moment equations with enhanced wall-boundary conditions. J Comp Phys 225:263–283
Guo Z, Zheng C (2008) Analysis of lattice Boltzmann equation for microscale gas flows: relaxation times, boundary conditions and the Knudsen layer. Int J Comput Fluid Dyn 22:465–473
Guo ZL, Zhao TS, Shi Y (2006) Physical symmetry, spatial accuracy, and relaxation time of the lattice Boltzmann equation for microgas flows. J Appl Phys 99:074903
Guo Z, Shi B, Zhao T, Zheng C (2007a) Discrete effects on boundary conditions for the lattice Boltzmann equation in simulating microscale gas flows. Phys Rev E 76:056704
Guo ZL, Shi BC, Zheng CG (2007b) An extended Navier–Stokes formulation for gas flows in the Knudsen layer near a wall. EPL 80:24001
Guo ZL, Zheng CG, Shi BC (2008) Lattice Boltzmann equation with multiple effective relaxation times for gaseous microscale flow. Phys Rev E 77:036707
Gusarov AV, Smurov I (2002) Gas-dynamic boundary conditions of evaporation and condensation: Numerical analysis of the Knudsen layer. Phys Fluids 14:4242–4255
Hadjiconstantinou NG (2000) Analysis of discretization in the direct simulation Monte Carlo. Phys Fluid 12:2634–2638
Hadjiconstantinou NG (2003) Comment on Cercignani’s second-order slip coefficient. Phys Fluid 15:2352–2354
Hadjiconstantinou NG (2006) The limits of Navier–Stokes theory and kinetic extensions for describing small-scale gaseous hydrodynamics. Phys Fluid 18:111301
Hadjiconstantinou NG, Simek O (2002) Constant-wall-temperature Nusselt number in micro and nano-channels. ASME J Heat Transfer 124:356–364
Hare LO, Lockerby DA, Reese JM, Emerson DR (2007) Near-wall effects in rarefied gas micro-flows: some modern hydrodynamic approaches. Inter J Heat Fluid Flow 28:37–43
Ho CM, Tai YC (1998) Micro-electro-mechanical-systems (MEMS) and fluid flows. Annu Rev Fluid Mech 30:579–612
Homayoon A, Meghdadi Isfahani AH, Shirani E, Ashrafizadeh M (2011) A novel modified lattice Boltzmann method for simulation of gas flows in wide range of Knudsen number. Int Commun Heat Mass Transf 38:827–832
Hossainpour S, Khadem MH (2010) Investigation of fluid flow and heat transfer characteristics of gases in microchannels with consideration of different roughness shapes at slip flow regime. Nanoscale Microscale Thermophys Eng 14:137–151
Hsia YT, Domoto GA (1983) An experimental investigation of molecular rarefaction effects in gas lubricated bearings at ultra-low clearances. ASME J Lubr Technol 105:120–130
Hu Y, Werner C, Li D (2003) Influence of three-dimensional roughness on pressure-driven flow through microchannels. ASME J Fluid Eng 125:871–879
Hwang CC, Fung RF, Yang RF, Weng CI, Li WL (1995) A new modified Reynolds equation for ultra-thin film gas lubrication. IEEE Trans Magn 32:344–347
Ivchenko IN, Loyalka SK, Tompson RV (1997) Slip coefficients for binary gas mixture. J Vac Sci Technol A 15:2375–2381
Jang J, Wereley ST (2006) Effective heights and tangential momentum accommodation coefficients of gaseous slip flows in deep reactive ion etching rectangular microchannels. J Micromech Microeng 16:493–504
Ji Y, Yuan K, Chung JN (2006) Numerical simulation of wall roughness on gaseous flow and heat transfer in a microchannel. Int J Heat Mass Transf 49:1329–1339
Jie D, Diao X, Cheong KB, Yong LK (2000) Navier–Stokes simulations of gas flow in micro devices. J Micromech Microeng 10:372–379
Jin S, Slemrod M (2001) Regularization of the Burnett equations via relaxation. J Stat Phys 103:1009–1033
Karniadakis GE, Beskok A (2002) Micro flows: fundamentals and simulation. Springer, New York
Karniadakis GE, Beskok A, Aluru N (2005) Microflows and nanoflows: fundamentals and simulation. Springer-Verlag, New York
Khadem MH, Shams M, Hossainpour S (2009) Numerical simulation of roughness effects on flow and heat transfer in microchannels at slip flow regime. Int Commun Heat Mass Transf 36:69–77
Kim SH, Pitsch H (2008) Analytic solution for a higher-order lattice Boltzmann method: Slip velocity and Knudsen layer. Phys Rev E 78:016702
Kim HM, Kim D, Kim WT, Chung PS, Jhon MS (2007) Langmuir slip model for air bearing simulation using the Lattice Boltzmann method. IEEE Trans Magnet 43:2244–2246
Kim SH, Pitsch H, Boyd ID (2008) Slip velocity and Knudsen layer in the lattice Boltzmann method for microscale flows. Phys Rev E 77:026704
Kleinstreuer C, Koo J (2004) Computational analysis of wall roughness effects for liquid flow in micro-conduits. ASME J Fluid Eng 126:1–9
Klinc T, Kuscer I (1972) Slip coefficients for general gas-surface interaction. Phys Fluid 15:1018
Koura K, Matsumoto H (1992) Variable soft sphere molecular model for inverse-power-lawor Lennard–Jones potential. Phys Fluid A 4:1083–1085
Kovalev V, Yakunchikov A, Li F (2011) Tangential momentum and thermal accommodation coefficients for hydrogen molecules on graphite surface. Acta Astronaut 69:744–746
Kuhlthau AR (1949) Air friction on rapidly moving surfaces. J Appl Phys 20:217–223
Kunert C, Harting J (2007) Roughness induced boundary slip in microchannel flows. Phys Rev Lett 99:176001
Langmuir I (1933) Surface chemistry. Chem Rev 13:147–191
Li B, Kwok DY (2003) Discrete Boltzmann equation for microfluidics. Phys Rev Lett 90:124502
Li ZX, Du DX, Guo ZY (2000) Characteristics of frictional resistance for gas flow in microtubes. In: Proceedings of symposium on energy engineering in the 21st Century, pp 658–664
Li W-L, Lin J-W, Lee S-C, Chen M-D (2002) Effects of roughness on rarefied gas flow in long microtubes. J Micromech Microeng 12:149–156
Li Q, He YL, Tang GH, Tao WQ (2011) Lattice Boltzmann modeling of microchannel flows in the transition flow regime. Microfluid Nanofluid 10:607–618
Lilley CR, Sader JE (2007) Velocity gradient singularity and structure of the velocity profile in the Knudsen layer according to the Boltzmann equation. Phys Rev E 76:1–4
Lilley CR, Sader JE (2008) Velocity profile in the Knudsen layer according to the Boltzmann equation. Proc R Soc A 464:2015–2035
Lilly TC, Duncan JA, Nothnagel SL, Gimelshein SF, Gimelshein NE, Ketsdever AD, Wysong IJ (2007) Numerical and experimental investigation of microchannel flows with rough surfaces. Phys Fluid 19:106101
Liu CF, Ni YS (2008) The effect of surface roughness on rarefied gas flows by lattice Boltzmann method. Chin Phys B 17:4554–4561
Lockerby DA, Reese JM (2008) On the modelling of isothermal gas flows at the microscale. J Fluid Mech 604:235–261
Lockerby DA, Reese JM, Emerson DR, Barber RW (2004) Velocity boundary condition at solid walls in rarefied gas calculations. Phys Rev E 70:017303
Lockerby DA, Reese JM, Gallis MA (2005a) Capturing the Knudsen layer in continuum-fluid models of nonequilibrium gas flows. AIAA J 43:1391–1393
Lockerby DA, Reese JM, Gallis MA (2005b) The usefulness of higher-order constitutive relations for describing the Knudsen layer. Phys Fluids 17:100609
Lord RG (1991) Some extensions to the Cercignani-Lampis gas-surface scattering kernel. Phys Fluid A: Fluid Dyn 3:706–710
Lord RG (1995) Some further extensions of the Cercignani-Lampis gas-surface interaction model. Phys Fluid 7:1159–1161
Lorenzani S (2011) Higher order slip according to the linearized Boltzmann equation with general boundary conditions. Phil Trans R Soc A 369:2228–2236
Loyalka SK (1969) Thermal transpiration in a cylindrical tube. Phys Fluids 12:2301–2305
Loyalka SK (1971) Approximate method in kinetic theory. Phys Fluid 14:2291–2294
Loyalka SK, Hickey KA (1989a) Plane Poiseuille flow: near continuum results for a rigid sphere gas. Phys A 160:395–410
Loyalka SK, Hickey HA (1989b) Velocity slip and defect: hard sphere gas. Phys Fluids A 1:612–614
Loyalka SK, Petrellis N, Stvorick ST (1975) Some numerical results for the BGK model: thermal creep and viscous slip problems with arbitrary accommodation of the surface. Phys Fluid 18:1094
Marques W, Kremer GM, Sharipov FM (2000) Couette flow with slip and jump boundary conditions. Contin Mech Thermodyn 12:379–386
Maurer J, Tabeling P, Joseph P, Willaime H (2003) Second-order slip laws in microchannels for helium and nitrogen. Phys Fluid 15:2613–2621
Maxwell JC (1879) On stresses in rarified gases arising from inequalities of temperature. Phil Trans Roy Soc 170:231–256
McCormick NG (2005) Gas-surface accommodation coefficients from viscous slip and temperature jump coefficients. Phys Fluid 17:107104
Mcnenly MJ, Gallis MA, Boyd ID (2005) Empirical slip and viscosity performance for microscale gas flow. Int J Numer Meth Fluids 49:1169–1191
Michalis VK, Kalarakis AN, Skouras ED, Burganos VN (2010) Rarefaction effects on gas viscosity in the Knudsen transition regime. Microfluid Nanofluid 9:847–853
Millikan RA (1923) Coefficients of slip in gases and the law of reflection of molecules from the surfaces of solids and liquids. Phys Rev 21:217–238
Mitsuya Y (1993) Modified Reynolds equation for ultra-thin film gas lubrication using 1.5-order slip flow model and considering surface accommodation coefficient. J Trib 115:289–294
Morini GL, Spiga M, Tartarini P (2004) The rarefaction effect on the friction factor of gas flow in microchannels. Superlattices Microstruct 35:587–599
Morini GL, Lorenzini M, Spiga M (2005) A criterion for experimental validation of slip-flow models for incompressible rarefied gases through microchannels. Microfluid Nanofluid 1:190–196
Myong RS (2001) A computational method for Eu’s generalized hydrodynamic equations of rarefied and microscale gas dynamics. J Comput Phys 168:47–72
Myong RS (2004a) Gaseous slip models based on the Langmuir adsorption isotherm. Phys Fluid 16:104–117
Myong RS (2004b) A generalized hydrodynamic computational model for rarefied and microscale diatomic gas flows. J Comput Phys 195:655–676
Myong RS, Reese JM, Barber RW, Emerson DR (2005) Velocity slip in microscale cylindrical Couette flow: the Langmuir model. Phys Fluid 17:087105
Naris S, Valougeorgis D, Sharipov F, Kalempa D (2004) Discrete velocity modelling of gaseous mixture flows in MEMS. Superlattices Microstruct 35:629–643
Neto C, Evans DR, Bonaccurso E, Butt H-J, Craig VSJ (2005) Boundary slip in Newtonian liquids: a review of experimental studies. Rep Prog Phys 68:2859–2897
Ng EY-K, Liu N (2002) Stress-density ratio slip-corrected Reynolds equation for ultra-thin film gas bearing lubrication. Phys Fluids 14:1450–1457
Ng EY-K, Liu N (2005) A multicoefficient slip-corrected Reynolds equation for micro-thin film gas Lubrication. Int J Rotat Mach 2:105–111
Ohwada T, Sone Y, Aoki K (1989) Numerical analysis of the shear and thermal creep flows of a rarefied gas over a plane wall on the basis of the linearized Boltzmann equation for hard sphere molecules. Phys Fluids A 1:1588–1599
Oran ES, Oh CK, Cybyk BZ (1998) Direct Simulation Monte Carlo: recent advances and application. Annu Rev Fluid Mech 30:403–441
Ozalp AA (2008) Roughness induced forced convective laminar-transitional micropipe flow: energy and exergy analysis. Heat Mass Transf 45:31–46
Ozalp AA (2011) Laminar-transitional micropipe flows: energy and exergy mechanisms based on Reynolds number, pipe diameter, surface roughness and wall heat flux. Heat Mass Transf. doi:10.1007/s00231-011-0832-6
Pan LS, Liu GR, Lam KY (1999) Determination of slip coefficient for rarefied gas flows using direct simulation Monte Carlo. J Micromech Microeng 9:89–96
Papadopoulos CI, Nikolakopoulos PG, Kaiktsis L (2011) Evolutionary optimization of micro-thrust bearings with periodic partial trapezoidal surface texturing. ASME J Eng Gas Turbines Power 133:012301
Park JH, Bahukudumbi P, Beskok A (2004) Rarefaction effects on shear driven oscillatory gas flows: a direct simulation Monte Carlo study in the entire Knudsen regime. Phys Fluid 16:317–330
Peng Y, Lu X, Luo J (2004) Nanoscale effect on ultrathin gas film lubrication in hard disk drive. ASME J Tribol 126:347–352
Pitakarnnop J, Varoutis S, Valougeorgis D, Geoffroy S, Baldas L, Colin S (2010) A novel experimental setup for gas microflows. Microfluid Nanofluid 8:57–72
Pollard WG, Present RD (1948) On gaseous self-diffusion in long capillary tubes. Phys Rev 73:762–774
Porodnov BT, Suetin PE, Borisov SF, Akinshin VD (1974) Experimental investigation of rarefied gas flow in different channels. J Fluid Mech 64:417–437
Rawool AS, Mitra SK, Kandlikar SG (2006) Numerical simulation of flow through microchannels with designed roughness. Microfluid Nanofluid 2:215–221
Reese JM, Zheng Y, Lockerby DA (2007) Computing the near-wall region in gas micro and nanofluidics: critical Knudsen layer phenomena. J Comput Theor Nanosci 4:807–813
Roohi E, Darbandi M (2009) Extending the Navier–Stokes solutions to transition regime in two-dimensional micro- and nanochannel flows using information preservation scheme. Phys Fluid 21:082001
Sbragaglia M, Succi S (2005) Analytical calculation of slip flow in lattice Boltzmann models with kinetic boundary conditions. J Phys Fluid 17:093602
Schaaf SA, Chambre PL (1961) Flow of rarefied gases. Princeton University Press, Princeton
Schamberg R (1947) The fundamental differential equations and the boundary conditions for high speed slip-flow, and their application to several specific problems. PhD thesis, California Institute of Technology
Seidl M, Steinheil E (1974) Measurement of momentum accommodation coefficients on surfaces characterized by Auger Spectroscopy. In: Rarefied Gas Dynamics, Ninth International Symposium, Germany, pp E 9.1–E 9.12
Shan X, Yuan X, Chen H (2006) Kinetic theory representation of hydrodynamics: a way beyond the Navier–Stokes equation. J Fluid Mech 550:413–441
Sharipov F (2003) Application of the Cercignani-Lampis scattering kernel to calculations of rarefied gas flows. II. Slip and jump coefficients. Eur J Mech B/Fluid 22:133–143
Sharipov F (2004) Data on the velocity slip and temperature jump coefficients. In: Proceedings of the 5th international conference on thermal and mechanical simulation and experiments in microelectronics and microsystems-EuroSimE, Shaker, Belgium, pp 243–249
Sharipov F (2011) Data on the velocity slip and temperature jump on a gas-solid interface. J Phys Chem Ref Data 40(2):023101
Sharipov F, Kalempa D (2003) Velocity slip and temperature jump coefficients for gaseous mixtures. I. Viscous slip coefficient. Phys Fluid 15:1800–1806
Sharipov F, Seleznev V (1998) Data on internal rarefied gas flows. J Phys Chem Ref Data 27(3):657–706
Shen S, Chen G, Crone RM, Dufresne MA (2007) A kinetic-theory based first order slip boundary condition for gas flow. Phys Fluids 19:086101
Siewert CE (2003) Viscous-slip, thermal-slip, and temperature-jump coefficients as defined by the linearized Boltzmann equation and the Cercignani-Lampis boundary condition. Phys Fluids 15:1696–1701
Siewert CE, Sharipov F (2002) Model equations in rarefied gas dynamics: Viscous-slip and thermal-slip coefficients. Phys Fluid 14:4123–4129
Siewert CE, Valougeorgis D (2004) Concise and accurate solutions to half-space binary-gas flow problems defined by the McCormack model and specular-diffuse wall conditions. Eur J Mech B/Fluid 23:709–726
Sone Y, Takata S, Ohwada T (1990) Numerical analysis of the plane Couette flow of a rarefied gas on the basis of the linearized Boltzmann equation for hard sphere molecules. Eur J Mech B/Fluids 9:273–288
Sreekanth AK (1969) Slip flow through long circular tubes. In: Proceedings of the sixth international symposium on rarefied gas dynamics, Academic, New York, pp 667–676
Stops DW (1970) The mean free path of gas molecules in the transition regime. J Phys D Appl Phys 3:685–696
Struchtrup H, Torrilhon M (2003) Regularization of Grid’s 13 moment equations: derivation and linear analysis. Phys Fluids 15:2668–2680
Struchtrup H, Torrilhon M (2008) Higher-order effects in rarefied channel flows. Phys Rev E 78:046301
Suetin PE, Porodnov BT, Chernjak VG, Borisov SF (1973) Poiseuille flow at arbitrary Knudsen numbers and tangential momentum accommodation. J Fluid Mech 60:581–592
Sun Y, Chan WK (2004) Analytical modeling of rarefied Poiseuille flow in microchannels. J Vac Sci Technol A 22:383–395
Sun H, Faghri M (2003) Effects of surface roughness on nitrogen flow in a microchannel using the direct simulation monte carlo method. Numer Heat Transf A 43:1–8
Sun J, Li ZX (2008) Effect of gas adsorption on momentum accommodation coefficients in microgas flows using molecular dynamic simulations. Molecular Phys 106:2325–2332
Sun Y, Chan WK, Liu N (2002) A slip model with molecular dynamics. J Micromech Microeng 12:316–322
Tang GH, He YL, Tao WQ (2007a) Comparison of gas slip models with solutions of linearized Boltzmann equation and direct simulation of Monte Carlo method. Int J Mod Phys C 18:203–216
Tang GH, Zhuo L, He YL, Tao WQ (2007b) Experimental study of compressibility, roughness and rarefaction influences on microchannel flow. Int J Heat Mass Transf 50:2282–2295
Tang GH, Zhang YH, Emerson DR (2008) Lattice Boltzmann models for nonequilibrium gas flows. Phys Rev E 77:046701
Tekasakul P, Bentz JA, Tompson RV, Loyalka SK (1996) The spinning rotor gauge: measurements of viscosity, velocity slip coefficients, and tangential momentum accommodation coefficients. J Vac Sci Technol A 14:2946–2952
Thomas LB, Lord RG (1974) Comparative measurements of tangential momentum and thermal accommodations on polished and on roughened steel spheres. Proc Int Symp On Rarefied Gas, Dynamics, pp 405–412
To QD, Bercegeay C, Lauriat G, Leonard C, Bonnet G (2010) A slip model for micro/nano gas flows induced by body forces. Microfluid Nanofluid 8:417–422
Turner SE, Lam LC, Faghri M, Gregory OJ (2004) Experimental investigation of gas flow in microchannels. ASME J Heat Transf 126:753
Veijola T, Turowski M (2001) Compact damping models for laterally moving microstructures with gas-rarefaction effects. J Microelectromech Syst 10:263–273
Veltzke T, Thoming J (2012) An analytically predictive model for moderately rarefied gas flow. J Fluid Mech 698:406–422
Wakabayashi M, Ohwada T, Golse F (1996) Numerical analysis of the shear and thermal creep flows of a rarefied gas over the plane wall of a Maxwell-type boundary on the basis of the linearized Boltzmann equation for hard-sphere molecules. Eur J Mech B/Fluids 15:175–201
Wang XQ, Yap C, Mujumdar AS (2005) Effects of two-dimensional roughness in flow in microchannel. ASME J Electron Packag 127:357–361
Watari M (2009) Velocity slip and temperature jump simulations by the three-dimensional thermal finite-difference lattice Boltzmann method. Phys Rev E 79:066706
Watari M (2010) Relationship between accuracy and number of velocity particles of the finite-difference lattice Boltzmann method in velocity slip simulations. ASME J Fluid Eng 132:101401
Weng HC, Chen CK (2008) A challenge in Navier–Stokes-based continuum modeling: Maxwell-Burnett slip law. Phys Fluid 20:106101
Weng CI, Li WL, Hwang CC (1999) Gaseous flow in microtubes at arbitrary Knudsen numbers. Nanotechnology 10:373–379
White J (2010) A gas lubrication equation for high Knudsen number flows and striated rough surfaces. ASME J Tribol 132:021701
Wu L (2008) slip model for rarefied gas flows at arbitrary Knudsen number. Appl Phys Lett 93:253103
Wu L, Bogy DB (2001) A generalized compressible Reynolds lubrication equation with bounded contact pressure. Phys Fluid 13:2237–2244
Wu L, Bogy DB (2003) New first and second order slip models for the compressible Reynolds equation. Trans ASME J Tribol 125:558–561
Xiong R, Chung JN (2010) Investigation of laminar flow in microtubes with random rough surfaces. Microfluid Nanofluid 8:11–20
Xue H, Fan Q (2000) A high order modification on the analytic solution of microchannel gaseous flows. In: Proceeding of ASME fluids engineering division summer meeting, Boston, USA, FEDSM2000-11313
Yamaguchi H, Hanawa T, Yamamoto O, Matsuda Y, Egami Y, Niimi T (2011) Experimental measurement on tangential momentum accommodation coefficient in a single microtube. Microfluid Nanofluid 11:57–64
Yamamoto K, Takeuchi H, Hyakutake T (2006) Characteristics of reflected gas molecules at a solid surface. Phys Fluid 18:046103
Young JB (2011) Calculation of Knudsen layers and jump conditions using the linearised G13 and R13 moment methods. Int J Heat Mass Transf 54:2902–2912
Yudistiawan WP, Ansumali S, Karlin IV (2008) Hydrodynamics beyond Navier–Stokes: the slip flow model. Phys Rev E 78:016705
Zahmatkesh I, Alishahi MM, Emdad H (2011) New velocity-slip and temperature-jump boundary conditions for Navier–Stokes computation of gas mixture flows in microgeometries. Mech Res Commun 38:417–424
Zhang J (2011) Lattice Boltzmann method for microfluidics: models and applications. Microfluid Nanofluid 10:1–28
Zhang WM, Meng G (2009) Property analysis of the rough slider bearings in micromotors for MEMS applications. IEEE/ASME Trans Mechatron 14:465–473
Zhang YH, Gu XJ, Barber RW, Emerson DR (2006a) Capturing Knudsen layer phenomena using a lattice Boltzmann model. Phys Rev E 74:046704
Zhang R, Shan X, Chen H (2006b) Efficient kinetic method for fluid simulation beyond the Navier–Stokes equation. Phys Rev E 74:046703
Zhang WM, Meng G, Zhou JB, Chen JY (2009) Slip model for the molecular gas film lubrication of the slider bearing in a micromotor. Microsys Technol 15:953–961
Zhang HW, Zhang ZQ, Zheng YG, Ye HF (2010a) Corrected second-order slip boundary condition for fluid flows in nanochannels. Phys Rev E 81:066303
Zhang WM, Meng G, Peng ZK (2010b) Random surface roughness effect on slider microbearing lubrication. Micro Nano Lett 5:347–350
Zhang WM, Zhou JB, Meng G (2011) Performance and stability analysis of gas-lubricated journal bearings in MEMS. Tribol Int 44:887–897
Zhang HW, Zhang ZQ, Zheng YG, Ye HF (2012a) Molecular dynamics-based prediction of boundary slip of fluids in nanochannels. Microfluid Nanofluid 12:107–115
Zhang WM, Meng G, Wei KX (2012b) Numerical prediction of surface roughness effect on slip flow in gas-lubricated journal microbearings. Tribol Trans 55:71–76
Zheng Y, Reese JM, Scanlon TJ, Lockerby DA (2006) Scaled Navier-Stokes-Fourier equations for gas flow and heat transfer phenomena in micro- and nanosystems. In: Proceedings of ASME ICNMM2006, June 19–21, Limerick, Ireland 96066
Zhong X, MacCormack RW, Chapman DR (1993) Stabilization of the Burnett equations and application to hypersonic flows. AIAA J 31:1036–1043
Acknowledgments
This work was supported by the National Science Foundation of China under Grant No. 11072147 and the Specialized Research Fund for State Key Laboratory of Mechanical System and Vibration under Grant No. MSVMS201106, and sponsored by Shanghai Rising-Star Program under Grant No. 11QA1403400.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhang, WM., Meng, G. & Wei, X. A review on slip models for gas microflows. Microfluid Nanofluid 13, 845–882 (2012). https://doi.org/10.1007/s10404-012-1012-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10404-012-1012-9