1 Introduction

Rapid advancements in micro and nano fabrication technologies over the past few years have triggered the introduction of intricate small-scale devices in several emerging applications (Karniadakis et al. 2005). The primary distinction between fluid flows in the micro-scale and the conventional devices originates from the pertinent surface area to volume ratios. This profoundly affects the mass, momentum and energy transport; and leads to additional effects like slip flow, rarefaction, etc. in gas flows. In highly rarefied system, deviations from local thermodynamic equilibrium are significant. The extent of this deviation is not merely dictated by the mean free path (λ) in an absolute sense, but also its comparability with the characteristic system length scale (L) that describes the relative importance of rarefaction in the system and the ratio of these two, known as the Knudsen number (Kn = λ/L).

It has commonly been proposed that the no-slip boundary condition may fail to be applicable when the Kn becomes greater than of the order of 10−3, although bulk continuum considerations still appear to hold appropriate within that limit. Experimental investigations by Arkilic et al. (1997), Harley et al. (1995), Maurer et al. (2003) and Ewart et al. (2007) have confirmed that the conventional forms of the Navier–Stokes equations together with the no-slip boundary condition may under-predict the experimentally observed mass flow rates, and the concerned discrepancies tend to become more severe for higher values of the Kn (Maurer et al. 2003; Ewart et al. 2007).

Several authors have theoretically addressed the phenomenon of enhanced mass flow rates by employing the continuum equations in conjunction with the application of the Maxwell slip boundary condition (Maxwell 1879). Identical considerations were also invoked by Smoluchowski for modelling the temperature jump boundary conditions at the walls (Karniadakis et al. 2005). Following the conceptual paradigm of Maxwell slip, Arkilic et al. (1997) obtained analytical expressions for the velocity components and the mass flow rate, which were further verified with their experimental measurements. However, these solutions were constrained to be applicable for infinitesimally small values of the Mach number and Reynolds number, with the Knudsen number being of the order of unity. To avoid the concerned anomalies, researchers subsequently postulated unified high-order slip-based models that are designed to be applicable for a wide range of Knudsen numbers, within the framework of the classical Navier–Stokes equations (Beskok and Karniadakis 1999; Dongari et al. 2007). Recently, Lockerby and Reese (2008) proposed a new model for slip boundary conditions with a near-wall scaling of the Navier–Stokes constitutive relations and obtained more accurate results at higher Knudsen numbers than the conventional second-order slip flow models.

One important inference from the slip models, mentioned as above, is the fact that in an effort to stretch the applicability of these models over a large range of Knudsen numbers, they have typically been closed with several fitting parameters. Such ad-hoc considerations, however, may not be physically complete in nature, since the fluid dynamic interactions occurring over disparate physical scales are intensely coupled with a number of significant thermodynamic criticalities and constraints in a rather complicated and dynamically evolving manner.

Fundamentally, the behaviour of a rarefied gas can be described by the Boltzmann equation (Sone 2002). While directly solving the Boltzmann equation for practical applications remains computationally expensive due to the complicated structure of the molecular collision term, the direct simulation Monte Carlo (DSMC) method (Bird 1994) is an excellent alternative approach for solving high-speed rarefied flows, although the computational cost for low-speed flows in the slip- and transition-flow regimes is still formidable.

The computational expenses associated with molecular simulations have motivated the exploration of alternative extended hydrodynamic models, valid over a wider range of Kn than the conventional NS equations. For many years, various macroscopic modelling and simulation strategies have been developed for capturing non-equilibrium phenomena in the transition regime (Muller and Ruggeri 1993; Struchtrup 2005; Dongari et al. 2009; Gu and Emerson 2009). One important bottleneck toward implementing standard continuum flow models following that notion lies in the fact that the macroscopic properties such as pressure and velocity are to be obtained by averaging over all the particles in an infinitesimal control volume around the point of interest. In the continuum regime, this elemental volume is likely to contain sufficient number of molecules to ensure acceptable continuity and differentiability of these macroscopic properties over space and time. For high Kn cases, however, this number of molecules may be considerably reduced, so that there are insufficient numbers of molecules to give a meaningful average. The values of the predicted macroscopic properties, thus, may fluctuate significantly over space and time. This is by no means a failure of the pertinent conservation considerations, rather the gradient terms in the conservation equations may have failed to capture the important changes in flow properties.

Recently, it has been suggested by several researchers (Öttinger 2005; Brenner 2005; Chakraborty and Durst 2007; Eu 2008; Dadzie et al. 2008) that the constitutive assumption in-built with the standard forms of the Navier–Stokes–Fourier (NSF) equations need to be extended, to render them applicable for fluid flows with strong local gradients of density and temperature. In a strict sense, the concept of continuum is an abstraction that does not exist in reality, because of the presence of discrete material entities (such as molecules) that have empty spaces separating between themselves. Such empty spaces are heavily interlinked with the extent of rarefaction or compression in the system. As a consequence, the presence of strong gradients of density may pose certain ambiguities in mathematically defining the ‘velocity’ of the continuum at a point. In an effort to avoid such ambiguities, one may refer to fluxes, instead of velocities. In that interpretation, the term ‘velocity’ that is commonly employed to describe the conservation of fluid mass (continuity equation) essentially describes a normalized flux density of a system of particles with a fixed mass and identity. With respect to an Eulerian control volume, the same can be interpreted as an advective flux density of mass across an element of the pertinent control surface. Superimposed on this advective flux, one may also have a phoretic or diffusive transport of mass across the control surface, which may be inherently actuated by local gradients of density and/or temperature. Physically, this phoretic flux can be manifested by the Lagrangian velocity of a passive and neutrally buoyant non-Brownian tracer particle introduced into the flow, relative to the advective transport. Because of such phoretic transport of fluid particles, one may have a net phoretic transport of mass across the control surface, without violating the constraining requirements of the conservation of mass from a continuum perspective, in a sense that individual molecules are free to enter and leave a material space with an invariant mass. This additional phoretic transport, however, has by far been grossly neglected in flow modelling of gases over microscopic length scales in an extended continuum limit.

Interestingly, a judicious employment of extended NSF equations is likely to obviate the need for an introduction of the Maxwellian slip boundary condition to explain phenomena such as thermophoresis (Brenner 2005; Brenner and Bielenberg 2005) and the Knudsen paradox (Dongari et al. 2009). Researchers have also demonstrated that the modified continuum conservation equations may yield more satisfactory predictions of the viscous structure of shock waves (Greenshields and Reese 2007) in the Mach number range of 1–11, as compared with the classical NSF based model which is known to fail beyond a Mach number of about 2.

In the present study, we employ extended forms of the NSF equations proposed by Chakraborty and Durst (2007) for modelling micro-scale gas flows over a wide range of Knudsen number. In this approach, the additional terms in the extended governing conservation equations originate through local temperature and density gradients, which implicitly take care of the complexities in the flow physics in a thermo-physically consistent sense, so that no special boundary treatment for rarefied gas flows becomes necessary. Recently, Dongari et al. (2009) employed extended continuum equations together with the effective Knudsen diffusion coefficient to model the isothermal pressure driven micro scale gas flows. Though Dongari et al. (2009) provided good results for the integral flow parameters such as mass flow rate in the transition regime using the Knudsen diffusion modelling, assessment of the correct prediction of field variables (such as cross-sectional velocity and streamwise density profiles) was beyond the scope of their study. Circumventing that limitation, here we obtain rigorous comparisons of velocity profiles with detailed DSMC computations over a wide range of Kn. This includes cases of high speed (Ma ~ 5) micro-scale compressible flows as well. Further, in contrast to the intuitive Knudsen diffusion modelling, we implement here detailed analysis of the geometry dependent effective mean free path based on the probability distribution function of free paths of gas molecules (Stops 1970).

Outline of the remaining part of this article is structured as follows. In Sect. 2, we describe the general forms of the extended NS equations considered in this study, and first present a limiting case with analytical solutions for low Mach number flows. Subsequently, we outline more general procedures for flows with high Mach numbers. In Sect. 3, we summarize the details of the DSMC computation strategies considered in this study, for necessary validation of the predictions from our extended continuum model. In Sect. 4, we present flow predictions for a wide range of Mach numbers, and compare those rigorously with predictions from other commonly used simulation techniques as well as with recently reported experimental data. In Sect. 5, we outline our concluding remarks based on the results of the present study.

2 Governing equations

2.1 Extended Navier–Stokes equations

Chakraborty and Durst (2007) proposed the derivations of the extended forms of the continuum conservation equations for ideal gas flows with heat and mass transfer, from upscaled molecular transport considerations, i.e., fluid particle analysis. According to Landau and Lifshitz (1958), the fluid particle velocity obeying the momentum conservation law is the velocity of a packet of molecular particles in elementary volume, which is sufficiently small in magnitude yet contains a sufficiently large number of molecular particles, so that it can be calculated by means of statistical mechanics if one so wishes. Therefore, a fluid particle in fluid mechanics clearly does not mean a molecular particle. Mathematically, in the fluid dynamics point of view, the fluid velocity is a solution of hydrodynamic equations in fluid mechanics and therefore a field variable like other deterministic hydrodynamic variables. Chakraborty and Durst (2007) proposed that the mean fluid velocity consists of two components; the center-of-gravity velocity of the packet of fluid molecules, which may be identified with the barycentric velocity in the phenomenological theory, and the phoretic (diffusive) contribution of its collective modes relative to the center of gravity, a contribution which does not vanish if there exist density and temperature gradients in the fluid, as follows:

$$ U_{i}^{\text{net}} = U_{i} + u_{i} , $$
(1)

where \( U_{i}^{\text{net}} \) is the mean fluid velocity, U i is the advective component of velocity and u i is the phoretic velocity; see also Eu (2008). It is important to note here that the advective component of velocity (U i ) invariably features in the calculations of the material or total derivatives appearing in the pertinent continuum conservation equations. For example, it does not explicitly appear in the entropy differential in the nonrelativistic local equilibrium assumption except that the time derivatives of thermodynamic variables—substantial time derivatives—are computed in the coordinates moving with the fluid velocity. Therefore, as far as the irreversible thermodynamics formalism is concerned, especially, for pure fluids, it is merely a quantity that can be calculated and known if the hydrodynamic equations, for example, the NSF equations, are appropriately solved. In a strict sense, this is not the true mean fluid velocity, but merely a description of a normalized flux density that advectively transports mass, momentum or energy within the fluid envisaged as a continuum. Superimposed on this advective flux, one can also have the phoretic or diffusive flux across the control surface, which may be actuated by local gradients of density and/or temperature, independent of action of any equivalent macroscopically resolvable imposed pressure gradient. A classical example of phoretic transport is the phenomenon of thermophoresis, in which heat-conducting, force-free and torque-free tracer particles (typically, spherical) move from hotter to colder regions in the fluid (usually, a gas), against an externally imposed temperature gradient, without necessitating the aid of any externally imposed pressure gradient. If the fluid is uniform in space or if the packet of fluid mass is rigid, the phoretic component vanishes.

Based on the local gradient-driven pheoretic transport considerations, Chakraborty and Durst (2007) derived the following extended constitutive forms (in Cartesian index notations) for the phoretic transport mechanisms of mass, momentum flux (shear stress components) and heat flux, respectively (for the salient features of the derivations of the extended model, please refer to the Appendix), augmenting the standard forms of the Navier–Stokes equations:

$$ \rho u_{i} = - \rho D\left[ {{\frac{1}{\rho }}\,{\frac{\partial \rho }{{\partial x_{i} }}} + \frac{1}{2T}{\frac{\partial T}{{\partial x_{i} }}}} \right]. $$
(2)
$$ \begin{aligned} \tau_{ij} & = - \mu \left( {{\frac{{\partial U_{j} }}{{\partial x_{i} }}} + {\frac{{\partial U_{i} }}{{\partial x_{j} }}}} \right) + \frac{2}{3}\mu \delta_{ij} {\frac{{\partial U_{k} }}{{\partial x_{k} }}} - \mu \left( {{\frac{{\partial u_{j} }}{{\partial x_{i} }}} + {\frac{{\partial u_{i} }}{{\partial x_{j} }}}} \right) + \frac{2}{3}\mu \delta_{ij} {\frac{{\partial u_{k} }}{{\partial x_{k} }}} \\ & = - \mu \left( {{\frac{{\partial U_{j}^{\rm net} }}{{\partial x_{i} }}} + {\frac{{\partial U_{i}^{\rm net} }}{{\partial x_{j} }}}} \right) + \frac{2}{3}\mu \delta_{ij} {\frac{{\partial U_{k}^{\rm net} }}{{\partial x_{k} }}}. \\ \end{aligned} $$
(3)
$$ q_{i} = - k\left( {{\frac{\partial T}{{\partial x_{i} }}}} \right) + \rho c_{p} Tu_{i} . $$
(4)

where ρ is the density, P is the pressure, T is the temperature, μ is the viscosity, k is the thermal conductivity, D is the phenomenological coefficient, which for the case of ideal gases, can be described as diffusion coefficient and C p is the specific heat at constant pressure. These equations are derived based on the consideration of ideal gases with Prandtl and Schmidt numbers of unity (satisfying the equation of state: P = ρℜT), so that \( D = \left( {1/3} \right)\bar{u}_{M} \lambda \) and ρD = μ (Bird et al. 1960); \( \bar{u}_{M} \) being the molecular mean velocity. The constitutive forms given by Eqs. 2–4 are consistent with the following conservation equations:

continuity:

$$ {\frac{\partial \rho }{\partial t}} + {\frac{{\partial \left( {\rho U_{i}^{\rm net} } \right)}}{{\partial x_{i} }}} = 0 \Rightarrow {\frac{\partial \rho }{\partial t}} + {\frac{{\partial (\rho U_{i} )}}{{\partial x_{i} }}} = - {\frac{{\partial (\rho u_{i} )}}{{\partial x_{i} }}}, $$
(5)

momentum:

$$ {\frac{{\partial \left( {\rho U_{j} } \right)}}{\partial t}} + {\frac{{\partial (\rho U_{i} U_{j} )}}{{\partial x_{i} }}} = - {\frac{\partial P}{{\partial x_{j} }}} - {\frac{{\partial \tau_{ij} }}{{\partial x_{i} }}}, $$
(6)

energy:

$$ \left( {{\frac{{\partial \left( {\rho C_{v} T} \right)}}{\partial t}} + {\frac{{\partial \left( {\rho C_{v} TU_{i} } \right)}}{{\partial x_{i} }}}} \right) = - {\frac{{\partial q_{i} }}{{\partial x_{i} }}} - \tau_{ij} {\frac{{\partial U_{j} }}{{\partial x_{i} }}} - P{\frac{{\partial U_{j} }}{{\partial x_{j} }}}. $$
(7)

2.2 Analytical model for low Mach number flows

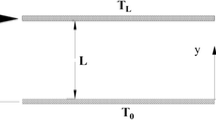
For gaining significant insight into the implications of incorporating the additional terms for phoretic transport in the conservation equations pertinent to gas microflows, we begin with a simple analytical treatment that is approximately valid for low Mach number flows (Ma ≪ 1). For that purpose, we consider gas flow through a rectangular microchannel with the geometrical characteristics as depicted in Fig. 1. Here the channel height h is assumed to be much smaller than the channel width w, so that the fluid essentially sees two infinite parallel plates, separated by a gap h.

Fig. 1
figure 1

Channel geometry, with the system of coordinates

Full size image

The continuity and momentum equations for compressible ideal gas flow can be reduced to the forms given by Eqs. 8 and 9, with the following assumptions:

  1. (a)

    the flow is laminar, steady and locally fully developed in the streamwise direction, so that U 2 = 0 and u 2 = 0;

  2. (b)

    temperature variations may be neglected for low Mach number flows in absence of any other heat source/sink and/or heating/cooling mechanisms, so that the energy equation need not to be solved;

  3. (c)

    the channel is substantially longer in the axial direction as compared with its height, so that the entry and exit effects are negligible;

  4. (d)

    low Reynolds numbers are considered so that the inertial terms may be neglected in the momentum equation;

  5. (e)

    the additional diffusive momentum transport term in the expression for \( \partial \tau_{11} /\partial x_{1} \) can be neglected as compared to that appearing in the term \( \partial \tau_{21} /\partial x_{2} , \) since the ratio between the height and the length of the considered channel is assumed to be very small \( \left( {h/L < < 1} \right); \)

  6. (f)

    volumetric dilation effects are neglected (Bird et al. 1960).

continuity:

$$ {\frac{{\partial \left( {\rho U_{z}^{\text{net}} } \right)}}{\partial z}} = 0, $$
(8)

z-momentum:

$$ 0 = - {\frac{\partial P}{\partial z}} - {\frac{{\partial \tau_{yz} }}{\partial y}}\;{\text{with}}\,\tau_{yz} = - \mu {\frac{{\partial U_{z}^{\text{net}} }}{\partial y}}, $$
(9)

where z ≡ x 1 and y ≡ x 2.

Equation 9, on integration, gives a parabolic profile for the mean fluid velocity. The three coefficients determining the form of the profile may be determined using the relation for the phoretic flux (see Eq. 2), the symmetry of the velocity profile with respect to the centreline, and using Eq. 9. Using Eq. 2, under isothermal conditions, the consequent phoretic velocity may be expressed as:

$$ u_{z} = - \mu \left( {{\frac{1}{{\rho^{2} }}}\,{\frac{{{\text{d}}\rho }}{\text{dz}}}} \right). $$
(10a)

Using the ideal gas law, the above may also be expressed as

$$ u_{z} = - \mu \left( {{\frac{1}{\rho P}}\,{\frac{{{\text{d}}P}}{{{\text{d}}z}}}} \right) $$
(10b)

The mean fluid velocity profile, thus, can be expressed as:

$$ U_{z}^{\rm net} \left( {y,z} \right) = - \left[ {{\frac{1}{\rho }}\,{\frac{{h^{2} }}{2\mu \Re T}}P{\frac{{{\text{d}}P}}{{{\text{d}}z}}}} \right]\left[ {\frac{y}{h} - \left( {\frac{y}{h}} \right)^{2} } \right] - \mu \left( {{\frac{1}{\rho P}}\,{\frac{{{\text{d}}P}}{{{\text{d}}z}}}} \right), $$
(11)

It is important to note that the phoretic transport introduces slip-kind of wall velocity but in a natural way as the phoretic flux only depends on the axial pressure gradient, which is uniform across the channel cross section.

Integrating Eq. 11 over the cross section, one can obtain the net mass flow rate as follows:

$$ \dot{M}_{\text{net}} = w\int\limits_{0}^{H} {\rho U_{z}^{\text{net}} } {\text{d}}y = - {\frac{{wh^{3} }}{24\mu \Re T}}{\frac{{{\text{d}}P^{2} }}{{{\text{d}}z}}} - wh\mu \left( {\frac{1}{P}\,{\frac{{{\text{d}}P}}{{{\text{d}}z}}}} \right). $$
(12)

Since the total mass flow rate is constant along the streamwise direction, one may obtain the analytical solution for the total mass flow rate in terms of inlet (P in) and outlet (P out) pressures of the channel, by integrating Eq. 13 between the limits z = 0 to z = L, as follows:

$$ \dot{M}^{\text{net}} = {\frac{{wh^{3} }}{24\mu \Re TL}}\left( {P_{\text{in}}^{2} - P_{\text{out}}^{2} } \right) + {\frac{wh\mu }{L}}\ln \left( {{\frac{{P_{\text{in}} }}{{P_{\text{out}} }}}} \right). $$
(13)

Dongari et al. (2009) obtained similar expression for mass flow rate and mentioned that the solution is accurate only up to Knudsen number around 0.8 and asymptotically reaches a constant value with decrease in pressure, which is unphysical (refer to Fig. 4 in Dongari et al. 2009). They have addressed this discrepancy by taking into account the Knudsen diffusion phenomenon and the behaviour in the transition regime is deduced through an interpolation scheme. In contrast to the interpolation scheme to model the Knudsen diffusion phenomenon in the transition regime, we provide kinetic theory based geometry dependent effective mean free path approach, which is discussed in detail in the section below.

2.3 Effective mean free path

The molecular mean free path (MFP), which is the average distance a gas molecule travels between consecutive collisions, is central to modelling transport phenomena in ideal gases. The influence of a solid wall on the MFP of the gas molecules can be analyzed in detail by considering the probability of the free path of a gas molecule. It is known from kinetic theory that, for an ideal gas, the free path of a molecule follows a probability distribution function of the form \( p(r) = \lambda^{ - 1} e^{ - r/\lambda } , \) which means that the probability that a given molecule will travel a distance in the range r to r + dr between two successive collisions is p(r)dr. If the gas is not bounded, the MFP of all molecules is just \( \int\nolimits_{0}^{\infty } {Nrp(r)dr/N} = \lambda , \) where N is the total number of gas molecules. If a solid bounding surface is included in the system, however, some molecules will hit the surface and their free flight paths will be terminated. As a result, the MFP of all the molecules in the system will be smaller than λ due to the boundary limiting effect. As an example, we consider a gas bounded by two parallel walls located at y = 0 and y = h, respectively. Considering the molecules within a plane located at 0 < y<h, for those moving toward the wall at y = 0, the MFP is found to be (Stops 1970):

$$ \lambda_{ - } (y) = \lambda \left[ {1 + \left( {\beta - 1} \right)e^{ - \beta } - \beta^{2} E_{i} \left( \beta \right)} \right], $$
(14)

where \( E_{i} \left( \beta \right) = \int\nolimits_{\beta }^{\infty } {y^{ - 1} } \exp \left( { - y} \right){\text{d}}y \) and \( \beta = {\frac{y}{\lambda }}. \)

Similarly for those moving toward the wall at y = h, the MFP can be written as:

$$ \lambda_{ + } (y) = \lambda_{{}} \left[ {1 + \left( {\alpha - 1} \right)e^{ - \alpha } - \alpha^{2} E_{i} \left( \alpha \right)} \right], $$
(15)

where \( E_{i} \left( \alpha \right) = \int\nolimits_{\alpha }^{\infty } {y^{ - 1} } \exp \left( { - y} \right){\text{d}}y \) and \( \alpha = {\frac{h - y}{\lambda }} = \frac{1}{Kn} - \beta . \)

Since a molecule can move toward either of these two walls with the same probability, the local mean free path for all the molecules in the flow domain can be determined by averaging these two parts:

$$ \lambda^{e} (y) = {\frac{{\lambda_{ + } (y) + \lambda_{ - } (y)}}{2}}. $$
(16)

It is well-known from the kinetic theory of gases that viscosity and thermal conductivity can be interpreted in terms of the collisions of gas molecules, and of the free paths which the molecules describe between collisions. The dynamic viscosity of an ideal gas can be expressed in terms of the MFP as (Kennard 1938):

$$ \mu = \frac{1}{3}\rho \bar{u}_{M} \lambda , $$
(17)

where \( \bar{u}_{M} \) is the mean molecular speed. From Eq. 17, the dynamic viscosity for ideal gases is independent of density and remains constant for a given temperature, as the bulk mean free path (λ) is inversely proportional to the density. However, for gas flows at high Knudsen numbers (λ/h > 1), the number of molecule/wall collisions will be increased relative to the molecule/molecule ones, and hence the effective viscosity close to the wall will be reduced due to the wall confinement. The effective viscosity can therefore be expressed as:

$$ \mu^{e} (y) = {\frac{{\mu \lambda^{e} (y)}}{\lambda }}. $$
(18)

If we are interested in the mean value of the effective viscosity, which is averaged over the cross section, the same may be obtained as:

$$ \mu_{m}^{e} = {\frac{\mu }{\lambda h}}\int\limits_{0}^{h} {\lambda^{e} (y)} {\text{d}}y. $$
(19)

In a similar way, other effective thermo-physical transport coefficients, e.g., effective thermal conductivity (k e(y)), etc., can also be obtained.

Using Eqs. 12 and 19, the effective net mass flow rate may be obtained as:

$$ \dot{M}_{e}^{\text{net}} = {\frac{{wh^{3} }}{{24\mu_{m}^{e} \Re TL}}}\left( {P_{\text{in}}^{2} - P_{\text{out}}^{2} } \right) + {\frac{{wh\mu_{m}^{e} }}{L}}\ln \left( {{\frac{{P_{\text{in}} }}{{P_{\text{out}} }}}} \right). $$
(20)

If one integrates Eq. 12 from the limits z = 0 to z = z 1, and including the effective properties, a semi-analytical solution for the pressure variation along the streamwise direction [P(z 1)] can be expressed as follows:

$$ \dot{M}_{e}^{\text{net}} = {\frac{{wh^{3} }}{{24\mu_{m}^{e} \Re T}}}\left( {P_{\text{in}}^{2} - P(z_{1} )^{2} } \right) + wh\mu_{m}^{e} \ln \left( {{\frac{{P_{\text{in}} }}{{P(z_{1} )}}}} \right), $$
(21)

where z 1 varies from 0 to L. If the fluid is uniform in space or if the packet of fluid mass is rigid, the phoretic component vanishes, and using Eqs. 9 and 19 and the no-slip boundary condition, the classical and effective advective component of the mass flow rates can be described as follows:

$$ \dot{M}_{z}^{A} = {\frac{{wh^{3} }}{24\mu \Re TL}}\left( {P_{\text{in}}^{2} - P_{\text{out}}^{2} } \right)\quad {\text{and}} $$
(22a)
$$ \dot{M}_{ez}^{A} = {\frac{{wh^{3} }}{{24\mu_{m}^{e} \Re TL}}}\left( {P_{\text{in}}^{2} - P_{\text{out}}^{2} } \right). $$
(22b)

Applying the continuity equation and the considerations of Kennard (1938) based on net velocity (see Eq. 1), one may express the phoretic mass flux as given below:

$$ \dot{M}_{ez}^{p} = \dot{M}_{e}^{\rm net} - \dot{M}_{ez}^{A} = - wh\mu_{m}^{e} \left( {1/p} \right)({\text{d}}p/{\text{d}}z). $$
(23)

The advective component of the mass flow rate, as given by Eqs. 22a, 22b, is solely driven by the imposed pressure difference between inlet and outlet of the capillary. However, in addition, one may have a phoretic mass transport, which may be solely dictated by the local density gradients prevailing in the system, as mentioned earlier. These density gradients, in turn, may be induced by local pressure gradients, which may originate because of the influence of the global pressure differential that acts across the channel. Accordingly, the externally imposed pressure gradient also induces a phoretic transport, not explicitly but in a rather implicit fashion.

On obtaining the streamwise variation of the pressure and its gradient, the effective mean fluid velocity profile may be computed by using Eqs. 11 and 18. The effective phoretic velocity \( \left[ {u_{e} = \dot{M}_{e}^{p} /\left( {wh\rho } \right)} \right] \) may accordingly be calculated using Eqs. 10b and 18.

2.4 Cases with high Mach number flows

We further consider high speed flows of Nitrogen gas in rectangular microchannels of height 1.5 μm and length of 6 μm. We assume the flow to be steady, laminar, two-dimensional and the fluid to be an ideal gas. In the case of high Mach number flows, we numerically solve the full compressible forms of the extended Navier–Stokes equations. We retain the inertial terms for these cases, since the corresponding Reynolds numbers may be significantly higher than those encountered for the low Mach number cases (Re ~ MaKn). Compressible steady-state Navier–Stokes–Fourier equations, as appropriate for describing such cases, become a mixed set of hyperbolic–elliptic equations which are difficult to solve because of the distinctive numerical techniques required for hyperbolic and elliptic types of equations (Anderson et al. 1984). Hence, unsteady terms are not dropped to solve above set of Eqs. 5–7, as they result in a set of hyperbolic–parabolic equations in time. The steady-state solution is obtained by marching the solution in time until convergence is achieved. For numerical solution of the system of governing transport equations, a finite difference method is employed. The systems of equations are discretized using the modified explicit MacCormack scheme (MacCormack 1971) and the time step is chosen based on the considerations given by MacCormack (1971) and Tannehill et al. (1975). In each time step, first Eqs. 5–7 are solved for ρ, m (m = ρU j ) and E (E = ρC v T). Pressure and phoretic flux are prescribed in terms of density and temperature by using the ideal gas law, in conjunction with Eq. 2. Mass, momentum and energy fluxes are evaluated through ρ, m and E. Subsequently, values of ρ, m and E are corrected through the obtained corresponding new flux estimates. The solution procedure is iterated till the relative error between the two successive iterations falls below 10−4, for all variables. To avoid undesirable under/over shoots in the computational solution, which may originate out of the highly non-linear nature of the governing transport equations, appropriate under-relaxation parameters are introduced for achieving controlled convergence. After reaching the convergence, the solver moves forward to the next time step and returns to the sequence of equations for ρ, m and E.

3 DSMC computations

3.1 Overview

In the DSMC method, the gas flow is modeled by considering the mechano-thermal transport of a system as a collection of discrete particles in the phase space. States of the particles evolve with time as the particles move and collide consistent with the constraints of the boundary conditions in a statistically simulated physical space. Unlike the deterministic molecular dynamics approach, the DSMC approach is based on a stochastic sampling of simulated molecules. The time-step (Δt) of simulation is chosen such that the streaming and collision processes are essentially decoupled during that interval. Given the initial positions and velocity distributions of the particles, they are allowed to evolve dynamically along their trajectories subjected to the boundary interactions. At the end of the time-step, the particles are sorted and their cell locations are rearranged. Subsequently, collision pairs are selected and intermolecular collisions are performed on a probabilistic basis. Flow properties such as velocity and temperature distributions are obtained by sampling the microscopic states of the particles in each computational cell. The linear dimensions of the computational cells are to be taken as substantially smaller than the length scales characterizing the system-scale flow gradients, so that the cell dimensions in the limiting condition approach the local molecular mean free path and the time-steps much less than the local mean collision time.

3.2 Kinetic theory, statistical considerations and computational constraints

One of the fundamental considerations in the DSMC computations is to assess the mean free path (λ) of flow. The traditional method of defining this parameter through a classical hard sphere model (Bird 1986) is somewhat inconsistent, since it yields a constant temperature-exponent of viscosity whereas in real gases the viscosity scales with temperature through an exponent ω that may range in between 0.6 and 0.9. To overcome such constraints, we consider the variable hard sphere (VHS) model in which particles are modelled as variable cross-sectional hard spheres, with the corresponding mean free path given as

$$ \lambda = {\frac{2\mu }{15}}\,{\frac{{\left( {7 - 2\omega } \right)\left( {5 - 2\omega } \right)\left( {2\pi \Re T} \right)^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}{\rho }}. $$
(24)

The mean free path is defined in a reference frame moving with the streaming speed of the gas molecules, and hence is related to the mean molecular thermal speed \( \left( {\overline{{c^{/} }} } \right) \) and the collision frequency (ν) as \( \lambda = \overline{{c^{/} }} /\nu . \) Further, the mean thermal speed is related to the most probable molecular speed \( \left[ {\beta^{ - 1} = \sqrt {2\Re T} } \right] \) as \( \overline{{c^{/} }} = 2/\left( {\sqrt \pi \beta } \right). \) Combining these considerations, the collision frequency may be expressed in terms of the mean free path as

$$ \nu = {\frac{2}{\lambda }}\sqrt {{\frac{2\Re T}{\pi }}} . $$
(25)

The importance of a correct estimation of the collision frequency in the DSMC simulation context lies in the fact that it implicitly dictates an upper limit of the computational time-step \( \left( {\Updelta t < < 1/\nu } \right). \) The choice of the time-step, in turn, determines the number of collision pairs (\( N_{p} \sim \Updelta tN_{c}^{2} /n_{\text{ref}} V_{c} ;V_{c} \) being the volume of a computational cell, N c the number of computational particles in the cell, n ref the number of simulated particles per unit volume or equivalently simulated number density), as well as the probability (p) that two simulated molecules collide amongst themselves over the time interval of Δt. The choice of a lower limit of N c in order to have sufficient numbers of collision pairs that yield consistent solutions is one of the important simulation considerations, which may be made according to the outcome of the rigorous sensitivity tests (Koura 1990; Kaburaki and Yokokawa 1994). As an outcome of these sensitivity tests, the recommended lower limit for N c ranges between 4 to 30.

The collision probability may be estimated in terms of other pertinent parameters as

$$ p = {\frac{{F_{N} \sigma_{\text{T}} c_{\text{r}} \Updelta t}}{{V_{c} }}}. $$
(26)

where c r is the relative speed between the colliding molecules, σ T is the total cross-section, and F N is the number of real molecules represented by each simulated molecule. The full set of collisions may be computed by considering pairs of simulated molecules in a cell at a time with the above collision probability. In order to enhance the simulation performance, only a fraction of these pairs is chosen, so that \( p_{\max } = F_{N} \left( {\sigma_{\text{T}} c_{\text{r}} } \right)_{\max } \Updelta t/V_{c} . \) Following the NTC method (Bird 1994), \( (1/2)N\bar{N}p_{\max } \) numbers of pairs are chosen from the cell at each time-step, where N is the fluctuating part and \( \bar{N} \) is the average of the number of molecules. The collision is then computed with a probability p/p max.

The total number of simulated particles (N tot) in the DSMC computations equals the product of the average number of simulated molecules per cell (N c ) and the total number of cells in the flow-field (C tot). In reality, one of the most challenging tasks in implementing the DSMC simulation strategies lies with an optimal selection of N tot so that it serves as an optimization between the thermo-physical requirements and the computational constraints. On one hand, the cell-size needs to be of the order of the molecular mean free path and on the other hand there should be enough number of simulated particles in each cell to render a statistical sampling appropriate for post-processing the simulated data to a reliable extent in predicting the flow behaviour. For the present simulations, we typically take 20 sampling cells for each μm of linear dimension, with each cell consisting of two collision sub-cells. In a typical array of 300 × 20 sampling cells, the total number of simulated particles is of the order of 105, with nearly 20 particles located in each collision sub-cell (the number of samplings is of the order of 104). Carrying out this computational burden is indeed a prohibitive task for many problems, if not impossible.

3.3 Implementation of boundary conditions

Traditionally, for high-speed flows, the inlet boundary conditions on the number density and free-stream velocity are prescribed from the information of the inlet Mach number, temperature and density. However, in cases of low number densities, this type of boundary treatment may give rise to numerical instabilities. Further, such parameters may not be experimentally well tractable. Hence, for the wide regime of micro-flows considered in this study, a more general boundary treatment may be recommended.

Based on the theory of characteristics (Wang and Li 2004), the inlet velocity boundary condition may be linked through pressure as follows:

$$ \left( {u_{\text{in}} } \right)_{j} = u_{j} + {\frac{{P_{\text{in}} - P_{j} }}{{\rho_{j} a_{j} }}}. $$
(27)

where the subscript j refers to the cell index; u in, P in are, respectively, the axial component of the inlet velocity and pressure; and a refers to the local sonic speed at a section immediately downstream to the inlet. Similarly, for the transverse component of the inlet velocity one may write

$$ \left( {v_{in} } \right)_{j} = v_{j} . $$
(28)

The number density may be obtained from the pressure and temperature information through the equation of state. The particle number fluxes as well as velocity components of the molecules entering the computational domain may be locally determined from the Maxwellian distribution.

For the exit (outflow) boundary, analogous treatments can be applied. For example, for an outflow boundary with direction normal along z, one may write (Liou and Fang 2001)

$$ \left( {\rho_{\text{ex}} } \right)_{j} = \rho_{j} + {\frac{{P_{\text{ex}} - P_{j} }}{{\left( {a_{j} } \right)^{2} }}}. $$
(29)
$$ \left( {u_{\text{ex}} } \right)_{j} = u_{j} + {\frac{{P_{j} - P_{\text{ex}} }}{{\rho_{j} a_{j} }}}. $$
(30)
$$ \left( {v_{ex} } \right)_{j} = v_{j} . $$
(31)
$$ \left( {T_{\text{ex}} } \right)_{j} = {\frac{{P_{\text{ex}} }}{{\rho_{\text{ex}} R}}} $$
(32)

where the subscript ‘ex’ refers to the exit section. Such characteristics-based expressions implicitly assure overall mass balance and aid in computational convergence to physically plausible solutions.

The mean quantities may be expressed in terms of sample-averaged values over simulated molecules as

$$ U_{j} = {\frac{{\sum\nolimits_{j} {u_{j} } }}{{N_{j} }}},V_{j} = {\frac{{\sum\nolimits_{j} {v_{j} } }}{{N_{j} }}}. $$
(33)

where N is the total number of molecules in a cell.

$$ \rho_{j} = n_{j} m. $$
(34)

where m is the molecular mass.

$$ T_{j} = {\frac{{3T_{\text{tr}} + \zeta T_{\text{rot}} }}{3 + \zeta }}. $$
(35)

where ζ is the number of rotational degrees of freedom; T tr and T rot are the translational and rotational temperatures (in K), respectively.

$$ p_{j} = n_{j} k_{B} T_{j} . $$
(36)

where k B is the Boltzmann constant.

Based on the above considerations, the properties of the molecules entering the computational domain may be iteratively updated by invoking the appropriate Maxwellian distribution functions.

It is important to mention here that from a microscopic viewpoint, gas molecules have a random thermal velocity component in addition to the mean molecular flow velocity component. For ultra high-speed flows, the thermal velocity may be negligible as compared to the mean flow velocity. However, for relatively lower flow speeds, the thermal velocities may be of comparable order as the mean molecular flow velocities. Keeping such consequences in consideration, an implicit boundary treatment may be employed for a correct determination of the molecular velocities at the inlet as well as the exit sections. A fundamental basis of such consideration lies in the fact that the number flux, F j of molecules through a cell face of the boundary may be described by the Maxwellian distribution function as

$$ F_{j} = {\frac{{n_{j} }}{2}}\sqrt {{\frac{{2RT_{j} }}{\pi }}} \left[ {\exp \left( { - s_{j}^{2} \cos^{2} \vartheta } \right) + \sqrt \pi s_{j} \cos \vartheta \left\{ {1 + erf\left( {s_{j} \cos \vartheta } \right)} \right\}} \right], $$
(37)

where \( s_{j} = U_{j} /\sqrt {2RT_{j} } ;\vartheta \) is zero for the inlet boundary and π for the exit boundary. The above distribution function may be employed to calculate the number flux of incoming molecules based on the local temperature and mean flow velocity. Following the acceptance-rejection criterion (Fang and Liou 2001), the streamwise thermal velocity component of molecules entering the computational domain is randomly sampled within the interval \( \left[ { - U_{j} ,3C_{\text{mp}} } \right], \) where C mp represents the local most probable thermal speed of the molecules \( \left( {C_{\text{mp}} = \sqrt {2RT_{j} } } \right). \) The resulting streamwise velocity component of the molecules entering the computational domain is accordingly given by

$$ u_{j} = \left( {U_{j} + 3C_{\text{mp}} } \right)R_{\text{f}} . $$
(38)

where R f is a fractional random number. The other components of the thermal velocity may also be analogously obtained from a Mawellian distribution function with an amplitude given by \( \sqrt { - \ln \left( {R_{\text{f}} } \right)} C_{\text{mp}} \) and a phase angle (ϕ) uniformly distributed between 0 and 2π (i.e., ϕ = 2πR f). For the exit boundary, similar conditions do apply with the term C mp replaced by −C mp in Eq. 38. The translational and rotational internal energy components may also be determined (considering diatomic molecules) as e tr = mc 2/2 and e rot = −ln (R f)k B T j ,  where c is molecular speed.

4 Results and discussions

4.1 Low Mach number flows

We first discuss our results corresponding to low Mach number flows (isothermal, pressure-driven), testing the quantitative prediction capabilities of the analytical model developed in this study. In the absence of any experimental data for the velocity profiles, we use DSMC predictions as an independent comparison basis. In addition, we also consider low Knudsen number flows (characteristically belonging to either the slip flow regime or the early transitional regime) for the results discussed in this sub-section, so that effective comparisons with various slip flow models reported in the literature may essentially be made.

Figure 2 depicts the variations in wall-adjacent phoretic velocity components (normalized with repect to the free stream inlet mean flow velocity) as a function of the dimensionless streamwise coordinates along the channel axis. These velocity components are compared with the normalized wall-slip velocities as obtained from DSMC predictions (Karniadakis et al. 2005) as well as those obtained from the first and second-order slip flow models (Arkilic et al. 1997; Dongari et al. 2007), acknowledging the notional analogies between slip velocities and phoretic flux of flow. Knudsen number and Mach number at the outlet are 0.20 and 0.212, respectively. Fundamentally, the non-zero flow velocities in the wall-adjacent layer are triggered in the present model through the additional phoretic transport considerations (under the influences of the local density or pressure gradients) in-built with the extended Navier–Stokes equations, unlike the traditionally used slip-flow based models in which wall-slip effects are diffused through viscous stresses in the wall-adjacent layer in accordance with the slip-based hydrodynamic boundary conditions prescribed at the walls. Interestingly, it is apparent from Fig. 2 that the phoretic velocity components predicted by the present model systematically underpredict the slip velocities obtained from the DSMC solutions in the upstream regions, although these become increasingly more comparable as one proceeds toward further downstream directions. On the other hand, both slip model results are in good agreement with the DSMC data in the upstream region and show deviations in the downstream region. This clearly corroborates the dependency of slip coefficients on the Knudsen number (Sreekanth 1969).

Fig. 2
figure 2

Normalized diffusion velocity variarions along the streamwise direction. Present theoretical results are compared with the DSMC predictions (Karniadakis et al. 2005), as well as predictions from the first and second-order slip flow models. The first-order slip coefficient (C1) is taken as 1 for the first-order slip model (Arkilic et al. 1997). The first (C1) and second (C2) order slip coefficients are, respectively, taken as 1.1466 and 0.14, as postulated by Sreekanth (1969) for the second-order slip flow model (Dongari et al. 2007). Here Pr represents the ratio between inlet and outlet pressures

Full size image

In order to obtain further significant insights on the above trends in theoretical predictions, we subsequently compare the variations in the normalized mass flow rate (S) as a function of Kn, against the first-order (Arkilic et al. 1997) and second-order (Dongari et al. 2007) slip flow model predictions, as shown in Fig. 3. Here the net mass flow rate (Eq. 21) is normalized with the classical advection mass flow rate (Eq. 22a). For substantially low values of Kn, the phoretic velocity components are negligibly small, so that the present model predictions and standard slip model predictions turn out be virtually identical. However, the differences between these model predictions tend to become more ominous with progressively increasing values of Kn within a critical limit of Kn, exhibiting the fact that the phoretic mass flux effects turn out to be slightly less prominent than the advective transport of mass within this regime. Over this regime (Kn < 0.3), the effective viscosity (Eq. 19) decrement with increments in Kn predominate over any other effects, which leads to an augmentation in the rate of advective transport of mass as compared to the rate of phoretic mass transport. On the other hand, beyond this threhold Kn (close to 0.3), the present model predictions tend to approach the higher order slip flow model predictions in an asymptotic sense. This is because of the fact that the phoretic phenomenon becomes significantly more important beyond that critical limit, which augments the predicted phoretic transport velocity considerably. It is also interesting to observe from Fig. 3 that the present model considerations impart significant levels of non-linearities to the Kn dependence of the predicted mass flow rates, unlike the standard slip flow models. This may be attributed to the non-linearities associated with the phoretic component of mass flux.

Fig. 3
figure 3

Normalized mass flow rate (S) variation as a function of Kn in the slip and early transition flow regimes. Dashed line corresponds to the first-order slip model (Arkilic et al. 1997), dash-dotted line to the second-order slip model (Dongari et al. 2007), and the solid line corresponds to the present theory. The slip coefficients are taken as mentioned in the caption of Fig. 3

Full size image

In order to elucidate the strengthened phoretic transport phenomena with progressively increasing Kn beyond a critical Kn limit, we demonstrate Fig. 4, which depicts the normalized velocity profiles along the cross-stream direction for low speed flow of Argon gas in rectangular channels of 2 mm height. Both the wall and the incoming gas temperatures are kept at 273 K. In the same plots, velocity profiles obtained by employing the DSMC method are also presented. One may infer from Fig. 4 that the normalized axial velocity components obtained from the present extended model exhibit good agreements with the corresponding DSMC predictions virtually over the entire transition flow regime (0.5 < Kn < 10). Such confluences may be attributed to the augmented rates of phoretic transport over this regime on account of strengthened Knudsen diffusion, which may be manifested through large phoretic velocity components in the wall-adjacent layer.

Fig. 4
figure 4

Normalized velocity profiles for micro-channel gas flows in the transitional regime (0.5 < Kn < 10). The Kn values referred in Fig. 5 correspond to the average of the inlet and outlet conditions. The mean Mach numbers (Ma) are 0.011, 0.015, 0.064 and 0.128, for a–d, respectively

Full size image

The assessments of the present analytical model, as already demonstrated in Figs. 2, 3, and 4, are somewhat relative in nature, since the velocities or the mass flow rates depicted in these figures have been normalized with respect to suitable reference parameters. Therefore, in an effort to obtain further quantitative assessments of the present model with regard to its predictive capabilities of the absolute values of the net mass flow rates, we also compare our theoretical predictions with the experimental data of Ewart et al. (2007) and the second order slip model (Dongari et al. 2007), encompassing a wide range of Kn (0.03–50). Figure 5a demonstrates the variation of net mass flow rate as a function of composite pressure drop (difference in squares of pressures), for the experimental conditions as reported in Ewart et al. (2007). Except for a few data points, agreements between the present analytical model predictions and the experimental predictions appear to be reasonably good. The second order slip model results deviate from the experimental data for highly rarefied conditions.

Fig. 5
figure 5

a Comparison of mass flow rate as a function of composite pressure drop (difference squares of pressure) against the experimental data (Ewart et al. 2007) and second order slip model (Dongari et al. 2007), for a pressure ratio of 5. b, c Percentage deviations of the theoretical predictions from the experimental data, as a function of the outlet Knudsen number. b Represents percentage deviation between the analytical solutions and the experimental predictions; c represents percentage deviation between the full-scale numerical solution and the experimental predictions. The experimental data are taken from the Table 3 reported in Ewart et al. (2007)

Full size image

For gaining more detailed insights on the percentage deviation of the theoretical predictions from the experimental findings, we plot Fig. 5b. From the figure, it may be observed that the discrepancy between the analytical predictions and the experimental measurements is relatively insignificant in both slip and early transition flow regimes (0.01 < Kn < 0.3). However, these deviations tend to get magnified with further increments in Kn. Such discrepancies may be attributed to the omission of some additional terms in the momentum equation to derive the present analytical model, which are likely to be progressively more significant in the transition flow regime. This may be verified by comparing the percentage deviations of the experimental predictions from the full-scale numerical solutions as obtained from the present theoretical model (see Fig. 5c). Here, Eqs. 5 and 6 are solved numerically, using the considerations given in Sect. 2.3, for isothermal, steady and laminar 2-D compressible flows. This implicitly indicates that full-scale numerical solution may deem to be more appropriate for the transition regime gas flows as compared to the more restricted analytical solutions, both being based on the same extended Navier–Stokes model as outlined in Sect. 2. The relatively larger percentage deviations observed in the free-molecular regime may not represent any systematic trend in the uncertainties in the predictive capabilities of the present model, primarily because of the restricted precision of the mass flow controllers that are employed for experimental studies in low mass flowrate (~10−13 kg/s) regimes. Overall, it is revealed that the average percentage deviation between the experimental results and the present analytical solutions is in the tune of 13%. This deviation is significantly less (~8.3% over the range of 0.01 < Kn < 50, and ~5.9% over the range of 0.01 < Kn < 10) when the full scale numerical solutions are used as references instead of the approximate analytical solutions, as the basis for comparison.

In order to assess the consequences of imposed pressure ratio on the mass flow rate predictions, we refer to Fig. 6. It is known from Knudsen’s (1909) and Gaede’s (1913) experiments in the transition flow regime that there is a minimum in the normalized volumetric flux, which occurs approximately at Kn ~ 1. This is referred as Knudsen paradox in the literature, as the classical NS solutions fail to predict this phenomenon. This behaviour has been rigorously explored by many researchers both theoretically as well as experimentally. In an effort to reveal the underlying consequences in perspective of the present theoretical considerations, we define a normalized volumetric flux, as (Ewart et al. 2007)

$$ {\text{G}} = {\frac{{ - \sqrt {2\Re T} \dot{M}_{e}^{\text{net}} }}{{wh^{2} \left( {{\text{d}}P/{\text{d}}z} \right)}}}. $$
Fig. 6
figure 6

Variation of normalized volume flux (G) as a function of inverse Knudsen number (δ). Triangles correspond to the DSMC data (Karniadakis et al. 2005) and rest of the symbols corresponds to experimental data (Ewart et al. 2007). The dashed line demonstrates the Boltzmann solution (Loyalka 1975) and the solid line represents results from the present theory (analytical solutions)

Full size image

The present theoretical results (analytical), with regard to the variations of G as a function of the inverse Knudsen number \( \left( {\delta \, = \sqrt \pi /(2Kn)} \right), \) are compared with the experimental data (Ewart et al. 2007) for pressure ratio (Pr, ratio of inlet to outlet pressure) values of 3, 4 and 5, as depicted in Fig. 6. This figure also shows the linearized Boltzmann solution (Loyalka 1975), as well as the DSMC predictions (Karniadakis et al. 2005). It interesting to observe that the present analytical solution of G has no dependence on the pressure ratio applied across the channel and the same is also obtained using the Boltzmann equation (Sone 2002). The present theory fair agreement with the experimental data from slip flow to the free-molecular regime (0.01 < Kn < 50), with deviations in the transition flow regime (0.3 < Kn < 1), as evident from Fig. 5b. The linearized Boltzmann solution has fair agreement with the present model as well as the DSMC and the experimental data, up to Kn = 10, which corresponds approximately to the end of the transition flow regime. However, in the limit of high Kn numbers, the flux predicted by the Boltzmann solution increases asymptotically to a value proportional to (1/π)1/2 ln (Kn) (Cercignani et al. 2004), whereas the DSMC approximately approach a constant value. This logarithmic behaviour of the Boltzmann solution is attributed to the degenerate geometry (infinite width) of the two-dimensional channel (Karniadakis et al. 2005). On the other hand, it was experimentally observed (Gaede 1913) that for finite width and long channel gas flows, the volume flux approaches a constant value, which is proportional to ln(L/h). In the free-molecular flow regime, the present model predictions are deviating from the Boltzmann solution and subsequently approach a constant value. Knudsen (1909) also experimentally reported that the normalized volume flux (G) reaches a constant value in the Knudsen regime (Kn → ∞), for rarefied internal flows. Later, it was theoretically shown by Knudsen that in the free-molecular regime, a diffusive mass transport, solely proportional to the pressure gradient but independent of the density, may be observed for pressure-driven isothermal gas flows, leading to a constant value of the normalized volume flux (Q); see Kennard (1938). However, to make reliable and accurate conclusions on the behaviour of G at large Kn (Kn > 100), one needs to have more rigorous experimental and DSMC data for different geometrical cases.

The good agreement of present analytical solutions with other benchmark solutions is achieved without incorporating any kind of adjustable or fitting parameters. This illustrates that the extended Navier–Stokes equations, along with appropriate treatment of phoretic mode of transport in the transition flow regime by taking into account the effective mean free path approach, indeed form a suitable framework to explain details of the micro-channel gas flow physics without explicitly resolving the molecular details.

4.2 High Mach number flows

In this section, we consider high speed flows of Nitrogen gas in rectangular microchannels of height 1.5 μm and length of 6 μm. Both the wall and the incoming gas temperatures are kept at 298 K. Inlet Mach number is specified as 5 and the back pressure is fixed to be atmospheric. The flow is assumed to be laminar, two-dimensional and steady. The upstream and downstream conditions are clearly defined through the Rankine–Hugonoit relations (Greenshields and Reese 2007), with all gradients of flow variables as well as the cross-stream velocity components taken to be zero at the far upstream and far downstream of the chosen computational domain. This condition also aids in achieving a rapid convergence to the steady-state solution. The inlet velocity and density are prescribed, based on the Mach number and the given inlet temperature and the inlet pressure, respectively (using the Rankine–Hugonoit relation). The shock is constrained to be stationary within the computational domain by application of the Rankine–Hugonoit velocity relation at the downstream boundary, as given in Eq. 3 of Greenshields and Reese (2007). The dynamic viscosity and thermal conductivity variations with density and temperature are taken in accordance with the kinetic theory of ideal gases and consistent with the Knudsen diffusion phenomenon. The Prandtl number (P r = k/μC p) is taken as unity for the numerical computations.

Figure 7 depicts the extended Navier–Stokes based predictions of the cross-streamwise velocity profiles at different axial locations (z/h = 0.8, 1.6, 2.4, 3.2, and 4.0), as compared to the DSMC solutions. At z/h = 0.8, the normalized velocity profile assumes virtually a flat shape, portraying the fact that the flow properties are sufficiently close to those corresponding to the channel inlet section. One may notice here that a significant change in the normalized velocity profiles occurs between the axial locations given by z/h = 0.8, 1.6 and 2.4, whereas relatively less differences are observed between the velocity profiles at z/h = 3.2 and 4.0. This implies that a major part of shock layer is confined within the upstream region. In all cases, excellent agreements between the present solutions and the DSMC predictions may be observed.

Fig. 7
figure 7

Velocity profiles at different axial locations of the microchannel and comparisons with DSMC data. Simulation conditions are described in the main text

Full size image

Figure 8a, b depicts the normalized axial velocity component and density variations, respectively, along the channel centerline, corresponding to the DSMC simulation data of Oh et al. (1997). Here, the non-dimensional parameter is defined as \( \left| {{{\left[ {\phi (z) - \min (\phi_{\text{in}} ,\phi_{\text{out}} )} \right]} \mathord{\left/ {\vphantom {{\left[ {\phi (z) - \min (\phi_{\text{in}} ,\phi_{\text{out}} )} \right]} {(\phi_{\text{in}} - \phi_{\text{out}} )}}} \right. \kern-\nulldelimiterspace} {(\phi_{\text{in}} - \phi_{\text{out}} )}}} \right|. \) For detailed descriptions of the simulation parameters, one may refer to Table 1 of Raju and Roy (2003). The shock layer predicted by the extended Navier–Stokes equations produce good agreement with the DSMC data. In effect, the phoretic transport of mass, as triggered by strong local gradients in density and temperature across the shock front, tends to smoothen out the pertinent flow property variations, when addressed through the present extended sets of continuum conservation equations. This also implicitly obviates many numerical instability issues, which are usually encountered with conventional continuum equations associated with the slip/jump boundary conditions for gas flows characterized by Mach numbers greater than 2 (Raju and Roy 2003). Slight discrepancies between the extended continuum predictions and DSMC data may be attributed to the additional ability of the DSMC technique in producing non-Maxwellian velocity distributions that may also differ in directions parallel and perpendicular to the bulk flow. Hydrodynamic models based on extended continuum considerations may not turn out to be precise enough in representing such direction-specific distinctive velocity distributions.

Fig. 8
figure 8

Centerline variations of a axial velocity and b density, with Kn = 0.14 and Ma = 5 at the inlet. Predictions from the solutions obtained from the present extended Navier–Stokes model are compared with DSMC simulation data (Oh et al. 1997)

Full size image

5 Conclusions

Traditional methodologies of analysis for micro-scale gas flows are either based the use of continuum conservation equations coupled with slip/jump based boundary conditions (in the slip flow regime), or are based on the employment of computationally more expensive molecular simulation techniques (in the transition flow). The former approach, though classically established for a long time, involves adjustable fitting parameters to address the non-equilibrium phenomenon in the transition regime flows. The molecular computational techniques, on the other hand, are computationally more involved and are often restricted by several constraints such as computational resources, statistical errors, and poor integrability with the traditional computational fluid dynamics algorithms. It is important to stress that we do not attempt to assess the accuracy of the present physical model underpinning the Boltzmann equation. However, an appropriate extension to the Navier–Stokes–Fourier equations would be less time-consuming and less demanding of computational capacity and our motivation is to compare the predictive capabilities of competing continuum equation sets relative to a more computationally expensive molecular technique.

To bridge the gap between the classical continuum considerations and the underlying molecular transport features, we have introduced here new unified and extended continuum approach that may be applicable for micro-scale gas flows over a wide range of Knudsen number and Mach number. This approach is based on an ‘extended’ version of the NSF equations, by taking the phoretic transport of mass into account, as triggered by the strong local gradients of density and temperature, which is neglected by the Navier–Stokes equations in their traditional forms. We have demonstrated that this approach is capable of capturing the physical details of micro-scale gas flows over a wide range of Knudsen numbers, without necessitating the employment of any slip/jump boundary conditions. Both field variables such as cross-sectional velocity and density profiles and integral flow parameters such as mass flow rate have been rigorously compared with the DSMC data, Boltzmann equation, experimental data and the conventional slip models. Good agreement is obtained in the early and late transition regime flows (0 < Kn < 0.3 and 1 < Kn < 10), with minor deviations in the core transition regime (0.3 < Kn < 1). These deviations are may be due the fact that the exponential distribution function of free paths of gas molecules, which is used to derive effective mean free path expression, is only valid for quasi-equilibrium gas flows. Using non-exponential/non-Gaussian free path probability distribution functions may reduce these deviations in the transition regime.