1 Introduction

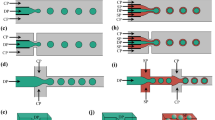
Digital microfluidic devices provide a new technology platform for controlled motion of small fluid volumes (Pollack et al. 2000 2002; Lee et al. 2002; Moon et al. 2002; Cho et al. 2003; Urbanski et al. 2006; Cooney et al. 2006; Fair 2007; Fouillet et al. 2008; Brassard et al. 2008; Abdelgawad and Wheeler 2008 2009; Fan et al. 2009). As it can be seen in Fig. 1, these systems can provide high-speed microdroplet transport on integrated electrode arrays. The generalized nature of these electrode architectures offers versatility, scalability and reconfigurability for numerous biomedical, chemical and sensing applications (Srinivasan et al. 2004; Wheeler et al. 2005; Chang et al. 2006; Moon et al. 2006; Fair et al. 2007; Nichols and Gardeniers 2007; Miller and Wheeler 2008; Sista et al. 2008; Jebrail and Wheeler 2009; Luk and Wheeler 2009; Hua et al. 2010; Malic et al. 2010). Furthermore, the incorporated actuation process being based largely upon electrocapillarity (Berge 1993; Vallet et al. 1996; Pollack et al. 2000; Lee and Kim 2000; Mugele and Baret 2005) between underlying electrodes and conductive liquids can provide high-throughput processing and rapid droplet transport with the rates up to 250 mm/s (Cho et al. 2002).

Fig. 1
figure 1

Microdroplet transport on electrode arrays

Full size image

The structural layout of digital microfluidic devices and the employed electrical activation schemes must be considered together in the design and operation of successful fluid actuation systems (Su et al. 2006; Fair 2007; Bhattacharjee and Najjaran 2010). The physical layout and electrode activation are closely linked, so one must carefully consider the architecture, materials and fluid characteristics in developing the appropriate electrode voltage switching algorithm. Ultimately, the optimal activation scheme will provide rapid droplet transport between neighboring electrodes, while inappropriate control can make continuous droplet motion impossible.

Microfluidic models provide an effective tool for predicting device performance and developing optimal designs. However, the development of such models is far from trivial as many complex physicochemical phenomena become involved in the transport. Driving forces (Baird et al. 2007) are balanced against opposing forces (such as three-phase contact line, shear and drag forces) (Ren et al. 2002; Bahadur and Garimella 2006; Kumari et al. 2008; Ahmadi et al. 2009), while threshold voltage conditions (Ren et al. 2002; Pollack et al. 2000) and saturation phenomena (Vallet et al. 1999) impede the droplet motion at low- and high-actuation voltages, respectively.

Given the above challenges in quantifying the electrical/physical characteristics of digital microfluidic architectures, the most recent microdroplet modeling efforts have treated these phenomena in isolation. Bahadur and Garimella (2006) modeled the dynamics of the microdroplet using an energy-based analysis. In their analytical approach, the size of the microdroplet is restricted to the electrode size, and microdroplet hydrodynamic effects are modeled as a simple one-dimensional flow. Walker et al. (2009) presented a partial differential equation model capable of capturing the evolution of the liquid–gas interface in two dimensions. Hele-Shaw type equations including the relevant boundary phenomena were used to model the fluid dynamics. Ahmadi et al. (2009) later included the effects of the microdroplet internal flow using a computational fluid dynamic (CFD) approach, though effects of electrostatic pressure on the microdroplet motion were not considered. Arzpeyma et al. (2008) considered both electrostatic and hydrodynamic effects in an electrohydrodynamic approach, however, the authors also recognized the limitations of their model in terms of hysteresis effects.

In this study, a novel multiphysics analysis is presented to model the complex physicochemical phenomena influencing the microdroplet motion by way of a pseudo-three-dimensional microdroplet transport model. Electrohydrodynamic governing equations (Zeng and Korsmeyer 2004; Arzpeyma et al. 2008) are numerically solved by way of the finite volume method (FVM) (Lomax et al. 2001) to obtain the electric field, electrostatic and hydrodynamic pressure and velocity distributions. These distributions are then used in a numerical electromechanical analysis to extract the driving and opposing forces. In carrying out this analysis, it is observed that the applied voltage and resulting electrostatic field also change the microdroplet shape via pressure distribution changes inside and outside the microdroplet. This change in the microdroplet–filler interface can then alter the force balance in the system and severely affect the voltage actuation process. Ultimately, it is shown that the coupling of electrostatic and hydrodynamic effects to the constituent microdroplet forces and shapes in this comprehensive model provides an accurate representation of microdroplet transport. Although the ideal behavior of the microdroplet is modeled without considering the saturation, dielectric loss and break down and three-dimensional pinning effects, the results of the model are shown to be in excellent agreement with experimental observations. The proposed pseudo-three-dimensional approach provides an efficient and accurate tool for modelling the microdroplet dynamics which decreases the computation time drastically. In the following sections, the governing equations of microdroplet motion are introduced, and the numerical procedure used for solving these electrohydrodynamic equations is explained. Finally, the results obtained from the model are presented and discussed.

2 Theory

To develop an accurate model for the microdroplet dynamics, the driving and opposing forces must be quantified. The governing transient equation for the microdroplet in the direction of the motion can be written as (Ren et al. 2002)

$$ m {\frac{{\text{d}}v_{\rm transport}}{\hbox{d}t}}=F_{\rm driving}-F_{\rm wall}-F_{\rm filler}-F_{\rm tpcl}, $$
(1)

where m is the mass of the microdroplet, \(v_{\rm transport}\) is the microdroplet transport velocity and \(F_{\rm driving}, F_{\rm wall}, F_{\rm filler} \hbox{ and } F_{\rm tpcl}\) are the driving, wall, filler and three-phase contact line forces, respectively. Accurate estimations for the driving and opposing forces were studied before (Ren et al. 2002; Bahadur and Garimella 2006; Ahmadi et al. 2009), and it has been shown that an accurate estimation of the opposing forces can be achieved if the microdroplet shape is calculated precisely as all the opposing forces depend on the wetted area of the microdroplet (Ahmadi et al. 2009). The electrostatic field outside the microdroplet and the hydrodynamic viscosity inside and outside the microdroplet are two main sources of changing the microdroplet shape, and each effect has been considered separately in the past (Buehrle et al. 2003; Baird et al. 2007; Arzpeyma et al. 2008; Ahmadi et al. 2009). The study presented here extends this study with an integrated methodology for coupling these electrostatic and hydrodynamic effects with the curvature of the microdroplet boundary conditions.

The relation between the electrostatic pressure, hydrodynamic pressure and microdroplet surface curvature can be expressed as (Zeng and Korsmeyer 2004)

$$ [[p_{\rm el}]]{\mathbf{n}}-[[p_{\rm hyd}]]{\mathbf{n}}=\gamma_{\rm df} (\varvec{\nabla}\cdot {\mathbf{n}}){\mathbf{n}}, $$
(2)

where \([[p_{\rm el}]]\) and \([[p_{\rm hyd}]]\) are the respective electrostatic and hydrodynamic pressure changes across the droplet–filler interface, \(\mathbf{n}\) is the normal unit vector to the interface and \(\gamma_{\rm df}\) is the droplet–filler surface tension. This discontinuity equation can be simplified by noting that the surface force density of electric origin must have no shearing component. The pressure and surface tension contributions are therefore normal to the interface (Kang 2002; Jones 2005). The curvature of the interface can then be extracted from Eq. 2 by determining the electrostatic pressure from the electric potential and field in the system and by determining the hydrodynamic pressure from Navier–Stokes and continuity equations inside the microdroplet and the filler.

The first step in solving Eq. 2 involves the determination of the electrostatic pressure from the electric potential and field outside the microdroplet by way of

$$ p_{\rm el}={\frac{\epsilon |{\mathbf{E}}|^2}{2}}, $$
(3)

where \(\epsilon\) is the permittivity of the filler and \(\mathbf{E}\) is the electric field vector at the interface. The electric field is obtained by solving the Maxwell equation (Buehrle et al. 2003)

$$ \varvec{\nabla}\cdot {\mathbf{D}}=\varvec{\nabla} \cdot(\epsilon {\mathbf{E}})=\varvec{\nabla}\cdot(-\epsilon \varvec{\nabla}{\Upphi})=0, $$
(4)

where \(\mathbf{D}\) is the electric displacement field vector. Note that Eq. 4 must be solved in three material regions: dielectric layers, filler and microdroplet interior.

The second step in solving Eq. 2 involves the solution of continuity and Navier–Stokes governing equations for the hydrodynamic pressure. The continuity equation for incompressible flow is

$$ \varvec{\nabla}\cdot {\mathbf{v}}=0, $$
(5)

where \(\mathbf{v}\) is the velocity vector of the fluid particles. The Navier–Stokes equation for the motion of the fluid is

$$ \rho [\partial_t{\mathbf{v}}+({\mathbf{v}}\cdot\varvec{\nabla}){\mathbf{v}}] =-\varvec{\nabla} p_{\rm hyd}+\mu \nabla^2 {\mathbf{v}}+\rho {\mathbf{g}}+\rho_{\rm f} {\mathbf{E}}, $$
(6)

where ρ and μ are the fluid density and viscosity, \(\mathbf{g}\) is the gravitational acceleration (which is ignored in this digital microfluidic analysis as the Bond number is smaller than 1; Arzpeyma et al. 2008), and \(\rho_{\rm f}\) is the free charge density. Since the Navier–Stokes equation is solved inside the conductive liquid microdroplet and a dielectric filler fluid, the last term of Eq. 6 vanishes. While both the velocity and hydrodynamic pressure of the fluid are unknown, it has been shown (Lomax et al. 2001) that the continuity Eq. 5 and Navier–Stokes equation 6 can be solved simultaneously using the numerical FVM.

It is important to note that the microdroplet transport velocity, \(v_{\rm transport},\) must be known for implementing accurate boundary conditions to Eqs. 5 and 6. A dilemma arises here as, in calculating the transport velocity from Eq. 1, Eqs. 5 and 6 have to be solved first to find the accurate shear forces acting on the microdroplet, \(F_{\rm wall}.\) With this in mind, a new iterative numerical procedure is proposed here for solving the hydrodynamic Eqs. 5 and 6 and electrostatic Eq. 4 and linking these solutions to the transport described by Eq. 1. In the proposed iterative algorithm, at each time step, the Navier–Stokes and Maxwell equations are numerically solved simultaneously using the FVM. As a result, the electrostatic and hydrodynamic pressures, and hence the shape of the microdroplet for the next time step, are calculated. By knowing the new shape, the actuation and opposing forces are then calculated accurately, and Eq. 1 is solved to find the transient velocity of the microdroplet. Finally, the transient velocity is used in a method based on the volume of fluid (VOF) method to model the moving boundary of the microdroplet. The algorithm used for these analyses is shown in Fig. 2, and the details of the numerical algorithm for coupling of the hydrodynamic and electrostatic equations are given in the following section.

Fig. 2
figure 2

The flowchart of the proposed numerical algorithm

Full size image

3 Methodology

In this section, the numerical procedure used for solving the overall electrohydrodynamic equations is explained. The FVM is used here to solve the electrostatic and hydrodynamic governing equations numerically by expressing the partial differential equations (PDEs) in volume integral form. Discretization is based on the evaluation of volume integrals over small control volumes, and the overall solution is represented by control volume averages.

It has been shown before (Ahmadi et al. 2009; Lu et al. 2008) that velocity fields inside the microdroplet deviate from the parabolic assumption used in most recent modeling efforts (Bahadur and Garimella 2006; Walker et al. 2009). As it is shown in Fig. 3, although significant recirculation has been observed near the microdroplet interface, streamlines are parallel far from the interfaces (Lu et al. 2008). Therefore, a pseudo-three-dimensional approach (Ahmadi et al. 2009) is employed in this study (see Fig. 4), and a standard two-dimensional grid is used for the FVM solution of the equations in the meridian plane (cross section A-A in Fig. 3). Governing equations are solved in the meridian plane, and the microdroplet is analyzed as a collection of planes parallel to this meridian plane. This analysis is carried out in dimensionless form such that the solution for the meridian plane can be extended to all the planes.

Fig. 3
figure 3

It is shown that although significant recirculation has been observed near the microdroplet interface, streamlines are parallel far from the interfaces

Full size image
Fig. 4
figure 4

The discretized regions of the digital microfluidic system are shown: microdroplet (region 1), filler (region 2), and dielectric layers (region 3). Black circles show the center of each cell and the dashed lines show the borders of each cell

Full size image

3.1 Electrostatics

3.1.1 Driving force

In this study, an electromechanical approach (Zeng and Korsmeyer 2004; Arzpeyma et al. 2008) is used to calculate the horizontal force acting on the microdroplet interface. A volume integral form of the Maxwell equation 4 can then be written as

$$ \int\limits_{\rm CV}\varvec{\nabla}\cdot {\mathbf{D}} \hbox{ d}v=\oint\limits_{\partial {\rm CV}}{\mathbf{D}}\cdot{\mathbf{n}} \hbox{ d}s=0, $$
(7)

where CV represents the control volume and \(\partial {\hbox{CV}}\) represents the control volume cell boundary. The divergence theorem allows the volume integral within the interior to be performed as a surface integral over the control volume cell boundary.

The implementation of Eq. 7 is shown in Fig. 5, and this equation can be written in discrete form for the control volume cell (i, j) as

$$ \begin{aligned} \oint\limits_{\partial{\rm CV}_{(i,j)}}{\mathbf{D}}\cdot{\mathbf{n}} \hbox{ d}s\,&= {\mathbf{D}}_{{(i+{\frac{1}{2}},j)}}\cdot{\mathbf{n}}_{{i+{\frac{1}{2}},j}}{\Updelta}y (1)\\ &\quad+{\mathbf{D}}_{{(i-{\frac{1}{2}},j)}}\cdot{\mathbf{n}}_{{i-{\frac{1}{2}},j}}{\Updelta}y (1)\\ &\quad+ {\mathbf{D}}_{{(i,j+{\frac{1}{2}})}}\cdot{\mathbf{n}}_{{i,j+{\frac{1}{2}}}}{\Updelta}x (1)\\ &\quad+{\mathbf{D}}_{{(i,j-{\frac{1}{2}})}}\cdot{\mathbf{n}}_{{i,j-{\frac{1}{2}}}}{\Updelta}x (1),\\ \end{aligned} $$
(8)

where \({\Updelta}x\) and \({\Updelta}y\) are the dimensions of the control volumes in the x and y directions. Since the electric displacement vector, \(\mathbf{D},\) has two components, \((D_x,D_y),\) and the normal vectors are oriented either horizontal or vertical, Eq. 8 can be written as

$$ D_{x,{(i+1/2,j)}}{\Updelta}y-D_{x,{(i-1/2,j)}}{\Updelta}y-D_{y,{(i,j-1/2)}}{\Updelta}y+D_{y,{(i,j+1/2)}}{\Updelta}y=0. $$
(9)

Equation 9 expresses the Maxwell equation for the cell (i, j) in terms of the electric displacements at the boundaries of the cell. The electric displacement can then be written as the electric field gradient as

$$ {\mathbf{D}}=(D_x,D_y)=\epsilon (E_x,E_y)=-\epsilon\left({\frac{\partial {\Upphi}}{\partial x}}, {\frac{\partial {\Upphi}}{\partial y}}\right), $$
(10)

where E x and E y are the x- and y-components of the electric field, respectively. Using Eq. 10, Eq. 9 can be written as

$$ \begin{aligned} & [ \epsilon_{{(i+1/2,j)}}\beta+\epsilon_{{(i-1/2,j)}}\beta+\epsilon_{{(i,j+1/2)}}+\epsilon_{(i,j-1/2)}] {\Upphi}_{(i,j)}\\ &\quad -\epsilon_{{(i+1/2,j)}}\beta{\Upphi}_{{(i+1,j)}}\\ &\quad -\epsilon_{{(i,j+1/2)}} {\Upphi}_{{(i,j+1)}}\\ &\quad -\epsilon_{{(i-1/2,j)}}\beta {\Upphi}_{{(i-1,j)}}\\ &\quad -\epsilon_{(i,j-1/2)}{\Upphi}_{{(i,j-1)}}=0,\\ \end{aligned} $$
(11)

where \(\beta={\frac{{\Updelta}y}{{\Updelta}x}},\) and \(\epsilon_{{(i+1/2,j)}},\) \(\epsilon_{{(i-1/2,j)}},\) \(\epsilon_{{(i,j+1/2)}}\) and \(\epsilon_{(i,j-1/2)}\) are the permittivities at the boundaries of the cell (i,j). There are three distinct permittivity regions in the overall system, and for sufficiently small cells, two distinct permittivity regions within cells along the microdroplet–filler interface. It should be noted that the mesh size is adjusted in a way that the cells at the microdroplet–solid and filler–solid interfaces contain one phase. Acquiring the permittivity values for interface cells is therefore a non-trivial task. A method based on the fractional VOF (Afkhami and Bussmann 2008; Arzpeyma et al. 2008) is developed here, and this method is shown in Fig. 6. The VOF method is based on the averaging phases at the interface, in which the volume fraction, f, is advected with the fluid flow. The volume fraction, f, for each cell is defined as

$$ f={\frac{V_{\rm liq}}{V_{\rm cell}}}, $$
(12)

where \(V_{\rm liq}\) and \(V_{\rm cell}\) are the liquid volume and total cell volume, respectively. Using the volume fraction, the permitivity of each interphase cell can be calculated as

$$ \epsilon_{(i,j)}=f{{(i,j)}}\epsilon_{\rm {microdroplet}}+(1-f{{(i,j)}})\epsilon_{\rm filler}, $$
(23)

where \(f{{(i,j)}}\) is the volume fraction of cell \({{(i,j)}}\) and \(\epsilon_{\rm microdroplet}\) and \(\epsilon_{\rm filler}\) are the microdroplet and filler permitivities, respectively.

Fig. 5
figure 5

The implementation of Eq. 7 is shown. The electric displacement vector, \(\mathbf{D},\) has two components, \((D_x,D_y),\) and the normal vectors are oriented either horizontal or vertical

Full size image
Fig. 6
figure 6

The concept of fractional VOF is shown. This method is based on averaging of phases at the interface, in which the volume fraction, f, is advected with the fluid flow

Full size image

Finally, Eq. 11 is solved using the Gauss–Seidel approach, and the electric potential, \({\Upphi},\) is found in all the regions. To accelerate the iterative procedure, Successive Overealaxation by Lines (SLOR) (Lomax et al. 2001) is implemented. An implicit Neumann boundary condition is therefore used. The electric potential at the actuated electrode is \({\Upphi}=V_{\rm {applied}},\) and the other electrodes are grounded.

After finding the electrostatic potential, \({\Upphi},\) the electric field and electrostatic pressure, \(p_{\rm el},\) can be found at the cells adjacent to the microdroplet–filler interface. This electrostatic pressure distribution is used to determine both the curvature of the interface and the driving force, \(F_{\rm {driving}},\) acting on the microdroplet.

To gain the curvature and driving force, the electric field is first calculated for the cells adjacent to the interface by way of the equation

$$ \begin{aligned} {\mathbf{E}}_{(i,j)}=({E}_{x,{(i,j)}},{E}_{y,{(i,j)}}) &=-\left({\frac{\partial{\Upphi}_{(i,j)}} {\partial x}},{\frac{\partial {\Upphi}_{(i,j)}}{\partial y}}\right)\\&= \left({\frac{{\Upphi}_{(i,j)}-{\Upphi}_{(i+1,j)}}{{\Updelta}x}},{\frac{{\Upphi}_{(i,j)}-{\Upphi}_{{(i,j+1)}}}{{\Updelta}y}}\right).\\ \end{aligned} $$
(14)

With this, the electrostatic pressure can now be calculated for these cells as

$$ p_{\rm el (i,j)}= {\frac{\epsilon |{\mathbf{E}}_{(i,j)}|^2}{2}}, $$
(15)

and the driving force can be calculated by integrating the electrostatic pressure along the interface (Kang 2002; Baird et al. 2007). The force element acting on one cell is therefore

$$ {\Updelta}F_{(i,j)}=p_{\rm el (i,j)}{\Updelta}A_{(i,j)}, $$
(16)

where \(F_{(i,j)}\) is the force acting on the interface. As it is shown in Fig. 7, this force is perpendicular to the surface element area \({\Updelta}A_{(i,j)}.\) Thus, considering the direction of the interface, the horizontal component of the force can be written as

$$ {\Updelta} F_{x,{{(i,j)}}}=p_{{\rm el} (i,j)}{\Updelta}A_{(i,j)}\sin(\theta_{(i,j)}), $$
(17)

where \(\theta_{(i,j)}\) is the angle of interface at the point of interest. It should be noted that the effetcs of the vertical component of the electrostatic force on the microdroplet dynamics are neglected here. Although it has been shown before that electric field (force) is singular at three-phase contact line (Thamida and Chang 2002), electrostatic pressure is integrable along the interface as

$$ F_{x,{\rm {interface}}}=\sum_jp_{{\rm el} (i,j)}{\Updelta}A_{(i,j)}\sin(\theta_{(i,j)}). $$
(18)

Finally, the total horizontal driving force will be sum of the forces acting on the advancing and receding faces given as

$$ F_{\rm driving, meridian}=F_{x,{\rm advancing}}-F_{x,{\rm receding}}. $$
(19)

This force is summed over planes parallel to the the meridian plane to give the total driving force.

Fig. 7
figure 7

Direction of the electrostatic force acting on the microdroplet interface is shown

Full size image

3.1.2 Threshold condition

It has been shown before that there exists a threshold force caused by pinning and hysteresis which prevents droplet motion prior to sufficient applied voltage (Gao and McCarthy 2006). However, implementing the threshold condition to the proposed algorithm is not a trivial task. Most of the recent modeling efforts suggest to subtract a constant threshold force from the driving force (Ren et al. 2002; Kumari et al. 2008; Bahadur and Garimella 2006; Ahmadi et al. 2009). However, since the threshold force cannot be greater than the driving force, subtracting a constant threshold force leads to inaccurate results. Therefore, in this article the hysteresis condition is implemented by considering an effective voltage as

$$ V_{\rm eff}=\sqrt{V_{\rm app}^2-V_{\rm tr}^2 }, $$
(20)

where \(V_{\rm eff}\) and \(V_{\rm tr}\) are the effective and the threshold voltage, respectively.

3.2 Hydrodynamics

The incompressible Navier–Stokes equations defined in Eq. 6 are a coupled system of non-linear elliptic PDEs. Similarly, the continuity equation defined in Eq. 5 is not an evolution equation but a partial differential constraint on the velocity field. Given these governing equations, the finite volume mesh for the electrostatic solution is also used to solve the hydrodynamics equation.

In our analysis, an artificial compressibility method (Lomax et al. 2001) is used to couple the continuity equation more tightly to the momentum equations which allows us to advance pressure and velocity in time together. The artificial compressibility method adds a physical time derivative of pressure to the continuity equation. This derivative is scaled by a parameter that effectively sets the pseudo-compressibility of the fluid. The artificial compressibility value is chosen according to the mesh size and over/under realaxation parameter to accelarate the convergence of the procedure. The details of the numerical procedure is beyond the scope of this article and can be found elsewhere (Ahmadi et al. 2009; Lomax et al. 2001).

The boundary condition used for the microdroplet and filler along the solid surfaces are the no-slip, no-penetration and zero pressure gradient condition. The microdroplet–filler interface is moving with the microdroplet transport velocity, \(v_{\rm transport},\) and is implemented by defining fictitious velocities within solid cells adjacent to fluid cells (Bussmann et al. 1999). As can be seen in Fig. 8, a method based on the VOF method can be used for modeling the moving boundary of the microdroplet. The main idea for the implementation is that the microdroplet–filler interface is moving with the transport velocity of the microdroplet, and in each time step the volume fraction of each cell, f, is updated according to the motion of the boundaries. This volume fraction of the cells must satisfy the advection equation

$$ [\partial_tf+v_{\rm transport}\partial_xf]=0. $$
(21)

Equations 5 and 6 are solved numerically, and the hydrodynamic pressure and velocity distributions are found. Using the volume fraction of each cell, density and viscosity of each cell are defined as

$$ \rho_{(i,j)}=f{(i,j)}\rho_{\rm microdroplet}+(1-f{(i,j)})\rho_{\rm filler} $$
(22)

and

$$ \mu_{(i,j)}=f{(i,j)}\mu_{\rm microdroplet}+(1-f{(i,j)})\mu_{\rm filler}, $$
(23)

where \(\rho_{\rm microdroplet}\) and \(\rho_{\rm filler}\) are the microdroplet and filler densities, and \(\mu_{\rm microdroplet}\) and \(\mu_{\rm filler}\) are the microdroplet and filler viscosities, respectively. After solving Eqs. 5 and 6, the velocity vector inside the microdroplet is then used to find the shear force on the wall \((F_{\rm wall})\) as

$$ {F}_{\rm wall}=\int\limits_{\rm walls}\tau \hbox{ d}A, $$
(24)

where τ is the shear stress.

Fig. 8
figure 8

The updating process for the advancing interface shape is shown. The volume fraction of each cell, f, is updated according to the motion of the boundaries

Full size image

3.3 Electrohydrodynamics

After finding the electrostatic and hydrodynamic pressures, Eq. 2 can be used to find the curvature of the advancing and receding surfaces. For conductive liquids, the electrostatic pressure inside the microdroplet is zero. Thus, as it is shown in Fig. 9, Eq. 2 (for the advancing face) becomes

$$ \begin{aligned} p_{{\rm el},{(i+1,j)}}&+p_{{\rm hyd},{(i+1,j)}}-p_{{\rm hyd},{(i-1,j)}}=\gamma_{\rm df}\left({\frac{1}{r}}+{\frac{1}{R}}\right)=\gamma_{\rm df}\left({\frac{{\text{d}}^2x_{{\rm interface},{(i,j)}}}{\hbox{d}y^2}}+{\frac{1}{R}}\right)\\ &=\gamma_{\rm df}\left({\frac{x_{{\rm interface},{(i,j+1)}}-2x_{{\rm interface}, {(i,j)}}+x_{{\rm interface},{(i,j-1)}}}{{\Updelta}y^2}}+ {\frac{1}{R}}\right),\\ \end{aligned} $$
(25)

where R is the microdroplet radius and r is the interphase radius of curvature in the x−y plane. Equation 25 is solved for \(x_{{\rm interface},{(i,j+1)}}\) for all the droplet–filler interface cells, and \(\theta_{(i,j)}\) can be obtained. Since the microdroplet voltage is known from the electrostatic solution, the Lippmann–Young equation can then be used to extract the static contact angle (which is need to find the dynamic contact angle) as

$$ \cos \theta_{\rm S,bottom,adv} = \cos \theta_0+{\frac{c}{2\gamma_{\rm df}}}(V_{\rm app}-V_{\rm drop})^2. $$
(26)

where \(\theta_{\rm {S,bottom,adv}}\) is the advancing lower (static) contact angle of the microdroplet, θ0 is the initial contact angle, c is the capacitance of the dielectric layers, \(V_{\rm app}\) is the applied voltage and \(V_{\rm drop}\) is the microdroplet voltage (which is uniform inside the conductive microdroplet).

Fig. 9
figure 9

The implementation of the Laplace law is shown for the advancing face where R is the radius of the microdroplet and r is the radius of curvature of the interface in the x−y plane

Full size image

Since the electrode underlying the receding interface is grounded, Eq. 29 for the receding face can be written in an analogous form as

$$ \cos \theta_{\rm {S,bottom,rec}} = \cos \theta_0+{\frac{c}{2\gamma_{\rm df}}}(V_{\rm drop})^2, $$
(27)

where \(\theta_{\rm S,bottom,rec}\) is the receding lower (static) contact angle of the microdroplet. It is shown that the contact angle of a moving microdroplet (dynamic contact angle) differs from its static value (static contact angle) at equilibrium (Blake and Coninck 2002; Keshavarz-Motamed et al. 2010). Using Frenkel–Eyring activated rate theory of transport in liquids (Blake and Coninck 2002; Keshavarz-Motamed et al. 2010), the static contact angle, \(\theta_{\rm S},\) and the dynamic contact angle, \(\theta_{\rm D},\) can be related to the microdroplet transport velocity as

$$ \cos \theta_{\rm S}-\cos \theta_{\rm D}={\frac{v_{\rm transport}\xi}{\gamma_{\rm df}}}, $$
(28)

where ξ = 0.04 is the friction factor. As it is shown in Fig. 10, the shape of the interface for the first two cells now can be expressed as

$$ {\frac{{x_{{\rm interface},{(i,j\rm {wall}+1)}}}-x_{{\rm interface},{(i,j{\rm wall})}}} {\Updelta y}}={\frac{1}{\tan (\theta_{\rm D, bottom})}}. $$
(29)
Fig. 10
figure 10

Use of the Lippmann–Young equation is shown for the advancing interface

Full size image

3.4 Multiphysics

After calculating the electrostatic and hydrodynamic pressures and finding the accurate shape of the microdroplet–filler interface, Eq. 1 has to be solved to obtain the microdroplet transport velocity. It is shown in the previous sections that the wall (shear) force and the driving force can be found from the electrostatic and the hydrodynamic solutions. As it can be seen in Eq. 1, effects of the filler fluid and three-phase contact line motion is brought into the effect by considering two forces: filler force, \(F_{\rm filler},\) and three-phase contact line force, \(F_{\rm tpcl}\)

3.4.1 Three-phase contact line force

Molecular-kinetic theory (Blake and Coninck 2002) states that attachment or detachment of fluid particles is the main source of energy dissipation at the moving three-phase contact line. Although dynamic of wetting can be described by the microdroplet velocity and the dynamic contact angle (Keshavarz-Motamed et al. 2010; Blake and Coninck 2002), it was shown (Ren et al. 2002; Ahmadi et al. 2009) that an additional force has to be added to the dynamic equation of the microdroplet motion. Using the molecular-kinetic theory, this three-phase contact line force can be expressed as

$$ F_{\rm tpcl} =2P\xi v_{\rm transport}, $$
(30)

where P is the perimeter length of the microdroplet. This linearly dependent friction force is especially accurate at low and intermediate velocities (Ren et al. 2002; Ahmadi et al. 2009).

3.4.2 Filler force

It was shown before (Ahmadi et al. 2009; Bahadur and Garimella 2006) that filler fluid plays an important role in the microdroplet dynamics. In this article, the effects of the filler fluid (silicone oil) on the microdroplet dynamics is considered by adding a force, \(F_{\rm filler},\) in the dynamic equation of the microdroplet motion as

$$ F_{\rm filler} ={\frac{1}{2}} C_{\rm D} \rho _{\rm f} v_{\rm transport}^{\rm 2} A_{\rm p}, $$
(31)

where \(A_{\rm P}\) is the microdroplet projected area, \(C_{\rm D}\) is the drag coefficient (Ahmadi et al. 2009), and \(\rho_{\rm f}\) is the filler density. Equation 1 now is solved to find the new transport velocity and to move the microdroplet–filler interface.

4 Results and discussion

In this section, the results of the developed model are presented and verified with experimental results. The experimental setup introduced by Pollack et al. (2002) is used here. An 800-nm thick film of parylene C provides insulation over the control electrodes. Both the top and bottom plates have a 60-nm thick top-coating of Teflon AF 1600. The filler fluid is 1 cSt silicon oil. The dynamics of a 900-nl droplet of 0.1 M KCl solution with an electrode pitch of \(L = 1.5\,\hbox{mm},\) gap spacing \(h = 0.3\,\hbox{mm}\) and droplet diameter of \(D = 1.9\,\hbox{mm}\) are observed in this experimental system and compared to the proposed model.

4.1 Verification of the model with single electrode transport

The proposed model must be accurate in terms of both displacement and velocity, as the model will be applied to the actuation analyses of the motion across numerous electrodes. As it can be seen in Fig. 11a and b, the microdroplet displacement and velocity obtained from the model show strong agreement with the experimental results. The model displacement in Fig. 11a closely follows the rising edge of the experimental displacement. The model then shows complete transport over the 1.5 mm electrode pitch over 1.0 s. The experimental results in Fig. 11a show nearly complete transport over the electrode pitch, but a misalignment in the microdroplet position and insufficient voltage lead to a final displacement of 1.2 mm in 0.4 s.

Fig. 11
figure 11

The a displacement and b velocity are compared to experimental results (Pollack et al. 2002). The applied voltage is 26 V, and the results are shown for a transition of the microdroplet over one electrode

Full size image

Figure 11a shows that the microdroplet velocity obtained from the model is in excellent agreement with the experimental values. The sharp peak around the maximum driving force originates from the sudden change in the wetted area increasing rate, and the observed difference between the experimental and modeling values at the beginning of its motion is attributed to the hysteresis effects in the system (Pollack et al. 2002) and the ideal nature of the model.

4.2 Application of the model to multiple electrode transport

The result in the previous section applied to transport with a single electrode. Practical devices will, however, implement multiple electodes with steady-state transport across many of these electrodes. For this reason, it is important to understand the electrohydrodynamic effects and their relationship to the applied voltage switching frequencies. The switching frequencies deliver appropriately timed voltages to the underlying electrodes, and it is important that the switching frequencies be optimized for the desired microdroplet average velocity. The relationship between these frequencies and the average velocity is studied in this subsection.

Figure 12 shows the arrival time for the microdroplet leading edge at various positions (i.e. displacements) across the three-electrode structure. Results are shown for four switching frequencies (2.5, 5, 10 and 15 Hz) and an applied voltage of 26 V. The optimal case for transport occurs with a switching frequency of approximately 13 Hz. It is immediately apparent from this figure that an increasing frequency leads to shorter arrival times at the end of the third electrode: the 2.5-Hz case has an arrival time of 0.91 s; the 5-Hz case has an arrival time of 0.48 s; the 10-Hz case has an arrival time of 0.24 s. Note that this trend does not apply to the 15-Hz case (which is above the 13-Hz case), as the microdroplet does not successfully complete its transport over each individual electrode. Such a phenomenon has been observed before (Pollack et al. 2002; Arzpeyma et al. 2008), as it has been noted that there exists a maximum allowable switching frequency for the applied voltages. This point is apparent from Fig. 13, which shows the maximum switching frequencies over a range of voltages for model results. The results from the proposed electrohydrodynamic model are compared to the experimental observations (Pollack et al. 2002) and the results obtained from the explicit electrostatic and hydrodynamic modeling approach (Ahmadi et al. 2009). The ability for the proposed approach to accurately replicate the experimental data is readily apparent, and compared to the previous approach, the new methodology models the microdroplet dynamics with greater accuracy for both low and high transport velocities.

Fig. 12
figure 12

The arrival time for the modeled microdroplet leading edge is shown for various positions (i.e. displacements) across the three-electrode structure. The applied voltage is 26 V, and the results are shown for four switching frequencies (2.5, 5, 10 and 15 Hz)

Full size image
Fig. 13
figure 13

The maximum switching frequencies for the proposed model are shown for a range of voltages and compared to the explicit electrostatic and hydrodynamic modeling (Ahmadi et al. 2009; Pollack et al. 2002) and experimental results

Full size image

To gain an insight into the switching frequency response, the model is applied next to the case of transport with a 10-Hz switching frequency at 26 V. Solutions of the microdroplet hydrodynamics (inside) and electrostatics (outside) are shown at four different times in Fig. 14. The relationship between the electrostatic solution and the hydrodynamic equations is apparent as the microdroplet is transported from the uncharged left electrode to the charged right electrode. Figure 14a shows the system under the condition of no applied voltage for which all the contact angles are 104° (i.e. the contact angle value defined for Teflon; Pollack et al. 2002). Figure 14b, c and d shows the moving microdroplet in three different positions (i.e. x = 0.3, 0.75 and 1.5 mm, respectively). As can be seen from Fig. 14, vortices form inside the microdroplet due to its motion (Ahmadi et al. 2009). These two-dimensional vortices (in the x–y plane) show that the flow inside the microdroplet is not one-dimensional, and therefore the Hele-Shaw flow assumption used in current microdroplet hydrodynamics modeling is not an accurate assumption. This is an important observation in terms of pressure. The multi-dimensional nature of the microdroplet internal flow causes a hydrodynamic pressure gradient along the microdroplet faces which plays a crucial role in determining the microdroplet shape. The streamlines inside the microdroplet represent the microdroplet internal flow as seen by an observer sitting on a coordinate system moving with the microdroplet velocity. The streamlines can be used to calculate the velocity gradient and the wall (shear) force acting on the microdroplet, \(F_{\rm {wall}}.\)

Fig. 14
figure 14

Modeled solutions of microdroplet hydrodynamics (inside) and electrostatics are shown at four instants: a time = 0 s with no applied voltage and contact angles of 104°, b time = 0.14 s, c time = 0.22 s and d time = 0.5 s

Full size image

Coupled multiphysics equations of the model are numerically solved simultaneously and plotted in Fig. 15 to characterize the electrohydrodynamics of the microdroplet motion. The results are shown as the microdroplet passes three electrodes. Figure 15 shows the values of different forces acting on the microdroplet. Since the gap spacing is relatively small \((h = 0.3\,\hbox{mm})\) compared to the microdroplet diameter \((D = 1.9\,\hbox{mm}),\) the filler force, \(F_{\rm filler},\) has the smallest value among all the forces, whereas the wall force, \(F_{\rm {wall}},\) is more significant. Moreover, it is observed that three-phase contact line force, \(F_{\rm tpcl},\) has a major contribution in the force balance, which shows that molecular adsorption and desorption processes around the contact-line could not be accounted for by viscous effects of the microdroplet and filler. Finally, the electric potential distribution changes as the microdroplet passes the electrodes (as shown by the color map of Fig. 14). This leads to the rising and falling of the driving force during transport. The driving force increases from zero to a maximum value, then it dips to a local minimum value as the advancing face of the microdroplet reaches the next electrode. This change in the driving force represents the change in the electrostatic pressure, microdroplet voltage and hence the microdroplet shape and contact angles. This observation is confirmed in Fig. 15 which shows the voltage of the microdroplet as a function of its position. The voltage of the microdroplet increases as it passes each electrode, and its potential drops to zero as it reaches the next electrode. Figure 15 shows the advancing bottom, receding bottom and top contact angles of the microdroplet as a function of position as it passes over three electrodes. The contact angle changes are due to the varying microdroplet voltages as it passes the electrodes: The advancing bottom static (and dynamic) contact angle increases from 70.6° (and 70.6°) to 75.9° (and 76.14°) as the microdroplet passes each electrode due to the increase in the microdroplet voltage from 0 to 2.2 V (or the decrease in the voltage drop across the dielectric layer). Changes in the top contact angles follow a different trend, as the contact angle decreases due to the increase of the voltage difference across the top layer (60 nm Teflon AF). Since the bottom layer is thicker than the top layer, the receding bottom contact angle does not change as much as the top contact angle. As can be seen here, the model accurately calculates the very small change in the contact angle due to the low applied voltage.

Fig. 15
figure 15

a Driving, contact line, filler and wall forces are shown as functions of microdroplet position. b The microdroplet voltage is shown as a function of its position. c Microdroplet advancing bottom, receding bottom and top contact angles are shown as a function of position. d Transient velocity of the microdroplet is shown as a function of its position

Full size image

The presented multiphysics model simultaneously solves the dynamic equation of microdroplet motion via Eq. 1 and ultimately tracks the microdroplet. The transient velocity of the microdroplet is shown as a function of its position in Fig. 15. Jerky motion of the microdroplet motion is apparent here. The microdroplet starts its motion with zero velocity, and its velocity reaches a maximum value. Interestingly, the velocity of the microdroplet does not reach to zero as it reaches to the next electrode due to its momentum. Since the force balance is changing (Fig. 15), the minimum values are not the same for different electrodes, and the microdroplet is accelerating as it passes the electrodes. This is a very interesting observation which highlights the crucial role of the optimum switching frequency for acheiving higher trasnport velocities.

5 Conclusion

In this article, ideal microdroplet transient motion in digital microfluidic systems was modeled to high accuracy. The model was based on the coupling of hydrodynamic and electrostatic governing equations, and the saturation, dielectric loss and break down and three-dimensional pinning effects were not included in the model. Important findings of the proposed methodology included the transient velocity and displacement of the microdroplet as well as the driving and opposing forces acting on the microdroplet as functions of time. It was shown that these time-varying effects all have important ramifications for the maximum allowable switching frequencies and overall device design for practical digital microfluidic systems.