1 Introduction

Recent advances in microfabrication techniques and applications have led to a rapidly growing interest in novel methods for fluid control at very small scales. Digital microfluidics, in which fluidic operations are achieved by manipulating individual fluid slugs instead of continuous flows, has been proposed for a variety of applications such as micro scale heat transfer and lab-on-a-chip chemical analysis. The use of individual droplets enables the fabrication of micro systems which are highly programmable, compact, and efficient (Jones 2002; Wang and Jones 2005; Saeki et al. 2001; Cho et al. 2003; Lee et al. 2002; Pollack et al. 2002; Zeng and Korsmeyer 2004; Zeng 2006; Cooney et al. 2006; Shapiro et al. 2003; Wheeler et al. 2004, 2005).

Several actuation methods for digital microfluidics are currently under research. Most of these methods scale linearly with the characteristic length of the droplet. These include the direct modulation of liquid surface tension through the application of a chemical or thermal gradient (Oleg and Alexander 2004; Mugele and Baret 2005; Darhuber et al. 2003; Chen et al. 2005), as well as electrostatic methods in which the driving force arises from the application of an electric field. The most promising actuation method for electrically conductive fluids currently under research is electrowetting on dielectric (EWOD) (Dolatabadi et al. 2006; Baird and Mohseni 2005; Mohseni et al. 2005; Moon 2002; Cho et al. 2002; Fair et al. 2003).

Droplet transport via EWOD can be carried out for sessile droplets on a flat surface, between two flat plates, or inside a micro channel or pipe. In each case, a patterned grid of electrodes is coated with a thin layer of insulation creating a high capacitance between the electrode array and the conducting fluid. Early discussions of EWOD focused primarily on Lippman’s equation to describe the actuation force:

$$ \text{cos}(\theta)=\text{cos}(\theta_0)+{\frac{1} {2\gamma_{ls}}}cV^2, $$
(1)

where θ is the fluid contact angle, θ0 is the contact angle with no applied voltage, c is the capacitance per unit area of the dielectric coating, and V is the voltage applied across the system. Lippman’s equation accurately predicts the contact angle for a cylindrically symmetric sessile droplet in which the outward EWOD force is balanced by the net inward effect of surface tension at the contact line. However, an accurate description of the EWOD force must not be limited to discussions of contact angles and surface tensions. Indeed, the EWOD force itself is a purely electrostatic phenomenon which applies equally to conducting solids, as well as fluids. Electrostatic descriptions of electrowetting on dielectric are discussed in (Kang 2002; Jones 2005). Bahadur and Garimella (2006) have recently used energy considerations similar to those in Sect. 2.1 of this article to concurrently derive lumped paramater formulae for net forces on circular droplets.

This paper presents a detailed description of the source and nature of the EWOD force. Simple algebraic expressions for the net force on a conducting body in EWOD configuration are derived and shown to depend on the instantaneous location of the droplet. In addition, numerical results for the electric potential near an EWOD-actuated droplet are presented and used to derive the charge distribution and force densities on the fluid’s leading and trailing interfaces. Numeric results from integrating the force density are shown to agree with net force calculations derived analytically. The effect of various system parameters on the force distribution, and subsequently on EWOD applications, is discussed.

2 Theoretical calculation of net force

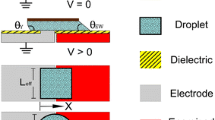
Consider a droplet of height h and length L in a microchannel, as seen in Fig. 1. The channel is coated with thin dielectric layers of thicknesses d l and d u , and dielectric constants ε l and ε u . We assume the droplet width, w, is much greater than its height, h, and that the problem is symmetric in the normal direction. All results will be derived per unit width—that is, the total force on a droplet is given by multiplying the results of this section by the transverse length of its contact line.

Fig. 1
figure 1

Conducting droplet in EWOD configuration

Full size image

2.1 Capacitive energy calculation

The force per unit width on the droplet is expected to scale with the electrostatic energy per unit area of the system (Beni et al. 1982). We first consider only the capacitive energy stored in the dielectric layers, then add the effect of the energy stored in the empty channel itself for completeness. When d≪h, the latter contribution becomes negligible.

While the net force on the droplet can be directly derived from capacitive energy considerations, it is not as simple as writing down \({{\frac{1}{2}}cV^2.}\)We consider here only the case of a continuous grounded electrode, with the opposite side of the droplet being in contact with a hot electrode with potential V app on its advancing face and a grounded electrode on its receding face. While patterning electrodes on both sides of the channel would allow for greater flexibility, the configuration considered here is most commonly used in practice due to its relative ease of fabrication. Ignoring the contributions of edge effects at the contact lines and the hot/cold electrode interface, the system energy is the sum of the capacitive energies in the four regions labeled in Fig. 1:

$$ \begin{aligned} U={\frac{1}{2}}c_l L V_{\rm drop}^2 &+ {\frac{1}{2}}c_u \left(x+{\frac{L}{2}}\right) (V_{\rm app}-V_{\rm drop})^2\\ & + {\frac{1}{2}}c_u\left({\frac{L}{2}}-x\right) (-V_{\rm drop})^2, \end{aligned} $$
(2)

where c u and c l are the capacitances per unit area of the top and bottom coatings, c = ε/d. The droplet voltage is found by minimizing the total energy with respect to V drop (Woodson and Melcher 1968a, b, c), giving a result of

$$ V_{\rm drop}={\frac{c_u V_{\rm app}}{c_u+c_l}}\left({\frac{x}{L}}+{\frac{1} {2}}\right). $$
(3)

Note that the droplet potential directly depends on its location with respect to the boundary between the hot and cold electrodes. Also note that differentiating the system energy with respect to V drop results in an equation of the form Q = C 1 V 1 + C 2 V 2 + C 3 V 3 + C 4 V 4 = 0; as the droplet is insulated by the dielectric layers, the net charge must always remain 0. As we have neglected the contribution of the fringing fields to the total energy, the approximation is therefore expected to be best when the asymmetric boundary condition is near the droplet’s center.

Note that when c l  ≫ c u , corresponding to very little or no insulation along the continuous grounded electrode, the droplet potential is always 0, as expected. When c u  ≫ c l , corresponding to the case where the ground electrode is omitted and the potential is allowed to float on this side of the droplet, the voltage reduces to

$$ V_{\rm drop}=V_{\rm app}\left({\frac{x} {L}}+{\frac{1}{2}}\right). $$
(4)

Equation (3) is substituted into Eq. (2) to derive an expression for the total system energy. The net force on the droplet in the x direction is given by differentiating the system energy with respect to the x coordinate, giving

$$ F_x={\frac{1}{2}}\,{\frac{c_u} {c_u+c_l}}V_{\rm app}^2\left(c_l-2c_u{\frac{x}{L}}\right). $$
(5)

When x = 0 and the droplet is centered, the force per unit width reduces to

$$ F_x={\frac{\hbox{d}U}{\hbox{d}x}}={\frac{1}{2}}\,{\frac{c_u c_l} {c_u+c_l}}V_{\rm app}^2, $$
(6)

which corresponds to the total capacitive energy per area stored in the dielectric layers when connected in series and placed at a voltage V app.

For a grounded droplet, the force is independent of position, taking on a constant value of

$$ F_x={\frac{1}{2}}c_uV_{\rm app}^2, $$
(7)

derived by taking the limit as c l approaches infinity. Taking the limit as c l approaches 0 for the droplet with no grounded electrode gives

$$ F_x=-{\frac{c_u V_{\rm app}^2} {L}}x. $$
(8)

In this case, the force is exactly harmonic with a ‘spring’ constant of c u V 2app /L. Due to the large effects of viscous drag and other nonconservative forces, such an EWOD oscillator can be considered overdamped, with the droplet ‘stalling’ atop the asymmetric interface (Cooney et al. 2006). It is interesting to note that with the battery holding the electrodes at constant potential, the droplet does not oscillate about a minimum in system energy, but a maximum (Jackson 1998; Landau et al. 1984; Griffith 1972). Plots of of system energy and net force as a function of droplet position for three configurations are given in Fig. 2.

Fig. 2
figure 2

Net forces (a) and capacitive energies (b) for droplets with c u ≪ c l (when the bottom dielectric layer is much thinner than the top), c u  = c l , and c u  ≫ c l

Full size image

When d and h are of the same order of magnitude, the energy stored in the channel itself between the hot electrode and ground becomes significant. The change in capacitive energy in the empty channel when the droplet is moved forward a distance dx is given by

$$ {\frac{\hbox{d}U_{\rm chan}}{\hbox{d}x}}={\frac{1}{2}}c_{\rm eq}V_{\rm app}^2, $$
(9)

where c eq is the equivalent capacitance of the channel and dielectric layers. This value is then subtracted from the net force.

2.2 Maxwell stress tensor calculation

The net EWOD force may also be found by integrating the Maxwell stress tensor around a suitably chosen path (Jackson 1998; Landau et al. 1984; Griffith 1972). A judicious choice of integration path allows the force to be calculated without any knowledge of the fringing fields. However, the electric field must again be known in the four regions of Fig. 1 sufficiently far from the contact lines and the voltage jump. Therefore, Eq. (3) is still used to calculate the voltage drop (and hence electric field) in each region.

We assume there is no magnetic field, and place the edges of the integration loop exactly along the top and bottom electrodes. This ensures that the field everywhere along the loop is always purely in the transverse direction, and all terms in the stress tensor have the form εE 2/2. To avoid integrating over the discontinuous jump in potential, separate loops are drawn around the front and rear faces of the droplet. The loop is extended far enough into the channel that the field will be uniform in these regions. This breaks the net force of the droplet into two parts: the driving force pulling on the front face, and an opposing but weaker force pulling on the back face. These forces are given by

$$ \begin{aligned} F_{\rm back}&={\frac{1}{2}}c_u V_{\rm drop}^2+{\frac{1}{2}}c_l V_{\rm drop}^2 \\ F_{\rm front} &={\frac{1}{2}}c_l V_{\rm drop}^2+{\frac{1} {2}}c_u (V_{\rm app}-V_{\rm drop})^2-{\frac{1}{2}}c_{\rm eq}V_{\rm app}^2, \end{aligned} $$
(10)

with V drop given by Eq. (3). The net force, given by subtracting F back from F front, is identical to the result derived through energy differentiation.

It is apparent from Eq. (10) that for a given c u and c l the net force is maximized by minimizing V drop. In practice, this is accomplished by patterning control electrodes narrow enough so that only a small fraction of the droplet’s length is in contact with the hot electrode at any time, and by using the thinnest possible layer of hydrophobization on the continuous grounded electrode. However, the limiting factor for droplet velocity is often dielectric breakdown of the capacitive layers at high voltages (Pollack 2001). When thicker layers are used, a higher voltage can be applied before breakdown is reached. When designing an EWOD system, consideration therefore needs to be given to whether a large force centered at one contact line or a more uniform force spread along the droplet is desired. Design considerations for fluidic operations such as droplet splitting, merging, and mixing are directly affected by a knowledge of the force distribution; e.g., droplet splitting can theoretically be accomplished by actuating only one electrode when the insulating coating atop the grounded side is thick.

In deriving the above expressions for the net EWOD force, fluid properties such as surface tension and contact angle are not important. EWOD should not be confused with actuation methods which modulate the fluid surface tension itself, such as thermal, chemical, or optical methods. In addition, the change in contact angle predicted by Lippman’s equation should be correctly interpreted as a consequence of the EWOD force, and not as the driving force itself (Jones 2005). For an axially symmetric static droplet, Lippman’s equation expresses the balance of the horizontal component of the EWOD force with the effect of surface tension. For a moving droplet, several forces including viscous drag along channel walls, contact angle hysteresis, wind resistance, added mass resistance and contact line friction counterbalance the EWOD effect. In addition, the system energy and Maxwell stress methods outlined above derive only the net axial force; electrostatic forces in the transverse direction may also be important for EWOD applications.

3 Numeric calculation of force distribution

While examinations of system energy and the Maxwell stress tensor are useful for giving simple formulae for net forces, they provide no detailed information of the force distribution on the droplet. To find the distribution, the electric field exactly at the surface of the fluid must be known. This requires a full numerical solution to the Maxwell equations for the electric potential in the region of the fluid. Integration from 0 to h of the force distributions derived in this section will be shown to agree with the lumped parameter results of Sect. 2.

When the potential is known, the charge distribution and electric field present on the droplet are given by (Jackson 1998; Landau et al. 1984; Griffith 1972)

$$ \sigma=\epsilon E = -\epsilon {\frac{\partial V}{\partial n}}, $$
(11)

where \({{\frac{\partial}{\partial n}}}\) represents the gradient of the potential along the outward normal to the droplet’s surface, E is the electric field evaluated at the surface, and ε is the electrical permittivity of the material external to the droplet where the derivative is calculated. This surface charge feels a force from the external electric field, giving rise to an electrostatic pressure which is always normally outward:

$$ f={\frac{1}{2}}\epsilon E^2. $$
(12)

Not surprisingly, the outward force per unit area on the droplet’s face is equal to the electrostatic energy per unit volume immediately outside. This is also the term which appears in the Maxwell stress tensor.

With no volumetric free charge in the solution region, the potential is found by solving Laplace’s equation with the boundary conditions shown in Fig. 3. The boundary condition on the surface of the conductor is

$$ \sigma = -\epsilon {\frac{\partial V}{\partial n}}, $$
(13)

with the entire droplet itself held at a constant V drop. The charge distribution and droplet potential are not known a priori, however, and must be found as part of the numerical solution. This is accomplished via a shooting method in which two initial guesses for the droplet are assumed, the net charge on the surface is calculated by integrating \({\sigma=-\epsilon {\frac{\partial V}{\partial n}}}\) over the boundary, and a subsequent guess for V drop is calculated via the secant method. Convergence is typically rapid, requiring only 4–6 iterations for the total charge to vanish within a reasonably strict tolerance.

Fig. 3
figure 3

Boundary conditions for solution of Laplace equation

Full size image

The Laplace equation was discretized on a 5-point stencil and iterated using successive over-relaxation. Second-order, one-sided finite differences were used to discretize the ‘jump’ conditions at the dielectric/dielectric interfaces and in calculating σ. All dielectric constants were nondimensionalized by ε0, voltages by V app, and lengths by the height h of the droplet. To reduce the need for extremely fine resolutions, dielectric layers were typically on the order of 0.1h; the capacitive energy of the empty channel was therefore taken into account when comparing numeric results for the total force to the results for Sect. 1.

A contour plot of the electric potential around a fluid slug is shown in Fig. 4. The droplet is centered over the voltage step, and d l  = d u  = 0.1h. Note that the contour lines are densely bunched around the four corners of the droplet, indicating the outward pressure along both faces.

Fig. 4
figure 4

Electric equipotentials surrounding a droplet in EWOD configuration

Full size image

The program was also run for the same geometry as Fig. 4 for several axial positions of the fluid relative to the electrode interface. Results for the droplet potential versus position, as well as the analytic result of Eq. (3), are shown in Fig. 5. As seen in the figure, the numerical data closely match the analytic prediction, especially when the droplet is centered over the voltage jump. When the droplet is near the edge of the boundary, no region of uniform field exists for use in the simple capacitive energy calculation; it is thus intuitive that Eq. (3) overestimates the droplet potential at these positions.

Fig. 5
figure 5

Analytic prediction and numerical results for droplet potential as a function of position

Full size image

The charge distribution for a straight-sided centered droplet is shown in Fig. 6a. On the rear interface, the distribution is symmetric about the center line and always of the same sign. On the front of the droplet, the charge changes sign at a location given roughly by

$$ y={\frac{V_{\rm drop}}{V_{\rm app}}}h. $$
(14)

At this position, the charge density and electric field at the surface change sign, and the electrostatic force has a local minimum of 0. This feature is clearly seen in Fig. 4 as the point at which the contours curving down from the top meet the contours curving up from the bottom.

Fig. 6
figure 6

Charge distributions (a) and force densities (b) on the leading and trailing interfaces of an EWOD-activated droplet

Full size image

Equation (12) is plotted for the same straight-sided droplet in Fig. 6b. As seen in the figure, the force distribution is strongly peaked exactly at the edges. While the integrable singularity is singular at the contact line, the force distribution does extend a significant distance over the droplet’s face. A characterization of the thickness of the force distribution in terms of system parameters is a topic of future research.

3.1 Net force integration

The net force is given by integrating the force density over the leading and trailing droplet fronts. This requires numerically integrating a function which is not well behaved (Kang 2002; Kang et al. 2003; Vallet et al. 1999). According to (Jackson 1998), extremely close to the channel wall the force density on a straight-sided droplet surrounded by a uniform dielectric is expected to scale as

$$ f \propto \epsilon \xi^{-2/3} $$
(15)

where ξ is the distance from the contact line. The net force was found by integrating the density using Simpson’s rule to within three grid points of the contact line, assuming the function goes as ξ−2/3 as it approaches the boundary, and extrapolating the contribution of the points nearest the contact line. With εlay/εchan = 1 and a resolution of 100 grid points or more along the droplet faces, the integrated force was found to be 2.5% lower than the prediction of Eq. (5). As εlay/εchan was increased from unity, the ratio of the numerically calculated force to the theoretically predicted value monotonically decreased. This is because the asymptotic behavior of the distribution no longer follows Eq. (15) with the addition of the jump condition exactly at the boundary. The presence of a material with ε > ε0 increases the charge density along the top of the droplet. This charge is distributed around the corner onto the face, increasing the strength of the singularity and causing an integration routine based on Eq. (15) to underestimate the contribution of the edge regions to the overall integral. A plot of the force distribution near the contact line adjacent to the actuated electrode for several values of εlay is given in Fig. 7. The force distribution is seen to become both greater in magnitude and steeper in shape as εlay increases. This observation led us to develop a leading-term analytical solution for the force distribution very near the tri-phase contact line (see Sect. 3.2).

Fig. 7
figure 7

Asymptotic force distribution for several values of ε

Full size image

The effect of the curvature of the droplet was also examined by comparing results for several different contact angles ranging from 90° to roughly 115°. As seen in Fig. 8, the droplet potential and the net forces on each interface remain constant, as predicted. The force distribution does change, however, according to the system curvature, as seen in Fig. 9. When integrating the force distribution to find the net result, the numerical integration needs to be modified at each step. From Jackson (1998), Kang (2002), Kang et al. (2003) and Vallet et al. (1999), we expect the singularity to become weaker as the contact angle is increased:

$$ f \propto \xi^{2(\pi/\beta-1)}, $$
(16)

where β = 2π − θ0 and θ0 is the contact angle. For the first three solution points closest to the contact lines, the asymptotic behavior is estimated using the tangent line at the interface. This behavior was then used to extrapolate the edge contributions for the total force. The accuracy of our results suggests that our numerical data are in excellent agreement with Eq. (16) except within one grid point of the boundary, where it is unable to capture the theoretical singularity. This asymptotic behavior is only expected to hold very close to the edge, implying the distribution is expected to follow Eq. (16) for distances less than about 0.1d from the boundary. As d is typically much smaller than h and h is in turn much smaller than the length of the solution domain, capturing the asymptotic behavior on a semi-uniform mesh becomes extremely expensive computationally. Future research will include a linear mapping near the contact line to increase resolution in its immediate vicinity.

Fig. 8
figure 8

Net forces and droplet potential as a function of contact angle. Theoretical predictions of Sect. 2 are given by solid lines, with numerical data presented as discrete points

Full size image
Fig. 9
figure 9

Force distributions near the contact line for several values of contact angle

Full size image

3.2 Asymptotic series solution of the EWOD force

Because of the complex geometry and boundary conditions, a full analytic solution for the electric potential everywhere in the region of a conducting droplet in EWOD configuration is not attempted here. In this chapter, we derive the leading term behavior of a series expansion solution near the triphase contact line, and examine its effect on EWOD actuation.

Very near the tri-phase line, we assume the curvature of the droplet is low enough that it can be approximated as a straight wedge at a slope given by the fluid’s contact angle. The leading term asymptotic solution will only be valid for distances which are small compared to the next smallest length scale of the problem, in this case given by d. As the droplet height is typically two orders of magnitude larger than this, the tangent line approximation is valid. This reduces the problem to solving for the potential near the intersection of two conducting planes held at a constant mutual voltage and an interface of two materials with varying dielectric constants. To match the geometry, we follow Jackson’s example and solve ∇2 V = 0 in polar coordinates (Jackson 1998) via separation of variables.

In polar coordinates, Laplace’s equation reduces to

$$ \nabla^2 V = {\frac{1}{r}}{\frac{\partial}{\partial r}} \left(r{\frac{\partial V}{\partial r}}\right)+{\frac{1}{r^2}}{\frac{\partial^2 V} {\partial \theta^2}}, $$
(17)

subject to the boundary conditions V(r, 0) = V drop, V(r, β) = V drop, and the ‘jump’ condition along the dielectric interface. Here, β is the exterior angle between the two conducting planes, as seen in Fig. 10. In addition, the potential must be defined and well-behaved everywhere in the solution region, including r = 0. The solution domain is split into two regions (see Fig. 10), region 1, with 0 ≤ θ ≤ π and dielectric constant ε1, and region 2, with π ≤ θ ≤ β and ε2. After considerable algebraic manipulation, application of all but the ‘jump’ boundary condition leads to the equation

$$ r^{\alpha_1-\alpha_2}=C{\frac{\text{sin}(\alpha_2 \pi)-\text{tan}(\alpha_2 \beta)\text{cos}(\alpha_2 \pi)}{\text{sin}(\alpha_1 \pi)}}, $$
(18)

where C is an unimportant overall constant. The variables in this equation are separated; the function \({r^{\alpha_1-\alpha_2}}\) is equal to a function which is independent of r. Both sides must therefore be equal to a constant, which is only possible if α1 = α2 = α. This is an intuitive and seemingly trivial result; however, it has significant physical meaning: even with the presence of the discontinuity in ε, the electric potential (and hence the electric field, charge distribution and force density) has the same asymptotic shape on both sides of the wedge in both media.

Fig. 10
figure 10

Geometry very close to the tri-phase contact line for asymptotic series solution of Laplace’s equation

Full size image

It remains to find the solution for α itself, and thus the leading term behavior. To this point, no restriction has been made, and a continuum of solutions has been possible. However, applying the jump condition at θ = π leads to the equation

$$ \epsilon_1 \text{cos}(\alpha \pi) = C \epsilon_2 [\text{cos}(\alpha \pi)+\text{tan}(\alpha \beta)\text{sin}(\alpha \pi)]. $$
(19)

The unimportant overall magnitude C can be eliminated by dividing the matching boundary condition [Eq. (18)] by the jump BC [Eq. (19)], resulting in a transcendental equation for α in terms of the wedge angle β and the dielectric ratio ε1/ε2:

$$ \text{tan}(\alpha \pi) = {\frac{\text{sin}(\alpha \pi)-\text{tan}(\alpha \beta)\text{cos}(\alpha \pi)}{\text{cos}(\alpha \pi)+\text{tan}(\alpha \beta)\text{sin}(\alpha \pi)}}{\frac{\epsilon_1}{\epsilon_2}}. $$
(20)

The leading term of the electric potential is proportional to r α, with the electric field then given by E ∝ r α − 1 and the force distribution by f ∝ r 2(α − 1). Equation 20 cannot be solved analytically in closed form, and is in general solved for α(β, ε1/ε2) numerically. The solution can, however, be checked for the case of ε1 = ε2. In this case, the solution of α = π/β can be verified by noting the tan(αβ) terms vanish; this is the solution obtained for this simplified scenario by Jackson (1998). Equation (20), with different notational conventions, was first derived in Buehrle et al. (2003). An examination of the effects of the asymptotic electric field on dielectric breakdown and contact angle saturation is given in Papathanasiou and Boudouvis (2005).

The result of Eq. (20) was used to integrate our numerically obtained force distributions. As seen in Fig. 8, numeric results using this value of α were in excellent agreement with analytical theory. The effect of α on these calculations should not be overlooked: with α = π/β but ε1 = 3ε2, the numerically obtained result for the total force is less than half the correct value. The close agreement in Fig. 8 and especially Fig. 11 indicates that the assumptions leading to Eq. (20) were valid for the geometries considered in our numerical code. A plot of α for several values of ε1/ε2 is given in Fig. 11a, along with a comparison of Eq. 5 given in Fig. 11b.

Fig. 11
figure 11

Exponent of leading term in series solution for the potential near a tri-phase contact line (a) and total integrated force on a droplet (b) as a function of ε1/ε2

Full size image

4 Conclusions and future research

This paper described the electrostatic force associated with electrowetting on dielectric. Both analytic results for integrated total forces and numeric results for the force distribution were presented, and shown to be in excellent agreement. The net force on a droplet was shown to be dependent on its instantaneous axial location and maximized when the narrowest possible control electrodes are used. The effects of dielectric constant, contact angle and system geometry were derived directly from fundamental equations describing the electrostatics of an EWOD system. Our future research will center on implementing our numerical scheme for the force density into a fully functional CFD code for detailed droplet dynamics. The effect of the divergent charge density on possible explanations for contact angle saturation such as charge trapping, local dielectric breakdown, and corona discharge is also being studied.