1 Introduction

Microfluidic systems used for biochemical analysis, drug delivery and sequencing or synthesis of nucleic acids, require rapid mixing (Nguyen and Wu 2005). Since the molecular diffusivity for most solutes in liquid solvents is very low, additional transport mechanisms must supplement molecular diffusion. However, it is challenging to induce advective mixing at microscale lengthscales and that are associated with relatively small velocities (Hessel et al. 2005), which has led to the design of passive and active micromixers (Nguyen and Wu 2005; Chang and Yang 2007).

Passive micromixers do not require external energy and, for instance, can enhance diffusion by creating thin adjacent high-gradient unmixed strips through chaotic advection. Active micromixers, on the other hand, use disturbances generated by an external field, e.g. pressure, temperature, electrokinetic, magnetohydrodynamic or acoustic perturbations. Although active micromixers require external power and involve more complicated design and integration, they are able to provide greater mixing control, particularly for intermittent and on-demand applications. Microscale mixing is more commonly implemented in flow-through configurations such as microchannels (Stone et al. 2004) although some sequential applications also require mixing to occur in discrete chambers (Lu et al. 2002).

For the low Reynolds number flows (Re ≪ 1) encountered in microfluidics, the inertia term in the Navier–Stokes equation can be neglected so that the flowfield is obtained by solving the Stokes equation. A linearized model for three-dimensional microchannel flow can thus be based on the superposition of one-dimensional axial channel flow upon the two-dimensional transverse flow along any of its cross-sections. The latter cross-sectional flow resembles that in a two-dimensional rectangular cavity.

Specific manufacturing processes and coatings can be used to induce an electric potential on a surface when it comes in contact with an ionic liquid. This surface potential, called the zeta (ζ) potential, enables a neutral electrolyte solution to develop an electric double layer (EDL) very close to a surface. The value of the zeta potential depends on the surface material (Soong and Wang 2003) and can be altered by use of specialized coatings (Towns and Reginer 1991). The EDL thickness, which is the Debye length, depends on the molarity of the liquid, the valencies of the ions present, and the permittivity of the medium. Negatively charged liquid ions within this layer arrange themselves to lie closer to a positively charged surface and vice versa. The ions contained in the EDL move when an external electric field is applied, causing liquid motion within it. This induces motion throughout the domain through viscous shearing. Such electroosmotic flows (EOFs) (Masliyah and Bhattacharya 2006) have been used to enable mixing in various microscale applications such as for sample injection, chemical reactions and species separation (Qiao and Aluru 2003; Paul et al. 1998).

Ng et al. (2004) performed numerical simulations of EOF and mixing by considering a steady electric field and a nonuniform surface potential and were able to generate both in- and out-of-plane vortices, which could be combined to create streamwise vortices. Qian and Bau (2002) provided closed form solutions for the flow and chaotic mixing in an electroosmotic stirrer by considering a two-dimensional conduit with electrodes placed repeatedly in the flow direction. They found that an unsteady flowfield, which gave rise to chaotic mixing, could be established by altering the magnitude and sign of the ζ-potential provided by the individual electrodes. Stroock and McGraw (2004) developed an analytical model by idealizing their configuration through a superposition of a pressure-driven axial flow and an electroosmotic transverse flow for a staggered herringbone mixer. They demonstrated chaotic mixing that was produced by two transverse alternating flow patterns. Pacheco et al. (2006) and Kim et al. (2006) simulated mixing in channel flows by combining axially and transversely generated electrokinetic flows. The former investigation analyzed time-dependent flows, and the latter considered steady flows with a relatively complex potential distribution.

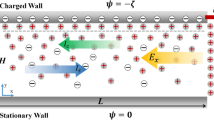
In contrast to these earlier studies, which relied on either unsteady flows or complex potential distributions, we present a relatively simpler scheme to achieve rapid mixing that uses a steady electric potential and a homogeneous zeta potential in an easily implemented configuration (Fig. 1). The previous investigations mostly considered flow-through configurations such as channels and did not address electroosmotic stirring in cavities whereas our work primarily addresses the latter configuration. In addition, for a very low Reynolds number, channel flow can be assumed to result from a superposition of the axial and two-dimensional cross-sectional flows. Our model, therefore, can also be used to simulate the electroosmotic flow that is generated across the channel cross-section, which can be superposed with the axial flow that is independent of it.

Fig. 1
figure 1

Schematic of electroosmotic cavity

Full size image

The simulation of EOF requires exceedingly fine grids in the EDL to simulate the essential features of the flow and transport phenomena (Qian and Bau 2005). A popular alternative strategy (Qian and Bau 2002; Pacheco et al. 2006; Kim et al. 2006) simplifies the treatment of the electroosmotic flow by considering a Helmholtz–Smoluchowsky velocity, which is the fluid velocity at the edge of the EDL. Since the EDL thickness (∼10–100 nm) is much smaller than the channel or cavity dimensions (∼10–100 μm), this approach takes the condition at the EDL edge and applies it directly to the wall. This eliminates the need for the superfine spatial resolution required for analysing the EDL flow and thus, considerably reduces the computational cost. Besides, the solution of electrostatic potential distribution is also not required. However, for smaller geometries, dilute solutions or relatively large EDL dimensions, the approximation is often questionable.

We have simulated the electroosmotic flow using the lattice Boltzmann method (LBM), which is linear and based on a fully explicit scheme, and is easily implemented on parallel computers (Ladd 1997). These features of LBM make it an attractive method for analyzing electrokinetic flows with sufficient spatial resolution in the EDL. The method has been used to investigate microfluidic (Chen and Doolen 1998; Succi 2001) and isothermal electrokinetic problems (Tang et al. 2006; Melchionna and Succi 2004). We have quantified the mixing generated through the mixing efficiency.

2 Mathematical modeling

2.1 Electroosmosis

The governing relations for EOF represent a coupled fluid-electrostatic phenomenon. The fluid motion is governed by the continuity and Navier–Stokes equations (which include the electroosmotic body force), i.e.,

$$ \nabla .{{\mathbf{u}}} = 0,\quad\hbox{and}\quad\rho \frac{\partial {{\mathbf{u}}}}{\partial t} + \rho {{\mathbf{u}}} \cdot \nabla {{\mathbf{u}}} = - \nabla p + \mu \nabla^{2} {{\mathbf{u}}} + \rho_{e} {{\mathbf{E}}}_{\rm eff}, $$
(1a,b)

where E eff denotes the effective electric field (both applied electric field and that due to the wall zeta potential). For a static or quasi-static irrotational electric field, it is related to electric potential Φ in the form E eff = −∇Φ. The electric potential results in a spatial charge distribution following the Poisson equation

$$ \nabla^{2} \Phi = - \frac{\rho_{e}}{\varepsilon}, $$
(2)

where ρ e denotes the volumetric free charge density and ɛ is the permittivity of the medium. The electric charge distribution depends both on the potential due to the applied electric field ϕ and the wall zeta potential ψ (i.e., Φ = ϕ + ψ). When, (1) the Debye thickness is small compared with the channel diameter or height (in our case the ratio of Debye length to channel dimension is 0.01) and (2) the charge at the walls is not large (i.e., zeψ/k B T ≤ 1), then ∇ϕ ≪ ∇ψ. At the same time, if the fluid velocity in the microchannel is very small (generally for microchannel flows, Re ≪ 1), Eq. (2) assumes the forms (Ng et al. 2004; Chang and Yang 2004)

$$ \nabla^{2} \phi = 0,\quad\hbox{and}\quad\nabla^{2} \psi = - \frac{\rho_{e}}{\varepsilon} = \frac{2n_{\infty} ze}{\varepsilon}\sinh {\left({\frac{ze\psi}{k_{\rm B} T}} \right)}, $$
(3a, b)

when the charge density ρ e follows the Boltzmann distribution for a symmetric electrolyte (z i  = ±z, n i  = n ∞). For small values of the zeta potential zeψ/k B T ≤ 1, using the Debye–Hückel approximation, Eq. (3b) assumes the form

$$ \nabla^{2} \psi = \frac{2n_{\infty} z^{2} e^{2} \psi}{\varepsilon k_{\rm B} T} = \kappa^{2} \psi, $$
(4)

where κ−1 denotes the Debye length. This approach has been adopted to simulate electrosmotic flows in cavities (Qian and Bau 2005) and rectangular channels (Kim et al. 2006) when a transverse potential gradient is applied. Equation (4) can be analytically solved by separating variables (O’Neil 2003) to determine the electric potential and charge distribution. The solution is of the form,

$$ \begin{aligned} \psi {\left({x,y} \right)} &= {\sum\limits_{n = 1}^\infty {\zeta_{1} \frac{2{\left({1 - {\left({- 1} \right)}^{n}} \right)}}{n\pi \sinh {\left({\mu_{n} L_{y}} \right)}}\sin {\left({\lambda_{n} x} \right)}\sinh {\left({\mu_{n} y} \right)}}} + {\sum\limits_{n = 1}^\infty {\zeta_{2} \frac{2{\left({1 - {\left({- 1} \right)}^{n}} \right)}}{n\pi \sinh{\left({\eta_{n} L_{x}} \right)}}\sinh {\left({\gamma_{n} x} \right)}\sin {\left({\eta_{n} y} \right)}}} \\ & \quad+ {\sum\limits_{n = 1}^\infty {\zeta_{3} \frac{2{\left({1 - {\left({- 1} \right)}^{n}} \right)}}{n\pi \sinh {\left({\mu_{n} L_{y}} \right)}}\sin {\left({\lambda_{n} x} \right)}\sinh {\left({\mu_{n} {\left({L_{y} - y} \right)}} \right)}}} + {\sum\limits_{n = 1}^\infty {\zeta_{4} \frac{2{\left({1 - {\left({- 1} \right)}^{n}} \right)}}{n\pi \sinh {\left({\eta_{n} L_{x}} \right)}}\sinh {\left({\gamma_{n} {\left({L_{x} - x} \right)}} \right)}\sin {\left({\eta_{n} y} \right)}}}, \\ \end{aligned} $$
(5)

where \(\lambda_{n} = \frac{{n\pi}}{{L_{x}}},\mu_{n} = {\sqrt {\lambda^{2}_{n} + \kappa^{2}}},\gamma_{n} = \frac{{n\pi}}{{L_{y}}},\eta_{n} = {\sqrt {\gamma^{2}_{n} + \kappa^{2}}}.\)

The details of the above solution are provided in the appendix. Equations (1a, b) are solved to generate the flowfield using LBM.

2.2 Lattice Boltzmann method

The fundamental concept defining the LBM (Succi 1997) is the construction of simplified kinetic models that incorporate the essential physics of microscopic and mesoscopic processes so that the averaged macroscopic properties obey the desired macroscopic equations (Chen and Doolen 1998). The Boltzmann equation with the Bhatnagar–Gross–Krook (BGK) approximation is (Succi 2001)

$$ \left(\frac{\partial}{\partial t} + {{\mathbf{e}}} \cdot \nabla_{\mathbf r} + {{\mathbf{a}}} \cdot \nabla_{\mathbf e}\right)f\left({{\mathbf{r}}},{{\mathbf{e}}},t \right) = - \frac{f -f_{\rm eq}}{\tau}, $$
(6)

where f(r, e, t) is a one-particle probability distribution function, defined such that, [f(r, e, t)·d3 r·d3 e] is the number of particles which, at time t, are located within a phase-space control element [d3 r·d3 e] about r and e (r is the particle’s co-ordinate in physical space and e is the particle’s discrete velocity; Nourgaliev et al. 2003). Here, a is the external force per unit mass acting on the particle. The last term of the above equation represents the collision between the two particles and is known as the "BGK collision operator" (Bhatnagar et al. 1954). The equilibrium distribution f eq is generally taken to be the Maxwell–Boltzmann distribution for molecules for which \(\nabla_{\bf e} f \approx \nabla_{\bf e} f_{{\rm eq}} = \frac{{{\mathbf{e}}}-{{\mathbf{u}}}}{RT}f_{\rm eq}.\) Thus,

$$ \frac{\partial f}{\partial t} + {{\mathbf{e}}} \cdot \nabla_{\bf r} f = - \frac{f - f_{\rm eq}}{\tau} + \frac{{{\mathbf{a}}} \cdot \left({{\mathbf{e}}} - {{\mathbf{u}}}\right)}{RT}f_{\rm eq}. $$
(7)

The velocity space e can be discretized into a finite set of velocities {e α }. Discretizing in time and space along a discretized velocity direction, we obtain the discrete Boltzmann equation on a lattice space or the lattice Boltzmann equation as follows,

$$ f_{\alpha} {\left({{{\mathbf{r}}}_{i} + \hbox{e}_{\alpha} {\rm \delta} t,t + {\rm \delta} t} \right)} - f_{\alpha} {\left({{{\mathbf{r}}}_{i}, t} \right)} = - \frac{1}{{\tau^{*}}}{\left[{f_{\alpha} {\left({{{\mathbf{r}}}_{i}, t} \right)} - f_{\alpha}^{\rm eq} {\left({{{\mathbf{r}}}_{i}, t} \right)}} \right]} + \frac{{{\mathbf{a}}} \cdot {\left({{{\mathbf{e}}}_{\alpha} - {{\mathbf{u}}}} \right)}\delta t}{RT}f_{\alpha}^{\rm eq} {\left({{{\mathbf{r}}}_{i}, t} \right)}. $$
(8)

The relaxation time is related to the fluid viscosity through the relation \(\nu = \frac{1}{3}{\left({\tau^{*} - 0.5} \right)}\frac{{{\rm \delta} x^{2}}}{{{\rm \delta} t}}.\) In Eq. (8), f α (r i , t) is the f distribution corresponding to the αth discrete velocity e α and f eq α is the corresponding equilibrium distribution in the discrete velocity space.

A popular lattice model is the two-dimensional nine-velocity (D2Q9) model (Fig. 2) for which the discrete velocities are

$$ {{\mathbf{e}}}_{\alpha} = \left\{{{\left({0,0} \right)},\alpha = 0;\quad c{\left\{{\cos {\left({\alpha - 1} \right)}\frac{\pi}{4}, \sin {\left({\alpha - 1} \right)}\frac{\pi}{4}} \right\}},\alpha = 1,3,5,7;\quad{\sqrt 2}c{\left\{{\cos {\left({\alpha - 1} \right)}\frac{\pi}{4}, \sin {\left({\alpha - 1} \right)}\frac{\pi}{4}} \right\}}, \alpha = 2,4,6,8} \right., $$
(9)

where c = δx/δt. The equilibrium distributions in the corresponding directions are

$$ f_{\alpha}^{\rm eq} = \rho w_{\alpha} {\left[{1 + \frac{3}{c^{2}}{{\mathbf{e}}}_{\alpha} \cdot {{\mathbf{u}}} + \frac{9}{2c^{4}}{\left({{{\mathbf{e}}}_{\alpha} \cdot {{\mathbf{u}}}} \right)}^{2} - \frac{3}{2c^{2}}{\left({{{\mathbf{u}}} \cdot {{\mathbf{u}}}} \right)}} \right]}. $$
(10)

The weights in Eq. (10) are

$$ w_{\alpha} = \left\{{\frac{4}{9},\alpha = 0;\quad\frac{1}{9},\alpha = 1,3,5,7;\quad\frac{1}{36},\alpha = 2,4,6,8} \right\}. $$
(11)

The fluid density and momentum are calculated from the moments of the distribution function,

$$ \rho = {\sum\limits_\alpha {f_{\alpha}}} = {\sum\limits_\alpha {f_{\alpha}^{\rm eq}}}\,\hbox{and}\, \rho {{\mathbf{u}}} = {\sum\limits_\alpha {f_{\alpha} {{\mathbf{e}}}_{\alpha}}} = {\sum\limits_\alpha {f_{\alpha}^{\rm eq} {{\mathbf{e}}}_{\alpha}}}. $$
(12)

The body force per unit mass responsible for the EOF is

$$ {{\mathbf{a}}} = \frac{\rho_{e}}{\rho}{\left({{{\mathbf{E}}} - \nabla \psi} \right)} = - \frac{{\kappa^{2} \varepsilon \psi}}{\rho}{\left({{{\mathbf{E}}} - \nabla \psi} \right)} = - \frac{\kappa^{2} \varepsilon}{\rho}{\left({\psi {{\mathbf{E}}} - \frac{1}{2}\nabla \psi^{2}} \right)}. $$
(13)

where E = −∇ϕ denotes the external electric field. The first term in parentheses is responsible for fluid flow along the wall and is used to calculate a. The second term 1/2∇ψ 2 is normally neglected in the literature on electroosmotic flow in comparison with the first tem in the parenthesis, ψ E. Our contribution is through the inclusion of this term which extends the formulation to cases involving large gradients in streaming potential. This term, can be added to ∇p to obtain an effective pressure gradient ∇p′ = ∇(p + 1/2ψ 2), which increases the pressure near the wall. A similar inclusion of gradients of scalar potentials has been reported in the context of buoyancy-driven flows (de Vahl Davis 1983; D’Orazio et al. 2004) and thermomagnetic convection (Mukhopadhyay et al. 2005) in enclosures. The pressure can be obtained form the relation \({p}^{\prime} = \frac{1}{3}\rho c^{2}.\)

Fig. 2
figure 2

Schematic of lattice Boltzmann nodes

Full size image

At all the four walls no-slip boundary condition is applied as proposed by Zou and He (1997). The boundary condition is based on bounce back of the non-equilibrium part of those distribution functions f, which are perpendicular to the wall. Therefore,

$$ f_{3}^{\rm neq} = f_{7}^{\rm neq} \,\hbox{and}\,f_{1}^{\rm neq} = f_{5}^{\rm neq} $$
(14a,b)

for horizontal and vertical walls, respectively.

For this boundary condition wall velocities are specified while the density and the unknown f distributions are calculated by using Eqs. (12) and (14a, b).

We consider electroosmotic mixing in a 10 μm × 10 μm cross-section square enclosure where the four walls can have different but homogenous ζ potentials (Fig. 1). We assume that the Debye length ∼100 nm, which can be generated in an aqueous monovalent ion solution of 10−6 M concentration. The electric potential ψ is normalized by the term k B T/ze (= 25.69 mV for z = 1). The normalized electric field E * = E/k B T/zeδx). For a square cavity of 10 μm sides with 501 node points (δx = 20 nm), E * = 1 is equivalent to a dimensional value of 1.28 V/μm. The fluid properties such as density, viscosity, and permittivity are assumed to be those of water.

3 Results and discussion

We consider fluid mixing due to different homogeneous wall zeta potentials in the presence of a steady applied electric field for which the various cases are listed in Table 1. At first, the flowfield is obtained by solving the lattice Boltzmann equation as discussed in the previous section. Once the steady flowfield is obtained a number of passive tracer particles are introduced in the flow. The motion of a tracer particle is obtained by solving the relation \(\frac{{\rm d}{{\mathbf{R}}}}{{{\rm d}t}} = {{\mathbf{u}}},\) where R = (x, y) denotes the particle position and u the fluid velocity at that location. The above equation is solved using an explicit Euler method and selecting the time step δt such that uδt ≈ 0.01 δr, where δr denotes the lattice spacing. Two types of passive tracer particles, white and black, are introduced into the top and bottom halves of the cavity, respectively. The resulting visualization of mixing by observing the motions of the passive tracers is purely that due to advection.

Table 1 The different configurations investigated
Full size table

Figure 3 presents the steady-state velocities and equilibrium tracer particle distributions for Cases I–V. Figure 3a presents results for Case I, when ζ = 1 for the top horizontal wall while ζ = 0 for all other walls, and an electric field E * X  = 0.01 is applied in the X-direction. This produces an EDL very close to the top surface, and the electric field forces the fluid to circulate clockwise inside the cavity. The center of the vortex is very close to the top surface and the circulation loops lie primarily within the top half of the cavity. Consequently, the tracer particles in the upper and lower halves of the cavity remain confined in those portions, although a few, close to the vertical wall, move between these halves. The white particles are mostly concentrated in the top half following the fluid circulation while a few others become sparsely distributed elsewhere.

Fig. 3
figure 3

Steady state velocity vector and passive tracer particle locations for different cases listed in Table 1

Full size image

Figure 3b corresponds to Case II when ζ = 1 for the right wall with the other walls at ζ = 0. An EDL is again produced close to the right wall. With E * Y  = 0.01 applied in the upward direction, the fluid near the right wall also moves upwards inducing circulation and good mixing in the right half of the cavity.

Figure 3c presents similar results for Case III when the two vertical walls are imparted unit zeta potentials while the horizontal walls are maintained at ζ = 0, and an upward field E * Y  = 0.01 is applied. Two EDLs are formed along the two vertical walls for this case, which induce upward fluid motion along both interfaces. This results in two symmetric circulations within the cavity, one clockwise and the other counter-clockwise. The tracer particles are thus able to move and mix vertically, except at the center of their respective vortices, but those that originate within the right or left halves remain confined to those sections.

The mixing for Case IV is presented in Fig. 3d for which the right and the left walls are given unit positive and negative zeta potentials, respectively, while the applied electric field acts upward. The fluid along the right wall starts moving upward while that along the left moves down, creating circulation in the entire cavity. At the end, particles of both kinds are well mixed throughout the domain.

Results for case V are shown in Fig. 3e when all walls have unit positive zeta potentials while the applied field is along both the X and Y directions (E * X  = 0.01, E * Y  = 0.01). This zeta potential distribution results in the formation of four EDLs, one along each wall. The fluid along the two vertical walls moves upward as a result while that along the horizontal walls moves rightward, which results in two triangular circulations inside the cavity. The tracer particles at the centers of vortices remain in the corners while other particles move diagonally creating two relatively unmixed triangular regions.

Mixing can be characterized through the mixing efficiency (Xia et al. 2006) or the Shannon entropy (Camesascal et al. 2005), which are interrelated. To do so, we divide the entire domain into a number of cells, and determine the number of white and black particles present in each of them. The i × j cells (i representing rows and j columns) in the domain are initially filled with N 1 and N 2 numbers of white and black particles respectively. Since the two mixing quantities provide equivalent descriptions, we present results for the mixing efficiency only.

The uniformity of mixing is measured through the mixing efficiency, which represents the standard deviation of mixing. If the kth cell has n k1 and n k2 particles, respectively, of the two types, the mixing efficiency (Xia et al. 2006)

$$ \sigma = \sqrt{\sum\limits_{k = 1}^{i \times j} \omega^{k} {\left[\frac{n_{1}^{k}}{n_{1}^{k} + n_{2}^{k}} - \frac{N_{1}}{N_{1} + N_{2}} \right]}^{2}}, $$
(15)

where, ω k = (n n1  + n k2 )/(N 1 + N 2) denotes the weighting factor. For binary mixing with the material ratio 1:1 (i.e., N 1 = N 2 = N), the standard deviation σ ranges from 0 for complete mixing to 0.5 for nonmixed particles.

The accuracy of these mixing parameters depends on the numbers of tracer particles and cells used in their determination. Considering a large number of cells increases the resolution but also increases the probability of finding spurious local nonhomogeneities, e.g., when only a single particle is present in a cell. It is therefore important to optimize the number of cells and particles used. We found that 104 particles and 20 × 20 cells provided useful measures of the mixing parameters for our simulations.

The temporal evolution of the mixing parameter is normalized by the time scale, t H-S = L/UH-S where UH-S = μ EOE is the Helmholtz–Smoluchowski electroosmotic velocity, Here, E denotes the applied electric field and μ EO the electroosmotic mobility of the ions. The ion mobility depends on the wall ζ potential, the permittivity of the medium, and the fluid viscosity through the relation μ EO = ɛζ/μ.

The tracer particles are initially entirely unmixed, i.e., σ = 0.5. The evolution of mixing efficiency is presented in Fig. 4. With the progression of mixing, the value of σ decreases. The mixing efficiency is overall poor for Cases I and V, reaching the minimum values σ min∼ 0.33. This result concurs with Fig. 3, which shows that for Case I most particles remain in their respective halves of the cavity, and form two discrete triangular regions for Case V. Mixing improves for Cases II, III and IV. Case II produces the most rapid mixing (σ min ∼ 0.12), while Cases III and IV produce slower but marginally better mixing (σ min ∼ 0.11).

Fig. 4
figure 4

Variation in the mixing efficiency with respect to the normalized time for the different cases listed in Table 1

Full size image

Next, we investigate the influence of varying E * Y between 0.01 and 1 for Case III. Figure 5 presents the corresponding changes in σ. The plots for the variation of σ over t * collapse on each other, yielding the relation σ = 0.67t *−1/4. This implies that the quality of mixing (i.e., the minimum value of σ) can be described by considering the normalized time alone. When the value of E increases but t * is held constant, the dimensional time t required to achieve a specific σ value decreases, i.e., mixing occurs more rapidly. Decreasing the mixing time involves decreasing the channel length thus aiding miniaturization. According to Fig. 5, the equilibrium value of σ is reached at t * ∼ 1,000. The actual mixing time can be calculated by using the relation t * = t/t H-S, as previously discussed. A time t * = 1,000 corresponds to t ∼ 73 s for E * Y  = 0.01, while for E * Y  = 0.1 and 1.0, the value of t ∼ 7.3 and 0.73 s, respectively. On the other hand, the diffusion time scale t D = L 2/D ∼ 103−104 s for L = 10 μm and diffusivity D of water-soluble organic molecules ∼10−14−10−13 m2/s (Elias 1983).

Fig. 5
figure 5

Variation of mixing efficiency with normalized time t * = t/t H-S for different electric field strengths

Full size image

Similar effects of electric field strength (E * X and E * Y ) on σ were observed for all other configurations in Table 1. Consequently, similar to the analysis of Case III, it is possible to generate different power series correlations between σ and t * for other configurations.

4 Conclusions

Stokes flow through a microchannel can be considered as the result of the superposition of a one-dimensional axial flow upon the two-dimensional transverse flow along any of its cross-sections. We have simulated the corresponding two-dimensional transverse EOF using LBM. Instead of the commonly used Helmholtz-Smoluchowski (H-S) slip velocity formulation, we have spatially resolved the EDL to determine the local EOF velocity. Our simulations show that rapid mixing can be achieved by using a homogeneous zeta potential and a steady electric field. The quality of mixing depends on the choice of wall which is provided with a zeta potential and the corresponding direction of the electric field. Mixing is enhanced when a ζ potential is imparted to the channel wall that is perpendicular to the initial particle distribution and when an electric field is also applied along the direction of this potential. The rapidity of mixing can be characterized by a normalized time that depends upon the electroosmotic time scale. In general, a stronger electric field induces more rapid mixing. This configuration decreases the mixing time for water-soluble organic molecules by four orders of magnitude.