1 Introduction

Micro-fluidic devices have found many applications in medical, biochemical and biological instruments in recent years [1]. These devices appropriate for transport, mixing, separations, and/or reactions, are necessary for LoC applications. Additionally, their operation defines the total performance of LoC systems; thus, their design is of crucial importance [2]. For example, a well-designed micromixer can reduce the analysis time as well as the footprint of LoC platforms [3]. The performance of these devices strongly depends on the surface property of the microchannel. It is well established that the surface property is a dominant factor to the behavior of micro-flows such as electrokinetic phenomena and flow resistance [4]. Electrokinetic phenomena are related to the electrochemical properties of both the surface and fluid, in which the fluid motion and electrical force are interacting with each other [5, 6]. One major category of these phenomena is the electro-osmotic phenomenon, in which the external electrical field causes the fluid to flow because the electrical field creases force the ions aggregated adjacent to the wall [7, 8]. This kind of flow has been extensively used for transfer and mixing of fluids in microflows which are the basis for lab-on-a-chip devices [9]. To determine the electro-osmotic flow field, in addition to the continuity and momentum equations, the equations that describe electrical potential and electric charges transfer need to be established and solved. Solving these equations for heterogeneous micro-channels either in geometry or properties, needs efficient numerical methods with significant computation cost [10, 11], hence some simple modeling approach such as Helmholtz–Smoluchowski model has been proposed [12,13,14], which reduces the computational cost considerably. Another surface phenomenon which plays an important role in micro-fluidic systems is the slip of fluid on the solid surface. Experimental studies have shown that considerable liquid slip occurs at walls with low energy level (hydrophobic), even at low Reynolds (Re < 10) [15,16,17]. Experimental observations have also shown that significant slip occurs on the highly charged surfaces [18]. Furthermore, there is an experimental evidence indicating that slip considerably enhances wall zeta-potential even for typical values of slip coefficient and Debye–Hückel parameter [19] which also has been confirmed with the theoretical model based on the free energy of binary mixtures [20]. In order to examine the effects of slip and the Electric Double Layer (EDL) simultaneously, the physically proper model needs to be employed. Fortunately, the molecular dynamic simulation of the water–solid interface has shown that the electric charges distribution in the presence of hydrodynamic slip can be well determined by conventional Poisson–Boltzmann equation [21].

The general features of electro osmotic flows have been examined thoroughly either by means of experimental studies [22, 23] or numerical simulations [24] and affecting parameters have been analyzed. Furthermore, the mixing performance of electro osmotic flows has been examined for both passive and active micro-mixers [25, 26]. Studies of electrokinetic mixing are mostly performed using Nernst–Planck equations [11, 26, 27] and there are a few investigations in which Helmholtz–Smoluchowski model [12,13,14] has been used to evaluate the mixing performance. On the other hand, examination of the results of Helmholtz–Smoluchowski model for mixing efficiency at various conditions indicates that this model can be used with acceptable accuracy if Debye–Hückel parameter and wall zeta-potential are properly selected [20, 28]. In many studies, mixing has been evaluated based on the averaged or standard deviation of concentration profiles [5, 6, 25, 29]. For simple flows without vortexes, this method presents a reasonable result; however, in complex flows containing vortexes, mixing efficiency exhibits some fluctuations in neighborhoods of the vortexes which are believed to be related to concentration gradients in the vortex area. An alternative method to evaluate the mixing efficiency is using an index based on the mixing entropy which has mostly been used in homogenous microchannels [30,31,32].

In this study, we employed the mixing entropy which was properly modified to examine the mixing performance of electroosmotic flows in heterogeneous microchannels. The effects of hydrodynamic slip have also been investigated on the mixing performance with both Nernst–Planck and Helmholtz–Smoluchowski (H–S) models. Furthermore, the conditions of H–S model in terms of governing parameters for relatively accurate predictions of electro-osmotic mixing in hydrophobic heterogeneous microchannels are clarified which was not properly examined in previous studies. It should be said that the heterogeneities are placed in a physical barrier in most previous studies while the nature of which is structurally and substantially different from the present paper. Actually, the innovation of the present paper relies on heterogeneous design on the surface properties of the microchannel wall (not with the help of heterogeneous geometry in fluid flow paths). This aspect of innovation will reduce the cost of building such electroosmotic heterogeneous micromixer and make them more applicable.

2 Governing equations

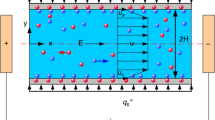
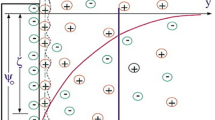
Solid surfaces in contact with electrolyte solutions gain charges and affect the distribution of electrolyte electric charges in the vicinity of the surface. The fluid layer adjacent to the solid surface, in which the electric charges have formed a new arrangement as shown in Fig. 1, is called the electric double layer or EDL [33]. The direct measurement of the electric potential on the interface of solid–liquid is difficult but it is possible at the shear plane with experimental methods. The electric potential in this plane is called zeta-potential and considered as a property for the interface of solid–liquid. In this case if an external electric field is applied, the fluid is then forced to move along the electric field known as Electro-osmotic flow. For a homogenous micro-channel with no-slip condition, the distributions of the electric potential and electro-osmotic velocity profile can be schematically shown in Fig. 1.

Fig. 1
figure 1

Velocity and electric potential distribution in an electroosmotic flow

Full size image

In this study it is assumed that the symmetric electrolyte solution flowing through the microchannel is an incompressible Newtonian fluid and the gravitational effects are negligible. Under these conditions the governing equations are introduced as follows:

2.1 Electric potential field

According to the electrostatic theory, the external potential field is governed by Laplace equation. Besides, the relation between electrochemical potential with electric charges distribution is described by Poisson’s equation. Hence, the equation for the total electric potential in the non-dimensional form is [34]:

$$\nabla^{2} \left( {\psi + \phi } \right) = \frac{{{\text{K}}^{2} }}{2}\left( {n^{ + } - n^{ - } } \right)$$
(1)

\({\text{K}} = H/\lambda\) is Debye–Hückel non-dimensional parameter and \(\lambda\) is the characteristic thickness of the electric double layer (EDL). \(\psi\) and \(\phi\) are the internal and external electric potentials, respectively.

2.2 Nernst–Planck equations

The distribution of ions in the electrolyte solution is obtained by solving the conservation of mass for electric charges known as Nernst–Planck equations. The non-dimensional form of this equation is as follows [34]:

$$\vec{\nabla } \cdot \left( {\vec{V}n^{i} } \right) = \frac{1}{{{\text{Re Sc}}^{\text{i}} }}\left\{ {\nabla^{2} n^{i} + \vec{\nabla } \cdot \left[ {n^{i} \left( {\vec{\nabla }\psi + {\text{A}}\vec{\nabla }\phi } \right)} \right]} \right\}$$
(2)

\(Sc\) is the Schmidt number, which is defined as the ratio of momentum diffusivity (\(\nu\)) and mass diffusivity (\(D\)) of ions. The reference velocity used in Eq. (2) is the known Helmholtz–Smoluchowski velocity defined as \(U_{H.S.} = \varepsilon E_{ref} \zeta /\mu\). The above equation is written for both negative and positive ions (i.e. \(n^{i} = n^{ + } ,n^{ - }\)). Also \({\text{A}} = E_{ref} H/(K_{b} T/{\text{z}}e)\) is a non-dimensional parameter which is the ratio of external induced voltage to the based voltage.

2.3 Navier–Stokes equations

The electro-osmotic flow field under steady conditions with the constant physical properties is governed by the non-dimensional Navier–Stokes equations in the form of [34]:

$$\vec{V} \cdot \nabla \left( {\vec{V}} \right) = - \vec{\nabla }{\text{P}} + \frac{1}{\text{Re}}\nabla^{2} \vec{V} - {\text{B}}\rho_{e} \left( {\vec{\nabla }\psi + {\text{A}}\vec{\nabla }\phi } \right)$$
(3)

\(B = n_{0} K_{b} T/\rho U_{ref}^{2}\). is a non-dimensional parameter presenting the ratio of ionic pressure to dynamic pressure. The last term on the right-hand side of Eq. (3) is the body force exerted by the electric field to the net charge of the fluid, which generates the electro-osmotic flow. In the case of the hydrophobic microchannels, the slip boundary condition is considered in its non-dimensional form as \({\text{u}} =\upbeta\left( {\partial {\text{u}}/\partial {\text{n}}} \right)\), where \(\upbeta\) is the slip coefficient.

2.4 Helmholtz–Smoluchowski model

For the electro-osmotic flow in a homogenous channel with thin EDL, it is possible to use Helmholtz–Smoluchowski approximation in which the effect of Coulomb force on the flow field is considered by applying an appropriate boundary condition for Momentum equation. For this purpose, a slip velocity is defined in terms of the applied electric field and wall zeta-potential as [35, 36]:

$$u_{s} = - \frac{{\varepsilon E_{\text{ext}} \zeta }}{\mu }$$
(4)

Implementing this condition, the effect of electric force in Navier–stokes equations is simulated. Hence there is no need to solve the Nernst-plank and Poisson’s equations, which saves considerable computational costs. The electro-osmotic flow field is then obtained by solving Navier–Stokes equations without the body force along with slip boundary condition [35, 36]:

$$\vec{V} \cdot \nabla \left( {\vec{V}} \right) = - \vec{\nabla }{\text{P}} + \frac{1}{\text{Re}}\nabla^{2} \vec{V}$$
(5)

2.5 The concentration equation

In order to investigate the mixing of electro-osmotic flows, the convection–diffusion equation for the concentration of a virtual species is considered. The non-dimensional form of the equation is [36]:

$$\vec{V} \cdot \vec{\nabla }C = \frac{1}{\text{Re Sc}}\nabla^{2} C$$
(6)

where \(Sc = \nu /D\) is the Schmitt number of the virtual species. The concentration distribution of species in the inlet of the microchannel is defined as:

$$C\left( {x = 0, y} \right) = \left\{ {\begin{array}{*{20}c} { 0 \quad 0 < y < \frac{H}{2}} \\ \\ {1\quad \frac{H}{2} < y < H} \\ \end{array} } \right.$$
(7)

2.6 Mixing entropy index

The Shannon’s entropy index, which reflects the diversity of species in a dataset has been used as a measure for evaluating the mixing performance according to the following equation [37, 38]:

$$S_{\text{mix}} = - \mathop \sum \limits_{j = 1}^{M} C_{j } {\text{Ln}}\left( {C_{j } } \right)$$
(8)

In this relation \(C_{j }\) indicates the concentration at each data point and \(M\) is the total number of the points. Based on Eq. (8) the modified diversity index for the moving species through a channel is presented as [31]:

$$S_{\text{mix}} = \frac{{ - \mathop \smallint \nolimits_{A}^{ } \left[ {C {\text{Ln}} C} \right] \rho u{\text{d}}y}}{{\mathop \smallint \nolimits_{A}^{ } \rho u {\text{d}}y}}$$
(9)

As a modification to relation (8), the mass flow rate has been considered as a weight function, which prevents local fluctuation near vortex regions. \(A\), is the cross-sectional area, \(u\) is the velocity component normal to the area and \(C\left( y \right)\) is the cross-sectional concentration distribution. Based on the weighted entropy index, the mixing efficiency at any cross-section of the microchannel is defined by Eq. (10):

$$\varepsilon_{s} = \frac{{S_{\text{mix}} - S_{\text{inlet}} }}{{S_{\infty } - S_{\text{inlet}} }}$$
(10)

According to the inlet concentration distributions given by Eq. (7), \(S_{inlet} = 0\) is obtained. In addition, \(S_{\infty }\) is evaluated at the outlet of an extremely long microchannel for which perfect mixing occurs with C = 0.5. Consequently, the mixing efficiency based on Eq. (10) is reduced to \(\varepsilon_{\text{s}} = {\text{S}}_{\text{mix}} /0.347\).

3 Micromixer details and notations

The schematic of the 2D flat microchannel designed for the purpose of an electro-osmotic micromixer is shown in Fig. 2. The microchannel has height H and length L = 6H, which is divided into three equal sections of length 2H.

Fig. 2
figure 2

Specifications of heterogeneous distribution of zeta-potential at microchannel walls

Full size image

In the middle section, the walls have heterogeneous zeta-potentials \(\zeta \left( {\text{x}} \right)\) composed of 4 patches with the same zeta-potential and length but different charge sign (i.e. positive or negative), while for the remaining walls constant zeta-potential is considered.

Clearly, three distinct arrangements of the patches in the middle section are possible if mirror image arrangements are discarded. For the first arrangement, the details of charges distribution and the corresponding flow field in middle section of the microchannel under the imposed electric field (from left to right) are shown in Fig. 3. This pattern will be denoted as the case (pn–np), since the upper wall has one positive (denoted by symbol p) and one negative (denoted by symbol n) patch, respectively, while a reverse arrangement is considered for the lower wall. According to this notation, two other arrangements are (np–np) and (pp–nn) cases.

Fig. 3
figure 3

Heterogeneous charge pattern (pn–np) and electro-osmotic flow streamlines with positive applied electric field from left to right

Full size image

4 Numerical solution and validation

The set of governing equations are highly coupled and hence a precise iterative procedure is performed to solve the flow and concentration fields and obtain the numerical solution for the set of coupled governing equations.

The calculations begin with the numerical solution of external electric field, which is the only uncoupled equation. Having been considered the proper initial distributions for electric field (both external and internal) and velocity field, Nernst–Planck equations are solved to obtain the distribution of electric charges. Actually, initial guesses for internal electric potential and velocity fields have been chosen to solve Nernst–Planck and Poisson equations, respectively. In this stage, the first estimation for electric body force can be evaluated.

Next, the electric body force is evaluated and consequently the resulting flow field can be obtained by solving momentum equations using the SIMPLEC algorithm. After this step, Navier–Stokes, Nernst–Planck and Poisson–Boltzmann equations are solved repeatedly until the adequate convergence is attained. The numerical iteration was performed until all the relative residuals were smaller than 10−16. Having the velocity field, the concentration equation will be solved in order to investigate the mixing performance.

It is worth to mention that a thorough mesh study has been performed and it is found that for transverse direction, grid refinement in the EDL is essential, while in the longitudinal direction uniformly fine grid results in a better convergence rather than locally refined grid. Therefore, for a channel with the length of L = 6H, a mesh with 251 longitudinal nodes and 151 lateral nodes has been considered for which at least 30 nodes exist within the EDL. In Fig. 4 a typical grid study with more focus in lateral direction has been performed for mixing efficiencies with charge pattern of (np–np) and \(\zeta_{p} /\zeta_{m} = 0.1\). As can be seen in this figure, the properties distribution on the wall is a discontinuous function so that the physical fluctuations are more intense at the discontinuity nodes, but the increasing number of the nodes improves the solution. In the microchannel entrance area where more intense mixing occurs, the achievement of independence of nodes is postponed while it is easier to achieve the independence of the node at the end of the microchannel. Although the amount of changes will not be well understood by the changing of the node for the curve with a slight slope, the changes are well visible for the curve with a greater gradient. In other words, there are changes in the results due to nodal changes everywhere so that these changes are more at the beginning and lower at the end of microchannel. Although these changes are not observed in the initial part because of the greater gradient of the curve, they are better seen in discontinuous areas with low gradients. In the Fig. 4, this area is magnified to observe obviously.

Fig. 4
figure 4

Investigation of mesh independency for mixing efficiency

Full size image

The validation for both full N–S and approximate H–S modeling has been presented in the case of no-slip flow for velocity profiles with two different values of Debye–Hückel parameter as shown in Fig. 5. It is seen that numerical solutions of full electroosmotic flow (i.e. Eqs. (1–3)) agree well with analytical solutions, while approximate simulations based on Helmholtz–Smoluchowski model (i.e. Eq. (5)) are independent of K and predict the analytical solutions only in the core region of the microchannel. We will examine the accuracy of the H–S model in more details in next sections, when mixing performances are discussed.

Fig. 5
figure 5

Comparison of full electro-osmotic and H–S approximate models velocity profiles with analytical solutions

Full size image

In order to examine the validity of the numerical procedure, the electroosmotic velocity profiles in a flat homogeneous microchannel has been solved with and without wall slip velocity and compared with the analytical solutions as described by Hunter [35, 36, 39]:

$$\frac{\psi \left( y \right)}{\zeta } = \frac{{\cosh \left( {{\text{K}}y - {\text{K}}/2} \right)}}{{\cosh \left( {{\text{K}}/2} \right)}}$$
(11)
$$\frac{u\left( y \right)}{{U_{\text{ref}} }} = 1 + {\text{K}}\upbeta\tanh \left( {{\text{K}}/2} \right) - \frac{\psi \left( y \right)}{\zeta }$$
(12)

In order to validate the numerical procedure with the presence of slip, the numerical solution of electro-osmotic velocity profiles in a homogeneous microchannel for two different values of slip coefficients were simulated and verified by the analytical solution presented in Fig. 6. This figure indicates that numerical results coincide perfectly well with analytical solutions.

Fig. 6
figure 6

Comparison of numerical velocity distributions in a homogeneous microchannel with analytical solutions with and without slip

Full size image

5 Results

As mentioned earlier, electrokinetic mixing is mostly studied using Nernst–Planck modeling and there are rather limited study in which H–S model is applied. In order to examine the validity of H–S model for electrokinetic mixing, the concentration field and mixing performance are obtained using Nernst–Planck modeling (Sect. 5.1) and then are compared to those of H–S modeling (Sect. 5.2).The last part of the results involves the examination of mixing performance in the hydrophobic microchannels with heterogeneous zeta-potentials which have been performed using Nernst–Planck model.

5.1 Mixing performance in heterogeneous microchannel without slip

As an illustration, the streamlines corresponding to the case (np–np) are shown in Fig. 7. It is seen that the existence of heterogeneities in the region \(2 < x \le 4\) forms strong vortexes near the positive patches where local electric body force acts against the bulk flow. These vortexes enhance the mixing significantly as will be discussed later. As mentioned earlier, the considered microchannel includes four patches in the middle section with the same absolute zeta-potential \((\zeta_{m}\)), while the remaining of the microchannel has a uniform zeta-potential represented by \(\zeta_{P}\). In fact, the middle section plays as mixing section, while the remaining of the channel provides pumping duty.

Fig. 7
figure 7

Streamline of heterogeneous microchannel with charge pattern (np–np) in middle section (Nernst–Planck solution)

Full size image

Variations of mixing efficiencies along the microchannel are shown in Fig. 8 for three different patterns discussed earlier. All patterns provide the same mixing efficiencies at the beginning of the channel but dramatically differ in the middle region where they have different zeta-potential distributions. From this figure, it is seen that the case (np–pn) provides better mixing efficiency at the channel exit as compared to other cases. For this case, the arrangement of charges in the middle section is more asymmetric than other cases and consequently higher mixing is attained. The worst mixing performance corresponds to the case which has the least asymmetry in the charge pattern.

Fig. 8
figure 8

Mixing efficiencies along the channel for different patterns of charges (\({\text{K}} = 41, \zeta_{\text{p}} /\zeta_{\text{m}} = 0.5\))

Full size image

One critical parameter affecting the electrokinetic mixing performance is the value of wall zeta-potential. In this study \(\upzeta_{m}\) has been assigned the value of 50 mV unless otherwise stated. Hence, the effects of wall zeta-potential on mixing efficiencies can be examined via different ratios of \(\upzeta_{p} /\upzeta_{m}\) as shown in Fig. 9. In this figure the axial variations of the mixing efficiencies for the case (np–np) at various ratios of \(\upzeta_{p} /\upzeta_{m}\) are compared. It is worthy to mention that when the zeta ratio (\(\upzeta_{p} /\upzeta_{m}\)) increases, the mass flow rate increases almost linearly due to the enhancement of EDL electric body force in the region that serves as pumping power.

Fig. 9
figure 9

Mixing efficiencies related to case (np–np) for different values of \(\zeta_{\text{p}} /\zeta_{\text{m}}\) and \({\text{K}} = 41\)

Full size image

In fact, the ratio of \(\upzeta_{p} /\upzeta_{m}\) can be interpreted as ratio of pumping power to mixing power of the electroosmotic flow. Therefore, at lower zeta ratios the residence time of the mixing fluid inside the channel increases and consequently higher mixing can occur. It is seen from Fig. 9 that almost perfect mixing (i.e. efficiency of 100%) has been achieved at \(\upzeta_{p} /\upzeta_{m} = 0.05\) right after the middle section of the channel, where \(x/H = 4\).

In order to investigate the effect of heterogeneities on the mixing performance, the mixing efficiency of the homogeneous microchannel is also plotted in Fig. 9 for the same conditions. It is seen that the existence of heterogeneities in the middle section of the microchannel significantly enhances the mixing efficiency. As a quantitative illustration, for the case with \(\upzeta_{p} /\upzeta_{m} = 0.05\), there is approximately 70% augmentation in mixing efficiency at the end of channel as compared to the homogenous channel.

A possible explanation for this significant augmentation is the formation of stronger circulation zones at relatively lower values of \(\upzeta_{p} /\upzeta_{m}\) due to the lower flow rates. The existence of vortexes in the confined space of microchannel creates a narrow and curly passage for the fluid flow, which the former increases the concentration gradients and the later increases the path-line of the species. Clearly, both higher gradients and longer path-line enhance the mixing performance.

Size and number of circulation zones depend on the flow and charge pattern in the intermediate section of the microchannel. Examination of different patterns indicates that highly heterogeneous microchannel provides better mixing in a shorter length as compared to the slightly heterogeneous or homogeneous microchannel. For example, as presented in Fig. 10, the mixing efficiency of the case (pp–nn) with \(\upzeta_{p} /\upzeta_{m} = 0.05\) approaches to its maximum value at about \(x \cong 2.5H\), while according to Fig. 9 for the same conditions, this level of efficiency for case (np–np) has been obtained at \(x \cong 4H\). This means that at the same settings microchannel with pattern (np–np) requires 60% extra length to provide mixing similar to that of the pattern (pp–nn).

Fig. 10
figure 10

Mixing efficiency along microchannel for case (pp–nn) at different values of \(\zeta_{\text{p}} / \zeta_{\text{m}}\) and \({\text{K}} = 41\)

Full size image

Another important parameter concerning the mixing performance is the Reynolds number. As it can be observed in Fig. 11, higher Reynolds numbers are associated with the lower mixing efficiencies.

Fig. 11
figure 11

Mixing efficiency along microchannel for case (np–np) at different Re numbers (\(\zeta_{\text{p}} / \zeta_{\text{m}} = 0.1\))

Full size image

The effect of Re number on the mixing is basically similar to the effect of zeta ratio \(\upzeta_{p} /\upzeta_{m}\). Lower Re number flows provide more time for diffusion of species, and therefore, higher mixing efficiencies are obtained at the channel exit. It is necessary to note that the reference velocity and the characteristic length in the Reynolds number are defined in term of wall zeta-potential and Debye–Hückel parameter, respectively. Therefore, Re number covers both effects of zeta-potential and Debye–Hückel parameter simultaneously.

5.2 Helmholtz–Smoluchowski model: accuracy and validation for mixing efficiency

The H–S approximate model has been frequently used and validated for predicting the electroosmotic flow field. However, for the purpose of mixing evaluation, there are rare studies in which validity of this model for mixing performance has been examined [10, 26]. In Fig. 12, the mixing efficiencies are plotted for three values of \(\upzeta_{\text{p}} /\upzeta_{\text{m}}\) for the case of (np–pn) with \({\text{K}} = 41\). The solid and dashed lines correspond to the results of the Nernst–Planck and the Helmholtz–Smoluchowski approximate solutions, respectively.

Fig. 12
figure 12

Axial variations of the mixing efficiencies; Nernst–Planck solution (solid lines); H–S approximate model (dashed lines) at different zeta-potential ratios for the case (np–np) with \({\text{K}} = 41\)

Full size image

According to Fig. 12, it is recognized that the H–S model slightly deviates from the Nernst–Planck solution as higher zeta-potential ratios. This feature is expected because H–S model is originally proposed for the channel with uniform zeta-potentials. Clearly, higher of zeta-potential ratios are associated with stronger non-uniformities of zeta-potential at intersections of patches. Figure 12 shows that at lower zeta-potential ratios (say \(\upzeta_{\text{p}} /\upzeta_{\text{m}} = 0.05\)) local deviations of the H–S model is fading along the channel such that the at the channel exit both models perform similarly. Similar findings have been observed for all arrangements of zeta-potential in the range of \(\upzeta_{p} /\upzeta_{m} \le 0.05\) and K > 21. For these circumstances, the accuracy of the H–S model at low zeta ratios is independent of both Debye–Hückel parameter and charge arrangement and is only determined by the value of the zeta-potentials ratio. Therefore, utilization of the approximate model in such conditions is suggested due to a significant saving in computational expenses. In order to make a quantitative comparison, Table 1 is prepared in which relative errors of H–S model in the evaluation of mixing efficiency (i.e. \((\varepsilon_{s, N - P} - \varepsilon_{s, H - S} )/\varepsilon_{s, N - P}\)) for \(K = 41\) are reported.

Table 1 Mixing efficiencies and relative errors of H–S model at the exit of the channel for different zeta-potential ratios (case (np–np), \({\text{K}} = 41\))
Full size table

It is expected that the Debye–Huckel parameter is also one of the parameters affecting the accuracy of the approximate model. In order to determine the effect of Debye–Hückel parameter on the accuracy of H–S model, the relative errors of H–S model are computed at different values of \(K\) and zeta-potential ratios for the case of (np–pn) and plotted in Fig. 13. It is observed that the relative error of Helmholtz–Smoluchowski model for mixing efficiency increases when \(K\) decreases. Furthermore, at relatively large zeta-potential ratios, the relative error increases rapidly when \(K\) decreases, while for small values of zeta-potential ratio the relative error is almost constant and independent of \(K\). For example, at \(\upzeta_{p} /\upzeta_{m} = 0.1\), when \(K\) reduces from 41 to 11, the relative error increases about \(0.29\%\). For the similar condition with \(\zeta_{p} /\zeta_{m} = 0.5\), the relative error increases to about \(10.5\%\).

Fig. 13
figure 13

Relative errors of mixing efficiency in terms of Debye–Hückel parameter at different zeta-potential ratios for case (np–pn)

Full size image

Therefore Helmholtz–Smoluchowski model predicts the mixing efficiencies with the relative error of less than one percent in the regions of low zeta ratios,\(\upzeta_{p} /\upzeta_{m} \le 0.1\), and high Debye–Hückel parameters, \(K > 11\). It is known that H–S model ignores the fact that EDL thickness is proportional to \(K^{ - 1}\). Therefore, for smaller values of \(K\), which correspond to the thicker EDLs, the effects of more extended region are neglected in H–S model, which leads to the less accurate results.

On the other hand, EDL thickness is also dependent on the wall zeta-potential such that the larger is the zeta ratio, the thicker is the EDL region. Consequently, at high zeta-potential ratios where EDL thickness becomes significant, H–S model fails to predict mixing efficiency accurately.

5.3 Effects of hydrophobicity on mixing efficiency

When microchannel walls are made of hydrophobic material, the no-slip boundary condition is no longer applicable because the liquid adjacent to the wall is allowed to have a slip velocity, which is proportional to the wall shear. In the non-dimensional form, it is convenient to consider this slip condition mathematically as u = βdu/dy. The effects of wall hydrophobicity can be examined through the coefficient of beta, known as slip coefficient. Figure 14 shows the effect of slip coefficient on the variation of mixing efficiencies for the arrangement (np–np).

Fig. 14
figure 14

Axial variations of the mixing efficiencies at different slip coefficients for case (np–pn) charge pattern and \({\text{Re}} = 0.003\)

Full size image

It is seen that presence of slip reduces the mixing efficiency significantly such that the maximum mixing happens in the case of no-slip. This is reasonable because slip velocity enhances the pumping effects rather than the mixing effects. According to Fig. 14 for Re = 0.003, when slip coefficient increases from 0.025 to 0.1, the value of mixing efficiency at the outlet decreases from 62.4 to 42% (i.e. 33% reduction) which is a significant reduction in mixing efficiency.

Figure 15 illustrates the corresponding flow fields of Fig. 14. It is seen that the size of circulating vortexes reduces when slip coefficient increases. As mentioned earlier, mixing efficiency is directly related to the vortex size. Hence, with the slip condition mixing efficiencies are less than their corresponding values with no slip condition.

Fig. 15
figure 15

Streamline for heterogeneous microchannel for case (np–pn) charge pattern

Full size image

The influence of Reynolds number on the mixing efficiency is shown in Fig. 16 for \(\upbeta = 0. 10\). From this figure, it is clear that velocity slip at all Reynolds numbers, causes severe reductions in mixing efficiencies as compared to the their corresponding cases of no-slip condition shown in Fig. 11.

Fig. 16
figure 16

Axial variations of mixing efficiencies along for different Reynolds numbers for (np–np) arrangement with \(\upbeta = 0.1\)

Full size image

The comparison between Fig. 11 and 16 at \(Re = 0.001\) indicates that when slip coefficient increases from zero to 0.1 the mixing efficiency decreases from 94.832 to 57.963% (i.e. 36.87% reduction), which is a significant reduction in mixing efficiency.

The axial variations of mixing efficiencies for (pp–nn) arrangement are shown in Fig. 17 for different slip coefficients at \(Re = 0.001.\) Similar to the case (np–pn) in Fig. 14, it is observed that the mixing efficiencies reduce when slip coefficient increases. In this case, the mixing efficiencies at the exit of the channel are relatively in a close range with no significant differences with the mixing efficiency of the homogenous channel (channel with no patch). Mixing efficiencies at the outlet are in the range of 82 to 95% and the efficiency of the homogenous channel at the channel exit is about 87%.

It is interesting to see that the mixing efficiencies of this case (pp–nn) at higher Re numbers are dramatically higher than the mixing efficiency of a homogeneous channel. To illustrate this point Fig. 18 is plotted for the same condition as Fig. 17 except for the Re number which is considered as 0.009.

Fig. 17
figure 17

Comparison of the mixing efficiencies of heterogeneous with homogeneous microchannel for the case (pp–nn) at Re = 0.001, \(\upzeta_{\text{p}} /\upzeta_{\text{m}} = 0.1\) and different slip coefficients

Full size image

It is seen that mixing efficiencies of non-homogenous channels at the outlet are in the range of 66% up to 76%. Surprisingly these values are dramatically different from the mixing efficiency of homogenous channel which is about 31.6%. Comparing Figs. 17 and 18 indicates that mixing efficiency enhances favorably with heterogeneous hydrophobic microchannel at large Reynolds numbers as compared to homogeneous microchannels. This is an important issue because at large Reynolds number the mixing performance is naturally weak as discussed earlier and any enhancement is favored.

Fig. 18
figure 18

Comparison of the mixing efficiencies of heterogeneous with homogeneous microchannel for the case (pp–nn) at Re = 0.009, \(\zeta_{\text{p}} /\zeta_{\text{m}} = 0.1\) and different slip coefficients

Full size image

6 Conclusions

In this article electro-osmotic mixing is studied by proposing a suitable mixing index (i.e., the mixing entropy) and the effects of influential parameters on mixing efficiency are discussed. The study shows that by means of electro-osmotic flow inside the heterogeneous hydrophobic microchannel and proper arrangement of heterogeneities, it is possible to design an electro-osmotic micromixer with a controllable mixing behavior. The behavior of such micromixers is affected by the arrangement of charge heterogeneities, the amount of wall zeta-potential, EDL thickness, Reynolds number and slip coefficient. The modeling of electro-osmotic mixing can be performed approximately by using the H–S model or accurately through the solution of Nernst–Planck equations. In this study, it is found that the accuracy of H–S model deteriorates with the decrease in Debye–Hückel parameter or with the increase in wall zeta-potential.

The numerical results show that in the range of \(K > 21\) and \(\zeta_{p} /\zeta_{m} < 0.10\), the relative error of H–S model in the computation of mixing efficiency is less than 0.5%. Examination of different charge patterns indicates that better mixing performances are achieved when the charge pattern is more asymmetric. Furthermore, it is seen that in non-homogenous microchannels, the mixing efficiency is mostly influenced by slip coefficient rather than Reynolds number. On the other hands, the mixing efficiencies of the non-homogenous channel with hydrophobic surface were no different from efficiencies of homogeneous microchannel at low Reynolds numbers. In contrary, at high Reynolds numbers mixing efficiencies of heterogeneous hydrophobic microchannel enhance successfully compared to the non-homogenous channel.