1 Introduction

Complex multi-physics fields, especially the coupling of mechanics and heat transfer, are a prominent issue in the design of modern engineering structures [1,2,3,4]. With high heat conduction demand for various mechanical and electronic components, a rational temperature range of the working environment should be considered. Due to the insufficient heat dissipation capacity, equipment may be damaged or users can be injured when the temperature exceeds the rated value. Meanwhile, structures should also withstand certain mechanical loads to prevent possible damage or complete fracture. How to advance a reasonable design approach, which can realize both temperature control and structural performance, is becoming a significant and challenging issue.

Topology optimization approaches evolved from an academic exercise into a forceful and practical tool and have been extensively explored to solve prominent problems for the conceptual design stage of engineering structures in the past decades, including the homogenization method [5], the density method [6, 7], the evolutionary method [8, 9], the level set method (LSM) [10], and the novel moving morphable component method (MMC) [11, 12]. Rodrigues and Fernandes [13] introduced an efficient optimization procedure of the 2D linear thermal-elastic structure using a material-based model. Sigmund and Torquato [14] utilized a numerical homogenization method to obtain composite materials with extremal thermal expansion coefficients. Then, a concurrent topology optimization method was proposed to minimize the structural compliance of thermo-elastic structures under thermal and mechanical loads [15, 16]. To characterize the dependence of the thermal stress loads upon the design variables, the penalization of thermal stress coefficient (TSC) was introduced to solve thermo-elastic problems with multiphase conditions [17]. The LSM based on a unified topological sensitivity was presented to solve the large-scale computational stress-constrained problems in thermo-elastic optimization [18]. In contrast to a volume constraint, Zhu et al. [19] presented a temperature-constrained method for thermo-elastic coupling problems. Furthermore, Meng et al. [20] proposed a stress-stabilizing control scheme to achieve volume minimization in thermo-elastic topology optimization. Numerical results in their work indicated that the proposed method can significantly reduce the temperature of the optimization structure. Therefore, topology optimization is a promising tool for achieving the ideal design of thermo-elastic structures. All the above-mentioned studies for thermo-elastic structures focused on uniform temperature fields or steady-state heat conduction problems.

In fact, most heat transfer phenomena are essentially transient in nature, which has received relatively more concerns due to their significance in recent years. Turteltaub [21] extended the method of solid isotropic material with penalization (SIMP) for transient heat conduction topology optimization, aiming to minimize the difference between actual and desired values of heat compliance at a prescribed time. Using a global heat compliance measure, the minimization of the peak value of transient heat compliance was implemented by Zhuang and Xiong [22, 23]. As mentioned by Wu et al. [24], a temperature control function for a transient heat conduction structure was proposed. The topology optimization model can precisely reflect the transient effect and generate adequate transient topological structures. Zhao et al. [25] investigated a non-Fourier transient heat conduction topology optimization method considering global thermal dissipation energy minimization. Li et al. [26] proposed a multi-material topology optimization method for transient heat conduction structures with several different optimization functions. These scholars have conducted in-depth studies around the transient heat conduction problem but have yet to extend their research to the transient problem of thermo-elastic coupling structures. Several scholars have paid attention to the transient thermo-elastic coupling problem and conducted related studies in recent years [27, 28]. However, these studies tend to solve the problem with the dynamic response as the objective function and the volume fraction as the constraint, thus neglecting the temperature control problem, which is of great concern to us. Therefore, how to achieve temperature control of transient thermo-elastic coupling structures by topology optimization still needs to be solved.

In this paper, a topology optimization design method for transient thermo-elastic structures is proposed. The regional temperature control scheme is developed to effectively constrain the maximum temperature value for the optimal topologies with the influences of heat loading time, material volume fraction, and maximum temperature constraint. Meanwhile, the minimization of structure compliance is considered as the objective function to increase the capacity of the topology results to withstand mechanical and thermal expansion loads. Several numerical examples are investigated to validate the proposed method.

2 Formulation of the Optimization Problem

2.1 Finite Element Parameterization

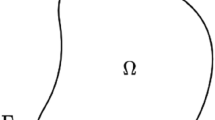
Figure 1 shows a generalized domain for transient linear thermo-elastic coupling optimization problem in two dimensions, which contains a design domain Ω with fixed displacement boundary Γd and temperature boundary ΓT. The invariable surface force f is exerted on boundary Γf, and the time-dependent heat flux q(t) is imposed on boundary Γq. All material properties are presumed to be isotropic. The transient thermo-elastic coupling problems can be specified as the following governing equations:

$$\left\{ \begin{gathered} - \nabla \cdot {\varvec{\sigma}}({\varvec{u}}(\Delta T(t))) = \user2{f } \hfill \\ {\varvec{u}}(t) = 0{\text{ on }}\Gamma _{d} \hfill \\ \end{gathered} \right.$$
(1)
$$\left\{ \begin{gathered} \rho c\frac{\partial T(t)}{{\partial t}} - \nabla \cdot k(\nabla T(t)) = Q(t) \hfill \\ - k\frac{\partial T(t)}{{\partial n}} = q(t){\text{ in }}\Gamma _{{{q}}} \hfill \\ T(t) = T_{{{f}}} {\text{ on }}\Gamma _{{{T}}} \hfill \\ T(t)\left| {_{t = 0} = T_{0} } \right. \hfill \\ \end{gathered} \right.$$
(2)

where σ is a stress tensor, t is the time variable of the transient process, u(t) is the displacement vector, T(t) is the structural temperature field, ρ is the material density, c denotes the specific heat of the material, Q(t) represents the internal heat energy generated, n is the unit outward normal vector of boundary, Tf is the prescribed temperature on boundary ΓT, ΔT(t) = T(t) − Tr, Tr is a reference temperature, k denotes the heat conduction coefficient, and T0 is the initial temperature.

Fig. 1
figure 1

Generalized thermo-elastic structural design domain

Full size image

In this article, the solution process of transient thermo-elastic coupling problems is based on the following assumptions. First, the external mechanical load of the thermo-elastic structure is static. Second, the heat energy is transferred by diffusion while the effect of convection and radiation is ignored. Third, the thermo-elastic coupling is one-way, in which the effect of structural deformation with respect to the heat transfer in the temperature field is negligible. Fourth, the thermo-elastic structure is considered to assume a small temperature variation range over time compared with the reference temperature so that inertia and damping effects can be neglected. Consequently, due to thermal expansion, the thermal stress analysis procedure is based on a quasi-static problem. When calculating the displacement and stress at a certain moment, the thermal load at that moment is regarded as static to solve the equilibrium equation.

With the above assumptions, the transient thermo-elastic problems can be considered as a combination of thermal and mechanical problems. Based on the application of the variational principle and finite element method (FEM), the thermal problem is governed by the discretized equation of transient heat conduction, which can be described as follows:

$${\varvec{C}}({\varvec{\rho}})\dot{\user2{T}}(t) + {\varvec{K}}_{{{T}}} ({\varvec{\rho}}){\varvec{T}}(t) = {\varvec{P}}(t)$$
(3)

where T is the node temperature vector, P(t) denotes the time-dependent nodal thermal load vector, KT(ρ) is the global heat conductivity matrix, C(ρ) is the heat capacity matrix, \({\varvec{\rho}}\) represents the density variable, and \(\dot{\user2{T}}\) is the derivative vector of the node temperature.

Based on a finite difference technique used to discretize the entire time step, \(\dot{\user2{T}}\) is given by:

$$\dot{\user2{T}} = \frac{{{\varvec{T}}_{k + 1} - {\varvec{T}}_{k} }}{\Delta t} + O(\Delta t)$$
(4)

where \(\Delta t = t_{k + 1} - t_{k}\); Tk+1 and Tk are the temperatures at the kth and the (k + 1)th levels, respectively.

Using a parameter θ, the temperature field and thermal load vector are, respectively, interpolated as follows:

$${\varvec{T}}_{k + \theta } = \theta {\varvec{T}}_{k + 1} + (1 - \theta ){\varvec{T}}_{k}$$
(5)
$${\varvec{P}}_{k + \theta } = \theta {\varvec{P}}_{k + 1} + (1 - \theta ){\varvec{P}}_{k}$$
(6)

Substituting Eqs. (4–6) into Eq. (3) yields:

$$\begin{aligned} ({\varvec{C}} &+ \theta \Delta t{\varvec{K}}_{T} ){\varvec{T}}_{k + 1} = [{\varvec{C}} - (1 - \theta )\Delta t{\varvec{K}}_{T} ]{\varvec{T}}_{k}\\& + \Delta t(\theta {\varvec{P}}_{k + 1} + (1 - \theta ){\varvec{P}}_{k} ) \end{aligned}$$
(7)

Using the above method, a discrete iterative approach can be obtained to calculate the temperature field for a specified time with a known initial temperature field. The quasi-static thermo-elastic relations are similar to the static problem, and the solved displacement and thermal stress are time-dependent. Therefore, the mechanical problem is described as follows:

$${\varvec{K}}_{{\text{m}}} {(}{\varvec{\rho}}{)}{\varvec{U}}(t) = {\varvec{F}}_{{\text{m}}} + {\varvec{F}}_{{{\text{th}}}} ({\varvec{\rho}},t)$$
(8)

where U(t) denotes the nodal displacement vector; Km(ρ)is the mechanical stiffness matrix; and Fm and Fth (ρ, t) are mechanical load vector and thermal expansion load vector, respectively.

The thermal expansion load Fth(ρ,t) can be assembled by accumulating the element thermal load as follows:

$${\varvec{F}}_{{{\text{th}}}} ({{\varvec{\rho}}},t) = \sum\limits_{e = 1}^{{N_{e} }} {E{(}\rho_{e} {)}\int_{{\Omega_{e} }} {{\varvec{B}}_{e}^{{\text{T}}} } {\varvec{D}}_{0} {{\varvec{\varepsilon}}}_{e} {(}\rho_{e} {)}\text{d}\Omega_{e} }$$
(9)
$${{\varvec{\varepsilon}}}_{e} {(}\rho_{e} {)} = \alpha {(}\rho_{e} {)}\Delta T_{e} (t){{\varvec{\omega}}}$$
(10)

where Ne is the total number of elements, E(ρe) is Young's modulus, Ωe represents the element domain, Be is the strain displacement matrix, D0 indicates the coefficient matrix for an element,\({{\varvec{\varepsilon}}}_{e} {(}\rho_{e} {)}\) is the thermal strain vector for the element,\(\alpha {(}\rho_{e} {)}\) is the material thermal expansion coefficient, and ω is a vector defined as {1, 1, 0}T for 2D problems.

It is worth noting that E(ρe) and α(ρe) are both concerned with the element density variables. Thus, by using the thermal stress coefficient (TSC), the parameters are combined into the single thermal stress coefficient:

$$\beta (\rho_{e} ) = E(\rho_{e} )\alpha (\rho_{e} )$$
(11)

Substituting Eq. (11) into Eq. (9), the thermal expansion load Fth(ρ,t) can be expressed as follows:

$${\varvec{F}}_{{{\text{th}}}} ({{\varvec{\rho}}},t) = \sum\limits_{e = 1}^{{N_{e} }} {\xi {(}\rho_{e} {)}\int_{{\Omega_{e} }} {{\varvec{B}}_{e}^{{\text{T}}} } {\varvec{D}}_{0} \Delta T_{e} (t){{\varvec{\omega}}}\text{d}\Omega_{e} }$$
(12)

By adopting the well-known SIMP method, Young’s modulus E(ρe), thermal conductivity coefficient λ(ρe), thermal stress coefficient β(ρe), and heat capacity coefficient c(ρe) of each designable element e are interpolated as follows:

$$\left\{ \begin{gathered} E(\rho_{e} ) = E_{{{\text{II}}}} + \rho_{e}^{{p_{1} }} (E_{{\text{I}}} - E_{{{\text{II}}}} ) \hfill \\ \lambda (\rho_{e} ) = \lambda_{{{\text{II}}}} + \rho_{e}^{{p_{2} }} (\lambda_{{\text{I}}} - \lambda_{{{\text{II}}}} ) \hfill \\ c(\rho_{e} ) = c_{{{\text{II}}}} + \rho_{e}^{{p_{3} }} (c_{{\text{I}}} - c_{{{\text{II}}}} ) \hfill \\ \beta (\rho_{e} ) = \beta_{{{\text{II}}}} + \rho_{e}^{{p_{4} }} (\beta_{{\text{I}}} - \beta_{{{\text{II}}}} ) \hfill \\ \end{gathered} \right.$$
(13)

where p1, p2, p3, and p4 represents the SIMP internal penalization parameter, EI, λI, cI, and βI are Young’s modulus, heat conductivity, heat capacity and thermal stress coefficient of material-I, respectively, and EII, λII, cII, and βII are Young’s modulus, heat conductivity, heat capacity, and thermal stress coefficient of material-II, respectively.

According to Eq. (11), βI and βII are written as follows:

$$\left\{ \begin{gathered} \beta_{{\text{I}}} = E_{{\text{I}}} \alpha_{{\text{I}}} \hfill \\ \beta_{{{\text{II}}}} = E_{{{\text{II}}}} \alpha_{{{\text{II}}}} \hfill \\ \end{gathered} \right.$$
(14)

where αI and αII represent thermal expansion coefficient of material-I and material-II, respectively.

2.2 Optimization Model

In this paper, the optimization objective is to minimize the global structural compliance over the entire time interval with volume and temperature constraints. By using the density-based approach, the topology optimization model for transient thermo-elastic coupling problems is formulated as follows:

$$\begin{gathered} {\text{find}}\, {\varvec{\rho}} \hfill \\ \min \, \varphi = \int_{0}^{{t_{f} }} {\chi ({\varvec{\rho}},t)\text{d}t} = \int_{0}^{{t_{f} }} {{\varvec{U}}^{\text{T}} (t){\varvec{K}}_{{\text{m}}} {\varvec{U}}(t)\text{d}t} \hfill \\ {\text{s}}.{\text{t}}.\,{\varvec{K}}_{{\text{m}}} ({\varvec{\rho}}){\varvec{U}}(t) = {\varvec{F}}_{{\text{m}}} + {\varvec{F}}_{{{\text{th}}}} ({\varvec{\rho}},t), \,\;\;\;\;\quad \quad t \in \left[ {0,t_{f} } \right] \hfill \\ \, {\varvec{C}}({\varvec{\rho}})\dot{\user2{T}}(t) + {\varvec{K}}_{T} ({\varvec{\rho}}){\varvec{T}}(t) = {\varvec{P}}(t) \hfill \\ \, \sum\limits_{e = 1}^{{N_{e} }} {\rho_{e} v_{e} \le f \cdot V_{0} \, } \hfill \\ \, T_{j} (t) \le T_{s} \,\qquad \qquad \qquad\quad ( \, j = 1,2, \ldots ,N_{j} ) \hfill \\ \, 0 \le \rho_{e} \le 1 \qquad \qquad \qquad\quad (e = 1,2, \ldots ,N_{e} ) \hfill \\ \end{gathered}$$
(15)

where φ represents the accumulated global structural compliance, ve is the elemental volume, f denotes the occupied volume fraction of the material, V0 is the volume of the solid material in the design domain, Tj(t) is the temperature of the jth node in the temperature-controlled area with respect to time t, j is the number of grid nodes, Nj is the total number of grid nodes for the temperature-controlled domain, and Ts is the value of temperature constraint.

2.3 Regional Temperature Control Scheme

The necessity of considering temperature constraints have previously explained in the introduction, which are implemented by making the maximum temperature in the design domain lower than a given constant. However, for transient thermo-elastic structures, the maximum temperature value varies in both time and space dimensions, and this discontinuous nature can complicate the solution of the optimization problem. In addition, the design domain has been discretized into meshes by the FEM, resulting in a certain number of nodes with each corresponding to a temperature value, which generates a large number of temperature constraints. Moreover, the simultaneous presence of multiple heat sources with high temperature in the design domain complicates the computational process for determining the maximum temperature.

Therefore, all the temperature values are aggregated into a region value at any given moment, and the region values are aggregated at all moments into a total value in the time dimension. In this way, the multiple temperature constraints are transformed and equated to a single constraint in the region of interest, typically the region near the heat source. Based on the smooth approximation theory, the regional temperature control function can be expressed in the form of an aggregation function as follows [29]:

$$\gamma_{{{t}}} = \frac{{\int_{\Omega } {T_{{{j}}} (t)\text{e}^{{\xi T_{{{j}}} }} {\text{d}}\Omega } }}{{\int_{\Omega } {\text{e}^{{\xi T_{{{j}}} }} {\text{d}}\Omega } }}{,}\quad \delta_{t} = \frac{{\int_{0}^{{t_{f} }} {\gamma_{{{t}}} \text{e}^{{\xi \gamma_{{{t}}} }} {\text{d}}t} }}{{\int_{0}^{{t_{f} }} {\text{e}^{{\xi \gamma_{{{t}}} }} {\text{d}}t} }}$$
(16)

where γt and δt represent the spatial temperature function and the time temperature function, respectively, and ξ is the aggregation parameter, when ξ →  + ∞, δt → Tmax.

It should be noted that since the parameter ξ cannot be infinite, it is difficult for the aggregated temperature value to efficiently approximate Tmax. Therefore, we build a temperature constraint function to implement a confinement on the aggregated temperature, which is defined as follows:

$$\overline{\psi }_{{t}} = cp \cdot \frac{{\delta_{{t}} }}{{T_{{s}} }} \le 1$$
(17)

where Ts is the limit value of maximum temperature, and cp is the adjustment parameter defined as Tmax/δt.

3 Sensitivity Analysis and Numerical Implementation

In this article, the method of moving asymptotes (MMA) [30], a gradient-based optimization algorithm, is utilized to accomplish the sensitivity analysis of the structural compliance as well as the temperature and volume constrains with respect to the design variables.

3.1 Structural Compliance Sensitivity

By the adjoint variable method (AVM), the modified objective function L is constructed as follows:

$$\begin{aligned}L &= \varphi + \int_{0}^{{t_{f} }} {{\varvec{\lambda}}_{{\text{m}}}^{{\text{T}}} \left[ {{\varvec{K}}_{{\text{m}}} {\varvec{U}} - {\varvec{F}}_{{\text{m}}} - {\varvec{F}}_{{{\text{th}}}} } \right]} {\text{d}}t \\&+ \int_{0}^{{t_{f} }} {{\varvec{\lambda}}_{{\text{t}}}^{{\text{T}}} \left[ {\user2{C\dot{T}}{ + }{\varvec{K}}_{{T}} {\varvec{T}} - {\varvec{P}}} \right]} {\text{d}}t\end{aligned}$$
(18)

where \({\varvec{\lambda}}_{{\text{m}}}\) and \({\varvec{\lambda}}_{{\text{t}}}\) denotes the vectors of Lagrange multipliers.

Therefore, the sensitivity of the global structural compliance corresponds to:

$$\begin{aligned} \frac{\partial L}{{\partial \rho_{e} }}& = \int_{0}^{{t_{f} }} {\frac{\partial \chi }{{\partial \rho_{e} }}{\text{d}}t} + \int_{0}^{{t_{f} }} {\left[ {\varvec{\lambda}_{{\text{t}}}^{{\text{T}}} \left( {\frac{{\partial {\varvec{C}}}}{{\partial \rho_{e} }}\dot{\user2{T}} + \frac{{\partial {\varvec{K}}_{{T}} }}{{\partial \rho_{e} }}{\varvec{T}} - \frac{{\partial} {\varvec{P}}}{{\partial \rho_{e} }}} \right)}\right.}\\&\quad {\left.{ + {\varvec{\lambda}}_{{\text{m}}}^{{\text{T}}} \left( {\frac{{\partial {\varvec{K}}_{{\text{m}}} }}{{\partial \rho_{e} }}{\varvec{U}} - \frac{{\partial {\varvec{F}}_{{\text{m}}} }}{{\partial \rho_{e} }} - \frac{{\partial {\varvec{F}}_{{{\text{th}}}} }}{{\partial \rho_{{\text{e}}} }}} \right)} \right]{\text{d}}t} \hfill \\ &\quad + \int_{0}^{{t_{f} }} {\left( {\frac{\partial \chi }{{\partial {\varvec{U}}}} + {\varvec{\lambda}}_{{\text{m}}}^{{\text{T}}} {\varvec{K}}_{{\text{m}}} } \right)\frac{{\partial {\varvec{U}}}}{{\partial \rho_{e} }}{\text{d}}t} \\ &\quad+ \int_{0}^{{t_{f} }} {\left[ { - {\varvec{\lambda}}_{{\text{m}}}^{{\text{T}}} \frac{{\partial {\varvec{F}}_{{{\text{th}}}} }}{{\partial} {\varvec{T}}} + {\varvec{\lambda}}_{{\text{t}}}^{{\text{T}}} {\varvec{K}} - \dot{\varvec{\lambda} }_{{\text{t}}}^{{\text{T}}} {\varvec{C}}} \right]} \frac{{\partial {\varvec{T}}}}{{\partial \rho_{e} }}{\text{d}}t \hfill \\ \end{aligned}$$
(19)

Correspondingly, the objective function sensitivity equation can be written as follows:

$$\begin{aligned}\frac{\partial L}{{\partial \rho_{e} }} &= \int_{0}^{{t_{f} }} {\frac{\partial \chi }{{\partial \rho_{e} }} + {\varvec{\lambda}}_{\text{t}}^{\text{T}} \left( {\frac{{\partial {\varvec{C}}}}{{\partial \rho_{e} }}\dot{\user2{T}} + \frac{{\partial {\varvec{K}}_{{T}} }}{{\partial \rho_{e} }}{\varvec{T}}} \right)}\\&\quad {+ {\varvec{\lambda}}_{{\text{m}}}^{{\text{T}}} \left( {\frac{{\partial {\varvec{K}}_{{\text{m}}} }}{{\partial \rho_{e} }}{\varvec{U}} - \frac{{\partial {\varvec{F}}_{{{\text{th}}}} }}{{\partial \rho_{e} }}} \right){\text{d}}t} \end{aligned}$$
(20)

The derivative of the structural volume with respect to the design variables can be obtained by:

$$\frac{\partial V}{{\partial \rho_{{\text{e}}} }} = \sum\limits_{{e = {1}}}^{{N_{e} }} {\frac{{\partial \rho_{{\text{e}}} v_{{\text{e}}} }}{{\partial \rho_{{\text{e}}} }}} = v_{{\text{e}}}$$
(21)

3.2 Temperature and Volume Constraints’ Sensitivity

By introducing the accompanying vector λc, the modified temperature constraint function R is constructed as follows:

$$R = \overline{\psi }_{{t}} + \int_{0}^{{t_{f} }} {{\varvec{\lambda}}_{{c}}^{{\text{T}}} \left( {\user2{C\dot{T}} + {\varvec{K}}_{{T}} {\varvec{T}} - {\varvec{P}}} \right)} {\text{d}}t$$
(22)

The sensitivity for the density variable ρi is derived as follows:

$$\begin{aligned} \frac{\partial R}{{\partial \rho_{{e}} }}&= \frac{{\partial \overline{\psi }_{{t}} }}{{\partial \rho_{{e}} }} + \int_{0}^{{t_{f} }} {{\varvec{\lambda}}_{c}^{{\text{T}}} \left( {\frac{{\partial {\varvec{C}}}}{{\partial \rho_{{e}} }}\dot{\user2{T}} + {\varvec{C}}\frac{{\partial \dot{\user2{T}}}}{{\partial \rho_{{e}} }} + \frac{{\partial {\varvec{K}}_{{T}} }}{{\partial \rho_{{e}} }}{\varvec{T}} }\right. }\\ & \quad {\left.{+ {\varvec{K}}_{{T}} \frac{{\partial {\varvec{T}}}}{{\partial \rho_{{e}} }} - \frac{{\partial {\varvec{P}}}}{{\partial \rho_{{e}} }}} \right)} {\text{d}}t = \mu_{{f}} \frac{cp}{{T_{{s}} }}\int_{0}^{{t_{f} }} {\left( {1 + \gamma_{t} \xi - \delta_{t} \xi } \right)\text{e}^{{\xi \gamma_{t} }} \frac{{\partial \gamma_{t} }}{{{\partial} \rho_{e} }}{\text{d}}t} \hfill \\ \; &\quad+ \int_{0}^{{t_{f} }} {\left[ {\mu_{{{f}}} \frac{cp}{{T_{{s}} }}\left( {1 + \gamma_{{t}} \xi - \delta_{{t}} \xi } \right)\text{e}^{{\xi \gamma_{t} }} \frac{{\partial \gamma_{{t}} }}{{\partial {\varvec{T}}}} + {\varvec{\lambda}}_{{c}}^{{\text{T}}} {\varvec{K}}_{{T}} - \dot{\user2{\varvec{\lambda} }}_{{c}}^{{\text{T}}} {\varvec{C}}} \right]}\\ &\quad \times{\frac{{\partial {\varvec{T}}}}{{\partial \rho_{{e}} }}} {\text{d}}t + \int_{0}^{{t_{f} }} {{\varvec{\lambda}}_{{c}}^{{\text{T}}} \left( {\frac{{\partial {\varvec{C}}}}{{\partial \rho_{{e}} }}\dot{\user2{T}} + \frac{{\partial {{\varvec{{K}}_T}}}}{{\partial \rho_{{e}} }}{\varvec{T}}} \right){\text{d}}t} \hfill \\ \end{aligned}$$
(23)

where \(\mu_{f} = {1 \mathord{\left/ {\vphantom {1 {\int_{0}^{{t_{f} }} {e^{{\xi \gamma_{t} }} {\text{d}}t} }}} \right. \kern-0pt} {\int_{0}^{{t_{f} }} {\text{e}^{{\xi \gamma_{t} }} {\text{d}}t} }}\).

Assuming that the thermal load is independent of the design variables, the sensitivity can be modified as follows:

$$\begin{aligned} \frac{\partial R}{{\partial \rho_{{e}} }} &= \mu_{{f}} \frac{cp}{{T_{{s}} }}\int_{0}^{{t_{f} }} {\left( {1 + \gamma_{{t}} \xi - \delta_{{t}} \xi } \right){\text{e}}^{{\xi \gamma_{t} }} \frac{{\partial \gamma_{{t}} }}{{\partial {\rho_{e}} }}{\text{d}}t} \\&\quad+ \int_{0}^{{t_{f} }} {{\varvec{\lambda}}_{c}^{{\text{T}}} \left( {\frac{{\partial {\varvec{C}}}}{{\partial \rho_{{e}} }}\dot{\user2{T}} + \frac{{\partial {\varvec{K}}_{{T}} }}{{\partial \rho_{{e}} }}{\varvec{T}}} \right)} {\text{d}}t \end{aligned}$$
(24)

where \({{\partial \gamma_{t} } \mathord{\left/ {\vphantom {{\partial \gamma_{t} } {\partial {\varvec{T}}}}} \right. \kern-0pt} {\partial {\varvec{T}}}}\) is expressed as follows:

$$\frac{{\partial \gamma_{t} }}{{\partial {\varvec{T}}}} = \frac{{\left[ {\left( {1 + \xi T_{j} (t)} \right)\text{e}^{{\xi T_{j} (t)}} - \xi \text{e}^{{\xi T_{j} (t)}} \gamma_{t} } \right]}}{{\sum\limits_{j = 1}^{{N_{j} }} {\text{e}^{{\xi T_{j} \left( t \right)}} } }}\frac{{\partial T_{j} (t)}}{{\partial {\varvec{T}}}}$$
(25)

3.3 Implementation Procedure

The MMA program is employed as the optimizer due to its applicability for multi-constraint topology optimization problems. The iterative process of the optimization algorithm for transient thermo-elastic structure topology optimization is described as follows:

Step 1 Input the basic parameters including EI, EII, λI, λII, cI, cII, αI, αII, p1, p2, p3, p4, and f.

Step 2 Initialize the design domain Ω, design variables ρe, boundary and load conditions including Γd, ΓT, Γf, Γq, Fm, and P(t).

Step 3 Assemble the global stiffness matrix, Km(ρ), heat capacity matrix, C(ρ), and heat conduction matrix, KT(ρ). Then calculate the nodal displacement vector, U(t), and thermal load, Fth(ρ,t).

Step 4 Evaluate the global structural compliance, φ, and the aggregated regional temperature, δt.

Step 5 Compute the sensitivity of the objective,\(\frac{\partial L}{{\partial \rho_{e} }}\), temperature constraint, \(\frac{\partial R}{{\partial \rho_{e} }}\), and volume constraint, \(\frac{\partial V}{{\partial \rho_{e} }}\).

Step 6 Modify the element sensitivity using the sensitivity filtering algorithm.

Step 7 Update the vector design variable, ρ, based on the MMA program.

Step 8 Check whether the convergence condition is satisfied. If satisfied, output the final optimization result and end the iteration procedure; otherwise, go back to Step 3 and repeat the steps.

4 Numerical Examples and Discussions

In this section, a total of two representative numerical experiments of topology optimization problems for transient thermo-elastic structures are introduced to verify the feasibility of the proposed method. The default parameters for all examples are set as follows: The properties of material-I are employed in the solid material region, and a constructed material-II is used in the weak-phase material region. The same materials are used in all examples, and these properties are listed in Table 1. Both the SIMP penalty terms p1 and p4 for Young’s modulus and thermal expansion coefficient are set to 3. In addition, p2 and p3 for heat conductivity and heat capacity are referenced as 3 and 2, respectively [24]. Unless otherwise specified, the value of aggregation parameter ξ is 15. The filter radius r = 1.5 for mesh independence is applied. The reference temperature Tr utilized to calculate the thermal stress is 0 K.

Table 1 Considered material properties
Full size table

4.1 Example 1: Square Thermo-elastic Structure with One Heat Source

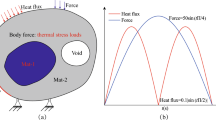
As shown in Fig. 2a, the square design domain has dimensions of 0.1 m × 0.1 m, and the thickness is 0.001 m. The whole structure is uniformly divided into 10,000 four-node quadrilateral elements. The uniformly distributed mechanical loads of Fm = 2000 N are imposed on all four sides of the domain. The four corners of the structure are set as simply supported boundaries and have a temperature value of 0 K. The heat flux P = 0.2 W at the center of the domain is a rectangular time function, as shown in Fig. 2b. The entire working time is 1000 s, and a suitable time step Δt aimed to improve computational efficiency is 5 s. To investigate the effect of the magnitude of the volume fraction f and heat load working time t on the final results, different volume fractions (40, 45, and 50) and heat loading times (800 s, 900 s, and 1000 s) are considered under different temperature constraints (Ts = 33, 31, and 29 K). Table 2 presents the topology optimization results for all the above cases.

Fig. 2
figure 2

a Design domain and boundary condition; b Rectangular heat load; and (c) the steady-state optimized solution of the topology optimization

Full size image
Table 2 Optimization results with one heat source for different volume fractions and working times
Full size table

The maximum temperature and volume fraction of the final optimized structure are given in Table 2. Meanwhile, the optimization results of the steady-state thermo-elastic structure under the same conditions are given in Fig. 2c. When the proposed topology optimization method for transient thermo-elastic structure is used, different topological results are obtained at different operating times of thermal load. Thus, the topology optimization of the transient thermo-elastic structure exhibits a significant transient effect. When the heating time is 800 s, the heat generated is insufficient to raise the maximum temperature to the constraint value, and the volume fraction of the structure satisfies the constraint. At this time, under the premise of meeting the temperature constraint, many beams are generated on the heat dissipation path to bear the external load to reduce the structural compliance. Of course, the maximum temperature value under different volume fractions significantly increases with increasing heating time. Under the same loading time, the increase in material enables higher volume fractions to exhibit lower maximum temperatures. When the heating time is 900 s and 1000 s, the loading time is sufficient, so the maximum temperature values reach the constraint value. In order to meet the temperature constraint value, more high-performance materials are concentrated in the heat dissipation path to improve the heat dissipation capacity. In general, the longer is the heating time, the higher is the material proportion of the heat dissipation path, which is in line with our expectation.

The iterative history of structural compliance values for each optimization result in Table 2 is given in Fig. 3. The overall structural compliance declines with increasing heating time at the same volume fraction. By comparing with other optimization results, when the working time is long and too much heat is generated, the material originally used to support the external load is utilized to dissipate heat to satisfy the temperature constraint preferentially. Of course, this comes at the cost of a rapid drop in the stiffness value of the optimized structure.

Fig. 3
figure 3

Optimization results with different volume fractions and working times under temperature constraints: a f = 40%; b f = 45%; and c f = 50%

Full size image

The above analysis and results show that the proposed transient thermo-elastic coupling model is effective, and the transient effect is noticeable. The desired optimal structure can be obtained in engineering applications by setting the volume and temperature constraints according to the required stiffness and maximum operating temperature. Therefore, the method can be used to derive optimal solutions considering transient thermo-elastic coupling problems.

4.2 Example 2: Square Thermo-elastic Structure with Four Heat Sources

As shown in Fig. 4a, the design domain of Example 2 has the same structural dimension and boundary conditions as Example 1. The difference is that there are four sine-type heat loads with the terminal time tf = 1000 s in the square domain as shown in Fig. 4b, and each point heat load is expressed as follows:

$$P{(}t{)} = {0}{\text{.15sin(}}\pi t{/1000)\quad(0} \le t \le {\text{1000s)}}$$
(26)
Fig. 4
figure 4

a Design domain and boundary conditions; b semi-sine heat load

Full size image

Assuming that the design domain is initially distributed with low-conductivity material-II, then, 40, 45, and 50 of the design domain is covered by high-conductivity material-I with a thickness of 0.001 m. For comparison purposes, Table 3 demonstrates the optimization results with four heat sources at t = 800 s, 900 s, and 1000 s and Ts = 52, 49, and 46 K. Obviously, the clear optimization results are obtained by the transient thermo-elastic topology optimization method with temperature constraints. We try to explain the topologies: In order to improve the heat dissipation efficiency with multiple heat sources, the high-conductivity material is distributed in an annulus at the location of the heat sources, which can connect various heat sources and enhance the energy flow between them.

Table 3 Optimization results with four heat sources for different volume fractions and working times
Full size table

These results demonstrate that the optimized topology varies with thermal loading, and the temperature constraint values can also significantly affect the optimization results for the design of transient thermo-elastic coupling structures. When the heating time is longer than 800 s, the heat generated by the four heat sources increases more rapidly than that by a single heat source. When the heating time increases to 900 s and 1000 s, the material at the boundary of the structure is utilized to reinforce the capacity of heat dissipation, and the heat source generates a local complex branchlike structure toward the center of the structure to achieve more efficient heat transfer. The temperature distribution of the final moment with different volume fractions at the heating time of 900 s is shown in Fig. 5. Figure 6 shows the iterative history of the objective function of the structure under different heating times, respectively. The longer is the loading time, the lower is the structural compliance, which demonstrates effective convergence and numerical stability of the proposed method. Therefore, the proposed method can reasonably determine the optimal distribution of high-conductivity materials in transient thermo-elastic coupling problems.

Fig. 5
figure 5

Comparison of the temperature distributions with different volume fractions at the heating time of 900 s: a f = 40%; b f = 45%; and c f = 50%

Full size image
Fig. 6
figure 6

Iterative histories of the objective function with the volume fraction of 40% at different heating times

Full size image

5 Conclusions

A transient thermo-elastic coupling structure topology optimization model targeting structural compliance is proposed, which is capable of effectively controlling the temperature, and has important practical significance for the structural design of mechanical or electronic devices. Using the SIMP interpolation scheme, a topology optimization that considers transient thermo-elastic coupling effects is established by integrating the transient objective function over a time interval relevant to the minimization of structural compliance. For the problem that the transient maximum temperature value is difficult to determine, the regional temperature function is used to aggregate all the temperature values in the time and space dimensions, which realizes the control of the transient temperature. Through numerical examples, some meaningful conclusions are drawn. First, topology optimization of transient thermo-elastic structures has significant transient effects. The optimal topology is closely related to the operating time, and different working hours of the thermal load lead to completely different optimal topology designs. Therefore, it is necessary to consider transient effects. Second, the optimized structure also exhibits different temperature and compliance values under different volume fractions, reflecting the influence of material ratio on the optimal topology. In the future, topology optimization for transient thermo-elastic structures considering temperature and stress constraints will be studied further.