1 Introduction

With the miniaturization and high capacity of the electronic equipment, keeping the working temperature of electronic components below an acceptable temperature level is a major concern (Hinton 2007; Ye et al. 2002), because the performance of equipment has a direct relationship with its temperature. Attaching or embedded heat conduction structure with high conductivity materials is a very important and widely used way to reduce and control the temperature through collecting, transferring and exchanging heat with the external environment automatically and rapidly (Bejan 1997). How to provide a rational distribution of highly conductive materials, which not only benefits to the temperature control but also can reduce the used materials and the manufacturing cost, is becoming a key and challengeable problem.

Due to this urgent practical demand, various methods were developed and a number of conducting paths have been designed in the past two decades (Dbouk 2017; Manuel and Lin 2017). For example, the construal design method was firstly proposed by Bejan (Bejan 1997), which was continuously increasing improvements and applications for various heat generating devices that were subject to different constraints (Almogbel and Bejan 2001; Bejan and Lorente 2004; Rocha et al. 2002). Various simple geometry structures with easy manufactures, such as T- (Lorenzini et al. 2017), H- (Chen et al. 2015), X- (Lorenzini et al. 2013), ‘+’- (Feng et al. 2015), fork-shaped (Hajmohammadi et al. 2013), ‘Phi-’ and ‘Psi’- (Hajmohammadi et al. 2014) conducting paths, have been shown to be very effective for heat conduction. Topology optimization of conductive structures has been an effective and important method for heat dissipation structure, and many topology optimization methods such as the SIMP method (Chen et al. 2010; Zhang and Liu 2008a), the ESO method (Li et al. 1999; Li et al. 2004) and the level set method (Jing et al. 2015; Zhuang et al. 2007) were employed to achieve optimal designs of heat conduction structure. More complicated problems, such as the design dependent heat load effect and combined structural and heat conduction optimization, were also addressed (Gao et al. 2008; Li et al. 2017). Theoretically, the topology optimization method may obtain an optimal solution for the distribution of highly conductive materials (Li et al. 2018; Yan et al. 2018). The complex geometries of the designed results are the inherent disadvantage of topology optimization. Fortunately, the progress of advanced manufacturing techniques, such as especially 3D printing, making it possible to fabricate them (Zegard and Paulino 2016). Thus, topology optimization is a promising way to achieve the ideal design of conducting path.

In the above-mentioned works, the conducting path designs were mainly obtained based on optimizing the objective calculated by the steady heat conduction analysis. However, many practical heat conduction problems are transient in nature, and in such applications, the temperature field varies with time. In addition, the steady-state topology optimization methods are unsuitable for solving the design problem of heat sink structure that entirely absorbs the heat input from the outside by itself. It is therefore obvious that the topology optimization method for the transient heat conduction problem is necessary and important, but the relative researches are inadequate and some basic problems remain unexplored. For example, intuitively, the different working time should have different optimal topologies for the transient thermal structure. However, there are still no relative results reported. As mentioned in (Zhuang et al. 2013), a level set based topology optimization model for transient thermal conduction structure is proposed, in which the heat compliance over a fixed time interval is regarded as the objective function. Subsequently, this topology optimization model was modified by using global heat compliance in order to minimize the peak value of transient heat compliance (Zhuang and Xiong 2014). The previous studies have been shown that minimizing the heat compliance and the maximum temperature are completely different objective functions (Zhang and Liu 2008b). Thus, how to minimize the maximum temperature of transient heat conduction structure by topology optimization is still an unsolved problem.

In this study, a new topology optimization model is proposed for transient heat conduction structure design to minimize the maximum temperature of the structure in the whole working period. The structure of this paper is as follows: first, the detailed topology optimization approach of transient thermal conduction structure including problem description, optimization model, sensitivity analysis, and implementation procedure is introduced in Section 2; then, the validity of the proposed optimization model is demonstrated by three numerical examples in Section 3; the conclusion is given in the final section.

2 Method

2.1 Problem description and topology optimization model

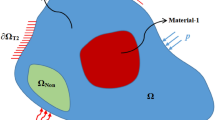
As shown in Fig. 1, the design domain heated by the discrete (or uniform) heat sources (red) are bounded by the solid line. There are two kinds of boundary conditions applied. One is the constant temperature condition, which is represented by the dashed line. The other is the adiabatic boundary, which restricts heat flux out of the domain. The Material-1 with low conductivity and high heat capacity is filled with the whole design domain. The initial ambient temperature is T0. In order to prevent the excess temperature in the design domain, the Material-2 with high thermal conductivity is inserted in order to improve the thermal diffusion efficiency. The transient-state conductive heat transfer across the domain is represented by the following governing equations.

$$ \rho c\frac{\partial T}{\partial t}-\nabla \cdot \left(k\nabla T\right)-\rho Q=0\kern0.87em on\;\varOmega $$
(1)
$$ T=\overline{T}\kern1.12em on\;{\varGamma}_1 $$
(2)
$$ -k\frac{\partial T}{\partial n}=q\kern0.87em on\;{\varGamma}_2 $$
(3)
$$ {\left.T\right|}_{t=0}={T}_0\kern1.5em on\;\varOmega $$
(4)

where T is the structural temperature field, ρ is the material density, c denotes the specific heat of the material, t is the time variable of the transient process, k denotes the heat conductivity, Q is the heat energy generated per unit mass inside the object, n denotes the unit outward normal vector of boundary, \( \overline{T}=\overline{T}\left(\varGamma, t\right) \) is a prescribed temperature on the boundary Γ1, and q = q(Γ, t) is a prescribed heat flux on the boundary Γ2.

Fig. 1
figure 1

Topology optimization problem for transient heat conduction with two-phase materials

Full size image

The main purpose of this study is to develop a new topology optimization method for designing the conducting paths constructed by Material-2 with high thermal conductivity in order to minimize the maximum temperature during the whole-time history. The topology optimization problem should be formulated mathematically as

$$ Find\kern2.28em \chi (x)=\Big\{{\displaystyle \begin{array}{c}1\kern0.36em if\kern1.2em x\in {\varOmega}_p\\ {}0\kern0.36em if\kern0.6em x\in \varOmega /{\varOmega}_p\end{array}} $$
(5)
$$ \mathit{\operatorname{Minimize}}\kern2.28em \mathit{\operatorname{Max}}\left(T\left(x,t\right)\right)\kern0.75em t\in \left[0,{t}_f\right] $$
(6)
$$ Subject\kern0.17em to\kern3.479999em {\int}_{\varOmega}\chi (x)d\mathrm{A}=\phi \mathrm{A} $$
(7)

where ϕ is the prescribed volume fraction of the high-conductivity material. The variable is the distribution denotation function of high conductive material, which is defined in (Eq. 5); the optimization objective in (Eq. 6) is to minimize the maximum temperature of structure all the transient process; the optimization procedure needs satisfying the volume limitation of high-conductivity material in (Eq. 7). Otherwise, the whole procedure needs satisfying the governing (Eq. 1), boundary conditions (Eq. 2, 3), and initial temperature condition (Eq. 4).

The position of the maximum temperature spot may change along with the change of material distribution, thus, the maximum temperature as a function of material distribution is non-continuous in some cases. The noncontinuity of the objective function often makes the solution of the optimization problem difficult (Zhang and Liu 2008b). Thus, the maximum temperature as the objective function is inadvisable. According to the smooth approximation theory of maximum function, the maximum temperature can be approximately expressed as a temperature control function.

$$ f(x)=\frac{\int_0^{t_f}\xi (t){a}^{\xi (t)} dt}{\int_0^{t_f}{a}^{\xi (t)} dt},\kern1em \xi (t)=\frac{\int_{\varOmega }T\left(x,t\right){a}^{T\left(x,t\right)}\mathrm{d}x}{\int_{\varOmega }{a}^{T\left(x,t\right)}\mathrm{d}x} $$
(8)

When a →  + ∝, f(x) → Tmax. As mentioned earlier, the objective of the optimization design is to make the highest temperature lowest in the entire region throughout the time. In fact, the maximum temperature often occurs near the heat source. According to the characteristics and design experience of the problem itself, to reduce the search scope in the optimization process, the most concerned area can be chosen to calculate as the temperature control area. The defined temperature control function is called the Regional Temperature Control Function (RTCF).

Because most of the transient heat conduction problems cannot get an analytical result, the finite element method is employed to solve the temperature field in this study. The quadrilateral element is used to mesh the design domain. The control equation for transient heat conduction problem (Eqs. 1–4) can be approximated as according to the finite element theory.

$$ \mathbf{C}\dot{\mathbf{T}}+\mathbf{KT}=\mathbf{P} $$
(9)

where C is the heat capacity matrix, K is the thermal conductivity matrix; P is the imposed heat load vector, T is the node temperature vector and \( \dot{\mathbf{T}} \) is the derivative vector of the node temperature to time.

In the finite element analysis, the material keeps unchanged in the domain of an element. In this case, the material distribution indication function is expressed as

$$ \chi (x)={\rho}_e,\kern0.75em x\in {\varOmega}_e,{\rho}_e=\Big\{{\displaystyle \begin{array}{l}1\kern0.75em \mathrm{if}\kern1.25em {\varOmega}_e\in {\varOmega}_p\ \\ {}0\kern0.75em \mathrm{if}\kern1.25em {\varOmega}_e\in \varOmega /{\varOmega}_p\end{array}},e=1,2,3\cdots {N}_e $$
(10)

where Ωe is the plane domain occupied by e-th element, Ne is the total number of the element. ρe= 1 (or 0) means that the e-th element is filled by Material-2 with high conductive material (or Material-1 with low conductive material).

According to the usual way of topology optimization, the design variable ρe is relaxed in order to avoid the difficulty in solving the 0–1 discrete valued design problem. It can cover the complete range of values from 0 (corresponding to Material-1) over intermediate value (composite) to 1 (Material-2). In the design process, the material properties are related to the design variables through Solid Isotropic Material with Penalization (SIMP), which is most widely used (Eschenauer and Olhoff 2001; Rietz 2001). The thermal conductivity and heat capacity of the e-th element can be expressed as

$$ {k}_e={k}_1+{\rho}_e^{pk}\left({k}_2-{k}_1\right) $$
(11)
$$ {c}_e={c}_1+{\rho}_e^{pc}\left({c}_2-{c}_1\right) $$
(12)

where ke is the thermal conductivity of the e-th element, ce is the heat capacity of the e-th element(The unit is J/(K ⋅ m3)), k1 and c1 are the thermal conductivity and heat capacity of Material-1, respectively, k2 and c2 are the thermal conductivity and heat capacity of Material-2, respectively, pk is the penalty factor for thermal conductivity, pc is the penalty factor for heat capacity. The penalty factor has the effect of penalizing the intermediate density 0 < ρe < 1 and pushes the topology design to the limit value ρe = 0 and ρe = 1, and thereby promotes more distinctive 0–1 design.

The constraint on the volume of Material-2 can be expressed as

$$ \phi \varOmega ={\int}_{\varOmega}\chi (x) d\varOmega =\sum \limits_{e=1}^{N_e}{\rho}_e{A}_e $$
(13)

where Ae is the area of e-th element.

Adopting the RTCF as the objective, the optimization model described by the finite element formula is as follows

$$ {\displaystyle \begin{array}{l} Find:X=\left({\rho}_1,{\rho}_2,...,{\rho}_e,...,{\rho}_{N_e}\right),{\rho}_e\in \left(0,1\right)\\ {}\mathit{\operatorname{Minimize}}:f(x)=\frac{\int_0^{t_f}\xi (t){a}^{\xi (t)} dt}{\int_0^{t_f}{a}^{\xi (t)} dt},\kern1em \xi (t)=\frac{\sum \limits_{i=1}^{N_c}{T}^{n_i}(t){a}^{T^{n_i}(t)}}{\sum \limits_{i=1}^{N_c}{a}^{T^{n_i}(t)}}\\ {} Subject\kern0.17em to:\kern1.44em \mathbf{C}\dot{\mathbf{T}}+\mathbf{KT}=\mathbf{P}\\ {}\kern7em \frac{1}{A}\sum \limits_{e=1}^{N_e}{A}_e{\rho}_e=\phi \end{array}} $$
(14)

Where ρe denotes the element density of the e-th element, ni is the node number of the i-th grid point in the overall grid in the temperature control area, NC represents the total number of grid nodes in the temperature control area, ϕ is the specified volume fraction, Ae is the volume of each element, A is the total volume of design domain.

2.2 Sensitivity analysis

In this paper, the optimization model of (Eq. 14) is solved by MMA algorithm (Svanberg 1987) that is a gradient-based optimization method. Thus, the sensitivity analysis to achieve the gradient information is very important. The explicit analytic derivative of the objective function with respect to the design variables can be expressed as followed:

$$ \frac{\partial f(x)}{\partial {\rho}_e}={\int}_0^{t_f}{\left\{l\left({t}_f-t\right)\right\}}^T\frac{\partial \left[C\right]}{\partial {\rho}_e}\left\{\dot{T}\right\} dt+{\int}_0^{t_f}{\left\{l\left({t}_f-t\right)\right\}}^T\frac{\partial \left[K\right]}{\partial {\rho}_e}\left\{T\right\} dt $$
(15)

where {l} is the Lagrange Multiplier which is a column vector related to time and can be obtained by the following adjoint state equation.

$$ \left[C\right]\left\{\dot{l}\right\}+\left[K\right]\left\{l\right\}=-\beta \left({t}_f-{t}^{\prime}\right){\left[\varLambda \right]}^T{\left[\chi \left({t}_f-{t}^{\prime}\right)\right]}^{\mathrm{T}},l\left({t}^{\prime }=0\right)=0 $$
(16)

The adjoint variable method is adopted to derive the sensitivity and the specific procedure is given as below.

First, the Lagrange Multiplier is introduced and the Lagrange Function is defined as followed:

$$ L=f(x)+{\int}_0^{t_f}{\left\{l(t)\right\}}^T\left(\left[C\right]\left\{\dot{T}\right\}+\left[K\right]\left\{T\right\}-\left\{P\right\}\right) dt,\kern1em {\left\{l(t)\right\}}^T=\left({l}_1,{l}_2,\cdots {l}_N\right) $$
(17)

where N is the number of nodes of the structure.

So the derivative of L with respect to an element density ρe is given as:

$$ \frac{\partial L}{\partial {\rho}_e}=\frac{\partial f(x)}{\partial {\rho}_e}+{\int}_0^{t_f}\left({\left\{l\right\}}^T\frac{\partial \left[C\right]}{\partial {\rho}_e}\left\{\dot{T}\right\}+{\left\{l\right\}}^T\left[C\right]\frac{\partial \left\{\dot{T}\right\}}{\partial {\rho}_e}+{\left\{l\right\}}^T\frac{\partial \left[K\right]}{\partial {\rho}_e}\left\{T\right\}+{\left\{l\right\}}^T\left[K\right]\frac{\partial \left\{T\right\}}{\partial {\rho}_e}\right) dt $$
(18)

For the initial value problem (in which the initial temperature field is given), \( {\left.\frac{\partial \left\{T\right\}}{\partial {\rho}_e}\right|}_{t=0}=0 \) is set and the following result can be achieved.

$$ {\left.{\int}_0^{t_f}{\left\{l\right\}}^T\left[C\right]\frac{\partial \left\{\dot{T}\right\}}{\partial {\rho}_e} dt={\left\{l\left(t={t}_f\right)\right\}}^T\left[C\right]\frac{\partial \left\{T\right\}}{\partial {\rho}_e}\right|}_{t={t}_f}-{\int}_0^{t_f}{\left\{\dot{l}\right\}}^T\left[C\right]\frac{\partial \left\{T\right\}}{\partial {\rho}_e} dt $$
(19)
(20)

The derivation of \( \frac{\partial f(x)}{\partial {\rho}_e} \) is shown as followed:

$$ \frac{\partial f(x)}{\partial {\rho}_e}=\frac{\int_0^{t_f}{a}^{\xi (t)}\left[1+\xi (t)\ln (a)\right]\frac{\partial \xi (t)}{\partial {\rho}_e}{dt}^{\ast }{\int}_0^{t_f}{a}^{\xi (t)} dt}{{\left({\int}_0^{t_f}{a}^{\xi (t)} dt\right)}^2}-\frac{\int_0^{t_f}\xi (t){a}^{\xi (t)}{dt}^{\ast }{\int}_0^{t_f}{a}^{\xi (t)}\ln (a)\frac{\partial \xi (t)}{\partial {\rho}_e} dt}{{\left({\int}_0^{t_f}{a}^{\xi (t)} dt\right)}^2} $$
(21)

\( A={\int}_0^{t_f}{a}^{\xi (t)} dt \) and \( B={\int}_0^{t_f}\xi (t){a}^{\xi (t)} dt \) are set here and the following result can be achieved.

$$ \frac{\partial f(x)}{\partial {\rho}_e}=\frac{1}{A}{\int}_0^{t_f}{a}^{\xi (t)}\left[1+\xi (t)\ln (a)\right]\frac{\partial \xi (t)}{\partial {\rho}_e} dt-\frac{B}{A^2}{\int}_0^{t_f}{a}^{\xi (t)}\ln (a)\frac{\partial \xi (t)}{\partial {\rho}_e} dt $$
(22)

Where,

$$ \frac{\partial \xi (x)}{\partial {\rho}_e}=\sum \limits_{i=1}^{N_c}\left\{{\left(\sum \limits_{i=1}^{N_c}{a}^{T_{n_i}}\right)}^{-1}{a}^{T_{n_i}}\left[1+{T}_{n_i}\ln (a)\right]-{\left(\sum \limits_{i=1}^{N_c}{a}^{T_{n_i}}\right)}^{-2}\left(\sum \limits_{i=1}^{Nc}{T}_{n_i}{a}^{T_{n_i}}\right)\ln (a){a}^{T_{n_i}}\right\}\frac{\partial {T}_{n_i}}{\partial {\rho}_e} $$
(23)

where the node temperature can be expressed as \( {T}^{n_l}={\varLambda}^{n_l}T \) and \( {\varLambda}^{n_l}=\left[0,0,...,1,...,0\right] \) is a row vector (in which the nlth column is 1 and the rest is 0). \( {\chi}_{n_i} \) can be expressed as followed.

$$ {\chi}_{n_i}={\left(\sum \limits_{i=1}^{N_c}{a}^{T_{n_i}}\right)}^{-1}{a}^{T_{n_i}}\left[1+{T}_{n_i}\ln (a)\right]-{\left(\sum \limits_{i=1}^{N_c}{a}^{T_{n_i}}\right)}^{-2}\left(\sum \limits_{i=1}^{N_c}{T}_{n_i}{a}^{T_{n_i}}\right)\ln (a){a}^{T_{n_i}} $$
(24)

Then:

$$ \frac{\partial \xi (x)}{\partial {\rho}_e}=\sum \limits_{l=1}^{N_c}{\chi}^{n_l}\left({\varLambda}^{n_l}\right)\frac{\partial T}{\partial {\rho}_e}=\left[\chi \right]\left[\varLambda \right]\left\{\frac{\partial T}{\partial {\rho}_e}\right\} $$
(25)

Where:

$$ \left[\chi \right]=\left({\chi}^1,{\chi}^2,\cdots, {\chi}^{n_{N_c}}\right),\kern1em \left[\varLambda \right]=\left[\begin{array}{c}{\varLambda}^1\\ {}{\varLambda}^2\\ {}\dots \\ {}{\varLambda}^{n_{N_c}}\end{array}\right] $$
(26)

β(t) can be given as below.

$$ \beta \left(\mathrm{t}\right)=\frac{1}{A}{a}^{\xi (t)}\left[1+\xi (t)\ln (a)\right]-\frac{B}{A^2}{a}^{\xi (t)}\ln (a) $$
(27)

Then

$$ \frac{\partial f(x)}{\partial {\rho}_e}={\int}_0^{t_f}\beta (t)\left[\chi \right]\left[\varLambda \right]\left\{\frac{\partial T}{\partial {\rho}_e}\right\} dt $$
(28)

Substituting (Eq. 28) into (Eq. 20) yields

(29)

The Lagrange Multiplier can be obtained by the following adjoint state equation.

$$ -\left[C\right]\left\{\dot{l}\right\}+\left[K\right]\left\{l\right\}=-\beta (t){\left[\varLambda \right]}^{\mathrm{T}}{\left[\chi \right]}^{\mathrm{T}},l\left(t={t}_f\right)=0 $$
(30)

To transform the (30) by introducingtf − t′ = t, the (Eq. 16) can be achieved and the sensitivity formulation of (Eq. 15) can also be obtained.

2.3 Implementation procedure

After attaining the sensitivity information, the whole optimization problem can be solved by the MMA algorithm (Svanberg 1987) in this paper. At the same time, to prevent the occurrence of checkerboard during the numerical solution process, the sensitivity filter technique is adopted (Sigmund and Petersson 1998). The complete iteration procedure based on the SIMP method for transient thermal conduction topology optimization is described as following:

  1. Step 1.

    Initialize the design domain, material property, boundary and load conditions;

  2. Step 2.

    Use finite elements to discretize the analysis domain and initialize the design variables;

  3. Step 3.

    Compute the material property of every element by using (Eqs. 11 and 12) and then achieve the temperature of the current structure under different time step;

  4. Step 4.

    Compute the objective function and the sensitivity information of (Eq. 15);

  5. Step 5.

    Modify the element sensitivity by the filtering method;

  6. Step 6.

    Update design variables based on the MMA method;

  7. Step 7.

    Check whether the convergence condition is satisfied. If satisfied, output the results and end the iteration; otherwise, return to the third step and repeat the procedure.

3 Numerical examples

Three numerical examples including conduction structure with the temperature boundary, heat sink structure, and multi-functional heat insulation structure are presented to confirm the utility of the proposed method. In all examples, the same materials are used. The properties of the used materials are listed in Table 1. In addition, the initial temperature of the whole structure is assumed to be 0K.

Table 1 The properties of the used materials
Full size table

3.1 Example 1: Square conduction structure with temperature boundary condition

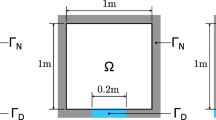
As shown in Fig. 2(a), the dimension of the square structure is 0.1m × 0.1m × 0.001m, the heat flux is 0.1 J/(m2 s) and the temperature of the four corners is fixed to 0K. Material-1 with low thermal conductivity is used. To improve the cooling efficiency of the structure, Material-2 with a thickness of 0.001m is covered on the surface of the square structure. The thermal conductivity of Material-2 is 100 times higher than one of Material-1. We suppose that the coverage area is 20% of the whole area. We try to determine the heat conduction paths of Material-2 in order to minimize the temperature of the center point during the whole working time under different heat load working times (100 s,250 s,500 s,1000s and 10,000 s).

Fig. 2
figure 2

a The design domain and boundary condition of example 1 b the steady-state optimized solution of the topology optimization

Full size image

If this example is solved by the topology optimization method for the steady-state thermal conduction structure, the only X-type conduction path can be obtained, as shown in Fig. 2(b). When the proposed topology optimization method for the transient heat conduction structure is used, the different topological results are gained under different working times of thermal loads, as shown in Table 2. Thus, topology optimization of the transient heat conduction structure exhibits remarkable transient effect, which is an important finding of this study.

Table 2 The comparison of the final topologies and maximum temperatures with different penalty factors under different working times
Full size table

Here there are two important aspects need paying more attention. One is that the penalty factors have a clear impact on the topology optimization results. They are shown in Table 2 for the different penalty factor combinations of thermal conductivity and heat capacity. Results indicate that the different penalty factors combinations will lead to the completely different topology design results in some cases. In most cases, the topology results are relatively clear and the corresponding design objective values are minimal as pc = 2 and pk = 3. Therefore, pc = 2 and pk = 3 are adopted in the following examples.

The other is the changing trend of the topological results obtained under different working times of heat load. With the working time increase of heat load, the stretching range of the heat conduction path is gradually increasing. When the time is long enough, the obtained topology result changes and is the same with the steady-state one, which is also in agreement with our intuition. The mechanism can be explained as follows.

This example is a square thermal conduction structure with temperature boundary conditions, as shown in Fig. 2(a). The temperature boundary can be regarded as a very strong heat sink, which can absorb any amount of heat. Thus, the steady solution is that the heat source is linked with the four temperature boundaries directly, as shown in Fig. 2(b). Obviously, this is reasonable.

When the heating time is short, the generated heat is less. Because the temperature boundary is far, the more economical way is that the material nearby absorbs the generated heat. As the increase of heating time, the optimum topologies are expanded gradually, the more material is utilized, as shown in Table 2 (100 s~1000s).

Obviously, the very short and enough long heating times are completely different heat dissipation mechanism. As the heating time is further increased, the high conductivity material may be expanded to the temperature boundary. Once the heat source is linked with the temperature boundary by high conductivity material, the optimum topology will jump to the X type (steady-state solution) rapidly.

It can be noted that the maximum temperatures of the final topology when the working time is 2000s, 4000 s, and 6000 s are sometimes even bigger than that of 10,000 s. This is a special phenomenon when two mechanisms are switched.

To verify whether the optimal design results are obtained at the different time of thermal load, three different topological design (100 s, 500 s, and 10,000 s) subjected the same working time (500 s) are estimated, as shown in Fig. 3. As seen from the diagram, the maximum temperature of the topology structure obtained under the heat load working time of 100 s is the lowest when the practical working time of thermal load is 100 s. However, it is not optimal when the practical working time of thermal loads increases to 500 s and the optimal solution becomes the topology result corresponding to the heat load working time of 500 s. It is worth noting that the maximum temperature of the steady-state solution is always higher than one of the two others. These results confirm that the optimal design solution of transient heat conduction structure can be obtained at the specific heat load working time by the new proposed topology optimization model. In addition, they also indicate that taking into account the transient effect is very necessary.

Fig. 3
figure 3

The curve of the central temperature of the topology results achieved when the working times are 100 s, 500 s, and 10,000 s (Steady-state)

Full size image

As mentioned before, the Transient Heat Compliance (THC) is also regarded as the objective function in current literature (Zhuang and Xiong 2014). The comparison of the topology optimization results with the different objective functions is shown in Fig. 4. It could be seen from the figure that there exists a great difference in topology optimization design results under different heat load working times using two different objective functions. Furthermore, the maximum temperature of the optimal solutions using the RTCF as the objective function has significantly reduced compared with ones using the THC at different heat load working times of heat loads. These results verify again that the proposed topology optimization model of transient heat conduction structure is highly effective, and the RTCF is more suitable as the optimization objective.

Fig. 4
figure 4

The contrast of maximum temperature values of the topological structures with different objective functions under different working times

Full size image

3.2 Example 2: Square heat sink structure

Example 2 has the same structural dimension with Example 1, which is a classic heat sink structure as shown in Fig. 5(a). The biggest difference with Example 1 is that there is no heat dissipation on the boundary in Example 2. The heat sink structure will entirely absorb all the heat generated from the sources by itself, which cannot be solved by topology optimization method of steady-state heat conduction structure. There are four point heat sources in the square domain as shown in Fig. 5(a), and the magnitude of each point heat source is p = 0.1 sin(πt/T)  0 ≤ t ≤ T, as shown in Fig. 5(b). Assuming that area of the square structure with Material-1 is 40% covered by Material-2 with a thickness of 0.001m. We try to determine the heat conduction paths of Material-2 in order to minimize the temperature of the center point during the whole working time under different heat load working times (50s,200s,400 s,500 s and 1000s).

Fig. 5
figure 5

a The design domain and boundary condition of example 2 b The relationship between the heat load and time in example 2

Full size image

Table 3 demonstrates the topology optimization results under different heat load working times (50s,200s,400 s,500 s and 1000s). The similar changed trend of the topological results with example 1 is obtained. As the working time of heat load increases, the stretching range of the heat conduction path is gradually increasing.

Table 3 The comparison of the final topologies under different working times
Full size table

To prove the optimality of the obtained topological optimization results, five different design schemes obtained under different heat loading times are analyzed. Fig. 6 illustrates the maximum temperatures of five different design schemes when the working time of heat load is 50s, 200 s, 400 s, 500 s, and 1000s respectively. Comparing Fig. 6 shows that the maximum temperature of the topology structure obtained under the heat load working time of 50s is the lowest when the practical working time of thermal load is 50s. When the practical working time of thermal loads increases to 200 s, the optimal solution becomes the topology result corresponding to the heat load working time of 200 s. When the practical working time of thermal loads increases to 400 s, the optimal solution becomes the topology result corresponding to the heat load working time of 400 s. When the practical working time of thermal loads increases to 500 s, the optimal solution becomes the topology result corresponding to the heat load working time of 500 s. When the practical working time of thermal loads increases to 1000s, the optimal solution becomes the topology result corresponding to the heat load working time of 1000s. These results show that the proposed topology optimization model can exactly reflect the transient effect and achieve ideal topology optimization results for heat sink structure.

Fig. 6
figure 6

The maximum temperature of the five different design schemes obtained under different working times when (a) the practical working time of heat load is 50s (b) the practical working time of heat load is 200 s (c) the practical working time of heat load is 400 s (d) the practical working time of heat load is 500 s (e) the practical working time of heat load is 1000s

Full size image

Figure 7 shows the topology optimization results adopting two different objective functions under different working times of heat load (50s, 200, 400, 500 s and 1000s). The topological structures obtained by the different objectives under the same working time are significantly different and the maximum temperature of the structure obtained by the RTCF as the objective is obviously lower. These results implicate again that the proposed topology optimization model of transient heat conduction structure is highly effective, and the RTCF is more suitable as the optimization objective.

Fig. 7
figure 7

The contrast of maximum temperature values of the topological structures with different objective functions under different working times

Full size image

3.3 Example 3: Multi-functional insulation structure

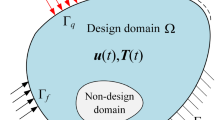
As shown in Fig. 8(a), the dimension of the square structure is 0.2m × 0.1m × 0.2m, which is a multi-functional insulation structure. In order to realize the other functionality (e.g. load bearing), the high conductivity material (Material-2, black) must be used as the non-design domain. The heat sources in a trapezoidal form with time as shown in Fig. 8(b) is applied to the upper surface of the structure and the other boundaries are insulated. The gray area is the design domain filled with Material-1. We try to determine the heat conduction paths of the embedding Material-2 to minimize the temperature of the center point during the whole working time under different heat load working times (1500s,2250s,3000 s,3750 s and 4500 s). We suppose that the embedding volume of Material-2 is 20% of the whole design domain.

Fig. 8
figure 8

a The design domain and boundary condition of example 3 b The relationship between the heat load and time in example 3

Full size image

Table 4 gives the topology optimization results under different heat load working times (1500s,2250s,3000 s,3750 s and 4500 s) and shows that the topological results achieved under different working times of heat load are obviously different, which indicates that the transient effect is also remarkable.

Table 4 The comparison of the final topologies under different working times
Full size table

Similar to Example 2, to prove the optimality of the obtained topological optimization results, five different design schemes obtained under different heat loading times are analyzed. Figure 9 illustrates the maximum temperatures of five different design schemes when the working time of heat load is 1500s, 2250 s, 3000 s, 3750 s, and 4500 s respectively. Comparing Fig. 9 shows that the maximum temperature of the topology structure obtained under the heat load working time of 1500s is the lowest when the practical working time of thermal load is 1500s. When the practical working time of thermal loads increases to 2250 s, the optimal solution becomes the topology result corresponding to the heat load working time of 2250 s. When the practical working time of thermal loads increases to 3000 s, the optimal solution becomes the topology result corresponding to the heat load working time of 3000 s. When the practical working time of thermal loads increases to 3750 s, the optimal solution becomes the topology result corresponding to the heat load working time of 3750 s. When the practical working time of thermal loads increases to 4500 s, the optimal solution becomes the topology result corresponding to the heat load working time of 4500 s. This result shows again that the proposed topology optimization model can exactly reflect the transient effect and achieve ideal topology optimization results for multi-functional structure.

Fig. 9
figure 9

The maximum temperature of the five different design schemes obtained under different working times when (a) The practical working time of heat load is 1500s (b) The practical working time of heat load is 2250 s (c) The practical working time of heat load is 3000 s (d) The practical working time of heat load is 3750 s (e) The practical working time of heat load is 4500 s

Full size image

Figure 10 shows the topology optimization results adopting two different optimization design objectives under different heat load working times (1500s,2250s,3000 s,3750 s and 4500 s). The topological structures obtained by the different objectives under the same working time are significantly different and the maximum temperature of the structure obtained by the RTCF as the objective is obviously lower. These results also implicate that the proposed topology optimization model of transient heat conduction structure is highly effective, and the RTCF is more suitable as the optimization objective.

Fig. 10
figure 10

The contrast of maximum temperature values of the topological structures with different objective functions under different working times

Full size image

4 Conclusions

A topology optimization model is proposed for transient heat conduction structure to minimize the maximum temperature. In this model, a new performance index, named as the Regional Temperature Control Function, was introduced as the objective function for representing the maximum temperature of specific areas during the whole working time. The explicit sensitivity analytic expression of the objective function is given. Some significant conclusions are obtained by some numerical examples.

First, topology optimization of the transient heat conduction structure exhibits the remarkable transient effect. That is to say, the optimal topology is closely related to the working time, and the different working times of thermal loads may result in the completely different optimal topological designs. Thus, it is very necessary to consider the transient effect. Second, the proposed topology optimization method of transient heat conduction structure can reflect the transient effects exactly and achieve ideal topology optimization results. Finally, the proposed topology optimization model of transient heat conduction structure is highly effective when minimizing the maximum temperature of specific areas, and the RTCF is more suitable as the optimization objective compared with the THC.