1 Introduction

In the past several decades, there have been substantial achievements in structural topology optimization in both theoretical research and practical applications due to the pioneering research [1,2,3,4]. However, topology optimization problems are still the most challenging and rewarding tasks in the structural optimization field owing to their difficulty and complexity. Several approaches for topology optimization have been presented so far. Bendsøe and Kikuchi [3] proposed the homogenization method, in which the sizes and angles of the microstructures in every element are optimized to achieve the optimal structural topology. Later, the solid isotropic material with penalization (SIMP) method was proposed to improve the efficiency of topology optimization [5, 6]. Xie and Steven [7] presented the evolutionary structural optimization (ESO) method that involved generating holes in the uniform isotropic continuum by deleting inefficient elements based on an optimality criterion. Wang et al. [8] proposed the level set method to optimize structural topology by optimizing the boundary lines of the holes in the continuum represented by the level set function. These methods have been widely applied to the numerical solution of topology optimization problems and received considerable attention [9,10,11]. For more details, readers should refer to the relevant literature and references therein for recent developments in the field of topology optimization [12, 13]. In addition, new advances have been made in topology optimization in the past several years. To realize the objective of achieving topology optimization in an explicit and geometric way, the moving morphable component (MMC)-based approach [14] and moving morphable void (MMV)-based approach [15] were proposed successively. However, most studies on structural topology optimization focus primarily on the uniform isotropic continuum. The optimal structural topology is considered in terms of the void and solid material, or the boundaries of the holes in the uniform isotropic continuum. All the aforementioned studies focused on the uniform isotropic perforated continuum.

Michell [16] revealed the characteristics of topology optimization structures that generally exist in the non-uniform anisotropic truss-like continua. Zhou and Li [17] presented a topology optimization method based on the truss-like material model, which can describe the topology optimization structures precisely. In particular, this method can closely approximate the analytical solution. Clear relations exist between the truss-like material-distributed field and the members, which indicate the force transferring paths in the truss-like structure. By deleting parts of the members in a truss-like structure, the truss-like structure can be transformed into a uniform isotropic perforated continuum. Without the suppression of the intermediate densities, there is no numerical instability. Therefore, the topology optimization method based on the truss-like material model is valuable. This study focuses on a method to optimize truss-like structures.

The structural topology optimization focuses primarily on structural compliance, which corresponds to the global structural performance. However, local structural performances play an important role in the design of industrial products and engineering structures. Among them, the local stress magnitude must be taken into consideration to guarantee the strength of a product or structure. The topology optimization with stress constraints is more complicated than the global structural performance-oriented topology optimization problems. Since the stress constraint is a local constraint, which introduces a large number of constraint equations into the optimization problem, the topology optimization with stress constraints represents a more difficult problem. By using the SIMP approach, Duysinx and Bendsøe [18] conducted pioneering research on the topology optimization involving stress constraints. On this basis, the topology optimization with stress constraints has been widely studied based on the SIMP method [19,20,21,22,23,24,25]. In addition, many level set-based methods have been proposed to solve the topology optimization problems involving stress constraints [26,27,28,29,30,31,32]. In actual situations, it is more likely that a product or structure is subjected to the MLC with stress constraints [33, 34]. In this paper, we present an approach for structural volume minimization under stress constraints and MLC to solve the three-dimensional topology optimization problems using a spatial truss-like material model.

A simple algorithm using the fitting-direction stiffness envelope was adopted to optimize planar truss-like structures with stress constraints under MLCs [35]. Only three design variables (two densities and one angle of the member in 2D) occur at every node. Therefore, it is easy to determine the densities and angles of members at every node by using the fitting-direction stiffness envelope. The idea here is to extend upon the previous work [35] by solving the three-dimensional topology optimization problem involving MLCs using a spatial truss-like material model. Compared to the two-dimensional topology optimization, the three-dimensional topology optimization problem is more challenging because there are six design variables (the densities and angles of three families of orthotropic members) at every node of a spatial truss-like structure. It is very difficult to determine the densities and directions of the three families of members at every node by using the fitting-direction stiffness envelope directly. To overcome this difficulty, the fitting problem of the direction stiffness envelope was converted to an eigenvalue problem. It shows that the eigenvalues and eigenvectors of the coefficient matrix of directional stiffness are the optimal densities and directions, respectively, of the three families of members.

In this study, the spatial truss-like continuum with stress constraint under an MLC is optimized by a new optimality criterion. First, under each SLC, the optimal truss-like continua are obtained based on the fully stressed criterion. Next, an optimality criterion for truss-like continua under MLC is suggested: The stiffness of the optimal structure under MLC should be as similar as possible to the maximum stiffness of all optimal structures under every SLC along any direction at any point. By using the fitting maximum stiffness obtained under all SLCs via the least-squares method, a quadric equation for the directional stiffness is established. Next, the eigenvectors and eigenvalues of the coefficient matrix of the quadric equation, which serve as the optimal directions and densities of the members under MLC, respectively, are solved. Consequently, the optimal truss-like continua under MLC are obtained.

2 Truss-Like Material Model and its Elastic Matrix

Generally, the optimal structure with stress constraints under an SLC is a non-uniform orthotropic truss-like structure. To simulate such a truss-like structure, a three-phase orthotropic truss-like material model is employed, in which three families of members along the three orthotropic directions are embedded continuously in a weak matrix as the spatial structure. There are an infinite number of members in the infinitesimal spaces at any point in the truss-like material. According to the character of truss-like material, there are no interactions between parallel members. Therefore, the Poisson’s ratio is assumed as zero.

If the three families of members are arranged along the axes \({{\varvec{e}}}_{b}\) with densities \(t_{b}\)\((b=1,2,3)\), the relationship between stress and strain can be expressed as

$$\begin{aligned} {\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {\{\sigma _x } &{} {\sigma _y } &{} {\sigma _z } &{} {\tau _{yz} } &{} {\tau _{zx} } &{} {\tau _{xy} } \\ \end{array} }\}^{{\mathrm{T}}}={{\varvec{D}}}(t_1 ,t_2 ,t_3 ,{{{\varvec{e}}}}_1 ,{{{\varvec{e}}}}_2 ,{{{\varvec{e}}}}_3 )\{{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {\varepsilon _x } &{} {\varepsilon _y } &{} {\varepsilon _z } &{} {\gamma _{yz} } &{} {\gamma _{zx} } &{} {\gamma _{xy} } \\ \end{array} }\}^{{\mathrm{T}}} \end{aligned}$$
(1)

where

$$\begin{aligned} {{{\varvec{D}}}}(t_1 ,t_2 ,t_3 ,{{{\varvec{e}}}}_1 ,{{{\varvec{e}}}}_2 ,{{{\varvec{e}}}}_3 )=E\cdot {\mathrm{diag}}[{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {t_1 } &{} {t_2 } &{} {t_3 } &{} {(t_2 +t_3 )/4} &{} {(t_3 +t_1 )/4} &{} {(t_1 +t_2 )/4} \\ \end{array} }] \end{aligned}$$
(2)

is the elastic matrix. The components \((t_{2}+t_{3})/4\), \((t_{3}+t_{1})/4\) and \((t_{1}+t_{2})/4\) are the assumed shear stiffnesses in the three coordinate planes; E is Young’s modulus; and the symbol “diag” denotes a diagonal matrix. Equation (2) can represent an isotropic material in the case of \(t_{1}=t_{2}=t_{3}\).

If the three families of members are laid along directions \({{{\varvec{n}}}}_b =\sum \nolimits _{i=1}^3 n_{ib} {{{\varvec{e}}}}_i (b=1,2,3)\), with the definition of coordinate transformation matrix

$$\begin{aligned}&{{{\varvec{T}}}}({{{\varvec{n}}}}_1 ,{{{\varvec{n}}}}_2 ,{{{\varvec{n}}}}_3 )\nonumber \\&\quad =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {n_{11}^2 }&{} {n_{12}^2 }&{} {n_{13}^2 }&{} {n_{12} n_{13} }&{} {n_{13} n_{11} }&{} {n_{11} n_{12} } \\ {n_{21}^2 }&{} {n_{22}^2 }&{} {n_{23}^2 }&{} {n_{22} n_{23} }&{} {n_{23} n_{21} }&{} {n_{21} n_{22} } \\ {n_{31}^2 }&{} {n_{32}^2 }&{} {n_{33}^2 }&{} {n_{32} n_{33} }&{} {n_{33} n_{31} }&{} {n_{31} n_{32} } \\ {2n_{21} n_{31} }&{} {2n_{22} n_{32} }&{} {2n_{23} n_{33} }&{} {n_{22} n_{33} +n_{32} n_{23} }&{} {n_{23} n_{31} +n_{33} n_{21} }&{} {n_{21} n_{32} +n_{31} n_{22} } \\ {2n_{31} n_{11} }&{} {2n_{32} n_{12} }&{} {2n_{33} n_{13} }&{} {n_{32} n_{13} +n_{12} n_{33} }&{} {n_{33} n_{11} +n_{13} n_{31} }&{} {n_{31} n_{12} +n_{11} n_{32} } \\ {2n_{11} n_{21} }&{} {2n_{12} n_{22} }&{} {2n_{13} n_{23} }&{} {n_{12} n_{23} +n_{22} n_{13} }&{} {n_{13} n_{21} +n_{23} n_{11} }&{} {n_{11} n_{22} +n_{21} n_{12} } \\ \end{array} }} \right] \end{aligned}$$
(3)

the elastic matrix can be expressed as

$$\begin{aligned} {{{\varvec{D}}}}(t_1 ,t_2 ,t_3 ,{{{\varvec{n}}}}_1 ,{{{\varvec{n}}}}_2 ,{{{\varvec{n}}}}_3 )={{{\varvec{T}}}}^{{\mathrm{T}}}({{{\varvec{n}}}}_1 ,{{{\varvec{n}}}}_2 ,{{{\varvec{n}}}}_3 ){{{\varvec{D}}}}(t_1 ,t_2 ,t_3 ,{{{\varvec{e}}}}_1 ,{{{\varvec{e}}}}_2 ,{{{\varvec{e}}}}_3 ){{{\varvec{T}}}}({{{\varvec{n}}}}_1 ,{{{\varvec{n}}}}_2 ,{{{\varvec{n}}}}_3 ) \end{aligned}$$
(4)

The element in the first row and the first column of the matrix in Eq. (4) is defined as the directional stiffness along \({{\varvec{e}}}_{1}\) and denoted as

$$\begin{aligned} S({{{\varvec{e}}}}_1 )=D_{11} =E\sum _{b=1}^3 {n_{1b}^2 t_b } =E\sum _{b=1}^3 {({{{\varvec{e}}}}_1 \cdot {{{\varvec{n}}}}_b )^{2}t_b } \end{aligned}$$
(5)

From Eq. (5), the directional stiffness along any unit vector \({{{\varvec{x}}}}=\sum \nolimits _{i=1}^3 {x_i {{{\varvec{e}}}}_i }\) can be expressed as

$$\begin{aligned} S({{{\varvec{x}}}})=E\sum _{b=1}^3 {({{{\varvec{x}}}}\cdot {{{\varvec{n}}}}_b )^{2}t_b } =E\sum _{i=1}^3 {\sum _{j=1}^3 {\left( \sum _{b=1}^3 {n_{ib} n_{jb} t_b } \right) x_i } x_j } =E{{{\varvec{x}}}}^{\mathrm{T}}{{{\varvec{Cx}}}} \end{aligned}$$
(6)

where

$$\begin{aligned} {[}{{{\varvec{C}}}}]_{ij} =\sum _{b=1}^3 {n_{ib} n_{jb} t_b } \end{aligned}$$
(7)

This is a quadratic equation about the unit vector x. The stiffness along any direction is illustrated by the black solid line in Fig. 1. To obtain the maximum stiffness in Eq. (6), the Lagrange function with constraint \(| {{{\varvec{x}}}} |=1\) is established as

$$\begin{aligned} L=S({{{\varvec{x}}}})+\lambda E(1-{{{\varvec{x}}}}^{\mathrm{T}}{{{\varvec{x}}}}) \end{aligned}$$
(8)

where \(\lambda \) is the Lagrange multiplier. The direction of the maximum stiffness can be obtained by setting the derivative of Eq. (8) with respect to the direction vector equal to zero, as

$$\begin{aligned} \frac{\partial L}{\partial {{{\varvec{x}}}}}=2E{{{\varvec{Cx}}}}-2\lambda E{{{\varvec{x}}}}=0 \end{aligned}$$
(9)

or

$$\begin{aligned} {{{\varvec{Cx}}}}=\lambda {{{\varvec{x}}}} \end{aligned}$$
(10)

This is an eigenvalue problem. Equations (6) and (10) show that the eigenvectors and eigenvalues are the directions and densities of the members, respectively.

Fig. 1
figure 1

Directional stiffness

Full size image

3 Finite Element Analysis

The elastic matrix at any point \((\xi ,\eta ,\zeta )\) within an element e can be calculated by the interpolation of the elastic matrices at the nodes belonging to the element

$$\begin{aligned} {{\varvec{D}}}_e (\xi ,\eta ,\zeta )=\sum _{j\in S_e } {N_j } (\xi ,\eta ,\zeta ){{\varvec{D}}}_j \end{aligned}$$
(11)

where \({{\varvec{D}}}_j \) is the elastic matrix at node j, \(N_{j}\) is the shape function and \(S_e \) is the set of nodes belonging to element e.

According to the finite element method, we can obtain the element stiffness matrix

$$\begin{aligned} {{\varvec{k}}}_e =\int _{V_e } {{{\varvec{B}}}^{\mathrm{T}}{{\varvec{D}}}_e {{\varvec{B}}}} \mathrm{d}V \end{aligned}$$
(12)

where B is the geometry matrix. The structural stiffness matrix K can be assembled from the element stiffness matrices

$$\begin{aligned} {{\varvec{K}}}=\sum _e {{{\varvec{k}}}_e } \end{aligned}$$
(13)

The structural stiffness equation can be written as

$$\begin{aligned} {{\varvec{KU}}}={{\varvec{F}}} \end{aligned}$$
(14)

where U and F denote the nodal displacement vector and the nodal force vector of the structure, respectively. The nodal displacement vector U can be obtained by solving the structural stiffness equation

$$\begin{aligned} {{{\varvec{U}}}}={{{\varvec{K}}}}^{-1}{{{\varvec{F}}}} \end{aligned}$$
(15)

The strain at node j is calculated by the average value of the strains at the nodes belonging to the element around node j

$$\begin{aligned} {{\varvec{\varepsilon }}}_j =\frac{1}{n_j }\sum _{e\in S_j } {{{{\varvec{B}}}}_j {{{\varvec{U}}}}_e } \end{aligned}$$
(16)

where \({{\varvec{B}}}_{j}\) is the geometry matrix of the elements around node j, \(S_{j}\) is the set of elements around node j, \(n_{j}\) is the number of elements around node j and \({{\varvec{U}}}_{e}\) is the nodal displacement vector of an element. For convenience, Eq. (16) is denoted simply as

$$\begin{aligned} {{\varvec{\varepsilon }} }_j ={{{\varvec{B}}}}_j {{{\varvec{U}}}}_e \end{aligned}$$
(17)

The nodal stress vector for each element is obtained as follows

$$\begin{aligned} {\varvec{\sigma }} ={{\varvec{DB}}}_j {{\varvec{U}}}_e \end{aligned}$$
(18)

The material volume is calculated by the summation of the integration of member densities over the structure

$$\begin{aligned} V=\sum _e \sum _{b=1}^3 \int _{V_e} {t_b {\mathrm{d}}V} \end{aligned}$$
(19)

where \(V_e \) is the volume of element e.

4 Envelope of Stiffness and Fitting

4.1 Optimal Densities and Directions of Member Under SLC

The optimization problem under each SLC l\((l=1,2,\ldots , L_c )\) can be described as

$$\begin{aligned} \begin{array}{l@{\quad }l} {\mathrm{find}}&{}\,\,\bar{{t}}_{bjl} ,{\bar{{{{\varvec{n}}}}}}_{bjl} \\ \min &{}\,\, V \\ {\mathrm{s.t.}}&{} \,\, | {\sigma _{bjl} } |\le \sigma _{\mathrm{p}} \\ \end{array} , \quad \begin{array}{l} b=1,2,3 \\ j{=1,2,}\ldots , J \\ l{=1,2,}\ldots , L_c \\ \end{array} \end{aligned}$$
(20)

where \(\bar{{t}}_{bjl} \), \({\bar{{{{\varvec{n}}}}}}_{bjl} =\{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {\bar{{n}}_{1bjl} }&{\bar{{n}}_{2bjl} }&{\bar{{n}}_{3bjl}}\end{array}\}^{\mathrm{T}}\) and \(\sigma _{bjl} \) denote the member densities, orientations and the stresses along the member (namely, the principal stresses in a truss-like continuum) at node j under load case l, respectively; \(\sigma _{\mathrm{p}} \) is the permissible stress; V is the structural volume; and \(L_{c}\) is the number of load cases. The optimal member densities under each SLC are optimized according to the fully stressed criterion

$$\begin{aligned} \bar{{t}}_{bjl}^{k+1} =\frac{\sigma _{bjl} }{\sigma _{\mathrm{p}} }\bar{{t}}_{bjl}^k\,\, (b=1,2,3;~j=1,2,\ldots ,~ J;~l=1,2,\ldots ,~ L_c ) \end{aligned}$$
(21)

where superscript k is the iterative index. The members are aligned with the principal stress directions.

According to Eq. (6), the stiffness along any direction x in the optimal structure under an SLC is expressed as

$$\begin{aligned} S_l ({{{\varvec{x}}}})=E\sum _{b=1}^3 \left( \sum _{i=1}^3 {x_i \bar{{n}}_{ibjl} } \right) ^{2}\bar{{t}}_{bjl} ~~ ( l=1,2,\ldots ,~ L_c ) \end{aligned}$$
(22)

The maximum stiffness along x under all single-load cases is expressed by

$$\begin{aligned} S_{\mathrm{m}} ({{{\varvec{x}}}})=\mathop {\max }\limits _l S_l ({{{\varvec{x}}}})=E\mathop {\max }\limits _l \sum _{b=1}^3 {\left( \sum _{i=1}^3 {x_i \bar{{n}}_{ibjl} } \right) ^{2}\bar{{t}}_{bjl} } \end{aligned}$$
(23)

The maximum stiffness is illustrated by the black thick line in Fig. 2.

4.2 Optimal Densities and Directions of Members Under MLCs

The optimization problem of minimum volume with stress constraints under MLCs is elaborated as follows. In the optimal structures under MLCs, the members at every node may exist in more than three directions, and the members may even be non-orthogonal to one another. To simplify the problem herein, a spatial truss-like material model with three families of orthotropic members is still employed.

Based on the fully stressed criterion, the optimal densities and directions of the members under a SLC can be determined easily. However, the optimization problem under an MLC becomes rather complicated. It is difficult to determine the directions of members at a node under MLC given three principal stress directions under each SLC. To overcome this difficulty, an optimality criterion based on the direction stiffness is suggested. According to Eq. (4), once the optimal truss-like continua under each SLC are obtained, the elastic matrix \({{{\varvec{D}}}}(\bar{{t}}_{1jl} ,\bar{{t}}_{2jl} ,\bar{{t}}_{3jl} ,{\bar{{{{\varvec{n}}}}}}_{1jl} ,{\bar{{{{\varvec{n}}}}}}_{2jl} ,{\bar{{{{\varvec{n}}}}}}_{3jl} )\)\((l=1,2,{\ldots },L_{c})\) of the optimal structure under the SLC at every node is determined. The elastic matrix \({{{\varvec{D}}}}(t_1 ,t_2 ,t_3 ,{{{\varvec{n}}}}_1 ,{{{\varvec{n}}}}_2 ,{{{\varvec{n}}}}_3 )\) of the optimal structures under an MLC can be estimated based on the elastic matrix \({{{\varvec{D}}}}(\bar{{t}}_{1jl} ,\bar{{t}}_{2jl} ,\bar{{t}}_{3jl} ,{\bar{{{{\varvec{n}}}}}}_{1jl} ,{\bar{{{{\varvec{n}}}}}}_{2jl} ,{\bar{{{{\varvec{n}}}}}}_{3jl} )\). As we know, the strains along the members in the optimal structures under an SLC should not exceed the allowable strain. Thus, the densities and directions of the members under an MLC can be adjusted to ensure that the maximum strains along the directions of the members under all SLCs are not allowed to exceed the allowable strain. Therefore, it is reasonable to assume that the stiffness along any direction at any point of the optimal structure under an MLC would not be less than the stiffness of the structure under every SLC.

$$\begin{aligned} S({{{\varvec{x}}}})\ge S_{\mathrm{m}} ({{{\varvec{x}}}}), \quad {{{\varvec{x}}}}\in {\mathbb {S}}^{2} \end{aligned}$$
(24)

where \(S_{\mathrm{m}} ({{{\varvec{x}}}})\) denotes the maximum stiffness under all SLCs and \({\mathbb {S}}^{2}\) is the surface of the unit sphere, which can express all directions.

Therefore, the optimization problem of minimum volume with stress constraints under MLC is transformed into

$$\begin{aligned} \begin{array}{l} \begin{array}{l@{\quad }l} {\mathrm{find}} &{} ~t_{bj} ,{{{\varvec{n}}}}_{bj} \\ {\min } &{} ~V \\ {\mathrm{s.t.}} &{} \begin{array}{l} S({{{\varvec{x}}}})\ge S_{\mathrm{m}} ({{{\varvec{x}}}}) \\ {{{\varvec{n}}}}_p^{\mathrm{T}} {{{\varvec{n}}}}_q =\left\{ \begin{array}{l@{\quad }l} 1&{}\quad ({p=q}) \\ 0&{}\quad ({p\ne q}) \\ \end{array} \right. \\ \end{array} \\ \end{array} , \quad \begin{array}{l} b=1,2,3 \\ j=1,2,\ldots , J \\ \end{array} \end{array} \end{aligned}$$
(25)

Unfortunately, it is very difficult to solve the optimization problem directly. To this end, we must consider other methods and tools. A greater stiffness is known to correspond to the requirement of a greater volume of material. To satisfy the constraint \(S({{{\varvec{x}}}})\ge S_{\mathrm{m}} ({{{\varvec{x}}}})\) with minimal volume, it is reasonable to assume that the stiffness along any direction at any point of the optimal structure under an MLC should be as close as possible to the stiffness under every SLC. The optimization problem in Eq. (25) is transformed into that of minimizing the summation of the difference between the stiffness under the MLC and the maximum stiffness under all SLCs. In other words, the volume of the shaded regions shown in Fig. 2 needs to be minimized. A surface, illustrated by the red solid line in Fig. 2, is used to fit with the stiffness under the MLC and approach the envelope surface of the stiffness under all SLCs. The distance from the center of symmetry to a point on the surface indicates the magnitude of the directional stiffness.

Fig. 2
figure 2

Envelope surface of stiffness under every SLC

Full size image

According to Eq. (6), the directional stiffness of the optimal structure under an MLC at any point is expressed as an equation for the quadric surface along any direction x

$$\begin{aligned}&S({{{\varvec{x}}}})={{{\varvec{P}}}}({{{\varvec{x}}}})\bar{{{{\varvec{C}}}}} \nonumber \\&{\bar{{{{\varvec{C}}}}}}=\{{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {c_1 }&{} {c_2 }&{} {c_3 }&{} {c_4 }&{} {c_5 }&{} {c_6 } \\ \end{array} }\}^{\mathrm{T}} \nonumber \\&{{{\varvec{P}}}}({{{\varvec{x}}}})=\{{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {x_1^2 }&{} {x_2^2 }&{} {x_3^2 }&{} {2x_1 x_2 }&{} {2x_2 x_3 }&{} {2x_3 x_1 } \\ \end{array} }\} \end{aligned}$$
(26)

or

$$\begin{aligned} S({{{\varvec{x}}}})={{{\varvec{x}}}}^{\mathrm{T}}{{\varvec{Cx}}},\quad {{{\varvec{C}}}}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {c_1 }&{} {c_4 }&{} {c_6 } \\ {c_4 }&{} {c_2 }&{} {c_5 } \\ {c_6 }&{} {c_5 }&{} {c_3 } \\ \end{array} }} \right] \end{aligned}$$
(27)

where \(c_{1}\)–\(c_{6}\) are constants to be determined.

The summation of the differences between the stiffness of the optimal structure under an MLC and the maximum stiffness under all SLCs over all directions, i.e., the volume of the shaded regions illustrated in Fig. 2, is defined as

$$\begin{aligned} \delta ^{2}= \oiint {[S({{{\varvec{x}}}})-S_{\mathrm{m}} ({{{\varvec{x}}}})]^{2}{\mathrm{d}}A} \end{aligned}$$
(28)

where the integral domain is the surface \(\mathbb {S}^{2}\) of the unit sphere, which represents all directions. To minimize Eq. (28), with the aid of Eq. (26), the differentiation of \(\delta ^{2}\) with respect to \({\bar{{{{\varvec{C}}}}}}\) yields

$$\begin{aligned} \frac{\partial \delta ^{2}}{\partial {\bar{{{{\varvec{C}}}}}}}=2 \oiint {{{{\varvec{P}}}}^{\mathrm{T}}({{{\varvec{x}}}})[{{{\varvec{P}}}}({{{\varvec{x}}}}){\bar{{{{\varvec{C}}}}}}-S_{\mathrm{m}} ({{{\varvec{x}}}})]{\mathrm{d}}A} =0 \end{aligned}$$
(29)

This leads to

$$\begin{aligned} \left[ \oiint {{{\varvec{P}}}}^{\mathrm{T}}({{{\varvec{x}}}}){{{\varvec{P}}}}({{{\varvec{x}}}}){\mathrm{d}}A\right] {\bar{{{{\varvec{C}}}}}}= \oiint {{{{\varvec{P}}}}^{\mathrm{T}}({{{\varvec{x}}}})S_{\mathrm{m}} ({{{\varvec{x}}}}){\mathrm{d}}A} \end{aligned}$$
(30)

Under the spherical coordinate system, the left-hand side of Eq. (30) is integrated as

$$\begin{aligned} \oiint {{{{\varvec{P}}}}^{\mathrm{T}}({{{\varvec{x}}}}){{{\varvec{P}}}}({{{\varvec{x}}}}){\mathrm{d}}A} =\int _0^{2\pi } {{\mathrm{d}}\theta \int _0^\pi {{{{\varvec{P}}}}^{\mathrm{T}}({{{\varvec{x}}}}){{{\varvec{P}}}}({{{\varvec{x}}}})\sin \varphi {\mathrm{d}}\varphi } } =\frac{4\pi }{15} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 3&{} 1&{} 1 &{}&{}\\ 1&{} 3&{} 1&{}&{} 0 &{} \\ 1&{} 1&{} 3 &{}&{}\\ &{}&{}&{}4&{} &{} \\ &{}0&{}&{}&{}4&{}\\ &{}&{}&{}&{} &{} 4 \\ \end{array} \right] \end{aligned}$$
(31)

Its inverse matrix is calculated by

$$\begin{aligned} \left[ \oiint {{{{\varvec{P}}}}^{\mathrm{T}}({{{\varvec{x}}}}){{{\varvec{P}}}}({{{\varvec{x}}}}){\mathrm{d}}A} \right] ^{-1}=\frac{3}{16\pi }\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 8 &{} {-2} &{} {-2} &{}&{}&{}\\ {-2} &{} 8 &{} {-2} &{}&{}0&{}\\ {-2} &{} {-2} &{} 8 &{}&{}&{}\\ &{}&{}&{}5&{}&{}\\ &{} 0&{}&{}&{}5&{} \\ &{}&{}&{}&{} &{} 5 \\ \end{array} \right] \end{aligned}$$
(32)

The coefficient in Eq. (26) is obtained by

$$\begin{aligned} {\bar{{{{\varvec{C}}}}}}=\left[ \oiint {{{{\varvec{P}}}}^{\mathrm{T}}({{{\varvec{x}}}}){{{\varvec{P}}}}({{{\varvec{x}}}}){\mathrm{d}}A} \right] ^{-1}\oiint {{{{\varvec{P}}}}({{{\varvec{x}}}})^{\mathrm{T}}S_{\mathrm{m}} ({{{\varvec{x}}}}){\mathrm{d}}A} \end{aligned}$$
(33)

The right-hand side of Eq. (30) is integrated by a numerical method in the spherical coordinate system

$$\begin{aligned} \oiint {{{{\varvec{P}}}}^{\mathrm{T}}({{{\varvec{x}}}})S_{\mathrm{m}} ({{{\varvec{x}}}}){\mathrm{d}}A} =\int _0^{2\pi } {\int _0^\pi {{{{\varvec{P}}}}^{\mathrm{T}}({{{\varvec{x}}}})S_{\mathrm{m}} ({{{\varvec{x}}}})\sin \varphi {\mathrm{d}}\theta {\mathrm{d}}\varphi } } \end{aligned}$$
(34)

At every node, vector \({\bar{{{{\varvec{C}}}}}}\) is established by Eq. (33). Subsequently, the coefficient matrix C in Eq. (27) is obtained accordingly. To determine the local extrema of the quadric surface subject to the condition that the points lie on the unit sphere, the corresponding Lagrange function is established as

$$\begin{aligned} L={{{\varvec{x}}}}^{\mathrm{T}}{{{\varvec{Cx}}}}+\lambda (1-{{{\varvec{x}}}}^{\mathrm{T}}{{{\varvec{x}}}}) \end{aligned}$$
(35)

The extremum condition of Eq. (35) is obtained by the differentiation of Eq. (35) with respect to unit vector x

$$\begin{aligned} \frac{\partial L}{\partial x_i }=2{{{\varvec{Cx}}}}-2\lambda {{{\varvec{x}}}}=0 \end{aligned}$$
(36)

which leads to the eigenvalue problem

$$\begin{aligned} {{{\varvec{Cx}}}}=\lambda {{{\varvec{x}}}} \end{aligned}$$
(37)

According to Eq. (10), we can find that the eigenvectors and eigenvalues of matrix C are the directions and densities of the three families of members, respectively.

The eigenvectors and eigenvalues of matrix C are taken as the optimal directions and densities, respectively, of the members under the MLC at the nodes. The optimal truss-like continua under the MLC are obtained.

5 Optimization Approach

The densities and directions of the three families of members at the nodes are taken as the design variables. The volume of the structure is the objective function. The densities of the members are optimized by the fully stressed criterion under each SLC. The optimal truss-like continua under each SLC are obtained. Next, the truss-like continua under the MLC are optimized based on the criterion that the stiffness of the optimal structure under the MLC along any direction should be as close as possible to the envelope surface of the stiffness under every SLC. The equation for the quadric surface is used to fit with the stiffness of the optimal structure under the MLC, which is close to the envelope surface of the stiffness under every SLC. Next, the coefficient matrix C of the quadric surface is determined by this optimality criterion. The eigenvectors and eigenvalues of the coefficient matrix of the direction stiffness are the optimal directions and densities, respectively, of the members under the MLC at every node. The concrete optimization procedure involves the following steps:

  1. (1)

    The design domain is meshed, and design variables are initialized.

  2. (2)

    The structures are analyzed by the finite element method. The densities and directions of the members in the structures under every SLC are determined by Eq. (21).

  3. (3)

    The stiffness under the MLC is fitted by a quadric surface represented in Eq. (26), based on Eq. (33), at every node.

  4. (4)

    The eigenvectors and eigenvalues of the coefficient matrix C in Eq. (27) are calculated. The eigenvectors and eigenvalues are taken as the optimal directions and densities of the members under the MLC at every node, respectively.

  5. (5)

    We return to step (2) if the maximum relative change in the densities and directions of the members in two successive iterations is larger than a given value (\(10^{-2}\) in this study). Otherwise, the iterations are terminated. The optimal truss-like continua under MLC are obtained.

  6. (6)

    The optimal truss-like continua are illustrated.

  7. (7)

    The optimal truss-like continua are discretized into frame structures.

Fig. 3
figure 3

Optimal configuration of the first example: a calculation model; b optimal truss-like structure; c optimal spatial frame

Full size image
Fig. 4
figure 4

Optimal configuration of the second example: a calculation model; b optimal truss-like structure; c optimal spatial frame

Full size image
Fig. 5
figure 5

Iterative history: a dimensionless volume; b stress ratio (\(\sigma /\sigma _{\mathrm{p}} \))

Full size image

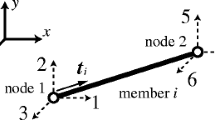
To demonstrate the truss-like structure, two types of figures are adopted with crossed lines and continuous lines, respectively. Using crossed lines, the densities and angles of members are presented using three short lines orthogonal to one another at every node. The angles and lengths of the three lines stand for the angles and densities of three families of members at every node. A few lines that are too long are cut short to make the figure distinguishable.

The structural topology is optimized in two steps. Firstly, an optimal truss-like material distribution field is formed, which is very close to the analytical solution. Clear relationship exists between the optimal truss-like material distribution field and the discrete truss used in engineering, which indicates the optimal force transferring paths. Secondly, by deleting and remaining parts of the members in a truss-like structure, the truss-like structure can be transformed into a uniform isotropic perforated continuum or a truss structure to achieve structural topology optimization.

6 Numerical Examples

Two cubes under multiple-load cases are optimized, measuring 1.0 meters on each side. They are supported at their four corners on the bottom surface. The cubes use \(10\times 10\times 10\) hexahedron elements with 8 nodes. The Young’s modulus and allowable stress are \(E=210\) GPa and \(\sigma _{\mathrm{p}} =160\) MPa, respectively. In the first example, two independent load sets \(F_{1}=F_{2} =10^{3}\) kN act at the center on the top surface along the two orthotropic directions in the horizontal plane as the two load cases. The mechanical model of the first example is illustrated in Fig. 3a. The truss-like material distribution field is optimized after 10 iterations. The optimal truss-like material distribution field is represented in Fig. 3b, in which the lengths and orientations of short lines stand for the densities and orientations of members at nodes, respectively. The optimal spatial frame structure is demonstrated in Fig. 3c.

In the second example, two groups of forces act on the top of the cube along the vertically downward direction as the two load cases. The mechanical model of the second example is illustrated in Fig. 4a. The truss-like material distribution field is optimized after 10 iterations. The optimal truss-like structure and optimal spatial frame structure are demonstrated in Fig. 4b, c, respectively.

The dimensionless volume is defined as

$$\begin{aligned} \bar{{V}}=\frac{V\sigma _{\mathrm{p}} }{Fh} \end{aligned}$$
(38)

where h is the structural height. The iteration histories of dimensionless structural volume and stress are given in Fig. 5, where the stress is the maximum stress in all members under all load case.

7 Conclusions

A new method of structural topology optimization is presented to minimize the volume of truss-like structures with stress constraints under an MLC. An optimality criterion is suggested such that the stiffness of the optimal structure under the MLC is as close as possible to the stiffness under every SLC along any direction at any point. The direction stiffness of the optimal structure under the MLC is fitted to approach the maximum direction stiffness under all SLCs. Next, the coefficient matrix of the direction stiffness is determined by the optimality criterion. The optimal directions and densities of the members under an MLC, which represent the eigenvectors and eigenvalues of the coefficient matrix of the direction stiffness, respectively, are determined at every node. Finally, the optimal spatial truss-like continua with stress constraints under an MLC are obtained. Two examples are presented to demonstrate the effectiveness and efficiency of the method.