Metaheuristic-based stochastic models for GNSS relative positioning planning

Abstract

A priori variance–covariance matrix (VCM) estimation of global navigation satellite systems (GNSS) double difference observations in relative positioning is challenging. Existing methods have been limited to estimate variances only or present variables challenging to acquire a priori, unfeasible for observation planning. Ignoring the covariances produces misleading results and compromises reliance on GNSS positioning design. In this study, we propose models to estimate the VCM a priori for planning, based on simple variables accessible to any professional: observation time span, vector length, and ephemeris type. Using a database of over 140,000 GNSS vectors with double difference (DD) observations, we group the data by time span and length range and extract standard deviations and covariances for the linear regression process. The Isolation Forest algorithm is employed to filter outlying observations. Our models provide standard deviations and root square covariances in a local coordinate system, requiring only vector length, observation time span, and ephemeris type as input. Additionally, the equations can be easily implemented in a simple spreadsheet. The results show high coefficients of determination (R² > 0.8). We tested the models in a simulated GNSS network and verified broadcast ephemeris resulted in 6.5 to 16.7 times larger error ellipsoids compared to the precise ephemeris, indicating higher uncertainty. Ellipsoids differed in flattening and orientation when compared to the null covariance (variance only) approach. Although VCM models better reflect the precision of relative positioning observations, they did not affect the number of non-controllable observations in the observation’s reliability tests.

Introduction

Relative positioning is widely used in several applications, producing three-dimensional (3D) baseline vectors to obtain the coordinates of the points of interest. The variance–covariance matrices (VCM) of these estimated vectors, which describe the uncertainty of the baseline components, are used as a quality measure, and the confidence region of the position solution depends directly on it. Estimating the uncertainty of these vectors a priori for planning activities can lead to better decision-making and cost reduction in the fieldwork. However, defining a priori VCM is challenging, and correlations are often neglected in the first phases. Incorrect estimation, or neglecting the covariances, leads to misleading precision and reliability values not accurately representing the real uncertainties in the field campaign (El-Rabbany 1994; Kermarrec and Schön 2016).

In the context of survey planning, it would be highly advantageous to predict covariances based on simple variables, such as observation time span and vector length. Several previous studies have successfully achieved this for variances in post-processed relative positioning (Eckl et al. 2001; Gatti 2004; Soler 2006; Schwieger 2007; Ozturk 2011; Soycan 2011; Firuzabadì 2012; Gond 2023), as well as in other methods like PPP (Precise Point Positioning) and RTK (Real Time Kinematic) (Geng 2010; Öğütcü 2018; Gökdaş 2020). Erdogan and Dogan (2019) and Kashani et al. (2004) studied the reliability and scaling of the VCM obtained from different GPS processing software. However, to the best of our knowledge, only one study considering a priori variances and covariances (or correlations) through simple variables such as vector length and observation time span is found in Gatti (2004).

Our study aims to provide models to estimate the VCM a priori for planning, based on simple variables accessible to any professional: observation time span, vector length and ephemeris type.

We have improved upon previous works by using over 140,000 global navigation satellite system (GNSS) vectors, covering an extensive range of values for the models' variables, and processed with global positioning system (GPS) and GLONASS signals. Also, this study provides models in a local coordinate system for broadcast and precise ephemeris. Our work also benefits from machine learning techniques for data filtering and modeling, combining linear regression, metaheuristics, and penalty functions to obtain better models.

By utilizing the outcomes of the models, professionals can adjust the observation time to meet established criteria and determine whether precise final ephemeris from the International GNSS Service (IGS)—which can take from 12 to 19 days—are necessary to achieve a desired level of quality. Moreover, it is important to consider that many developing countries lack dense networks of active stations, making post-processed relative positioning a daily reality for professionals in those regions.

In this study, the processed vectors are grouped by observation time span (t), length (l), and ephemeris type to check for patterns in the discrepancies (north, east, and up) predicated on these three variables (t, l and ephemeris). First, we computed and defined benchmark values of the 3D components of each baseline used in this study. Second, the discrepancies of each of the estimated vectors are set as input in the filtering process using the Isolation Forest algorithm (IFA) to remove outlying vectors (Liu et al. 2008, 2012). Third, the standard deviations and covariances computed for each group of vectors are fed to the proposed procedure for the models building. Each variance and covariance component are modeled separately, also distinguishing between broadcast and precise ephemeris.

A simulated GNSS network is established and both cases with null covariances (VM) and VCM are tested. Reliability measures proposed in Prószyński (2010) are computed to evaluate the observations’ quality and controllability to outliers. Error ellipsoids of the stations are also drawn and compared as measures of precision.

The next section presents the data we used, the pre-processing filtering, and its organization. In the later section, the regression procedure, and the metaheuristic Independent Vortices Search (IVS) are presented, along with the strategy to compute reliability measures and their application in a simulated GNSS network. Following that, we present the models obtained to estimate the VCM (available online at https://docs.google.com/spreadsheets/d/1zvMk7J_TYmkZYdgujIZVsZOKIHmcpelIIj4NLMBdBzI/edit?usp=sharing) and the outcomes from the implementation in the GNSS network and discuss the significance of the results. Finally, we summarize the findings and discuss final considerations.

GNSS vectors data, filtering, and organization

The investigation of variance and covariances models was based on a massive database of processed GNSS vectors, based on 43 stations of the Brazilian Network for Continuous Monitoring of GNSS Systems (RBMC) (Fig. 1). 761 three-dimensional (3D) baselines ranging from 2.3 to 950 km had their data collected on 32 different days, from January to May 2019. This period avoids data collection on high ionospheric activity. Each vector for each day of observation was processed with eight (8) unique time spans (1/2, 1, 2, 4, 6, 8, 12, and 24 hours) and separately for broadcast and precise final ephemeris. The vector processing was carried out using the software Trimble Business Center (TBC).

Fig. 1

Location of the RBMC stations for the GNSS relative positioning. Concentrated in the middle-west, south, and southeast of Brazil. Ranges: latitude from −18° to −28°; longitude from −43° to −58°

The TBC processing configuration was mostly kept unchanged from the default settings, as follows: the accepted solution types were fixed, and in case of failure, float; all available frequencies of satellite signals were used; the epoch processing time interval was set to automatic; the elevation mask was 10 degrees, and the enabled GNSS constellations were GPS and GLONASS. The method used to solve ambiguity varies according to the length of the vector. For vectors considered very short, less than two kilometers, TBC uses the double differences processing mode for all signal frequencies. For vectors between 2 and 20 km, double differences for all frequencies, but with ionosphere modeling. Vectors with medium lengths, from 20 to 200 km, are processed with the combination of ionosphere-free and wide lane carrier phase measurements without ionosphere modeling. For baselines from 200 to 1000 km, the software generates a mixed solution of the previous method and the Melbourne-Wübbena mode (Trimble Inc. 2018). The epoch processing time interval varies automatically according to the observation duration. While there are various alternative processing strategies, it is important to emphasize that the proposed models are applicable for processing configurations similar to the one utilized here (whether in TBC or in other software). Investigating the effect of different processing strategies on the model could be the subject of future works. Additionally, the methodology proposed for obtaining VCM models in this study is general and can be applied to different processing strategies.

All 3D vectors were transformed into a local 3D coordinate system by using the midpoint of each baseline as the reference for the transformation, applying the following (Leick et al. 2015),

$${{\varvec{X}}}_{enu}={\varvec{R}}\Delta {{\varvec{X}}}_{XYZ}$$

(1)

where X_enu is the vector with the transformed coordinates in the local 3D coordinate system, ∆X_XYZ is the vector in the Earth-centered, Earth-fixed (ECEF) coordinate system, given by

$$\Delta {{\varvec{X}}}_{XYZ} = \left[\begin{array}{c}\Delta X\\ \Delta Y\\ \Delta Z\end{array}\right] = \left[\begin{array}{c}{X}_{P}-{X}_{0}\\ {Y}_{P}-{Y}_{0}\\ {Z}_{P}-{Z}_{0}\end{array}\right]$$

(2)

where (·)_P are the coordinates to be transformed and (·)₀ the origin coordinates. R is the rotation matrix given by (Leick et al. 2015),

$${\varvec{R}} = \left[\begin{array}{ccc}-sin{\lambda }_{0}& cos{\lambda }_{0}& 0\\ -sin{\phi }_{0}cos{\lambda }_{0}& -sin{\phi }_{0}sin{\lambda }_{0}& cos{\phi }_{0}\\ cos{\phi }_{0}cos{\lambda }_{0}& cos{\phi }_{0}sin{\lambda }_{0}& sin{\phi }_{0}\end{array}\right]$$

(3)

Here, λ₀ and ϕ₀ are the longitude and latitude at the origin of the local coordinate system.

We obtained benchmark values for 761 baselines by averaging vectors processed using twenty-four (24) hours of relative positioning with double differences observations and precise ephemeris. We then compared the standard deviation of the length variability with the residual of each 24-h vector. Any vector with a residual higher than three standard deviations (σ > 3) was removed, and we recalculated the average length to obtain the best benchmark values. The residuals higher than 3σ were eliminated as they may indicate problems with the baseline observation. We defined the error-free benchmark values of each baseline as the 3D components of the averaged vector.

Next, all processed vectors had their length components (e, n, u) subtracted from their benchmark pair to get the discrepancy values. Vectors with minor timespan observations or longer baselines are likely to present higher differences (Koch et al. 2022). Nevertheless, these discrepancies may indicate outlying values as GNSS vectors are also susceptible to errors. The most common causes are multipath errors, in which the satellite signal is dispersed over a surface and perceived by the receiver from different directions, and equipment errors, among others (Hofmann-Wellenhof et al. 2008).

A filtering process was conducted to identify outliers using the Isolation Forest algorithm (IFA). IFA uses a relatively simple concept, isolating the anomalies through a binary tree structure called the Isolation Tree. It contrasts with most approaches, where a model is built on the data followed by outlier detection techniques. IFA allows us to clean the database beforehand, not depending on a previous model which could have already suffered bias in the regression. Another feature that draws attention is that IFA has only two training parameters and one evaluation parameter. The number of trees (n_T) to be built and the sample size (ψ) belong to the training parameters. The tree height limit (h_lim) for the sample scoring makes the evaluation parameter. More details on IFA can be found at Liu et al. (2008, 2012).

Although it is possible to use a threshold-based approach to remove outliers by analyzing residuals that exceed a certain limit, IFA is capable of handling non-Gaussian distributions and correlations between variables, making it more suitable for identifying outliers for diverse data sets. IFA can detect outliers that may not be easily identified by just looking at the residuals. Overall, IFA provides a more robust and automated approach to outlier detection than a threshold-based approach.

For the vector database, n_T was set at 2,000 and ψ at 25%, defined by a trial-and-error process while checking the results and behavior of the algorithm. Based on the heterogeneity of the data, the sample size must retain a good amount of normal data, while a higher number of trees assures thousands of sample combinations are tested, pursuing better isolations.

The remaining data contained 141.391 vectors. Approximately 4.1% and 3.9% were detected as anomalies for relative positioning processed with broadcast and precise ephemeris. All outlying vectors were removed from later experiments.

The filtered data were organized in intervals of baseline lengths, categories of eight (8) distinct time spans, and vectors processed with broadcast or precise orbits. Table 1 presents the north component standard deviations for each group of vectors. As the observation time span increases the standard deviations lower, while for longer ranges these values increase. The other two components (east and up) show a similar pattern, i.e., the shorter the time span and vector length, the lower the standard deviation. IFA identified vectors up to 50 km in length with 24 h of observation as anomalies. This could be explained by the limited number of short vectors in the database, causing them to be wrongly identified as anomalous due to their relative position (away) from other data points in the set space. However, this did not impede the construction of the models since other intervals were present. Moreover, in most real-life applications, 24-h observations on short length vectors are rare.

Table 1 Standard deviations from reference baselines (mm) for the North component. Values shaded in orange represent more significant deviations, while values in blue indicate smaller deviations

The covariances were also computed from each group of vectors, assembled by the same variables as in Table 1. Here we chose to work with the squared root of the covariances values to produce better models. Table 2 presents the covariances for X and Y axes (σ(X, Y)) in absolute squared values (mm).

Table 2 Absolute square XY covariances (mm). Values shaded in orange represent more significant covariances, while blue shades indicate smaller values

A small GNSS network was also designed to simulate the application of the models we produced. Four stations of the RBMC (MSMN, MSAQ, SPBO, SPFE) forming six 3D vectors with a single control point (MSMN). This resulted in nine (9) parameters to estimate, 18 observations and nine (9) degrees of freedom. The observation time simulated was six hours and the vectors ranged from 340 to 610 km long.

Estimation approach

To build the models, a linear regression was set up using the data from the three variables we investigated: time span (t), length (l), and ephemeris type. The two first variables were repeated in the equation by adding an unknown exponent to each, plus a relation within the two (l/t) and a constant (b₆). The ephemeris type was treated in different regressions to produce models for each type of orbit. This equation was set for all three standard deviation and covariance components in a local coordinate system (Koch et al. 2022),

$$\upsigma \left(\cdot \right)\left(t,l\right)={b}_{0}\frac{1}{t}+{b}_{1}l+{b}_{2}\frac{l}{t}+{b}_{3}{\left(\frac{1}{t}\right)}^{x}+{b}_{4}{l}^{y}+{b}_{5}{\left(\frac{l}{t}\right)}^{z}+{b}_{6}$$

(4)

where σ(·) stands for the standard deviation of the respective component (e, n, u, X, Y or Z), while t and l represent the observation time span in hours and the length of the vector in kilometers, respectively. The exponents ^x, ^y and ^z are determined during the regression process by a metaheuristic algorithm (MH). The same equation is reproduced for the covariances models where σ(·) becomes σ(·,·) for en, eu, nu, XY, XZ, and YZ covariances.

Independent vortices search

To define the exponents of (4) and evaluate the penalty function result, the metaheuristic Independent Vortices Search algorithm (IVS) was implemented (Koch et al. 2019). IVS is applied for optimizing numerical functions with a unique solution. It is based on the idea of vortices that move through the search space, narrowing the production of new candidate solutions around the best solution for each vortex. The center of each vortex coincides with the best solution at that moment, and all vortices behave independently.

The candidates are produced using a normal distribution around the center where the extent (radius) of the vortex equals 1σ. Because the radius size is decreased over the cycles, the search shifts from a global to a local search (exploration to investigation) (Koch et al. 2019).

A fitness function evaluates the result for each candidate solution produced by any vortex and normalizes the values of f_i within the range of [0;1].

$${\mathrm{fit}}_{\mathrm{i}}=\frac{1}{1+|{f}_{i}|}$$

(5)

where f_i results from the objective function of the i-th candidate.

IVS only needs a few parameters to be determined: the size of the search space common to all metaheuristics, the total count of cycles; the number of vortices; and the number of candidate solutions generated by each vortex in each cycle. For more details on IVS, the reader can refer to Koch et al. (2019) and Dogan and Olmez (2015).

Penalizing and approach overview

In the regression process, a penalty function was introduced based on Koch et al. (2022) study.

$$\mathrm{min}{\sum }_{0}^{n}\left|\frac{{r}_{n}^{p}}{{r}_{n}}-1\right|$$

(6)

For the regressions, Eq. (6) provides better adjustment to the more precise data (less discrepancies). where n is the number of data points, r_n^p is the n-th estimated value from the regression, and r_n is the n-th value in the dataset. As the proportion of the i-th estimated discrepancy (r_i^p) and i-th discrepancy in the dataset (r_i) approaches 1, the sum will tend to 0, reducing the penalty value applied.

Once the penalized result is computed, it returns to IVS, and the fitness of the result is evaluated. If IVS has reached a stopping criterion (the number of fitness evaluations), the algorithm verifies the null hypothesis at 5%. Any variable that presents a p-value higher than 5% is removed from the model. In case two or more variables presented p-values higher than 5%, the variable associated with the highest p-value is removed. The algorithm restarts with the remaining variables and adjusts the number of fitness evaluations in IVS when necessary.

If IVS reaches the stopping condition and all variables pass the null hypothesis test at 5%, the linear regression coefficients are returned along with the exponents estimated by the metaheuristic. The equation can then be fulfilled based on the initial model (4). A diagram detailing the procedure is presented in Fig. 2.

Fig. 2

Procedure for linear regression with the application of IVS and penalty function

Occasionally, none of the exponent variables might remain in the expression (4) after continuously removing them based on their p-value. If so, the MH execution can be skipped as no exponents remain in the model. The null hypothesis test is still applied directly after the linear regression. The disadvantage of such a situation is that the penalty function is no longer activated as it only influenced the estimation of the exponents by the MH.

Validating models results in a network

To validate the VM and VCM models, they were applied for the network we presented and considered for both orbits, precise and broadcast. The network adjustment was computed using the Gauss–Markov model for linear or linearized problems, computing the residuals and comparing error ellipsoids of the adjusted vertices. Reliability measures were also evaluated for the observations.

Reliability measures

For the VM model, the local redundancy number indicates the fraction of a possible (non-random) error in an observation that is reflected in the respective residue of that observation. It is obtained by computing the redundancy matrix ${{\varvec{R}}}_{L}$ given by

$${{\varvec{R}}}_{{\varvec{L}}}={\varvec{I}}-{\varvec{A}}{\left({{\varvec{A}}}^{T}{{\varvec{W}}}_{d}{\varvec{A}}\right)}^{-1}{{\varvec{A}}}^{T}{{\varvec{W}}}_{d}$$

(7)

where I is an identity matrix. Here, ${{\varvec{W}}}_{d}={\upsigma }^{2}{{\varvec{\Sigma}}}_{d}^{-1}$ with ${{\varvec{\Sigma}}}_{d}$ as a diagonal matrix composed by the VM of each observation. If 0.5 < r_i ≤ 1 for r_i representing the i-th diagonal element of ${{\varvec{R}}}_{{\varvec{L}}}$, i.e., r_i = diag(${{\varvec{R}}}_{{\varvec{L}}}$)_ii, than the i-th related observation will have at least half possible (non-random) error reflected in the respective residual. The observation has good controllability.

Similarly, for the VCM model, a two-parameter reliability measure was adopted as proposed in Prószyński (2010) for the tests with covariances. It transforms the observations into correlated dimensionless variables of equal accuracy by dividing the system by ${\upsigma }_{s}=\sqrt{\mathrm{diag}\left({\varvec{\Sigma}}\right)}$.

The system chosen to obtain the network LS solutions is also transformed, resulting in (Prószyński 2010):

$${{\varvec{v}}}_{s}={{\varvec{A}}}_{s}{\varvec{x}}-{{\varvec{l}}}_{s}\, \mathrm{with} \,{{\varvec{\Sigma}}}_{s}={{\varvec{\upsigma}}}_{s}^{-1}{\varvec{\Sigma}}{{\varvec{\upsigma}}}_{s}^{-1}$$

(8)

where l_s, A_s, and v_s are the transformed vector of observations, design matrix, and vector of residuals, respectively, obtained by ${{\varvec{l}}}_{{\varvec{s}}}={{\varvec{\upsigma}}}_{s}^{-1}$, ${{\varvec{A}}}_{\mathrm{s}}={{\varvec{\upsigma}}}_{\mathrm{s}}^{-1}{\varvec{A}}$, ${{\varvec{v}}}_{s}={{\varvec{\upsigma}}}_{s}^{-1}{\varvec{v}}$ (Prószyński 2010).

The two parameters that measure the reliability of each observation in the network are then evaluated. h_ii, is the i-th diagonal element of H (Prószyński 2010):

$${\varvec{H}}={\varvec{I}}-{{\varvec{A}}}_{s}{\left({{\varvec{A}}}_{s}^{T}{{\varvec{\Sigma}}}_{s}^{-1}{{\varvec{A}}}_{s}\right)}^{-1}{{\varvec{A}}}_{s}^{T}{{\varvec{\Sigma}}}_{s}^{-1}$$

(9)

if 0.5 < h_ii ≤ 1 then the first criteria is met, here meaning that at least half the error will be reflected on the i-th residual, similar to r_i from (7) which in this study yields the same result (Prószyński 2010).

The second parameter is computed as

$${k}_{i}=\frac{1}{{h}_{ii}}-\frac{{w}_{ii}}{{h}_{ii}^{2}}-1$$

(10)

which gives the relation to observations disturbance on local and quasi-global errors. If 0 < k_i < 1 then the local error effect of the i-th observation is greater on the i-th residual than on the quasi-global effect on all other residuals (Prószyński 2010). w_ii is defined by

$${w}_{ii}={h}_{ii}-{\left({{\varvec{H}}}^{T}{\varvec{H}}\right)}_{ii}$$

(11)

where w_ii is the effect of the asymmetry of the i-th row and the i-th column of H.

Since our VCM models are designed for GNSS observations and geodetic network planning, establishing readability measures is very important. Regarding network responses to outlying observations, these reliability measures produce interpretable results. The reader can find more details in Prószyński (2010).

Results and discussion

We applied the proposed procedure to obtain standard deviations and covariances estimation equations according to the ephemeris chosen. The equations were used in a GNSS network, and null covariances and a complete VCM were compared.

Models

By implementing the procedure detailed in Fig. 2, 24 equations were obtained that model the standard deviations and covariances of the GNSS DD relative positioning as a function of the time span (t in hours) and vector length (l in kilometers). Based on the collected data, all components have different models for broadcast and precise ephemeris. Standard deviations are given in meters (m) and covariances were squared in the estimation process, meaning they are also represented in meters (m) (Table 3).

Table 3 Comparative analysis: quality metrics of obtained models vs. Eckl et al. (2001) regression models

All equations kept at least one coefficient related to l and t, for both orbit products. It is essential to note that using values of l and t outside the studied intervals may produce undesirable and misleading results. Nevertheless, this study covers most practical applications since quantities beyond these intervals are rarely employed, allowing for widespread use of the models.

Regressions were also run with Eckl et al. (2001) equation to compare the models produced for standard deviations and root squared covariances. The obtained models were based on the same data, but without IVS and penalty functions, using only the four coefficients proposed in Eckl et al. (2001). The models’ results were analyzed and summarized in Table 3.

The procedure to obtain the models presented in Table 4 showed better results when comparing the R² and RMSE values. Models with more coefficients and IVS better represented standard deviations and root squared covariances in all components (Figs. 3 and 4). For vectors with 8 to 24h of observation time span and up to 650 km long, where smaller deviation values are expected, our models reduced RMSE by 75.5% and 22% for standard deviation and root squared covariances models, respectively. This is mostly accomplished by the penalization function presented in Eq. 6, which provides better adjustment to the more precise data.

Table 4 Equations resulted from the proposed procedure for the standard deviations and covariances. σ(·) stands for the standard deviation of (·) given in meters (m), and √σ(·,·) indicates the square root of the covariance of (·,·) also given in meters (m). R² is the coefficient of determination of the statistical model, and RMSE is the root-mean-square error

Fig. 3

Comparison of the R² values obtained for each component of standard deviations and root squared covariances. In blue color, values for the models produced from Koch et al. (2022) procedure with IVS and penalizing function. In gray color, values from the regressions with four components (Eckl et al. 2001)

Fig. 4

Comparison of the RMSE values obtained for each component of standard deviations and root squared covariances. In blue color, RMSE values produced from Koch et al. (2022) procedure with IVS and penalizing function. In gray color, RMSE with four components models (Eckl et al. 2001)

The resulting equations can be easily applied to planning GNSS relative positioning with double differences applications and require only two variables to be known: the time span of the observation, which is easily managed, and the vector length that can be planned without difficulty.

Application

All models were tested on the simulated network presented earlier, which consisted of four RBMC stations, one control point, and six 3D observation vectors. Adjustments were computed using both VCM and VM (null covariances), and the error ellipsoids and reliability measures were analyzed for each station. The volume values of the ellipsoids for each network station are presented in Fig. 5.

Fig. 5

Vertices volumes in the network, for broadcast and precise ephemeris and both models of variance and covariance matrices. Broadcast ephemeris present larger volumes meaning more uncertainty

The error ellipsoids for the stations computed using the broadcast ephemeris were found to have larger volumes, indicating that the uncertainty of these points is substantially higher compared to using precise final orbits. For the studied network, the error ellipsoids from the broadcast models were found to have volumes ranging from 6.5 to 16.7 times greater than with the final ephemeris, with a mean value of approximately 12.4 times greater. Comparing the error ellipsoids computed using the VCM and VM approaches showed no significant difference in the volumes. Figure 6 illustrates the error ellipsoids for station MSAQ using the local models.

Fig. 6

Ellipsoids of station MSAQ. On the left, the error ellipsoids using the VCM for both broadcast and precise ephemeris. On the right, the ellipsoids produced when computing the errors only with the VM. Different volumes, orientations and flattening reinforce the need to work with a full VCM

Reliability measures were used to evaluate how controllable the observations in the network is. Figure 7 illustrates the percentage of rejected vectors in the tests. In the case of VCM models, both h_ii and k_i are considered for controllability, while only r_i is used for VM models.

Fig. 7

Percentage of non-controllable observations. No change is detected for VCM or VM or broadcast and precise ephemeris

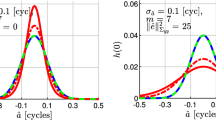
The VCM models consider more uncertainty in the observations and therefore better reflect the precision involved in relative positioning observations, although no difference is detected in the number of non-controllable observations. The reliability metrics of Prószyński (2010) for individual observations generally vary with the type of ephemeris, with the broadcast ephemeris showing greater variation. However, the number of controlled observations within the outlier exposing area did not change with the type of ephemeris or the model (VM or VCM). This is the first study to make this type of comparison, and therefore further investigations with other networks would be necessary. Figure 8 illustrates the two-parameter reliability measure for the observations computed with the VCM models. The precise orbits resulted in less dispersion on h, but the number of observations that fit within the reliability area does not appear to improve.

Fig. 8

Reliability measures of the observations (points) computed with the VCM models, divided into broadcast (right) and precise (left) ephemeris. The green area represents the space where the reliability measures are both met. Although precise orbits presented less dispersion on h, they did not seem to improve the controllability of the observations on the network

The final summation of the squared residuals from the network’s adjustments is also assessed. Figure 9 shows the absolute difference between the sum of the squared residuals computed with VCM and VM.

Fig. 9

Absolute difference of the sum of the squared residuals. Discrepancies between VCM and VM models resulted in negligible residuals in terms of magnitude; however, working with precise ephemeris ensures less difference

The differences in the final sum of squared residuals between the VCM and VM models were found to be negligible, with values under 100 mm². Precise orbits yielded even lower values, under 1 mm². This confirms that the weight matrix, which is built from variance and covariance models, has a low impact on the estimator but more on the VCM and reliability measures.

When adjusting networks, it is always advisable to use the VCM models, even if they may not improve the final solution. The VCM provides a more realistic error ellipsoid in terms of its flattening and orientation, which helps prevent the overestimation of the final precision of the computed variables. Furthermore, even though the total number of controlled observations did not change (in the global analysis), the reliability of each individual observation (local) did change. Therefore, the VCM model is also recommended in terms of observation reliability.

Conclusion

This study proposed to provide models to estimate the VCM of GNSS DD vectors a priori for planning, based on observation time span, vector length and ephemeris type. These values are critical for decision-making in structural displacement monitoring, GNSS networks, and several civil infrastructures that use GNSS observations. The study expanded the results of previous research by applying data from various vector lengths and time spans for both broadcast and precise orbits based on 140,000 GNSS relative positioning with double difference vectors. The models obtained are easy to implement with low computational cost and were tested on a simulated GNSS network.

The proposed procedure combines the IVS metaheuristic algorithm with a penalty function to better fit lower discrepancy values. It resulted in 24 models for standard deviations and covariances using broadcast and precise ephemeris for a local coordinate system.

The obtained models require only two variables to be known: the time span of the observation and vector length, which can be planned in any project’s design phase. The RMSE ranged from 7.59 × 10^–4 to 5.92 × 10^–3 m for the models, and the high coefficients of determination (R² > 0.8).

When tested on a simulated GNSS network, error ellipsoids obtained with the broadcast ephemeris presented larger volumes, indicating that the uncertainty of these points is substantially higher than with precise ephemeris. Despite not presenting big changes in the volumes, in terms of flattening and orientation the use of a complete VCM brings differences when compared to the VM (null covariances) approach.

Although the VCM models consider more uncertainty in the observations and therefore better reflect the precision involved in relative positioning observations, no difference is detected in the number of non-controllable observations by reliability measures applied in this study.

Final residuals produced by adjusting the networks with VCM and VM presented negligible differences in terms of the residual magnitude. In general, the variance and covariance models have a low effect on the estimator and more on the VCM and reliability measures. When comparing orbits, precise ephemeris reduced the differences in residuals.

In conclusion, this study demonstrated that using the VCM is essential for obtaining more reasonable a priori error ellipsoids, avoiding misleading predictions in planning observations. The linear regression-based models led to uncomplicated implementation of the models for simulations and practical use. Future research could extend the experiments with tests on high ionospheric activity and high variations in height within the stations. Also, we recommend comparing our method with expert models based on the physical properties involved, considering factors such as the elevation angles of the satellites and the temporal correlation in the process of constructing the double differences.