Best integer equivariant position estimation for multi-GNSS RTK: a multivariate normal and t-distributed performance comparison

Abstract

The best integer equivariant (BIE) estimator for the multivariate t-distribution was introduced in Teunissen (J Geod, 2020. https://doi.org/10.1007/s00190-020-01407-2), where it was shown that the BIE-weights will be different from that of the normal distribution. In this contribution, we analyze these BIE estimators while making use of multi global navigation satellite system (GNSS) data. The BIE-estimators are also compared to their least-squares (LS) and integer least-squares (ILS) contenders. Monte Carlo simulations are conducted so as to realize controlled performance comparisons of the different estimators for the purpose of multi-GNSS (GPS, Galileo, BDS and QZSS) single-frequency real-time kinematic positioning. The analyses are done in a qualitative sense by means of positioning scatter plots, and in a quantitative sense by means of numerical mean-squared-error (MSE) curves for the different estimators under different model strengths (receiver-satellite geometries and varying degrees of freedom). Particular attention is given to the difference in impact the multivariate t-distribution has when either only its cofactor matrix is in common with the normal distribution or its complete variance-covariance matrix. It will be shown that the BIE-estimators give better MSEs to both the LS- and ILS-estimator when the ILS success rate is different from zero and one, respectively. We also demonstrate that using the same BIE-estimator on different data distributions can give users an unrealistic sense of their solution quality, while the usage of two different BIE-estimators on the same data can have a marginal impact.

1 Introduction

In this contribution, we will study the real-time kinematic (RTK) positioning performance of the best integer equivariant (BIE) estimator for the multivariate t-distribution, as introduced by Teunissen (2020). This estimator is a member of the class of integer equivariant estimators, the theory of which was introduced and developed in Teunissen (2003). Our study will focus in particular on the sensitivity of the BIE estimator for different aspects of the distributional assumptions (Kibria and Joarder 2006) and different strengths of the underlying multi-GNSS model.

In Teunissen (2003), the BIE estimator was derived for when the data can be assumed to be normally distributed. Verhagen and Teunissen (2005) used simulation to study the distributional properties and performance of the BIE estimator when compared to the float and ILS fixed counterparts, while (Wen et al 2012) showed how to use this BIE estimator for global navigation satellite system (GNSS) precise point positioning (PPP). In Brack (2019), Brack et al (2014), a sequential approach to BIE estimation was developed and tested, while (Odolinski and Teunissen 2020b) analyzed the normal distribution-based BIE estimation for low-cost single-frequency (SF) multi-GNSS RTK positioning. Odolinski and Teunissen (2020a) analyzed subsequently also the corresponding BIE performance for low-cost dual-frequency long baseline multi-GNSS RTK positioning, and found that the estimated BIE positions follow a ’star-like’ pattern when the ILS SRs are high.

However, several GNSS studies have shown that working with a distribution with heavier tail probabilities than that of the normal distribution would be more appropriate. For instance Heng et al (2011) showed that many GPS satellite clock errors have heavier tails than that of the normal distribution. In inertial navigation system (INS) and GPS integration studies, the Student’s t-distribution was proposed as the more suitable distribution (Zhu et al 2012; Zhong et al 2018; Wang and Zhou 2019). Similar findings were found for multi-sensor GPS fusion in Dhital et al (2013), Xiao et al (2016) and Al Hage et al (2019).

It is therefore important to understand the BIE estimator’s behavior under the multivariate t-distribution and when compared to the usually assumed multivariate normal distribution. The purpose of our study is thus to analyze the properties and performance of the BIE-estimator when the data would be multivariate t-distributed. In this contribution, we therefore perform sensitivity analyses by means of Monte Carlo simulations so as to be able to vary the degrees of freedom for a large range of values for the multivariate t-distribution, and to have a complete control over the properties to be studied. This will be done in the context of GPS, Galileo, BDS and QZSS SF and single-epoch RTK for a location in Perth, Australia. We highlight that future studies can assess the BIE estimator for other heavy tailed distributions, like the contaminated normal distribution (Teunissen 2020).

This contribution is organized as follows. In Sect. 2 we briefly review best integer equivariant estimation and provide the explicit expressions of the BIE-estimators for when the data are multivariate normal and t-distributed. In Sect. 3, we describe the Monte Carlo simulations conducted to simulate the multi-GNSS data and also detail how to efficiently compute the float LS, the ILS and the approximate BIE solutions, respectively. In Sect. 4, we provide a qualitative analysis of the SF RTK positioning performance under the multivariate t-distribution and show by means of scatter plots how the BIE-estimator compares with its LS and ILS contenders under different model strengths. The qualitative analysis is then complemented in Sect. 5 with a quantitative performance comparison of the different estimators under different distributional regimes. It is also here that we bring attention to the importance of discriminating between a multivariate t-distribution that only has its cofactor matrix in common with the normal distribution, or one that has an identical observational variance-covariance (vc) matrix as the normal distribution. The analyses are conducted for both regimes and the implications for the different estimators are described and explained. Finally Sect. 6 contains the summary and conclusions.

2 Best integer equivariant estimation

2.1 Multivariate normal distribution

We generally assume our GNSS data to be normally distributed as,

$$\begin{aligned} \begin{aligned}&y \overset{M_{1}}{\sim } N_{m}\left( Aa+Bb, \Sigma _{yy}\right) \end{aligned} \end{aligned}$$

(1)

where y is the m-vector of double-differenced (DD) observations, $M_{1}$ denotes the first model, A is the $m \times n$ design matrix of the DD integer ambiguities in the n vector a, B corresponds to the design matrix of size $m\times p$ of the p vector of real-valued baseline components in b, and finally $\Sigma _{yy}$ represents the $m\times m$ variance-covariance (vc) matrix of the observations. The probability density function (PDF) of the multivariate normal distribution reads,

$$\begin{aligned} \begin{aligned}&f_{y}\left( y\right) =\frac{1}{\left( 2\pi \right) ^{\frac{m}{2}}\sqrt{|\Sigma _{yy}|}}\text {exp}\left\{ -\frac{1}{2}||y-Aa-Bb||^{2}_{\Sigma _{yy}}\right\} \end{aligned} \end{aligned}$$

(2)

where $||\cdot ||_{\Sigma _{yy}}^{2}=\left( \cdot \right) ^T\Sigma _{yy}^{-1}\left( \cdot \right)$ and $|\cdot |$ denotes the determinant. Note here that $E\left( y\right) =Aa+Bb$ and $D\left( y\right) =\Sigma _{yy}$, with $E\left( \cdot \right)$ and $D\left( \cdot \right)$ the expectation and dispersion operator, respectively.

The BIE estimator of the ambiguity vector a, denoted with ‘overline’, for elliptically contoured distributions reads (Teunissen 2020),

$$\begin{aligned} \begin{aligned}&\overline{a} = \sum _{z\in \mathbb {Z}^{n}}z\frac{h(z)}{ \sum _{u\in \mathbb {Z}^{n}}h(u)} \end{aligned} \end{aligned}$$

(3)

Two such elliptically contoured distributions are the multivariate normal and t-distribution. In case of normally distributed data, h(z) in (3) can be expressed as (Teunissen 2003),

$$\begin{aligned} \begin{aligned} h(z) \overset{M_{1}}{\propto } \exp \left\{ -\tfrac{1}{2}||\hat{a}-z||_{\Sigma _{\hat{a}\hat{a}}}^{2}\right\} \end{aligned} \end{aligned}$$

(4)

where $\propto$ means ’proportional to’ and $\hat{a}$ is the vector of the float ambiguities. The BIE baseline solution can then be derived as,

$$\begin{aligned} \begin{aligned}&\overline{b}=\hat{b}-\Sigma _{\hat{b}\hat{a}}\Sigma _{\hat{a}\hat{a}}^{-1}\left( \hat{a}-\overline{a}\right) \end{aligned} \end{aligned}$$

(5)

where $\hat{b}$ is the float baseline vector (15), $\Sigma _{\hat{b}\hat{a}}$ is the float covariance matrix and $\Sigma _{\hat{a}\hat{a}}$ is the vc-matrix of the float ambiguities $\hat{a}$.

Fig. 1

The BIE-’weights’ $h_{N}(0)$ (cf. 4) and $h_{t}(0)$ (cf. 9) as function of $\hat{a} \in [-0.5,+0.5]$ cycles, for varying values of m, $||\hat{e}||_{\Sigma _{yy}}^{2}$, and $\sigma _{\hat{a}}$, with $p = 1$. Full blue line corresponds to $h_{N}(0)$, whereas full red line, dashed red line and dashed green line correspond to $h_{t}(0)$ for degrees of freedom $d = 3$, $d = 10$, and $d = \infty$

The BIE estimator is unbiased and it minimizes the mean squared errors (MSEs) in the class of integer equivariant (IE) estimators (Teunissen 2003). And since it was also shown in (ibid) that the IE-class includes the class of integer-estimators, as well as the class of linear estimators, the MSE of the BIE estimator is never larger than that of the integer least squares (ILS) estimator and float LS estimator. We therefore have:

$$\begin{aligned} \begin{aligned}&D\left( \overline{b}\right) \le D\left( \check{b}\right) \\&D\left( \overline{b}\right) \le D\left( \hat{b}\right) \end{aligned} \end{aligned}$$

(6)

where $\check{b}$ is the fixed ILS baseline solution (18). The BIE estimator becomes similar to the float solution when the success rate (SR) is very low, and similar to the ILS solution when the SR is very high (Teunissen 2003).

2.2 Multivariate t-distribution

Now assume that $M_{1}$ (1) is not the correct model, but that the observations have a multivariate t-distribution with $d>2$ degrees of freedom instead,

$$\begin{aligned} \begin{aligned} y \overset{M_{2}}{\sim } T_{m}\big (Aa+Bb, \Sigma _{yy},d\big ) \end{aligned} \end{aligned}$$

(7)

where $M_{2}$ denotes the second model. The PDF of the multivariate t-distribution reads (Teunissen 2020),

$$\begin{aligned} \begin{aligned}&f_{y}\left( y\right) \\&\quad =\frac{\Gamma \left( \frac{m+d}{2}\right) }{\left( d\pi \right) ^{\frac{m}{2}}\Gamma \left( \frac{d}{2}\right) |\Sigma _{yy}|^{1/2}}\left[ 1+\frac{||y-Aa-Bb||^{2}_{\Sigma _{yy}}}{d}\right] ^{-\frac{m+d}{2}} \end{aligned} \end{aligned}$$

(8)

in which $\Gamma \left( \cdot \right)$ denotes the gamma function. Note here that again $E\left( y\right) =Aa+Bb$, however the vc-matrix of the t-distributed observations is now given as $D\left( y\right) =\frac{d}{d-2}\Sigma _{yy}$. Hence the smaller the degrees of freedom d, the less precise the observation vector becomes when compared to the normal distribution $D\left( y\right) =\Sigma _{yy}$. In Teunissen (2020) it was shown that h(z) in (3) for the BIE estimator, when having a multivariate t-distribution, can be expressed as

$$\begin{aligned} \begin{aligned} h(z) \overset{M_{2}}{\propto } \left[ 1+\frac{c_{z}}{d}\right] ^{-\frac{m+d}{2}+p} \end{aligned} \end{aligned}$$

(9)

in which $c_{z}= ||\hat{e}||_{\Sigma _{yy}}^{2}+||\hat{a}-z||_{\Sigma _{\hat{a}\hat{a}}}^{2}$ and $\hat{e}=y-A\hat{a}-B\hat{b}$ is the LS residual vector. Note that as the t-distribution converges to the normal distribution for $d\rightarrow \infty$, it was shown in Teunissen (2020) that h(z) in (9) then also converges toward that of (4) for the normal distribution.

To get some insight into the difference between the BIE-‘weights’ $h_{N}(z)$ (cf. 4) and $h_{t}(z)$ (cf. 9), we have shown them in Fig. 1, for the case $p=1$ and $n=1$, as function of $\hat{a} \in [-0.5,+0.5]$ cycles, for varying values of m, $||\hat{e}||_{\Sigma _{yy}}^{2}$, and $\sigma _{\hat{a}}$. In the first three subfigures, $h_{N}(0)$ remains unchanged, but $h_{t}(0)$ varies, from less-peaked curves, when $m=2$ and $||\hat{e}||_{\Sigma _{yy}}^{2}=0$, to more-peaked curves, when $m=7$ and $||\hat{e}||_{\Sigma _{yy}}^{2}=0$, to less-peaked curves again, having thick tails, when $m=7$ and $||\hat{e}||_{\Sigma _{yy}}^{2}=25$. Finally, all curves get flattened when $\sigma _{\hat{a}}$ increases, since $\frac{\hat{a}^2}{\sigma _{\hat{a}}^2}$ will then become smaller for all values of $\hat{a}$.

3 On the computation of the single-epoch float, ILS and BIE solutions

3.1 Multi-GNSS Monte Carlo simulations

In this, section we describe the Monte Carlo simulations that are used to assess the properties of the BIE estimator. This simulation is necessary so as to have a complete control over the properties to be studied, and to be able to systematically investigate how sensitive the BIE estimates are to the two underlying assumptions: (1) that the data are multivariate normal distributed (1), or (2) multivariate t-distributed (7).

We simulate SF GPS, BDS, Galileo and QZSS observations, where BDS refers to the BDS-2 regional system (Odolinski et al 2013; Yang et al 2014). In the single-baseline RTK model $E(y)=Aa+Bb$ we assume residual atmospheric delays to be absent in b. We also take a common reference satellite on the overlapping frequencies between the systems to further strengthen the model. The inter-system biases (ISBs) on the overlapping frequencies are neglected since we assume to have similar receiver types with the same firmware version (Odijk and Teunissen 2013). The zenith-referenced and undifferenced standard deviations (STDs) in Table 1 are used, together with an exponential elevation weighting function (Euler and Goad 1991), to formulate an undifferenced observational vc-matrix $\Sigma _{yy}^{UD}$. In this model, we assume that cross-correlation between frequencies, satellites, and code p and phase $\phi$ observations is absent. To make our simulation as realistic as possible, the code and phase STDs we employ here were estimated with least-squares variance component estimation (LS-VCE) and based on the real data in Odolinski and Teunissen (2020a), for low-cost SF ublox EVK-M8T receivers and patch antennas. We transform this undifferenced vc-matrix $\Sigma _{yy}^{UD}$ into a DD one through the linear law of error propagation to finally obtain,

$$\begin{aligned} \begin{aligned} \Sigma _{yy}=\overline{D}\Sigma _{yy}^{UD}\overline{D}^{T} \end{aligned} \end{aligned}$$

(10)

with $\overline{D}$ the DD operator (Teunissen 1997) for code and phase. In our case with one frequency, two receivers and $q+1$ satellites, we have,

$$\begin{aligned} \begin{aligned} \overline{D} = I_{2}\otimes [-1, 1] \otimes D^{T} \end{aligned} \end{aligned}$$

(11)

with $I_{2}$ the identity matrix of dimension 2 corresponding to code and phase, $[-1, 1]$ is corresponding to the between-receiver differencing with respect to pivot receiver 1, $D^{T}=\left[ -e_{q},I_{q}\right]$ is for the between-satellite differences assuming pivot satellite 1, where $e_{q}$ is a vector of ones of size $q\times 1$, and finally $\otimes$ is the Kronecker product (Rao 1973).

Table 1 Undifferenced and zenith-referenced STDs for code and phase for a SF GPS + Galileo + QZSS + BDS model, derived by using real data collected by ublox EVK-M8T receivers and patch antennas

Fig. 2

Skyplot of L1 + E1 + L1 + B1 GPS + Galileo + QZSS + BDS (19 satellites) with an elevation cut-off angle of $30^{\circ }$ for the simulated data from a position in Perth, AU

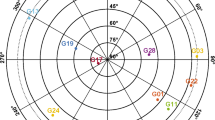
The Monte Carlo simulations to produce the multivariate normally distributed data (1) are then conducted as follows (Teunissen 1998). First we use a random generator with m independent samples drawn from the univariate standard normal distribution, say $s_{1},\ldots ,s_{m}$ from N(0, 1). We collect this in a vector $s=\left[ s_{1},\ldots ,s_{m}\right] ^T$, where m equals the number of DD code and phase observations to be employed in our SF multi-GNSS single-baseline RTK model. We subsequently transform this vector as $y_0=Gs$, with G the Cholesky factor of the vc-matrix $\Sigma _{yy}$ (10), i.e., $\Sigma _{yy}=GG^T$. This makes $y_0$ to become a sample from $N_{m}(0,\Sigma _{yy})$. To make our simulation realistic for a ’real-world’ experiment, the multi-GNSS satellite constellation in Fig. 2 is used as obtained through the broadcast ephemeris for a position in Perth, AU. The corresponding satellite coordinates and receiver benchmark coordinates are assumed to be true coordinates so that we can compute a (DD) known range vector $\rho$ to replace the above zero mean vector, i.e., we have

$$\begin{aligned} \begin{aligned}&y \overset{M_{1}}{\sim } N_{m}(\rho ,\Sigma _{yy}) \end{aligned} \end{aligned}$$

(12)

The estimated receivers coordinates will thus be unbiased, and the mean of the float ambiguities will be zero.

When we generate the multivariate t-distributed data (7), we repeat the above procedure, but now instead of generating the independent samples in s drawn from $N_1(0,1)$ we use samples drawn from Student’s t-distribution $T_{1}(0,1,d)$ for varying degrees of freedom d. This means that through using the Cholesky factor G from $\Sigma _{yy}=GG^T$, we have $D(y)=\frac{d}{d-2}\Sigma _{yy}$. Note that matrix $\Sigma _{yy}$ is now thus not the vc-matrix of the t-distributed data. We finally get,

$$\begin{aligned} \begin{aligned}&y \overset{M_{2}}{\sim } T_{m}(\rho ,\Sigma _{yy},d) \end{aligned} \end{aligned}$$

(13)

Since we will also investigate the differences between the normal and BIE estimator when the variances of the observations between the two distributions are the same, some further simulations need to be conducted. To do this simulation we generate $y_0=Gs$ with G the Cholesky factor of $\frac{d-2}{d}\Sigma _{yy}$ rather than $\Sigma _{yy}$, so that $D(y)=\Sigma _{yy}$, thus achieving that the t-distributed data will have the same vc-matrix as that of the normally distributed data. We then finally have,

$$\begin{aligned} \begin{aligned} y \overset{M_{3}}{\sim } T_{m}\left( \rho ,\tfrac{d-2}{d}\cdot \Sigma _{yy},d\right) \end{aligned} \end{aligned}$$

(14)

where $M_{3}$ now refers to the third model, so that we can distinguish it from that of (13). We repeat the above procedure N = 200,000 times for (12), (13) and (14), respectively, so that we have large samples of observations. A sufficiently large number of samples are needed in order to get good approximations of the ILS SRs, i.e., probability of correct integer estimation. Using the Chebyshev inequality, similar to Eq. (18) in Teunissen (1998), such large number of samples gives $0.5\%$ as upperbound on the probability that the relative frequency (to compute the ILS SR) differs more than $10^{-3}$ from that of the actual probability, when the ILS SR is $99.9\%$.

3.2 Integer least squares estimation

3.2.1 The float solution

Making use of the simulated samples of observations being either multivariate normal distributed (12) or multivariate t-distributed through (13) and (14), we can now estimate the ambiguities as real-valued parameters $a\in \mathbb {R}^{n}$ and perform a LS adjustment. By doing so we obtain the so called float solution of the ambiguities a and baseline components b, denoted with a ’hat’, as,

$$\begin{aligned} \begin{aligned}&\hat{a}=\left( \overline{A}^{T}\Sigma _{yy}^{-1}\overline{A}\right) ^{-1}\overline{A}^{T}\Sigma _{yy}^{-1}y\\&\hat{b}=\left( B^{T}\Sigma _{yy}^{-1}B\right) ^{-1}B^{T}\Sigma _{yy}^{-1}\left( y-A\hat{a}\right) \end{aligned} \end{aligned}$$

(15)

with $\overline{A}=P_{B}^{\bot }A$, and the orthogonal projector defined as $P_{B}^{\bot }=I_{m}-B\left( B^T\Sigma _{yy}^{-1}B\right) ^{-1}B^T\Sigma _{yy}^{-1}$. The float vc matrices, in case of normally distributed data, of the ambiguities and baseline components in (15) read,

$$\begin{aligned} \begin{aligned}&\Sigma _{\hat{a}\hat{a}}=\left( \overline{A}^{T}\Sigma _{yy}^{-1}\overline{A}\right) ^{-1}\\&\Sigma _{\hat{b}\hat{b}}=\left( \overline{B}^{T}\Sigma _{yy}^{-1}\overline{B}\right) ^{-1} \end{aligned} \end{aligned}$$

(16)

with $\overline{B}=P_{A}^{\bot }B$ and $P_{A}^{\bot }=I_{m}-A\left( A^T\Sigma _{yy}^{-1}A\right) ^{-1}A^T\Sigma _{yy}^{-1}$. Note that when the data are t-distributed the above matrices become cofactor matrices, and to then obtain the float vc matrices we need to scale them with the appropriate function of the degrees of freedom. Next step is to solve the ILS problem by making use of the float ambiguities $\hat{a}\in \mathbb {R}^{n}$ in (15) and search for its corresponding integer solution $\check{a}\in \mathbb {Z}^{n}$.

3.2.2 Integer ambiguity estimation

There are several different integer estimators that can be used. We choose ILS as it is optimal in the sense of having the largest possible SRs of all integer estimators, both under the normal distribution and under the t-distribution (Teunissen 1999a). The ILS ambiguity estimator is denoted with a ’check’ and defined as,

$$\begin{aligned} \begin{aligned}&\check{a}=\mathop {\text {arg min}}_{z\in \mathbb {Z}^{n}}||\hat{a}-z||^{2}_{\Sigma _{\hat{a}\hat{a}}} \end{aligned} \end{aligned}$$

(17)

This ILS problem is then efficiently solved by means of the LAMBDA method (Teunissen 1995; De Jonge and Tiberius 1996).

3.2.3 Fixed solution

Table 2 Elevation cut-off angle, frequency, and GNSS constellation combination (c.f. skyplot in Fig. 2)

In the final step we compute the fixed baseline solution as,

$$\begin{aligned} \begin{aligned}&\check{b}=\hat{b}-\Sigma _{\hat{b}\hat{a}}\Sigma _{\hat{a}\hat{a}}^{-1}\left( \hat{a}-\check{a}\right) \end{aligned} \end{aligned}$$

(18)

Provided the uncertainty in $\check{a}$ can be neglected we have,

$$\begin{aligned} \begin{aligned}&\Sigma _{\check{b}\check{b}}=\Sigma _{\hat{b}\hat{b}}-\Sigma _{\hat{b}\hat{a}}\Sigma _{\hat{a}\hat{a}}^{-1}\Sigma _{\hat{a}\hat{b}}<\Sigma _{\hat{b}\hat{b}} \end{aligned} \end{aligned}$$

(19)

where $\Sigma _{\hat{b}\hat{a}}^{T}=\Sigma _{\hat{a}\hat{b}}$ are the float covariance matrices under the assumption of normally distributed data. Again we note that the matrix $\Sigma _{\check{b}\check{b}}$ in (19) is a vc-matrix under the assumption of normally distributed data and a cofactor matrix in case the data is t-distributed, and to then obtain its vc-matrix we need to scale it with the appropriate function of the degrees of freedom. We note in (19) that the precision of the fixed baseline is driven by the very-precise carrier-phase data while that of $\hat{b}$ in the single-epoch case is merely driven by the pseudorange data (c.f. Table 1). This means that the standard deviations of $\check{b}$ will then be a two-order of magnitude smaller than those of $\hat{b}$. However, for this to hold true, the uncertainty in the resolved integer ambiguities must be negligible, implying that their SR should be sufficiently close to one.

3.2.4 Integer least squares success rate

To determine the ILS SR one can count how many times, say $N_{z}$, out of the N samples of observations that the estimated integer ambiguities become the null vector. This gives us the ILS SR as,

$$\begin{aligned} \begin{aligned} P_s=\frac{N_{z}}{N}\cdot 100\hbox { }\ [\%] \end{aligned} \end{aligned}$$

(20)

We assess in the following results the ILS SRs for both the simulated multivariate normal distributed (12) and multivariate t-distributed data (13) and (14).

Table 2 depicts in the first three columns the elevation cut-off angle, frequency and GNSS constellation combinations used for our simulations, respectively. The ILS SRs when the data are assumed normally distributed (12) are depicted in the last column, based on the stochastic model settings in Table 1 and the GNSS constellation in Fig. 2. We set the elevation cut-off angle to high values of $30^{\circ }$ and $35^{\circ }$ degrees at the bottom row, respectively, so as to simulate the scenario of constrained environments, for example in urban canyons or when low-elevation multipath is present. We also remove arbitrary satellites, so that all four GNSSs can ultimately be included (bottom row) without achieving the $100\%$ single-epoch ILS SR (where the BIE positioning precision will become equal to that of the ILS solution).

3.3 Best integer equivariant approximation

The BIE solution in (3) involves an infinite weighted sum over the whole space of integers, which is not possible to compute in practice. Teunissen (2005) has shown that one can make use of a finite integer set $\Theta _{\hat{a}}^{\lambda }$ while still maintaining the property of integer-equivariance,

$$\begin{aligned} \begin{aligned}&\Theta _{\hat{a}}^{\lambda }=\left\{ z\in \mathbb {Z}^{n}|\text { }\Vert \hat{a}-z\Vert _{\Sigma _{\hat{a}\hat{a}}}^{2}<\lambda ^2\right\} \end{aligned} \end{aligned}$$

(21)

The integers that reside in the set $\Theta _{\hat{a}}^{\lambda }$ depends then on the ellipsoidal region around the float solution $\hat{a}$ with its radius defined in the metric of $\Sigma _{\hat{a}\hat{a}}$. When making use of this finite integer set, the BIE estimator in (3) reads,

$$\begin{aligned} \begin{aligned}&\overline{a}^{\lambda } = \sum _{z\in \Theta _{\hat{a}}^{\lambda }}z\frac{h(z)}{ \sum _{u\in \Theta _{\hat{a}}^{\lambda }}h(u)} \end{aligned} \end{aligned}$$

(22)

where $z\in \mathbb {Z}^{n}$ in (3) has been replaced by $z\in \Theta _{\hat{a}}^{\lambda }$ in (22). When the data are normally distributed, the threshold $\lambda ^2$ (21) can be determined from (Teunissen 2005),

$$\begin{aligned} \begin{aligned} P\left[ \chi ^{2}(n)\le \lambda ^2\right] =1-\alpha \end{aligned} \end{aligned}$$

(23)

i.e., from a central Chi-squared distribution $\chi ^{2}$ with n degrees of freedom and a small significance level $\alpha$.

The threshold $\lambda ^2$ (21) for a multivariate t-distribution can be defined as (Teunissen 2020),

$$\begin{aligned} \begin{aligned} P\left[ F(n,d)\le \lambda ^2\right] =1-\alpha \end{aligned} \end{aligned}$$

(24)

where F is a central F-distribution with n and d degrees of freedom, respectively.

Throughout the following results, we choose $\alpha =10^{-9}$ so as to avoid any computational burden. The LAMBDA method is again used to efficiently find the integer vectors residing in the ellipsoidal region (21).

4 SF RTK positioning under the t-distribution

Fig. 3

Simulated (200,000 samples, see Table 1, Fig. 2) horizontal (North/East) scatter of the instantaneous BIE (green dots), ILS (magenta dots), and ambiguity-float (black dots) SF (cut-off $30^{\circ }$) RTK positioning errors (c.f. Table 2). The data are t-distributed according to (14), i.e., we have $M_{3}$, where left column corresponds to the $M_{1}|M_{3}$ BIE results assuming normal h(z) (4), whereas right column shows $M_{3}|M_{3}$ BIE results using the correct h(z) (9). From top to bottom rows we depict the results for $d=3$, $d=10$ and $d=\infty$, respectively. The largest magenta dots are for ILS positioning solutions that have the same integer ambiguity vector and exceeds a cluster of $\ge 5000$ positioning solutions, where the corresponding number for the second largest magenta dots, etc. are 500 to $<5000$, 50 to $<500$, 5 to $<50$ and a single ILS solution. This multi-modal distribution of the ILS solutions is also depicted by the ILS histogram in Fig. 4

Fig. 4

Example histograms (bin size of 5 mm) of simulated North positioning errors in Fig. 3 for $95.0\%$ $M_{3}$ ILS SR and $d=3$ degrees of freedom (200,000 samples, see Table 1, Fig. 2). The BIE solutions $M_{3}|M_{3}$ using the correct h(z) (9) are shown as green bars, BIE $M_{1}|M_{3}$ using the normal h(z) (4) are plotted underneath the green bars as red bars in the right column, ILS as magenta bars in the middle column, and ambiguity-float as in the left column. The theoretical t-distribution is plotted for the float solutions and kernel smoothing (Wand and Jones 1995) is used to fit a distribution to the BIE solutions and ILS solutions depicted in the zoom-in windows, respectively, which are all given as gray lines. The zoom-in windows depict the spread of the sample solutions of North errors between $-0.05$ m and 0.05 m and 1.0 m to 5.0 m, respectively

In this section a qualitative comparison is made between the BIE, ILS and LS positioning estimators when the data are multivariate t-distributed. This comparison is done under the M3-data regime, for different degrees of freedom. Figure 3 depicts horizontal scatter plots in local North and East errors for the case of having a $M_{1}$ $98.5\%$ ILS-SR when using the simulated data in Table 2. The instantaneous BIE, ILS and LS SF positioning errors are shown as green, magenta and black dots, respectively. The comparison is made for two different BIE-estimators: the M1-BIE estimator in figure’s left column ($M_{1}|M_{3}$) and the M3-BIE estimator in figure’s right column ($M_{3}|M_{3}$). As the data are M3-based, the M1-BIE estimator has its weights incorrectly based on the the normal-weights (4), while the M3-BIE estimator is using the correct weights (9).

The three rows of Fig. 3 are based on M3-data with different degrees of freedom. The first row is based on M3-data with $d=3$ degrees of freedom, having an $95.0\%$ ILS-SR, the second row is based on M3-data with $d=10$ degrees of freedom, having an $96.3\%$ ILS-SR, while the last row corresponds with $d=\infty$, and thus with the case that $M3=M1$, i.e., the normally distributed case, having an $98.5\%$ ILS-SR.

The ILS positioning results in Fig. 3 follow a multi-modal distribution (Teunissen 1999b). To depict this clearly, all the ILS solutions that have the same integer ambiguity vector are grouped into different clusters if they exceed a certain number of positioning solutions. A cluster of $\ge 5000$ positioning solutions is denoted as the largest magenta dot, where the corresponding number for the second largest magenta dots, etc. are 500 to $<5000$, 50 to $<500$, 5 to $<50$, and finally a single ILS solution, respectively. The zoom-in window in Fig. 3 is depicted to show the two-order of magnitude improvement when going from the ambiguity-float LS-solutions to the successfully ambiguity fixed ILS-solutions. In this zoom-in window all ILS solutions are shown as their single-epoch ILS solutions (small magenta dots).

Figure 3 clearly shows the impact of the degrees of freedom. Its top row shows many occurrences of BIE (green dots), LS (black dots) and ILS solutions (magenta dots) with errors well above 2 m in both Northing and Easting when the degrees of freedom is low ($d=3$). The occurrence of such positioning solutions decreases significantly when the degrees of freedom increases ($d=10$) at the middle and particularly bottom row ($d=\infty$), when the data converge to following a normal distribution. This is due to the heavier tails of the t-distribution for lower degrees of freedom.

The impact of the degrees of freedom is also visible when comparing the performance of the M1-BIE estimator (left column) with the M3-BIE estimator (right column). The impact of using incorrect weights for the BIE-estimator is felt more when the tail probabilities are heavier and thus at the lower end of the degrees-of-freedom spectrum. This is clearly seen when comparing the respective zoom-in windows.

We also note, when the degrees of freedom increase and the tail probabilities become less heavy, that we obtain fewer number of incorrectly fixed solutions. This gives rise to a ’star-like’ scattering of the BIE solutions as explained in Odolinski and Teunissen (2020a). As the BIE-weight is larger the closer the integer vector is to the LS float solution in the metric of the ambiguity variance matrix, the more the ’star’ symmetry will point in the directions of integer vectors that have a larger probability of being an ILS solution.

Complementary to Fig. 3, we show in Fig. 4 the histograms of the North positioning errors that correspond with the scatter plots for $d=3$, where, from left to right, the LS, ILS, and BIE results are depicted. The East and Up positioning errors behave in a similar manner and are thus not shown. The M1-BIE results are shown as red bars ($M_{1}|M_{3}$) and the M3-BIE results as green bars on top of the red bars ($M_{3}|M_{3}$). On top of the LS float solutions (black bars), we also plot the corresponding theoretical t-distribution as gray lines, and we used kernel smoothing (Wand and Jones 1995) to fit the BIE and the ILS distribution in the zoom-in windows. The zoom-in windows clearly show the multi-modality of the ILS distribution. Figure 4 also shows that the BIE solutions are much more peaked than that of the LS float solution, and at the same time that ILS has more instances than both BIE estimators with large North positioning errors of say above 1 m. For example the highest PDF peak for ILS is close to $0.1\%$ with errors above 1 m, whereas BIE has a much smaller PDF value for the similar magnitude of positioning error (especially when $M_{3}|M_{3}$).

5 BIE positioning performance comparison for t- and normal distribution

In this section, we provide a quantitative performance comparison of the BIE estimator with its LS and ILS contenders. We first compare between the M1 and M2 models (cf. 12 and 13), followed by a comparison between the M1 and M3 models (cf. 12 and 14). In all our results note that the MSEs refer to the MSEs of the 3D position vectors.

5.1 BIE MSE comparison for M1 and M2 models

Fig. 5

SF RTK positioning MSE-ratio curves with equal cofactor matrix for normal (M1) and t (M2) distribution: $\tfrac{\mathrm{(M1}\;\mathrm{BIE-MSE)_\mathrm{M1}}}{\mathrm{(Float-MSE)_\mathrm{M1}}}$ (full green), $\tfrac{\mathrm{(M2}\;\mathrm{BIE-MSE)_\mathrm{M2}}}{\mathrm{(Float-MSE)_\mathrm{M2}}}$ (dashed green), $\tfrac{\mathrm{(ILS-MSE)}_\mathrm{M1}}{\mathrm{(Float-MSE)}_\mathrm{M1}}$ (full magenta), $\tfrac{\mathrm{(ILS-MSE)}_\mathrm{M2}}{\mathrm{(Float-MSE)}_\mathrm{M2}}$ (dashed magenta), $\tfrac{\mathrm{(M1}\;\mathrm{BIE-MSE)_\mathrm{M2}}}{\mathrm{(Float-MSE)_\mathrm{M2}}}$ (dashed red)

Figure 5 depicts the MSE performance of the BIE and ILS estimators for the two different data sets M1 and M2 (200,000 samples, see Table 1, Fig. 2). Their MSEs, as function of the degrees of freedom, are shown as ratios with respect to the MSEs of their own float solution. From top to bottom and left to right, the panels of Fig. 5 depict results when the satellite-geometry model-strength increases (from weak to strong), as measured by the M1 ILS SR being $9.1\%$, $40.6\%$, $84.6\%$, $95.1\%$, $98.5\%$ and $99.9\%$, respectively (c.f. Table 2).

In the figure we also show a reference line as a black horizontal line at the reference-value 1. Since BIE is MSE-superior over the LS float-solutions, all MSE-ratio curves lie below this reference line. As the tail probabilities of the M2 data get smaller with increasing degrees of freedom, the strength of the model also increases. Note, since the MSE ratios are shown with respect to their own float solution, that both the numerator and denominator of the ratio will change when the strength of the underlying model changes. Hence, if the ratio gets smaller, the implication is that the numerator benefits more from the stronger model than the denominator. First we discuss the M1-data results and then the M2-data results.

M1-data These results concern the ratios

(25)

Both their curves are horizontal as the M1 data are independent of the degrees of freedom. The M1-BIE ratio gets smaller when the model gets stronger. For an M1 ILS SR of $9.1\%$ (top row, left column) it is close to one (i.e., BIE is close to LS), and at $99.9\%$ ILS SR (bottom row, right column) it is close to zero (BIE as good as correctly fixed ILS). As the ratio gets smaller with increasing model strength, the BIE benefits more from the stronger model than its own float MSE.

Fig. 6

PDF of the standard normal (blue line) and Student’s t-distribution, with $d=3$ (red line), $d=10$ (dotted red line) and $d=\infty$ (dashed green line), respectively, with a zoom-in given for the tail probabilities of errors ranging from 2.5 to 5. a shows the PDFs when $D(y)=d/(d-2)$ for the Student’s t-distribution, whereas b shows the corresponding results when $D(y)=1$. Finally the dashed gray lines indicate the instances when the PDF becomes higher or lower for the normal distribution when compared to that of the t-distribution with $d=3$

For ILS such property only holds if the model is sufficiently strong. When the model is weak, an increase in strength may improve the float MSE more than that of ILS, which thus results in an increase in ratio. This is seen when going from an ILS SR of $9.1\%$ (top row, left column) to $40.6\%$ (top row, right column). In these cases the ILS MSE is also poorer than that of its float. The ILS MSE is only better than its float solution when the model is sufficiently strong, as can be seen when the ILS SR reaches $84.6\%$ (middle row, left column). In all cases however, the ILS MSE is poorer than that of the M1-BIE.

M2-data These results concern the ratios

(26)

All three type of curves show their dependence on the degrees of freedom and converge to the M1-data results when the degrees of freedom are at infinity ($d \rightarrow \infty$). As was the case with the M1-data, the BIE benefits more from an increase in model strength than its own float LS solution. The ILS-curve shows that the MSE of ILS only outperforms that of its float solution when the model is sufficiently strong (in Fig. 5 when the M1 ILS SR is larger than $95\%$). In all cases it is outperformed by the BIE, with particularly large differences for the weaker models.

The two BIE-ratio curves of Fig. 5 show a similar behavior, with, of course, the M2-BIE outperforming the M1-BIE, as the latter has no minimum MSE (MMSE) property under the M2-data. Their difference is however small, which is a consolation, as it implies that in this case one cannot be too wrong when using the wrong BIE estimator, i.e., when using M1-BIE instead of M2-BIE.

We also note however, particularly for the lower end of the degree-of-freedom spectrum, that the values of the two curves are significantly higher than under the M1-data regime. Hence, with M2-data, the larger tail probabilities of the t-distribution, make the BIE-estimator, relative to its own float solution, less beneficial than it is with M1-data. Thus the M1-BIE estimator has a significantly better performance with M1-data than with M2-data. This difference gets less the stronger the model becomes.

5.2 Only same cofactor matrix or same vc-matrix?

Up till now we have been comparing the performance of the estimators under the M1 and M2 data-regimes. These comparisons however, although based on different distributions, are still based on using the same cofactor matrix $\Sigma _{yy}$ for both distributions. This is indeed the usual way in which the two distributions, $N_{m}(Ax, \Sigma _{yy})$ and $T_{m}(Ax, \Sigma _{yy}, d)$, are compared. The consequence of such comparison is however that one thereby implicitly assumes the data to have different vc-matrices. We believe that such assumption does not do justice to the way vc-matrices, and thereby the observational precisions, are generally determined in practice. Many variance-component estimation methods, such as the LS-VCE method, estimate the observational precisions without the a-priori need to specify the distribution (Teunissen and Amiri-Simkooei 2008). This implies that it is more natural to make a comparison on the basis of the two distributions having the same vc-matrix, and thus comparing the estimator performances for $N_{m}(Ax, \Sigma _{yy})$ and $T_{m}(Ax, \tfrac{d-2}{d}\Sigma _{yy}, d)$, respectively.

To get an easy insight in the consequences of comparing when only the cofactor matrices are the same or when the vc-matrices are the same, we first compare the corresponding univariate distributions. For that purpose, Fig. 6 depicts the continuous PDF of the standard normal distribution $N_{1}\left( 0,1\right)$ as a blue line and the Student’s t-distribution $T_{1}\left( 0,1,d\right)$ with $d=3$, $d=10$ and $d=\infty$ degrees of freedom as red, dotted red and dashed green lines, respectively. A zoom-in window is further shown so as to compare the tail probabilities between the two distributions. In the right column of Fig. 6 we show the corresponding PDFs when the variances of the Student’s t-distributions have been scaled with $\frac{d-2}{d}$, i.e., $T_{1}\left( 0,(d-2)/d,d\right)$. The dashed gray lines indicate the instances (PDF intersections) when the PDF-values become larger or smaller for the normal distribution when compared to that of the t-distribution with $d=3$.

Fig. 7

ILS SRs for M2 (cf. 13) (dashed blue lines) and M3 (cf. 14) (full blue lines) as a function of the degrees of freedom for SF RTK positioning (200,000 samples, see Table 1, Fig. 2). The cases, from top to bottom, show the results for different model strengths having M1 ILS SRs of $99.9\%$, $95.1\%$, $40.6\%$ and $9.1\%$

Fig. 8

SF RTK positioning MSE-ratio curves with equal observation precision for normal (M1) and t (M3) distribution: $\tfrac{\mathrm{(M1}\;\mathrm{BIE-MSE)_\mathrm{M1}}}{\mathrm{(Float-MSE)_\mathrm{M1}}}$ (full green), $\tfrac{\mathrm{(M3}\;\mathrm{BIE-MSE)_\mathrm{M3}}}{\mathrm{(Float-MSE)_\mathrm{M3}}}$ (dashed green), $\tfrac{\mathrm{(ILS-MSE)}_\mathrm{M1}}{\mathrm{(Float-MSE)}_\mathrm{M1}}$ (full magenta), $\tfrac{\mathrm{(ILS-MSE)}_\mathrm{M3}}{\mathrm{(Float-MSE)}_\mathrm{M3}}$ (dashed magenta), $\tfrac{\mathrm{(M1}\;\mathrm{BIE-MSE)_\mathrm{M3}}}{\mathrm{(Float-MSE)_\mathrm{M3}}}$ (dashed red)

Figure 6 and the left column shows the much heavier tails for the PDF of the t-distribution when compared to the normal distribution as the degrees of freedom d remains low at $d=3$ and $d=10$, depicted as full and dotted red lines, respectively. Whereas when the degrees of freedom increases $d\rightarrow \infty$ (dashed green line), the PDF of the t-distribution will then converge to the normal distribution (blue line). The right column of Fig. 6 reveals that when $D(y)=1$ for the t-distribution, it becomes more peaked (when $d=3$) than the PDF of the normal distribution for errors ranging between about $-0.63$ and 0.63. Whereas in the left column the corresponding normal distribution PDF is more peaked than the t-distribution for errors ranging between about $-1.67$ and 1.67. The right column also reveals that the t-distribution will then still have heavier tails than that of normal distribution (although less prominently so).

The two relevant conclusions that can be drawn from the above univariate description are:

• 1. Although the t-distribution is in both instances heavier tailed than the normal distribution, this is less pronounced in case the two distributions have the same observational precision.

• 2. In case of equal observational precision, the t-distribution is more peaked than both the standard t-distribution and the normal distribution

When translated to the multivariate case, the implication of the increase in peakedness, in particular for the lower end of the degrees-of-freedom spectrum, is that the M3 ILS-SR will be larger than the M2 ILS-SR. This is shown in Fig. 7 as function of the degrees of freedom, for different satellite-geometry model-strengths. With this important difference in mind between the M2 and M3 data sets, we now compare the estimator performances using the M3-regime.

5.3 BIE MSE comparison for M1 and M3 models

In analogy with Fig. 5 and Fig. 8 shows the MSE-ratio curves of (25) and the M3-based MSE-ratio curves that concern,

(27)

As the general trend is similar to that of Fig. 5, we only show in Fig. 8 the model-strength cases of $40.6\%$, $84.6\%$ and $99.9\%$ M1 ILS SRs. Although the general trend is similar, there are a number of important differences that need highlighting.

First note that the MSE-ratios of (27) are smaller than their counterparts of (26). The MSEs of the BIE and ILS benefit more than their float solutions do from the improved observational precision of the M3-data over the M2-data. We also noted that due to the heavier tails of the t-distribution, the BIE MSE-ratio of (25), as shown in Fig. 5, is in all cases smaller than the BIE MSE-ratios of (26). However, this is not the case anymore in case of the M3-data for weaker models. As Fig. 8 shows for the weaker model strength of $40.6\%$ M1 ILS SR, now the BIE MSE-ratio of (25) is larger than those of (27).

We also note, both in Figs. 5 and 8, that the difference between the BIE MSE-ratio curves (dashed green and dashed red) get smaller the stronger the model becomes. This implies that the differences in their benefits with respect to their float solution get smaller. However, one should not automatically conclude from this that the MSE-differences between the BIE-solutions themselves get small as well. To make this point clear, we consider the following two important BIE-MSE ratios,

$$\begin{aligned} \tfrac{\mathrm{(M1}\;\mathrm{BIE-MSE)_\mathrm{M3}}}{\mathrm{(M1}\;\mathrm{BIE-MSE)_\mathrm{M1}}}\;\;\mathrm{and}\;\;\tfrac{\mathrm{(M1}\;\mathrm{BIE-MSE)_\mathrm{M3}}}{\mathrm{(M3}\;\mathrm{BIE-MSE)_\mathrm{M3}}} \end{aligned}$$

(28)

The first ratio measures the deterioration in the BIE-MSE when one works with the M1-BIE thinking that one has normally distributed M1-data, while in actual fact one is working with t-distributed M3-data. The second ratio measures the deterioration in the BIE-MSE when one should work with the optimal BIE under M3, but in actual fact one is working with the suboptimal M1-BIE. Both ratios are shown as function of the degrees of freedom in Fig. 9 for a strong model. The two curves show a marked difference for a large range of degrees of freedom. As $\mathrm{(M1}\;\mathrm{BIE-MSE)}_\mathrm{M3}$ is much larger than $\mathrm{(M1}\;\mathrm{BIE-MSE)}_\mathrm{M1}$ for the lower degrees of freedom, the implication is that users computing the BIE under an assumed normal distribution $M_{1}$, while the data are actually t-distributed $M_{3}$, will believe to have a much smaller MSE than their solution actually has. The second ratio-curve however, is much flatter and shows that the difference between $\mathrm{(M1}\;\mathrm{BIE-MSE)}_\mathrm{M3}$ and $\mathrm{(M3}\;\mathrm{BIE-MSE)}_\mathrm{M3}$ is marginal. Hence, these results show that using the same estimator on different data can have a big impact on the quality, while the impact of using two different estimators on the same data can be marginal. This last property is an important practical consolation as it implies that one cannot be too wrong when using a suboptimal BIE.

Fig. 9

BIE MSE-ratios $\tfrac{\mathrm{(M1}\;\mathrm{BIE-MSE)_\mathrm{M3}}}{\mathrm{(M1}\;\mathrm{BIE-MSE)_\mathrm{M1}}}$ (dashed-blue) and $\tfrac{\mathrm{(M1}\;\mathrm{BIE-MSE)_\mathrm{M3}}}{\mathrm{(M3}\;\mathrm{BIE-MSE)_\mathrm{M3}}}$ (dashed-green) as function of the degrees of freedom for the case $98.5\%$ M1 ILS-SR

6 Summary and conclusions

The best integer equivariant (BIE) estimator for the multivariate t-distribution was introduced by Teunissen (2020), where it was shown that the BIE-weights for such data will be different from that of BIE assuming normally distributed data. This contribution analyzed the performance of the BIE estimator and compared it with its LS and ILS contenders, for both multivariate t-distributed and normally distributed global navigation satellite system (GNSS) data. We provided the analytical expressions for the two types of BIE-estimators and discussed how they can be computed while maintaining their property of integer equivariance. Sensitivity analyses based on Monte Carlo simulations were then conducted to assess the performances of the various estimators for single-frequency multi-GNSS (GPS, Galileo, BDS and QZSS) instantaneous real-time kinematic (RTK) positioning. This was done in a qualitative sense by means of positioning scatter plots and in a quantitative sense by means of numerical mean-squared-error (MSE) curves for the different estimators under different model strengths.

The results confirm that the BIE-estimator is MSE-superior to both the LS- and ILS-estimator. The BIE-estimator automatically, and in a smooth way, adapts to the strength of the underlying model. The BIE-solution is close to the float LS-solution when the model is weak and it is close the ILS-solution when the model is strong.

Although it is well known that the t-distribution is heavier tailed than the normal distribution, we pointed out and demonstrated that the heaviness of the tail probabilities, and therefore the impact it has on the BIE, ILS, and LS-performances, depends on whether the comparison between the normal distribution and the t-distribution is conducted on the basis of the standard formulations, $N_{m}(Ax, \Sigma _{yy})$ and $T_{m}(Ax, \Sigma _{yy}, d)$, or on the basis of the two distributions having the same observational vc-matrix, $N_{m}(Ax, \Sigma _{yy})$ and $T_{m}(Ax, \tfrac{d-2}{d}\Sigma _{yy}, d)$. It is therefore crucial in the performance comparison of the normal distribution and the t-distribution to be very clear on this difference, not only for the BIE-evaluation, but also for the ILS-evaluation (see Fig. 7). We motivated why we believe that the second comparison does more justice to daily practice.

It was shown that the BIE-solutions benefit more from model strengthening (i.e., better receiver-satellite geometry and/or larger degrees of freedom) than the corresponding LS float solutions. It was also shown that the MSE-gain the BIE has over its LS float solution is higher for the normal distribution than for the t-distribution, in particular at the lower end of the degree-of-freedom spectrum when the tails are heavier. This difference in gain becomes less pronounced however when the t-distribution is taken to have the same observational precision as the normal distribution.

It was also shown for the models considered that the ILS success-rate under the t-distribution $T_{m}(Ax, \tfrac{d-2}{d}\Sigma _{yy}, d)$ is larger than under the normal distribution $N_{m}(Ax, \Sigma _{yy})$. This was explained by the fact that, although the t-distribution is still heavier tailed than the normal distribution in case of equal observational precision, the distribution is now also more peaked than the normal distribution, thus providing for more probability mass over the origin-centred pull-in region. For the same reason the BIE-estimators of the t- and normal distribution having the same vc-matrix outperform the BIE-estimator under the distribution $T_{m}(Ax, \Sigma _{yy}, d)$. This underlines the care one has to take in considering the type of t-distribution when comparing the performances of the different estimators. Finally, we demonstrated that using the same BIE-estimator on different data can have a big impact and thus give users an unrealistic sense of their solution quality, while on the other hand, the usage of two different BIE-estimators on the same data can have a marginal impact.