Influence measures in nonparametric regression model with symmetric random errors

Abstract

In this paper we present several diagnostic measures for the class of nonparametric regression models with symmetric random errors, which includes all continuous and symmetric distributions. In particular, we derive some diagnostic measures of global influence such as residuals, leverage values, Cook’s distance and the influence measure proposed by Peña (Technometrics 47(1):1–12, 2005) to measure the influence of an observation when it is influenced by the rest of the observations. A simulation study to evaluate the effectiveness of the diagnostic measures is presented. In addition, we develop the local influence measure to assess the sensitivity of the maximum penalized likelihood estimator of smooth function. Finally, an example with real data is given for illustration.

1 Introduction

As was noted by some authors in nonparametric regression analysis, the estimation of the nonparametric function is influenced when there are outlying observations. For this reason, diagnostic analysis is a fundamental process in the statistical modelling and have been largely investigated in the statistical literature. Some of the diagnostic techniques frequently used are global influence (elimination of cases) and local influence. The majority of the works have given emphasis in studying the effect of eliminating observations on the results from the fitted model.

This approach has also been extended to nonparametric and semiparametric models. For example, Eubank (1984, 1985) derives influence diagnostic measures based on the leverage and residuals for spline regression. Silverman (1985) discusses the application of residuals in spline regression. Eubank and Gunst (1986) derive some influence diagnostic measures for penalized least-squares estimates from a Bayesian perspective. Eubank and Thomas (1993) propose diagnostic tests and graphics for assessing heteroscedasticity in spline regression. Kim (1996) discusses the application of residuals, leverage and Cook-type distance for smoothing spline. Wei (2004) presents some influence diagnostic and robustness measures for smoothing spline. Kim et al. (2002) derive influence measures for the partial linear models based on residuals and leverage for the estimates of the regression coefficients and the nonparametric function suggested in Speckman (1988). Fung et al. (2002) studied influence diagnostics for normal semiparametric mixed models with longitudinal data. They consider single influential case or subject for the maximum penalized likelihood estimates suggested in Zhang et al. (1998). Peña (2005) defined for normal regression model a new way to measure the influence of an observation based on how this observation is being influenced by the rest of the data and Türkan and Toktamis (2013) extended these diagnostic measure for semiparametric regression model. Vanegas and Paula (2016) studied the log-symmetric regression models. In this context, the mean and skewness were modeled through nonparametric functions based on P-splines and cubic spline considering an arbitrary number of knots. In addition, they developed some diagnostic measures which were computerized in R-project. The main idea of the local influence technique, introduced by Cook (1986), is to evaluate the sensitivity of the parameters estimators when small perturbations are introduced in the assumptions of the model or in the data (for example, in the response or explanatory variables). This method has the advantage, with respect to elimination of cases, that it is not necessary to calculate the estimates of the parameters for each case excluded. Some of the works related to the technique of local influence are the following. Thomas (1991) developed local influence diagnostics for the smoothing parameter under nonparametric regression model. Ibacache-Pulgar et al. (2012, 2013) derived the local influence curvature for elliptical semiparamteric mixed and symmetric semiparametric additive models, respectively. Ferreira and Paula (2017) extended the local influence technique for different perturbation schemes considering a skew-normal partially linear model and Emami (2018) applied the local influence analysis to the Liu penalized least squares estimators. Recently, Zhu et al. (2003) and Ibacache-Pulgar and Paula (2011) to provide local influence measures under different perturbation schemes in normal and Student-t partially linear models, respectively. The aim of the work is to derive some diagnostic measures such as global and local influence in nonparametric regression model under symmetric random errors. Here, the nonparametric components is estimated by incorporating a quadratic penalty function in the log-likelihood function and whose solution leads to cubic spline functions. The work is presented as follows. In Sect. 2, we introduce the nonparametric regression models under symmetric random errors and a penalized log-likelihood function is proposed for the parameter estimation. In Sect. 3, we propose some diagnostic measures based on the global influence and we develop the local influence method for various perturbations schemes. In Sect. 4, a set of real data is used to illustrate the methodologies proposed in this paper. A simulation study to evaluate the effectiveness of the diagnostic measures derived in this paper is presented in Sect. 5. The last section deals with some concluding remarks.

2 Nonparametric regression model with symmetric random errors

In this section we present the nonparametric regression model under symmetrical random errors and penalized likelihood function, which is often required for maximizing the penalized likelihood function. The symmetric class (see, for instance, Fang et al. (1990)) includes all symmetric continuous distributions such as normal, Student-t, power exponential, logistics I and II, contaminated normal, among others. The variety of error distributions with different kurtosis coefficients gives more flexibility for modelling data sets from light- and heavy-tailed distributions.

2.1 The model

The nonparametric regression model is a powerful tool in statistical modelling due to their flexibility to model explanatory variable effect that can contribute in the nonparametric way, when there is no linear relationship between the variables. Such models assume the following relationship between the response and the explanatory variable values:

$$\begin{aligned} y_{i}=f(t_{i})+\epsilon _{i}, \quad i=1, \ldots , n, \end{aligned}$$

(1)

where $y_{i}$ denotes the ith response value at design point $t_{i}$, $f(\cdot )$ is an unknown smooth function that belongs to the Sobolev function space $W_{2}^{2}[a, b]=\{ f: f \in [a, b], f, f^{(1)}$ absolutely continuous and $f^{(2)} \in L^{2}[a, b]\}$, where $f^{(2)}({t})=\frac{{d}^{2}}{{dt}^{2}} f({t})$, and $\epsilon _{i}$ are independent random errors such that $\epsilon _{i}$ follows a symmetric distribution with location parameter 0, scale parameter $\phi >0$ and density function, given by

$$\begin{aligned} h_{\varvec{\epsilon}_{i}}({\varvec{\epsilon }})=\frac{1}{\sqrt{\phi }} g(\varvec{\epsilon }^{2}/\phi ), \end{aligned}$$

(2)

where ${\varvec\epsilon}\in {\mathcal {R}}$ and ${g}:{\mathcal {R}} \rightarrow [0,\infty ]$ is typically known as the density generator function that satisfies

$$\begin{aligned} \int _{0}^{\infty } g(u) {\mathrm {d}}u < \infty \quad \text {with}\quad u=\frac{(y-\mu )^2}{\phi }. \end{aligned}$$

Let now ${\mathbf {f}}=(\xi _{1}, \ldots , \xi _{r})^{T}$ a $(r \times 1)$ vector such that $\xi _{j}=f(t_{j}^{0}),$ with $t_{j}^{0} (j=1, \ldots , r)$ denoting the distinct and ordered values of the explanatory variable t called knots, and ${\mathbf {N}}$ an $(n \times r)$ incidence matrix whose (i, j)th element equals the indicator function $I(t_{i}=t_{j}^{0})$ for $j= 1, \ldots , r$ and $i=1,\ldots ,n$. Then, we may rewrite model (1) as follows:

$$\begin{aligned} {\mathbf {y}}={\mathbf {N f}}+{\varvec{\epsilon }}, \end{aligned}$$

(3)

where ${\mathbf {y}}$ is the $(n \times 1)$ vector of response values and ${\varvec{\epsilon }}=\left( {\varvec\epsilon}_{1}, \ldots , {\varvec\epsilon}_{n}\right) ^{T}$ is a $(n \times 1)$ vector of random errors.

2.2 The penalized log-likelihood function

From (2)we have that $y_{i}$ follows a symmetric distribution with location parameter $\mu _{i}$ and scale parameter $\phi$ whose density function is given by

$$\begin{aligned} h_{y}({y}_{i})=\frac{1}{\sqrt{\phi }} g(\delta _{i}), \end{aligned}$$

where $\delta _{i}=\phi ^{-1}\left( \textit{y}_{i}-\mu _{i}\right) ^{2}$ and $\mu _{i}={\mathbf {n}}_{i}^{T} {\mathbf {f}}$, with ${\mathbf {n}}_{i}^{T}$ denoting the ith row of the incidence matrix ${\mathbf {N}}$. We have, when they exist, that ${\mathrm {E}}(\textit{y}_{i})=\mu _{i}={\mathbf {n}}_{i}^{T} {\mathbf {f}}$ and Var$(\textit{y}_{i})=\varrho \phi ,$ where $\varrho >0$ is a constant that may be obtained from the derivative of the characteristic function (see, for instance, Fang et al. (1990)). Then, the log-likelihood function for $\varvec{\theta }=({\mathbf {f}}^{T}, \phi )^{T}$ is given by

$$\begin{aligned} L({\varvec{\theta }})=-\frac{n}{2} \mathop {\mathrm{log}}\nolimits \phi +\sum _{i=1}^{n} \mathop {\mathrm{log}}\nolimits \{g(\delta _{i})\}, \end{aligned}$$

(4)

where $\varvec{\theta } \in \varvec{\varTheta } \subseteq {\mathcal {R}}^{p^{*}},$ with $p^{*}=r+1$. A well known procedure for estimating f is based on the idea of log-likelihood penalization and consists in incorporing a penalty function in the log-likelihood function. Following, for instance, Green and Silverman (1993), we will consider the penalty function given by

$$\begin{aligned} J(f) = -\frac{\alpha }{2} \int _{a}^{b} \left[ f^{(2)}({\mathrm {t}})\right] ^{2} {\mathrm {dt}}= -\frac{\alpha }{2} {\mathbf {f}}^{T} {\mathbf {K f}}, \end{aligned}$$

where ${\mathbf {K}} \in {\mathcal {R}}^{r \times r}$ is a positive-definite matrix that depends only on the knots $t_{j}^{0}$. Therefore, the penalized log-likelihood function associated to $\varvec{\theta }$ can be expressed as

$$\begin{aligned} L_{\mathrm {p}}(\varvec{\theta }, \alpha )=L(\varvec{\theta })-\frac{\alpha }{2} {\mathbf {f}}^{T} {\mathbf {K}} {\mathbf {f}}, \end{aligned}$$

(5)

where the smoothing parameter $\alpha$ controls the tradeoff between goodness of fit, measured by large values of $L(\varvec{\theta })$, and the smoothness estimated function, measured by small values of J(f). It is important to note that large values of $\alpha$ generate smoother curves while smaller values produce more oscillating curves. In practice situations the smoothing parameter should be selected from the data. When a smoothing spline is used, for example, it is usual to consider the cross-validation method or the generalized cross-validation method Craven and Wahba (1978). Alternatively, this parameter may be selected by applying the Akaike information criterion (Akaike, 1973) or the Bayesian information criterion (Schwarz, 1978).

An alternative approach for estimating the smooth function is to use a set of base functions which are more local in their effects compared to other methods such as fourier expansion. For example, Eilers and Marx (1996) proposed P-splines, whose penalty is direct on the coefficients, instead the curve, and is based on finite differences of the coefficients of adjacent B-splines (Boor, 1978), allowing a good discrete approximation to the integrated square of the dth derivative. Such penalties are more flexible since it is independent of the degree of the polynomial used to construct the B-splines. The study of other types of base can be found, for instance, in Wood (2003).

2.3 Estimation process

Differenting the penalized log-likelihood function (5) with respect to $\varvec{\theta }=\left( {\mathbf {f}}^{T}, \phi \right) ^{T}$ and equating the elements to zero, we have the following estimating equations:

$$\begin{aligned} \frac{1}{\phi } {\mathbf {N}}^{T} {\mathbf {D}}_{v}({\mathbf {y}}-{\mathbf {N}} {\mathbf {f}})-\alpha {\mathbf {K}} {\mathbf {f}}= & {} 0\\ (2 \phi )^{-1} \left\{ \phi ^{-1}({\mathbf {y}}-{\mathbf {N}} {\mathbf {f}})^{T} {\mathbf {D}}_{v}({\mathbf {y}}-{\mathbf {N}} {\mathbf {f}})-n\right\}= & {} 0, \end{aligned}$$

with ${\mathbf {D}}_{v}=$diag$_{1 \le i \le n}(v_{i})$ and $v_{i}=-2 \zeta _{i},$ with $\zeta _{i}=\frac{{\mathrm {d}} \mathop {\mathrm{log}}\nolimits g(\delta _{i})}{{\mathrm {d}} \delta _{i}}$. The quantity $v_{i}$’s can be interpreted as weights since $g\left( \delta _{i}\right)$ is, for the majority of the symmetrical distributions, a positive decreasing function. Exceptions are Kotz, generalized Kotz and double exponential distributions. Consequently, the solution to estimating equations leads to the following two-step iterative process:

Step 1 Denoted by $\varvec{\theta }^{(0)}$ and $\varvec{\theta }^{(m+1)}$ the starting and current values of $\varvec{\theta }$, for $m=0,1,\ldots$ and $\alpha$ fixed. In this stage, ${\mathbf {f}}$ can be estimated by using the equation

$$\begin{aligned} {\mathbf {f}}^{(m+1)}=\left( {\mathbf {N}}^{T} {\mathbf {D}}_{v}^{(m)} {\mathbf {N}}+\alpha \phi ^{(m)} {\mathbf {K}}\right) ^{-1} {\mathbf {N}}^{T} {\mathbf {D}}_{v}^{(m)} {\mathbf {y}}, \end{aligned}$$

where ${\mathbf {D}}_{v}^{(m)}=$ diag$_{1 \le i \le n}\left( v_{i}\right) |_{\mathbf {\theta }^{(m)}}$

Step 2 Update ${\phi }$ by using the following equation:

$$\begin{aligned} \phi ^{(m+1)}=n^{-1}\left( {\mathbf {y}}-{\mathbf {N}} {\mathbf {f}}^{(m)}\right) ^{T} {\mathbf {D}}_{v}^{(m)}\left( {\mathbf {y}}-{\mathbf {N}} {\mathbf {f}}^{(m)}\right) . \end{aligned}$$

Note that in first step of iterative process we maximize the penalized log-likelihood function with regard ${\mathbf {f}}$ given $\phi$ while in the second step we maximize the penalized log-likelihood function with regard $\phi$ given ${\mathbf {f}}$. Thus, alternating between stages 1 and 2, this iterative process leads to the maximum penalized likelihood estimate (MPLE) of $\varvec{\theta }$.

2.4 Approximate standard errors

Analogously to the parametric regression model with normal random errors, the approximate covariance matrix of ${\widehat{\varvec{\theta }}}$ is derived from the inverse of the expected information matrix. In fact,

$$\begin{aligned} {\widehat{\mathrm {Cov}}}_{\mathrm {approx}}({\widehat{\varvec{\theta }}})=\left. {\jmath }_{\mathrm {p}}^{-1}\right| _{\widehat{\varvec{\theta }}}, \end{aligned}$$

where the matrix ${\jmath }_{\mathrm {p}}$ is defined by (see, for instance, Ibacache-Pulgar et al. (2013))

$$\begin{aligned} {{\jmath }_{\mathrm {p}}}=\left( \begin{array}{cc}{{\mathbf{N}}^{T} {\mathbf {D}}_{d} {\mathbf {N}}+\alpha {\mathbf {K}}} &{} {0} \\ {0} &{} {\frac{n\left( 4 f_{g}-1\right) }{4 \phi ^{2}}}\end{array}\right) , \end{aligned}$$

where ${\mathbf {D}}_{d}=\frac{4 d_{g}}{\phi } {\mathbf {I}},$ with $d_{g}={\mathrm {E}}\left( \zeta _{g}^{2}\left( \epsilon _{i}^{2}\right) \epsilon _{i}^{2}\right) ,f_{g}={\mathrm {E}}\left( \zeta _{g}^{2}\left( \epsilon _{i}^{2}\right) \epsilon _{i}^{4}\right)$, ${\mathbf {I}}$ denoting an $(n \times n)$ identity matrix and $\epsilon _{i}$ follows a symmetric distribution with location parameter 0, scale parameter $\phi$ and generator function g; see, for example, Ibacache-Pulgar and Paula (2011). In particular, if we are interested in drawing inferences for f and $\phi$, the approximate covariance matrices can be estimated by using the corresponding block-diagonal matrices obtained from ${\jmath }_{\mathrm {p}}^{-1}$, that is,

$$\begin{aligned} {\widehat{\mathrm {Cov}}}_{\mathrm {approx}}({\widehat{\mathbf {f}}})=\left. \left( {\mathbf {N}}^{T} {\mathbf {D}}_{d} {\mathbf {N}}+\alpha {\mathbf {K}}\right) ^{-1}\right| _{\widehat{\varvec{\theta }}} \end{aligned}$$

(6)

and

$$\begin{aligned} {\widehat{\mathrm {Cov}}}_{\mathrm {approx}}({\widehat{\phi }})=\left. \frac{4 \phi ^{2}}{n(4 f_{g}-1)}\right| _{\widehat{\varvec{\theta }}} . \end{aligned}$$

An approximate pointwise standard error band (SEB) for $f(\cdot )$ which allows us to assess how accurate the estimator ${\widehat{f}}(\cdot )$ is at different locations within the range of interest it is given by ${\widehat{f}}({\mathrm {t}}_{j}^{0}) \pm 2 \sqrt{\widehat{\mathrm {Var}}_{\mathrm {approx}}({\widehat{f}}({\mathrm {t}}_{j}^{0}))}$, where ${\widehat{\mathrm {Var}}}_{\mathrm {approx }}({\widehat{f}}({\mathrm {t}}_{j}^{0}))$ denotes the estimated approximate variance of ${\widehat{f}}({\mathrm {t}}_{j}^{0}),$ for $j=1, \ldots , r,$ obtained from Eq. (6).

3 Global and local influence measures

In this section, we propose some diagnostics measures such as: leverage, standardized residuals, Cook’s distance, Peña measured and likelihood displacement for detecting misspecifications of the error distribution as well as the presence of outlying observations.

3.1 Leverage

Considering that in the iterative process the weights $v_{i}$’s are calculated based on previous iteration, it is not possible to obtain an explicit expression for the smoother matrix (hat matrix). However, for the final iteration, the estimates not depend on ${\varvec{\theta }}$ and therefore the hat matrix has the same role as the hat matrix in linear regression that is detecting atypical observation for the predicted values of y. Considering $\alpha , \phi$ and ${\mathbf {D}}_{v}$ fixed, the vector of predictions from the fitted model (3) is given by

$$\begin{aligned} {\widehat{\mathbf {y}}} = \widehat{\varvec{\mu }} ={\mathbf {H}}(\alpha ) {\mathbf {y}}, \end{aligned}$$

(7)

where ${\mathbf {H}}(\alpha )= {\mathbf {N}}\left( {\mathbf {N}}^{T} {\mathbf {D}}_{v} {\mathbf {N}}+\alpha \phi {\mathbf {K}}\right) ^{-1} {\mathbf {N}}^{T} {\mathbf {D}}_{v} = \left\{ h_{i j}(\alpha )\right\} _{i,j=1}^{n}$ is called smoother or hat matrix and $\widehat{y}_{i}=\widehat{\mu }_{i}=\sum _{j=1}^{n} h_{i j}(\alpha ) y_{j}.$ The diagonal elements of the matrix defined as

$$\begin{aligned} h_{i i}(\alpha )={\mathbf {n}}_{i}^{T}\left( {\mathbf {N}}^{T} {\mathbf {D}}_{v} {\mathbf {N}}+\alpha \phi {\mathbf {K}}\right) ^{-1} {\mathbf {n}}_{i} v_{i} \end{aligned}$$

are called leverage values and indicate how much influence ${\mathrm {y}}_{i}$ has on the fit of ${\mathrm {y}}_{i}$. In general, the hat matrix ${\mathbf {H}}(\alpha )$ is not a projection operator, except under normally distributed random errors (see, for instance, Eubank 1984). However, for purposes of diagnostic analysis, this matrix has the same role as the hat matrix in classical linear regression. Then, considering that the hat matrix ${\mathbf {H}}(\alpha )$ is not a projection operator, we have that the conditional covariance matrix of the prediction vector is given by

$$\begin{aligned} {\mathrm {Cov}}_{\mathrm {approx}}({\widehat{\varvec{\mu }}})=\varrho \phi {\mathbf {H}}(\alpha ) {\mathbf {H}}^{T}(\alpha ). \end{aligned}$$

(8)

Note that Var$_{\mathrm {approx}}\left( {\widehat{\mathrm {\mu }}}_{i}\right) =\varrho \phi h_{i i}^{2}(\alpha ),$ for $i=1, \ldots , n.$

3.2 Effective degrees of freedom and smoothing parameter

In the literature concerning nonparametric regression models there are different definitions for the degrees of freedom, depending on the context in which they are used. A natural candidate to measure the contribution of the nonparametric component (see, for instance, Buja et al. 1989) is given by

$$\begin{aligned} {\mathrm {df}}(\alpha ) = \text {tr}\{\mathbf{H}(\alpha )\} , \end{aligned}$$

(9)

where $\mathbf{H}(\alpha )$ is defined above. According to Eilers and Marx (1996), if we consider $\mathbf{Q}_{\mathbf{N}}=\mathbf{N}^{T} \mathbf{D}_{v} \mathbf{N}$ and $\mathbf{Q}_{\alpha } = \alpha \phi \mathbf{K}$, the trace of $\mathbf{H}(\alpha )$ can be written as

$$\begin{aligned} \text {tr}\big \{\mathbf{H}(\alpha ) \big \}= & {} \text {tr}\big \{ (\mathbf{Q}_{\mathbf{N}} + \mathbf{Q}_{\alpha })^{-1} \mathbf{Q}_{\mathbf{N}} \big \} \\= & {} \text {tr}\big \{ \mathbf{Q}_{\mathbf{N}}^{1/2} (\mathbf{Q}_{\mathbf{N}} + \mathbf{Q}_{\alpha })^{-1} \mathbf{Q}_{\mathbf{N}}^{1/2} \big \} \nonumber \\= & {} \text {tr}\big \{ (\mathbf{I}_{(r \times r)} + \mathbf{Q}_{\mathbf{N}}^{-1/2} \mathbf{Q}_{\alpha } \mathbf{Q}_{\mathbf{N}}^{-1/2})^{-1} \big \} \nonumber . \end{aligned}$$

Consequently, this can be written as (see, for instance, Hastie and Tibshirani 1990)

$$\begin{aligned} \text {tr}\big \{\mathbf{H}(\alpha ) \big \}= & {} \text {tr}\big \{ (\mathbf{I}_{(r \times r)} + \mathbf{P}_{(r \times r)})^{-1} \big \} \\= & {} \sum _{j=1}^{r} \frac{1}{1 + \alpha \phi \ell _{j}} \nonumber \\\approx & {} 2 + \sum _{j=3}^{r} \frac{1}{1 + \alpha \phi \ell _{j}} \nonumber , \end{aligned}$$

(10)

where $\ell _{\jmath }$, for $\jmath = 1,\ldots , r$, are the eigenvalues of $\mathbf{P}= \mathbf{Q}_{\mathbf{N}}^{-1/2} \mathbf{Q}_{\alpha } \mathbf{Q}_{\mathbf{N}}^{-1/2}$. The calculation of ${\mathrm {df}}(\alpha )$ from Eq. (9) involves a matrix of order n, while the calculation from expression (10) involves matrices of order r ($r < n$), which minimizes the computational cost. It is important to note that (i) ${\mathrm {df}}(\alpha )=\text {tr}\{ \mathbf{H}(\alpha ) \}$ is a monotonically decreasing function of $\alpha$, given $\phi$; (ii) ${\mathrm {df}}(\alpha ) \rightarrow 2 + r$ as $\alpha \rightarrow 0$; (iii) ${\mathrm {df}}(\alpha ) \rightarrow 2$ as $\alpha \rightarrow \infty$; (iv) $2 \le {\mathrm {df}}(\alpha ) \le 2 + r$; and (v) once we have obtained the eigenvalues $\ell _{\jmath }$’s, the calculation of the degrees of freedom ${\mathrm {df}}(\alpha )$, given $\phi$ and $\alpha$, is computationally simple, and can be used to determine a value for the smoothing parameter given its decreasing monotonic relationship.

3.3 Residual

As an extension for the nonparametric regression model with symmetric random errors, we will consider the ordinary residual for checking the assumption of our model. It follows from (7) that the vector of ordinary residuals is given by

$$\begin{aligned} {\mathbf {e}}={\mathbf {y}}-\widehat{\varvec{\mu }}= \left( {\mathbf {I}}_{n}-{\mathbf {H}}(\alpha )\right) {\mathbf {y}}, \end{aligned}$$

where the ith residual is ${\mathrm {e}}_{i}=y_i-\widehat{\mu }_{i}$, for $i=1, \ldots , n .$ From (8), follows that the approximate variance of the ith ordinary residual is given by

$$\begin{aligned} {\mathrm {Var}}_{\mathrm {approx}} \left( {\mathrm {e}}_{i}\right) =\varrho \phi \left\{ 1-h_{i i}(\alpha )\right\} ^{2}. \end{aligned}$$

Then, following Eubank (1985) and Silverman (1985), for $\phi$ and $\alpha$ fixed, we can use the standardized residuals,

$$\begin{aligned} {\mathrm {r}}_{i}^{2}=\frac{\mathrm {e}_{i}^{2}}{\varrho \phi \left( 1-h_{i i}(\alpha )\right) ^{2}} \end{aligned}$$

for assessing the quality of the fit to ${\mathrm {y}}_{i}$. Alternatively, one might consider the versions of the studentized residuals given by

$$\begin{aligned} {\mathrm {r}}_{i}^{2}=\frac{\mathrm {e}_{i}^{2}}{\left( \varrho \widehat{\phi }^{*}\right) \left( 1-h_{i i}(\alpha )\right) ^{2}} \quad \text {and} \quad {\mathrm {t}}^{[i]^{2}}=\frac{\mathrm {e}_{i}^{2}}{\left( \varrho \widehat{\phi }^{*[i]}\right) \left( 1-h_{i i}(\alpha )\right) ^{2}} , \end{aligned}$$

where $\widehat{\phi }^{*}$ is the estimator of $\phi$ defined as (see, for instance, Wahba 1983)

$$\begin{aligned} \widehat{\phi }^{*}=\frac{({\mathbf {y}}-\widehat{\varvec{\mu }})^{T} {\mathbf {D}}_{v}({\mathbf {y}}-\widehat{\varvec{\mu }})}{\text {tr}\left\{ \mathbf {I}-{\mathbf {H}}(\alpha )\right\} }, \end{aligned}$$

and $\widehat{\phi }^{*[i]}$ is the estimator of $\phi$ but without the ith observation (see, for instance, Eubank 1984), this is,

$$\begin{aligned} \widehat{\phi }^{*[i]}=\sum _{j=1, j \ne i}^{n} v_{j}\frac{\left[ {\mathrm {e}}_{j}+v_{i} h_{j i} (\alpha ){\mathrm {e}}_{i}/\left( 1-v_{i} h_{ii}(\alpha )\right) \right] ^{2}}{\left[ n-1-\text {tr}\left\{ \mathbf {H}^{[i]}(\alpha )\right\} \right] }, \end{aligned}$$

with

$$\begin{aligned} \text {tr} \left\{ \mathbf {H}^{[i]}(\alpha )\right\} =\sum _{j=1, j \ne i}^{n}\left[ h_{j j}(\alpha )+v_{i} h_{j i}^{2}(\alpha ) /\left( 1-v_{i} h_{i i}(\alpha )\right) \right] . \end{aligned}$$

Alternatively, we can consider the quantile residuals proposed by Dunn and Smyth (1996) and which are defined as

$$\begin{aligned} {\mathrm {r}}_{q_{i}} = \varPhi ^{-1}\{F_{Y_{i}}(y_{i},{\varvec{\theta }})\} , \end{aligned}$$

where $\varvec{\theta }=({\mathbf {f}}^{T}, \phi )^{T}$, $\varPhi (\cdot )$ and $F_{Y_{i}}(y_{i},{\varvec{\theta }})$ denote, respectively, the fda’s of the standard normal distribution and the postulated symmetric distributions. Under the model one has that ${\mathrm {r}}_{q_{i}}$ are independent and equally distributed N(0, 1), for $i=1,\ldots ,n$.

3.4 Cook’s distance

In ordinary linear regression models, Cook (1977) proposed measuring the influence of a point by the squared norm of the vector of forecast changes. Analogously, Hastie and Tibshirani (1990) defined a version of Cook’s distance for measuring the influence of the ith observation on the fit of a nonparametric regression model. Based on those works, we define Cook’s distance as follows:

$$\begin{aligned} D_{i}=\frac{\left( {\widehat{\varvec{\mu }}}-{\widehat{\varvec{\mu }}}^{[i]}\right) ^{T} {\mathrm {Cov}}_{\mathrm {approx}}^{-1}({\widehat{\varvec{\mu }}})\left( {\widehat{\varvec{\mu }}}-{\widehat{\varvec{\mu }}}^{[i]}\right) }{\text {tr}\{\mathbf {H}(\alpha )\}}, \end{aligned}$$

where $\widehat{\varvec{\mu }}^{[i]}={\mathbf {N}} \widehat{\mathbf {f}}^{[i]}$ denote the cubic smoothing spline fit to the data when the ith observation, $\left( {\mathrm {t}}_{i}, {\mathrm {y}}_{i}\right)$, has been deleted, and by assuming that $\alpha {\mathbf {K}}$ remains approximately constant removing the ith observation one has that

$$\begin{aligned} \widehat{\mathbf {f}}^{[i]}=\widehat{\mathbf {f}}-\frac{\left( {\mathbf {N}}^{T} {\mathbf {D}}_{v} {\mathbf {N}}+\alpha \phi {\mathbf {K}}\right) ^{-1} {{\mathbf {n}}_{i}} v_{i} {\mathrm {e}}_{i}}{\left( 1-h_{i i}(\alpha )\right) }. \end{aligned}$$

(11)

A more convenient way of writing $D_{i}$ follows from relation (see, for instance, Craven and Wahba 1978),

$$\begin{aligned} \begin{aligned} \widehat{\mu }_{i}-\widehat{\mu }_{i}^{[i]}&= {\mathbf {n}}_{i}^{T} \widehat{\mathbf {f}}-{\mathbf {n}}_{i}^{T} \widehat{\mathbf {f}}^{[i]}\\&=\frac{\mathbf {n}_{i}^{T}\left( {\mathbf {N}}^{T} {\mathbf {D}}_{v} {\mathbf {N}}+\alpha \phi {\mathbf {K}}\right) ^{-1} {\mathbf {n}}_{i} v_{i} {\mathrm {e}}_{i}}{\left( 1-h_{ii}(\alpha )\right) }\\&=\frac{h_{i i}(\alpha ) {\mathrm {e}}_{i}}{1-h_{i i}(\alpha )}. \end{aligned} \end{aligned}$$

(12)

Then, by using the Eqs. (11) and (12), we may write statistic $D_{i}$ as

$$\begin{aligned} \begin{aligned} D_{i}&=\frac{\left( \widehat{\mathbf {f}}-\widehat{\mathbf {f}}^{[i]}\right) ^{T} {\mathbf {n}}_{i} {\mathrm {Cov}}_{\mathrm {approx}}^{-1}({\widehat{\varvec{\mu }}}){\mathbf {n}}_{i}^{T}\left( {\widehat{\mathbf {f}}}-{\widehat{\mathbf {f}}}^{[i]}\right) }{\text {tr}\{\mathbf {H}(\alpha )\}} \\&=\frac{1}{\text {tr}\{\mathbf {H}(\alpha )\}} \frac{1}{\varrho \phi h_{i i}^{2}(\alpha )} \frac{h_{i i}^{2}(\alpha ) {\mathrm {e}}_{i}^{2}}{\left( 1-h_{i i}(\alpha )\right) ^{2}} \\&=\frac{1}{\varrho \phi \text {tr}\{\mathbf {H}(\alpha )\}} \frac{\mathrm {e}_{i}^{2}}{\left( 1-h_{i i}(\alpha )\right) ^{2}} \\&=\frac{1}{\text {tr}\{\mathbf {H}(\alpha )\}} {\mathrm {r}}_{i}^{2} \end{aligned} \end{aligned}$$

Then, motivated by practices in ordinary regression analysis, influential observations are detected by large values of their Cook’s distance; this is, when $D_{i} > 2\bar{D}$, with $\bar{D} = \sum _{i=1}^{n} \frac{D_{i}}{n}$. Note that under normality, this is $v_{i}=1$ and ${\text {Var}}\left( {\mathrm {y}}_{i}\right) =\phi h_{i i}(\alpha )$, the statistic $D_{i}$ agree with statistic proposed, for example, by Eubank (1985).

3.5 Peña measure

In the normal linear regression model, Peña (2005) proposed a statistic called S-statistic, to measure sensitive in the forecast of the ith observation when each observation is deleted. This type of influence analysis complements the traditional one and is able to indicate features in the data, such as clusters of hight-leverage outliers. In addition, this new statistics is very simple to compute and with an intuitive interpretation, that can be a useful tool in regression analysis, mainly with large datasets in high dimension. As an extension on nonparametric regression model with symmetric random errors, such statistic can be defined analogously by

$$\begin{aligned} S_{i}=\frac{\left\| {\mathbf {s}}_{i}\right\| ^{2}}{\text {tr}\{\mathbf {H}(\alpha )\} {\text {Var}}_{\mathrm {approx}}^{-1}({\widehat{\mathrm {\mu }}}_{i})}, \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l}{\qquad \begin{array}{c}{\mathbf {s}_{i}=\left( \widehat{\mu }_{i}-\widehat{\mu }_{i}^{[1]}, \ldots , \widehat{\mu }_{i}-\widehat{\mu }_{i}^{[n]}\right) ^{T}} \end{array}} \end{array} \end{aligned}$$

Considering Var$_{\mathrm {approx}}({\widehat{\mu }_{i}})=\varrho \phi h_{i i}^{2}(\alpha )$ and by using the identity (see, for instance, Eubank 1985)

$$\begin{aligned} {\widehat{\mu }}_{i}-{\widehat{\mu }}_{i}^{[j]}= \frac{h_{ij}(\alpha ) {\mathrm {e}}_{j}}{ ( 1-h_{jj}(\alpha ))}, \end{aligned}$$

we can write statistic $S_{i}$ as

$$\begin{aligned} S_{i}&=\frac{\left\| {\mathbf {s}}_{i}\right\| ^{2}}{\text {tr}\{{\mathbf {H}}(\alpha )\} \varrho \widehat{\phi } {h_{i i}^{2}}(\alpha )} \\&=\frac{1}{\varrho \widehat{\phi } \text {tr}\{{\mathbf {H}}(\alpha )\} {h_{i i}^{2}}(\alpha )} \sum _{j=1}^{n} \frac{h_{i j}^{2}(\alpha ) {\mathrm {e}}_{j}^{2}}{\left( 1-h_{j j}(\alpha )\right) ^{2}} \\&=\sum _{j=1}^{n} \rho _{j i}^{2} D_{j}, \end{aligned}$$

where $\rho _{j i}=\left\{ h_{i j}(\alpha ) / h_{i i}(\alpha ) h_{j j}(\alpha )\right\} \le 1$ is the correlation between forecast ${\widehat{\mu }}_{i}-{\widehat{\mu }}_{j}$ and ${D_{j}=\frac{1}{\text {tr}\{\mathbf {H}(\alpha )\}}{\mathrm {r}}_{j}^{2}}$. An alternative way of writing $S_{i}$ is given by

$$\begin{aligned} S_{i}=\frac{1}{\varrho \widehat{\phi } \text {tr}\{\mathbf {H}(\alpha )\}} \sum _{j=1}^{n} w_{j i}(\alpha ) {\mathrm {e}}_{j}^{[j]^{2}}, \end{aligned}$$

where ${\mathrm {e}}_{j}^{[j]}={\mathrm {e}}_{j} /\left( 1-h_{j j}(\alpha )\right)$ and $w_{ji}(\alpha )=h_{i j}^{2}(\alpha ) / h_{i i}^{2}(\alpha ).$ In this case, the cutoff point is considered as $4.5MAD(S_{i})$, where $MAD(S_{i}) = {\mathrm {median}} \left| S_i - {\mathrm {med}}(S) \right|$, with ${\mathrm {med}}(S)$ being the median of the $S_{i}$ values. A observation is considered heterogeneous if $|S_{i} - {\mathrm {med}}(S)| \ge {\mathrm {cutoff}}$. The properties of the S-statistic are discussed in Peña (2005).

3.6 Likelihood displacement

Let $L_{\mathrm {p}}(\varvec{\theta }, \alpha )$ the penalized log-likelihood function under nonparametric regression model with symmetric random errors and $\varvec{\theta }=({\mathbf {f}}^{T}, \phi )^{T}$. Following Cook (1986), we define the penalized likelihood displacement as

$$\begin{aligned} L D_{i}(\varvec{\theta }, \alpha )=2\Big [L_{\mathrm {p}}({\widehat{\varvec{\theta }}}, \alpha )-L_{\mathrm {p}}({\widehat{\varvec{\theta }}}^{[i]}, \alpha )\Big ], \end{aligned}$$

where ${\widehat{\varvec{\theta }}}^{[i]}=\left( {\widehat{\mathbf {f}}}^{[i]^{T}}, \widehat{\phi }^{[i]}\right) ^{T}$ denotes the MPLE of ${\varvec{\theta }}$ by dropping the $i$th observation, $L_{\mathrm {p}}({\widehat{\varvec{\theta }}}, \alpha )$ is the penalized log-likelihood function evaluated in ${\varvec{\theta }}=\widehat{\varvec{\theta }},$ and

$$\begin{aligned} L_{\mathrm {p}}\Big ({\widehat{\varvec{\theta }}}^{[i]}, \alpha \Big )=-\frac{n}{2} \mathop {\mathrm{log}}\nolimits {\widehat{\phi }}^{[i]}+\sum _{i=1}^{n} \mathop {\mathrm{log}}\nolimits \left(g\left( {\widehat{\delta }}_{i}^{[i]} \right) \right)-\frac{\alpha }{2} {\widehat{\mathbf {f}}}^{[i] T} {\mathbf {K}} {\widehat{\mathbf {f}}}^{[i]}. \end{aligned}$$

Then, we have that likelihood displacement may be expressed in the form

$$\begin{aligned} LD_{i}({\varvec{\theta }}, \alpha )=n \mathop {\mathrm{log}}\nolimits \left( \frac{\widehat{\phi }^{[i]}}{\widehat{\phi }}\right) +2 \sum _{i=1}^{n} \mathop {\mathrm{log}}\nolimits \left( \frac{g\left( {\widehat{\delta }}_{i}\right) }{g\left( {\widehat{\delta }}_{i}^{[i]}\right) }\right) +\alpha \left( {\mathbf {f}}^{[i]^{T}} {\mathbf {K}} {\mathbf {f}}^{[i]}-{\widehat{\mathbf {f}}}^{T} {\mathbf {K}} {\widehat{\mathbf {f}}}\right) . \end{aligned}$$

In particular, under normal random errors we have that the likelihood displacement may be expressed in the form

$$\begin{aligned} \begin{aligned} LD_{i}(\varvec{\theta }, \alpha )=n \mathop {\mathrm{log}}\nolimits \left[ \left( \frac{n}{n-1}\right) \frac{\left( n-1-p^{\prime }\right) }{\left( {\mathrm {r}}_{i}^{2}+n-1-p^{\prime }\right) }\right] +&\frac{(n-1)\left( 1-h_{i i}(\alpha )\right) ^{-1} {\mathrm {r}}_{i}^{2}}{\left( n-1-p^{\prime }\right) }\\ \ \ \ -1 -\alpha \text {tr}\left\{ \widetilde{\mathbf {H}}(\alpha )\left( \mathbf {y} {\mathbf {y}}^{T}-{\mathbf {y}}^{*} {\mathbf {y}}^{*^{T}}\right) \right\} , \end{aligned} \end{aligned}$$

where $p^{\prime }=\text {tr}\left\{ \mathbf {H}^{[i]}(\alpha )\right\}$ and $\tilde{\mathbf {H}}(\alpha )={\mathbf {H}}(\alpha )^{T} {\mathbf {K}} {\mathbf {H}}(\alpha )$. According Green and Silverman (1993) (Lemma 3.1) the vector $\widehat{\mathbf{f}}^{[i]}$ satisfies equality $\widehat{\mathbf{f}}^{[i]}=\mathbf{H}(\alpha ) \mathbf{y}^{*}$, where the vector $\mathbf{y}^{*}$ is defined by

$$\begin{aligned} \textit{y}_{j}^{*}= & {} \textit{y}_{j} \quad \mathrm{for} \quad j \ne i \\ \textit{y}_{i}^{*}= & {} \widehat{f}^{[i]}(\mathrm{t}_{i}). \end{aligned}$$

Note that part of $LD_{i}(\varvec{\theta }, \alpha )$, due to the nonparametric regression model, coincides with expression (5.2.9) given in Cook and Weisberg (1982) under normal linear regression model.

3.7 Local influence measure

Let $\varvec{\omega }=\left( \omega _{1}, \ldots , \omega _{n}\right) ^{T}$ be an $(n \times 1)$ vector of perturbations restricted to some open subset $\varOmega \in {\mathcal {R}}^{n}$ and the logarithm of the perturbed penalized likelihood denoted by $L_{\mathrm {p}}(\varvec{\theta }, \alpha | \varvec{\omega }).$ Suppose that there is a point $\omega _{0} \in \varOmega$ that represents no perturbation of the data so that $L_{\mathrm {p}}\left( \varvec{\theta }, \alpha | \varvec{\omega }_{0}\right) =L_{\mathrm {p}}(\varvec{\theta }, \alpha ) .$ To assess the influence of minor perturbations on $\widehat{\varvec{\theta }},$ we consider the likelihood displacement $LD(\varvec{\omega })=2\left[ L_{\mathrm {p}}(\widehat{\varvec{\theta }}, \alpha )-L_{\mathrm {p}}\left( \widehat{\varvec{\theta }}_{\omega }, \alpha \right) \right] \ge 0,$ where $\hat{\varvec{\theta }}_{\omega }$ is the MPLE under $L_{\mathrm {P}}(\varvec{\theta }, \alpha | \varvec{\omega }) .$ The measure $L D(\varvec{\omega })$ is useful for assessing the distance between $\widehat{\varvec{\theta }}$ and $\widehat{\varvec{\theta }}_{\omega }$. Cook (1986) suggested studying the local behavior of $L D(\varvec{\omega })$ around $\varvec{\omega }_{0} .$ The procedure consists in selecting a unit direction $\ell \in \varOmega (\Vert \ell \Vert =1),$ and then to consider the plot of $L D\left( \varvec{\omega }_{0}+a \ell \right)$ against $a,$ where $a \in {\mathcal {R}} .$ This plot is called lifted line. Each lifted line can be characterized by considering the normal curvature $C_{\ell }(\varvec{\theta })$ around $a=0 .$ The suggestion is to consider the direction $\ell =\ell _{\max }$ corresponding to the largest curvature $C_{\ell _{\max }}(\varvec{\theta }) .$ The index plot of $\ell _{\text{ max }}$ may reveal those observations that under small perturbations exercise notable influence on $LD(\omega ).$ According to Cook (1986) the normal curvature in the unitary direction $\ell$ is given by $C_{\ell }(\varvec{\theta })=-2\left\{ \ell ^{T} \varvec{\varDelta }_{\mathrm {p}}^{T} {\mathbf {L}}_{\mathrm {p}}^{-1} \varvec{\varDelta }_{\mathrm {p}} \ell \right\} ,$ where ${\mathbf {L}}_{\mathrm {p}}$ is the Hessian matrix and $\varvec{\varDelta }_{\mathrm {p}}$ is the perturbation matrix. These matrices are defined in the appendix.

4 Application and results

To illustrate the methodology described in this paper we consider the house price data set that has been analyzed by various authors. The aim of the study is to assess the association of the house prices with the air quality of the neighborhood by using regression models. The response variable LMV (logarithm of the median house price in USD 1000) is related with 14 explanatory variables. Altogether there are 506 observations. Here we only consider the explanatory variable LSTAT (% lower status of the population) due to its non-linear relationship with the response variable; see Fig. 1 .

Fig. 1

Scatter plot: LMV versus LSTAT

Indeed, we consider the nonparametric regression model

$$\begin{aligned} \textit{y}_{i}=f\left( {\mathrm {t}}_{i}\right) +\epsilon _{i}, \quad i=1, \ldots , 506, \end{aligned}$$

where $\textit{y}_{i}$ denotes the logarithm value of the median house price in USD 1000 and ${\mathrm {t}}_{i}$ denotes the value of % lower status of the population. For comparative purposes, we will assume that random errors $\epsilon _{i}$ follow a normal, Student-t and power exponential distribution. The smoothing parameters associated with both models were selected such that the effective degrees of freedom are close to 3. The degrees of freedom $\nu =5$ and shape parameter ($k=0.3$) for the Student-t and power exponential models, respectively, were obtained by applying the Akaike information criterion. Table  1 shows a summary of the fit of models.

Table 1 Maximum penalized likelihood estimates, estimated standard errors and AIC values under normal, Student-$\text {t}$ ($\nu =5$) and power exponential ($k=0.3$) models fitted to house price data

Comparing these results, we observe that the estimate $\widehat{\phi }$ under the power exponential model is lower (as is the standard error) with respect to the normal and Student-t models, however these are not comparable with each other. In addition, we may notice that the AIC value under the Student-$\text {t}$ model is smaller compared to the normal and power exponential models, indicating a superiority of the heavy-tailed model, which is confirmed through the normal probability plots presented in Fig. 2a–c. The estimated smooth function under three models and their corresponding approximate standard error band are presented in Fig. 2d–f.

Fig. 2

Scatter plots: a normal probability plot under normal errors, b normal probability plot under Student-t errors, c normal probability plot under power exponential errors, d estimated smooth function under normal errors, e estimated smooth function under Student-t errors, f estimated smooth function under power exponential errors, with its approximate pointwise standard error band denoted by red lines

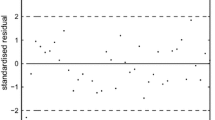
Figs. 3,  4 and  5 show some plots of residuals and global influence under normal, Student- t and power exponential errors, respectively. Specifically, the index plots of the residuals (left side of the first row), leverage values (right side of the first row) and Cook’s distance (left side of the second row), the scatterplot Cook’s distance versus the $S$-statistic (right side of the second row), and the index plot of the $S$-statistic (bottom of the figure) considering the cutoff point proposed by Peña (2005).

In Fig. 3 (under normal errors), the plot of the residual does not show the presence of outliers, while the plot of the leverage values reveals that the observations $\# 375$ and $\# 415$ are intermediate-leverage outliers. For its part, Cook’s distance plot shows that observations $\# 375$ and $\# 413$ are outliers. On the other hand, the scatterplot of Cook’s distance versus the $S$-statistic clearly indicates the presence of some outliers; this is, the observations $\# 375, \# 399, \# 406, \# 413$ and $\# 415 .$ This is confirmed by comparing the values of $S$-statistic with the cutoff point mentioned above.

Fig. 3

Global influence analysis of the Boston data under normal errors: a index plot of residuals, b index plot of leverage values, c index plot of Cook’s distance, dispersion plot of S-statistics, d Cook’s distance, e index plot of S-statistics

In Fig. 4 (under Student-t errors), the plot of the residual shows the presence of five outliers, observations $\# 215, \# 372, \# 406, \# 413$ and $\# 506,$ while the plot of the leverage values reveals that the observation $\#375, \# 415$ and $\# 439$ are intermediate-leverage outliers. Cook’s distance plot shows that observations $\# 142, \# 374, \# 375$ and $\# 413$ are outliers, while the plot of dispersion between Cook’s distance and the $S$-statistic indicates gain the presence of some outliers, specifically, observations $\# 142 , \# 215, \# 375$ and $\# 413$ being confirmed, for some observations, by comparing the values of $S$-statistic.

Fig. 4

Influence analysis of the Boston data under Student-t errors: a index plot of residuals, b index plot of leverage values, c index plot of Cook’s distance, dispersion plot of S-statistics, d Cook’s distance, e index plot of S-statistics

In Fig. 5 (under power exponential errors), the plot of the residual does not show the presence of outliers, while the plot of the leverage values reveals that the observations $\# 415$ and $\# 439$ are intermediate-leverage outliers. For its part, Cook’s distance plot shows that observation $\# 145, \#215, \# 375$ and $\# 415$ are outliers. On the other hand, the scatterplot of Cook’s distance versus the $S$-statistic clearly indicates the presence of some outliers; this is, the observations $\# 142, \# 215, \# 375$ and $\# 415$ . This is confirmed by comparing the values of $S$-statistic. It is important to mention that the observations $\#215$, and $\#406$ that appear as possible outliers under the Student-t model, the estimation process assigns them small weights, confirming the robust aspects of the MPLEs against outlying observations under heavier-tailed error models; see Fig. 8.

Fig. 5

Influence analysis of the Boston data under power exponential errors: a index plot of residuals, b index plot of leverage values, c index plot of Cook’s distance, dispersion plot of S-statistics, d Cook’s distance, e index plot of S-statistics

On the other hand, Figs. 6 and  7 show the local influence plots for the case-weight and response variable perturbation schemes assuming normal, Student-t and power exponential errors, respectively. The results of local influence for f obtained under the scale perturbation scheme are the same as those obtained for the case-weight scheme, and therefore are omitted. Based on Fig. 6 we notice that observations 215#, 375#, #413 and #414 are more influential under the normal model (left side) whereas the observations #215 and #142 appear slightly influential under Student-t model (middle). Under power exponential model, the 142#, 213#, #215 and #415 are more influential (right side). Looking at Fig. 7 we observe that no observation appears highly influential under the three models. Based on these local influence graphics we can conclude that $\widehat{f}$ appear to be less sensitive in the Student-t model under case-weight perturbation, whereas the sensitivity of $\widehat{f}$ appears to be similar for the three fitted models under response variable perturbation.

Fig. 6

Local influence analysis of the Boston data under case-weight perturbation: a normal errors, b Student-t errors, c power exponential errors

Fig. 7

Local influence analysis of the Boston data under response variable perturbation: a normal errors, b Student-t errors, c power exponential errors

It is important to note that for Student-t model the current weight $v_{i}^{(m)}=(\nu + 1)/\left(\nu + \delta _{i}^{(m)}\right)$, with $\delta _{i}^{(m)}=\left(\mathop {\mathrm{y}}\nolimits _{i} - \mu _{i}^{(m)}\right)^{2}/\phi ^{(m)}$, is inversely proportional to the distance between the observed value $y_{i}$ and its current predicted value $\mu _{i}^{(m)}$, so that outlying observations tend to have small weights in the estimation process. Therefore, we may expected that the MPLEs from the Student-t model are less sensitive to outlying observations than the MPLEs from normal models. Fig. 8 shows the plot between the standardized residual and estimated weights, and estimated weights under Student-t and power exponential models. We can be seen that observations #215 and #406 have a large and small residual, respectively, and a high estimated weight; see Fig. 8a–b. Looking Fig. 8c–d we can see that observations #215 and #406 have a large and small residual respectively, and a high estimated weight. Finally, it is important to note that the iterative process under Student-t model generates a reduction in the weights associated with the observations detected as discrepant. Hence such estimators present some characteristics of robustness similar to the associated with the weight function described by Huber (2004).

Fig. 8

Scatter plots between: a the standardized residual and estimated weights and b estimated Mahalanobis distance and estimated weights, under the Student-t model; c the standardized residual and estimated weights and d estimated Mahalanobis distance and estimated weights, under power exponential model

5 Simulation study

To evaluate further the effectiveness of the diagnostic measures derived in this paper, specifically Cook’s distance and Peña Measure, we consider a simulated data set with two forced outliers. We simulated data from the model

$$\begin{aligned} y_{i}=\sin \left( \frac{2 \pi i}{n}\right) +\epsilon _{i} \quad (i=1, \ldots , n) \end{aligned}$$

where $\epsilon _{i}$ follows a symmetric distribution. To perform the simulation, we will consider the models ${\mathrm {N}}\left( 0,0.1^{2}\right)$ and ${\mathrm {t}}\left( 0,0.1^{2}, 3\right) ,$ and implement an ${\mathrm {R}}$ routine that calculates the proportion of times that forced outlier observations are detected by diagnostic measures $D_{i}$ and $S_{i},$ for $n \in \{25,50,10\}$ and 1000 replicates each. To obtain the two outlier observations we change the values of the responses for the 1 th and n th observations in the form $y_{1}^{*}=$ $y_{1}+1.5$ and $y_{n}^{*}=y_{n}-1.5,$ respectively. A summary of our simulation study is presented in Table 2; see also Figs. 9,  10,  11 and  12. We can observe, for example, that for normal errors and sample size 50 in $100 \%$ of the simulations the 1 th and n th observation is detected as influential for both measures, while for Student-t errors with the same sample size in the $100 \%$ and $96.6 \%$ of the simulations, the 1 th and n th observation are detected as influential by the measures $D_{i}$ and $S_{i}$, respectively. This confirmed in Figs. 13 and  14, respectively, where it is observed that the values of $D_{i}$ and $S_{i}$ associated with observations 1 th and n th are the highest. In conclusion, in this simulation study, the two forced outliers are correctly identified by the diagnostic measures that we derive in Sect. 3. Similar results were found for the $L D_{i}(\varvec{\theta }, \alpha )$ measure but were omitted in this study.

Table 2 Number of times (in %) in which the forced outlier observations were detected as influential through the measures $D_{i}$ and $S_{i}$

Fig. 9

Index plots of the $D_{i}$ and $S_{i}$ measures for $n=25$ and 1000 simulations under normal errors

Fig. 10

Index plots of the $D_{i}$ and $S_{i}$ measures for $n=25$ and 1000 simulations under Student-t errors

Fig. 11

Index plots of the $D_{i}$ and $S_{i}$ measures for $n=100$ and 1000 simulations under normal errors

Fig. 12

Index plots of the $D_{i}$ and $S_{i}$ measures for $n=100$ and 1000 simulations under Student-t errors

Fig. 13

Index plots of the $D_{i}$ and $S_{i}$ measures for $n=50$ and 1000 simulations under normal errors

Fig. 14

Index plots of the $D_{i}$ and $S_{i}$ measures for $n=50$ and 1000 simulations under Student-t errors

6 Concluding remarks

In this paper we consider some diagnostic measures of global and local influence for the nonparametric regression model with symmetric random errors. In the context of global influence, we derive expressions for the residuals, leverage values and Cook’s distance similar to those obtained in classical regression under the assumption of normality. In addition, we extend the influence measure proposed by Peña (2005) in order to measure the influence of an observation when it is influenced by the rest of the observations and we use the Boston house price as an illustration. In the context of local influence, we derive the normal curvature for three perturbation schemes, with the purpose of evaluating the sensitivity of the maximum penalized likelihood estimator of smooth function. Both global and local influence measures were illustrated through a set of data. The study provides evidence on the robust aspects of the MPLEs from Student-t with small degrees of freedom against outlying observations. However, these robust aspects do not seem to the extended to all perturbation schemes of the local influence approach, indicating the usefulness to the normal curvature derived in this paper for assessing the sensitivity of the MPLEs from the symmetric nonparametric regression model.

Appendix

1.1 Hessian matrix

Let ${\mathbf {L}}_{\mathrm {p}}\left( p^{*} \times p^{*}\right)$ be the Hessian matrix with $\left( j^{*}, \ell ^{*}\right)$ -element given by $\partial ^{2} L_{\mathrm {p}}(\varvec{\theta }, \varvec{\alpha }) / \partial \theta _{j^{*}} \theta _{\ell ^{*}}$ for $j^{*}, \ell ^{*}=1, \ldots , p^{*} .$ After some algebraic manipulations we find

$$\begin{aligned} \begin{array}{l}{ \frac{\partial ^{2} L_{\mathrm {p}}(\varvec{\theta }, \varvec{\alpha })}{\partial {\mathbf {f}} \partial {\mathbf {f}}^{T}}=-\frac{1}{\phi } {\mathbf {N}}^{T} {\mathbf {D}}_{a} {\mathbf {N}}-\alpha {\mathbf {K}}} , \\ {\frac{\partial ^{2} L_{\mathrm {p}}(\varvec{\theta }, \varvec{\alpha })}{\partial \phi ^{2}}=\frac{1}{\phi ^{2}}\left\{ \frac{n}{2}+\varvec{\delta }^{T} {\mathbf {D}}_{\zeta ^{\prime }} \varvec{\delta }-\frac{1}{\phi } \varvec{\epsilon }^{T} {\mathbf {D}}_{v} \varvec{\epsilon }\right\} } {\mathrm {and}}\\ {\frac{\partial ^{2} L_{\mathrm {p}}(\varvec{\theta }, \varvec{\alpha })}{\partial {\mathbf {f}} \partial \phi }=\frac{2}{\phi ^{2}} {\mathbf {N}}^{T} {\mathbf {b}}}, \end{array} \end{aligned}$$

where ${\mathbf {D}}_{a}={\mathrm {diag}}_{1 \le i \le n}\left( a_{i}\right) , {\mathbf {D}}_{\zeta ^{\prime }}={\mathrm {diag}}_{1 \le i \le n}\left( \zeta _{i}^{\prime }\right) , {\mathbf {b}}=\left( b_{1}, \ldots , b_{n}\right) ^{T}, \varvec{\delta }=\left( \delta _{1}, \ldots , \delta _{n}\right) ^{T}$, $\varvec{\epsilon } = \left( \epsilon _{1}, \ldots , \epsilon _{n}\right) ^{T}, a_{i}=-2\left( \zeta _{i}+2 \zeta _{i}^{\prime } \delta _{i}\right) , b_{i}=\left( \zeta _{i}+\zeta _{i}^{\prime } \delta _{i}\right) \epsilon _{i}, \epsilon _{i} = \textit{y}_{i} - \mu _{i}, \zeta _{i}^{\prime }=\frac{d \zeta _{i}}{d \delta _{i}}$ and $\delta _{i}=\phi ^{-1} \epsilon _{i}^{2}.$

1.1.1 Cases-weight perturbation

Let us consider cases-weight perturbation for the observations in the penalized log-likelihood function as

$$\begin{aligned} L_{\mathrm {p}}(\varvec{\theta }, \alpha | \varvec{\omega })=\sum _{i=1}^{n} \omega _{i} L_{i}(\varvec{\theta })-\frac{\alpha }{2} {\mathbf {f}}^{T} {\mathbf {K f}}, \end{aligned}$$

where $\varvec{\omega }=\left( \omega _{1}, \ldots , \omega _{n}\right) ^{T}$ is the vector of weights, with $0 \le \omega _{i} \le 1,$ for $i=1, \ldots , n$. In this case, the vector of no perturbation is given by $\varvec{\omega }_{0}=(1, \ldots , 1)^{T}$. Differentiating $L_{\mathrm {p}}(\varvec{\theta }, \alpha | \varvec{\omega })$ with respect to the elements of $\varvec{\theta }$ and $\omega _{i},$ we obtain after some algebraic manipulation

$$\begin{aligned} \left. \frac{\partial ^{2} L_{\mathrm {p}_{i}}(\varvec{\theta }, \alpha | \varvec{\omega })}{\partial {\mathbf {f}} \partial \omega _{i}}\right| _{\theta =\hat{\theta }, \omega =\omega _{0}}= & {} -\frac{2}{\widehat{\phi }} \widehat{\zeta }_{i} \widehat{\epsilon }_{i} {\mathbf {n}}_{i} \quad \text {and}\\ \left. \frac{\partial ^{2} L_{\mathrm {p}_{i}}(\varvec{\theta }, \alpha | \varvec{\omega })}{\partial \phi \partial \omega _{i}}\right| _{\theta =\hat{\theta }, \omega =\omega _{0}}= & {} -\frac{1}{2 \widehat{\phi }}-\frac{1}{2 \widehat{\phi }} \widehat{\zeta }_{i} \widehat{\delta }_{i} , \end{aligned}$$

where $\widehat{\epsilon }_{i} = y_i - \widehat{\mu {_i}}$, for $i=1, \ldots , n$.

1.1.2 Scale perturbation

Under scale parameter perturbation scheme it is assumed that ${\mathrm {y}}_{i} \sim S(\mu _{i}, \omega _{i}^{-1} \phi , g ),$ where $\omega =\left( \omega _{1}, \ldots , \omega _{n}\right) ^{T}$ is the vector of perturbations, with $\omega _{i}>0,$ for $i=1, \ldots , n .$ In this case, the vector of no perturbation is given by $\omega _{0}=(1, \ldots , 1)^{T}$ such that $L_{\mathrm {p}}(\varvec{\theta }, \alpha | \varvec{\omega =\omega _{0}})=L_{\mathrm {p}}(\varvec{\theta }, \alpha ).$ Taking differentials of $L_{\mathrm {P}}(\varvec{\theta }, \alpha | \varvec{\omega })$ with respect to the elements of $\varvec{\theta }$ and $\omega _{i},$ we obtain after some algebraic manipulation

$$\begin{aligned} \frac{ \partial ^{2} L_{\mathrm {p}_{i}} (\varvec{\theta }, \alpha | \varvec{\omega })}{\partial {\mathbf {f}} \partial \omega _{i}}|_{\theta =\hat{\theta }, \omega =\omega _{0}}= & {} -\frac{2}{\widehat{\phi }}\left\{ \widehat{\zeta }_{i}^{\prime } \hat{\delta }_{i}+\widehat{\zeta }_{i}\right\} \widehat{\epsilon }_{i} {\mathbf {n}}_{i}^{T}\\ \frac{\partial ^{2} L_{\mathrm {p}_{i}}(\varvec{\theta }, \alpha | \varvec{\omega })}{\partial \phi \partial \omega _{i}}|_{\theta =\hat{\theta }, \omega =\omega _{0}}= & {} -\frac{1}{2\widehat{\phi }}-\frac{1}{\hat{\phi }}\left\{ \widehat{\zeta }_{i}^{\prime } \hat{\delta }_{i}+\widehat{\zeta }_{i}\right\} \hat{\delta }_{i} , \end{aligned}$$

where $\widehat{\epsilon }_{i} = y_i - \widehat{\mu {_i}}$, for $i=1, \ldots , n$.

1.1.3 Response variable perturbation

To perturb the response variable values we consider $y_{i \omega }=y_{i}+\omega _{i},$ for $i=1, \ldots , n$, where $\omega =\left( \omega _{1}, \ldots , \omega _{n}\right) ^{T}$ is the vector of perturbations. Here, the vector of no perturbation is given by $\varvec{\omega }_{0}=(0, \ldots , 0)^{T}$ and the perturbed penalized log-likelihood function is constructed from (5) with ${\mathrm {y}}_{i}$ replaced by ${\mathrm {y}}_{i \omega },$ that is,

$$\begin{aligned} L_{\mathrm {p}}(\varvec{\theta }, \alpha | \varvec{\omega })=L(\varvec{\theta } | \varvec{\omega })-\frac{\alpha }{2} {\mathbf {f}}^{T} {\mathbf {K}} {\mathbf {f}}, \end{aligned}$$

where $L(\cdot )$ is given by (4) with $\delta _{i \omega }=\phi ^{-1}\left( {\mathrm {y}}_{i \omega }-\mu _{i}\right) ^{2}$ in the place of $\delta _{i} .$ Differentiating $L_{\mathrm {p}}(\varvec{\theta }, \alpha | \varvec{\omega })$ with respect to the elements of $\varvec{\theta }$ and $\omega _{i},$ we obtain, after some algebraic manipulation, that

$$\begin{aligned} \frac{\partial ^{2} L_{\mathrm {p}_{i}}({\varvec{\theta }}, \alpha | {\varvec{\omega }})}{\partial {\mathbf {f}} \partial \omega _{i}}|_{\theta =\hat{\theta }, \omega =\omega _{0}}= & {} -\frac{1}{\widehat{\phi }}\left\{ 2 \widehat{\zeta _{i}}^{\prime } \widehat{\delta }_{i}+2 \widehat{\zeta }_{i} \right\} \quad \text {and} \\ \frac{\partial ^{2} L_{\mathrm {P}_{i}}({\varvec{\theta }}, \alpha | {\varvec{\omega }})}{\partial \phi \partial \omega _{i}}|_{\theta =\hat{\theta }, \omega =\omega _{0}}= & {} -\frac{\widehat{\epsilon }_{i}}{\widehat{\phi }^{2}}\left\{ 2 \widehat{\zeta }_{i}^{\prime } \widehat{\delta }_{i}+2 \widehat{\zeta }_{i}\right\} , \end{aligned}$$

where $\widehat{\epsilon }_{i} = y_i - \widehat{\mu {_i}}$, for $i=1, \ldots , n$.