Heterogeneous players in a Cournot model with differentiated products

Abstract

In this article, we analyse a duopolistic Cournotian game with firms producing differentiated goods, marginal costs are constant and demand functions are microfounded. We consider firms adopting different decisional mechanisms which are based on a reduced degree of rationality. In particular, we assume that a firm adopts the local monopolistic approximation approach, while the rival adjusts its output level according to the gradient rule. We provide conditions for the stability of the Nash equilibrium and investigate some bifurcation scenarios as parameters vary. The main finding of the article is that both a high level and a low level in goods differentiation may have a destabilising role in the system.

1 Introduction

The purpose of this article is to discuss the role of horizontal product differentiation in a nonlinear Cournot duopoly in which firms adopt different decisional mechanisms.

Based on the pioneering work of Cournot (1838), in the last decades, several works have shown that oligopoly models may lead to complex behaviours, as described in Rand (1978), who discussed the emergence of random-like exotic effects in the dynamics of a simple Cournot duopoly, and in Puu (1991). In particular, the latter one proposed a duopoly model with unimodal reaction functions obtained by solving the profit maximisation problem for the two firms. In the case of constant marginal costs, Cobb–Douglas preferences and isoelastic demand function, the author showed that the outputs of each firm can evolve through a sequence of period-doubling bifurcations leading to chaos. As the firms have a perfect knowledge of the market demand, the decision mechanism analysed by Puu (1991) is the myopic best reply. By assuming that the rival does not change its decisions on the production, the firm solves its profit maximisation problem. Following these seminal works, the focus has shifted to less demanding decisional mechanisms regarding the ability of firms in exploring the demand side of the market. In particular, the literature has greatly deepened two mechanisms known as (i) the gradient-like mechanism and (ii) the local monopolistic approximation (LMA hereafter).

The gradient-like approach describes firms that do not have a complete knowledge of demand and cost functions (see Bischi et al. 1999). They use a local estimation of the marginal profit to update the production level. In particular, the output increases (decreases, respectively) if the marginal profit is positive (negative, respectively). A crucial role in defining the stability is then played by the parameter measuring the magnitude of this deviation in production, called speed of adjustment (see Cavalli and Naimzada 2014; Cavalli et al. 2015).

In the LMA approach, proposed for the first time in Silvestre (1977), firms conjecture a linear demand function and estimate it through the current knowledge of the market in terms of quantities and price. Based on this estimate and assuming that competitors do not vary their production levels, the firm chooses the output that maximises the conjectured profit function (see Tuinstra 2004; Bischi et al. 2007).

Recently, several authors have started to investigate the effects generated by the interaction of firms adopting different decision-making mechanisms. Assuming firms that produce a homogeneous good, their analysis focused on the heterogeneity in the supply side of the market. In particular, (Tramontana 2010) analysed a duopoly model where one firm has incomplete information and adopts the gradient-like mechanism, whereas the rival has complete information and adopts the best reply. Instead, Cavalli and Naimzada (2014) and Cavalli et al. (2015)¹ have characterised the dynamic properties of a model in which firms are heterogeneous in decisional mechanisms and they have restricted information on market demands (gradient-like approach vs. LMA).

Unlike the works mentioned above, whose analysis focuses on the supply side of the market, a strand of the literature focused on the study of the effects generated by product differentiation, or how the features related to the consumers’ perception of goods may affect the duopolistic dynamics. To this purpose, this analysis has been carried out especially in Bertrand models where the product differentiation allows to overcome the so-called Bertrand paradox.² In particular, Ahmed et al. (2015), Brianzoni et al. (2015) and Gori and Sodini (2017) analyse the dynamics of a Bertrand duopoly where homogeneous decisional mechanisms and horizontal product differentiation are considered. In such models, the authors showed that the degree of product differentiation may play a destabilising role when it is set at too high or too low levels. Instead, Agliari et al. (2016) discussed the effects of product differentiation in a Cournot framework where firms adopt the same decisional mechanism (the gradient rule) and showed that unlike the literature on Bertrand models, only high levels of differentiation may have a destabilising effect on the system.

By removing the assumption that firms adopt the same decisional mechanism and assuming a not overly demanding framework in terms of rationality and information, we consider a duopoly with nonlinear market demands for products of both varieties where firms (i) adopt, respectively, the gradient rule and the LMA approach and (ii) produce heterogeneous goods. In the analysis, we discuss how some relevant parameters (such as the speed of adjustment, the degree of differentiation and the marginal costs ratio) affect the stability of the Nash equilibrium and we show how the assumption of heterogeneous decisional mechanisms induces a partial change in the role played by the differentiation on the stability. Indeed, our investigation confirms the result shown in Agliari et al. (2016). Indeed, starting from a situation of stability for the Nash equilibrium, an increase in the differentiation destabilises the system, but we further show that also a low extent of product differentiation may be destabilising. From a dynamic point of view, we notice that a destabilisation may occur through Flip and/or Neimark–Sacker bifurcations. Finally, we prove the existence of complex dynamics and the coexistence of attractors.

The economic intuition behind our findings is the following: (i) if the degree of product differentiation is high, then the goods will tend to be independent and consequently, competition is less. In a context of isoelastic demands, this implies that prices will react little to changes in quantities produced and are not able to bring the market back to a stationary equilibrium; on the other hand, (ii) if the degree of product differentiation is low, then the goods will tend to be indistinguishable and consequently, competition is high. This implies that prices will react excessively to changes in quantities produced and are not able to bring the market back to a stationary equilibrium.

The rest of the paper is organised as follows: Sect. 2 shows the main features of the static duopolistic game and proves the existence of the Nash equilibrium; Sect. 3 describes the adjustment process of the firms; Sect. 4 refers to the local and global analysis of the model and Sect. 5 concludes.

2 The static model

We consider a duopoly market in which every firm i produces a differentiated good, whose prices and quantities are denoted by $p_{i}$ and $q_{i}$, respectively, with $i\in \{1,2\}$. Moreover, a continuum of identical consumers with preferences towards the two commodities $q_{1}$ and $q_{2}$ is assumed.In particular, following Agliari et al. (2016), we determine the nonlinear demand functions from a monotonic transformation of a CES utility function (Mas-Colell et al. 1995) where the exponent is associated with the degree of product differentiation. Then, the utility function of the agents is

$$\begin{aligned} U(q_{1},q_{2})=q_{1}^{\alpha }+q_{2}^{\alpha }, \end{aligned}$$

(1)

where $0<\alpha \le 1$³ represents the degree of substitutability (differentiation) among the commodities. This utility function is maximised subject to the budget constraint

$$\begin{aligned} p_{1}q_{1}+p_{2}q_{2}=1, \end{aligned}$$

(2)

in which the consumers’ income is assumed to be constant and equal to 1.From the agents’ allocative problem, the following inverse demand functions are derived:

$$\begin{aligned} p_{1}= & {} g_{1}(q_{1},q_{2}):={\frac{{{q_{1}^{\alpha -1}}}}{{{q_{1}^{\alpha }}}+{{q_{2}^{\alpha }}} }} \end{aligned}$$

(3)

$$\begin{aligned} p_{2}= & {} g_{2}(q_{1},q_{2}):={\frac{{{q_{2}^{\alpha -1}}}}{{{q_{2}^{\alpha }}}+{{q_{1}^{\alpha }}} }}. \end{aligned}$$

(4)

We notice that if $\alpha =1$, the commodities are indistinguishable and consumers regard them as identical. Lower values of $\alpha$ make the commodities as interchangeable, and furthermore, as $\alpha$ tends to zero, they become independent.

On the production side, the two duopolistic firms are characterised by a linear cost function given by

$$\begin{aligned} C_{i}(q_{i})=c_{i}q_{i} \quad \text {with}\;i=1,2 \end{aligned}$$

(5)

where $c_{i}$ represent the positive constant marginal costs. Then, the expected profit function for the i-th firm is

$$\begin{aligned} \pi _{i}(q_{i},q_{j}^{e})=p_{i}(q_{i},q_{j}^{e})q_{i}-c_{i}q_{i} \quad \text {with} \;i,j=1,2;\ i\ne \,j \end{aligned}$$

(6)

in which $q_{j}^{e}$ is the expected output level of the rival.

Therefore, the unique Nash equilibrium of the Cournotian game can be derived (see Agliari et al. 2016):

Proposition 1

The Nash equilibrium of the static Cournotian game is unique, and it is given by

$$\begin{aligned} E^{*}=\bigg ({\frac{\alpha {c_{1}^{\alpha -1}}{{c_{2}^{\alpha }}}}{\left( {{c_{1}^{\alpha }} }+{{c_{2}^{\alpha }}}\right) ^{2}}},{\frac{\alpha \,{{c_{1}^{\alpha }}}{{\ c_{2}^{\alpha -1}}}}{\left( {{c_{1}^{\alpha }}}+{{c_{2}^{\alpha }}}\right) ^{2}}}\bigg ). \end{aligned}$$

3 LMA versus gradient learning

In an oligopolistic competition, the Nash equilibrium notion is based on the assumption that each firm knows what the rivals decide to do. In particular, each firm is assumed to know the entire demand curve for the good it produces. Then, the Nash equilibrium turns out to be highly demanding in terms of rationality and information. Indeed, it becomes interesting to investigate whether the Nash equilibrium describes the long-run behaviour of the market, that is if there exist mechanisms that, although they do not allow to achieve such equilibrium in one shot, lead to the Nash equilibrium at least asymptotically. In this case, we consider two different adjustment mechanisms requiring a low degree of rationality: the LMA approach and the gradient adjustment process.

To be precise, we assume that firm 1 adopts the LMA approach that is a bounded rational adjustment process based on the assumption that the firm has only a limited knowledge of the demand function (see Bischi et al. 2007; Naimzada and Tramontana 2009; Cavalli et al. 2015). We assume that the firm 1 knows the market price, the output produced by the firm and the output produced by the rival at time t, that is $p_{1,t}$, $q_{1,t}$ and $q_{2,t}$, respectively. Moreover, the firm is able to get a correct estimate of the partial derivative $\frac{\partial \,g_{1}(q_{1,t},q_{2,t})}{\partial \,q_{1,t}}$. As in Bischi et al. (2007), firm 1 conjectures that $q_{2,t+1}=q_{2,t}$ and a linear price function. Therefore, the expected price at time $t+1$ is

$$\begin{aligned} p_{1,t+1}^{e}=p_{1,t}+\frac{\partial \,g_{1}(q_{1,t}, q_{2,t})}{\partial \,q_{1,t}}(q_{1,t+1}-q_{1,t}) \end{aligned}$$

(7)

from which, by considering the expression in (3), we get the following:

$$\begin{aligned} p_{1,t+1}^{e}={\frac{{{q_{1,t}^{\alpha -1}}}}{{{q_{1,t}^{\alpha }}}+{{q_{2,t}^{\alpha }}} }}-{\frac{ \left( \left( 1-\alpha \right) {{q_{1,t}^{\alpha -2}}}{{ \ q_{2,t}^{\alpha }}}+{{q_{1,t}^{2\,\alpha -2}}} \right) }{ \left( {{q_{1,t}^{\alpha }}}+{{\ q_{2,t}^{\alpha }}} \right) ^{2}}}\left( {q_{1,t+1}}-{ q_{1,t}}\right) . \end{aligned}$$

(8)

The output to produce at $t+1$ can be determined as the solution of the maximisation problem for the expected profit:

$$\begin{aligned} q_{1,t+1}=\underset{q_{1,t+1}}{\arg \max } [p_{1,t+1}^{e}q_{1,t+1}-c_{1}q_{1,t+1}], \end{aligned}$$

(9)

which leads to the equation⁴

$$\begin{aligned} q_{1,t+1}=\frac{1}{2}\left[ \frac{\left( {\frac{{{q_{1,t}^{\alpha -1}}}}{{{ q_{1,t}^{\alpha }}}+{{q_{2,t}^{\alpha }}}}-c_{1}}\right) \left( {{q_{1,t}^{\alpha }}}+ {{q_{2,t}^{\alpha }}}\right) ^{2}}{{{q_{1,t}^{\alpha -2}}}\left[ (1-\alpha ){{ q_{2,t}^{\alpha }}}+{{q_{1,t}^{\alpha }}}\right] }+{q_{1,t}}\right] \end{aligned}$$

(10)

Differently, we assume that firm 2 adopts the gradient rule. In particular, we assume that firm 2 does not have a global knowledge of the demand function and tries to investigate how the market responds to its production changes through an empirical estimate of the marginal profit. This estimate may be obtained by market researches carried out at the beginning of the period t, and then we assume that although the firm is unaware of the market demand, it can obtain a correct empirical estimate of the marginal profit, $\frac{\partial \pi _{2}}{\partial {q_{2}}}$. With this type of information, the firm increases (decreases, respectively) its production if it perceives a positive (negative, respectively) marginal profit. We assume that the dynamic adjustment mechanism for firm 2 reads as

$$\begin{aligned} q_{2,t+1}=q_{2,t}+k\frac{\partial \pi _{2}(q_{1,t},q_{2,t})}{\partial { q_{2,t}}}, \end{aligned}$$

(11)

where $k>0$ represents the coefficient measuring the speed of adjustment of the output for firm 2 at time $t+1$ with respect to the marginal profit at time t.⁵By taking into account expressions in (10) and (11), the two-dimensional system characterising the dynamics of the Cournot duopoly with differentiated products is the following:

$$\begin{aligned} M: {\left\{ \begin{array}{ll} q_{1}^{^{\prime }}=\frac{1}{2}\left[ \frac{\left( {\frac{{{q_{1}^{\alpha -1}}} }{{{q_{1}^{\alpha }}}+{{q_{2}^{\alpha }}}}-c_{1}}\right) \left( {{q_{1}^{\alpha }}} +{{q_{2}^{\alpha }}}\right) ^{2}}{{{q_{1}^{\alpha -2}}}\left[ (1-\alpha ){{q_{2}^{\alpha }}}+{{q_{1}^{\alpha }}}\right] }+{q_{1}} \right] \\ q_{2}^{^{\prime }}={q_{2}}+k\left( {\frac{\alpha \,{{q_{2}^{\alpha -1}}}{{ q_{1}^{\alpha }}}}{\left( {{q_{1}^{\alpha }}}+{{q_{2}^{\alpha }}}\right) ^{2} }}-{c_{2}}\right) \end{array}\right. } \end{aligned}$$

(12)

where the symbol $^{\prime }$ is the unit-time advancement operator and, as aforementioned, $\alpha \in (0,1]$ while $k,c_{1},c_{2}>0$. Due to the presence of a denominator with $q_{1}$ and $q_{2}$, we focus on dynamics which stay in the set FS for any iterations, where

$$\begin{aligned} FS= \big \{(q_{1},q_{2}): q_{1}>0, q_{2}>0\}. \end{aligned}$$

(13)

Analogously to Agliari et al. (2016), we have the following result:

Proposition 2

The Nash equilibrium $E^{*}$ is a steady state of the system M described in (12). Contrariwise, the unique steady state of (12) is the Nash equilibrium.

4 Dynamic properties of the model

In order to investigate the local stability of the Nash equilibrium, we consider the Jacobian matrix of the system (12), evaluated at $E^{*}$, $J_{E^{*}}=$

$$\begin{aligned} ={\left[ \begin{array}{cc} -\frac{1}{2}\,{\frac{({\alpha }^{2}-3\, \alpha +2) {{c_{1}^{2\,\alpha }}}-{{ c_{2}^{\alpha }}}(\alpha +4)(\alpha -1) {{c_{1}^{\alpha }}}+2\,{{c_{2}^{2\,\alpha }}} }{\left( (\alpha -1) {{c_{1}^{\alpha }}}-{{c_{2}^{\alpha }}}\right) ({{c_{1}^{\alpha }}} +{{\ c_{2}^{\alpha }})}}} &{} \frac{1}{2}\,{\frac{{{c_{1}^{\alpha }}}{ c_{2}}\,\left( {{c_{1}^{\alpha }}}-{{c_{2}^{\alpha }}}\right) {\alpha }^{2}}{\left( ( \alpha -1){{ c_{1}^{\alpha }}}-{{c_{2}^{\alpha }}}\right) \left( {{c_{1}^{\alpha }}}+{{c_{2}^{\alpha }}}\right) { c_{1}}}} \\ {\frac{k{c_{1}}\,{c_{2}}\,\left( {{c_{1}^{\alpha }}}-{{c_{2}^{\alpha }}}\right) \left( {{c_{1}^{\alpha }}}+{{c_{2}^{\alpha }}}\right) }{{{c_{1}^{\alpha }}}{{c_{2}^{ \alpha }}}}} &{} -{\frac{{{c_{2}^{2}}}k( \alpha +1) {{c_{1}^{2\,\alpha }}}+\left( 2\,{{ c_{2}^{2}}}k-\alpha \right) {{c_{2}^{\alpha }}}{{c_{1}^{\alpha }}}-{{c_{2}^{2\alpha +2}}} k( \alpha -1) }{{{c_{2}^{\alpha }}}\alpha \,{{c_{1}^{\alpha }}}}} \end{array} \right] .} \end{aligned}$$

The Nash equilibrium is locally asymptotically stable if the following Jury conditions (Elaydi 2007) are satisfied:

$$\begin{aligned} {\left\{ \begin{array}{ll} 1-\mathrm{Tr}(J_ {E^{*}})+\mathrm{Det}(J_ {E^{*}})>0 \\ 1+\mathrm{Tr}(J_ {E^{*}})+\mathrm{Det}(J_ {E^{*}})>0 \\ 1-\mathrm{Det}(J_ {E^{*}})>0. \end{array}\right. } \end{aligned}$$

(14)

We can notice that the first condition in (14)

$$\begin{aligned} 1-\mathrm{Tr}(J_ {E^{*}})+\mathrm{Det}(J_ {E^{*}})=\frac{1}{2}\bigg [\frac{{{c_{2}}}^{2}k({{c_{1}}}^{\alpha }+{{ c_{2}}}^{\alpha })^{2}}{{{c_{2}}^{\alpha }((1-\alpha ){{c_{1}}}^{\alpha }+{{c_{2} }}^{\alpha })}}\bigg ]>0 \end{aligned}$$

(15)

is always fulfilled.

In order to determine the stability region of the Nash equilibrium in the space of parameters, in what follows we will characterise the boundary of such a region, defined by the equations

$$\begin{aligned} 1+\mathrm{Tr}(J_ {E^{*}})+\mathrm{Det}(J_ {E^{*}})=0, \end{aligned}$$

(16)

and

$$\begin{aligned} 1-\mathrm{Det}(J_ {E^{*}})=0. \end{aligned}$$

(17)

By introducing the change of variable $x:=\big (\frac{c_{1}}{c_{2}}\big )^{\alpha }$, if

$$\begin{aligned} h(\alpha ,x)= & {} \left( {\alpha }^{2}+\frac{1}{4}\,\alpha -1\right) {x}^{2}-\left( {\alpha }^{2}-\frac{5}{4}\,\alpha +2\right) x+\alpha -1, \end{aligned}$$

(18)

$$\begin{aligned} z(\alpha ,x)= & {} \left( {\alpha }^{2}+\frac{1}{2}\,\alpha -1\right) {x}^{2}-\left( {\alpha }^{2}-\frac{3}{2}\,\alpha +2\right) x+\alpha -1 \end{aligned}$$

(19)

are different from zero, both the relationships in (16) and (17) define k as function of $\alpha$, $c_{1}$ and $c_{2}$, namely $F_{l}(\alpha ,c_{1},c_{2})$ with $l=1,2$, respectively. Since these functions are both homogeneous of degree $-2$ with respect to $c_{1}$ and $c_{2}$, without loss of generality, (16) and (17) define the following functions $f_{l}:(\alpha ,x)\rightarrow \,\widetilde{k}$ with $l=1,2$, respectively:⁶

$$\begin{aligned} f_{1}(\alpha ,x):= & {} \frac{1}{2}\,\bigg (\frac{\alpha \,x}{(x+1)^{2}}\bigg ){\frac{-({\alpha }^{2}-5\,\alpha +4){x}^{2}+({\alpha }^{2}+5\,\alpha -8) {x}-4}{h(\alpha ,x)}}; \end{aligned}$$

(20)

$$\begin{aligned} f_{2}(\alpha ,x):= & {} \frac{1}{2}\,\bigg (\frac{\alpha \,x}{x+1}\bigg )^{2}{\frac{(1-\alpha ){x}+(\alpha +1)}{z(\alpha ,x)}} \end{aligned}$$

(21)

where $\widetilde{k}=\frac{k}{c_{2}^{2}}$. We note that x is increasing with respect to $\frac{c_{1}}{c_{2}}$ and it varies in the interval $(0+\infty )$.

The (i) shape of the graphs of these functions, (ii) their intersection points and (iii) the study of inequalities in (14) allow characterising the different dynamic properties of the Nash equilibrium and the local bifurcations around it in terms of k and x. It is worth noting that since $\alpha$ appears in the definition of x, the analysis will be set in terms of the original parameters of the model, by fixing $\alpha$. This investigation will then allow us to define the dynamic properties of the model in terms of marginal costs’ ratio and the speed of adjustment, for a fixed level of $\alpha$.

Remark 1

The case in which both denominators in (20) and (21) are equal to zero simplifies the analysis, and such occurrence will be discussed at the end of the section.

Remark 2

The expressions in (20) and (21) do not allow to obtain a functional relation binding $\alpha$ to k and the marginal costs’ ratio. Because of the crucial role of differentiation, we will discuss through numerical analysis how the parameter $\alpha$ is decisive in defining the dynamics of the model.

4.1 Shapes of graphs of $f_{1}$ and $f_{2}$

In order to describe the behaviour of the graphs of the functions defined in (20) and (21), we can first notice that (i) $\lim \nolimits _{x\rightarrow \,0}f_{1}(\alpha ,x)=\lim \nolimits _{x\rightarrow \,0}f_{2}(\alpha ,x)=0$ that is both curves approach the origin of the axes in the plane $(x,\widetilde{k})$ and (ii) $\lim \nolimits _{x\rightarrow +\infty }f_{l}(\alpha ,x)=0$ with $l=1,2$ that is the x-axis represents a horizontal asymptote for both curves. By a direct inspection of $h(\alpha ,x)$ and $z(\alpha ,x)$, we get the following Lemma:

Lemma 1

Let $h(\alpha ,x)$, $z(\alpha ,x)$, $f_{1}(\alpha ,x)$ and $f_{2}(\alpha ,x)$ be defined in (18), (19), (20) and (21), respectively.

• (a) If ${\alpha }^{2}+\frac{1}{4}\,\alpha -1>0$, then there exists a unique $\overline{x}_{1}\in (0,+\infty )$ such that $h=0$. Therefore, $f_{1}$ is not defined in $x=\overline{x}_{1}$. Otherwise, $f_{1}$ is defined for every x in $(0,+\infty )$;

• (b) if ${\alpha }^{2}+\frac{1}{2}\,\alpha -1>0$, then there exists a unique $\overline{x}_{2}\in (0,+\infty )$ such that $z=0$. Therefore, $f_{2}$ is not defined in $x=\overline{x}_{2}$. Otherwise, $f_{2}$ is defined for every x in $(0,+\infty )$.

Proof

(a) Consider the function $h(\alpha ,x)$ defined in (18). We have that ${\alpha }^{2}-\frac{5}{4}\,\alpha +2>0$. Being the $\Delta$ of $h(\alpha ,x)$ always positive, we can notice that the potential changes of sign for $h(\alpha ,x)$ depend on the sign assumed by ${\alpha }^{2}+\frac{1}{4}\,\alpha -1$. In particular, for ${\alpha }^{2}+\frac{1}{4}\,\alpha -1>0$, we have that $h(\alpha ,x)$ changes its sign at most one time and then there exists a unique positive value $\overline{x}_{1}$ such that $h(\alpha ,\overline{x}_{1})=0$; for ${\alpha }^{2}+\frac{1}{4}\,\alpha -1=0$, $h(\alpha ,x)$ becomes a polynomial of degree 1 w.r.t. x and it assumes only negative values; for ${\alpha }^{2}+\frac{1}{4}\,\alpha -1<0$, $h(\alpha ,x)$ is the sum of three negative terms and then it assumes always negative values. Finally, the result follows.

(b) Analogously, consider the function $z(\alpha ,x)$, defined in (19). We have that ${\alpha }^{2}-\frac{3}{2}\,\alpha +2>0$. Being the $\Delta$ of $z(\alpha ,x)$ always positive, we can notice that changes of sign in $z(\alpha ,x)$ depend on the sign assumed by ${\alpha }^{2}+\frac{1}{2}\,\alpha -1$. In particular, for ${\alpha }^{2}+\frac{1}{2}\,\alpha -1>0$, the sign of $z(\alpha ,x)$ changes at most one time and there exists a unique positive $\overline{x}_{2}$ such that $z(\alpha ,\overline{x}_{2})=0$; for ${\alpha }^{2}+\frac{1}{2}\,\alpha -1=0$, $z(\alpha ,x)$ becomes a polynomial of degree 1 w.r.t. x and it assumes only negative values; for ${\alpha }^{2}+\frac{1}{2}\,\alpha -1<0$, $z(\alpha ,x)$ is the sum of three negative terms and then it assumes only negative values. Therefore, the result follows. $\square$

On the basis of the previous Lemma, we can state the following proposition:

Proposition 3

Let $\alpha _{1}=\frac{1}{8}(\sqrt{65}-1)$ and $\alpha _{2}=\frac{1}{4}(\sqrt{17}-1)$. Then,

• (a) For $\alpha \in (0,\alpha _{2})$, $\overline{x}_{1}$ and $\overline{x}_{2}$ do not exist;

• (b) for $\alpha \in (\alpha _{2},\alpha _{1})$, $\overline{x}_{2}$ exists while $\overline{x}_{1}$ does not exist;

• (c) for $\alpha \in (\alpha _{1},1)$, $\overline{x}_{1}$ and $\overline{x}_{2}$ exist.

Proof

By solving ${\alpha }^{2}+\frac{1}{4}\,\alpha -1=0$ and ${\alpha }^{2}+\frac{1}{2}\,\alpha -1=0$, we obtain the values of $\alpha _{1}$ and $\alpha _{2}$,respectively. Therefore, the relation $\alpha _{2}<\alpha _{1}$ is straightforward.

(a) From Lemma 1, we can deduce that in the interval $(0,\alpha _{2})$, $\overline{x}_{2}$ does not exist and then the inequality $\alpha _{2}<\alpha _{1}$ guarantees that also $\overline{x}_{1}$ does not exist. (b) The same inequality implies that there exists a range $(\alpha _{2},\alpha _{1})$ in which only $\overline{x}_{2}$ exists and then the asymptote for $f_{2}$ is the unique admitted. (c) Finally, at the right of $\alpha _{1}$, both $\overline{x}_{1}$ and $\overline{x}_{2}$ exist. $\square$

Remark 3

In the previous proposition, we analyse the conditions for which $\overline{x}_{1}$ and $\overline{x}_{2}$ exist. We notice that both values are exclusively dependent on $\alpha$ ($\overline{x}_{1}=\overline{x}_{1}(\alpha ), \overline{x}_{2}=\overline{x}_{2}(\alpha )$). Regarding the original parameters of the model, given $\alpha$, we have that positive values of $c_{1}$ and $c_{2}$ exist such that

$$\begin{aligned} \bigg (\frac{c_{1}}{c_{2}}\bigg )^{\alpha }=\overline{x}_{i},\ \ \ i=1,2 \end{aligned}$$

holds. In particular, being $\alpha \in (0,1]$, if $\overline{x}_{i}>1$, we have $\frac{c_{1}}{c_{2}}>1$ while if $\overline{x}_{i}<1$, we have $\frac{c_{1}}{c_{2}}<1$.

In order to have a graphical insight into what is shown above, we refer the reader to Fig. 1.

4.2 Intersections between graphs of $f_{1}$ and $f_{2}$

The existence of intersection points between $f_{1}$ and $f_{2}$ can be analysed in the plane $(x,\widetilde{k})$, as $\alpha$ varies. As far as this is concerned, the following proposition holds:

Proposition 4

There exists a unique intersection point $(x^{*},\widetilde{k}^{*})=\big (\frac{4}{5\alpha -4},\frac{8(5\alpha -4)}{25\alpha }\big )$ between the curves $\widetilde{k}=f_{1}$ and $\widetilde{k}=f_{2}$ in the plane $(x,\widetilde{k})$. It is feasible that is $x^{*},\widetilde{k}^{*}>0$, if and only if $\alpha >\alpha ^{*}=\frac{4}{5}$.

Proof

Solving the equation

$$\begin{aligned} f_{1}(\alpha ,x)=f_{2}(\alpha ,x) \end{aligned}$$

(22)

in terms of x, we have that a unique solution $x^{*}=\frac{4}{5\alpha -4}$.

Therefore, $x^{*}\in (0,+\infty )$ if and only if $\alpha >\frac{4}{5}$. By evaluating $f_{1}$ (or $f_{2}$) at $x^{*}$, the positive value $\widetilde{k}^{*}=\frac{8(5\alpha -4)}{25\alpha }$ is derived. $\square$

Corollary 1

The positive intersection point $(x^{*},\widetilde{k}^{*})=\big (\frac{4}{5\alpha -4},\frac{8(5\alpha -4)}{25\alpha }\big )$ exists if and only if $\overline{x}_{2}$ exists, where $\overline{x}_{2}$ is defined in Lemma 3.

Proof

Recalling the definition of $\overline{x}_{2}$ in Lemma 1 and that $\alpha _{2}=\frac{1}{4}(\sqrt{17}-1)$, the proof is straightforward because $\alpha _{2}<\alpha ^{*}$. $\square$

Remark 4

The equation

$$\begin{aligned} \bigg (\frac{c_{1}}{c_{2}}\bigg )^{\alpha }=\frac{4}{5\alpha -4} \end{aligned}$$

has a solution in terms of $\alpha$ in the interval $(\frac{4}{5},1]$ only if $\frac{c_{1}}{c_{2}}>1$. The equation has no solutions when $\frac{c_{1}}{c_{2}}<1$.

Remark 5

The previous propositions allow to deduce that (i) in the interval $(0,\alpha _{2})$, $f_{1}$ assumes only positive values while $f_{2}$ assumes only negative ones and (ii) in the interval $(\alpha _{2},\alpha ^{*})$, both $f_{1}$ and $f_{2}$ assume only positive values but $f_{2}$ assumes higher values than $f_{1}$.

4.3 Local stability of the Nash Equilibrium

In the light of the results discussed above, we can formulate the following proposition on the local stability of $E^{*}$:

Proposition 5

• (a) If (i) $\alpha \in \,(0,\alpha ^{*})$, then $E^{*}$ is locally asymptotically stable for $\widetilde{k}<f_{1}(\alpha ,x)$; (ii) for $\alpha =\alpha ^{*}$, $E^{*}$ loses its stability through a Flip bifurcation; (iii) otherwise, $E^{*}$ is unstable.

• (b) If (i) $(0,x^{*})$ the following cases arise: for $\alpha =\alpha ^{*}$, $E^{*}$ loses its stability through a Flip bifurcation while, for $\alpha \in \,(\alpha ^{*},1)$, $E^{*}$ is locally asymptotically stable for $\widetilde{k}<f_{1}(\alpha ,x)$. (ii) If $(x^{*},+\infty )$, the following cases arise: for $\alpha =\alpha ^{*}$, $E^{*}$ loses its stability through a Neimark–Sacker bifurcation while, for $\alpha \in \,(\alpha ^{*},1)$, $E^{*}$ is locally asymptotically stable for $\widetilde{k}<f_{2}(\alpha ,x)$. (iii) Otherwise, $E^{*}$ is unstable.

Proof

• (a) By recalling Remark 5, in the interval $(0,\alpha ^{*})$ we have that $E^{*}$ is stable for every $\widetilde{k}<f_{1}(\alpha ,x)$. On the contrary, for every $\widetilde{k}>f_{1}(\alpha ,x)$ $E^{*}$ loses its stability due to a Flip bifurcation, generated in the geometric place of the points $(x,\widetilde{k})$ such that $\widetilde{k}=f_{1}(\alpha ,x)$.

• (b) In the interval $(\alpha ^{*},1)$, the positive intersection point $x^{*}$ exists. By considering that $\lim \nolimits _{x\rightarrow \,0}f_{l}(\alpha ,x)=\lim \nolimits _{x\rightarrow +\infty }f_{l}(\alpha ,x)=0$ with $l=1,2$, we have that $E^{*}$ is stable for $\widetilde{k}<f_{1}$ in the interval $(0,x^{*})$ and for $\widetilde{k}<f_{2}$ in the interval $(x^{*},+\infty )$. On the contrary, the couples $(x,\widetilde{k})$ such that $\widetilde{k}=f_{1}$ define the geometric place of points in which the fixed point is destabilised through a Flip bifurcation in the interval $(0,x^{*})$, while the couples $(x,\widetilde{k})$ such that $\widetilde{k}=f_{2}$ the geometric place of points in which the fixed point is destabilised through a Neimark–Sacker bifurcation in the interval $(x^{*},+\infty )$.

$\square$

For the sake of completeness, the following proposition discusses the stability of $E^{*}$ in such cases where $h(\alpha ,x)$ or $z(\alpha ,x)$ vanish:

Proposition 6

• (a) If $h(\alpha ,x)=0$ and $\alpha \in \,(\alpha _{1},1)$, then $E^{*}$ may lose its stability via Neimark–Sacker bifurcation;

• (b) if $z(\alpha ,x)=0$ and $\alpha \in \,(\alpha _{2},1)$, then $E^{*}$ may lose its stability via Flip bifurcation.

Proof

(a) $h(\alpha ,x)$ is equal to zero if and only if $x=x_{1}^{*}$ or $x=x_{2}^{*}$ where

$$\begin{aligned} x_{1,2}^{*}=\frac{1}{2}\,{\frac{4\,{\alpha }^{2}-5\,\alpha +8\pm \sqrt{137\,{\alpha }^{2}-104 \,{\alpha }^{3}+16\,{\alpha }^{4}}}{4\,{\alpha }^{2}+\alpha -4}}. \end{aligned}$$

We have that $x_{1}^{*}>0$ for $\alpha \in \,(\alpha _{1},1)$ while $x_{2}^{*}<0$ for every $\alpha$. By substituting $x_{1}^{*}$ in the second condition of (14), we have that the inequality $1+\mathrm{Tr}(J_ {E^{*}})+\mathrm{Det}(J_ {E^{*}})>0$ is fulfilled by every $\alpha \in \,(\alpha _{1},1)$. This implies that in the interval $(\alpha _{1},1)$, the Jury conditions are satisfied if and only if the condition $1-\mathrm{Det}(J_ {E^{*}})>0$ is satisfied; (b) $z(\alpha ,x)$ is equal to zero if and only if $x=x_{3}^{*}$ or $x=x_{4}^{*}$, where

$$\begin{aligned} x_{3,4}^{*}=\frac{1}{2}\,{\frac{2\,{\alpha }^{2}-3\,\alpha +4\pm \sqrt{33\,{\alpha }^{2}-28\, {\alpha }^{3}+4\,{\alpha }^{4}}}{2\,{\alpha }^{2}+\alpha -2}}. \end{aligned}$$

We have that $x_{3}^{*}>0$ for $\alpha \in \,(\alpha _{2},1)$ while $x_{4}^{*}<0$ for every $\alpha$. By substituting $x_{3}^{*}$ in the third condition of (14), we have that the inequality $1-\mathrm{Det}(J_ {E^{*}})>0$ is fulfilled by every $\alpha \in \,(\alpha _{2},1)$. This implies that, in the interval $(\alpha _{2},1)$, the Jury conditions are satisfied if and only if the condition $1+\mathrm{Tr}(J_ {E^{*}})+\mathrm{Det}(J_ {E^{*}})>0$ is satisfied. $\square$

Remark 6

Proposition 5 allows to deduce that a destabilisation via Neimark–Sacker with respect to the parameter $\widetilde{k}$ may occur only for high values of $\alpha$ ($\alpha \in (\alpha ^{*},1)$). In addition, by combining Propositions 4 and 5, it must hold:

$$\begin{aligned} \frac{c_{1}}{c_{2}}>\bigg (\frac{4}{5\alpha -4}\bigg )^{\frac{1}{\alpha }}. \end{aligned}$$

(23)

The inequality in (23) implies that for $\alpha \in (\alpha ^{*},1)$, $E^{*}$ may be destabilised via Neimark–Sacker only if $c_{1}$ is at least the quadruple of $c_{2}$.

Fig. 1

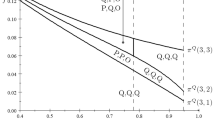
Different stability regions (areas in green) of $E^{*}$ in the plane $(x,\widetilde{k})$, defined by the bifurcation curves $f_{1}$ (depicted in black) and $f_{2}$ (depicted in red). a The fixed point may lose its stability only through a Flip bifurcation, $\alpha =0.55$; b both the bifurcations curve are in the positive plane, but $E^{*}$ may destabilise itself only through a Flip bifurcation, $\alpha =0.798$; c the stability region when both the bifurcation curves are in the positive plane and intersect each other in $x^{*}$, $\alpha =0.83$; d the stability region when there exist both the intersection point $(x^{*},\widetilde{k}^{*})$ and the asymptotes $\overline{x}_{1}$ and $\overline{x}_{2}$, $\alpha =0.95$ (colour figure online)

The graphs in Fig. 1 illustrate the main results stated in Propositions 3, 4 and 5. In particular, Panels (a) and (b) refer to the case (a) in Proposition 5 while Panel (c) shows a numerical example of case (b) in Proposition 5. Finally, Panel (d) describes the stability region for a value of $\alpha$ such that (i) $f_{1}$ and $f_{2}$ are not defined at a point ($\overline{x}_{1}$ and $\overline{x}_{2}$, respectively), as stated in Proposition 3 and (ii) $f_{1}$ and $f_{2}$ have an intersection point $(x^{*},\widetilde{k}^{*})$, as stated in Proposition 4. Moreover, with regard to the results shown in Proposition 6, Panel (d) in Fig. 1 allows to notice that, at $\overline{x}_{1}$ and $\overline{x}_{2}$, the Nash equilibrium is stable if the configuration of the parameters defines a point in the region depicted in green.⁷

Considering the results of the local analysis, in what follows we will discuss some dynamic scenarios.

4.4 Bifurcations and stability

The stability conditions provided in Proposition 5 allow us to deduce relevant information on the effect of both the speed of adjustment and the marginal costs ratio. In particular, starting from a parameter configuration for which the equilibrium is stable, an increase of k, leaving all the other parameters as fixed, implies a destabilisation of $E^{*}$ through a Flip or Neimark–Sacker bifurcation, in line with the results of Agliari et al. (2016) and the majority of literature focused on dynamic interactions in duopoly markets. The hump-shaped behaviour of the graph of $f_{1}$ induces a twofold role for x. Indeed, as suggested by the Panel (a) in Fig. 1, for a not too large value of the speed of adjustment, as x varies, we have that starting from zero the Nash equilibrium is first unstable, then stable and finally unstable again.

The bifurcation diagrams in Fig. 2, performed with respect to the speed of adjustment k, numerically show the theoretical results proved in Proposition 5. In Panel (a) of Fig. 2, we can notice that the Nash equilibrium is locally stable for low values of k and it undergoes a Flip bifurcation at $k=k_\mathrm{Flip}\simeq \,0.18859649$ generating a stable two-period cycle. As the speed of adjustment further increases, a sequence of period-doubling bifurcations generates cycles of a higher period leading to chaos. Differently, Panel (c) of Fig. 2 shows an example in which, as k varies, a Neimark–Sacker bifurcation takes place for $k=k_{ns}\simeq \,0.036752$. Finally, Panel (d) of Fig. 2 describes a numerical example of how instability and complex phenomena may occur regardless of marginal costs ratio. Indeed, the graph shows that for both $c_{1}<c_{2}$ and $c_{1}>c_{2}$, chaotic regimes may arise. From an economic point of view, we can then observe that scenarios of instability may occur both if the largest impact on the market is held by the firm adopting the LMA (case $c_{1}<c_{2}$) and if the largest impact is held by the firm adopting the gradient-like mechanism (case $c_{1}>c_{2}$).

Fig. 2

(i) Bifurcation diagrams of strategy $q_{2}$ as k varies: a Parameter set: $\alpha =0.4, c_{1}=0.064, c_{2}=1$. The Nash equilibrium loses its stability through a Flip bifurcation; b largest Lyapunov exponent with respect to k associated with Panel (a); c Parameter set: $\alpha =0.97, c_{1}=10, c_{2}=1$. $E^{*}$ undergoes a Neimark–Sacker bifurcation. d Parameter set: $\alpha =0.19, c_{2}=1, k=0.13$. Bifurcation diagram of strategy $q_{2}$ as $c_{1}$ varies in the interval [0.002, 3], where $E^{*}$ is destabilised in both cases $c_{1}<c_{2}$ and $c_{1}>c_{2}$

In order to deepen the dynamic properties of the system with respect to $\alpha$, we focus on the study of the Jury conditions assuming, without loss of generality, $c_{2}=1$. By studying the system defined by the second and third inequalities in (14) in the space of parameters $(c_{1},k,\alpha )$, we notice that as $\alpha$ varies, different stability switchings may arise (see Fig. 3).⁸

Fig. 3

a Portion of the stability region S in the space of parameters $(k,c_{1},\alpha )$, bounded by multicolour surface and a light-red surface. b Parameter set: $c_{1}=15.8$. A slice of the stability region (depicted in green) in the plane $(\alpha ,k)$ (colour figure online)

This result reveals that the degree of differentiation may have an ambiguous role and as a consequence, given an appropriate parameter set, both low and high values of $\alpha$ may induce instability. In particular, we have that (i) $\alpha$ is destabilising when it assumes low values (as in Agliari et al. 2016) and (ii) differently from Agliari et al. (2016), the fixed point may be destabilised also for high levels of $\alpha$ (that is, when goods are increasingly perceived as indistinguishable) via Flip bifurcation and, if $c_{1}$ is sufficiently larger than $c_{2}$ (see Remark 6), via Neimark–Sacker bifurcation. From an economic point of view, these results induce interesting conclusions. The results (i) suggest that for $\alpha \rightarrow \,0$ goods are basically independent and firms operate in distinct markets, characterised by isoelastic demands with elasticity close to 1, where they act as monopolists. In such a case, prices react little to changes in the number of goods placed on the market and are not able to bring the market back to a stationary equilibrium.⁹ Instead, The result (ii) suggests that for a low degree of product differentiation, the goods start to be perceived as indistinguishable and competition is high. In such a case, prices excessively react to changes in the amount of goods and are not able to bring the market back to a stationary equilibrium. A quite unexpected result considering that also if the market is composed of two firms adopting LMA, stability persists as a increases.¹⁰ Therefore, we can conclude that the main element generating instability is specifically the interaction between heterogeneous decisional mechanisms, namely the gradient-like mechanism and LMA.

Fig. 4

Parameter set: $c_{1}=15.8, c_{2}=1, k=0.1125$. The bifurcation diagram with respect to $\alpha$ shows several stability switchings for the Nash equilibrium and the destabilising role of both low and high values of the parameter

Fig. 5

Bifurcation diagram with respect to k for $\alpha =0.985$, $c_{1}=10$, and $c_{2}=1$

Fig. 6

Parameter set: $\alpha =0.985, c_{1}=10, c_{2}=1$. From left to right, top to bottom. Phase plane diagrams for different values of the parameter k. a $k=0.0303597$; b $k=0.0335548$; c $k=0.0336313$ d $k=0.0336568$; e $k=0.03449750$

Fig. 7

Parameter set: $\alpha =0.88, c_{1}=5, c_{2}=1, k=0.22857$. The stable 4-cycle, represented by the time series depicted in blue ($q_{1}(0)=0.018606$), coexists with the stable 12-cycle described by the time series depicted in red ($q_{1}(0)=0.02$) (colour figure online)

The occurrence of several stability switchings, as $\alpha$ varies, is highlighted by the bifurcation diagram in Fig. 4. In particular, by starting from the initial condition $(q_{1}^{0},q_{2}^{0})=(0.00416,0.079)$, we observe that as $\alpha$ is really close to 0 (not shown in the graph), the system is completely unstable (that is, almost all trajectories diverge). By increasing $\alpha$, dynamics become chaotic and then, as $\alpha$ continues to increase, the Nash equilibrium becomes stable until the value $\alpha =\alpha _\mathrm{Flip}\simeq \,0.6813$ where it undergoes a Flip bifurcation. By considering values of $\alpha$ larger than 0.6813, we notice (i) the existence of quasiperiodic orbits around a cycle of period 4 and then, after a phase of stability for $\alpha \in [0.8261,0.8756)$, (ii) the fixed point undergoes a Neimark–Sacker bifurcation for $\alpha =\alpha _{NS}\simeq \,0.8756$, leading to a quasiperiodic regime around the Nash equilibrium.

Remark 7

Numerical experiments performed above suggest that the Flip bifurcation has always a supercritical nature. Differently, the Neimark–Sacker bifurcation may experience a switch from a supercritical nature to a subcritical one.

Figure 5 furnishes another interesting numerical example. More in depth, the graph shows that starting from the initial condition $(q_{1}^{0},q_{2}^{0})=(0.0016,0.1)$ and varying the speed of adjustment k, a Neimark–Sacker bifurcation takes place at $k=\hat{k}_{ns}\simeq \,0.02924342$. Passing the critical value $\hat{k}_{ns}$, a quasiperiod behaviour starts and lasts until $k\simeq \,0.03254934$ from which such regime is replaced by a sequence of frequency-locking intervals. In these intervals, the motion along the stable closed invariant curve becomes captured by a periodic cycle therein contained. As the graph suggests, for values of k sufficiently high, the system falls in a chaotic regime.

Regarding the role of k, in Fig. 6 we provide some phase plane diagrams, which show (i) the initial quasiperiodic dynamics with an attracting invariant closed curve (see Panels (a) and (b)), (ii) the successive period-46 cycle generated by one of the frequency-locking intervals (see Panel (c)) and (iii) the unconnected cyclical areas after the frequency-locking (Panels (d)). As the speed of adjustment further increases, (iv) a nine-piece chaotic attractor appears (see Panel (e)). For $k\simeq \,0.03449750$, a final bifurcation occurs and almost all trajectories become unfeasible.

Finally, Fig. 7 shows that starting from two different initial conditions for $q_{1}$ (given the same initial value for $q_{2}$), after the transient phase, dynamics settle down to different periodic cycles. Then, the coexistence of two attractors appears.

5 Conclusions

In this article, we analysed the dynamics of a Cournot duopoly with differentiated goods and boundedly rational firms adopting heterogeneous decisional mechanisms to adjust the quantity of output produced. We showed that the differentiation parameter has an ambiguous role because both high and low levels of product differentiation may destabilise the Nash equilibrium, leading to cyclical behaviours and chaotic dynamics as well. This is a really counterintuitive result both compared with those presented in Agliari et al. (2016), where both firms adopt a gradient-like decisional mechanism, and the possible scenario in which the market is composed of two firms adopting LMA, for whom stability persists as the degree of differentiation varies. Therefore, we can conclude that the main element generating instability is specifically the interaction between heterogeneous decisional mechanisms, namely the gradient-like mechanism and LMA. With regard to this destabilising role of product differentiation, we also provided different parameter configurations for which the equilibrium loses its stability through Flip and/or Neimark–Sacker bifurcations.

In addition, we have found ranges of parameters for which chaotic dynamics, as well as coexistence of attractors, appear.