Cournot–Bertrand endogenous behavior in a differentiated oligopoly with entry deterrence

Abstract

This paper presents a new theoretical justification for the Cournot–Bertrand model to arise in equilibrium when firms have, at the outset, the same cost structure and sell symmetrically differentiated products. The Cournot–Bertrand model assumes some firms compete on price, adjusting their production to meet demand, while others set quantities and let their price adjust until market equilibrium is reached. We show that this may occur endogenously due to the possibility of entry, which may be deterred when some of the incumbents decide to set prices, while others free ride on this behavior and choose quantities.

1 Introduction

Although most of the Industrial Organization literature assumes that firms compete either by choosing prices or by choosing quantities, there is some empirical evidence that, in the same industry, some firms use price as the relevant strategic variable, while others compete by choosing quantities.¹ This situation was first developed by Bylka and Komar (1976) and the now called Cournot–Bertrand duopoly was later extended by Singh and Vives (1984) with the inclusion of a stage in which the choice of the strategic variable by the duopolists is made endogenous. Probably, because the Cournot model corresponds to the subgame perfect Nash equilibrium (SPNE) when the two firms’ products are substitutes and the Bertrand model corresponds to the SPNE when firms sell complements, the “hybrid case”, in which one firm chooses quantity and the other selects price as their strategic variables, has failed to receive enough attention from the literature.²

This article contributes to the understanding of how this mixed behavior may emerge endogenously and is in line with several authors that have established that Cournot–Bertrand competition may indeed arise in equilibrium. Sakai et al. (1995) show that the Cournot–Bertrand outcome may emerge in a triopoly when some products are substitutes and others are complements. Correa-López (2007) concludes that, in a vertically differentiated duopoly with an upstream market for an input, the high quality firm may choose to be a price competitor, whereas the low quality firm may choose to be a quantity setter. Reisinger and Ressner (2009) discuss the role of demand uncertainty on the endogenous strategic variables and show that the hybrid case can take place when demand uncertainty is neither too high or too low when compared to the degree of product substitutability.³ Tremblay et al. (2013) show that the Cournot–Bertrand duopoly may result from sequential decisions (with endogenous or exogenous timing) or, in the case of simultaneous moves, from higher fixed costs when choosing to compete in quantities.⁴ With the exception of Reisinger and Ressner (2009), significant asymmetry between firms is usually required to obtain the hybrid outcome in equilibrium.

Many other papers have just taken the Cournot–Bertrand structure as given: Kopel and Putz (2021) study information sharing in this context, Tremblay and Tremblay (2011) discuss stability and profitability in a Cournot–Bertrand duopoly, Barthel and Hoffman (2020) study the existence and stability of equilibrium with a general number of firms, and Askar (2014) discusses the uniqueness and stability of the Cournot–Bertrand duopoly when demand is a nonlinear function of price. For a survey of this literature, see Tremblay and Tremblay (2019).

In this article, we show that the Cournot–Bertrand model may occur endogenously even when all active firms have the same objective function, make their decisions simultaneously, have the same cost structure and sell symmetrically differentiated substitutes.

Our framework differs from previous works in assuming that there is the possibility of entry. As showed by Cellini et al. (2004) and Mukherjee (2005), the free entry number of firms in a differentiated oligopoly is not the same if firms compete a la Cournot or a la Bertrand. This means that the strategic variable that firms choose can influence the number of competitors they will face or, in other words, that it may be used to deter entry. When entry is considered, committing to behave more aggressively, that is to compete on price, may occur with the purpose of deterring entry. However, some incumbents may prefer to compete on quantity and free ride on the entry deterrence behavior of some of the others.

To illustrate this possibility, we assume exactly the same setup as in Mukherjee (2005) with a major difference: instead of assuming all firms are Cournot or Bertrand competitors, we allow the decision to be a Bertrand or a Cournot competitor to become endogenous. We share many other assumptions with the above mentioned literature: we assume a non-delegation game in which firms maximize their profit,⁵ use a linear demand/linear cost model, a symmetric cost structure and we assume that before the competition stage firms can credibly commit to use price or quantity as a strategic variable. As explained in Singh and Vives (1984), if a firm chooses to offer the price contract “it will have to supply the amount the consumers demand at a predetermined price, whatever action the competitor (...) takes.” If a firm opts for offering the quantity contract “it is committed to supplying a predetermined quantity independently of the action of the competitor”.

It may be difficult, a priori, to assume that the differences in production flexibility between the two types of contracts described above will result in firms having the same cost structure, regardless of their strategic variable choice. In particular, as Tremblay et al. (2013) point out when explaining different firm behavior in the market for small cars: “Fixed costs are higher for output competition than price competition, because output competition requires a dealer to have sufficient inventory and a large car lot relative to a firm that competes in price and receives a car from the factory only after a customer order is placed”.⁶ However, the assumption of a symmetric cost structure is standard in the literature, essentially for tractability as far as marginal costs are concerned. Although we follow this assumption, we illustrate with a specific example that the main results do not depend on it.

It should be noted that the term “Coutnot-Bertrand” oligopoly has also been used to refer to a different situation in which firms do not choose between setting prices or setting quantities but, instead, choose a price and quantity pair (see d’Aspremont and Dos Santos Ferreira 2009, and also d’Aspremont et al. 2007). This line of literature allows for parameterizing the degree of “competitive aggressiveness” of the active firms and these parameters can be strategically chosen by firms (e.g., d’Aspremont et al, 2016) before competition takes place. This constitutes a richer approach, as there is a continuum of possibilities for each firm’s level of aggressiveness. We focus on the extreme cases of pure price or quantity competition.⁷

The remainder of the paper is organized as follows. The next section presents the main assumptions in the model. Section 3 presents the equilibrium and illustrates the main ideas in the paper with a three-firm example, followed by the results for the general case. Finally, Sect. 4 concludes. All proofs are presented in the appendix.

2 The model

We assume that there are $n\ge 2$ incumbents that make their strategic variable choice (price or quantity) simultaneously before one entrant makes the decision of whether to enter the industry or not. In the former case, the entrant also selects its strategic variable. Afterward, competition takes place and the firms that are active simultaneously choose the specific value for their strategic variable, price or quantity.

With respect to notation, we denote the strategies of not entering the market, choosing price as the strategic variable and choosing quantity as the strategic variable, respectively, by O, P and Q, that is, each incumbent’s set of admissible strategies in the first stage is $\left\{ P,Q\right\}$ and the entrant’s set of admissible actions is $\left\{ O,P,Q\right\}$.

When the final competition stage is reached we have an industry with n or $n+1$ competitors, that include k firms that compete by setting quantities (Cournot competitors), while the remaining firms compete by setting prices (Bertrand competitors). The former firms choose their output and let price adjust, so that demand equals supply, whereas the latter post their prices and produce the quantity that is demanded. We refer to this distinction as firms of different “types”.

Following Mukherjee (2005), we assume the Singh and Vives (1984) demand structure given by

$$\begin{aligned} p_{i}=a-bq_{i}-b\gamma \sum _{j\ne i}q_{j} \end{aligned}$$

(1)

where $p_{i}$ and $q_{i}$ denote firm i’s unit price and quantity, with $a>0$, $b>0$ and $\gamma \in \left[ 0,1\right)$ measures the degree of substitutability between the products: for $\gamma =0$ the products belong to independent markets and when $\gamma \rightarrow 1$ products become homogeneous.

We further assume that the marginal production cost is constant and equal to $c<a$ for all firms in the industry, regardless of which strategic variable was chosen.⁸ In case of entry, the entrant faces an entry fixed cost $F\$which we denote in its normalized form by $f=F/\frac{\left( a-c\right) ^{2}}{b}.$ The profit when not entering the market is assumed to be 0.

Results similar to those presented below can be obtained for the alternative case in which the demand structure follows Shubik and Levitan (1980) and the inverse demand for firm i is

$$\begin{aligned} p_{i}=v-\frac{1}{1+u}(nq_{i}+uQ) \end{aligned}$$

where $Q=\sum _{i=1}^{n}q_{i}$ and v and u are two positive parameters with u measuring the degree of substitutability between the n products. When $u=0$ firms sell completely independent products and when $u\rightarrow +\infty$ all products are perfect substitutes. As highlighted in Motta (2004), this demand structure has several appealing properties such as the fact that market size does not vary with the number of products and with the degree of substitutability.⁹

3 Equilibria

This section presents the equilibrium of the game, which is obtained by backward induction. The first subsection refers to the equilibrium of the competition stage and the second subsection addresses the choice of strategic variables and the entry decision.

3.1 Cournot–Bertrand competition stage

We start by presenting the equilibrium profits that result from the final stage of the game, as a function of the number of active firms and of the number of quantity and price setters. Afterward, we discuss how individual profits compare in different market configurations. In Lemma 1, profits have been normalized by dividing by $\left( a-c\right) ^{2}/b$, and any entry costs are not included.

Lemma 1

Assume there are n active firms that include k Cournot competitors and $n-k$ Bertrand competitors. Individual profits of the two types of firms are

$$\begin{aligned} \pi _{i}^{Q}(n,k)&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1\right) }{\left( 1-\gamma +\gamma \left( n-k\right) \right) }\frac{\left( \gamma -2\gamma \left( n-k\right) -2+2\gamma \right) ^{2} }{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}}\end{aligned}$$

(2)

$$\begin{aligned} \pi _{i}^{P}(n,k)&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-k-1\right) +1-\gamma \right) }{\left( 1-\gamma +\gamma \left( n-k\right) \right) }\frac{\left( \gamma -2\gamma \left( n-k\right) -2\right) ^{2} }{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}} \end{aligned}$$

(3)

with $\pi _{i}^{Q}(n,k)$ and $\pi _{i}^{P}(n,k)$ denoting, respectively, the individual profit of a Cournot and a Bertrand competitor. For the particular case in which firms are all of the same type ($k=n$ or $k=0$ ):

$$\begin{aligned} \pi _{i}^{Q}(n,n)&=\frac{1}{\left( \gamma \left( n-1\right) +2\right) ^{2}}\end{aligned}$$

(4)

$$\begin{aligned} \pi _{i}^{P}(n,0)&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-2\right) +1\right) }{\left( \gamma \left( n-1\right) +1\right) \left( \gamma \left( n-3\right) +2\right) ^{2}} \end{aligned}$$

(5)

Proof

See Appendix A.

$\square$

Comparing the equilibrium profit levels in Lemma 1, it is possible to establish that (i) each Cournot competitor has a higher profit than each Bertrand competitor, that is $\pi _{i}^{Q}(n,k)>\pi _{i}^{P}(n,k)$, and (ii) keeping the total number of firms constant, a higher number of Cournot competitors (or a lower number of Bertrand competitors) increases the profit of each Cournot competitor, that is $\pi _{i}^{Q}(n,k+1)>\pi _{i}^{Q}(n,k)$. Thus, it is straightforward to conclude that any price setter would have had a higher profit if it had decided instead to be a quantity setter: $\pi ^{Q}(n,k+1)>\pi ^{P}(n,k)$.¹⁰

In addition, (iii) if firms are all of the same type, the profit of each of the n Cournot competitors is higher than the profit of each of the n Bertrand competitors, $\pi _{i}^{Q}(n,n)>\pi _{i}^{P}(n,0)$, and (iv) entry by an additional Cournot competitor will lower the profit of all incumbents, regardless of which strategic variable they have chosen: $\pi _{i}^{Q} (n,k)>\pi _{i}^{Q}(n+1,k+1)$ and $\pi _{i}^{P}(n,k)>\pi _{i}^{P}(n+1,k+1)$.¹¹

These results hint at the possibility that, in the first stage of the game, some incumbents may deter entry by deciding to be price setters. If entering, the entrant will decide to be a Cournot competitor, which will lower the profit of any type of incumbent. However, the entrant’s profit decreases with the number of price setters. Thus, depending on the cost of entry, entry may be deterred if there is a sufficiently high number of price setters. In some cases, characterized in the remainder of the paper, this may lead firms which are symmetric at the outset to choose different strategic variables in equilibrium, thus leading endogenously to the Cournot–Bertrand structure.

It should be noted that if one considered the possibility of different fixed costs between Cournot and Bertrand competitors, all the profit inequalities above would hold trivially except $\pi _{i}^{Q}(n,k)>\pi _{i}^{P}(n,k)$, which would become $\pi _{i}^{Q}(n,k)-F^{Q}>\pi _{i}^{P}(n,k)-F^{P}$, where $F^{Q}$ and $F^{P}$ denote, respectively, the fixed cost of a Cournot and of a Bertrand competitor, and which is equivalent to $F^{Q}-F^{P}<\pi _{i} ^{Q}(n,k)-\pi _{i}^{P}(n,k)$.¹² Thus, the results above would be similar if, when $F^{Q}>F^{P}$ the differences in fixed costs were sufficiently small or if $F^{Q}<F^{P}$. The same would apply for differences in marginal costs, in the sense that the relevant inequalities would hold if the differences in marginal costs were sufficiently small. This is illustrated in the next section, where, at the end, an example with cost asymmetry is presented.

3.2 Choice of strategic variables and entry decision

Having observed the incumbents’ strategic choices, the entrant will have higher profits if it is a Cournot competitor than if it is a Bertrand competitor, that is $\pi _{i}^{Q}(n+1,k+1)>\pi _{i}^{P}(n+1,k),$ which follows from $\pi _{i}^{Q}(n+1,k+1)>\pi _{i}^{Q}(n+1,k)>\pi _{i}^{P}(n+1,k).$ Therefore, the entrant will decide to enter the market as a quantity setter if this profit exceeds the entry cost: $\pi _{i}^{Q}(n+1,k+1)>f$.

We now turn to the simultaneous decisions of the n incumbents with respect to their strategic variable choices. The next section presents a three firm game to illustrate our results and the general case is discussed afterward.

3.2.1 Three-firm example

Most papers in the literature on Cournot–Bertrand competition assume the case of duopoly. Here, we add a third firm, to allow for the possibility of entry. As mentioned above, when deciding to enter, the entrant will compete by setting quantities as this dominates setting prices.

To solve the game, we need to rank several payoffs that result from the final competition stage and that are particular cases of the expressions presented in Lemma 1. The ranking between $\pi ^{Q}(3,3)$ and $\pi ^{Q}(2,1)$ is ambiguous: in the former case there are more competitors, whereas in the latter case there are less competitors but one competes more aggressively. For entry deterrence by a single incumbent to occur, we need that its profit when chosing to be a price competitor, $\pi ^{P}(2,1)$, is higher than the profit when choosing to be a quantity competitor and allowing entry, $\pi ^{Q}(3,3).$ A necessary condition for this to happen is that $\pi ^{Q}(2,1)>\pi ^{Q} (3,3)$  because, as seen above, $\pi ^{Q}(2,1)>\pi ^{P}(2,1).$ Thus, we assume that $\pi ^{Q}(3,3)<\pi ^{Q}(2,1)$ or, equivalently, that $\gamma <\overline{\gamma }:=0.94808$.

Then, the following ranking of payoffs holds:

$$\begin{aligned} \pi ^{Q}(3,1)<\pi ^{Q}(3,2)<\pi ^{Q}(3,3)<\pi ^{Q}(2,1) \end{aligned}$$

Finally, we define a relevant threshold for the product differentiation parameter $\gamma$, $\gamma <\gamma _{1}:=0.78078$, which ensures that $\pi ^{P}(2,1)>\pi ^{Q}(3,3)$ and note that $\pi ^{P}(2,0)>\pi ^{Q}(3,2)$ for all $\gamma$.

We now consider several possibilities for the entry cost:

(i) $f>\pi ^{Q}(3,3)$. For high values of f entry is blockaded and incumbents choose to compete in quantities.

(ii) $\pi ^{Q}(3,2)<f<\pi ^{Q}(3,3).$ In this case, there is no entry if at least one of the incumbents chooses to compete on price. Otherwise there will be entry and the entrant will compete in quantities. Thus, the two incumbents play the following game:

	P	Q
P	$\pi ^{P}(2,0),\pi ^{P}(2,0)$	$\pi ^{P}(2,1),\pi ^{Q}(2,1)$
Q	$\pi ^{Q}(2,1),\pi ^{P}(2,1)$	$\pi ^{Q}(3,3),\pi ^{Q}(3,3)$

Bertrand competition, (P,P), would be an equilibrium outcome of this game if and only if $\pi ^{P}(2,0)>\pi ^{Q}(2,1),$ but this is impossible.

Cournot–Bertrand competition, (P,Q) or (Q,P), however, occurs in equilibrium if and only if $\pi ^{P}(2,1)>\pi ^{Q}(3,3)$ which is equivalent to $\gamma <\gamma _{1}$ and $\pi ^{Q}(2,1)>\pi ^{P}(2,0),$ which is always true.

Finally, Cournot competition, (Q,Q), is an equilibrium if and only if $\pi ^{Q}(3,3)>\pi ^{P}(2,1)$ or, equivalently, $\gamma >\gamma _{1}.$

(iii) $\pi ^{Q}(3,1)<f<\pi ^{Q}(3,2).$ In this case, there is no entry if and only if both incumbents choose to compete by setting prices. Otherwise, firm 3 decides to enter the market and choose to compete by setting quantities. The two incumbents play the following game:

	P	Q
P	$\pi ^{P}(2,0),\pi ^{P}(2,0)$	$\pi ^{P}(3,2),\pi ^{Q}(3,2)$
Q	$\pi ^{Q}(3,2),\pi ^{P}(3,2)$	$\pi ^{Q}(3,3),\pi ^{Q}(3,3)$

Cournot–Bertrand competition is never an equilibrium, because $\pi ^{P}(3,2)<\pi ^{Q}(3,3)$.

Bertrand competition, leading to no entry, is an equilibrium if and only if $\pi ^{P}(2,0)>\pi ^{Q}(3,2)$ which is always true.

Cournot competition, leading to entry, is always an equilibrium, because $\pi ^{Q}(3,3)>\pi ^{P}(3,2).$ Neither of the incumbents profits from unilaterally deviating from Q to P as this does not deter entry.

(iv)$\ f<\pi ^{Q}(3,1).$ In this case entry will always take place. The two incumbents compete in quantities and there is entry by the third competitor, who also sets quantities.

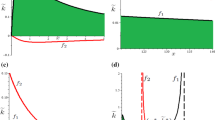
Figure 1 presents the relevant areas in the $(\gamma ,f)$ space.

Fig. 1

Equilibria of the 3-firm game, as a function of $\gamma$ and f

For Cournot–Bertrand competition to arise in equilibrium, the entry cost must take intermediate values (so that entry is not blockaded or impossible to deter by a single firm) and the products must be sufficiently differentiated. If products are relatively homogeneous, the existence of a price setter will lead to lower profits by both duopolists and the price setter would increase its profits when deviating to become a quantity setter, despite the fact that this leads to entry.

Different marginal costs

As mentioned in the Introduction, we have assumed that each firm’s cost structure is the same, regardless of the strategic variable the firms have chosen. Alternatively, one could assume that the marginal cost differs. In particular, let the marginal cost of the firms that compete in price be written as $\alpha c$, with $\alpha \ge 0$, where c is the marginal cost of the firms that compete in quantity. Let $Z=\frac{(1-\alpha )c}{a-c}$. This parameter measures the (normalized) cost disadvantage (or, if negative, advantage) of the output setters when compared to firms that compete by setting prices. In appendix B, we present the general expressions for profits, $\pi ^{Q}(n,k,Z)$ and $\pi ^{P}(n,k,Z)$, and the relevant constraints on Z, such that (i) the preliminary assumption above:

$$\begin{aligned} \pi ^{Q}(3,1,Z)<\pi ^{Q}(3,2,Z)<\pi ^{Q}(3,3,Z)<\pi ^{Q}(2,1,Z), \end{aligned}$$

holds, (ii) the outputs of both types of firms are always positive and (iii) conditions for a Cournot–Bertrand competition equilibrium are verified: $\pi ^{P}(2,1,Z)>\pi ^{Q}(3,3,Z)$ and $\pi ^{Q}(2,1,Z)>\pi ^{P}(2,0,Z).$

All these inequalities hold for $\underline{Z}<Z<\overline{Z}$. The thresholds $\underline{Z}$ and $\overline{Z}$ are defined in appendix B and presented in Fig. 2. The shaded area represents the pairs of values ($\gamma ,Z$) such that there is a duopoly in equilibrium with one firm choosing to set quantities and the other one choosing to set prices.

Fig. 2

Cournot–Bertrand equilibrium with cost asymmetry

The original symmetric example corresponds to the particular case of $Z=0$ (along the horizontal axis), which requires, as already shown, $\gamma <\gamma _{1}=0.78078$. Interestingly, if products are not very differentiated ($\gamma _{1}>0.78078$) a Cournot–Bertrand duopoly may arise in equilibrium only if Cournot competitors are sufficiently less efficient than Bertrand competitors. The reason is that this reduces the incentive of the low cost Bertrand competitor to deviate and become a high cost Cournot competitor.

As one might expect, for intermediate values of the product differentiation parameter, Cournot–Bertrand competition arises endogenously for a wider range of cost asymmetries.

3.2.2 General case

In this section we present the equilibrium of the whole game and, in particular, the conditions under which it is possible to have an equilibrium in which some of the n incumbents decide to set prices with the purpose of deterring entry, while the remaining firms choose quantities.

As expected, whether entry deterrence is possible (and profitable) or not depends on the entry cost. When $\pi ^{Q}(n+1,1)<f<\pi ^{Q}(n+1,n+1)$ it is possible to deter entry provided that the number of price setters is sufficiently large. With n incumbents, let the minimum number of price setters that result in entry deterrence be defined by $g^{*}(f)\in \mathbb {N}$, such that

$$\begin{aligned} \pi ^{Q}(n+1,n-g^{*}(f)+1)<f<\pi ^{Q}(n+1,n-(g^{*}(f)-1)+1) \end{aligned}$$

(6)

This condition ensures that the entry cost is such that with $g^{*}(f)$ price setters active in the industry, entry of an additional quantity setter is not profitable, but it would be profitable if a single price setter changed its behavior to become a quantity setter.

Assuming $\pi ^{Q}(n+1,1)<f<\pi ^{Q}(n+1,n+1)$, we have $g^{*} (f)\in \left[ 1,n\right]$. With respect to the subgame perfect Nash equilibria of this game, it is relevant to distinguish between two cases: when $g^{*}(f)=1$ any single firm can, unilaterally, deter entry by deciding to be a price competitor, whereas when $g^{*}(f)>1$ this is not possible. There are also several trivial cases. When $f>\pi ^{Q}(n+1,n+1)$ entry is blockaded: it is not profitable to enter the industry even if all firms are Cournot competitors. In this case, we say that $g^{*}(f)=0$. Finally, when $f<\pi ^{Q}(n+1,1)$ entry is impossible to deter, a case we denote by $g^{*}(f)>n.$

The next Proposition presents the equilibria of this game.

Proposition 1

• (a) Let $g^{*}(f)=0$. In the subgame perfect Nash equilibrium all n incumbents choose to be Cournot competitors and there is no entry.

• (b) Let $g^{*}(f)=1.$

  • (i) If $\pi ^{P}(n,n-1)>\pi ^{Q}(n+1,n+1),$ which is equivalent to $n<\frac{2-\gamma }{\gamma ^{2}}$, there are n subgame perfect Nash equilibria in which one incumbent chooses to be a Bertrand competitor, $n-1$ incumbents choose to be Cournot competitors and entry is deterred.

  • (ii) Otherwise, in the subgame perfect Nash equilibrium all n incumbents choose to be Cournot competitors and there is entry by a Cournot competitor.

• (c) Let $g^{*}(f)\in \left( 1,n\right] .$

  • (i) For all f there is a subgame perfect Nash equilibrium in which all n incumbents choose to be Cournot competitors and there is entry by a Cournot competitor.

  • (ii) For values of f such that $\pi ^{P}(n,n-g^{*}(f))>\pi ^{Q}(n+1,n-(g^{*}(f)-1)+1)$ there are $\frac{n!}{g^{*}!(n-g^{*})!}$ subgame perfect Nash equilibria in which $g^{*}(f)$ incumbents choose to be Bertrand competitors, $n-g^{*}(f)$ incumbents choose to be Cournot competitors and entry is deterred.

• (d) Let $g^{*}(f)>n.$ In the subgame perfect Nash equilibrium all n incumbents choose to be Cournot competitors and there is entry by a Cournot competitor.

Proof

See Appendix A. $\square$

The intuition for the Cournot–Bertrand equilibria motivated by entry deterrence, which happens in cases (b) (i) and (c) (ii) of Proposition 1, is the following. The only reason for a firm to decide to be a price competitor is the possibility of deterring entry. Thus, the entry cost f must be sufficiently high ($f>\pi ^{Q}(n+1,n-g^{*}(f)+1)$), so that it is possible to deter entry. However, it must also be sufficiently low ($f<\pi ^{Q}(n+1,n-(g^{*}(f)-1)+1)$), so that if a given price setter unilaterally decided to become a quantity setter this would trigger entry and, eventually, render such deviation unprofitable. These two thresholds on f correspond to requiring that $g^{*}(f)\in \left[ 1,n\right]$. In addition, entry deterrence must be profitable, which is ensured by the parameter constraints presented in (b) (i) and (c) (ii). These conditions ensure that being a price setter and avoiding entry is more profitable than setting quantities and facing an additional competitor.

When $g^{*}(f)=1,$ the hybrid equilibrium emerges under relatively simple conditions on the degree of product differentation and on the number of firms.

When $1<g^{*}(f)<n$, a subset of firms may choose quantity in equilibrium and free ride on the entry deterrence behavior of the others, who, by deciding to be price competitors, will have a lower equilibrium profit. The conditions for this to happen are not as clear cut unless one considers particular cases for n and k. One case may be of particular interest. It corresponds to the symmetric case in which, with an even number of incumbents, in equilibrium there is the same number of price and quantity setters. The conditions under which this case occurs in equilibrium are presented in Corollary 1.

Corollary 1

With an even number of firms n,  there is an equilibrium in which n/2 incumbents set quantities and n/2 incumbents set prices and entry is deterred if and only if:

(i) $\pi ^{Q}(n+1,n/2+1)<f<\pi ^{Q}(n+1,n/2+2)$ and;

(ii) $n\ge 6$ or $(n=4$ and $\gamma <0.87067)$ or $(n=2$ and $\gamma <0.78078).$

Proof

See Appendix A. $\square$

The first condition corresponds to requiring that $g^{*}(f)=n/2$ and the second one ensures that deterring entry is profitable. For large values of n this is always true and if n is small (that is $n=2$ or $n=4$) the products must be sufficiently differentiated to ensure the firms that are setting prices find it profitable to do so.

Equilibrium stability

These results also have implications for the stability of equilibria in Cournot–Betrand markets. They allow us to discuss the impact that potential entry has on the stability of equilibria. Without the prospect of entry, all firms would be Cournot competitors. As seen above, in the presence of the threat of further entry we may have $g^{*}(f)$ Bertrand players in equilibrium, as defined in Barthel and Hoffman (2020). This different mix of firm types will affect the stability of the equilibrium in the price or quantity setting stage. Theorem 3 in Barthel and Hoffman (2020) establishes how the set of values for parameter $\gamma$, the degree of substitutability, under which the equilibrium is stable changes as the number of Cournot players or Bertrand players change. Denoting this set by $P(n-k,k)$, this Theorem establishes that it becomes larger when the number of Bertrand players increases (that is, $P(n-k,k)\subset P(n-k+1,k))$ and smaller when the number of Cournot players increases (that is, $P(n-k,k+1)\subset P(n-k,k))$, provided that $\gamma <1/2$.¹³

In the absence of entry deterrence, all $n+1$ firms would be Cournot players but with entry-deterrence behavior, and when f takes intermediate values, there are equilibria in which $g^{*}(f)$ firms are Bertand competitors. Simple manipulation of the above inclusions yields

$$\begin{aligned} P(0,n+1)\subset P(0,n)\subset P(g^{*}(f),n)\subset P(g^{*}(f),n-g^{*}(f)) \end{aligned}$$

and hence $g^{*}(f)$ firms switching from Cournot to Bertrand competitors promotes stability in the sense that there are more values for $\gamma$ such that the equilibrium is stable.¹⁴

Numeric example

Proposition 1 relies heavily on $g^{*}(f),$the minimum number of price setters required for entry deterrence. In this section we present $g^{*}(f)$, for an arbitrary numeric example: $n=10$ and $\gamma =\frac{1}{3}$. For each value of f, $g^{*}$ is defined by

$$\begin{aligned} \pi ^{Q}(n+1,n-g^{*}+1)<f<\pi ^{Q}(n+1,n-g^{*}+2) \end{aligned}$$

which, in this numeric example, is equivalent to

$$\begin{aligned} \frac{\left( g^{*}+3\right) \left( 2g^{*}+3\right) ^{2}}{6\left( g^{*}+2\right) \left( 5g^{*}+8\right) ^{2}}<f<\frac{\left( g^{*}+2\right) \left( 2g^{*}+1\right) ^{2}}{6\left( 5g^{*}+3\right) ^{2}\left( g^{*}+1\right) }. \end{aligned}$$

The condition in Proposition 1 (b) (i) or (c) (ii):

$$\begin{aligned} \pi ^{P}(n,n-g^{*})>\pi ^{Q}(n+1,n-g^{*}+2), \end{aligned}$$

is equivalent to

$$\begin{aligned} \frac{6\left( 2g^{*}+5\right) ^{2}\left( g^{*}+1\right) }{\left( 28g^{*}+45\right) ^{2}\left( g^{*}+2\right) }>\frac{\left( g^{*}+2\right) \left( 2g^{*}+1\right) ^{2}}{6\left( 5g^{*}+3\right) ^{2}\left( g^{*}+1\right) }\end{aligned}$$

and always holds for any $g^{*}\ge 1$.

In Fig. 3, for each value of f,  the step function depicted in black presents the corresponding $g^{*}$: for high entry costs it suffices that one incumbent behaves as a price setter to deter entry, but more firms are required to do so to have the same outcome as f decreases. Given that $\pi ^{P}(n,n-g^{*})$ is represented by the thicker curve, it is clear that $\pi ^{P}(n,n-g^{*})>\pi ^{Q}(n+1,n-g^{*}+2),$ as long as $g^{*}\ge 1$. Thus, for any f belonging to $\left[ \pi ^{Q}(n+1,1),\pi ^{Q}(n+1,n+1)\right] ,$ there are equilibria in which entry is deterred. The number of firms that, in equilibrium, choose to be price setters and are, therefore, the ones responsible for entry deterrence changes (is decreasing) with f.

Fig. 3

$g^*$ as a function of f for $n=10$ and $\gamma =\frac{1}{3}.$

4 Conclusions

There is some empirical evidence that firms in the same industry use different strategic variables: some firms compete on price, adjusting their production to meet demand, while others set quantities and let their price adjust until market equilibrium is reached. Several papers have made the decision of which strategic variable to use endogenous by introducing a preliminary stage in which firms decide which of two types of contracts they make with consumers: the price contract or the quantity contract. As defined by Singh and Vives (1984), if a firm opts for the price contract “it will have to supply the amount the consumers demand at a predetermined price, whatever action the competitor (...) takes.” If a firm chooses the quantity contract “it is committed to supplying a predetermined quantity independently of the action of the competitor”. In general, some sort of firm asymmetry is required for the hybrid outcome to emerge in equilibrium, with some firms choosing prices and others choosing quantities as their main strategic variable. This asymmetry may result from exogenous product differentiation, cost differences, timing differences or differences in the firms’ objective functions.

In this paper, we present a context in which firms that are symmetric at the outset in terms of objective function, costs and timing of decisions, and sell symmetrically differentiated products may choose different strategic variables in equilibrium, with some firms serving as industry “watchdogs”, setting prices to prevent new rivals’ entry. In other words, we present a new theoretical justification for the Cournot–Bertrand model to arise in equilibrium: entry deterrence. It is well-known that price competition usually leads to lower profits than quantity competition, due to its more aggressive nature. Therefore, if the number of price setters is sufficiently high, an entrant may find entry unprofitable and an equilibrium may emerge in which a given number of firms decide to set prices, while others free ride on this behavior and set quantities. For this to happen in equilibrium, products must be sufficiently differentiated.

Even though authorities cannot intervene on competitors’ strategic variables choices (and, besides, the welfare effect of such choices is not clear as entry deterrence may increase or decrease welfare), the results obtained may shed some light on firms’ behavior, especially in contestable industries.

Appendices

Appendix A

Proof of Lemma 1: Let there be n firms, k of which set quantities with $k\in \left[ 1,n-1\right]$. Without loss of generality let these firms be firm $1,\ldots ,k$. Firms $k+1,\ldots ,n$ set prices. There are such $n-k$ firms.

Aggregating the demand functions (1) for the two types of firms we obtain, respectively, for the firms that set quantities and for the firms that set prices

$$\begin{aligned} P_{k}&=ka-bQ_{k}\left( 1-\gamma \right) -kb\gamma Q\\ P_{n-k}&=(n-k)a-bQ_{n-k}\left( 1-\gamma \right) -(n-k)b\gamma Q \end{aligned}$$

with $P_{k}=\sum _{j=1}^{k}p_{j}$ and $P_{n-k}=\sum _{j=k+1}^{n}p_{j}$ and likewise for quantities. As $Q=Q_{k}+Q_{n-k}$, we have

$$\begin{aligned} P_{k}&=ka-bQ_{k}\left( 1-\gamma \right) -kb\gamma \left( Q_{k} +Q_{n-k}\right) \\ P_{n-k}&=(n-k)a-bQ_{n-k}\left( 1-\gamma \right) -(n-k)b\gamma \left( Q_{k}+Q_{n-k}\right) \end{aligned}$$

or

$$\begin{aligned} Q_{k}&=\frac{ka-P_{k}-kb\gamma Q_{n-k}}{b\left( 1-\gamma +k\gamma \right) }\end{aligned}$$

(7)

$$\begin{aligned} Q_{n-k}&=\frac{(n-k)a-P_{n-k}-(n-k)b\gamma Q_{k}}{b\left( 1-\gamma +(n-k)\gamma \right) } \end{aligned}$$

(8)

Consider one of the quantity setting firms. Its inverse demand is

$$\begin{aligned} p_{i}=a-bq_{i}\left( 1-\gamma \right) -b\gamma \left( Q_{k}+Q_{n-k}\right) \end{aligned}$$

(9)

We want to write this as a function of the quantities of the other quantity setting firms, $Q_{k-i}$, and of the sum of prices of the price setting firms, $P_{n-k}$. Plugging (8) into (9) and simplifying we obtain

$$\begin{aligned} p_{i}=\frac{a\left( 1-\gamma \right) -bq_{i}\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1\right) +\gamma P_{n-k}-Q_{k-i}b\gamma \left( 1-\gamma \right) }{1-\gamma +\left( n-k\right) \gamma } \end{aligned}$$

(10)

where $Q_{k-i}=Q_{k}-q_{i}$.

Consider now one of the price setting firms. The demand for its product is

$$\begin{aligned} q_{i}=\frac{a-p_{i}-b\gamma \left( Q_{k}+Q_{n-k}\right) }{b\left( 1-\gamma \right) } \end{aligned}$$

(11)

We want to write this as a function of the quantities of the other quantity setting firms, $Q_{k}$, and of the sum of the prices of the other price setting firms, $P_{n-k-i}$. Plugging (8) into (11) and simplifying we obtain

$$\begin{aligned} q_{i}=\frac{a\left( 1-\gamma \right) -p_{i}\left( \gamma \left( n-k-1\right) +1-\gamma \right) +\gamma P_{n-k-i}-b\gamma \left( 1-\gamma \right) Q_{k}}{b\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1-\gamma \right) } \end{aligned}$$

(12)

where $P_{n-k-i}=\left( P_{n-k}-p_{i}\right)$.

The profit function of the quantity setting firms is then

$$\begin{aligned} \pi _{i}^{Q}&=(p_{i}-c)q_{i}\\&=\left( \frac{a\left( 1-\gamma \right) -bq_{i}\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1\right) +\gamma \sum _{j=k+1}^{n}p_{j} -\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^{k}q_{j}b\gamma \left( 1-\gamma \right) }{1-\gamma +\gamma \left( n-k\right) }-c\right) q_{i} \end{aligned}$$

and the first-order conditions for profit maximization are

$$\begin{aligned} \frac{\partial \pi _{i}^{Q}}{\partial q_{i}}=\frac{a\left( 1-\gamma \right) -2bq_{i}\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1\right) +\gamma \sum _{j=k+1}^{n}p_{j}-\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^{k}q_{j} b\gamma \left( 1-\gamma \right) }{1-\gamma +\gamma \left( n-k\right) }-c=0 \end{aligned}$$

The profit function of the price setting firms is then

$$\begin{aligned} \pi _{i}^{P}&=(p_{i}-c)q_{i}\\&=(p_{i}-c)\frac{a\left( 1-\gamma \right) -p_{i}\left( \gamma \left( n-k-1\right) +1-\gamma \right) +\gamma \sum _{\begin{array}{c} j=k+1\\ j\ne i \end{array} }^{n}p_{j}-b\gamma \left( 1-\gamma \right) \sum _{j=1}^{k}q_{j}}{b\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1-\gamma \right) } \end{aligned}$$

and the first-order conditions for profit maximization are

$$\begin{aligned} \frac{\partial \pi _{i}^{P}}{\partial p_{i}}&=\frac{a\left( 1-\gamma \right) -p_{i}\left( \gamma \left( n-k-1\right) +1-\gamma \right) +\gamma \sum _{\begin{array}{c} j=k+1\\ j\ne i \end{array}}^{n}p_{j}-b\gamma \left( 1-\gamma \right) \sum _{j=1}^{k}q_{j}}{b\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1-\gamma \right) }\\&\quad +(p_{i}-c)\frac{-\left( \gamma \left( n-k-1\right) +1-\gamma \right) }{b\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1-\gamma \right) }=0 \end{aligned}$$

Under symmetry we have $q_{1}=\cdots =q_{k}=q$ and $p_{k+1}=\cdots =p_{n}=p$. Solving the system of first-order conditions with respect to p, q yields:

$$\begin{aligned} p^{P}&=c+\frac{\left( 1-\gamma \right) \left( 2-\gamma +2\gamma \left( n-k\right) \right) }{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) }\left( a-c\right) \\ q^{Q}&=\frac{2\left( \gamma \left( n-k\right) +1\right) -3\gamma }{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) }\frac{a-c}{b} \end{aligned}$$

Plugging these prices and quantities into (12) and (10) yields the quantity of a price setting firm (say firm $k+1$):

$$\begin{aligned} q_{k+1}=\frac{\left( \gamma \left( n-k-2\right) +1\right) \left( \gamma \left( 2\left( n-k-1\right) +1\right) +2\right) }{\left( \gamma \left( n-k-1\right) +1\right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) }\frac{a-c}{b} \end{aligned}$$

and the price of a quantity setting firm (say firm 1):

$$\begin{aligned} p_{1}=c+\frac{\left( 1-\gamma \right) \left( 2-3\gamma +2\gamma \left( n-k\right) \right) \left( \gamma \left( n-k\right) +1\right) }{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) \left( 1-\gamma +\gamma \left( n-k\right) \right) }\left( a-c\right) \end{aligned}$$

It can be showed that the quantities of both types of firms are always positive.

Finally, normalized equilibrium profits (i.e., profits divided by $\frac{\left( a-c\right) ^{2}}{b})$ are

$$\begin{aligned} \pi _{i}^{Q}(n,k)&=(p_{1}-c)q^{Q}\\&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1\right) }{\left( 1-\gamma +\gamma \left( n-k\right) \right) } \frac{\left( \gamma -2\gamma \left( n-k\right) -2+2\gamma \right) ^{2} }{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}} \end{aligned}$$

and

$$\begin{aligned} \pi _{i}^{P}(n,k)&=(p^{P}-c)q_{k+1}\\&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-k-1\right) +1-\gamma \right) }{\left( 1-\gamma +\gamma \left( n-k\right) \right) } \frac{\left( \gamma -2\gamma \left( n-k\right) -2\right) ^{2}}{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}} \end{aligned}$$

with

$$\begin{aligned} \pi _{i}^{Q}(n,n)=\frac{1}{\left( \gamma \left( n-1\right) +2\right) ^{2}} \end{aligned}$$

and

$$\begin{aligned} \pi _{i}^{P}(n,0)=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-2\right) +1\right) }{\left( \gamma \left( n-1\right) +1\right) \left( -3\gamma +n\gamma +2\right) ^{2}} \end{aligned}$$

Given the equilibrium profits presented above, it is straightforward to check that:

(i) $\pi _{i}^{Q}(n,k)-\pi _{i}^{P}(n,k)>0:$

$$\begin{aligned}&\pi _{i}^{Q}(n,k)-\pi _{i}^{P}(n,k)\\&\quad =\frac{2\gamma ^{3}\left( 1-\gamma \right) }{\left( 1-\gamma +\gamma \left( n-k\right) \right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}}>0 \end{aligned}$$

(ii) $\pi _{i}^{Q}(n,k+1)>\pi _{i}^{Q}(n,k).$

Let $k\le n-1$. The result follows from the sign of

$$\begin{aligned}&\frac{\partial \pi _{i}^{Q}(n,k)}{\partial k}=\gamma ^{3}\left( 1-\gamma \right) \left( 2-\gamma +2\gamma \left( n-k-1\right) \right) \\&\quad \times \frac{4k^{2}\gamma ^{2}\left( n+1\right) -2k\gamma \left( 4n+3\gamma -2n\gamma +4n^{2}\gamma -2\right) +\gamma ^{2}\left( 15n-8n^{2}+4n^{3} -9\right) +2\gamma \left( 4n^{2}-8n+9\right) +4\left( n-2\right) }{\left( 1-\gamma +\gamma \left( n-k\right) \right) ^{2}\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{3}} \end{aligned}$$

This expression has the same sign as the numerator, which is a U-shaped parabola in k minimized at

$$\begin{aligned} k^{*}=\frac{2\left( 2n-1\right) \left( n\gamma +1\right) +3\gamma }{4\gamma \left( n+1\right) } \end{aligned}$$

As $k^{*}>n-1\$if and only if $n>\frac{2-7\gamma }{2\left( 2-\gamma \right) }$, which is always true, we have that the minimum of the numerator occurs at $k=n-1$ and is equal to

$$\begin{aligned} 4\left( 1-\gamma \right) \left( n-2\right) +6\gamma +\gamma ^{2}\left( n+1\right) >0 \end{aligned}$$

Therefore, the derivative is positive.

If $k>n-1$ we have that

$$\begin{aligned}&\pi _{i}^{Q}(n,n)-\pi _{i}^{Q}(n,n-1)\\&\quad =\gamma ^{3}\frac{\left( n-2\right) \left( 4\gamma ^{2}+n\gamma ^{3}+8\right) +24\gamma +\gamma ^{3}+8n\gamma ^{2}-20n\gamma +4n^{2}\gamma \left( 1-\gamma \right) }{\left( \gamma \left( n-1\right) +2\right) ^{2}\left( 4\gamma -2n\gamma +\gamma ^{2}+n\gamma ^{2}-4\right) ^{2}} \end{aligned}$$

The numerator is minimized in n at $n^{*}=\frac{\gamma ^{2}+2-4\gamma }{\gamma \left( \gamma -2\right) }<1$. Therefore, the minimum occurs at $n=2$ and the numerator takes value $\left( 2-2\right) \left( 4\gamma ^{2}+2\gamma ^{3}+8\right) +24\gamma +\gamma ^{3}+8*2\gamma ^{2}-20*2\gamma +4*2^{2}\gamma \left( 1-\gamma \right) =\gamma ^{3}>0.$

(iii) If firms are of the same type, profits decrease with the number of firms

$$\begin{aligned} \frac{\partial \pi _{i}^{Q}(n,n)}{\partial n}&=\frac{-2\gamma }{\left( \gamma \left( n-1\right) +2\right) ^{3}}<0\\ \frac{\partial \pi _{i}^{P}(n,0)}{\partial n}&=-\gamma \left( 1-\gamma \right) \frac{2n^{2}\gamma ^{2}+n\left( 4\gamma -7\gamma ^{2}\right) -8\gamma +7\gamma ^{2}+2}{\left( \gamma \left( n-1\right) +1\right) ^{2}\left( \gamma \left( n-3\right) +2\right) ^{3}}<0 \end{aligned}$$

because $2n^{2}\gamma ^{2}+n\left( 4\gamma -7\gamma ^{2}\right) -8\gamma +7\gamma ^{2}+2$ is increasing in n for $n\ge 2$, and evaluated at $n=2$ is equal to $\gamma ^{2}+2>0.$ In addition

$$\begin{aligned} \pi _{i}^{Q}(n,n)-\pi _{i}^{P}(n,0)=\frac{\gamma ^{3}\left( n-1\right) ^{2}\left( \gamma \left( n-2\right) +2\right) }{\left( \gamma \left( n-1\right) +1\right) \left( \gamma \left( n-3\right) +2\right) ^{2}\left( \gamma \left( n-1\right) +2\right) ^{2}}>0 \end{aligned}$$

(iv) $\pi _{i}^{Q}(n,k)>\pi _{i}^{Q}(n+1,k+1)$ and $\pi _{i} ^{P}(n,k)>\pi _{i}^{P}(n+1,k+1).$

Let the number of price setters be given by g: then $k=\left( n-g\right)$. If $g=0$ the result follows from the fact that if all firms are Cournot competitors profits decrease with the number of firms. If $g\ge 1,$

$$\begin{aligned} \frac{\partial \pi _{i}^{Q}(n,n-g)}{\partial n}&=-\frac{2\gamma \left( 1-\gamma \right) \left( g\gamma +1\right) \left( 2\gamma \left( g-1\right) +2-\gamma \right) ^{3}}{\left( \gamma \left( g-1\right) +1\right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) g\right) ^{3}}<0\\ \frac{\partial \pi _{i}^{P}(n,n-g)}{\partial n}&=-\frac{2\gamma \left( 1-\gamma \right) \left( \gamma \left( g-1\right) +1-\gamma \right) \left( \gamma \left( 2g-1\right) +2\right) ^{2}\left( 2\gamma \left( g-1\right) +2-\gamma \right) }{\left( \gamma \left( g-1\right) +1\right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) g\right) ^{3}}<0 \end{aligned}$$

$\blacksquare$

Proof of Proposition 1:

Parts (a) and (d) are trivial. If the number of firms does not depend on the incumbents’ decision no firm would profit from being a price competitor instead of a quantity competitor.

(b) Assume that $g^{*}(f)=1$. Having $n-1$ quantity setters and one price setter is an equilibrium if any quantity setter does not profit from changing to become a price setter, and the price setter does not profit from changing to become a quantity setter, which will trigger entry.

The first part is implied by

$$\begin{aligned} \pi _{i}^{Q}(n,n-1)>\pi _{i}^{Q}(n,n-2)>\pi _{i}^{P}(n,n-2). \end{aligned}$$

As for the second part, the price setter changing to become a quantity setter, which will trigger entry, is not profitable if

$$\begin{aligned} \pi _{i}^{P}(n,n-1)>\pi _{i}^{Q}(n+1,n+1) \end{aligned}$$

which, with

$$\begin{aligned} \pi _{i}^{Q}(n+1,n+1)&=\frac{1}{\left( \gamma n+2\right) ^{2}}\\ \pi _{i}^{P}(n,n-1)&=\frac{\left( 1-\gamma \right) ^{2}\left( \gamma +2\right) ^{2}}{\left( 4\gamma -2n\gamma +\gamma ^{2}+n\gamma ^{2}-4\right) ^{2}} \end{aligned}$$

is equivalent to

$$\begin{aligned} 1-\frac{\left( 1-\gamma \right) \left( \gamma +4\right) \left( \gamma +2\right) }{\gamma \left( 4-2\gamma -\gamma ^{2}\right) }<n<\frac{2-\gamma }{\gamma ^{2}} \end{aligned}$$

with the first inequality verified trivially.

(c) Assume that $g^{*}(f)>1$.

(i) Having all n firms choosing quantities is a Nash equilibrium (with entry), because no firm profits from changing its decision. If any single firm decides to be a price setter this is not enough to deter entry and the profit of this firm will decrease.

(ii) Having $n-g^{*}(f)$ firms choosing quantities and the remaining $g^{*}(f)$ firms choosing prices is a Nash equilibrium (with no entry) if no firm wants to change its decision.

Any price setter does not want to change its decision (which leads to entry) if and only if

$$\begin{aligned} \pi ^{P}(n,n-g^{*}(f))>\pi ^{Q}(n+1,n-g^{*}(f)+2) \end{aligned}$$

Any quantity setter does not want to change its decision (which leads to no entry) if and only if

$$\begin{aligned} \pi ^{Q}(n,n-g^{*}(f))>\pi ^{P}(n,n-g^{*}(f)-1) \end{aligned}$$

which is always true.

Finally, regardless of the value taken by $g^{*}(f)$, having more than $g^{*}(f)$ firms choosing prices is not an equilibrium as, if one of these firms deviated to become a quantity setter, this would not lead to entry and would be profitable. In addition, having at least one but less than $g^{*}(f)$ firms choosing prices is not also an equilibrium as the deviation to become a quantity setter would still lead to entry and would be profitable.$\blacksquare$

Proof of Corollary 1: For this equilibrium to exist, we need

$$\begin{aligned} \pi ^{Q}(n+1,k+1)&<f<\pi ^{Q}(n+1,k+2)\\ \pi ^{P}(n,k)&>\pi ^{Q}(n+1,k+2) \end{aligned}$$

with $k=\frac{n}{2}$.

The interval in the first condition always exists.

We now move to the second condition, assuming n is even and $k=n/2$ and using

$$\begin{aligned} \pi ^{P}(n,n/2)&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-4\right) +2\right) \left( \gamma \left( n-1\right) +2\right) ^{2} }{\left( \gamma \left( n-2\right) +2\right) \left( 4+4\gamma \left( n-2\right) +\gamma ^{2}\left( n^{2}-5n+3\right) \right) ^{2}}\\ \pi ^{Q}(n+1,n/2+2)&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-2\right) +2\right) \left( \gamma \left( n-5\right) +2\right) ^{2} }{\left( \gamma \left( n-4\right) +2\right) \left( 4+2\gamma \left( 2n-5\right) +\gamma ^{2}\left( n^{2}-6n+2\right) \right) ^{2}} \end{aligned}$$

It can be shown that $\pi ^{P}(n,n/2)-\pi ^{Q}(n+1,n/2+2)$ has the same sign as

$$\begin{aligned} g(n,\gamma )&=-\gamma ^{3}\left( -n^{3}+12n^{2}-37n+22\right) +\gamma ^{2}\left( 6n^{2}-44n+62\right) \\&\quad +\gamma \left( 12n-40\right) +8 \end{aligned}$$

for $n\ge 6$.

Both roots of $\frac{\partial g(n,\gamma )}{\partial \gamma }$ with respect to $\gamma$ are negative for $n\ge 8$, so this derivative is always positive and $g(n,\gamma )$ increases with $\gamma$. As $g(n,0)=8>0$ we have that $g(n,0)>0$ for all $\gamma$ if $n\ge 8$.

For the other values of n we proceed case by case. Inequality $\pi ^{P}(n,k)>\pi ^{Q}(n+1,k+2)$ with $k=n/2$ is equivalent to:

(i) if $n=2$: $\gamma <0.78078$ as presented in the numeric example.

(ii) if $n=4$:

$$\begin{aligned} \frac{\left( 1-\gamma \right) \gamma \left( 4\gamma -9\gamma ^{2}-\gamma ^{3}+4\right) \left( 44\gamma +8\gamma ^{2}-27\gamma ^{3}+\gamma ^{4}+16\right) }{4\left( \gamma +1\right) \left( -8\gamma +\gamma ^{2}-4\right) ^{2}\left( -3\gamma +3\gamma ^{2}-2\right) ^{2}}>0 \end{aligned}$$

which holds if and only if $\gamma <0.87067$.

(iii) if $n=6$:

$$\begin{aligned} \frac{\gamma \left( 1-\gamma \right) \left( 2-\gamma \right) \left( 9\gamma +8\gamma ^{2}+2\right) \left( 108\gamma +228\gamma ^{2}+161\gamma ^{3}+28\gamma ^{4}+16\right) }{4\left( \gamma +1\right) \left( 2\gamma +1\right) \left( 16\gamma +9\gamma ^{2}+4\right) ^{2}\left( 7\gamma +\gamma ^{2}+2\right) ^{2}}>0 \end{aligned}$$

which is true for any $\gamma \in \left( 0,1\right) .$

This concludes the proof.$\blacksquare$

Appendix B

In this appendix we detail the three firm example in Sect. 3.2.1 for the case of cost asymmetries.

It is straightforward to show, following the same steps as in the proof of Lemma 1, that in the presence of cost asymmetries the equilibrium profits are given by

$$\begin{aligned} \pi _{i}^{Q}(n,k,Z)&=\frac{\left( 1+\gamma \left( n-k\right) \right) \left( \left( \gamma -1\right) \left( 3\gamma +2k\gamma -2n\gamma -2\right) +Z\gamma \left( n-k\right) \left( 2\gamma +k\gamma -n\gamma -1\right) \right) ^{2}}{\left( 1-\gamma \right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}\left( 1-\gamma +\gamma \left( n-k\right) \right) }\\ \pi _{i}^{P}(n,k,Z)&=\frac{\left( 1+\gamma \left( n-k-2\right) \right) \left( \left( 1-\gamma \right) \left( 2-\gamma +2\gamma \left( n-k\right) \right) -Z\left( \begin{array}{c} \gamma \left( k-2n+3\right) +\\ \gamma ^{2}\left( 2n+k\left( k-n-1\right) -1\right) -2 \end{array} \right) \right) ^{2}}{\left( 1-\gamma \right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}\left( 1-\gamma +\gamma \left( n-k\right) \right) } \end{aligned}$$

where $Z=\frac{c(1-\alpha )}{a-c}$ is a normalization of the difference in the marginal costs of quantity setters, c, and price setters, $\alpha c.$

The payoffs involved in Sect. 3 are:

$$\begin{aligned} \pi _{i}^{Q}(3,3,Z)&=\frac{1}{4\left( \gamma +1\right) ^{2}}\\ \pi _{i}^{Q}(3,2,Z)&=\frac{\left( 1-\gamma \right) \left( \gamma +1\right) \left( \gamma +Z\gamma -2\right) ^{2}}{4\left( -\gamma +2\gamma ^{2}-2\right) ^{2}}\\ \pi _{i}^{Q}(3,1,Z)&=\frac{\left( \left( \gamma +2\right) \left( 1-\gamma \right) -2\gamma Z\right) ^{2}\left( 2\gamma +1\right) }{4\left( 1-\gamma \right) \left( \gamma +1\right) \left( \gamma ^{2}-3\gamma -2\right) ^{2}}\\ \pi _{i}^{Q}(2,1,Z)&=\frac{\left( \gamma +1\right) \left( 1-\gamma \right) \left( 2-\gamma \left( Z+1\right) \right) ^{2}}{\left( 3\gamma ^{2}-4\right) ^{2}} \end{aligned}$$

All quantities involved in these cases must be positive, that is, cost differences cannot be too large to ensure positive quantities for all firms involved.

The equilibrium quantities (divided by $\frac{a-c}{b}$) are

$$\begin{aligned} q^{Q}&=\frac{\left( 3\gamma -2\left( \gamma \left( n-k\right) +1\right) \right) \left( 1-\gamma \right) +\gamma \left( n-k\right) \left( \gamma \left( n-k\right) +1-2\gamma \right) Z}{\left( 1-\gamma \right) \left( 2\left( \gamma \left( 2k-3n+4\right) -2\right) +\gamma ^{2}\left( 7n+2kn-2n^{2}-4k-3\right) \right) }\\ q^{P}&=\frac{\left( \begin{array}{c} \left( \gamma \left( n-k-2\right) +1\right) \left( \gamma \left( 2\left( n-k-1\right) +1\right) +2\right) \left( 1-\gamma \right) \\ -\left( \gamma \left( k-2n+3\right) +\gamma ^{2}\left( -k+2n-kn+k^{2} -1\right) -2\right) \left( \gamma \left( n-k-2\right) +1\right) Z \end{array} \right) }{-\left( 1-\gamma \right) \left( \gamma \left( n-k-1\right) +1\right) \left( 2\left( \gamma \left( 2k-3n+4\right) -2\right) +\gamma ^{2}\left( -4k+7n+2kn-2n^{2}-3\right) \right) } \end{aligned}$$

The following table presents the upper and lower bounds on Z, such that all quantities are positive.

	$q^{Q}>0$	$q^{P}>0$
$n=3;k=2$	$Z<\frac{2-\gamma }{\gamma }$	$Z>\frac{\gamma +\gamma ^{2} -2}{\left( \gamma +1\right) (2-\gamma )}$
$n=3;k=1$	$Z<\frac{1}{2}\frac{2-\gamma }{\gamma }-\frac{1}{2}\gamma$	$Z>\frac{1}{2}\left( 3\gamma +2\right) \frac{1-\gamma }{-\gamma +\gamma ^{2}-1}$
$n=2;k=1$	$Z<\frac{2-\gamma }{\gamma }$	$Z>\frac{\gamma +\gamma ^{2} -2}{\left( 2-\gamma ^{2}\right) }$

All these are implied by¹⁵

$$\begin{aligned} \underline{Z_{1}}:=\frac{\gamma +\gamma ^{2}-2}{\left( \gamma +1\right) (2-\gamma )}<Z<\overline{Z_{1}}:=\frac{1}{2}\frac{2-\gamma }{\gamma }-\frac{1}{2}\gamma \end{aligned}$$

This merely states that the cost differences between the two types of firms cannot be too large.

With respect to the preliminary assumption in Sect. 3:

$$\begin{aligned} \pi ^{Q}(3,1,Z)<\pi ^{Q}(3,2,Z)<\pi ^{Q}(3,3,Z)<\pi ^{Q}(2,1,Z) \end{aligned}$$

one needs that $\pi ^{Q}(3,3)<\pi ^{Q}(2,1),$ $\pi _{i}^{Q}(3,2)<\pi _{i} ^{Q}(3,3)$, $\pi _{i}^{Q}(3,1)<\pi _{i}^{Q}(3,2)$, which yield, respectively:

$$\begin{aligned} \text { }Z&<\overline{Z_{2}}:=\frac{2-\gamma }{\gamma }-\frac{\left( 4-3\gamma ^{2}\right) }{2\gamma \sqrt{\left( 1-\gamma \right) \left( \gamma +1\right) ^{3}}}<1\\ Z&>\underline{Z_{2}}:=\frac{2-\gamma }{\gamma }-\frac{\left( \gamma -2\gamma ^{2}+2\right) }{\gamma \sqrt{\left( 1-\gamma \right) \left( \gamma +1\right) ^{3}}}\\ \underline{Z_{3}}&<Z<\overline{Z_{3}} \end{aligned}$$

with

$$\begin{aligned} \underline{Z_{3}}&:=\frac{\left( \gamma -1\right) \left( \begin{array}{c} -28\gamma -18\gamma ^{2}+23\gamma ^{3}+25\gamma ^{4}+2\gamma ^{5}-8\gamma ^{6}-7\gamma ^{7}+\gamma ^{8}-8\\ +\sqrt{2\gamma +1}\left( \gamma +1\right) \left( \gamma ^{2}-3\gamma -2\right) \left( 2\gamma ^{2}-\gamma -2\right) \left( 2-\gamma +\gamma ^{2}\right) \end{array} \right) }{\gamma \left( 36\gamma +7\gamma ^{2}-42\gamma ^{3}-11\gamma ^{4}+8\gamma ^{5}-3\gamma ^{6}+6\gamma ^{7}-\gamma ^{8}+12\right) }\\ \overline{Z_{3}}&:=\frac{\left( \gamma -1\right) \left( \begin{array}{c} -28\gamma -18\gamma ^{2}+23\gamma ^{3}+25\gamma ^{4}+2\gamma ^{5}-8\gamma ^{6}-7\gamma ^{7}+\gamma ^{8}-8\\ -\sqrt{2\gamma +1}\left( \gamma +1\right) \left( \gamma ^{2}-3\gamma -2\right) \left( 2\gamma ^{2}-\gamma -2\right) \left( 2-\gamma +\gamma ^{2}\right) \end{array} \right) }{\gamma \left( 36\gamma +7\gamma ^{2}-42\gamma ^{3}-11\gamma ^{4}+8\gamma ^{5}-3\gamma ^{6}+6\gamma ^{7}-\gamma ^{8}+12\right) } \end{aligned}$$

The first (second) condition imposes that the individual profit in a “pure” Cournot tripoloy is lower (higher) than a quantity setters’ profit when it is competing with a price setter. This is easier to verify if the quantity setter’s cost disadvantage (advantage) is sufficiently low (high). The third condition imposes that the profit of a quantity setter when competing with another quantity setter plus a price setter is higher than when competing with two price setters.

In addition, two more conditions are needed to have an equilibrium with Bertrand-Cournot competition:

(i) $\pi ^{P}(2,1)>\pi ^{Q}(3,3)$, which holds for

$$\begin{aligned} Z>\underline{Z_{4}}:=\gamma \frac{\gamma +2\gamma ^{2}-2}{2\left( \gamma +1\right) \left( 2-\gamma ^{2}\right) } \end{aligned}$$

and;

(ii) $\pi ^{Q}(2,1)>\pi ^{P}(2,0)$, which holds for

$$\begin{aligned} Z<\overline{Z_{4}}:=\frac{\gamma ^{3}}{\left( \gamma +2\right) \left( 2-\gamma ^{2}\right) } \end{aligned}$$

The first condition ensures that it is more profitable to deter entry by being a price setter than to be a quantity setter and allow entry. This is more likely to happen the greater the cost disadvantage of quantity setters. The second condition ensures that the quantity setter in the Cournot–Bertrand duopoly does not want to switch to be a price competitor, which is easier to verify when the quantity setters’ cost disadvantage is small.

Let $\underline{Z}=\max \left\{ \underline{Z_{1}},\underline{Z_{2} },\underline{Z_{3}},\underline{Z_{4}}\right\}$ and $\overline{Z} =\min \left\{ \overline{Z_{1}},\overline{Z_{2}},\overline{Z_{3}} ,\overline{Z_{4}}\right\}$. Figure 2 presents these thresholds and for $\underline{Z}<Z<\overline{Z}$ an equilibrium with Cournot–Bertrand competition exists.