An evolutionary model with best response and imitative rules

Abstract

We formulate an evolutionary oligopoly model where quantity setting players produce following either the static expectation best response or a performance-proportional imitation rule. The choice on how to behave is driven by an evolutionary selection mechanism according to which the rule that brought the highest performance attracts more followers. The model has a stationary state that represents a heterogeneous population where rational and imitative rules coexist and where players produce at the Cournot–Nash level. We find that the intensity of choice, a parameter representing the evolutionary propensity to switch to the most profitable rule, the cost of the best response implementation as well as the number of players have ambiguous roles in determining the stability property of the Cournot–Nash equilibrium. This marks important differences with most of the results from evolutionary models and oligopoly competitions. Such differences should be referred to the particular imitative behavior we consider in the present modeling setup. Moreover, the global analysis of the model reveals that the above-mentioned parameters introduce further elements of complexity, conditioning the convergence toward an inner attractor. In particular, even when the Cournot–Nash equilibrium loses its stability, outputs of players little differ from the Cournot–Nash level and most of the dynamics is due to wide variations of imitators’ relative fraction. This describes dynamic scenarios where shares of players produce more or less at the same level alternating their decision mechanisms.

1 Introduction

The most common decisional mechanism considered in the game theory is based on best response functions and was proposed by Cournot in his seminal work (Cournot 1838). Such a decisional mechanism was replaced in the literature concerning oligopoly competition by heuristic behaviors that imply lower degrees of rationality from players in terms of computational abilities and limited information set exploited by the players. An example is the gradient rule, introduced by Bischi and Naimzada (2000), Bischi et al. (1999, 2001), Agiza et al. (2002) and recently considered by Askar (2014a, b) and Fanti et al. (2015), according to which players ignore the market demand and adjust their outputs in the direction of increasing earnings based on local estimations of the slope of their profit function at the actual market state. Another example is the local monopolistic approximation (LMA) rule, introduced by Tuinstra (2004), considered in the framework of repeated oligopolies by Bischi et al. (2007), Naimzada and Sbragia (2006), Naimzada and Tramontana (2009) and in a monopolistic framework in Naimzada and Ricchiuti (2011). According to the LMA rule, players optimize their profits using a linear approximation of the true demand estimated by means of the local knowledge at the actual market state. The simultaneous presence of different decisional mechanisms is considered when the presence of heterogeneous degrees of rationality and computational abilities among players is assumed. Various pairings of heterogeneous behaviors, including the best response, the gradient rule and the LMA rule, are considered in Leonard and Nishimura (1999), Den Haan (2001), Agiza and Elsadany (2003, 2004), Angelini et al. (2009), Tramontana (2010), Cavalli and Naimzada (2014), Andaluz and Jarne (2015), Cavalli et al. (2015b), Cavalli and Naimzada (2015), Pireddu (2015), Tramontana et al. (2015), Naimzada and Tramontana (2015) and Andaluz et al. (2017). The presence of heterogeneous decisional mechanisms has also been considered in evolutionary frameworks that account for the changing propensity of players to behave according to a certain rule over a finite set of possible decision mechanisms. Along the line marked by Droste et al. (2002), the decisional mechanism that brought the best relative performances will attract more followers. Several contributions in this direction are provided in Bischi et al. (2009, 2015, 2018), Kopel et al. (2014), Cavalli et al. (2015a), Cerboni Baiardi et al. (2015), Radi (2017), among others. Noteworthy, endogenous fluctuations and evolutionary stable heterogeneities, where different behaviors coexist along complex dynamics, are often observed.

Here, we consider that the presence of heterogeneous decisional mechanisms is detected in experimental oligopolies, where both the imitative and the rational behaviors emerge (see Apesteguia et al. 2007; Oechssler et al. 2016; Huck et al. 2004; Bigoni and Fort 2013 or Offerman et al. 2002, among others). Motivated by this, we formulate an evolutionary oligopoly model where players behave following, alternatively, the static expectation best response or the performance-proportional imitation rule introduced in Cerboni Baiardi et al. (2018). The changing attitude to adopt one rule instead of the other one is driven by the differences in the past performances that each decision mechanism has generated. In particular, we assume that the performances of an output, which have been obtained by means of the static expectation best response behavior, result from the profit which that particular choice has generated. However, that profit is to be reduced by a constant average per-period implementation cost, due to the burden requirements that the best response behavior implies. Differently, we consider that the performances of an output coming from the exploitation of the imitation rule correspond to the profit it has generated. In other words, we assume that the imitation rule is free of charge.

We obtain a three-dimensional discrete-time dynamic system that approximates the dynamics of a population of N agents. Our model has a stationary state at which productions match the Cournot–Nash equilibrium and that represents a heterogeneous population, where both rational and imitative rules coexist. We find that the equilibrium production has lowered, whereas the number of players involved in the competition has increased. Moreover, the share of imitators at the Cournot–Nash equilibrium gets higher as the propensity of agents to switch to the most profitable rule increases. The same occurrence is observed when the costs for the best response rule exploitation grow.

The Cournot–Nash equilibrium may lose its stability either through flip or Neimark–Sacker bifurcations, which occur at certain variations of the intensity of choice, of the implementation costs and the number of players. Remarkably, those parameters have an unexpected ambiguous role in determining the local stability of the Cournot–Nash equilibrium. In fact, most of the evolutionary models state the destabilizing role of both the intensity of choice (see e.g., Hofbauer and Sigmund 2003) and the implementation costs (see e.g., Hommes (2013), where several models assume per-period information gathering costs to be associated with highly sophisticated decision mechanisms). In addition, starting from Theocharis (1960), most of the literature concerning oligopoly competition highlights the destabilizing role of the number of players.

The global analysis, performed through numerical simulations, highlights the effects of parameters variations on both the dynamic complexities of attractors and the shapes of their basins of attraction. Indeed, inner attractors should be the stationary state, periodic orbits, closed invariant curves as well as chaotic trajectories. They describe the dynamics of heterogeneous populations where both rational and imitative rules coexist. Remarkably, we find that increasing values in the intensity of choice widen the basin of attraction of the inner attractor around the Cournot–Nash equilibrium. In addition, even when the Cournot–Nash equilibrium is unstable, outputs of players that occur along periodic or chaotic trajectories little differ from the Cournot–Nash level. Most of the dynamics consists in variations of the imitators’ relative fraction, thus describing scenarios where shares of players produce at the same level alternating their decision mechanisms.

The paper is organized as follows. In Sect. 2, the model is formulated. In Sect. 3, the stationary states of the model and their relative stability conditions are provided in analytic forms when possible. In Sect. 4, the global dynamics that the model describes is discussed. Section 5 concludes.

2 The model

We consider a linear oligopoly model where a population of $N\ge 2$ quantity setting players compete producing homogeneous goods and bearing the same constant marginal production cost $c>0$. Let $q_{k}\ge 0$ be the output strategy adopted by agent k, for all $k=1,...,N$, and let the aggregate supply by all agents be $Q = \sum _{k=1}^Nq_{k}$. We assume that the market structure is summarized by the inverse demand function $P(Q) = \max \{a-bQ,0\}$, where the parameter $a>0$ represents the maximum price and $b>0$ is the slope of the price with respect to Q in the interval where it is positive. Hence, the generic kth player’s profit results as

$$\begin{aligned} \pi _k:=\pi (q_k) = (P(Q)-c)q_k. \end{aligned}$$

(2.1)

Game-theoretic arguments show that at the Cournot–Nash equilibrium each player produces at the level

$$\begin{aligned} q^{*} = \dfrac{a-c}{b(N+1)} \end{aligned}$$

(2.2)

and earns the profit

$$\begin{aligned} \pi ^{*} = \dfrac{1}{b}\left( \dfrac{a-c}{N+1}\right) ^2. \end{aligned}$$

(2.3)

Since producing at the Cournot–Nash level is very demanding in terms of rationality and information set owned by players, we assume that the players’ strategies come from the adoption of certain decisional mechanisms that can be implemented with limited information sets and, in one case, with limited rationality. Even so, we consider that the exploitation of a behavioral rule may require efforts in terms of computational abilities and the use of information set for its implementation. With this, the performance from an outcome can be measured by means of the profits it has brought, diminished by the costs needed for the implementation of the involved decisional mechanism. Hence, if agent k choose $q_k$, she gets the performance $U_k = \pi (q_k) - C_k$, where $C_k$ represents the per-period implementation cost related to the rule adopted by k.

We consider here that players can choose, alternatively, between the static expectation best response rule and a performance-proportional imitation rule involving weighed averages of previous period outputs, similarly to the rule proposed in Cerboni Baiardi et al. (2018). Since the static expectation best response requires relevant computational abilities and the holding of an important information set, which includes the knowledge of the market demand, we assume this to be implemented at a constant average per-period cost C. Differently, imitation-like behaviors are simple heuristics that imply limited implementation efforts that are negligible with respect to C and we set it free of charges. This is to say $C_k = C$ if k denotes a best responder player, while $C_k = 0$ if k denotes an imitator player.

Remark 1

For the economic consistency of the model, we assume the implementation cost C to be small enough not to determine negative or vanishing performances at the Cournot–Nash level, namely

$$\begin{aligned} C<\pi ^{*}, \end{aligned}$$

(2.4)

where $\pi ^{*}$ is the profit of each player at the Cournot–Nash equilibrium (see (2.3)).

The model is developed in a discrete-time framework where each player, at the beginning of each period, chooses which decisional mechanism to exploit and determines her production level accordingly. Following Droste et al. (2002) (see also Bischi et al. 2015; Cerboni Baiardi et al. 2015 or Lamantia and Radi 2018, among others) we assume that, if agent i produces according to the best response rule, she adapts her production optimally to the average output of the rest of the industry that has been observed in the previous period. Then, player i sets her output, at the generic time period $t+1$, to the level

$$\begin{aligned} q_i(t+1)&= \arg \max _{q_i\ge 0}\;\pi _i\left( q_i,(N-1){\bar{q}}(t)\right) \nonumber \\&=\arg \max _{q_i\ge 0}\left( \dfrac{1}{2b}\left( a-c-b(N-1){\bar{q}}(t)\right) \right) , \end{aligned}$$

(2.5)

where the “$\max$” operator prevents best responders from adopting negative outputs and where $(N-1){\bar{q}}(t)$ is the average production of the rest of the industry at time period t. Under static expectations, the value $(N-1){\bar{q}}(t)$ is taken as a proxy for the aggregate quantity $Q^{(e)}_{-i}(t+1)$ that player i expects to be produced by her competitors at the time period $t+1$.

Alternatively, if agent i determines her output by exploiting the performance-proportional imitation rule, she sets at time period $t+1$ the weighted average of the previous period outputs in the market, where weights are given by the associated relative performances. More precisely, let ${\mathcal {S}}(t)$ be the set of the quantities in the market at time t given by

$$\begin{aligned} {\mathcal {S}}(t):=\{q\in {\mathbb {R}}_+:\exists \; j\in {\mathbb {N}} \mathrm {\;s.t.\;} q=q_j(t) \}. \end{aligned}$$

In terms of ${\mathcal {S}}$, the set of best responders and imitators’ indexes choosing, respectively, different outputs can be expressed as

$$\begin{aligned} {\mathcal {B}}(t)&= \{i\in {\mathbb {N}}:q_i\in {\mathcal {S}}(t) \text{ and } i\text { is a best responder}\}\\ {\mathcal {I}}(t)&= \{j\in {\mathbb {N}}:q_j\in {\mathcal {S}}(t) \text { and }j\text { is an imitator}\}. \end{aligned}$$

Letting ${\mathcal {A}}(t) := I(t)\cup {\mathcal {B}}(t)$, the performance-proportional imitation rule we consider is

$$\begin{aligned} q_{i}(t+1)&=\dfrac{\sum _{k\in {\mathcal {A}}(t)}U_{k}q_{k}}{\sum _{k\in {\mathcal {A}}(t)}U_{k}}. \end{aligned}$$

(2.6)

The rule (2.6) considers that imitators are aware of the presence of strategic interactions and that an action that brought high performance (or the highest performance) in the previous period may not produce so good a result in the present time. Because of the indeterminacy about the performances that an action produces, imitators will tackle the problem of whom to imitate by considering, prudently, all the previous period outputs with weighted importance. This allows to mitigate the uncertainty on which outcome should arise from imitating a single previous period output. In addition, weights measure the relative importance of each output in proportion to the performances it has generated. Therefore, the higher the performance from a certain output is, the more the imitators’ production approaches that output.

Remark 2

The imitation rule (2.6) is defined at time $t+1$ whenever performances at time t are nonnegative, namely $U_k\ge 0$ for all $k\in {\mathcal {A}}(t)$, with at least one of them that is strictly positive. This restriction ensures that each weight $U_{k}/\sum _{k'}U_{k'}$, with $k\in {\mathcal {A}}(t)$ is included in the interval [0, 1] and, in turn, implies that production levels of imitator players at time $t+1$ are nonnegative, provided that positive outputs at time t are given.

The recurrences (2.5) and (2.6) can be aggregated into two unidimensional discrete maps by assuming the same initial conditions for players adopting the same rule. Indeed, this implies that best responders produce at the same output also in subsequent periods and their actions can be summarized by a single dynamic variable $q_1$ interpreted as the choice of the representative best responder earning profits $\pi _1$ with $U_1 = \pi _1-C$ performance. The same implication holds for imitators’ outputs that can be summarized by a single dynamic variable $q_2$ interpreted as the choice of the representative imitator earning profits $\pi _2$ with $U_2 = \pi _2$ performance. The splitting of the population between best responders and imitators can be described by the variable $\omega (t)\in (0,1)$ representing the fraction of imitators at time t. Clearly, the complementary fraction $(1-\omega (t))$ represents the fraction of best responders. Then, the average level of production can be expressed, at the generic period t, in terms of the share $\omega (t)$ of imitators as

$$\begin{aligned} {\bar{q}}(t) = (1-\omega (t))q_1(t)+\omega (t)q_2(t) \end{aligned}$$

and recurrence (2.5) reduces to

$$\begin{aligned} q_1(t+1)&= \max \left\{ 0,\dfrac{a-c}{2b} - \dfrac{1}{2}(N-1)\left( (1-\omega (t))q_1(t) + \omega (t) q_2(t)\right) \right\} . \end{aligned}$$

(2.7)

At the same time, the assumption of identical initial conditions of players can be expressed as

$$\begin{aligned} q_2(t+1)&= \dfrac{U_1(t)}{U_1(t) +U_2(t)}q_1(t) +\dfrac{U_2(t)}{U_1(t) +U_2(t)}q_2(t), \end{aligned}$$

(2.8)

where performances explicitly read as

$$\begin{aligned} U_1(t) :&= \pi _1(t)-C = (a-c-bN((1-\omega (t)) q_1(t) + \omega (t) q_2))q_1(t)-C\\ U_2(t) :&= \pi _2(t) = (a-c-bN((1-\omega (t))q_1(t) + \omega (t) q_2(t)))q_2(t). \end{aligned}$$

The changing propensity of each player to adopt a certain decisional mechanism is driven by differences in performances from past choices. As a consequence, the rule with better performance will attract more followers. Along the line marked by McFadden (1973) the propensity to follow the imitative rule changes in time according to the logit model

$$\begin{aligned} \omega (t+1) = \dfrac{e^{\beta U_2(t)}}{e^{\beta U_2(t)} + e^{\beta U_1(t)}}, \end{aligned}$$

(2.9)

where the parameter $\beta$ is the intensity of choice and measures the propensity of players to adopt the decision mechanism that brought the best performances in the past period. If $\beta = 0$, players do not value differences in performances and the fraction of imitators is fixed over time at 1 / 2. Otherwise, if $\beta = \infty$, players perfectly distinguish differences in performances and, in each period, all agents choose the previous-time best decision rule.

The dynamics of best responders and imitators’ productions, described by means of recurrences (2.7) and (2.8), respectively, together with recurrence (2.9), is given by the three-dimensional discrete-time nonlinear map T that explicitly reads as

$$\begin{aligned} T&:\left\{ \begin{array}{l} q_1' = \max \left\{ 0,\dfrac{a-c}{2b} - \dfrac{1}{2}(N-1)\left( (1-\omega )q_1 + \omega q_2\right) \right\} \\ q_2' = \dfrac{(a-c-bN((1-\omega )q_1 + \omega q_2))(q_1^2 + q_2^2) - Cq_1}{ (a-c-bN((1-\omega )q_1 + \omega q_2))(q_1 + q_2) - C}\\ \omega ' = \dfrac{1}{1+e^{\beta \left\{ (a-c-bN((1-\omega )q_1 + \omega q_2))(q_1 - q_2)-C\right\} }} \end{array}\right. \end{aligned}$$

(2.10)

where unlabeled variables are intended at the generic time t and accents denote one-step time advancements.

3 Local analysis

Stationary states of the model are provided in the following proposition.

Proposition 1

Map T has the stationary state $E^{*} = (q^{*},q^{*},\omega ^{*})$ where

$$\begin{aligned} q_1 = q_2 = q^{*} = \dfrac{a-c}{b(N+1)},\; \;\omega ^{*} = \dfrac{1}{1+e^{-\beta C}}. \end{aligned}$$

In addition, if condition (2.4) is met, then map T has the further stationary state $E^{0} = (q_1^0,q_2^0,\omega ^{0})$ where

and $\omega ^{0}\in (0,1)$ is the unique root in the interval [0, 1] of the equation $G(\omega ) = 0$, where

$$\begin{aligned} G(\omega )= -\dfrac{C}{q_1^0}q_2^0 - \dfrac{1}{\beta }\ln \left( \dfrac{1}{\omega }-1\right) . \end{aligned}$$

(3.1)

Proof

See Appendix 6$\square$

At the stationary state $E^{*}$ best responders and imitators produce the same output $q^{*}$, $E^{*}$ matches the Cournot–Nash equilibrium. Moreover, we mention that, at the stationary state $E^{*}$, the equilibrium share of imitators $\omega ^{*}$ increases with increasing values of both $\beta$ and C. This follows from the fact that the performances of the representative best responder player are lower than those of the representative imitator player because of the implementation costs C required by the best response behavior. Hence, the increase in $\beta$, which corresponds to the increasing capacity of players to distinguish differences in performances, makes the imitation heuristic more appealing. At the same time, the increase in C discourages the adoption of the best response behavior because of its increasing burden.

We further mention that, in the special occurrence where $C\rightarrow 0$, the stationary state $E^{0}$ can be interpreted as the Walrasian equilibrium of the oligopoly, where players produce at the market clearing price and earn null profits. Indeed, in this case, it results

$$\begin{aligned} \lim _{C\rightarrow 0}P(Q) = \lim _{C\rightarrow 0} \max \left\{ 0,a-bN((1-\omega ^0)q_1^0 + \omega ^0q_2^0)\right\} = c. \end{aligned}$$

The following proposition claims sufficient conditions for the asymptotic stability of the Cournot–Nash equilibrium.

Proposition 2

The stationary state $E^{*}$ is locally asymptotically stable provided that $\omega _f<\omega ^{*}<\omega _{ns}$, where

$$\begin{aligned} \omega _f := \dfrac{1}{2}\cdot \dfrac{3\pi ^{*}-C}{2\pi ^{*}-C}\cdot \dfrac{N-3}{N-1},\;\; \omega ^{*} = \dfrac{1}{1+e^{-\beta C}}\;\; \text{ and } \; \omega _{ns} = \dfrac{2}{N-1}+\dfrac{\pi ^{*}}{2\pi ^{*}-C} \end{aligned}$$

At $\omega ^{*}=\omega _f$, $E^{*}$ undergoes a flip bifurcation, while at $\omega ^{*} = \omega _{ns}$, $E^{*}$ undergoes a Neimark–Sacker bifurcation.

Proof

See Appendix 6$\square$

Analytic stability conditions cannot be obtained for the fixed point $E^{0}$ since the equilibrium fraction $\omega ^0$ cannot be obtained in an analytical form. However, in several numerical simulations performed at a wide range of parameters’ values, the stationary state $E^{0}$ is never found to be stable. The instability of the stationary state $E^0$ is an important outcome of our model whenever it is interpreted as the Walrasian equilibrium in the case in which implementation costs tend to zero. This is a consequence of our modeling setup where imitator players are coupled with profit maximizers, whose actions tend to move the oligopoly competition away from the market clearing price production and, hence, from $E^0$. Indeed, best responders have incentive to deviate from having vanishing performances that correspond to negative profits.

We remark that the instability occurrence of the Walrasian equilibrium deviates from various theoretical and experimental results concerning Cournot competitions, where imitation heuristics are considered (see e.g., Vega-Redondo 1997; Apesteguia et al. 2007). In detail, as shown in Vega-Redondo (1997), the Walrasian equilibrium emerges as players imitate the best or, alternatively, set random outputs with a nonvanishing mutation probability. Then, the emergence of the Walrasian equilibrium in that model should be explained by means of the players’ lack of awareness of strategic interactions. A similar argument can be used to explain the emergence of the mentioned equilibrium in the model proposed in Apesteguia et al. (2007) and tested through experiments. In fact, according to that model, players follow imitation-like rules. We also mention that the emergence of the Walrasian equilibrium in an evolutionary setting has been found by Radi (2017), where the author considers firms competing in a Cournot oligopoly by choosing to behave as profit maximizers or as price takers.

In the remainder of the section, we outline the role of the relevant parameters of the model, that is, the intensity of choice $\beta$, the implementation costs C and the number of players N, in their influencing the stability property of the Cournot–Nash equilibrium. As for this subject, we first mention that the stability conditions for the Cournot–Nash equilibrium provided in Proposition 2 can be rewritten in terms of the parameter $\beta$.

Corollary 1

The stationary state $E^{*}$ is locally asymptotically stable provided that $\beta _f<\beta <\beta _{ns}$ where

$$\begin{aligned} \beta _f = -\dfrac{1}{C}\log \left( \dfrac{1}{\omega _f}-1\right) ,\;\;\;\; \beta _{ns} = -\dfrac{1}{C}\log \left( \dfrac{1}{\omega _{ns}}-1\right) . \end{aligned}$$

The Corollary shows that a double stability threshold exists at increasing values of $\beta$. This occurrence is due to the presence of the imitative heuristic, and it is quite unexpected since, in most models endowed with logit-like evolutionary mechanisms, the intensity of choice has just a destabilizing effect (see e.g., Brock and Hommes 1997; Hommes 2013 or Hofbauer and Sigmund 2003). Bifurcation diagrams, which show the long-run dynamics of the three dynamic variables $q_1$, $q_2$ and $\omega$ varying $\beta$, are reported in Fig. 1. In the simulation, the stationary state $E^{*}$ is unstable, provided values of $\beta$ below the threshold $\beta _f$ are given. If parameter $\beta$ increases, a stable period-2 cycle appears and merges with the stationary state $E^{*}$ as $\beta$ matches the threshold value $\beta _f$. This causes a flip bifurcation, after which the Cournot–Nash equilibrium $E^{*}$ becomes locally asymptotically stable. The stability of $E^{*}$ is maintained as $\beta$ is further increased until it reaches the second threshold value $\beta _{ns}$ at which $E^{*}$ undergoes Neimark–Sacker bifurcation. From this point onwards, further increases in $\beta$ beyond $\beta _{ns}$ determine the loss of stability of $E^{*}$ and the appearance of stable invariant curves, periodic cycles and chaotic trajectories. The amplitudes of fluctuations of those trajectories widen as $\beta$ grows, until a contact of the stable attractor with the boundary of its basin of attraction occurs, thus causing a global bifurcation (contact bifurcation) after which only unfeasible trajectories take place.

Fig. 1

Bifurcation diagram of $q_1$ (left), $q_2$ (center) and $\omega$ (right). Parameters are $a = 100$, $b=c=1$, $C=3$ and $N=15$

In order to underline the role of $\beta$ at a wider spectrum of parameters variations, we provide numerical simulations in Fig. 2, giving examples of stability regions in the $C-\beta$ and $N-\beta$ parameters spaces (panels a) and b), respectively). In detail, stability regions, which denote parameters combinations for which $E^{*}$ is stable, are highlighted by the gray points, while the white points denote parameters configurations for which $E^{*}$ is unstable. Flip and Neimark–Sacker bifurcation thresholds are also shown by the orange and blue lines, respectively. The simulations confirm the double stability threshold for $\beta$, as stated in Corollary 1.

Fig. 2

Parameter spaces where stability regions are highlighted by the gray points. Common parameters are $a = 100$, $b = c = 1$, while $C_{\max }$ and $N_{\max }$ denote maximum values of C and N such that condition (2.4) is satisfied. a $C - \beta$ planes. $N = 7$ (left), $N = 15$ (right). b $N - \beta$ planes. $C = 1$ (left), $C = 10$ (right)

Simulations in panels a) highlight also the ambiguous role of implementation costs C in influencing the stability properties of $E^{*}$. Indeed, several bifurcation values exist along different bifurcation paths where C increases and to which various stability losses and stability retrievals of $E^{*}$ may correspond. In detail, the left panel a) where $N=7$ shows that, given a fixed value of $\beta$, $E^{*}$ is stable provided that implementation costs C are at sufficiently low values. Then, the increase in C determines, at first, the loss of stability of the Cournot–Nash equilibrium through Neimark–Sacker bifurcation and then its stability retrieval through Neimark–Sacker bifurcation. Differently, in the right panel a) where $N = 15$, $E^{*}$ is unstable provided that C is at sufficiently low values. Then, the increase in C may determine the stability retrieval of $E^{*}$ through flip bifurcation, its loss of stability through Neimark–Sacker bifurcation and, again, its stability retrieval through Neimark–Sacker bifurcation.

We remark that the variety of results that emerges with increasing C is an unexpected occurrence since, usually, implementation costs in evolutionary settings have just a destabilizing effect (see Brock and Hommes 1997; Hommes 2013 or Hofbauer and Sigmund 2003). By contrast, in the present modeling setup, the ambiguous role of C should be referred to its presence both within the evolutionary selection mechanism and within the imitative rule. In particular, we note that the first stability retrieval of $E^{*}$ through flip bifurcation, which takes place when the number N of players is sufficiently high, can be explained by noting that, as C increases, the equilibrium share of imitators $\omega ^{*}$ increases as well. Then, the share of imitators with a stabilizing role reaches a sufficient size so that the destabilizing action of best responders is compensated. Differently, the successive loss of stability of $E^{*}$ through Neimark–Sacker bifurcation, which may occur in both the scenarios where $N = 7$ and $N = 15$, should be referred to the overcrowding imitators and the scarcity of best response players to drive the dynamics toward convergence. Moreover, both the above-mentioned simulations show that $E^{*}$ is stable whenever implementation costs C are sufficiently high, provided that sufficiently high values of $\beta$ are given. This circumstance can be proved by analytical computations. To this purpose, let us define the value $C_{\max }$ to be the least upper bound of values of C such that condition (2.4) is satisfied. Clearly, it results $C_{\max } = \pi ^{*}$. Then, the stability conditions of $E^{*}$ given in Proposition 2, namely $\omega _f<\omega ^{*}<\omega _{ns}$, can be rewritten¹ in the limit $C\rightarrow C_{\max }$ as

$$\begin{aligned} 1 -\dfrac{2}{N-1}<\dfrac{1}{1+e^{-\beta \pi ^{*}}}<1+\dfrac{2}{N-1}. \end{aligned}$$

Those relations are always satisfied for whichever $\beta$ if $N\le 3$, while, if $N> 3$, the same relations are satisfied provided that

$$\begin{aligned} \beta >\dfrac{1}{\pi ^{*}}\log \left( \dfrac{N-3}{2}\right) . \end{aligned}$$

The consequence of such a circumstance is that as players support increasingly burden efforts to implement the best response behavior, the emergence of the Cournot–Nash equilibrium is favored, provided that players have sufficient capability to distinguish differences in performances.

Fig. 3

Bifurcation diagram of $q_1$ (left), $q_2$ (center) and $\omega$ (right) as N varies. Other parameters are $a = 100$, $b=c=1$, $C = 10$ and $\beta =0.2$

In order to highlight the role of the number of players in determining the stability of the stationary state $E^{*}$, we provide the bifurcation diagram in Fig. 3 where the long-run dynamics of the state variables are shown as N increases. The diagram reveals three stability threshold values of N to which the same number of changes in the stability of the stationary state $E^{*}$ corresponds. In detail, provided sufficiently low values of N, the Cournot–Nash equilibrium is stable. We remark that this circumstance is always true. Indeed, the two relations that ensure the local asymptotic stability of $E^{*}$ given in Proposition 2 are both matched² at the extreme value $N=2$. Then, as N increases, the first loss of stability of $E^{*}$ takes place through a Neimark–Sacker bifurcation, thus giving rise to a stable closed invariant curve. The curve widens as N increases and, then, disappears due to a global bifurcation that should be explained by the contact of the attractor with its basin of attraction. Just after that global bifurcation no feasible trajectory occurs. However, as N is sufficiently increased, a stable attractor (which is again a closed invariant curve) acquires stability and merges with the stationary state $E^{*}$ that becomes stable through a second Neimark–Sacker bifurcation. Moreover, at higher values of N, the stationary state $E^{*}$ loses again its stability through the flip bifurcation and a stable period-2 cycle arises. The stability property of the cycle $C_2$ evolves with N as well and, after the usual period doubling cascade, it originates periodic and chaotic trajectories. Finally, a new global bifurcation determines the disappearance of any stable attractor and bound trajectories can no more exist.

Fig. 4

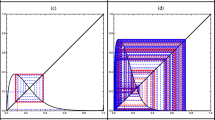
Sections of the phase space at fixed $q_1 = q^{*}$ at $N = 8$ (left) and $N = 11$ (right). The blue points represent the basin of attraction of inner attractors, while the white points represent the basin of unfeasible trajectories. Common parameters are $a = 100$, $b = c=1$, $C = 10$ and $\beta = 0.04$

The ambiguous role of N is also highlighted in the simulations provided in Fig. 2 panels b), where stability regions in the $N-\beta$ parameters space are shown for $C = 1$ and $C=10$ (left and right panels b), respectively). The simulations highlight the occurrence of possible stability changes in the stationary state $E^{*}$ that may be observed at increasing values of N. Again, the ambiguous role of the number of players should be referred to the presence of imitative behavior. It represents an unexpected circumstance since, according to the Theocharis’ result provided in Theocharis (1960), most of the literature concerning oligopoly competition highlights the destabilizing role of the number of players.

4 Global analysis

The global analysis, performed through numerical simulations, reveals further interesting dynamic phenomena that cannot be deduced through the local analysis provided in the previous section. Before proceeding with simulations, we observe that the segment ${\mathcal {L}}:=\{(q^{*}, q^{*},\omega ):\omega \in (0,1)\}$ is invariant under the action of map T, i.e., $T({\mathcal {L}})\subset {\mathcal {L}}$. In particular, initial conditions lying on ${\mathcal {L}}$ are mapped toward $E^{*}\in {\mathcal {L}}$ in one step. This implies that the set ${\mathcal {L}}$ is included in the basin of attraction of $E^{*}$. The role of the segment ${\mathcal {L}}$ in shaping basins of attraction of feasible trajectories is highlighted in simulations. Indeed, Figs. 4 and 5 show vertical sections of the phase space where the variable standing for the output of best responders is kept fixed at the equilibrium level $q^{*}$ and the invariant segment ${\mathcal {L}}$ is highlighted by the dashed red lines. In all the scenarios, where the share of imitators lies between the extreme values 0 and 1, an inner attractor is present and represents heterogeneous populations where rational and imitative rules coexist in the long run. Basins of attraction of inner attractors are represented by the blue points, while the white points denote initial conditions from which unfeasible trajectories originate. The shapes of the basins highlight that the possibility for non-diverging dynamics to occur is conditioned upon initial conditions. Indeed, feasible trajectories are likely to be observed as initial productions are closer to the Cournot–Nash level. Also, whenever the initial productions sufficiently approach the Cournot–Nash level, the convergence toward $E^{*}$ occurs regardless the share of imitators. At the same time, if the share of best responders increases, the initial deviation from the Cournot–Nash production, which still leads to non-divergent paths, grows larger.

Moreover, the simulations in Fig. 4 show two different dynamic scenarios obtained at different values in the number of players. In particular, in the left panel where $N = 8$, the stationary state $E^{*}$ is locally asymptotically stable. Differently, in the right panel where $N = 11$, $E^{*}$ has lost its stability through the flip bifurcation and a stable inner period-2 cycle $C_2$ is present. Noteworthy, the increase in N not only determines the stability loss of the stationary state $E^{*}$, but it also influences the shapes of basins of feasible trajectories by shrinking them around the invariant segment ${\mathcal {L}}$. This circumstance limits the feasible trajectories to the ones starting from productions that are closer and closer to the Cournot–Nash level as N increases.

Other interesting dynamic scenarios obtained at different values of the intensity of choice $\beta$ are represented in Fig. 5. In detail, in the left panel where $\beta = 0.1$, the stationary state $E^{*}$ is stable, while, in the right panel, $E^{*}$ has lost its stability through a Neimark–Sacker bifurcation. This is due to the increase in $\beta$ up to $\beta = 0.15$, beyond the threshold $\beta _{ns}$, and an inner chaotic attractor is present. Noteworthy, when chaotic dynamics arise, outputs of best responder and imitator players little differ from the Cournot–Nash production level and feasible trajectories take place in the neighborhood of the invariant segment ${\mathcal {L}}$. In addition, most of the dynamics of the system is due to the wide variations of imitators’ relative fraction. This means that the loss of stability of $E^{*}$ represents a transition from a scenario where each player produces according to a given rule in time toward a new scenario where shares of players produce at the same level alternating their decision mechanisms. Moreover, the comparison of scenarios provided in Fig. 5 highlights that the intensity of choice influences the shapes of the basins of inner attractors. Indeed, increasing values of $\beta$ widen the set of convergent initial conditions around the invariant segment ${\mathcal {L}}$, at the expense of the extension of the basin of unfeasible trajectories. Then, convergence toward the inner attractor is more likely to be achieved when players increase their ability to distinguish differences in performances.

Fig. 5

Sections of the phase space at fixed $q_1 = q^{*}$ at $\beta = 0.1$ and $\beta = 0.15$. The blue points represent the basin of attraction of the stable Cournot–Nash equilibrium, while the white points represent the basin of unfeasible trajectories. Common parameters are $N = 10$, $a = 100$, $b = c=1$ and $C = 10$

5 Conclusion

The oligopoly competition among static expectation best responders and imitators is considered. Players select which decisional mechanism to exploit according to an evolutionary selection mechanism such that the rule that brought the highest performance in the past attracts more followers. The model we consider describes the dynamics of N players by means of a discrete-time three-dimensional map and has a stationary state with an important economic interpretation, representing a heterogeneous population where rational and imitative rules coexist and where players produce at the Cournot–Nash level. We found that the intensity of choice, a parameter representing the evolutionary propensity to switch to the most profitable rule, and the cost of the best response implementation have ambiguous roles in determining the stability property of the mentioned stationary state. This is due to the presence of the imitative rule and marks an important difference with most of the results from evolutionary models (see e.g., Brock and Hommes 1997; Hommes 2013 or Hofbauer and Sigmund 2003). A similar occurrence has been found as the number of players involved in the competition increases. This, again, should be referred to the presence of imitative behavior and represents an unexpected circumstance because most of the literature concerning oligopoly competition, starting from the Theocharis rule (see Theocharis 1960), highlights the destabilizing role of the number of players. The global analysis of the model, performed by means of numerical simulations, reveals that variations of both the number of players and the intensity of choice lead to the loss of stability of the Cournot–Nash equilibrium and to the emergence of inner and stable periodic cycles or chaotic attractors. We found that the increase in the number of players or the increase in the intensity of choice influences the shape of the basin of the inner attractor by, respectively, shrinking or widening that basin around the Cournot–Nash production level.

Appendix

1.1 Proof of Proposition 1

Stationary states of map T are the solutions of the following algebraic system of equation:

$$\begin{aligned} \left\{ \begin{array}{l} q_1 = \max \left\{ 0,\dfrac{a-c}{2b} - \dfrac{1}{2}(N-1)\left( (1-\omega )q_1 + \omega q_2\right) \right\} \\ q_2 = \dfrac{(a-c-bN((1-\omega )q_1 + \omega q_2))(q_1^2 + q_2^2) - Cq_1}{ (a-c-bN((1-\omega )q_1 + \omega q_2))(q_1 + q_2) - C}\\ \omega = \dfrac{1}{1+e^{\beta \left\{ (a-c-bN((1-\omega )q_1 + \omega q_2))(q_1 - q_2)-C\right\} }} \end{array}.\right. \end{aligned}$$

(6.1)

We observe that the second equation in (6.1) can be re-expressed as

$$\begin{aligned} q_2 = \dfrac{\pi _1-C}{\pi _1+\pi _2-C}q_1+\dfrac{\pi _2}{\pi _1+\pi _2-C}q_2 \end{aligned}$$

which is equivalent to

$$\begin{aligned} (q_2-q_1)(\pi _1-C)=0. \end{aligned}$$

This equation is satisfied if either $q_1=q_2$ or $\pi _1-C=0$. In the former case, the condition $q_1=q_2$, together with the first equation in (6.1), implies either $q_1=q_2=q^{*}$ or $q_1=q_2=0$. Moreover, since the condition $q_1=q_2$ implies $\pi _1 = \pi _2$, the stationary share of imitators satisfying the third equation in (6.1) is fixed at the level $\omega ^{*} = 1/(1 + e^{-\beta C})$. However, only the point $(q^{*},q^{*},\omega ^{*})$ is a feasible stationary state of map T. Indeed, provided that both the representative best responder and imitator set null productions, namely $q_1=q_2=0$, the imitation rule (2.6) is not defined (see Remark 2).

Let us consider the latter occurrence in which $\pi _1-C=0$. In this case, the condition $q_1(t+1)=q_1(t)$ can be rewritten to express the stationary value $q_2$ in terms of $q_1$ as

$$\begin{aligned} q_2 = \dfrac{2}{(N-1)\omega }\left( \dfrac{a-c}{2b}-q_1\left( 1+\dfrac{1}{2}(N-1)(1-\omega )\right) \right) . \end{aligned}$$

(6.2)

Hence, the condition $\pi _1-C=0$ turns to a second-order polynomial in the variable $q_1$:

$$\begin{aligned} \pi _1-C = \left( 2b\dfrac{N}{N-1}q_1-\dfrac{a-c}{N-1}\right) q_1-C=0 \end{aligned}$$

(6.3)

whose positive root is $q_1^0$. Then, by substituting the value $q_1^0$ in Eq. (6.2), the value $q_2^0$ is obtained. We observe that, provided that condition (2.4) holds, $q_2^0$ is positive. Indeed,

$$\begin{aligned} q_2^0&=\dfrac{1}{4bN(N-1)\omega }\bigg ((a-c)(3N-1+\omega (N-1))\\&-(N+1-\omega (N-1))\sqrt{(a-c)^2+8bN(N-1)C}\bigg )\\&>\dfrac{1}{4bN(N-1)\omega }\bigg ((a-c)(3N-1+\omega (N-1))\\&\quad -(N+1-\omega (N-1))\sqrt{(a-c)^2+8N(N-1)\left( \dfrac{a-c}{N+1}\right) ^2}\bigg )\\&=\dfrac{a-c}{4bN(N-1)\omega }\bigg (2N+(N+1)\left( 1-\sqrt{1+\dfrac{8N(N-1)}{(N+1)^2}}\right) \\&\quad +\omega (N-1)\left( 1+\sqrt{1+\dfrac{8N(N-1)}{(N+1)^2}}\right) \bigg ) \\&=\dfrac{a-c}{4bN(N-1)\omega }\bigg (2+\omega (N-1)\left( 1+\dfrac{3N-1}{N+1}\right) \bigg )>0. \end{aligned}$$

Finally, the condition $\omega (t+1) = \omega (t)$ computed at $q_1 = q_1^0$ and $q_2 = q_2^0$ leads to the equation $G(\omega ) = 0$, where

$$\begin{aligned} G(\omega )&=\left( a-c-bN((1-\omega ) q_1^0+\omega q_2^0)\right) (q_1^0-q_2^0)-C- \dfrac{1}{\beta }\ln \left( \dfrac{1}{\omega }-1\right) . \end{aligned}$$

By Eq. (6.3), $G(\omega )$ can be simplified as follows:

$$\begin{aligned} G(\omega )&= -\dfrac{C}{q_1^0}q_2^0 - \dfrac{1}{\beta }\ln \left( \dfrac{1}{\omega }-1\right) . \end{aligned}$$

Equation $G(\omega ) = 0$ has a unique root $\omega ^0$ within the interval [0, 1] such that $\omega ^0\in (0,1)$ provided that condition 2.4 holds. Indeed, in this case, there holds

$$\begin{aligned} \lim _{\omega \rightarrow 0^+}G(\omega )&= -\infty ,\;\; \lim _{\omega \rightarrow 1^-}G(\omega ) = +\infty \end{aligned}$$

and $G'(\omega )>0$ for all $\omega \in (0,1)$.

1.2 Proof of Proposition 2

The Jacobian matrix of map T computed at $E^{*}$ is given by

$$\begin{aligned} J(E^{*})&=\left( \begin{array}{cccc} -(N-1)(1-\omega ^{*})/2&{} &{}-(N-1)\omega ^{*}/2&{}0\\ \dfrac{\pi ^{*}-C}{2\pi ^{*}-C}&{} &{}\dfrac{\pi ^{*}}{2\pi ^{*}-C}&{}0\\ -\beta N\cdot \dfrac{a-c}{N+1}\cdot \dfrac{e^{-\beta C}}{(1+e^{-\beta C})^2}&{} &{} \beta N\cdot \dfrac{a-c}{N+1}\cdot \dfrac{e^{-\beta C}}{(1+e^{-\beta C})^2}&{}0 \end{array}\right) . \end{aligned}$$

The Jacobian matrix $J(E^{*})$ has a vanishing column, and its characteristic polynomial can be factorized as $P(\lambda ) = -\lambda {\hat{P}}(\lambda )$, where

$$\begin{aligned} {\hat{P}}(\lambda )&= \lambda ^2 - \lambda \left( -\dfrac{N-1}{2}(1-\omega ^{*})+ \dfrac{\pi ^{*}}{2\pi ^{*}-C}\right) \\&\quad -\dfrac{N-1}{2}\cdot \dfrac{\pi ^{*}}{2\pi ^{*}-C}(1-\omega ^{*}) + \dfrac{N-1}{2}\cdot \dfrac{\pi ^{*}-C}{2\pi ^{*}-C}\omega ^{*} \end{aligned}$$

is the characteristic polynomial of the $2\times 2$ matrix ${\hat{J}}$ representing the Jacobian matrix related to the first two recurrences of map T computed at $q_1 = q_2 = q^{*}$. Hence, the stability conditions for $E^{*}$ are the Jury’s conditions for the stability of equilibria in two-dimensional discrete-time maps and read as

$$\begin{aligned} {\hat{P}}(1)&>0\;\Longrightarrow \; N+1>0\text { (always satisfied)}\\ {\hat{P}}(-1)&>0\;\Longrightarrow \; \omega ^{*}>\omega _f:=\dfrac{1}{2}\cdot \dfrac{3\pi ^{*}-C}{2\pi ^{*}-C}\cdot \dfrac{N-3}{N-1}\\ \text {det}{\hat{J}}&<1\;\Longrightarrow \;\omega ^{*}<\omega _{ns}:=\dfrac{2}{N-1}+\dfrac{\pi ^{*}}{2\pi ^{*}-C} \end{aligned}$$

and the thesis follows.