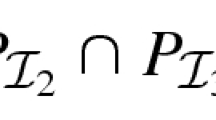1 Introduction

Some combinatorial optimisation problems are well-understood in the sense that they can be solved in polynomial time and the complete description of the associated polytope is known. Examples are the spanning tree problem, the optimisation over matroids or over the intersection of two matroids as well as the matching problem, see e. g. , [10, 11, 27]. Combinatorial optimisation problems with general polynomial objective functions are often solved by introducing new variables for each monomial, see e. g. , [13, 15, 16, 21, 29] and considering the associated linear problem, for the quadratic unconstrained case see e. g. , [25]. Recently, the polyhedral structure of linearised unconstrained polynomial 0–1 problems has been considered in more detail, see e. g. , [6, 8]. Approaches for solving some kinds of non-linear matroid optimization problem can be found, e. g. , in [1, 7, 23].

In this paper we study a simpler but related problem with the aim to better understand the structure of polytopes arising from linearisations. Instead of considering an arbitrary polynomial objective function, we restrict to linear terms and a set of nested monomials or in a special case one additional monomial of arbitrary degree. Studying the polynomially-solvable matroid optimisation problem, we will show that the corresponding problem with this particular polynomial objective function is solvable in polynomial time (see Remark 2). But although the well-known “separation equals optimisation” result [18] then implies that the separation problem for our problem can be solved in polynomial time, we want to find the exact complete description of the associated linearised polytope and combinatorial separation algorithms for the newly derived cutting planes.

Our main motivation is that this study can also be helpful for (matroid) problems with general linearised polynomial objective functions because the strengthened inequalities for the case with linearised nested monomials usually remain valid for the general case and the respective separation algorithms can be used as well (but in most cases the facet defining inequalities of the case with few linearised monomials will not remain facet defining for the general case). One advantage of our approach in comparison to general linearisation techniques, like the procedure of Sherali and Adams [28, 29], is that we strengthen the constraints of the original linear problem without introducing new variables for non-linear monomials that are not explicitly contained in the objective function.

Focusing on exactly one additional non-linear monomial has first been suggested by Buchheim and Klein [3, 4] for the quadratic case. Results for the spanning tree and forest problem with exactly one additional quadratic monomial can be found in [3, 4, 12]. Buchheim and Klein also showed that the use of strengthened cutting planes can reduce the number of nodes of a branch-and-cut tree in the solution of general quadratic spanning tree problems significantly. Furthermore, bipartite and general matching problems with exactly one quadratic term have been in the focus of research, see [19, 20, 30]. In this paper we extend the results for the quadratic forest problems to general matroid optimisation problems with one monomial of arbitrary degree and to a set of nested monomials to be described below.

In the following we will describe our setting in more detail. We start with a short review of matroids and their associated polytopes [24, 31]. In 1970 Edmonds [10] presented a complete description of the polytope \(P_M\)  associated with a matroid \(M=(E, {\mathcal {I}})\) (the convex hull over all incidence vectors of independent sets) with finite set E and a family \({\mathcal {I}}\) of subsets of E satisfying the three matroid properties

  1. (M1)

    \(\emptyset \in {\mathcal {I}}\),

  2. (M2)

    \(T\in {\mathcal {I}}, S\subset T\) \(\Rightarrow \) \(S\in {\mathcal {I}}\),

  3. (M3)

    \(S,T \in {\mathcal {I}}, |S|<|T|\Rightarrow \exists \,e\in T{\setminus } S\) with \(S\cup \{e\}\in {\mathcal {I}}\).

A pair \(M=(E, {\mathcal {I}})\) satisfying only (M1) and (M2) is called independence system. We denote by \({\mathcal {P}}(X)\) the power set of a finite set X. Then the rank function \(r{:}\,{\mathcal {P}}(E) \rightarrow {\mathbb {N}}_0\) of an independence system \(M=(E, {\mathcal {I}})\) is defined as \(r(T) = \max \{|B|{:}\,B\subseteq T, B\in {\mathcal {I}}\}\). For some \(T\subseteq E\) a set B with \(B\subseteq T, B\in {\mathcal {I}}\) and \(r(T)=|B|\) is called basis (of T). It is well known that the rank function of a matroid has the following properties (see e. g. , [24, 31]):

  1. (R1)

    subcardinality: \(\forall \,X\subseteq E{:}\,r(X) \le |X|\),

  2. (R2)

    monotonicity: \(\forall \,X \subseteq Y \subseteq E{:}\,r(X) \le r(Y)\),

  3. (R3)

    submodularity: \(\forall \,X,Y \subseteq E{:}\,r(X \cap Y) + r(X \cup Y) \le r(X) + r(Y)\).

Furthermore, we will often make use of the following well-known theorem.

Theorem 1

(Brualdi [2], also Strong Basis Exchange Theorem) Let \(S,S'\) be two different bases of a matroid M. Then for any \(e \in S {\setminus } S'\) there is an \(f \in S' {\setminus } S\) so that \((S{\setminus } \{e\})\cup \{f\}\), \((S'{\setminus } \{f\})\cup \{e\}\) are both bases of M.

For further results on matroid theory we refer the reader to the excellent books [24, 31].

Let \(M =(E, {\mathcal {I}})\) be a matroid with rank function \(r{:}\,{\mathcal {P}}(E) \rightarrow {\mathbb {N}}_0\) and \(\bar{E}:=\{e_1, \cdots , e_k\} \subseteq E\), \(|\bar{E}|\ge 2\), be a set with cardinality k. We set \(\bar{E}_{i,j} := \{e_i, \cdots , e_j\}\) for all \(i,j\in \{1, \cdots , k\},i\le j,\) and \(\bar{E}_{1,0}:=\emptyset \). Throughout the paper we assume, w. l. o. g. , that the following conditions are satisfied:

$$\begin{aligned} \forall \; e\in E{:}\,\{e\}\in {\mathcal {I}}\quad {\text {and}}\quad \bar{E}\in {\mathcal {I}}. \end{aligned}$$
(1)

This will allow us to consider full-dimensional polytopes later on. In the following we assume that M is given via a rank oracle where a rank oracle returns the rank r(X) for arbitrary sets \(X\subseteq E\). Furthermore, we use the following notation. Let \(S, T\subseteq E\) and let \(e\in E\). If the meaning is clear from the context, we will often simply write \(S+T\) and \(S-T\) instead of \(S\cup T\) and \(S{\setminus } T\) as well as \(S+e\) and \(S-e\) instead of \(S\cup \{e\}\) and \(S{\setminus } \{e\}\).

We can now state our optimisation problem. Given an index set \(K:=\{k_1, \cdots , k_l\}\subseteq \{2, \cdots , k\}, k_1< \cdots < k_l=k\), that contains the degrees of the (non-linear) nested monomials and cost functions \(c{:}\,E\rightarrow {\mathbb {R}}\) and \(\bar{c}{:}\,K\rightarrow {\mathbb {R}}\) we consider the maximisation problem

figure a

where \(P_M\)  is the polytope that is associated with the matroid M. So \(\bar{E}\) contains all elements of E that belong to some non-linear monomial. Furthermore we set \(k_0:=0\). An important special case of (OPT-K) is the problem

figure b

where \(K=\{k\}\) in (OPT-K) with exactly one non-linear monomial. A visualisation of the structure of the objective function can be found in Fig. 1.

Fig. 1
figure 1

Visualisation of the structure of the objective function of (OPT-K). In this example we have \(E = \{f_1,\ldots , f_8\}\cup \{e_1, \ldots , e_8\},\bar{E}=\{e_1, \ldots , e_8\}\) as well as \(l =4, K=\{2,5,6,8\}\). The elements contained in each ellipse correspond to one of the four non-linear nested monomials

Full size image

Although we are mainly interested in the structure of the associated polytopes, we first note that these problems can be solved in polynomial time. This motivates us by the “separation equals optimisation” result to detect the complete descriptions of the associated linearised polytopes.

Remark 2

The optimisation problem (OPT-K) can be solved in polynomial time.

Proof

We solve (OPT-K) with \(K=\{k_1, \cdots , k_l\}\) in two main steps. First, we consider the l cases that \(\prod _{j=1}^{k_h}x_{e_j}=0\), but \(\prod _{j=1}^{k_{h-1}}x_{e_j}=1\) for \(h\in \{1, \ldots , l\}\). So the contribution of the non-linear monomial is fixed in these cases. For each \(h\in \{1, \cdots , l\}\) we determine a solution \(X^{*}_h \in {\mathcal {I}}\) with \( \bar{E}_{1,k_{h-1}}\subseteq X^{*}_h \), such that not all \(k_h-k_{h-1}\) elements of \(\bar{E}_{k_{h-1}+1,k_h}\) are contained in \(X^{*}_h\) and that has maximum objective value with respect to c. This can be done by solving a matroid intersection problem of matroid M and a matroid \(M_h'=(E, {\mathcal {I}}_h')\) with \({\mathcal {I}}_h'=\{X\subseteq E {:}\,|X\cap \bar{E}_{k_{h-1}+1,k_h}|\le k_h-k_{h-1}-1\}\). The objective value of problem (OPT-K) evaluated for \(X^{*}_h\) equals \(\sum _{e\in X^{*}_h} c(e) + \sum _{j=1}^{h-1} \bar{c}(k_j)\) in this case. Furthermore we solve one additional matroid optimisation problem in order to determine a set \(X^{*}_{l+1}\in {\mathcal {I}}, \bar{E}_{1,k_l} \subseteq X^*_{l+1}\) (so \(\prod _{j=1}^{k_l}x_{e_j}=1\)) such that \(\sum _{e\in X^{*}_{l+1}}c(e)\) is maximised. The objective value of problem (OPT-K) evaluated for \(X^{*}_{l+1}\) is then \(\sum _{e\in X^{*}_{l+1}} c(e) + \sum _{j=1}^l \bar{c}(k_j)\). At the end we take a set \(X_h^*\) with \(h\in \{1, \cdots , l+1\}\) with maximum objective value. \(\square \)

Because (OPT-k) is a special case of (OPT-K) the problem (OPT-k) can be solved by one matroid optimisation and one matroid intersection problem. Alternatively one can solve (OPT-K) by comparing the optimal values of \(k+1\) matroid optimisation problems.

Our aim is to present a complete description of the linearised polytopes

$$\begin{aligned} P_{M}^{\bar{E},K}&:= {{\mathrm{conv}}}\bigg \{ (x,y)\in {\{0,1\}}^{E+K}{:}\,x\in P_M\,, y_{k_j} = \prod _{i=1}^{k_j} x_{e_i}, j=1, \cdots , l\bigg \},\\ P_{M}^{\bar{E},k}&:= {{\mathrm{conv}}}\bigg \{ (x,y)\in {\{0,1\}}^{E+k}{:}\,x\in P_M\,, y = \prod _{i=1}^{k} x_{e_i}\bigg \}. \end{aligned}$$

Note, if \(K=\{k\}\), we often simply write y instead of \(y_k\) or \(y_{k_1}\).

Starting point of our work is a result of Edmonds on the polytope \(P_M\) associated with a matroid M. Before repeating this result we need some notation. For any \(S \subseteq E\) we define the characteristic vector \(\chi ^S \in {\{0, 1\}}^E\) by

$$\begin{aligned} \chi ^S_e = {\left\{ \begin{array}{ll} 1, &{}\quad e \in S,\\ 0, &{}\quad e \notin S, \end{array}\right. } \end{aligned}$$

(in slight abuse of notation, we often do not distinguish between the characteristic vector of an independent set \(J\in {\mathcal {I}}\) and the set J). Then the polytope associated with the matroid M is

$$\begin{aligned} P_M\,= {{\mathrm{conv}}}\left\{ \chi ^S \in {\{0,1\}}^{E} {:}\,S\in {\mathcal {I}}\right\} . \end{aligned}$$

Theorem 3

(Edmonds [10]) Let M be a matroid with rank function \(r{:}\,{\mathcal {P}}(E)\rightarrow {\mathbb {N}}_0\), then

$$\begin{aligned} P_M=\left\{ x\in {\mathbb {R}}^E_+ {:}\,\sum _{e\in T}x_e\le r(T), T\subseteq E \right\} . \end{aligned}$$

The inequalities

$$\begin{aligned} x_T \le r(T), \quad T\subseteq E \end{aligned}$$
(2)

with \(x_T:=\sum _{e\in T} x_e\) are often called rank constraints/inequalities. Together with the non-negativity constraints \(x_e\ge 0, e\in E\), they form a complete description of \(P_M\) . Edmonds also characterised which sets T lead to facet defining inequalities of \(P_M\) , details are given in Sect. 3.

The paper is structured as follows. In Sect. 2 we present complete descriptions of \(P_{M}^{\bar{E},k}\)  and \(P_{M}^{\bar{E},K}\) . A main part of the proof consists of showing that apart from the standard linearisation, i. e. , all constraints that are needed in the unconstrained case (\({\mathcal {I}}={\mathcal {P}}(E)\)) as well, all coefficients of facet defining inequalities \(a^T x + \alpha ^T y \le b\) of the polytopes are non-negative. We start with proving this result for \(P_{M}^{\bar{E},k}\)  and extend this to \(P_{M}^{\bar{E},K}\)  with \(K=\{2, \cdots , k\}\). Based on the complete description in this case, we show that it is possible to derive a complete description of \(P_{M}^{\bar{E},K}\)  for arbitrary sets \(K\subseteq \{2, \cdots , k\}\). In Sect. 3 we study the facetial structure of \(P_{M}^{\bar{E},K}\) . So we have a closer look at the so called trivial facets and give some necessary conditions for some specially lifted rank inequalities to be facet defining for \(P_{M}^{\bar{E},K}\) . For \(P_{M}^{\bar{E},k}\)  we even fully characterise all facets. In Sect. 4 we show that the separation problem for \(P_{M}^{\bar{E},K}\)  can be solved in strongly polynomial time by complete enumeration of the trivial facets and by submodular function minimisation. Finally, in Sect. 5, we describe further possible extensions of our results and give suggestions for future work. Some rather technical proofs are deferred to the “Appendix”.

2 Complete description of \(P_{M}^{\bar{E},K}\) 

In this section we provide a complete description of \(P_{M}^{\bar{E},K}\)  for arbitrary sets \(K\subseteq \{2, \cdots , k\}\). Before we present a formulation of (OPT-K) we need some definitions.

Definition 4

Let \(T \subseteq E\). The closure of set T is the set

$$\begin{aligned} {{\mathrm{cl}}}(T) := T\cup \left\{ e\in E{:}\,r(T)=r(T+e)\right\} . \end{aligned}$$

The set T is called closed if \(T = {{\mathrm{cl}}}(T)\).

Later we will need the following simple result that follows directly from the last definition and the submodularity of the rank function:

Observation 5

Let \(T\subseteq E\) and let \(e\in {{\mathrm{cl}}}(T)\). Then \(r(T+S)=r(T+S+e)\) for all \(S\subseteq E\).

A proof of Observation 5 can be found in the “Appendix”.

We will present strengthened versions of the rank inequalities (2). In order to express the coefficients of the y-variables corresponding to the linearised monomials we introduce the following objects:

Definition 6

For a matroid \(M=(E,{\mathcal {I}})\) with rank function r we define \(\alpha {:}\,{\mathcal {P}}(E) \rightarrow {\mathbb {N}}_0^k\) with \(\alpha (T)=(\alpha _1(T),\ldots , \alpha _k(T))\) for \(T\subseteq E\) where

$$\begin{aligned} \alpha _i(T) := |\{e_i\}{\setminus } T| + r(T+\bar{E}_{1,i-1}) - r(T+\bar{E}_{1,i}), \quad i=1, \cdots , k. \end{aligned}$$

Furthermore we set \(\alpha _0 (T) := 0\) and write \(\alpha _{i,j}(T) := \sum _{m=i}^j \alpha _m(T)\) for \(i,j\in \{1, \ldots , k\}, i\le j\).

The \(\alpha _i(T)\) for some \(T\subseteq E\) can be interpreted in the following way. First, if \(e_i \in T\), then \(\alpha _i(T)=0\), because \(T+\bar{E}_{1,i-1}=T+\bar{E}_{1,i}\). Moreover, if \(e_i\notin T\), then \(\alpha _i(T)=1\) if and only if \(r(T+\bar{E}_{1,i-1})=r(T+\bar{E}_{1,i} )\), i. e. , if and only if the rank does not increase even if the second set strictly contains the first one. Figure 2 illustrates \(\alpha _i(T)\) for some sets \(T\subseteq E\) for the graphical matroid on a complete graph \(G=(V,E)\) with six nodes and \(\bar{E}=\{e_1,e_2,e_3,e_4\}\). The edges of \(T\subset E\) are drawn solid and the edges of \(\bar{E}\) are drawn with dotted lines.

Fig. 2
figure 2

Illustration of \(\alpha (\cdot )\). We consider the graphical matroid on a complete graph \(G=(V,E)\) with six nodes and \(\bar{E}=\{e_1,e_2,e_3,e_4\}\). The edges of \(T\subset E\) are drawn solid and the edges of \(\bar{E}\) are drawn with dotted lines. All other edges are omitted in the picture for the sake of clarity. Note that \(\alpha _1(T)=0\) in all four cases because T is closed

Full size image

The following results follow directly from the definition of \(\alpha _i(\cdot )\).

Observation 7

Let \(T\subseteq E\).

(A1) :

If T is closed, \(\alpha _1(T) = 0\).

(A2) :

We have \(\alpha _{1,j}(T) = |\bar{E}_{1,j}{\setminus } T|+r(T)- r(T+\bar{E}_{1,j})\) for all \(j\in \{1, \cdots , k\}\).

(A3) :

Let \(i\in \{1, \cdots , k\}\) and \(e\in {{\mathrm{cl}}}(T){\setminus } \{e_i\}\). Then \(\alpha _i(T)=\alpha _i(T+e)\).

(A4) :

Let \(i\in \{1, \cdots , k\}\) and \(e_i \in {{\mathrm{cl}}}(T){\setminus } T\). Then \(\alpha _i(T)=1=\alpha _i(T+e_i) + 1\).

We deferred the proof of this result to the “Appendix”.

Studying (OPT-K) we define for each set \(S \subseteq E\) the vector \(y^S=(y_{k_1}^S, \ldots , y_{k_l}^S)\) where the jth (linearised) monomial term of S is defined as

$$\begin{aligned} y_{k_j}^S := \prod \limits _{i=1}^j \chi ^S_{e_i}= {\left\{ \begin{array}{ll} 1, &{}\quad \bar{E}_{1,k_j} \subseteq S,\\ 0, &{}\quad \bar{E}_{1,k_j} \nsubseteq S, \end{array}\right. } \end{aligned}$$

for \(j\in \{1, \cdots , l\}\). Note that for each \(j\in \{1, \ldots , l\}, S\subset E, e\in \bar{E},\) we have \(y_{k_j}^{S-e}\le y_{k_j}^S\) as well as \(y_{k_j}^{S-e}= y_{k_j}^S\) if \(e\in \bar{E}_{k_j+1,k_l}\). So \(P_{M}^{\bar{E},K}\)  can also be written as

$$\begin{aligned} P_{M}^{\bar{E},K}\,= {{\mathrm{conv}}}\left\{ (\chi ^S,y^S)\in {\{0,1\}}^{E+K}{:}\,S\in {\mathcal {I}}\right\} . \end{aligned}$$

With these definitions we are able to give a formulation of (OPT-K):

Lemma 8

A formulation of (OPT-K) is given by:

$$\begin{aligned}&{{\mathrm{maximise}}}\quad \sum _{e\in E} c(e)x_e + \sum _{j=1}^l \bar{c}(k_j)y_{k_j}\nonumber \\&-y_{k_l} \le 0, \end{aligned}$$
(3)
$$\begin{aligned}&y_{k_j} - y_{k_{j-1}} \le 0,\quad j\in \{2, \cdots , l\}, \end{aligned}$$
(4)
$$\begin{aligned}&x_{\bar{E}_{1,k_1}} - y_{k_1} \le k_1-1, \end{aligned}$$
(5)
$$\begin{aligned}&x_{\bar{E}_{k_{j-1}+1,k_j}} + y_{k_{j-1}}- y_{k_j} \le k_j-k_{j-1},\quad j \in \{2, \cdots , l\}, \end{aligned}$$
(6)
$$\begin{aligned}&-x_{e_i}+y_{k_j} \le 0,\quad j \in \{1, \cdots , l\},\quad i\in \{k_{j-1}+1, \cdots , k_j\}, \end{aligned}$$
(7)
$$\begin{aligned}&-x_e \le 0,\quad e \in E{\setminus } \bar{E}, \end{aligned}$$
(8)
$$\begin{aligned}&x_T + \sum _{j=1}^l \alpha _{k_{j-1}+1,k_j} (T) y_{k_j} \le r(T),\quad T \subseteq E,\end{aligned}$$
(9)
$$\begin{aligned}&(x,y) \in {\{0,1\}}^{E+K}. \end{aligned}$$
(10)

Note, we often denote \((y_{k_1}, \ldots , y_{k_l})\) by y.

Proof

Constraints (3)–(7) are the standard linearisation of the non-linear monomials in this case and (8) are the non-negativity conditions for the x-variables. By the integrality conditions (10) and the complete description of the matroid polytope \(P_M\)  in Theorem 3 it remains to show the validity of the strengthened rank inequalities (9). Let \(T \subseteq E\) be an arbitrary set and let \(S\in {\mathcal {I}}\). If \(\bar{E}_{1,k_1}\not \subseteq S\), then the validity follows from the validity of (2) for \(P_M\)  because \(y_{k_j}^S=0\) for all \(j\in \{1, \ldots , l\}\). So let \(\bar{E}_{1,k_i}\subseteq S\) for some \(i\in \{1, \cdots , l\}\) with \(\bar{E}_{1,k_{i+1}} \nsubseteq S\) in the case \(i<l\). Then by (A2) we have

$$\begin{aligned} \sum _{e\in T}\chi ^{S}_e + \sum _{j=1}^l \alpha _{k_{j-1}+1,k_j}(T) y_{k_j}^S&= |S\cap T| + \underbrace{|\bar{E}_{1,k_i}{\setminus } T|+r(T)-r(T\cup \bar{E}_{1,k_i})}_{=\alpha _{1,k_i}(T)} \\ ({\text {by }}(S\cap T)\cap (\bar{E}_{1,k_i}{\setminus } T)=\emptyset )&= | (S\cap T) \cup (\bar{E}_{1,k_i}{\setminus } T)|-r(T\cup \bar{E}_{1,k_i})+r(T) \\ ({\text {by }} S\in {\mathcal {I}}, \bar{E}_{1,k_i}\subseteq S)&= r( (S\cap T) \cup (\bar{E}_{1,k_i}{\setminus } T))-r(T\cup \bar{E}_{1,k_i})+r(T) \\ ({\text {by }} ((S\cap T) \cup (\bar{E}_{1,k_i}{\setminus } T)) \subseteq T\cup \bar{E}_{1,k_i})&\le r(T{\cup } \bar{E}_{1,k_i})-r(T{\cup } \bar{E}_{1,k_i})+r(T) {=} r(T). \end{aligned}$$

\(\square \)

Furthermore, we want to note that the non-negativity constraints of the x- and the y-variables in (3) and (8) are implied by the integrality conditions (10). We included them in the formulation because our aim is to prove that (3)–(9) completely describe the associated polytope.

A visualisation of the extended rank inequalities (9) on the example of a graphical matroid is given in Fig. 3.

Remark 9

With the last result the formulation of (OPT-k) reduces to

$$\begin{aligned}&{{\mathrm{maximise}}}\,\sum _{e\in E} c(e)x_e + \bar{c}(k)y \nonumber \\&x_{\bar{E}} - y \le |\bar{E}| - 1, \end{aligned}$$
(11)
$$\begin{aligned}&-x_e + y \le 0, \quad e \in \bar{E},\end{aligned}$$
(12)
$$\begin{aligned}&x \ge 0,\quad y \ge 0,\end{aligned}$$
(13)
$$\begin{aligned}&x_T + \alpha _{1,k}(T) y \le r (T), \quad T \subseteq E,\\&x,y {\text { binary}}.\nonumber \end{aligned}$$
(14)
Fig. 3
figure 3

Visualisation of the extended rank inequalities (9). We consider the graphical matroid on an undirected graph with six nodes with different sets K for a given \(\bar{E}\). The set T is visualised with bold lines, the edges associated with \(\bar{E}\) with dotted lines. All other edges are omitted in the pictures for the sake of clarity. Note, all sets T are closed, see also Remark 10

Full size image

Remark 10

In the formulation and the complete description of \(P_{M}^{\bar{E},K}\)  and \(P_{M}^{\bar{E},k}\)  it is sufficient to restrict to closed sets \(T\subseteq E\) for the extended rank inequalities (9) and (14), respectively, i. e. ,

$$\begin{aligned} x_T + \sum _{j=1}^l \alpha _{k_{j-1}+1,k_j} (T) y_{k_j} \le r(T),\quad T \subseteq E, {{\mathrm{cl}}}(T)=T, \end{aligned}$$
(15)

for arbitrary sets K and in the case \(K=\{k\}\) we can restrict to

$$\begin{aligned} x_T + \alpha _{1,k} (T) y \le r(T), \quad T\subseteq E, {{\mathrm{cl}}}(T)=T. \end{aligned}$$
(16)

For proving this results, let \(T\subseteq E\) be an arbitrary set. Then we define \(\bar{T} := {{\mathrm{cl}}}(T){\setminus } T\). By (A3) and (A4) we get \(\alpha _i(T)=\alpha _i({{\mathrm{cl}}}(T)) + |\{e_i\}{\setminus } \bar{T}|\) for all \(i=1, \ldots , k\). For this, note that for some arbitrary \(i\in \{1, \ldots , k\}\) we have \(\alpha _i(T)=\alpha _i(T+e)\) for some \(e\in E\) as long as \(e\ne e_i\) and \(\alpha _i(T)=1\) if \(e_i\in \bar{T}\). Let \((\bar{x}, \bar{y})\) be a point that satisfies (3)–(8) as well as (15), then

$$\begin{aligned}&\bar{x}_T + \sum _{j=1}^l \alpha _{k_{j-1}+1,k_j}(T) \bar{y}_{k_j} \\&\quad \le \bar{x}_T + \underbrace{\bar{x}_{\bar{T} \cap \bar{E}} - \sum _{j=1}^l \left| \bar{T}\cap \bar{E}_{k_{j-1}+1, k_j} \right| \bar{y}_{k_j}}_{\ge 0 \text { by }(7)} + \sum _{j=1}^l \alpha _{k_{j-1}+1,k_j}(T) \bar{y}_{k_j} \\&\quad \le \bar{x}_T + \bar{x}_{\bar{T}\cap \bar{E}} + \underbrace{\bar{x}_{\bar{T}{\setminus } \bar{E}}}_{\ge 0 \text { by }(8)} + \sum _{j=1}^l \underbrace{\alpha _{k_{j-1}+1,k_j} ({{\mathrm{cl}}}(T))}_{\begin{array}{c} =\,\alpha _{k_{j-1}+1,k_j}(T)\\ -|\bar{T}\cap \bar{E}_{k_{j-1}+1, k_j}| \end{array}} \bar{y}_{k_j} \\&\quad \le \bar{x}_{{{\mathrm{cl}}}(T)} + \sum _{j=1}^l \alpha _{k_{j-1}+1,k_j} ({{\mathrm{cl}}}(T)) \bar{y}_{k_j} \mathop {\le }\limits ^{(15)} r({{\mathrm{cl}}}(T)) = r(T). \end{aligned}$$

So all extended rank inequalities (9) for non-closed sets \(T\subseteq E\) are implied by (3)–(8) and (15).

In the remaining section we will prove that (3)–(8) and (15) are a complete description of \(P_{M}^{\bar{E},K}\)  and therefore that (11)–(13) and  (16) are a complete description of \(P_{M}^{\bar{E},k}\) . The proof for \(P_{M}^{\bar{E},K}\)  consists of three steps. First, we consider the special case \(K=\{2, \cdots , k\}\). Indeed one can show that then each facet defining inequality of \(P_{M}^{\bar{E},K}\)  that is not a positive multiple of one of (3)–(8) is an inequality of the type \(a^T x + \alpha ^T y \le b\) with \(a\ge 0, \alpha \ge 0\). This result then allows to derive the complete description of \(P_{M}^{\bar{E},K}\)  in this special case. Finally, we consider the complete description of \(P_{M}^{\bar{E},K}\)  for arbitrary sets \(K\subseteq \{2, \cdots , k\}\). In the special case of \(l=2\) and \({\mathcal {I}}={\mathcal {P}}(E)\) (then we have an unconstrained polynomial 0–1 problem) our linearisation of the non-linear monomials leads to a complete description of the associated polytope, which can be found in [6] as well.

We start with an observation about the structure of facet defining inequalities \(a^T x + \alpha ^T y \le b\) of \(P_{M}^{\bar{E},K}\)  that are not a positive multiple of one of (3)–(8). Note, (7) of the standard linearisation and the non-negativity constraints (8) will suffice to prove the desired structural property. Nonetheless will always refer to the whole standard linearisation (and the non-negativity constraints).

Observation 11

Let \(a^T x + \alpha ^T y \le b\) be a facet defining inequality of \(P_{M}^{\bar{E},K}\)  that is not a positive multiple of one of (3)–(8). Then \(a \ge 0\).

Before proving this result we want to mention that in several proofs throughout the paper we use the following well-known result from polyhedral combinatorics. Suppose that \(a^T x +\alpha ^T y \le b\) is a facet-defining inequality of \(P_{M}^{\bar{E},K}\)  that is not a positive multiple of the valid inequality \(\tilde{a}^T x +\tilde{\alpha }^T y \le \tilde{b}\). Then there exists an \(S\in {\mathcal {I}}\) such that \(a^T \chi ^S +\alpha ^T y^S = b\), but \(\tilde{a}^T \chi ^S +\tilde{\alpha }^T y^S < \tilde{b}\).

Proof

Let \(a^T x +\alpha ^T y\le b\) be a facet defining inequality of \(P_{M}^{\bar{E},K}\)  that is not a positive multiple of one of (3)–(8). We consider two cases.

  1. 1.

    \(a (e) < 0\) for some \(e \in E {\setminus } \bar{E}\): Because \(a^T x +\alpha ^T y\le b\) is not a positive multiple of \(x_e \ge 0\) (8), there exists a set \(S \in {\mathcal {I}}\) with \(e \in S\) and \(a^T \chi ^S + \alpha ^T y^S = b\). Assumption \(e \notin \bar{E}\) implies \(y_{k_i}^S = y_{k_i}^{S - e}\) for all \(i\in \{1, \cdots , l\}\), thus \(b=a^T \chi ^{S} + \alpha ^T y^S < a^T \chi ^{S - e} + \alpha ^T y^{S - e}\). This contradicts the validity of \(a^T x +\alpha ^T y\le b\).

  2. 2.

    \(a (e) < 0\) for some \(e=e_i \in \bar{E}\): Because \(a^T x +\alpha ^T y\le b\) is not a positive multiple of \(y_{k_m} \le x_{e_i}\) for \(m\in \{1, \cdots , l\}\) such that \(i\in \{k_{m-1}+1, \cdots , k_m\}\) [see (7)], there exists some \(S \in {\mathcal {I}}\) with \(e \in S\), \(y_{k_m}^S = 0\) and \(a^T \chi ^S + \alpha ^T y^S = b\). With \(0=y_{k_j}^S = y_{k_j}^{S-e}\) for all \(j\in \{m, \cdots , l\}\) and \(y_{k_j}^S = y_{k_j}^{S-e}\) for all \(j\in \{1, \cdots , m-1\}\) by the choice of \(e\in \bar{E}_{k_{m-1}+1,k_m}\), this implies \(b=a^T \chi ^S + \alpha ^T y^S < a^T \chi ^{S - e} + \alpha ^T y^{S-e}\), again a contraction to validity. \(\square \)

Next, we consider the coefficients of the y-variables of facet defining inequalities \(a^T x + \alpha ^T y \le b\). Although the result for \(P_{M}^{\bar{E},k}\)  will be implied by the results for \(P_{M}^{\bar{E},K}\)  we will present next the proof in detail because it is much shorter than in the general case and already shows the main ideas.

Lemma 12

Each facet defining inequality \(a^T x + \alpha y \le b\) of \(P_{M}^{\bar{E},k}\)  that is not a positive multiple of one of (11)–(13) satisfies \(\alpha \ge 0\).

Proof

Let \(a^T x + \alpha y \le b\) be a facet defining inequality of \(P_{M}^{\bar{E},k}\)  that is not a positive multiple of one of (11)–(13). By Observation 11 we may assume \(a \ge 0\). Because \(a^T x + \alpha y \le b\) is not a positive multiple of \(x_{\bar{E}} - y \le |\bar{E}|-1\) [(see (11)] there exists an \(S \in {\mathcal {I}}\) with \(|\bar{E}{\setminus } S| \ge 2\) (so \((\chi ^{\bar{E}})^T\chi ^S_{\bar{E}} - y^S < |\bar{E}|-1\)) and \(a^T \chi ^{S} = b\). Similarly, because \(a^T x + \alpha y \le b\) is not a positive multiple of \(y \ge 0\) [see (13)], there exists an \(S' \in {\mathcal {I}}\) with \(\bar{E}\subseteq S'\) (so \(y^S > 0\)) and \(a^T \chi ^{S'} + \alpha y^{S'}= a^T \chi ^{S'} + \alpha = b\). Set \(T := \{e \in E {\setminus } \bar{E}{:}\,a_e > 0\} \cup (S \cap \bar{E})\). We may assume \(S \subseteq T\) (otherwise we can use the set \(S \cap T\) instead of S because \(a \ge 0\) implies \(a_e = 0\) for all \(e \in S{\setminus } T\) and so \(a^T \chi ^{S} + \alpha y^{S} = a^T \chi ^{S}=a^T \chi ^{S\cap T}= b\) in this case) and \(r(S) = r(T)\) (otherwise there would be an \(e \in T {\setminus } S\) (and so \(e\notin \bar{E}\)) with \(S + e \in {\mathcal {I}}\), implying \(a^T\chi ^{S+e}+\alpha y^{S+e}= a^T\chi ^{S+e}= a^T\chi ^{S} + a_e > a^T\chi ^{S} = b\), a contradiction to the validity of \(a^T x + \alpha y \le b\)). Analogously we may assume \(S' \subseteq T \cup \bar{E}\) (similarly to above we could otherwise use \(S'\cap (T\cup \bar{E})\) instead of \(S'\)) as well as \(r(S') = r(T \cup \bar{E})\) (similarly to above we would otherwise get a contradiction to the validity of \(a^T x + \alpha y \le b\)). We distinguish two cases.

  1. 1.

    \(r(T) < r(T \cup \bar{E})\). Then there exists an \(e \in \bar{E}{\setminus } T\) with \(r(T + e) > r(T) = r(S)\), so \(S + e \in {\mathcal {I}}\) with \(\bar{E}\not \subseteq (S+e)\) by the choice of S. Therefore \( a^T\chi ^{S+e}\le b\) while \(a^T\chi ^{S} = b\). With \(a_e\ge 0\) we get \(a_e = 0\). But since \(y^{S'} = 1\) and \(e \in \bar{E}\subseteq S'\), this implies \(y^{S' - e} = 0\) and so \(a^T\chi ^{S'} = a^T\chi ^{S'-e} \le b = a^T \chi ^{S'} + \alpha \). This proves \(\alpha \ge 0\).

  2. 2.

    \(r(T) = r(T \cup \bar{E})\). By assumption S, \(S'\) are both bases of \(T \cup \bar{E}\). We may assume that \(|S \cap S'|\) is maximum. By Theorem 1 there exists for each \(f \in S'{\setminus } S\) an \(e \in S{\setminus } S'\) so that \(S-e+f, S'+e-f \in {\mathcal {I}}\). Because \(y^{S-e+f}=0\) and \(a^T \chi ^{S-e+f} \le b = a^T \chi ^S\) we get \(a_e \ge a_f\). We choose \(f \in (S'{\setminus } S)\cap \bar{E}\ne \emptyset \), then \(y^{S'+e-f}=0\) and so \(a^T \chi ^{S'+e-f} \le b = a^T \chi ^{S'} + \alpha \) implying \(a_e \le a_f + \alpha \). This proves \(\alpha \ge 0\). \(\square \)

Now, we extend the previous result to \(P_{M}^{\bar{E},K}\)  in the case \(K=\{2, \cdots , k\}\). This is done in three main steps, which make use of the following observation. For further details and the complete, rather technical proofs we refer to the “Appendix”.

Observation 13

Let \(a^T x + \alpha ^T y \le b\) be a facet defining inequality of \(P_{M}^{\bar{E},K}\)  with \(K=\{2, \cdots , k\}\) and let S be a root of it, i. e. , the incidence vector \(\chi ^S\) associated with S satisfies \(a^T \chi ^S + \alpha ^T y^S= b\). Let \(X\subseteq E\). We define

$$\begin{aligned} {{\mathrm{lhs}}}(X) := a^T\chi ^X + \alpha ^T y^{X} \quad {\text { and }}\quad \tilde{a}(X,e) := {{\mathrm{lhs}}}(X) - {{\mathrm{lhs}}}(X-e), e\in X. \end{aligned}$$

Then the following conditions are satisfied:

  1. (i)

    for all \(e \in S{:}\,\tilde{a}(S,e) \ge 0\),

  2. (ii)

    for all \(e \notin S\) with \(S+e \in {\mathcal {I}}{:}\,\tilde{a}(S+e,e) \le 0\),

  3. (iii)

    for all \(e \in S, f \notin S\) with \(S-e+f \in {\mathcal {I}}{:}\,\tilde{a}(S,e) \ge \tilde{a}(S-e+f,f)\).

Proof

Immediately clear because otherwise \(a^T x + \alpha ^T y \le b\) would not be valid for the sets \(S-e\), \(S+e\) or \(S-e+f\), respectively. \(\square \)

First one can show that for each facet defining inequality of \(P_{M}^{\bar{E},K}\)  (\(K=\{2, \cdots , k\}\)) there exists a root with a certain structure.

Lemma 14

Let \(a^T x +\alpha ^T y \le b \) be a facet defining inequality of \(P_{M}^{\bar{E},K}\)  with \(K=\{2, \cdots , k\}\) that is not a positive multiple of one of (3)–(8) and let \(m \in \{2, \cdots , k\}\). Then there exists a root S of \(a^T x +\alpha ^T y \le b \) with the structure

$$\begin{aligned} \bar{E}_{1,m} {\setminus } \{e_j,e_m\} = S \cap \bar{E}_{1,m} {\text { for some }}j \in \left\{ 1, \cdots , m-1\right\} . \end{aligned}$$

Lemma 14 implies the non-negativity of particular sums of coefficients of facet defining inequalities satisfying certain structures:

Lemma 15

Let \(a^T x+\alpha ^T y\le b\) be a facet defining inequality of \(P_{M}^{\bar{E},K}\)  with \(K=\{2, \cdots , k\}\) that is not a positive multiple of one of (3)–(8). Let \(m \in \{2, \cdots , k\}\) so that there is a root S of \(a^T x+\alpha ^T y\le b\) satisfying \(S \cap \bar{E}_{1,m} = \bar{E}_{1,m} {\setminus } \{e_j,e_m\}\) for some \(j \in \{1, \cdots , m-1\}\). Then \(\alpha _m + \cdots + \alpha _h \ge 0\) for all \(h \in \{m, \cdots , k\}\) with \(h=k\) or with \(e_{h+1} \notin S\).

This leads to the following result.

Lemma 16

Let \(a^T x + \alpha ^T y\le b\) be a facet defining inequality of \(P_{M}^{\bar{E},K}\)  with \(K=\{2, \cdots , k\}\) that is not a positive multiple of one of (3)–(8). Then \(\alpha _m + \cdots + \alpha _h \ge 0\) for all \(m,h \in \{2, \cdots , k\}\), \(m \le h\).

The following corollary summarises Observation 11, Lemmas 15 and 16.

Corollary 17

Let \(a^T x + \alpha ^T y \le b\) be a facet defining inequality of \(P_{M}^{\bar{E},K}\)  with \(K=\{2, \cdots , k\}\), that is not a positive multiple of one of (3)–(8). Then \(a \ge 0\) and \(\alpha \ge 0\).

Proof

Let \(a^T x + \alpha ^T y \le b\) be a facet defining inequality of \(P_{M}^{\bar{E},K}\)  with \(K=\{2, \cdots , k\}\) satisfying the requirements. Then \(a \ge 0\) follows from Observation 11 and \(\alpha \ge 0\) follows from Lemma 16 for \(m=h\). \(\square \)

This allows us to prove our main result for \(P_{M}^{\bar{E},K}\)  in the case \(K=\{2, \cdots , k\}\).

Theorem 18

The inequalities (3)–(8) and (15) are a complete description of \(P_{M}^{\bar{E},K}\) , \(K=\{2, \cdots ,k\}\).

Proof

Let \(a^T x + \alpha ^T y \le b\) be a facet defining inequality of \(P_{M}^{\bar{E},K}\) , \(K=\{2, \cdots , k\}\), that is not a positive multiple of one of (3)–(8) and (15). Then Corollary 17 implies \(a \ge 0\) and \(\alpha \ge 0\). Let \(T' := \{ e \in E {:}\,a_e > 0 \}\) and \(T := {{\mathrm{cl}}}(T')\).

If we can prove for some \(S \in {\mathcal {I}}\) with \(a^T \chi ^S + \alpha ^T y^S = b\) that there exists an \(e \in T' {\setminus } S\) so that \(S + e \in {\mathcal {I}}\), then \(a^T \chi ^{S + e} + \alpha ^T y^{S+e} > a^T \chi ^S + \alpha ^T y^S = b\), hence the inequality would not be valid, a contradiction. We distinguish two cases.

We consider the constraint (15) associated with T. Because \(a^T x + \alpha ^T y \le b\) is not a positive multiple of this constraint, there exists an \(S \in {\mathcal {I}}\) with \(\sum _{e\in T}\chi ^S_e + \sum _{j=1}^l \alpha _{k_{j-1}+1,k_j}{(T)} y_{k_j}^S < r (T)\) and \(a^T \chi ^S + \alpha ^T y^S = b\). In particular, \(r (S \cap T) =\sum _{e\in T} \chi ^S_e\) implies

$$\begin{aligned} r (S \cap T) + \sum _{j=1}^l \alpha _{k_{j-1}+1,k_j}{(T)} y_{k_j}^S < r (T). \end{aligned}$$
(17)

Let \(\hat{\imath } \in \{1, \cdots , k\}\) be maximum so that \(y_i = 1 \,\Leftrightarrow \, i \le \hat{\imath }\) (\(\hat{\imath }=1\) means that \(\bar{E}_{1,2}\not \subseteq S\)). Note that \(\hat{\imath } > 1\) implies \(\bar{E}_{1,\hat{\imath }} \subseteq S\) and \(\hat{\imath } < k\) implies \(\bar{E}_{1,\hat{\imath }+1} \nsubseteq S\) as well. We first consider the case \(\hat{\imath }> 1\). Then we may assume \(S \subseteq T' \cup \bar{E}_{1,\hat{\imath }}\) (otherwise use \(\bar{S} := S \cap (T' \cup \bar{E}_{1,\hat{\imath }})\) with \(a^T \chi ^{\bar{S}} + \alpha ^T y^{\bar{S}} = a^T \chi ^S + \alpha ^T y^{S} = b\)). Note that \(\alpha ^T y^{S} = \alpha _{1,\hat{\imath }}(T)\), so (17) and (A2) imply \(r(S \cap T) < r(T \cup \bar{E}_{1,\hat{\imath }}) - |\bar{E}_{1,\hat{\imath }} {\setminus } T|\). Therefore

$$\begin{aligned} r(S)&= r(S \cap T) + |S {\setminus } T| < r(T \cup \bar{E}_{1,\hat{\imath }}) \underbrace{- |\bar{E}_{1,\hat{\imath }} {\setminus } T| + |S {\setminus } T|}_{=0 {\text { by }}\bar{E}_{1,\hat{\imath }}\subseteq S\subseteq T\cup \bar{E}_{1,\hat{\imath }} } \\&= r(T \cup \bar{E}_{1,\hat{\imath }}) = r(T' \cup \bar{E}_{1,\hat{\imath }}). \end{aligned}$$

Here the last equation follows from Observation 5. So there exists an \(e \in (T' \cup \bar{E}_{1,\hat{\imath }}) {\setminus } S = T' {\setminus } S\) with \(S + e \in {\mathcal {I}}\), which contradicts the validity of \(a^T x + \alpha ^T y \le b\).

It remains to consider the case \(\hat{\imath }=1\). But then \(y^S=0\) and we know with \(S':=S\cap T'\) that \(r(S')\le r(S\cap T)< r(T)=r(T')\) by (17). Hence there exists an \(e\in T'{\setminus } S'\) with \(S'+e\in {\mathcal {I}}\), a contradiction. \(\square \)

Remark 19

If we consider (OPT-k), i. e. , (OPT-K) with \(K=\{k\}\), the proof of Theorem 18 in combination with Lemma 12 also shows that (11)–(13) and (16) define a complete description of \(P_{M}^{\bar{E},k}\)  because setting \(\hat{\imath }=k\) implies \(\alpha _{1,k}(T) = \sum _{j=1}^{\hat{\imath }} \alpha _j(T)\).

In our last step we extend the previous results to the complete description of \(P_{M}^{\bar{E},K}\)  with arbitrary \(K=\{k_1, \cdots , k_l\} \subseteq \{2, \cdots , k\}\).

Theorem 20

Inequalities (3)–(8) and (15) are a complete description for \(P_{M}^{\bar{E},K}\)  with arbitrary set \(K=\{k_1, \cdots , k_l\}\subseteq \{2, \cdots , k\}\).

Proof

We prove this result by induction. We know that (3)–(8) and (15) are a complete description for \(P_{M}^{\bar{E},K}\)  if \(K=\{2, \cdots , k\}\).

Let \(j \in \{1, \cdots , l\}\) so that either \(j \ge 2\) and \(k_j - k_{j-1} \ge 2\) or \(j=1\) and \(k_1 > 2\). Set

$$\begin{aligned} \hat{k} := {\left\{ \begin{array}{ll} k_{j-1}+1, &{}\quad j \ge 2, \\ 2, &{}\quad j = 1. \end{array}\right. } \end{aligned}$$

It will be convenient throughout the proof to identify formally \(\bar{y}_1 := x_{e_1}\). We show that the complete description for K can be derived from the complete description for \(P_M^{\bar{E},K'}\) with \(K'=K\cup \{\hat{k}\}\). For this note that our aim is to prove that a point \((\bar{x}, \bar{y})\) satisfying (3)–(8) as well as (15) for (OPT-K) can be written as a convex combination of incidence vectors (x- and y-part) of independent sets of M. The idea is now to extend \((\bar{x}, \bar{y})\) by one entry that corresponds to the one extra variable in \(K'\). If the enlarged vector is feasible for \(P_M^{\bar{E},K'}\), then the complete description for \(P_M^{\bar{E},K'}\) yields a convex combination of incidence vectors (x- and y-part) of independent sets. Deleting the extra component of these vectors then yields the desired convex combination for \(P_M^{\bar{E},K}\).

Let \((\bar{x}, \bar{y})\) be a point that satisfies (3)–(8) as well as (15) for (OPT-K). We want to extend \((\bar{x}, \bar{y})\) by component \(\bar{y}_{\hat{k}}\) in order to get a feasible point \((\bar{x}, \hat{y}) := (\bar{x}, \bar{y}_{k_1}, \cdots , \bar{y}_{k_{j-1}}, \bar{y}_{\hat{k}}, \bar{y}_{k_j}, \cdots , \bar{y}_{k_l}) \in P_M^{\bar{E},K'}\). Indeed, we prove next that \(\bar{y}_{\hat{k}} = \max \{\bar{y}_{k_j},\bar{y}_{\hat{k}-1} + \bar{x}_{e_{\hat{k}}} - 1\}\) leads to a feasible point.

Case 1 :

If \(\bar{y}_{\hat{k}-1} + \bar{x}_{e_{\hat{k}}} \le 1 + \bar{y}_{k_j}\) we set \(\bar{y}_{\hat{k}} := \bar{y}_{k_j}\). Then (6) is satisfied. It remains to check if the point \((\bar{x},\hat{y})\) is feasible for \(P_M^{\bar{E},K'}\), because then the desired statement immediately follows from the complete description of the known case. Constraints (3)–(8) are satisfied by assumption, by the feasibility of \((\bar{x}, \bar{y})\) for (OPT-K) and by the fact that \(\bar{x}_e\le 1, e\in E\) [by (15)]. For (15) with \(T\subseteq E\), T closed, we just split \(\alpha _{\hat{k},k_j}(T)\bar{y}_{k_j}\) into \(\alpha _{\hat{k},\hat{k}}(T)\bar{y}_{\hat{k}} + \alpha _{\hat{k}+1,k_j}(T)\bar{y}_{k_j}\) (note, in the case \(\hat{k}=2\) the coefficient of \(\bar{y}_{\hat{k}}\) is \(\alpha _{1,\hat{k}}(T)\), but T closed implies \(\alpha _1(T)=0\) and so \(\alpha _{1,\hat{k}}(T)=\alpha _{\hat{k},\hat{k}}(T)\)).

Case 2 :

Otherwise we set \(\bar{y}_{\hat{k}} := \bar{y}_{\hat{k}-1} + \bar{x}_{e_{\hat{k}}} - 1 > \bar{y}_{k_j}\). Then the point \((\bar{x}, \hat{y})\) might possibly violate (15) of the formulation of \(P_M^{\bar{E}, K'}\). All other constraints of the formulation of \(P_M^{\bar{E},K'}\) [(3)–(8)] remain satisfied by this definition of \(\bar{y}_{\hat{k}}\), either trivially or because

$$\begin{aligned} \quad \sum _{i=\hat{k}+1}^{k_j} \bar{x}_{e_i} {+} \underbrace{\bar{x}_{e_{\hat{k}}} {+} \bar{y}_{\hat{k}-1}}_{=\bar{y}_{\hat{k}}+1} \le \bar{y}_{k_j}{+}k_j{-}k_{j-1} \;{\Leftrightarrow } \; \sum _{i=\hat{k}+1}^{k_j} \bar{x}_{e_i} + \bar{y}_{\hat{k}} \le \bar{y}_{k_j} + (k_j - \hat{k}). \end{aligned}$$

Let \(T \subseteq E\), \({{\mathrm{cl}}}(T) = T\), (see also Remark 10) be a closed set and consider the associated rank constraint (15). If \(\alpha _{\hat{k}}(T) = 0\), then the validity of this rank constraint for \(P_M^{\bar{E},K'}\) follows directly from the validity of the associated rank constraint for \(P_{M}^{\bar{E},K}\) . So we may assume \(\alpha _{\hat{k}}(T) = 1\). This implies \(r(T+\bar{E}_{1,\hat{k}-1})=r(T+\bar{E}_{1,\hat{k}})\) and with \(T' := T+e_{\hat{k}}\)

$$\begin{aligned}&\alpha _{1,m} (T') {-} \alpha _{1,m}(T)=1{-}r(T'+\bar{E}_{1,m})+r(T{+}\bar{E}_{1,m}) \ge 0, m=1, \cdots , \hat{k}-1,\nonumber \\&\alpha _{1,\hat{k}-1}(T') {-} \alpha _{1,\hat{k}-1}(T){=}1 {-} r(T{+}\bar{E}_{1,\hat{k}}){+}r(T{+}\bar{E}_{1,\hat{k}-1}) {=} 1. \end{aligned}$$
(18)

Let us define \(\gamma _i := \bar{y}_{k_i} - \bar{y}_{k_{i+1}}\ge 0\) for \(i=1, \cdots ,j-2\). Then we can write \(\bar{y}_{k_i}=\bar{y}_{\hat{k}-1}+\sum _{m=i}^{j-2} \gamma _m\) by the definition of \(\hat{k}\) and using the method of differences. Using these relations we get for the rank constraint associated with T for \(K'\)

$$\begin{aligned}&\qquad \bar{x}_T + \sum _{i=1}^{j-1} \alpha _{k_{i-1}+1,k_i}(T) \bar{y}_{k_i} + \underbrace{\alpha _{\hat{k}}(T)}_{=1}\bar{y}_{\hat{k}} + \underbrace{\alpha _{\hat{k}+1,k_j}(T)}_{=\alpha _{\hat{k}+1,k_j}(T')} \bar{y}_{k_j} + \sum _{i=j+1}^l \underbrace{\alpha _{k_{i-1}+1,k_i}(T)}_{=\alpha _{k_{i-1}+1,k_i}(T')} \bar{y}_{k_i} \\&\qquad = \bar{x}_T+\underbrace{\alpha _{1,\hat{k}-1}(T)}_{= \alpha _{1,\hat{k}-1}(T')-1} \bar{y}_{\hat{k}-1} + \sum _{i=1}^{j-2} \underbrace{\alpha _{1,k_i}(T)}_{\le \alpha _{1,k_i}(T')}\gamma _i + \bar{y}_{\hat{k}} + \underbrace{\alpha _{\hat{k}+1,k_j}(T')}_{=\alpha _{\hat{k},k_j}(T')}\bar{y}_{k_j}\\&\qquad \quad + \sum _{i=j+1}^{l}\alpha _{k_{i-1}+1,k_i}(T') \bar{y}_{k_i} \end{aligned}$$

and using \(\bar{y}_{\hat{k}} = -\bar{y}_{\hat{k}-1} + \bar{x}_{e_{\hat{k}}} - 1\) and the definition of the \(\gamma _{\bullet }\)

$$\begin{aligned}&\le \bar{x}_{T'} + \sum _{i=1}^l \alpha _{k_{i-1}+1,k_i}(T') \bar{y}_{k_i} - 1 \\&\le \bar{x}_{{{\mathrm{cl}}}(T')} + \sum _{i=1}^l \alpha _{k_{i-1}+1,k_i}({{\mathrm{cl}}}(T')) \bar{y}_{k_i} - 1 \le r({{\mathrm{cl}}}(T')) - 1 = r(T). \end{aligned}$$

For the last step we used that each rank constraint associated with \(T'\) is always dominated by the rank constraint associated with \({{\mathrm{cl}}}(T')\) by Remark 10. So the result follows again by the known complete description of \(P_M^{\bar{E},K'}\). \(\square \)

So the complete description of \(P_{M}^{\bar{E},K}\)  for arbitrary sets \(K\subseteq \{2, \cdots ,k\}\) can easily be derived from the complete description of \(P_M^{\bar{E}, K'}\) with \(K'=\{2, \cdots , k\}\) by adapting the constraints of the standard linearisation and by adjusting the extended rank inequalities. Indeed, the coefficient of \(y_{k_j}, k_j\in K\), equals the sum of the coefficients of variables \(y_i, i=k_{j-1}+1, \cdots , k_j,\) in the problem with \(K'\). Although feasibility of the extended rank inequalities is trivially preserved by this approach, it is remarkable that we even get the complete description of \(P_{M}^{\bar{E},K}\)  in this way.

3 Facetial structure of \(P_{M}^{\bar{E},K}\)  and \(P_{M}^{\bar{E},k}\) 

The polytope \(P_M\)  of some matroid M is well-understood. In 1970 Edmonds [10] presented a complete description of \(P_M\)  and characterised its facetial structure, see also [17]. We will extend these results to the polytopes \(P_{M}^{\bar{E},k}\)  and \(P_{M}^{\bar{E},K}\)  and study their facetial structures in more detail. This includes the dimension of the polytopes as well as results on the facetness of the constraints of the standard linearisation. Furthermore, we have a closer look at the extended rank inequalities (9). If a closed set T does not satisfy certain non-separability conditions (to be defined below) the associated rank inequality cannot be facet defining for \(P_{M}^{\bar{E},K}\) . For \(P_{M}^{\bar{E},k}\)  we even exactly characterise the facet defining inequalities and provide a minimal description.

We start with studying the dimension and the trivial facets of \(P_{M}^{\bar{E},K}\) . One can easily prove the following result:

Observation 21

Under the assumptions (1) the polytope \(P_{M}^{\bar{E},K}\)  is full-dimensional. The inequalities (3)–(8) define facets of \(P_{M}^{\bar{E},K}\) .

Details of the proof are deferred to the “Appendix”. Recent studies on the facial structure of linearisations of unconstrained 0–1 polynomial optimisation problems can be found, e. g. , in [6, 8].

In the next step we consider the extended rank inequalities (14). These are extensions of the rank inequalities (2). Before repeating results on the facetness of (2) for \(P_M\)  we need a definition, which will be extended to our setting later on.

Definition 22

Let \(T\subseteq E\). A set T is called separable if there exists a partition \(T_1,T_2\subsetneq T, T_1\cup T_2=T, T_1\cap T_2=\emptyset \) such that \(r(T_1)+r(T_2) = r(T)\), otherwise it is called non-separable.

Indeed, all closed and non-separable sets \(T\subseteq E\) lead to facet defining rank inequalities (2) of \(P_M\)  [10, 17]. The next proposition shows that they also lead to facet defining inequalities (9) of \(P_{M}^{\bar{E},K}\)  whenever \(\alpha _{k_{j-1}+1,k_j}(T) > 0\) for all \(j\in \{1, \ldots , l\}\).

Proposition 23

Let \(T\subseteq E\) be a closed and non-separable set associated with a facet defining inequality (2) of \(P_M\) . If \(\alpha _{k_{j-1}+1,k_j}(T) > 0\) for all \(j\in \{1, \ldots , l\}\), then the inequality (9) is facet defining for \(P_{M}^{\bar{E},K}\) , too.

Proof

Because \(x_T \le r(T)\) is facet defining for \(P_M\)  there exist \(d := \dim P_M\,\) affinely independent \(S_i \in {\mathcal {I}}\), \(S_i \subseteq T\) with \(r(S_i)=r(T)\) for \(i=1, \cdots , d\). By our assumption \(\alpha _{k_{j-1}+1,k_j}(T) > 0\) for all \(j\in \{1, \ldots , l\}\), we know \(\bar{E}_{k_{j-1}+1,k_j}\nsubseteq T\) for all \( j\in \{1, \ldots , l\}\), hence \(\bar{E}_{k_{j-1}+1,k_j} \nsubseteq S_i\) for all \(i \in \{1, \cdots , d\}, j\in \{1, \ldots , l\}\). If we choose for each \(j\in \{1, \ldots , l\}\) a set \(\hat{S}_j \in {\mathcal {I}}\) satisfying the two properties \(\bar{E}_{1,k_j} \subseteq \hat{S}_j \subseteq T + \bar{E}_{1,k_j}\) and \(|\hat{S}_j| = r(\hat{S}_j) = r(T + \bar{E}_{1,k_j})\) (such a set exists because we can extend \(\bar{E}_{1,k_j}\) to a basis of \(T + \bar{E}_{1,k_j}\) for each \(j\in \{1, \ldots , l\}\)), the left-hand side of

$$\begin{aligned} \chi ^{\hat{S}_j}_T + \sum _{\hat{\imath }=1}^l \alpha _{k_{\hat{\imath }-1}+1,k_{\hat{\imath }}}(T) y_{k_{\hat{\imath }}}^{\hat{S}_j} \le r(T) \end{aligned}$$

computes to

$$\begin{aligned} r(\hat{S}_j \cap T) + \alpha _{1,k_j}(T)&= r(T + \bar{E}_{1,k_j}) - |\hat{S}_j {\setminus } T| + \alpha _{1,k_j}(T)\\&= r(T + \bar{E}_{1,k_j}) - |\bar{E}_{1,k_j} {\setminus } T| + \alpha _{1,k_j}(T) = r(T) \end{aligned}$$

by (A2). So there exist \(d+l\) affinely independent sets that are roots of (9), which proves the statement. \(\square \)

Considering the first type of extended subtour elimination constraints (constraints (5) in [4]) for the spanning forest problem with one linearised quadratic monomial in [4], the facetness of these inequalities follows directly from the previous result. But as already observed by Buchheim and Klein [4] for this problem (see constraints (6) in [4]), not all facet defining inequalities of \(P_{M}^{\bar{E},K}\)  are directly related to facet defining inequalities of \(P_M\) . So we need further properties that allow us to describe the facetial structure of \(P_{M}^{\bar{E},K}\) .

Definition 24

Let \(T \subseteq E\) be closed and \(K=\{k_1, \cdots , k_l\}\subset \{2, \cdots , k\}\). A set T is called \((\bar{E},K)\)-separable if there exists a partition \(T_1, T_2 \subsetneq T\), \(T_1 \cap T_2 = \emptyset \), \(T_1 \cup T_2 = T\) with

$$\begin{aligned} r(T)&= r(T_1) + r(T_2), \;{\text { and }}\; \alpha _{k_{j-1}+1,k_j}(T) = \alpha _{k_{j-1}+1,k_j}(T_1) +\alpha _{k_{j-1}+1,k_j}(T_2), \nonumber \\&j=1, \cdots , l, \end{aligned}$$
(19)

otherwise it is called \((\bar{E},K)\)-non-separable.

Note, the definition of separability by Edmonds [10] only included the first equation of the last definition (see Definition 22). A visualisation of the new setting is given in Fig. 4.

Fig. 4
figure 4

Visualisation of \((\bar{E},K)\)-(non)-separability. We consider the graphical matroid on an undirected graph with four nodes. Although set T (bold lines) is the same on both sides, depending on \(\bar{E}\) (dotted lines), it is \((\bar{E},\{2\})\)-separable or not. Note, T is separable with \(T_1=\{f_1\}, T_2=\{f_2\}\) by Definition 22

Full size image

A closed set \(T\subseteq E\) that is \((\bar{E},K)\)-separable does not lead to a facet defining rank inequality (9) of \(P_{M}^{\bar{E},K}\) .

Observation 25

Let (9) be a facet defining inequality of \(P_{M}^{\bar{E},K}\)  associated with a closed set \( T\subseteq E\). Then T is \((\bar{E},K)\)-non-separable.

Proof

Let \(T\subseteq E\) be closed and assume that T is \((\bar{E},K)\)-separable with partition \(T_1,T_2\subsetneq T, T_1\cap T_2=\emptyset , T_1\cup T_2=T\) satisfying (19). Then we can derive (9) by adding the two rank inequalities (9) for \(T_1,T_2\):

$$\begin{aligned} \underbrace{x_{T_1}+x_{T_2}}_{=x_T} + \sum _{j=1}^l \underbrace{(\alpha _{k_{j-1}+1,k_j}(T_1) + \alpha _{k_{j-1}+1,k_j}(T_2))}_{=\alpha _{k_{j-1}+1,k_j}(T)}y_{k_j} \le r(T). \end{aligned}$$

So the extended rank inequality associated with T does not define a facet of \(P_{M}^{\bar{E},K}\) . \(\square \)

However, not all \((\bar{E},K)\)-non-separable sets \(T\subseteq E\) lead to facet defining rank inequalities (9). This may depend on the structure of K as well. If, for instance, \(k_{j-1},k_j\in K\) with \(k_{j-1}+1=k_j\), then the inequality \(x_{e_{k_j}}\le 1\) can be derived by adding \(-y_{k_{j-1}}+y_{k_j}\le 0\) and \(y_{k_{j-1}}+x_{e_{k_j}}-y_{k_j}\le 1\) [see also property \((\mathbf{P1}^k)\) to be defined below for the case \(K=\{k\}\)].

In the following we will fully characterise the facetial structure of \(P_{M}^{\bar{E},k}\) . We start with some easy results that follow directly from the definition of \((\bar{E},\{k\})\)-separability. The proofs of all three following observations can be found in the “Appendix”.

Observation 26

Let \(T\subseteq E\) be a closed set with \(|T| \ge 2\).

  1. 1.

    If \(T \subseteq \bar{E}\), then T is \((\bar{E},\{k\})\)-separable.

  2. 2.

    If \(\alpha _{1,k}(T{\setminus } \bar{E})=0\) and \(\bar{E}\cap T \ne \emptyset \), then T is \((\bar{E},\{k\})\)-separable.

In addition to closedness and \((\bar{E},\{k\})\)-non-separability it will turn out that a set \(T\subseteq E\) leading to facet defining extended rank inequalities (14) has to satisfy the following properties:

Definition 27

Let \(T\subseteq E\) be a closed and \((\bar{E},\{k\})\)-non-separable set. We say it satisfies properties

\((\mathbf{P1}^k)\) :

if \(\bar{E}\nsubseteq T\) and if in the case \(|\bar{E}|=2\) additionally \(T\ne \{e\}, e\in \bar{E}\),

\((\mathbf{P2}^k)\) :

if \(\bar{E}\subseteq T\) and \(\alpha _{1,k}(T {\setminus } \bar{E}) \ge 2\).

These properties are necessary conditions that a set \(T\subseteq E\) leads to a facet defining rank inequality (14) of \(P_{M}^{\bar{E},k}\) .

Observation 28

Let \(T\subseteq E\) be a closed and \((\bar{E},\{k\})\)-non-separable set. If the rank inequality associated with T is facet defining for \(P_{M}^{\bar{E},k}\) , then it satisfies either \((\mathbf{P1}^k)\) or \((\mathbf{P2}^k)\).

Next we will prove that for a set \(T\subseteq E\) closedness, \((\bar{E},\{k\})\)-non-separability and properties \((\mathbf{P1}^k)\), \((\mathbf{P2}^k)\) lead to facetness of the associated inequality (14). In the proof of this result we need the following observation:

Observation 29

Let \(T\subseteq E\) be a closed set with \(\bar{E}\subseteq T\). If \(\alpha _{1,k}(T{\setminus } \bar{E})\ge 2\), then there exists a basis B of T such that \(|B\cap \bar{E}| \le |\bar{E}|-2\).

Lemma 30

Let \(T \subseteq E\) be a closed and \((\bar{E},\{k\})\)-non-separable set satisfying properties \((\mathbf{P1}^k)\) or \((\mathbf{P2}^k)\). Then the extended rank inequality (14) defines a facet of \(P_{M}^{\bar{E},k}\) .

Proof

Let \(T \subseteq E\) be a closed, \((\bar{E},\{k\})\)-non-separable set satisfying  \((\mathbf{P1}^k)\) or \((\mathbf{P2}^k)\). Further we assume that \(a^T x + \bar{a} y \le b\) is a facet defining inequality of \(P_{M}^{\bar{E},k}\)  so that \(a^T \chi ^S + \bar{a} y^S = b\) whenever S is a root of \(x_T+\alpha _{1,k}(T)y\le r(T)\), the extended rank constraint associated with T. We will show that in this case \(a^T x + \bar{a} y \le b\) is a positive multiple of \(x_T+\alpha _{1,k}(T)y\le r(T)\). Our proof consists of four main steps.

Claim 1

Under the given assumptions the constraints (14) are not implied by the constraints of the standard linearisation (see Observation 21).

Proof of Claim 1

In order to prove that \(x_T+\alpha _{1,k}(T)y\le r(T)\) is not implied by (11)–(13) we can easily determine in each of the cases an independent set \(J\in {\mathcal {I}}\) such that J is a root of the rank inequality (14), but J is not a root of one of (11)–(13). Technical details can be found in the “Appendix”.

So by Lemma 12 we know that \(a\ge 0, \bar{a}\ge 0\). Next we prove the following:

Claim 2

A coefficient \(a_e, e\in E\), or \(\bar{a}\) is zero if the corresponding coefficient in \(x_T+\alpha _{1,k}(T)y\le r(T)\) is zero.

Proof of Claim 2

Assume, for a contradiction, \(a_e > 0\) for some \(e \notin T\). Let S be a basis of T. Then S is a root of \(x_T+\alpha _{1,k}(T)y\le r(T)\) and consequently of \(a^T x + \bar{a} y \le b\), too. Because T is closed \(S + e \in {\mathcal {I}}\), but \(S + e\) violates \(a^T x + \bar{a} y \le b\), a contradiction.

Now assume the coefficient \(\alpha _{1,k}(T)\) of y is zero in \(x_T+\alpha _{1,k}(T)y\le r(T)\), i. e. ,

$$\begin{aligned} r(T)+|\bar{E}{\setminus } T|=r(T + \bar{E}) \end{aligned}$$
(20)

by (A2). First, if \(\bar{E}\nsubseteq T\), we choose a basis B of T with \((T\cap \bar{E})\subseteq B\). Then by (20) we know \(B+(\bar{E}{\setminus } T)\in {\mathcal {I}}\) and this independent set is also a root of \(x_T+\alpha _{1,k}(T)y\le r(T)\). However, because \(y^{B+(\bar{E}{\setminus } T)}=1\) it follows \(\bar{a}=0\). Second, let \(\bar{E}\subset T\). Let \(\bar{B}\) be a basis of T with \(\bar{E}\subseteq \bar{B}\). Furthermore, by assumption \((\mathbf{P2}^k)\) we may apply Observation 29, and find a basis B of T with \(|B \cap \bar{E}| \le |\bar{E}| - 2\). So there exist two elements \(e_i,e_j \in (\bar{B} {\setminus } B) \cap \bar{E}, i\ne j\). Because M is a matroid there exists an \(f_i \in B {\setminus } \bar{B} \subseteq B {\setminus } \bar{E}\) with \(\bar{B} - e_i + f_i \in {\mathcal {I}}\) and an \(f_j \in B {\setminus } (\bar{B} - e_i + f_i) \subseteq B {\setminus } \bar{E}\) with \(\bar{B} - e_i - e_j + f_i + f_j \in {\mathcal {I}}\). Note that all three sets \(\bar{B}\), \(\bar{B} - e_i + f_i\), \(\bar{B} - e_i - e_j + f_i + f_j\) are bases of T and define roots of \(x_T+\alpha _{1,k}(T)y\le r(T)\). In particular, this implies \(a_{e_i} + \bar{a} = a_{f_i}\) and \(a_{e_j} = a_{f_j}\). Submodularity gives

$$\begin{aligned} \underbrace{r(\bar{B} - e_j)}_{=r(T)-1} + \underbrace{r(\bar{B} - e_j + f_i + f_j)}_{=r(T)} \le r(\bar{B} - e_j + f_j) + r(\bar{B} - e_j + f_i), \end{aligned}$$

so at least one of \(\bar{B} - e_j + f_j\), \(\bar{B} - e_j + f_i\) is a basis of T. If \(\bar{B} - e_j + f_j\) is a basis then comparing with \(\bar{B} - e_i - e_j + f_i + f_j\) shows \(a_{e_i} = a_{f_i}\), hence \(\bar{a} = 0\). Otherwise, if \(\bar{B} - e_j + f_j\) is not a basis but \(\bar{B} - e_j + f_i\) is a basis, we have similarly \(a_{e_i} = a_{f_j}\) and submodularity implies

$$\begin{aligned} \underbrace{r(\bar{B} - e_i - e_j + f_j)}_{=r(T)-1} + \underbrace{r(\bar{B} + f_j)}_{=r(T)} \le r(\bar{B} - e_i + f_j) + \underbrace{r(\bar{B} - e_j + f_j)}_{=r(T)-1}, \end{aligned}$$

hence \(\bar{B} - e_i + f_j\) is a basis and so \(a_{f_i} = a_{e_j}\). Together we have \(a_{e_i} = a_{f_j} = a_{e_j} = a_{f_i}\) and again \(\bar{a} = 0\). This proves Claim 2.

It remains to prove that all coefficients \(a_e, e\in T\), have the same value and that the coefficient \(\bar{a}\) of y has the correct value. We start with the first statement.

Claim 3

All coefficients \(a_e\), \(e \in T\), have the same value.

Proof of Claim 3

We define the simple undirected graph \(G=(T,A)\) with set of nodes T and set of edges

$$\begin{aligned} A&:= \left\{ \{e,f\}{:}\,\exists \,B \subseteq T, e,f \in T {\setminus } B, B + e, B + f {\text { bases of }}T \right\} \\&\cup \left\{ \{e,f\}{:}\,\exists \,B \subseteq T + \bar{E}, e,f \in T {\setminus } B, \bar{E}\subseteq B, B+e, B+f {\text { bases of }}T + \bar{E}\right\} . \end{aligned}$$

We prove the statement in two steps.

Claim 3.1

If \(\{e,f\}\in A\), then we have \(a_e=a_f\).

Proof of Claim 3.1

Let \(\{e,f\} \in A\). If, on the one hand, there exists \(B \subseteq T\), \(e,f \in T{\setminus } B\), with \(B + e, B + f\) bases of T, then both bases define roots of \(x_T+\alpha _{1,k}(T)y\le r(T)\) and consequently \(\sum _{e' \in B+e} a_{e'} + \bar{a} y^{B + e} = \sum _{e' \in B+f} a_{e'} + \bar{a} y^{B+f}\), hence \(a_e + \bar{a} y^{B+e} = a_f + \bar{a} y^{B+f}\). If \(\bar{E}\nsubseteq T\), then \(y^{B+e} = y^{B+f} = 0\), otherwise \(\alpha _{1,k}(T)=r(T)+|\bar{E}{\setminus } T|-r(T + \bar{E})=r(T)+0-r(T)= 0\) by (A2) implying \(\bar{a} = 0\), so \(a_e = a_f\) follows. On the other hand, if there exists \(B \subseteq T + \bar{E}\), \(e,f \in T {\setminus } B\), with \(\bar{E}\subseteq B\) and \(B + e\), \(B + f\) bases of \(T + \bar{E}\), then \(y^{B + e} = y^{B + f} = 1\). Furthermore

$$\begin{aligned} |(B+e) \cap T| + \alpha _{1,k}(T) y^{B+e}&= |(B+e) \cap T| + r(T) + |\bar{E}{\setminus } T| - r(T + \bar{E}) \\&= |(B+e) \cap T| + r(T) + |(B+e) {\setminus } T| - r(T + \bar{E}) \\&= r(T + \bar{E}) + r(T) - r(T + \bar{E}) = r(T) \end{aligned}$$

by (A2), so \(B+e\) defines a root of \(x_T+\alpha _{1,k}(T)y\le r(T)\) (and, analogously, \(B+f\)). As above we conclude \(a_e = a_f\) and Claim 3.1 follows. Therefore, if we can prove that G is connected, all coefficients \(a_e\), \(e \in T\), must be equal.

Claim 3.2

Graph G is connected.

Proof of Claim 3.2

Assume, for a contradiction, that G is not connected, i. e. , there exist \(T_1, T_2 \subseteq T\), \(T_1, T_2 \ne \emptyset \), \(T_1 \cap T_2 = \emptyset \) and \(T_1 \cup T_2 = T\) such that there do not exist edges between \(T_1\) and \(T_2\). First assume \(r(T) < r(T_1) + r(T_2)\) and let \(B'\) be a basis of T with \(r(T_1) = r(B' \cap T_1)\). Then \(r(T_2) > r(B' \cap T_2)\), so there exists an \(e \in T_2 {\setminus } B'\) so that \((B' \cap T_2) + e \in {\mathcal {I}}\). However, \(B' + e \notin {\mathcal {I}}\) (\(B'\) basis), but because M is a matroid there exists an \(f \in (T_1 \cap B')\) so that \(B' + e - f\) is a basis of T. Consequently, choosing \(B := B' - f\) proves \(\{e,f\} \in A\), a contradiction.

Secondly, if \(r(T) = r(T_1) + r(T_2)\) then \((\bar{E},\{k\})\)-non-separability and (A2) imply \(|\bar{E}| + r(T + \bar{E}) < r(T_1 + \bar{E}) + r(T_2 + \bar{E})\). Let \(B'\) be a basis of \(T + \bar{E}\) with \(\bar{E}\subseteq B'\) and \(r(B' \cap (T_1 + \bar{E})) = r(T_1 + \bar{E})\). Consequently,

$$\begin{aligned} r(B' \cap (T_2 + \bar{E}))&= |\bar{E}| + |B' \cap (T_2 {\setminus } \bar{E})| \\&< r(T_1 + \bar{E}) + r(T_2 + \bar{E}) - r(T + \bar{E}) + |B' \cap (T_2 {\setminus } \bar{E})| \\&= |B' \cap (T_1 + \bar{E})| + r(T_2 + \bar{E}) - r(T + \bar{E}) + |B' \cap (T_2 {\setminus } \bar{E})| \\&= |B'| + r(T_2 + \bar{E}) - r(T + \bar{E}) = r(T_2 + \bar{E}). \end{aligned}$$

Hence there exists an \(e \in T_2 {\setminus } B'\) so that \((B' + e) \cap (T_2 + \bar{E}) \in {\mathcal {I}}\), but \(B' + e \notin {\mathcal {I}}\). Because M is a matroid there exists an \(f \in T_1\) such that \(B' + e - f\) is a basis of T, too. Consequently, choosing \(B := B' - f\) proves \(\{e,f\} \in A\), a contradiction. So G is connected and this proves Claim 3.2 and so Claim 3. Finally, it remains to prove:

Claim 4

The coefficient \(\bar{a}\) of y has the correct value.

Proof of Claim 4

By Claim 2 we know that \(\bar{a}=0\) if \(\alpha _{1,k}(T)=0\). So, e. g. , in the cases \(T\subseteq \bar{E}\) or \(\bar{E}\subseteq T\) the statement follows. So assume \(T\nsubseteq \bar{E}\), \(\bar{E}\nsubseteq T\) and \(\alpha _{1,k}(T) > 0\). Let B be a basis of \(T + \bar{E}\) with \(r(B \cap (T \cap \bar{E})) = r(T \cap \bar{E})\) and \(r(B \cap T) = r(T)\). Then \(\bar{E}{\setminus } B \ne \emptyset \) because

$$\begin{aligned} |\bar{E}{\setminus } B|&= |B \cap T| + |\bar{E}{\setminus } T| - |B| = r(T) + |\bar{E}{\setminus } T| - r(T + \bar{E}) = \alpha _{1,k}(T) > 0. \end{aligned}$$

In particular, \(y^B = 0\). Let \(B'\) be a basis of \(T + \bar{E}\) with \(\bar{E}\subseteq B'\). Then \(B,B'\) are roots of \(x_T + \alpha _{1,k}(T)y \le r(T)\) and so of \(a^T x + \bar{a} y \le b\). Therefore, with \(\tilde{a} := a_e\) being the value of all coefficients \(a_e\), \(e \in T\), we get

$$\begin{aligned} \sum _{e \in B \cap T} a_e + \bar{a} \underbrace{y^B}_{=0} = \sum _{e \in B' \cap T} a_e + \bar{a} \underbrace{y^{B'}}_{=1}, \end{aligned}$$

so by the choice of \(B'\)

$$\begin{aligned} \bar{a}= & {} (|B \cap T| - |B' \cap T|) \cdot \tilde{a} = (|B \cap T| - |B'| + |B' {\setminus } T|) \cdot \tilde{a} \\= & {} (|B \cap T| - |B| + |\bar{E}{\setminus } T|) \cdot \tilde{a} = \alpha _{1,k}(T) \tilde{a}. \end{aligned}$$

Consequently Claim 4 follows. In total, this proves that \(a^T x + \bar{a}y\le b\) is a positive multiple (with factor \(\tilde{a}\)) of \(x_T+\alpha _{1,k}(T)y\le r(T)\). \(\square \)

The following theorem summarises the results on the facetial structure of \(P_{M}^{\bar{E},k}\) .

Theorem 31

All facet defining inequalities of \(P_{M}^{\bar{E},k}\)  are given by (11) and (12), \(x_e\ge 0, e\in E{\setminus } \bar{E}, y\ge 0\) and all extended rank inequalities (14)

$$\begin{aligned} x_T+\alpha _{1,k}(T)y\le r(T),\quad {}&T\subseteq E, T {\text { closed, }}(\bar{E},\{k\}){\text {-non-separable and}}\\&T{\text { satisfies property }}(\mathbf{P1}^k){\text { or }}(\mathbf{P2}^k). \end{aligned}$$

4 Separation

By the well-known “optimisation equals separation” result [18] we know that the separation problem for the polytope \(P_{M}^{\bar{E},K}\)  can be solved in polynomial time because the corresponding optimisation problem can be solved in polynomial time. But the proof of the next result shows how to separate the extended rank inequalities more directly. Note, all inequalities of the standard linearisation (3)–(7) as well as the non-negativity constraints (8) can be separated in polynomial time by complete enumeration.

Theorem 32

Let \(K=\{k_1, \cdots , k_l\}\subset \{2, \cdots , k\}\). Given a point \((\bar{x}, \bar{y})\) the separation problem for the extended rank inequalities (9) of \(P_{M}^{\bar{E},K}\)  can be solved in (strongly) polynomial time if \(\bar{y}_{k_j}\ge \bar{y}_{k_{j+1}}\) for all \(j=1, \cdots , l-1\), as well as \(\bar{y}_{k_1}\le 1, \bar{y}_{k_l}\ge 0\).

Proof

Let \((\bar{x}, \bar{y})\) be a point that satisfies all requirements. Then we want to find a set \(T\subseteq E\) such that (9) evaluated for \((\bar{x}, \bar{y})\) is violated or we want to prove that there does not exist such a set T. Therefore we define the function \(d{:}\,{\mathcal {P}}(E) \rightarrow {\mathbb {R}}\),

$$\begin{aligned} d(T):= r(T)-\bar{x}_T - \sum _{j=1}^l \alpha _{k_{j-1}+1, k_j}(T) \bar{y}_{k_j}. \end{aligned}$$

Our separation problem is then equivalent to the problem to decide whether the optimal value of

$$\begin{aligned} \min _{T\subseteq E} d(T) \end{aligned}$$

is negative or not. Using (A2) we can write d(T) as:

$$\begin{aligned} d(T)=\,&r(T)\cdot \underbrace{(1-\bar{y}_{k_1})}_{\ge 0} + \sum _{j=1}^{l-1}\left( r(T\cup \bar{E}_{1,k_j})\cdot \underbrace{\left( \bar{y}_{k_j}-\bar{y}_{k_{j+1}}\right) }_{\ge 0}\right) + r(T\cup \bar{E}_{1,k_l})\cdot \underbrace{\bar{y}_{k_l}}_{\ge 0}\\&-\bar{x}_T- |\bar{E}_{1,k_1} {\setminus } T|\bar{y}_{k_1} -\sum _{j=2}^l \left( |\bar{E}_{k_{j-1}+1, k_j}{\setminus } T|\cdot \bar{y}_{k_j}\right) . \end{aligned}$$

So, d(T) is submodular by the submodularity of the rank function \(r(\cdot )\) and our separation problem reduces to minimising the submodular function d(T), which can be done in strongly polynomial time [14, 22], e. g. , using a combinatorial algorithm [26, 27]. \(\square \)

5 Extensions and future work

A natural question is if it is possible to extend the previous results to related problems. For instance, Edmonds [10] also provided a complete description for the polytope that is associated with the intersection of two matroids. However, the following example shows that even in the case with exactly one additional quadratic monomial there exist facet defining inequalities \(a^T x + \bar{a} y\le b\) of the associated linearised polytope that are not a positive multiple of the standard linearisation but with \(a\ge 0\) and \(\bar{a} < 0\). Thus, it might be necessary to extend the line of arguments in Sect. 2 significantly.

Example 33

We consider the directed graph \(G=(V,E)\) in Fig. 5I with four nodes and four arcs \(E=\{e_1,e_2,f_1,f_2\}\) and the branching problem [9] (intersection of two matroids) with \(\bar{E}=\{e_1,e_2\}\). Then one can check by direct computations that the inequality \(x_{f_1}+x_{f_2}+x_{e_1}+x_{e_2}-y_{e_1e_2} \le 2\) is facet defining for the associated linearised polytope although the coefficient of \(y_{e_1e_2}\) is \(-1\). Note, the inequality above is of the form

$$\begin{aligned} x_T + x_{e_1} + x_{e_2} - y_{e_1e_2} \le r(T), \end{aligned}$$

with \(T\subseteq E, r(T) = r(T+e_1) = r(T+e_2) = r(T+e_1+e_2)-1\) (r denotes the minimum of the rank of T for \(M_1\) and \(M_2\)) where in our example \(T=\{f_1,f_2\}\). Furthermore, considering the branching problem in Fig. 5II the inequality \( 2x_{e_1}+x_{e_2}+x_{f_1}+x_{f_2}-y_{e_1e_2} \le 2 \) is facet defining. So, also coefficients of the x-variables larger than one may appear. This is a large contrast to the results by Edmonds for the polytope associated with the intersection of two matroids [10]. Indeed, given two matroids \(M_1=(E, {\mathcal {I}}_1), M_2=(E, {\mathcal {I}}_2)\) with rank functions \(r_i{:}\,E\rightarrow {\mathbb {N}}_0, i=1,2\), the convex hull of all sets \(I\subseteq E\) with \(I\in {\mathcal {I}}_1, I\in {\mathcal {I}}_2\) can be described by the non-negativity constraints and the rank inequalities for the two single matroids [10].

Fig. 5
figure 5

Visualisation of the four different graphs in Examples 33–35

Full size image

To the best of our knowledge the only matroid intersection problem combined with one non-linear monomial that has been considered in the literature before is the bipartite matching problem. Recently, Walter [30] proved a conjecture in [20] on the complete description of the linearised polytope in this case. In comparison to the branching problem coefficients of two for x-variables do not appear there. So the situation is a bit easier. It remains for future work to study which other matroid intersection problems can be treated with the approach in [30]. Unfortunately, this approach cannot easily be extended to larger sets of monomials.

Furthermore, it is interesting to extend the results to two or more monomials that are not necessarily nested. But again, this might lead to facet defining inequalities containing variables with negative coefficients apart from the standard linearisation. We start with an example where the two monomials are in pairwise conflict.

Example 34

We consider the undirected graph \(G=(V,E)\) in Fig. 5III with four nodes and five edges \(E=\{f_1,e_1,e_2,e_3, e_4\}\) and the optimisation problem over the graphical matroid with the two additional monomials \(x_{e_1}x_{e_2}, x_{e_3}x_{e_4}\). Then the inequality \(x_{f_1}+y_{e_1e_2}+x_{e_3}+x_{e_4}-y_{e_3e_4} \le 2\) is facet defining. So one of the coefficients of the linearised variables is negative although the inequality does not belong to the standard linearisation in this case.

One might think that the problem in Example 34 arises because \(\{e_i{:}\,i=1,\cdots , 4\} \notin {\mathcal {I}}\). But even if the union of all elements contained in the additional monomials is an independent set and none of the elements \(e\in E\) appears in more than one of these non-linear monomials, facet defining inequalities can contain variables with negative coefficients apart from the standard linearisation.

Example 35

We consider the undirected graph \(G=(V,E)\) in Fig. 5IV with six nodes and set of edges \(E=\{f_1,f_2,f_3,e_1,e_2,e_3,e_4\}\) and the optimisation problem over the graphical matroid with the two additional monomials \(x_{e_1}x_{e_2}, x_{e_3}x_{e_4}\) and \(\{e_1, \cdots ,e_4\}\in {\mathcal {I}}\). Then the inequality \(x_{f_1}+x_{f_2}+x_{f_3}+y_{e_1e_2}+x_{e_3}+x_{e_4}-y_{e_3e_4} \le 4\) is facet defining for the associated polytope.

Let, in general, a matroid \(M=(E, {\mathcal {I}})\) be given and let \(x_{e_1}x_{e_2}\), \(x_{e_3}x_{e_4}\), \(\{e_1,e_2\}\cap \{e_3,e_4\}=\emptyset \), denote the two additional quadratic monomials with associated variables \(y_{e_1e_2},y_{e_3e_4}\). Then inequalities

$$\begin{aligned} x_T + y_{e_1e_2} + x_{e_3}+x_{e_4}-y_{e_3e_4} \le r(T)+1, \end{aligned}$$

\(T\subset E{\setminus } \{e_1,e_2, e_3, e_4\}, r(T+e_3+e_4) > r(T)+1, (T+e_1+e_2+e_i)\notin {\mathcal {I}}, i=3,4\), are valid for the associated linearised polytope. The facet defining inequalities in Examples 34 and 35 are exactly of this type with \(T=\{f_1\}\) and \(T=\{f_1,f_2,f_3\}\), respectively.

Extending our results to problems with objective functions with more than one non-linear monomial, a good starting point might be to consider the three quadratic monomials \(x_{e_1}x_{e_2}\), \(x_{e_1}x_{e_3}\), \(x_{e_2}x_{e_3}\) and the associated cubic monomial \(x_{e_1}x_{e_2}x_{e_3}\) on the three elements \(e_1,e_2,e_3\in E\) with \(\{e_1,e_2,e_3\} \in {\mathcal {I}}\) or \(\{e_1,e_2,e_3\}\) forming a circuit. In both mentioned cases the monomials then satisfy some kind of up- and downwards compatibility, see [5]. Furthermore, it remains for future work to extend the results to (integral) polymatroids [10], see also [14, 27]. Here, the setting might be quite different because the variables are not necessarily binary. One possible way might be to transform the integral polymatroid to a matroid by the standard transformation, but then even a single quadratic monomial leads to several quadratic monomials in the extended problem. So a better understanding of the multiple monomial case is essential.