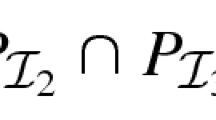Approximate Multi-matroid Intersection via Iterative Refinement

Abstract

We introduce a new iterative rounding technique to round a point in a matroid polytope subject to further matroid constraints. This technique returns an independent set in one matroid with limited violations of the other ones. On top of the classical steps of iterative relaxation approaches, we iteratively refine/split involved matroid constraints to obtain a more restrictive constraint system, that is amenable to iterative relaxation techniques. Hence, throughout the iterations, we both tighten constraints and later relax them by dropping constraints under certain conditions. Due to the refinement step, we can deal with considerably more general constraint classes than existing iterative relaxation/rounding methods, which typically round on one matroid polytope with additional simple cardinality constraints that do not overlap too much.

We show how our rounding method, combined with an application of a matroid intersection algorithm, yields the first 2-approximation for finding a maximum-weight common independent set in 3 matroids. Moreover, our 2-approximation is LP-based, and settles the integrality gap for the natural relaxation of the problem. Prior to our work, no upper bound better than 3 was known for the integrality gap, which followed from the greedy algorithm. We also discuss various other applications of our techniques, including an extension that allows us to handle a mixture of matroid and knapsack constraints.

A. Linhares and C. Swamy—Research supported by NSERC grant 327620-09 and an NSERC DAS Award.

N. Olver—Supported by NWO VIDI grant 016.Vidi.189.087.

R. Zenklusen—Supported by Swiss National Science Foundation grant 200021_165866.

1 Introduction

Matroids are among the most fundamental and well-studied structures in combinatorial optimization. Recall that a matroid M is a pair $M=(N,\mathcal {I})$, where N is a finite ground set and $\mathcal {I}\subseteq 2^N$ is a family of sets, called independent sets, such that (i) $\emptyset \in \mathcal I$, (ii) if $A\in \mathcal {I}$ and $B\subseteq A$, then $B\in \mathcal {I}$, and (iii) if $A,B\in \mathcal {I}$ with $|A| > |B|$, then there is an element $e\in A\setminus B$ such that $B\cup \{e\}\in \mathcal {I}$. We make the standard assumption that a matroid is specified via an independence oracle, which, given $S\subseteq N$ as input, returns if $S\in \mathcal I$. Matroids capture many interesting problems, and matroid-optimization algorithms provide a powerful tool in the design and analysis of efficient algorithms. A key matroid optimization problem is matroid intersection, wherein we seek a maximum-weight set that is independent in two matroids, for which various efficient algorithms are known, and we also have a celebrated min-max theorem and a polyhedral understanding of the problem. The versatility of matroid intersection comes from the fact that the intersection of matroids allows for describing a very broad family of constraints.

Unfortunately, as soon as the intersection of 3 or more matroids is considered, already the unweighted version of determining a maximum cardinality common independent set becomes APX-hard. Due to its fundamental nature, and many natural special cases, the problem of optimizing over 3 or more matroids has received considerable attention. In particular, there is extensive prior work ranging from the study of maximum cardinality problems [15], the maximization of submodular functions over the intersection of multiple matroids (see [4, 8, 11, 16, 17] and the references therein), to various interesting special cases like k-dimensional matching (see [3, 6, 7, 12, 13] and the references therein; many of these results apply also to the k-set packing problem which generalizes k-dimensional matching).

Nevertheless, there are still basic open questions regarding the approximability of the optimization over 3 or more matroids. Perhaps the most basic problem of this type is the weighted 3-matroid intersection problem, defined as follows.

Weighted 3-Matroid Intersection. Given matroids $M_i=(N,\mathcal I_i)$, for $i=1,2,3$, on a common ground set N, and a weight vector $w\in \mathbb R^N$, solve

$$\begin{aligned} \max \ \left\{ w(I):\ I\in \mathcal {I}_1 \cap \mathcal {I}_2 \cap \mathcal {I}_3 \right\} , \end{aligned}$$

where we use the shorthand for any set $S\subseteq N$.

The unweighted 3-matroid intersection problem, which is also sometimes called the cardinality version of 3-matroid intersection, is the special case where $w(e)=1$ for all $e\in N$, so $w(S)=|S|$ for $S\subseteq N$.

The 3-matroid intersection problem has a natural and canonical LP-relaxation:

where, for a matroid $M=(N,\mathcal {I})$, we denote by $P_{\mathcal {I}}\subseteq [0,1]^N$ the matroid polytope of M, which is the convex hull of all characteristic vectors of sets in $\mathcal {I}$. It has a well known inequality description given by

$$\begin{aligned} P_{\mathcal {I}} = \bigl \{ x\in \mathbb {R}_{\ge 0}^N:\ x(S)\le r(S) \;\;\forall S\subseteq N \bigr \}\,, \end{aligned}$$

where $r:2^N \longrightarrow \mathbb {Z}_{\ge 0}$ is the rank function of M, which, for $S\subseteq N$, is defined by . The rank function is submodular, and r(S) can be computed for any $S\subseteq N$ using an independence oracle. It will therefore often be convenient to assume that a matroid M is specified via its rank oracle that, given $S\subseteq N$ as input, returns r(S). In particular, one can efficiently optimize any linear function over $P_{\mathcal I}$ given a rank oracle (or equivalently an independence oracle). The above LP-relaxation extends naturally to the k-matroid intersection problem, which is the extension of 3-matroid intersection to k matroids.

Whereas ($\mathrm{LP}_{3\text {-}\mathrm{mat}}$), and its extension ($\mathrm {LP}_{k{\text {-mat}}}$) to k-matroid intersection, are well-known LP-relaxations, there remain various gaps in our understanding of these relaxations. It is widely known that the greedy algorithm is a k-approximation for k-matroid intersection. Moreover, this approximation is relative to the optimal value of ($\mathrm {LP}_{k{\text {-mat}}}$), which leads to the current best upper bound of k on the integrality gap of ($\mathrm {LP}_{k{\text {-mat}}}$), for all $k\ge 3$. However, the best lower bound on the integrality gap of ($\mathrm {LP}_{k{\text {-mat}}}$) is $k-1$, whenever $k-1$ is a prime power; this is known to be achievable in instances where the involved matroids are partition matroids, and for unweighted instances [3, 9, 15, 18].

Significant progress on approximating k-matroid intersection was achieved by Lee, Sviridenko, and Vondrák [17], who presented, for any fixed $\epsilon >0$, a local search procedure with running time exponential in $\epsilon$ that leads to a $(k-1+\epsilon )$-approximation (i.e., the weight of the set returned is at least (optimum)/$(k-1+\epsilon )$). Unfortunately, apart from its high running time dependence on $\epsilon$, this approach does not shed any insights on ($\mathrm {LP}_{k{\text {-mat}}}$), as the above guarantee is not relative to ${ OPT }_{\mathrm {LP}_{k{\text {-mat}}}}$. Further progress on understanding the quality of the LP-relaxations has only been achieved in special cases. In particular, for unweighted k-matroid intersection, Lau, Ravi and Singh [15] give an LP-based $(k-1)$-approximation through iterative rounding. Their proof is based on identifying an element with “large” fractional value, picking it, and altering the fractional solution so that it remains feasible; the last step crucially uses the fact that the instance is unweighted to control the loss in the LP objective value. For the intersection of k unitary partition matroids, a problem also known as k-dimensional matching, Chan and Lau [3] were able to obtain a $(k-1)$-approximation based on ($\mathrm {LP}_{k{\text {-mat}}}$), and Parekh and Pritchard [18] later obtained the same approximation factor for the intersection of k (not necessarily unitary) partition matroids.

Although it is generally believed that a $(k-1)$-approximation for k-matroid intersection should exist, and that the integrality gap of ($\mathrm {LP}_{k{\text {-mat}}}$) is equal to the known lower bound of $k-1$, this has remained open even for 3-matroid intersection (prior to our work). Recall that in this case, the best known upper and lower bounds on the integrality gap of  ($\mathrm{LP}_{3\text {-}\mathrm{mat}}$) are 3 (via the classical greedy algorithm) and 2 respectively. Moreover, the only method to beat the trivial 3-approximation of the greedy algorithm is the non-LP based and computationally quite expensive $(2+\epsilon )$-approximation in [17]. One main reason for the limited progress is the lack of techniques for rounding points in the intersection of multiple matroid polytopes with sufficiently strong properties. In particular, one technical difficulty that is encountered is that the tight constraints (even at an extreme point) may have large overlap, and we do not know of ways for dealing with this.

Our Results. We introduce a new iterative rounding approach to handle the above difficulties, that allows for dealing with a very general class of optimization problems involving matroids. Before delving into the details of this technique, we highlight its main implication in the context of 3-matroid intersection.

Theorem 1

There is an LP-relative 2-approximation for weighted 3-matroid intersection. That is, for any instance, we can efficiently find a common independent set R with $w(R)\ge {{ OPT }_{\mathrm{LP}_{3\text {-mat}}}}/{2}$; thus, the integrality gap of ($\mathrm{LP}_{3\text {-}\mathrm{mat}}$) is at most 2.

This is the first 2-approximation for 3-matroid intersection (with general weights). Moreover, our result settles the integrality gap of ($\mathrm{LP}_{3\text {-}\mathrm{mat}}$) due to the known matching integrality gap lower bound of 2.

The chief new technical ingredient that leads to Theorem 1, and results for other applications discussed in Sect. 3, is an approximation result based on a novel iterative refinement technique (see Sect. 2) for problems of the following type. Let $N=N_0$ be a finite ground set, and $M_i=(N_i,\mathcal {I}_i)$ for $i=0,\ldots ,k$ be $k+1$ matroids with rank functions $\{r_i\}$, where $N_i\subseteq N$, and $w\in \mathbb R^N$ be a weight vector (note that negative weights are allowed). We consider the problem

$$\begin{aligned} \max \ \bigl \{w(I): \ I \in \mathcal {B}_0, \quad I \cap N_i \in \mathcal {I}_i \, \, \forall i \in [k] \bigr \}, \end{aligned}$$

(1)

where $\mathcal {B}_0$ is the set of all bases of $M_0$ and $[k] := \{1, \dots , k\}$. The reason we consider matroids $M_i$ for $i\in [k]$ defined on ground sets $N_i$ that are subsets of N, is because, as we show below, we obtain guarantees depending on how strongly the sets $N_i$ overlap; intuitively, problem (1) becomes easier as the overlap between $N_1,\ldots ,N_k$ decreases, and our guarantee improves correspondingly.

We cannot hope to solve (1) optimally, as this would enable one to solve the NP-hard k-matroid intersection problem. Our goal will be to find a basis of $M_0$ of large weight that is “approximately independent” in the matroids $M_1,\ldots ,M_k$.

How to quantify “approximate independence”? Perhaps the two notions that first come to mind are additive and multiplicative violation of the rank constraints. Whereas additive violations are common in the study of degree-bounded MST problems, which can be cast as special cases of (1), it turns out that such a guarantee is impossible to obtain (in polytime) for (1). More precisely, we show in Appendix A (via a replication idea) that, even for $k=2$, if we could find in polytime a basis B of $M_0$ satisfying $|B|\le r_i(B)+\alpha$ for $i=1,2$ for $\alpha = O(|N|^{1-\epsilon })$ for any $\epsilon > 0$, then we could efficiently find a basis of $M_0$ that is independent in $M_1$, $M_2$; the latter problem is easily seen to be NP-hard via a reduction from Hamiltonian path. We therefore consider multiplicative violation of the rank constraints. We say that $S\subseteq N$ is $\alpha$-approximately independent, or simply $\alpha$-independent, for a matroid $M=(N,\mathcal I)$, if $|T|\le \alpha \cdot r(T)\ \forall T\subseteq S$ (equivalently, $\chi ^S\in \alpha P_{\mathcal I}$, where $\chi ^S$ is the characteristic vector of S). This is much stronger than simply requiring that $|S|\le \alpha \cdot r(S)$, and it is easy to give examples where this weaker notion admits sets that one would consider to be quite far from being independent. An appealing feature of the stronger definition is that, using the min-max result for matroid-intersection (or via matroid partition; see, e.g., [5]), it follows easily that if $\alpha \in \mathbb Z_{\ge 1}$, then S is $\alpha$-independent iff S can be partitioned into at most $\alpha$ independent sets of M. We now state the guarantee we obtain for (1) precisely. We consider the following canonical LP relaxation of (1):

where for a set $S\subseteq N$, we use $x\vert _{S}\in \mathbb {R}^S$ to denote the restriction of x to S, and is the matroid base polytope of $M_0$. For ease of notation, we will sometimes write $x\in P_{\mathcal {I}_i}$ and $R\in \mathcal I_i$ instead of $x\vert _{N_i} \in P_{\mathcal {I}_i}$ and $R\cap N_i\in \mathcal I_i$, respectively. Our main result for (1), based on a new iterative rounding algorithm for ($\mathrm{LP}_\mathrm{mat}$) described in Sect. 2, is the following.

Theorem 2

Let $q_1,\ldots , q_k \in \mathbb {Z}_{\ge 1}$ such that

$$\begin{aligned} \sum _{i\in [k]: e\in N_i} q_i^{-1} \le 1 \qquad \forall e\in N\,. \end{aligned}$$

(2)

If  ($\mathrm{LP}_\mathrm{mat}$) is feasible, then one can efficiently compute $R \subseteq N$ such that (i) $R\in \mathcal {B}_0$; (ii) $w(R)\ge { OPT }_{\mathrm{LP}_{mat}}$ ; and (iii) R is $q_i$-independent in $M_i$ $\forall i \in [k]$.

Note that, in particular, taking $q_i=\max _{e\in N}\bigl |\{j\in [k]: e\in N_j\}\bigr |$ for all $i \in [k]$ satisfies (2). Thus, we violate the constraints imposed by the other matroids $M_1,\ldots , M_k$ by a multiplicative factor depending on how strongly the $N_i$s overlap.

While we have stated Theorem 2 in terms of bases of $M_0$, the following natural variant is easily deduced from it (we defer the proof to Appendix B).

Corollary 3

Theorem 2 also holds when R is required only to be an independent set in $M_0$ (as opposed to a basis), and we replace $P_{\mathcal {B}_0}$ in ($\mathrm{LP}_\mathrm{mat}$) by $P_{\mathcal I_0}$.

A variety of problem settings can be handled via Theorem 2 and Corollary 3 in a unified way. We first show how to obtain a crisp, simple proof of Theorem 1.

Proof of Theorem

1. Given matroids $M_i = (N,\mathcal {I}_i)$ for $i=0,1,2$, and a weight vector $w \in \mathbb {R}^N$, we first solve  ($\mathrm{LP}_{3\text {-}\mathrm{mat}}$) to obtain an optimal solution $x^*$. Now we utilize Corollary 3 with the same three matroids, and $q_1=q_2=2$. Clearly, these q-values satisfy (2), and $x^*$ is a feasible solution to ($\mathrm{LP}_\mathrm{mat}$), when we replace $P_{\mathcal {B}_0}$ by $P_{\mathcal I_0}$. Thus, we obtain a set $A\in \mathcal I_0$ with $w(A)\ge w^Tx^*$ and $\chi ^A\in 2P_{\mathcal I_1}\cap 2P_{\mathcal I_2}$.

It is well known that $P_{\mathcal I_1}\cap P_{\mathcal I_2}$ is a polytope with integral extreme points (see, e.g., [5]). So since $\chi ^A/2\in P_{\mathcal I_1}\cap P_{\mathcal I_2}$, by using an algorithm for (weighted) matroid intersection applied to matroids $M_1$ and $M_2$ restricted to A, we can find a set $R\subseteq A$ such that $R\in \mathcal I_1\cap \mathcal I_2$ and $w(R)\ge w^T\chi ^A/2\ge w^T x^*/2$. Finally, since $R\subseteq A$ and $A\in \mathcal I_0$, we also have that $R\in \mathcal I_0$.    $\square$

Beyond 3-matroid intersection, Theorem 2 is applicable to various constrained (e.g., degree-bounded) spanning tree problems; we expand on this below. In Sect. 3, we discuss an application in this direction, wherein we seek a min-cost spanning tree satisfying matroid-independence constraints on the edge-sets of a given disjoint collection of node sets. Using Theorem 2, we obtain a spanning tree with a multiplicative factor-2 violation of the matroid constraints.

In Sect. 3, we also present a noteworthy extension of Theorem 2 with t knapsack constraints in addition to k matroid constraints, where we obtain bounded multiplicative violations of all involved constraints. The only other such result we are aware of that applies to a mixture of matroid and knapsack constraints is by Gupta et al. [10]; their result in our setting yields an O(kt)-approximation with no constraint violation, which is incomparable to our result.

Related Work and Connections. By choosing $M_0$ to be a graphic matroid, problem (1) generalizes many known constrained spanning tree problems, including degree-bounded spanning trees, and generalizations thereof considered by Bansal et al. [2], Király et al. [14], and Zenklusen [21]. Theorem 2 thus yields a unified way to deal with various spanning tree problems considered in the literature, where the soft/degree constraints are violated by at most a constant factor. However, as noted earlier, whereas the above works obtain stronger, additive violation results, such guarantees are not possible for our general problem (1) (see Appendix A). This hardness (of obtaining small additive violations) carries over to the spanning tree application that we consider in Sect. 3 (which generalizes the matroidal degree-bounded spanning tree problem considered in [21]).

To showcase how Theorem 2 can be used for such problems, consider the minimum degree-bounded spanning tree problem, where given is a graph $G=(V,E)$ with edge weights $w:E\rightarrow \mathbb {R}$ and degree bounds $B_v\in \mathbb {Z}_{\ge 1}$ for $v\in V$. The nominal problem asks to find a spanning tree $T\subseteq E$ with $|T\cap \delta (v)|\le B_v$ for $v\in V$ minimizing w(T), where $\delta (v)$ denotes the set of edges incident with v. Here one can apply Theorem 2 with $M_0$ being the graphic matroid of G, and for each $v\in V$ we define a uniform matroid $M_v$ with ground set $\delta (v)$ and rank $B_v$. Theorem 2 with $q_v=2 \;\forall v\in V$ and negated edge weights leads to a spanning tree T with $|T\cap \delta (v)|\le 2B_v \; \forall v\in V$ and weight no more than the optimal LP-weight. Whereas this is a simple showcase example, Theorem 2 can be used in a similar way for considerably more general constraints than just degree constraints.

Finally, we highlight a main difference of our approach compared to prior techniques. Prior techniques for related problems, as used, for example, by Singh and Lau [20], Király et al. [14], and Bansal et al. [2], successively drop constraints of a relaxation. Also, interesting variations have been suggested that do not just drop constraints but may relax constraints by replacing a constraint by a weaker family (see work by Bansal etal. [1]). In contrast, our method does not just relax constraints, but also strengthens the constraint family in some iterations, so as to simplify it and enable one to drop constraints later on.

2 Our Rounding Technique

Our rounding technique heavily relies on a simple yet very useful “splitting” procedure for matroids, which we call matroid refinement.

Matroid Refinement. Let $M=(N,\mathcal {I})$ be a matroid with rank function $r:2^N\rightarrow \mathbb {Z}_{\ge 0}$, and let $S\subsetneq N$, $S\ne \emptyset$. Refining M with respect to S yields the two matroids $M_1=M\vert _{S}$ obtained by restricting M to S, and $M_2=M/S$ obtained by contracting S in M. Formally, the independent sets of the two matroids $M_1=(S,\mathcal {I}_1), M_2=(N\setminus S, \mathcal {I}_2)$ are given by $\mathcal {I}_1=\left\{ I\subseteq S: I\in \mathcal {I} \right\}$, and $\mathcal {I}_2= \left\{ I\subseteq N\setminus S: I\cup I_S \in \mathcal {I} \right\}$, where $I_S\in \mathcal {I}$ is a maximum cardinality independent subset of S. It is well-known that the definition of $\mathcal {I}_2$ does not depend on which set $I_S$ is chosen. The rank functions $r_1:2^S\rightarrow \mathbb {Z}_{\ge 0}$ and $r_2:2^{N\setminus S} \rightarrow \mathbb {Z}_{\ge 0}$ of $M_1$ and $M_2$, respectively, are given by

$$\begin{aligned} r_1(A) = r(A) \;\;\forall A\subseteq S, \text { and} \quad r_2(B) = r(B\cup S) -r(S) \;\;\forall B\subseteq N\setminus S. \end{aligned}$$

(3)

We refer the reader to [19, Volume B] for more information on matroid restrictions and contractions. The following lemma describes two basic yet important relations between a matroid $M=(N,\mathcal {I})$ and its refinements $M_1=M\vert _S$ and $M_2=M/S$. These relations easily follow from well-known properties of matroids; we omit the proofs here, but include them in the full version.

Lemma 4

(i) If $x\in \mathbb {R}^N$ satisfies $x\vert _S\in P_{\mathcal {I}_1}$ and $x\vert _{N\setminus S}\in P_{\mathcal I_2}$, then $x\in P_{\mathcal {I}}$. (ii) Let $x\in P_{\mathcal {I}}$ be such that $x(S)=r(S)$. Then $x\vert _{S}\in P_{\mathcal {I}_1}$ and $x\vert _{N\setminus S}\in P_{\mathcal I_2}$.

Intuitively, matroid refinement serves to partly decouple the matroid independence constraints for M, thereby allowing one to work with somewhat “simpler” matroids subsequently, and we leverage this carefully in our algorithm.

An Algorithm Based on Iterative Refinement and Relaxation. Algorithm 1 describes our method to prove Theorem 2. Recall that the input is an instance of problem (1), which consists of $k+1$ matroids $M_i=(N_i,\mathcal {I}_i)$ for $i=0,\ldots ,k$, where each $N_i$ is a subset of a finite ground set $N=N_0$, and a weight vector $w\in \mathbb {R}^N$. We are also given integers $q_i\ge 1$ for $i\in [k]$ satisfying (2).

Algorithm 1 starts by solving the natural LP-relaxation in step 2 to obtain an optimal extreme point $x^*$. As is common in iterative rounding algorithms, we delete all elements of value 0 and fix all elements of value 1 through contractions in step 3. Apart from these standard operations, we refine the matroids in step 5, as long as there is a matroid $M'=(N',\mathcal {I}')$ in our collection $\mathcal {M}$ with a nontrivial $x^*$-tight set $S\subseteq N'$, i.e., $x^*(S) = r'(S)$ and $S\notin \{\emptyset , N'\}$. Notice that after step 5, the q-values for the matroids in the new collection $\mathcal M$ continue to satisfy (2). Step 6 is our relaxation step, where we drop a matroid $M'=(N',\mathcal {I}')$ if $|N'|-x^*(N') < q_{M'}$. This is the step that results in a violation of the matroid constraints, but, as we show, the above condition ensures that even if we select all elements of $N'$ in the solution, the violation is still within the prescribed bounds. Moreover, we will show in the proof of Lemma 6 that, whenever Algorithm 1 is at step 6, there is a matroid $M'=(N',\mathcal {I}')\in \mathcal {M}$ that can be dropped, i.e., $x^*(N') = r'(N')$ and $|N'| - x^*(N') < q_{M'}$. We remark that, in step 6, one could also drop all matroids $M'\in \mathcal {M}$ fulfilling this condition, instead of just a single one, without impacting the correctness of the algorithm.

One can find an $x^*$-tight set $\emptyset \ne S\subsetneq N'$ (if one exists) in step 5 by minimizing the submodular function $r'(A)-x^*(A)$ over the sets $\emptyset \ne A\subsetneq N'$. Depending on the matroids involved, faster specialized approaches can be employed.

It is perhaps illuminating to consider the combined effect of all the refinement steps and step 6 corresponding to a given basic optimal solution $x^*$. Using standard uncrossing techniques, one can show that for each matroid $M'=(N',\mathcal I')\in \mathcal M$, there is a nested family of sets $\emptyset \subsetneq S_1\subsetneq \ldots \subsetneq S_p\subseteq N'$ whose rank constraints span the $x^*$-tight constraints of $M'$. Let $p' := p$ if $p = 0$ or $S_p \ne N'$, and let $p' := p - 1$ otherwise; so any $S_i$ with $i \in [p']$ can be used to refine $M'$. The combined effect of steps 5 for $M'$ can be seen as replacing $M'$ by the matroids $\bigl (M'\vert _{S_\ell }\bigr )/S_{\ell -1}$ for $\ell =1,\ldots ,p'+1$, where and . Step 6 chooses some $M'\in \mathcal M$ and a “ring” $S_\ell \setminus S_{\ell -1}$ of its nested family satisfying $|S_\ell \setminus S_{\ell -1}|-x^*(S_\ell \setminus S_{\ell -1})<q_{M'}$, and drops the matroid created for this ring.

Analysis. Lemma 5 shows that if Algorithm 1 terminates, then it returns a set with the desired properties. In Lemma 6, we show that the algorithm terminates in a polynomial number of iterations. In particular, we show that in step 6, there will always be a matroid in our collection that we can drop.

Lemma 5

Suppose that Algorithm 1 returns a set $R\subseteq N$. Then, R satisfies the properties stated in Theorem 2.

Proof

Note that $R\in \mathcal {B}_0$, as $M_0$ is only modified via deletions or contractions. Moreover, $w(R)\ge { OPT }$, where ${ OPT }$ is the optimal value of ($\mathrm{LP}_\mathrm{mat}$) for the input instance. Indeed, if $x^*$ is the current optimal solution, and we update our instance (via deletions, contractions, refinements, or dropping matroids), then $x^*$ restricted to the new ground set remains feasible for ($\mathrm{LP}_\mathrm{mat}$) for the new instance. This is immediate for deletions and contractions, and if we drop a matroid; it holds for refinements due to Lemma 4 (ii). So if the optimal value of ($\mathrm{LP}_\mathrm{mat}$) decreases, this is only because we contract elements with $x^*(e)=1$, which we include in R. It follows that $w(R)\ge { OPT }$.

It remains to show that R satisfies property (iii) of Theorem 2, i.e., R is $q_i$-independent in $M_i$ for all $i\in [k]$. To this end, consider the state of the algorithm at a point during its execution right before step 2. Hence, the instance may already have been modified through prior refinements, contractions, deletions, and relaxations. We claim that the invariant below holds throughout the algorithm:

If a subset $R'$ of the current ground set satisfies the properties of Theorem 2 with respect to the current instance, then the set R consisting of $R'$ and all elements contracted so far fulfills the properties of Theorem 2 with respect to the original instance.

To show the claim, it suffices to show that the invariant is preserved whenever we change the instance in the algorithm. Note that $R=R'$ unless the change involves contracting an element. First, one can observe that if the instance changes by deleting an element of value 0 or contracting an element of value 1, then the invariant is preserved. Next, consider step 5, where we refine $M'=(N',\mathcal {I}')\in \mathcal M$ to obtain $M'\vert _S=(S,\mathcal I'_1)$ and $M'/S=(N'\setminus S,\mathcal I'_2)$ whose q-values are set to $q_{M'}$. We are given that $\chi ^{R'}\vert _{S}\in q_{M'}P_{\mathcal I'_1}$ and $\chi ^{R'}\vert _{N'\setminus S}\in q_{M'}P_{\mathcal I'_2}$, and we have $R=R'$. So by Lemma 4 (i), we have $\chi ^R/q_{M'}\in P_{\mathcal I'}$, or equivalently $\chi ^R\in q_{M'}P_{\mathcal I'}$.

Finally, consider the case where a matroid $M'=(N',\mathcal {I}')\in \mathcal M$ gets dropped in step 6. We have $R=R'$, and we need to show that $\chi ^R\vert _{N'}\in q_{M'} P_{\mathcal {I'}}$. Let $x^*$ be the optimal solution used in the algorithm when $M'$ was dropped. We have $|N'| - x^*(N') < q_{M'}$, and since $x^*(N')=r'(N')$, and both $|N'|$ and $q_{M'}$ are integral, this implies $|N'| - x^*(N') \le q_{M'}-1$. So $N'$ can be partitioned into a basis of $M'$, which has size $r'(N')=x^*(N')\ge |N'|-(q_{M'}-1)$, and at most $q_{M'}-1$ other singleton sets. Each singleton $\{e\}$ is independent in $M'$, since $0<x^*(e)\le r'(\{e\})$ as $x^*\vert _{N'}\in P_{\mathcal I'}$. Therefore, $N'$ can be partitioned into at most $q_{M'}$ independent sets of $M'$. Intersecting these sets with R shows that $R\cap N'$ can be partitioned into at most $q_{M'}$ independent sets of $M'$.    $\square$

We now prove that the algorithm terminates. Note that refinements guarantee that whenever the algorithm is at step 6, then for any $M'=(N',\mathcal I')\in \mathcal M$, only the constraint of $P_{\mathcal {I}'}$ corresponding to $N'$ may be $x^*$-tight. This allows us to leverage ideas similar to those in [2, 14] to show that step 6 is well defined.

Lemma 6

Algorithm 1 terminates in at most $(2k+1)|N|$ iterations.

Proof

We show that whenever the algorithm is at step 6, then at least one matroid in our collection can be dropped. This implies the above bound on the number of iterations as follows. There can be at most |N| deletions or contractions. Each matroid $M_i=(N_i,\mathcal I_i)$ in our input spawns at most $|N_i|$ refinements, as each refinement of a matroid creates two matroids with disjoint (nonempty) ground sets. This also means that step 6 can be executed at most k|N| times.

We focus on showing that step 6 is well defined. Consider the current collection of matroids $\mathcal M$. (Recall that $\mathcal M$ does not contain the current version of $M_0$.) Let $x^*$ be the current basic solution, which is not integral; otherwise every element would have been deleted or contracted in step 3 and we would have terminated in step 4. Since we deleted all elements e with $x^*(e)=0$, the current ground set N satisfies .

Consider a full-rank subsystem of ($\mathrm{LP}_\mathrm{mat}$), $Ax=b$, consisting of linearly independent, $x^*$-tight constraints. By standard uncrossing arguments, we may assume that the constraints of $Ax=b$ coming from a single matroid correspond to a nested family of sets. The system $Ax=b$ must contain some constraint corresponding to a matroid $M'\in \mathcal M$. Otherwise, we would have a full-rank system consisting of constraints coming from only one matroid, namely $M_0$, which would yield a unique integral solution; but $x^*$ is not integral. Furthermore, for a matroid $M'=(N',\mathcal I')\in \mathcal M$, the only constraint of $P_{\mathcal {I}'}$ that can be $x^*$-tight corresponds to $N'$, as otherwise, $M'$ would have been refined in step 5. So a matroid $M'\in \mathcal M$ gives rise to at most one row of A, which we denote by $A_{M'}$ if it exists. Let $\emptyset \subsetneq S_1\subsetneq \ldots \subsetneq S_p\subseteq N_0=N$ denote the nested family of sets that give rise to the constraints of $M_0$ in our full-rank system.

Consider the following token-counting argument. Each $e\in N$ gives $x^*(e)$ tokens to the row of A corresponding to the smallest set $S_\ell$ containing e (if one exists). It also supplies $\bigl (1-x^*(e)\bigr )/q_{M'}$ tokens to every row $A_{M'}$ corresponding to a matroid $M'\in \mathcal M$ whose ground set contains e. Since the q-values satisfy (2), every $e\in N$ supplies at most one unit of token in total to the rows of A. Every row of A corresponding to a set $S_\ell$ receives $x^*(S_\ell )-x^*(S_{\ell -1})$ tokens, where . This is positive and integer, and thus at least 1. We claim that there is some $e\in N$ that supplies strictly less than one token unit. Given this, it must be that there is a row $A_{M'}$ corresponding to a matroid $M'=(N',\mathcal I')\in \mathcal M$ that receives less than 1 token unit; thus $|N'|-x^*(N')<q_{M'}$ as desired.

Finally, we prove the claim. If every element supplies exactly one token unit, then it must be that: (i) $S_p=N$, (ii) inequality (2) is tight for all $e\in N$, and (iii) for every $e\in N$, every matroid $M'=(N',\mathcal I')\in \mathcal M$ with $e\in N'$ gives rise to a row $A_{M'}$. But then $\sum _{M'\in \mathcal M}\frac{1}{q_{M'}}\cdot A_{M'}=\chi ^N$, which is the row of A corresponding to the constraint of $M_0$ for the set $S_p$. This contradicts that A has full rank.    $\square$

3 Further Applications and Extensions

Generalized Matroidal Degree-Bounded Spanning Tree $(\textsc {gmdst})$. In this problem, we are given an undirected graph $G=(V,E)$ with edge costs $c\in \mathbb R^E$, disjoint node-sets $S_1,\ldots ,S_k$, and matroids $M_i=(\delta (S_i),\mathcal I_i)$ for all $i\in [k]$, where $\delta (S_i)$ is the set of edges of G that cross $S_i$. We want to find a spanning tree T of minimum cost such that $T\cap \delta (S_i)\in \mathcal I_i$ for all $i\in [k]$. This generalizes the matroidal degree-bounded MST problem considered by [21], wherein each node $\{v\}$ is an $S_i$ set. Clearly, each edge belongs to at most 2 ground sets of the matroids $\{M_i\}_{i \in [k]}$. Thus, by taking $M_0$ to be the graphic matroid and setting $w=-c$, Theorem 2 leads to a tree T of cost at most the optimum such that $T\cap \delta (S_i)$ is 2-independent in $M_i$ for all $i\in [k]$.

We remark that, whereas [21] obtains an O(1)-additive violation of the matroid constraints for matroidal degree-bounded MST problem, such a polytime additive guarantee is not possible for gmdst unless ${\textit{P}} = {\textit{NP}}$. This follows from the same replication idea used in Appendix A to rule out small additive violations for (1).

Extension to Knapsack Constraints. We can consider a generalization of (1), where, in addition to the matroids $M_0, \dots , M_k$ (over subsets of N) and weight vector $w\in \mathbb R^N$, we have t knapsack constraints, indexed by $i = k + 1, \dots , k + t$. The i-th knapsack constraint is specified by a ground set $N_i\subseteq N$, cost vector $c^i\in \mathbb {R}^{N_i}_{\ge 0}$, and budget $U_i\ge 0$. The goal is to find a maximum-weight set R such that $R\in \mathcal {B}_0\cap \mathcal I_1\cap \ldots \cap \mathcal I_k$, and satisfying $c^i(R\cap N_i)\le U_i$ for all $i=k+1,\ldots ,k+t$.

We consider the natural LP-relaxation ($\mathrm{LP}_\mathrm{matkn}$) for this problem, and extend Theorem 2 to obtain the following result; we sketch the proof in Appendix B.

Theorem 7

Let $q_1,\ldots , q_{k + t} \in \mathbb {Z}_{\ge 1}$ be such that $\sum _{i\in [k + t]: e\in N_i} \frac{1}{q_i} \le 1$ for all $e\in N$. If ($\mathrm{LP}_\mathrm{matkn}$) is feasible, then one can efficiently compute $R \subseteq N$ such that (i) $R\in \mathcal {B}_0$; (ii) $w(R)\ge { OPT }_{\mathrm{LP}_{matkn}}$; (iii) R is $q_i$-independent in $M_i$ for all $i \in [k]$; and (iv) $c^i(R \cap N_i) \le U_i + q_i\cdot \bigl (\max _{e\in N_i}c^i_e\bigr )$ for all $i\in \{k + 1, \dots , k + t\}$.

Appendices

A Impossibility of Achieving Small Additive Violations

We show that Theorem 2 for problem (1) cannot be strengthened to yield a basis of $M_0$ that has small additive violation for the matroid constraints of $M_1,\ldots ,M_k$, even when $k=2$.

We first define additive violation precisely. Given a matroid $M = (N,\mathcal {I})$ with rank function r, we say that a set $R \subseteq N$ is $\mu \text {-}additively\,independent$ in M if $|R|-r(R) \le \mu$; equivalently, we can remove at most $\mu$ elements from R to obtain an independent set in M. Unlike results for degree-bounded spanning trees, or matroidal degree-bounded MST [21], we show that small additive violation is not possible in polytime (assuming P $\ne$ NP) even for the special case of (1) where $k=2$, so we seek a basis of $M_0$ that is independent in $M_1,M_2$.

Theorem 8

Let $f(n) = O(n^{1-\varepsilon })$, where $\varepsilon > 0$ is a constant. Suppose we have a polytime algorithm $\mathcal {A}$ for (1) that returns a basis B of $M_0$ satisfying $|B|\le r_i(B)+f(|N|)$ for $i=1,2$ (where $r_i$ is the rank function of $M_i$). Then we can find in polytime a basis of $M_0$ that is independent in $M_1,M_2$.

The problem of finding a basis of $M_0$ that is independent in $M_1,M_2$ is NP-hard, as shown by an easy reduction from the directed Hamiltonian path problem. Thus, Theorem 8 shows that it is NP-hard to obtain an additive violation for problem (1) that is substantially better than linear violation.

Proof of Theorem

8. Choose t large enough so that $t > 2f(t|N|)$. Since $f(n) = O\bigl (n^{1-\varepsilon }\bigr )$, this is achieved by some $t={{\,\mathrm{poly}\,}}(|N|)$. For each $i \in \{0, 1, 2\}$, let $M'_i$ be the direct sum of t copies of $M_i$. Let $N'$ be the ground set of these matroids, which consists of t disjoint copies of N, which we label $N_1,\ldots ,N_t$.

Clearly, the instance $(M'_0, M'_1, M'_2)$ is feasible iff the original instance is feasible. Suppose that running $\mathcal {A}$ on the replicated instance yields a basis $R'$ of $M'_0$ that has the stated additive violation for the matroids $M'_1, M'_2$. Hence, there are two sets $Q_1,Q_2\subseteq R'$ with $|Q_1|,|Q_2|\le f(t|N|)$, such that $R'\setminus Q_i$ is independent in $M'_i$ for $i = 1, 2$. Hence, $R'\setminus (Q_1\cup Q_2)$ is independent in both $M'_1$ and $M'_2$. Because $|Q_1\cup Q_2| \le 2f(t|N|) < t$, we have by the pigeonhole principle that there is one $j\in [t]$ such that $(Q_1\cup Q_2)\cap N_j=\emptyset$. This implies that $R = R'\cap N_j = (R'\setminus (Q_1\cup Q_2))\cap N_j$, when interpreted on the ground set N, is independent in both $M_1$ and $M_2$. Moreover, the elements of R, when interpreted on the ground set N, are a basis in $M_0$ because $R'$ is a basis in $M'_0$. Hence, R is the desired basis without any violations.    $\square$

B Omitted Proofs

Proof of Corollary

3. Extend N by adding a set F of $r(N_0)$ additional elements with 0 weight, where r is the rank function of $M_0$. We modify $M_0$ to a matroid $\widehat{M}_0$ on the ground set $N_0\,\cup \,F$, given by the rank function . That is, $\widehat{M}_0$ is the union of $M_0$ with a free matroid on F, but then truncated to have rank $r(N_0)$. Let $P_{\widehat{\mathcal {B}}_0}$ be the matroid base polytope of $\widehat{M}_0$. It is now easy to see that if $x\in \mathbb R^{N_0\cup F}$ lies in $P_{\widehat{\mathcal {B}}_0}$, then $x\vert _{N_0}\in P_{\mathcal I_0}$. Moreover, we can extend $x\in \mathbb R^{N_0}$ with $x\in P_{\mathcal I_0}$ to $x'\in \mathbb R^{N_0\cup F}$ so that $x'\in P_{\widehat{\mathcal {B}}_0}$ and $x'\vert _{N_0}=x$. The corollary thus follows by applying Theorem 2 to $\widehat{M}_0, M_1, \ldots , M_k$.    $\square$

Proof sketch of Theorem

7. We first state the LP-relaxation ($\mathrm{LP}_\mathrm{matkn}$).

The algorithm leading to Theorem 7 is quite similar to Algorithm 1, and so is its analysis, and we highlight the main changes.

In the algorithm, whenever we contract an element e, for each knapsack constraint with $e\in N_i$, we now update $U_i\leftarrow U_i-c^i_e$ and drop e from $N_i$. After performing all possible deletions, contractions, and refinements, we now either drop a matroid $M'\in \mathcal M'$ in step 6 as before, or, we drop a knapsack constraint for some $i\in \{k+1,\ldots ,k+t\}$ if $|N_i|-x^*(N_i)\le q_i$.

To prove termination, we need only argue that we can always drop a matroid constraint, or a knapsack constraint in step 6 (modified as above). This follows from the same token-counting argument as in the proof of Lemma 6. Recall that if $Ax=b$ is a full-rank subsystem of ($\mathrm{LP}_\mathrm{matkn}$) consisting of linearly independent $x^*$-tight constraints, then we may assume that the rows of A corresponding to the $M_0$-constraints form a nested family $\mathcal {C}$. We define a token-assignment scheme, where each $e\in N$ supplies $x^*(e)$ tokens to the row of A corresponding to the smallest set in $\mathcal {C}$ containing e (if one exists), and $\bigl (1-x^*(e)\bigr )/q_{M'}$ to each row $A_{M'}$ coming from a matroid $M'\in \mathcal M$ in our collection whose ground set contains e. Additionally, every $e\in N$ now also supplies $\bigl (1-x^*(e)\bigr )/q_i$ tokens to each row of A originating from a knapsack constraint whose ground set contains e. Under this scheme, as before, given the constraint on our q-values, it follows that every $e\in N$ supplies at most 1 token unit. Also, as before, each row of A corresponding to an $M_0$ constraint receives at least 1 token unit. So either there is some row $A_{M'}$ coming from a matroid in $\mathcal M$ that receives strictly less than 1 token-unit, or there must be some row of A corresponding to a knapsack constraint that receives at most 1 token-unit; the latter case corresponds to a knapsack constraint i with $|N_i|-x^*(N_i)\le q_i$.

The proof of parts (i)–(iii) is exactly as before. To prove part (iv), consider the i-th knapsack constraint. Note that the only place where we possibly introduce a violation in the knapsack constraint is when we drop the constraint. If $x^*$ is the optimal solution just before we drop the constraint, then we know that $(c^i)^Tx^*\vert _{N_i}\le U_i$. (Note that $N_i$ and $U_i$ refer to the updated ground set and budget.) It follows that if S denotes the set of elements included from this residual ground set $N_i$, then the additive violation in the knapsack constraint is

$$\begin{aligned} c^i(S)-U_i\le c^i(N_i)-U_i\le \bigl (\max _{e\in N_i}c^i_e\bigr )\bigl (|N_i|-x^*(N_i)\bigr ) \le q_i\cdot \bigl (\max _{e\in N_i}c^i_e\bigr ). \end{aligned}$$

   $\square$