Introduction

The installation and maintenance of pre-tensioned fully grouted bolts sealed to the rock mass represents a high cost in the operating budget of transport infrastructures prone to rock hazard. In this context, clarifying different aspects of bolt performance and behavior is a substantial challenge which needs to be thoroughly investigated.

In the passive type of grouted bolt, a small sliding of the rock blocks leads the bolts to be activated. A shear and a tension force are developed in the bolt due to the confinement of sliding plane movements (Bjurstrom 1974; Dight 1982; Xiurun and Jianwu 1988; Spang and Egger 1990; Ferrero 1995; Pellet and Egger 1996; Li and Stillborg 1999; Hutchinson and Falmagne 2000; Oreste and Cravero 2008; Jalalifar and Aziz 2010a, b; Deb and Das 2011, 2014; Martin et al. 2013; Cao et al. 2013; Wang et al. 2014; Wyllie and Mah 2014; Nemcik et al. 2014; Aziz et al 2016; Li et al. 2016; Mohammadi et al. 2017; Bi et al. 2019; Saadat and Taheri 2020). However, the pre-tensioned type is installed under tension force before any rock block sliding occurs, and hence, the bolt contribution is enhanced through the applying a greater normal stress on the sliding plane, which permits an increase of the resistance against sliding movements (Ranjbarnia et al. 2016a, b). Therefore, two performances can be expected for active bolts:

  • The pre-tensioned force or the resultant normal stress prevents any sliding of rock blocks. In this case, no further forces are developed in rockbolts, and the grouting along the bolt length has no influence on its behavior. It will only protect the bolt from corrosion.

  • The pre-tensioned rockbolts cannot fully prevent the blocks from sliding. This performance can be due to the increase of the external load on the block, the generation of water pressure, and the creep of the rock. In this case, a small sliding will occur in the blocks, which will apply a shear and tension force to the active rockbolt similar to the passive one. Therefore, the bolt contribution is first activated by the pre-tensioned force and then by the subsequent axial and shear forces.

The issue of the rock slope stability by passive and pre-tensioned grouted rockbolts has been studied by variety of approaches such as laboratory, analytical, and numerical methods. While all of these studies has been devoted to find the bolt contribution against discontinuity sliding, some of them have also investigated to the issue of plastic hinges development on the bolt, and some others have focused on effective parameters of bolt performance.

In the first group, Spang and Egger (1990), by experimental study, explained that the rock blocks’ sliding imposes a shear deformation to rockbolts. It causes two points along the bolt that are then created: the first point is at the intersection of the joint and the bolt where the curvature of the deformed bolt and the bending moment are null. The other point is the location of the greatest curvature where the bending moment and the shear force are the maximum and zero, respectively. In the other similar investigation, Grasselli (2005) carried out large-scale experiments on various bolts and resulted in two plastic hinges that are produced in the bolt, symmetrically on either side of the joint plane, and the traction concentrated between these two plastic hinges is the primary reason of bolts failure. Jalalifar and Aziz (2010a, b) illustrated that the failure of a bolt occurred at its intersection with the joint plane where the combination of shear and axial forces is activated. In this study, a theoretical relation was suggested to find the positions of plastic hinges under various loading conditions, and it was shown that these positions are almost independent of pre-tensioned force. Wang et al. (2014) proposed an analytical approach in which the bolt was considered as a statically indeterminate beam with two fixed ends between of plastic hinges and discussed the relation of the axial and shear forces acting along with the bolt.In the other group of researches, Pellet and Egger (1996), by assuming the bolt as a semi-infinite beam with a trapezoidal distribution, presented an analytical approach for prediction of the bolt contribution in which the bolts are exposed to transverse and axial loads. The proposed method was unable to predict the bolt contribution when the bolt is perpendicular to the joint. Oreste and Cravero (2008), through an analytical simulation, showed that both of axial and transverse contribution of a bolt should to sliding be taken into account, and consideration of only axial force is not sufficient. Liu and Li (2017) conducted experimental studies and presented an analytical method for a bolted rock joint subjected to shearing. The results indicated that the angle between the bolt axis and the joint plane and the friction angle of the joint have a significant influence on the bolt contribution to prevent shearing. For a bolt inclination lower than the friction angle, they found that the bolt contribution is primarily provided by the axial forces rather than the shear forces. However, the rock strength at the joint/bolt interaction was ignored. In the other study, Chen et al. (2018) studied the shear behavior of bolted rock joints considering different roughness. It was found that the bolt deformation is directly in relation to the roughness, due to opening of the joint. Saadat and Taheri (2020), by direct shear tests bolted rock joints, observed that the shear strength of rock joints significantly improved for those having high roughness. Liu and Li (2020) used the minimum total potential energy principle and explored the bolt diameter, the rock strength, the bolting angle, and the friction angle of the joint affect the bolt’s contribution.

Despite the valuable achievements, there are still some shortcomings that need to be bridged. The influence of joint roughness angle (which is the case in reality) on the bolt contribution needs to be investigated. Furthermore, the role of pre-tensioning force has not been explored in the response of bolted joint sliding. In this regard, the interaction of pre-tensioned force with various factors such as bolt inclination, the rock strength, joint friction angle, and particularly the joint roughness is of great interest. Finally, the precise value of bolt deflection length (the locations of plastic hinges) is required to be used to exactly predict the bolt contribution.

Therefore, this paper presents a theoretical model to simulate the mechanical contribution of a pre-tensioned bolt to the confinement of a joint sliding. The proposed analytical model can be used for passive bolts, too. The problem is modeled by a 3D numerical to investigate the plastic state of bolt, which is not addressed in the proposed analytical simulation.

Analytical simulation

Problem definition and general assumptions

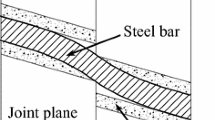
Tensioned rockbolts are installed across potential slide surfaces and bonded to sound rock beyond the surface. The application of a tensile force on the bolt, which is transmitted into the rock by a reaction plate at the rock surface, produces compression in the rock mass, and modifies the normal and shear stresses on the slide surface. The normal force and its corresponding stress on the joint plane improve when a pre-tensioned force is applied to the bolt, so the shear strength of the joint increases. However, if the added shear strength is not sufficient to prevent the rock block from sliding, a bolted rock joint will be subjected to a shear displacement, and additional bolt forces will be developed. Therefore, a shear force and an axial force are developed in the bolt due to the sliding and opening of the joint, respectively. In this case, considering the reinforcement performance of the rockbolt in rock slopes should include three components as follows:

  • The total axial force component, perpendicular to the joint plane, which increases the normal stress on the joint plane. The total axial force results from the applied pre-tensioned force and from the joint opening due to roughness when the sliding occurs.

  • The axial force component, parallel to the joint plane direction, applies a resistance against the joint sliding.

  • The bolt effect, which restrains the sliding of the joint by providing a transverse shear resistance

However, the following conditions are assumed to be satisfied for these effects:

  • The shear deformation of the bolted rock joint is perpendicular to the bolt axis.

  • There is a close and complete contact between the bolt and its surrounding medium (i.e., grout and rock) so that the rock mass immediately applies a transverse load to the bolt once sliding of the joint occurs.

  • The bolt should have proper shear strength and stiffness.

Figure 1 depicts a bolted rock joint subjected to shearing. The bolt deflects anti-symmetrically with respect to the joint plane and is separated from the grout in the joint vicinity. According to Fig. 2, after yielding, two plastic hinges are created in the bolt. Liu and Li (2017) proposed that the deflection length (distance between these two plastic hinges, i.e., points A and B in Fig. 2) is 2 to 3 times the bolt diameter, while Grasselli (2005) found a value of 1 to 2 times the bolt diameter. Therefore, the bolt contribution cannot be calculated directly due to uncertainty associated with the deflection length under shearing, which varies between 1 and 3db. Furthermore, Jalalifar and Aziz (2010a) demonstrated that the location of a hinge point from the joint plane is influenced by the rock strength and the applied axial force. The proposed relation is given by Eq. (1):

$${l}_{p}=\frac{1}{2}\sqrt{\frac{A{f}_{y}-\left(T+{N}_{O}\right)}{{\sigma }_{c}}}$$
(1)

where \({l}_{p}\) is the reaction length (hinge length), A is the cross-sectional area of the bolt, and \({f}_{y}\),T, \({\sigma }_{c}\), and \({N}_{O}\) are the yield strength of the rockbolt, pre-tensioned force, the uniaxial compressive strength of the rock/grout, and the bolt axial force at the rock joint, respectively.

Fig. 1
figure 1

Anti-symmetric deflection of bolt and it separation from the grout when joint subjected to shearing

Full size image
Fig. 2
figure 2

Plastic hinges formation at points A and B due to a shear displacement and load distribution on bolt from surrounding medium reaction

Full size image

If the bolt is separated from the grout under the shear displacement, the friction force at the bolt-grout interface along the deflection length is assumed to be equal to zero (Fig. 1; Liu and Li 2017, 2020).

The distribution of the reaction loading from the surrounding medium on the bolt perimeter surface (due to rock blocks sliding) can be considered as a trapezoidal one (Pellet and Egger 1996; Jalalifar and Aziz 2010a, b). Its magnitude depends on the compressive strength of the grout and rock and the applied force. Due to ribs at the bolt surface and the interlocking between the bolts and grout (friction force distribution), the distance between two plastic hinges is considered as a statically indeterminate beam with two ends fixed, as shown in Fig. 3 (Wang et al. 2014; Liu and Li 2017, 2020).

Fig. 3
figure 3

Beam model for deflecting length of bolt

Full size image

Structural analysis of the rockbolt

By releasing point B of Fig. 3, a statically determinate beam model is obtained as shown in Fig. 4. If the axial force, shear force, and bending moment at B are respectively named \({X}_{1}\), \({X}_{2}\), and \({X}_{3}\), the corresponding axial displacement, deflection, and rotation are \({\Delta }_{1}\), \({\Delta }_{2}\), and \({\Delta }_{3}\), respectively. Based on the force method equations and deformation compatibility relationships (Hibbeler 2012), the following can be written:

$$\left\{\begin{array}{c}{\delta }_{11}{X}_{1}+{\delta }_{12}{X}_{2}+{\delta }_{13}{X}_{3}+{\Delta }_{1q}={\Delta }_{1}\\ {\delta }_{21}{X}_{1}+{\delta }_{22}{X}_{2}+{\delta }_{23}{X}_{3}+{\Delta }_{2q}={\Delta }_{2}\\ {\delta }_{31}{X}_{1}+{\delta }_{32}{X}_{2}+{\delta }_{33}{X}_{3}+{\Delta }_{3q}={\Delta }_{3}\end{array}\right.$$
(2)

where \({\delta }_{ij}\) represents displacements of the primary structure due to the unit primary unknowns; these coefficients are called the unit displacements.\({\Delta }_{iq}\) represents displacements along the direction of unknown \({X}_{j}\). They are due to the action of the actual loads in the primary system. Displacements \({\Delta }_{iq}\) caused by the applied loads are called the loaded terms or free terms (Hibbeler 2012). These can be found by the virtual work principle as follows:

$${\delta }_{ij}=\left[\begin{array}{ccc}\frac{{2l}_{p}}{EA}& 0& 0\\ 0& \frac{8{l}_{p}^{3}}{3EI}& \frac{2{l}_{p}^{2}}{EI}\\ 0& \frac{2{l}_{p}^{2}}{EI}& \frac{2{l}_{p}}{EI}\end{array}\right]$$
(3)

and

$${\Delta }_{iq}=\left[\begin{array}{ccc}0& \frac{\kappa {q}_{0}{l}_{p}^{2}}{GA}+\frac{17}{12}\frac{{q}_{0}{l}_{p}^{4}}{EI}& \frac{{q}_{0}{l}_{p}^{3}}{EI}\end{array}\right]$$
(4)

where E and G are the elasticity modulus and shear modulus of the bolt, respectively. Parameters A and I indicate the area and the moment of inertia of the bolt section, respectively. Also, κ is a dimensionless parameter depending on the shape of the cross section. For circular sections, it is equal to 10/9 (Hibbeler 2012). The parameter q0 represents the maximal collection degree of the compressive load which can be applied to the bolt, so it remains in an elastic state, and 2lp is the bolt deflection length.

Fig. 4
figure 4

Simplification of beam model for rockbolt

Full size image

At point B, there is a plastic hinge; therefore, X2 = 0, and it is reasonable to assume that \({\Delta }_{3}=0\) (fixed support). Hence, substituting Eqs. (3) and (4) into Eq. (2) results in the following:

$$\left\{\begin{array}{c}\frac{2{l}_{p}}{EA}{X}_{1}={\Delta }_{1}\\ -\frac{2{l}_{p}^{2}}{EI}{X}_{3}+\frac{\kappa {q}_{0}{l}_{p}^{2}}{GA}+\frac{17}{12}\frac{{q}_{0}{l}_{p}^{4}}{EI}={\Delta }_{2}\\ \frac{2{l}_{p}}{EI}{X}_{3}=\frac{{q}_{0}{l}_{p}^{3}}{EI}\end{array}\right.$$
(5)

From Eq. (5), it can be obtained

$$\left\{\begin{array}{c}{X}_{1}=\frac{EA}{2{l}_{p}}{\Delta }_{1}\\ {q}_{0}=\frac{{\Delta }_{2}}{\frac{5}{12}\frac{{l}_{p}^{4}}{EI}+\frac{10}{9}\frac{{l}_{p}^{2}}{GA}}\\ {X}_{3}= \frac{1}{2}{q}_{0}{l}_{p}^{2}\end{array}\right.$$
(6)

Finally, the distribution of internal forces along the deflection length can be calculated by Eqs. (7) and (8).

$${Q}_{q}\left(x\right)=\left\{\begin{array}{ll}{q}_{0}x& 0\le x\le {l}_{p}\\ -{q}_{0}x+2{q}_{0}{l}_{p}& {l}_{p}\le x\le 2{l}_{p}\end{array}\right.$$
(7)
$${M}_{q}\left(x\right)=\left\{\begin{array}{ll}-\frac{1}{2}{q}_{0}{x}^{2}+\frac{1}{2}{q}_{0}{l}_{p}^{2}& 0\le x\le {l}_{p}\\ \frac{1}{2}{q}_{0}{x}^{2}-2{q}_{0}{l}_{p}x+\frac{3}{2}{q}_{0}{l}_{p}^{2}& {l\le }_{p}x\le 2{l}_{p}\end{array}\right.$$
(8)

where \({Q}_{q}\left(x\right)\) and \({M}_{q}\left(x\right)\) are respectively the shear force and bending moment equations, and \(x\) is the local coordinate system parallel to the bolt axis (Fig. 4).

Therefore, the shear force Qo and axial force No at the intersection (x = lp) can be calculated by the following:

$${Q}_{o}={q}_{0}{l}_{p}=\frac{{\Delta }_{2}}{\frac{5}{12}\frac{{l}_{p}^{3}}{EI}+\frac{10}{9}\frac{{l}_{p}}{GA}}$$
(9)
$${N}_{o}=\frac{EA}{2{l}_{p}}{\Delta }_{1}$$
(10)

From Fig. 5, for the point B, one can obtain the following:

$$\left\{\begin{array}{l}{\Delta }_{1}=u\ \mathrm{sin}\ \alpha +v\ \mathrm{cos}\ \alpha \\ {\Delta }_{2}=v\ \mathrm{sin}\ \alpha -u\ \mathrm{cos}\ \alpha \end{array}\right.$$
(11)

where u and v are the opening and shear displacements of the rock joint, respectively, and \(\alpha\) is the angle between the bolt axis and joint plane.

Fig. 5
figure 5

Deformation compatibility condition

Full size image

Denoting the dilation angle of the joint as i, the following equation can be obtained:

$$u=v\ \mathrm{tan}\ i$$
(12)

Combining Eqs. (11) and (12) results in the following:

$$\frac{{\Delta }_{2}}{{\Delta }_{1}}=\mathrm{tan}(\alpha -i)$$
(13)

The expression describing the relationship between Qo and No is then obtained by substituting Eqs. (9) and (10) into Eq. (13)

$$\frac{{Q}_{o}}{{N}_{o}}=K\ \mathrm{tan}(\alpha -i)$$
(14)
$$K=\frac{1}{\frac{5}{24}\frac{{l}_{p}^{2}A}{I}+\frac{5}{9}\frac{E}{G}}$$
(15)

where K is the bolt coefficient. The value of K depends on the deflection length and the geometric and mechanical parameters of the rockbolt. Furthermore, according to Eq. (1), the deflection length (lp) is affected by the rock strength (\({\sigma }_{c}\)), the axial forces (T + No), and the cross-sectional area of the bolt (A).

Calculation of the bolt contribution

The contributions of a pre-tensioned bolt to support a joint against sliding are provided by shear force Qo, axial force due to opening of joint No, and pre-tensioned force T as shown in Fig. 6:

$${R}_{Q}={Q}_{o}\ \mathrm{sin}\ \alpha - {Q}_{o}\ \mathrm{cos}\ \alpha\ \mathrm{tan}({\phi }_{r}+i)$$
(16)
$${R}_{N}={N}_{o}\ \mathrm{cos}\ \alpha + {N}_{o}\ \mathrm{sin}\ \alpha\ \mathrm{tan}({\phi }_{r}+i)$$
(17)
$${R}_{T}=T\ \mathrm{cos}\ \alpha +T\ \mathrm{sin}\ \alpha\ \mathrm{tan}({\phi }_{r}+i)$$
(18)

where \({\phi }_{r}\) is the residual friction angle of the joint plane.

Fig. 6
figure 6

Activated forces in the bolt at the rock joint

Full size image

According to Eqs. (16), (17), and (18), the components of \({Q}_{O}\ \mathrm{sin}\ \alpha\), \({N}_{O}\ \mathrm{cos}\ \alpha\), and \(T\ \mathrm{cos}\ \alpha\) directly prevent slipping and the components of \({N}_{O}\ \mathrm{sin}\ \alpha\ \mathrm{tan}\left({\phi }_{r}+i\right)\) and \(T\ \mathrm{sin}\ \alpha\ \mathrm{tan}({\phi }_{r}+i)\) create frictional resistance.

Based on previous studies (Pellet and Egger 1996; Jalalifar and Aziz 2010b; Liu and Li 2017), the bolt failure occurs at the joint (Fig. 6) where the Tresca failure criterion in terms of shear and axial forces reaches the following value:

$${Q}_{o}^{2}+\frac{1}{4}{({N}_{o}+T)}^{2}=\frac{1}{4}{(A{f}_{y})}^{2}$$
(19)

where \({f}_{y}\) is the yielding bolt stress.

According to Eq. (1), the hinges distance (i.e., 2 \({l}_{p}\)) depends on the developed bolt axial forces (No + T) while Eq. (14) calculates No and Qo in terms of lp. For finding the (lp), it is required to know the maximum value of the bolt axial force. Meanwhile, to calculate the (No), it is necessary to know the (lp). By the combination of Eqs. (1) and (15), we can obtain the following:

$$K=\frac{1}{\frac{5}{24{r}^{2}}\left(\frac{A{f}_{y}-(T+{N}_{o})}{{\sigma }_{c}}\right)+\frac{5}{9}\frac{E}{G}}$$
(20)

where r is the rockbolt cross section radius. Replacing Eqs. (19) and (20) into Eq. (14) gives Eq. (21) which calculates the value of (No):

$$\begin{aligned}4{\left(X-T\right)}^{2}{\mathrm{tan}}^{2}\left(\alpha -i\right)+{X}^{2}{\left[\frac{5}{24{r}^{2}}\left(\frac{A{f}_{y}-X}{{\sigma }_{c}}\right)+\frac{5}{9}\frac{E}{G}\right]}^{2}\\={(A{f}_{y})}^{2}{\left[\frac{5}{24{r}^{2}}\left(\frac{A{f}_{y}-X}{{\sigma }_{c}}\right)+\frac{5}{9}\frac{E}{G}\right]}^{2}\end{aligned}$$
(21)

where

$${N}_{o}=X-T$$

Therefore, the maximum axial force can be calculated for an elastic state due to the displacement of the rock (No). Afterward, the bolt coefficient (K) and maximum shear force in the bolt (Qo) can be found for the elastic state, using Eqs. (20) and (14), respectively.

The design support force provided by a pre-tensioned bolt against sliding for the yielding state can be expressed as follows:

$$\begin{aligned}R=&T\left(\mathrm{sin}\ \alpha\ \mathrm{tan}\left({\phi }_{r}+i\right)+\mathrm{cos}\ \alpha \right)+{N}_{o}\left[(\mathrm{cos}\ \alpha +\mathrm{sin}\ \alpha\ \mathrm{tan}({\phi }_{r}+i))\right. \\ & \left.+K\ \mathrm{tan}\left(\alpha -i\right)(\mathrm{sin}\ \alpha\ -\mathrm{cos}\ \alpha\ \mathrm{tan}\left({\phi }_{r}+i\right))\right]\end{aligned}$$
(22)

In the absence of pre-tension force, Eq. (22) gives the design support force for a passive grouted rockbolt.

Influence of the pre-tensioned force on the roughness angle

According to the Barton-Bandis joint model, the roughness angle of joints depends on the effective normal stress via Eq. (23) (Barton 1973; Barton and Choubey 1977; Barton et al. 1985):

$$i=\left[JRC\ {\mathrm{log}}_{10}\left(\frac{JCS}{{\sigma }_{n}}\right)\right]$$
(23)

where JRC is the joint roughness coefficient, JCS is the compressive strength of the rock at the fracture surface, and \({\sigma }_{n}\) is the effective normal stress which is created by two factors: the sliding block weight (\({\sigma }_{nW}\)) and the pre-tensioned load (\({\sigma }_{nT}\)). Thus

$${\sigma }_{n}={\sigma }_{nW}+{\sigma }_{nT}$$
(24)

where

$${\sigma }_{nT}=\frac{T\mathrm{sin}\alpha }{{s}_{l}{s}_{t}}$$
(25)

where \({s}_{l}\) and \({s}_{t}\) are the longitudinal and transverse bolt distances in a block if a systematic bolting pattern is used to stabilize a rock slope. The inclusion of the roughness angle into Eq. (22) gives the contribution of an active or passive bolt against the joint sliding:

$$\begin{aligned}R=&T\left(\mathrm{cos}\ \alpha +\mathrm{sin}\ \alpha\ \mathrm{tan}\left({\phi }_{r}+\left[JRC\ {\mathrm{log}}_{10}\left(\frac{JCS}{{\sigma }_{nW}+\frac{T\ \mathrm{sin}\ \alpha }{{s}_{l}{s}_{t}}}\right)\right] \right)\right)\\&+{N}_{o}\left[\left(\mathrm{cos}\ \alpha +\mathrm{sin}\ \alpha\ \mathrm{tan}\left({\phi }_{r}+\left[JRC\ {\mathrm{log}}_{10}\left(\frac{JCS}{{\sigma }_{nW}+\frac{T\ \mathrm{sin}\ \alpha }{{s}_{l}{s}_{t}}}\right)\right]\right)\right)\right. \\ & \left.+K\ \mathrm{tan}\left(\alpha -\left[JRC\ {\mathrm{log}}_{10}\left(\frac{JCS}{{\sigma }_{nW}+\frac{T\ \mathrm{sin}\ \alpha }{{s}_{l}{s}_{t}}}\right)\right]\right)\right. \\ & \left.\left(\mathrm{sin}\ \alpha -\mathrm{cos}\ \alpha\ \mathrm{tan}\left({\phi }_{r}+\left[JRC\ {\mathrm{log}}_{10}\left(\frac{JCS}{{\sigma }_{nW}+\frac{T\ \mathrm{sin}\ \alpha }{{s}_{l}{s}_{t}}}\right)\right]\right)\right)\right]\end{aligned}$$
(26)

Comparison between the results of proposed analytical approach and laboratory tests

In the case of passive grouted bolts, the results of experimental tests by Liu and Li (2017) are employed for the verification of presented analytical approach. In this case, four following combinations of bolt inclinations (with respect to the joint plane), i.e., α and joint effective friction angles i.e., \(\phi ={\phi }_{r}+i\), were considered for the experiments. The other parameters are shown in Table 1.

  • α = 90°, ϕr + i = 36.4°;

  • α = 75°, ϕr + i = 42.5°;

  • α = 60°, ϕr + i 38.7°; and

  • α = 45°, ϕr + i = 42.1°.

Table 1 Mechanical parameters of the steel bar and material (Liu and Li 2017)
Full size table

The current analytical approach predicts the yielding state of the bolt contribution. The ratio of the bolt's ultimate contribution to its yield contribution is almost equal to the bolt’s failure strength to its yield strength. Therefore, by multiplying the bolt contributions calculated from the analytical model by the ratio of the failure strength to the yield strength of the bolt, the ultimate bolt contributions are found by the analytical approach (Grasselli 2005; Liu and Li 2017, 2020). Figure 7 compares the ultimate bolt contribution by the reported laboratory tests and the analytical approach. As observed, there is a good agreement between the results.

Fig. 7
figure 7

Comparison between analytical model and experimental results for passive bolt

Full size image

For active bolts, the proposed analytical approach predictions are compared with the reported experimental data by Jalalifar and Aziz (2010a, b), which shear load was calculated at the yielding point under various conditions. According to Table 2, the maximum difference between two approaches is 9%, which is satisfactory.

Table 2 Comparison of the resistance predicted by the proposed analytical approach and experimental results
Full size table

Parametric analysis

A parametric analysis is performed to find the weight of some effective parameters. The resistance generated by the bolt to keep the joint from moving is influenced by the following:

  • The angle between the bolt axis and joint plane (\(\alpha\))

  • The roughness and friction angles of the rock joint (i and  \({\phi }_{r}\))

  • The uniaxial compressive strength of the rock or the grout (\({\sigma }_{c}\))

  • The pre-tensioned force (T)

For each investigated parameter, three values are selected so that they almost cover encountered practical conditions. For example, the joint roughness coefficient (JRC) varies from zero for smooth, planar, and particularly slickenside surfaces to as much as 20 for rough, undulating surfaces (Barton 1973). Also, the range of the pre-tensioning bolt varies from 0 to 50% of the bolt’s yielding capacity, and the rock strengths vary from medium strong rock to very strong rock.

Some bolt parameters are fixed as standard values of E = 206 GPa, G = 79 GPa, fy = 600 MPa, db = 25 mm, JCS = 50 MPa, =\(\frac{\mathrm{JCS}}{{\sigma }_{nW}}\)  = 3.17, and sl = st = 1 m. A parametric analysis is performed to evaluate the \(\alpha\), i, \({\sigma }_{c}\), and T with basic values of \({\phi }_{r}\) = 35 \(^\circ\), JRC = 10, \({\sigma }_{c}\) = 50 MPa, and T = 80 kN.

Influence of the joint roughness, rock strength and pre-tensioned force on (\(\frac{{Q}_{0}}{{N}_{0}+T}\))

In this part, the contribution of the pre-tensioned bolt is given in terms of a dimensionless parameter (\(\frac{{Q}_{0}}{{N}_{0}+T}\)), which corresponds to the ratio of the shear force to the axial force. If this ratio decreases, the bolt contribution improves the stability of the joint, because, according to the Tresca strength criterion, the axial loading capacity of a steel bolt is higher than the shear one (i.e., the No + T is activated in the bolt, so RN and RT are created in the joint plane).

The influence of the joint roughness on the bolt contribution for different bolt inclination angles is presented in Fig. 8. As observed, when the bolt inclination angle is equal to the joint roughness angle, the bolt is subjected to a pure tension force. In this case, the shear force component is not developed. When the inclination of the bolt increases, the shear force (Qo) is activated gradually, which rapidly decreases the total capacity of the bolt. This trend is intensified for \(\alpha >70^\circ\), particularly for smaller roughness angles. When the roughness angle is increased, the value of the No rises due to the use of the axial capacity of the bolt, which increases not only the RN but also the RT (influence on No and \(({\phi }_{r}+i)\)).

Fig. 8
figure 8

Influence of JRC on \(\frac{{Q}_{o}}{{N}_{o}+T}\) for different values of bolt inclination angles (case of \({\sigma }_{c}\) = 50 MPa and T = 80 kN)

Full size image

Figure 9 illustrates the effect of the rock strength (or grout strength) on the bolt contribution. For high inclination angles (where great shear force is induced in the bolt), the rock mass strength surrounding the bolt is more important than small inclination angles, which no effect is observed for \(\alpha <30^\circ\). A great shear force is induced in the bolt when the rock mass strength rises because \({\sigma }_{c}\) has an inverse relationship with the distance of plastic hinges (2lp). Therefore, for the high-strength rock, the length of the beam becomes small, which reduces the bolt contribution.

Fig. 9
figure 9

Influence of \({\sigma }_{c}\) on \(\frac{{Q}_{o}}{{N}_{o}+T}\) for different values of bolt inclination angles (case of JRC = 10 and T = 80 kN)

Full size image

As expected, when the bolt inclination is greater than the sum of the friction and roughness angles (\(\alpha >{\phi }_{r}+i\)), the \(\frac{{Q}_{0}}{{N}_{0}+T}\) decreased for high pre-tensioned force cases, particularly for perpendicular installed bolt. This is not only the benefit due to the pre-tensioned bolt, but also the frictional resistance is activated due to the initial tension. Therefore, the sliding potential and shear movements are reduced, and the bolt is less sheared (Fig. 10). Furthermore, the No and Qo components are activated by the movement of the rock block and cause the resistances of RN and RQ on the rock joint, respectively. For \(\alpha \le {\phi }_{r}+i\), the value of shear force (Qo) is low and it is expected that the bolt contribution will increase due to the rise of (No + T).

Fig. 10
figure 10

Influence of pre-tensioned force on \(\frac{{Q}_{o}}{{N}_{o}+T}\) for different values of the bolt inclination angle (case of JRC = 10, \({\sigma }_{c}\) = 50 MPa)

Full size image

For passive bolts, when the inclination of the bolt is less than the friction angle of the joint, the component of No is activated by the sliding of the rock block and used from the axial capacity of the bolt, but the active bolt can generate the component of T for any inclination without sliding. Therefore, the difference between T = 0 kN and T = 150 kN is small when the inclination of the bolt is less than the friction angles of the joint. Both cases utilize the axial capacity of the bolt.

The effect of different parameters on the bolt’s support force

To evaluate the effect of the bolt pre-tension in detail, the effects of the joint roughness and rock strength are combined with bolt pre-tensioned force values. Figure 11 depicts how joint roughness and pre-tensioned force can affect the maximum and minimum bolt contribution. According to Fig. 11, it seems that the joint roughness, similar to pre-tensioned force, is a beneficial parameter for enhancing the bolt contribution (the pre-tensioned force is equal to 27% of the bolt yielding capacity). However, for different conditions, the position of the greatest bolt contribution is not unique and depends on the joint roughness angle. In these cases, the maximum bolt contribution occurs in the join plane where the bolt inclination angle is equal to the sum of the friction and roughness angles (\({\phi }_{r}+i\)). Furthermore, the bolt contribution quickly falls at a unique rate (for all cases) from maximum to minimum values when the inclination angle becomes great. Also, for the same bolt inclination, the cases with low pre-tensioned force or roughness angle lead to the minimum bolt contribution.

Fig. 11
figure 11

Influence of JRC on the contribution of pre-tensioned bolts (case of \({\phi }_{r} =\) 35°, \({\sigma }_{c}=\) 50 MPa)

Full size image

Figure 12 shows that the maximum and minimum contributions of the bolt are also influenced by the strength of the rock/grout. A high-strength rock leads to the distance between the plastic hinges decreasing, so it reduces the resistance developed by the deformation of the bolt. Therefore, the pre-tension of the bolt is more effective for the high-strength rocks than the low-strength rocks.

Fig. 12
figure 12

Influence of \({\sigma }_{c}\) on the contribution of pre-tensioned bolts (case of \({\phi }_{r} =\) 35°, JRC = 10)

Full size image

The position of the maximum bolt contribution is influenced by the rock/grout strength and the pre-tensioned force. In contrast to the pre-tensioned force, the great value of the rock/grout strength leads to the bolt inclination angle becoming smaller than the sum of the roughness and friction angles for creating the maximum bolt contribution (\({\phi }_{r}+i\)).

Finally, according to Fig. 13, the bolt contribution improves with increasing the pre-tensioned force, especially when the bolt is steeply inclined with respect to the joint plane. In general, increasing the joint roughness and pre-tensioned force causes an improvement in the bolt contribution because these factors activate the axial resistance.

Fig. 13
figure 13

Influence of pre-tensioned load on the contribution of pre-tensioned bolts (case of \({\phi }_{r} =\) 35°, JRC = 10, \({\sigma }_{c}=\) 50 MPa)

Full size image

Plastic behavior of the bolt and modeling procedure

In rock slope engineering, it is strictly advised the ultimate load of rockbolt should not exceed than 60% of the ultimate strength of the steel (e.g., Wyllie and Mah 2014). Therefore, it is completely avoided from the plastic state of bolt for design purpose. However, for further investigation of the problem that might probably occur in very rare circumstances, this study is extended to the plastic state of bolt. Due to inherent limitations associated to the analytical approaches, it is carried out by a three-dimensional numerical simulation using a finite element software.

The modeling procedure includes creating a two blocks geometry with dimensions of 40 × 40 × 20 cm and the simulation of the rockbolt (db = 8 mm) and the surrounding grout (Fig. 14). Linear elasticity with perfect plasticity and elasticity were assumed to consider the bolt and grout behavior, respectively. The assigned properties of these materials are presented in Table 3 (Liu and Li 2017). For the boundary conditions, the lateral faces are closed in their normal direction. After inserting the bolt, the pre-tensioned load is applied in three steps: including pulling of the bolt, applying the reaction of the pre-tensioned force to the block, and applying the shear load. The used magnitudes of the pre-tensioned forces are T = 5 kN and 10 kN. Figure 15 represents the mesh of the rockbolt (twenty nodes finite elements of C3D20R type). For the length of the bolt located in the vicinity of the joint, a finer mesh was employed. The contact between the grout and bolt was simulated with no friction along the deflection length and with a rough contact in the remaining length (no-slip condition for remaining length).

Fig. 14
figure 14

Half of the geometry of modeling for inclination 45°

Full size image
Table 3 Mechanical parameters of materials (Liu and Li 2017)
Full size table
Fig. 15
figure 15

Meshing of the bolt

Full size image

Finally, the interaction module is used to assign joint plane properties, where its basic concept is the Coulomb friction model. The effective friction angle (sum of basic friction angle and roughness angle (\({\phi }_{r}+i\)) was introduced to the Coulomb friction model. That is to say, joint roughness was not directly introduced to ABAQUS software but was considered in the total value of friction angle.

Validation of the numerical model

For the passive rockbolt, the numerical predictions were compared with experimental and analytical results to validate the numerical results (Liu and Li 2017). Furthermore, analytical results were used to validate the active rockbolt. Figure 16 shows the shear displacements versus the shear loads for the passive rockbolts with different bolt inclinations. The results prove a good agreement between the numerical and experimental results. Furthermore, Table 4 compares the results of the analytical and numerical methods in yielding states, where the differences between the analytical and numerical results for passive bolts are satisfactory. Furthermore, for cases of pre-tensioned bolts, the differences between the analytical and numerical simulations are acceptable. In the case of α = 90 \(^\circ\), \(\left({\phi }_{r}+i\right)\) = 36.4 \(^\circ\), the greatest effect of the pre-tensioned force is seen due to reducing the shear force in the rockbolt.

Fig. 16
figure 16

Shear displacement versus shear load of the passive rock-bolts with different inclination

Full size image
Table 4
figure 17

Comparison of the resistance predicted by the numerical and analytical approach

Full size image

Results and discussions

Figure 17 shows a passive bolt which reaches the plastic state. As observed, the stress distribution is anti-symmetric on the deflection length of the bolt, and the maximum shear stress is concentrated at the bolt-joint intersection. Furthermore, the bolt yields at the vicinity of the rock joint and the displacement contour showed that the blocks are separated in the upper part of the bolt (Z direction) when the bolt yields (part A). Therefore, the friction between the blocks is not activated in the upper part of the bolt (part A). Meanwhile, in the lower part of the block, the blocks collide together and friction is activated (part B). Furthermore, the pre-tensioning of the bolt decreases the deformation of the block at the Z direction.

Fig. 17
figure 18

Deformation of the bolted rock block for cases of a α = 45°, T = 0 kN and b α = 45 \(^\circ\), T = 10 kN. c α = 90 \(^\circ\), T = 0 kN and d α = 90 \(^\circ\), T = 10 kN

Full size image

Figure 18 shows the shear displacement versus the shear load for 75 \(^\circ\) and 45° inclination and pre-tensioned forces. When the pre-tensioned force does not apply, the rockbolt yields with great shear deformation. Furthermore, the pre-tensioned force is more effective in the case of 75 \(^\circ\) than the case of 45 \(^\circ\) due to reducing the shear force at the bolt.

Fig. 18
figure 19

Shear displacement versus shear load of the bolts for case of a α = 75°, \(\left({\phi }_{r}+i\right)\) = 42.5° and b α = 45°, \(\left({\phi }_{r}+i\right)\) = 42.1°

Full size image

Conclusions

This paper presented a straightforward theoretical simulation of mechanical performance of grouted pre-tensioned (active) and passive rockbolts in the stability of a layered rock slope. The proposed analytical method can also predict the resistance role of the bolt in its starting yielding state. The general outcome of this study which could be drawn is that the bolt inclination, the strength of the medium around the bolt, the joint friction and roughness, and the pre-tensioned force all have an effective role in the activation of the bolt’s contribution against sliding. The extent of each parameter’s role depends upon the conditions, e.g.:

  • For higher pre-tensioned force, the bolt contribution is the maximum when the bolt inclination is equal to the sum of the friction angle and roughness angle (\({\phi }_{r}+i)\).

  • The minimum bolt resistance is generated where the bolt axis is perpendicular to the joint plane, because the maximum shear component of bolt force is mobilized.

  • The maximum bolt contribution is developed when both the shear and axial components of bolt forces are activated.

  • A high-strength rock block reduces the distance between the plastic hinges, and the resistance developed by the deformation of the bolt decreases. Furthermore, the pre-tensioning of the bolt is more effective for the high-strength rocks than the low-strength rocks.

  • Like the pre-tensioned force, the joint roughness severely stimulates the axial component of the bolt contribution due to the opening of the joint.

However, the presented theoretical approach has some limitations, such as not considering the plastic state of grouted bolts that might unintentionally occur in very rare circumstances. Therefore, the problem was simulated by numerical method (ABAQUS software). The distinguished results from numerical study are:

  • The developed stress distribution on the rockbolt, due to shear movement of joint, is anti-symmetric with respect to joint plane;

  • An increase in the pre-tensioned force leads to a reduction in the shear movement of the joint. However, a slight shear deformation may cause the bolt to become plastic, which is avoided in practice. The more pre-tensioned force, the less required shear deformation to plasticize the bolt, and the more caution to prevent shear deformation.

  • When the bolt is in the plastic state, if the shearing of the joint plane continues, a part of the moving (unstable) rock block located on one side of the bolt is separated from the stable rock block; therefore, the friction resistance between the blocks at this part of the joint plane is gradually diminished.

Finally, it should be remembered that the presented simulations do not address the issue of rock slopes with random discontinuities. In fact, this study covers all of planner joint movements.