Stability of bolt-supported concealed bedding rock slopes with respect to bi-planar failure

Abstract

Bi-planar failure is one of the most common issues encountered in concealed bedding rock slopes (CBRSs). Fully grouted bolts are widely adopted to improve the stability of slopes and prevent failure due to their high efficacy and low cost. In this study, a bi-planar mechanical model is first established for the sliding body based on the interactions between active and passive blocks. The supporting forces supplied by fully grouted bolts are then introduced and limit equilibrium theory is used to analyze the stability of the bolted CBRSs. A parametric analysis is conducted to investigate the effects of varying the bolt angle (angle of the bolt with respect to the joint plane), bolt diameter, and bolt location on the stability of the CBRSs. Finally, comparisons are made between results obtained using the proposed method of analysis and discrete element modeling. The results obtained using the two different approaches are in good agreement. There is an optimal bolt angle that maximizes the stability of the bolted CBRSs–its value is approximately equal to the friction angle of the joint. The slope stability (and contribution made by the bolts) also increases with the diameter of the bolts used, the variation increasing according to a power function. The proposed method of analysis offers a sound basis for better understanding the mechanism by which fully grouted bolts reinforce such slopes and can be used as a useful design aid for protecting CBRSs against bi-planar failure.

Introduction

A bedding rock slope is a layered rock slope in which the slope surface has approximately the same trend and dip direction as the rock strata. They are commonly encountered in engineering projects in a wide range of situations, e.g., construction of mountain roads and railways, building hydroelectric power stations, and open-pit mining (Li et al. 2018; Lu and Cai 2019; Sun et al. 2019; Zhao et al. 2019; Wu et al. 2020; Sun et al. 2022). Such slopes can be further subdivided into “overdip” and “concealed” slopes depending on the relationship between the slope angle and dip angle of the rock strata (Cruden 2000; Huang 2007).

Overdip slopes have slope angles that are steeper than the dip of the rock strata. In this case, the failure modes encountered are easy to identify and prevent as the potential slip surfaces are exposed on the slope. In contrast, concealed slopes have slope angles that are less than or equal to the dip of the rock strata. This means that their potential slip surfaces are not directly exposed on the slope surface. As a result, they can readily accumulate energy, and this can lead to large-scale landslides. Moreover, there are no obvious signs that a landslide is imminent and so they can be extremely hazardous phenomena (Yin et al. 2011; Havaej et al. 2015; Song et al. 2022). Bi-planar failure is the most common form of instability in such slopes. In this failure mode, the slip surface is composed of both steeply and gently dipping joints (Fisher 2009; Alejano et al. 2011; Chen et al. 2020; Huang et al. 2020).

The stability of concealed bedding rock slopes (CBRSs) with respect to bi-planar failure is primarily governed by the strength of the pre-existing joints. Bi-planar failure mechanisms have been extensively investigated and numerous methods of analysis used to evaluate the stability of CBRSs. Fisher (2009) provided specific guidance for assessing the stability state of bedding slopes based on an extensive literature review, numerical modeling, and parametric evaluation. Ning et al. (2011) and Havaej et al. (2014) analyzed bi-planar failure in CBRSs using numerical manifold and finite-discrete element methods, respectively. Alejano et al. (2011) performed a solid analytical work on the stability of CBRSs based on the tilt test, discrete element modeling and limit equilibrium theory, and proposed an accurate evaluation method for the stability of CBRSs. In addition, Sun et al. (2019, 2020) evaluated the stability of CBRSs against bi-planar failure by considering two conditions: one with and one without the daylighting joint at the toe of the slope, and Sun et al. (2021) assessed the stability of CBRSs with talus deposits accumulated at their toes.

Fully grouted bolts are widely employed to improve the stability of slopes due to their high efficacy and low cost (Liu and Li 2017; Zheng et al. 2019). The bolts contribute to the failure resistance of the slope by virtue of the combined effect of the shear and axial supporting forces mobilized within. Grasselli (2005) investigated the behavior of bolted rock joints using experimental tests and numerical modeling and hence presented the characteristics of the shear and traction contributions made by the bolts. Oreste and Cravero (2008) used a block reinforcement procedure to represent the dowel–rock interaction using a Winkler approach in both the normal and axial directions of the dowel, which is a more effective way of designing a passive reinforcing system. Cai et al. (2015) and Tan (2016) used elastoplastic analysis to assess the mechanical behavior of a reinforced mass according to the characteristics of the interaction between the grouted bolts and rock mass. Liu and Li (2017) proposed a mechanical model for a bolt-supported slope based on equations describing the forces and deformation–compatibility relationships. They hence described the contributions made by the axial and shear forces acting inside the bolts. These studies have enriched our understanding of the tension-shear coupling failure mechanism of the bolts in bolt-supported rock masses and provided methods for the analysis of the contribution made by the bolts to axial and shear resistance, but few studies have applied these methods to the stability evaluation of bedding rock slopes.

Siad (2001) analyzed the stability of bolt-supported jointed rock slopes using a kinematic method based on yield design theory and revealed the positive effect of using bolts as stabilizing reinforcements. Zheng et al. (2019) proposed a mechanical model to predict the stability of bolt-supported anti-dip bedding slopes and elucidated the optimal positions of the rock bolts. These studies have enhanced our understanding of the mechanisms by which fully grouted bolts reinforce slopes. However, only a few studies have been conducted on the stability of bolt-supported jointed slopes and even less research has been carried out on bi-planar failure in bolted CBRSs.

In this paper, a new method for evaluating the stability of bolt-supported CBRSs with respect to bi-planar failure is proposed. A bi-planar mechanical model for the sliding body is established based on the interactions occurring between active and passive blocks. The supporting force provided by the fully grouted bolts is then introduced and limit equilibrium theory is used to analyze the stability of the bolted CBRSs. Subsequently, a parametric analysis is carried out to investigate the effects of the bolt angle (i.e., the angle of the bolts with respect to the joint plane), bolt diameter, and bolt location on the stability of the CBRSs. Finally, the results obtained using the new analysis method are compared with those obtained via discrete element modeling.

Mechanical model and analytical method

Bi-planar failure model

Monoclinic sequences are the most important geological features of CBRSs and joints that are steeply dipping along the slope are very developed in such slopes. Under the influences of external factors, such as rainfall and earthquakes, it is easy for gently dipping joints to penetrate the surface at the toe of the slope. As a result, bi-planar sliding failure occurs along these joints. This type of sliding body can be further divided into active and passive blocks (Huang 2007; Alejano et al. 2011; Yin et al. 2011; Sun et al. 2020). The active block, driven by the sliding force of its own weight, slides along the interlayer structural surface of the slope. The passive block at the toe of the slope is passively squeezed due to the anti-slip effect–eventually, this squeezing exceeds a critical amount, equilibrium is lost, and a landslide occurs.

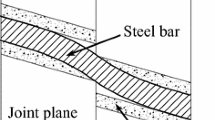
Fully grouted bolts are widely used in slope reinforcement as they are an effective and low-cost measure capable of preventing landslides. A typical bolt-supported CBRS is shown in Fig. 1a and the corresponding conceptual diagram is illustrated in Fig. 1b.

Fig. 1

A typical bolt-supported CBRS: a photograph and b conceptual diagram

The boundary between the active and passive blocks is the key to establishing a good mechanical model for bi-planar failure. Various assumptions are often made about the nature of this interblock boundary but the main assumption relates to its orientation which is often taken to be vertical, horizontal, or perpendicular to the surface of the slope (Chen and Peng 1996; Siad and Megueddem 1998; Alejano et al. 2011).

In this paper, the interblock boundary is assumed to pass through the point where the steeply dipping and gently dipping joints intersect and is oriented perpendicular to the gently dipping joint. This is because an internal shear surface is generated inside the bi-planar sliding body, according to the bi-planar failure mechanism (Fisher 2009; Sun et al. 2019). In order to better match the internal shear surface and more conveniently perform force analysis of the active and passive blocks, the mechanical model is thus established for bi-planar failure, as shown in Fig. 2.

Fig. 2

Mechanical model for bi-planar failure: a block model and b force diagram

Analysis of the CBRS

To account for the complex behavior of the CBRS when bi-planar failure occurs, the following assumptions are made from a theoretical point of view: (1) the interblock boundary passes through the point of intersection of the steeply and gently dipping joints and is oriented perpendicular to the gently dipping joint, (2) the slip surface of the active block is much longer than that of the passive block, and (3) the safety factors of the active and passive blocks are equivalent and equal to the safety factor of the slope.

According to the force analysis of the active and passive blocks (Fig. 2b), the safety factors of these blocks can be obtained by dividing the sliding resistance (R_ij) by the sliding force (T_ij) acting on them. The formulae for the safety factors of the active and passive blocks are combined and the safety factor for the slope derived by eliminating the unknown normal force acting on the interblock boundary.

The shear force acting at the interblock boundary is difficult to determine accurately. The magnitude of the shear force, however, lies between two extreme states wherein: (1) the shear force is zero and (2) the shear force reaches the Mohr–Coulomb friction strength. It is noteworthy that although the Hoek–Brown criterion can be more suitable for describing the strength behavior of rock mass (Gharsallaoui et al. 2020; Chen et al. 2021, 2022a, b; Xia et al. 2022), the simple and commonly used Mohr–Coulomb criterion is used for the strength criterion in this work to facilitate practical engineering applications.

If the shear force ($S_{ra}$) on the interblock boundary is zero, the sliding force (T_1a) and sliding resistance force ($R_{1a}$) on the active block are given by

$${T}_{1a}={W}_{1} \sin {\theta }_{1}$$

(1)

$$\begin{aligned}R_{1a} =&\; \left[ {W_{1} \cos \theta_{1} + N_{ra} \sin \left( {\theta_{1} - \theta_{2} } \right)} \right]\\&\;\tan \varphi_{1} + c_{1} l_{1} + N_{ra} \cos \left( {\theta_{1} - \theta_{2} } \right)\end{aligned}$$

(2)

respectively, where W₁ is the weight of the active block, $l_{1}$ is the length of the slip surface of the active block, $l_{1} = l_{s} - t\cot \left( {\theta_{1} - \theta_{2} } \right) + t\cot \theta_{1}$ wherein $l_{s}$ is the length of the slope and t is the depth of the sliding body, $\theta_{1}$ and θ₂ are the dip angles of the steeply and gently dipping joints, respectively, $N_{ra}$ is the normal force acting on the interblock boundary, and c₁ and $\varphi_{1}$ are the cohesion and friction angle of the steeply dipping joint, respectively.

Similarly, the sliding force (T_2a) and sliding resistance force ($R_{2a}$) on the passive block are given by

$${T}_{2a}={W}_{2} \sin {\theta }_{2}+{N}_{ra}$$

(3)

$$R_{2a} = W_{2} \cos \theta_{2} \tan \varphi_{2} + c_{2} l_{2}$$

(4)

respectively, where W₂ is the weight of the passive block, $l_{2}$ is the length of the slip surface of the passive block, $l_{2} = t\csc \left( {\theta_{1} - \theta_{2} } \right)$, and c₂ and $\varphi_{2}$ are the cohesion and friction angle of the gently dipping joint, respectively.

Combining Eqs. (1)–(4), the safety factor of the slope (F_s) is obtained by eliminating the normal force acting at the interblock boundary ($N_{ra}$), as follows:

$$\left.\begin{array}{c}{F}_{s}={R}_{1a}/{T}_{1a}\\ {F}_{s}={R}_{2a}/{T}_{2a}\end{array}\right\}$$

(5)

If the shear force ($S_{rb}$) on the interblock boundary reaches the Mohr–Coulomb friction strength, ${S}_{rb}={N}_{rb} \tan {\varphi }_{r}+{c}_{r}{l}_{r}$ (where $N_{rb}$ is the normal force on this boundary, c_r and $\varphi_{r}$ represent, respectively, the cohesion and friction angle of the rock mass, and $l_{r}$ is the length of the interblock boundary, $l_{r} = t\sec \left( {\theta_{1} - \theta_{2} } \right)$, the sliding force (T_1b) and sliding resistance force ($R_{1b}$) on the active block are given by

$${T}_{1b}={W}_{1} \sin {\theta }_{1}$$

(6)

$$\begin{aligned} R_{1b} =&\; \left[ {W_{1} \cos \theta_{1} + N_{rb} \sin \left( {\theta_{1} - \theta_{2} } \right) - S_{rb} \cos \left( {\theta_{1} - \theta_{2} } \right)} \right]\tan \varphi_{1} \\& + c_{1} l_{1} + N_{rb} \cos \left( {\theta_{1} - \theta_{2} } \right) + S_{rb} \sin \left( {\theta_{1} - \theta_{2} } \right) \end{aligned}$$

(7)

Similarly, the sliding force (T_2b) and sliding resistance force ($R_{2b}$) on the passive block are given by

$${T}_{2b}={W}_{2} \sin {\theta }_{2}+{N}_{rb}$$

(8)

$$R_{2b} = \left( {W_{2} \cos \theta_{2} + S_{rb} } \right)\tan \varphi_{2} + c_{2} l_{2}$$

(9)

A similar derivation for the safety factor of the slope (F_s) can be carried out, giving

$$\left. \begin{array}{l} F_{s} = {{R_{1b} } \mathord{\left/ {\vphantom {{R_{1b} } {T_{1b} }}} \right. \kern-0pt} {T_{1b} }} \\ F_{s} = {{R_{2b} } \mathord{\left/ {\vphantom {{R_{2b} } {T_{2b} }}} \right. \kern-0pt} {T_{2b} }} \end{array} \right\}$$

(10)

These two hypothetical scenarios correspond to two extreme states of the slope stability. The actual safety factor for the slope must fall between these two scenarios. Therefore, for practical purposes, the mean value of these two safety factors is used to assess the stability of the CBRS with respect to bi-planar failure.

Analysis of the support provided by a bolt

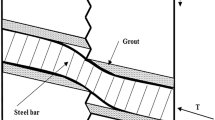
The fully grouted bolts generate a supporting force when there is a small transverse displacement of the bolted rock mass. This “dowel effect” of the bolts is activated by a small shear displacement which produces a shear supporting force in the bolts that contributes to the stability of the slope. In addition, the “pull-out” effect is activated by axial displacement which produces an axial supporting force in the bolts. Thus, the shear and axial forces in the bolts contribute to the forces acting to prevent sliding along the joint and hence play an important role in improving the stability of the slope (Fig. 3).

Fig. 3

Sketch of a bolt-reinforced joint

According to Fig. 3, the supporting force provided by one bolt (R) can be expressed as:

$$R = R_{N} + R_{Q} = N_{0} (\cos \alpha + \sin \alpha \tan \varphi_{j} ) + Q_{0} (\sin \alpha - \cos \alpha \tan \varphi_{j} )$$

(11)

where $\alpha$ is the angle of the bolt with respect to the joint, $\varphi_{j}$ is the friction angle of the joint, $R_{N}$ and $R_{Q}$ are the support forces provided by the axial and shear forces, respectively, and $N_{0}$ and $Q_{0}$ are the axial and shear forces acting in the bolt, respectively.

By considering the contributions the bolts make to the forces acting against bi-planar sliding failure, expressions can be obtained for the safety factor of the bolted CBRS by combining Eqs. (5), (10), and (11). Two sets of formulae can be obtained in the following ways:

• 1. If the shear force on the interblock boundary is assumed to be zero, the safety factor of the bolted CBRS is given by

  $$\left. \begin{array}{l} F_{s} = {{(R_{1a} + n_{1} R)} \mathord{\left/ {\vphantom {{(R_{1a} + n_{1} R)} {T_{1a} }}} \right. \kern-0pt} {T_{1a} }} \\ F_{s} = {{(R_{2a} + n_{2} R^{*} )} \mathord{\left/ {\vphantom {{(R_{2a} + n_{2} R^{*} )} {T_{2a} }}} \right. \kern-0pt} {T_{2a} }} \end{array} \right\}$$

  (12)

  where n₁ and n₂ are the numbers of bolt rows penetrating the steeply dipping and gently dipping joints, respectively, per unit width along the slope strike direction. In addition, R^* denotes the supporting force provided by one bolt at the gently dipping joint when the installation angle is the same as that of the bolt installed at the steeply dipping joint. Since the dip angles of the steeply dipping and gently dipping joints are different, α should be replaced with α^* ($\alpha^{*} = \theta_{1} - \theta_{2} + \alpha$) in Eq. (11) to calculate the value of R^*.

• 2. If the shear force on the interblock boundary is assumed to reach the Mohr–Coulomb friction strength, the safety factor of the bolted CBRS is given by

  $$\left. \begin{array}{l} F_{s} = {{(R_{1b} + n_{1} R)} \mathord{\left/ {\vphantom {{(R_{1b} + n_{1} R)} {T_{1b} }}} \right. \kern-0pt} {T_{1b} }} \\ F_{s} = {{(R_{2b} + n_{2} R^{*} )} \mathord{\left/ {\vphantom {{(R_{2b} + n_{2} R^{*} )} {T_{2b} }}} \right. \kern-0pt} {T_{2b} }} \end{array} \right\}$$

  (13)

As mentioned earlier, these two cases represent two extreme states describing the stability of the bolted CBRS. Also, the mean value of the safety factors in these two formulae is used for practical purposes to assess the stability of the bolted CBRS.

Effects of the bolt parameters

The fully grouted bolts used to support the CBRS are usually made of common materials (e.g., HRB400 steel and M30 grout), so their main design objects are the bolt angles used and their diameters. Moreover, the joint strength has a significant influence on the stability of the bolted CBRS based on the description given in Eqs. (12) and (13). Therefore, this section mainly focuses on the effects of bolt angle and diameter for joints of different strengths as well as the bolt location.

A generalized bolt-supported CBRS model is established based on the road cutting bedding slopes in the mountains (Liu et al. 2012; Zhao et al. 2019), as shown in Fig. 4. The model has a width of 190 m, height of 77 m, a slope angle (i.e., the dip angle of the steeply dipping joints) of 50°, and a gently dipping joint that dips at 30°. The length and depth of the sliding body are taken to be 50 m and 5 m, respectively.

Fig. 4

Geometry of the model slope considered

According to the basic quality (BQ) value analyzed from the geological characteristics of the slope, the BQ index of the rock mass is about III, so the values of the rock mass parameters can be taken based on the BQ index of the rock mass (National Standards Compilation Group of People’s Republic of China, GB/T 50218-2014 2014). In addition, the capacity of the fully grouted bolt mainly relies on the strength of the steel bar (Liu and Li 2017; Ranjbarnia et al. 2022), so the parameters of the bolt are obtained based on the properties of the HRB400 steel (National Standards Compilation Group of People’s Republic of China, GB 50010-2010 2015).

The specific values of the parameters used for the rock mass (unit weight γ_r, cohesion c_r, and friction angle φ_r) and bolts (elasticity modulus E, shear modulus G, and yield strength f_y) in the current work are listed in Table 1. Referring to the range of the dilation angle of the joint suggested by Bahrani and Tannant (2011) and Liu and Li (2017), it is taken to be 5° in the present work. The friction angle of the joint is the parameter with the most important influence, so three representative values of this parameter (20°, 30°, and 40°) are considered in this research.

Table 1 Main parameters used for the bolted slope

The bolts are assumed to be made of HRB400 steel and M30 grout, and they are applied to reinforce the main slip surface of the slope (i.e., the slip surface of the active block) and pass through the main slip surface over at least 1 m along their length. It is assumed that there are six rows of bolts per unit width along the slope strike direction, i.e., n₁ is taken to be 6 and n₂ is 0. The bolt angle (α) and diameter (d) also play major roles in determining the stability of the bolted CBRS; thus, nine different values of α (10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, and 90°) and seven values of d (10, 16, 20, 22, 25, 28, and 32 mm) are considered.

As mentioned above, the contribution the bolts make to the force suppressing bi-planar sliding failure is provided by the shear and axial forces acting between the bolts and joints. These forces have been studied by many scholars (Grasselli 2005; Oreste and Cravero 2008; Liu and Li 2017). Recent research (Liu and Li 2017) indicates that the relationship between the shear force ($Q_{0}$) and normal force ($N_{0}$) can be determined based on a structural mechanical model of the deflecting section of the bolt, with the form:

$${{Q_{0} } \mathord{\left/ {\vphantom {{Q_{0} } {N_{0} }}} \right. \kern-0pt} {N_{0} }} = K\tan \left( {\alpha - \beta } \right)$$

(14)

where $\beta$ is the dilation angle of the joint and K is a constant related to the deflecting length, the geometric and mechanical parameters of the bolts. To be more specific, $K = \left( {{{3Al^{2} } \mathord{\left/ {\vphantom {{3Al^{2} } {80I}}} \right. \kern-0pt} {80I}} + {{kE} \mathord{\left/ {\vphantom {{kE} {3G}}} \right. \kern-0pt} {3G}}} \right)^{ - 1}$, where A is the cross-sectional area of the bolt, I is the section moment of inertia, l is the length of the shear deformation section ($l = 3d$), and k is a coefficient related to the cross-section shape (e.g., $k = {{10} \mathord{\left/ {\vphantom {{10} 9}} \right. \kern-0pt} 9}$ for a bolt of circular cross-section).

In this work, the Mises yield criterion is adopted to describe the yield criterion of the bolts at the shearing point:

$$\left( {\frac{{N_{0} }}{{Af_{y} }}} \right)^{2} + 3\left( {\frac{{Q_{0} }}{{Af_{y} }}} \right)^{2} = 1$$

(15)

This criterion is more suitable for metal materials and improves on the criterion used in the original literature (Liu and Li 2017).

Combining Eqs. (14) and (15), we have

$$\left. \begin{array}{l} Q_{0} = \frac{{K\tan \left( {\alpha - \beta } \right)}}{{\sqrt {3K^{2} \tan^{2} \left( {\alpha - \beta } \right) + 1} }}Af_{y} \\ N_{0} = \frac{1}{{\sqrt {3K^{2} \tan^{2} \left( {\alpha - \beta } \right) + 1} }}Af_{y} \end{array} \right\}$$

(16)

Using Eq. (11), the axial, shear, and resultant forces describing the contribution the bolts make to deformation resistance are given by:

$$R_{N} = N_{0} (\cos \alpha + \sin \alpha \tan \varphi_{j} ) = \frac{{(\cos \alpha + \sin \alpha \tan \varphi_{j} )Af_{y} }}{{\sqrt {3K^{2} \tan^{2} \left( {\alpha - \beta } \right) + 1} }}$$

(17)

$$R_{Q} = Q_{0} (\sin \alpha - \cos \alpha \tan \varphi_{j} ) = \frac{{K\tan \left( {\alpha - \beta } \right)(\sin \alpha - \cos \alpha \tan \varphi_{j} )Af_{y} }}{{\sqrt {3K^{2} \tan^{2} \left( {\alpha - \beta } \right) + 1} }}$$

(18)

$$R = \frac{{\left[ {\cos \alpha + K\tan \left( {\alpha - \beta } \right)\sin \alpha } \right] + \left[ {\sin \alpha - K\tan \left( {\alpha - \beta } \right)\cos \alpha } \right]\tan \varphi_{j} }}{{\sqrt {3K^{2} \tan^{2} \left( {\alpha - \beta } \right) + 1} }}Af_{y}$$

(19)

Effect of bolt angle

Figure 5 presents plots showing how the bolt angle (α) affects the resultant supporting force provided by one bolt ($R$) and the increase in the safety factor of the bolted slope ($\Delta F_{s}$). The plots correspond to three different joint strengths ($\varphi_{j}$) and the bolt diameter ($d$) is fixed at 25 mm. Each of the curves increase at first, peak, and then decrease as α increases. Thus, there is an optimal bolt angle that maximizes the stability of the bolted CBRS. Moreover, this optimal value of α is approximately equal to the friction angle of the joint.

Fig. 5

Effects of bolt angle α on R and $\Delta F_{s}$ for different $\varphi_{j}$ values ($d = 25{\text{ mm}}$)

The optimal α value yields increase in the values of R and $\Delta F_{s}$ of about 37.2% and 39.5%, respectively, compared to the worst bolt angle (α = 90°). Obviously, it is necessary to give priority to maximizing the reinforcement effect by choosing the optimal bolt angle when designing support for a bolted CBRS. However, the optimal bolt angle may not necessarily be a convenient angle to use when it comes to drilling and grouting construction. Hence, it is also necessary to take into account convenience when choosing the bolt angle.

Figure 5 also indicates that R and ${\Delta F}_{s}$ both increase as $\varphi_{j}$ increases. This is because the rough joint enhances its frictional strength under the Coulomb criterion (Zheng et al. 2021). Therefore, for a given axial force from the bolt, the greater the joint friction angle, the larger the support force from the bolt, and the greater the increase in the safety factor of the bolted CBRS.

Figure 6 further depicts the effect that α has on the support forces ($R$, $R_{N}$, and $R_{Q}$) and force ratios ${{R_{N} } \mathord{\left/ {\vphantom {{R_{N} } R}} \right. \kern-0pt} R}$ and ${{R_{Q} } \mathord{\left/ {\vphantom {{R_{Q} } R}} \right. \kern-0pt} R}$ when the joint friction angle is 30° and the bolt diameter is 25 mm. The figure shows that $R_{N}$ first increases as α increases, reaches a peak at 30° (i.e., the joint friction angle), and then decreases. On the other hand, $R_{Q}$ increases very slowly to begin with (essentially remaining very close to zero) and then increases more rapidly. It can also be seen that the value α = 30° acts, in some ways, as a boundary. That is, ${{R_{N} } \mathord{\left/ {\vphantom {{R_{N} } R}} \right. \kern-0pt} R}$ essentially remains unchanged at first and then starts to decrease when the boundary is reached. Similarly, ${{R_{Q} } \mathord{\left/ {\vphantom {{R_{Q} } R}} \right. \kern-0pt} R}$ essentially remains unchanged at first and then increases when the boundary is reached. This means that if a small bolt angle is selected, it is the axial force in the bolt that make the major contribution to the deformation resistance (and so the bond strength of the bolt is particularly important at this time). However, as the bolt angle is gradually increased, the shear force acting in the bolt gradually begins to contribute more to the resistance. That is, the larger the bolt angle, the greater the contribution made by the shear resistance of the bolt and the more obvious the dowel effect.

Fig. 6

Effects of α on the support forces R, $R_{N}$, and $R_{Q}$, and force ratios ${{R_{N} } \mathord{\left/ {\vphantom {{R_{N} } R}} \right. \kern-0pt} R}$ and ${{R_{Q} } \mathord{\left/ {\vphantom {{R_{Q} } R}} \right. \kern-0pt} R}$ ($\varphi_{j} = 30^\circ$ and $d = 25{\text{ mm}}$)

Effect of bolt diameter

Figure 7 presents plots showing how the bolt diameter (d) affects the resultant supporting force provided by one bolt (R) and the increase in the safety factor of the bolted slope ($\Delta F_{s}$). The plots correspond to three different joint strengths ($\varphi_{j}$) and the bolt angle (α) is fixed at 30°. The curves all increase according to power functions as d increases. In addition, it can also be seen that R and $\Delta F_{s}$ increase much more rapidly with d when the diameter exceeds 16 mm. Clearly, it is important that this power function reinforcement effect is considered when selecting the bolts to use to support the CBRS so that the bolt design is both reasonable and economical.

Fig. 7

Effects of bolt diameter d on R and $\Delta F_{s}$ for different $\varphi_{j}$ values ($\alpha = 30^\circ$)

Effect of bolt location

Figure 8 shows how the bolt location (n₁ and n₂) affects the safety factor of the slope (F_s). The plots correspond to the bolt angle (α) and the joint strength (φ_j) which are both fixed at 30°. The total number of n₁ and n₂ is taken as six rows; F_s increases as n₂ increases when the total number of n₁ and n₂ is constant. It means that it will be more effective to have several bolts penetrating the gently dipping joint; however, it should be noted that on such slopes, the slip surface of the active block is generally much longer than that of the passive block, and only a few bolts can be installed to penetrate the gently dipping joint.

Fig. 8

Effects of the bolt location (n₁ and n₂) on $F_{s}$ for different $\theta_{2}$ values ($\alpha = 30^\circ$)

Numerical simulations

The widely used discrete element package Universal Distinct Element Code (UDEC) has a mature simulation element for local reinforcement structures such as bolts which makes it ideal for studying the deformation and failure of bolted bedding rock slopes (Zheng et al. 2019). Therefore, UDEC is used to model the bolt-supported CBRS in this work.

Numerical model and parameters

A numerical model is established using UDEC for the bolt-supported CBRS shown in Fig. 4. The geometric characteristics of the numerical model shown in Fig. 9 are identical to those of the model in Fig. 4. The horizontal displacement of the numerical model is constrained along its two lateral boundaries, and both the vertical and horizontal displacements are fixed at the bottom boundary. The displacement monitoring point (M) is installed at the shoulder of the slope.

Fig. 9

Numerical (UDEC) model for the bolt-supported CBRS

The Mohr–Coulomb plasticity and Coulomb slip models are used to characterize the mechanical behavior of the rock mass and joints in the UDEC model, respectively. Furthermore, the local reinforcement model “REINFORCE” is used to simulate the local effect of reinforcement where it passes through existing joints. Two springs are used in this model to simulate the shear deformation characteristics of the bolt, and the two springs are located at the joint interface and oriented perpendicular and parallel to the axis of bolt (Fig. 10).

Fig. 10

The shear and axial springs in the local reinforcement model and their orientations representing reinforcements a before and b after shear displacement

Following shear displacement, the shear spring maintains the same direction and the axial spring produces a small displacement along the direction of shearing, causing a change in the bolt angle, resulting in shear deformation of the bolt along both sides of the joint (Fig. 11). The length of the shear deformation section is called the active length. It is found that this length is generally about several times the bolt diameter (Liu and Li 2017; Ranjbarnia et al. 2022). The UDEC manual also indicates that the active length extends approximately the distance of one to two reinforcing element diameters on each side of the joint (Itasca Consulting Group Inc. 2004).

Fig. 11

Assumed reinforcement geometry after shear displacement, ∆u_s

The force-displacement models with continuous and nonlinear algorithms are used for the axial and shear behaviors of the bolts (Itasca Consulting Group Inc. 2004). They are employed to determine forces arising in the springs from incremental displacements at the end points of the active length. The reinforcement model generates two resistance forces, axial and shear, to describe that the contribution of the bolt subjected to the combined load. Furthermore, the axial and shear forces will increase with their deformation until they reach their ultimate capacities, respectively. When both axial and shear forces reach their ultimate capacities, it means that the bolt is damaged under the combined load. In addition, the resultant axial and shear forces are resolved into components perpendicular and parallel to the joint. Forces are then applied to the neighboring blocks to provide local reinforcement.

The ultimate axial capacity (P_ult) of the bolt depends on the tensile capacity of the steel bar (P₁), the pull force between the grout and the steel bar (P₂), and the pull force between the grout and the rock (P₃), which is equal to the minimum value among these three forces; the ultimate axial (P_ult) and shear ($F_{s,b}^{\max }$) capacities can be obtained as follows (Itasca Consulting Group Inc. 2004; National Standards Compilation Group of the People’s Republic of China, GB 50330-2013 2013):

$$P_{1} = f_{y} \pi (0.5d_{1} )^{2}$$

(20)

$$P_{2} = f_{gb} \pi d_{1} L$$

(21)

$$P_{3} = f_{gr} \pi d_{2} L$$

(22)

$$F_{s,b}^{\max } = 0.67d_{1}^{2} (f_{y} \sigma_{c} )^{0.5}$$

(23)

where d₁ and d₂ refer to the diameters of the bolt and hole, respectively; f_gb is the bond strength between the grout and the steel bar; f_gr is the bond strength between the grout and the surrounding rock; L is the band length; and σ_c denotes the uniaxial compressive strength of massive rocks.

The values of the parameters required to describe the rock mass, joint, and bolts in the UDEC model are chosen to be consistent with those used in the theoretical analysis. Furthermore, the additional bolt parameters required are available from Eqs. (20)–(23) and the UDEC Manual. The specific values of the parameters used are shown in Tables 2, 3, and 4, respectively.

Table 2 Numerical parameters used for the rock mass in the UDEC model

Table 3 Numerical parameters used for the joints in the UDEC model

Table 4 Numerical parameters used for the bolts in the UDEC model

The parameters required to describe the rock mass include unit weight γ_r, elasticity modulus E_r, Poisson’s ratio μ, cohesion c_r, friction angle φ_r, and tensile strength σ_t; those required for the joint are cohesion c_j, friction angle φ_j, tensile strength σ_jt, and dilation angle β; and those for the bolts are axial stiffness K_a, shear stiffness K_s, ultimate axial capacity P_ult, ultimate shear capacity $F_{s,b}^{\max }$, 1/2 active length l_a, and spacing in the out-of-plane direction, Spacing.

Stability of the bolted CBRS

To analyze the stability of the bolted CBRS, calculations are first run to allow the slope model to equilibrate in order to generate the initial stress field present under its own weight and boundary conditions. Rock masses in the designated cut area are then deleted to simulate the evolution of the CBRS excavation process. Bolts are installed after the excavation of the rock masses in the area awaiting reinforcement. Finally, a strength reduction technique is used to determine the slope safety factor by simultaneously reducing the strength parameters of rock mass and joint.

Figure 12 shows the joint failure occurring in the slope when the slope is not reinforced and when bolts are used with different bolt angles. In Fig. 12a (no bolts), the failure surfaces of the steeply dipping and gently dipping joints are connected to each other, forming a through slip surface. That is, bi-planar failure occurs in this CBRS if it is not reinforced with bolts.

Fig. 12

Joint failure in slopes reinforced by a no bolts, b bolts with bolt angles of 30°, c bolts with bolt angles of 50°, and d bolts with bolt angles of 70°. (Red cracks denote shear failure; cyan cracks represent tensile failure)

It can also be seen from Fig. 12a that the slip surface mainly results from tensile failure–some shear failure is involved, however, which occurs locally at the intersection of the steeply and gently dipping joints as well as the top of the steeply dipping joint. This indicates that the sliding body deforms and further rotates around the intersection of the joints after the slip surface penetrates, which is consistent with the bi-planar sliding failure mechanism (Wang et al. 2004; Yin et al. 2011).

Figure 12b–d show that the failure surface of the steeply dipping joint is not complete when bolts are used (as shown by the arrows). In addition, the amount of tensile failure occurring along the gently dipping joint is much less than that occurring in Fig. 12a. This indicates that after the slope is reinforced, the dowel effect of the bolts limits the displacement of the slope which prevents the deformation and rotation of the potential sliding body. This restricts the opening of the gently dipping joint and restrains the penetration of the sliding surface, thus improving the stability of the slope.

In the UDEC simulations, the slope calculation does not converge when bolt reinforcement is not used. However, the calculations do converge when bolts are used (for each bolt angle used here). To obtain all calculation results for slopes with and without bolt reinforcement, a larger fixed number of steps (100,000 steps) could be used as the calculation end condition for the unreinforced slope model without convergence. This fixed number of steps is approximately five times the number of steps to convergence used in the analysis of the bolted slope. Figure 13 displays contour maps of the slope displacements with and without bolt reinforcement and Fig. 14 shows a plot of the displacements of the monitoring point M located at the shoulder of the slope.

Fig. 13

Displacement contour maps of slopes reinforced by a no bolts, b bolts with bolt angles of 30°, c bolts with bolt angles of 50°, and d bolts with bolt angles of 70°

Fig. 14

Displacement of the slope shoulder as a function of bolt angle

Figures 13 and 14 clearly show the improved stability of the slope resulting from the dowel effect of the bolts. The displacement of the bi-planar sliding body in the CBRS is clearly effectively controlled after the slope is reinforced with bolts. More specifically, the unreinforced sliding body undergoes a displacement of 171 mm but bolt reinforcement reduces this to about 0.24 mm thus ensuring the stability of the slope.

Figure 14 also demonstrates that the displacements of the bolted slopes with different bolt angles are all approximately the same. However, the smallest shoulder displacement occurs when the bolt angle is equal to the friction angle of the joint (30°). This finding shows that there is an optimal bolt angle which is consistent with the results of the previous theoretical analysis.

Verification and comparison

To further verify the rationality and accuracy of the theoretical method, the support force provided by the bolts and the safety factor of the bolted slope are calculated using the two methods (theoretical and numerical) and compared.

Since the supporting force of each row of the bolts is approximately the same in UDEC, the average value of support force from six rows of bolts can be used for the analysis of the support force contribution of the bolts. Figure 15 shows a comparison of the values of the support force calculated for one bolt (R) for a variety of bolt angles. This force is calculated in UDEC by extracting the axial ($N_{0}$) and shear ($Q_{0}$) forces on the reinforcement element at the intersection between the slip surface and bolt when the slope is in the limit equilibrium state. The support forces calculated using the two methods are almost the same (the mean percentage difference is just 0.5% over the range of bolt angles considered). Moreover, they both predict the same optimal bolt angle for maximizing the resistance contribution of the bolts, and this angle is consistent with that found by Pellet and Egger (1996) and Liu and Li (2017). Therefore, the two methods are mutually verified: on the one hand, the results verify the rationality of using the proposed method to evaluate the stability of bolted CBRSs; on the other, it demonstrates the feasibility of using UDEC to study bolted CBRSs.

Fig. 15

Comparison of the bolt contributions calculated using the theoretical and numerical methods for a variety of different bolt angles

Figure 16 shows a comparison of the safety factors of the bolted slope ($F_{s}$) calculated using the theoretical and numerical methods. The theoretical results include three aspects: (1) the safety factor (F_sav) obtained when the shear force acting at the interblock boundary is zero (S_r = S_ra), (2) the safety factor (F_sbv) obtained when that force reaches the Mohr–Coulomb friction strength (S_r = S_rb), and (3) the mean value (F_smv) of the safety factors obtained from the first two. The average percentage difference between F_smv and the safety factor (F_sn) calculated by numerical simulation is 7.6%, while the average percentage difference between F_sav and F_sn is 33.9%, and the average percentage difference between F_sbv and F_sn is 18.8%. Therefore, the mean values of the theoretical results are the closest to the numerical results. This also proves the rationality of the mean value results suggested in engineering practice in the present work.

Fig. 16

Comparison of slope safety factors calculated using the theoretical and numerical methods for a variety of different bolt angles

In addition, the reinforcement effect provided by the bolts effectively improves the safety factor of the slope. The bolts increase the theoretical slope safety factor by 0.185, on average, which is an increase of 20.5% compared to the unreinforced slope. The increase in safety factor calculated using UDEC is 0.275, on average, compared to the unreinforced slope which is an increase of 30.6%. The average percentage difference between the safety factors of the bolted CBRS calculated using the two methods is approximately 10%. This means the results are relatively consistent and the agreement is generally acceptable from both rock mechanical and practical points of view (Alejano et al. 2011; Sun et al. 2020). The differences between the two sets of results may be mainly attributed to that the theoretical method ignores the effect of the distributed support force provided by multiple rows of bolts. This results in smaller safety factors being calculated for the bolted CBRS. Fortunately, this means the calculated results are more conservative which is good for practical engineering applications (Sun et al. 2019; 2020).

Discussion

The CBRSs have slope angles that are less than or equal to the dip of the rock strata. When the slope angle is equal to the dip of the rock strata, the slope can be called a dip slope, and the slope can be called an underdip slope when its slope angle is less than the dip of the rock strata (Cruden 2000). Both types of slopes are subject to bi-planar sliding failure along the steeply dipping and gently dipping joints (Huang 2007), and their analytical models are the same. The difference between these two is that the active and the passive blocks have different areas.

To elucidate the bi-planar failure mechanism of the underdip slopes, a typical slope model is established (see Fig. 17). The slope angle (θ_s) is 35°, and the dip angles of the steeply dipping (θ₁) and gently dipping (θ₂) joints are taken to be 50° and 20°, respectively. The orientations of the steeply dipping and gently dipping joints of a real slope can be determined by the statistical analysis of a pole plot of the joints. Here, the steeply and gently dipping joints are assumed to be persistent.

Fig. 17

Calculation model of the underdip slope considered

Figure 18 shows the comparison of the stability of the underdip slopes calculated by numerical and theoretical methods. Figure 18a illustrates the bi-planar failure mechanism caused by the penetration damage of steeply dipping and gently dipping joints in the underdip slopes. This is consistent with the sliding mechanism of active and passive blocks of the dip slope developed in this work.

Fig. 18

Comparison of the stability of the underdip slopes calculated by a numerical simulation and b proposed theoretical method

The safety factor of the slope calculated by UDEC is 1.225, and the rear edge of the slip surface located at the second steeply dipping joint behind the shoulder of the slope, as shown in Fig. 18a. In addition, using the method proposed in this work to calculate the safety factor of the slope for different rear edge locations (i.e., the location of the steeply dipping slip surface marked by numbers in Fig. 18b), there exists a minimum safety factor of the slope, which corresponds to the most dangerous potential slip surface. Figure 18b shows that the minimum safety factor of the slope is 1.342, which differs from the numerical calculation result by 8.7%; the steeply dipping slip surface corresponding to the minimum safety factor is located at the 5th steeply dipping joint (i.e., the first steeply dipping joint position behind the slope shoulder), as shown by the pink slip surface, which differs from the numerical simulation result by only one rock layer thickness. These differences are mainly caused by the different nature of the two methods. The proposed method is based on the limit equilibrium principle of rigid bodies, while UDEC simulation adopts the stress–strain analysis of deformable bodies.

Figure 19 presents plots showing how the various slope angles (θ_s) influence the safety factor (F_s) of CBRSs. The plots correspond to the dip angle (θ₁) of the steeply dipping joint that is 50°, and the joint strength (φ_j) and the bolt angle (α) which are both 30°. The bi-planar slip surface of CBRSs is shown as the pink line in the figure. The variation in the safety factor of the slope is approximately the same as that of the dip angle of gently dipping joints at 20° and 30°.

Fig. 19

Effects of slope angle θ_s on F_s for different θ₂ values (θ₁ = 50°)

The safety factors of the underdip slopes are greater than that of the dip slope, and the smaller the slope angle, the greater the safety factor of underdip slope. This is because the smaller the slope angle of underdip slope, the greater the area of the passive block at the toe of slope, thus the better the anti-slip stability of the slope (Huang 2007; Sun et al. 2019, 2021).

With the support provided by the bolts, the safety factors of the bolted CBRSs are all improved. Moreover, the safety factors of the bolt-supported underdip slopes are all greater than that of bolted dip slope. However, the changes in the safety factors of the bolted underdip slopes are not significant with changes in slope angle. The main reason for this may be that the area ratio of the active and passive blocks of the underdip slope is different for different slopes, resulting in different reinforcement effects arising from the bolts.

Conclusions

In this work, a new method for evaluating the stability of bolt-supported CBRSs with respect to bi-planar failure is proposed. A parametric analysis is then performed to investigate the effects of varying the bolt angle (angle of the bolt with respect to the joint plane) and bolt diameter on the stability of the CBRS. The key conclusions drawn are:

• 1. Fully grouted bolts are an effective and economical means of reinforcing CBRSs. The shear and axial forces acting in the bolts create dowel and pull-out effects that restrain the sliding of the rock strata and increase their shear strength.

• 2. There exists an optimal bolt angle that maximizes the stability of the bolted CBRS; its value is approximately equal to the friction angle of the joint. Using this bolt angle provides the largest support force and hence maximizes the safety factor of the bolted CBRS.

• 3. The support force provided by the bolts and safety factor of the bolted CBRS both increase according to power functions as the diameter of the bolts is increased. Thus, it is necessary to consider this power function reinforcement effect when selecting the bolt diameter in order to achieve an effective and economical design.

• 4. The support forces provided by the bolts and safety factors of the bolted CBRSs calculated using the proposed method are relatively consistent which those calculated numerically. This finding verifies the rationality of using the proposed method to evaluate the stability of bolted CBRSs; it also demonstrates the feasibility of using UDEC to study bolted CBRSs.