Introduction

With the rapid development of large-scale projects constructed in mountainous areas worldwide in recent decades, there is a growing interest in understanding the stability of the rock wedges caused by anthropogenic excavations. Owing to the influence of excavation unloading, the stability of rock slopes may drop remarkably, which poses a direct threat to the safety of construction projects (Kumsar et al. 2000; Lee et al. 2007; Song et al. 2010). Many types of rock slope reinforcement problems arise from the development and construction of such projects. The anchor cable reinforcement system is now recognized as one of the most effective and convenient reinforcement measures for rock slopes and foundations (Danziger et al. 2006; Sun et al. 2010). The current study relates to anchored slopes and focuses on stability of the rock slope, mechanical calculation of anchor cables and optimization of anchor cable design.

The methods used to design the stability of rock slopes vary widely, and include analytical solutions and numerical modeling approaches. Avcı et al. (1999), Sagaseta et al. (2001), Hack et al. (2003), Kentli and Topal (2003), Di Luzio et al. (2004) and Liu et al. (2014) examined the stability of rock slopes using analytical approaches. In addition, a number of monitoring experiments have been conducted to investigate the stability of rock slopes (Yang et al. 2001; Shu et al. 2005a, b; Lin et al. 2014). Due to the rapid development of numerical modeling technologies, numerical simulation is an efficient alternative method with which to study the stability of a slope (Griffiths and Marquez 2007; Tan and Sarma 2008; Bui et al. 2011; Pain et al. 2014), and has attracted worldwide attention. Stead et al. (2006), Song et al. (2010), Böhme et al. (2013), He et al. (2013) and Wong and Wu (2014) analyzed the stability and deformation of rock slopes using numerical modeling methods. In particular, Park and West (2001), Yoon et al. (2002), Tonon and Asadollahi (2008), Li et al. (2009), Indraratna et al. (2010) and Jiang et al. (2013) examined the stability and failure of rock wedges.

Anchor cables are now used widely to support rock slopes, and the corresponding theoretical calculation methods of anchor cables have been examined in several studies. Shu et al. (2005a) and Sasiharan et al. (2006) investigated the results of field tests conducted on anchors used to support wire mesh and cable net rockfall protection systems. Tang et al. (2010) developed calculation methods to obtain the axial force of anchors in rock slopes. Zhang et al. (2010) discussed the effect of reinforcement of a rock slope with group anchorage cables and the stress characteristics of pre-stressed anchorage cables in the fractured surface. Koca et al. (2011) examined anchor applications using the example of a Karatepe andesite rock slope. A dynamic simplified model for anchor rod frame ground beam to support slopes based on the elastic ground beam theory and structural dynamics theory was proposed by Yuan and Liu (2012). By using the FLAC3D numerical simulation, the roadway full-length anchor support mechanism was investigated by Dong and Wang (2012) to analyze the full-length anchor force-transferring mechanism and stress-field distribution formed by rocks surrounding roadways. Blanco-Fernandez et al. (2011, 2013) analyzed the different hypotheses assumed in the calculation methods for flexible systems and the technique of flexible systems anchored to the ground for slope stabilization.

Optimization of the design of anchor cables is crucial to engineering practice in rock slopes. Zhang et al. (2002) proposed an optimized method based on analysis of the failure factors of the anchorage system. The dynamic finite element strength reduction method was employed by Ye et al. (2010) to evaluate the dynamic stability of rock slopes supported with anchors. Liu et al. (2012) carried out an optimum arrangement of prestressed cables in rock anchorage by using different lengths of prestressed cables. The anchor spacing and inclined angles optimization of cables were studied by Zheng et al. (2012) based on an equivalent pseudo-static force analysis method.

The computational methods and application of anchor cables have been examined in depth in recent decades; however, most existing studies focus on the behavior of a single cable or several cables within a limit area, few studies in the literature have addressed the issue of the overall layout of anchor cables according to the realistic characteristics of the whole spatial distribution of rock wedges. The conservation and design of evenly distributed anchor cables indeed can ensure the safety of rock slopes; however, a great number of useless anchor cables or bolts can waste a tremendous amount of investment, especially in the case of rock wedges. Consequently, the main purpose of this paper was to present a novel optimal overall layout and length of anchor cables for slope reinforcement based on a study of the actual three-dimensional characteristics of rock wedges. Note that the layout and length optimization of the anchor cables described in this paper can also apply to bolts reinforcement projects.

Theoretical background

Sliding failure of single-faced rock slopes

Generally, the wedge failures of single-faced rock slopes can be divided into two modes in terms of sliding planes of wedges, namely single plane sliding (Fig. 1a) and double plane sliding (Fig. 1b), which is the general form of wedge failure (Hocking 1976). If two joint planes bound a sliding wedge, single plane sliding (Fig. 1a) is defined as a sliding on only one of the joints bounding the base of the wedge, whereas double plane sliding (Fig. 1b) is defined as a sliding on both joint planes parallel to the line of intersection (Yoon et al. 2002).

Fig. 1
figure 1

Sliding failure for sliding of a single-faced slope. a Single plane sliding. b Double plane sliding (Hocking 1976). J1, J2 Joint planes; SL slope surface

Full size image

To explain the sliding failure of single-faced rock slopes with two typical rock wedges as above, a stereographic projection graph can be used to conduct the analysis (Fig. 2; after Hocking 1976, with minor revision), where J1 and J2 denote the joint planes; SL denotes the slope surface (large circle); NJ1 and NJ2 are the true dip of the joint planes J1 and J2, respectively; NSL denotes the true dip of slope surface (SL); and NI denotes the intersection of joint planes. If NJ1 or NJ2 of either of the joint planes (J1 or J2) lies within the shaded area between NI and SL, as shown in Fig. 2a, single plane sliding can occur (Hocking 1976). On the other hand, if NI is located in the sliding envelope and both NJ1 and NJ2 lie outside the area (shaded area in Fig. 2b), then double plane sliding can occur (Hocking 1976; Yoon et al. 2002).

Fig. 2
figure 2

Stereographic solution for sliding of a single-faced slope. a Single plane sliding. b Double plane sliding (after Hocking 1976 with minor revision). J1, J2 Joint planes; SL slope surface (large circle); NJ1, NJ2 true dip of joint planes J1 and J2, respectively; NSL true dip of slope surface (SL); NI intersection of joint planes

Full size image

Simplified theoretical model of rock wedges

Considering rock wedges of single-faced rock slopes (Fig. 1), a generalized analysis model can be established as shown in Fig. 3, where ABD and BCD denote the slip surface developed by two groups of preferred discontinuities, respectively, and ADC denotes the free surface of the slope in which to set anchor cables.

Fig. 3
figure 3

A generalized analysis model for rock wedges. L Maximum length of slope cross-section; H vertical height of free surface; a, b side length in major section, respectively; section T is the longitudinal profile with distance x to the major section, a(x) and b(x) are corresponding side lengths in section T, respectively

Full size image

In an attempt to perform quantitative analysis for a generalized rock wedge, we made an effort to conduct a symmetrical analysis on rock wedges. Assuming a symmetrical simplified model, the following geometrical relationships can be set: (1) AB equals BC, AD equals DC, respectively; point O is the center of AC; consequently, BO and OD are perpendicular to AC, respectively; (2) the thickest position of the sliding mass generally occurs in the central part (major section BOD), and the thickness decreases gradually along the distance from the central section to the side boundaries. The driving force of the rock slope in major section can be obtained by the rigid equilibrium limit method [Code for Investigation of Geotechnical Engineering. National Standard of People’s Republic of China GB 50021-2001 (2009 Revised); Li et al. 2010]. The related arbitrary longitudinal section (section T) of the rock slope can be presented as in Fig. 4, which corresponds to the red section region in Fig. 3.

Fig. 4
figure 4

Longitudinal profile of section T with distance x to the major section. α Angle between the corresponding slip plane of the arbitrary longitudinal section of slope and horizontal plane, θ 1 angle between the free surface and the slip surface, θ 2 angle between free surface and crest surface

Full size image

Rational spacing and length calculation for anchor cables

Area of any longitudinal section T

On the basis of the above simplified theoretical model of rock wedges (Fig. 3) and the geometrical relationship (Fig. 4), the area of the arbitrary longitudinal section (section T) of the slope, namely S(x), can be calculated out:

$$ S\, (x ) { = }\frac{1}{2}a\,(x)\,b\,(x)\sin \theta_{2} $$
(1)

where θ 2 denotes the angle between free surface and crest surface.

Furthermore, as can be noted from the geometrical relationship shown in Fig. 3, the equations of free surface a(x) and free surface b(x) at the location of section x can be expressed as:

$$ a(x) = \left( {1 - \frac{2x}{L}} \right) \times a $$
(2)
$$ b(x) = \left( {1 - \frac{2x}{L}} \right) \times b $$
(3)

Expression function for driving force in section T

The scale factor is defined as the ratio between the original slope model and the calculated slope model, which can be expressed as follows (Li et al. 2010):

$$ \varepsilon = \frac{{Z_{\text{o}} }}{{Z_{\text{c}} }} $$
(4)

where ε denotes the scale factor; Z c denotes the height of the calculated slope model; and Z o denotes the height of the original slope model.

Considering the scale factor and the limit equilibrium analysis of slope stability, the formula in the Fellennius method can be rewritten as (Li et al. 2010):

$$ K = \frac{{\sum {\left( {\frac{1}{\varepsilon }c_{I} l_{I} + \frac{1}{{\varepsilon^{2} }}W_{I} \cos \alpha_{I} \tan \varphi_{I} } \right)} }}{{\sum {\frac{1}{{\varepsilon^{2} }}W_{I} \sin \alpha_{I} } }} $$
(5)

where W I denotes the weight of no. I slice; c I denotes the cohesion of no. I slice; φ I denotes the friction angle of no. I slice; l I denotes the slip surface length of no. I slice; α I denotes the slip surface dip angle of no. I slice; and K x denotes the stability coefficient at section T.

The study of the relationship between the driving force and scale factor by Li et al. (2010) indicates that the hyperbolic model can be used to describe the relationship between driving force and scale factor. Consequently, suppose the driving force along the major driving direction is F max, the driving force F(x) along the arbitrary longitudinal section T can be expressed as:

$$ F(x) = \frac{1}{{\varepsilon^{2} }}F_{\hbox{max} } = \frac{1}{{\left( {\frac{S}{S(x)}} \right)^{2} }}F_{\hbox{max} } = \left( {1 - \frac{2x}{L}} \right)^{2} \times F_{\hbox{max} } $$
(6)

Equation (6) indicates that the distribution pattern of the driving force along the arbitrary longitudinal section T is accordance with the expression of parabolic function. Consequently, we obtain the sketch of distribution of driving force along the rock wedge shown in Fig. 5.

Fig. 5
figure 5

Sketch of distribution discipline for anchor cables in a rock wedge

Full size image

Rational spacing model for anchor cables

The height H(x) of the anchor cables installed in the arbitrary longitudinal section T of slope can be expressed as follows:

$$ H(x) = \left( {1 - \frac{2x}{L}} \right) \times H $$
(7)

It is generally accepted that the driving force F(x) of the rock slope is transferred to the bedrock by the corresponding anchor cables. Specifically, the driving force F(x) is usually obtained by the two-dimensional rigid equilibrium limit method along longitude section T. Consequently, we visualize the layout of anchor cables in the horizontal direction in rows and in the vertical direction in columns (see Fig. 6). Each column of anchor cables affords the slope driving force F of the corresponding scale near this column. For instance, as can be noted from Fig. 6, the first column of anchor cables affords the slope driving force F 1 within the section J 1 region, and the second column of anchor cables shares the slope driving force within the J 2 region, and so on. Here, S 1 and S 2 correspond to the spacing of anchor cables of the first and second columns, respectively.

Fig. 6
figure 6

Sketch of anchor cables sharing the driving force of the rock wedge

Full size image

It can be seen that the number of anchor cables depends on the corresponding driving force. Therefore, the number of anchor cables should correspond to the driving force of the calculation section, i.e., the spacing of anchor cables is determined by the corresponding driving force. As mentioned above, the distribution pattern of driving force along the arbitrary longitudinal section T is a parabolic function. Consequently, the spacing of anchor cables should be adjusted to the parabolic change in the driving force, which will result in a non-uniform layout: closer in the central part and sparser near the side boundaries.

On the basis of the above non-uniform layout principle for anchor cables, for any column of anchor cables, the relationship among J I, S I and the calculation location x I can be described as:

$$ x_{I} = \frac{1}{2}\left( {\sum\limits_{1}^{i} {J_{I} } + \sum\limits_{1}^{i - 1} {J_{I} } - J_{1} } \right) = \sum\limits_{1}^{i} {S_{I - 1} } $$
(8)
$$ S_{I} = \frac{{J_{I} + J_{I + 1} }}{2} $$
(9)

where I denotes the number of each column of anchor cables, namely 1, 2, 3,……; J I denotes the distance of the number I column anchor cables resisting the slope driving force; and S I denotes the anchor cable spacing between the cable numbers of (I) and (I + 1).

Considering the mechanical equilibrium between the driving force and the resistance provided by the anchor cables, we can establish the following equation:

$$ F_{I} \times J_{I} = \frac{{P_{a} }}{\eta } \times \left[ {\frac{{H(x_{I} )}}{{S_{\text{v}} }}} \right] $$
(10)

where F I denotes the driving force along the number I column of anchor cables; S v denotes the vertical spacing of anchor cables; \( \left[ {\frac{{H(x_{I} )}}{{S_{\text{v}} }}} \right] \) denotes rounding function, which stands for the necessary number of rows for anchor cables; P a denotes the anchorage force of single anchor cable; η denotes the coefficient for importance of structure.

The required number and rational spacing of anchor cables in any distance J I resisting the driving force can be solved by a system of equations (Eqs. 6–10).

Determination of rational length of anchor cables

The total length of an anchor cable comprises two sections, namely a free section length and an anchorage length. The anchorage length can be calculated according to the stress condition of anchor cables along the slope section (GB 50330-2013, 2013, Technical Code for Building Slope Engineering). We assumed that the anchorage length maintains a conservative necessary length constant along a specific slope section; therefore, the length of an anchor cable depends on changes in the spatial morphology of rock wedges. The longitudinal profile of the layout of anchor cables with distance x to the major slip section is presented in Fig. 7, where 1, 2,…, N and N + 1 denote the number of anchor cables, respectively; β denotes the angle between the axis of the anchor cable and the horizontal plane; H(x) denotes the vertical height of the free surface with distance x to the major slip section.

Fig. 7
figure 7

Layout of anchor cable with distance x to the major slip section

Full size image

The layout of the number N anchor cable with x distance to the major slip section is presented in Fig. 8, where l xN denotes the free section length of number N anchor cable, and H xN denotes the vertical height of the number N anchor head. As can be noted from the geometric relationship in Fig. 8 and Eq. (7), the following equation can be proposed:

$$ \frac{{l_{xN} }}{{\sin \theta_{1} }} = \frac{{H_{xN} }}{{\sin \gamma \times \sin \left( {\alpha + \theta_{1} } \right)}} = \frac{{H(x) - S_{\text{v}} \times N}}{{\sin (\alpha + \beta ) \times \sin \left( {\alpha + \theta_{1} } \right)}} $$
(11)

where N denotes the number of anchor cables, and \( 1 \le N \le \left[ {\frac{H(x)}{{S_{\text{v}} }}} \right] \), \( \left[ {\frac{H(x)}{{S_{\text{v}} }}} \right] \) denotes the rounding function; \( \gamma \) denotes the angle between the anchor cable and the slip surface, \( \gamma = \alpha + \beta \).

Fig. 8
figure 8

Sketch of the length calculation of the number N anchor cable

Full size image

The expression of l xN can then be obtained as follows:

$$ l_{xN} = \frac{{\left( {H(x) - S_{\text{v}} \times N} \right) \times \sin \theta_{1} }}{{\sin \gamma \times \sin \left( {\alpha + \theta_{1} } \right)}} $$
(12)

By solving the free section length in Eq. (12), we can obtain the total length of the anchor cables, which is the sum of free section length and unchanged anchorage length. The expression can be written as:

$$ l_{{{\text{t}}N}} = l_{xN} + l_{{{\text{a}}N}} $$
(13)

where l tN denotes the total length of anchor cables in number N row; l xN denotes the free section length of anchor cables in number N row; l aN denotes the anchorage length of anchor cables in number N row.

Case study

Project background

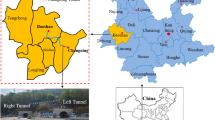
The Shuige sewage treatment plant is located in Lishui City, Zhejiang Province, China (see Fig. 9). Due to construction of the Shuige sewage treatment plant in the hilly Shuige industrial zone, the ground leveling involved excavation of the original slope (see Fig. 10), which requires evaluation of the stability of the cut slope and the proposal of corresponding reinforcement measures.

Fig. 9
figure 9

Engineering geology plane of the Shuige slope

Full size image
Fig. 10
figure 10

Site photo of the Shuige slope during construction. The bold red line delineates the optimization region

Full size image

The lithology of this slope is mainly argillaceous sandstone, belonging to the Chaochuan Formation of the Early Cretaceous period. The total length of the slope is about 400 m. The altitudes of crown and toe after the excavation were 121.8 and 69.00–71.00 m, respectively. The stability of the slope will be affected seriously by the excavation. The Shuige sewage treatment plant was designed to be built on the levelled platform, with a safety grade of “second-class” according the specifications in China (Zhejiang Jiatu Survey and Design Co. Ltd. 2008). A site photo of the Shuige slope (K0 + 000 m–K0 + 120 m) is shown in Fig. 10—the zone within the red line is the area studied in this paper.

The site investigation data revealed two major sets of preferred discontinuities in the Shuige rock slope (K0 + 000 m–K0 + 120 m), at 213∠36 (bedding plane) and 270∠52 (joint plane), respectively. Combined with the attitude of the excavated slope surface (222∠53), the wedged rock block can be formed by the cutting the two sets preferred discontinuities and the excavated slope surface (see Fig. 11).

Fig. 11
figure 11

Stereographic projection of the two sets of preferred discontinuities and the excavated slope surface of the Shuige rock slope

Full size image

As can be seen from Fig. 11, the line of intersection (NI) is located within the sliding envelope and both NJ1 and NJ2 lie outside this area (shaded area in Fig. 11); therefore, double plane sliding could occur according to the failure models presented in Figs. 1 and 2. Furthermore, the dip angle of the intersection (NI) can be seen to be about 36°.

Distribution of driving force in rock wedges

Combined with the preferred discontinuities in the Shuige rock slope, the actual geometry of the slope can be determined by the method presented in Fig. 12. Points A′ and C′are the projections of A and C in the horizontal plane, respectively. The attitudes of planes ABD, BCD and ADC are 213∠36, 270∠52 and 222∠53, respectively (see Fig. 12a). The occurrence of intersecting lines DA and DC can be identified in Fig. 11, and followed by the azimuthal angle of DA′ and DC′ in the horizontal plane oxy. Finally, the actual length of OA and OC can be calculated as in Fig. 12b.

Fig. 12
figure 12

Sketch of the projection of the actual geometry of wedge slope in the horizontal plane. a Overall view. b Partial enlarged detail

Full size image

On the basis of the site investigation and laboratory tests, as well as the calculation results of the slope above, the recommended parameters for slope reinforcement in the Shuige slope are listed in Table 1 (Zhejiang Jiatu Survey and Design Co., Ltd. 2008).

Table 1 Calculation parameters for slope reinforcement in the Shuige slope (K0 + 000 m–K0 + 120 m)
Full size table

The driving force F(x) on both sides of the wedge slope along the arbitrary longitudinal section T can be rewritten by Eq. (6) as follows:

$$ F_{\text{OA}} (x) = \left( {1 - \frac{x}{{L_{\text{OA}} }}} \right)^{2} \times F_{\hbox{max} } $$
(14)
$$ F_{\text{OC}} (x) = \left( {1 - \frac{x}{{L_{\text{OC}} }}} \right)^{2} \times F_{\hbox{max} } $$
(15)

The corresponding height H(x) of the anchor cables installed in the arbitrary longitudinal section T of slope can be rewritten as:

$$ H_{\text{OA}} (x) = \left( {1 - \frac{x}{{L_{\text{OA}} }}} \right) \times H $$
(16)
$$ H_{\text{OC}} (x) = \left( {1 - \frac{x}{{L_{\text{OC}} }}} \right) \times H $$
(17)

Combined with Eqs. (14) and (15) and relevant parameters in Table 1, the curve of the driving force on both sides of the major slip section can be shown as in Fig. 13.

Fig. 13
figure 13

Driving force in the arbitrary longitudinal section T of slope

Full size image

Spacing optimization of anchor cables

The single anchorage force P a in the Shuige slope project is designed to be 1000 kN, and the layout of anchor cables is 4 × 4 m square (Zhejiang Jiatu Survey and Design Co., Ltd. 2008).

To demonstrate the optimization effect of the layout of anchor cables, we emphasise the effect of the actual characteristics of rock slope driving force on anchor spacing by employing anchor cables with the same single anchorage force. Taking construction conditions into consideration, the longitudinal spacing remains unchanged at 4 m.

As mentioned above, the vertical spacing of anchor cables S v is 4 m, and the coefficient for importance of structure η is 1.2. Therefore, Eq. (10) can be rewritten as:

$$ F_{I} \times J_{I} \, = \,J_{I} \times \left( {1 - \frac{x}{107}} \right)^{2} \times \, F_{\hbox{max} } \, = \,\frac{{P_{a} }}{1.2} \times \left[ {\frac{{H_{\text{OA}} (x)}}{4}} \right] $$
(18)
$$ F_{I} \times J_{I} = J_{I} \times \left( {1 - \frac{x}{13}} \right)^{2} \times \, F_{\hbox{max} } = \frac{{P_{a} }}{1.2} \times \left[ {\frac{{H_{\text{OC}} (x)}}{4}} \right] $$
(19)

Substituting the related parameters in Table 1 and the above design parameters into Eqs. (8), (9), (18) and (19), we can obtain all the corresponding distances J I of the anchor cables sharing the slope driving force and spacing (S I) of anchor cables, as listed in Table 2. A comparison of the calculated horizontal spacing (OA) and the conventional uniformly distributed anchor cables is presented in Fig. 14.

Table 2 Calculated spacing of the anchor cables resisting the slope driving force
Full size table
Fig. 14
figure 14

Comparison of the calculated horizontal spacing and the conventional uniformly distribution anchor cables (left side of major slip, Section OA)

Full size image

Taking safety conservation and construction convenience into account, anchor spacing is kept to just one decimal place. Consequently, the final spacing S if can be determined as in Table 3.

Table 3 Final spacing of the anchor cables resisting the slope driving force
Full size table

As can be noted from Fig. 14, the shape of the curve of optimized spacing of anchor cables can be described approximately by a parabolic distribution, and the spacing of anchor cables increases gradually along the distance from the major intersection section to the side boundaries. Compared with the conventional uniform layout of anchor cables in Fig. 15, we can conclude that the optimal layout scheme reduces the number of anchor cables markedly, especially nearby the side boundaries of the slope. The conventional layout of anchor cables is uniformly spaced, without considering the actual characteristics of the three-dimensional distribution of the driving forces of rock wedges. Actually, the maximum slope driving force usually occurs in the central intersection plane; it then decreases steadily along the distance from the intersection plane to the side boundaries. Consequently, the conventional layout of anchor cables under a uniform spacing scheme includes some redundant anchor cables, which causes a great waste of investment.

Fig. 15
figure 15

Conventional layout of the Shuige slope supported by anchor cables with connecting beams

Full size image

The conventional layout of anchor cables under a uniform spacing scheme and an optimized layout of anchor cables under a non-uniform spacing scheme for reinforcing the rock wedges are presented in Figs. 16 and 17, respectively. The conventional layout of anchor cables is uniformly spaced, without considering the influence of the actual spatial distribution of the rock slope driving force. In contrast, the optimized layout of anchor cables under a non-uniform spacing scheme is more reasonable due to consideration of the three-dimensional driving force. The maximum driving force occurs in the major slip section of the slope; therefore, a correspondingly smaller spacing is required to maintain slope stability. Similarly, greater spacing can be used in the region far from the major intersection plane. On the whole, considering the actual characteristics of spatial distribution of rock slope driving forces, the corresponding spacing of anchor cables should be closer near the intersection region and sparser near the side boundaries. In comparison with actual engineering practice, the optimized scheme can reduce the amount of anchor cables from 71 to 54—a saving in terms of number of cables of 23.9 %.

Fig. 16
figure 16

Conventional layout design of anchor cables under a uniform spacing scheme for reinforcing rock wedges

Full size image
Fig. 17
figure 17

Optimized layout of anchor cables under a non-uniform spacing scheme for reinforcing a wedged slope

Full size image

Length optimization of anchor cables

As noted previously, we assumed that the anchorage length remains a conservative necessary length along a specific slope section. Consequently, we focused on determination of the free section length l xN of anchor cables, which, plus the l aN anchorage length of anchor cables, is l tN the total length of anchor cables in row number N. According to the specifications (GB 50330-2013, Technical Code for Building Slope Engineering), we set the conservative necessary anchorage length of anchor cables as 10.0 m, i.e., l aN = 10.0 m. Then, Eq. (13) can be rewritten as:

$$ l_{tN} = l_{xN} + 10.0 $$
(20)

On the basis of Eq. (12) and the relevant parameters of the Shuige slope in Table 1, the free section length l xN of anchor cables can be calculated (see Table 4).

Combined with the anchorage length of anchor cables of 10.0 m, the corresponding total length l tN of anchor cables can be obtained (see Table 5). Figure 18 shows the distribution characteristics of the total length l tN of anchor cables at different positions varying from the first row to the ninth row, starting from bottom to top on the free surface.

Table 4 Calculated free section length l xN of anchor cables from rows 1–9 (unit m)
Full size table
Table 5 Calculated total length l tN of anchor cables from rows 1–9 (unit m)
Full size table
Fig. 18
figure 18

Distribution chart of the total length of anchor cables at different positions. Row numbering starts from top to bottom on the free surface

Full size image

Discussion

The upper limit of anchor cable spacing

Due to the possible existence of secondary discontinuities in rock wedges, too large a spacing of anchor cables could induce local instability. Consequently, an upper limit for spacing of anchor cables for engineering practice should be determined.

There is a marked turning point in the x–S I curve in Fig. 19, which is induced by the parabolic distributed driving force. For safety considerations, we set the limit of maximum spacing (limit of S max) at this turning point (see Fig. 19). There is an exit threshold for spacing in the x–S f curve, at about 5.2 m. Therefore, to fulfil both safety and economic considerations, we chose 5.2 m as the upper limit of cable spacing S max, i.e., this close spacing is applied in the major intersection profile of the slope, with spacing then increasing slowly along the distance to the side boundaries, finally reaching the upper limit value of spacing (see Fig. 19). We can then adjust the former optimized layout of anchor cables on the free surface of the wedge, and the newly adjusted rational layout scheme is presented in Fig. 20. As can be seen from the layout graph in Fig. 20, we need only 59 anchor cables in total; compared with the 71 anchor cables in the conventional uniform scheme, we can therefore obtain a saving of 16.9 % in the number of anchor cables.

Fig. 19
figure 19

Sketch determining the limit of maximum spacing

Full size image
Fig. 20
figure 20

Adjusted rational layout of anchor cables for reinforcing rock wedges

Full size image

Application of asymmetrical rock wedges

We assumed that rock wedges are symmetrical as in the model shown in Fig. 3. However, actual rock wedges may not be perfectly symmetrical objects. Indeed, due to the cutting of different sets of discontinues, actual rock wedges are more likely to be asymmetrical. However, the non-uniform layout principal presented above for anchor cables also applies to asymmetrical rock wedges. The spacing and total length of anchor cables can be obtained according to actual spatial characteristics. The optimal asymmetrical layout of anchor cables can then be obtained as presented in the case study of the Shuige rock wedge in Lishui City, China.

Specification considerations for length of anchor cables

Considering the length of anchor cables, the National Norm of China (GB 50330-2013) “Technical code for building slope engineering” states the designated specification length, for instance, 20, 25, 30, 35, 40 m, etc. Therefore, in order to meet the requirement of the designated specification length for construction convenience, the presented total length of anchor cables can also be adjusted to suit. Furthermore, due to the particular shape of the wedge, it is possible to cut down the length of anchor cables at the lower rows. For instance, Fig. 8 indicates that the thickness of the rock wedges is quite small in the lowest row; therefore, we can consider cutting down the length of anchor cables or replacing them with anchor bolts so as to obtain a more reasonable and economical design.

As can be seen in Fig. 14, the curve of each column of anchor cables with distances x to the major intersection profile of the slope is parallel to the others. For each row of anchor cables, the total length has the same value in the major intersection profile and to the side boundaries. For each column of anchor cables, the total length increases along with the height of the anchor cables. The above two varying trends of anchor cable lengths depend on the three-dimensional distribution characteristics of the driving force as well as the shape of the rock wedges. Therefore, the conventional scheme with uniform length of anchor cables is an over-conservative scheme, which could result in longer anchor cables than necessary, thereby resulting in wasted investment. However, the actual shape characteristics of the slope are not always prefect wedges. Taking account of the actual situation and construction convenience, the final length of the anchor cables can be determined from Table 6.

Table 6 Adjusted final total length l f of anchor cables from rows 1–9 (units m)
Full size table

The maximum length of anchor cables was 30 m in the actual project, and we suppose the average length to be approximately 25 m. Comparing the adjusted final length results of anchor cables in Table 6 with the conventional uniform length design scheme, we can conclude that the adjusted scheme can reduce the anchor cables by 18.9 % in total length.

Conclusions

From the perspective of the three-dimensional geological characteristics of rock wedges, this paper presents an optimization study on the layout and length of anchor cables stabilizing rock wedges.

A generalized theoretical model of rock wedges was abstracted from a site investigation to represent the three-dimensional characteristics of rock wedges. On the basis of the hyperbolic model between driving force and scale factor, a parabolic function can be deduced to describe the distribution pattern of driving force along an arbitrary longitudinal section.

For a given longitudinal section, the number of anchor cables depends on the corresponding driving force, which is usually obtained by the two-dimensional rigid equilibrium limit method. Consequently, the required number of anchor cables should correspond to the driving force of the calculation section. Therefore, due to the remarkable characteristics of parabolic curves in the expression of driving forces, a corresponding non-uniform layout principle of anchor cables was proposed, with closer layout in the central part and sparse layout nearer the side boundaries.

The total length of an anchor cable is comprised of two sections, namely a free section length and an anchorage length. Anchorage length can be calculated according to the stress condition of anchor cables along the slope sections. The rational length of anchor cables was quantified on the basis of specification and the three-dimensional spatial characteristics of the rock wedges.

In addition, considering safety, an upper limit spacing of anchor cables was proposed by the spacing threshold caused by the parabolic distributed driving force.

The spacing distribution of the optimized anchor cables was verified to be a parabolic distribution according to the case study of the Shuige rock wedge in Lishui City, China. The results indeed show that the curve of optimized anchor cables spacing is verified to be a parabolic distribution. Compared with conventional uniform spacing and length design schemes, the adjusted optimal non-uniform scheme can reduce anchor cables by 16.9 % in number and 18.9 % in total length, respectively.