1 Introduction

Optical couplers employing the energy exchange of evanescent waves have been of great interest since its first introduction over a decade ago. These are composed of linearly coupled waveguides with significant distance between each other to control the rate of energy-transfer adjacently, and have potentials to be key components in various optoelectronics and photonics applications. To enhance the capabilities, various kinds of couplers employing different mechanisms and processes have been studied in the literature, e.g., bundle optical coupler [1], unidirectional coupler [2], and coaxial directional coupler [3].

Directional coupler with nonlinear coupling medium possesses great potentials as a quantum light generator. Several kinds of nonlinear couplers with different nonlinear processes, such as second-harmonic generation [4], Raman or Brillouin processes [5], and optical Kerr effect [6], have been given much attention. Since the reports by Jensen [7] as a two-channel single-mode device, the properties of nonlinear directional couplers (NLDCs) has been theoretically investigated, and many interesting non-classical effects have been reported analytically [8,9,10,11] and semi-analytically [12,13,14,15].

Subsequently, the two-channel two-mode devices have been extended to three- [16, 17] and four-mode devices [18] with many interesting quantum effects. These studies demonstrate significant advantages of the multimode interaction of optical fields in nonlinear media, as opposed to the two-channel system, and allow the possibility of designing quantum light amplifiers (based on these devices) for applications beyond the standard quantum limit. One of the most challenging problems in optical technology has been the restrictions on device performance set by the quantum limit, resulting from the intrinsic noise inherited in quantum systems [19].

Even though multimode interaction of two-channel device exhibits a considerable reduction in quantum noise, this comes at the expense of reducing the propagation length [18] of the squeezed states. In addition, one of the conditions for an effective estimation of the solution requires the field modes to propagate at the same velocity [17]. This can be strenuous to achieve due to the difficulty in controlling the property of individual modes in each waveguide throughout the propagation length. This is due to the fact that multimode waveguides induce different individual propagation velocity for each mode compared with single-mode waveguides. Therefore, we believe that a single-mode multichannel coupler provides a more convenient alternative to generate squeezed states via multimode interaction compared with a multimode two-channel coupler. The proposed system offers more flexibility on the coupled-mode interactions. Thus, an effective production and mode transmission of squeezed states is possible via single- and mixed-mode quadrature correlations.

Various kinds of geometrical arrangements of couplers with interesting quantum properties have been reported. The switching mechanism of an optical coupler, composed of three symmetric waveguides with Kerr-like nonlinear intensity-dependent media, has been characterized using the eigenmodes of the structure [20]. The all-optical switching mechanism and wavelength demultiplexing of an asymmetric version of the three-waveguide directional coupler with thin photorefractive grating have been investigated [21]. In another version of this device, quantum-statistical properties of light have been studied in three-channel directional coupler composed of nonlinear waveguide operated by the second-harmonic generator placed between two linear waveguides [22]. Furthermore, the optical switching operation in a three-channel NLDC has also been studied when the power is initially launched into the center waveguides [23].

Despite being a simple optical system, the three-channel Kerr NLDC provides a good mechanism for generating quantum states of light. Moreover, the fact that Kerr effect does not require phase matching (together with the fast nonlinear optical response of mediums) contributes to further enhancement of quantum effects. Nevertheless, three-channel coupler employs the center excitation model, permitting thereby the energy transfer only to the adjacent waveguide from the center where the power is initially fed into. While the isolation of waveguides may be beneficial to quantum phase gate application of bandgap quantum coupler [24], such arrangement will disadvantageously limit the possible number of coupling modes.

The work reported in this communication is pivoted to the investigation of dynamical quantum properties of single-mode Kerr NLDC composed of four coupled waveguides, in the context of phase-space representation. In the proposed four-channel system, waveguides are arranged so that all the modes are involved in evanescent field coupling. Particularly, the modeling of system is focused on the generation and dynamics of quantum noise below the standard quantum limit, and its comparison with the two-channel device. The novelty of this work is that a quad-channel nonlinear coupler, based on Kerr nonlinearities, exhibits reliable quantum effects to a significant extent, as compared with its conventional two-channel counterparts. This is because the propagating fields in quad-channel system are involved in multiple multimode linear interactions supported by the Kerr self-action nonlinearity. Given that the surrounding waveguides are isolated from each other, the system will be reduced to four-channel bandgap quantum coupler, which would be useable for quantum logical gate application [24].

2 Design and modeling

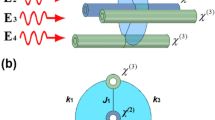
Figure 1 shows the arrangement of four Kerr waveguides with the physical characteristics chosen such that they share identical physical geometries. Only one waveguide is initially pumped (with power), and the energy flow in the other guides (via the evanescent field coupling) remains under observation. The periodical range of energy exchange between the coupled modes is specified by the coupling factor that is essentially the reciprocal of the distance of separation of guides. Accordingly, the waveguides have to be arranged in close proximity to allow energy transfer. Figure 1 also depicts the interaction scheme of the proposed system. The quantum mechanical treatment of the problem allows the Hamiltonian (to describe the system adequately) to be of the form.

Fig. 1
figure 1

Schematic representation of the cross-section of a quad-directional coupler; \({a}_{1}\), \({a}_{2}\), \({a}_{3}\) and \({a}_{4}\), respectively, denote the fundamental, second, third and fourth mode propagating in the channels

Full size image
$${\hat {H}_t}\;=\;{\hat {H}_{{\text{system}}}}+{\hat {H}_{{\text{Kerr}}}}+{\hat {H}_{{\text{coupling}}}}.$$
(1)

Carrying the description of optical modes, the total Hamiltonian is comprised of system Hamiltonian, nonlinear Hamiltonian due to the third-order nonlinear mediums, and coupling Hamiltonian of the coupled modes. The system Hamiltonian, in general, may be modeled through the equation

$${\hat {H}_{{\text{system}}}}=\hbar \omega \sum\limits_{{n=1}}^{4} {\left\{ {\hat {a}_{n}^{\dag }{{\hat {a}}_n}} \right\}} ,$$
(2)

where \({\widehat{a}}_{i}\) and \({\widehat{a}}_{i}^{\dag}\) are the creation and annihilation operators, respectively, satisfying the commutation relation \(\left[\widehat{a},{\widehat{a}}^{\dag}\right]=1\). The coefficients ω and \(\hbar\) give the standard definition of operating frequency and Planck constant, respectively. The practical estimation of operating frequency ω lies around ≈ 1014 Hz. The nonlinear interaction is modeled by the Kerr Hamiltonian

$${\hat {H}_{{\text{Kerr}}}}=\hbar g\sum\limits_{{n=1}}^{4} {\left\{ {\hat {a}{{_{n}^{\dag }}^2}\hat {a}_{n}^{2}} \right\}} ,$$
(3)

where the coupling constant g is the nonlinear coupling strength, and the term \({\widehat{a}}_{i}^{\dag2}{\widehat{a}}_{i}^{2}\) is responsible for self-action process having positive proportionality to the third-order susceptibility in Kerr nonlinear mediums. Following the classical anharmonic oscillator equation, the coupling constant g may be conveniently approximated using the classical formula [25]

$$g=\left( {\frac{{{\varepsilon _0}{m^3}}}{{N{e^4}}}} \right)\chi _{{iiii}}^{{(3)}}{\left( {\omega _{0}^{2} - {\omega ^2} - i\omega \xi } \right)^4},$$
(4)

where e and m are, respectively, the electronic charge and mass. The coefficient χ(3) denotes the third-order nonlinear dielectric susceptibility, and N gives the number density of bound electrons. For a typical dielectric material, the third-order nonlinear dielectric susceptibility is approximately χ(3) ≈ 10−22 m2/V2 and N ≈ 5.3 × 1028 m−3. The parameter g is approximated within 1.5 × 105 to 8 × 1012 /s. In this newly proposed system, we think of investigating an ideal situation without dissipation, which displays the maximum possible squeezing from the conceptual point of view.

The coupling Hamiltonian, that represents the interaction of the coupled modes, is given by

$$\begin{aligned}{\hat {H}_{{\text{coupling}}}}\;&=\hbar \left\{ {{k_1}\left( {\hat {a}_{1}^{\dag }{{\hat {a}}_2}+\hat {a}_{1}^{\dag }{{\hat {a}}_3}+\hat {a}_{1}^{\dag }{{\hat {a}}_4}} \right)} \right.\\ &\left. {\quad+\;{k_2}\left( {\hat {a}_{2}^{\dag }{{\hat {a}}_3}+\hat {a}_{2}^{\dag }{{\hat {a}}_4}+\hat {a}_{3}^{\dag }{{\hat {a}}_4}} \right)+{\text{h.c}}.} \right\}, \end{aligned}$$
(5)

where h.c. denotes the Hermitian conjugate. In addition, the coefficients kn (n = 1, 2) control the evanescent field linear cross-coupling strength, and may be approximated by the formula [26] k ≈ π/2Lc; Lc being the separation length between the adjacent waveguides. The parameter k has a dimension of wavenumber. For convenience in numerical simulation, the parameter k can be converted to unit frequency, which is estimated assuming optical velocity in nonlinear fibre (for example, using silica glass) in this paper. Following the standard method for Hamiltonian, the master equation for the reduced density operator \(\widehat{\rho }\) in Schrödinger picture is given by [27]

$$i\hbar \frac{{\partial \hat {\rho }}}{{\partial t}}=\left[ {{{\hat {H}}_t},\hat {\rho }} \right].$$
(6)

One way of solving Eq. (6) is to expand the density operator \(\widehat{\rho }\) with a coherent state basis in phase-space using suitable quasiprobability distribution [28], such as positive-\(P\) [29] representation. The transformation of quantum equation to its classical description, using the positive-\(P\) representation, allows the density matrix of quantum fields to be represented in a diagonal form of coherent state. By the application of operator algebra rules [30], the Fokker–Planck equation is derived using the positive-\(P\) representation as

$$\begin{gathered} \frac{{\partial P}}{{\partial \tau }}=\left[ {\sum\limits_{{n=1}}^{4} {\frac{\partial }{{\partial {\alpha _n}}}\left\{ {i\omega {\alpha _n}+2ig{\beta _n}\alpha _{n}^{2}} \right\} - \sum\limits_{{n=1}}^{4} {\frac{\partial }{{\partial {\beta _n}}}\left\{ {i\omega {\beta _n}+2ig{\alpha _n}\beta _{n}^{2}} \right\}} } } \right. \hfill \\ \quad \quad +\frac{\partial }{{\partial {\alpha _1}}}\left\{ {i{k_1}{\alpha _2}+i{k_2}\left( {{\alpha _3}+{\alpha _4}} \right)} \right\} - \frac{\partial }{{\partial {\beta _1}}}\left\{ {i{k_1}{\beta _2}+i{k_2}\left( {{\beta _3}+{\beta _4}} \right)} \right\} \hfill \\ \quad \quad +\frac{\partial }{{\partial {\alpha _2}}}\left\{ {i{k_1}{\alpha _1}+i{k_2}\left( {{\alpha _3}+{\alpha _4}} \right)} \right\} - \frac{\partial }{{\partial {\beta _2}}}\left\{ {i{k_1}{\beta _1}+i{k_2}\left( {{\beta _3}+{\beta _4}} \right)} \right\} \hfill \\ \quad \quad +\frac{\partial }{{\partial {\alpha _3}}}\left\{ {i{k_1}{\alpha _1}+i{k_2}\left( {{\alpha _2}+{\alpha _4}} \right)} \right\} - \frac{\partial }{{\partial {\beta _3}}}\left\{ {i{k_1}{\beta _1}+i{k_2}\left( {{\beta _2}+{\beta _4}} \right)} \right\} \hfill \\ \quad \quad +\frac{\partial }{{\partial {\alpha _4}}}\left\{ {i{k_1}{\alpha _1}+i{k_2}\left( {{\alpha _2}+{\alpha _3}} \right)} \right\} - \frac{\partial }{{\partial {\beta _4}}}\left\{ {i{k_1}{\beta _1}+i{k_2}\left( {{\beta _2}+{\beta _3}} \right)} \right\} \hfill \\ \quad \quad +\frac{1}{2}\frac{{{\partial ^2}}}{{\partial \alpha _{1}^{2}}}\left\{ { - 2ig\alpha _{1}^{2}} \right\}+\frac{1}{2}\frac{{{\partial ^2}}}{{\partial \beta _{1}^{2}}}\left\{ {2ig\beta _{1}^{2}} \right\}+\frac{1}{2}\frac{{{\partial ^2}}}{{\partial \alpha _{2}^{2}}}\left\{ { - 2ig\alpha _{2}^{2}} \right\} \hfill \\ \quad \quad +\frac{1}{2}\frac{{{\partial ^2}}}{{\partial \beta _{2}^{2}}}\left\{ {2ig\beta _{2}^{2}} \right\}+\frac{1}{2}\frac{{{\partial ^2}}}{{\partial \alpha _{3}^{2}}}\left\{ { - 2ig\alpha _{3}^{2}} \right\}+\frac{1}{2}\frac{{{\partial ^2}}}{{\partial \beta _{3}^{2}}}\left\{ {2ig\beta _{3}^{2}} \right\} \hfill \\ \left. {\quad \quad +\frac{1}{2}\frac{{{\partial ^2}}}{{\partial \alpha _{4}^{2}}}\left\{ { - 2ig\alpha _{4}^{2}} \right\}+\frac{1}{2}\frac{{{\partial ^2}}}{{\partial \beta _{4}^{2}}}\left\{ {2ig\beta _{4}^{2}} \right\}} \right]P. \hfill \\ \end{gathered}$$
(7)

In Eq. (7), \(P\) is a quasi-probability positive function of the evolution parameter giving normally ordered averages, and τ denotes the propagation direction. The variables αn and βn are complex-valued functions of τ. Equation (7) can be converted to Langevin Stochastic equations by applying it to rules [31]. Furthermore, for the convenience of simulations, the resulting set of equations can be of the following form:

$${\dot {\alpha }_1}= - i\left\{ {{\alpha _1}\left( {\tilde {\omega }+2\tilde {g}{\beta _1}{\alpha _1}} \right)+{{\tilde {k}}_1}\left( {{\alpha _2}+{\alpha _3}+{\alpha _4}} \right)} \right\}+\sqrt {2\tilde {g}} {\alpha _1}{\lambda _1}{\eta _1}(\tilde {\tau }),$$
(8)
$${\dot {\beta }_1}=i\left\{ {{\beta _1}\left( {\tilde {\omega }+2\tilde {g}{\alpha _1}{\beta _1}} \right)+{{\tilde {k}}_1}\left( {{\beta _2}+{\beta _3}+{\beta _4}} \right)} \right\}+\sqrt {2\tilde {g}} {\beta _1}{\lambda _2}{\eta _2}(\tilde {\tau }),$$
(9)
$${\dot {\alpha }_2}= - i\left\{ {{\alpha _2}\left( {\tilde {\omega }+2\tilde {g}{\beta _2}{\alpha _2}} \right)+{{\tilde {k}}_1}{\alpha _1}+{{\tilde {k}}_2}\left( {{\alpha _3}+{\alpha _4}} \right)} \right\}+\sqrt {2\tilde {g}} {\alpha _2}{\lambda _1}{\eta _3}(\tilde {\tau }),$$
(10)
$${\dot {\beta }_2}=i\left\{ {{\beta _2}\left( {\tilde {\omega }+2\tilde {g}{\alpha _2}{\beta _2}} \right)+{{\tilde {k}}_1}{\beta _1}+{{\tilde {k}}_2}\left( {{\beta _3}+{\beta _4}} \right)} \right\}+\sqrt {2\tilde {g}} {\beta _1}{\lambda _2}{\eta _4}(\tilde {\tau }),$$
(11)
$${\dot {\alpha }_3}= - i\left\{ {{\alpha _3}\left( {\tilde {\omega }+2\tilde {g}{\beta _3}{\alpha _3}} \right)+{{\tilde {k}}_1}{\alpha _1}+{{\tilde {k}}_2}\left( {{\alpha _2}+{\alpha _4}} \right)} \right\}+\sqrt {2\tilde {g}} {\alpha _3}{\lambda _1}{\eta _5}(\tilde {\tau }),$$
(12)
$${\dot {\beta }_3}=i\left\{ {{\beta _3}\left( {\tilde {\omega }+2\tilde {g}{\alpha _3}{\beta _3}} \right)+{{\tilde {k}}_1}{\beta _1}+{{\tilde {k}}_2}\left( {{\beta _2}+{\beta _4}} \right)} \right\}+\sqrt {2\tilde {g}} {\beta _3}{\lambda _2}{\eta _6}(\tilde {\tau }),$$
(13)
$${\dot {\alpha }_4}= - i\left\{ {{\alpha _4}\left( {\tilde {\omega }+2\tilde {g}{\beta _4}{\alpha _4}} \right)+{{\tilde {k}}_1}{\alpha _1}+{{\tilde {k}}_2}\left( {{\alpha _2}+{\alpha _3}} \right)} \right\}+\sqrt {2\tilde {g}} {\alpha _4}{\lambda _1}{\eta _7}(\tilde {\tau }),$$
(14)
$${\dot {\beta }_4}=i\left\{ {{\beta _4}\left( {\tilde {\omega }+2\tilde {g}{\alpha _4}{\beta _4}} \right)+{{\tilde {k}}_1}{\beta _1}+{{\tilde {k}}_2}\left( {{\beta _2}+{\beta _3}} \right)} \right\}+\sqrt {2\tilde {g}} {\beta _3}{\lambda _2}{\eta _8}(\tilde {\tau }).$$
(15)

In the above set of Eqs. (8)–(15), the overdot represents partial derivative of variables over dimensionless direction of propagation τ. The dimensionless variables are related to its dimensional counterparts by \(\tilde {\tau }\) = ωτ, g͂ = g/ω, k͂ = k/ω, ῶ = ω/ω, and ηn(τ) = η(t)/ω1/2. The intrinsic Gaussian white noise is given by the coefficient ηn(t), satisfying both the correlations of < ηn(t) > = 0 and < ηn(t) ηm(t′)> = δnmδ(t−tʹ) accordingly. The coefficient ω1/2 sets the level of quantum noise, and λn (n = 1, 2) are given by λ1 = cos(π/4)−isin(π/4) and λ2 = cos(π/4) + isin(π/4).

As long as the integration process converges, the positive-\(P\) representation remains a powerful tool to model the dynamics of system. In certain cases, the numerical solution of stochastic equations, derived using the positive-\(P\) representation, has an instability issue due to the double number of variables, in comparison with the classical equations resulting from other representations. To investigate the system dynamics, where the implementation of positive-\(P\) go astray, an approximate “truncated Wigner” may be considered. For the present consideration, the positive-\(P\) representation is found to be stable in practice, and therefore, can be used to investigate the system properties for longer interaction length. This is as opposed to the conventional short-length solution, where the interaction length can be limited.

3 Quantum dynamical properties

Random noise is usually derived from environmental factors. In usual classical practice, the effective way of eliminating the influence of such noise is achieved by carefully designed light source. Quantum optical systems, in contrast, adhere to the laws of quantum mechanics, and have an inherent quantum indeterminacy of field fluctuation. The fundamental noise is permanent, no matter how carefully the light source is controlled [32]. Laser-based devices are at disadvantage from the quantum noise, because it sets a fundamental limit on their resolution.

To overcome the quantum limit, light with significant amount of squeezing is usually used. The quantum noise is naturally distributed equally in both the optical phase quadrature components, in accordance with Heisenberg’s uncertainty principle with minimized uncertainty product. The phase distribution of fluctuations is random, and the standard quantum limit, known as the zero-point fluctuation, gives the highest noise reduction in the field. By squeezing the fluctuation, the quantum noise in one quadrature is able to surpass the standard quantum limit. This phenomenon will lead to an increase in fluctuation in the canonical variable to ensure that the fluctuation product does not violate the uncertainty relation, and also, the area in phase-space is conserved.

To investigate squeezing, we define the field quadratures of coherent radiation for the most elementary case as [33]

$${\hat {X}_f}=\frac{1}{2}\sum\limits_{{j=1}}^{f} {\left( {{{\hat {a}}_j}+\hat {a}_{j}^{\dag }} \right)} ;\;\;{\hat {Y}_f}\;=\;\frac{1}{{2i}}\sum\limits_{{j=1}}^{f} {\left( {{{\hat {a}}_j} - \hat {a}_{j}^{\dag }} \right)} ,$$
(16)

with the arbitrary subscript f being the controlling parameter for specifying the quadrature linear combinations. For example, f = 1 accounts for single-mode and f > 1 for mixed-mode quadrature. In the present system, maximal f is set at f = 4. Fluctuation of uncertainty in the variances of \({\hat {X}_f}\) and \({\hat {Y}_f}\) yields [17]

$$\left\langle {{{(\Delta {{\hat {X}}_f})}^2}\rangle \langle {{(\Delta {{\hat {Y}}_f})}^2}} \right\rangle \; \geq \;\frac{{{{\left| {{c_f}} \right|}^2}}}{{16}},$$
(17)

where cf takes the value of 1 to 4 for single- to four-mode squeezing, respectively. Rearrangement of Eq. (17) gives the expressions for general first-order squeezing [17]

$${S_{x,f}}=4\langle {(\Delta {\hat {X}_f})^2}\rangle - \left| {{c_f}} \right| \leq 0,$$
(18)
$${S_{y,f}}=4\langle {(\Delta {\hat {Y}_f})^2}\rangle - \left| {{c_f}} \right| \leq 0.$$
(19)

Making use of the positive-\(P\) representations, the possibility of squeezing appearing in the four-channel system is to be investigated. It must be noted that, in the present approach, the normally ordered equations are very sensitive to the value of the input parameters. Therefore, in predicting the presence of squeezed light, the numerical solution of the system is performed with input parameters adopted from the literature [34, 35] to ensure that the integration is stable and optimal. For an experimentally realizable results, perhaps these input parameters needs to be modified to tailor an experimental scheme.

Figure 2 illustrates single-mode squeezing in the quad-coupler as a function of dimensionless interaction length ωτ with asymmetrical initialization mechanism. A small value of initial state (viz. \({\alpha }_{1}=0.1\)) in the first mode to initialize the launching mechanism enables squeezing to be generated. Figure 2a, b shows comparative features of the first and second quadrature, respectively, in both channel one and channel two. The first and second quadrature in channel one (Fig. 2a) show similar squeezing patterns, in terms of squeezing range and shape. It is observed that, the fluctuation amplitude of squeezing is relatively large, considering that the coherent initialization state is small. The device shows usual pattern of squeezing where the quantum noise is being distributed equally between the quadrature components. In addition, squeezing increases with the increase of dimensionless interaction length ωτ, and the maximal squeezing is found to be at the longest ωτ. On the other hand, in the second channel (Fig. 2b), at certain interaction range (from 0 to ≈ 10), squeezing is not observed in the quadrature evolution for both components. The absence of squeezing is due to the implication of asymmetric initialization, where the second channel is launched with vacuum excitation a2 = 0. Without the transfer of energy from the first channel, the field remains in a vacuum state. For weak coupling condition, the rotating wave approximation of Hamiltonian Eq. (5) remains relevant, quantum state transfer occurs only when the condition ωτ > 10 is achieved. From this range (ωτ > 10), both quadrature components start to surpass the quantum limit periodically. This shows that the second channel of quad-coupler exhibits redistribution of noise between the two quadrature fields, henceforth induce considerable stochastic reduction over ranges of evolution distances.

Fig. 2
figure 2

Variation of the single-mode squeezing as a function of dimensionless interaction length ωτ with asymmetrical initialization mechanism; a channel one; b channel two. The input parameters are taken as ain1 = 0.1, ain2 = ain3 = ain4 = 0, ω = 1014 Hz, g = 0.5×1011 s−1, k1 = 1011/s and k2 = 0.5 k1

Full size image

One of the special features of Kerr NLDC is that it allows switching of squeezed light from one input beam to other. The first channel is capable of generating quantum light with oscillatory behavior. At sufficient strength of evanescent coupling, there would be an interaction between waveguides, thereby transferring quantum light from one channel to another. Parallel squeezing obtained with symmetrical state initialization is given in Fig. 3a.

Fig. 3
figure 3

Variation of the single-mode squeezing as a function of dimensionless interaction length ωτ with symmetrical and asymmetrical initialization mechanism. a Parallel squeezing in channel one and channel two with symmetrical initialization; b squeezing in channel one for both symmetrical and asymmetrical initialization. The input parameters are taken as ω = 1014 Hz, g = 0.5 × 1011/s, k1 = 1011/s, k2 = 0.5 k1, ain1 = ain2 = ain3 = ain4 = 0.1 for (a) and ain1 = ain2 = ain3 = ain4 = 0.1, ain1 = 0.1, ain2 = ain3 = ain4 = 0 for (b)

Full size image

For a symmetrical choice of input parameters, squeezing is found to be equal in all channels. Nevertheless, the absence of coupling constant k1,2 reduced the system to four independent waveguides, and squeezing disappears entirely. The linear coupling constant permits multichannel interaction to switch the squeezed oscillation between waveguides, and the entire oscillation will then have an identical evolution throughout the remainder of their interaction paths. Figure 3b illustrates a comparison between squeezing exhibited in the first channel for both symmetric and asymmetric initializations. It is found that the symmetrical initialization state is relevant to invoke a greater degree of squeezing. To note, the same squeezing effects are observed in the other channels as well.

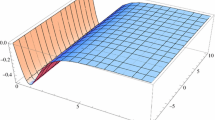
The multichannel structure of system extends the number of possibilities for correlation between the modes in different channels. As such, a more flexible combination of the coupled modes, i.e., the second-, third-, and fourth-order mixed-mode, are available. For this reason, a quad-channel system could be useful in enhancing the generation of squeezing via the mixed-mode interaction. The manifestation of mixed-mode in multichannel structure is presented in Fig. 4a. It follows that a strong non-classical transition of coherent states is observed for single- and mixed-mode propagation of field operators. The states of maximal squeezing, in this case, depend upon the order of combination of field operators; the strongest squeezing always appears in the highest combination. Figure 4b depicts a comparison between the quadrature evolution in the first channel for both the two-channel and the present system. The solid curves give the quadrature fluctuation for maximal achievable squeezing in the two-channel coupler, whereas the dotted curves show the maximal achievable squeezing in the present system. In this scenario, the quadrature variances exhibit greater maximal squeezing in both canonically conjugate quadrature. The spectrum of both quadrature squeezing in the present system is remarkably larger than that observed in the two-channel system. Moreover, the quantum behavior of quadrature components (∆Xf, ∆Yf) periodically depends on the self-action nonlinear coupling with negative proportionality relationship between each other. At longer distances, the quadrature variances propagate erratically as random phase fluctuating fields rather than reaching a steady state, as usually predicted in Kerr NLDC.

Fig. 4
figure 4

Variation of the mixed-mode squeezing as a function of dimensionless interaction length ωτ with symmetrical initialization mechanism. a Channel one; b comparison between maximal achievable squeezing for two-channel and quad-channel system. The input parameters are taken as ain1 = ain2 = ain3 = ain4 = 0.1, ω = 1014 Hz, g = 0.5 × 1011/s, k1 = 1011/s and k2 = 0.5 k1

Full size image

Figure 5a shows the evolution of the quadrature variances in the first channel as a function of ωτ with several initial coherent states, while the other input parameters remain fixed. Numerical estimations of quadrature evolution indicate that the maximal squeezing is dependent on the initial value of coherent field, and the device is generating greater maximal squeezing at higher values of initial intensity. The result obtained here is consistent with the case of three-mode oscillator interaction [34] where a very strong squeezing is achievable via effective manipulation of the initial value of coherent excitation. Higher values of initial conditions of coherent fields, however, affect the stability of positive-\(P\) representation. This is because the integration in positive-\(P\) representation converges for longer distances at low initial intensities of coherent signals. A comparison between the first quadrature in the second channel with different initial coherent states is given in Fig. 5b. This demonstrates that the second channel assumes similar squeezing properties to that of the first channel, in response to the varying initial states. Similarly, it appears that the same effect is subjected to the third and fourth channels as well.

Fig. 5
figure 5

Single-mode squeezing as a function of dimensionless interaction length ωτ for different asymmetrical initializations. a Channel one; b channel two. The input parameters are taken as ω = 1014 Hz, g = 0.5×1011/s, k1 = 1011/s and k2 = 0.5 k1

Full size image

4 Conclusion

As a conclusion, four-channel Kerr waveguides have been modeled by phase-space representation. Quantum dynamics describing quadrature variances of system have been obtained by integrating the stochastic equations of the respective representation. Single- and mixed-mode squeezing are predicted in response to variations in input parameters. The effect of symmetry in the initial state, the initial state of the coherent field, the number of waveguides involved in interaction, and the nonlinear coupling parameter on the propagation of quadrature squeezing have been studied. Depending on system initialization, parallel squeezing (in all channels) is achievable via quantum state transfer and the squeezing levels depend on the channels. As opposed to the asymmetrical initialization, symmetrical excitation provides a greater degree of squeezing. Moreover, larger squeezing is possible with a larger input field. The present system is found to be useful in enhancing squeezing via mixed-mode interaction and can be better than the two-channel system. A remarkable improvement of maximal squeezing is possible via multichannel interaction and higher value of nonlinear coupling constant. Even though numerous ways exist to achieve robust squeezing, such as the parametric process. Nevertheless, it turns out that parametric processes are physically complicated9. Alternatively, the present system could give us access to the new possibilities of manipulating squeezing in simple systems with more flexibility through effective manipulation of modes correlation induced by multichannel interaction. A greater amount of squeezing is possible via increasing the number of channel waveguides involved in interaction, i.e., a stronger squeezing is expected to be observed in a system implementing higher number of single-mode waveguides. Rather than relying on devices with complicated structures, the present system may stimulate further interests in generating squeezed states of light using multichannel waveguides. Finally, the system presented here provides a better squeezing compared with the two-channel device, and may be used as an alternative source of squeezed light, in general.