1 Introduction

Quantum mechanics not only helps us understand the framework of physics and its principle, but also the mainly responsible to future technological advance such as quantum information, teleportation, computation and many other branches. The important features of this advance are nonclassical properties of quantum systems which are called quantum correlations and can be firmness to transmit reserve and manipulate information. These lead to the speedy development of a particular interest in research of quantum correlations in various types of quantum systems. Recently experiments also show the convincing evidence of higher-order nonclassical properties in some quantum systems. It has been clearly observed that we may easily discover a weak nonclassicality when using the criterion of higher-order nonclassicality. In fact, squeezed states have played an important role for the teleportation of coherent states and continuous variable quantum cryptography (Hillery 2000). The single photon sources are built by using antibunched states (Ekert 1991). The essential states for the implementation of quantum key distribution, quantum teleportation, quantum cryptography and dense-coding are entangled states (Lee 1990; Furusawa et al. 1998; Bennett et al. 1993; Bennett and Wiesner 1992). Studying the possibility of generation of such correlations in different quantum systems has recently become extremely significant and important for the researchers, who are working in different aspects of quantum information theory and quantum optics.

In recent decades, there exists a rapid development of a particular interest in research of quantum correlations in multi-parties systems consisting of two or more subsystems. Many scientists have focused on the generation of quantum correlations in terms of nonclassicalities in the Kerr-like nonlinear coupler systems such as antibunching (Zou and Mandel 1990), steering (Olsen 2015; Kalaga et al. 2017), squeezing (Lukš et al. 1988), and intermodal entanglement (Duan et al. 2000; Hillery and Zubairy 2006). These systems usually contain two Kerr nonlinear oscillators interacting linearly (Leoński and Miranowicz 2004; Miranowicz and Leoński 2006) or nonlinearly (Kowalewska-Kudłaszyk and Leoński 2006; Le Duc and Cao Long 2016) with each other and may be driven by the external fields in one (Leoński and Miranowicz 2004; Miranowicz and Leoński  2006; Kowalewska-Kudłaszyk and Leoński 2006) or two modes (Miranowicz and Leoński 2006; Le Duc and Cao Long 2016). These oscillators are described by effective Hamiltonians, which is similar to those described optical Kerr systems. These systems have been extended to the case of three Kerr-like nonlinear oscillators (Kalaga et al. 2016, 2018; Kalaga and Leoński 2017). When the strength of mutual coupling and the external excitation satisfy the conditions related to Kerr-like nonlinearity, the system’s evolution will be closed within finite set of n-photon Fock states. Applying the method of nonlinear quantum scissors (Leoński and Kowalewska-Kudłaszyk 2011; Leoński 1997; Leoński et al. 1997), the nondissipation models can be considered as the perfect qubit–qubit systems. Then, one concentrated on the system’s possibility to generation of maximally entangled states (Bell-like states) and shows that such states can be produced with high accuracy in these models. One shows that the models discussed here can be dealt with a potential source of maximally entangled states. Especially, when the cross-coupling interaction is present, such processes become more effective (Nguyen et al. 2013). Moreover, one shows how damping processes can destructively influence such generation effects. It also showed that sudden death of the entanglement (and its sudden rebirth) appears in the system (Kowalewska-Kudłaszyk et al. 2014). In addition, it shows that under special conditions, some amount of the entanglement can survive despite the presence of decoherence process.

In all papers mentioned above, it is assumed that the laser light is monochromatic. However, in the experiments, real laser is never absolutely monochromatic as it is often assumed in theoretical models that have fluctuations in both amplitude and phase. These quantum fluctuations are the subjects of both theoretical and experimental research of a wide community of physicists in the world because they have potential applications for the quantum technology, in particular quantum information technology. To avoid complicated microscopic description, laser light is usually considered as a classical stochastic process. Even then, the dynamics equations describing the optical systems are stochastic equations, which are usually difficult to be solved analytically even for the case when real laser light is modeled by a random Gaussian noise, apart from some special cases as so-called white noise. In this case, we have obtained some interesting results (Doan Quoc et al. 2012a, b, 2016a, b, 2018).

The objective of this paper is to consider the influence of the external and coupling field width on the generation of maximally entangled states in the Kerr nonlinear couplers, including two quantum nonlinear oscillators located inside one cavity. These oscillators are linearly coupled to each other and one of them is pumped by an external classical field, which is supposed to be divided into two components: a coherent component and a randomly fluctuating chaotic component that is so-called white noise. What is more the analytical solutions of stochastic differential equation of the probability amplitude depicting the system dynamics will be derived as well as represented by graphs and compared them with the results obtained previously in the literature.

Our paper is structured as followed: In Sect. 2, the model of the Kerr nonlinear coupler pumped in one mode and analytic solutions for the complex probability amplitudes are described. The change of entangled entropy and Bell-like states generation in the presence of parameter related to the chaotic component are discussed in the next section. The last part is the conclusions.

2 The Kerr nonlinear coupler pumped in one mode

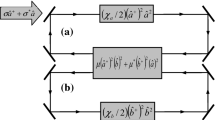
The model of the Kerr nonlinear coupler that is considered in our work includes two nonlinear oscillators linearly coupled to each other. One of them is excited by an external classical field as shown in Fig. 1. We suggest that this excitation is linear and has invariable amplitude. This system is expressed by the Hamiltonian in following form (Miranowicz and Leoński 2006) (\(\hbar = 1\)):

$$\hat{H} = \hat{H}_{0} + \hat{H}_{NL(a)} + \hat{H}_{NL(b)} + \hat{H}_{\text{int}} + \hat{H}_{ext(a)} ,$$
(1)

where

$$\hat{H}_{0} = \omega_{a} \hat{a}^{ + } \hat{a} + \omega_{b} \hat{b}^{ + } \hat{b},$$
(2)
$$\hat{H}_{NL(a)} = \frac{{\chi_{a} }}{2}\left( {\hat{a}^{ + } } \right)^{2} \hat{a}^{2} ,$$
(3)
$$\hat{H}_{NL(b)} = \frac{{\chi_{b} }}{2}\left( {\hat{b}^{ + } } \right)^{2} \hat{b}^{2} ,$$
(4)
$$\hat{H}_{\text{int}} = \varepsilon \hat{a}^{ + } \hat{b} + \varepsilon^{*} \hat{a}\hat{b}^{ + } ,$$
(5)
$$\hat{H}_{ext\left( a \right)} = \alpha \hat{a}^{ + } + \alpha^{*} \hat{a},$$
(6)

in which \(\hat{H}_{NL(a)}\) and \(\hat{H}_{NL(b)}\) describe nonlinear oscillators a and b with Kerr nonlinearities \(\chi_{a}\) and \(\chi_{b}\), respectively. \(\hat{H}_{\text{int}}\) corresponds to an internal coupling and \(\hat{H}_{ext(a)}\) describes a linear coupling between the external classical field and the mode of the field inside cavity corresponding to the oscillator a. The parameter α depicts the strength of coupling between the external classical field and the cavity mode a, and the parameter ε is the strength of the linear coupling between the two Kerr nonlinear oscillators.

Fig. 1
figure 1

The model of a Kerr nonlinear coupler pumped in one mode

Full size image

In our model, damping processes are neglected, thus the system’s evolution can be described by a time-dependent wave function, which can be written in the n-photon Fock basis as

$$\left| {\psi (t)} \right\rangle = \sum\limits_{m,n = 0}^{\infty } {c_{mn} (t)} \left| {mn} \right\rangle ,$$
(7)

in which \(c_{mn} \left( t \right)\) are the complex probability amplitudes for finding our system in the m-photon and n-photon states for mode a and b, respectively.

We have comprised here an external coupling and, thus, the energy inside the cavity is not preserved. As a consequence, one can wait in the evolution of the system many of the states, corresponding to a high number of photons will be included. However, we can surmount this difficulty by applying the method of nonlinear quantum scissors. Quantum scissors are known in literature as a group of methods or physical devices permitting the creation of the number states finite superpositions by the state truncation of the system that is defined in infinite-dimensional Hilbert space. Thus, they pertain to a wider group of engineering methods of the quantum states. The scissors debated here are relied on the optical methods in which the truncation can be obtained in different manners. When only linear optical elements or nonlinear optical media are used for achieving finite-dimensional states one can talk about linear quantum scissors or nonlinear quantum scissors devices, respectively (Leoński and Kowalewska-Kudłaszyk 2011). We can see that \(\hat{H}_{NL(a)}\) and \(\hat{H}_{NL(b)}\) produce degenerate levels of the energy equal to zero, corresponding to the following four states: \(\left| {00} \right\rangle\), \(\left| {01} \right\rangle\), \(\left| {10} \right\rangle\) and \(\left| {11} \right\rangle\). Moreover, all couplings described here have invariable envelopes, and, likewise as in Leoński and Kowalewska-Kudłaszyk (2011), Leoński (1997) and Leoński et al. (1997), we suppose that they are weak. Thus, we can study transitions within the mentioned set of the states as of resonant nature. The evolution of the considered system is closed inside the set of these four states and interactions with other states can be omitted in our approximation. Therefore, we can obtain the wave function, which depicts our model in the following form

$$\left| {\psi (t)} \right\rangle_{cut} = c_{00}^{{\left( {ij} \right)}} (t)\left| {00} \right\rangle + c_{01}^{{\left( {ij} \right)}} (t)\left| {01} \right\rangle + c_{10}^{{\left( {ij} \right)}} (t)\left| {10} \right\rangle + c_{11}^{{\left( {ij} \right)}} (t)\left| {11} \right\rangle ,$$
(8)

where \(i,j = 0,1\) are the symbol of cavity modes that are initially in states \(\left| {ij} \right\rangle\). Thus, the motion equations for the system are

$$\begin{aligned} i\frac{d}{dt}c_{00}^{{\left( {ij} \right)}} (t) & = \alpha^{*} c_{10}^{{\left( {ij} \right)}} (t), \\ i\frac{d}{dt}c_{01}^{{\left( {ij} \right)}} (t) & = \varepsilon^{*} c_{10}^{{\left( {ij} \right)}} (t) + \alpha^{*} c_{11}^{{\left( {ij} \right)}} (t), \\ i\frac{d}{dt}c_{10}^{{\left( {ij} \right)}} (t) & = \varepsilon c_{01}^{{\left( {ij} \right)}} (t) + \alpha c_{00}^{{\left( {ij} \right)}} (t), \\ i\frac{d}{dt}c_{11}^{{\left( {ij} \right)}} (t) & = \alpha c_{01}^{{\left( {ij} \right)}} (t). \\ \end{aligned}$$
(9)

It is clear that exact analytical averaging of stochastic differential equations with Gaussian noise, which has finite correlation time, is a hard task. Almost only the extreme case of white noise—Gaussian noise with the correlation time is equal to zero has been well investigated. We now suppose that \(\alpha\) is separated from two parts as

$$\alpha = \alpha_{0} + \gamma \left( t \right),$$
(10)

where \(\alpha_{0}\) is a deterministic coherent part of the external classical field amplitude and stochastic process \(\gamma \left( t \right)\) is characterized by a white noise with the following form

$$\left\langle {\left\langle {\gamma \left( t \right)\gamma *\left( {t^{{\prime }} } \right)} \right\rangle } \right\rangle = a_{0} \delta \left( {t - t^{{\prime }} } \right),$$
(11)

the double brackets in (11) indicate an average over the ensemble of realisations of the \(\gamma \left( t \right)\). In this case, the set of equations of motion (9) has the form of the following stochastic differential equation

$$\frac{dX}{dt} = \left[ {C_{1} + x\left( t \right)C_{2} + x^{*} \left( t \right)C_{3} } \right]X,$$
(12)

where X is a vector function of time and \(C_{1} ,C_{2} ,C_{3}\) are constant matrices. As known from the multiplicative stochastic process theory, the function \(\left\langle {\left\langle X \right\rangle } \right\rangle\) satisfies the equation:

$$\frac{d}{dt}\left\langle {\left\langle X \right\rangle } \right\rangle = \left[ {C_{1} + a_{0} \left\{ {C_{2} ,C_{3} } \right\}/2} \right]\left\langle {\left\langle X \right\rangle } \right\rangle ,$$
(13)

in which \(\left\{ {C_{2} ,C_{3} } \right\}\) is the anticommutator of C2 and C3.

Then, by using Eq. (13) and restrict ourselves to the case of all coupling constants are real and the same strength (\(\alpha = \varepsilon\)), we derive the system of equations for stochastic averages of the variables as (for convenience double brackets have been dropped)

$$\begin{aligned} i\frac{d}{dt}c_{00}^{{\left( {ij} \right)}} (t) & = \frac{{a_{0} }}{2}c_{00}^{{\left( {ij} \right)}} \left( t \right) + \frac{{a_{0} }}{2}c_{01}^{{\left( {ij} \right)}} \left( t \right) + \alpha_{0}^{*} c_{10}^{{\left( {ij} \right)}} (t), \\ i\frac{d}{dt}c_{01}^{{\left( {ij} \right)}} (t) & = \frac{{a_{0} }}{2}c_{00}^{{\left( {ij} \right)}} \left( t \right) + a_{0} c_{01}^{{\left( {ij} \right)}} \left( t \right) + \alpha_{0}^{*} c_{10}^{{\left( {ij} \right)}} (t) + \alpha_{0}^{*} c_{11}^{{\left( {ij} \right)}} (t), \\ i\frac{d}{dt}c_{10}^{{\left( {ij} \right)}} (t) & = \alpha_{0} c_{00}^{{\left( {ij} \right)}} (t) + \alpha_{0} c_{01}^{{\left( {ij} \right)}} (t) + a_{0} c_{10}^{{\left( {ij} \right)}} \left( t \right) + \frac{{a_{0} }}{2}c_{11}^{{\left( {ij} \right)}} (t), \\ i\frac{d}{dt}c_{11}^{{\left( {ij} \right)}} (t) & = \alpha_{0} c_{01}^{{\left( {ij} \right)}} (t) + \frac{{a_{0} }}{2}c_{10}^{{\left( {ij} \right)}} (t) + \frac{{a_{0} }}{2}c_{11}^{{\left( {ij} \right)}} (t). \\ \end{aligned}$$
(14)

In addition, we suppose that both cavity modes are initially in vacuum states \(\left| {00} \right\rangle\). Then we obtain the solutions for the complex probability amplitudes \(c_{mn}^{ij} \left( t \right)\), \(m,n = 0,1.\) in the following form:

$$\begin{aligned} c_{00}^{{\left( {00} \right)}} (t) & = \frac{1}{2}e^{{ - \frac{{3ia_{0} t}}{4}}} \left[ {e^{{\frac{{i\alpha_{0} t}}{2}}} \left( {\cos x_{1} t + \frac{i}{\sqrt 5 }\sin x_{1} t} \right) + e^{{ - \frac{{i\alpha_{0} t}}{2}}} \left( {\cos x_{2} t + \frac{i}{\sqrt 5 }\sin x_{2} t} \right)} \right], \\ c_{01}^{{\left( {00} \right)}} (t) & = - \frac{i}{\sqrt 5 }e^{{ - \frac{{3ia_{0} t}}{4}}} \left[ {e^{{\frac{{i\alpha_{0} t}}{2}}} \sin x_{1} t + e^{{ - \frac{{i\alpha_{0} t}}{2}}} \sin x_{2} t} \right], \\ c_{10}^{{\left( {00} \right)}} (t) & = \frac{i}{\sqrt 5 }e^{{ - \frac{{3ia_{0} t}}{4}}} \left[ {e^{{\frac{{i\alpha_{0} t}}{2}}} \sin x_{1} t - e^{{ - \frac{{i\alpha_{0} t}}{2}}} \sin x_{2} t} \right], \\ c_{11}^{{\left( {00} \right)}} (t) & = - \frac{1}{2}e^{{ - \frac{{3ia_{0} t}}{4}}} \left[ {e^{{\frac{{i\alpha_{0} t}}{2}}} \left( {\cos x_{1} t + \frac{i}{\sqrt 5 }\sin x_{1} t} \right) - e^{{ - \frac{{i\alpha_{0} t}}{2}}} \left( {\cos x_{2} t + \frac{i}{\sqrt 5 }\sin x_{2} t} \right)} \right], \\ \end{aligned}$$
(15)

where \(x_{1} = \frac{\sqrt 5 }{4}\left( {a_{0} - 2\alpha_{0} } \right)\) and \(x_{2} = \frac{\sqrt 5 }{4}\left( {a_{0} + 2\alpha_{0} } \right)\). We can easily see that when the parameter related to the chaotic component is absent \(\left( {a_{0} = 0} \right)\), our results become exactly the same as those in Miranowicz and Leoński (2006). However, when we suppose that one cavity mode is initially in vacuum state and other cavity mode is initially in Fock states, namely state \(\left| {01} \right\rangle\), the solutions for \(c_{mn}^{ij} \left( t \right)\) have the form as

$$\begin{aligned} c_{00}^{{\left( {01} \right)}} (t) &= c_{01}^{{\left( {00} \right)}} (t), \hfill \\ c_{01}^{{\left( {01} \right)}} (t) &= \frac{1}{2}e^{{ - \frac{{3ia_{0} t}}{4}}} \left[ {e^{{\frac{{i\alpha_{0} t}}{2}}} \left( {\cos x_{1} t - \frac{i}{\sqrt 5 }\sin x_{1} t} \right) + e^{{ - \frac{{i\alpha_{0} t}}{2}}} \left( {\cos x_{2} t - \frac{i}{\sqrt 5 }\sin x_{2} t} \right)} \right], \hfill \\ c_{10}^{{\left( {01} \right)}} (t) &= - \frac{1}{2}e^{{ - \frac{{3ia_{0} t}}{4}}} \left[ {e^{{\frac{{i\alpha_{0} t}}{2}}} \left( {\cos x_{1} t - \frac{i}{\sqrt 5 }\sin x_{1} t} \right) - e^{{ - \frac{{i\alpha_{0} t}}{2}}} \left( {\cos x_{2} t - \frac{i}{\sqrt 5 }\sin x_{2} t} \right)} \right], \hfill \\ c_{11}^{{\left( {01} \right)}} (t) &= c_{10}^{{\left( {00} \right)}} (t). \hfill \\ \end{aligned}$$
(16)

The main purpose of this paper is focused on the generation of maximally entangled states of the system.

3 Entanglement and the generation of maximally entangled states

In this section we shall express the obtained wave function in the basic Bell states as

$$\left| \psi \right\rangle = \sum\limits_{k = 1}^{4} {b_{k}^{{\left( {ij} \right)}} \left| {B_{k}^{{\left( {ij} \right)}} } \right\rangle } ,$$
(17)

where \(i,j = 0,1\), the states \(\left| {B_{k}^{{\left( {ij} \right)}} } \right\rangle\) are Bell-like states that can be represented as functions of the n-photon Fock states examined here:

$$\begin{aligned} \left| {B_{1}^{{\left( {ij} \right)}} } \right\rangle & = \frac{1}{\sqrt 2 }\left( {\left| {00} \right\rangle + i\left| {11} \right\rangle } \right)^{{\left( {ij} \right)}} ,\quad \left| {B_{2}^{{\left( {ij} \right)}} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {11} \right\rangle + i\left| {00} \right\rangle } \right)^{{\left( {ij} \right)}} , \\ \left| {B_{3}^{{\left( {ij} \right)}} } \right\rangle & = \frac{1}{\sqrt 2 }\left( {\left| {01} \right\rangle - i\left| {10} \right\rangle } \right)^{{\left( {ij} \right)}} ,\quad \left| {B_{4}^{{\left( {ij} \right)}} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {10} \right\rangle - i\left| {01} \right\rangle } \right)^{{\left( {ij} \right)}} . \\ \end{aligned}$$
(18)

We can see that Bell-like states are different from the commonly discussed Bell states in the existence of the phase factor—for the case debated here, one of the n-photon Fock states is multiplied with i. From (17) and (8), we can obtain the coefficients \(b_{k}^{{\left( {ij} \right)}}\) as

$$\begin{aligned} b_{1}^{{\left( {ij} \right)}} & = \frac{1}{\sqrt 2 }\left( {c_{00}^{{\left( {ij} \right)}} (t) - ic_{11}^{{\left( {ij} \right)}} (t)} \right),\quad b_{2}^{{\left( {ij} \right)}} = \frac{1}{\sqrt 2 }\left( {c_{11}^{{\left( {ij} \right)}} (t) - ic_{00}^{{\left( {ij} \right)}} (t)} \right), \\ b_{3}^{{\left( {ij} \right)}} & = \frac{1}{\sqrt 2 }\left( {c_{01}^{{\left( {ij} \right)}} (t) + ic_{10}^{{\left( {ij} \right)}} (t)} \right),\quad b_{4}^{{\left( {ij} \right)}} = \frac{1}{\sqrt 2 }\left( {c_{10}^{{\left( {ij} \right)}} (t) + ic_{01}^{{\left( {ij} \right)}} (t)} \right). \\ \end{aligned}$$
(19)

Then the states in our system become Bell-like states when \(\left| {b_{k}^{{\left( {ij} \right)}} } \right|^{2}\) are equal to unity. We can easily see that \(\left| {b_{1}^{{\left( {01} \right)}} } \right|^{2} = \left| {b_{4}^{{\left( {00} \right)}} } \right|^{2}\) and \(\left| {b_{2}^{{\left( {01} \right)}} } \right|^{2} = \left| {b_{3}^{{\left( {00} \right)}} } \right|^{2}\), so we do not need to draw the graphs of probabilities for obtaining the system in the Bell-like states \(\left| {B_{1}^{{\left( {01} \right)}} } \right\rangle\) and \(\left| {B_{2}^{{\left( {01} \right)}} } \right\rangle\). In cases the initial states are the two-mode vacuum \(\left| {00} \right\rangle\) and n-photon Fock \(\left| {01} \right\rangle\) states, the probabilities for the Bell-like states creation as a time function are depicted in Figs. 2, 3 and 4. When the parameter a0 is absent, the plots are completely identical to the results obtained in Miranowicz and Leoński (2006). Figure 2 shows the states \(\left| {B_{1}^{{\left( {00} \right)}} } \right\rangle\) and \(\left| {B_{2}^{{\left( {00} \right)}} } \right\rangle\), being superpositions of \(\left| {00} \right\rangle\) and \(\left| {11} \right\rangle\), can be generated the entangled states come closing maximally entangled states. Whereas, the states \(\left| {B_{3}^{{\left( {00} \right)}} } \right\rangle\) and \(\left| {B_{4}^{{\left( {00} \right)}} } \right\rangle\) in Fig. 4, being superpositions of \(\left| {01} \right\rangle\) and \(\left| {10} \right\rangle\), cannot be generated the entangled states approaching maximally entangled states. As a consequence, the states \(\left| {01} \right\rangle\) and \(\left| {10} \right\rangle\) cannot become maximally entangled states with the initial vacuum states. However, creation of maximally entangled states for \(\left| {B_{3}^{{\left( {01} \right)}} } \right\rangle\) and \(\left| {B_{4}^{{\left( {01} \right)}} } \right\rangle\) would be likely by assuming that the system is initially in the n-photon Fock states \(\left| {01} \right\rangle\), which are shown in Fig. 3. Nevertheless, when the parameter \(a_{0} \ne 0\), Figs. 2, 3 and 4 show the maximally entangled states \(\left| {B_{1}^{{\left( {00} \right)}} } \right\rangle\) to \(\left| {B_{4}^{{\left( {00} \right)}} } \right\rangle\) and \(\left| {B_{1}^{{\left( {01} \right)}} } \right\rangle\) to \(\left| {B_{4}^{{\left( {01} \right)}} } \right\rangle\) are not created, namely the probabilities for \(\left| {B_{1}^{{\left( {00} \right)}} } \right\rangle\) to \(\left| {B_{4}^{{\left( {00} \right)}} } \right\rangle\) and \(\left| {B_{1}^{{\left( {01} \right)}} } \right\rangle\) to \(\left| {B_{4}^{{\left( {01} \right)}} } \right\rangle\) can reach only 0.793, 0.929, 0.798, 0.790 and 0.790, 0.798, 0.943, 0.844, respectively. These may explain that the presence of the parameter a0 causes the quantum interference of the system to be weakened when compared to the absence of this parameter.

Fig. 2
figure 2

Probabilities for finding the coupler in the Bell-like states \(\left| {B_{1}^{{\left( {00} \right)}} } \right\rangle\) and \(\left| {B_{2}^{{\left( {00} \right)}} } \right\rangle\) with \(\alpha_{0} = 10^{6} \pi\) rad/s. Solid curve is for a0 = 0, dashed curve is for \(a_{0} = 10^{5} \pi\) rad/s and dashed dotted curve is for \(a_{0} = 2 \times 10^{5} \pi\) rad/s

Full size image
Fig. 3
figure 3

Probabilities for finding the coupler in the Bell-like states \(\left| {B_{3}^{{\left( {01} \right)}} } \right\rangle\) and \(\left| {B_{4}^{{\left( {01} \right)}} } \right\rangle\) with \(\alpha_{0} = 10^{6} \pi\) rad/s. Solid curve is for a0 = 0, dashed curve is for \(a_{0} = 10^{5} \pi\) rad/s and dashed dotted curve is for \(a_{0} = 2 \times 10^{5} \pi\) rad/s

Full size image
Fig. 4
figure 4

Probabilities for finding the coupler in the Bell-like states \(\left| {B_{3}^{{\left( {00} \right)}} } \right\rangle\) and \(\left| {B_{4}^{{\left( {00} \right)}} } \right\rangle\) with \(\alpha_{0} = 10^{6} \pi\) rad/s. Solid curve is for a0 = 0, dashed curve is for \(a_{0} = 10^{5} \pi\) rad/s and dashed dotted curve is for \(a_{0} = 2 \times 10^{5} \pi\) rad/s

Full size image

Especially, we see that when the parameter a0 is present, in Fig. 4a, the probabilities for obtaining the system in state \(\left| {B_{3}^{{\left( {00} \right)}} } \right\rangle\) is greater and in Fig. 3, the higher the peaks, the more strongly reduce while the lower the peaks the more are enhanced in comparison with the case when the parameter a0 is absent. These mean that the probabilities of obtaining the system in the entangled states are more stable. Moreover, on the left side of the maximally entangled state, if the parameter a0 is increasing then probabilities for \(\left| {B_{1}^{{\left( {00} \right)}} } \right\rangle\) and \(\left| {B_{2}^{{\left( {00} \right)}} } \right\rangle\) in Fig. 2 are decreasing and the peaks of probability tend to split into two peaks starting at the maximum peak, whereas the right side of this state, the probabilities for \(\left| {B_{1}^{{\left( {00} \right)}} } \right\rangle\) and \(\left| {B_{2}^{{\left( {00} \right)}} } \right\rangle\) are increasing or decreasing are not as regular as its left. In addition, the maximum values of the probabilities for \(\left| {B_{1}^{{\left( {00} \right)}} } \right\rangle\) to \(\left| {B_{4}^{{\left( {00} \right)}} } \right\rangle\) shift towards the zero of time in comparison to the case of chaotic part are absent.

We can use the form of the von Neumann entropy of the reduced density matrix \(\rho_{a} = Tr_{b} \rho\) or \(\rho_{b} = Tr_{a} \rho\), which built on the basis of the full density matrix \(\rho = \left| \psi \right\rangle \left\langle \psi \right|\) that depicts the evolution of the system to depict the capability for generation of maximally entangled states. Equivalently, the Shannon entropy S for the squared Schmidt coefficients \(\xi_{k}\) is employed with the following form (Vedral 2002):

$$E^{{\left( {ij} \right)}} = - Tr\rho_{a} \log_{2} \rho_{a} = - Tr\rho_{b} \log_{2} \rho_{b} = S\left\{ {\xi_{k} } \right\} = - \sum\limits_{k} {\xi_{k} } \log_{2} \xi_{k} .$$
(20)

This measurement is usually used for bipartite pure states to as the entropy of entanglement. For the case of two qubits in a pure state, the value of entangled entropy varies from zero for separable states to 1 ebit for the maximally entangled, and it is simply given in the form of the binary entropy as follows

$$E^{{\left( {ij} \right)}} (t) = - \xi \cdot \log_{2} \xi - (1 - \xi ) \cdot \log_{2} (1 - \xi ),$$
(21)

with \(\xi = \frac{{1 + \sqrt {1 - \left( {C^{{\left( {ij} \right)}} } \right)^{2} } }}{2}\) and \(C^{{\left( {ij} \right)}} = 2\left| {c_{00}^{{\left( {ij} \right)}} (t)c_{11}^{{\left( {ij} \right)}} (t) - c_{01}^{{\left( {ij} \right)}} (t)c_{10}^{{\left( {ij} \right)}} (t)} \right|\). The evolution of entangled entropy are shown in Fig. 5, which describes evolutions of entangled entropy with varies values of parameter a0. In Fig. 5a, for a0 = 0, our result becomes exactly the similar to those derived in Miranowicz and Leoński (2006). The entropy of entanglement can reach a limit of 1 ebit or close to it for the Bell-like states are constituted. So, it demonstrates that the Kerr nonlinear couplers with linear interactions between field modes can be behaved as a source of maximally entangled states. We can see that in Fig. 5b, the entropy of entanglement can reach a limit of 1 ebit or close to it are more in comparison with Fig. 5a and the numbers of peaks are more than twice the peaks of Fig. 5a, i.e. the oscillations are twice faster. For \(a_{0} \ne 0\), we see that for \(E^{{\left( {00} \right)}}\), the entropy of entanglement increases slowly for \(0 < t < 2 \times 10^{ - 6} s\), decreases quickly for \(2 \times 10^{ - 6} s < t < 6 \times 10^{ - 6} s\) and increases fast for \(6 \times 10^{ - 6} s < t < 8 \times 10^{ - 6} s\) in comparison with the case of parameters a0 are not present. For \(E^{{\left( {01} \right)}}\), when the parameter a0 is present, the entropy of entanglement almost decreases and the peaks with lower height disappear gradually, but when a0 increases, the peaks split again into two peaks of nearly equal height. It can be concluded that if the chaotic part is present, maxima values of the entangled entropy reduce in comparison to the case of a0 = 0 and the values of entangled entropy are almost greater than zero, which means the system is almost in the entangled states. As a consequence, the parameter a0 related to the chaotic part is an important parameter which controls the generation of maximally entangled states.

Fig. 5
figure 5

Evolution of the entangled entropies \(E^{{\left( {00} \right)}}\) and \(E^{{\left( {01} \right)}}\) of the truncated states with \(\alpha_{0} = 10^{6} \pi\) rad/s. Solid curve is for a0 = 0, dashed curve is for \(a_{0} = 10^{5} \pi\) rad/s and dashed dotted curve is for \(a_{0} = 2 \times 10^{5} \pi\) rad/s

Full size image

Until now, both cavity modes have been initially supposed in vacuum states \(\left| {00} \right\rangle\) and the n-photon Fock state \(\left| {01} \right\rangle\). We consider other cases for the evolution of the system when cavity modes are initially in states \(\left| {10} \right\rangle\) and \(\left| {11} \right\rangle\), which means \(\left| {\psi \left( 0 \right)} \right\rangle \equiv \left| {\psi^{{\left( {pq} \right)}} \left( 0 \right)} \right\rangle = \left| {pq} \right\rangle\), where \(p,q = 0,1\). Hence, the evolutions of the initial states of the system, which is considered here, have the following form

$$\left| {\psi^{{\left( {10} \right)}} \left( t \right)} \right\rangle_{cut} = c_{10}^{{\left( {00} \right)}} \left| {00} \right\rangle + c_{10}^{{\left( {01} \right)}} \left| {01} \right\rangle + c_{01}^{{\left( {01} \right)}} \left| {10} \right\rangle + c_{01}^{{\left( {00} \right)}} \left| {11} \right\rangle ,$$
(22)

and

$$\left| {\psi^{{\left( {11} \right)}} \left( t \right)} \right\rangle_{cut} = c_{11}^{{\left( {00} \right)}} \left| {00} \right\rangle + c_{10}^{{\left( {00} \right)}} \left| {01} \right\rangle + c_{01}^{{\left( {00} \right)}} \left| {10} \right\rangle + c_{00}^{{\left( {00} \right)}} \left| {11} \right\rangle ,$$
(23)

From there we can easily obtain the entropies of entanglement as

$$E^{{\left( {11} \right)}} \left( t \right) = E^{{\left( {00} \right)}} \left( t \right)\quad E^{{\left( {10} \right)}} \left( t \right) = E^{{\left( {01} \right)}} \left( t \right),$$
(24)

and the complex probability amplitudes

$$b_{1}^{{\left( {10} \right)}} = b_{2}^{{\left( {01} \right)}} ,\quad b_{2}^{{\left( {10} \right)}} = b_{1}^{{\left( {01} \right)}} ,\quad b_{3}^{{\left( {10} \right)}} = b_{4}^{{\left( {01} \right)}} ,\quad b_{4}^{{\left( {10} \right)}} = b_{3}^{{\left( {01} \right)}} ,$$
(25)

and

$$b_{1}^{{\left( {11} \right)}} = b_{2}^{{\left( {00} \right)}} \quad b_{2}^{{\left( {11} \right)}} = b_{1}^{{\left( {00} \right)}} ,\quad b_{3}^{{\left( {11} \right)}} = b_{4}^{{\left( {00} \right)}} ,\quad b_{4}^{{\left( {11} \right)}} = b_{3}^{{\left( {00} \right)}} .$$
(26)

It is worth noting that when the parameter a0 is absent, our system for the initial states \(\left| {00} \right\rangle\) or \(\left| {11} \right\rangle\) quasi-periodically evolves into the maximally entangled states \(\left| {B_{1}^{{\left( {00} \right)}} } \right\rangle\), \(\left| {B_{2}^{{\left( {00} \right)}} } \right\rangle\) or \(\left| {B_{1}^{{\left( {11} \right)}} } \right\rangle\), \(\left| {B_{2}^{{\left( {11} \right)}} } \right\rangle\), respectively with high accuracy but does not evolve into states \(\left| {B_{3}^{{\left( {01} \right)}} } \right\rangle\), \(\left| {B_{4}^{{\left( {01} \right)}} } \right\rangle\) or \(\left| {B_{3}^{{\left( {10} \right)}} } \right\rangle\), \(\left| {B_{4}^{{\left( {10} \right)}} } \right\rangle\). This is in contradiction with the evolutions of our system for the initial states \(\left| {01} \right\rangle\) or \(\left| {10} \right\rangle\). When the parameter a0 is present, our system is almost in the entangled states but does not generate the maximally entangled states for all initial states. In brief, we do not show any graphs of the evolution systems for the initial states \(\left| {10} \right\rangle\) and \(\left| {11} \right\rangle\) because they have been presented in the Figs. 2, 3, 4 and 5 for the initial states \(\left| {00} \right\rangle\) and \(\left| {01} \right\rangle\).

4 Conclusions

In this work, we have studied a Kerr nonlinear coupler, which include two nonlinear oscillators linearly coupled to each other and one of them pumped by external classical field. This field is supposed to be split into two parts: coherent component and white noise. We have used formalism of the nonlinear quantum scissors and shown that the evolution of our system is closed within a finite set of four states: \(\left| {00} \right\rangle\), \(\left| {01} \right\rangle\), \(\left| {10} \right\rangle\) and \(\left| {11} \right\rangle\). We have reviewed in detail the evolution of the system for all cases of the cavity modes, which is initially in vacuum states or in n-photon Fock states. The result shows that when the parameter a0 is absent, the system has generated the entangled states that become closing maximally entangled states. Moreover, when one cavity mode is initially in vacuum state and other cavity mode is initially in n-photon Fock states, the entropy of entanglement can reach a limit of 1 ebit or close to it are more in comparison with the cases of both cavity modes are initially in vacuum or n-photon Fock states. So, our system can be seen as a source of maximally entangled states. Conversely, when the parameter a0 is present, the maximally entangled states in our system are not generated. The entropy of entanglement almost decreases and the system is almost in the entangled states in comparison to the absence of the parameter a0. As a result, the parameter a0 related to the chaotic part is an important parameter that controls the generation of maximally entangled states. Because of the strengths of the laser field amplitude used in experimental always contain some fluctuation component, we believe that our model is more realistic than that described in the case as the white noise is absent. In the near future the influence of the white noise and nonlinear quantum scissors adopted here can be expanded to the research on the generation of entangled states in other optical couplers such as a codirectional symmetric or asymmetric nonlinear optical coupler that have been recently reported (Thapliyal et al. 2014, 2016).