Exponential Stability of Non-Autonomous Neural Networks with Heterogeneous Time-Varying Delays and Destabilizing Impulses

Abstract

In this paper, the problem of global exponential stability analysis of a class of non-autonomous neural networks with heterogeneous delays and time-varying impulses is considered. Based on the comparison principle, explicit conditions are derived in terms of testable matrix inequalities ensuring that the system is globally exponentially stable under destabilizing impulsive effects. Numerical examples are given to demonstrate the effectiveness of the obtained results.

1 Introduction

During the past few years, qualitative and asymptotic behavior of neural networks have been intensively studied due to their potential applications in many fields such as image and signal processing, pattern recognition, associative memory, parallel computing, solving optimization problems [6, 7, 38]. In most of the practical applications, it is of prime importance to ensure that the designed neural networks are stable [2]. On the other hand, in modeling neural networks and general complex dynamical networks, time delays are often encountered in real applications due to the finite switching speed of amplifiers [40] which usually become a source of oscillation, divergence, instability, and poor performance [4, 33]. Considerable attention from researchers has been devoted to the problem of stability analysis and control of delayed neural networks recently, see, [3, 10, 11, 15, 16, 18, 20, 25–27, 31, 41] and the references therein.

It is well known that, for simple circuits with a small number of cells, the use of fixed constant delays may provide a good approximation when modeling them. However, in practical implementation, neural networks usually have a spatial nature due to the presence of an amount of parallel pathways with a variety of axon sizes and lengths. As a consequence of facts, the time-delay in neural networks is usually time-varying. Therefore, the study of neural networks with time-varying delay is more relevant and important in practice than that of neural networks with constant delay which has attracted increasing interest of many researchers recently, see, for example, [3, 11, 12, 17, 18, 25, 44]. In addition, it is important to note that the transmission of the signals experiencing different segments of networks, on one hand, may cause different time delays [19]. On the other hand, the time required for transmitting signal from a neuron to another neuron is generally different [8]. If a neural network is designed for such an application with a single delay, the time delay is treated as the maximal delay of the network. This obviously leads to certain conservatism when analyzing stability of the network. Therefore, it is reasonable and essential to study the stability of neural networks with heterogeneous delays which contain the neural networks with single and/or multiple delays as some special ones.

Besides the delay effect, the states of various dynamical networks in the fields of artificial systems such as mechanics, electronic, and telecommunication networks, often suffer from instantaneous disturbances and undergo abrupt changes at certain instants [36]. These may arise from switching phenomena or frequency changes, and thus, they exhibit impulsive effects [42]. With the effect of impulses, stability of the networks may be destroyed [43] (see also the next section in this paper). Therefore, delays and impulses heavily affect the dynamical behaviors of the networks, and thus, it is necessary to study both effects of time-delay and impulses on the stability of neural networks. Up to now, considerable effort of researchers has been devoted to investigating stability and asymptotic behavior of neural networks with impulses [21, 23, 24, 29, 30, 35, 37, 42, 43].

However, the aforementioned works have been devoted to neural networks with constant coefficients. As discussed in [11], non-autonomous phenomena often occur in realistic systems; for instance, when considering a long-term dynamical behavior of the system, the parameters of the system usually change along with time [32, 39]. Also, the problem of stability analysis for non-autonomous systems usually requires specific and quite different tools from the autonomous ones (systems with constant coefficients). There are only few papers concerning the stability of non-autonomous neural networks with heterogeneous time-varying delays and impulsive effects. Based on a new non-autonomous Halanay inequality developed from the result of [36], a set of sufficient conditions ensuring the exponential stability of a class of non-autonomous neural networks with impulses and time-varying delays was proposed in [22]. Although the proposed stability conditions in [22] were shown more effective than those in some previous results, they are still conservative, especially in estimating the exponential convergent rate of the network. Specifically, the derived conditions guarantee exponential stability of the corresponding system without impulses. Then, in order to ensure exponential stability of the impulsive model, a uniform upper bound of the growth of impulsive strengths is imposed which produces much conservatism for models with time-varying impulses in a wide range.

Motivated by the aforementioned discussions, in this paper, we investigate the exponential stability of a class of non-autonomous neural networks with heterogeneous delays and time-varying impulses. Based on the comparison principle, an explicit criterion is derived in terms of inequalities for M-matrices ensuring the global exponential stability of the model under destabilizing impulsive effects. The obtained results are shown to improve some recent existing results. Finally, numerical examples are given to demonstrate the effectiveness of the proposed conditions.

The remainder of this paper is organized as follows. Section 2 presents the model description, notations and some preliminaries. In Section 3, an explicit stability criterion of the system is derived in terms of inequalities for M-matrices. Illustrative examples and discussions to the existing results are given in Section 4. The paper ends with a conclusion and cited references.

Notation

Throughout this paper, we denote $\underline {n}:=\{1,2,\ldots , n\}$ for a positive integer $n\in \mathbb {Z}^{+}$. $\mathbb {R}^{n}$ and $\mathbb {R}^{m\times n}$ denote the n-dimensional vector space with the vector norm $\|x\|_{\infty }=\max _{i\in \underline n}|x_{i}|$ and the set of m×n-matrices, respectively. Comparison between vectors will be understood componentwise. Specifically, for u=(u _i ), v=(v _i ) in $\mathbb {R}^{n}$, we write u≥v and u≫v, respectively, if u _i ≥v _i and u _i >v _i for all $i\in \underline {n}$. $\mathbb {R}^{n}_{+}$ denotes the positive orthant of $\mathbb {R}^{n}$, that is, $\mathbb {R}^{n}_{+}=\{\eta \in \mathbb {R}^{n}: \eta \gg 0\}$. For a continuous real-valued function v(t), D ⁺ v(t) denotes the upper-right Dini derivative of v(t) defined by $D^{+}v(t)=\limsup _{h\to 0^{+}}\frac {v(t+h)-v(t)}{h}$.

2 Model Description and Preliminaries

2.1 A Motivation Example

Consider a two-dimensional neural network of the following form

$$ \left\{\begin{array}{ll} \dot x(t)=-D(t)x(t)+W_{0}f(x(t))+W_{1}f(x(t-\tau(t))),\quad t>0,\\ x(t)=\phi(t)\in C([-\tau,0],\mathbb{R}^{2}), \end{array} \right. $$

(1)

where $D(t)=\text {diag}(4+e^{-t^{2}},4-|\sin (2t)|)$, $W_{0}=\left (\begin {array}{ll} 2&1\\0 &1\end {array}\right ),W_{1}=\left (\begin {array}{ll}1&2\\ 0&1\end {array}\right )$, τ(t)∈[0,τ] is a time-varying delay, f(x)=(f _i (x _i )),i=1,2, and $f_{i}(x_{i})=\frac {1}{2}(|x_{i}+1|-|x_{i}-1|)$.

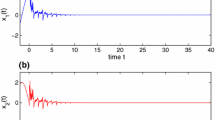
By Theorem 3.2 in [12], the neural network (1) is globally exponentially stable for any delay τ(t). A state trajectory of (1) with $\tau (t)=1+|\sin (t)|$ and $\phi (t)=(1, -1)^{T}\in \mathbb {R}^{2}$, t∈[−2,0], is presented in Fig. 1. This simulation result illustrates the stability of (1).

Fig. 1

A state trajectory of (1) with $\tau (t)=1+|\sin (t)|$

We now consider system (1) in the presence of impulsive effects. By incorporating impulses, the impulsive neural network can be modeled in the form

$$ \left\{\begin{array}{ll} \dot x(t)=-D(t)x(t)+W_{0}f(x(t))+W_{1}f(x(t-\tau(t))),\quad t\neq t_{k},\\ x(t_{k}^{+})=\gamma_{k}x(t_{k}^{-}),\quad k\in\mathbb{Z}^{+}. \end{array}\right. $$

(2)

For illustrative purpose, we consider uniform impulsive times t _k = k T _s , where T _s >0 is a sampling time. As mentioned before, system (1) is exponentially stable. However, in the presence of impulses, stability of system (1) may be destroyed. For instance, in (2), we let sampling time T _s =0.2, impulsive strengths γ _k =1.6(−1)^k. The simulation result given in Fig. 2 shows that (2) is unstable. It should be noted that, in this case, |γ _k |>1∀k, which we refer to as destabilizing impulses.

Fig. 2

A state trajectoy of (2) with T _s =0.2,γ _k =1.6(−1)^k

An important and natural question is that, with destabilizing impulses, can neural network (2) be exponentially stable? In other words, in which conditions the stability of (1) is preserved for (2) with destabilizing impulses. This will be addressed in this paper.

2.2 Model Description and Preliminaries

Consider a class of non-autonomous impulsive neural networks with heterogeneous time-varying delays of the following form

$$ \left\{\begin{array}{rl} x_{i}^{\prime}(t)=& -d_{i}(t)x_{i}(t)+\sum\limits_{j=1}^{n}a_{ij}(t)f_{j}(x_{j}(t))\\ &+\sum\limits_{j=1}^{n}b_{ij}(t)g_{j}(x_{j}(t-\tau_{ij}(t)))+I_{i}(t), \quad t>0, t\neq t_{k},\\ {\Delta} x_{i}(t_{k}):=&x_{i}(t_{k}^{+})-x_{i}(t_{k}^{-})=-\sigma_{ik}x_{i}(t_{k}^{-}),\quad t = t_{k}, k\in\mathbb{Z}^{+},\\ x_{i}(t)=&\phi_{i}(t),\quad t\in[-\tau,0], i\in\underline{n}, \end{array} \right. $$

(3)

where n is the number of neurons of the network, x _i (t), $i\in \underline {n}$, is the state associated with neuron ith at time t, f _j (⋅), g _j (⋅), are neural activation functions, d _i (t) is the rate at which the ith neuron will reset its potential to the resting state in isolation when disconnected from the network and external inputs, a _{i j} (t), b _{i j} (t) are time-varying connection weights, $I(t)=(I_{i}(t))\in \mathbb {R}^{n}$ is the external input signal, τ _{i j} (t), $i,j\in \underline {n}$, are possibly heterogeneous communication delays of the neurons satisfying $0\leq \tau _{ij}(t)\leq \tau ^{+}_{ij}$, $\tau =\max _{ij}\tau ^{+}_{ij}$ and $\phi \in C([-\tau ,0],\mathbb {R}^{n})$ is an initial function specifying the initial state of the network on [−τ,0]. The sequence of impulsive moments $(t_{k})_{k\in \mathbb {Z}^{+}}$ is strictly increasing, $\lim _{k\to \infty }t_{k}=\infty$ and $(\sigma _{ik})_{i\in \underline {n}}$, $k\in \mathbb {Z}^{+}$, are real sequences representing the abrupt changes of the state x _i (t) at impulsive time t _k . It is assumed that I _i (t), τ _{i j} (t), $i,j\in \underline {n}$, are piecewise continuous on $\mathbb {R}^{+}$ with possible discontinuities at t = t _k , $k\in \mathbb {Z}^{+}$.

For convenience, system (3) shall be rewritten in the following vector form:

$$ \left\{\begin{array}{l} x^{\prime}(t)= -D(t)x(t)+A(t)f(x(t))+B(t)g(x(t-\tau(t)))+I(t), \quad t>0, t\neq t_{k},\\ x(t_{k}^{+})=J_{k}x(t_{k}^{-}),\quad t = t_{k}, k\in\mathbb{Z}^{+}, \end{array}\right. $$

(4)

where J _k =diag(1−σ _1k ,1−σ _2k ,…,1−σ _{n k} ).

For system (3), we make the following assumptions.

• (A1) The matrices D(t)=diag(d ₁(t),d ₂(t),…,d _n (t)), A(t)=(a _{i j} (t)) and B(t)=(b _{i j} (t)) are continuous on each interval (t _k ,t _k+1), k≥0, and there exist scalars $\hat {d}_{i}$, $a^{+}_{ij}$, $b^{+}_{ij}$ such that

  $$d_{i}(t)\geq \hat{d}_{i}>0,\quad |a_{ij}(t)|\leq a^{+}_{ij},\quad |b_{ij}(t)|\leq b^{+}_{ij} \quad \forall t\geq 0, i, j\in\underline{n}. $$

• (A2) The neural activation functions f _i ,g _i , $i\in \underline {n}$, satisfy

  $$l_{i1}^{-}\leq\frac{f_{i}(x)-f_{i}(y)}{x-y}\leq l_{i1}^{+},\quad l_{i2}^{-}\leq\frac{g_{i}(x)-g_{i}(y)}{x-y}\leq l_{i2}^{+}\quad \forall x,y\in\mathbb{R}, x\neq y, $$

  where $l_{ik}^{-}, l_{ik}^{+}$, k=1,2, are known constants.

• (A3) There exists a positive sequence $(\gamma _{k})_{k\in \mathbb {Z}^{+}}$ such that $1-\gamma _{k}\leq \sigma _{ik}\leq 1+\gamma _{k}\forall i\in \underline {n}$, $k\in \mathbb {Z}^{+}$.

Remark 1

The constants $l_{ik}^{-}$, $l_{ik}^{+}$, $i\in \underline {n}$, k=1,2, in Assumption (A2) are allowed to be positive, negative or zero. As discussed in the existing literature, for autonomous neural networks, Assumption (A2) can lead to less conservative stability conditions than the descriptions on the Lipschitz-type activation functions or the sigmoid activation functions. However, in order to establish stability conditions for non-autonomous impulsive neural network (3) we utilize the following estimations which can be easily derived from (A2)

$$f_{i}(x)-f_{i}(y)\leq\max\{l_{i1}^{+},-l_{i1}^{-}\}|x-y|,\quad g_{i}(x)-g_{i}(y)\leq\max\left\{l_{i2}^{+},-l_{i2}^{-}\right\}|x-y|. $$

Hereafter, let us denote for $i\in \underline {n}$ the constants $F_{i}=\max \{l_{i1}^{+},-l_{i1}^{-}\}$ and G _i =$\max \left \{l_{i2}^{+},-l_{i2}^{-}\right \}$.

Remark 2

Under Assumptions (A1), (A2), for each initial function $\phi \in C([-\tau ,0],\mathbb {R}^{n})$, there exists a unique solution x(t,ϕ) of (3) which is piecewise continuous on $\mathbb {R}^{+}$ with possible discontinuities at t = t _k , $k\in \mathbb {Z}^{+}$ (see, for example, [1, 28]).

Remark 3

When γ _k >1, the absolute value of the state can be enlarged and the impulses can potentially destroy the stability of system (3). We refer this type of impulses to as destabilizing impulses. When γ _k ≤1, the impulsive effects are inactive or stabilizing. In this paper, and as mentioned in the preceding section, we assume that the impulses are destabilizing and taking values in a finite set {μ ₁,μ ₂,…,μ _q }, where μ _i >1, $i\in \underline {q}$.

Let us denote by t _{j k} , $j\in \underline {q}$, the activation times of the destabilizing impulses with impulsive strength μ _j , that means t _{j k} = t _k if γ _k = μ _j .

Remark 4

It is well-known that when the network dynamics are stable but the impulsive effects are destabilizing, the impulses should not occur too frequently in order to guarantee stability [23]. In this paper, we derive conditions ensuring that the non-autonomous neural network (3) is globally exponentially stable under destabilizing impulsive effects. In regard to this observation, we assume that

• (A4) There are positive numbers ρ _j such that

  $$t_{j(k+1)}-t_{jk}\geq \rho_{j}\quad \forall j\in\underline{q}, k\in\mathbb{Z}^{+}. $$

Remark 5

In the case of constant impulse [23, 34], q=1, and Assumption (A4) can be replaced by the average impulsive interval condition; that is, there exist positive integer N ₀ and positive number T _a such that

$$ \frac{t-s}{T_{a}}-N_{0}\leq N_{\zeta}(t,s)\leq\frac{t-s}{T_{a}}+N_{0}\quad \forall t>s\geq 0, $$

(5)

where N _ζ (t,s) denotes the number of impulsive times of the impulsive sequence ζ={t ₁,t ₂,…} on interval (s,t).

Definition 1

The impulsive neural network (3) is said to be globally exponentially stable if there exist positive constants α,β such that, for any two solutions x(t), $\hat {x}(t)$ of (3) with respectively initial functions $\phi ,\psi \in C([-\tau ,0],\mathbb {R}^{n})$, the following inequality holds

$$ \|x(t)-\hat{x}(t)\|_{\infty}\leq \beta\|\phi-\psi\|_{\infty}e^{-\alpha t}\quad t\geq 0. $$

(6)

The main objective of this paper is to derive new conditions in terms of testable matrix inequalities ensuring the global exponential stability of the neural network (3) based on M-matrix theory and some efficient techniques which have been developed for time-varying systems with bounded delays [13].

3 Stability Conditions

To facilitate in presenting our results, let us introduce the following matrix notations:

$$\begin{array}{@{}rcl@{}} \mathcal{D}&=&\text{diag}(\hat{d}_{1},\hat{d}_{2},\ldots,\hat{d}_{n}),\quad \hat{A}=(a^{+}_{ij}),\quad \hat{B}=\left( e^{\sigma_{0}\tau_{ij}^{+}}b^{+}_{ij}\right),\quad \sigma_{0}= \sum\limits_{j=1}^{q}\frac{\ln{\mu_{j}}}{\rho_{j}},\\ F&=&\text{diag}(F_{1}, F_{2},\ldots, F_{n}),\quad G=\text{diag}(G_{1},G_{2},\ldots, G_{n}),\\ \mathcal{M}&=&\hat{A}F+\hat{B}G+\sigma_{0}I-\mathcal{D}. \end{array} $$

We have the following result.

Theorem 1

Let Assumptions (A1)–-(A4) hold. Then the impulsive neural network ( 3 ) is globally exponentially stable if there exists a vector $\chi \in \mathbb {R}^{n}_{+}$ such that

$$ (\hat{A}F+\hat{B}G+\sigma_{0}I-\mathcal{D})\chi\ll 0. $$

(7)

Proof

We present a constructive proof in the following three steps.

Step 1 Prior estimates :

Let x(t)=(x _i (t)) and $\hat {x}(t)=(\hat {x}_{i}(t))$ be solutions of (3) with initial conditions $\phi ,\psi \in C([-\tau ,0],\mathbb {R}^{n})$, respectively. Define $z_{i}(t)=x_{i}(t)-\hat {x}_{i}(t)$, t≥0, and z _i (t) = ϕ _i (t)−ψ _i (t), t∈[−τ,0], $i\in \underline {n}$, then from (3) we have

$$\begin{array}{@{}rcl@{}} z_{i}^{\prime}(t) &=&-d_{i}(t)z_{i}(t)+\sum\limits_{j=1}^{n} a_{ij}(t)\big[f_{j}(x_{j}(t))-f_{j}(\hat{x}_{j}(t))\big]\\ &&+\sum\limits_{j=1}^{n}b_{ij}(t)\big[g_{j}(x_{j}(t-\tau_{ij}(t)))-g_{j}(\hat{x}_{j}(t-\tau_{ij}(t)))\big] , \quad t\neq t_{k}. \end{array} $$

(8)

By (8) and (A1), the upper-right Dini derivative of z _i (t) is bounded as follows:

$$\begin{array}{@{}rcl@{}} D^{+}|z_{i}(t)|&=&\text{sgn}(z_{i}(t))z_{i}^{\prime}(t)\\ &\leq& -d_{i}(t)|z_{i}(t)|+\sum\limits_{j=1}^{n} |a_{ij}(t)||f_{j}(x_{j}(t))-f_{j}(\hat{x}_{j}(t))|\\ && +\sum\limits_{j=1}^{n}|b_{ij}(t)||g_{j}(x_{j}(t-\tau_{ij}(t)))-g_{j}(\hat{x}_{j}(t-\tau_{ij}(t)))|\\ &\leq&-\hat{d}_{i}|z_{i}(t)|+\sum\limits_{j=1}^{n}a^{+}_{ij}F_{j}|z_{j}(t)| +\sum\limits_{j=1}^{n}b^{+}_{ij}G_{j}|z_{j}(t-\tau_{ij}(t))|, t\in[t_{k-1},t_{k}),\quad \end{array} $$

(9)

where, for convenience, we let t ₀=0.

At the impulsive moment t = t _k , from (3) and (A3), we have

$$ |z_{i}(t_{k}^{+})|=|1-\sigma_{ik}||z_{i}(t_{k}^{-})|\leq \gamma_{k}|z_{i}(t_{k}^{-})|, \quad k\in\mathbb{Z}^{+}. $$

(10)

Step 2 Constructing a comparative system :

In regard to (9) and (10), we now consider the following impulsive system in the vector form

$$ \left\{\begin{array}{ll} \hat{z}^{\prime}(t)=-\mathcal{D}\hat{z}(t)+\hat{A}F\hat{z}(t)+B^{+}G\hat{z}(t-\tau(t)),\quad t\neq t_{k},\\ \hat{z}(t_{k})=\gamma_{k}\hat{z}(t_{k}^{-}),\quad t=t_{k},\\ \hat{z}(t)=|\phi(t)-\psi(t)|,\quad t\in[-\tau,0], \end{array}\right. $$

(11)

where $B^{+}=\left (b_{ij}^{+}\right )$.

As mentioned in Remark 2, and by similar approach proposed in [1], it can be verified that, for given $\phi ,\psi \in C([-\tau ,0],\mathbb {R}^{n})$, system (11) has a unique solution $\hat {z}(t)$ on $[-\tau ,\infty )$. Since $M_{1}=-\mathcal {D}+\hat {A}F$ is a Metzler matrix and M ₂ = B ⁺ G≥0, (11) is a positive system [34]. Furthermore, by some similar lines used in the proof of Lemma 2.1 in [14], it is found that $|z_{i}(t)|\leq \hat {z}_{i}(t)$, ∀t≥0, $i\in \underline {n}$.

Let $\chi \in \mathbb {R}^{n}_{+}$ satisfy condition (7), that is $\mathcal {M}\chi \ll 0$. Then we have

$$ \sigma_{0}\chi_{i}+\sum\limits_{j=1}^{n}\left( a^{+}_{ij}F_{j} +b^{+}_{ij}e^{\sigma_{0}\tau_{ij}^{+}}G_{j}\right)\chi_{j} <\hat{d}_{i}\chi_{i},\quad i\in\underline{n}. $$

(12)

Consider the function H _i (λ), $i\in \underline {n}$, defined by

$$H_{i}(\lambda)=\sum\limits_{j=1}^{n}\left( a^{+}_{ij}F_{j}+b^{+}_{ij}e^{\lambda\tau_{ij}^{+}}G_{j}\right)\chi_{j} +(\lambda-\hat{d}_{i})\chi_{i},\quad \lambda\in[0,\infty). $$

Clearly, H _i (λ) is continuous and strictly increasing on $[0,\infty )$, H _i (0)<0 by (12) and H _i (λ) tends to infinity as λ tends to infinity. Thus, there exists a unique positive solution λ _i of the scalar equation H _i (λ)=0. Let $\lambda _{*}=\min _{1\leq i\leq n}\lambda _{i}>0$ then $H_{i}(\lambda _{*})\leq 0,\;\forall i\in \underline {n}$, which yields

$$ -\hat{d}_{i}\chi_{i} +\sum\limits_{j=1}^{n}\left( a^{+}_{ij}F_{j}+b^{+}_{ij}e^{\lambda\tau_{ij}^{+}}G_{j}\right)\chi_{j} <-\lambda\chi_{i},\quad i\in\underline{n}, \lambda\in(0,\lambda_{*}). $$

(13)

In addition, since H _i (σ ₀)<0, and by the monotonicity of H _i (λ), then λ _∗>σ ₀.

Inspired by the technique used in the proof of generalized Halanay inequalities [14, 36], we now show that

$$ \hat{z}(t)\leq\frac{\chi}{\min_{1\leq i\leq n}\chi_{i}} \|\phi-\psi\|_{\infty} e^{-\lambda t}\prod\limits_{t_{s}\leq t}\gamma_{s},\quad t > 0, $$

(14)

where σ ₀<λ<λ _∗. To this end, let us consider the functions v _i (t), $i\in \underline {n}$, defined as follows:

$$ \left\{\begin{array}{ll}\displaystyle v_{i}(t)=k_{i}e^{-\lambda t}\prod\limits_{s=0}^{k-1}\gamma_{s},\quad t\in[t_{k-1},t_{k}),\\ v_{i}(t_{k})=v_{i}\left( t_{k}^{+}\right)=\gamma_{k}v_{i}\left( t_{k}^{-}\right),\quad t=t_{k}, k\in\mathbb{Z}^{+}, \end{array}\right. $$

(15)

where γ ₀=1, $k_{i}=\frac {\chi _{i}}{\chi _{+}}\|\phi -\psi \|_{\infty }$ and $\chi _{+}=\min _{1\leq i\leq n}\chi _{i}$. It can be verified from (15) that, for each $i\in \underline {n}$, the function v _i (t) is piecewise continuous on $[0,\infty )$. More precisely, v _i (t) is continuous on intervals (t _k ,t _k+1) and right continuous at t = t _k .

Step 3 Exponential estimate :

For a given 𝜃 > 1, $\sup _{-\tau \leq t\leq t_{0}}\hat {z}_{i}(t)<\theta v_{i}(t_{0})\;\forall i\in \underline {n}$. Assume that there exist $i\in \underline {n}$ and t _∗∈(t ₀,t ₁) such that $\hat {z}_{i}(t_{*})=\theta v_{i}(t_{*})$ and $\hat {z}_{l}(t)-\theta v_{l}(t)\leq 0 \forall t\in [t_{0},t_{*}]$, $l\in \underline {n}$. Then $D^{+}(\hat {z}_{i}-\theta v_{i})(t_{*})\geq 0$. On the other hand, it follows from (11) that

$$\begin{array}{@{}rcl@{}} D^{+}\hat{z}_{i}(t_{*})&\leq& -\hat{d}_{i}\hat{z}_{i}(t_{*})+\sum\limits_{j=1}^{n}a_{ij}^{+}F_{j}\hat{z}_{j}(t_{*}) + \sum\limits_{j=1}^{n}b^{+}_{ij}G_{j}\sup_{t_{*}-\tau^{+}_{ij}\leq t\leq t_{*}}\hat{z}_{j}(t)\\ &\leq& \left( -\hat{d}_{i}k_{i}+\sum\limits_{j=1}^{n}a^{+}_{ij}F_{j}k_{j} + \sum\limits_{j=1}^{n}b^{+}_{ij}e^{\lambda\tau^{+}_{ij}}G_{j}k_{j}\right)\theta e^{-\lambda t_{*}}\\ &<& -\lambda\theta v_{i}(t_{*}), \end{array} $$

(16)

hence $D^{+}(\hat {z}_{i}-\theta v_{i})(t_{*})< 0$. This is clearly a contradiction. Therefore, $\hat {z}_{i}(t)<\theta v_{i}(t)$ holds for all $i\in \underline {n}$ and t∈[t ₀,t ₁) from which we obtain

$$ \hat{z}(t)\leq \frac{\chi}{\chi_{+}}\|\phi-\psi\|_{\infty} e^{-\lambda t},\quad t\in[t_{0},t_{1}), $$

(17)

by letting 𝜃→1⁺.

Suppose that for some positive integer k, the estimate

$$ \hat{z}(t)\leq\frac{\chi}{\chi_{+}}\|\phi-\psi\|_{\infty}\prod\limits_{t_{s}\leq t}\gamma_{s}e^{-\lambda t},\quad t\in[t_{l-1},t_{l}), $$

(18)

holds for all l=1,2,…,k. Then, from (11) and (18), we readily obtain

$$ \hat{z}\left( t_{k}^{+}\right)\leq \frac{\chi}{\chi_{+}}\|\phi-\psi\|_{\infty}\prod\limits_{s=0}^{k}\gamma_{s}e^{-\lambda t_{k}}=v\left( t_{k}^{+}\right). $$

(19)

On the other hand, for t∈[t _k ,t _k+1) and $\upsilon \in \left [-\tau _{ij}^{+},0\right ]$, we have

$$v_{j}(t+\upsilon)=k_{j}e^{-\lambda(t+\upsilon)}\prod\limits_{t_{l}\leq t+\upsilon}\gamma_{l} \leq e^{\lambda\tau_{ij}^{+}}v_{j}(t) $$

which leads to $\sup _{t-\tau ^{+}_{ij}\leq s \leq t}v_{j}(s)\leq e^{\lambda \tau _{ij}^{+}}v_{j}(t)$. Similar to (16) we have

$$\begin{array}{@{}rcl@{}} &&-\hat{d}_{i}v_{i}(t)+\sum\limits_{j=1}^{n}a_{ij}^{+}F_{j}v_{j}(t)+\sum\limits_{j=1}^{n}b_{ij}^{+}G_{j}\sup_{t-\tau_{ij}^{+}\leq s\leq t}v_{j}(s)\\ &&\qquad\leq -\hat{d}_{i}v_{i}(t)+\sum\limits_{j=1}^{n}\big(a_{ij}^{+}F_{j}+b_{ij}^{+}G_{j}e^{\lambda\tau_{ij}^{+}}\big)v_{j}(t)\\ &&\qquad=\left[-\hat{d}_{i}k_{i}+\sum\limits_{j=1}^{n}\big(a_{ij}^{+}F_{j}+b_{ij}^{+}G_{j}e^{\lambda\tau_{ij}^{+}}\big)k_{j}\right]\prod\limits_{l=0}^{k}\gamma_{l}e^{-\lambda t}\\ &&\qquad\leq -\lambda k_{i}\prod\limits_{l=0}^{k}\gamma_{l}e^{-\lambda t}. \end{array} $$

Therefore,

$$ D^{+}v_{i}(t)\geq -\hat{d}_{i}v_{i}(t)+\sum\limits_{j=1}^{n}a_{ij}^{+}F_{j}v_{j}(t) +\sum\limits_{j=1}^{n}b_{ij}^{+}G_{j}\sup_{t-\tau_{ij}^{+}\leq s\leq t}v_{j}(s),\quad t\in[t_{k},t_{k+1}). $$

(20)

By similar arguments used in deriving (17), it follows from (11), (19), and (20) that $\hat {z}_{i}(t)\leq v_{i}(t)$ holds for all $i\in \underline {n}$ and t∈[t _k ,t _k+1). Consequently, estimate (18) holds for t∈[t _k ,t _k+1), and thus, by induction, (14) holds.

For any t>0, let $N_{\mu _{j}}(t)$ denote the number of impulses with the impulsive strength μ _j in interval (0,t). Then, by (A4), we have $(N_{\mu _{j}}(t)-1)\rho _{j}\leq t$, and hence

$$\prod\limits_{t_{s}\leq t}\gamma_{s}= \prod\limits_{j=1}^{q}\mu_{j}^{N_{\mu_{j}}(t)} \leq \prod\limits_{j=1}^{q}\mu_{j}^{\frac{t}{\rho_{j}}+1} = \prod\limits_{j=1}^{q}\mu_{j}e^{\left( \sum\limits_{j=1}^{q}\frac{\ln\mu_{j}}{\rho_{j}}\right)t} = \prod\limits_{j=1}^{q}\mu_{j}e^{\sigma_{0} t}. $$

This, together with (14), leads to

$$\|\hat{z}(t)\|_{\infty}\leq\beta\|\phi-\psi\|_{\infty} e^{-(\lambda-\sigma_{0})t},\quad t>0, $$

where $\beta =C_{\chi }{\prod }_{j=1}^{q}\mu _{j}$ and $C_{\chi }=\frac 1{\chi _{+}}\max _{1\leq j\leq n}\chi _{j}$. Note that α = λ−σ ₀>0 as λ>σ ₀. By Step 1, we finally obtain

$$ \|x(t)-\hat{x}(t)\|_{\infty}\leq \beta\|\phi-\psi\|_{\infty} e^{-\alpha t},\quad t>0. $$

(21)

Estimate (21) shows that the neural network (3) is exponentially stable. The proof is complete.

□

Remark 6

Since $-\mathcal {M}$ is an M-matrix [5], condition (7) is satisfied if and only if $-\mathcal {M}$ is a nonsingular M-matrix. Therefore (7) can be verified by various criteria (see, for example, Chapter 6 in [5] and Proposition 2.1 in [12]).

Remark 7

It can be found in many existing works which deal with time-varying impulses, the impulsive strength sequence (γ _k ) is usually assumed to be bounded; that is, there exists a constant μ>0 such that $\gamma _{k}\leq \mu \; \forall k\in \mathbb {Z}^{+}$. In this case, by the same arguments used in the proof of Theorem 1, we have the following result.

Corollary 1

Assume that Assumptions (A1)–(A3) hold and there exists a T _a >0 satisfying ( 5 ). Then the neural network ( 3 ) is globally exponentially stable if there exist a constant μ≥1 and a vector $\tilde {\chi }\in \mathbb {R}^{n}_{+}$ such that γ _k ≤μ, $k\in \mathbb {Z}^{+}$ , and

$$ (\hat{A}F+\tilde{B}G+\tilde{\sigma}_{0}I-\mathcal{D})\tilde{\chi}\ll 0, $$

(22)

where $\tilde {\sigma }_{0}=\frac {\ln \mu }{T_{a}}$ and $\tilde {B}=(e^{\tilde {\sigma }_{0}\tau _{ij}^{+}}b^{+}_{ij})$.

Remark 8

It should be pointed out that Theorem 1 and Corollary 1 are devoted to non-autonomous neural networks with bounded impulses. However, it can be seen from the proof of Theorem 1 that our approach can also be used for non-autonomous neural networks with unbounded impulses. In that case, the following condition which is widely used in the literature (see, for example, [22, 36]) can be employed

$$ \exists \gamma_{0}\geq 0:\qquad \frac{\ln\gamma_{k}}{t_{k}-t_{k-1}}\leq\gamma_{0}\quad \forall k\geq 1. $$

(23)

Then, stability conditions of the network (3) incorporating (23) are formulated in the following corollary.

Corollary 2

Let Assumptions (A1)-(A3) and condition ( 23 ) hold. Then, the neural network ( 3 ) is globally exponentially stable if there exists a vector $\hat {\chi }\in \mathbb {R}^{n}_{+}$ satisfying

$$ (\hat{A}F+\check{B}G+\gamma_{0}I-\mathcal{D})\hat{\chi}\ll 0, $$

(24)

where $\check {B}=(e^{\gamma _{0}\tau ^{+}_{ij}}b^{+}_{ij})$.

As a special case, when σ _{i k} =0, $i\in \underline {n}$, k≥1, and I(t)=0, system (3) becomes the following nonlinear non-autonomous system without impulses

$$ \left\{\begin{array}{ll} x_{i}^{\prime}(t)=-d_{i}(t)x_{i}(t)+\sum\limits_{j=1}^{n}a_{ij}(t)f_{j}(x_{j}(t)) +\sum\limits_{j=1}^{n}b_{ij}(t)g_{j}(x_{j}(t-\tau_{ij}(t))),\quad t\geq 0,\\ x_{i}(t)=\phi_{i}(t),\quad t\in[-\tau,0]. \end{array}\right. $$

(25)

From the proof of Theorem 1 we get the following result.

Corollary 3

Under Assumptions (A1), (A2), assume that there exists a vector $\upsilon \in \mathbb {R}^{n}_{+}$ such that

$$ (\hat{A}F+B^{+}G-\mathcal{D})\upsilon\ll 0, $$

(26)

where $B^{+}=\left (b^{+}_{ij}\right )$ . Then system ( 25 ) is globally exponentially stable. Furthermore, every solution x(t,ϕ) of ( 25 ) satisfies

$$\|x(t,\phi)\|_{\infty}\leq C_{\upsilon}\|\phi\|_{\infty} e^{-\eta_{0}t},\quad t\geq 0, $$

where $C_{\upsilon }=\max _{1\leq i\leq n}\left (\frac {\upsilon _{i}}{\min _{1\leq j\leq n}\upsilon _{j}}\right )$ , $0<\eta _{0}\leq \min _{1\leq i\leq n}\eta _{i}$ and η _i is the unique positive solution of the scalar equation

$$ -\hat{d}_{i}+\frac1{\upsilon_{i}}\sum\limits_{j=1}^{n}\left( a^{+}_{ij}F_{j} +b^{+}_{ij}e^{\eta_{i}\tau_{ij}^{+}}G_{j}\right)\upsilon_{j}+\eta_{i}=0. $$

(27)

Remark 9

It is worth mentioning here that Corollary 3 in this paper encompasses Theorem 3 in [9] as a special case. More precisely, system (25) includes linear time-invariant (LTI) systems with time-varying delays as its particular form. For LTI systems with single delay, the result of Corollary 3 is same as that of Theorem 3 in [9].

4 Examples

In this section, we give some numerical examples to illustrate the effectiveness and less conservativeness of the proposed conditions in this paper.

Example 1

Let us reconsider model (2) with heterogeneous delays, where $\tau _{11}(t)=0.2|\sin (2t)|$, $\tau _{12}(t)=\tau _{21}(t)=1+0.5|\cos (3t)|$ and $\tau _{22}(t)=0.1|\sin (4t)|$. We have

$$\mathcal{D}=\text{diag}(4,3),\quad \hat{A}=\left( \begin{array}{ll}2&1\\ 0&1\end{array}\right),\quad \hat{B}=\left( \begin{array}{ll}1& 2\\ 0 &1\end{array}\right),\quad F=G=I $$

and $\tau =\max _{i,j=1,2}\tau ^{+}_{ij}=1.5$. With periodic impulsive times t _k = k T _s and σ _{i k} =1.6(−1)^k, i=1,2, we have $\sigma _{0}=\frac {0.47}{T_{s}}$. Therefore,

$$\mathcal{M}=\left( \begin{array}{cc} -2+\frac{0.47}{T_{s}}+e^{\frac{0.094}{T_{s}}} & 1+2e^{\frac{0.705}{T_{s}}}\\ 0 &-2+\frac{0.47}{T_{s}}+e^{\frac{0.047}{T_{s}}}\end{array}\right). $$

It is easy to verify that condition (7) holds if and only if

$$\frac{0.47}{T_{s}}+e^{\frac{0.094}{T_{s}}}<2 $$

which yields T _s >0.5722. A simulation result with sampling time T _s =0.58 is given in Fig. 3 which illustrates the obtained theoretical result.

Fig. 3

State trajectories of the network with T _s =0.58

Example 2

Consider a three-dimensional non-autonomous neural network in the following vector form

$$ \left\{\begin{array}{ll} x^{\prime}(t)=-D(t)x(t)+A(t)f(x(t))+B(t)g(x(t-\tau(t))),\quad t\geq 0,\\ x(t)=\phi(t),\; t\in[-\tau,0], \end{array}\right. $$

(28)

where $D(t)=\text {diag}(1+4e^{-0.1|\sin t|},3e^{-0.1\cos ^{2}t}, 4-0.2|\cos (2t)|)$ and

$$\begin{array}{@{}rcl@{}} A(t)&=&\left( \begin{array}{ccc}\sin^{2}t & 2|\cos(2t)|\quad &0\hspace*{2pt} \\ 0&|\sin(\sqrt{2}t)|{\kern5pt}&0\\ \frac{\sqrt{t}\sin t}{1+t^{2}}& 0 & te^{-0.5t} \end{array}\right),\\ B(t)&=&\left( \begin{array}{cc}|\sin(3t)| \quad\qquad0 &e^{-0.5t}\cos(4t)\\ 1+0.2\cos^{2}(4t)\;\frac{\sqrt{t}\cos t}{1+t^{2}} &0\\ te^{-0.8t}\qquad\qquad0& 1+0.1|\sin(\sqrt{3}t)|\end{array}\right). \end{array} $$

Activation functions $f(x), g(x), x\in \mathbb {R}^{3}$, are given by

$$\begin{array}{@{}rcl@{}} f(x)&=&\big(f_{1}(x_{1}),f_{2}(x_{2}),0\big),\quad f_{i}(x_{i})=0.5\big(|x_{i}+1|-|x_{i}-1|\big),\quad i=1,2,\\ g(x)&=&(0,\tanh(x_{2}),\tanh(x_{3})), \end{array} $$

and heterogeneous time-varying delays

$$\tau_{13}(t)=|\sin(\sqrt{3}t)|,\quad \tau_{22}(t)=0.5|\cos(4t)|,\quad \tau_{33}(t)=0.5|\sin(5t)|. $$

• (a) It is easy to verify that Assumptions (A1), (A2) are satisfied. In addition, we have

  $$\begin{array}{@{}rcl@{}} F&=&\text{diag}(1,1,0),\quad G=\text{diag}(0,1,1),\quad \mathcal{D}=\text{diag}(1+4e^{-0.1},3e^{-0.1},3.8),\\ \hat{A}&=&\left( \begin{array}{ccc} 1&2&0\\ 0&1&0\\ \frac{3}{4\sqrt[4]{3}} &0&2e^{-1}\end{array}\right),\quad B^{+}=\left( \begin{array}{ccc} 1&0&1\\ 1.2&\frac{3}{4\sqrt[4]{3}}&0\\ \frac54e^{-1} &0&1.1\end{array}\right), \end{array} $$

  and $\tau ^{+}_{13}=1$, $\tau ^{+}_{22}=\tau ^{+}_{33}=0.5$. Therefore, condition (26) is equivalent to

  $$ \left\{\begin{array}{ll} -4e^{-0.1}\upsilon_{1}+2\upsilon_{2}+\upsilon_{3}<0,\\ \upsilon_{i}>0,\quad i=1,2,3. \end{array}\right. $$

  (29)

  It is obvious that the solution region of (29) is nonempty. By Corollary 3, system (28) is globally exponentially stable. Let us take υ=(1,0.5,1)^T satisfying (29) then, by solving (27), the exponential convergent rate η ₀=0.6683 and every solution x(t,ϕ) of (28) satisfies

  $$\|x(t,\phi)\|_{\infty}\leq 2\|\phi\|_{\infty} e^{-0.6683t},\quad t\geq 0. $$

Remark 10

In [22], an improved stability criterion was derived for a class of non-autonomous neural networks with time-varying delays. However, the proposed method of [22] leads to a hard constraint in deriving the exponential convergent rate. Specifically, by [22], the matrices P(t)=−D(t)+|A(t)|F and Q(t)=|B(t)|G will be estimated as follows

$$P(t)\leq \underbrace{\left( \begin{array}{ccc}-1-4e^{-0.1}&0&0\\ 0&-3e^{-0.1}&0\\ 0&0&-4\end{array}\right)}_{\hat{P}} +\underbrace{\left( \begin{array}{ccc}\sin^{2}t & 2|\cos(2t)|&0\\ 0&|\sin(\sqrt{2}t)|&0\\ 0&0&0.2|\cos(2t)|\end{array}\right)}_{(\hat{\alpha}_{ij}(t))} $$

and $Q(t)\leq \hat {Q}=\text {diag}(0,\frac {3}{4\sqrt [4]{3}},1.1)$. It can be seen that there exists a vector $\upsilon \in \mathbb {R}^{3}_{+}$ satisfying $(\lambda I_{3}+\hat {P}+e^{\lambda \tau }\hat {Q})\upsilon \ll 0$, where $\tau =\max _{ij}\tau ^{+}_{ij}=1$, if and only if λ<1.0025. In that case, let υ=(1,1,1)^T then the exponential convergent rate is defined by 0<α<λ−μ, where μ>0 is a constant satisfying the following estimate for some b≥0

$${{\int}_{0}^{t}}\hat{\theta}(s)ds\leq \mu t+b\quad \forall t\geq 0, $$

where $\hat {\theta }(s)=\max _{1\leq i\leq 3}{\sum }_{j=1}^{3}\hat {\alpha }_{ij}(s)$. Firstly, it is hard to compute ${{\int }_{0}^{t}}\hat {\theta }(s)ds$. Secondly, the estimate $\mu \geq \frac 1{t}{{\int }_{0}^{t}}(\sin ^{2}(s)+2|\cos (2s)|)ds-\frac {b}{t}\,\forall t>0$, implies that $\alpha <\lambda -\liminf _{t\to \infty }\frac {1}{t}{{\int }_{0}^{t}}\left (\sin ^{2}(s)+2|\cos (2s)|\right )ds$. Since $\sin ^{2}(t)+2|\cos (2t)|\geq \frac 12\,\forall t\geq 0$, the exponential convergent rate derived by the method of [22] does not exceed 0.5025, which is obviously less than η ₀.

• (b) Now, we consider the neural network (28) with impulsive effects specified by

  $$ \left\{\begin{array}{cc} \gamma_{k}=1.6+0.5\sin\frac{k\pi}{2},\quad k\in\mathbb{Z}^{+},\\ t_{k}-t_{k-1}=1-\frac{1}{k(k+1)},\quad t_{0}=0. \end{array}\right. $$

  (30)

  Note at first that (t _k ) is a strictly increasing sequence, $t_{k}={\sum }_{j=1}^{k}\left (1-\frac 1{j(j+1)}\right )=k-1+\frac {1}{k+1}\to \infty$. Also, it is evident that γ _k ∈{μ ₁,μ ₂,μ ₃} ∀k≥1, where μ ₁=2.1, μ ₂=1.6, μ ₃=1.1. In addition, (A4) holds with $\rho _{1}=\inf _{k\geq 1}\left \{4-\frac {4}{(k+1)(k+5)}\right \}=\frac {11}{3}$, $\rho _{2}=\inf _{k\geq 2}\left \{2-\frac {2}{(k+1)(k+3)}\right \}=\frac {28}{15}$ and $\rho _{3}=\inf _{k\geq 3}\left \{4-\frac {4}{(k+1)(k+5)}\right \}=\frac {31}{8}$. Therefore $\sigma _{0}={\sum }_{j=1}^{3}\frac {\ln \mu _{j}}{\rho _{j}}=0.4787$ and

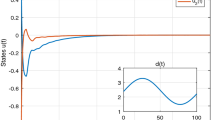
  $$\mathcal{M}=\hat{A}F+\hat{B}G+\sigma_{0}I_{3}-\mathcal{D} =\left( \begin{array}{ccc} -3.1406&2&1.6140\\ 0&-0.5118 & 0\\ 0&0 &-1.9238\end{array}\right). $$

  Let $\chi =(1,0.5,1)^{T}\in \mathbb {R}^{3}_{+}$ then $\mathcal {M}\chi \ll 0$. By Theorem 1, the impulsive neural network (28) and (30) is globally exponentially stable. According to (21), every solution x(t,ϕ) of (28), (30) satisfies the following exponential estimate

  $$\|x(t,\phi)\|_{\infty}\leq 7.392\|\phi\|_{\infty} e^{-0.1396t},\quad t\geq 0. $$

  A state trajectory of (28) with impulsive effects defined by (30) is given in Fig. 4 which illustrates the obtained theoretical results.

Fig. 4

A state trajectory of (28), (30)

Remark 11

It is found from (30) that a constant γ satisfies $\frac {\ln \gamma _{k}}{t_{k}-t_{k-1}}\leq \gamma \forall k\geq 1$, if and only if $\gamma \geq 2\ln (2.1)$. Therefore, a positive number λ satisfying condition

$$\left\{\begin{array}{ll} (\lambda I_{3}+\hat{P}+e^{\lambda\tau}\hat{Q})\upsilon\ll 0,\quad \upsilon\in\mathbb{R}^{3}_{+},\\ \lambda>\gamma, \end{array}\right. $$

does not exist. Thus, stability conditions proposed in [22] cannot be applied to the impulsive neural network (28), (30).

Example 3

Consider the following linear system with constant impulsive strength μ

$$ \left\{\begin{array}{ll} \dot x(t)=-x(t)+B(t)x(t-0.2),\quad t\neq kT_{s}, k\in\mathbb{Z}^{+},\\ x(t)=\mu x(t^{-}),\quad t=kT_{s}, \end{array}\right. $$

(31)

where T _s >0 is a sampling time and $B(t)=\left (\begin {array}{cc}0.8&\;\; 1+0.5|\sin (2t)|\\ 0&0.8\end {array}\right )$.

Let T _s =0.25. Theorem 1 ensures that system (31) is globally exponentially stable for impulsive strength |μ|<1.0439. However, the system can be stable for |μ|<1.0499 by simulation results. This result shows that, for this example, the sufficient conditions proposed in Theorem 1 are very closed to the critical result which demonstrates the effectiveness of the proposed method in this paper.

5 Concluding Remarks

In this paper, the problem of global exponential stability analysis has been addressed for a class of non-autonomous neural networks with heterogeneous delays and time-varying impulsive effects. Based on the comparison principle, sufficient delay-dependent conditions have been derived using M-matrix theory ensuring that, under destabilizing impulsive effects, the system is globally exponentially stable. The effectiveness of the derived conditions has been illustrated by numerical examples.

The approach presented in this paper can also be extended to some related important problems such as state bounding or synchronization analysis and control of non-autonomous impulsive networks where the existing methods, for example, based on the Lyapunov–Krasovskii functionals or using fixed-point theorems are not effective. However, as mentioned above, a gap between the derived sufficient conditions and necessary-type conditions still exists which produces conservativeness in the derived stability conditions. Reducing this gap or furthermore establishing if and only if-type conditions is an interesting issue. In addition, unlike autonomous systems, for non-autonomous systems, the rate of change of the system parameters affects stability of the system. How to utilize the rate of change of the system parameters to derive stability conditions is another interesting and challenging problem. These issues require further investigations in the future works.