1 Introduction

In the past few years, there has been increasing interest in neural networks due to their extensive applications in many fields such as pattern recognition, parallel computing, associative memory, signal and image processing and combinatorial optimization. As is well known, in both biological and man-made neural networks, delays occur due to finite switching speed of the amplifiers and communication time. The stability analysis problem for neural networks with delays has gained much research attention, and a large amount of results related to this problem have been published, (see, e.g., [1–12]).

However, besides delay, impulsive effects are also likely to exist in the neural network system. For example, in implementation of electronic networks in which state is subject to instantaneous perturbations and experiences abrupt change at certain moments, which may be caused by switching phenomenon, frequency change or other sudden noise, that is, does exhibit impulsive effects. Some interesting results about the stability for impulsive neural networks with delays have been obtained [13–18].

On the other hand, a real system is usually affected by external perturbations which in many cases are of great uncertainty and hence may be treated as random, as pointed out by [19] that in real nervous systems synaptic transmission is a noisy process brought on by random fluctuations from the release of neurotransmitters, and other probabilistic causes. Therefore, it is significant and of prime importance to consider stochastic effects to the dynamics behavior of impulsive neural networks with delays[20, 21]. In recent years, a large number of stability criteria of neural networks with impulsive and stochastic effects have been reported, see [22–27]. For example, Song and Wang [26] investigated the existence, uniqueness and exponential p-stability of the equilibrium point for impulsive stochastic Cohen-Grossberg neural networks with mixed time delays by employing a combination of the M-matrix theory and stochastic analysis technique. In [27], Wang et al. studied the impulsive stochastic Cohen-Grossberg neural networks with mixed delays by establishing an L-operator differential inequality with mixed delays and using the properties of M-cone and stochastic analysis technique. In [22–24], Zhang et al. studied the dynamical behavior of impulsive stochastic autonomous nonlinear systems.

It is well known that the non-autonomous phenomenon often occurs in many realistic systems. Particularly, when we consider a long-term dynamical behavior of a system, the parameters of the system are usually subjected to environmental disturbances and frequently vary with time. In this case, non-autonomous neural network model can even accurately depict evolutionary processes of networks. Thus the research on the non-autonomous neural networks is also important like on autonomous neural networks [28–35]. Motivated by the above discussions, in this work, we consider a class of impulsive non-autonomous stochastic neural networks with mixed delays. By establishing a new generalized Halanay inequality with impulses which improves the generalized Halanay inequality with impulses established by Li in [18], we obtain some sufficient conditions ensuring global mean square exponential stability of the addressed neural networks.

The rest of this paper is organized as follows. In the next section, we introduce our notations and some basic definitions. Section 3 is devoted to the global exponential stability of the following Eq. (1). We end this paper in Sect. 4 with an illustrative example.

2 Preliminaries

For convenience, we introduce several notations and recall some basic definitions.

Let \(\mathcal {N}=\{1,2,\ldots ,n\}\). C(X, Y ) denotes the space of continuous mappings from the topological space X to the topological space Y. Especially, \(C \buildrel \Delta \over = C( {\left( { -\infty ,0} \right] ,{R^n}} )\) .

$$\begin{aligned} PC(J,H)=&\Big \{\psi (t): J\rightarrow H\mid \psi (t)\,\, \text {is continuous for all but at most countable points } s\in J\\&\text { and at these points}\, s\in J,\, \psi (s^{+}) \,\, \text{ and } \,\, \psi (s^{-})\,\, \text {exist}, \, \psi (s^{+})=\psi (s) \Big \}, \end{aligned}$$

where \(J \subset R\) is an interval, H is a complete metric space, \(\psi (s^{+})\) and \(\psi (s^{-})\) denote the right-hand and left-hand limit of the function \(\psi (s)\), respectively. Especially, let \(PC \buildrel \Delta \over = PC\left( {\left( { - \infty ,0} \right] ,{R^n}} \right) \).

$$\begin{aligned} \wp =&\Big \{\psi (t): R_+\rightarrow R_+\mid \psi (t)\,\, \text {is piecewise continuous and }\int _{0}^{\infty } e^{\lambda _0s}\psi (s)\,\mathrm {d}t<\infty \Big \}, \end{aligned}$$

where \(\lambda _0\) is a positive constant.

For any \(\varphi \in C\) or \(\varphi \in PC\), we always assume that \(\varphi \) is bounded and introduce the following norm:

$$\begin{aligned} \Vert \varphi \Vert =\sup _{-\infty < s\le 0}|\varphi (s)|. \end{aligned}$$

Let \((\Omega ,\mathscr {F},\{\mathscr {F}_t\}_{t\ge 0},P)\) be a complete probability space with a filtration \(\{\mathscr {F}_t\}_{t\ge 0}\) satisfying the usual conditions \((\text {i.e, it is right continuous and}\) \(\mathscr {F}_0 \; \text {contains all P-null sets})\). Denote by \(PC^b_{\mathscr {F}_0}\left( {\left( { - \infty ,0} \right] ,{R^n}} \right) \) the family of all bounded \(\mathscr {F}_0\)-measurable, PC-valued random variables \(\varphi \), satisfying \(\left\| \varphi \right\| _{{L^2}}^2 = \mathop {\sup } \limits _{ - \infty < s \le 0} E{\left| {\phi \left( s \right) } \right| ^2} < \infty \) , where E[f] means the mathematical expectation of f.

In this work, we consider the following impulsive non-autonomous stochastic neural networks:

$$\begin{aligned} \left\{ \begin{array}{l} dx_i \left( t \right) = - a_i \left( t \right) x_i \left( t \right) + \sum \limits _{j = 1}^n {b_{ij} \left( t \right) f_j \left( {x_j \left( t \right) } \right) } + \sum \limits _{j = 1}^n {c_{ij} \left( t \right) g_j \left( {x_j \left( {t - \tau _{ij} \left( t \right) } \right) } \right) } \\ \quad \quad \quad \quad \quad + \sum \limits _{j = 1}^n {d_{ij} \left( t \right) \int _{ - \infty }^t {k_j \left( {t - s} \right) h_j \left( {x_j \left( s \right) } \right) ds} } \\ \quad \quad \quad \quad \quad + \sum \limits _{j = 1}^n {\sigma _{ij} \left( {t,x_i \left( t \right) ,x_i \left( {t - \tau _{ij} \left( t \right) } \right) } \right) }dw_j(t) ,\,\,t \ge t_0 ,\,\,t \ne t_k , \\ x_i \left( {t_k } \right) = \sum \limits _{j = 1}^n {w_{ij}^k x_j \left( {t_k^ - } \right) } +\sum \limits _{j = 1}^n {e_{ij}^k x_j \left( {t_k^ --\tau } \right) } ,\,\,t = t_k, \\ x_i(t_0+s)=\varphi _i(s),\quad -\infty <s\le 0, \,i=1,2,\ldots ,n,\\ \end{array} \right. \end{aligned}$$
(1)

where n corresponds to the number of units in a neural network; \(x_i(t)\) corresponds to the state of the ith unit at time t; \(f_j (x_j (t))\), \(g_j (x_j (t))\) and \(h_j (x_j (t))\) denote the activation functions of the jth unit at time t; \(a_i(t) \ge 0\) represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs; \((b_{ij}(t))_{n\times n}\), \((c_{ij}(t))_{n\times n}\) and \((d_{ij}(t))_{n\times n}\) are connection matrices; the delay kernels \(k_j(t),\,j=1,2,\ldots ,n,\) are piecewise continuous and satisfy that \(|k_{j}(t)|\le k(t)\in \wp \); \(0\le \tau _{ij}(t)\le \tau \) is the transmission delay, where \(\tau \) is a positive constant. \(\sigma \left( { \cdot , \cdot , \cdot } \right) = \left( {{\sigma _1}\left( { \cdot , \cdot , \cdot } \right) , \ldots ,{\sigma _n}\left( { \cdot , \cdot , \cdot } \right) } \right) :\left[ {{t_0},\infty } \right) \times {R^n} \times {R^n} \rightarrow {R^{n \times n}}\) is the diffusion coefficient matrix; \(w(t) = (w_1 (t), \cdots ,w_n (t))^T \) is an n-dimensional Brownian motion defined on \((\Omega , \mathscr {F},\{\mathscr {F}_t\}_{t\ge 0},P)\). The initial condition \(\varphi (s)=(\varphi _1(s),\varphi _2(s),\ldots ,\varphi _n(s))^T \in PC^b_{\mathscr {F}_0}\left( { (- \infty ,0],{R^n}} \right) .\) \(t_0<t_1<t_2<\cdots \) are fixed impulsive points with \(\mathop {\lim }\limits _{k \rightarrow \infty } {t_k} = \infty ,\) \(k=1,2,\ldots .\)

As a standing hypothesis, we assume that for any initial value \(\varphi \in PC^b_{\mathscr {F}_0}\left( { (- \infty ,0],{R^n}} \right) \) there exists one solution of system (1) which is denoted by \(x(t, t_0,\varphi )\), or, x(t), if no confusion occurs. We will also assume that \(f_j(0) = 0,\ g_j (0) = 0,\ h_j (0) = 0, \,\text {and}\, \sigma _{ij}(t, 0,0) = 0, i\in \mathcal {N},\,t\ge t_0\), for the stability purpose of this work. Then system (1) admits an equilibrium solution \(x(t)\equiv 0\).

Definition 2.1

The zero solution of system (1) is said to be mean square globally exponentially stable if there exist positive constants \(\alpha \) and \(K\ge 1\) such that for any solution \(x(t,t_0,\varphi )\) with the initial condition \(\varphi \in PC^b_{\mathscr {F}_0}\left( { (- \infty ,0],{R^n}} \right) \),

$$\begin{aligned} {E\left\| {x\left( t,t_0,\varphi \right) } \right\| ^2} \le K\left\| \varphi \right\| _{L^2}^2{e^{ - \alpha \left( {t - {t_0}} \right) }}, \quad t \ge {t_{0.}} \end{aligned}$$
(2)

3 Global Exponential Stability

In this section, we will first establish a generalized Halanay inequality with impulses and then give some sufficient conditions on the global exponential stability of zero solution for Eq. (1).

Theorem 3.1

Let u(t) be a solution of the impulsive integro-differential inequality

$$\begin{aligned} \left\{ \begin{array}{l} D^ + u\left( t \right) \le - \alpha \left( t \right) u\left( t \right) +\beta \left( t \right) [u(t)]_\tau + \gamma \left( t \right) \int _0^\infty {k\left( s \right) u\left( {t - s} \right) } ds,\quad t \ge t_0,\,t\ne t_k \\ u\left( {t_k } \right) \le p_k u\left( {t_k^ - } \right) +q_k u(t_k^--\tau ),\quad k =1,2,\ldots , \\ u\left( {t_0 + s} \right) \le \phi \left( s \right) ,\quad s \in ( - \infty ,0], \\ \end{array} \right. \end{aligned}$$
(3)

where u(t) is continuous at \(t\ne t_k\), \(t\ge t_0\), \(\phi \in PC\), k(s) is the same as defined in Sect. 2, \(\alpha (t)\), \(\beta (t)\) and \(\gamma (t)\) are nonnegative continuous functions with \(\alpha (t)\ge \alpha _0>0\) and \(0\le \beta (t)+\gamma (t) \int _0^\infty {k(s)}ds<q\alpha (t)\) for all \(t\ge t_0\) with \(0\le q<1.\) Further assume that there exits a constant \(\rho >0\) such that

$$\begin{aligned} \prod \limits _{k = 1}^n {\delta _k } \le e^{\rho \left( {t_n - t_0 } \right) } ,\quad n = 1,2, \ldots , \end{aligned}$$
(4)

where \(\delta _k : = \max \left\{ {1,\left| {p_k } \right| +\left| {q_k } \right| e^{\lambda \tau } } \right\} \). Then

$$\begin{aligned} u\left( t \right) \le \Vert \phi \Vert e^{ - (\lambda -\rho ) (t-t_0)} ,\quad t \ge t_0 , \end{aligned}$$
(5)

where \(\lambda \in (0,\lambda _0)\) is defined as

$$\begin{aligned} 0 < \lambda < \lambda ^ * = \mathop {\inf }\limits _{t \ge t_0 } \left\{ {\lambda \left( t \right) :\lambda \left( t \right) - \alpha \left( t \right) +\beta (t)e^{\lambda (t)\tau } + \gamma \left( t \right) \int _0^\infty {k\left( s \right) e^{\lambda \left( t \right) s} } ds = 0} \right\} . \end{aligned}$$
(6)

Proof

Denote

$$\begin{aligned} H\left( \lambda \right) = \lambda \ - \alpha \left( t \right) + \beta \left( t \right) e^{\lambda \tau }+\gamma (t)\int _0^\infty {k\left( s \right) e^{\lambda s} } ds. \end{aligned}$$

By assumption \(\alpha (t)\ge \alpha _0>0\) and \(0\le \beta (t)+\gamma (t) \int _0^\infty {k(s)}ds<q\alpha (t)\) for all \(t\ge t_0\) with \(0\le q<1,\) then for any given fixed \(t\ge t_0\), we see that \( H\left( 0 \right) = - \alpha \left( t \right) + \beta \left( t \right) +\gamma (t) \int _0^\infty {k(s)}ds \le - \left( {1 - q} \right) \alpha \left( t \right) \le - \left( {1 - q} \right) \alpha _0 < 0, \mathop {\lim }\limits _{\lambda \rightarrow \infty } H\left( \lambda \right) = \infty , \) and the fact that \(H(\lambda )\) is a strictly increasing function. Therefore, for any \(t\ge t_0\) there is a unique positive \(\lambda (t)\) such that \( \lambda \left( t \right) - \alpha \left( t \right) + \beta \left( t \right) e^{\lambda (t)\tau }+\gamma (t)\int _0^\infty {k\left( s \right) e^{\lambda \left( t \right) s} } ds = 0. \) From the definition, one has \(\lambda ^ * \ge 0\). We have to prove \(\lambda ^ *>0\). Suppose this is not true. Fix \(\tilde{q}\) satisfying \( 0 \le q < \tilde{q} < 1 \) and pick a small enough \(\varepsilon >0\) satisfying \(e^{\varepsilon \tau }<\frac{1}{\tilde{q}},\, \int _0^\infty {k\left( s \right) e^{\varepsilon s} } ds < \frac{1}{{\tilde{q}}}\int _0^\infty {k(s)}ds \), and \( \varepsilon < \left( {1 - \frac{q}{{\tilde{q}}}} \right) \alpha _0. \) Then there is a \(t^*\ge t_0\) such that \(\lambda (t^*)<\varepsilon \) and

$$\begin{aligned} \lambda \left( {t^ * } \right) - \alpha \left( {t^ * } \right) + \beta \left( {t^ * } \right) e^{\lambda \left( {t^ * } \right) \tau }+\gamma (t^*)\int _0^\infty {k\left( s \right) e^{\lambda \left( {t^ * } \right) s} } ds = 0. \end{aligned}$$

Now we have

$$\begin{aligned} 0= & {} \lambda \left( {t^ * } \right) - \alpha \left( {t^ * } \right) + \beta \left( {t^ * } \right) e^{\lambda \left( {t^ * } \right) \tau }+\gamma (t^*)\int _0^\infty {k\left( s \right) e^{\lambda \left( {t^ * } \right) s} } ds \\< & {} \varepsilon - \alpha \left( {t^ * } \right) +\beta \left( {t^ * } \right) e^{\varepsilon \tau } + \gamma \left( {t^ * } \right) \int _0^\infty {k\left( s \right) e^{\varepsilon s} } ds \\< & {} \varepsilon - \alpha \left( {t^ * } \right) + \frac{1}{{\tilde{q}}}\beta \left( {t^ * } \right) +\frac{1}{{\tilde{q}}}\gamma \left( {t^ * } \right) \int _0^\infty {k(s)}ds \\\le & {} \varepsilon - \left( {1 - \frac{q}{{\tilde{q}}}} \right) \alpha \left( {t^ * } \right) \\\le & {} \varepsilon - \left( {1 - \frac{q}{{\tilde{q}}}} \right) \alpha _0 < 0, \end{aligned}$$

this contradiction shows that \(\lambda ^*> 0\), so there at least exists a constant \(\lambda \) such that \(0 < \lambda < \min \{\lambda _0,\lambda ^*\}\), that is, the definition of \(\lambda \) for (6) is reasonable.

As \(\phi \in PC\), we always have

$$\begin{aligned} u\left( t \right) \le \Vert \phi \Vert e^{ - \lambda \left( {t - t_0 } \right) } ,\quad - \infty < t \le t_0. \end{aligned}$$
(7)

We first prove for any given \(k > 1\),

$$\begin{aligned} u\left( t \right) < k\Vert \phi \Vert e^{ - \lambda \left( {t - t_0 } \right) } =v(t),\quad t \in [t_0 ,\, t_1 ). \end{aligned}$$
(8)

If (8) is not true, then from (7) and the continuity of u(t) for \(t \in [t_0 ,t_1) \), there must exist a \(\hat{t} \in [t_0 ,t_1) \) such that

$$\begin{aligned}&u\left( \hat{t} \right) = v\left( \hat{t} \right) ,\quad D^ + u\left( \hat{t} \right) \ge v^{'}\left( \hat{t} \right) , \end{aligned}$$
(9)
$$\begin{aligned}&u\left( t \right) \le v\left( t \right) , \quad \quad \quad \quad - \infty < t \le \hat{t}. \end{aligned}$$
(10)

By using (3),(6) and (10), we obtain that

$$\begin{aligned} D^ + u\left( \hat{t} \right)\le & {} - \alpha \left( \hat{t} \right) u\left( t \right) + \beta \left( \hat{t} \right) [u(\hat{t})]_\tau +\gamma \left( \hat{t} \right) \int _0^\infty {k\left( s \right) u\left( {\hat{t} - s} \right) } ds \\\le & {} - \alpha \left( \hat{t} \right) k\Vert \phi \Vert e^{ - \lambda \left( {\hat{t} - t_0 } \right) } + \beta \left( \hat{t} \right) e^{\lambda \tau }k\Vert \phi \Vert e^{ - \lambda \left( {\hat{t} - t_0 } \right) }\\&+\gamma \left( \hat{t} \right) \int _0^\infty {k\left( s \right) k\Vert \phi \Vert e^{ - \lambda \left( {\hat{t} - s - t_0 } \right) } } ds \\= & {} \left[ { - \alpha \left( \hat{t} \right) +\beta \left( \hat{t} \right) e^{\lambda \tau }+ \gamma \left( \hat{t} \right) \int _0^\infty {k\left( s \right) e^{\lambda s} } ds} \right] k\Vert \phi \Vert e^{ - \lambda \left( {\hat{t} - t_0 } \right) } \\< & {} \left[ { - \alpha \left( \hat{t} \right) +\beta \left( \hat{t} \right) e^{\lambda (\hat{t})\tau } + \gamma \left( \hat{t} \right) \int _0^\infty {k\left( s \right) e^ {\lambda \left( \hat{t} \right) s} } ds} \right] k\Vert \phi \Vert e^{ - \lambda \left( {\hat{t} - t_0 } \right) } \\= & {} - \lambda \left( \hat{t} \right) k\Vert \phi \Vert e^{ - \lambda \left( {\hat{t} - t_0 } \right) } \\< & {} - \lambda k\Vert \phi \Vert e^{ - \lambda \left( {\hat{t} - t_0 } \right) } = v^{'} \left( \hat{t} \right) , \end{aligned}$$

which contradicts the inequality in (9), and so (8) holds for \(t\in [t_0,\,\,t_1)\). Letting \(k\rightarrow 1\), then we have

$$\begin{aligned} u\left( t \right) \le \Vert \phi \Vert e^{ - \lambda \left( {t - t_0 } \right) },\quad t \in [t_0 ,\, t_1 ). \end{aligned}$$
(11)

Using the result above and the discrete part of (3), we can get

$$\begin{aligned} u\left( {t_1 } \right)\le & {} p_1 u\left( {t_1^ - } \right) + q_1 u\left( {t_1^ --\tau } \right) \\\le & {} (\left| {p_1 } \right| +\left| {q_1 } \right| e^{\lambda \tau })\Vert \phi \Vert e^{ - \lambda \left( {t_1 - t_0 } \right) }\\\le & {} \delta _1 \Vert \phi \Vert e^{ - \lambda \left( {t_1 - t_0 } \right) } . \end{aligned}$$

Therefore

$$\begin{aligned} u\left( t \right) \le \delta _1 \Vert \phi \Vert e^{ - \lambda \left( {t_1 - t_0 } \right) } , \quad t \in \left( { - \infty ,t_1 } \right] . \end{aligned}$$

Suppose for all \(q = 1, 2,\ldots ,k\), the inequalities

$$\begin{aligned} u\left( t \right) \le \delta _0 \delta _1 \cdots \delta _{q - 1} \Vert \phi \Vert e^{ - \lambda \left( {t_1 - t_0 } \right) } ,\quad t \in \left[ {t_{q - 1} ,t_q } \right) . \end{aligned}$$
(12)

hold, where \(\delta _0=1\). Then, from (12), the discrete part of (3) satisfies that

$$\begin{aligned} u\left( {t_k } \right)\le & {} p_k u\left( {t_k^ - } \right) +q_k u\left( {t_k^ --\tau } \right) \nonumber \\\le & {} \big (\left| {p_k } \right| +\left| {q_k} \right| e^{\lambda \tau }\big )\Vert \phi \Vert e^{ - \lambda \left( {t_k - t_0 } \right) } \nonumber \\\le & {} \delta _k \Vert \phi \Vert e^{ - \lambda \left( {t_k - t_0 } \right) }. \end{aligned}$$
(13)

This, together with (12), leads to

$$\begin{aligned} u\left( t \right) \le \delta _0 \delta _1 \cdots \delta _{k} \Vert \phi \Vert e^{ - \lambda \left( {t - t_0 } \right) } , \quad t \in \left[ {t_{k} ,\,t_{k+1} } \right) . \end{aligned}$$

By the mathematical induction, we can conclude that

$$\begin{aligned} u\left( t \right) \le \delta _0 \delta _1 \cdots \delta _{k - 1} \Vert \phi \Vert e^{ - \lambda \left( {t - t_0 } \right) }\le \Vert \phi \Vert e^{ - (\lambda -\rho ) \left( {t - t_0 } \right) },\quad t \in \left[ {t_{k - 1} ,t_k } \right) ,\quad k=1,2,\ldots . \end{aligned}$$

The proof is completed.\(\square \)

Remark 3.1

If \(\alpha (t)\equiv \alpha \), \(\beta (t)\equiv \beta \) and \(\gamma (t)\equiv \gamma \), \(t\ge t_0\), Theorem 3.1 becomes the lemma 1 in [18].

Theorem 3.2

[18, Lemma 1] Let \(\alpha ,\beta ,\gamma \) and \(p_k,k=1,2,\ldots ,\) denote nonnegative constants and let u(t) be a solution of the impulsive integro-differential inequality

$$\begin{aligned} \left\{ \begin{array}{l} D^ + u\left( t \right) \le - \alpha u\left( t \right) + \beta [u(t)]_\tau + \gamma \int _0^\infty {k\left( s \right) u\left( {t - s} \right) } ds,\quad t \ge t_0,\,t\ne t_k \\ u\left( {t_k } \right) \le p_k u\left( {t_k^ - } \right) + q_ku\left( {t_k^ - }-\tau \right) ,\quad k \in N, \\ u\left( {t_0 + s} \right) \le \phi \left( s \right) ,\quad s \in ( - \infty ,0], \\ \end{array} \right. \end{aligned}$$
(14)

where u(t) is continuous at \(t\ne t_k\), \(t\ge t_0\), \(\phi \in PC\), k(s) is the same as defined in Sect. 2. Assume that

  1. (i)

    \(\alpha >\beta +\gamma \int _0^\infty k\left( s \right) ds\);

  2. (ii)

    there exits a constant \(\rho >0\) such that

    $$\begin{aligned} \prod \limits _{k = 1}^n {\delta _k } \le e^{\rho \left( {t_n - t_0 } \right) } ,\quad n = 1,2, \ldots , \end{aligned}$$

    where \(\delta _k : = \max \left\{ {1,\left| {p_k } \right| +\left| {q_k } \right| e^{\lambda \tau } } \right\} .\)

Then

$$\begin{aligned} u\left( t \right) \le \Vert \phi \Vert e^{ - (\lambda -\rho ) (t-t_0)} ,\quad t \ge t_0 , \end{aligned}$$

where \(\lambda \in (0,\lambda _0)\) is defined as

$$\begin{aligned} {\lambda - \alpha + \beta e^{\lambda \tau }+ \gamma \int _0^\infty {k\left( s \right) e^{\lambda s} } ds \le 0} . \end{aligned}$$

We remark here that the autonomous condition (14) is replaced by the non-autonomous condition (3), it is more useful for practical purpose, please see the following example.

Example 3.1

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{dx\left( t \right) }}{{dt}} = - \left( {1 + 2t} \right) x\left( t \right) +\left( {\frac{1}{4} + \frac{1}{2}t} \right) x(t-1) + \left( {\frac{1}{4} + \frac{1}{2}t} \right) \int _0^\infty {e^{ - s} x\left( {t - s} \right) ds,\quad t \ge 0,\,t \ne t_k ,} \\ x\left( t_k \right) = -e^{0.2k} x\left( {t_k^ - } \right) , \\ x\left( {0 + s} \right) = \sin s,\, - \infty < s \le 0, \\ \end{array} \right. \end{aligned}$$
(15)

where \(t_k=t_{k-1}+2k, k=1,2,\ldots \). It is clear that Theorem 3.2 fails to apply to Eq. (15). However, from Theorem 3.1, we can easily see that the trivial solution of (15) satisfies \(x\left( t \right) \le e^{ - 0.1t} ,\, t\ge 0\).

Theorem 3.3

Assume that

\((A_1)\) There exist nonnegative constants \(L_j^f , L_j^g ,\) and \(L_{j}^h\) , \(j = 1,\ldots n,\) such that

$$\begin{aligned} \begin{array}{l} \left| {f_j \left( x \right) - f_j \left( y \right) } \right| \le L_j^f \left| {x - y} \right| ,\quad \left| {g_j \left( x \right) - g_j \left( y \right) } \right| \le L_j^g \left| {x - y} \right| , \\ \left| {h_{j} \left( x \right) - h_{j} \left( y \right) } \right| \le L_{j}^h \left| {x - y} \right| ,\quad \forall x,y\in R^n. \\ \end{array} \end{aligned}$$

\((A_2)\) There exist nonnegative continuous functions \(\alpha _i(t)\) and \(\beta _i(t)\), \(i=1,2,\ldots ,n,\) such that

$$\begin{aligned} \sigma _i \left( {t,x,y} \right) \sigma _i^T \left( {t,x, y} \right) \le \alpha _i \left( t \right) x^2 + \beta _i \left( t \right) y^2. \end{aligned}$$

\((A_3)\) There exist nonnegative continuous functions \(\eta (t)\), \(\zeta (t)\) and \(\rho (t)\) , \(t\ge t_0\), such that

$$\begin{aligned} \eta (t)\ge \eta _0>0,\quad 0\le \zeta (t)+\rho (t) \int _0^\infty {k(s)}ds<q\eta (t) ,\quad 0\le q<1, \end{aligned}$$

where

$$\begin{aligned} \eta \left( t \right)= & {} \mathop {\min }\limits _{1 \le i \le n} \left\{ 2a_i \left( t \right) - \sum \limits _{j = 1}^n \left| {b_{ij} \left( t \right) } \right| L_j^f - \sum \limits _{j = 1}^n {\left| {b_{ji} \left( t \right) } \right| L_i^f } - \sum \limits _{j = 1}^n \left| {c_{ij} \left( t \right) } \right| L_j^g \right. \\&\left. - \sum \limits _{j = 1}^n {\left| {d_{ij} \left( t \right) } \right| L_j^h - \alpha _i \left( t \right) } \right\} ,\\ \zeta \left( t \right)= & {} \mathop {\max }\limits _{1 \le i \le n} \left\{ {\sum \limits _{j = 1}^n {\left| {c_{ji} \left( t \right) } \right| L_i^g + \beta _i \left( t \right) } } \right\} ,\quad \text {and} \quad \rho \left( t \right) = \mathop {\max }\limits _{1 \le i \le n} \left\{ {\sum \limits _{j = 1}^n {\left| {d_{ji} \left( t \right) } \right| L_i^h } } \right\} . \end{aligned}$$

\((A_4)\) There exists a positive constant \(\gamma \) satisfying

$$\begin{aligned} \frac{{\ln \gamma _k }}{{t_k - t_{k - 1} }} \le \gamma < \lambda ,\quad k=1,2,\ldots , \end{aligned}$$
(16)

where \( \gamma _k = \max \left\{ 1,\mathop {2n\max }\limits _{1 \le i \le n} \left\{ {\sum \limits _{j = 1}^n {\left( {w_{ij}^k } \right) ^2 } }\right\} +\mathop {2n\max }\limits _{1 \le i \le n} \left\{ {\sum \limits _{j = 1}^n {\left( {e_{ij}^k } \right) ^2 } }\right\} e^{\lambda \tau } \right\} \) and \(0<\lambda \le \lambda _0\) is defined as

$$\begin{aligned} 0 < \lambda < \lambda ^ * = \mathop {\inf }\limits _{t \ge t_0 } \left\{ {\lambda \left( t \right) :\lambda \left( t \right) - \eta \left( t \right) + \zeta \left( t \right) \int _0^\infty {k\left( s \right) e^{\lambda \left( t \right) s} } ds = 0} \right\} . \end{aligned}$$
(17)

Then the zero solution of (1) is mean square globally exponentially stable.

Proof

By a similar argument with (6), one can know that the \(\lambda \) defined by (17) is reasonable.

By the assumptions \((A_1)\)–\((A_4)\), the theorem 4.1 in [36], and the following proof, we know that for any \(\varphi \in PC^b_{\mathscr {F}_0}\left( { (- \infty ,0],{R^n}} \right) \), there exists a unique global solution x(t) through \((t_0, \varphi )\).

Define \( V\left( t \right) = \sum \limits _{i = 1}^n { {x^2_i \left( t \right) } } \). From (1), \((A_1)\), and Itô formula [37] we have

$$\begin{aligned} dV\left( t \right) = LV\left( t \right) dt + \sum \limits _{i = 1}^n {2x_i \left( t \right) } \sum \limits _{j = 1}^n {\sigma _{ij} \left( {t,x_i \left( t \right) ,\quad x_i \left( {t - \tau _{ij} \left( t \right) } \right) } \right) } dw_j \left( t \right) , \end{aligned}$$
(18)

where \(LV\left( t \right) \) is defined by

$$\begin{aligned} LV\left( t \right)= & {} \sum \limits _{i = 1}^n {2x_i \left( t \right) } \left\{ { - a_i \left( t \right) x_i \left( t \right) + \sum \limits _{j = 1}^n {b_{ij} \left( t \right) f_j \left( {x_j \left( t \right) } \right) } } \right. \\&+ \sum \limits _{j = 1}^n {c_{ij} \left( t \right) g_j \left( {x_j \left( {t - \tau _{ij} \left( t \right) } \right) } \right) } + \left. {\sum \limits _{j = 1}^n {d_{ij} \left( t \right) \int _{ - \infty }^t {k_j \left( {t - s} \right) h_j \left( {x_j \left( s \right) } \right) ds} } } \right\} \\&+ \sum \limits _{i = 1}^n {\sigma _i } \left( {t,x_i \left( t \right) ,x_i \left( {t - \tau _{ij} \left( t \right) } \right) } \right) \sigma _i^T \left( {t,x_i \left( t \right) ,x_i \left( {t - \tau _{ij} \left( t \right) } \right) } \right) . \end{aligned}$$

It follows from \((A_1)-(A_3)\) that

$$\begin{aligned} LV\left( t \right)\le & {} - 2\sum \limits _{i = 1}^n {a_i \left( t \right) x_i^2 \left( t \right) } + 2\sum \limits _{i = 1}^n {\sum \limits _{j = 1}^n {\left| {b_{ij} \left( t \right) } \right| } } \left| {x_i \left( t \right) } \right| L_j^f \left| {x_j \left( t \right) } \right| \\&+ 2\sum \limits _{i = 1}^n {\sum \limits _{j = 1}^n {\left| {c_{ij} \left( t \right) } \right| } } \left| {x_i \left( t \right) } \right| L_j^g \left| {x_j \left( {t - \tau _{ij} \left( t \right) } \right) } \right| \\&+ 2\sum \limits _{i = 1}^n {\sum \limits _{j = 1}^n {\left| {d_{ij} \left( t \right) } \right| } } \left| {x_i \left( t \right) } \right| L_j^h \int _0^\infty {k_j \left( s \right) \left| {x_j \left( {t - s} \right) } \right| ds} \\&+ \sum \limits _{i = 1}^n {\alpha _i \left( t \right) x_i^2 \left( t \right) } + \sum \limits _{i = 1}^n {\beta _i \left( t \right) x_i^2 \left( {t - \tau _{ij} \left( t \right) } \right) } \\\le & {} - 2\sum \limits _{i = 1}^n {a_i \left( t \right) x_i^2 \left( t \right) } + \sum \limits _{i = 1}^n {\sum \limits _{j = 1}^n {\left| {b_{ij} \left( t \right) } \right| } } L_j^f \left( {x_i^2 \left( t \right) + x_j^2 \left( t \right) } \right) \\&+ \sum \limits _{i = 1}^n {\sum \limits _{j = 1}^n {\left| {c_{ij} \left( t \right) } \right| } } L_j^g \left( {x_i^2 \left( t \right) + x_j^2 \left( {t - \tau _{ij} \left( t \right) } \right) } \right) \\&+ \sum \limits _{i = 1}^n {\sum \limits _{j = 1}^n {\left| {d_{ij} \left( t \right) } \right| } } L_j^h \int _0^\infty {k_j \left( s \right) \left( {x_i^2 \left( t \right) + x_j^2 \left( {t - s} \right) } \right) ds} \\&+ \sum \limits _{i = 1}^n {\alpha _i \left( t \right) x_i^2 \left( t \right) } + \sum \limits _{i = 1}^n {\beta _i \left( t \right) x_i^2 \left( {t - \tau _{ij} \left( t \right) } \right) } \end{aligned}$$
$$\begin{aligned}\le & {} - \mathop {\min }\limits _{1 \le i \le n} \left\{ {2a_i \left( t \right) - } \right. \sum \limits _{j = 1}^n {\left| {b_{ij} \left( t \right) } \right| L_j^f - \sum \limits _{j = 1}^n {\left| {b_{ji} \left( t \right) } \right| L_i^f } - \sum \limits _{j = 1}^n {\left| {c_{ij} \left( t \right) } \right| L_j^g } } \nonumber \\&\left. { - \sum \limits _{j = 1}^n {\left| {d_{ij} \left( t \right) } \right| L_j^h - \alpha _i \left( t \right) } } \right\} \sum \limits _{i = 1}^n {x_i^2 \left( t \right) } \nonumber \\&+ \mathop {\max }\limits _{1 \le i \le n} \left\{ {\sum \limits _{j = 1}^n {\left| {c_{ji} \left( t \right) } \right| L_i^g + \beta _i \left( t \right) } } \right\} \sum \limits _{i = 1}^n {x_i^2 \left( {t - \tau _{ij} \left( t \right) } \right) } \nonumber \\&+ \mathop {\max }\limits _{1 \le i \le n} \left\{ {\sum \limits _{j = 1}^n {\left| {d_{ji} \left( t \right) } \right| L_i^h } } \right\} \int _0^\infty {k_j \left( s \right) \sum \limits _{i = 1}^n {x_i^2 \left( {t - s} \right) } ds}\nonumber \\\le & {} -\eta (t)V(t)+\zeta (t)[V(t)]_\tau +\rho (t)\int _0^\infty {k(s)V(t-s)}ds. \end{aligned}$$
(19)

Integrating (18) from \(t_k\) to t, \(t\in [t_k,t_{k+1}),\,k=0,1,2,\ldots ,\) we have

$$\begin{aligned} V\left( t \right) = V\left( {t_k } \right) + \int _{t_k }^t {LV\left( s \right) ds} + \int _{t_k }^t {\sum \limits _{i = 1}^n {2x_i \left( s \right) } \sum \limits _{j = 1} ^n {\sigma _{ij} \left( {s,x_i \left( s \right) ,x_i \left( {s - \tau _{ij} \left( s \right) } \right) } \right) } dw_j \left( s \right) }. \end{aligned}$$

Taking the mathematical expectation, we get that

$$\begin{aligned} EV\left( t \right) = EV\left( {t_k } \right) + \int _{t_k }^t {{ ELV}\left( s \right) ds}, \end{aligned}$$
(20)

and for small enough \(\Delta t > 0,\)

$$\begin{aligned} EV\left( t+\Delta t \right) = EV\left( {t_k } \right) + \int _{t_k }^{t+\Delta t} {{ ELV}\left( s \right) ds}. \end{aligned}$$
(21)

Thus, from (20) and (21), it follows that

$$\begin{aligned} EV\left( {t + \Delta t} \right) - EV\left( t \right) = \int _t^{t + \Delta t} {{ ELV}\left( s \right) ds}, \end{aligned}$$

together with (19), which implies

$$\begin{aligned} D^ + EV\left( t \right)= & {} { ELV}\left( t \right) \nonumber \\\le & {} - \eta \left( t \right) EV\left( t \right) + \zeta \left( t \right) \left[ {{ EV}\left( t \right) } \right] _\tau + \rho \left( t \right) \int _0^\infty {k\left( s \right) } { EV}\left( {t - s} \right) ds. \end{aligned}$$
(22)

On the other hand, from (1) and Hölder inequality, we can get

$$\begin{aligned} EV\left( {t_k } \right)= & {} E\sum \limits _{i = 1}^n {x_i^2 \left( {t_k } \right) } = E\sum \limits _{i = 1}^n {\left( {\sum \limits _{j = 1}^n {w_{ij}^k x_j \left( {t_k^ - } \right) } }+{\sum \limits _{j = 1}^n {e_{ij}^k x_j \left( {t_k^ --\tau } \right) } } \right) } ^2 \\\le & {} 2E\sum \limits _{i = 1}^n {\left[ {\sum \limits _{j = 1}^n {\left( {w_{ij}^k } \right) ^2 \sum \limits _{j = 1}^n {x_j^2 \left( {t_k^ - } \right) } } }+{\sum \limits _{j = 1}^n {\left( {e_{ij}^k } \right) ^2 \sum \limits _{j = 1}^n {x_j^2 \left( {t_k^ --\tau } \right) } } } \right] } \\\le & {} \mathop {2n\max }\limits _{1 \le i \le n} \left\{ {\sum \limits _{j = 1}^n {\left( {w_{ij}^k } \right) ^2 } } \right\} E\sum \limits _{i = 1}^n {x_i^2 \left( {t_k^ - } \right) } +\mathop {2n\max }\limits _{1 \le i \le n} \left\{ {\sum \limits _{j = 1}^n {\left( {e_{ij}^k } \right) ^2 } } \right\} E\sum \limits _{i = 1}^n {x_i^2 \left( {t_k^ --\tau } \right) } \\= & {} \mathop {2n\max }\limits _{1 \le i \le n} \left\{ {\sum \limits _{j = 1}^n {\left( {w_{ij}^k } \right) ^2 } }\right\} EV\left( {t_k^ - } \right) +\mathop {2n\max }\limits _{1 \le i \le n} \left\{ {\sum \limits _{j = 1}^n {\left( {e_{ij}^k } \right) ^2 } }\right\} EV\left( {t_k^ --\tau } \right) ,k = 1,2, \ldots . \end{aligned}$$

It follows from (16) in condition \((A_4)\) that

$$\begin{aligned} \prod \limits _{k = 1}^n {\gamma _k } \le \prod \limits _{k = 1}^n {e^{\gamma \left( {t_k - t_{k - 1} } \right) } } = e^{\gamma \left( {t_n - t_0 } \right) } ,\quad n = 1,2, \ldots . \end{aligned}$$
(23)

Then, all conditions of Theorem 3.1 are satisfied by (22), (23) and condition \((A_3)\), so

$$\begin{aligned} EV\left( t \right) \le E\Vert {V\left( {t_0 } \right) } \Vert _\infty e^{ - \left( {\lambda - \gamma } \right) \left( {t - t_0 } \right) } ,\quad t \ge t_0 . \end{aligned}$$

i.e,

$$\begin{aligned} {E\left\| {x\left( t,t_0,\varphi \right) } \right\| ^2} \le \left\| \varphi \right\| _{L^2}^2{e^{ - \left( {\lambda - \gamma } \right) \left( {t - {t_0}} \right) }}, \quad t \ge {t_{0.}} \end{aligned}$$

The proof is complete.\(\square \)

Remark 3.2

The stability of non-autonomous neural networks has been investigated in Refs.[32, 33]. However, the parameters appearing in [32, 33] are bounded. Note in our results, we do not require that the parameters \(a_i(t),\,b_{ij}(t)\,c_{ij}(t),\,d_{ij}(t),\,i,j=1,2,\ldots ,\) in the system (1) are bounded.

If \(w_{ij}^k = 0,i \ne j,e_{ij}^k = 0,i,j = 1,2, \ldots n,\,k=1,2,\ldots \), then the model (1) reduces the following simpler impulsive system.

$$\begin{aligned} \left\{ \begin{array}{l} dx_i \left( t \right) = - a_i \left( t \right) x_i \left( t \right) + \sum \limits _{j = 1}^n {b_{ij} \left( t \right) f_j \left( {x_j \left( t \right) } \right) } + \sum \limits _{j = 1}^n {c_{ij} \left( t \right) g_j \left( {x_j \left( {t - \tau _{ij} \left( t \right) } \right) } \right) } \\ \quad \quad \quad \quad \quad + \sum \limits _{j = 1}^n {d_{ij} \left( t \right) \int _{ - \infty }^t {k_j \left( {t - s} \right) h_j \left( {x_j \left( s \right) } \right) ds} } \\ \quad \quad \quad \quad \quad + \sum \limits _{j = 1}^n {\sigma _{ij} \left( {t,x_i \left( t \right) ,x_i \left( {t - \tau _{ij} \left( t \right) } \right) } \right) }dw_j(t) ,\,\,t \ge t_0 ,\,\,t \ne t_k , \\ x_i \left( {t_k } \right) = {w_{ii}^k x_i \left( {t_k^ - } \right) } ,\,\,t = t_k, \\ x_i(t_0+s)=\varphi _i(s),\quad -\infty <s\le 0, \,i=1,2,\ldots ,n,\\ \end{array} \right. \end{aligned}$$
(24)

Corollary 3.1

Assume that \((A_1 )-(A_3 )\) and \((A_4)\) with \(\gamma _k=\max \{1,(w_{ii}^k)^2\}\) hold. Then the zero solution of (24) is mean square globally exponentially stable.

Proof

The proof is similar to that of Theorem 3.3. So we omit it.\(\square \)

Remark 3.3

In the particular case when the parameters \(a_i(t),\,b_{ij}(t),\,c_{ij}(t),\,d_{ij}(t)\) and \(\sigma _{ij}(t,x_i(t),x_i(t-\tau _{ij}(t))),\,i,j=1,2,\ldots ,\) in the system (1) are independent on t, by using Theorem 3.2 with \(q_k=0\), \(k=1,2,\ldots ,\) and the same Lyapunov function V(t) defined in Theorem 3.3, Li[25] obtain some sufficient conditions ensuring global mean square exponential stability of the system (24). As Theorem 3.1 generalizes Theorem 3.2 from autonomous case to non-autonomous case, Corollary 3.1 also generalizes Theorem 3.2 in [25] from autonomous case to non-autonomous case.

Corollary 3.2

Assume that \((A_1 )-(A_3 )\) hold. Then the zero solution of (24) is mean square globally exponentially stable if \(-1\le w_{ii}^k\le 1 \).

Proof

As \(-1\le w_{ii}^k\le 1\), a direct calculation shows that when we take \(\gamma _k=1\) and \(\gamma =0\), the condition \((A_4)\) is satisfied. It follows from Corollary 3.1 that zero solution of (24) is mean square globally exponentially stable. The proof is completed.\(\square \)

If \(w_{ii}^k = 1,w_{ij}^k = 0,i \ne j,e_{ij}^k = 0,i,j = 1,2, \ldots n,\,k=1,2,\ldots \), then the model (1) becomes delay stochastic neural networks without impulses

$$\begin{aligned} \left\{ \begin{array}{l} dx_i \left( t \right) = - a_i \left( t \right) x_i \left( t \right) + \sum \limits _{j = 1}^n {b_{ij} \left( t \right) f_j \left( {x_j \left( t \right) } \right) } + \sum \limits _{j = 1}^n {c_{ij} \left( t \right) g_j \left( {x_j \left( {t - \tau _{ij} \left( t \right) } \right) } \right) } \\ \quad \quad \quad \quad \quad + \sum \limits _{j = 1}^n {d_{ij} \left( t \right) \int _{ - \infty }^t {k_j \left( {t - s} \right) h_j \left( {x_j \left( s \right) } \right) ds} } \\ \quad \quad \quad \quad \quad + \sum \limits _{j = 1}^n {\sigma _{ij} \left( {t,x_i \left( t \right) ,x_i \left( {t - \tau _{ij} \left( t \right) } \right) } \right) }dw_j(t) ,\,\,t \ge t_0, \\ x_i(t_0+s)=\varphi _i(s),\quad -\infty <s\le 0, \,i=1,2,\ldots ,n,\\ \end{array} \right. \end{aligned}$$
(25)

By using of Theorem 3.3, we can easily get the following corollary.

Corollary 3.3

Assume that \((A_1 )-(A_3 )\) hold. Then the zero solution of (25) is mean square globally exponentially stable with exponential convergent rate \(\lambda \).

4 Example

In this section, we will give an example to illustrate the exponential stability of (1).

Example 4.1

Consider the following impulsive non-autonomous stochastic neural networks:

$$\begin{aligned} \left\{ \begin{array}{l} dx_1 \left( t \right) = \left[ { - \left( {3 + 5t} \right) x_1 \left( t \right) + t\arctan x_1 \left( t \right) + \frac{1}{2}t\arctan x_2 \left( t \right) } \right. \\ \quad \quad \quad \quad \quad + \frac{1}{2}\sin x_1 (t - 1) + t\sin x_2 (t - 2) \\ \quad \quad \quad \quad \quad \left. { + \frac{1}{2}\left( {1 + t} \right) \int _{ - \infty }^t {e^{ - \left( {t - s} \right) } x_1 \left( s \right) ds + t\int _{ - \infty }^t {e^{ - \left( {t - s} \right) } x_2 \left( s \right) ds} } } \right] ds \\ \quad \quad \quad \quad \quad + x_1 \left( t \right) dw_1 \left( t \right) + x_2 \left( t \right) dw_2 \left( t \right) , \\ dx_2 \left( t \right) = \left[ { - \left( {2 + 4t} \right) x_2 \left( t \right) + t\arctan x_1 \left( t \right) + \frac{1}{2}t\arctan x_2 \left( t \right) } \right. \\ \quad \quad \quad \quad \quad + t\sin x_1 (t - 1) + \frac{1}{2}\sin x_2 (t - 2) \\ \quad \quad \quad \quad \quad \left. { + t\int _{ - \infty }^t {e^{ - \left( {t - s} \right) } x_1 \left( s \right) ds + \frac{1}{3}\int _{ - \infty }^t {e^{ - \left( {t - s} \right) } x_2 \left( s \right) ds} } } \right] ds \\ \quad \quad \quad \quad \quad + x_1 \left( t \right) dw_1 \left( t \right) + x_2 \left( t \right) dw_2 \left( t \right) ,\,\, t \ge 0,t \ne t_k , \\ x_1 \left( {t_k } \right) = - 0.9e^{0.1k} x_1 \left( {t_k^ - } \right) \\ x_2 \left( {t_k } \right) = - e^{0.1k} x_2 \left( {t_k^ - } \right) \\ \end{array} \right. \end{aligned}$$
(26)

where \(t_k=t_{k-1}+k,\,k=1,2,\ldots ,\) and \(\int _0^\infty e^{-s}ds=1<\infty \) satisfying the condition (H). We can easily find that Conditions \((A_1)\) and \((A_2)\) are satisfied with \(L_j^f=L_j^g=L_j^h=1,\,j=1,2\), \(\alpha _i(t)\equiv 2,\,\beta _i(t)\equiv 0,\,i=1,2.\) By simple computation, we can get from \((A_3)\) that \(\eta (t)=3+4t\), \(\zeta (t)=\frac{1}{2}+t\), and \(\rho (t)=\frac{1}{2}+\frac{3}{2}t\). Let \(\gamma _k=e^{0.2k} =\max \left\{ {1,e^{0.2k} } \right\} \) and \(\lambda =0.3\) which satisfies inequality (16). Therefore, we obtain that there exists a \(\gamma = 0.2>0 \) such that

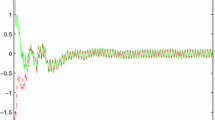
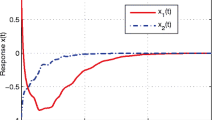
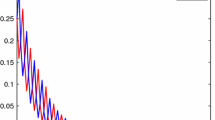
$$\begin{aligned} \frac{{\ln \gamma _k }}{{t_k - t_{k - 1} }} = \frac{{0.2k}}{k} = 0.2 \le \gamma < \lambda . \end{aligned}$$

As all the conditions of Corollary 3.1 are satisfied, we conclude that the solution of (26) is mean square globally exponentially stable with exponential convergent rate 0.1. We employ the Euler scheme to discretize this equation, where the integral term is approximated by using the composite \(\Theta \)-rule as a quadrature [38]. The simulation results are illustrated in Fig. 1.

Fig. 1
figure 1

Simulation result of Example 4.1

Full size image

Remark 4.1

Since \( \mathop {\min }\limits _{t \ge 0} \left\{ {\eta \left( t \right) } \right\} = 3,\) \(\mathop {\max }\limits _{t \ge 0} \left\{ {\zeta \left( t \right) } \right\} = + \infty \) and \(\mathop {\max }\limits _{t \ge 0} \left\{ {\rho \left( t \right) } \right\} = + \infty \), It is clear that the lemma 1 in [15] fails to apply to Eq. (26).