1 Introduction

The experimental determination of the blood serum dynamic viscosity (ηS) is very important for the clinical evaluation and management of patients who suffer the blood hyperviscosity syndrome (BHS) or can be affected by this medical condition [1, 2]. It is particularly important in pathologies as the Waldenström Macroglobulinemia (WM) and Multiple Myeloma (MM), where the blood concentration of monoclonal immunoglobulin (IgM, IgG and IgA) is increased [2]. Nevertheless; the traditional methods to determine ηS have a limited clinical application because of the sample volume needed, the necessity of to wash the viscometer to be used in different patients and the additional determinations required to convert the kinematic viscosity (ν) in absolute dynamic viscosity (η) [1, 3].

Magnetic resonance has been employed to determine η in protein solutions [3,4,5,6,7,8], which reduces in one order of magnitude the minimal sample volume to be employed with respect to the classical viscometers, avoids the viscometer washing between determinations and supplies directly the value of η without additional experimental evaluations. Nevertheless, experiments based on the nitroxide radicals electronic paramagnetic resonance (EPR) spectra, the longitudinal magnetic relaxation of 13C in molecules of Glicine and glutathione belonging to the red blood cells (RBC), the water self-diffusion coefficient and the proton dispersion profiles underestimate the values of η in protein solutions [5, 6]. On the other hand, other methods based on nuclear magnetic relaxation [7, 8] modify the sample using superparamagnetic particles [7] or employ calibration curves obtained using samples with a very different nature with respect to the protein solutions [8]. In spite of these results, another approach to evaluate ηS, starting from transverse proton magnetic relaxation, can be introduced as follows.

Proton magnetic relaxation in protein solutions is determined by the dominant contribution of the water protons [3, 9,10,11]. The other protons, belonging to the macromolecular structure, have magnetic relaxation times very short; much shorter than the magnetic relaxation times of the water protons at the protein solution and than the dead times of the majority of the equipment utilized to measure relaxation, then its contribution can be neglected [10]. The physical model most commonly used to describe proton magnetic relaxation in protein solutions is the two sites water exchange model [12], which considers two types of water: the water bound to the macromolecular surface (b) and the free water (bulk). In this model, the bound water is considered as irrotationally bound to the protein surface, such as its residence time (\(\tau_{{{\text{res}}}}^{b}\)) is much bigger than the macromolecular rotational correlation time (\(\tau_{R}^{{}}\)) and much shorter than the measured values of the transverse (\(T_{2}\)) and longitudinal (\(T_{1}\)) proton magnetic relaxation times. Then, a fast exchange of water molecules between the bound and free water states will be established; and, for heterogeneous protein solutions, the transverse water proton relaxation rate (\(R_{2} = \frac{1}{{T_{2} }}\)) can be calculated as follows [3, 10,11,12,13,14]:

$$ R_{2} = P_{{{\text{bulk}}}} R_{2w}^{{{\text{bulk}}}} + \sum\limits_{i} {P_{b}^{i} } R_{2b}^{i} $$
(1)

In Eq. (1), \({\text{R}}_{{{\text{2w}}}}^{{{\text{bulk}}}}\) and \({\text{R}}_{{{\text{2b}}}}^{{}}\) represent the transverse proton magnetic relaxation rates of the free and bound water protons, respectively. Pb and Pbulk are the fractions of bound and free water, such as \(\sum\limits_{i} {{\text{P}}_{{\text{b}}}^{i} } + P_{{{\text{bulk}}}} = 1\). \({\text{P}}_{{\text{b}}}^{{}}\) can be calculated using the following equation [3, 10, 13, 14]:

$$ \begin{gathered} P_{b}^{i} = \frac{{h_{i}^{{}} C_{i} }}{{M_{i} N_{w} \left( {1 - \varphi_{i} } \right)}} \hfill \\ \hfill \\ \end{gathered} $$
(2)

where M and C are the molecular weight in g Mol−1 and the concentration in gl−1 of the protein, respectively, Nw = 55.5 Mol l−1 is the molarity of water, and \(h_{i}^{{}}\) represents the number of sites available for the water binding to the protein surface. \(\varphi\) is the partial volume occupied by the protein in the total volume of the sample. In one heterogeneous protein solution, i runs by the different types of proteins at the solution, in the case of blood serum (S) i = albumin (Al) and globulins (Gb) [15]. Starting from all the analyzed above, Eq. (1) can be rewritten as follows [13,14,15,16]:

$$ \begin{gathered} R_{2}^{{\text{S}}} = R_{2w}^{{{\text{bulk}}({\text{S}})}} + \sum\limits_{i} {\frac{{g_{i}^{{\text{S}}} }}{{M_{i} }}} C_{i}^{{\text{S}}} \hfill \\ g_{i}^{{\text{S}}} = 0.018h_{i} \left( {R_{2b}^{i(S)} - R_{2w}^{{{\text{bulk}}({\text{S}})}} } \right) \hfill \\ R_{2}^{{\text{S}}} = R_{2w}^{{{\text{bulk}}({\text{S}})}} + \left[ {\frac{{g_{{{\text{Al}}}}^{{\text{S}}} }}{{M_{{{\text{Al}}}} }}C_{{{\text{Al}}}}^{{\text{S}}} + \frac{{g_{{{\text{Gb}}}}^{{\text{S}}} }}{{M_{{{\text{Gb}}}} }}C_{{{\text{Gb}}}}^{{\text{S}}} } \right] \hfill \\ \end{gathered} $$
(3)

Here, the blood serum has been considered an extremely diluted solution of proteins (Pbulk≈1, \(\varphi\) <  < 1) [13,14,15] and \(g_{i}^{{\text{S}}}\) is constant, in the range of concentration from zero to the physiological concentration, for albumin and globulins [13].

If we consider to \(C_{{{\text{Al}}}}^{{\text{S}}}\) and \(C_{{{\text{Gb}}}}^{{\text{S}}}\) as a function of the total concentration of proteins in blood serum (\(C_{{{\text{tot}}}}^{{\text{S}}}\)) [14],

$$ \begin{gathered} R_{2}^{{\text{S}}} = R_{2w}^{{{\text{bulk}}({\text{S}})}} + C_{{{\text{tot}}}}^{{\text{S}}} \left[ {\frac{1}{\sigma + 1}\left( {\frac{{\sigma g_{{{\text{Al}}}}^{{\text{S}}} }}{{M_{{{\text{Al}}}} }} + \frac{{g_{{{\text{Gb}}}}^{{\text{S}}} }}{{M_{{{\text{Gb}}}} }}} \right)} \right] \hfill \\ C_{{{\text{tot}}}}^{{\text{S}}} = C_{{{\text{Al}}}}^{{\text{S}}} + C_{{{\text{Gb}}}}^{{\text{S}}} \hfill \\ \sigma = \frac{{C_{{{\text{Al}}}}^{{\text{S}}} }}{{C_{{{\text{Gb}}}}^{{\text{S}}} }} \hfill \\ C_{{{\text{Gb}}}}^{{\text{S}}} = \frac{{C_{{{\text{tot}}}}^{{\text{S}}} }}{\sigma + 1} \hfill \\ C_{{{\text{Al}}}}^{{\text{S}}} = \frac{{\sigma C_{{{\text{tot}}}}^{{\text{S}}} }}{\sigma + 1} \hfill \\ \end{gathered} $$
(4)

In one extremely diluted solution of proteins, ηS is a function of \(C_{{{\text{tot}}}}^{{\text{S}}}\) in agreement with the Einstein’s equation [5]:

$$ \begin{gathered} \eta_{{\text{S}}} = \eta_{0}^{{\text{S}}} \left( {1 + 2.5\overline{\nu }^{{\text{S}}} C_{{{\text{tot}}}}^{{\text{S}}} } \right) \hfill \\ C_{{{\text{tot}}}}^{{\text{S}}} = \frac{{\eta_{{\text{S}}} }}{{2.5\overline{\nu }^{{\text{S}}} \eta_{0}^{{\text{S}}} }} - \frac{1}{{2.5\overline{\nu }^{{\text{S}}} }} \hfill \\ \end{gathered} $$
(5)

where \(\eta_{0}\) is the absolute dynamic viscosity of the solvent, at the absolute temperature T, and \(\overline{\nu }\) is the mean value of the contributions from the specific partial volumes of the albumin and globulins. Merging Eqs. (4) and (5), we obtain

$$ \begin{gathered} R_{2}^{{\text{S}}} = \eta_{{\text{S}}} \left[ {\frac{1}{{2.5\overline{\nu }^{{\text{S}}} \eta_{0}^{{\text{S}}} \left( {\sigma + 1} \right)}}\left( {\frac{{\sigma g_{{{\text{Al}}}}^{{\text{S}}} }}{{M_{{{\text{Al}}}} }} + \frac{{g_{{{\text{Gb}}}}^{{\text{S}}} }}{{M_{{{\text{Gb}}}} }}} \right)} \right] + R_{2w}^{{{\text{bulk}}({\text{S}})}} - \left[ {\frac{1}{{2.5\overline{\nu }^{{\text{S}}} \left( {\sigma + 1} \right)}}\left( {\frac{{\sigma g_{{{\text{Al}}}}^{{\text{S}}} }}{{M_{{{\text{Al}}}} }} + \frac{{g_{{{\text{Gb}}}}^{{\text{S}}} }}{{M_{{{\text{Gb}}}} }}} \right)} \right] \hfill \\ \hfill \\ \end{gathered} $$
(6)

From Eq. (6) it is possible to see that, from a theoretical point of view, \(R_{2}^{S}\) depends linearly of ηS with slope \(\left[ {\frac{1}{{2.5\overline{\nu }^{{\text{S}}} \eta_{0}^{{\text{S}}} \left( {\sigma + 1} \right)}}\left( {\frac{{\sigma g_{{{\text{Al}}}}^{{\text{S}}} }}{{M_{{{\text{Al}}}} }} + \frac{{g_{{{\text{Gb}}}}^{{\text{S}}} }}{{M_{{{\text{Gb}}}} }}} \right)} \right]\) and intercept \(R_{2w}^{{{\text{bulk}}({\text{S}})}} - \left[ {\frac{1}{{2.5\overline{\nu }^{{\text{S}}} \left( {\sigma + 1} \right)}}\left( {\frac{{\sigma g_{{{\text{Al}}}}^{{\text{S}}} }}{{M_{{{\text{Al}}}} }} + \frac{{g_{{{\text{Gb}}}}^{{\text{S}}} }}{{M_{{{\text{Gb}}}} }}} \right)} \right]\). The slope and the intercept depend of the temperature, the types of proteins inside the solution and its structure and dimensions. Starting from this theoretical approach, it is possible to develop an experimental method in which ηS could be directly determined from the value of T2.

This theoretical approach is more rigorous than the theoretical analysis performed by us in the case of blood plasma (P) [3], where only was considered the contribution of albumin, starting from its dominant contribution to \(C_{{{\text{tot}}}}^{P}\), thus neglecting the contributions of globulins and fibrinogen (Fn). This was a limited point of view, which does not consider the dominant role of fibrinogen in the plasma dynamic viscosity of the healthy individuals because of the dimensions and the asymmetry of this macromolecule [2]. Something similar occurs in the case of pathologies as MW and MM, where the increasing of plasma dynamic viscosity is determined by the concentration of monoclonal globulins as IgG, IgA and IgM. Thus, for the case of blood plasma, performing a similar analysis to those performed above for the case of blood serum, we obtain:

$$ \begin{gathered} R_{2}^{P} = \eta_{P} \left[ {\frac{1}{{2.5\overline{\nu }^{P} \eta_{0}^{P} }}\left( {\frac{{\sigma_{{{\text{Al}}}} g_{{{\text{Al}}}}^{P} }}{{M_{{{\text{Al}}}} }} + \frac{{\sigma_{{{\text{Fn}}}} g_{{{\text{Fn}}}}^{P} }}{{M_{{{\text{Fn}}}} }} + \frac{{\sigma_{{{\text{Gb}}}} g_{{{\text{Gb}}}}^{P} }}{{M_{{{\text{Gb}}}} }}} \right)} \right] + \hfill \\ R_{2w}^{{{\text{bulk}}(P)}} - \left[ {\frac{1}{{2.5\overline{\nu }^{P} }}\left( {\frac{{\sigma_{{{\text{Al}}}} g_{{{\text{Al}}}}^{P} }}{{M_{{{\text{Al}}}} }} + \frac{{\sigma_{{{\text{Fn}}}} g_{{{\text{Fn}}}}^{P} }}{{M_{{{\text{Fn}}}} }} + \frac{{\sigma_{{{\text{Gb}}}} g_{{{\text{Gb}}}}^{P} }}{{M_{{{\text{Gb}}}} }}} \right)} \right] \hfill \\ C_{{{\text{tot}}}}^{P} = C_{{{\text{Al}}}}^{P} + C_{{{\text{Fn}}}}^{P} + C_{{{\text{Gb}}}}^{P} \hfill \\ C_{i}^{P} = \sigma_{i} C_{{{\text{tot}}}}^{P} \hfill \\ \end{gathered} $$
(7)

Now, i = Al, Fn, Gb. Using this type of theoretical approach, our group has developed and presented previously two methods, based on proton magnetic relaxation, to evaluate η in blood plasma and hemoglobin solutions [3, 4], reporting values which match with those measured utilizing traditional viscometers and, moreover, offering the advantages previously discussed for the magnetic resonance methods. In this work, we present a similar method for the case of blood serum.

2 Materials and Methods

Fresh whole blood was voluntary obtained, using venipuncture, from healthy individuals and patients with MM at the clinical laboratory of the “Juan Bruno Zayas Alfonso” general hospital located in Santiago de Cuba, Cuba. The blood serum samples were prepared collecting the whole blood in a dry tube without anticoagulant, waiting 10 min under room temperature and centrifuging (2500 rpm, 10 min) to take the blood serum from the supernatant [17]. A set of samples of blood serum with different protein concentration was prepared by continuous dilution using Fosfate Saline Buffer (PBS, pH 7.4, Sigma Chemicals Co.) starting from the blood serum samples corresponding to 10 healthy individuals.

An Ostwald viscometer [1] and a pycnometer (25 ml, 20 °C) were used to evaluate ηS in the set of blood serum samples with different protein concentrations and in those samples belonging to 20 additional healthy individuals. The temperature for the measurement was 20 °C and ηS was calculated according to

$$ \eta_{{\text{S}}} = \varsigma \rho_{{\text{S}}} \delta t $$
(8)

where ρS is the density of the blood serum sample measured with the pycnometer, \(\delta t\) is the time interval during which the blood serum go through the capillary tube of the Ostwald viscometer and \(\varsigma\) = 1.62 10–7 m2/s2 is an instrumental parameter related with the geometry and dimensions of the viscometer [18].

For the proton magnetic relaxation measurements, a LapNMR magnetic resonance console was employed (Tecmag, Houston, USA) coupled to a magnet of 0.095 T (4.07 MHz for protons) and the measurement temperature was 20 °C. T2 was determined using the Carr–Purcell–Meiboom–Gill (CPMG) pulse sequence [19, 20] with 6 μs and 12 μs as the width for the 90˚ and 180˚ radio frequency pulses, respectively, 15,000 echoes and echo time (TE) of 1600 μs [3, 4]. In the CPMG pulse sequence, the measured R2 (\(\frac{1}{{T_{2e} }}\)) is affected by the diffusion of water molecules in a magnetic field gradient as follows [5, 19, 20]:

$$ \begin{gathered} \frac{1}{{T_{2e} }} = \frac{1}{{T_{2} }} + \frac{{\gamma^{2} G^{2} D\tau^{2} }}{3} \hfill \\ D = \frac{kT}{{6\pi \eta_{s} r}} \hfill \\ \end{gathered} $$
(9)

In Eq. (9), \(\gamma = 2.678 \times 10^{8} \frac{1}{sT}\) is the proton gyromagnetic ratio, \(G = 0.060\frac{T}{m}\) is the magnetic field gradient affecting the sample inside of our magnet, \(D\) is the water molecules translational diffusion coefficient and \(\tau = 800 \times 10^{ - 6} s\) is the time between the 90˚ and the first 180˚ radiofrequency pulses (TE/2). In addition, r = 1.4 10–10 m is the radius of the water molecule, k = 1.38 10−23 J/K is the Boltzmann’s constant and T = 293 K is the absolute temperature.

For the set of samples of blood serum with different protein concentrations, the values of 1/T2e were plotted versus the ηS values determined employing the Ostwald viscometer to obtain a calibration curve. This curve was used to evaluate ηS in 20 healthy individuals (different individuals to those used to obtain the calibration curve) and 24 patients with MM. Equation (5) was used to explain the behavior of ηS in MM patients.

The values of ηS were reported in mPa s as usual in the literature and the clinical practice [1,2,3,4,5,6,7,8]. For the statistical analysis, a Student test (t-test) was applied to compare the means (α = 0.05).

This research has been performed in agreement with all the ethical rules corresponding to scientific research in human beings in accordance with the provisions of the Declaration of Helsinki (1964, updated until 2013) of the World Medical Association.

3 Results and Discussion

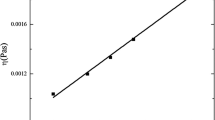
Figure 1 shows the calibration curve obtained after plotting \(\frac{1}{{T_{2e} }}\) as a function of the ηs values, determined using the Ostwald viscometer, in the set of samples of blood serum with different protein concentration. A linear behavior of the \(\frac{1}{{T_{2e} }}\) as a function of ηs can be observed according to

$$ \begin{gathered} \frac{1}{{T_{2e} }} = 0.002\eta_{{\text{S}}} - 0.001 \hfill \\ \hfill \\ \end{gathered} $$
(10)

where the units of \(\frac{1}{{T_{2e} }}\) and ηs are ms−1 and mPa s, respectively.

Fig. 1
figure 1

The behavior of \(\frac{1}{{T_{2e} }}\) as a function of ηs obtained in samples of blood serum with different concentration at 20 °C

Full size image

To explain the experimental behavior showed in Fig. 1 and Eq. (10) a detailed analysis of the values of \(\frac{1}{{T_{2e} }}\) was performed considering it is affected by the diffusion of the water molecules in a magnetic field gradient according to Eq. (9). Starting from the values of ηS measured using the Ostwald viscometer, and using the Eq. (9), it is possible to calculate \(\frac{{DG^{2} \gamma^{2} \tau^{2} }}{3}\) and to compare it with \(\frac{1}{{T_{2e} }}\) for all points in Fig. 1 (Table 1) observing that \(\frac{1}{{T_{2e} }}\) >  > \(\frac{{DG^{2} \gamma^{2} \tau^{2} }}{3}\). Therefore, in Eq. (9), \(\frac{1}{{T_{2e} }} = \frac{1}{{T_{2} }}\) and Eq. (10) can be rewritten according to

$$ \begin{gathered} R_{2}^{S} = \frac{1}{{T_{2} }} = 0.002\eta_{S} - 0.001 \hfill \\ \hfill \\ \end{gathered} $$
(11)
Table 1 Values of \(\frac{1}{{T_{2e} }}\) and \(\frac{{\gamma^{2} G^{2} D\tau^{2} }}{3}\) in samples of blood serum with different ηS at 20 °C
Full size table

It means that we are measuring the “real” T2 values of the water protons inside the blood serum solutions and the linear behavior observed in Eq. (10) can be supported by the theoretical approach described by Eq. (6). In our experiment to obtain the calibration curve, the temperature is constant as well as all others parameters at the right member of Eq. (6), except ηS. The values of g are constant for Albumin and immunoglobulin at the range of concentration used [13]. In spite of the concentrations of albumin and immunoglobulin change with dilution, at the set of blood serum samples with different concentration, the ratio between them (σ) remains constant. The same occurs with \(\overline{\nu }^{S}\) considering it is only related with the shape and dimensions of the proteins that are unchangeable with dilution. The viscosity of the solvent, the transverse proton relaxation rate of the solvent and the molecular weight of the proteins also do not change with dilution. Then, Eq. (6) describes that 1/T2 only depends on ηS in our experiment.

The experimental results presented in Fig. 1 and the Eq. (10) are the basis of a new method to determine ηS. Table 2 shows the results obtained during the application of this new method in 20 healthy individuals and 24 patients suffering MM.

Table 2 Values of ηS determined using proton magnetic relaxation (PMR) in the case of 20 healthy individuals and 24 patients suffering MM
Full size table

The values of ηS determined using proton magnetic relaxation (PMR), in the case of the healthy individuals, statistically match (P = 0.104319 > 0.05, α = 0.05) with those measured using the Ostwald viscometer. On the other hand, the method based on PMR allows observing, in the case of the patients suffering MM, an increasing of ηS with respect to the values obtained in healthy individuals (P = 0.0137509 < 0.05, α = 0.05). It can be explained, according to the Eq. (5), because of the increasing in the concentration of immunoglobulin, particularly IgG and IgA, which take place in MM [1,2,3]. The dimensions and the asymmetry of these macromolecules increase its contribution to ηS in comparison with Albumin, through its contributions to \(\overline{\nu }\).

The developed method to determine ηS, based on PMR, is very useful because it decreases, in one order of magnitude, the volume of sample needed to perform the experiment; avoids the washing of the viscometer between measurements; is fast (around 5 min per measurement, 30 min per patient); is not affected by the turbidity of the sample and the skills of the technician performing the measurement and allows reporting directly the value of ηS. Despite these advantages, the PMR is an expensive experimental method with respect to the traditional methods to measure ηS, nevertheless, this disadvantage can be minimized when we added other potential medical applications [11, 16, 19].

In spite of the good results obtained with the method based on PMR to determine ηS, it is important to take into account some requirements to avoid unexpected or undesired changes in the values of T2, which are not naturally related with ηS. During the sample preparation, it is important to avoid: the mixing with paramagnetic compounds; water; protein solutions and cells or tissues. The temperature inside the sample should be constant and, to use Eq. (10), it must be 20 °C; when other temperature is used, it should be minor than 40 °C and the calibration curve (Fig. 1) should be obtained again for the new temperature value. We recommend to use a magnetic system homogeneous enough to guarantee that the second term at the right member of Eq. (9) can be neglected; on the contrary, we recommend to calculate this term and to use at the calibration curve \(\frac{1}{{T_{2} }} = \frac{1}{{T_{2e} }} - \frac{{\gamma^{2} G^{2} D\tau^{2} }}{3}\). For values of the frequency of resonance (\(\omega_{0}\)) such as \(50\;{\text{KHz}} > \frac{{\omega_{0} }}{2\pi } > 2\;{\text{MHz}}\), the same calibration curve can be used, nevertheless, for \(50\;{\text{KHz}} \le \frac{{\omega_{0} }}{2\pi } \le 2\;{\text{MHz}}\), a new calibration curve is needed for each value of \(\omega_{0}\).

4 Conclusions

A new method, based on proton magnetic relaxation, to determine the absolute dynamic viscosity of blood serum was developed, obtaining results which statistically match with the values obtained using an Ostwald viscometer. This method improves this kind of measurements because of it reduces the volume of sample needed for the experiment, avoids the washing of the viscometer between measurements, is less time consumer, reports directly the parameter under study and does not depend of the technician skills. It was demonstrated the potential medical utility of this method observing how the values of the absolute dynamic viscosity of blood serum in patients suffering Multiple Myeloma increase with respect to those obtained in healthy individuals.